Abstract
One of the most challenging problems that are still open in the field of materials science is the 3D reconstruction of porous media using information from a single 2D thin image of the original material. Such a reconstruction is only feasible subject to some important assumptions that need to be made as far as the statistical properties of the material are concerned. In this study, the aforementioned problem is investigated as an explicitly formulated optimization problem, with the phase of each porous material point being decided such that the resulting 3D material model shows the same statistical properties as its corresponding 2D version. Based on this problem formulation, herein for the first time, several traditional (genetic algorithms—GAs, particle swarm optimization—PSO, differential evolution—DE), as well as recently proposed (firefly algorithm—FA, artificial bee colony—ABC, gravitational search algorithm—GSA) nature-inspired optimization algorithms were applied to solve the 3D reconstruction problem. These algorithms utilized a newly proposed data representation scheme that decreased the number of unknowns searched by the optimization process. The advantages of addressing the 3D reconstruction of porous media through the application of a parallel heuristic optimization algorithm were clearly defined, while appropriate experiments demonstrating the greater performance of the GA algorithm in almost all the cases by a factor between 5%–84% (porosity accuracy) and 3%–15% (auto-correlation function accuracy) over the PSO, DE, FA, ABC, and GSA algorithms were undertaken. Moreover, this study revealed that statistical functions of a high order need to be incorporated into the reconstruction procedure to increase the reconstruction accuracy.
1. Introduction
Nowadays, porous media have attracted multidisciplinary attention due to their notable properties, which have broadened their applications in the petroleum [1] and chemical industries [2], hydrology [3], etc. This increased interest makes the accurate analysis of the microstructural behavior of the examined porous media a great field of research. To accurately measure the transport properties of a porous material, e.g., diffusivity, permeability, and conductivity, the 3D material structure needs to be known. However, the acquisition of the 3D structure of a material requires microscopes of high technology and high cost, as well as a high processing time.
Alternatively, the 3D material structure can be derived by applying a computational reconstruction technique that uses a single 2D image of the material that is acquired using conventional imaging equipment [4]. The first reconstruction method was proposed quite early by Quiblier [5] in the years when imaging systems were limited and displayed marginal performance. Lately, Adler et al. [6] generalized Quiblier’s method to measure the flow in porous media, while Bentz and Martys [7] proposed a simplified version of Quiblier’s method, which is free of filter parameter calculations but adds a significant computational overhead. Since then, several algorithms have been proposed [8,9,10,11] aiming to improve the reconstruction accuracy. Almost all algorithms make use of specific correlation functions for measuring the morphology of the material’s microstructure. The spatial correlation functions [12], such as auto-correlation functions, have proved to be good descriptors of the porous space morphology, while their simplicity accelerates the overall reconstruction procedure.
More recent attempts to develop a reliable 3D reconstruction of porous media from a single 2D image were targeted toward investigating the connectivity of the flow paths by utilizing reconstruction approaches using multiple-point statistics [13,14,15], cross-correlation functions [16,17,18], spatial correlation functions [19], and multiple statistical functions [20]. The majority of these approaches consist of several simple processing steps in an iterative manner, where the 3D material is reconstructed layer by layer through repetitive comparisons with the 2D slice reference image. Of course, the reconstruction accuracy is higher if more information is retrieved from the initial 2D image. Very recent works [21,22,23] have tried to utilize the advantages of the deep learning models to represent some initial information (2D thin image) with massive abstract features and to generate possible 3D reconstructions as adversarial images of the input information. However, these approaches are time-consuming and need many annotated samples from the same material for model training, which in most cases are difficult to collect.
Among the reconstruction methods presented in the literature, the work of Yeong and Torquato [9,10] exhibits some remarkable properties relative to its simplicity and efficiency. In their work Yeong and Torquato tackled the reconstruction procedure as an optimization problem, which they solved by applying the simulated annealing (SA) algorithm. Of course, the main weakness of this method is the high computation time stemming from the low convergence time of the SA algorithm. Motivated by the method of Yeong and Torquato [9,10], in this study, we examine the reconstruction performance of porous media when several traditional, as well as recently proposed, nature-inspired optimization algorithms are used instead of SA. The application of the standard genetic algorithm (GA) [24], particle swarm optimization (PSO) [25], differential evolution (DE) [26], firefly algorithm (FA) [27], artificial bee colony (ABC) [28], and gravitational search algorithm (GSA) [29] optimization evolutionary algorithms showed some important advantages: (1) they could provide a global solution to the problem via exploitation and exploration of the solution space, (2) they were free from complex mathematics, (3) they did not require the objective function being optimized to have specific mathematical properties, (4) they provided flexibility in combining multiple objectives, (5) they had a parallel nature and could be executed very fast by applying high-performance computing frameworks (GPU, Spark, etc.).
The contributions of this work are as follows:
- (1)
- The 3D porous media reconstruction was formulated as a generic optimization problem described using a multi-objective function that was able to incorporate any type and any combination of statistical functions, alleviating the restrictions of the past techniques that used a single statistical measure.
- (2)
- For the first time, the nature-inspired algorithms were applied in 3D porous media reconstruction.
- (3)
- A novel and efficient material data representation that enabled the reliable deployment of the evolutionary algorithms with a fast execution rate was proposed.
- (4)
- The emergence of the existing auto-correlation functions’ weaknesses and the highlight of the needs for more descriptive auto-correlation functions.
It is worth mentioning that although the standard versions of the abovementioned evolutionary algorithms were applied in this study, the generic nature of the derived optimization problem permitted the application of more sophisticated and advanced evolutionary algorithms [30,31,32,33,34].
The paper is organized as follows: Section 2 reviews the main principles of porous media 3D reconstruction and briefly describes the theory of some popular and efficient nature-inspired optimization algorithms. Section 3 presents the problem formulation in terms of optimization and illustrates the scheme of the proposed reconstruction methodology. Section 4 evaluates the reconstruction performance of the applied optimization algorithms. Section 5 summarizes the main conclusions derived from the previous experimental study, while future research directions are defined toward the development of a more efficient porous media 3D reconstruction technique.
2. Material and Methods
2.1. 3D Porous Media Reconstruction
To study the macroscopic behavior of a porous media, the geometry and topology of the pore space need to be determined. However, the acquisition of the porous media microstructure requires the application of specialized and expensive equipment (TEM, GEM, etc.) that can accurately capture the distribution of the pores in a short time. Another, less equipment-demanding way to derive the 3D porous media structure is to apply a 3D reconstruction algorithm, utilizing the material information enclosed in a single 2D thin slice of the material, which can be captured easily using a conventional microscope.
Mainly, there are two categories of 3D material reconstruction algorithms: (1) statistical/stochastic methods that apply linear and non-linear filters to an uncorrelated Gaussian distribution [5,7,8,35] and (2) optimization-based methods that tackle the reconstruction process as an optimization problem [9,10]. The former methods are characterized by lower accuracy and higher computation time compared to the latter ones. However, both types of algorithms use the same measures for encoding the porous space and describing the morphological properties of the material, such as multiple-point and auto-correlation functions [36]. These functions are capable of statistically describing the microstructures of the 2D slice of porous media and thus can be used to construct 3D models with the same statistical properties.
A recent work investigating the role of the correlation function in 3D material reconstruction [37] has shown that among the diverse number of correlation functions, the following two-point auto-correlation function exhibits a high reconstruction performance:
where is the vector of the coordinates of each image pixel, is the distance vector, is the average operator, and is the phase function defined as:
Moreover, corresponds to the porosity of the material.
It is worth noting that when calculating the auto-correlation function of the 2D slice image, the method of periodic boundaries is applied for the coordinates lying outside the image’s dimensions. The porosity and the auto-correlation function of Equation (1) corresponds to the first two statistical moments of the 2D image, which describe the distribution of the pixel values inside the material image space.
In this study, the 3D reconstruction of a material using an algorithm belonging to the second abovementioned category was examined. The defined optimization problem was solved by applying several nature-inspired optimization algorithms discussed in the next section.
2.2. Nature-Inspired Optimization Algorithms
It is well known that for the optimization of a specific procedure/function, a common practice is to apply a gradient-based algorithm [38], e.g., Newton’s method. However, the gradient-based optimization algorithms have two significant limitations: (1) can be trapped at a local minimum and (2) require that the function being minimized is differentiable. These limitations do not make the gradient-based optimization algorithms applicable in complex problems where the analytical definition of the objective function is not easy to derive.
To handle the abovementioned limitations of the traditional optimization algorithms, the nature-inspired algorithms were proposed. These algorithms use a population of candidate solutions, where their fitness to solve the problem under investigation were examined in parallel, while a set of operators inspired by several natural processes were applied in each algorithm’s iteration. Some of the most popular, as well as modern, nature-inspired optimization algorithms are briefly discussed in the next section and are applied in the 3D reconstruction of porous media in the experimental section.
2.2.1. Genetic Algorithm (GA)
A simple genetic algorithm (GA) is a stochastic method that searches in wide search spaces, subject to some probability values. For these reasons, it can converge to the global minimum or maximum, depending on the specific application, and can skip possible local minima or maxima. Genetic algorithms were proposed by Holland [24] who tried to find a method to mimic the evolutionary process that characterizes the evolution of living organisms. This theory is based on the mechanism representing the survival of the fittest individuals over a population. Genetic algorithms have been widely applied to several disciplines, such as feature selection [39], biomedicine [40], mechanical systems [41], etc.
Initially, a population of candidate solutions (chromosomes), satisfying the constraints of the problem, is randomly constructed. In each iteration (generation) of the algorithm, a fitness is assigned to each chromosome, which is a real number value that indicates how suitable the solution for the problem under consideration is. In each generation, a set of operators, aiming to produce new unexplored solutions, is applied to the entire population. The most popular operators are:
Selection is an operator applied to the current population like the one used by natural selection found in biological systems. The fitter individuals are promoted to the next population and poorer individuals are discarded.
Crossover is the second operator and follows selection. This operator allows for solutions to exchange information that the living organisms use to reproduce themselves. Specifically, two solutions are selected to exchange their substrings from a single point and after, according to a predefined probability . The resulting offsprings carry some information from their parents.
Mutation is the third operator and follows crossover. According to this operation, a small part of the chromosome is changed (e.g., a single bit of a binary string is flipped) according to a predefined probability .
Elitism is the procedure according to which a fraction of the fittest chromosomes in a generation is ensured to be maintained in the next generation.
After the application of the above operators to the current population, a new population is formed and the generational counter is increased by one. This process is repeated until a predefined number of generations is attained or some form of convergence criterion is met.
2.2.2. Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) was proposed by Kennedy and Eberhart [25] as a new optimization method based on swarming theory, such as bird flocking and fish schooling. Similar to a genetic algorithm, a population of potential solutions (particles) is created randomly. Each particle is characterized by its position and velocity . In each iteration, the velocity and position of the particle are defined as follows:
where [27] are the learning parameters; are random numbers; is the current best of particle ; and is the current global best of the entire population.
From the above equations, it is obvious that the movements of the particles are guided by their own best-known position in the search space, as well as the entire swarm’s best-known position. This algorithm is simpler than the GA since it does not apply any advanced operator; instead, some simple mathematical calculations are incorporated.
2.2.3. Differential Evolution (DE)
According to the differential evolution (DE) algorithm [26], a population (with NP size) of candidate solutions (agents) is initially randomly selected. New solutions are produced by adding the weighted difference between two population agents to a third one . This operation is called mutation and its mathematical expression is as follows:
where are randomly selected and is called the differential weight, which controls the amplification of the differential variation of Equation (5). Next, a crossover operator is applied to the resultant mutant agent subject to a crossover , according to the following rule:
where is the trial solution in the n-dimensional search space, is a random number, and is a random index. Finally, the produced solution is compared with its value in the previous iteration (generation) with respect to the objective function being minimized. If the new solution yields a smaller objective function value than its old value, then is set to ; otherwise, the old value is retained.
The main advantages of the DE algorithm are its simplicity (few control parameters and simple operators) and the fast convergence to the global optimum.
2.2.4. Firefly Algorithm (FA)
The firefly algorithm (FA) was recently proposed by Yang [27] as an alternative population-based optimization method that mimics the natural process of the flashing behavior of the fireflies. It is known that the flashing light of the fireflies is used to attract mating partners and potential prey. The variation of light intensity (light intensity decreases with the distance increase because the air absorbs the light) and the formulation attractiveness are the main functional principles of FA that need to be handled. The movement of a firefly toward another attractive one is determined by:
where (usually equal to 1) corresponds to the attractiveness, (usually between 0.1 and 10) is the absorption coefficient, is the Euclidean distance between fireflies and , is the step size, and is a random vector drawn from a Gaussian or normal distribution. It is worth noting that the light intensity is associated with the objective function that needs to be optimized, while the entire population tends to be attracted by the brightest firefly during the algorithm.
2.2.5. Artificial Bee Colony (ABC)
The artificial bee colony (ABC) algorithm is a heuristic optimization algorithm based on the intelligent behavior of a honey bee swarm, which was proposed by Karaboga and Basturk [28]. In the ABC algorithm, the colony of artificial bees contains three groups of bees: employed bees (bees going to the food source visited by themselves previously), onlookers (bees waiting to decide on a food source), and scouts (bees carrying out a random search). In the ABC algorithm, the first half of the colony consists of employed artificial bees and the second half consists of onlookers. For every food source (a possible solution), there is only one employed bee (the number of employed bees is equal to the number of food sources around the hive). Each cycle of the search consists of three steps: sending the employed bees to the food sources and then measuring their nectar amounts, selection of the food sources by the onlookers after the information is shared by the employed bees and determining the nectar amount of the foods, and determining the scout bees and then sending them to possible food sources [28,42]. The colony has to optimize the overall efficiency of nectar collection, where each possible solution has a specific amount of nectar. An artificial employed or onlooker bee probabilistically produces a modification on the position (solution) in her memory for finding a new food source and tests the nectar amount (fitness value) of the new source (new solution).
An onlooker bee evaluates the nectar information taken from all the employed bees and chooses a food source with a probability related to its nectar amount according to the following definition:
where is the fitness value of the th solution. This probabilistic selection is equal to a roulette wheel selection mechanism.
Each employed bee generates a new candidate solution (food position) in the neighborhood of its present position according to the following rule:
where and , are randomly chosen indexes, is the number of employed bees, and is a random number.
2.2.6. Gravitational Search Algorithm (GSA)
The gravitational search algorithm (GSA) is a new nature-inspired optimization algorithm proposed by Rashedi et al. [29] based on the law of gravity and mass interactions. The GSA emulates a small artificial world of masses obeying the Newtonian laws of gravitation and motion. According to the GSA algorithm, a population (with NP size) of candidate solutions (masses) is randomly initialized and the force acting to each other (from mass to mass at time ) is calculated based on the following equation:
where is the active gravitational mass related to mass , is the passive gravitational mass related to mass , is a gravitational constant at time , is a small constant, and is the Euclidean distance between the two masses and . The total force that acts on mass is calculated as follows:
where is a random number.
Based on the law of motion, the acceleration of mass is defined as follows:
where is the inertial mass of solution .
The velocity and position of each mass of the population is calculated as follows:
where is a random number.
It is worth noting that the gravitational and inertial masses are updated according to the following equations:
where is the fitness of mass , and and are the worst and best fitness of the entire population at time , respectively.
2.2.7. Discussion
All the above-discussed nature-inspired optimization algorithms share some common properties even though each one applies different operators that control the method for producing better solutions. These common characteristics are summarized as follows:
- −
- A set of candidate solutions (population) are examined in parallel by avoiding trapping in a local optimum.
- −
- Several variants of each algorithm are proposed to handle real, integer, and binary unknowns (solutions).
- −
- The diversity of the population should be retained during the algorithm execution to avoid its premature convergence to a local optimum.
- −
- Each algorithm aims to compromise between exploration and exploitation of the search space.
- −
- The cost (objective) non-differentiable function that measures the utility of each solution in the real problem under study needs to be determined carefully.
- −
- The same termination criteria are applied, where either a fixed number of iterations is attained or a predefined accuracy is reached.
The nature-inspired optimization algorithms discussed in the previous section are used to solve the problem of 3D porous media reconstruction as long as it is defined in terms of optimization, as follows in the next section.
3. 3D Reconstruction as an Optimization Problem
The 3D reconstruction of a material by using statistical methods, such as the well-known Quiblier’s method [5] and its variants [7,8,35], has the following weaknesses:
- The computation of the coefficients needed to define the linear and the non-linear filters is a laborious task.
- Only one correlation function can be incorporated into the algorithm at a time to code the morphological properties of the material.
- There is no proof of optimality for the resultant porous media distribution.
- The need to binarize the computed 3D model to derive the final porous media distribution.
On the other hand, the nature-inspired, optimization-based 3D reconstruction algorithms exhibit the following properties, which alleviate the aforementioned limitations of the statistical methods:
- There is no need to compute coefficients of any filter (they do not exist).
- Several correlation functions can be used simultaneously in the same objective function and therefore the morphological properties of the material can be described more accurately.
- Although there is no analytical proof, regarding the optimality of the solutions derived by the nature-inspired optimization algorithms, experience has shown that the solutions are near optimal.
- There is no need to apply a binarization method in order to derive the final 3D model since the optimization algorithms can directly provide the solutions in a binary form.
To apply a nature-inspired optimization algorithm for reconstructing a 3D model of porous media, two important issues need to be addressed appropriately. First, the task of 3D reconstruction should be defined in terms of optimization, where the appropriate cost (objective) function needs to be defined to describe the fitness of each solution of the real system. Second, the solutions should be coded appropriately through an efficient data representation scheme such that the algorithm operates in the real search space with the lowest possible complexity. Both issues are hereafter discussed in detail.
3.1. Problem Formulation
Based on the previous analysis, it was concluded that the application of a nature-inspired optimization algorithm will significantly enhance the 3D reconstruction of porous media. However, the application of any nature-inspired optimization algorithm is highly dependent on the successful formulation of the optimization problem related to the definition of the cost (objective) function being minimized. A generic objective function consisting of multiple correlation functions was proposed in this work for the set of N unknowns (the phases of the 3D model’s pixels) , according to the following form:
where is the number of different functions (correlation and/or statistical) used to measure the morphological properties of the material; and are the th function and its reference value (of the 2D slice image); and are the dimension and the normalization factor of the function, respectively; and is its weight defining its importance satisfying the following condition:
Based on the objective function of Equation (18), the 3D reconstruction optimization problem is defined as follows:
The flowchart of the proposed reconstruction methodology, applied for each one of the algorithms of Section 2, is depicted in Figure 1. Based on this figure, the proposed 3D porous media reconstruction consists of the following phases: (1) initial random candidate solutions: in this phase, random material phases are generated and the proposed data representation scheme is applied to reduce the number of unknowns that need to be found by the evolutionary algorithm, (2) application of the specific operators of the applied evolutionary algorithm to produce solutions with higher fitnesses, (3) reconstruction of a 3D material model for each candidate solution, and (4) fitness calculation of each candidate solution using Equation (18). The execution of these four phases is repeated until a termination criterion is met. After the termination of the algorithm, the fittest solution corresponds to the reconstructed 3D porous media.
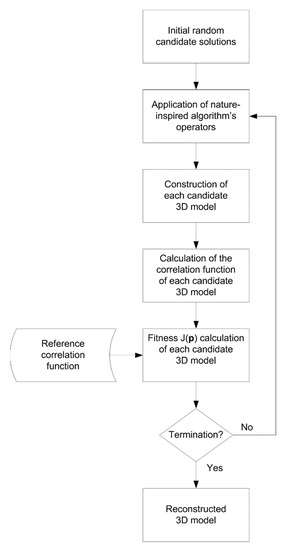
Figure 1.
Flowchart of the proposed reconstruction algorithm.
3.2. Data Representation
In the above-defined optimization problem, the unknowns that need to be found are the phase values of each material image pixel. Therefore, for an image of pixels in size, the number of unknowns is , and thus the corresponding search space where any nature-inspired algorithm needs to be executed is extremely complex. For example, if a 3D model of pixels size needs to be derived, a total of 2,097,152 unknowns should be found by the algorithm.
To overcome the above problem of high dimensional data, an efficient data representation is proposed in this work. For this purpose, the notion of the fundamental element (fe), which controls the representation accuracy of the reconstructed 3D material model, was introduced. Considering that the material is composed of homogenous cubic (all pixels of the cube have the same phase) elements of pixels in size, the number of unknowns can be reduced to , achieving a significant reduction in the problem’s dimension.
Moreover, considering the case of a two-phase porous media and without loss of generality, each cubic element can be decoded as a single bit. In this way, by using a 64-bit arithmetic representation, one can compactly encode the phase of 64 cubic elements in a single integer value. By applying the proposed data representation, the problem dimension is finally reduced to .
3.3. Complexity Analysis
The main overhead of the proposed methodology is the fitness computation of each candidate solution consisting of the 3D model construction and the computation of its auto-correlation function. However, the former process is of order of complexity, whereas the latter one is of . This improvement in the data representation decreases the solution space and accelerates the convergence of the deployed evolutionary algorithms.
4. Experimental Study
A set of experiments was conducted to investigate the reconstruction performance of the proposed methodology under several configurations. For experimental purposes, the specific software was developed in the MATLAB 2012b integrated development environment, where experiments were executed on an Intel i5 3.3 GHz PC with 8 GB RAM.
4.1. Data Description and Preparation
For the sake of the experiments, two porous media were selected as test materials for evaluating the reconstruction performance of the proposed methodology. The first material was sintered copper (SC) used in Bodla et al. [43] and the second one is the SBA-15 acquired in the Hephaestus Lab [44], as illustrated in Figure 2.

Figure 2.
Test material data and their thresholded versions: (a) sintered copper and (b) SBA-15.
Before applying the proposed method, preprocessing was applied to both materials. Both SC and SBA-15 materials were thresholded (white pixels correspond to the pores and black ones to the material) (Figure 2), by applying the Otsu [45] binarization method, with derived thresholds equal to 0.3490 and 0.2745, respectively. Moreover, in Figure 2, the porosity of each material is also depicted.
4.2. Simulations
The test materials of Figure 2 were pixels in size, thus the size of the reconstructed 3D model should be pixels in size, whereas the selected fundamental element was pixels in size. Moreover, according to the analysis of Section 3.2, the number of unknowns that needed to be found by the algorithms was 512 64-bit length values. The algorithms were configured such that they operated with the same population size and number of iterations to fairly compare their performances. The detailed configuration of each algorithm is presented in Table 1. It is mentioned that the applied configurations were not optimal; rather, they were decided by trial and error and a more optimal parameter set can be derived using a grid search. Note that the execution time of each algorithm for these configurations was 3–4 h per reconstruction experiment.

Table 1.
Configuration of the algorithms: genetic algorithm (GA), particle swarm optimization (PSO), differential evolution (DE), firefly algorithm (FA), artificial bee colony (ABC), and gravitational search algorithm (GSA).
The reconstruction performance of each nature-inspired algorithm is depicted in Figure 3, Figure 4 and Figure 5 and Figure 6, Figure 7 and Figure 8 for the SC and SBA-15, respectively. In these figures, the resultant 3D model, its first 2D slice, and its corresponding auto-correlation function are illustrated. Moreover, along with the , the corresponding auto-correlation function of the binary reference 2D slice image is plotted for comparison.
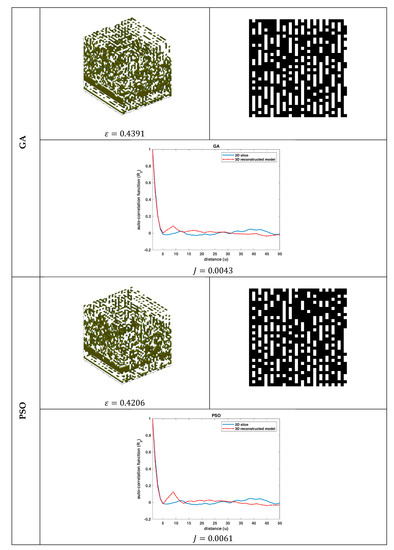
Figure 3.
Reconstruction performance for sintered copper (SC): The 3D reconstructed model, the first slice of the 3D model, and its auto-correlation function, along with the auto-correlation function of the binary reference image of Figure 2a, for the GA and PSO algorithms.
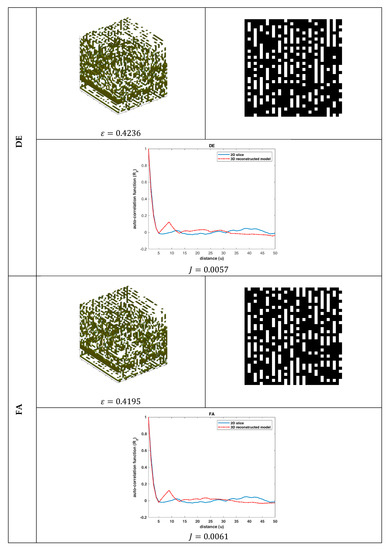
Figure 4.
Reconstruction performance (SC): The 3D reconstructed model, the first slice of the 3D model, and its auto-correlation function, along with the auto-correlation function of the binary reference image of Figure 2a, for the DE and FA algorithms.
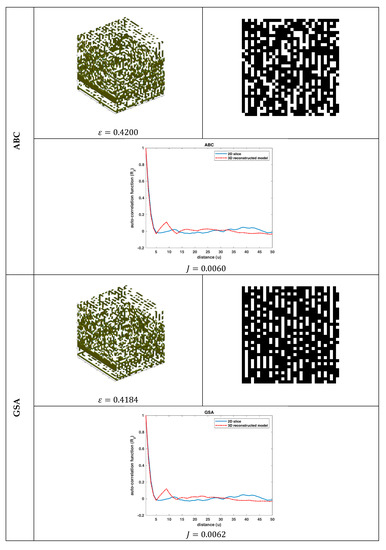
Figure 5.
Reconstruction performance (SC): The 3D reconstructed model, the first slice of the 3D model, and its auto-correlation function, along with the auto-correlation function of the binary reference image of Figure 2a, for the ABC and GSA algorithms.
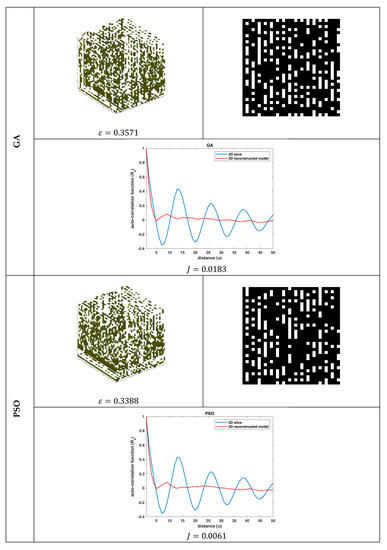
Figure 6.
Reconstruction performance (SBA-15): The 3D reconstructed model, the 1st slice of the 3D model and its auto-correlation function along with the auto-correlation function of the binary reference image of Figure 2b, for the GA and PSO algorithms, respectively.
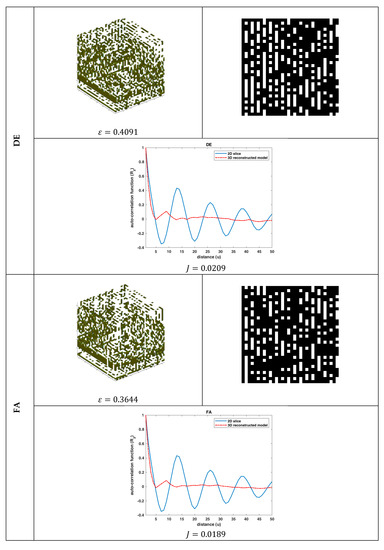
Figure 7.
Reconstruction performance (SBA-15): The 3D reconstructed model, the first slice of the 3D model, and its auto-correlation function, along with the auto-correlation function of the binary reference image of Figure 2b, for the DE and FA algorithms.
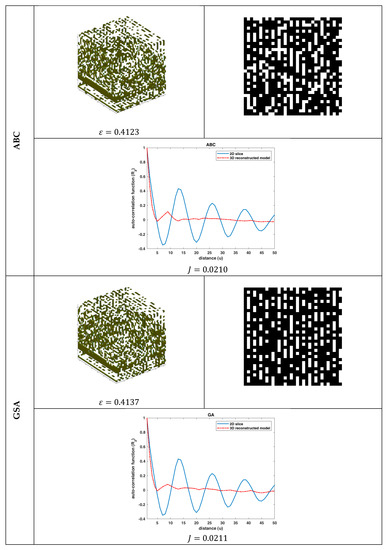
Figure 8.
Reconstruction performance (SBA-15): The 3D reconstructed model, the first slice of the 3D model, and its auto-correlation function, along with the auto-correlation function of the binary reference image of Figure 2b, for the ABC and GSA algorithms.
4.2.1. Qualitative Analysis
By qualitatively studying all the reconstruction results (Figure 3–8), some useful conclusions can be drawn. All the algorithms showed almost the same performance with small variations, as far as the values of the objective function and the porosity are concerned, meaning that the problem was very complex. The porosity of the reconstructed 3D model was quite close to the targeted porosity of the 2D slice, but the auto-correlation of the 2D slice and that of the 3D model differed in absolute values. However, the results revealed that the reconstructed model could simulate the trends of the 2D slice’s auto-correlation function. Moreover, the differences in the resultant 3D models and their sample 2D slices revealed that different 3D structures had similar statistical properties and vice versa. Thus, it was concluded that the statistical functions and ε seemed to be unable to adequately describe the morphological properties of the material microstructure. Instead, higher-order statistics, rather than the first- and second-order ones, are needed to guarantee that the minimized objective function corresponds to a unique solution (3D model). It is worth noting that this property of the objective function is highly connected to what is called a one-to-one function (“1–1”) in mathematics. However, since the procedure to analytically prove that the objective function is a “1–1” function is laborious, one can limit the search space by applying more and higher-order correlation functions.
4.2.2. Quantitative Analysis
To quantitatively study the reconstruction results, the following mean squared error (MSE) was introduced:
where , is the number of slices, and the superscripts 3D and 2D indicate the 3D model and the 2D slice image, respectively.
Table 2 summarizes the reconstruction results of the algorithms using Equation (21), where the highest performance in each case is indicated with boldface.

Table 2.
Reconstruction performance indexes of the algorithms.
The results of Table 2 reveal that the GA algorithm outperformed the PSO, DE, FA, ABC, and GSA algorithms in almost all the cases by between 5%–84% (porosity accuracy) and 3%–15% (auto-correlation function accuracy). Moreover, it is worth mentioning that the performance of all algorithms was worst for the case of the SC material (higher average MSE(ε)) in terms of porosity accuracy, although the 2D slices of the 3D model were more correlated in this case (lower average MSE(ε)). This was justified by the fact that the morphology of the SC material is more complex than that of the SBA-15. This complex distribution of SC material phases makes the optimization problem more difficult to solve using evolutionary algorithms.
5. Conclusion and Future Work
The problem of the 3D reconstruction of porous media from a single 2D material image using six nature-inspired optimization algorithms was studied. Although the reconstruction results were very accurate in terms of MSE for the case of the statistical functions, the visual representation deviated significantly from the desired materials’ microstructures. This contradiction between the numerical and visual performance of the reconstruction methodology was due to the existence of more than one different 3D microstructure having the same statistical properties . Moreover, the suboptimal configuration of the algorithms also affected the numerical accuracy of the methodology, and a sensitivity analysis of the optimization algorithms regarding their free parameters is needed. However, this study sheds light on two important issues: (1) a nature-inspired algorithm could reconstruct the 3D porous media by applying an appropriate data representation scheme despite the complex search space and (2) there are needs for more descriptive and higher-order [46,47] functions for measuring the material’s phase distribution to increase the fidelity of the reconstructed microstructure. These outcomes pave the way for future research toward the development of an efficient reconstruction algorithm in terms of accuracy and processing time.
As far as the computation time is concerned, the high computational burden stemming from the sources described in Section 3.3 can be reduced by applying modern parallel computing frameworks (e.g., MPI – Message Passing Interface, GPU programming, thread programming, MapReduce, SparK, cluster computing, and grid computing). For example, the high parallelism of all the nature-inspired algorithms enables the implementation of the algorithms (fitness computation) by utilizing the parallel computing capabilities of a GPU (graphics processing unit) Nvidia card within the CUDA architecture [48]. The development of an accelerated nature-inspired algorithm in conjunction with the proposed data representation scheme will allow for the execution of an algorithm with a larger population size and more iterations that can increase the reconstruction accuracy.
Finally, additional research should be arranged toward the direction of applying higher-order statistics to describe the microstructure of the material uniquely. The proposed generic form of the objective function can help in this direction since it enables the incorporation of any number and type of functions with minimal modifications.
Author Contributions
Methodology, G.A.P., J.W.N., and A.C.M.; software, G.A.P. and J.W.N.; validation, J.W.N. and A.C.M.; investigation, G.A.P.; writing—original draft preparation, G.A.P.; writing—review and editing, J.W.N. and A.C.M.; supervision, G.A.P. and J.W.N.; project administration, A.C.M.; funding acquisition, A.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Thalis “NANOCAPILLARY MIS 375233” research project of the Greek Ministry of National Education and Religious Affairs.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, Y.; Zhang, L.; Zhu, G.; Yao, J.; Sun, H.; Song, W.; Yang, Y.; Zhao, J. A Pore-Scale Investigation of Residual Oil Distributions and Enhanced Oil Recovery Methods. Energies 2019, 12, 3732. [Google Scholar] [CrossRef]
- Poonoosamy, J.; Haber-Pohlmeier, S.; Deng, H.; Deissmann, G.; Klinkenberg, M.; Gizatullin, B.; Stapf, S.; Brandt, F.; Bosbach, D.; Pohlmeier, A. Combination of MRI and SEM to Assess Changes in the Chemical Properties and Permeability of Porous Media due to Barite Precipitation. Minerals 2020, 10, 226. [Google Scholar] [CrossRef]
- Duan, R.; Dong, Y.; Zhang, Q. Characteristics of Aggregate Size Distribution of Nanoscale Zero-Valent Iron in Aqueous Suspensions and Its Effect on Transport Process in Porous Media. Water 2018, 10, 670. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, C.; Zhang, C.; Zhou, X.; Zhang, Z.; Nie, X.; Liu, W.; Zhu, B. Challenges and prospects of digital core-reconstruction research. Geofluids 2019, 2019. [Google Scholar] [CrossRef]
- Quiblier, J.A. A new three-dimensional modeling technique for studying porous media. J. Coll. Interface Sci. 1984, 98, 84–102. [Google Scholar] [CrossRef]
- Adler, P.M.; Jacquin, C.G.; Quiblier, J.A. Flow in simulated porous media. Int. J. Multiph. Flow 1990, 16, 691–712. [Google Scholar] [CrossRef]
- Bentz, D.P.; Martys, N.S. Hydraulic radius and transport in reconstructed model three-dimensional porous media. Transp. Porous Media 1994, 17, 221–238. [Google Scholar] [CrossRef]
- Liang, Z.R.; Fernandes, C.P.; Magnani, F.S.; Philippi, P.C. A reconstruction technique for three-dimensional porous media using image analysis and Fourier transforms. J. Petroleum Sci. Eng. 1998, 21, 273–283. [Google Scholar] [CrossRef]
- Yeong, C.L.Y.; Torquato, S. Reconstructing random media. Phys. Rev. E 1998, 57, 495. [Google Scholar] [CrossRef]
- Yeong, C.L.Y.; Torquato, S. Reconstructing random media. II. Three-dimensional media from two-dimensional cuts. Phys. Rev. E 1998, 58, 224. [Google Scholar] [CrossRef]
- Sabbagh, R.; Kazemi, M.A.; Soltani, H.; Nobes, D.S. Micro- and Macro-Scale Measurement of Flow Velocity in Porous Media: A Shadow Imaging Approach for 2D and 3D. Optics 2020, 1, 71–87. [Google Scholar] [CrossRef]
- Berryman, J.G. Measurement of spatial correlation functions using image processing techniques. J. Appl. Phys. 1985, 57, 2374–2384. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. Multiple-point geostatistical modeling based on the cross-correlation functions. Comput. Geosci. 2012, 16, 779–797. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Sahimi, M. Reconstruction of three-dimensional porous media using a single thin section. Phys. Rev. E 2012, 85, 066709. [Google Scholar] [CrossRef]
- Xu, Z.; Teng, Q.; He, X.; Li, Z. A reconstruction method for three-dimensional pore space using multiple-point geology statistic based on statistical pattern recognition and microstructure characterization. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 97–110. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Sahimi, M. Cross-correlation function for accurate reconstruction of heterogeneous media. Phys. Rev. Lett. 2013, 110, 078002. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Javadpour, F.; Sahimi, M. Three-dimensional stochastic characterization of shale SEM images. Transp. Porous Media 2015, 110, 521–531. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Sahimi, M.; Kohanpur, A.H.; Valocchi, A. Pore-scale simulation of flow of CO2 and brine in reconstructed and actual 3D rock cores. J. Petroleum Sci. Eng. 2017, 155, 21–33. [Google Scholar] [CrossRef]
- Karsanina, M.V.; Gerke, K.M.; Skvortsova, E.B.; Mallants, D. Universal spatial correlation functions for describing and reconstructing soil microstructure. PLoS ONE 2015, 10, e0126515. [Google Scholar] [CrossRef]
- Tahmasebi, P. Accurate modeling and evaluation of microstructures in complex materials. Phys. Rev. E 2018, 97, 023307. [Google Scholar] [CrossRef]
- Mosser, L.; Dubrule, O.; Blunt, M.J. Stochastic reconstruction of an oolitic limestone by generative adversarial networks. Transp. Porous Media 2018, 125, 81–103. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; Catherine Brinson, L.; Choudhary, A.N.; Chen, W.; Agrawal, A. Microstructural materials design via deep adversarial learning methodology. J. Mech. Des. 2018, 140. [Google Scholar] [CrossRef]
- Shams, R.; Masihi, M.; Boozarjomehry, R.B.; Blunt, M.J. Coupled generative adversarial and auto-encoder neural networks to reconstruct three-dimensional multi-scale porous media. J. Petroleum Sci. Eng. 2020, 186, 106794. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Garg, H. A hybrid GSA-GA algorithm for constrained optimization problems. Inf. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Patwal, R.S.; Narang, N.; Garg, H. A novel TVAC-PSO based mutation strategies algorithm for generation scheduling of pumped storage hydrothermal system incorporating solar units. Energy 2018, 142, 822–837. [Google Scholar] [CrossRef]
- Garg, H.; Sharma, S.P. Multi-objective reliability-redundancy allocation problem using particle swarm optimization. Comput. Ind. Eng. 2013, 64, 247–255. [Google Scholar] [CrossRef]
- Shah, H.; Tairan, N.; Garg, H.; Ghazali, R. Global Gbest Guided-Artificial Bee Colony Algorithm for Numerical Function Optimization. Computers 2018, 7, 69. [Google Scholar] [CrossRef]
- Kainourgiakis, M.E.; Kikkinides, E.S.; Stubos, A.K. Diffusion and flow in porous domains constructed using process-based and stochastic techniques. J. Porous Mater. 2002, 9, 141–154. [Google Scholar] [CrossRef]
- Blair, S.C.; Berge, P.A.; Berryman, J.G. Using two-point correlation functions to characterize microgeometry and estimate permeabilities of sandstones and porous glass. J. Geophys. Res. Solid Earth 1996, 101, 20359–20375. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Nolan, J.W.; Vordos, N.; Gkika, D.; Kainourgiakis, M.E.; Mitropoulos, A.C. On 3D reconstruction of porous media by using spatial correlation functions. J. Eng. Sci. Technol. Rev. 2015, 8, 78–83. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Papakostas, G.A. Improving the recognition performance of moment features by selection. In Feature Selection for Data and Pattern Recognition; Springer: Berlin, Germany, 2015; pp. 305–327. [Google Scholar]
- Papakostas, G.A.; Karras, D.A.; Mertzios, B.G.; Van Ormondt, D.; Graveron-Demilly, D. In vivo MRS metabolite quantification using genetic optimization. Meas. Sci. Technol. 2011, 22, 114004. [Google Scholar] [CrossRef]
- Saad, A.; Dong, Z.; Karimi, M. A comparative study on recently-introduced nature-based global optimization methods in complex mechanical system design. Algorithms 2017, 10, 120. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Bodla, K.K.; Garimella, S.V.; Murthy, J.Y. 3D reconstruction and design of porous media from thin sections. Int. J. Heat Mass Transf. 2014, 73, 250–264. [Google Scholar] [CrossRef]
- Hephaestus Laboratory. Available online: http://hephaestus.teikav.edu.gr/ (accessed on 1 December 2019).
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Boutalis, Y.S.; Karras, D.A.; Mertzios, B.G. A new class of Zernike moments for computer vision applications. Inf. Sci. 2007, 177, 2802–2819. [Google Scholar] [CrossRef]
- Papakostas, G.A.; Koulouriotis, D.E.; Karakasis, E.G. Computation strategies of orthogonal image moments: A comparative study. Appl. Math. Comput. 2010, 216, 1–17. [Google Scholar] [CrossRef]
- Mussi, L.; Daolio, F.; Cagnoni, S. Evaluation of parallel particle swarm optimization algorithms within the CUDATM architecture. Inf. Sci. 2011, 181, 4642–4657. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).