Performance Assessment of Predictive Control—A Survey
Abstract
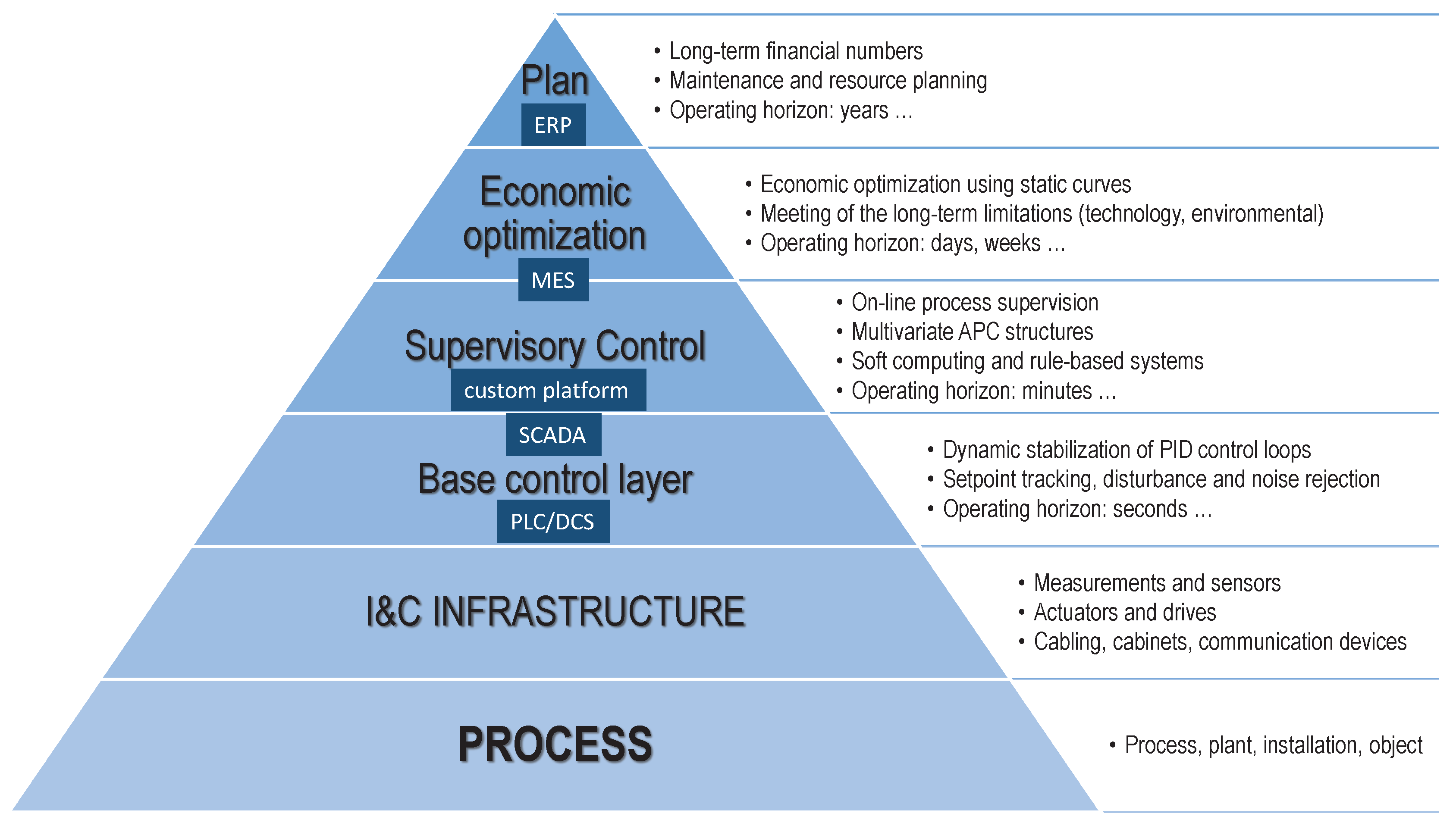
1. Introduction
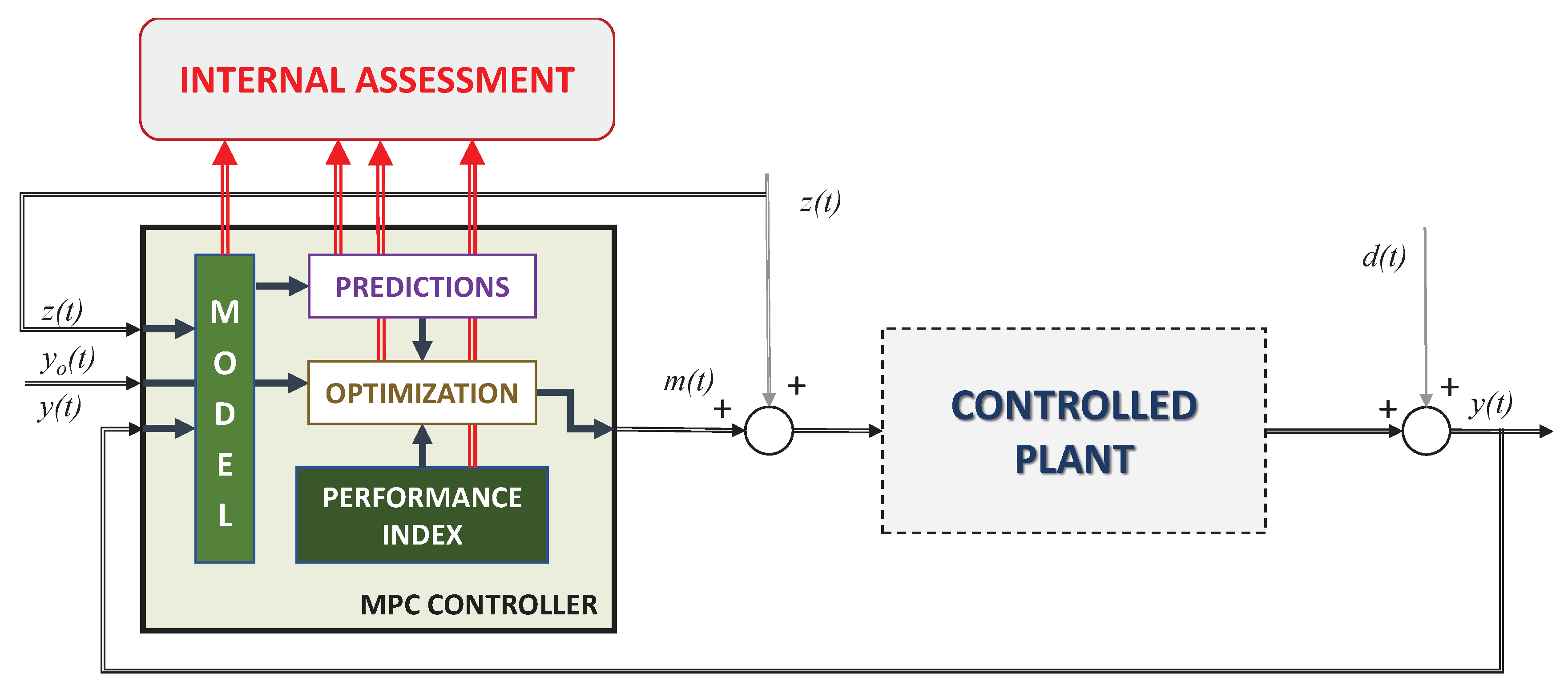
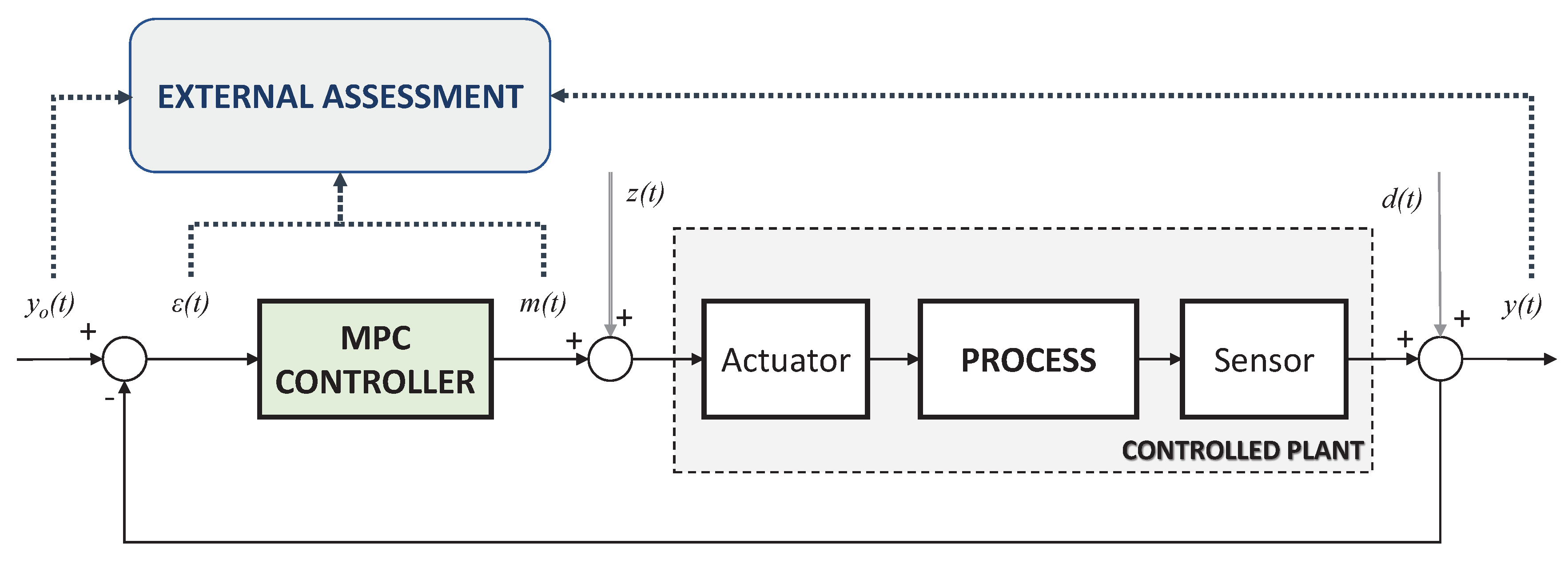
2. Model Predictive Control
General MPC Rule
- on their minimal and maximal permissible limits and ;
- on their future changes with a limiting value of ; and
- on process output predictions (also over the prediction horizon) denoted as and .
- process model;
- performance index formulation;
- utilized optimization algorithm; or
- algorithm numerical representation.
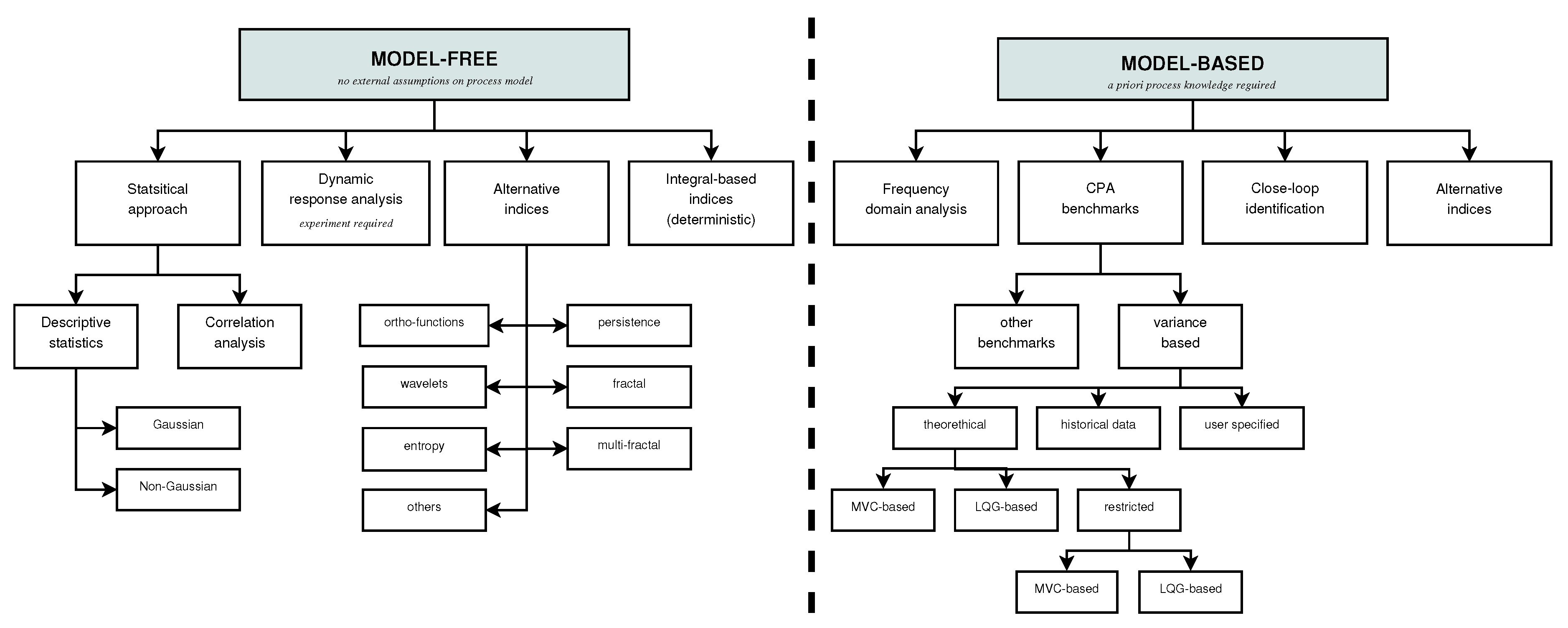
3. Control Performance Assessment
- Model-free means that no process model is required.
- Process model-based approaches require performing the modeling of the controlled plant.
- Methods requiring plant experiment:
- measures that use setpoint step response, such as overshoot, undershoot, rise, peak and settling time, decay ratio, offset (steady state error), and peak value [71]; and
- Model-based methods:
- frequency methods starting from classical Bode, Nyquist and Nichols charts with phase and gain margins [69] followed by deeper investigations, such as with the use of Fourier transform [80], sensitivity function [81], reference to disturbance ratio index [82], and singular spectrum analysis [83]; and
- Data-driven methods:
- benchmarking methods [97]; and
4. MPC Performance Assessment
4.1. Model-Based Approaches
- design-case approach [121], which uses the MPC controller criterion as the measure performance index ;
- constraint benchmarking taking into account an economic performance assessment [122];
- Harris-based benchmarking [123] applied to the multivariate cases;
- multi-parametric quadratic programming analysis has been used to develop maps of minimum variance performance for constrained control over the state-space partition [124];
- predictive DMC structures used to compare and assess implemented as a single controller or as a supervisory level over PID regulatory control [125];
- orthogonal projection of the current output onto the space spanned by past outputs, inputs or setpoint using normal routine close loop data [126];
- the infinite-horizon MPC [65];
- Filtering and Correlation Analysis algorithm (FCOR) approach used to evaluate the minimum variance control problem and the performance assessment index [127]; and
4.2. Data-Driven Approaches
4.3. Industrial Implementations
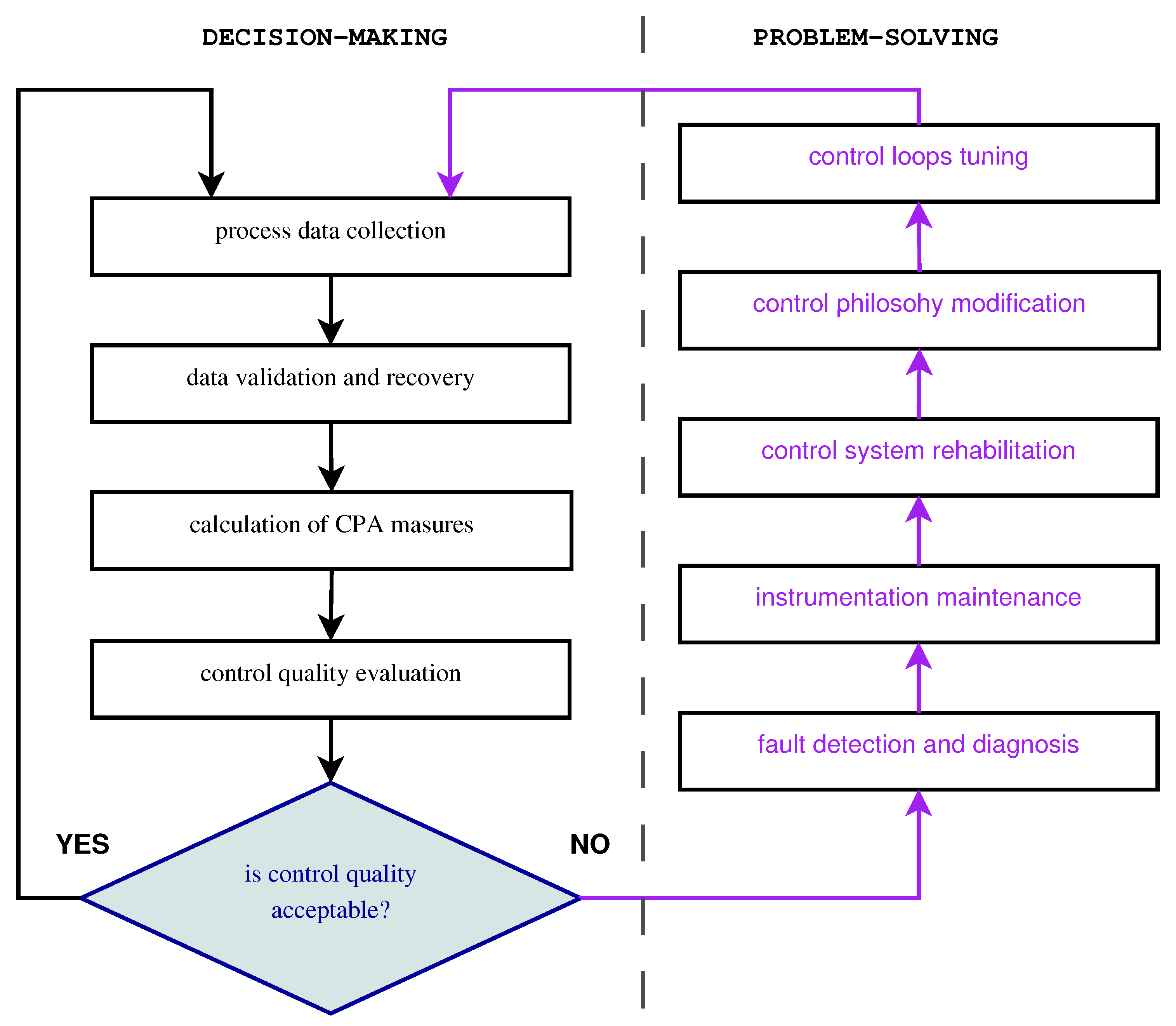
5. MPC Assessment Procedure
- (1)
- Take a plant walk-down and talk to the plant personnel: operators, control and technology engineers.
- (2)
- Review relevant variables time trends using plant control system.
- (3)
- Investigate AUTO/MAN mode of operation for the considered controllers.
- (4)
- Collect historical data for the assessed control loops.
- (5)
- Calculate basic and simple data statistics, such as minimum, maximum, mean, median, standard deviation, skewness, kurtosis, MAD, etc.
- (6)
- If the step response is available or can be calculated, estimate the settling time and the overshoot.
- (7)
- Prepare static curves (MV-CV plots) to assess nonlinearities and noise ratios.
- (8)
- Calculate control error integral indexes: MSE and IAE, though MSE should be used with caution.
- (9)
- Check the stationarity of the process variables, search for possible trends, and try to remove them.
- (10)
- Identify potential oscillations, assess their frequency, and try to remove them.
- (11)
- Draw control error histogram, check its shape, validate normality tests, and look for possible fat tails.
- (12)
- Fit underlying distributions, select the best fitting function, and estimate its coefficients with the aim to identify an underlying generation mechanism.
- (a)
- If signals are Gaussian, normal standard deviation and other moments may be used.
- (b)
- Once fat tails exist, -stable distribution seems to be a reliable choice with its coefficients: scaling , skewness , or characteristic exponent .
- (c)
- Calculate robust scale estimators .
- (d)
- Otherwise, select coefficients for the another best fitting PDF.
- (13)
- In case of fat tails, data non-stationarity, or self-similarity, conduct the persistence analysis using rescaled range R/S and estimate Hurst exponents and crossover points.
- (14)
- Translate obtained numbers into verbal conclusions.
- (15)
- Suggest relevant improvement actions.
6. Discussion and Further Research
Funding
Conflicts of Interest
Abbreviations
| CPA | Control Performance Assessment |
| Probabilistic Density Function | |
| MPC | Model Predictive Control |
| MIMO | Multi Input Multi Output |
| SISO | Single Input Single Output |
| PID | Proportional, Integral and Derivative |
| LQR | Linear, Quadratic Regulator |
| DMC | Dynamic Matrix Control |
| LP-DMC | Linear Programming Dynamic Matrix Control |
| QDMC | Quadratic Dynamic Matrix Control |
| GPC | Generalized Predictive Control |
| MAC | Model Algorithmic Control |
| MV | Manipulated Variable |
| CV | Controlled Variable |
| DV | Disturbance Variable |
| PV | Process Variable |
| ARMA | Auto-Regressive Moving Average |
| ARIMAX | Auto-Regressive Integrated Moving Average with auXiliary Input |
| CARIMA | Controlled Auto-Regressive Integrated Moving Average |
| NO-MPC | Nonlinear Optimization Model Predictive Control |
| MPC-NPLPT | MPC with Nonlinear Prediction and Linearization Along the Predicted Trajectory |
| MSE | Mean Square Error |
| IAE | Integral Absolute Error |
| ITAE | Integral Time Absolute Value |
| ISTC | Integral of Square Time derivative of the Control input |
| TSV | Total Squared Variation |
| AMP | Amplitude Index |
| LQG | Linear Quadratic Gaussian |
| PCA | Principal Component Analysis |
| FCOR | Filtering and CORrelation analysis |
| KPI | Key Performance Indicator |
| EWMA | exponentially weighted moving averages |
| SVM | support vector machine |
| MAD | Mean Absolute Deviation |
| MADAM | Mean Absolute Deviation Around Median |
| SFA | Slow Feature Analysis |
References
- Knospe, C. PID control. IEEE Control Syst. Mag. 2006, 26, 30–31. [Google Scholar]
- Åström, K.J.; Murray, R. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2012; Available online: http://www.cds.caltech.edu/~murray/amwiki (accessed on 25 October 2019).
- Samad, T. A Survey on Industry Impact and Challenges Thereof [Technical Activities]. IEEE Control Syst. Mag. 2017, 37, 17–18. [Google Scholar]
- Soltesz, K. On Automation of the PID Tuning Procedure. Ph.D. Thesis, Department of Automatic Control, Lund University, Lund, Sweden, 2012. [Google Scholar]
- Leiviskä, K. Industrial Applications of Soft Computing: Paper, Mineral and Metal Processing Industries; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Betlem, B.; Roffel, B. Advanced Practical Process Control; Advances in Soft Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Ordys, A.; Uduehi, D.; Johnson, M.A. Process Control Performance Assessment—From Theory to Implementation; Springer: London, UK, 2007. [Google Scholar]
- Ribeiro, R.N.; Muniz, E.S.; Metha, R.; Park, S.W. Economic evaluation of advanced process control projects. Rev. O Pap. 2013, 74, 57–65. [Google Scholar]
- Domański, P.D. Control Performance Assessment: Theoretical Analyses and Industrial Practice; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Tatjewski, P. Disturbance modeling and state estimation for offset-free predictive control with state-space process models. Int. J. Appl. Math. Comput. Sci. 2014, 24, 313–323. [Google Scholar] [CrossRef]
- Tatjewski, P. Advanced Control of Industrial Processes, Structures and Algorithms; Springer: London, UK, 2007. [Google Scholar]
- Tatjewski, P. Supervisory predictive control and on-line set-point optimization. Int. J. Appl. Math. Comput. Sci. 2010, 20, 483–495. [Google Scholar] [CrossRef]
- Yang, X.; Maciejowski, J.M. Fault tolerant control using Gaussian processes and model predictive control. Int. J. Appl. Math. Comput. Sci. 2015, 25, 133–148. [Google Scholar] [CrossRef]
- Domański, P.D. Optimization Projects in Industry—Much ado about nothing. In Proceedings of the VIII National Conference on Evolutionary Algorithms and Global Optimization KAEiOG, Korbielów, Poland; Warsaw University of Technology Press: Warsaw, Poland, 2005; pp. 45–54. [Google Scholar]
- Maciejowski, J.M. Predictive Control with Constraints; Prentice Hall: Harlow, UK, 2002. [Google Scholar]
- Kalman, R.E. Contribution to the theory of optimal control. Bol. Soc. Math. Mex. 1960, 5, 102–119. [Google Scholar]
- Richalet, J.; Rault, A.; Testud, J.; Papon, J. Model algorithmic control of industrial processes. IFAC Proc. Vol. 1977, 10, 103–120. [Google Scholar] [CrossRef]
- Cutler, C.R.; Ramaker, B. Dynamic matrix control—A computer control algorithm. In Proceedings of the AIChE National Meeting, Houston, TX, USA, 1–5 April 1979. [Google Scholar]
- Clarke, W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Clarke, W.; Mohtadi, C.; Tuffs, P.S. Generalized predictive control—II. Extensions and interpretations. Automatica 1987, 23, 149–160. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: London, UK, 1999. [Google Scholar]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control. Autom. Syst. 2011, 9, 415. [Google Scholar] [CrossRef]
- Forbes, M.G.; Patwardhan, R.S.; Hamadah, H.; Gopaluni, R.B. Model Predictive Control in Industry: Challenges and Opportunities. IFAC-PapersOnLine 2015, 48, 531–538. [Google Scholar] [CrossRef]
- Zanoli, S.M.; Cocchioni, F.; Pepe, C. MPC-based energy efficiency improvement in a pusher type billets reheating furnace. Adv. Sci. Technol. Eng. Syst. J. 2018, 3, 74–84. [Google Scholar] [CrossRef]
- Stentoft, P.; Munk-Nielsen, T.; Møller, J.; Madsen, H.; Vezzaro, L.; Mikkelsen, P.; Vangsgaard, A. Green MPC—An approach towards predictive control for minimimal environmental impact of activated sludge processes. In Proceedings of the 10th IWA Symposium on Modelling and Integrated Assessment, Copenhagen, Denmark, 1–4 September 2019. [Google Scholar]
- Cychowski, M. Explicit Nonlinear Model Predictive Control, Theory and Applications; VDM Verlag Dr. Mueller: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Khaled, N.; Pattel, B. Practical Design and Application of Model Predictive Control; Butterworth-Heinemann: Cambridge, MA, USA, 2018. [Google Scholar]
- Guo, J.; Luo, Y.; Li, K. Adaptive neural-network sliding mode cascade architecture of longitudinal tracking control for unmanned vehicles. Nonlinear Dyn. 2017, 87, 2497–2510. [Google Scholar] [CrossRef]
- Sawulski, J.; Ławryńczuk, M. Optimization of control strategy for a low fuel consumption vehicle engine. Inf. Sci. 2019, 493, 192–216. [Google Scholar] [CrossRef]
- Sardarmehni, T.; Rahmani, R.; Menhaj, M.B. Robust control of wheel slip in anti-lock brake system of automobiles. Nonlinear Dyn. 2014, 76, 125–138. [Google Scholar] [CrossRef]
- Takács, G.; Batista, G.; Gulan, M.; Rohal’-Ilkiv, B. Embedded explicit model predictive vibration control. Mechatronics 2016, 36, 54–62. [Google Scholar]
- Xu, F.; Chen, H.; Gong, X. Fast nonlinear Model Predictive Control on FPGA using particle swarm optimization. IEEE Trans. Ind. Electron. 2016, 63, 310–321. [Google Scholar] [CrossRef]
- Zhu, B. Nonlinear adaptive neural network control for a model-scaled unmanned helicopter. Nonlinear Dyn. 2014, 78, 1695–1708. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Dötlinger, A.; Kennel, R.M. Near time-optimal model predictive control using an L1-norm based cost functional. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 3504–3511. [Google Scholar]
- Bemporad, A.; Borrelli, F.; Morari, M. Model predictive control based on linear programming—The explicit solution. IEEE Trans. Autom. Control 2002, 47, 1974–1985. [Google Scholar] [CrossRef]
- Gallieri, M. ℓasso-MPC—Predictive Control with ℓ1-Regularised Least Squares; Springer Theses, Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Arabas, J.; Białobrzeski, L.; Chomiak, T.; Domański, P.D.; Świrski, K.; Neelakantan, R. Pulverized Coal Fired Boiler Optimization and NOx Control using Neural Networks and Fuzzy Logic. In Proceedings of the AspenWorld’97, Boston, MA, USA, 12–16 October 1997. [Google Scholar]
- Ławryńczuk, M. Practical nonlinear predictive control algorithms for neural Wiener models. J. Process Control 2013, 23, 696–714. [Google Scholar] [CrossRef]
- Ławryńczuk, M. Computationally Efficient Model Predictive Control Algorithms: A Neural Network Approach; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2014; Volume 3. [Google Scholar]
- Ławryńczuk, M. Nonlinear State–Space Predictive Control with On–Line Linearisation and State Estimation. Int. J. Appl. Math. Comput. Sci. 2015, 25, 833–847. [Google Scholar] [CrossRef]
- Lahiri, S.K. Multivariable Predictive Control: Applications in Industry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cutler, C.R.; Ramaker, B.L. Dynamic matrix control—A computer control algorithm. Jt. Autom. Control Conf. 1980, 17, 72. [Google Scholar]
- Prett, D.M.; Gillette, R.D. Optimization and constrained multivariable control of a catalytic cracking unit. Jt. Autom. Control Conf. 1980, 17, 73. [Google Scholar]
- Cutler, C.R.; Haydel, J.J.; Moshedi, A.M. An Industrial Perspective on Advanced Control. In Proceedings of the AIChE Diamond Jubilee Meeting, Washington, DC, USA, 4 November 1983. [Google Scholar]
- Plamowski, S. Implementation of DMC algorithm in embedded controller—Resources, memory and numerical modifications. In Trends in Advanced Intelligent Control, Optimization and Automation; Mitkowski, W., Kacprzyk, J., Oprzędkiewicz, K., Skruch, P., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 335–343. [Google Scholar]
- Xu, J.; Pan, X.; Li, Y.; Wang, G.; Martinez, R. An improved generalized predictive control algorithm based on the difference equation CARIMA model for the SISO system with known strong interference. J. Differ. Equ. Appl. 2019, 25, 1255–1269. [Google Scholar] [CrossRef]
- Solís-Chaves, J.S.; Rodrigues, L.L.; Rocha-Osorio, C.M.; Sguarezi Filho, A.J. A Long-Range Generalized Predictive Control Algorithm for a DFIG Based Wind Energy System. IEEE/CAA J. Autom. Sin. 2019, 6, 1209. [Google Scholar] [CrossRef]
- Rodríguez, M.; Pérez, D. First principles model based control. In European Symposium on Computer-Aided Process Engineering-15, 38th European Symposium of the Working Party on Computer Aided Process Engineering; Puigjaner, L., Espuña, A., Eds.; Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume 20, pp. 1285–1290. [Google Scholar]
- Zhang, Z.; Wu, Z.; Rincon, D.; Christofides, P.D. Real-Time Optimization and Control of Nonlinear Processes Using Machine Learning. Mathematics 2019, 7, 890. [Google Scholar] [CrossRef]
- Gabor, J.; Pakulski, D.; Domański, P.D.; Świrski, K. Closed loop NOx control and optimization using neural networks. In Proceedings of the IFAC Symposium on Power Plants and Power Systems Control, Brussels, Belgium, 26–29 April 2000; pp. 188–196. [Google Scholar]
- Afram, A.; Janabi-Sharifi, F.; Fung, A.S.; Raahemifar, K. Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy Build. 2017, 141, 96–113. [Google Scholar] [CrossRef]
- Patwardhan, R.S.; Lakshminarayanan, S.; Shah, S.L. Constrained nonlinear MPC using hammerstein and wiener models: PLS framework. AIChE J. 1998, 44, 1611–1622. [Google Scholar] [CrossRef]
- Espinosa, J.J.; Vandewalle, J. Predictive Control Using Fuzzy Models. In Advances in Soft Computing; Roy, R., Furuhashi, T., Chawdhry, P.K., Eds.; Springer: London, UK, 1999; pp. 187–200. [Google Scholar]
- Huang, Y.; Lou, H.H.; Gong, J.P.; Edgar, T.F. Fuzzy model predictive control. IEEE Trans. Fuzzy Syst. 2000, 8, 665–678. [Google Scholar]
- Schultz, P.; Golenia, Z.; Grott, J.; Domański, P.D.; Świrski, K. Advanced Emission Control. In Proceedings of the Power GEN Europe 2000 Conference, Helsinki, Finland, 20–22 June 2000; pp. 171–178. [Google Scholar]
- Subathra, B.; Seshadhri, S.; Radhakrishnan, T. A comparative study of neuro fuzzy and recurrent neuro fuzzy model-based controllers for real-time industrial processes. Syst. Sci. Control Eng. 2015, 3, 412–426. [Google Scholar] [CrossRef]
- Jain, A.; Nghiem, T.; Morari, M.; Mangharam, R. Learning and Control Using Gaussian Processes. In Proceedings of the 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), Porto, Portugal, 11–13 April 2018; pp. 140–149. [Google Scholar]
- Hewing, L.; Kabzan, J.; Zeilinger, M.N. Cautious Model Predictive Control Using Gaussian Process Regression. IEEE Trans. Control Syst. Technol. 2019, 1–8. [Google Scholar] [CrossRef]
- Jain, A.; Smarra, F.; Behl, M.; Mangharam, R. Data-Driven Model Predictive Control with Regression Trees—An Application to Building Energy Management. ACM Trans. Cyber-Phys. Syst. 2018, 2, 1–21. [Google Scholar] [CrossRef]
- Smarra, F.; Di Girolamo, G.D.; De Iuliis, V.; Jain, A.; Mangharam, R.; D’Innocenzo, A. Data-driven switching modeling for MPC using Regression Trees and Random Forests. Nonlinear Anal. Hybrid Syst. 2020, 36, 100882. [Google Scholar] [CrossRef]
- Ernst, D.; Glavic, M.; Capitanescu, F.; Wehenkel, L. Reinforcement Learning Versus Model Predictive Control: A Comparison on a Power System Problem. IEEE Trans. Syst. Man, Cybern. Part B (Cybern.) 2009, 39, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Smuts, J.F.; Hussey, A. Requirements for Successfully Implementing and Sustaining Advanced Control Applications. In Proceedings of the 54th ISA POWID Symposium, Charlotte, NC, USA, 6–8 June 2011; pp. 89–105. [Google Scholar]
- Domański, P.D.; Leppakoski, J. Advanced Process Control Implementation of Boiler Optimization driven by Future Power Market Challenges. In Proceedings of the Pennwell Conference Coal-GEN Europe 2012, Warsaw, Poland, 14–16 February 2012. [Google Scholar]
- Jelali, M. Control Performance Management in Industrial Automation: Assessment, Diagnosis and Improvement of Control Loop Performance; Springer: London, UK, 2013. [Google Scholar]
- Starr, K.D.; Petersen, H.; Bauer, M. Control loop performance monitoring—ABB’s experience over two decades. IFAC-PapersOnLine 2016, 49, 526–532. [Google Scholar] [CrossRef]
- Bauer, M.; Horch, A.; Xie, L.; Jelali, M.; Thornhill, N. The current state of control loop performance monitoring—A survey of application in industry. J. Process Control 2016, 38, 1–10. [Google Scholar] [CrossRef]
- Åström, K.J. Computer control of a paper machine—An application of linear stochastic control theory. IBM J. 1967, 11, 389–405. [Google Scholar] [CrossRef]
- Shardt, Y.; Zhao, Y.; Qi, F.; Lee, K.; Yu, X.; Huang, B.; Shah, S. Determining the state of a process control system: Current trends and future challenges. Can. J. Chem. Eng. 2012, 90, 217–245. [Google Scholar] [CrossRef]
- O’Neill, Z.; Li, Y.; Williams, K. HVAC control loop performance assessment: A critical review (1587-RP). Sci. Technol. Built Environ. 2017, 23, 619–636. [Google Scholar] [CrossRef]
- Spinner, T.; Srinivasan, B.; Rengaswamy, R. Data-based automated diagnosis and iterative retuning of proportional-integral (PI) controllers. Control Eng. Pract. 2014, 29, 23–41. [Google Scholar]
- Hägglund, T. Automatic detection of sluggish control loops. Control Eng. Pract. 1999, 7, 1505–1511. [Google Scholar]
- Visioli, A. Method for Proportional-Integral Controller Tuning Assessment. Ind. Eng. Chem. Res. 2006, 45, 2741–2747. [Google Scholar]
- Salsbury, T.I. A practical method for assessing the performance of control loops subject to random load changes. J. Process Control 2005, 15, 393–405. [Google Scholar]
- Harris, T.J. Assessment of closed loop performance. Can. J. Chem. Eng. 1989, 67, 856–861. [Google Scholar]
- Grimble, M.J. Controller performance benchmarking and tuning using generalised minimum variance control. Automatica 2002, 38, 2111–2119. [Google Scholar]
- Harris, T.J.; Seppala, C.T. Recent Developments in Controller Performance Monitoring and Assessment Techniques. In Proceedings of the Sixth International Conference on Chemical Process Control, Tucson, AZ, USA, 7–12 January 2001; pp. 199–207. [Google Scholar]
- Meng, Q.W.; Gu, J.Q.; Zhong, Z.F.; Ch, S.; Niu, Y.G. Control performance assessment and improvement with a new performance index. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 4081–4084. [Google Scholar]
- Salsbury, T.I. Continuous-time model identification for closed loop control performance assessment. Control Eng. Pract. 2007, 15, 109–121. [Google Scholar]
- Schlegel, M.; Skarda, R.; Cech, M. Running discrete Fourier transform and its applications in control loop performance assessment. In Proceedings of the 2013 International Conference on Process Control (PC), Strbske Pleso, Slovakia, 18–21 June 2013; pp. 113–118. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. A flexible MATLAB tool for optimal fractional-order PID controller design subject to specifications. In Proceedings of the 2012 31st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2012. [Google Scholar]
- Alagoz, B.B.; Tan, N.; Deniz, F.N.; Keles, C. Implicit disturbance rejection performance analysis of closed loop control systems according to communication channel limitations. IET Control Theory Appl. 2015, 9, 2522–2531. [Google Scholar]
- Yuan, H. Process Analysis and Performance Assessment for Sheet Forming Processes. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2015. [Google Scholar]
- Zhou, Y.; Wan, F. A neural network approach to control performance assessment. Int. J. Intell. Comput. Cybern. 2008, 1, 617–633. [Google Scholar]
- Pillay, N.; Govender, P. Multi-Class SVMs for Automatic Performance Classification of Closed Loop Controllers. J. Control Eng. Appl. Inform. 2017, 19, 3–12. [Google Scholar]
- Shinskey, F.G. How Good are Our Controllers in Absolute Performance and Robustness? Meas. Control 1990, 23, 114–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Xie, W.; Tu, X. Performance-based parameter tuning method of model-driven PID control systems. ISA Trans. 2012, 51, 393–399. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B. Analysis and Auto-Tuning of Supply Air Temperature PI Control in Hot Water Heating Systems. Ph.D. Thesis, University of Nebraska, Lincoln, NE, USA, 2007. [Google Scholar]
- Yu, Z.; Wang, J. Performance assessment of static lead-lag feedforward controllers for disturbance rejection in PID control loops. ISA Trans. 2016, 64, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Horch, A. A simple method for detection of stiction in control valves. Control Eng. Pract. 1999, 7, 1221–1231. [Google Scholar] [CrossRef]
- Howard, R.; Cooper, D. A novel pattern-based approach for diagnostic controller performance monitoring. Control Eng. Pract. 2010, 18, 279–288. [Google Scholar] [CrossRef]
- Choudhury, M.A.A.S.; Shah, S.L.; Thornhill, N.F. Diagnosis of poor control-loop performance using higher-order statistics. Automatica 2004, 40, 1719–1728. [Google Scholar] [CrossRef]
- Li, Y.; O’Neill, Z. Evaluating control performance on building HVAC controllers. In Proceedings of the BS2015—14th Conference ofInternational Building Performance Simulation Association, Hyderabad, India, 7–9 December 2015; pp. 962–967. [Google Scholar]
- Zhong, L. Defect distribution model validation and effective process control. Proc. SPIE 2003, 5041, 31–38. [Google Scholar]
- Domański, P.D. Non-Gaussian Statistical Measures of Control Performance. Control Cybern. 2017, 46, 259–290. [Google Scholar]
- Domański, P.D.; Golonka, S.; Marusak, P.M.; Moszowski, B. Robust and Asymmetric Assessment of the Benefits from Improved Control—Industrial Validation. IFAC-PapersOnLine 2018, 51, 815–820. [Google Scholar] [CrossRef]
- Hadjiiski, M.; Georgiev, Z. Benchmarking of Process Control Performance. In Problems of Engineering, Cybernetics and Robotics; Bulgarian Academy of Sciences: Sofia, Bulgaria, 2005; Volume 55, pp. 103–110. [Google Scholar]
- Nesic, Z.; Dumont, G.; Davies, M.; Brewster, D. CD Control Diagnostics Using a Wavelet Toolbox. In Proceedings of the CD Symposium, IMEKO, Tampere, Finland, 1–6 June 1997; Volume XB, pp. 120–125. [Google Scholar]
- Lynch, C.B.; Dumont, G.A. Control loop performance monitoring. IEEE Trans. Control Syst. Technol. 1996, 4, 185–192. [Google Scholar] [CrossRef]
- Pillay, N.; Govender, P. A Data Driven Approach to Performance Assessment of PID Controllers for Setpoint Tracking. Procedia Eng. 2014, 69, 1130–1137. [Google Scholar] [CrossRef]
- Domański, P.D. Non-Gaussian and persistence measures for control loop quality assessment. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 043105. [Google Scholar] [CrossRef] [PubMed]
- Domański, P.D. Control quality assessment using fractal persistence measures. ISA Trans. 2019, 90, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Jiang, M.; Chen, J. Minimum entropy-based performance assessment of feedback control loops subjected to non-Gaussian disturbances. J. Process Control 2015, 24, 1660–1670. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, Y.; Jiang, H.; Fan, S. Non-Gaussian Systems Control Performance Assessment Based on Rational Entropy. Entropy 2018, 20, 331. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Lee, F.; Chen, Q.; Sun, Z. Improved Renyi Entropy Benchmark for Performance Assessment of Common Cascade Control System. IEEE Access 2019, 7, 6796–6803. [Google Scholar] [CrossRef]
- Domański, P.D.; Gintrowski, M. Alternative approaches to the prediction of electricity prices. Int. J. Energy Sect. Manag. 2017, 11, 3–27. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Y.Q.; Domański, P.D.; Zhang, X. A Novel Method for Control Performance Assessment with Fractional Order Signal Processing and Its Application to Semiconductor Manufacturing. Algorithms 2018, 11, 90. [Google Scholar] [CrossRef]
- Liu, K.; Chen, Y.; Domański, P.D. Control Performance Assessment of the Disturbance with Fractional Order Dynamics. In Nonlinear Dynamics and Control; Lacarbonara, W., Balachandran, B., Ma, J., Tenreiro Machado, J.A., Stepan, G., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 255–264. [Google Scholar]
- Khamseh, S.A.; Sedigh, A.K.; Moshiri, B.; Fatehi, A. Control performance assessment based on sensor fusion techniques. Control Eng. Pract. 2016, 49, 14–28. [Google Scholar] [CrossRef]
- Salsbury, T.I.; Alcala, C.F. Two new normalized EWMA-based indices for control loop performance assessment. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 962–967. [Google Scholar]
- Dziuba, K.; Góra, R.; Domański, P.D.; Ławryńczuk, M. Multicriteria control quality assessment for ammonia production process (in Polish). In 1st Scientific and Technical Conference Innovations in the Chemical Industry; Zalewska, A., Ed.; Polish Chamber of Chemical Industry: Warsaw, Poland, 2018; pp. 80–90. [Google Scholar]
- Domański, P.D.; Ławryńczuk, M.; Golonka, S.; Moszowski, B.; Matyja, P. Multi-criteria Loop Quality Assessment: A Large-Scale Industrial Case Study. In Proceedings of the IEEE International Conference on Methods and Models in Automation and Robotics MMAR, Międzyzdroje, Poland, 26–29 August 2019; pp. 99–104. [Google Scholar]
- Knierim-Dietz, N.; Hanel, L.; Lehner, J. Definition and Verification of the Control Loop Performance for Different Power Plant Types; Technical Report; Institute of Combustion and Power Plant Technology, University of Stutgart: Stutgart, Germany, 2012. [Google Scholar]
- Hugo, A. Performance assessment of DMC controllers. In Proceedings of the 1999 American Control Conference, San Diego, CA, USA, 2–4 June 1999; Volume 4, pp. 2640–2641. [Google Scholar]
- Julien, R.H.; Foley, M.W.; Cluett, W.R. Performance assessment using a model predictive control benchmark. J. Process Control 2004, 14, 441–456. [Google Scholar] [CrossRef]
- Sotomayor, O.A.Z.; Odloak, D. Performance Assessment of Model Predictive Control Systems. IFAC Proc. Vol. 2006, 39, 875–880. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, Y.; Su, H.; Huang, B. Economic performance assessment of advanced process control with LQG benchmarking. J. Process Control 2009, 19, 557–569. [Google Scholar] [CrossRef]
- Zhao, C.; Su, H.; Gu, Y.; Chu, J. A Pragmatic Approach for Assessing the Economic Performance of Model Predictive Control Systems and Its Industrial Application. Chin. J. Chem. Eng. 2009, 17, 241–250. [Google Scholar] [CrossRef]
- Ko, B.S.; Edgar, T.F. Performance assessment of multivariable feedback control systems. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, USA, 28–30 June 2000; Volume 6, pp. 4373–4377. [Google Scholar]
- Ko, B.S.; Edgar, T.F. Performance assessment of constrained model predictive control systems. AIChE J. 2001, 47, 1363–1371. [Google Scholar] [CrossRef]
- Shah, S.L.; Patwardhan, R.; Huang, B. Multivariate Controller Performance Analysis: Methods, Applications and Challenges. In Proceedings of the Sixth International Conference on Chemical Process Control, Tucson, AZ, USA, 7–12 January 2001; pp. 199–207. [Google Scholar]
- Xu, F.; Huang, B.; Tamayo, E.C. Assessment of Economic Performance of Model Predictive Control through Variance/Constraint Tuning. IFAC Proc. Vol. 2006, 39, 899–904. [Google Scholar] [CrossRef]
- Yuan, Q.; Lennox, B. The Investigation of Multivariable Control Performance Assessment Techniques. In Proceedings of the UKACC International Conference on Control 2008, Cardiff, UK, 3–5 September 2008. [Google Scholar]
- Harrison, C.A.; Qin, S.J. Minimum variance performance map for constrained model predictive control. J. Process Control 2009, 19, 1199–1204. [Google Scholar] [CrossRef]
- Pour, N.D.; Huang, B.; Shah, S. Performance assessment of advanced supervisory-regulatory control systems with subspace LQG benchmark. Automatica 2010, 46, 1363–1368. [Google Scholar] [CrossRef]
- Sun, Z.; Qin, S.J.; Singhal, A.; Megan, L. Control performance monitoring via model residual assessment. In Proceedings of the 2012 American Control Conference (ACC), Montréal, QC, Canada, 27–29 June 2012; pp. 2800–2805. [Google Scholar]
- Borrero-Salazar, A.A.; Cardenas-Cabrera, J.; Barros-Gutierrez, D.A.; Jiménez-Cabas, J. A comparison study of MPC strategies based on minimum variance control index performance. Rev. ESPACIOS 2019, 40, 12–38. [Google Scholar]
- Xu, F.; Huang, B.; Akande, S. Performance Assessment of Model Pedictive Control for Variability and Constraint Tuning. Ind. Eng. Chem. Res. 2007, 46, 1208–1219. [Google Scholar] [CrossRef]
- Wei, W.; Zhuo, H. Research of performance assessment and monitoring for multivariate model predictive control system. In Proceedings of the 2009 4th International Conference on Computer Science Education, Nanning, China, 25–28 July 2009; pp. 509–514. [Google Scholar]
- Huang, B.; Shah, S.L.; Kwok, E.K. On-line control performance monitoring of MIMO processes. In Proceedings of the 1995 American Control Conference, Seattle, WA, USA, 21–23 June 1995; Volume 2, pp. 1250–1254. [Google Scholar]
- Zhang, R.; Zhang, Q. Model predictive control performance assessment using a prediction error benchmark. In Proceedings of the 2011 International Symposium on Advanced Control of Industrial Processes (ADCONIP), Hangzhou, China, 23–26 May 2011; pp. 571–574. [Google Scholar]
- Patwardhan, R.S.; Shah, S.L. Issues in performance diagnostics of model-based controllers. J. Process Control 2002, 12, 413–427. [Google Scholar] [CrossRef]
- Schäfer, J.; Cinar, A. Multivariable MPC system performance assessment, monitoring, and diagnosis. J. Process Control 2004, 14, 113–129. [Google Scholar] [CrossRef]
- Loquasto, F.; Seborg, D.E. Monitoring Model Predictive Control Systems Using Pattern Classification and Neural Networks. Ind. Eng. Chem. Res. 2003, 42, 4689–4701. [Google Scholar] [CrossRef]
- Agarwal, N.; Huang, B.; Tamayo, E.C. Assessing Model Prediction Control (MPC) Performance. 1. Probabilistic Approach for Constraint Analysis. Ind. Eng. Chem. Res. 2007, 46, 8101–8111. [Google Scholar] [CrossRef]
- Agarwal, N.; Huang, B.; Tamayo, E.C. Assessing Model Prediction Control (MPC) Performance. 2. Bayesian Approach for Constraint Tuning. Ind. Eng. Chem. Res. 2007, 46, 8112–8119. [Google Scholar] [CrossRef]
- Kesavan, P.; Lee, J.H. Diagnostic Tools for Multivariable Model-Based Control Systems. Ind. Eng. Chem. Res. 1997, 36, 2725–2738. [Google Scholar] [CrossRef]
- Kesavan, P.; Lee, J.H. A set based approach to detection and isolation of faults in multivariable systems. Comput. Chem. Eng. 2001, 25, 925–940. [Google Scholar] [CrossRef]
- Harrison, C.A.; Qin, S.J. Discriminating between disturbance and process model mismatch in model predictive control. J. Process Control 2009, 19, 1610–1616. [Google Scholar] [CrossRef]
- Badwe, A.S.; Gudi, R.D.; Patwardhan, R.S.; Shah, S.L.; Patwardhan, S.C. Detection of model-plant mismatch in MPC applications. J. Process Control 2009, 19, 1305–1313. [Google Scholar] [CrossRef]
- Sun, Z.; Qin, S.J.; Singhal, A.; Megan, L. Performance monitoring of model-predictive controllers via model residual assessment. J. Process Control 2013, 23, 473–482. [Google Scholar] [CrossRef]
- Chen, J. Statistical Methods for Process Monitoring and Control. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 2014. [Google Scholar]
- Pannocchia, G.; De Luca, A.; Bottai, M. Prediction Error Based Performance Monitoring, Degradation Diagnosis and Remedies in Offset-Free MPC: Theory and Applications. Asian J. Control 2014, 16, 995–1005. [Google Scholar] [CrossRef]
- Zhao, Y.; Chu, J.; Su, H.; Huang, B. Multi-step prediction error approach for controller performance monitoring. Control Eng. Pract. 2010, 18, 1–12. [Google Scholar] [CrossRef]
- Botelho, V.; Trierweiler, J.O.; Farenzena, M.; Duraiski, R. Methodology for Detecting Model–Plant Mismatches Affecting Model Predictive Control Performance. Ind. Eng. Chem. Res. 2015, 54, 12072–12085. [Google Scholar] [CrossRef]
- Botelho, V.; Trierweiler, J.O.; Farenzena, M.; Duraiski, R. Perspectives and challenges in performance assessment of model predictive control. Can. J. Chem. Eng. 2016, 94, 1225–1241. [Google Scholar] [CrossRef]
- Lee, K.H.; Huang, B.; Tamayo, E.C. Sensitivity analysis for selective constraint and variability tuning in performance assessment of industrial MPC. Control Eng. Pract. 2008, 16, 1195–1215. [Google Scholar] [CrossRef]
- Godoy, J.L.; Ferramosca, A.; González, A.H. Economic performance assessment and monitoring in LP-DMC type controller applications. J. Process Control 2017, 57, 26–37. [Google Scholar] [CrossRef]
- Rodrigues, J.A.D.; Maciel Filho, R. Analysis of the predictive DMC controller performance applied to a feed-batch bioreactor. Braz. J. Chem. Eng. 1997, 14. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, S. Performance Monitoring and Diagnosis of Multivariable Model Predictive Control Using Statistical Analysis. Chin. J. Chem. Eng. 2006, 14, 207–215. [Google Scholar] [CrossRef]
- AlGhazzawi, A.; Lennox, B. Model predictive control monitoring using multivariate statistics. J. Process Control 2009, 19, 314–327. [Google Scholar] [CrossRef]
- Chen, Y.T.; Li, S.Y.; Li, N. Performance analysis on dynamic matrix controller with single prediction strategy. In Proceeding of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 1694–1699. [Google Scholar]
- Khan, M.; Tahiyat, M.; Imtiaz, S.; Choudhury, M.A.A.S.; Khan, F. Experimental evaluation of control performance of MPC as a regulatory controller. ISA Trans. 2017, 70, 512–520. [Google Scholar] [CrossRef]
- Shang, L.Y.; Tian, X.M.; Cao, Y.P.; Cai, L.F. MPC Performance Monitoring and Diagnosis Based on Dissimilarity Analysis of PLS Cross-product Matrix. Acta Autom. Sin. 2017, 43, 271–279. [Google Scholar]
- Shang, L.; Wang, Y.; Deng, X.; Cao, Y.; Wang, P.; Wang, Y. An Enhanced Method to Assess MPC Performance Based on Multi-Step Slow Feature Analysis. Energies 2019, 12, 3799. [Google Scholar] [CrossRef]
- Shang, L.; Wang, Y.; Deng, X.; Cao, Y.; Wang, P.; Wang, Y. A Model Predictive Control Performance Monitoring and Grading Strategy Based on Improved Slow Feature Analysis. IEEE Access 2019, 7, 50897–50911. [Google Scholar] [CrossRef]
- Domański, P.D.; Ławryńczuk, M. Assessment of the GPC Control Quality using Non-Gaussian Statistical Measures. Int. J. Appl. Math. Comput. Sci. 2017, 27, 291–307. [Google Scholar] [CrossRef]
- Domański, P.D.; Ławryńczuk, M. Assessment of Predictive Control Performance using Fractal Measures. Nonlinear Dyn. 2017, 89, 773–790. [Google Scholar] [CrossRef]
- Domański, P.D.; Ławryńczuk, M. Multi-Criteria Control Performance Assessment Method for Multivariate MPC. In Proceedings of the 2020 American Control Conference, Denver, CO, USA, 1–3 July 2020. accepted for publication. [Google Scholar]
- Domański, P.D.; Ławryńczuk, M. Control Quality Assessment of Nonlinear Model Predictive Control Using Fractal and Entropy Measures. In Nonlinear Dynamics and Control; Lacarbonara, W., Balachandran, B., Ma, J., Tenreiro Machado, J.A., Stepan, G., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 147–156. [Google Scholar]
- Xu, Y.; Li, N.; Li, S. A Data-driven performance assessment approach for MPC using improved distance similarity factor. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 1870–1875. [Google Scholar]
- Xu, Y.; Zhang, G.; Li, N.; Zhang, J.; Li, S.; Wang, L. Data-Driven Performance Monitoring for Model Predictive Control Using a mahalanobis distance based overall index. Asian J. Control 2019, 21, 891–907. [Google Scholar] [CrossRef]
- Gao, J.; Patwardhan, R.; Akamatsu, K.; Hashimoto, Y.; Emoto, G.; Shah, S.L.; Huang, B. Performance evaluation of two industrial MPC controllers. Control Eng. Pract. 2003, 11, 1371–1387. [Google Scholar] [CrossRef]
- Jiang, H.; Shah, S.L.; Huang, B.; Wilson, B.; Patwardhan, R.; Szeto, F. Performance Assessment and Model Validation of Two Industrial MPC Controllers. IFAC Proc. Vol. 2008, 41, 8387–8394. [Google Scholar] [CrossRef]
- Claro, É.R.; Botelho, V.; Trierweiler, J.O.; Farenzena, M. Model Performance Assessment of a Predictive Controller for Propylene/Propane Separation. IFAC-PapersOnLine 2016, 49, 978–983. [Google Scholar] [CrossRef]
- Botelho, V.R.; Trierweiler, J.O.; Farenzena, M.; Longhi, L.G.S.; Zanin, A.C.; Teixeira, H.C.G.; Duraiski, R.G. Model assessment of MPCs with control ranges: An industrial application in a delayed coking unit. Control Eng. Pract. 2019, 84, 261–273. [Google Scholar] [CrossRef]
- Domański, P.D. Statistical measures for proportional–integral–derivative control quality: Simulations and industrial data. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2018, 232, 428–441. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domański, P.D. Performance Assessment of Predictive Control—A Survey. Algorithms 2020, 13, 97. https://doi.org/10.3390/a13040097
Domański PD. Performance Assessment of Predictive Control—A Survey. Algorithms. 2020; 13(4):97. https://doi.org/10.3390/a13040097
Chicago/Turabian StyleDomański, Paweł D. 2020. "Performance Assessment of Predictive Control—A Survey" Algorithms 13, no. 4: 97. https://doi.org/10.3390/a13040097
APA StyleDomański, P. D. (2020). Performance Assessment of Predictive Control—A Survey. Algorithms, 13(4), 97. https://doi.org/10.3390/a13040097




