Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models
Abstract
1. Introduction
2. Material and Method
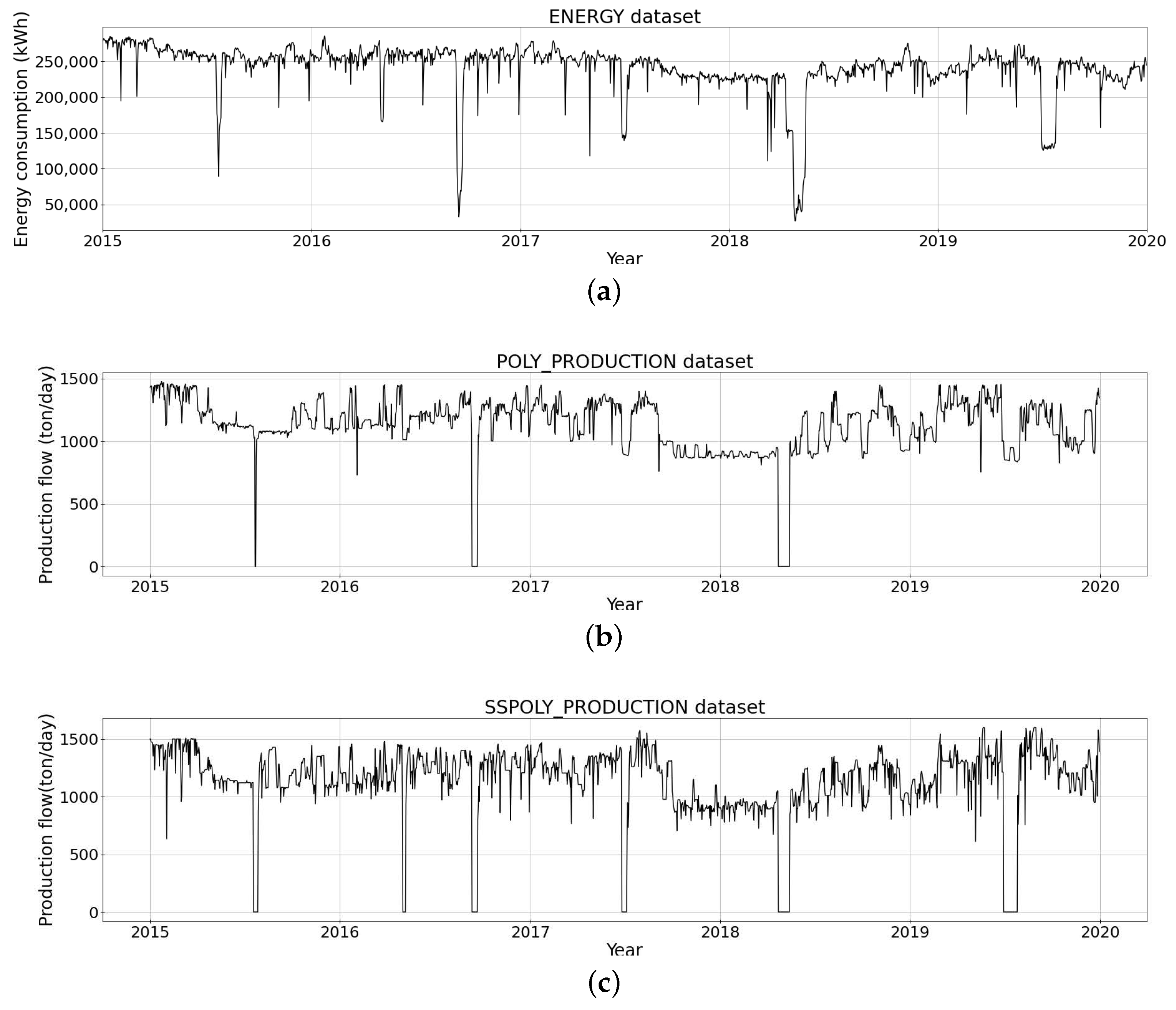
2.1. Dataset
2.2. Data Preprocessing
2.3. Evaluation Metric
3. Finding Models to Predict Energy Consumption
3.1. Deep Learning Models
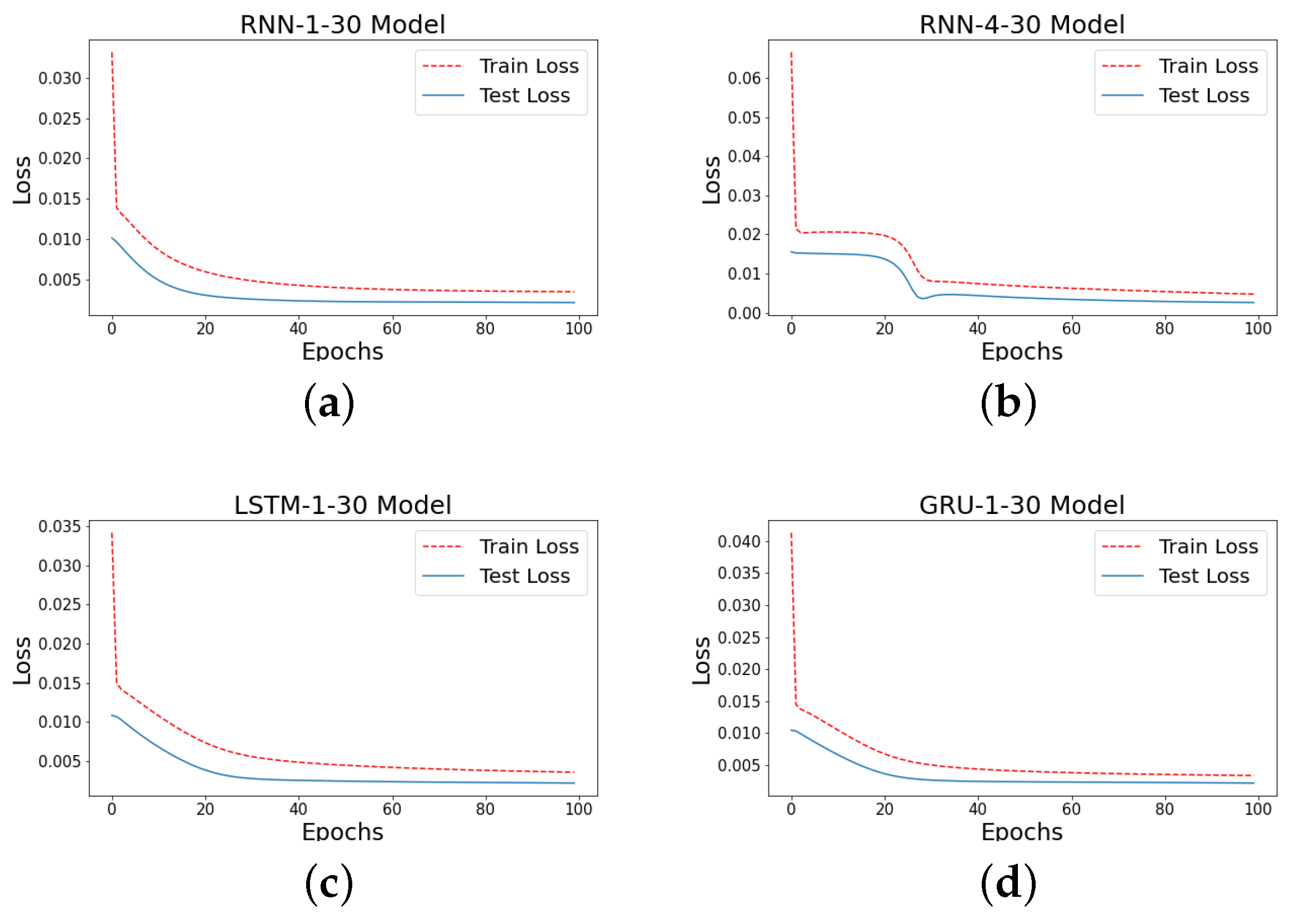
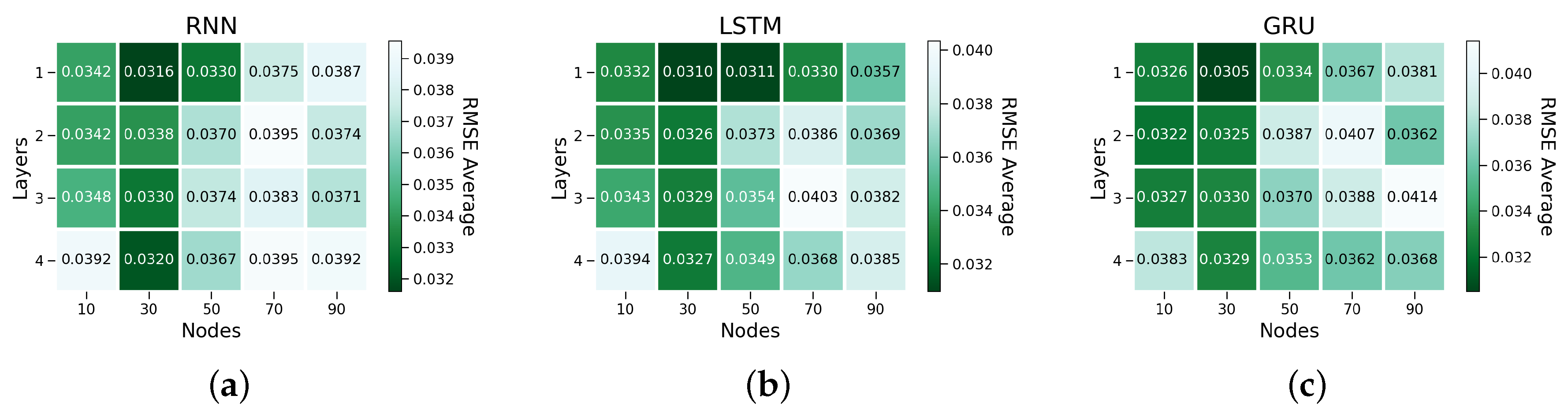
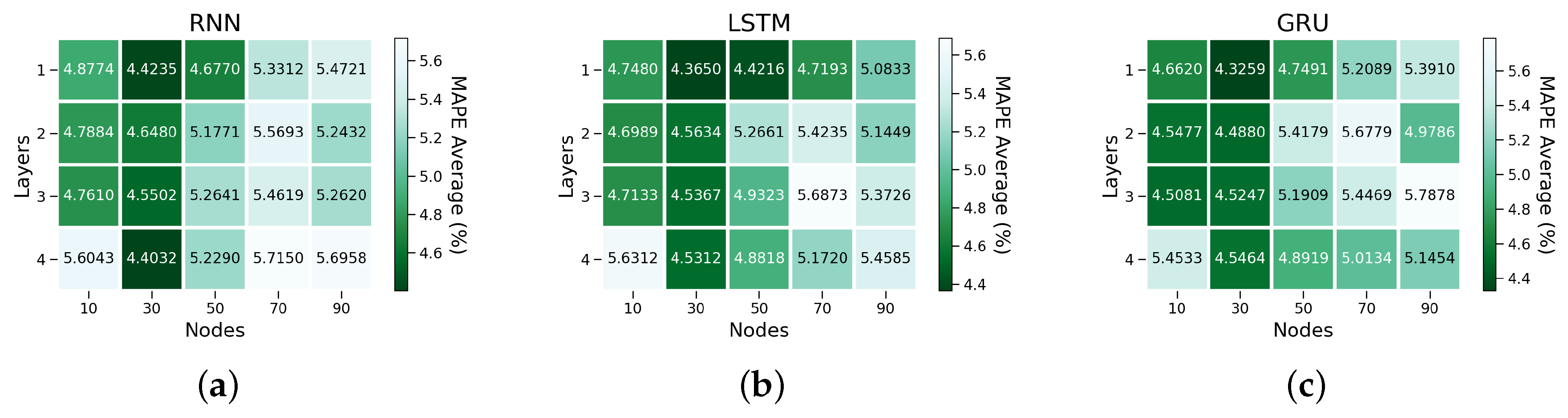
Deep Learning Model Settings
3.2. Machine-Learning Models
Machine-Learning Model Settings
3.3. Benchmarks
4. Results and Discussions
Diebold–Mariano Statistical Test
5. Related Work
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Networks |
| ARIMA | Autoregressive Integrated Moving Average |
| Btu | British Thermal Units |
| CNN | Convolutional Neural Network |
| CO2 | Carbon Dioxide |
| DFNN | Deep Feed Forward Neural Networks |
| DNN | Deep Neural Network |
| DRNN | Deep Recurrent Neural Networks |
| DSHW | Double Seasonal Holt–Winters |
| DT | Decision Tree |
| EAF | Electric Arc Furnace |
| GRU | Gated Recurrent Unit |
| HVAC | Heating, Ventilation, and Air Conditioning |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LR | Linear Regression |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percent Error |
| MLP | Multi-Layer Perceptrons |
| MSE | Mean Squared Error |
| POLY | Polymerization |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Networks |
| RRMSE | Relative Root Mean Square Error |
| SDG | Sustainable Development Goals |
| SNN | Shallow Neural Network |
| SSPOLY | Solid-State Polymerization |
| STLF | Short-Term Load Forecasting |
| SVM | Support Vector Machines |
| SVR | Support Vector Machine Regression |
| TECI | Technical Energy Consumption Index |
| VSTLF | Very Short-Term Load Forecasting |
References
- EIA. International Energy Outlook 2019. Available online: https://www.eia.gov/outlooks/ieo/ (accessed on 24 April 2020).
- EIA. International Energy Outlook 2016 with Projections to 2040; Government Printing Office: Washington, DC, USA, 2016.
- Gozgor, G.; Lau, C.K.M.; Lu, Z. Energy consumption and economic growth: New evidence from the OECD countries. Energy 2018, 153, 27–34. [Google Scholar] [CrossRef]
- SDG. Build Resilient Infrastructure, Promote Inclusive and Sustainable Industrialization and Foster Innovation. Available online: https://sustainabledevelopment.un.org/sdg9 (accessed on 24 April 2020).
- Sundarakani, B.; De Souza, R.; Goh, M.; Wagner, S.M.; Manikandan, S. Modeling carbon footprints across the supply chain. Int. J. Prod. Econ. 2010, 128, 43–50. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2017, 10, 3. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Kumar, M.; Qin, J. Energy consumption modelling using deep learning technique—A case study of EAF. Procedia CIRP 2018, 72, 1063–1068. [Google Scholar] [CrossRef]
- Demirhan, H.; Renwick, Z. Missing value imputation for short to mid-term horizontal solar irradiance data. Appl. Energy 2018, 225, 998–1012. [Google Scholar] [CrossRef]
- Andiojaya, A.; Demirhan, H. A bagging algorithm for the imputation of missing values in time series. Expert Syst. Appl. 2019, 129, 10–26. [Google Scholar] [CrossRef]
- Peppanen, J.; Zhang, X.; Grijalva, S.; Reno, M.J. Handling bad or missing smart meter data through advanced data imputation. In Proceedings of the 2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Azadeh, A.; Ghaderi, S.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Berriel, R.F.; Lopes, A.T.; Rodrigues, A.; Varejao, F.M.; Oliveira-Santos, T. Monthly energy consumption forecast: A deep learning approach. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 4283–4290. [Google Scholar]
- Kuo, P.H.; Huang, C.J. A high precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Debnath, K.B.; Mourshed, M. Forecasting methods in energy planning models. Renew. Sustain. Energy Rev. 2018, 88, 297–325. [Google Scholar] [CrossRef]
- Yeom, K.R.; Choi, H.S. Prediction of Manufacturing Plant’s Electric Power Using Machine Learning. In Proceedings of the 2018 Tenth International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018; pp. 814–816. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Hsieh, T.J.; Hsiao, H.F.; Yeh, W.C. Forecasting stock markets using wavelet transforms and recurrent neural networks: An integrated system based on artificial bee colony algorithm. Appl. Soft Comput. 2011, 11, 2510–2525. [Google Scholar] [CrossRef]
- Kolomvatsos, K.; Papadopoulou, P.; Anagnostopoulos, C.; Hadjiefthymiades, S. A Spatio-Temporal Data Imputation Model for Supporting Analytics at the Edge. In Proceedings of the Conference on e-Business, e-Services and e-Society, Trondheim, Norway, 18–20 September 2019; pp. 138–150. [Google Scholar]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Xiang, F. Short-term Load Forecasting: A Case Study in Chongqing Factories. In Proceedings of the 2019 6th International Conference on Information Science and Control Engineering (ICISCE), Shanghai, China, 20–22 December 2019; pp. 892–897. [Google Scholar]
- Güngör, O.; Akşanlı, B.; Aydoğan, R. Algorithm selection and combining multiple learners for residential energy prediction. Future Gener. Comput. Syst. 2019, 99, 391–400. [Google Scholar] [CrossRef]
- Lago, J.; De Ridder, F.; De Schutter, B. Forecasting spot electricity prices: Deep learning approaches and empirical comparison of traditional algorithms. Appl. Energy 2018, 221, 386–405. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Sundermeyer, M.; Schlüter, R.; Ney, H. LSTM neural networks for language modeling. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association, Oregon, Portland, 9–13 September 2012. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. In Proceedings of the 1999 Ninth International Conference on Artificial Neural Networks ICANN 99. (Conf. Publ. No. 470), Edinburgh, UK, 7–10 September 1999; Volume 2, pp. 850–855. [Google Scholar] [CrossRef]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2342–2350. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Liao, J.M.; Chang, M.J.; Chang, L.M. Prediction of Air-Conditioning Energy Consumption in R&D Building Using Multiple Machine Learning Techniques. Energies 2020, 13, 1847. [Google Scholar]
- Yoon, H.; Kim, Y.; Ha, K.; Lee, S.H.; Kim, G.P. Comparative evaluation of ANN-and SVM-time series models for predicting freshwater-saltwater interface fluctuations. Water 2017, 9, 323. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Modeling and prediction of Turkey’s electricity consumption using Support Vector Regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Samsudin, R.; Shabri, A.; Saad, P. A comparison of time series forecasting using support vector machine and artificial neural network model. J. Appl. Sci. 2010, 10, 950–958. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; pp. 1–5. [Google Scholar]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. In From Natural to Artificial Neural Computation; Mira, J., Sandoval, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory (p. 189); Springer: New York, NY, USA, 1995; Volume 10, p. 978. [Google Scholar]
- Müller, K.R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 8–10 October 1997; pp. 999–1004. [Google Scholar]
- Simon, H. Neural Networks: A Comprehensive Foundation; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 1–6 December 1997; pp. 155–161. [Google Scholar]
- Golkarnarenji, G.; Naebe, M.; Badii, K.; Milani, A.S.; Jazar, R.N.; Khayyam, H. Support vector regression modelling and optimization of energy consumption in carbon fiber production line. Comput. Chem. Eng. 2018, 109, 276–288. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Li, C.; Tao, Y.; Ao, W.; Yang, S.; Bai, Y. Improving forecasting accuracy of daily enterprise electricity consumption using a random forest based on ensemble empirical mode decomposition. Energy 2018, 165, 1220–1227. [Google Scholar] [CrossRef]
- Caruana, R.; Karampatziakis, N.; Yessenalina, A. An empirical evaluation of supervised learning in high dimensions. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 96–103. [Google Scholar]
- Pushp, S. Merging Two Arima Models for Energy Optimization in WSN. arXiv 2010, arXiv:1006.5436. [Google Scholar]
- Diebold, F.X. Comparing predictive accuracy, twenty years later: A personal perspective on the use and abuse of Diebold—Mariano tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]
- Qiu, X.; Ren, Y.; Suganthan, P.N.; Amaratunga, G.A. Empirical mode decomposition based ensemble deep learning for load demand time series forecasting. Appl. Soft Comput. 2017, 54, 246–255. [Google Scholar] [CrossRef]
- Dong, X.; Qian, L.; Huang, L. Short-term load forecasting in smart grid: A combined CNN and K-means clustering approach. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Korea, 13–16 February 2017; pp. 119–125. [Google Scholar]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002858–002865. [Google Scholar]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2017, 9, 5271–5280. [Google Scholar] [CrossRef]
- Xypolytou, E.; Meisel, M.; Sauter, T. Short-term electricity consumption forecast with artificial neural networks—A case study of office buildings. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Petri, I.; Li, H.; Rezgui, Y.; Chunfeng, Y.; Yuce, B.; Jayan, B. Deep learning for household load forecasting—A novel pooling deep RNN. Renew. Sustain. Energy Rev. 2014, 38, 990–1002. [Google Scholar] [CrossRef]
- Olanrewaju, O.A. Predicting Industrial Sector’s Energy Consumption: Application of Support Vector Machine. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macao, China, 15–18 December 2019; pp. 1597–1600. [Google Scholar]
- Hobby, J.D.; Tucci, G.H. Analysis of the residential, commercial and industrial electricity consumption. In Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies (ISGT), Perth, WA, Australia, 13–16 November 2011; pp. 1–7. [Google Scholar]
- Hadera, H.; Labrik, R.; Mäntysaari, J.; Sand, G.; Harjunkoski, I.; Engell, S. Integration of energy-cost optimization and production scheduling using multiparametric programming. Comput. Aided Chem. Eng. 2016, 38, 559–564. [Google Scholar]
- Mawson, V.J.; Hughes, B.R. Deep Learning techniques for energy forecasting and condition monitoring in the manufacturing sector. Energy Build. 2020, 217, 109966. [Google Scholar] [CrossRef]
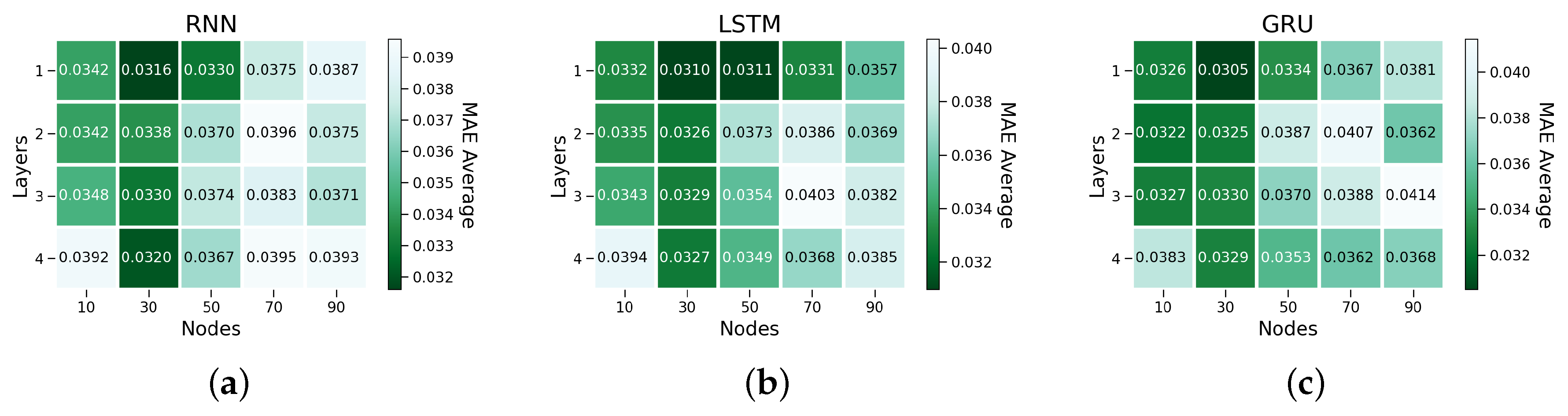
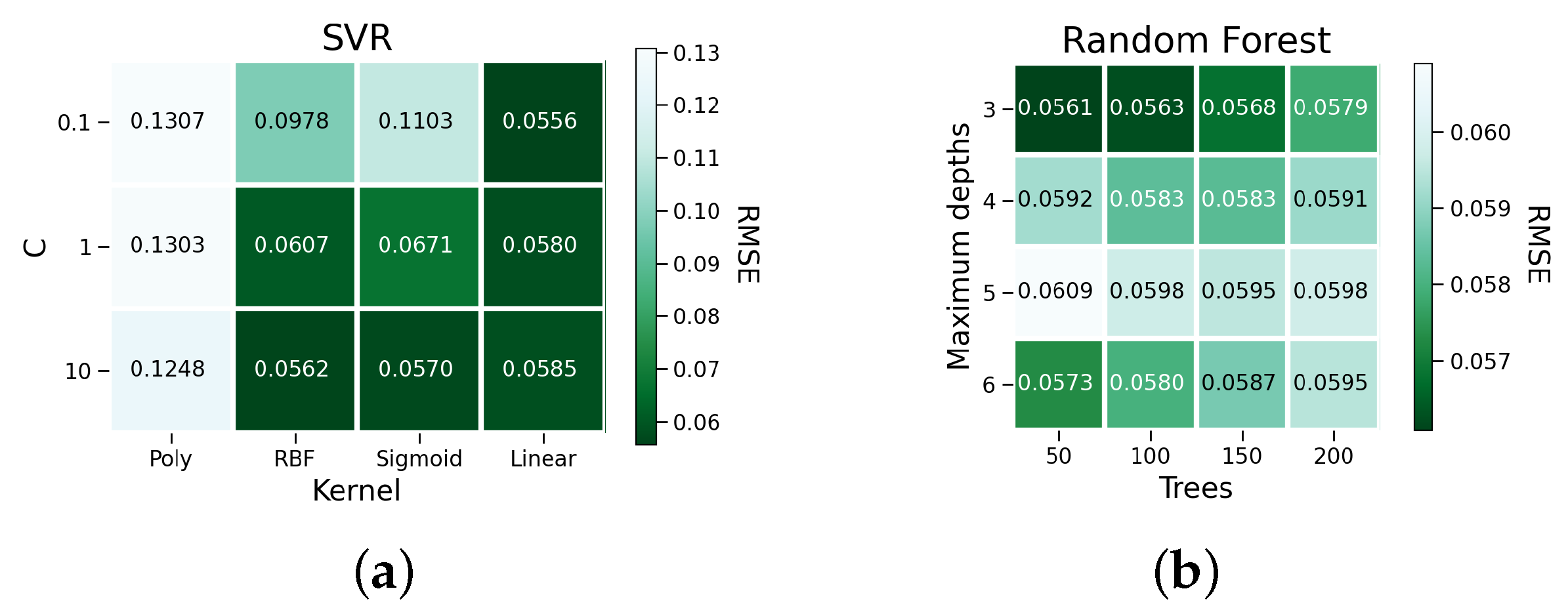
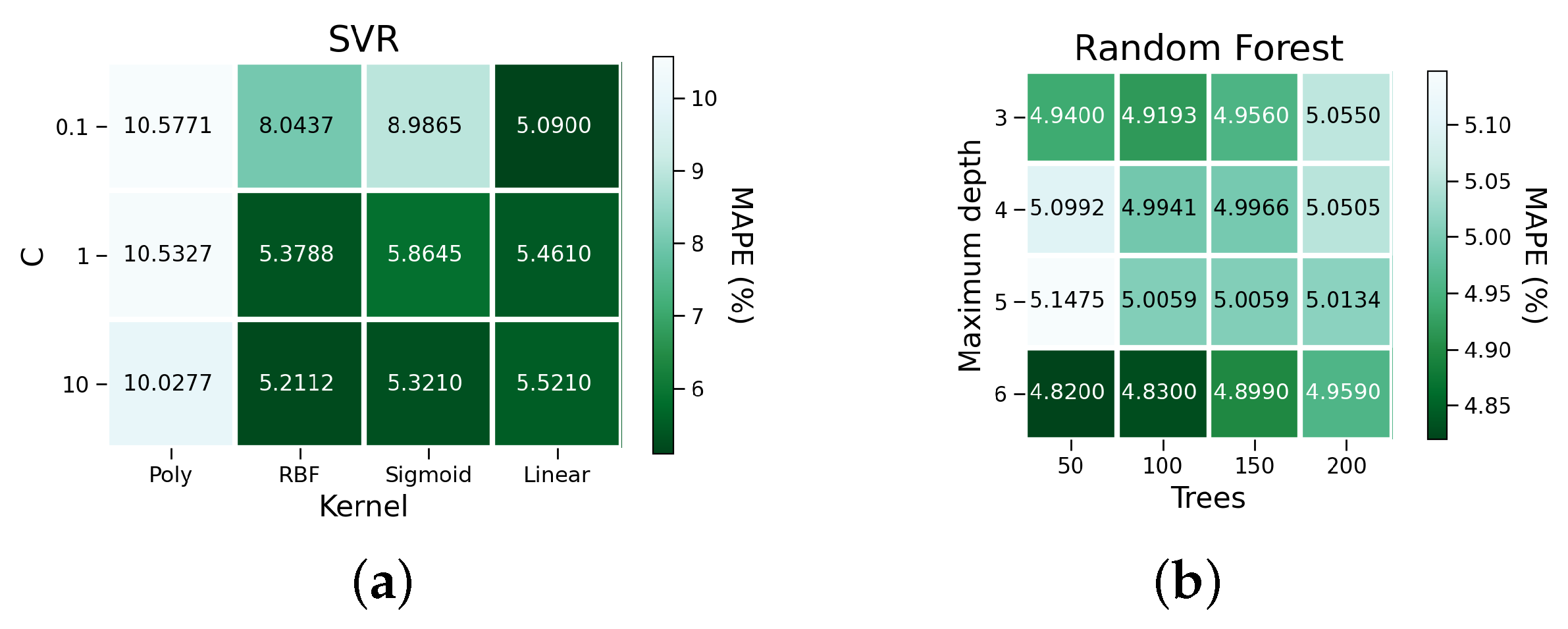
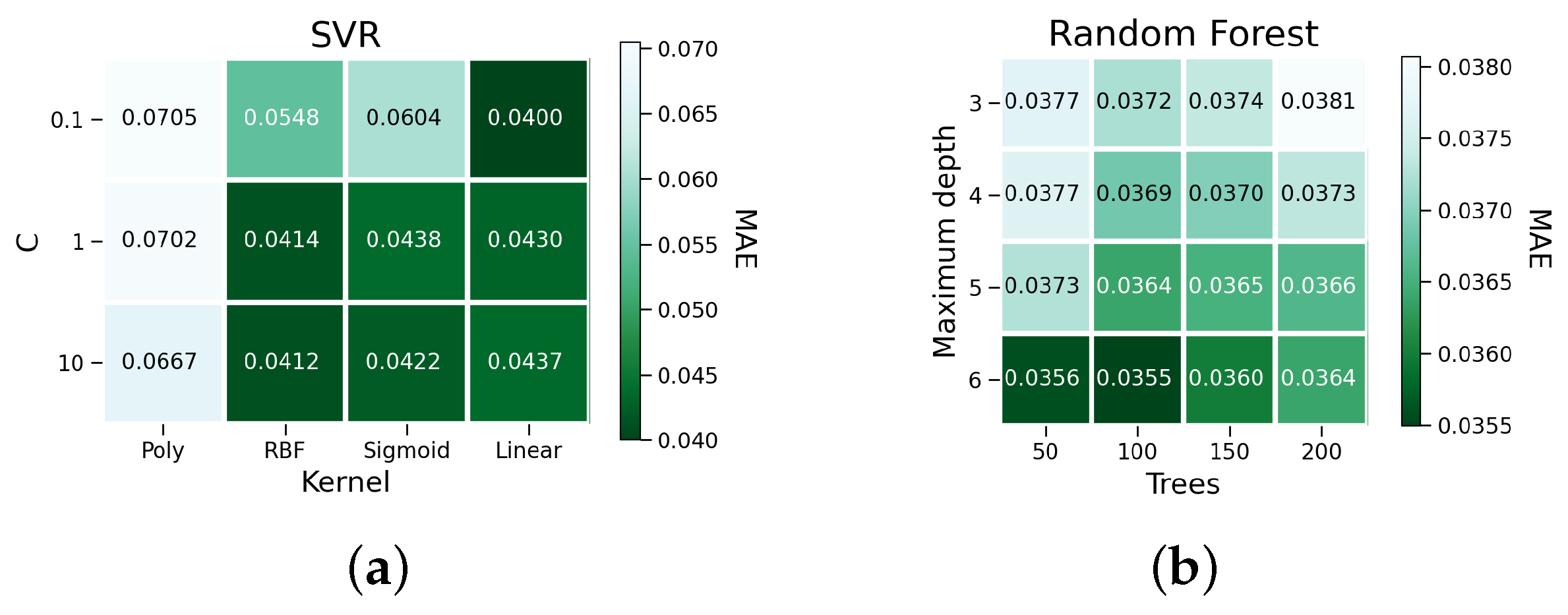
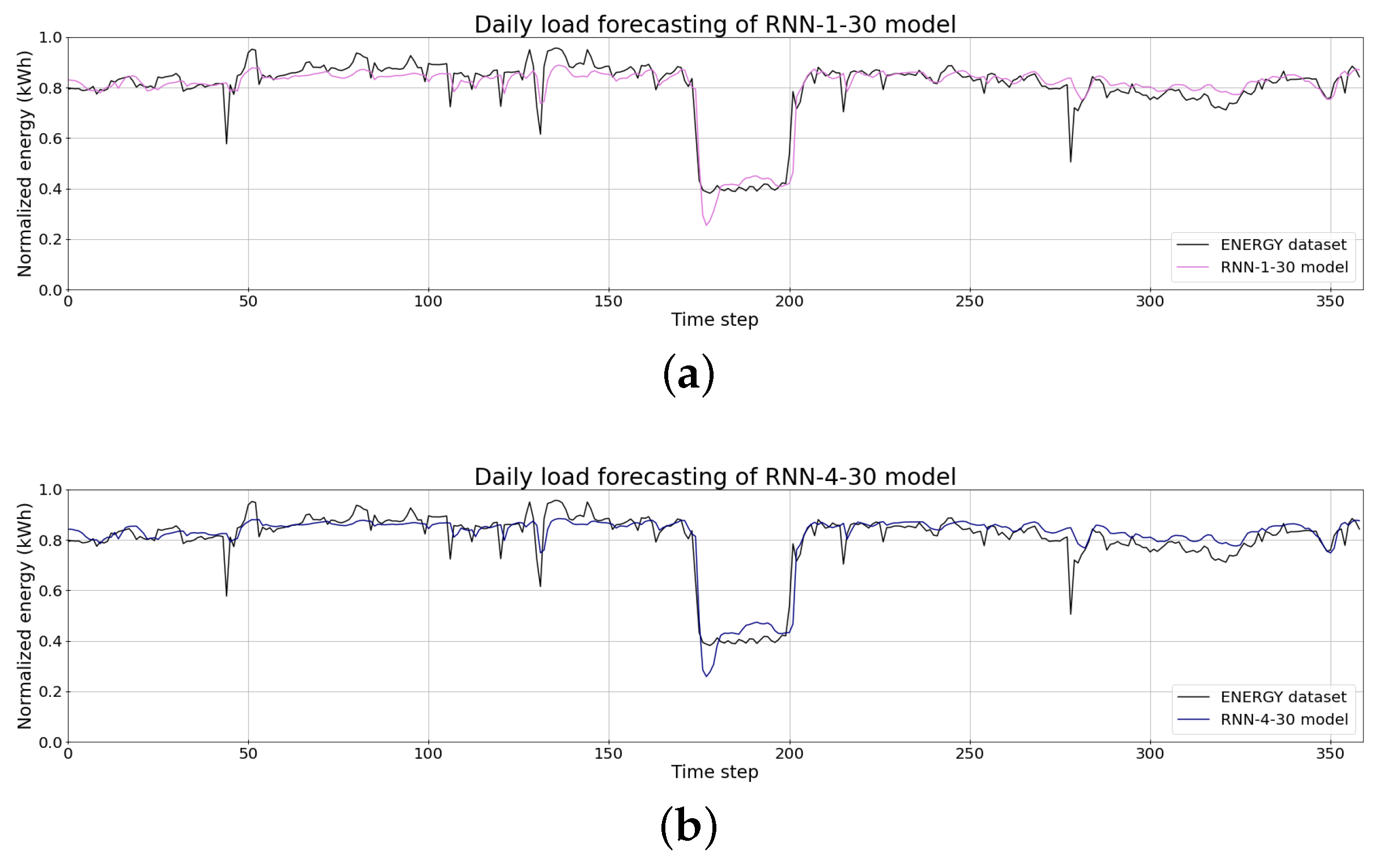
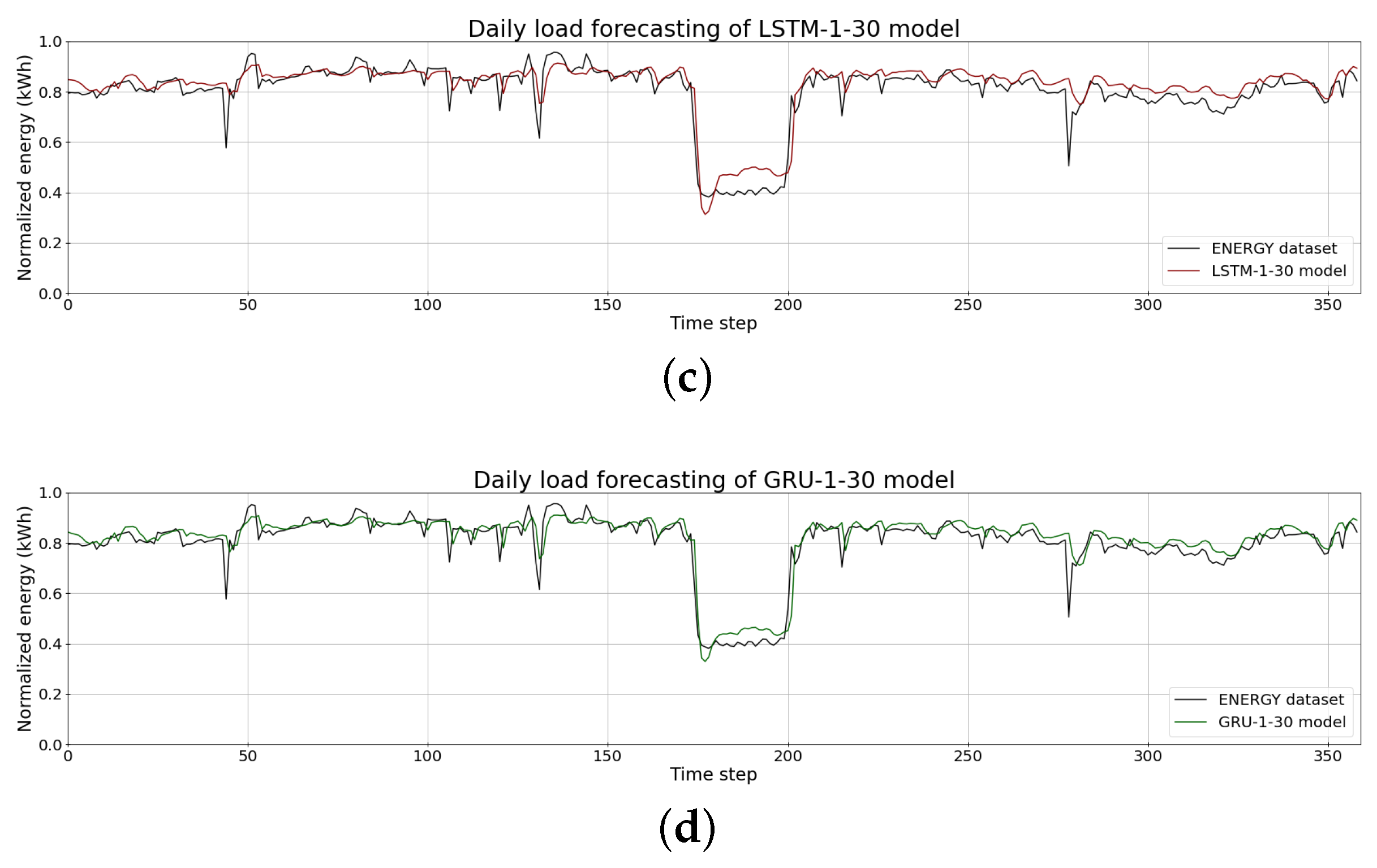
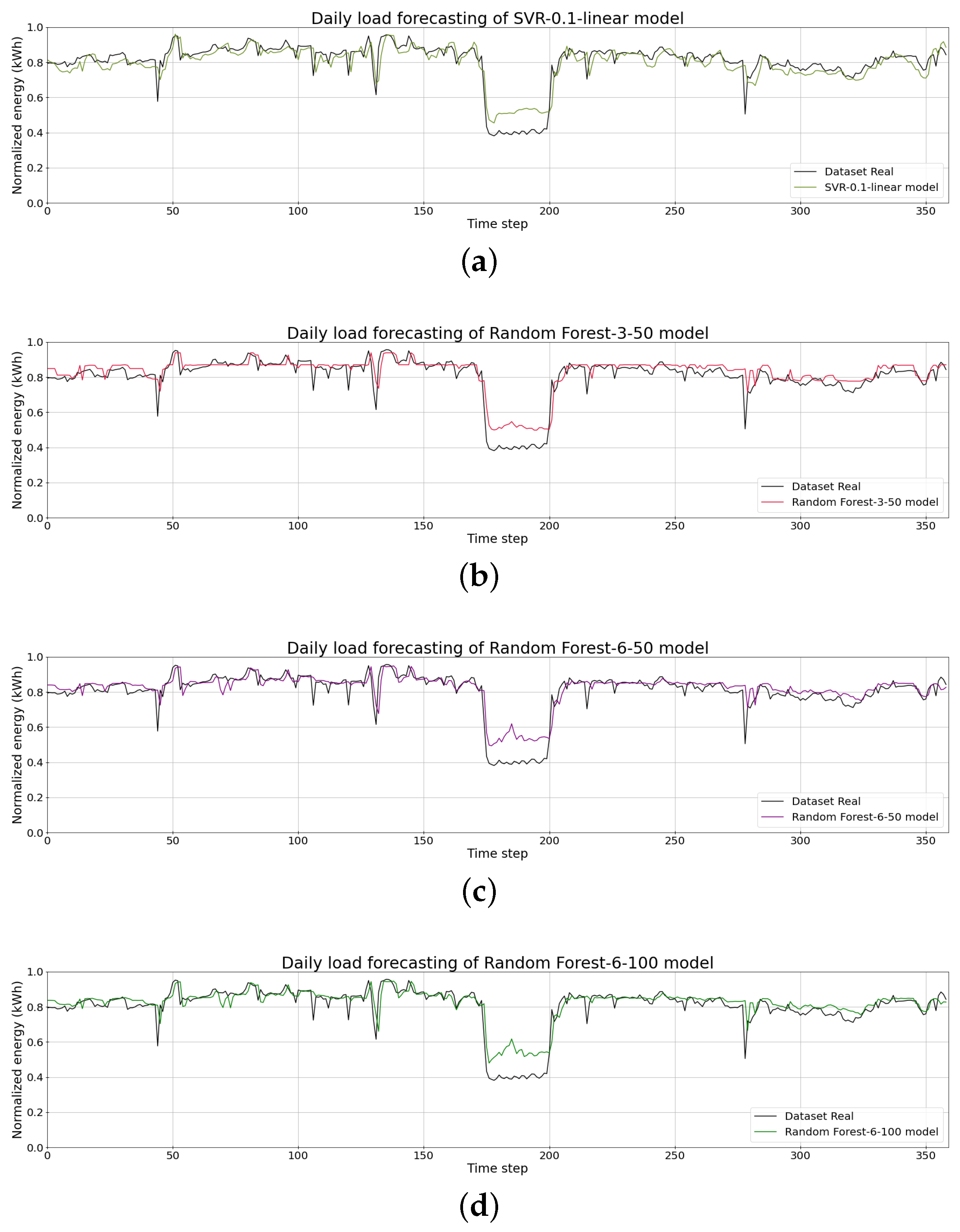
| Parameter | Levels |
|---|---|
| Number of nodes | From 10 to 90, step 20 |
| Number of layers | From 1 to 4, step 1 |
| Technique | Parameter | Levels |
|---|---|---|
| SVR | Number of C | 0.1, 1 and 10 |
| SVR | Type of kernel | Linear, polinomial and RBF |
| Random Forest | Number of max. depth | From 3 to 6, step 1 |
| Random Forest | Number of trees | From 50 to 200, step 50 |
| Models | RMSE | MAPE (%) | MAE |
|---|---|---|---|
| ARIMA | 0.0471 | 3.52 | 0.0249 |
| RNN-1-30 | 0.0316 | 4.42 | 0.0316 |
| RNN-4-30 | 0.0320 | 4.40 | 0.0320 |
| LSTM-1-30 | 0.0310 | 4.37 | 0.0310 |
| GRU-1-30 | 0.0305 | 4.33 | 0.0305 |
| SVR-0.1-linear | 0.0556 | 5.09 | 0.0400 |
| Random Forest-3-50 | 0.0561 | 4.94 | 0.0377 |
| Random Forest-6-50 | 0.0573 | 4.82 | 0.0356 |
| Random Forest-6-100 | 0.0580 | 4.83 | 0.0355 |
| Case site technique | 0.4119 | 51.61 | 0.4039 |
| Models | Inference Time Average (s) |
|---|---|
| ARIMA | 56.3565 ± 0.6802 |
| RNN-1-30 | 0.3896 ± 0.1289 |
| RNN-4-30 | 0.5939 ± 0.2070 |
| LSTM-1-30 | 0.6751 ± 0.2480 |
| GRU-1-30 | 0.7058 ± 0.2866 |
| SVR-0.1-linear | 0.0014 ± 0.0004 |
| Random Forest-3-50 | 0.0043 ± 0.0004 |
| Random Forest-6-50 | 0.0046 ± 0.0001 |
| Random Forest-6-100 | 0.0080 ± 0.0012 |
| ARIMA | RNN-1-30 | RNN-4-30 | LSTM-1-30 | GRU-1-30 | SVR-0.1- Linear | Random Forest-3-50 | Random Forest-6-50 | Random Forest-6-100 | |
|---|---|---|---|---|---|---|---|---|---|
| Case site technique | 51.38 | 51.55 | 51.27 | 50.79 | 51.30 | 51.06 | 50.20 | 49.76 | 49.70 |
| ARIMA | - | −0.54 | −0.83 | −1.46 | 0.45 | −2.96 | −3.36 | −2.95 | −3.18 |
| RNN-1-30 | - | - | −1.39 | −1.34 | 1.99 | −2.43 | −2.76 | −2.41 | −2.56 |
| RNN-4-30 | - | - | - | −0.99 | 3.04 | −2.07 | −2.57 | −2.25 | −2.40 |
| LSTM-1-30 | - | - | - | - | 6.56 | −1.96 | −2.81 | −2.37 | −2.54 |
| GRU-1-30 | - | - | - | - | - | −3.87 | −4.47 | −3.61 | −3.71 |
| SVR-0.1-linear | - | - | - | - | - | - | −0.24 | −0.78 | −1.08 |
| Random Forest-3-50 | - | - | - | - | - | - | - | −0.76 | −1.15 |
| Random Forest-6-50 | - | - | - | - | - | - | - | - | −1.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, A.M.N.C.; do Carmo, P.R.X.; Rodrigues, I.R.; Sadok, D.; Lynn, T.; Endo, P.T. Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models. Algorithms 2020, 13, 274. https://doi.org/10.3390/a13110274
Ribeiro AMNC, do Carmo PRX, Rodrigues IR, Sadok D, Lynn T, Endo PT. Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models. Algorithms. 2020; 13(11):274. https://doi.org/10.3390/a13110274
Chicago/Turabian StyleRibeiro, Andrea Maria N. C., Pedro Rafael X. do Carmo, Iago Richard Rodrigues, Djamel Sadok, Theo Lynn, and Patricia Takako Endo. 2020. "Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models" Algorithms 13, no. 11: 274. https://doi.org/10.3390/a13110274
APA StyleRibeiro, A. M. N. C., do Carmo, P. R. X., Rodrigues, I. R., Sadok, D., Lynn, T., & Endo, P. T. (2020). Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models. Algorithms, 13(11), 274. https://doi.org/10.3390/a13110274






