Abstract
Cotton constitutes a significant commercial crop and a widely traded commodity around the world. The accurate prediction of its yield quantity could lead to high economic benefits for farmers as well as for the rural national economy. In this research, we propose a multiple-input neural network model for the prediction of cotton’s production. The proposed model utilizes as inputs three different kinds of data (soil data, cultivation management data, and yield management data) which are treated and handled independently. The significant advantages of the selected architecture are that it is able to efficiently exploit mixed data, which usually requires being processed separately, reduces overfitting, and provides more flexibility and adaptivity for low computational cost compared to a classical fully-connected neural network. An empirical study was performed utilizing data from three consecutive years from cotton farms in Central Greece (Thessaly) in which the prediction performance of the proposed model was evaluated against that of traditional neural network-based and state-of-the-art models. The numerical experiments revealed the superiority of the proposed approach.
1. Introduction
Cotton is a significant commercial crop and a widely traded commodity around the world, which constitutes a critical link in the chain of agricultural activities. It is also commonly known as “white gold” due to its high influence in the rural national economy. The cotton crop is a perennial plant and it is grown primarily for seed and fiber, while it is grown commercially as an annual with a biological cycle between 140–210 days [1].
In general, the key objective in precision farming and agriculture is the improvement of crop yield quality and production as well as the reduction in environmental pollution and operating costs [2]. Nevertheless, farm mechanization and the application of new technologies lead to the transformation of crop management from a rather qualitative science, which was mainly based on observations of a more quantitative science, which is now based on measurements. In this new data-driven area, a variety of different production features including soil and climate conditions, irrigation management, and nutrient availability significantly influence the potential cotton yield and growth [1,2,3,4,5]. Therefore, the prediction of cotton’s yield, as well as the factors which mostly affect it, could lead to production optimization through the early modification of harvest settings and adjustments.
The traditional way to forecast cotton production is mainly based on the empirical knowledge of the farmer or mostly by the agricultural expert [6,7,8]. Cultivation and weather information are processed by agriculturists who attempt to perform accurate predictions about future yield production. Nevertheless, the quantity of cotton production possesses, by nature, nonlinear behavior since it is affected by several soil and climate factors and it is characterized by by spatio-temporal variability [9,10]. As a result, the problem of conducting accurate predictions is considered a considerably hard problem. Moreover, the fact that yield monitors revealed that the cotton’s production was different even in different parts of the same field [11] makes this prediction problem even more challenging. Therefore, the use and the development of sophisticated decision support tools is considered essential for potentially assisting agricultural investors and farmers gaining significant profits.
During the last decade, the application of artificial intelligence techniques and methodologies sparked the interest of the scientific community, since they constitute the appropriate tools to deal with the noisy and sometimes chaotic nature of cotton’s yield production and lead to more accurate predictions. Along this line, research focused on the development of expert systems for the prediction of agriculture production for assisting growth operations [2]. These intelligent systems exploit the high predictive ability of machine learning algorithms, focusing on increasing crop’s efficiency and economic benefits, while simultaneously reducing risks and losses [11,12,13,14,15].
In this work, we propose a new neural network model for predicting cotton production, which is based on a multiple-input architecture and constitutes the main contribution. The proposed model utilizes as input three different kinds of data, namely soil data, cultivation management data, and yield management data. To the best of our knowledge, this is the first approach which utilizes three different types of features. The selected neural network architecture provides that each kind of input data are processed and handled in a different and independent way. The motivation behind our approach is to develop a learning system which is capable of efficiently exploiting information from different kinds of data, since these kinds of data usually require separate treatment. A series of experiments was conducted for evaluating the prediction performance of the proposed model by comparing it against traditional neural network-based and other state-of-the-art models. For our experiments, we utilized data from three consecutive years from cotton farms in Central Greece (Thessaly). The presented results demonstrate the prediction accuracy of the proposed model, providing empirical evidence that the proposed approach is able to develop an accurate and reliable model.
The remainder of this paper is organized as follows: Section 2 presents a brief survey of rewarding studies, regarding the application of machine learning methodologies for cotton prediction. Section 3 presents a detailed description of the utilized data as well as the data preparation process. Section 4 presents the proposed prediction multiple-input neural network model focusing on its advantages and benefits. Section 5 presents state-of-the-art prediction models. Section 6 presents our numerical experiments. Finally, Section 7 discusses our methodology and the findings of this research, and presents our conclusions.
2. Related Work
During the last decade, the significant advances in digital technology and machine learning have renewed the interest of the scientific community for the development of efficient expert systems for assisting agriculture precision and production. Chlingaryana et al. [2] conducted an excellent review and presented in detail the recent developments performed within the last two decades, focusing on the application of machine learning methods for accurate crop prediction as well as the estimation of nitrogen status. The main findings of this research were that machine learning techniques provide complete and cost-effective solutions for efficiently estimating crop and environment state as well as significant assistance in decision-making. Additionally, the authors attempted to gain significant insights on crop prediction by identifying the factors which affect it, and possible directions to support and improve precision agriculture through artificial intelligence. To the best of our knowledge, the application of machine learning methods for predicting cotton crop has been limited compared to other types of crops. In the sequel, we briefly discuss some rewarding studies regarding cotton yield prediction using machine learning models.
Papageorgiou et al. [12] proposed an intelligent knowledge-based model for modeling the behavior of crop cotton yield in precision farming. The proposed model was based on using a soft computing methodology based on Fuzzy Cognitive Maps (FCMs) and on the unsupervised learning algorithm for FCMs for assessing measurement data and updating initial knowledge. The performance of the proposed model was extensively evaluated for 360 cases in a 5 hectare experimental farm for predicting the cotton yield using a two-level classification (“Low” and “High”). Moreover, their used data were collected from central Greece, during the years 2001, 2003, and 2006. Based on the brief experimental analysis, the authors stated that the proposed FCMs model is able to assist agriculture managers with better understanding cotton yield requirements. Along this line, in [11], the authors extended their previous work, including more elegant conditions to increase the efficiency of their intelligent model. Their numerical experiments reported that the updated model outperformed traditional prediction models such as artificial neural networks (ANNs), decision trees, and Naive–Bayes. Finally, the authors highlighted that the proposed updated model consists a convenient decision support tool for cotton production due to its sufficient simplicity and interpretability.
Jamuna et al. [13] studied the problem of classifying the quality of cotton’s seed utilizing several growth stages of the crop. Their dataset consists of 900 records and 24 features from a set of different cotton categories. The authors conducted a performance evaluation of state-of-art prediction models, including decision trees, Naive–Bayes and ANNs for identifying the quality of cotton’s seed (“Good”, “Average” and “Bad”). Their experiments showed that ANNs and decision trees provided almost identical performance, reporting 98.58% classification accuracy. However, the decision trees reported significantly lower training time and computational cost.
Haghverdi et al. [14] attempted to determine cotton lint yield in irrigated fields using remote sensing technology. More specifically, they utilized ANNs for extracting information from remotely-sensed crop indices in order to predict and map the cotton lint yield of a field in two successive cropping seasons. The data in their research were obtained after conducting an on-farm irrigation experiment on a property of 73 hectares in west Tennessee during the years 2013 and 2014. Their numerical experiments presented some interesting results, revealing that neural networks can efficiently exploit crop indices phenology for predicting crop yield. Additionally, based on their detailed experiments, the authors stated that the use of remote sensing-based ANN models has a great potential to provide reliable and accurate predictions of cotton yield maps.
Nguyen et al. [15] proposed a spatial-temporal multi-task learning model for predicting within-field crop yield. The proposed model was based on a deep dense neural network enforced with dropout layers and a new weighted regularization technique to improve the prediction performance. It exploits different spatial-temporal features by integrating multiple heterogeneous data from difference sources. The data used in their study were collected from a cotton field in west Texas from 2001 to 2003 and include soil properties, weather data, normalized difference vegetation index data, and spectral data. Their proposed model was evaluated against state-of-the-art models such as linear regression, decision tree regression, support vector regression as well as ensemble models, such as random forest and XGBoost. Their experimental analysis provided empirical evidence about the superiority of the proposed model against traditional models; hence, the authors stated that it could effectively assist the field of crop prediction.
In this research, we propose a different approach for the development of an accurate model for the prediction of cotton’s yield production. More specifically, we propose a new multiple-input neural network model, which exploits mixed features as inputs from three different kinds of data: soil data, cultivation management data, and yield management data. The contribution of our approach is that the proposed neural network architecture processes and handles each type of input in an independent way, which benefits the prediction performance more, since mixed features of data usually require separate treatment. To the best of our knowledge, none of the mentioned approaches considered exploiting information from three different kinds of cotton data and developing a prediction model by handling them separately. An advantage provided by the proposed architecture is the considerable flexibility and adaptivity for low computational effort, compared to that of a fully connected neural network with two or more hidden layers.
3. Data
In our research, the data concern the cotton yield in kilograms per 0.1 hectare from 350 sampling sites of the Thessaly plain, during the years 2008–2010. For each sampling site, a number of features were obtained from three main categories: soil features, cultivation management features, and yield management features. The data were divided into a training set (273 instances) which consists of the yield production during 2008 and 2009, which ensures a substantial amount of data for training and testing set (119 instances) containing yield production during 2010, which ensures that it will be performed with a considerable amount of unseen data. It is also worth mentioning that the maximum cotton production in Greece indicated no significant year-to-year fluctuations and has remained rather stable during the last twenty years. This implies that the current productions are not considerably different from the potential. Finally, the used data contained no missing values, while the outlier prices were not removed for not destroying the dynamics of data.
Table 1, Table 2 and Table 3 present the set of features concerning soil, cultivation management and yield management features, respectively, as well as a brief description for each feature.

Table 1.
List of soil features.

Table 2.
List of cultivation management features.

Table 3.
List of yield management features.
Finally, it is worth noticing that, for maximizing the performance of all prediction models, we applied a variety of feature selection techniques such as univariate feature selection, recursive feature elimination, and selection based on feature importance [16,17,18] as well as attempting to reduce the number of features by analyzing the correlation [19] between them. Nevertheless, any attempt of selecting a subset of the presented features resulted in slightly decreasing the overall performance of all prediction models; thus, all features presented in Table 1, Table 2 and Table 3 were utilized, even the least significant.
4. Proposed Multiple-Input Neural Network Prediction Model
The main contribution of this research is the development of a prediction model for efficiently predicting cotton yield production, which is based on a multiple-input single-output structure. The motivation behind our approach is to develop a learning system that is capable of efficiently exploiting useful information from mixed features of data, since these kinds of data usually require separate treatment. To this end, each input kind of data is processed and handled in a different and independent way.
The architecture of the proposed Multiple-input Neural Network (MNN) model is depicted in Figure 1. It consists of three separate input layers (Input Layer -1-, Input Layer -2-, and Input Layer -3-), each one has as inputs the soil (Table 1), the cultivation management (Table 2), and the yield management features (Table 3), respectively. Each input layer is followed by a hidden layer (Hidden Layer -1-, Hidden Layer -2-, Hidden Layer -3-), which independently processes the input data. It is worth noticing that each hidden layer could be constituted by a classical dense layer or by a more sophisticated recurrent layer such as Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU). Next, the outputs of the three hidden layers are imported and merged by a concatenate layer. This layer is followed by a dense layer and a final output layer of one neuron.
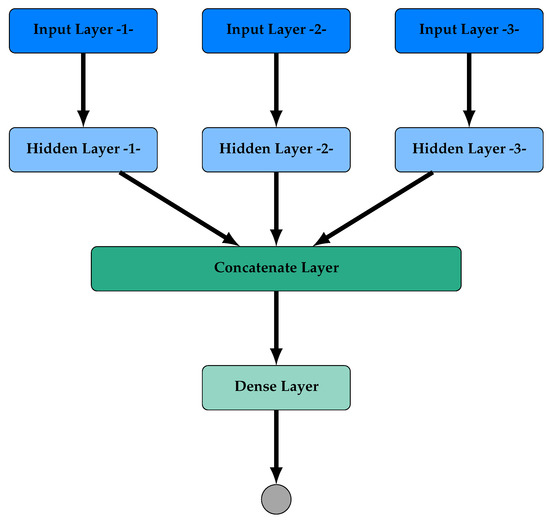
Figure 1.
Proposed architecture of a Multiple-input Neural Network (MNN).
An advantage of the proposed architecture is that, although stacking many hidden layers allows a traditional neural network model to analyze and encode a very complex function from the input to the output, it is usually difficult to train such a model due to the vanishing gradient problem, which implies that the convergence of the training process may be degradated. Additionally, each category of mixed features of data are handled independently and subsequently the processed data are merged and further processed. As a result, the proposed architecture offers more flexibility and adaptivity for a low development cost compared to that of a fully connected neural network with two or more hidden layers, which implies that computational effort of the training process is reduced.
In the sequel, we present a brief description of the Dense, LSTM, and GRU layers which constitute the main elements of the proposed MNN model.
- Dense layer: Dense layers [20] constitute the traditional and the most popular choice for composing a hidden layer in a multilayer neural network. A dense layer is composed of neurons which are connected with all neurons in the previous layer. The operations performed by each neuron can be summarized bywhere is the output of the i-neuron of the layer, is the vector of weights, x is the input vector, is the bias vector, and f is the activation function.
- LSTM layer: Long Short-Term Memory (LSTM) layers [21] constitute a special type of Recurrent Neural Networks layers which are characterized by their ability to learn long-term dependencies.Each LSTM unit in the layer is composed of a memory cell and three gates: input, output, and forget. At time t, the input gate and a second gate modulate the amount of information that are stored into the memory state . The forget gate modulates the past information which must be vanished or must be kept on the memory cell at the previous time . Finally, the hidden state constitutes the output of the memory cell and it is calculated using memory state and the output gate which modulates the information used for the output of the memory cell. In summary, the following equations describe the operations performed by an LSTM unit:where denotes the input of each unit, and are matrices of weights, and are the bias vectors with , the operator ⊙ denotes the Hadamard product (component-wise multiplication), is the sigmoid function, and is the output of the memory cell which denotes the hidden state.
- GRU layer: Gated Recurrent Units (GRU) were originally proposed by Cho et al. [22] and were inspired by the LSTM units, but with simpler implementation and calculations. Its main difference is that a GRU unit only has two gates (update and reset) which modulate the flow of information, without the utilization of memory gates, since it exposes the full hidden content without any control.The update gate controls the level the unit updates its content, by taking into consideration a linear sum between the previous state and the input . The reset gate is computed in a similar manner with the update gate . Finally, the activation of a GRU unit constitutes the linear combination between the previous and the candidate activation , which is computed similarly to the traditional recurrent unit. The operations performed by an GRU unit are briefly described bywhere denotes the input vector and and are matrices of weights with and are the bias vectors.
In our numerical experiments, the performance of the proposed MNN model was evaluated using three different architectures (Figure 2), namely:
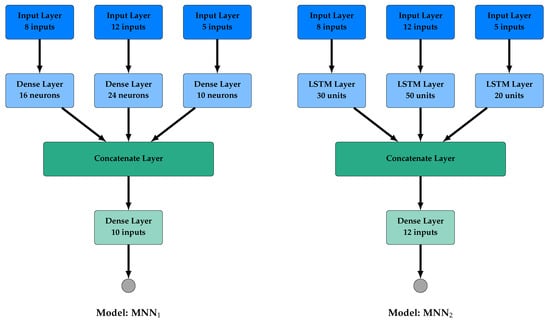
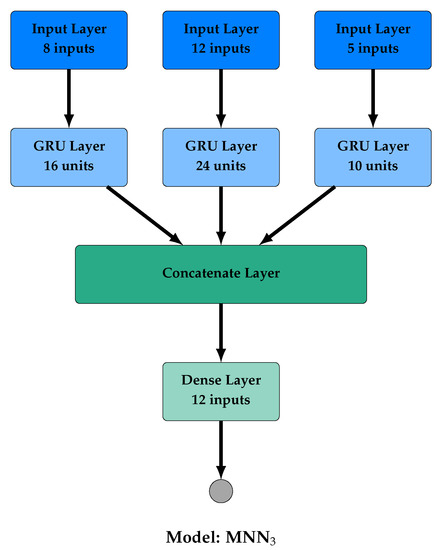
Figure 2.
Architecture of the proposed MNN, MNN, and MNN models.
- MNN utilizes three dense layers of 16, 24, and 10 neurons in Hidden Layer -1-, Hidden Layer -2-, and Hidden Layer -3-, respectively, and a dense layer of 10 neurons after the concatenate layer.
- MNN utilizes three LSTM layers of 30, 50, and 20 units in Hidden Layer -1-, Hidden Layer -2-, and Hidden Layer -3-, respectively, and a dense layer of 12 neurons after the concatenate layer.
- MNN utilizes three GRU layers of 16, 24, and 10 units in Hidden Layer -1-, Hidden Layer -2-, and Hidden Layer -3-, respectively, and a dense layer of 12 neurons after the concatenate layer.
All neurons in the hidden layers used a Rectifier Linear Unit (ReLU) activation function while the neuron in the output layer used sigmoid activation. The kernel and bias initializer in all layers were set as the default as well as the recurrent initializer in the recurrent layers.
5. State-of-the-Art Machine Learning Models
In this section, we briefly present the state-of-the-art machine learning models which have been established in the literature to address prediction benchmarks. These models will be utilized to base models in order to explore and highlight the performance of the proposed model.
More specifically, the models are: Decision Tree Regressor (DTR) [23], Gaussian Processes (GP) [24], k-Nearest Neighbor Regression (kNN) [25], Least Absolute Shrinkage and Selection Operator (LASSO) [26], Linear Regression (LR) [27], and Support Vector Regression (SVR) [28], which are described below:
- DTR is a decision tree dedicated for regression problems, which constructs a model tree based on splitting criteria. More analytically, this algorithm develops a tree with decision nodes and leaf nodes, in which the leaves predict the output continuous value utilizing the linear regression algorithm.
- GP constitutes a collection of random variables depending on time or space, in which every collection of those variables has a multivariate normal distribution. The prediction value of this machine learning algorithm is a one-dimensional Gaussian distribution, and it is calculated by the similarity between the training instances and the unseen instances.
- kNN is a popular machine learning algorithm, which utilizes various distance mathematic formulas to compute feature similarity between each new instance and a predefined number k of instances in the training data. For regression problems, the output value is defined by the average value of its k nearest neighbors.
- LASSO is a linear model trained with prior as a regularizer. This algorithm performs both regularization and variable selection in order to enhance the prediction accuracy. Due to its simplicity and efficiency, it has been successfully extended and applied to a wide variety of statistical models.
- LR probably constitutes the most commonly used algorithm for developing an efficient regression model. This prediction algorithm aims to determine the relationship between one or more explanatory (independent) variables and the dependent variable based on the linear mathematical model.
- SVR is a classical machine learning algorithm which is utilized for predicting continuous values. Its main objective is to fit the error within a specified threshold, in contrast to traditional regression algorithms like LR, which focuses on minimizing the error.
Additionally, the performance of the proposed MNN model was also compared against that of three widely utilized neural network-based models i.e., a fully connected Feed-Forward Neural Network (FFNN), a GRU-based network (GRU), and a Long Short-Term Memory (LSTM) network. Notice in our numerical experiments the hyper-parameters of all regression models were optimized under exhaustive experimentation and are briefly presented in Table 4.

Table 4.
Hyper-parameter specification of all prediction models.
6. Numerical Experiments
In this section, we evaluate the performance of the proposed MNN model and compare it against that of three widely utilized neural network-based models i.e., Feed-Forward Neural Network (FFNN), a GRU-based network (GRU) and a Long Short-Term Memory (LSTM) network. Additionally, it was also compared against the state-of-the art models: Decision Tree Regressor (DTR), Gaussian Processes (GP), k-Nearest Neighbor Regression (kNN), Least Absolute Shrinkage and Selection Operator (LASSO), Linear Regression (LR) and Support Vector Regression (SVR).
In order to avoid overfitting and maximize the efficiency of the proposed models as well as the neural network-based models, 15% of training data were used for validation and early stopping technique based on ’validation loss’ was used. Furthermore, any attempt to use regularizers or dropout decreased the overall performance of all these models.
The performance of all prediction models was measured utilizing the metrics: Mean Absolute Error (MAE), Root-Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), and symmetric Mean Absolute Percentage Error (sMAPE), which are respectively defined by
where N is the number of forecasts, is the actual value, and is the predicted value. In addition, the implementation code was written in Python 3.7 on a laptop (Intel(R) Core(TM) i7-6700HQ CPU 2.6 GHz, 16 GB RAM) using libraries Tensorflow [29] sand Scikit-learn [30].
Table 5 presents the performance of all compared models, regarding the performance metrics RMSE, MAE, MAPE, and sMAPE. Additionally, a more representative visualization of all performance metrics is presented in Figure 3. Clearly, the proposed models MNN, MNN, and MNN exhibited the best performance, considerably outperforming all neural network-based and state-of-the-art prediction models. More specifically, all versions of the proposed MNN model presented the lowest MAE and RMSE scores. MNN reported the best performance, closely followed by MNN, relative to MAE and RMSE scores. Regarding MAPE and sMAPE performance metrics, MNN reported the lowest (best) scores, followed by MNN, which exhibited slightly worse performance. MNN reported 11.8–41.36% and 8.24–48.98% lower MAPE and sMAPE scores, respectively, compared to the performance of the state-of-the-art models. Additionally, MNN exhibited 10.5–22.6% and 13.6–23.4% lower MAPE and sMAPE scores, respectively compared to the performance of the neural network-based models. LSTM, GP, kNN, and LR presented competitive performance to MNN; however, they were considerably outperformed by the versions of the proposed model which utilized recurrent hidden layers, i.e., MNN and MNN. This implies that the utilization of hidden layers with recurrent units favored the performance of the proposed MNN model. Additionally, LASSO and SVR reported the worst performance, regarding all metrics.

Table 5.
Performance of the proposed MNN model and the state-of-the-art prediction models.
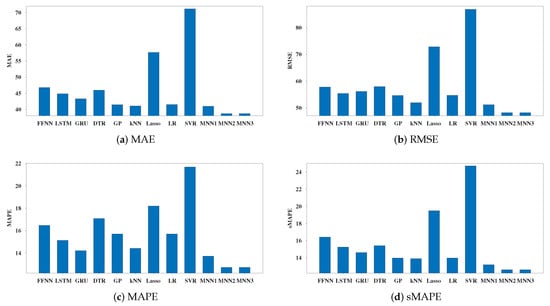
Figure 3.
Box-plot for the performance of the proposed MNN model and the state-of-the-art prediction models based on (a) MAE; (b) RMSE; (c) MAPE; (d) sMAPE.
In summary, the interpretation of Table 5 reveals that the three different architectures of the proposed MNN model exhibited the best overall performance, regarding all metrics. Furthermore, the utilization of the recurrent layers (LSTM and GRU), instead of the traditional dense layers, benefited its performance considerably. It is also worth mentioning that the proposed model exhibited slightly better performance utilizing GRU layers, instead of LSTM layers. This may be due to the fact that each LSTM unit has more gates for the gradients to flow through, causing steady progress to be more difficult to maintain [22,31]. Nevertheless, this is surprising since GRU frequently suffers from the vanishing gradient problem [32]. By taking these into consideration, we are able to conclude that the vanishing gradient problem rarely or did not occur in our experiments. A possible explanation for this could be the utilization of ReLU activation function, the less complex architecture of the proposed model compared to that of a fully connected network, as well as the complexity and size of the used dataset. This is certainly worth being investigated in the near future.
7. Discussion and Conclusions
In this work, we proposed a multiple-input neural network model, called MNN, for the prediction of cotton’s yield. The proposed model uses as inputs three different kinds of data (soil, cultivation management, and yield management) which are treated and handled independently. A significant advantage of the selected architecture is that it is able to efficiently exploit information in mixed data, since these kinds of data usually require being processed separately. Additionally, the proposed architecture is superior to the traditionally fully connected neural network architecture in terms of flexibility and adaptivity for low computational cost.
An empirical study was performed utilizing data from three consecutive years from cotton farms in Central Greece, in which the prediction performance of the proposed model was evaluated against that of traditional neural network-based and other state-of-the-art models. Our numerical experiments revealed the superiority of the proposed approach, providing empirical evidence that agricultural datasets, which consists of different types of data, should be treated utilizing the proposed approach.
Additionally, the performance of the proposed model was evaluated utilizing three different types of hidden layers, i.e., dense, LSTM, and GRU. It is worth noticing that the utilization of the recurrent layers benefitted the performance of MNN considerably, compared with the utilization of traditionally dense layers. Furthermore, the proposed MNN model exhibited slightly better performance utilizing GRU layers instead of LSTM layers. A possible explanation for this is that each LSTM unit has more gates for the gradients to flow through, causing steady progress to be more difficult to maintain [22,31]. In addition, by comparing the performance of MNN and MNN, we can conclude that the vanishing gradient problem was rarely or not occurring in our experiments. This is probably due to the utilization of the ReLU activation function and to the “sparse” architecture of the proposed multi-input neural network model. More analytically, the utilization of ReLU activation function is able to frequently prevent the vanishing gradient problem from occurring, since it only saturates in one direction, while the “sparse” architecture of the proposed model makes it considerably less complicated compared to a fully connected neural network. Another possible reason could be the complexity of the utilized dataset as well its relative small number of training instances. To this end, more experiments utilizing more cotton and other crop datasets are needed, which is definitely included in our future research.
Furthermore, it is worth mentioning that the features used in this research do not constitute a conclusive list. An extension could introduce new features and other criteria, which may potentially influence the prediction performance. Clearly, it is still under consideration which feature has a greater impact for predicting cotton production or which of them should be used by an intelligent model. These questions constitute an interesting aspect for future research. Nevertheless, it is likely that the research to answer these questions could reveal additional information about the cotton yield behavior.
A limitation of this work is that the utilized dataset contained only 349 samples. Based on the preliminary experimental results, it seems that the proposed approach is able to develop a reliable and accurate model. However, we intend to enlarge our database with data from more sample sites and more years in order to perform a exhaustive performance evaluation of the compared models on various datasets as well as a comprehensive statistical analysis (use of a nonparametric test and/or a post-hoc tests).
Since the presented numerical experiments are quite encouraging, an interesting next step could be to evaluate the proposed model for the prediction of yield of other crop species such as wheat, trees, maize, and vineyards. In our future research, we intend to incorporate ensemble learning strategies (see [33,34,35,36,37] and the references therein) and also incorporate sophisticated preprocessing methodologies [11,12] in our framework for improving the prediction performance. Finally, it is worth noticing that our main expectation is that the proposed approach could be utilized as a reference for decision-making in agricultural production.
Author Contributions
Conceptualization, I.E.L.; methodology, I.E.L.; software, I.E.L.; validation, I.E.L. and S.D.D.; formal analysis, I.E.L. and S.D.D.; investigation, I.E.L.; resources, D.P.K.; data curation, D.P.K.; writing–original draft preparation, I.E.L.; writing–review and editing, I.E.L. and S.D.D; visualization, I.E.L.; supervision, G.K.P. and D.P.K.; project administration, I.E.L. funding acquisition, I.E.L. and S.D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kalivas, D.; Kollias, V. Effects of soil, climate and cultivation techniques on cotton yield in Central Greece, using different statistical methods. Agronomie 2001, 21, 73–90. [Google Scholar] [CrossRef][Green Version]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Hayat, A.; Amin, M.; Afzal, S. Statistical investigation to explore the impact of soil and other characteristics on cotton yield. Commun. Soil Sci. Plant Anal. 2020, 51, 1434–1442. [Google Scholar] [CrossRef]
- Sawan, Z.M. Climatic variables: Evaporation, sunshine, relative humidity, soil and air temperature and its adverse effects on cotton production. Inf. Process. Agric. 2018, 5, 134–148. [Google Scholar] [CrossRef]
- Dai, J.; Li, W.; Zhang, D.; Tang, W.; Li, Z.; Lu, H.; Kong, X.; Luo, Z.; Xu, S.; Xin, C. Competitive yield and economic benefits of cotton achieved through a combination of extensive pruning and a reduced nitrogen rate at high plant density. Field Crop. Res. 2017, 209, 65–72. [Google Scholar] [CrossRef]
- Ahmad, S.; Hasanuzzaman, M. Cotton Production and Uses: Agronomy, Crop Protection, and Postharvest Technologies; Springer Nature: London, UK, 2020. [Google Scholar]
- Jabran, K.; Chauhan, B.S. Cotton Production; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Khan, M.A.; Wahid, A.; Ahmad, M.; Tahir, M.T.; Ahmed, M.; Ahmad, S.; Hasanuzzaman, M. World Cotton Production and Consumption: An Overview. In Cotton Production and Uses; Springer: Berlin, Germany, 2020; pp. 1–7. [Google Scholar]
- Ullah, K.; Khan, N.; Usman, Z.; Ullah, R.; Saleem, F.Y.; Shah, S.A.I.; Salman, M. Impact of temperature on yield and related traits in cotton genotypes. J. Integr. Agric. 2016, 15, 678–683. [Google Scholar] [CrossRef]
- Zonta, J.H.; Brandão, Z.N.; Sofiatti, V.; Bezerra, J.R.C.; Medeiros, J.d.C. Irrigation and nitrogen effects on seed cotton yield, water productivity and yield response factor in semi-arid environmernt. Aust. J. Crop. Sci. 2016, 10, 118–126. [Google Scholar]
- Papageorgiou, E.I.; Markinos, A.T.; Gemtos, T.A. Fuzzy cognitive map based approach for predicting yield in cotton crop production as a basis for decision support system in precision agriculture application. Appl. Soft Comput. 2011, 11, 3643–3657. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Markinos, A.; Gemptos, T. Application of fuzzy cognitive maps for cotton yield management in precision farming. Expert Syst. Appl. 2009, 36, 12399–12413. [Google Scholar] [CrossRef]
- Jamuna, K.; Karpagavalli, S.; Vijaya, M.; Revathi, P.; Gokilavani, S.; Madhiya, E. Classification of seed cotton yield based on the growth stages of cotton crop using machine learning techniques. In Proceedings of the 2010 International Conference on Advances in Computer Engineering, Bangalore, India, 21–22 June 2010; pp. 312–315. [Google Scholar]
- Haghverdi, A.; Washington-Allen, R.A.; Leib, B.G. Prediction of cotton lint yield from phenology of crop indices using artificial neural networks. Comput. Electron. Agric. 2018, 152, 186–197. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Zhu, J.; Lin, Z.; Du, H.; Yang, Z.; Guo, W.; Jin, F. Spatial-temporal Multi-Task Learning for Within-field Cotton Yield Prediction. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Cham, Switzerland, 2019; pp. 343–354. [Google Scholar]
- Brownlee, J. Machine Learning Mastery with Python: Understand Your Data, Create Accurate Models, and Work Projects End-to-End; Machine Learning Mastery: Melbourne, Australia, 2016. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Khalid, S.; Khalil, T.; Nasreen, S. A survey of feature selection and feature extraction techniques in machine learning. In Proceedings of the 2014 Science and Information Conference, Warsaw, Poland, 7–10 September 2014; pp. 372–378. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Loh, W.Y. Classification and regression tree methods. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Paul, W.; Baschnagel, J. Stochastic Processes; Springer: Berlin, Germany, 2013; Volume 1. [Google Scholar]
- Aha, D. Lazy Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 329. [Google Scholar]
- Deng, N.; Tian, Y.; Zhang, C. Support Vector Machines: Optimization Based Theory, Algorithms, and Extensions; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI’ 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Dey, R.; Salemt, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar]
- Hu, Y.; Huber, A.; Anumula, J.; Liu, S.C. Overcoming the vanishing gradient problem in plain recurrent networks. arXiv 2018, arXiv:1801.06105. [Google Scholar]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning; Springer: Berlin, Germany, 2012; pp. 1–34. [Google Scholar]
- Dietterich, T.G. Ensemble learning. Handb. Brain Theory Neural Netw. 2002, 2, 110–125. [Google Scholar]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: Berlin, Germany, 2012. [Google Scholar]
- Brown, G. Ensemble Learning. Encycl. Mach. Learn. 2010, 6, 312. [Google Scholar]
- Pintelas, P.; Livieris, I.E. Special Issue on Ensemble Learning and Applications. Algorithms 2020, 13, 140. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).