Characterization and Modeling of Out-of-Plane Behavior of Fiber-Based Materials: Numerical Illustration of Wrinkle in Deep Drawing
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Material Characterization Experiments
2.2.1. In-Plane Uniaxial Tensile Test
2.2.2. In-Plane Shear Test
2.2.3. Out-of-Plane Compression Test
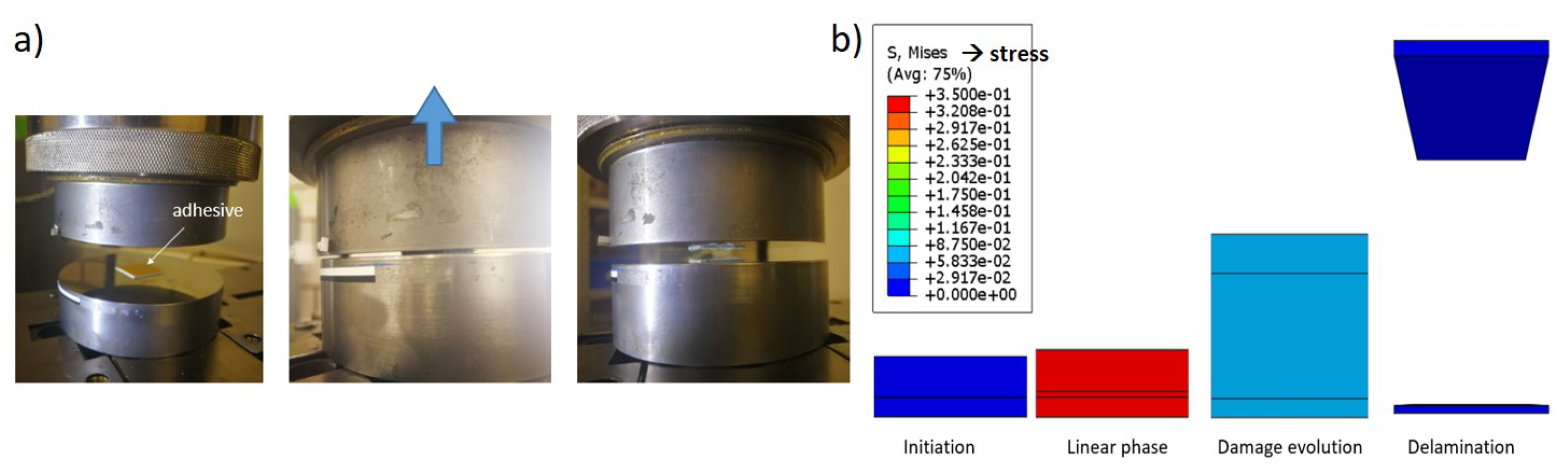
2.2.4. Out-of-Plane Tensile Test
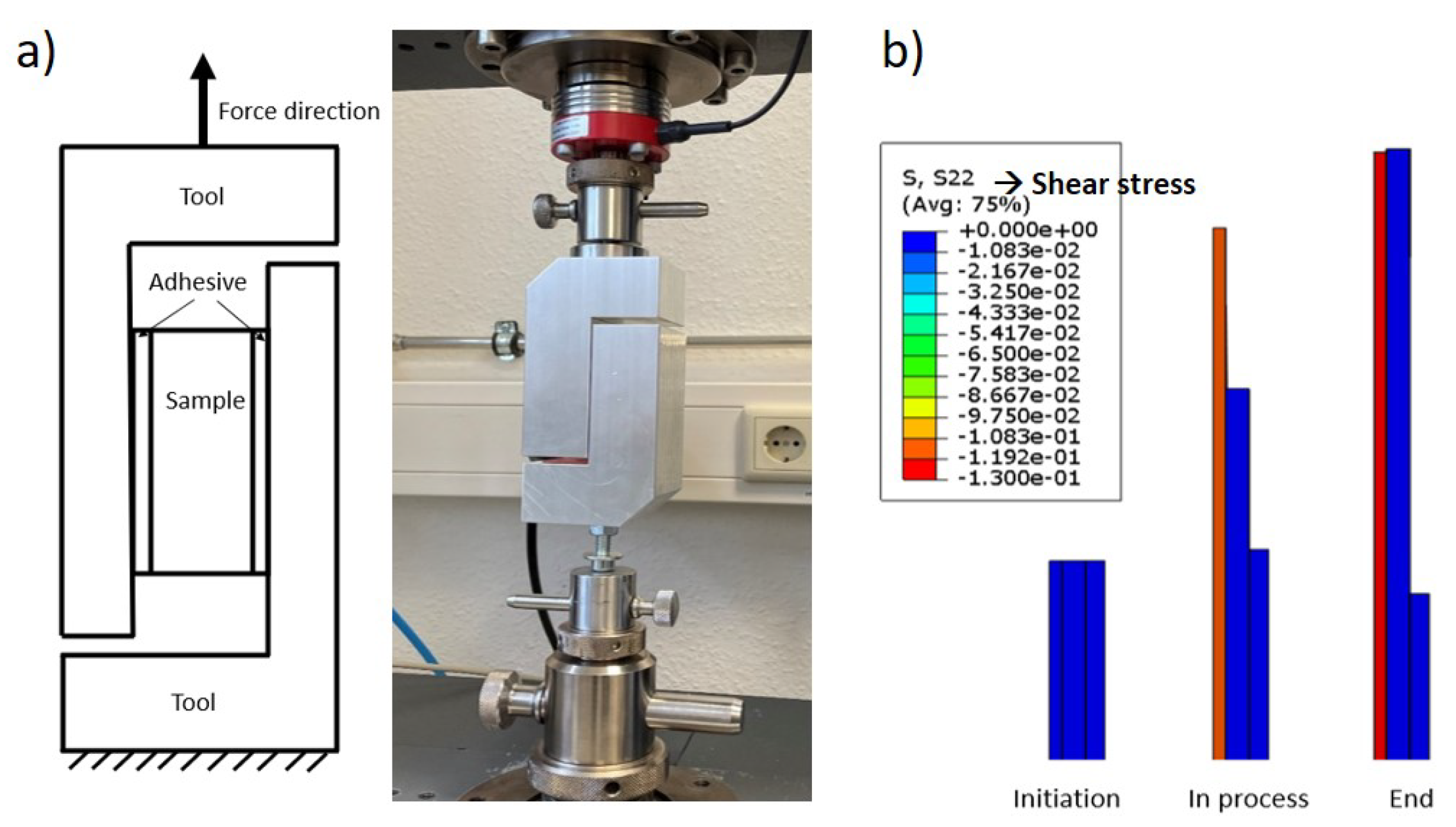
2.2.5. Out-of-Plane Shear Test
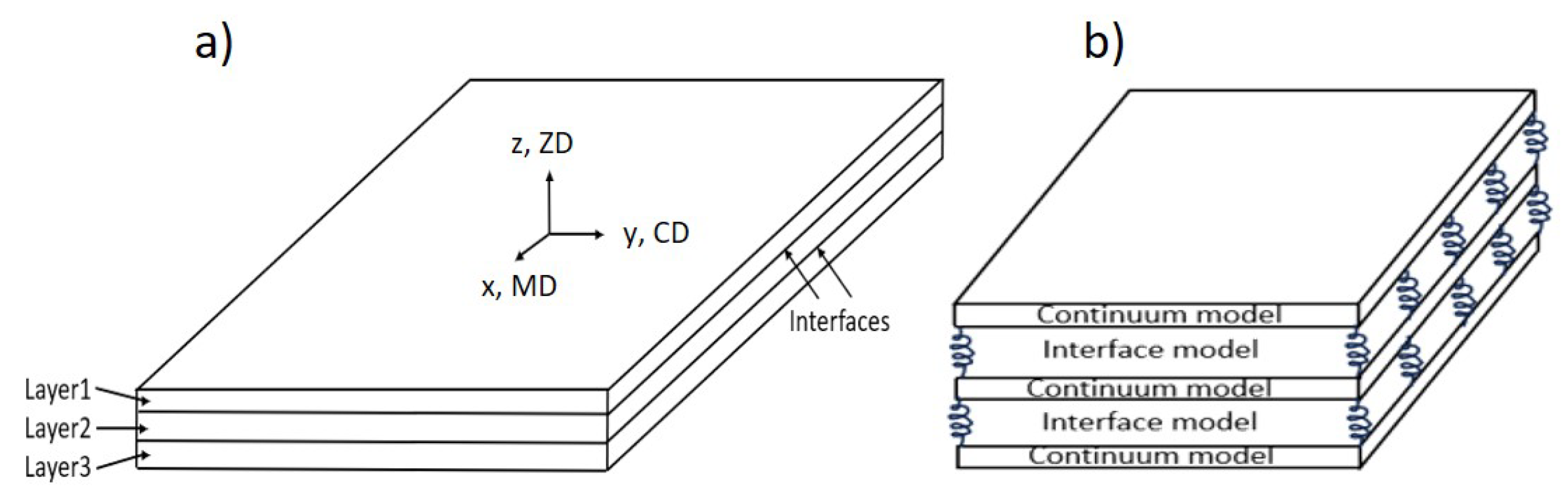
2.3. Material Modeling
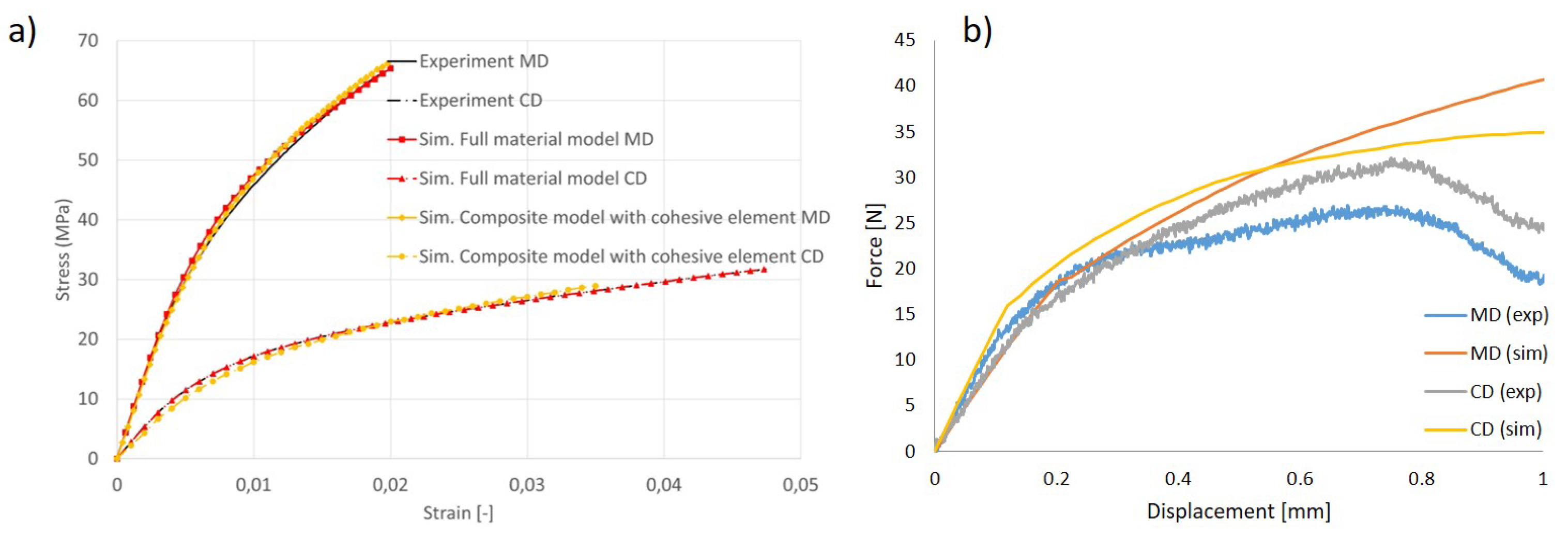
2.3.1. In-Plane Continuum Modeling and Validation
2.3.2. Out-of-Plane Interface Modeling
2.4. Validation Experiments and Deep Drawing Process
3. Results
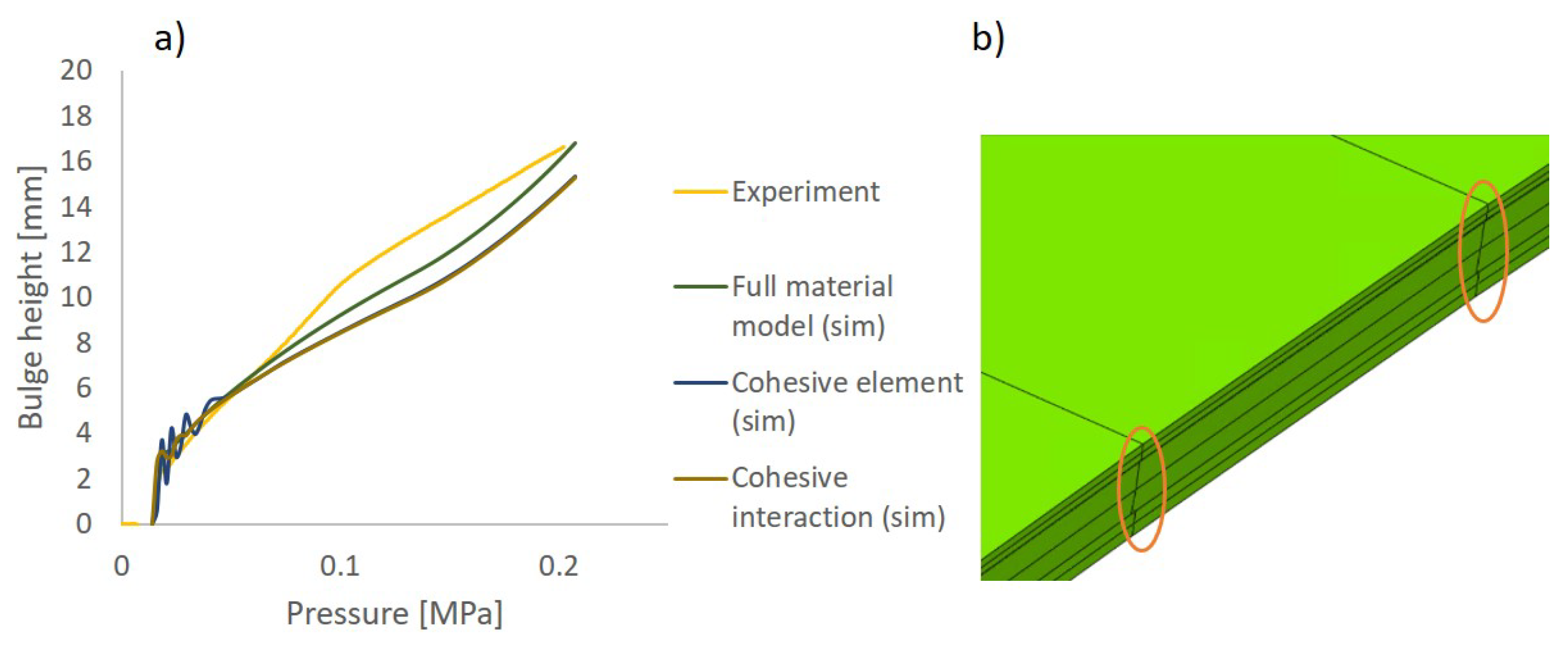
3.1. Validation Results of Bending and Bulge Tests
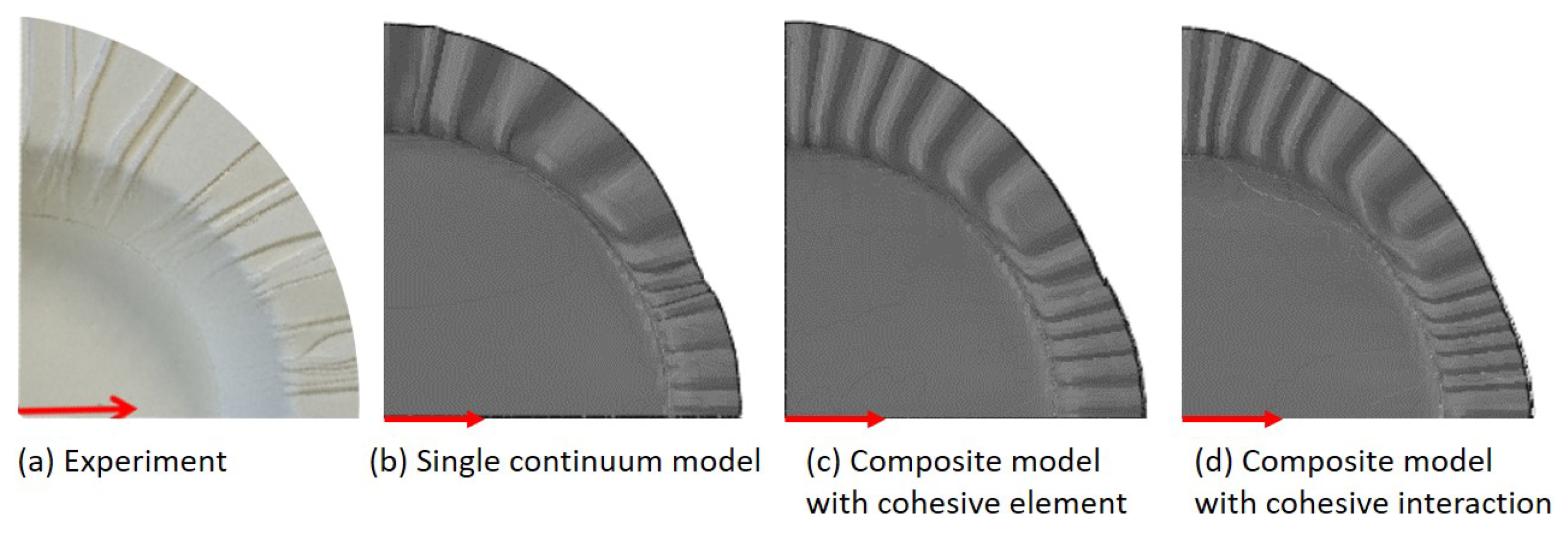
3.2. Simulation of Wrinkles in the Deep Drawing Process
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hagman, A.; Nygårds, M. Short compression testing of multi-ply paperboard, influence from shear strength. Nord. Pulp Pap. Res. J. 2016, 31, 123–134. [Google Scholar] [CrossRef]
- Simon, J.W. A review of recent trends and challenges in computational modeling of paper and paperboard at different scales. Arch. Comput. Methods Eng. 2021, 28, 2409–2428. [Google Scholar] [CrossRef]
- Wallmeier, M.; Linvill, E.; Hauptmann, M.; Majschak, J.P.; Östlund, S. Explicit FEM analysis of the deep drawing of paperboard. Mech. Mater. 2015, 89, 202–215. [Google Scholar] [CrossRef]
- Choi, D.D.; Lavrykov, S.A.; Ramarao, B.V. Delamination in the scoring and folding of paperboard. Tappi 2012, 11, 61–66. [Google Scholar] [CrossRef]
- Dunn, H.M. Micromechanisms of Paperboard Deformation. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2000. [Google Scholar]
- Stenberg, N. A model for the through-thickness elastic–plastic behaviour of paper. Int. J. Solids Struct. 2003, 46, 7483–7498. [Google Scholar] [CrossRef]
- Stenberg, N.; Fellers, C.; Östlund, S. Measuring the stress-strain properties of paperboard in the thickness direction. J. Pulp Pap. Sci. 2001, 27, 213–221. [Google Scholar]
- Byrd, V.L.; Setterholm, V.C.; Wichmann, J.F. Method for measuring the interlaminar shear properties of paper. TAPPI 1975, 58, 132–135. [Google Scholar]
- Qiu, Y.P.; Millan, M.; Lin, C.H.; Gerhardt, T.D. Nonlinear properties of high strength paperboards. J. Eng. Mater. Technol. 1999, 121, 272–277. [Google Scholar] [CrossRef]
- Nygårds, M.; Fellers, C.; Östlund, S. Measuring out-of-plane shear properties of paperboard. Journal of pulp and paper science 2007, 33, 105–109. [Google Scholar]
- Fellers, C.; Östlund, S.; Mäkelä, P. Evaluation of the Scott bond test method. Nord. Pulp Pap. Res. J. 2012, 27, 231–236. [Google Scholar] [CrossRef]
- Nygårds, M.; Just, M.; Tryding, J. Experimental and numerical studies of creasing of paperboard. Int. J. Solids Struct. 2009, 46, 2493–2505. [Google Scholar] [CrossRef]
- Stenberg, N.; Fellers, C.; Östlund, S. Plasticity in the thickness direction of paperboard under combined shear and normal loading. J. Eng. Mater. Technol. 2001, 123, 184–190. [Google Scholar] [CrossRef]
- Hallbäck, N.; Girlanda, O.; Tryding, J. Finite element analysis of ink-tack delamination of paperboard. Int. J. Solids Struct. 2006, 43, 899–912. [Google Scholar] [CrossRef]
- Xia, Q.S.; Boyce, M.C.; Parks, D.M. A constitutive model for the anisotropic elastic–plastic deformation of paper and paperboard. Int. J. Solids Struct. 2002, 39, 4053–4071. [Google Scholar] [CrossRef]
- Nygårds, M. Modelling the out-of-plane behaviour of paperboard. Nord. Pulp Pap. Res. J. 2008, 10, 142–149. [Google Scholar] [CrossRef]
- Borgqvist, E.; Wallin, M.; Ristinmaa, M.; Tryding, J. An anisotropic in-plane and out-of-plane elasto-plastic continuum model for paperboard. Compos. Struct. 2015, 126, 184–195. [Google Scholar] [CrossRef]
- Li, Y.; Stapleton, S.E.; Reese, S.; Simon, J.W. Anisotropic elastic-plastic deformation of paper: Out-of-plane model. Int. J. Solids Struct. 2018, 130, 172–182. [Google Scholar] [CrossRef]
- Simonetto, E.; Singh, P.; Ghiotti, A.; Bruschi, S.; Jessen, N.; Groche, P. Creasing and folding of paper-based sandwich material–Phenomena and modelling. CIRP Ann. 2024, 73, 221–224. [Google Scholar] [CrossRef]
- Arora, N.; Batan, A.; Li, J.; Slesarenko, V.; Rudykh, S. On the influence of inhomogeneous interphase layers on instabilities in hyperelastic composites. Materials 2019, 12, 763. [Google Scholar] [CrossRef]
- Greco, F.; Luciano, R.; Pranno, A. Effects of interfacial debonding on the stability of finitely strained periodic microstructured elastic composites. Philos. Trans. A 2024, 382, 20230356. [Google Scholar] [CrossRef]
- Awais, M.; Sorvari, J.; Tanninen, P.; Leppänen, T. Finite element analysis of the press forming process. Int. J. Mech. Sci. 2017, 131, 767–775. [Google Scholar] [CrossRef]
- Linvill, E.; Wallmeier, M.; Östlund, S. A constitutive model for paperboard including wrinkle prediction and post-wrinkle behavior applied to deep drawing. Int. J. Solids Struct. 2017, 117, 143–158. [Google Scholar] [CrossRef]
- Lindberg, G.; Kulachenko, A. Tray forming operation of paperboard: A case study using implicit finite element analysis. Packag. Technol. Sci. 2022, 35, 183–198. [Google Scholar] [CrossRef]
- Optimized Specimen for In-Plane Shear Test. Available online: https://www.lbf.fraunhofer.de/en/press-releases/in-plane-shear-test.html (accessed on 9 November 2020).
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. A 1948, 193, 281–297. [Google Scholar]
- Nygårds, M. Experimental techniques for characterization of elastic-plastic material properties in paperboard. Nord. Pulp Pap. Res. J. 2008, 23, 432–437. [Google Scholar] [CrossRef]
- Baum, G.A.; Habeger, C.C.; Fleischman, E.H. Measurement of the Orthotropic Elastic Constants of Paper; Trans. of Symp. on The Role of Fundamental Research in Paper Making: Appleton, Wisconsin, 1981; pp. 453–478.
- Huang, H.; Nygårds, M. MECHANICAL PULPING: Numerical and experimental investigation of paperboard folding. Nord. Pulp Pap. Res. J. 2011, 26, 452–467. [Google Scholar] [CrossRef]
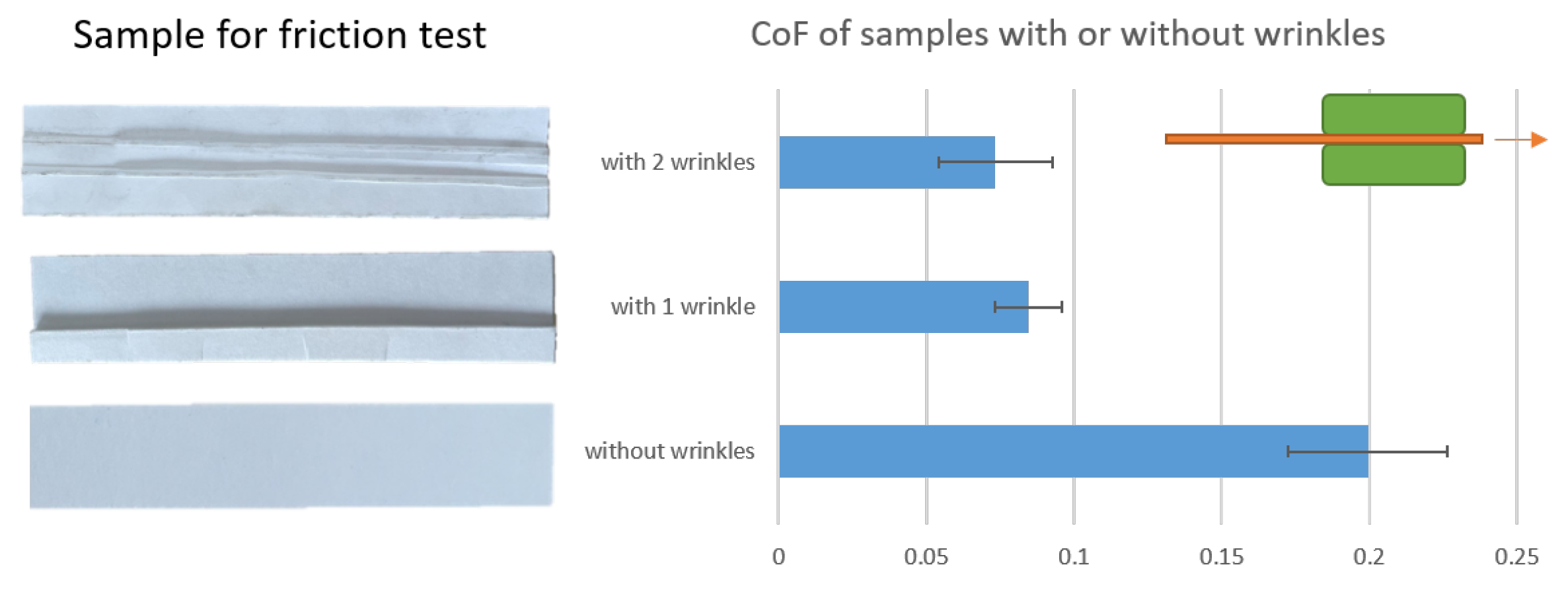
- Lenske, A.; Müller, T.; Penter, L.; Schneider, M.; Hauptmann, M.; Majschak, J. Evaluating the factors influencing the friction behavior of paperboard during the deep drawing process. BioResources 2017, 12, 8340–8358. [Google Scholar] [CrossRef]


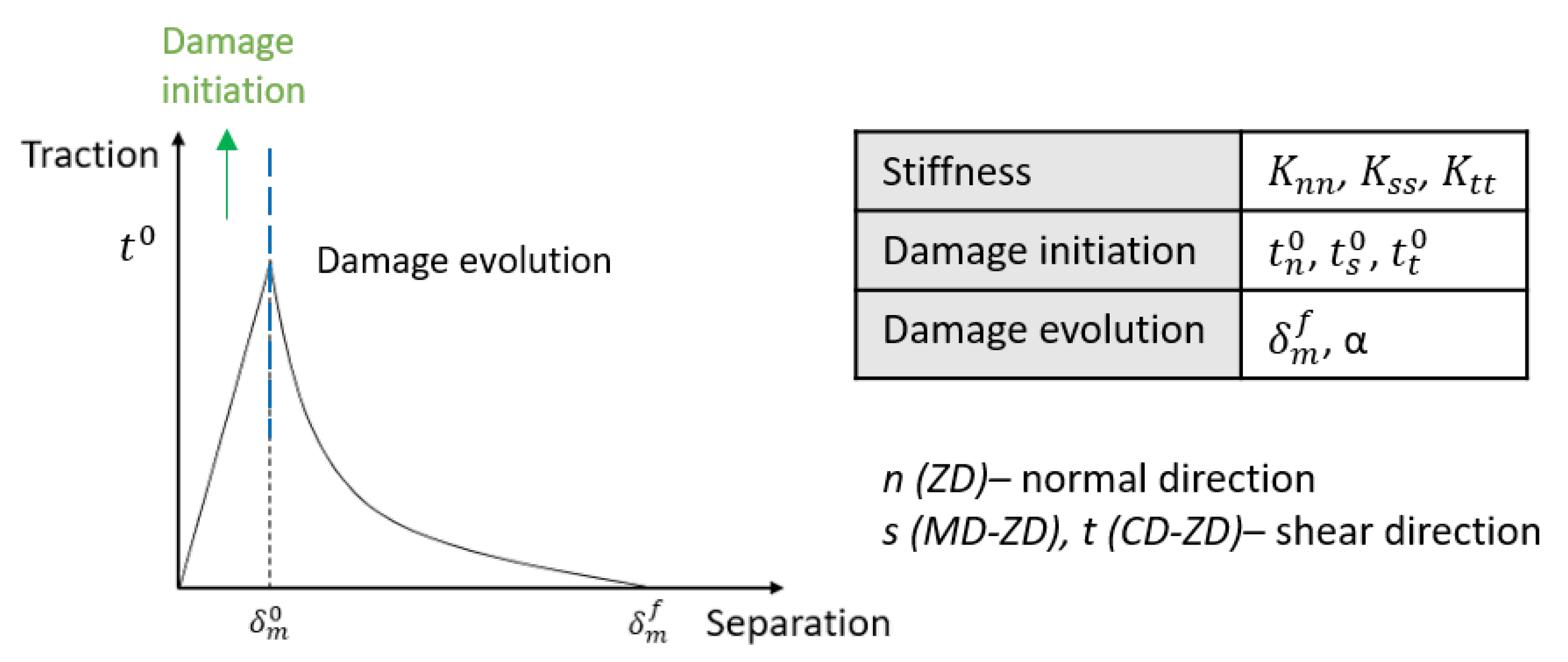
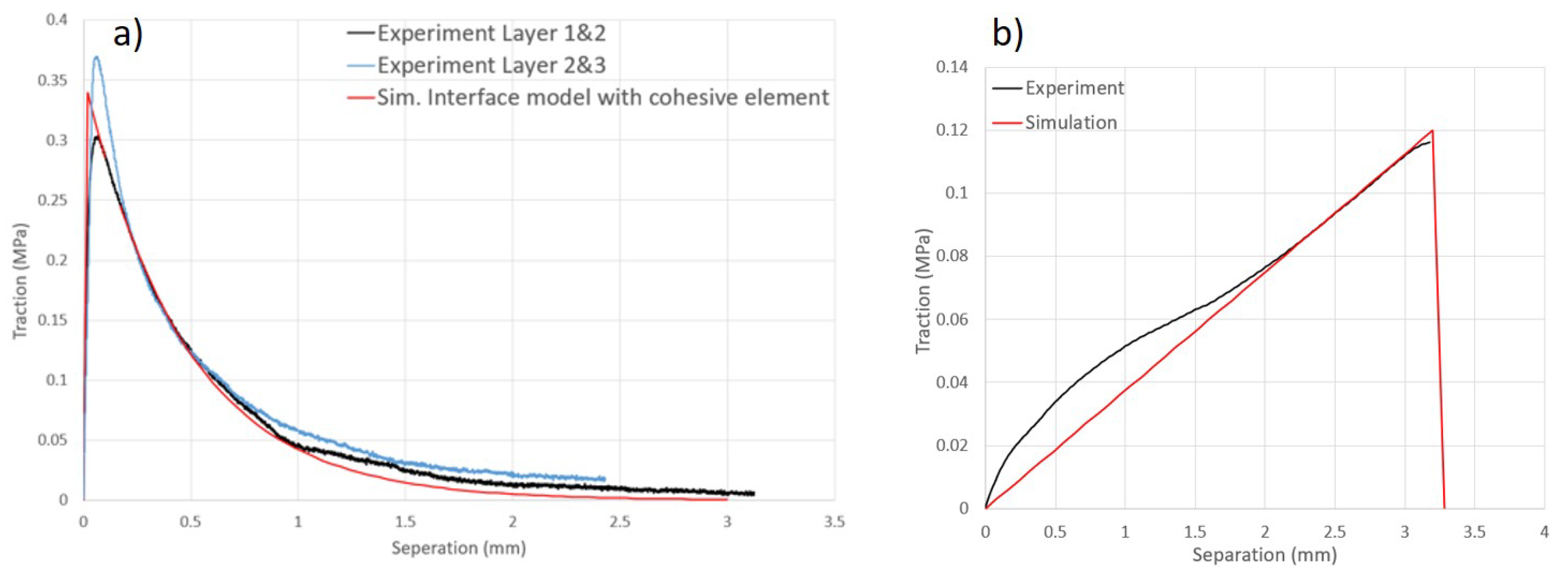
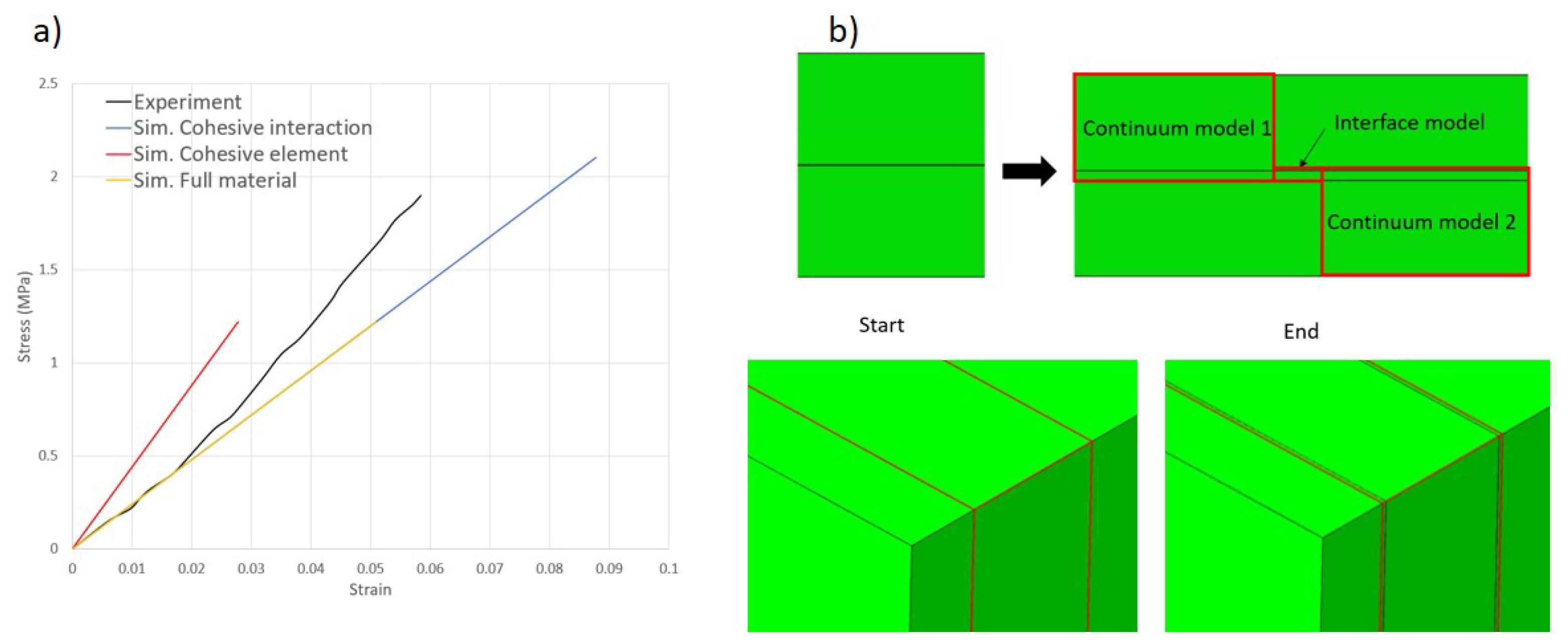
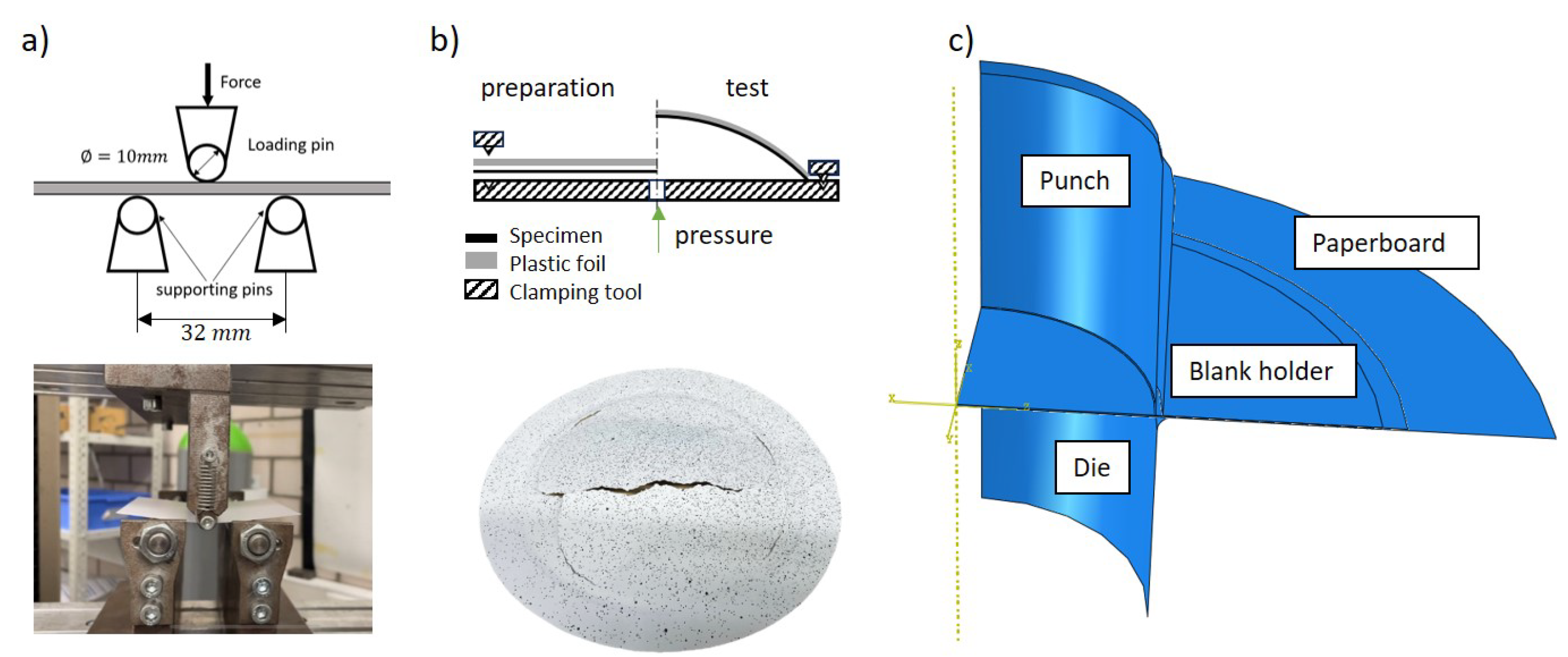




| Parameter [Unit] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | a | b | c | d | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Continuum | 7200 | 2750 | 24 | 1806 | 3.7 | −29.04 | 34.47 | 233.28 | 2.13 | 2.33 | 0.82 |
| Layer1 | 7100 | 2300 | 24 | 2421 | 5.4 | −93.55 | 21.88 | 688.79 | 1.56 | 2.52 | 0.97 |
| Layer2 | 5450 | 1650 | 24 | 1972 | 7.3 | −146.60 | 11.05 | 687.37 | 1.45 | 2.36 | 1 |
| Layer3 | 6650 | 2300 | 24 | 1744 | 6.5 | −31.84 | 24.70 | 271.53 | 1.90 | 2.22 | 0.9 |
| Parameter [Unit] | [MPa/mm] | [MPa/mm] | [MPa/mm] | [MPa] | [MPa] | [MPa] | [mm] | [-] |
|---|---|---|---|---|---|---|---|---|
| Constants | 25 | 0.075 | 0.075 | 0.34 | 0.12 | 0.12 | 5.2 | 11 |
| Parameter [Unit] | Geometric Parameter | Process Parameter | ||||
|---|---|---|---|---|---|---|
| Components | Paperboard | Punch | Blank Holder | Die | ||
| Distance to centerline [mm] | 0 | 0 | 41 | 40 | Friction coefficient [-] | 0.08 |
| Height [mm] | 0.42 | 58 | 50 | 50 | Blank holder force [N] | 1250 |
| Width/Radius [mm] | 65 | 39.55 | 49 | 80 | Drawing depth [mm] | 15 |
| Chamfer diameter [mm] | - | R 0.2 | 0 | R 3 | ||
| Model | Advantages | Disadvantages | Application |
|---|---|---|---|
| Single continuum mode |
|
| Processes without delamination, mainly in-plane deformation, such as 3D forming processes (deep drawing, press forming, and hydroforming) and embossing |
| Composite model with cohesive elements |
|
| Process with delamination, no apparent compressive stress in thickness direction, like folding and opening process of packaging |
| Composite model with cohesive interface |
|
| Process involving delamination with apparent compressive stress in the thickness direction, such as creasing and wrinkling in deep drawing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanjon, C.W.; Leng, Y.; Yan, Y.; Groche, P.; Hauptmann, M.; Ludat, N.; Majschak, J.-P. Characterization and Modeling of Out-of-Plane Behavior of Fiber-Based Materials: Numerical Illustration of Wrinkle in Deep Drawing. Materials 2024, 17, 4177. https://doi.org/10.3390/ma17174177
Sanjon CW, Leng Y, Yan Y, Groche P, Hauptmann M, Ludat N, Majschak J-P. Characterization and Modeling of Out-of-Plane Behavior of Fiber-Based Materials: Numerical Illustration of Wrinkle in Deep Drawing. Materials. 2024; 17(17):4177. https://doi.org/10.3390/ma17174177
Chicago/Turabian StyleSanjon, Cedric W., Yuchen Leng, Yi Yan, Peter Groche, Marek Hauptmann, Nicole Ludat, and Jens-Peter Majschak. 2024. "Characterization and Modeling of Out-of-Plane Behavior of Fiber-Based Materials: Numerical Illustration of Wrinkle in Deep Drawing" Materials 17, no. 17: 4177. https://doi.org/10.3390/ma17174177
APA StyleSanjon, C. W., Leng, Y., Yan, Y., Groche, P., Hauptmann, M., Ludat, N., & Majschak, J.-P. (2024). Characterization and Modeling of Out-of-Plane Behavior of Fiber-Based Materials: Numerical Illustration of Wrinkle in Deep Drawing. Materials, 17(17), 4177. https://doi.org/10.3390/ma17174177







