Materials Properties Prediction (MAPP): Empowering the Prediction of Material Properties Solely Based on Chemical Formulas
Abstract
1. Introduction
2. Materials and Methods
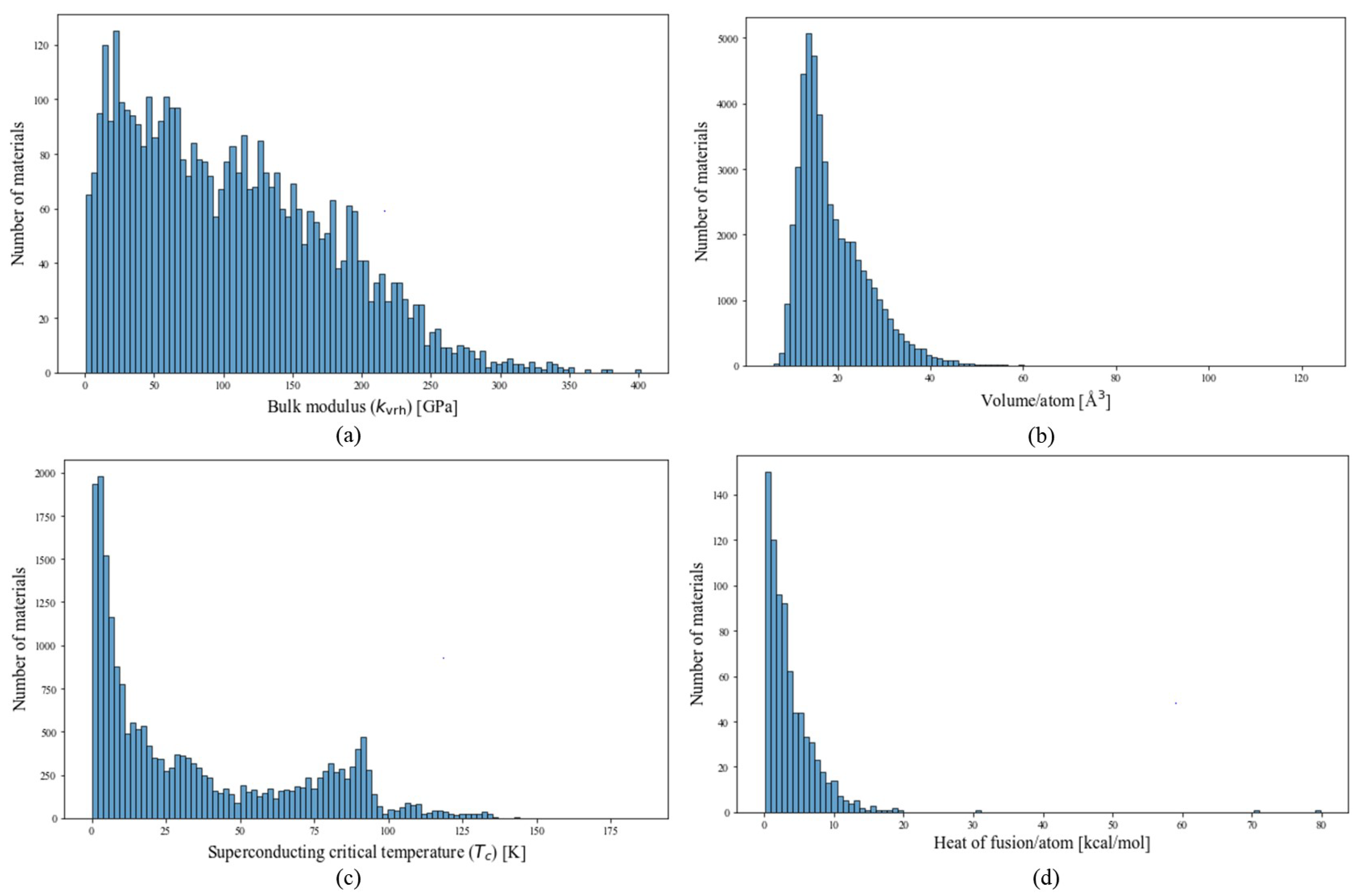
2.1. Data
2.1.1. Melting Temperature and Heat of Fusion
2.1.2. Bulk Modulus and Volume
2.1.3. Superconducting Critical Temperature
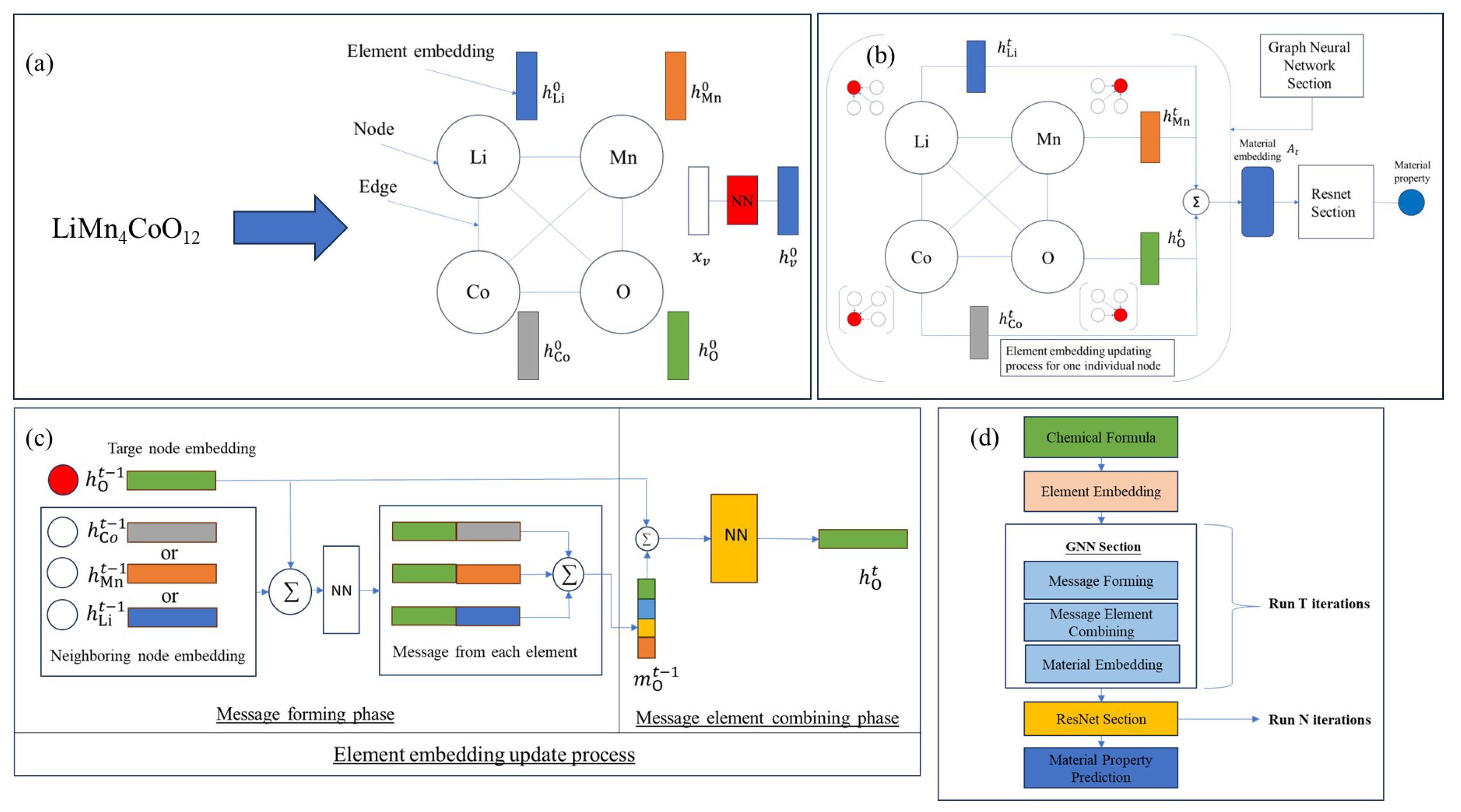
2.2. Model Architecture
2.2.1. Element Embedding
2.2.2. Graph Neural Network Section
2.2.3. Property Prediction Section with ResNet Architecture
2.2.4. Ensemble Model and Uncertainty Estimation
3. Results and Discussion
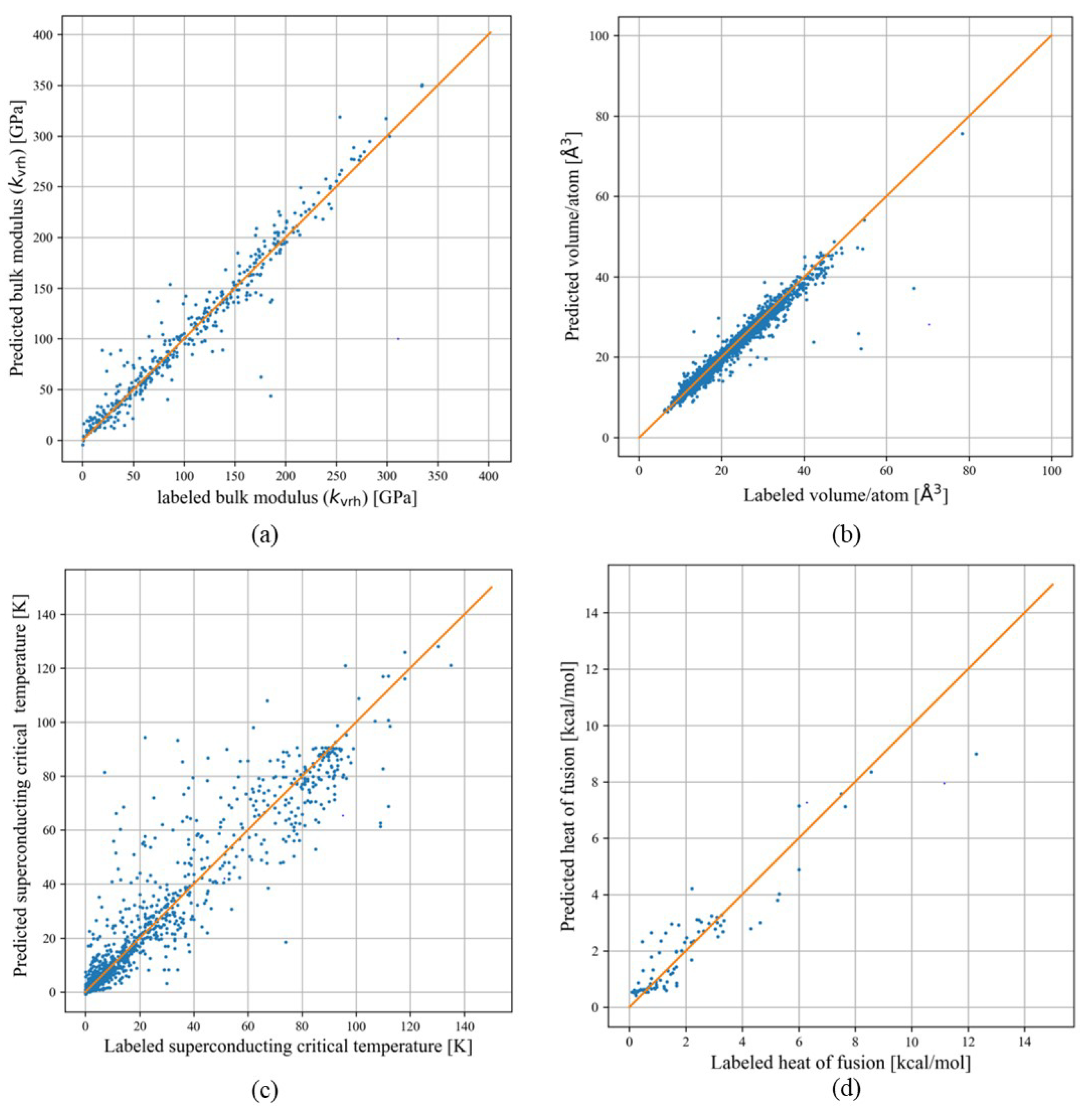
3.1. Bulk Modulus
3.2. Volume
3.3. Superconducting Critical Temperature
3.4. Heat of Fusion
3.5. Discussion
4. Conclusions
- Evaluate material properties across large datasets;
- Run interactive simulations for the design and discovery of materials with extreme properties;
- Include material properties as new features for their models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choudhary, K.; Garrity, K.F.; Reid, A.C.; DeCost, B.; Biacchi, A.J.; Hight Walker, A.R.; Trautt, Z.; Hattrick-Simpers, J.; Kusne, A.G.; Centrone, A.; et al. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. NPJ Comput. Mater. 2020, 6, 173. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. NPJ Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Wang, S.; Xue, J.; Yang, K.; Taylor, R.H.; Nelson, L.J.; Hart, G.L.; Sanvito, S.; Buongiorno-Nardelli, M.; et al. AFLOWLIB. ORG: A distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 2012, 58, 227–235. [Google Scholar] [CrossRef]
- Hellenbrandt, M. The inorganic crystal structure database (ICSD)—Present and future. Crystallogr. Rev. 2004, 10, 17–22. [Google Scholar] [CrossRef]
- Zakutayev, A.; Wunder, N.; Schwarting, M.; Perkins, J.D.; White, R.; Munch, K.; Tumas, W.; Phillips, C. An open experimental database for exploring inorganic materials. Sci. Data 2018, 5, 1–12. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Choudhary, K.; DeCost, B.; Chen, C.; Jain, A.; Tavazza, F.; Cohn, R.; Park, C.W.; Choudhary, A.; Agrawal, A.; Billinge, S.J.; et al. Recent advances and applications of deep learning methods in materials science. Npj Comput. Mater. 2022, 8, 59. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine learning and artificial neural network accelerated computational discoveries in materials science. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1450. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Jha, D.; Ward, L.; Paul, A.; Liao, W.k.; Choudhary, A.; Wolverton, C.; Agrawal, A. Elemnet: Deep learning the chemistry of materials from only elemental composition. Sci. Rep. 2018, 8, 17593. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Zheng, P.; Zhang, R.Z. Machine learning material properties from the periodic table using convolutional neural networks. Chem. Sci. 2018, 9, 8426–8432. [Google Scholar] [CrossRef]
- Le, T.D.; Noumeir, R.; Quach, H.L.; Kim, J.H.; Kim, J.H.; Kim, H.M. Critical temperature prediction for a superconductor: A variational bayesian neural network approach. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Schmidt, J.; Pettersson, L.; Verdozzi, C.; Botti, S.; Marques, M.A. Crystal graph attention networks for the prediction of stable materials. Sci. Adv. 2021, 7, eabi7948. [Google Scholar] [CrossRef] [PubMed]
- Allotey, J.; Butler, K.T.; Thiyagalingam, J. Entropy-based active learning of graph neural network surrogate models for materials properties. J. Chem. Phys. 2021, 155, 174116. [Google Scholar] [CrossRef]
- Stanev, V.; Oses, C.; Kusne, A.G.; Rodriguez, E.; Paglione, J.; Curtarolo, S.; Takeuchi, I. Machine learning modeling of superconducting critical temperature. NPJ Comput. Mater. 2018, 4, 29. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Bi, S.; Yin, J.; Zhang, G.; Eisenbach, M. Robust data-driven approach for predicting the configurational energy of high entropy alloys. Mater. Des. 2020, 185, 108247. [Google Scholar] [CrossRef]
- Hong, Q.J.; van de Walle, A.; Ushakov, S.V.; Navrotsky, A. Integrating computational and experimental thermodynamics of refractory materials at high temperature. Calphad 2022, 79, 102500. [Google Scholar] [CrossRef]
- Hong, Q.J.; Ushakov, S.V.; van de Walle, A.; Navrotsky, A. Melting temperature prediction using a graph neural network model: From ancient minerals to new materials. Proc. Natl. Acad. Sci. USA 2022, 119, e2209630119. [Google Scholar] [CrossRef] [PubMed]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Glushko, V.P.; Gurvich, L. Thermodynamic Properties of Individual Substances: Volume 1, Parts 1 and 2. 1988. Available online: https://www.osti.gov/biblio/6862010 (accessed on 20 August 2024).
- Database of Thermodynamic Properties of Individual Substances. Available online: http://www.chem.msu.su/cgi-bin/tkv.pl?show=welcome.html (accessed on 7 July 2024).
- Hong, Q.J.; van de Walle, A. Direct first-principles chemical potential calculations of liquids. J. Chem. Phys. 2012, 137, 094114. [Google Scholar] [CrossRef]
- Hong, Q.J.; van de Walle, A. Solid-liquid coexistence in small systems: A statistical method to calculate melting temperatures. J. Chem. Phys. 2013, 139, 094114. [Google Scholar] [CrossRef] [PubMed]
- Hong, Q.J.; van de Walle, A. A user guide for SLUSCHI: Solid and Liquid in Ultra Small Coexistence with Hovering Interfaces. Calphad 2016, 52, 88–97. [Google Scholar] [CrossRef]
- Hong, Q.J.; Liu, Z.K. A generalized approach for rapid entropy calculation of liquids and solids. arXiv 2024, arXiv:2403.19872. [Google Scholar]
- Hamidieh, K. A data-driven statistical model for predicting the critical temperature of a superconductor. Comput. Mater. Sci. 2018, 154, 346–354. [Google Scholar] [CrossRef]
- Materials Data Repository SuperCon Datasheet. Available online: https://mdr.nims.go.jp/collections/5712mb227 (accessed on 7 July 2024).
- Zeng, S.; Zhao, Y.; Li, G.; Wang, R.; Wang, X.; Ni, J. Atom table convolutional neural networks for an accurate prediction of compounds properties. NPJ Comput. Mater. 2019, 5, 84. [Google Scholar] [CrossRef]
- Konno, T.; Kurokawa, H.; Nabeshima, F.; Sakishita, Y.; Ogawa, R.; Hosako, I.; Maeda, A. Deep learning model for finding new superconductors. Phys. Rev. B 2021, 103, 014509. [Google Scholar] [CrossRef]
- Gilmer, J.; Schoenholz, S.S.; Riley, P.F.; Vinyals, O.; Dahl, G.E. Neural message passing for quantum chemistry. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1263–1272. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778, ISSN 1063-6919. [Google Scholar] [CrossRef]
- Mansouri Tehrani, A.; Oliynyk, A.O.; Parry, M.; Rizvi, Z.; Couper, S.; Lin, F.; Miyagi, L.; Sparks, T.D.; Brgoch, J. Machine Learning Directed Search for Ultraincompressible, Superhard Materials. J. Am. Chem. Soc. 2018, 140, 9844–9853. [Google Scholar] [CrossRef] [PubMed]
- Kaner, R.B.; Gilman, J.J.; Tolbert, S.H. Designing Superhard Materials. Science 2005, 308, 1268–1269. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Mann, A. High-temperature superconductivity at 25: Still in suspense. Nature 2011, 475, 280–282. [Google Scholar] [CrossRef] [PubMed]
- Bednorz, J.G.; Müller, K.A. Possible high T c superconductivity in the Ba- La- Cu- O system. Z. Für Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Crawshaw, M. Multi-task learning with deep neural networks: A survey. arXiv 2020, arXiv:2009.09796. [Google Scholar]
- Hong, Q.J. Melting temperature prediction via first principles and deep learning. Comput. Mater. Sci. 2022, 214, 111684. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [PubMed]
- Hong, Q.J. MAPP. 2023. Available online: https://faculty.engineering.asu.edu/hong/materials-properties-prediction-mapp/ (accessed on 7 July 2024).
- MAPP-API. Available online: https://github.com/qjhong/mapp_api (accessed on 7 July 2024).


| Model Type | Single Model | Ensemble Mode | ||||
|---|---|---|---|---|---|---|
| Material Properties | Score | RMSE | MAE | Score | RMSE | MAE |
| Bulk modulus () [GPa] | 0.95 | 17.04 | 9.96 | 0.93 | 19.41 | 11.2 |
| Unit cell volume/atom [] | 0.97 | 1.56 | 0.65 | 0.97 | 1.36 | 0.84 |
| Superconducting critical temperature () [K] | 0.91 | 10.16 | 6.91 | 0.88 | 12.64 | 7.54 |
| Heat of fusion/atom [kcal/mol] | - | - | - | 0.70 | 1.15 | 0.74 |
| Heat of fusion/atom (multi-task learning) [kcal/mol] | - | - | - | 0.74 | 1.01 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, S.-D.; Hong, Q.-J. Materials Properties Prediction (MAPP): Empowering the Prediction of Material Properties Solely Based on Chemical Formulas. Materials 2024, 17, 4176. https://doi.org/10.3390/ma17174176
Xue S-D, Hong Q-J. Materials Properties Prediction (MAPP): Empowering the Prediction of Material Properties Solely Based on Chemical Formulas. Materials. 2024; 17(17):4176. https://doi.org/10.3390/ma17174176
Chicago/Turabian StyleXue, Si-Da, and Qi-Jun Hong. 2024. "Materials Properties Prediction (MAPP): Empowering the Prediction of Material Properties Solely Based on Chemical Formulas" Materials 17, no. 17: 4176. https://doi.org/10.3390/ma17174176
APA StyleXue, S.-D., & Hong, Q.-J. (2024). Materials Properties Prediction (MAPP): Empowering the Prediction of Material Properties Solely Based on Chemical Formulas. Materials, 17(17), 4176. https://doi.org/10.3390/ma17174176






