Inductive Determination of Rate-Reaction Equation Parameters for Dislocation Structure Formation Using Artificial Neural Network
Abstract
1. Introduction
2. Methodology
2.1. Reaction-Diffusion Equation by Walgraef-Aifantis
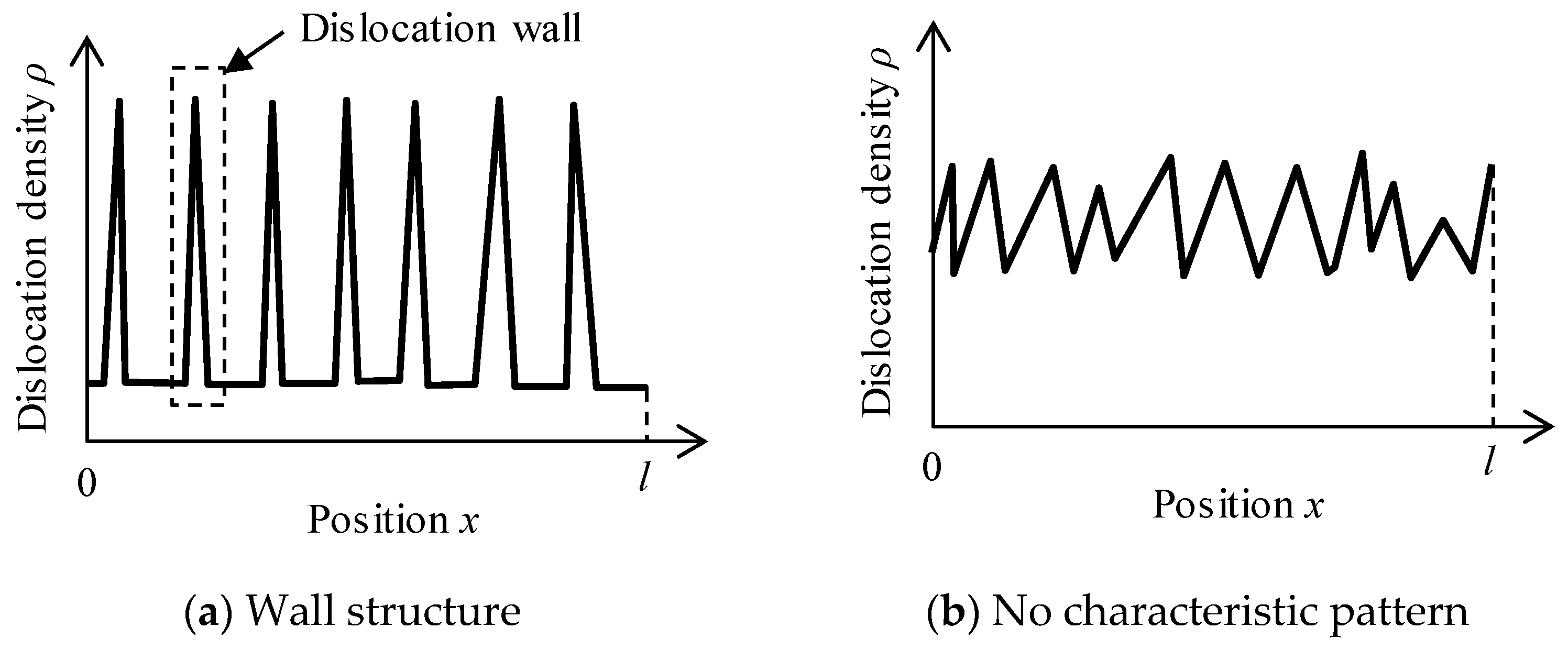
2.2. Characterization of Resulting Dislocation Structure
2.3. Mapping of WA Parameters and Resulting Dislocation Structure
2.3.1. Structure of Artificial Neural Network model
2.3.2. Training of ANN
2.3.3. Test of ANN
3. Results and Discussion
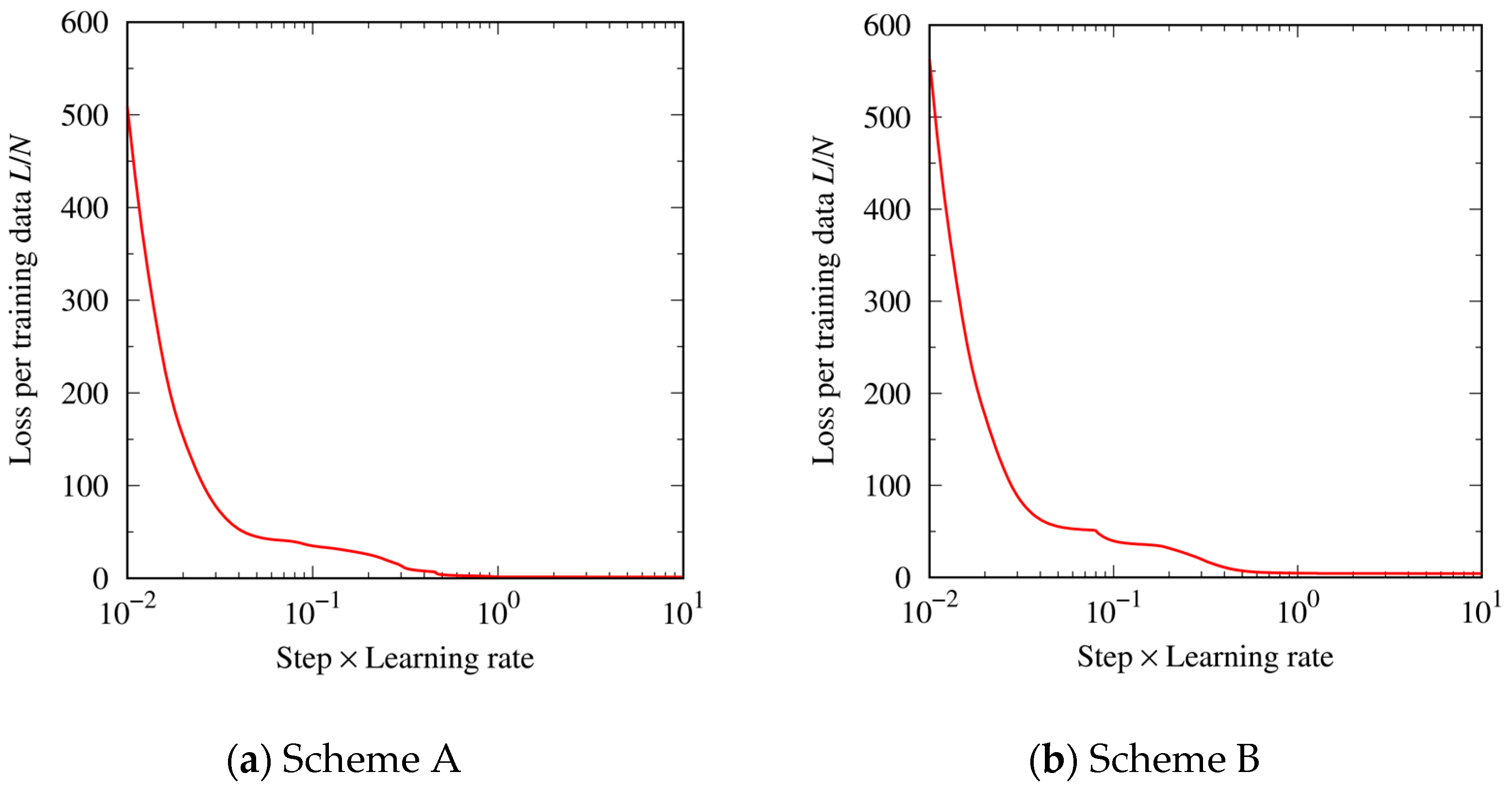
3.1. Training of ANN
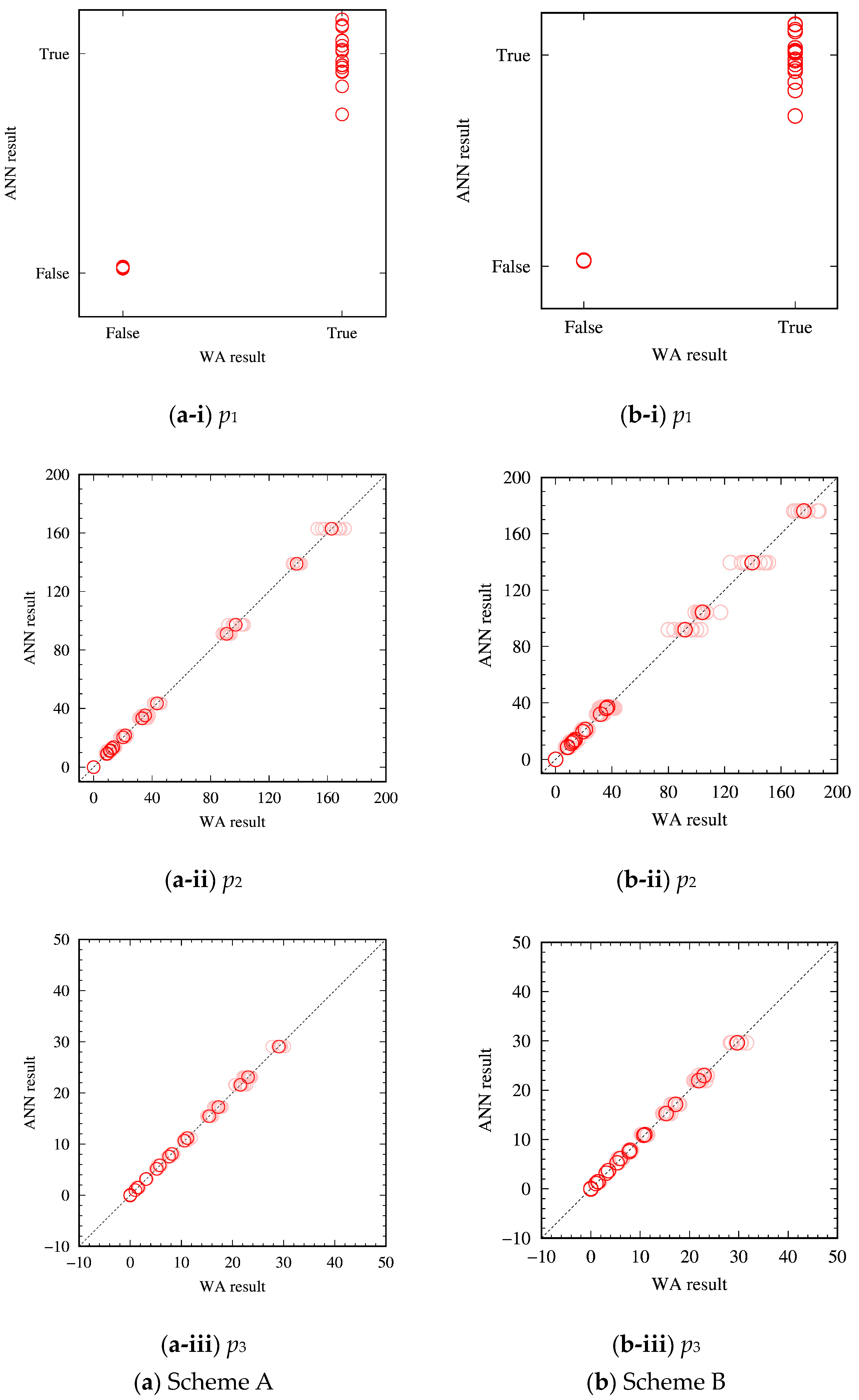
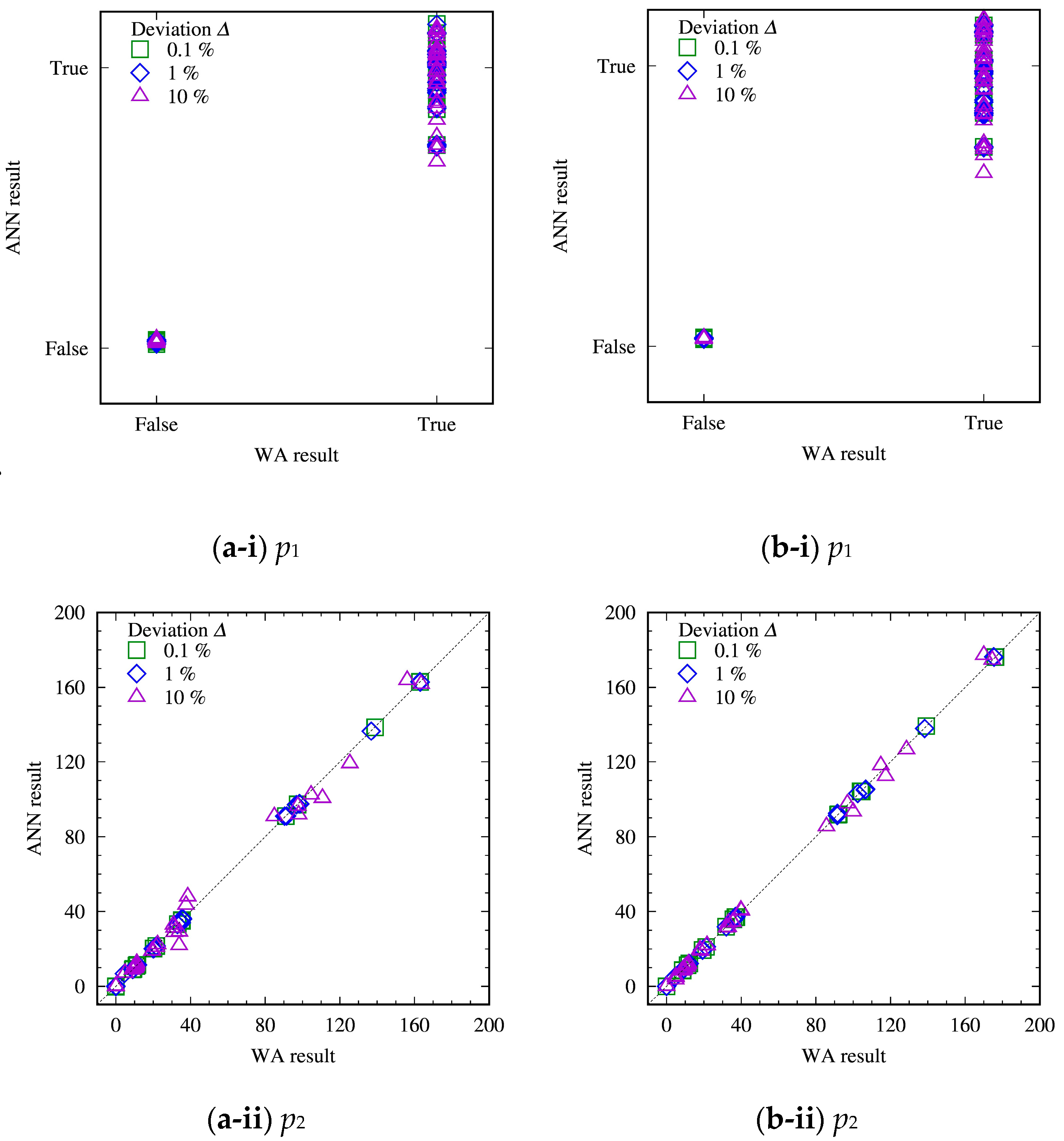
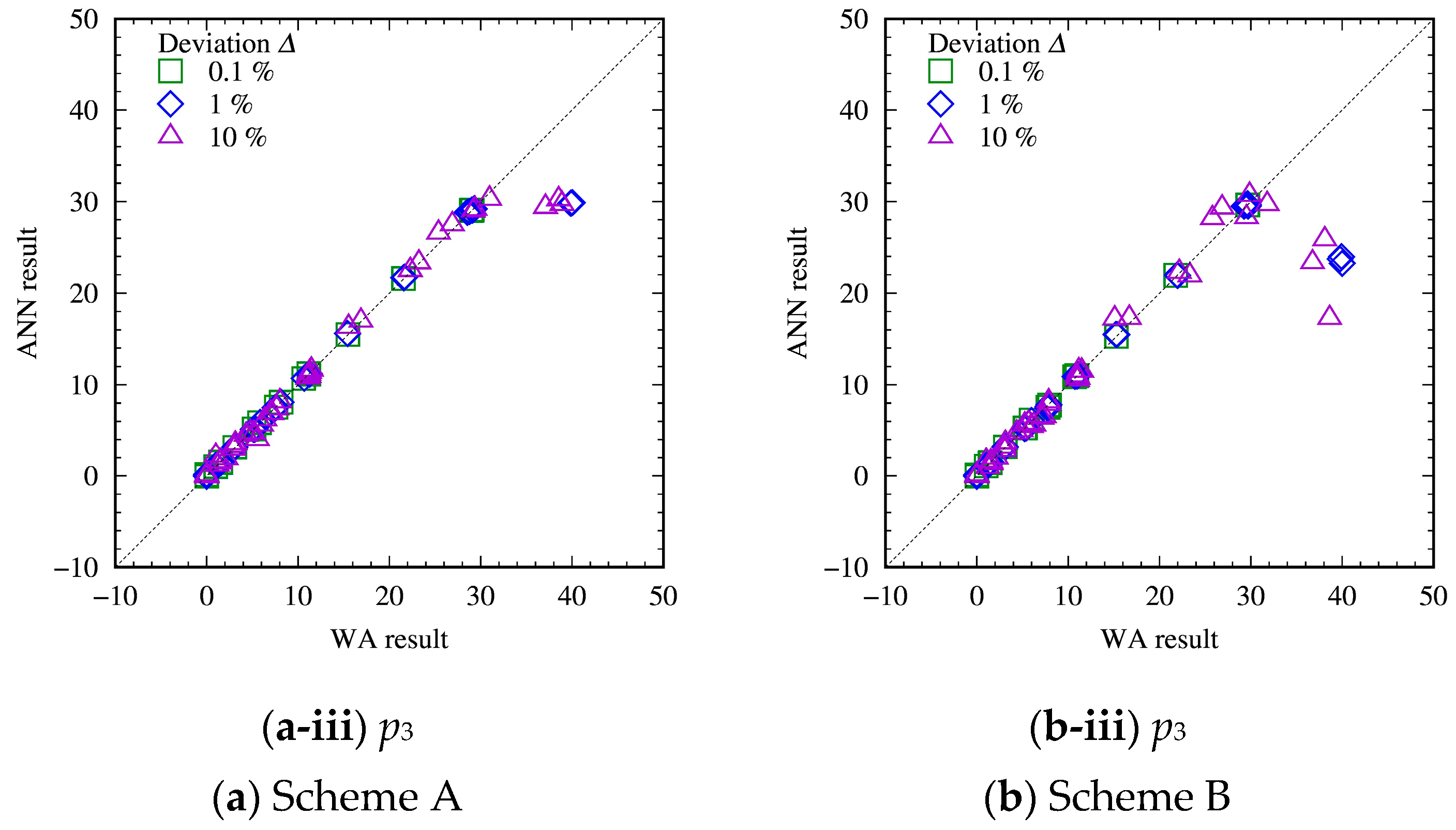
3.2. Evaluation of ANN with Test Datasets
3.3. Possibility of Inductive Construction of a Simulation Model
- (A)
- Finding solution of partial differential equationsThe function forms and parameters of partial differential equations (PDEs) are known. Initial and boundary conditions are given at discrete sampling points. A neural network mimicking the solution of the PDEs is to be found.
- (B)
- Finding parameter of partial differential equationsThe function forms of PDEs are known while their parameters are unknown. The solution of the PDEs is given at discrete sampling points. A neural network as the solution of the PDEs is to be found, resulting in the determination of the PDE parameters.
- (C)
- Finding latent physical quantities in observationsThe function forms and parameters of PDEs are known. A physical quantity in the considered system is given by observation. A neural network giving the observed physical quantity and other (latent) physical quantities appearing in the PDEs is to be found so that the prediction of the quantities is consistent with the observation and the PDEs.
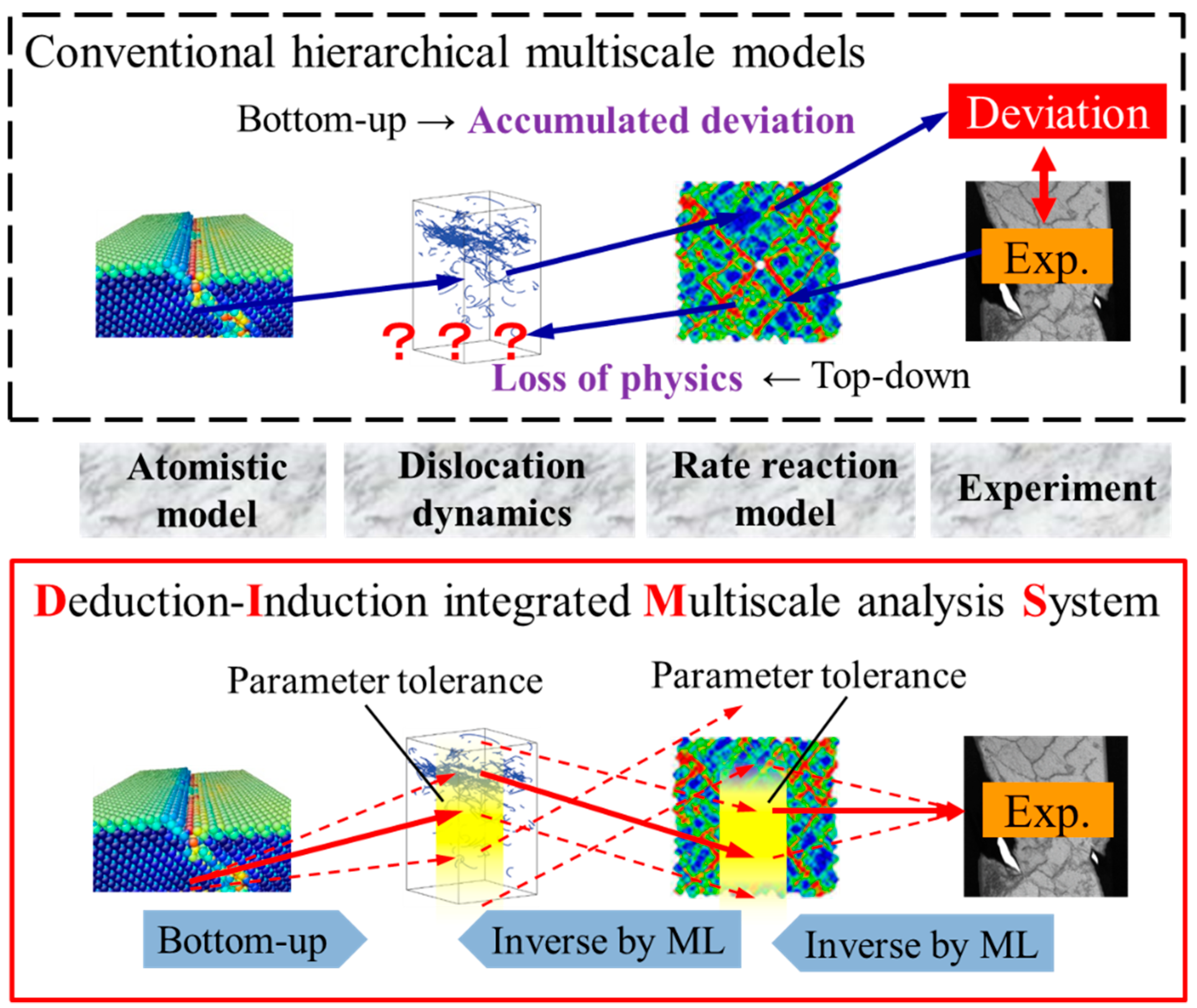
3.4. Integration of Deduction and Induction Approaches in Multiscale Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Auxiliary parameter for Equations (5)–(7) | |
| Diffusion coefficient of immobile dislocation | |
| Diffusion coefficient of mobile dislocation | |
| Uniform random number | |
| Activation function | |
| L | Loss function |
| Simulation cell size for WA equation | |
| Mean free path of immobile dislocation | |
| Number of test data | |
| ANN output | |
| Training data | |
| Reference data | |
| Uniform random number | |
| Time | |
| Effective velocity of mobile dislocation | |
| Bias parameter | |
| Weight parameter | |
| Position | |
| State of ANN nodes | |
| Walgraef–Aifantis parameter | |
| Walgraef–Aifantis parameter | |
| sampled for machine learning | |
| Critical value of at Turing instability | |
| Critical value of at Hopf bifurcation | |
| Walgraef–Aifantis parameter | |
| Deviation for test dataset | |
| Density of immobile dislocation | |
| Density of mobile dislocation | |
| Maximum dislocation density | |
| Minimum dislocation density | |
| Threshold dislocation density | |
| Walgraef–Aifantis parameter |
Appendix A
| Immobile Dislocation | Mobile Dislocation | |
|---|---|---|
| 17 | 23 | |
| 0.5 | 0.5 | |
| 6 | 6 | |
| 1.0 | 1.0 | |
| 0.2 | 0.2 |
References
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012; pp. 53–79. [Google Scholar]
- Sumigawa, T.; Uegaki, S.; Yukishita, T.; Arai, S.; Takahashi, Y.; Kitamura, T. FE-SEM in situ observation of damage evolution in tension-compression fatigue of micro-sized single-crystal copper. Mater. Sci. Eng. A 2019, 764, 138218. [Google Scholar] [CrossRef]
- Sumigawa, T.; Hikasa, K.; Kusunose, A.; Unno, H.; Masuda, K.; Shimada, T.; Kitamura, T. In situ TEM observation of nanodomain mechanics in barium titanate under external loads. Phys. Rev. Mater. 2020, 4, 054415. [Google Scholar] [CrossRef]
- Lavenstein, S.; Gu, Y.; Madisetti, D.; El-Awady, J.A. The heterogeneity of persistent slip band nucleation and evolution in metals at the micrometer scale. Science 2020, 370, 190. [Google Scholar] [CrossRef] [PubMed]
- Walgraef, D.; Aifantis, E.C. Dislocation patterning in fatigued metals as a result of dynamical instabilities. J. Appl. Phys. 1985, 58, 688–691. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the formation and stability of dislocation patterns—I: One-dimensional considerations. Int. J. Eng. Sci. 1985, 23, 1351–1358. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the formation and stability of dislocation patterns—II: Two-dimensional considerations. Int. J. Eng. Sci. 1985, 23, 1359–1364. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On the dynamical origin of dislocation patterns—III: Three-dimensional considerations. Int. J. Eng. Sci. 1985, 23, 1365–1372. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the dynamical origin of dislocation patterns. Mater. Sci. Eng. 1986, 81, 563–574. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. Dislocation patterning in fatigued metals: Labyrinth structures and rotational effects. Int. J. Eng. Sci. 1986, 24, 1789–1798. [Google Scholar] [CrossRef]
- Romanov, A.E.; Aifantis, E.C. On the kinetic and diffusional nature of linear defects. Scr. Metall. Mater. 1993, 29, 707–712. [Google Scholar] [CrossRef]
- Aifantis, E.C. Non-linearity, periodicity and patterning in plasticity and fracture. Int. J. Non-Linear Mech. 1996, 31, 797–809. [Google Scholar] [CrossRef]
- Walgraef, D.; Aifantis, E.C. On certain problems of deformation-induced material instabilities. Int. J. Eng. Sci. 2012, 59, 140–155. [Google Scholar] [CrossRef]
- Spiliotis, K.G.; Russo, L.; Siettos, C.; Aifantis, E.C. Analytical and numerical bifurcation analysis of dislocation pattern formation of the Walgraef–Aifantis model. Int. J. Non-Linear Mech. 2018, 102, 41–52. [Google Scholar] [CrossRef]
- Schiller, C.; Walgraef, D. Numerical simulation of persistent slip band formation. Acta Metall. 1988, 36, 563–574. [Google Scholar] [CrossRef]
- Saito, Y. Deep Learning from Scratch; O’Reilly Japan: Tokyo, Japan, 2016; pp. 39–122. [Google Scholar]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Inferring solutions of differential equations using noisy multi-fidelity data. J. Comput. Phys. 2017, 335, 736–746. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 2017, 348, 683–693. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Numerical Gaussian Processes for Time-Dependent and Nonlinear Partial Differential Equations. SIAM J. Sci. Comput. 2018, 40, A172–A198. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Fan, J. Multiscale Analysis of Deformation and Failure of Materials; John Wiley & Sons. Ltd.: Chichester, UK, 2011; pp. 261–341. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umeno, Y.; Kawai, E.; Kubo, A.; Shima, H.; Sumigawa, T. Inductive Determination of Rate-Reaction Equation Parameters for Dislocation Structure Formation Using Artificial Neural Network. Materials 2023, 16, 2108. https://doi.org/10.3390/ma16052108
Umeno Y, Kawai E, Kubo A, Shima H, Sumigawa T. Inductive Determination of Rate-Reaction Equation Parameters for Dislocation Structure Formation Using Artificial Neural Network. Materials. 2023; 16(5):2108. https://doi.org/10.3390/ma16052108
Chicago/Turabian StyleUmeno, Yoshitaka, Emi Kawai, Atsushi Kubo, Hiroyuki Shima, and Takashi Sumigawa. 2023. "Inductive Determination of Rate-Reaction Equation Parameters for Dislocation Structure Formation Using Artificial Neural Network" Materials 16, no. 5: 2108. https://doi.org/10.3390/ma16052108
APA StyleUmeno, Y., Kawai, E., Kubo, A., Shima, H., & Sumigawa, T. (2023). Inductive Determination of Rate-Reaction Equation Parameters for Dislocation Structure Formation Using Artificial Neural Network. Materials, 16(5), 2108. https://doi.org/10.3390/ma16052108








