Near-Surface-Defect Detection in Countersunk Head Riveted Joints Based on High-Frequency EMAT
Abstract
1. Introduction
- The propagation of ultrasonic waves in a CHRJ with a defect is analyzed using the theory of the reflection and transmission of ultrasonic waves.
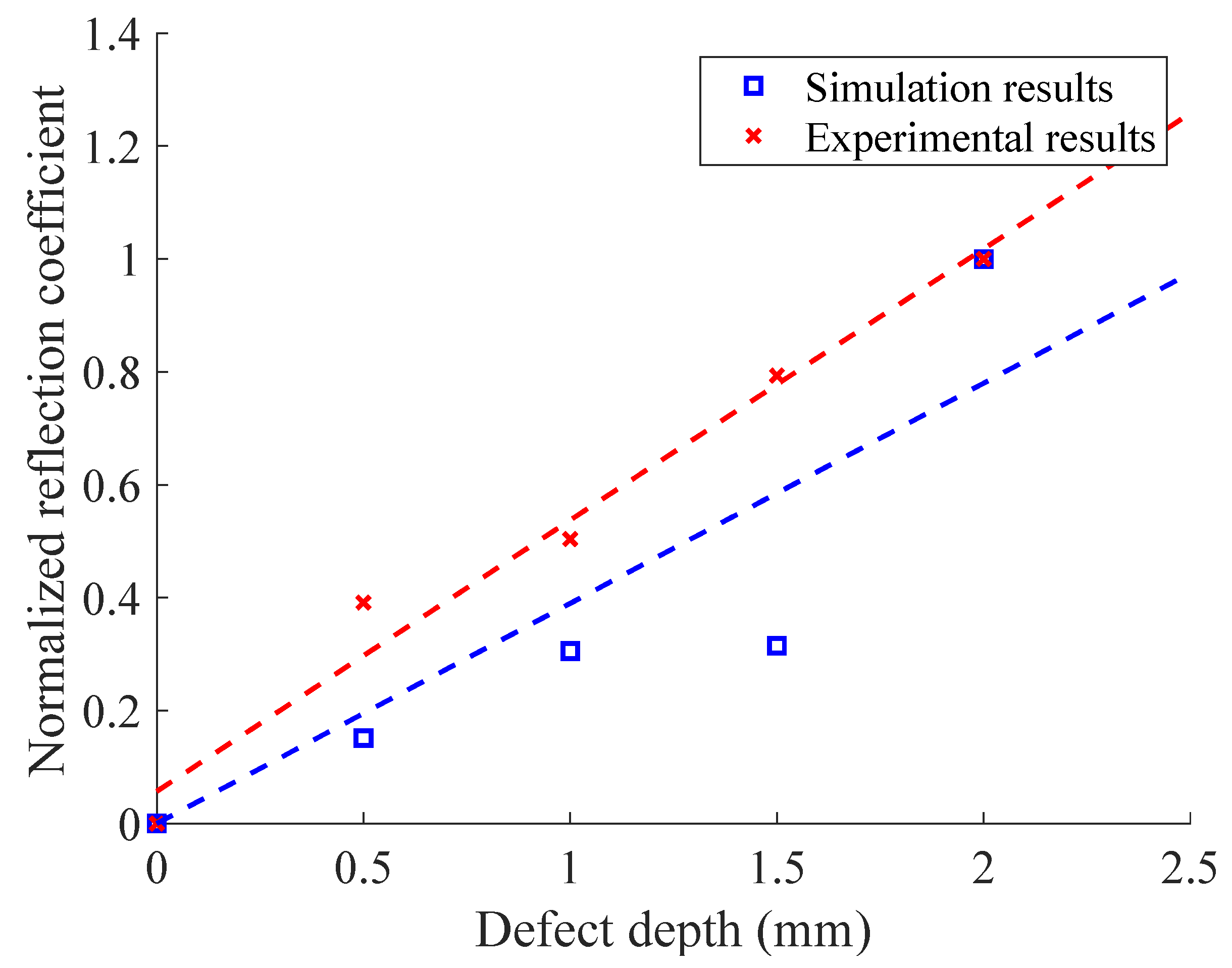
- The principle of defect-echo generation is studied using the FES, and the relationship between the defect depth and the reflection coefficient is investigated.
- An experimental verification of the simulation results was performed, the experimental signal was processed using the WTD, and the simulation results were in good agreement with the experimental results.
2. Theory
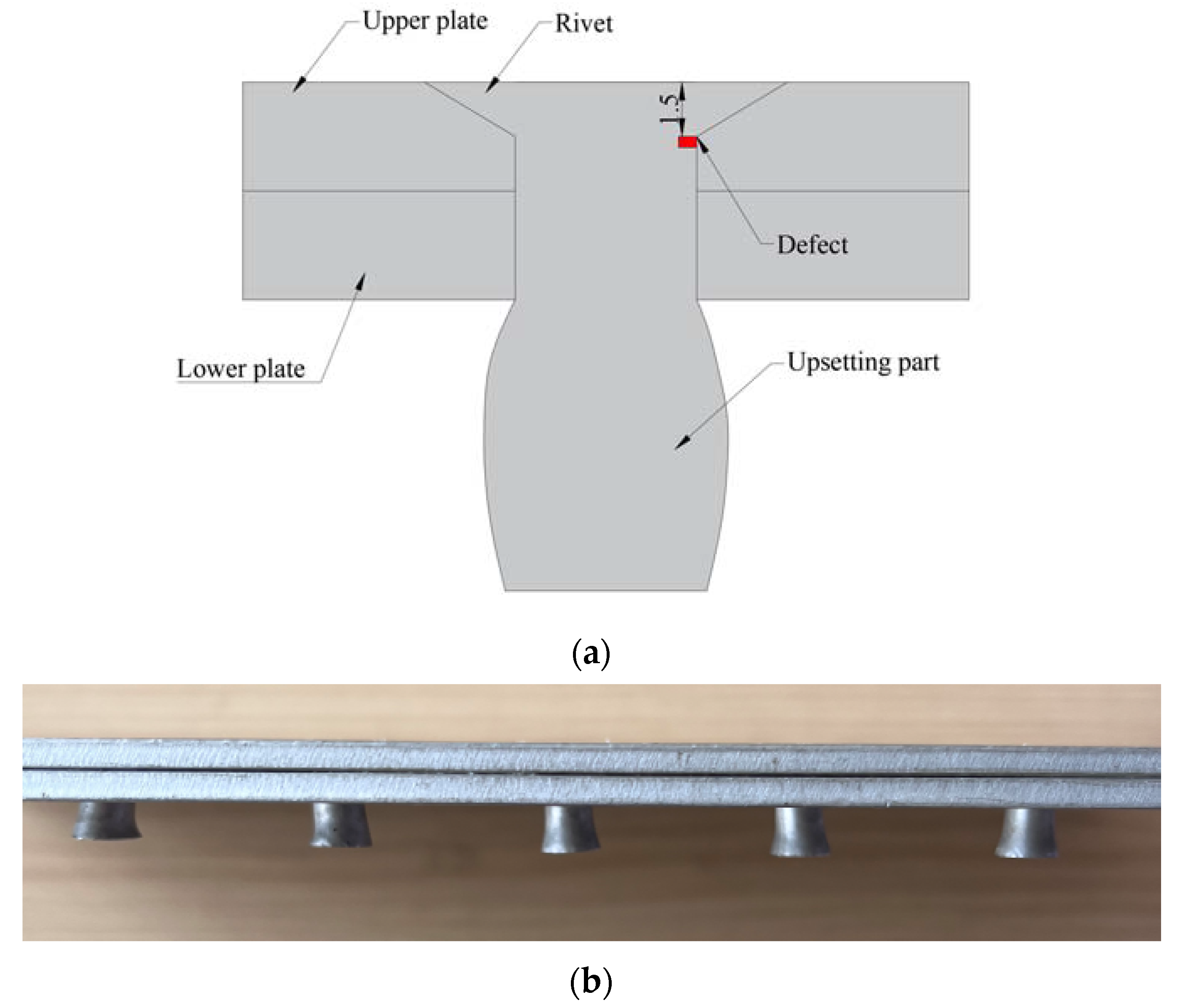
2.1. Propagation of Ultrasonic Waves in the CHRJ with a Defect
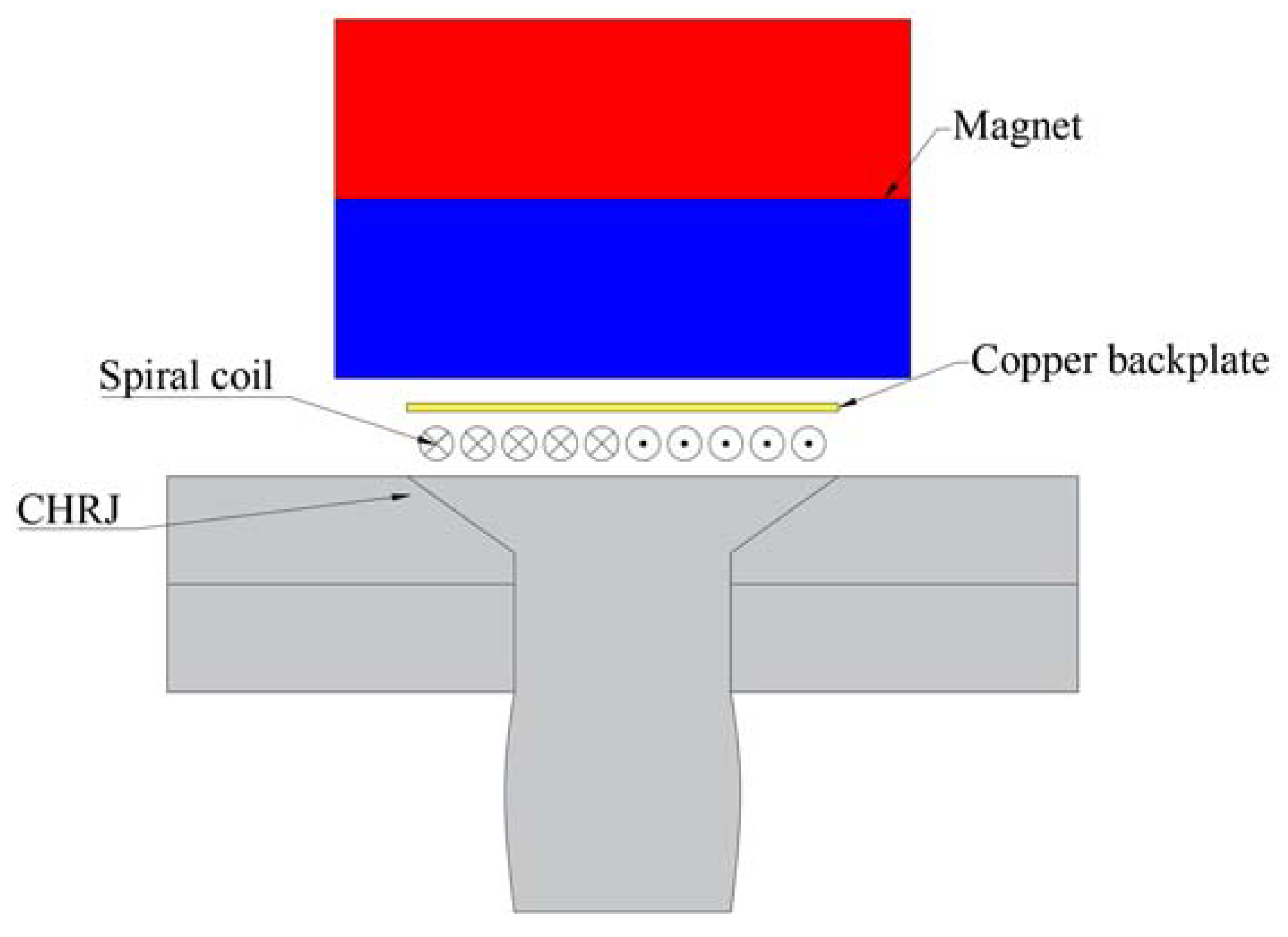
2.2. High-Frequency Transverse-Wave EMAT for the CHRJ
3. FES of Defect Detection
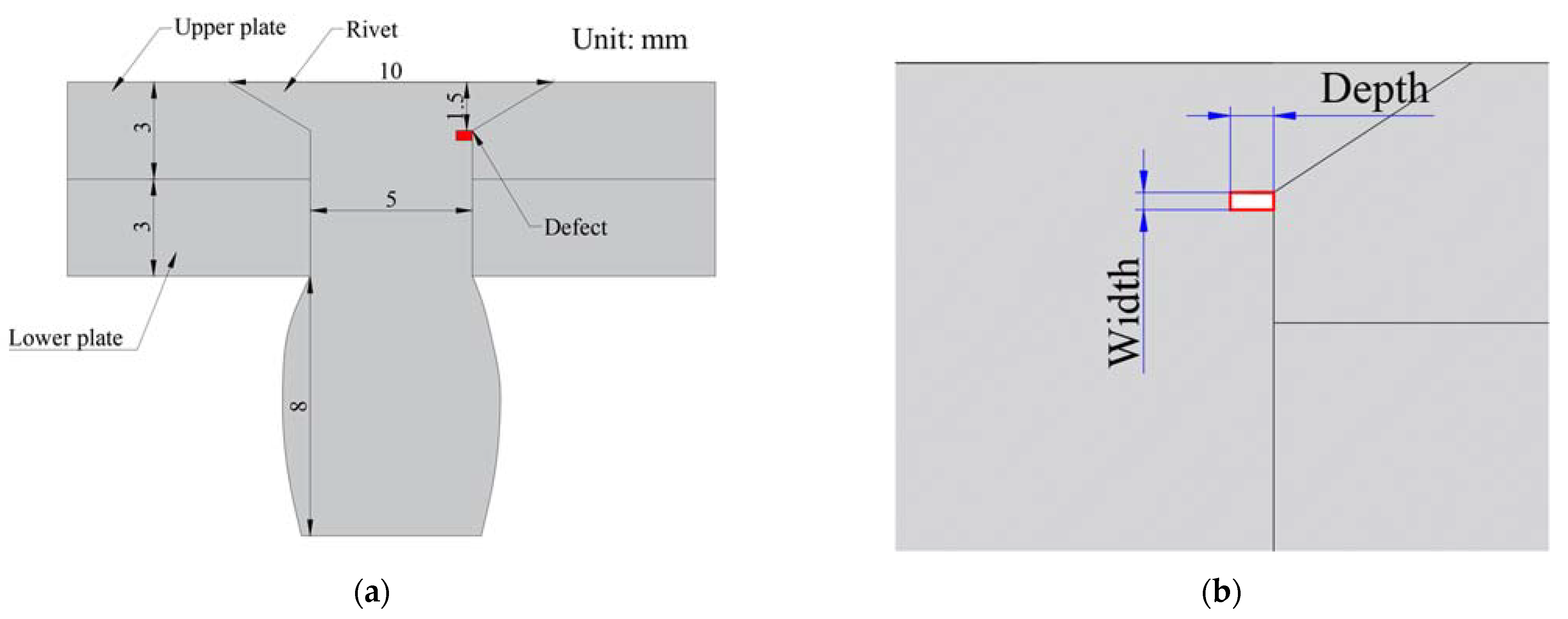
3.1. Modeling
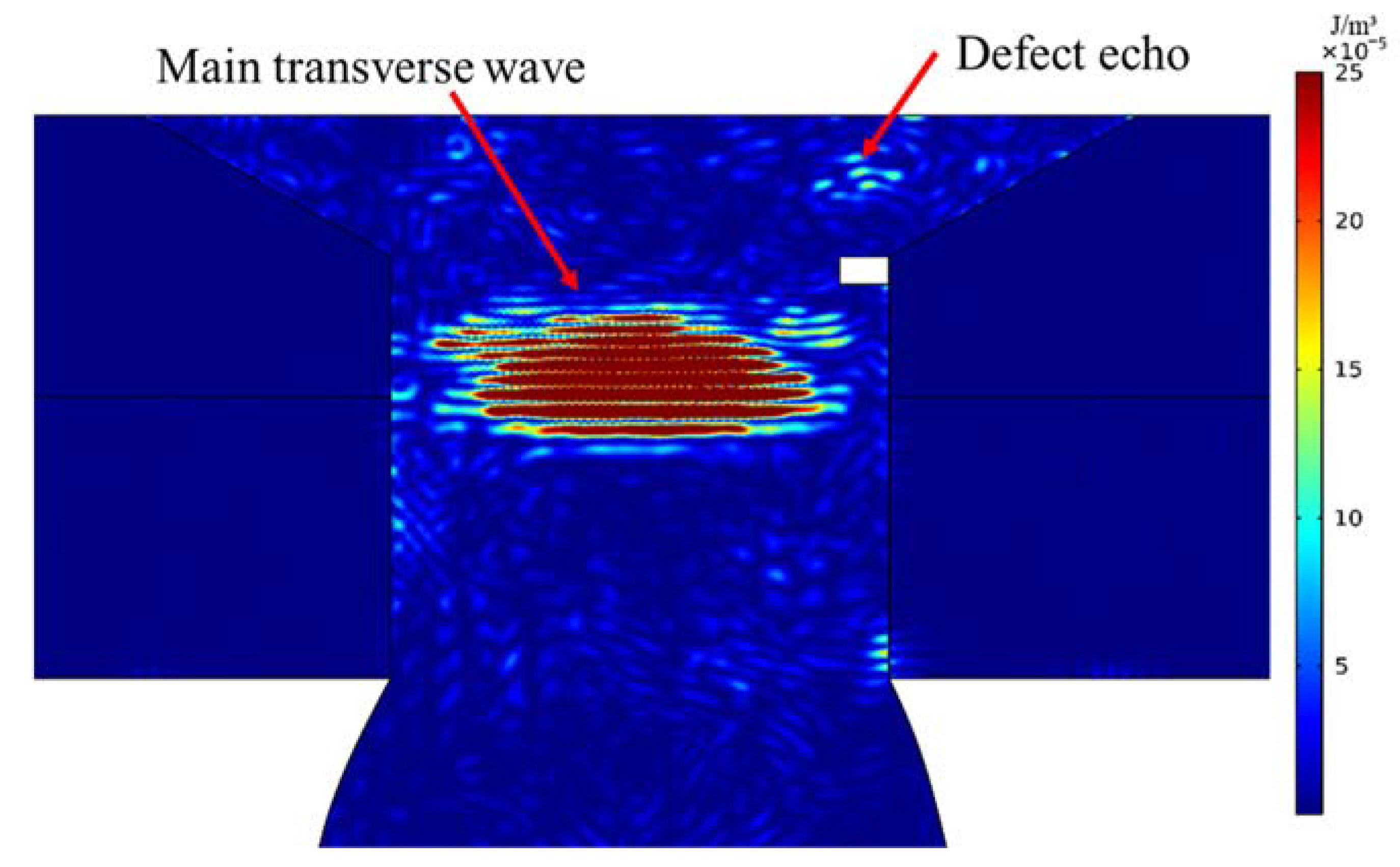
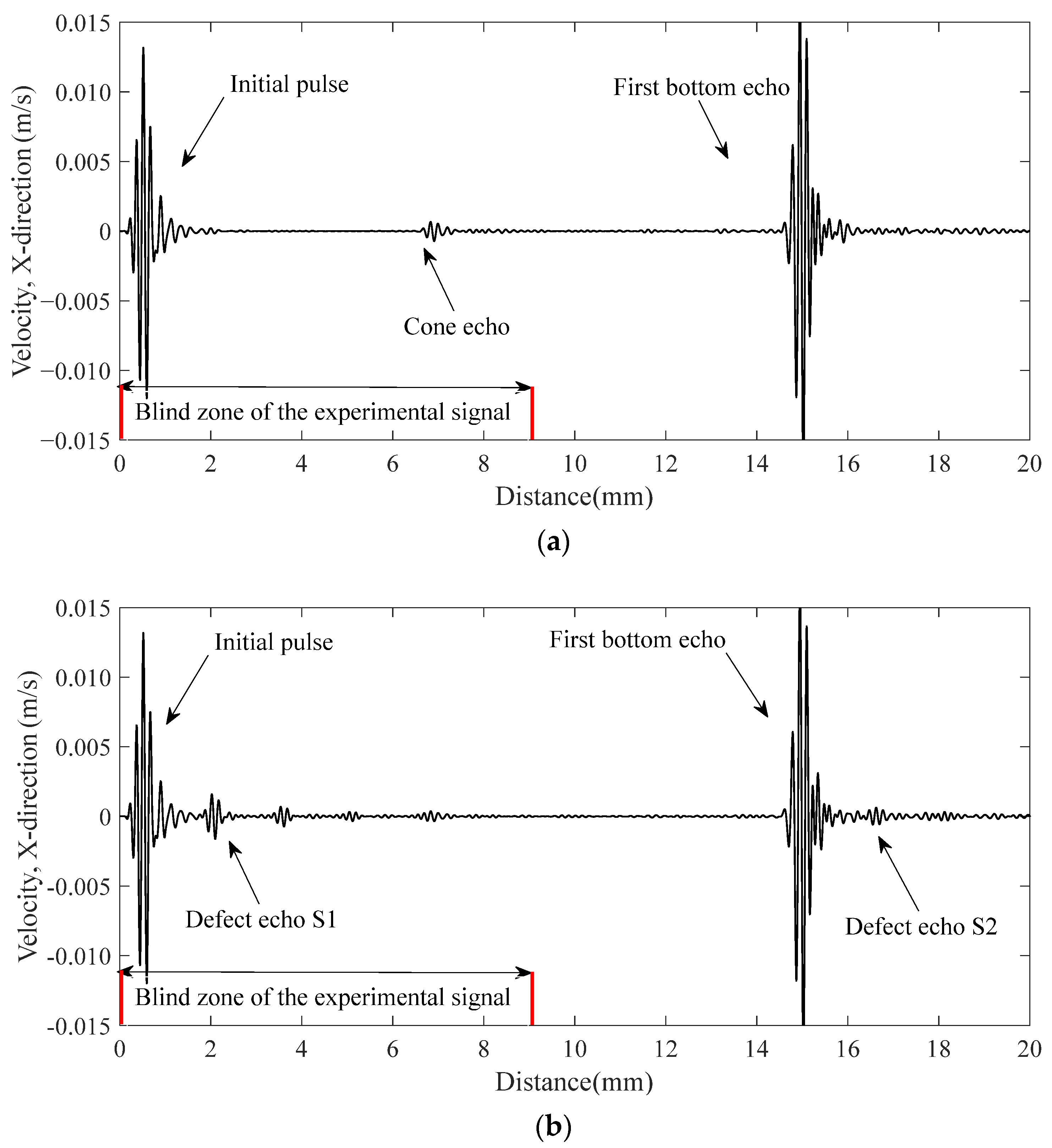
3.2. Simulation Results
4. Experiments
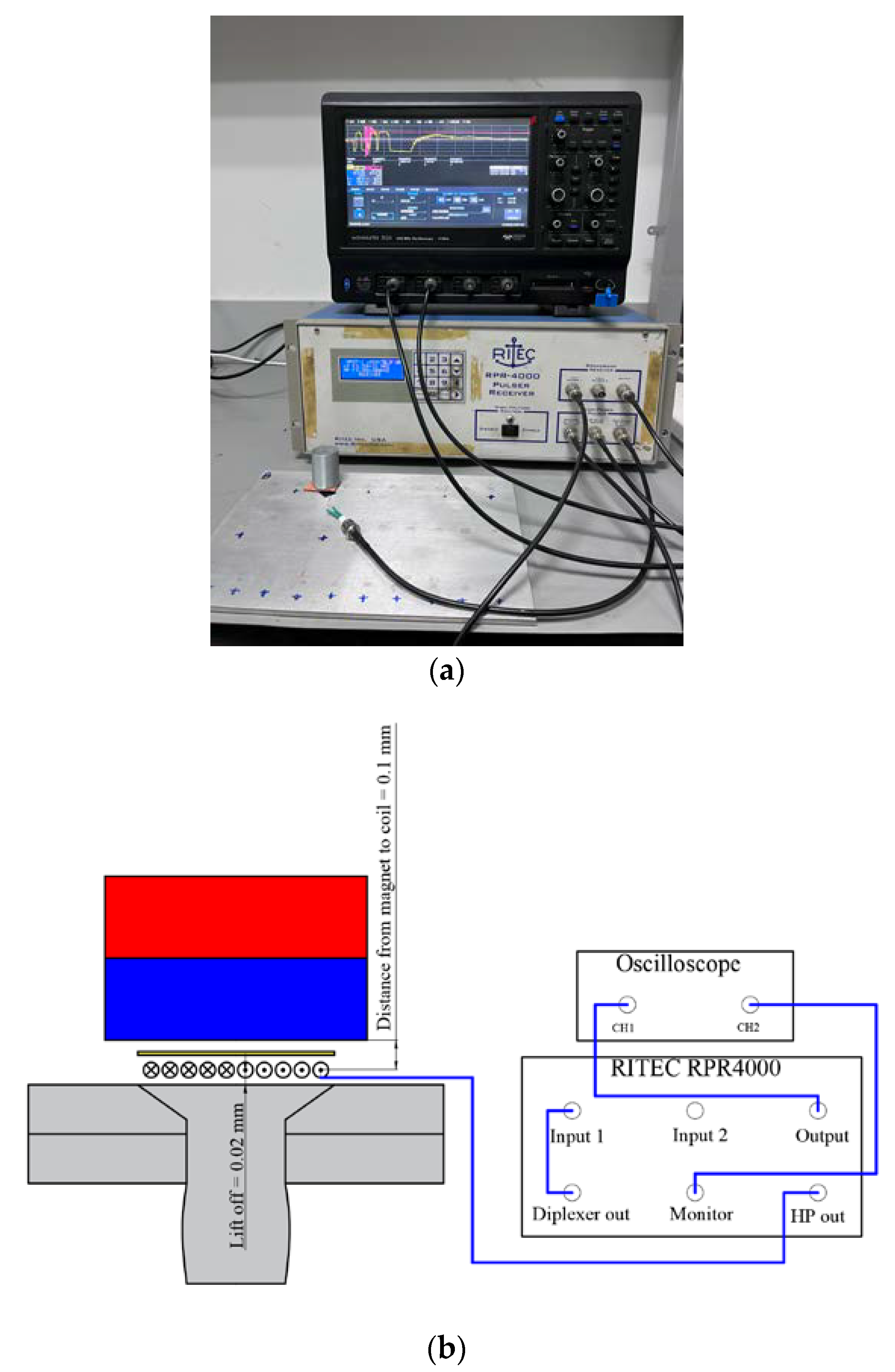
4.1. Experiment Setup
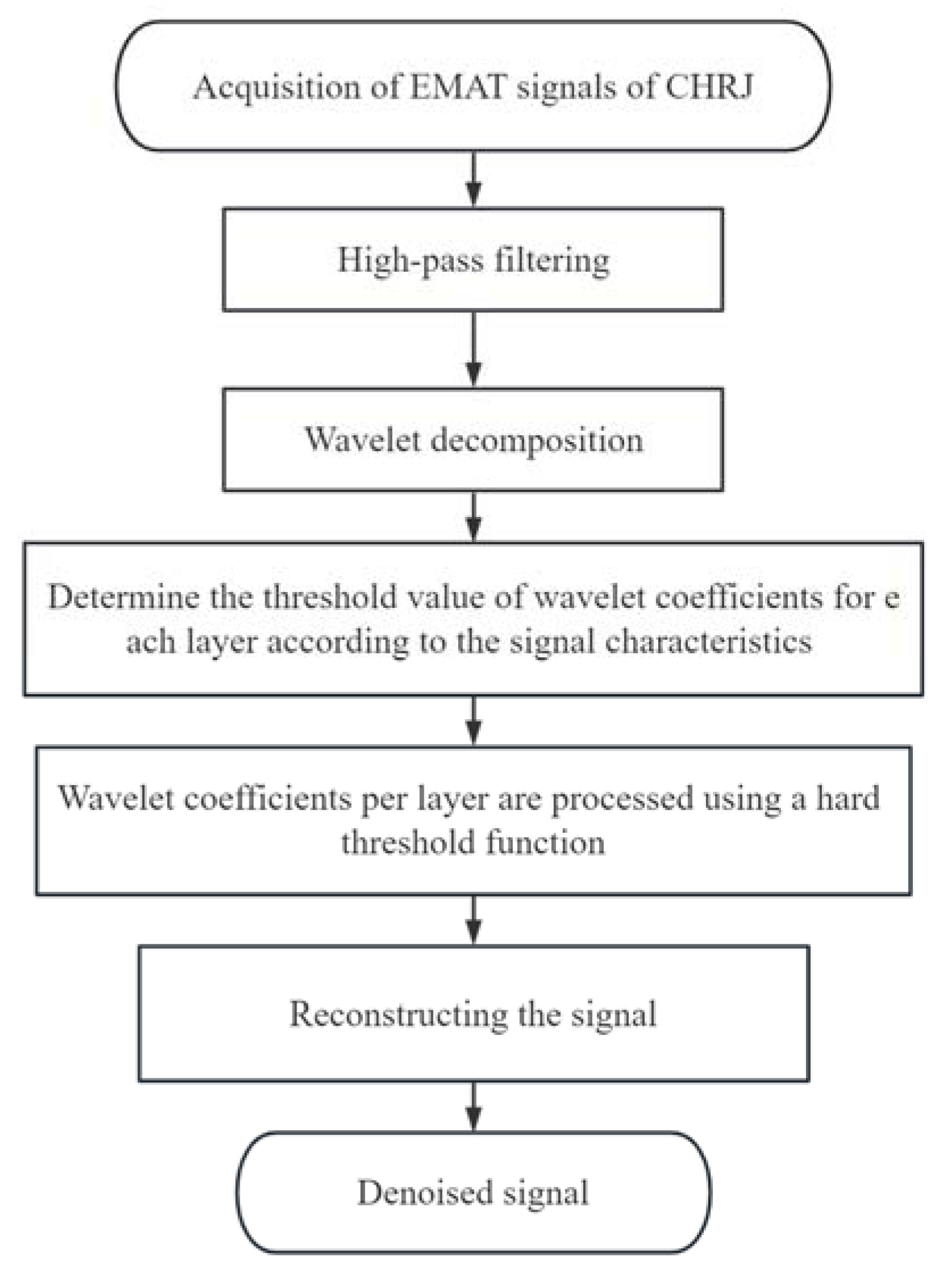
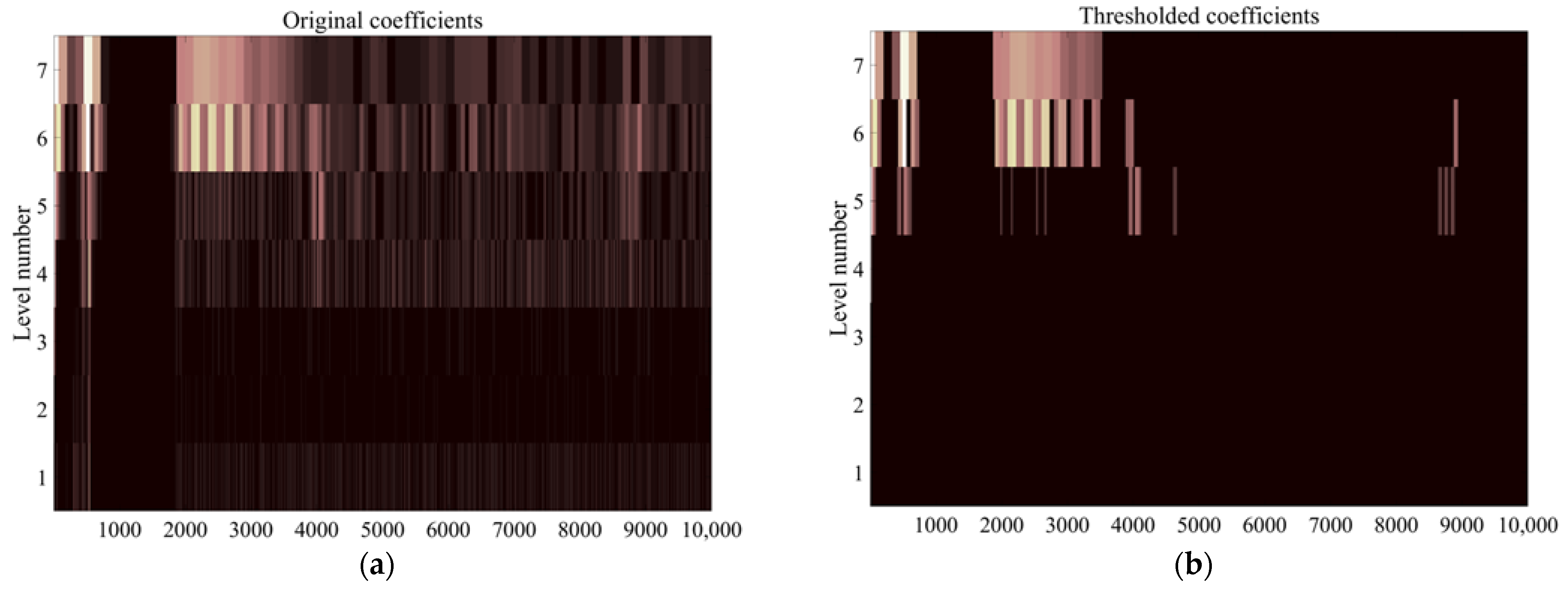
4.2. Signal Process Based on WTD
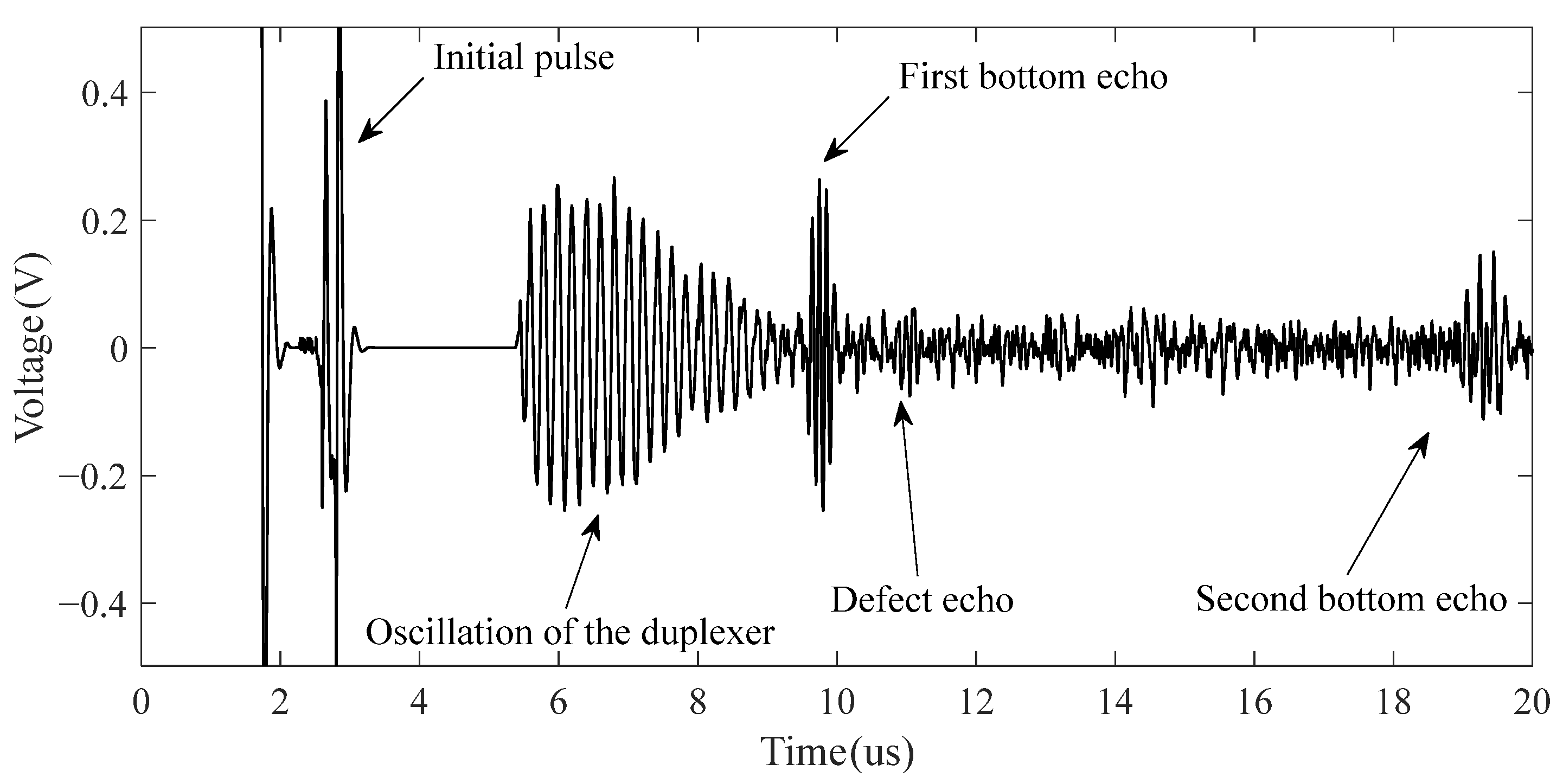
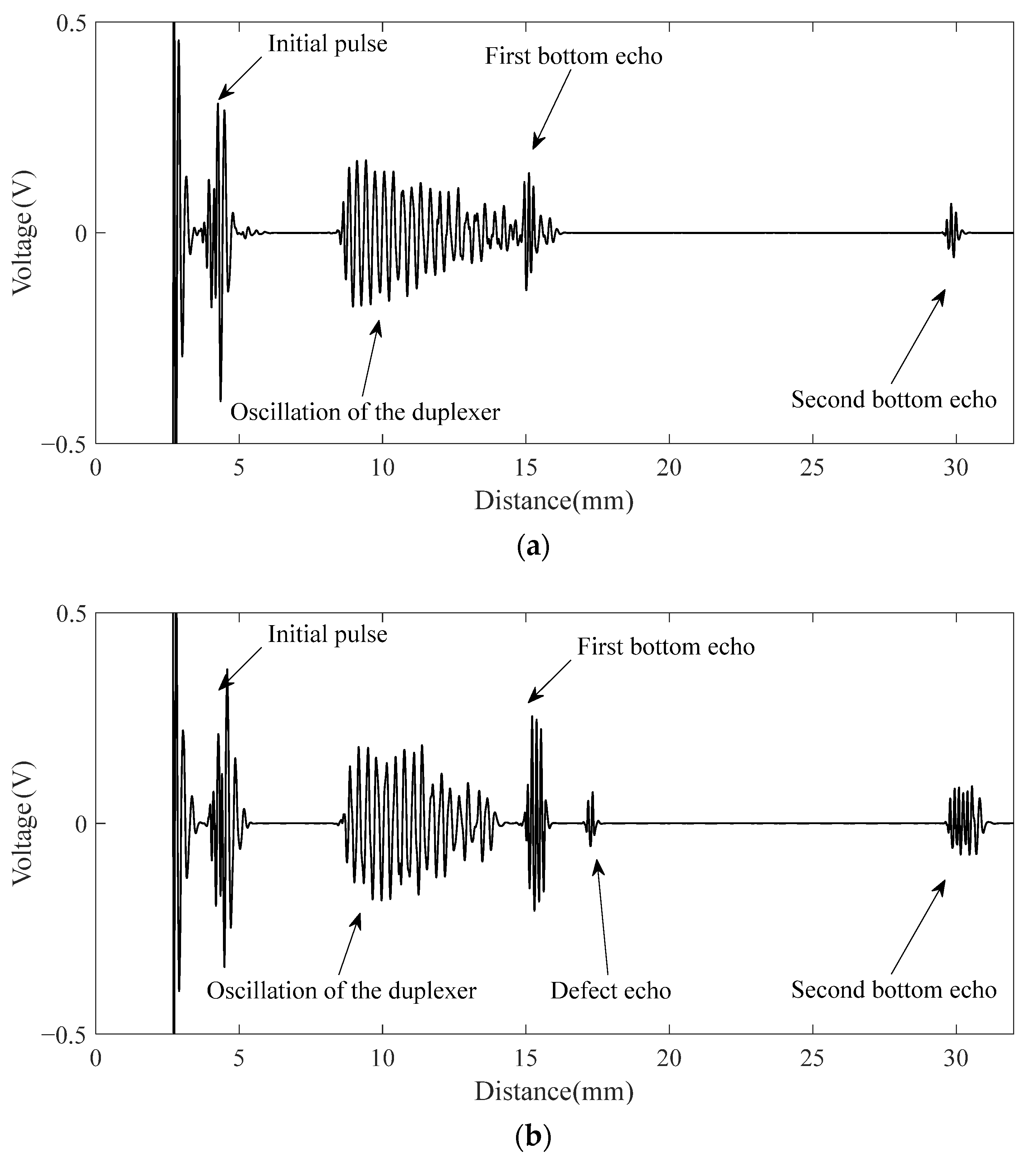
4.3. Results and Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Li, X.; Zhu, Y.; Shao, X. Experimental study on flexural behavior of damaged reinforced concrete (RC) beam strengthened by toughness-improved ultra-high performance concrete (UHPC) layer. Compos. Part B Eng. 2020, 186, 107834. [Google Scholar] [CrossRef]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and Thermodynamic Analysis of the Porous ZrO2/(ZrO2+Ni) Functionally Graded Bolted Joint. Compos. B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Korbel, A. Effect of aircraft rivet installation process and production variables on residual stress, clamping force and fatigue behaviour of thin sheet riveted lap joints. Thin Walled Struct. 2022, 181, 110041. [Google Scholar] [CrossRef]
- Sophian, A.; Tian, G.Y.; Taylor, D.; Rudlin, J. Design of a pulsed eddy current sensor for detection of defects in aircraft lap-joints. Sensors Actuators A Phys. 2002, 101, 92–98. [Google Scholar] [CrossRef]
- Abidin, I.Z.; Mandache, C.; Tian, G.Y.; Morozov, M. Pulsed Eddy Current Testing with Variable Duty Cycle on Rivet Joints. NDT E Int. 2009, 42, 599–605. [Google Scholar] [CrossRef]
- He, Y.; Luo, F.; Pan, M.; Weng, F.; Hu, X.; Gao, J.; Liu, B. Pulsed eddy current technique for defect detection in aircraft riveted structures. NDT E Int. 2010, 43, 176–181. [Google Scholar] [CrossRef]
- Sieber, L.; Urbanek, R.; Bär, J. Crack-Detection in old riveted steel bridge structures. Procedia Struct. Integr. 2019, 17, 339–346. [Google Scholar] [CrossRef]
- Fromme, P.; Sayir, M.B. Detection of cracks at rivet holes using guided waves. Ultrasonics 2002, 40, 199–203. [Google Scholar] [CrossRef]
- Le, M.; Kim, J.; Kim, S.; Lee, J. B-scan ultrasonic testing of rivets in multilayer structures based on short-time Fourier transform analysis. Measurement 2018, 128, 495–503. [Google Scholar] [CrossRef]
- Amosov, O.S.; Amosova, S.G.; Iochkov, I.O. Defects Detection and Recognition in Aviation Riveted Joints by Using Ul-trasonic Echo Signals of Non–Destructive Testing. IFAC PapersOnLine 2021, 54, 484–489. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. Electromagnetic Acoustic Transducers; Springer: Tokyo, Japan, 2017. [Google Scholar]
- Parra-Raad, J.; Khalili, P.; Cegla, F. Shear waves with orthogonal polarisations for thickness measurement and crack detection using EMATs. NDT E Int. 2020, 111, 102212. [Google Scholar] [CrossRef]
- Petcher, P.A.; Dixon, S. Weld Defect Detection Using PPM EMAT Generated Shear Horizontal Ultrasound. NDT E Int. 2015, 74, 58–65. [Google Scholar] [CrossRef]
- Park, J.; Lee, J.; Min, J.; Cho, Y. Defects Inspection in Wires by Nonlinear Ultrasonic-Guided Wave Generated by Electromagnetic Sensors. Appl. Sci. 2020, 10, 4610. [Google Scholar] [CrossRef]
- He, C.; Deng, P.; Lu, Y.; Liu, X.; Liu, Z.; Jiao, J.; Wu, B. Estimation of Surface Crack Depth using Rayleigh Waves by Electromagnetic Acoustic Transducers. Int. J. Acoust. Vib. 2017, 22, 541–548. [Google Scholar] [CrossRef]
- Parra-Raad, J.; Lan, B.; Cegla, F. Orthogonally polarised shear waves for evaluating anisotropy and cracks in metals. NDT E Int. 2021, 121, 102440. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Miao, Y.; Yuan, W.; Liu, Z. Study of a spiral-coil EMAT for rail subsurface inspection. Ultrasonics 2020, 108, 106169. [Google Scholar] [CrossRef]
- Andruschak, N.; Saletes, I.; Filleter, T.; Sinclair, A. An NDT guided wave technique for the identification of corrosion defects at support locations. NDT E Int. 2015, 75, 72–79. [Google Scholar] [CrossRef]
- Si, D.; Gao, B.; Guo, W.; Yan, Y.; Tian, G.Y.; Yin, Y. Variational Mode Decomposition Linked Wavelet Method for EMAT Denoise with Large Lift-Off Effect. NDT E Int. 2019, 107, 102151. [Google Scholar] [CrossRef]
- Huang, S.; Sun, H.; Wang, S.; Qu, K.; Zhao, W.; Peng, L. SSWT and VMD Linked Mode Identification and Time-of-Flight Extraction of Denoised SH Guided Waves. IEEE Sens. J. 2021, 21, 14709–14717. [Google Scholar] [CrossRef]
- Zhao, S.; Zhou, J.; Liu, Y.; Zhang, J.; Cui, J. Application of Adaptive Filtering Based on Variational Mode Decomposition for High-Temperature Elec-tromagnetic Acoustic Transducer Denoising. Sensors 2022, 22, 6483. [Google Scholar] [CrossRef]
- Kubinyi, M.; Kreibich, O.; Neuzil, J.; Smid, R. EMAT noise suppression using information fusion in stationary wavelet packets. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1027–1036. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zheng, L.; Chen, C.; Long, Z.; Wang, Y. Ultrasonic Detection Method for Grouted Defects in Grouted Splice Sleeve Connector Based on Wavelet Pack Energy. Sensors 2019, 19, 1562. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Tong, Y.; Zhao, W. A denoising algorithm for an electromagnetic acoustic transducer (EMAT) signal by envelope regulation. Meas. Sci. Technol. 2010, 21, 085102. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, J.; Yang, X. Influences of Upsetting on the Propagation Characteristic of the Elastic Wave in the Countersunk Head Riveted Joints. Appl. Acoust. 2023, 208, 109406. [Google Scholar]


| Name | Meaning |
|---|---|
| ADe | Amplitude of defect echo |
| AFbe | Amplitude of the first bottom echo |
| E | Total energy of the ultrasonic waves |
| r | Reflection coefficient |
| t | Transmission coefficient |
| a | Energy-loss coefficient |
| Name | Meaning |
|---|---|
| dax | Axial resolution |
| c | Wave speed |
| n | Cycles of the ultrasonic wave |
| f | Frequency |
| h | Distance between the defect and the upper surface |
| Name | Meaning |
|---|---|
| Flor | Lorenz force in the specimen |
| Jind | Current density of induced eddy currents in the specimen |
| Bstatic | Magnetic flux intensity of static magnetic field |
| Jre | Current density in the conductor during reception |
| η | Conductivity of the specimen |
| v | Velocity of the particle in the specimen |
| Object | Name | Value |
|---|---|---|
| RITEC RPR4000 | Frequency | 10 MHz |
| Cycles | 3 | |
| Excitement peak voltage | 500 V | |
| Gain | 72.4 dB | |
| Passband of filter | 800 kHz–22 MHz | |
| Oscilloscope | Sampling rate | 100 MHz |
| Average number of samples | 256 | |
| Data-acquisition resolution | 10 ns |
| Object | Name | Value |
|---|---|---|
| Cylindrical magnet | Height | 40 mm |
| Radius | 15 mm | |
| Material | N52 | |
| Residual magnetic flux density | 1.48 T | |
| Distance from magnet to coil | 0.1 mm | |
| Spiral coil | Spacing | 10 mil |
| Line width | 5 mil | |
| Number of turns | 18 | |
| Radius | 5 mm | |
| Copper thickness | 0.5 oz | |
| Number of layers | 2 | |
| Lift-off | 0.02 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Xu, J.; Yang, X.; Lin, H. Near-Surface-Defect Detection in Countersunk Head Riveted Joints Based on High-Frequency EMAT. Materials 2023, 16, 3998. https://doi.org/10.3390/ma16113998
Zhang S, Xu J, Yang X, Lin H. Near-Surface-Defect Detection in Countersunk Head Riveted Joints Based on High-Frequency EMAT. Materials. 2023; 16(11):3998. https://doi.org/10.3390/ma16113998
Chicago/Turabian StyleZhang, Shuchang, Jiang Xu, Xin Yang, and Hui Lin. 2023. "Near-Surface-Defect Detection in Countersunk Head Riveted Joints Based on High-Frequency EMAT" Materials 16, no. 11: 3998. https://doi.org/10.3390/ma16113998
APA StyleZhang, S., Xu, J., Yang, X., & Lin, H. (2023). Near-Surface-Defect Detection in Countersunk Head Riveted Joints Based on High-Frequency EMAT. Materials, 16(11), 3998. https://doi.org/10.3390/ma16113998







