Debonding Detection in Aluminum/Rigid Polyurethane Foam Composite Plates Using A0 Mode LAMB Wave EMATs
Abstract
1. Introduction
2. Theory Background
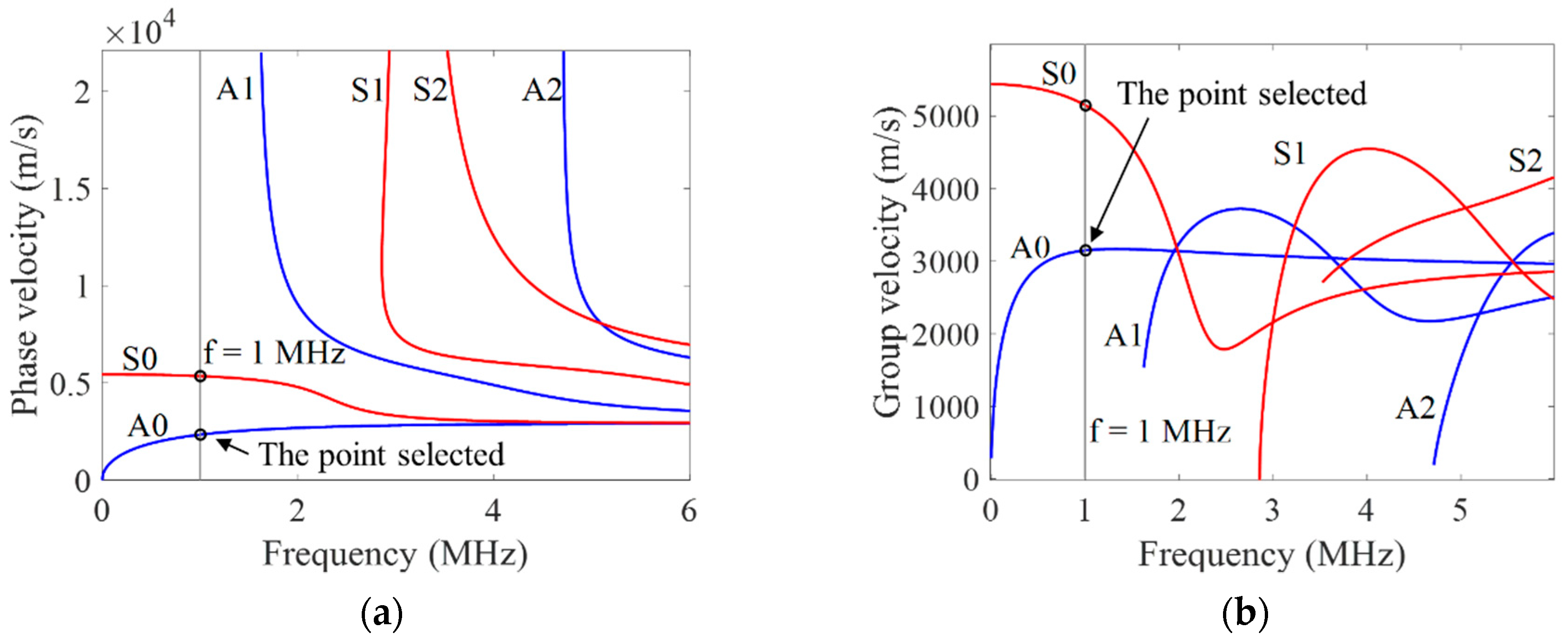
2.1. Mode Selection
- (1)
- To avoid the superposition of multimode Lamb wave signals, the frequency should be lower than the cutoff frequency of the A1 mode Lamb wave.
- (2)
- The phase velocity and group velocity are equal at the point with a slope of zero on the group velocity dispersion curve, which means that the Lamb wave does not disperse. Therefore, the point with a slope closer to zero on the group velocity dispersion curve is preferred.
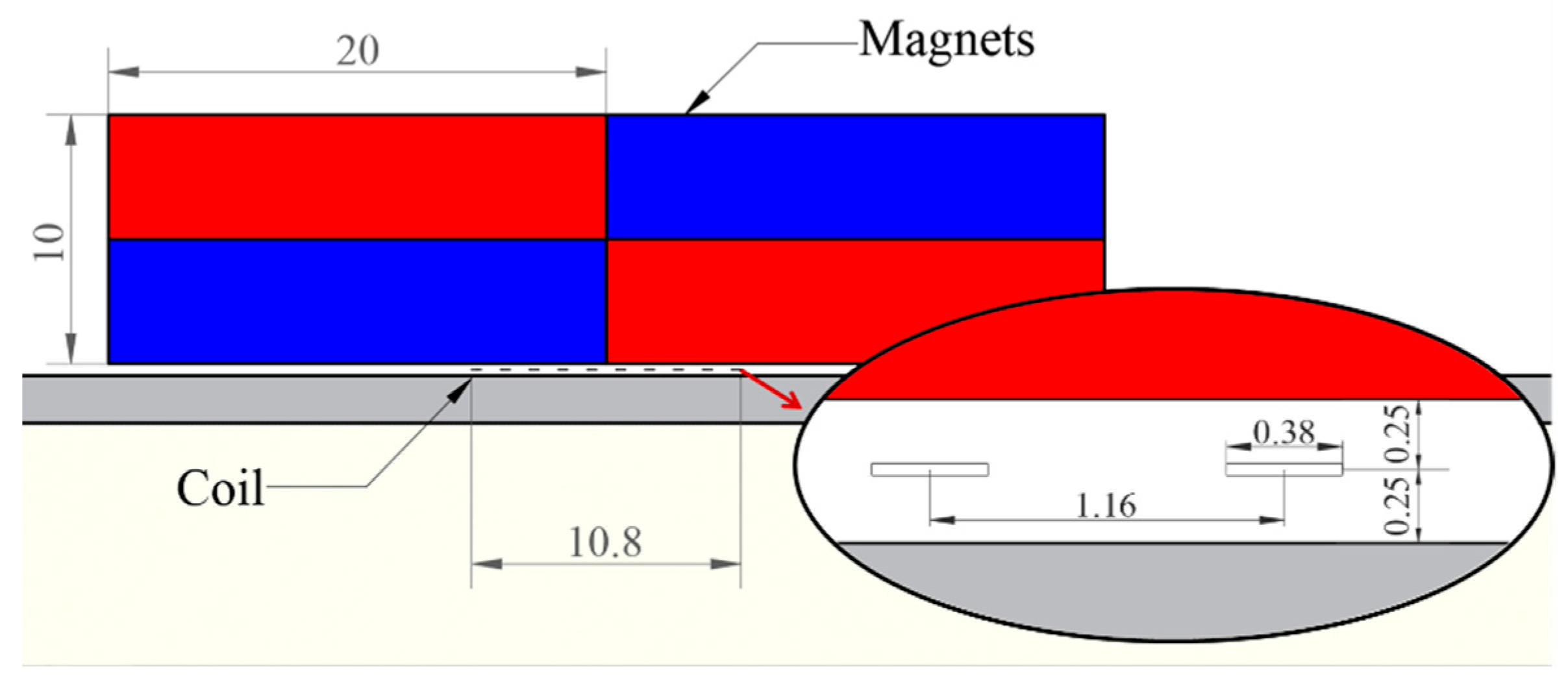
2.2. Principle of the A0 Mode Lamb Wave EMAT
3. FES of the Propagation of A0 Mode Lamb Waves in an ARCP
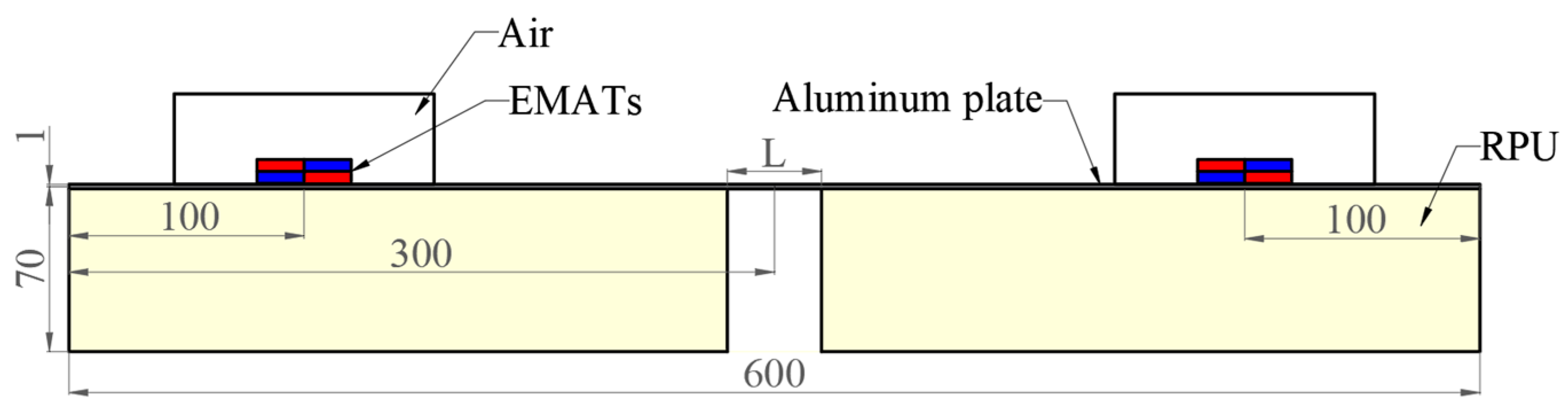
3.1. FES Modeling
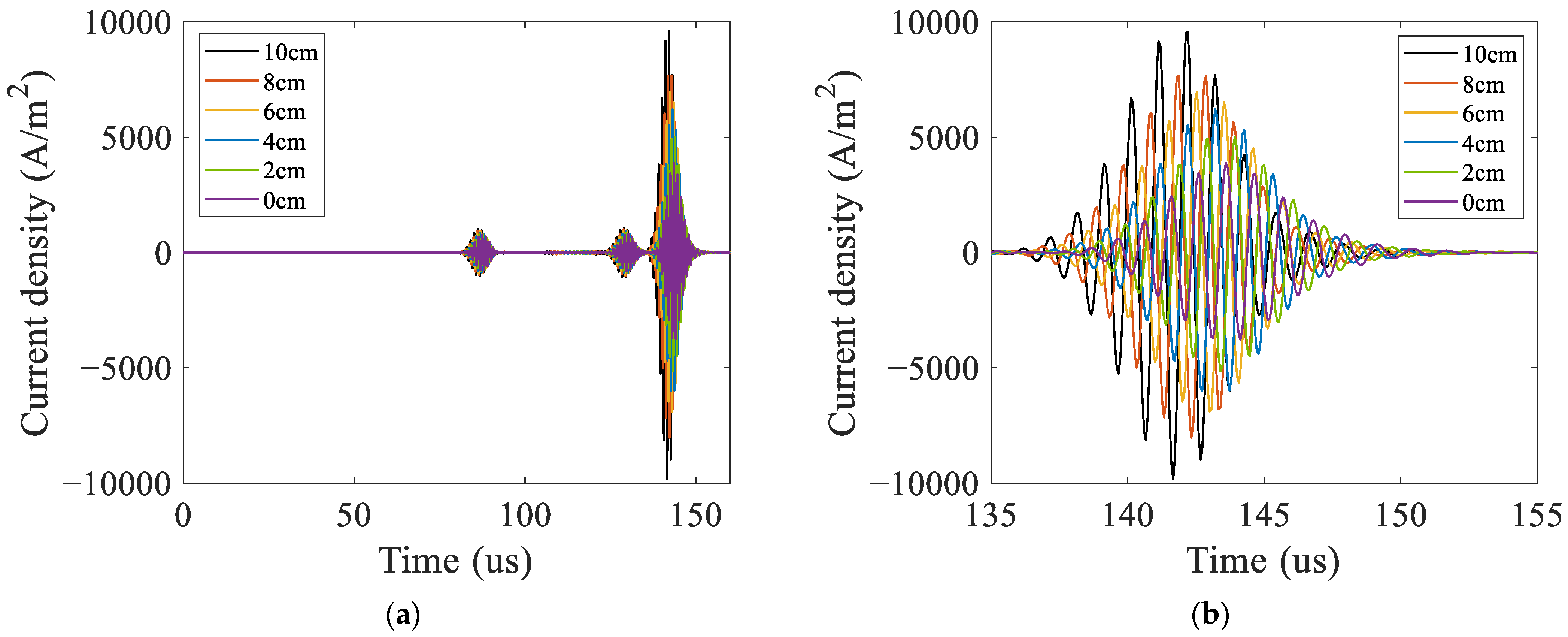
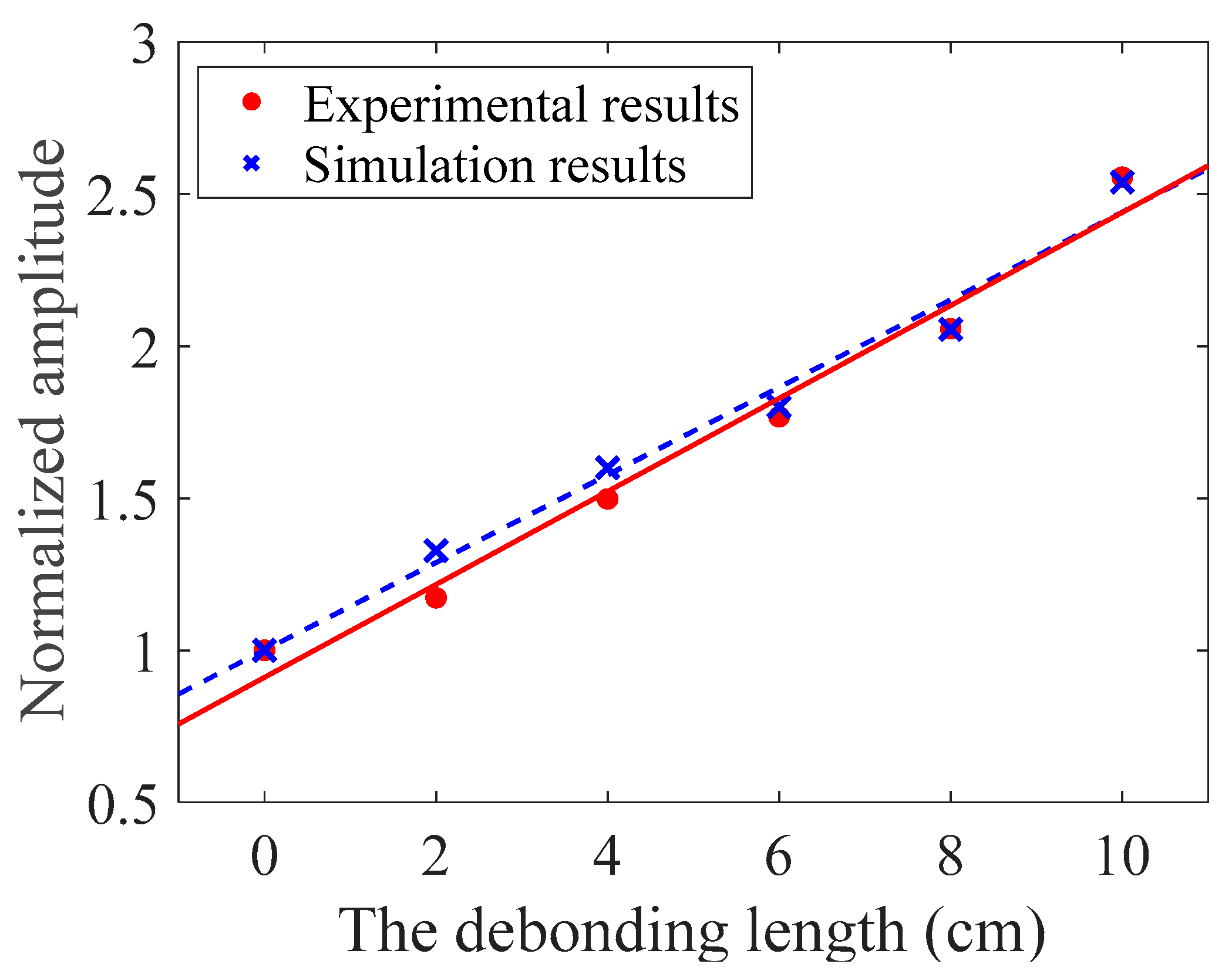
3.2. Simulation Results
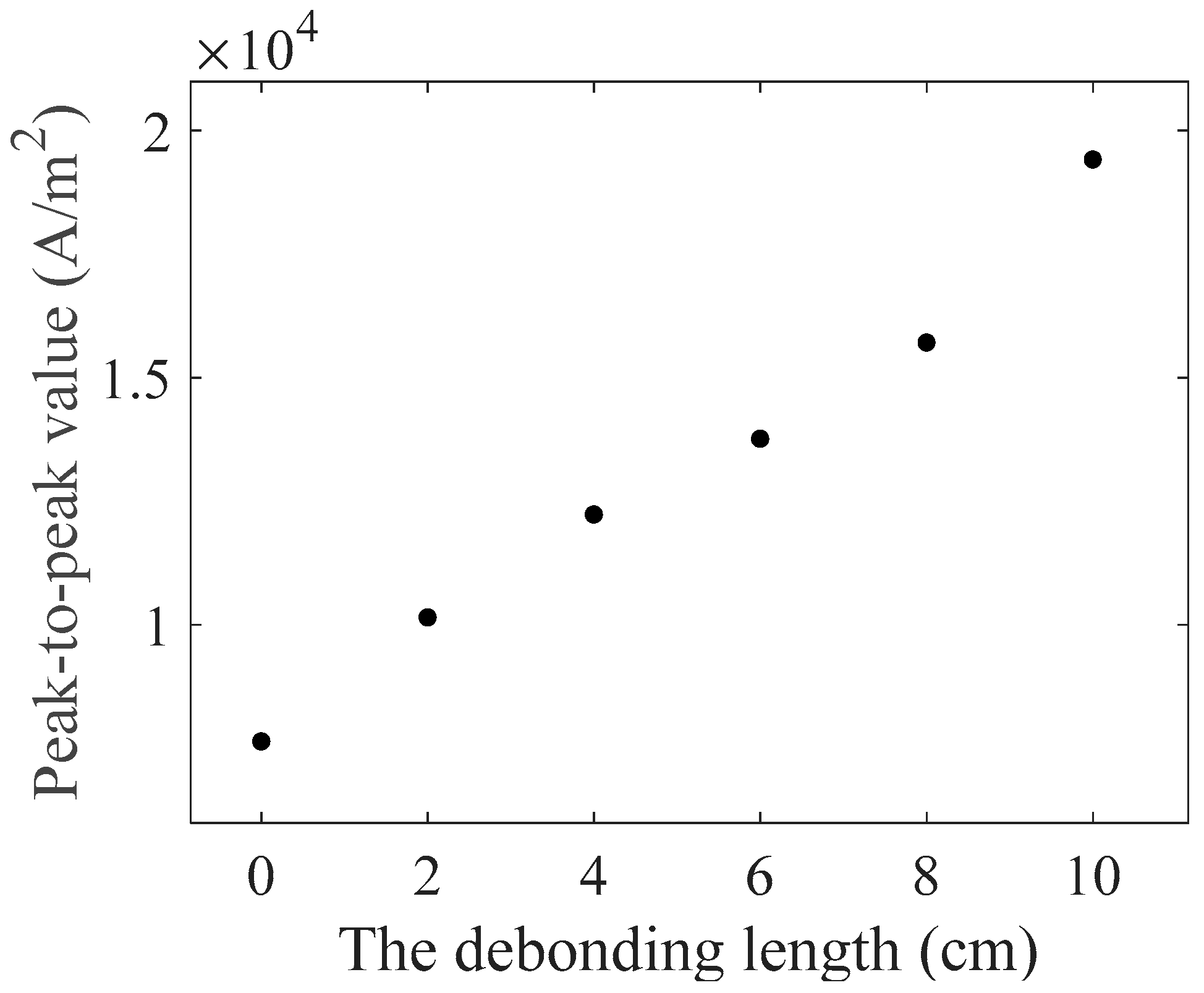
4. Experimental Verification
4.1. Experiment Setup
4.2. Results and Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Choe, H.; Choi, Y.; Kim, J.H. Threshold Cell Diameter for High Thermal Insulation of Water-blown Rigid Polyurethane Foams. Ind. Eng. Chem. 2019, 73, 344–350. [Google Scholar] [CrossRef]
- Hou, L.; Li, H.; Liu, Y.; Niu, K.; Shi, Z.; Liang, L.; Yao, Z.; Liu, C.; Tian, D. Synergistic Effect of Silica Aerogels and Hollow Glass Microspheres on Microstructure and Thermal Properties of Rigid Polyurethane Foam. J. Non-Cryst. Solids 2022, 592, 121753. [Google Scholar] [CrossRef]
- Wegrzyk, G.; Grzeda, D.; Ryszkowska, J. The Effect of Mixing Pressure in a High-Pressure Machine on Morphological and Physical Properties of Free-Rising Rigid Polyurethane Foams-A Case Study. Materials 2023, 16, 857. [Google Scholar] [CrossRef] [PubMed]
- Henriques, I.R.; Rouleau, L.; Castello, D.A.; Borges, L.A.; Deü, J.F. Viscoelastic Behavior of Polymeric Foams: Experiments and Modeling. Mech. Mater 2020, 148, 103506. [Google Scholar] [CrossRef]
- Balasubramaniam, K.; Sikdar, S.; Soman, R.; Malinowski, P. Multi-step Structural Health Monitoring Approaches in Debonding Assessment in A Sandwich Honeycomb Composite Structure Using Ultrasonic Guided Waves. Measurement 2022, 194, 111057. [Google Scholar] [CrossRef]
- Liu, T.; Pei, C.; Cheng, X.; Zhou, H.; Xiao, P.; Chen, Z. Adhesive Debonding Inspection with A Small EMAT in Resonant Mode. NDT E Int. 2018, 98, 110–116. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, T.; Song, G.; Gu, H. Active Interface Debonding Detection of A Concrete-filled Steel Tube with Piezoelectric Technologies Using Wavelet Packet Analysis. Mech. Syst. Signal Proc. 2013, 36, 7–17. [Google Scholar] [CrossRef]
- Li, J.; Lu, Y.; Lee, Y.F. Debonding Detection in CFRP-reinforced Steel Structures Using Anti-symmetrical Guided Waves. Compos. Struct. 2020, 253, 112813. [Google Scholar] [CrossRef]
- Ghose, B.; Panda, R.S.; Balasubramaniam, K. Guided A0 Wave Mode Interaction with Interfacial Disbonds in An Elastic-Viscoelastic Bilayer Structure. NDT E Int. 2021, 124, 102543. [Google Scholar] [CrossRef]
- Ghose, B.; Panda, R.S.; Balasubramaniam, K. A Study on the Use of Fundamental Antisymmetric-like Guided Wave for Health Monitoring of Elastic–viscoelastic Bilayer Structures. Struct. Health Monit. 2022, 22, 1193–1210. [Google Scholar] [CrossRef]
- Sun, H.; Kosukegawa, H.; Hashimoto, M.; Uchimoto, T.; Takagi, T. Electromagnetic-pulse-induced Acoustic Testing for Nondestructive Testing of Plastic Composite/Metal Adhesive Bonding. Int. J. Hydrogen Energy 2020, 45, 31303–31314. [Google Scholar] [CrossRef]
- Ng, C.T.; Veidt, M. Prediction and Measurement of Lamb Wave from Debondings at Structural Features in Composite Laminates. Key Eng. Mater 2013, 558, 139–148. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, X.; Scarpa, F.; Barton, D.; Zhu, Y.; Lang, Z.; Zhang, D. A Dynamic Poroelastic Model for Auxetic Polyurethane Foams Involving Viscoelasticity and Pneumatic Damping Effects in the Linear Regime. Mech. Syst. Signal Proc. 2022, 179, 109375. [Google Scholar] [CrossRef]
- Hameed, M.S.; Li, Z.; Zheng, K. Damage Detection Method Based on Continuous Wavelet Transformation of Lamb Wave Signals. Appl. Sci. 2020, 10, 8610. [Google Scholar] [CrossRef]
- Lee, S.E.; Hong, J.W. Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves. Materials 2020, 13, 3823. [Google Scholar] [CrossRef] [PubMed]
- Hosoya, N.; Umino, R.; Kanda, A.; Kajiwara, I.; Yoshinaga, A. Lamb Wave Generation Using Nanosecond Laser Ablation to Detect Damage. J. Vib. Control 2017, 24, 5842–5853. [Google Scholar] [CrossRef]
- Xue, Z.; Xu, W.; Peng, Y.; Wang, M.; Pelenovich, V.; Yang, B.; Zhang, J. Measuring the Depth of Subsurface Defects in Additive Manufacturing Components by Laser-Generated Ultrasound. Metals 2022, 12, 437. [Google Scholar] [CrossRef]
- Sun, H.; Kosukegawa, H.; Takagi, T.; Uchimoto, T.; Hashimoto, M.; Takeshita, N. Electromagnetic Pulse-induced Acoustic Testing and the Pulsed Guided Wave Propagation in Composite/Metal Adhesive Bonding Specimens. Compos. Sci. Technol. 2021, 201, 108499. [Google Scholar] [CrossRef]
- Pei, C.; Zhao, S.; Xiao, P.; Chen, Z. A Modified Meander-line-coil EMAT Design for Signal Amplitude Enhancement. Sens. Actuator A-Phys. 2016, 247, 539–546. [Google Scholar] [CrossRef]
- Lan, J.; Zhang, J.; Jia, X.; Gao, R. Optimization Design of Surface Wave Electromagnetic Acoustic Transducers Based on Simulation Analysis and Orthogonal Test Method. Sensors 2022, 22, 524. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, Y. The Effect of Magnet-to-Coil Distance on the Performance Characteristics of EMATs. Sensors 2020, 20, 5096. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, W.; Wu, Y.; Wu, Y.; Zhang, T. An EMAT for Improving the Purity and Amplitude of S0 Lamb Waves. Meas. Sci. Technol. 2022, 33, 095114. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, L.; Zhang, Y.; Li, A.; Bin, W.; He, C. Development of An Omni-directional Magnetic-concentrator-type Electromagnetic Acoustic Transducer. NDT E Int. 2020, 109, 102193. [Google Scholar] [CrossRef]
- Sun, W.; Liu, G.; Xia, H.; Xia, Z. A Modified Design of the Omnidirectional EMAT for Antisymmetric Lamb Wave Generation. Sens. Actuator A-Phys. 2018, 282, 251–258. [Google Scholar] [CrossRef]
- Kang, L.; Wang, S.; Jiang, T.; Zhai, G. Optimal Design of Lamb Wave Electromagnetic Acoustic Transducers for Improving Their Excitation Performance. Jpn. J. Appl. Phys. 2011, 50, 07HD01. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, W.; Qiu, X.; Xiang, Y. A Lorentz Force EMAT Design with Racetrack Coil and Periodic Permanent Magnets for Selective Enhancement of Ultrasonic Lamb Wave Generation. Sensors 2022, 23, 96. [Google Scholar] [CrossRef]
- Huber, A. Dispersion Calculator User’s Manual; DLR: Augsburg, Germany, 2019. [Google Scholar]
- Liu, Z.; Hu, Y.; Xie, M.; Wu, B.; He, C. Development of Omnidirectional A0 Mode EMAT Employing A Concentric Permanent Magnet Pairs with Opposite Polarity for Plate Inspection. NDT E Int. 2018, 94, 13–21. [Google Scholar] [CrossRef]
- Wang, S.; Huang, S.; Velichko, A.; Wilcox, P.; Zhao, W. A Multi-objective Structural Optimization of An Omnidirectional Electromagnetic Acoustic Transducer. Ultrasonics 2017, 81, 23–31. [Google Scholar] [CrossRef]
- Zhang, Y.; Qian, Z.; Wang, B. Modes Control of Lamb Wave in Plates Using Meander-Line Electromagnetic Acoustic Transducers. Appl. Sci. 2020, 10, 3491. [Google Scholar] [CrossRef]
- Koodalil, D.; Rajagopal, P.; Balasubramaniam, K. Bond Stiffness Estimation with Shear Horizontal Guided Waves Generated Using PPM-EMATs. Int. J. Adhes. Adhes. 2021, 104, 102761. [Google Scholar] [CrossRef]
- Koodalil, D.; Barnoncel, D.; Rajagopal, P.; Balasubramaniam, K. Detection of Interfacial Weakness in a Lap-shear Joint Using Shear Horizontal Guided Waves. NDT E Int. 2020, 112, 102248. [Google Scholar] [CrossRef]
- Koodalil, D.; Rajagopal, P.; Balasubramaniam, K. Quantifying Adhesive Thickness and Adhesion Parameters Using Higher-order SH Guided Waves. Ultrasonics 2021, 114, 106429. [Google Scholar] [CrossRef] [PubMed]
- Drinkwater, B.W.; Dwyer-Joyce, R.S.; Cawley, P. A Study of the Interaction between Ultrasound and A Partially Contacting Solid--Solid Interface. Proc. R. Soc. A-Math. Phys. Eng. Sci. 1996, 452, 2613–2628. [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.; Chen, D. PPM EMAT for Defect Detection in 90-Degree Pipe Bend. Materials 2022, 15, 4630. [Google Scholar] [CrossRef] [PubMed]










| Material | Density/kg·m−3 | Young’s Modulus/GPa | Poisson’s Ratio |
|---|---|---|---|
| Aluminum | 2700 | 70 | 0.33 |
| RPUF | 40 | 0.16 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Xu, J.; Zhang, S.; Tu, J. Debonding Detection in Aluminum/Rigid Polyurethane Foam Composite Plates Using A0 Mode LAMB Wave EMATs. Materials 2023, 16, 2797. https://doi.org/10.3390/ma16072797
Yang X, Xu J, Zhang S, Tu J. Debonding Detection in Aluminum/Rigid Polyurethane Foam Composite Plates Using A0 Mode LAMB Wave EMATs. Materials. 2023; 16(7):2797. https://doi.org/10.3390/ma16072797
Chicago/Turabian StyleYang, Xin, Jiang Xu, Shuchang Zhang, and Jun Tu. 2023. "Debonding Detection in Aluminum/Rigid Polyurethane Foam Composite Plates Using A0 Mode LAMB Wave EMATs" Materials 16, no. 7: 2797. https://doi.org/10.3390/ma16072797
APA StyleYang, X., Xu, J., Zhang, S., & Tu, J. (2023). Debonding Detection in Aluminum/Rigid Polyurethane Foam Composite Plates Using A0 Mode LAMB Wave EMATs. Materials, 16(7), 2797. https://doi.org/10.3390/ma16072797







