Establishment of Analytical Model for CFRP Cutting Force Considering the Radius of the Edge Circle
Abstract
:1. Instruction
2. CFRP Finite Element Micro-Cutting Model
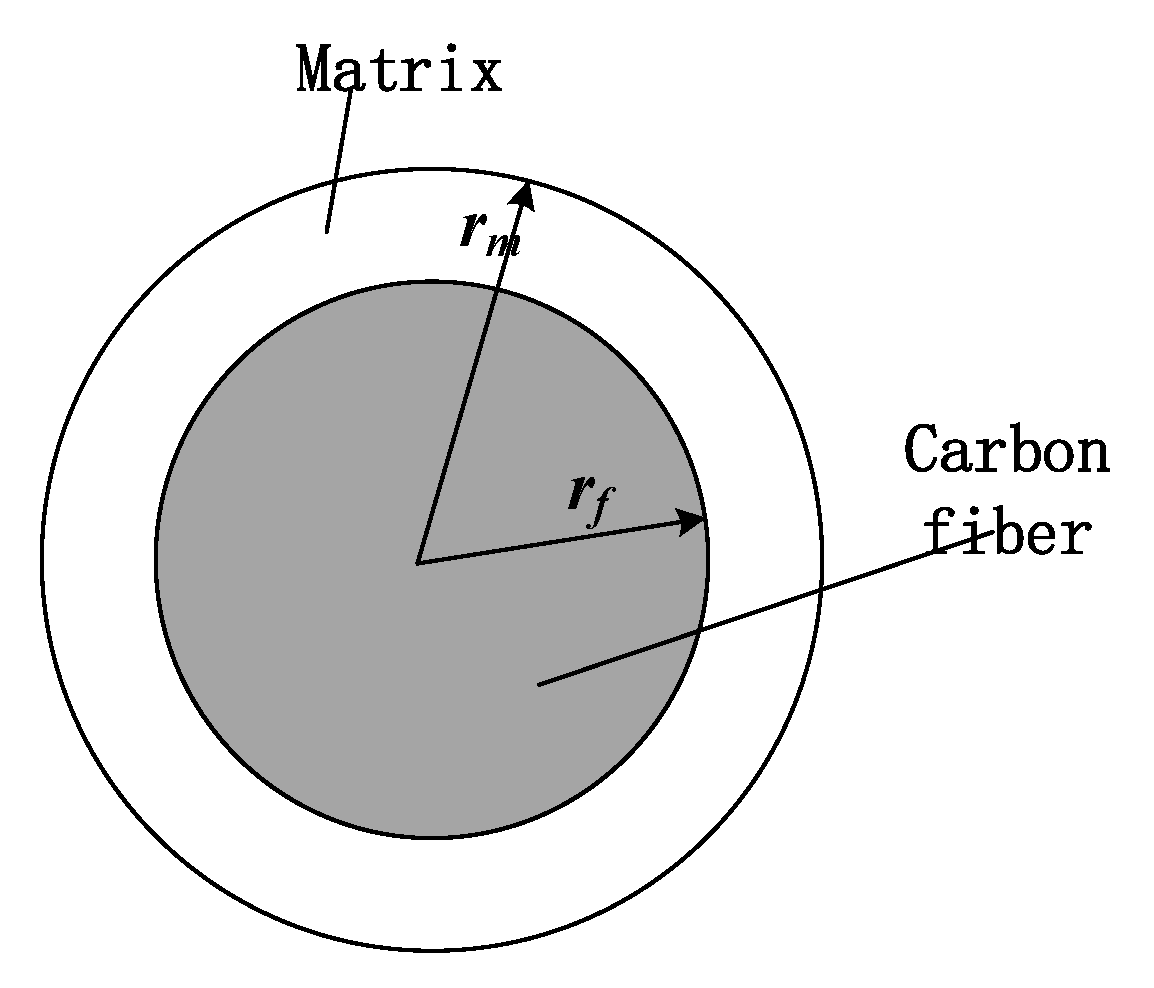
2.1. Geometric Model and Mesh
2.2. Material Parameters and Boundary Conditions
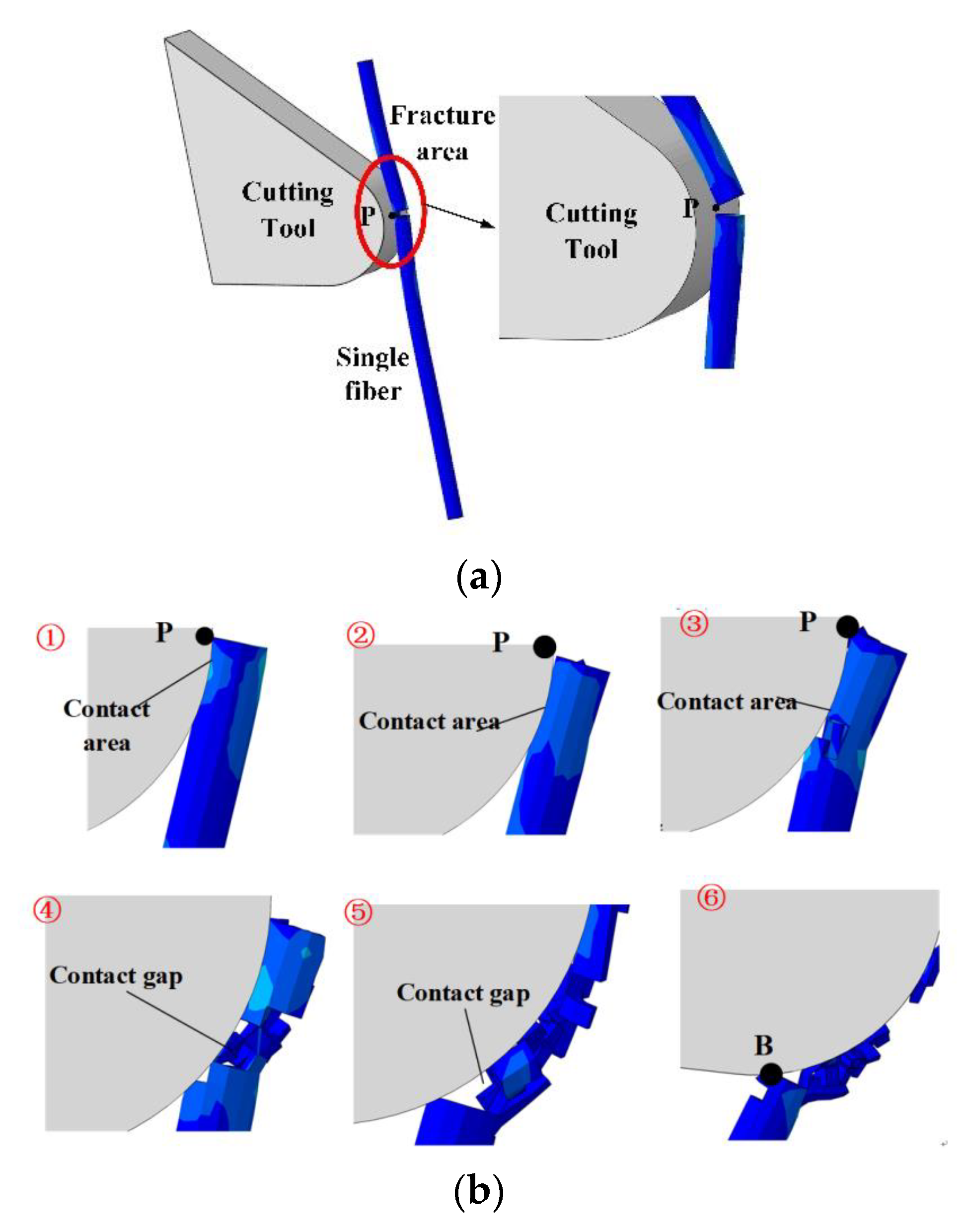
3. Analysis of Finite Element Simulation Results
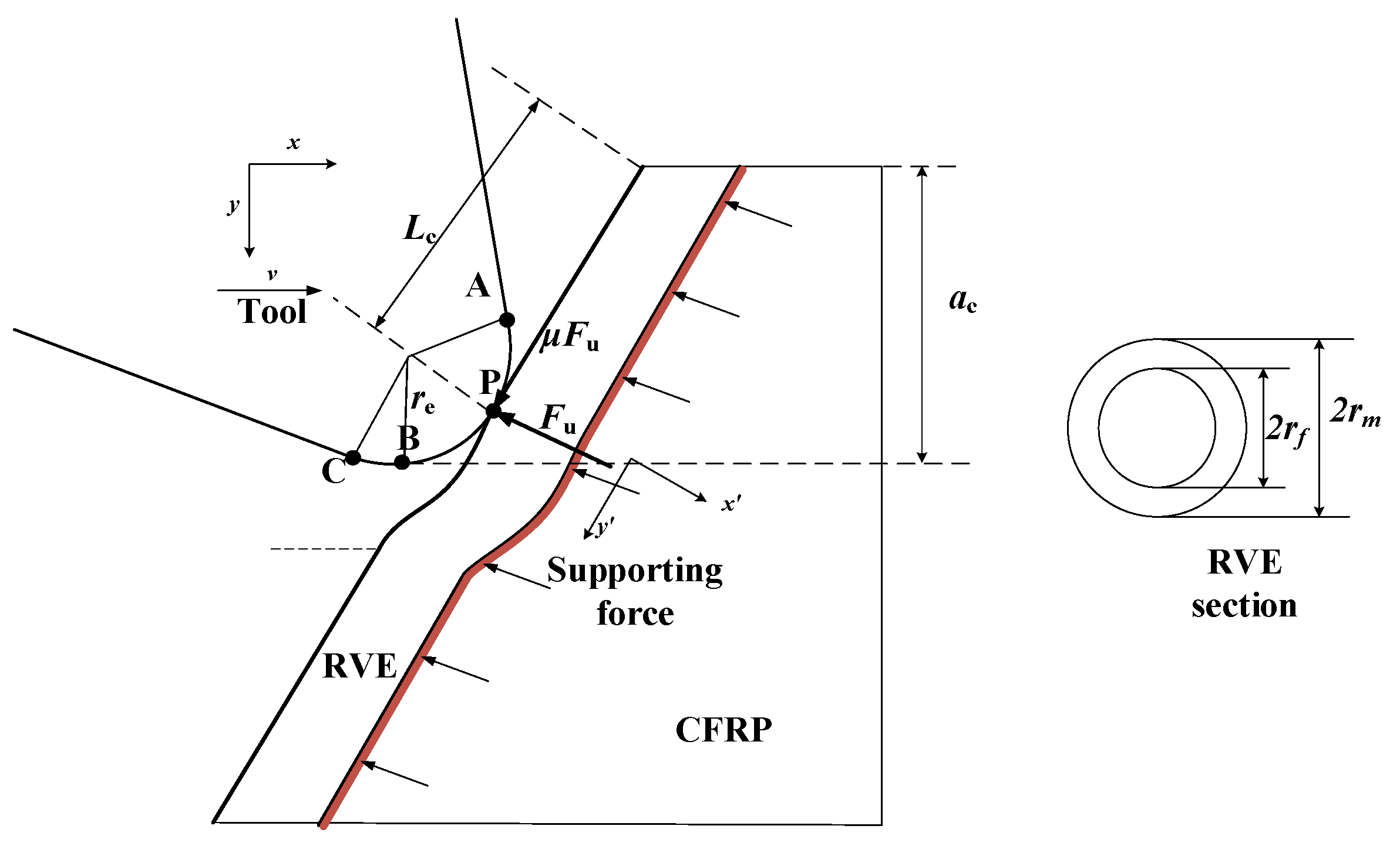
4. CFRP Cutting Force Analytical Model
4.1. Cutting Slip Zone (Zone I)
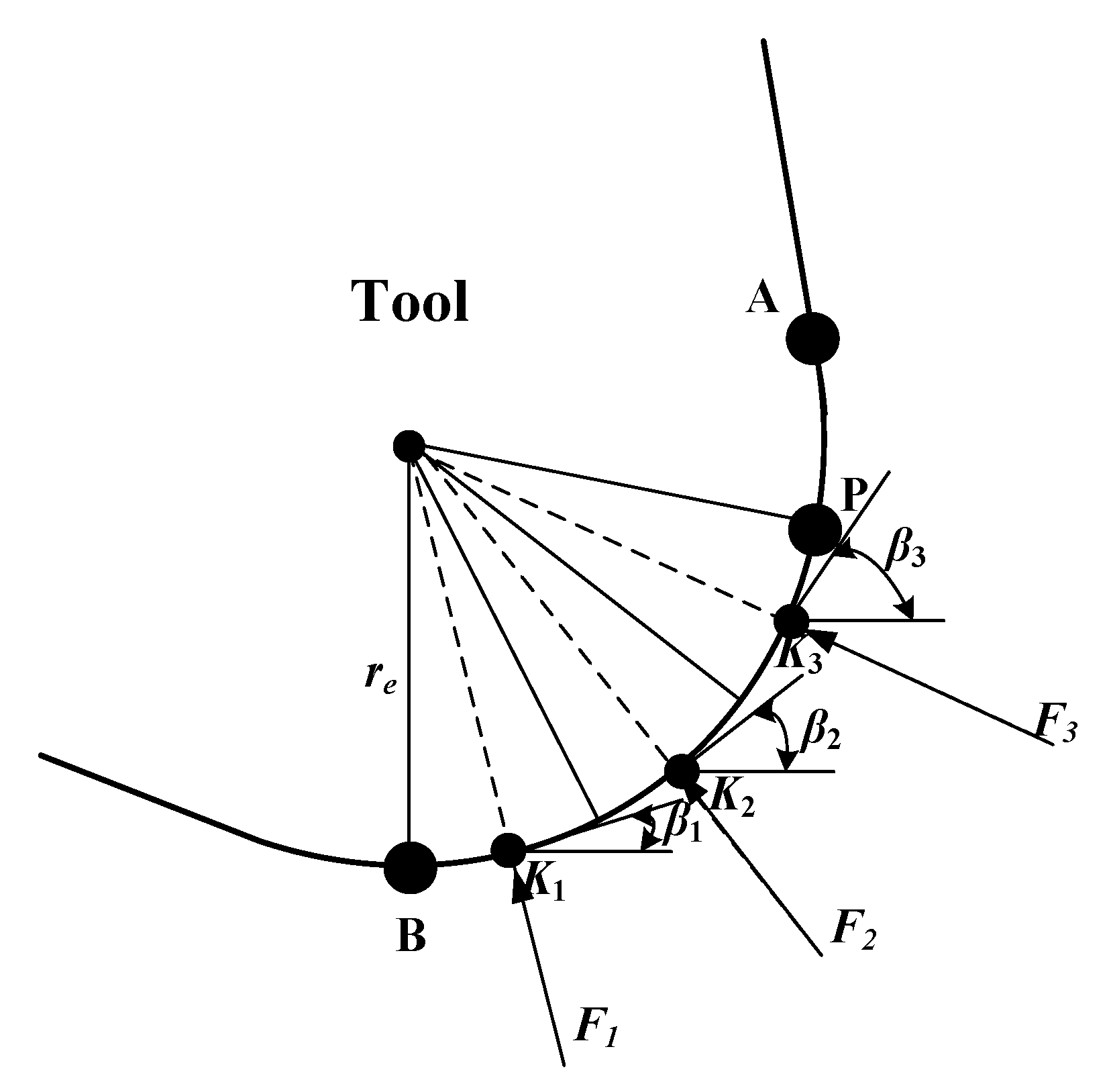
4.2. Fiber Resin Fracture Zone (Zone II)
- Fracture occurs when the fiber is in contact with the tool for the first time,
- The residual material of the fiber further contacts the tool and may cause secondary fractures.
4.3. Rebound Zone (Zone Ⅲ)
4.4. Cutting Force Evaluation
5. CFRP Cutting Force Analytical Model Verification
5.1. Experimental Design
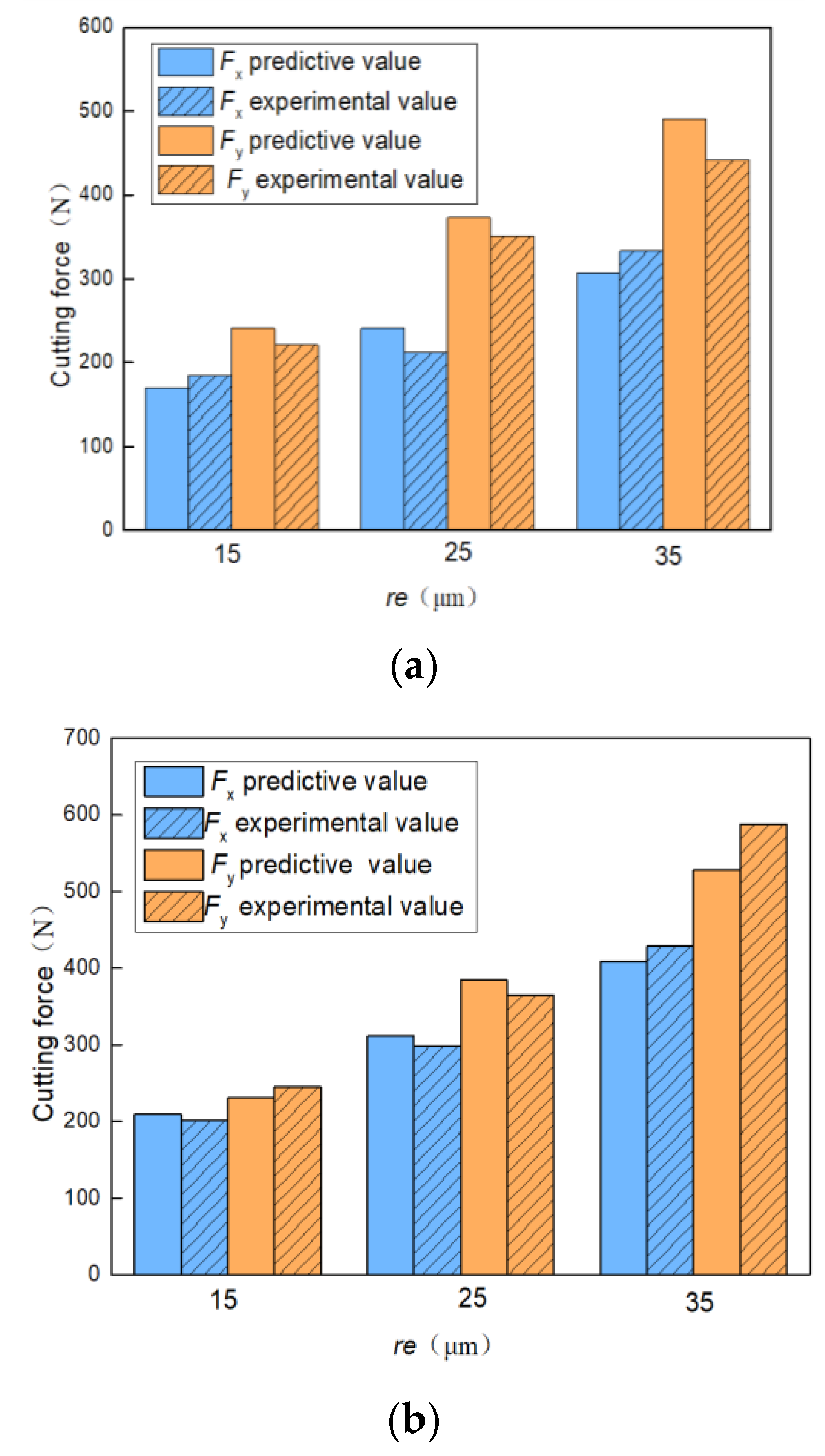
5.2. Cutting Force Model Verification
6. Conclusions
- In the CFRP cutting process, the tool tooth and a single carbon fiber first come into contact, eventually breaking at that point. The residual fibers may also interact with the tool teeth and break multiple times.
- The tool edge radius has a direct influence on the cutting force, and the model correctly reflects the dependence in the different cases analyzed on the fiber cutting angle.
- The comparison with measured forces shows that the maximum relative deviation of the model predicted value of the cutting force was below 15%, which proves that the analytical model built for the CFRP cutting force can provide values within a limited uncertainty, useful for many evaluations and machining applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Em | Elastic modulus of the matrix | re | Radius of the edge circle |
| θ | Fiber cutting angle | tn | Normal stress |
| Eb | Equivalent Young’s modulus | ts, tt | Shear stresses |
| γ | Rake angle of the tool | ac | Cutting depth |
| Fiber strain energy | b | Thickness about CFRP laminate | |
| Ef1 | Longitudinal elastic modulus | G12 | Shear modulus |
| Moment of inertia of the section | re | Radius of the edge circle | |
| Matrix strain energy | k | Dimensionless number | |
| Gm | Shear modulus of the matrix | Radius of the RVE | |
| Fracture energy density | Radius of the carbon fiber | ||
| Fracture energy | Fiber volume fraction | ||
| Um | Matrix strain energy | Average cutting force | |
| Work done by the the external force | Fiber strain energy | ||
| Work done by the supporting force | Pressure on the flank surface | ||
| Transverse elastic modulus of fiber | ae | Radial depth of cut |
References
- Norcahyo, R.; Soepangkat, B.O.P.; Effendi, M.K. Minimization of the hole entry and hole exit delamination on drilling process of carbon fiber reinforced polymer using BPNN-PSO. AIP Conf. Proc. 2019, 2114, 060005. [Google Scholar]
- John, K.M.; Kumaran, S.T. A feasible strategy to produce quality holes using temperature-assisted drilling on CFRP. Int. J. Adv. Manuf. Technol. 2020, 110, 3113–3127. [Google Scholar] [CrossRef]
- Dong, S.; Liao, W.; Zheng, K.; Ma, W. Investigation on thrust force in rotary ultrasonic drilling of CFRP/aluminum stacks. Proc. Inst. Mech. Eng. Part C 2020, 234, 394–404. [Google Scholar] [CrossRef]
- Tamura, S.; Matsumura, T. Delamination-free drilling of carbon fiber reinforced plastic with variable feed rate. Precis. Eng. 2010, 70, 70–76. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Qiao, W.; Li, Z.; Wang, N.; Zhang, J.; Wang, T. High-speed milling of CFRP composites: A progressive damage model of cutting force. Int. J. Adv. Manuf. Technol. 2020, 106, 1005–1015. [Google Scholar] [CrossRef]
- Wang, F.; Bi, G.; Ning, F. Modeling of dynamic milling forces considering the interlaminar effect during milling multidirectional CFRP laminate. J. Reinf. Plast. Compos. 2021, 40, 437–449. [Google Scholar] [CrossRef]
- Chen, T.; Wang, C.; Xiang, J.; Wang, Y. Study on tool wear mechanism and cutting performance in helical milling of CFRP with stepped bi-directional milling cutters. Int. J. Adv. Manuf. Technol. 2020, 111, 2441–2448. [Google Scholar] [CrossRef]
- Calzada, K.A.; Kapoor, S.G.; DeVor, R.E.; Samuel, J.; Srivastava, A.K. Modeling and interpretation of fiber orientation-based failure mechanisms in machining of carbon fiber-reinforced polymer composites. J. Manuf. Process. 2012, 14, 141–149. [Google Scholar] [CrossRef]
- Dandekar Chinmaya, R.; Shin Yung, C. Multiphase Finite Element Modeling of Machining Unidirectional Composites: Prediction of Debonding and Fiber Damage. J. Manuf. Sci. Eng. 2008, 130, 051016. [Google Scholar] [CrossRef]
- Liu, X. Three-Dimensional Finite Element Analysis and Experimental Research on the Macro and Micro Mechanism of CFRP Cutting. Ph.D. Thesis, Hunan University of Science and Technology, Xiangtan, China, 2019. [Google Scholar]
- Wang, F.; Wang, X.; Yang, R.; Gao, H.; Su, Y.; Bi, G. Research on the carbon fibre-reinforced plastic (CFRP) cutting mechanism using macroscopic and microscopic numerical simulations. J. Reinf. Plast. Compos. 2017, 36, 555–562. [Google Scholar] [CrossRef]
- Rong, C.; Shujian, L.; Pengnan, L.; Xiaopeng, L.; Xinyi, Q.; Ko, T.J.; Yong, J. Effect of fiber orientation angles on the material removal behavior of CFRP during cutting process by multi-scale characterization. Int. J. Adv. Manuf. Technol. 2020, 106, 5017–5031. [Google Scholar] [CrossRef]
- Pwu, H.Y.; Hocheng, H. Chip formation of cutting fiber-reinforced plastics perpendicular to fiber axis. J. Manuf. Sci. Eng. 1998, 120, 192–196. [Google Scholar] [CrossRef]
- Zhang, L.C.; Zhang, H.J.; Wang, X.M. A force prediction model for cutting unidirectional fibre-reinforced plastics. Mach. Sci. Technol. 2001, 5, 293–305. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, K.; Cheng, H.; Wang, D.; Meng, Q. Microscopic mechanism based force prediction in orthogonal cutting of unidirectional CFRP. Int. J. Adv. Manuf. Technol. 2015, 79, 1209–1219. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, C.; Wang, G.; Huang, P. Investigation on the effects of microstructure on machining unidirectional carbon fiber reinforced polymer composites with a modified force model. J. Reinf. Plast. Compos. 2019, 38, 379–394. [Google Scholar] [CrossRef]
- Voss, R.; Seeholzer, L.; Kuster, F.; Wegener, K. Analytical force model for orthogonal machining of unidirectional carbon fibre reinforced polymers as a function of the fibre orientation. J. Mater. Process. Technol. 2018, 263, 440–469. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, K.; Cheng, H.; Liu, S.; Jiang, S. An analytical method for predicting the fluctuation of thrust force during drilling of unidirectional carbon fiber reinforced plastics. J. Compos. Mater. 2014, 49, 699–711. [Google Scholar] [CrossRef]
- Gao, C.; Xiao, J.; Xu, J.; Ke, Y. Factor analysis of machining parameters of fiber-reinforced polymer composites based on finite element simulation with experimental investigation. Int. J. Adv. Manuf. Technol. 2016, 83, 1113–1125. [Google Scholar] [CrossRef]
- Li, H.N.; Wang, J.P.; Wu, C.Q.; Zhao, Y.J.; Xu, J.; Liu, X.; Zhu, W.Q. Damage behaviors of unidirectional CFRP in orthogonal cutting: A comparison between single- and multiple-pass strategies. Compos. Part B Eng. 2020, 185, 107774. [Google Scholar] [CrossRef]
- Zhenchao, Q. Research on Drilling Force Modeling and Layered Control Method of CFRP/Metal Laminated Structure. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2015. [Google Scholar]
- Yan, X.; Reiner, J.; Bacca, M.; Altintas, Y.; Vaziri, R. A study of energy dissipating mechanisms in orthogonal cutting of UD-CFRP composites. Compos. Struct. 2019, 220, 460–472. [Google Scholar] [CrossRef]
- Xu, X.; Jin, X. 3-D finite element modeling of sequential oblique cutting of unidirectional carbon fiber reinforced polymer. Compos. Struct. 2021, 256, 113127. [Google Scholar] [CrossRef]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials. Cengage Learn. Emea 2012, 29, 224. [Google Scholar]
- Winkler, E. Theory of Elasticity and Strength; Dominicus: Prague, Czechoslovakia, 1867. [Google Scholar]

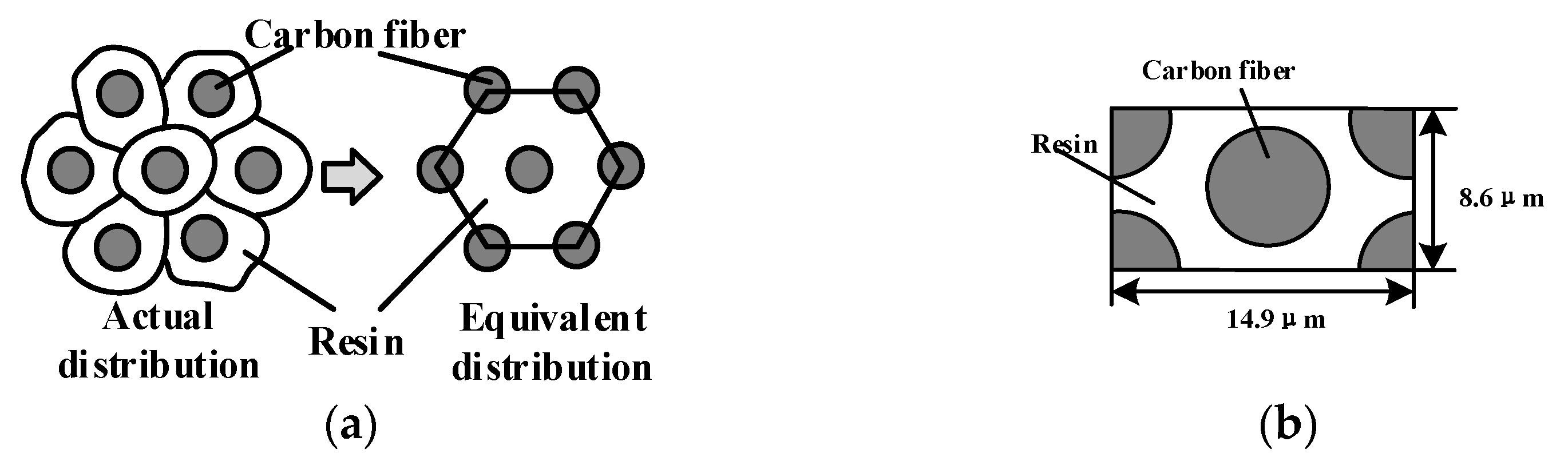

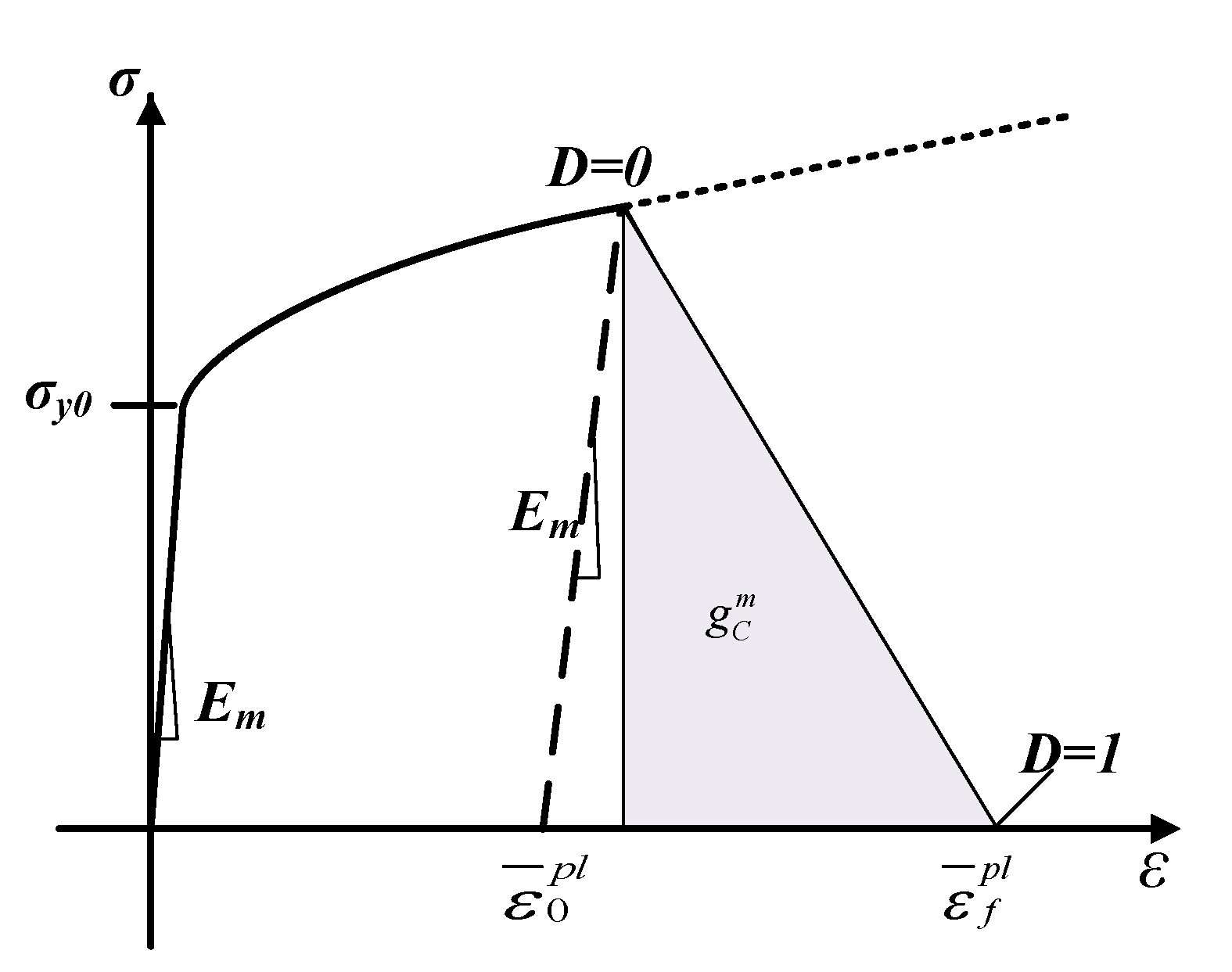
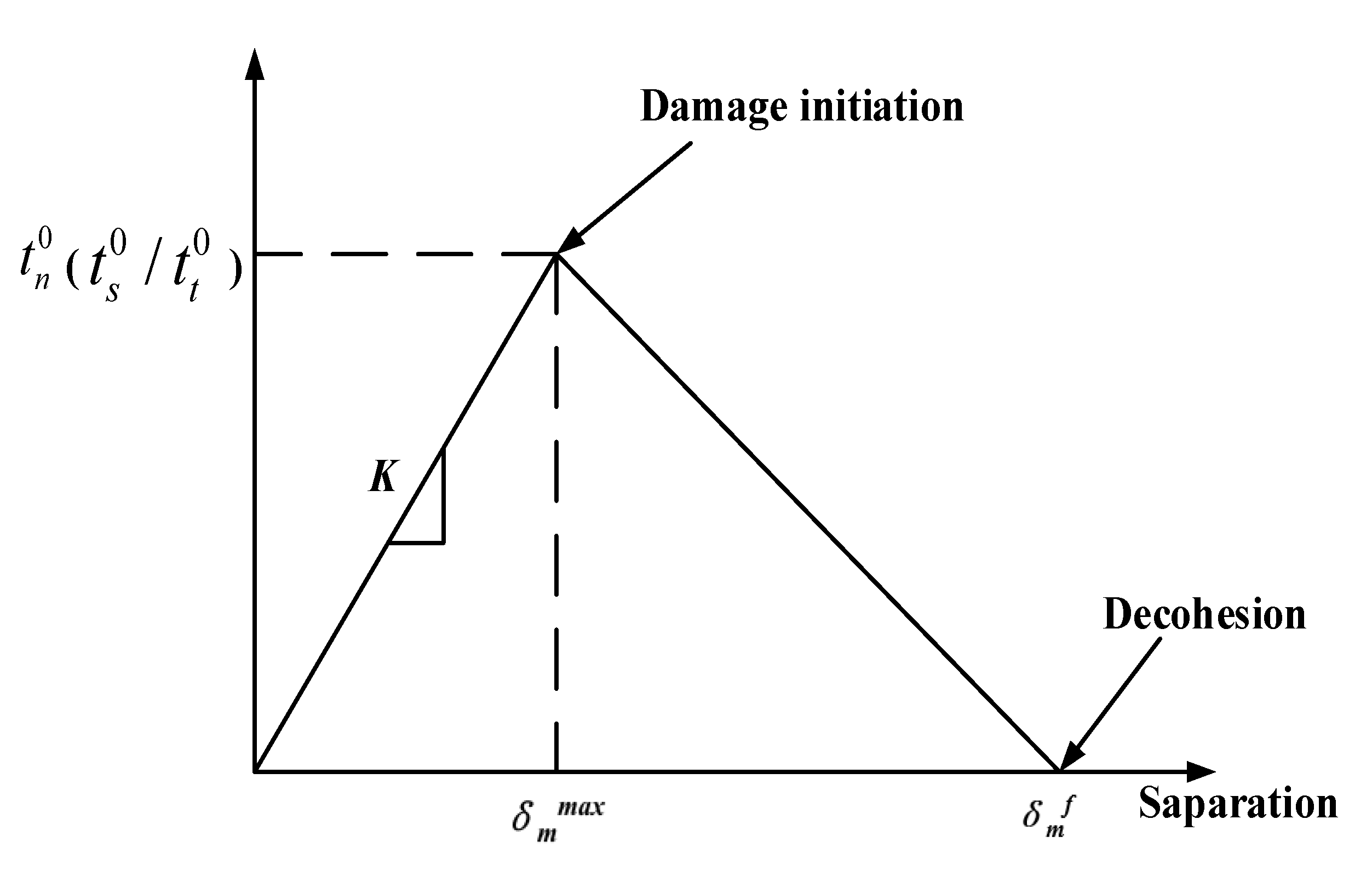
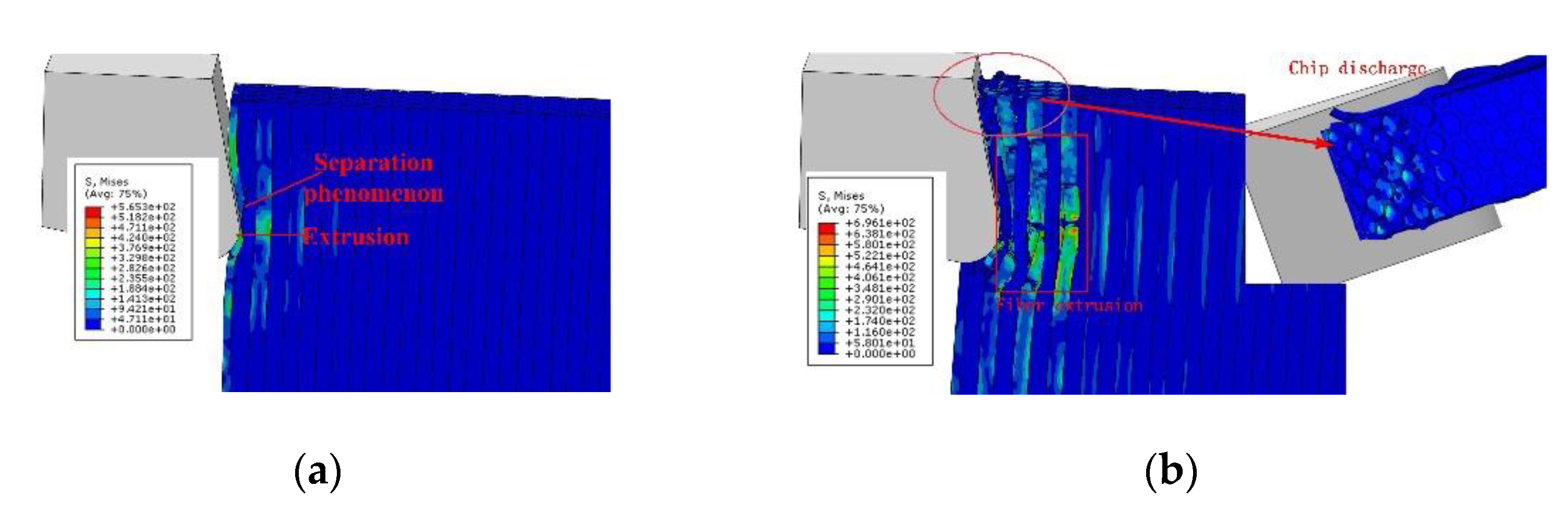






| Density | Longitudinal Elastic Modulus | Transverse Elastic Modulus | Poisson’s Ratio | Shear Modulus | Tensile Strength | Compressive Strength | |||
|---|---|---|---|---|---|---|---|---|---|
| ρ (kg/m3) | Ef1 (GPa) | Ef2 (GPa) | G12 = G13 (GPa) | G23 (GPa) | Xt (GPa) | Xc (GPa) | Yt (GPa) | Yc (GPa) | |
| 1760 | 230 | 8.2 | 0.2 | 28 | 5.5 | 4.9 | 3.96 | 3.34 | 1.5 |
| Elastic Modulus | Poisson’s Ratio | Shear Modulus | Shear Strength | Density | Yield Strength | Damage Plastic Strain | Fracture Energy |
|---|---|---|---|---|---|---|---|
| Em (GPa) | Gm (GPa) | ρ (kg/m3) | |||||
| 3.5 | 0.33 | 1.02 | 62 | 980 | 27 | 5% | 0.1 |
| Normal Strength | Shear Strength | Elastic Stiffness | Fracture Energy | Mixed-Mode | |
|---|---|---|---|---|---|
| (MPa) | Knn = Kss = Ktt (N/mm3) | ηa | |||
| 167.5 | 25 | 100,000 | 0.002 | 0.006 | 1.45 |
| Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio |
|---|---|---|
| 14,450 | 640 | 0.22 |
| Spindle Speed | Cutting Speed | Fiber Cutting Angle | Radial Depth of Cut | Axial Depth of Cut | Feed per Tooth | The Cutter Radius |
|---|---|---|---|---|---|---|
| n (r/min) | v (mm/s) | θ (°) | ae (mm) | ap (mm) | vf (mm/tooth) | re (μm) |
| 500 | 3.8 | 45°/90° | 1 | 4 | 0.225 | 15/25/35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, H.; Zheng, H.; Wang, G. Establishment of Analytical Model for CFRP Cutting Force Considering the Radius of the Edge Circle. Materials 2022, 15, 2127. https://doi.org/10.3390/ma15062127
Ning H, Zheng H, Wang G. Establishment of Analytical Model for CFRP Cutting Force Considering the Radius of the Edge Circle. Materials. 2022; 15(6):2127. https://doi.org/10.3390/ma15062127
Chicago/Turabian StyleNing, Haifeng, Hualin Zheng, and Guixin Wang. 2022. "Establishment of Analytical Model for CFRP Cutting Force Considering the Radius of the Edge Circle" Materials 15, no. 6: 2127. https://doi.org/10.3390/ma15062127
APA StyleNing, H., Zheng, H., & Wang, G. (2022). Establishment of Analytical Model for CFRP Cutting Force Considering the Radius of the Edge Circle. Materials, 15(6), 2127. https://doi.org/10.3390/ma15062127





