Analysis of Deep Drawing Process for Stainless Steel Micro-Channel Array
Abstract
:1. Introduction
2. Basic Theory
2.1. Stiffness Equation
2.2. Selective Reduced Integration Formulation
2.3. Scale Factors for Micro-Forming Process of Sheet Metal
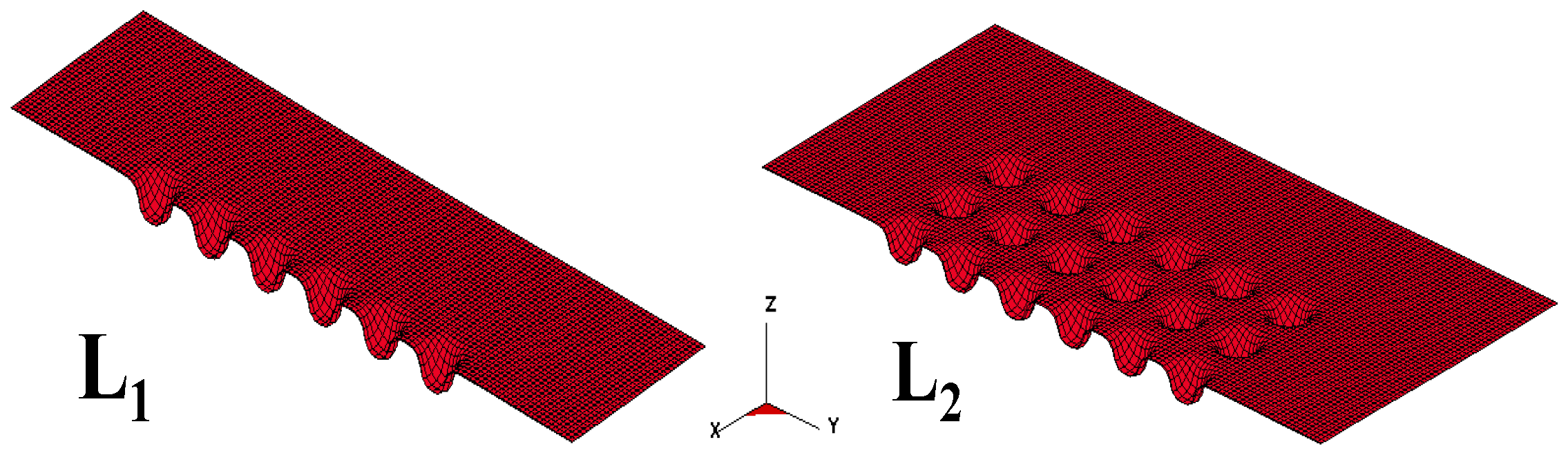
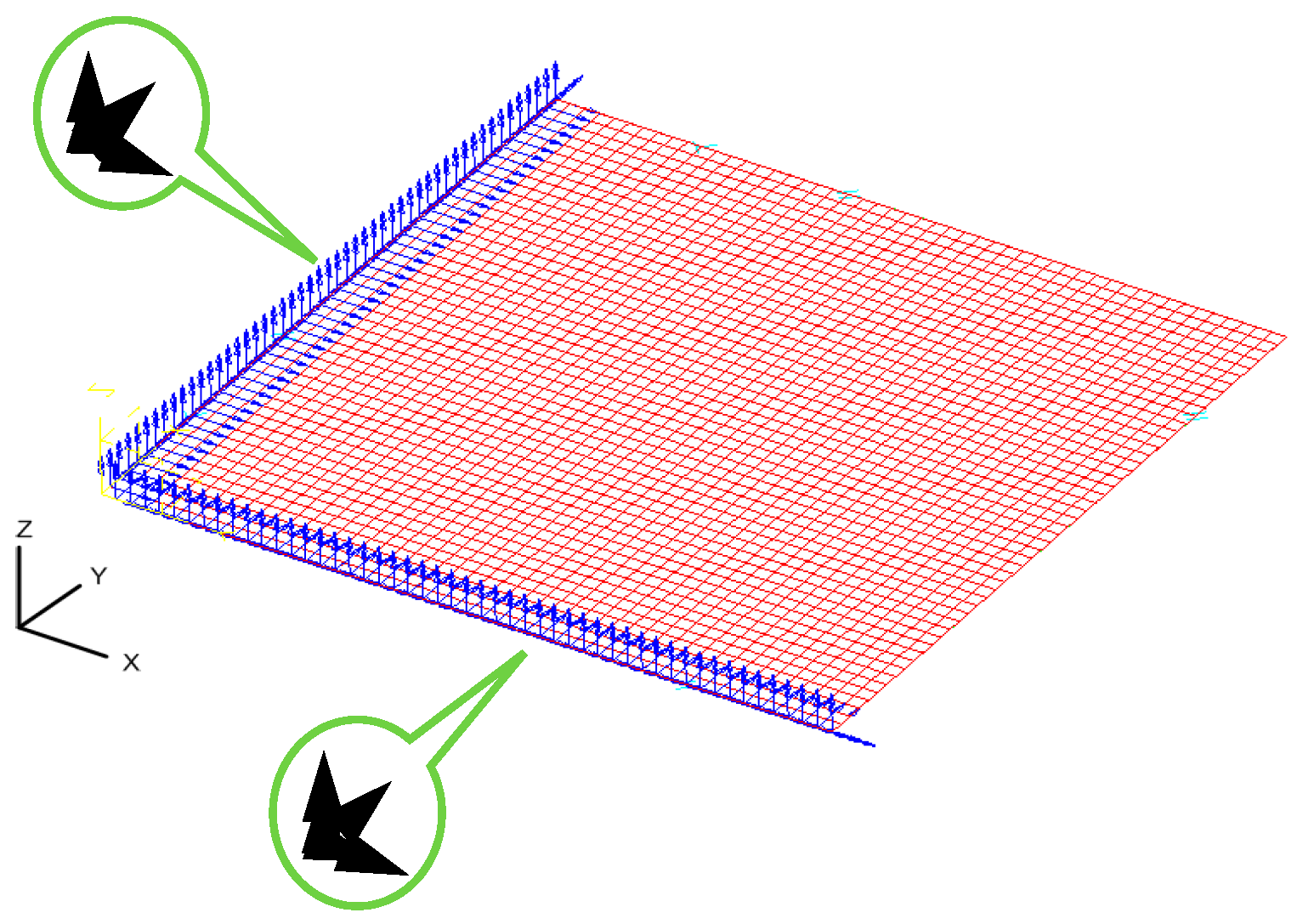
3. Numerical Analysis for Micro-Channel Array Forming Process
4. Experimental Results and Discussion
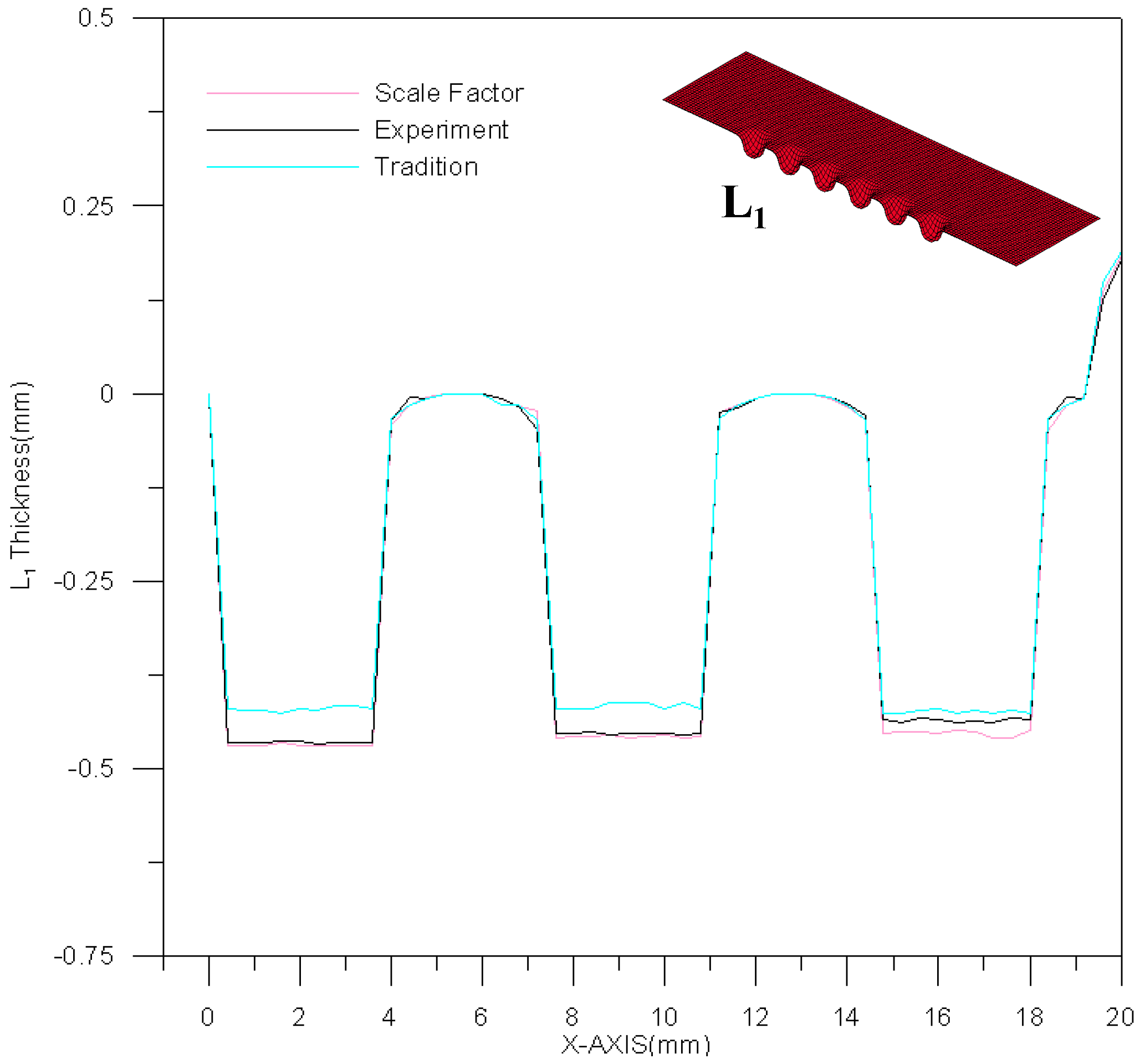
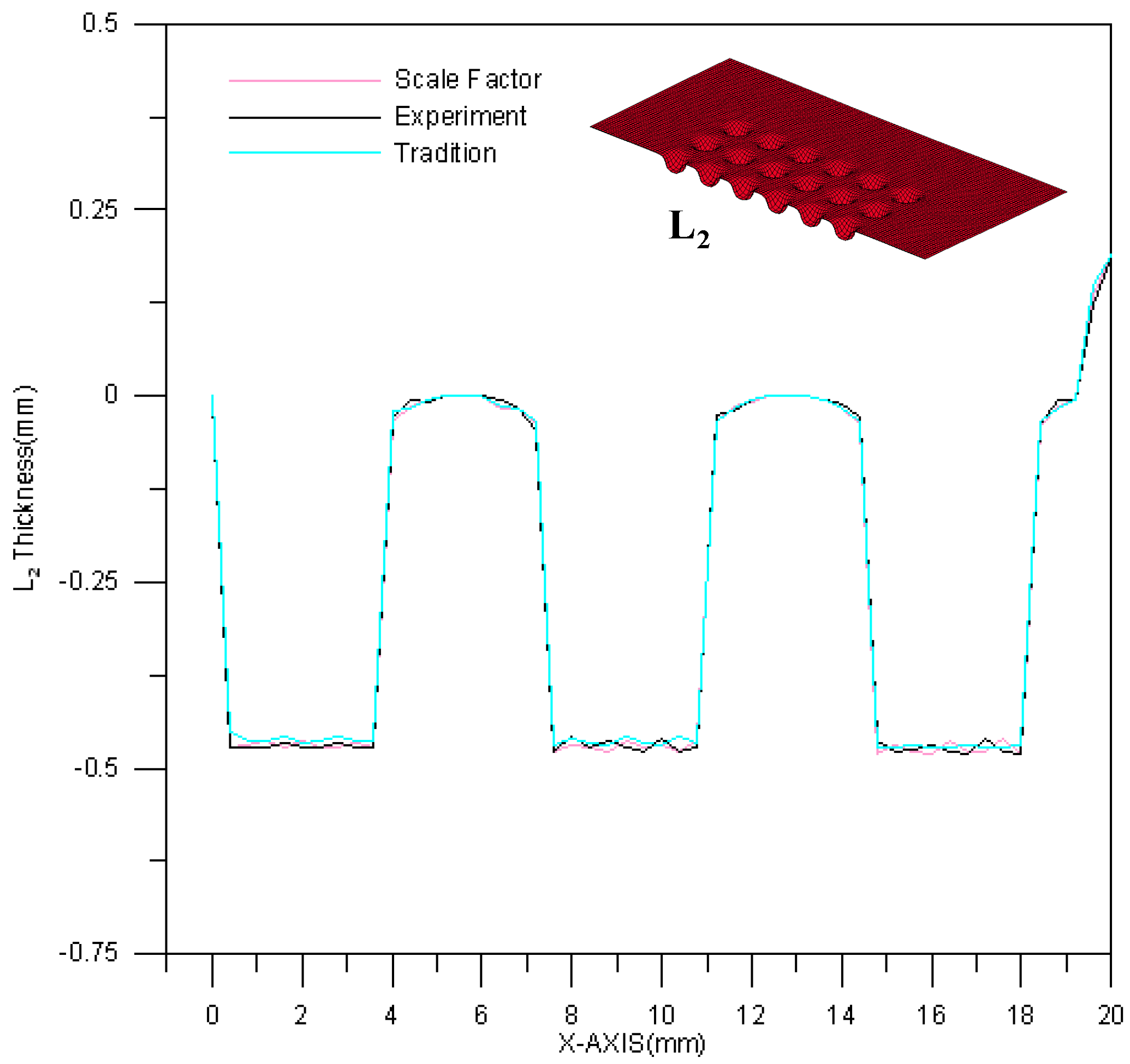
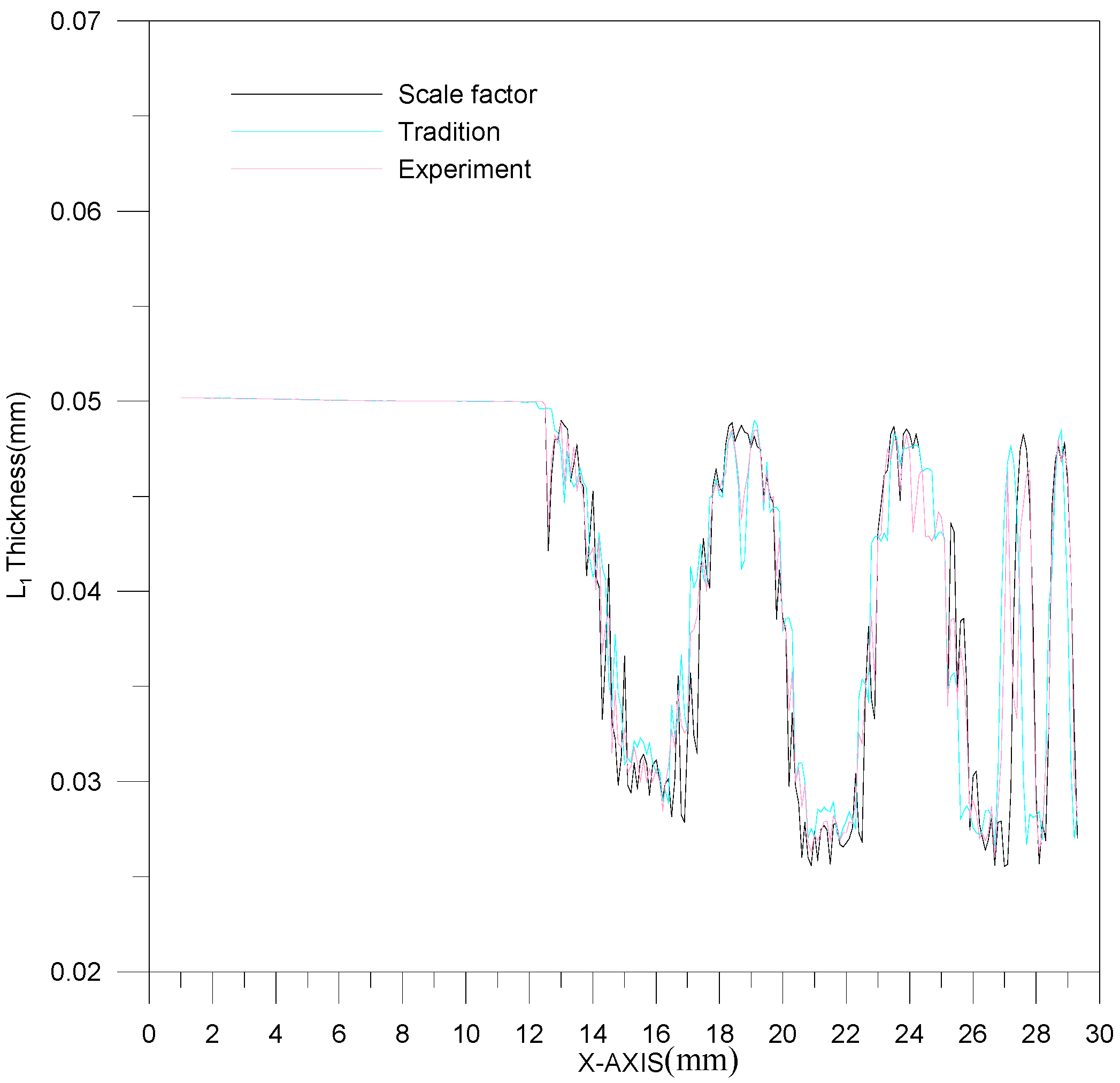
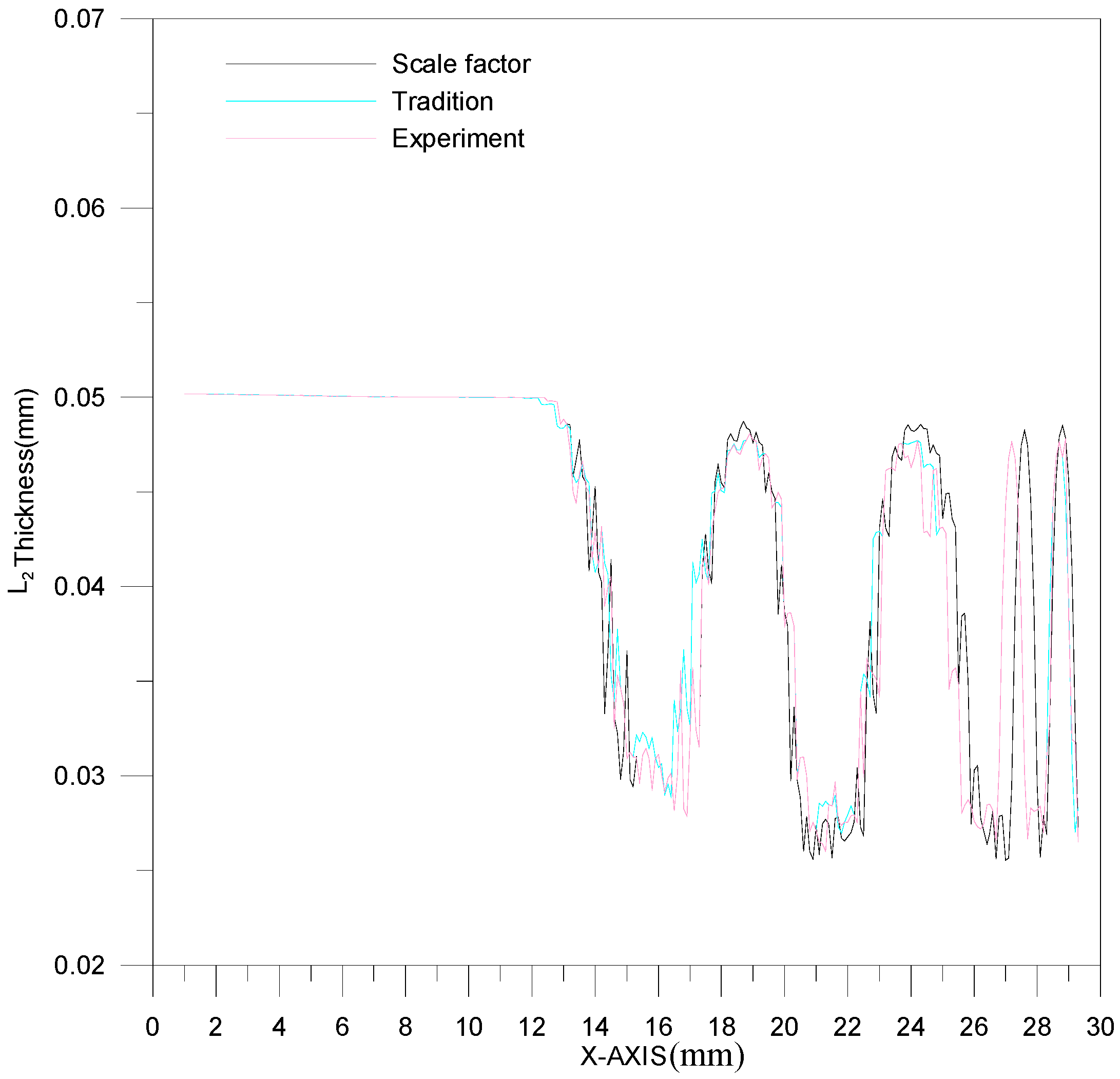
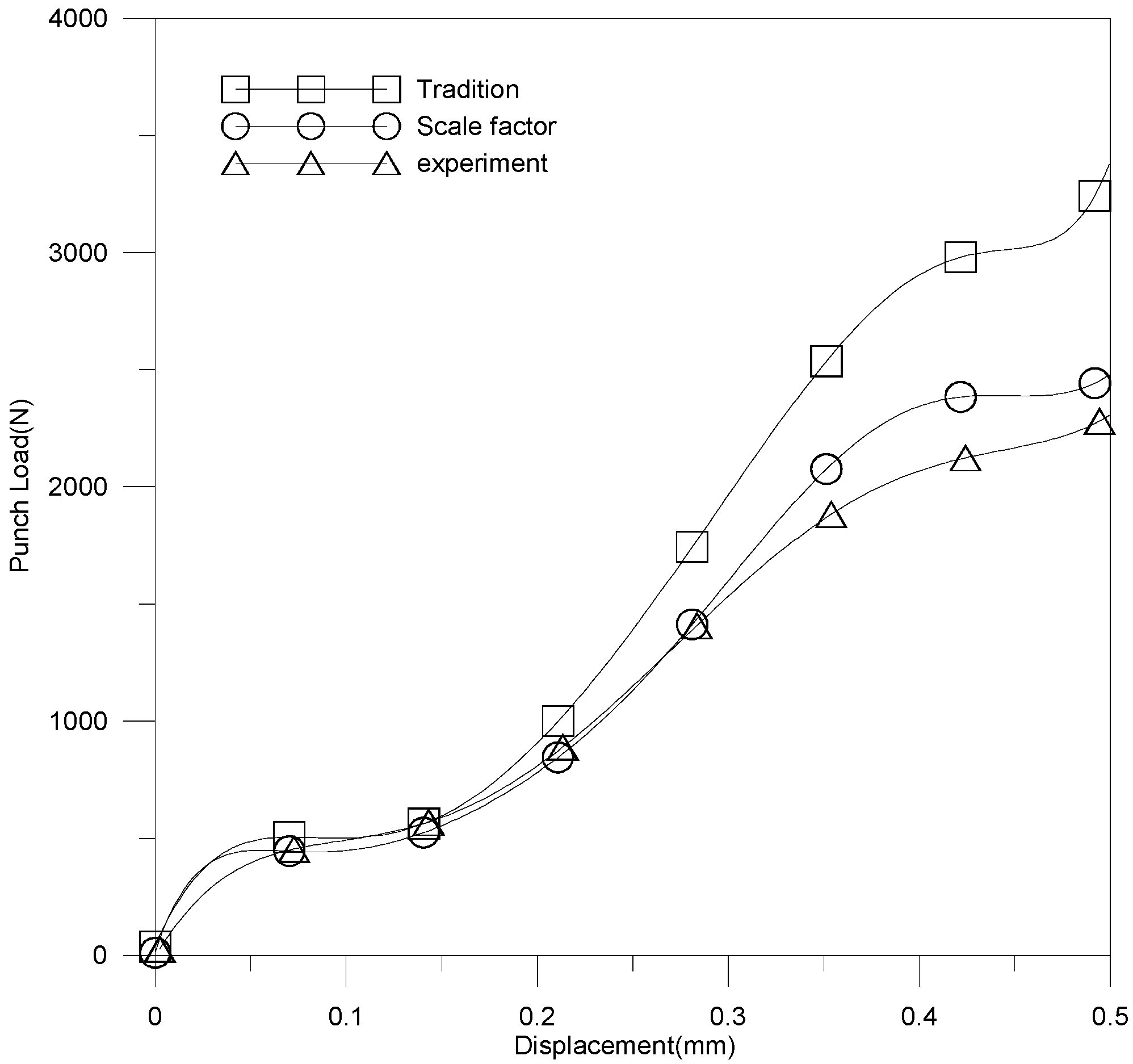
4.1. Comparisons between Experimental Results and Simulation Results
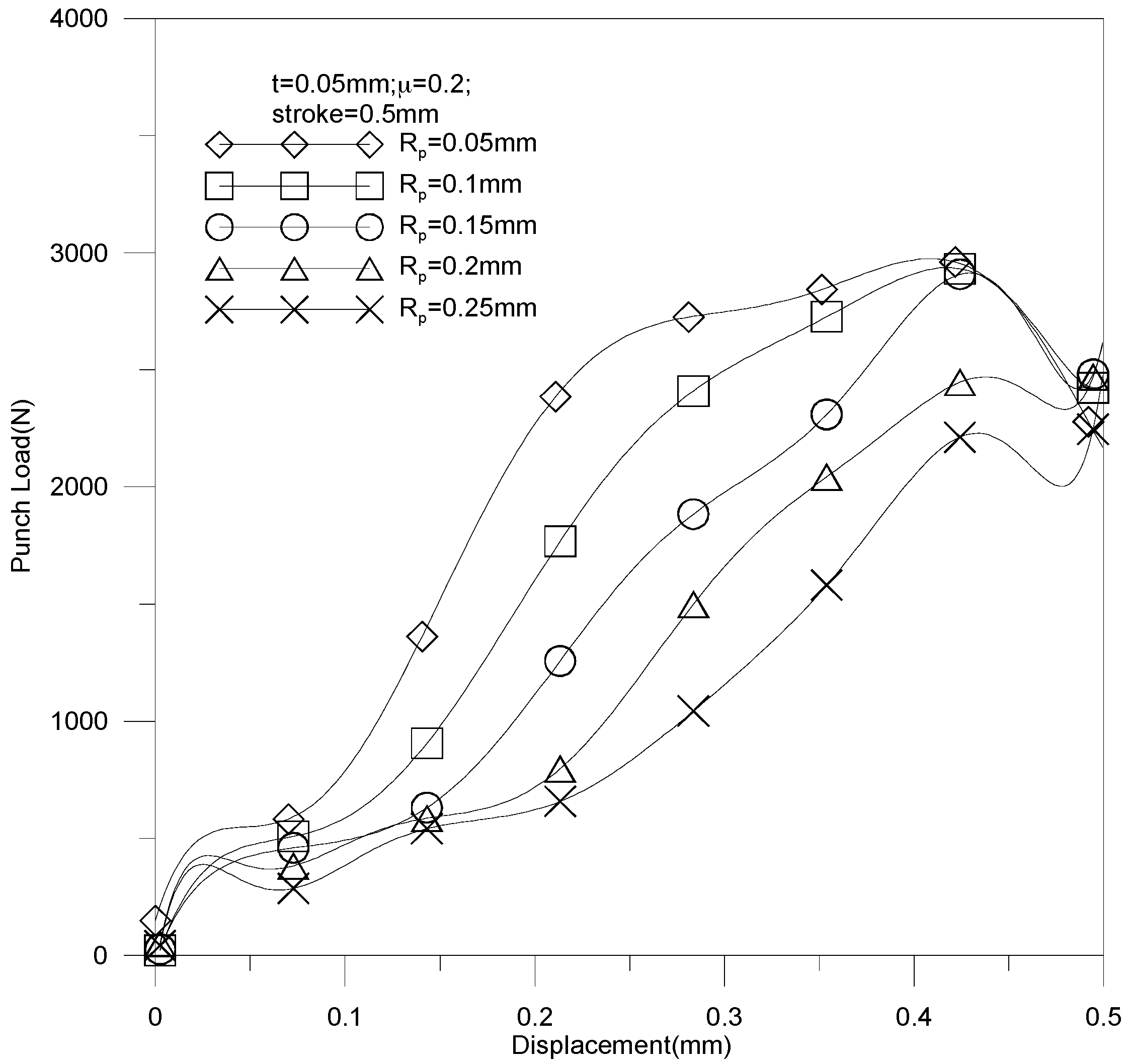
4.2. Effect of Tool Radius on the Micro-Channel Array Forming Process of Stainless Steel Plates
- *
- Punch fillet radius: 0.05 mm, 0.1 mm, 0.15 mm, 0.2 mm, and 0.25 mm
- *
- Stroke: 0.5 mm
- *
- Coefficient of friction: 0.2
- *
- Blank thickness: 0.5 mm
5. Conclusions
- (1)
- The maximum channel depth for a 50 μm stainless steel sheet is about 0.5 mm. This is verified by both of the simulation results and the experimental results.
- (2)
- On the basis of the finished workpieces, the material fracture is mainly located in the contact area between the punch and the bottom die fillet. As a result, more attention should be devoted to fillet radius design.
- (3)
- The deep drawing process can be performed more smoothly when a large fillet radius is applied. In other words, a small tool fillet radius may lead to an increase of fracture.
- (4)
- The simulation performance of the modified scale-factor material model is better than that of the traditional material model.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yu, H.N.; Lim, J.W.; Suh, J.D.; Lee, D.G. A graphite-coated carbon fiber epoxy composite bipolar plate for polymer electrolyte membrane fuel cell. J. Power Sources 2011, 196, 9868–9875. [Google Scholar] [CrossRef]
- Kumar, A.; Ricketts, M.; Hirano, S. Ex situ evaluation of nanometer range gold coating on stainless steel substrate for automotive polymer electrolyte membrane fuel cell bipolar plate. J. Power Sources 2010, 195, 1401–1407. [Google Scholar] [CrossRef]
- Peng, L.; Lai, X.; Liu, D.; Hu, P.; Ni, J. Flow channel shape optimum design for hydroformed metal bipolar plate in PEM fuel cell. J. Power Sources 2008, 178, 223–230. [Google Scholar] [CrossRef]
- Petrach, E.; Abu-Isa, I.; Wang, X. Investigation of elastomer graphite composite material for proton exchange membrane fuel cell bipolar plate. J. Fuel Cell Sci. Technol. 2009, 6, 0310051–0310056. [Google Scholar] [CrossRef]
- Gautam, R.K.; Banerjee, S.; Kar, K.K. Bipolar plate materials for proton exchange membrane fuel cell application. Recent Pat. Mater. Sci. 2015, 8, 15–45. [Google Scholar] [CrossRef]
- Koc, M.; Mahabunphachai, S. Feasibility investigations on a novel micro-manufacturing process for fabrication of fuel cell bipolar plates: Internal pressure-assisted embossing of micro-channels with in-die mechanical bonding. J. Power Sources 2007, 172, 725–733. [Google Scholar] [CrossRef]
- Iranzo, A.; Munoz, M.; Lopez, E.; Pino, J.; Rosa, F. Experimental fuel cell performance analysis under different operating conditions and bipolar designs. Int. J. Hydrogen Energy 2010, 35, 11434–11447. [Google Scholar] [CrossRef]
- Kakati, B.K.; Yamsani, V.K.; Dhathathreyan, K.S.; Sathiyamoorthy, D.; Verma, A. The electrical conductivity of a composite bipolar plate for fuel cell applications. Carbon 2009, 47, 2413–2418. [Google Scholar] [CrossRef]
- Mahabunphachai, S.; Koc, M. Fabrication of micro-channel arrays on thin metallic sheet using internal fluid pressure: Investigations on size effects and development of design guidelines. J. Power Sources 2008, 175, 363–371. [Google Scholar] [CrossRef]
- Hu, P.; Peng, L.; Zhang, W.; Lai, X. Optimization design of slotted-interdifitated channel for stamped thin metal bipolar plate in proton exchange membrane fuel cell. J. Power Sources 2009, 187, 407–414. [Google Scholar] [CrossRef]
- Park, Y.-C.; Lee, S.-H.; Kim, S.-K.; Lim, S.; Jung, D.-H.; Lee, D.-Y.; Choi, S.-Y.; Ji, H.; Peck, D.-H. Performance and long-term stability of Ti metal and stainless steels as a metal bipolar plate for a direct methanol fuel cell. Int. J. Hydrogen Energy 2010, 35, 4320–4328. [Google Scholar] [CrossRef]
- Peng, L.F.; Hu, P.; Lai, X.M.; Mei, D.Q.; Ni, J. Investigation of micro/meso sheet soft punch stamping process-simulation and experiments, materials and design. Mater. Des. 2009, 30, 783–790. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Y.F.; He, H.; Li, J.M.; Yuan, Z.Y.; Na, C.R.; Liu, X.W. Development and performance analysis of a metallic micro-direct methanol fuel cell for high-performance applications. J. Power Sources 2010, 195, 7338–7348. [Google Scholar] [CrossRef]
- Chen, Y.L.; Zhan, H.B.; Lee, S.J.L.; Zhu, S.M. Micro-ECM of maze flow channel on bipolar plates of fuel cell. Key Eng. Mater. 2011, 458, 125–130. [Google Scholar] [CrossRef]
- Qiu, D.; Yi, P.; Peng, L.; Lai, X. Channel dimensional error effect of stamped bipolar plates on the characteristics of gas diffusion layer contact pressure for proton exchange membrane fuel cell stacks. J. Fuel Cell Sci. Technol. 2015, 12, 041002. [Google Scholar] [CrossRef]
- Imanmehr, S.; Pourmahmod, N. A parameteric study of bipolar plate structural parameters on the performance of proton exchange membrane fuel cell. J. Fuel Cell Sci. Technol. 2012, 9, 051003. [Google Scholar] [CrossRef]
- Kianimanesh, A.; Yu, B.; Yang, Q.; Freiheit, T.; Xue, D.; Park, S.S. Investigation of bipolar plate geometry on direct ethanol fuel cell performance. Int. J. Hydrogen Energy 2012, 37, 18403–18411. [Google Scholar] [CrossRef]
- Park, W.T.; Jin, C.K.; Kang, C.G. Improving channel depth of stainless steel bipolar plate in fuel cell using process parameters of stamping. Energy Convers. Manag. 2016, 124, 51–60. [Google Scholar] [CrossRef]
- McMeeking, R.M.; Rice, J.R. Finite-element formulations for problems of large elastic-plastic deformation. Int. J. Solids Struct. 1975, 11, 601–616. [Google Scholar] [CrossRef]
- Hinton, E.; Owen, D.R. Finite Element Software for Plates and Shell; Pineridge: Swansea, UK, 1984. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method; Prentice-Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Hughes, T.J.R. Generalization of selective integration procedures to anisotropic and nonlinear media. Int. J. Numer. Methods Eng. 1980, 15, 1413–1418. [Google Scholar] [CrossRef]
- Adam, F.M.; Mohamed, E.; Hassaballa, A.E. Degenerated four nodes shell element with drilling degree of freedom. J. Eng. 2013, 3, 10–20. [Google Scholar]
- Peng, L.F.; Liu, F.; Ni, J.; Lai, X.M. Size effects in thin sheet metal forming and its elastic-plastic constitutive model. Mater. Des. 2007, 28, 1731–1736. [Google Scholar] [CrossRef]
- Huang, Z.G.; Li, J.W. Heating and thermostatic analysis of an oven-controlled quartz crystal oscillator. Smart Sci. 2016, 4, 45–51. [Google Scholar] [CrossRef]
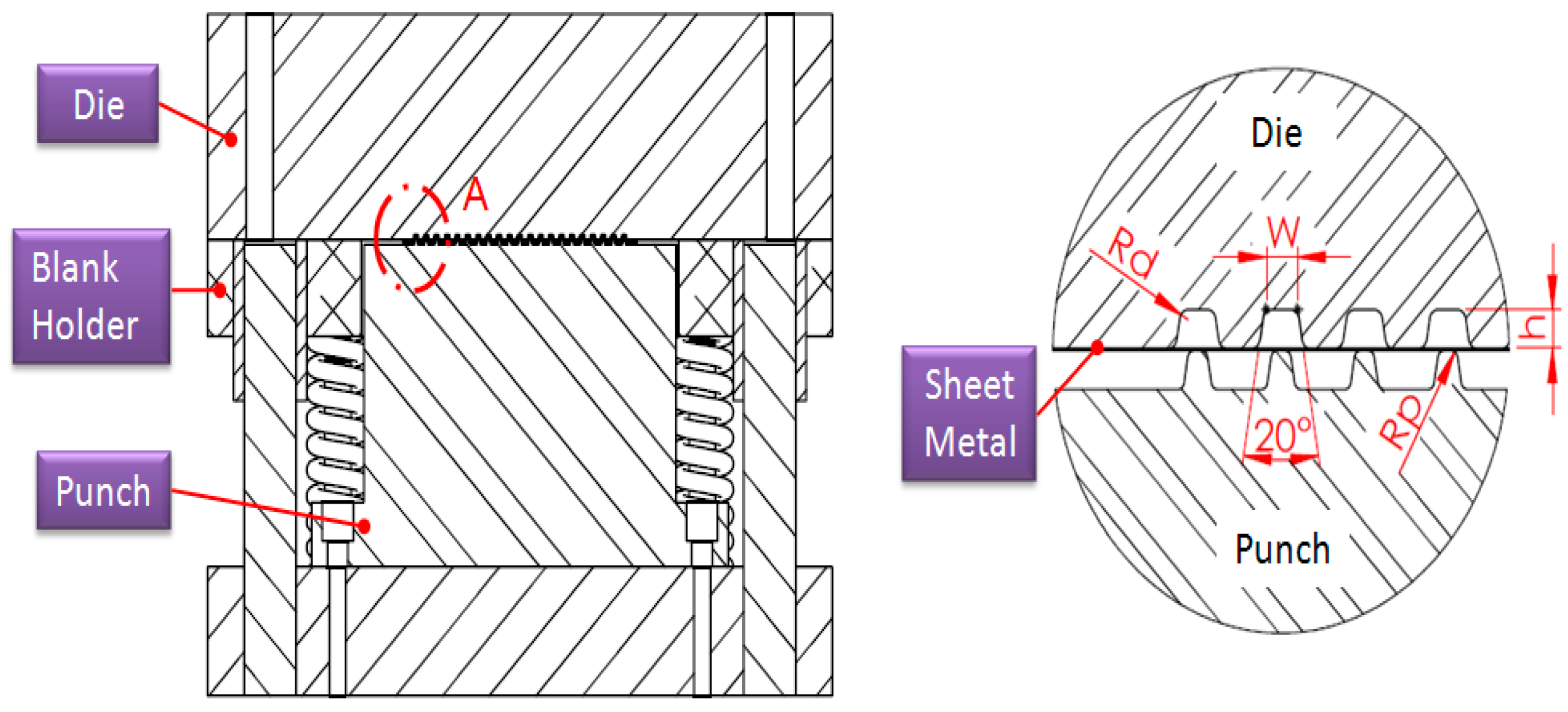







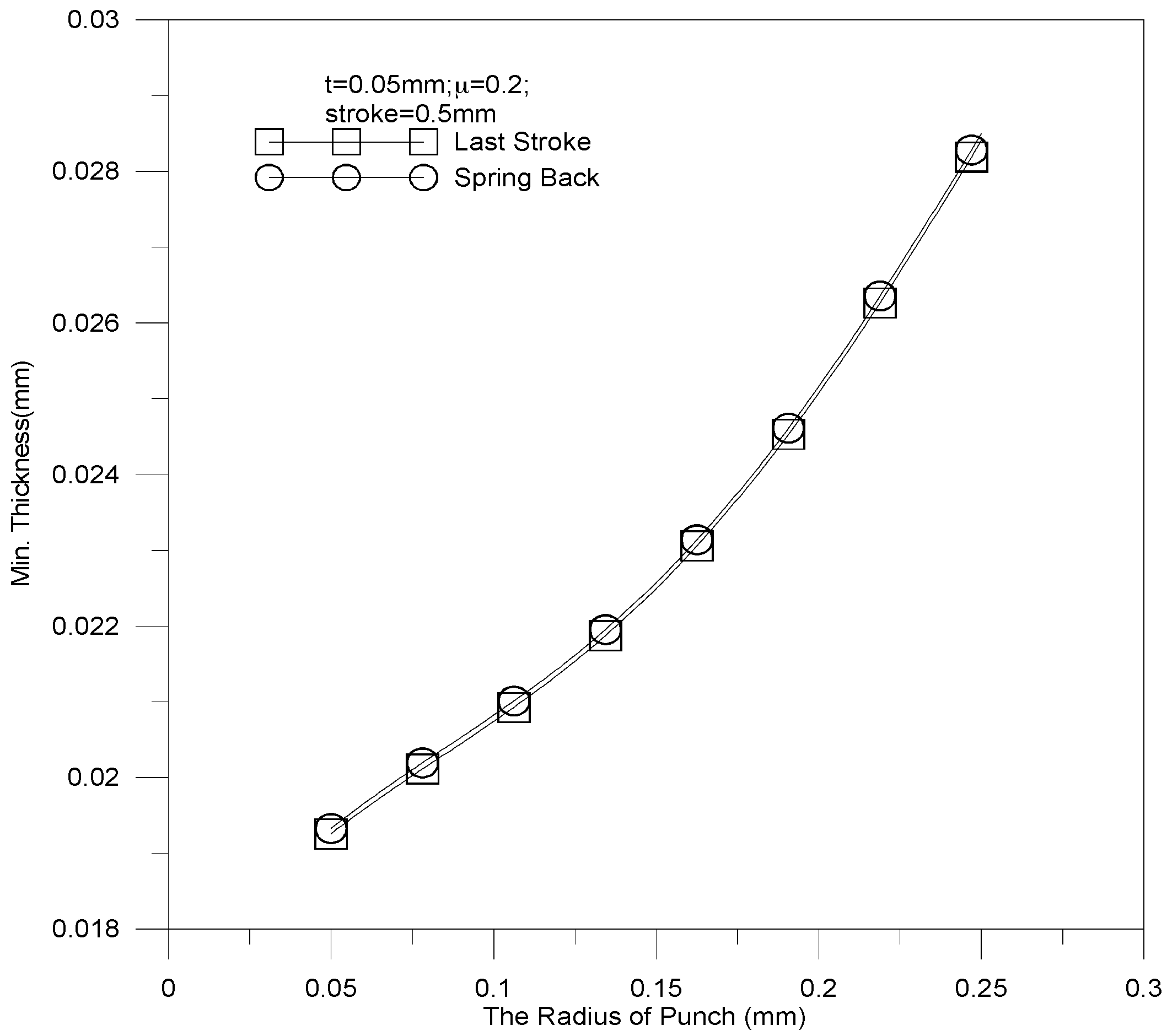



| Items | Dimensions (mm) |
|---|---|
| Width of channel (W) | 0.75 |
| Height of channel (h) | 0.5 |
| Radius of die (Rd) | 0.25 |
| Radius of punch (Rp) | 0.2 |
| Material (SUS304) | E (GPa) | ν | σy (MPa) | K (MPa) | n | ε0 |
|---|---|---|---|---|---|---|
| Tradition | 207 | 0.3 | 341 | 1819 | 0.576 | 0.077 |
| Scale Factor | 198 | 0.3 | 306 | 1361 | 0.582 | 0.077 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.-C.; Lin, J.-C.; Lee, R.-M. Analysis of Deep Drawing Process for Stainless Steel Micro-Channel Array. Materials 2017, 10, 423. https://doi.org/10.3390/ma10040423
Chen T-C, Lin J-C, Lee R-M. Analysis of Deep Drawing Process for Stainless Steel Micro-Channel Array. Materials. 2017; 10(4):423. https://doi.org/10.3390/ma10040423
Chicago/Turabian StyleChen, Tsung-Chia, Jiang-Cheng Lin, and Rong-Mao Lee. 2017. "Analysis of Deep Drawing Process for Stainless Steel Micro-Channel Array" Materials 10, no. 4: 423. https://doi.org/10.3390/ma10040423
APA StyleChen, T.-C., Lin, J.-C., & Lee, R.-M. (2017). Analysis of Deep Drawing Process for Stainless Steel Micro-Channel Array. Materials, 10(4), 423. https://doi.org/10.3390/ma10040423





