Data-Driven Load Forecasting in Microgrids: Integrating External Factors for Efficient Control and Decision-Making

Abstract

Accurate load forecasting is essential for optimizing microgrid and smart grid operations, thereby supporting Energy Management Systems (EMSs). Load forecasting also plays a key role in integrating renewable energy, ensuring grid stability, and facilitating decision-making. In this regard, we present a comprehensive literature review that combines both bibliometric analysis and critical literature synthesis to evaluate state-of-the-art forecasting techniques. Based on a screened corpus of over 200 scientific publications from 2015 to 2024, our analysis reveals a significant shift in the field: AI-based approaches, including Machine Learning (ML) and Deep Learning (DL), represent more than 55% of the analyzed literature, overtaking traditional statistical models. The bibliometric results highlight a 300% increase in publications focusing on ML-based models (e.g., SVM, CNN, LSTM) over the years. Furthermore, approximately 70% of the total reviewed works use at least one exogenous variable, such as weather variables, socioeconomic indicators, and cultural behavior. These findings reflect the transition from traditional statistical models to more flexible and scalable approaches. However, socioeconomic and cultural variables remain underutilized in the literature, particularly for long-term planning. Despite the progress load forecasting processes have made in recent years, thanks to advanced modeling, a few hurdles remain to realizing their full potential in modern microgrids. Thus, we argue that future research should focus on three key areas: (i) scalable real-time adaptive models, including computational complexity characterization, (ii) standardization in data collection for seamless integration of exogenous variables, and (iii) real-world application of forecasting models in decision-making that supports EMSs. Progress in these areas may enhance grid stability, optimize resource allocation, and accelerate the transition to sustainable energy systems.

1. Introduction

Load forecasting plays a key role in the operation and optimization of microgrids and smart grids, serving as a fundamental enabler of sustainable Energy Management Systems (EMSs) [1]. In the context of the global energy transition, where Renewable Energy Sources (RESs), such as solar, wind, and hydropower, are rapidly expanding [2], these forecasts are critical for ensuring grid stability, optimizing energy generation, reducing costs, and minimizing environmental impacts [3]. They enable utility providers to allocate resources efficiently, prevent supply-demand imbalances, and enhance grid resilience [4], while also supporting the integration of decentralized energy systems and reducing reliance on fossil fuels [5].

The growing complexity of modern energy systems has further underscored the need for advanced forecasting techniques [6]. Traditional power grids, characterized by unidirectional energy flow from centralized generation facilities to end users, are now being replaced by smart grids. Smart grids are equipped with Advanced Metering Infrastructure (AMI), Internet of Things (IoT)-enabled devices, and big data collection systems [3]. Smart grids allow bidirectional energy flows and integrate Distributed Energy Resources (DERs), such as rooftop solar panels, battery storage systems, and electric vehicles [7]. However, this transformation also introduces new challenges, including increased variability in both energy consumption and generation patterns, the unpredictability of renewable energy production, and the need for sophisticated decision-making mechanisms applied to real-world microgrid scenarios [8]. Historically, traditional statistical models, such as Autoregressive Integrated Moving Average (ARIMA) and exponential smoothing, have been widely used for load forecasting, even before the emergence of smart grids [9]. These techniques were effective in traditional power systems, where load demand followed relatively predictable patterns and fluctuations were mainly influenced by seasonal factors [7]. However, as power grids have evolved to accommodate a more decentralized and dynamic structure, these models have struggled to capture the increasing complexity of load demand and generation [10]. Their reliance on predefined assumptions and limited adaptability makes them less suitable for handling the nonlinearity and high dimensionality of modern grid systems [8].

Consequently, the field of smart grids has increasingly adopted machine learning (ML) and Deep Learning (DL) techniques. These techniques offer increased flexibility in analyzing large-scale datasets, identifying complex and nonlinear relationships, and making adaptive predictions, ultimately leading to more scalable systems [11]. These data-driven approaches offer significant advantages in forecasting load demand, optimizing grid operations, and improving overall system resilience in the face of uncertainty [12]. One of the key factors driving this shift is the growing recognition that energy consumption and generation are influenced by a wide range of external factors (hereafter referred to as exogenous variables in this work), including climatic conditions, socioeconomic factors, and consumer behavior [11,12]. Weather factors, such as temperature, humidity, wind speed, and solar radiation, are key for determining demand fluctuations and renewable energy availability [13]. At the same time, economic activity, population density, and industrial output significantly affect long-term consumption patterns [14,15]. Additionally, cultural factors, such as responses to dynamic pricing and shifts in lifestyle trends, tend to introduce further complexity into demand forecasting [14]. The need to incorporate these external influences into modern predictive models is even more critical given the dynamic and highly interdependent nature of current energy systems [16].

To process this high-dimensional and interdependent data, ML models such as Support Vector Machine (SVM), Decision Tree (DT), Random Forest (RF), and Gradient-Boosting (GB) algorithms have been widely employed, as they excel at detecting hidden patterns and interactions within large datasets [17]. These methods often rely on manual feature engineering and struggle to fully capture the temporal dependencies and complex nonlinear dynamics of load demand and renewable energy generation [18]. In contrast, DL architectures offer an automated approach by directly extracting relevant features from raw data, enabling the modeling of complex patterns without requiring extensive data preprocessing [11,19]. For instance, Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), particularly Long Short-Term Memory (LSTM) networks, have demonstrated high effectiveness in processing time-series data. These DL models can capture both short-term and long-term dependencies, making them well-suited for load forecasting applications in smart grids [20]. LSTM networks are specifically designed to retain information over extended time intervals, enabling them to model the complex temporal relationships inherent in energy consumption and generation data [21,22]. This ability is especially valuable for handling the variability of RESs, where generation is subject to fluctuations driven by unpredictable factors such as changing weather patterns and seasonal effects [23]. Moreover, DL models can dynamically adapt to evolving consumption behaviors and external conditions, enhancing forecasting accuracy in scenarios where classical ML models might require frequent retraining and manual parameter adjustments [24,25]. Beyond standalone ML and DL models, hybrid models have emerged as a powerful alternative, combining the strengths of both approaches with advanced data decomposition methods [26]. Techniques such as the wavelet transform and empirical mode decomposition enable forecasting models to break down complex time-series data into simpler components, allowing them to focus on specific trends while reducing noise [27,28]. By leveraging the structured feature-extraction capabilities of ML and the advanced sequence-modeling strengths of DL, hybrid models provide a more robust framework for capturing both short-term fluctuations and long-term consumption trends. As a result, these models have significantly improved forecasting accuracy, making them particularly effective for managing load demand volatility and integrating renewable energy [26].

Despite recent advances in modeling, the implementation and scalability of the aforementioned predictive systems remain significant challenges [29]. The massive volume of data generated by smart grids and the high computational requirements of most sophisticated models represent considerable obstacles [30]. Many algorithms require intensive optimization and lengthy training, making them both resource- and time-consuming [31]. Moreover, efficient forecasting models are essential for smart grid applications in systems that aim to respond dynamically to sudden changes in load demand or generation, often triggered by weather anomalies, network disturbances, or unexpected consumer behavior [32]. Without this timely response capability, the practical utility of predictive models is limited, especially in scenarios where the volatility of renewable energy sources introduces greater uncertainty into energy systems [33]. Additionally, the forecast horizon itself introduces layered complexity: (i) short-term predictions (minutes to days) must account for high-frequency fluctuations in weather variables, user behavior, and distributed renewable generation, often requiring near-real-time updates and fine-grained data. (ii) Medium-term horizons (weeks to months) involve seasonal cycles, special events, and coordination across system components like storage and scheduled maintenance, which makes prediction difficult due to the overlap of seasons and events, changes in the number of users, and emerging technologies. (iii) Long-term forecasts (years) are shaped by demographic shifts, technological adoption, infrastructure planning, and policy impacts, all of which introduce deep uncertainty and require models that can adapt to slow but impactful structural changes. In particular, demographic and socioeconomic data are often scarce due to limited public availability and the annual collection cycle. Adapting load forecasting models to different forecasting horizons requires preprocessing the data. Techniques such as resampling or interpolation may be employed based on specific needs. In some cases, additional transformations are required to capture temporal patterns effectively. However, specific forecasting models, such as LSTMs, can handle time-series data directly without extensive preprocessing.

Given the extensive literature on data-driven strategies for load forecasting, especially with the rise in DL applications in smart grids and their integration with external information sources, limitations in current approaches, such as the lack of generalizability across different contexts, insufficient inclusion of diverse external variables, and limited real-world validation, remain critical barriers. Figure 1 shows the methodology applied in this review paper for conducting a comprehensive and robust literature analysis, similar to [34]. We employ a hybrid methodology that combines bibliometric analysis with a critical and systematic review of the existing literature to evaluate current load forecasting techniques. We examine traditional statistical, ML, and DL models that have been developed and applied to enhance predictive accuracy in the load forecasting field. By analyzing the strengths and weaknesses of various approaches, this literature review aims to identify the most effective strategies to address the distinct challenges of load forecasting in contemporary energy systems. Special emphasis is placed on incorporating exogenous variables, such as weather conditions, socioeconomic data, and cultural behavior. Furthermore, this review highlights key areas for future research, including the development of scalable and adaptive models, as well as the exploration of innovative forecasting paradigms, such as hybrid models. While there are numerous reviews on electricity load forecasting [7,35,36,37,38,39,40,41,42,43,44], many focus on specific approaches, such as DL, or primarily showcase optimal outcomes often neglecting the influence of exogenous variables and the validation of these models in real-world scenarios. In particular, there is a lack of detailed analyses examining how variables such as weather conditions and socioeconomic indicators affect the accuracy and applicability of these forecasting strategies in different contexts. Furthermore, the absence of rigorous bibliometric analyses in these studies limits our understanding of emerging research trends in load forecasting. To address these gaps and demonstrate the need for this study, this review offers a comprehensive examination of the most relevant approaches. It also emphasizes the impact of exogenous variables, presenting them as inputs for forecast models. This provides researchers with insight into trends and relationships between load demand, climatic factors, and socioeconomic indicators, while also identifying the most relevant or strongly correlated variables. Additionally, a bibliometric analysis is included to identify key research directions and potential future developments in this field. By combining bibliometric and systematic review methods, the study outlines existing strategies and identifies remaining challenges to guide future research.

The remainder of this paper is organized as follows. Section 2 provides a detailed analysis of the differences between this work and the previously mentioned works. Section 3 presents a bibliometric analysis conducted with the Bibliometrix tool in the programming environment R, examining trends in key concepts for load prediction in electrical microgrids. An in-depth analysis is conducted of key topics across categories, including themes, driving themes, essential themes, and emerging or declining themes. Lastly, this section presents a hierarchical analysis of key concepts, organized into clusters, that illustrate the progress made in this field of research. Section 4 categorizes strategies for predicting electrical load in microgrids and smart grids. This section divides the techniques into traditional statistical models, classical ML, DL, and hybrid models. At the end of the article, Section 5 presents a detailed analysis of each of the reviewed works on electric load forecasting, covering approaches ranging from traditional statistical models to hybrid models. The section also examines the use of exogenous variables (such as climatic, socioeconomic, and cultural factors) as predictors in the proposed models, as well as the electrical system’s intrinsic variables. Finally, Section 6 presents the paper’s conclusions.

2. Related Review Articles

In this section, we present the different ways in which other review articles have addressed electric load prediction using data-driven strategies.

One of the most comprehensive review articles on load forecasting for smart grids/microgrids is [7]. In that work, the authors provide a comprehensive literature review that spans traditional methods to AI-based strategies, along with an in-depth examination of the theory behind each approach. However, they focus exclusively on forecasting techniques, without addressing the climatological or socioeconomic factors that affect load forecasts in electrical microgrids. Furthermore, they fail to distinguish between classical ML and DL models, a crucial consideration when selecting a tool for load forecasting in a specific microgrid (especially when prioritizing effectiveness or interpretability).

Building on a similar attempt at a broad review but with a different focus, in [35], the authors present a systematic review of load forecasting strategies. While they conduct a relatively thorough bibliometric analysis based on search queries incorporating relevant field-specific keywords (similar to the approach taken in this work), their focus is confined to Reinforcement Learning (RL) strategies, and the number of references available for comparison is relatively limited. Unlike [7], authors in [35] incorporate bibliometric analysis, even though it does not examine the role of exogenous variables in load forecasts.

Shahinzadeh et al. [36] extend the discussion by reviewing DL and hybrid models. Compared to the previous two works, this review offers a more technical breakdown of how each forecasting strategy operates, discussing advantages and disadvantages. However, unlike [35], their work does not include a bibliometric component, and unlike [7], it lacks a comprehensive comparison among the works; for instance, the only table summarizing the models omits references and practical applications.

A different perspective is adopted by Ardabili et al. [37], who concentrate exclusively on ensemble and hybrid models, neglecting a broader array of potential forecasting methods. They assess the sustainability and reliability of these models. However, while they provide a brief overview of the number of documents on ensemble and hybrid approaches, they do not analyze trends or conduct cluster analysis to identify groups of similar articles that could aid in developing a taxonomy for the two types of models they define.

More recently, Dong et al. [38] analyzed various forecasting strategies, ranging from traditional statistical models to DL and hybrid approaches, with a particular focus on short-term prediction (i.e., forecasting for the upcoming hours). A notable strength of their work is the inclusion of a section that compiles the datasets used across the studies, as well as the use of specialized databases to conduct the literature search, an element missing in earlier reviews. However, the review also presents several limitations: although the authors acknowledge that exogenous variables strongly influence load forecasts, they do not thoroughly analyze these variables. Moreover, their analysis remains mostly descriptive, focusing solely on the number of publications per year without offering deeper insights.

Unlike the aforementioned reviews, Fida et al. [39] conducted a comprehensive literature review that thoroughly analyzed the societal impact of load forecasting. They present the theoretical basis of the forecasting techniques implemented through 2024 in a comprehensive and detailed manner, and provide a brief demonstration of the exogenous variables that most significantly influence behavior. However, this latter aspect is not the article’s primary focus. In addition, several groups of forecasting strategies (such as traditional statistical models or classical ML models) are excluded. In a complementary manner, Wang et al. [40] include anomaly detection in their survey of forecasting models, thereby expanding the scope beyond pure prediction. Yet, most reviews do not include a bibliometric analysis or a detailed consideration of exogenous variables.

A different angle is provided by [41], who conduct a systematic literature review based on an in-depth bibliometric analysis, highlighting the application areas where various load forecasting techniques have been used, such as marketing, compatibility with existing infrastructure, and infrastructure costs in the planning of potato supply chains within the Algerian context. Unlike the global perspective sought in works such as [38], this review is strongly localized, limiting comparability across regions with diverse climatic or socioeconomic conditions.

Finally, Hasan et al. [42] classify forecasting models according to horizon length (short, medium, and long), emphasizing the different types of load forecasting that can be carried out depending on the horizon (load management, financial planning, transmission planning, and general system planning), which is new in comparison to the reviews were mentioned above. This structure provides clarity but is less critical than the evaluative one, and, once again, long-term forecasting receives relatively less attention than short-term approaches. Additionally, it offers limited discussion on the real-world applicability of the reviewed methods under data, computational, and institutional constraints.

In summary, the growing complexity of microgrids and the rapid evolution of data-driven forecasting methods have led to a diverse range of literature reviews, each with valuable contributions but also notable gaps. Many of these studies, summarized in

Table 1. Summary of related review articles on electric load forecasting (key focus, strengths, and gaps).

Reference	Scope/Focus	Methods Covered	Strengths	Limitations/Gaps
[7]	Broad review (smart grids/microgrids)	Traditional to AI-based methods	Comprehensive theoretical treatment	Omits exogenous variables; no clear ML vs DL taxonomy
[35]	Systematic + bibliometric (RL focus)	Reinforcement learning methods	Bibliometric approach	Narrow focus; limited comparative set; exogenous variables not analyzed
[36]	DL and hybrid models	Deep learning and hybrid approaches	Technical breakdown of methods	No bibliometrics; comparative tables lack refs/applications
[37]	Ensembles and hybrids	Ensemble/hybrid methods	Assesses sustainability/reliability	Narrow scope; lacks cluster/taxonomy analysis
[38]	Short-term forecasting emphasis	Traditional, DL, hybrid; short-term methods	Dataset compilation; specialized DB search	Limited exogenous analysis; mostly descriptive
[39]	Societal-impact oriented review	Theoretical methods up to 2024	Thorough societal discussion	Exogenous variables not main focus; some model families excluded
[40]	Forecasting + anomaly detection	Forecasting and anomaly detection	Expands scope beyond prediction	Limited bibliometrics; shallow exogenous treatment
[41]	Systematic + bibliometric; localized case studies	Application-aware forecasting methods	Detailed bibliometric analysis	Highly localized (limits global generalizability)
[42]	Classification by horizon (short/med/long)	Models mapped to horizon-specific tasks	Clarifies horizon use-cases	Less evaluative; long-term forecasting underrepresented

, focus narrowly on specific approaches (such as reinforcement learning, hybrid models, or short-term forecasting) and often lack a holistic view of the broader methodological landscape. Others fail to distinguish between classical ML and DL models, omit exogenous variables such as weather or socioeconomic factors, or exclude bibliometric evidence that could support the structure of their analysis. This work aims to address those limitations by providing a comprehensive review that (i) covers the full spectrum of forecasting techniques, from traditional statistical models to advanced AI-based and hybrid strategies, (ii) incorporates a robust bibliometric analysis to uncover trends, thematic clusters, and emerging areas, and (iii) explicitly examines the role of exogenous variables in forecasting accuracy, as well as practical implementation challenges such as scalability, interpretability, and data integration.

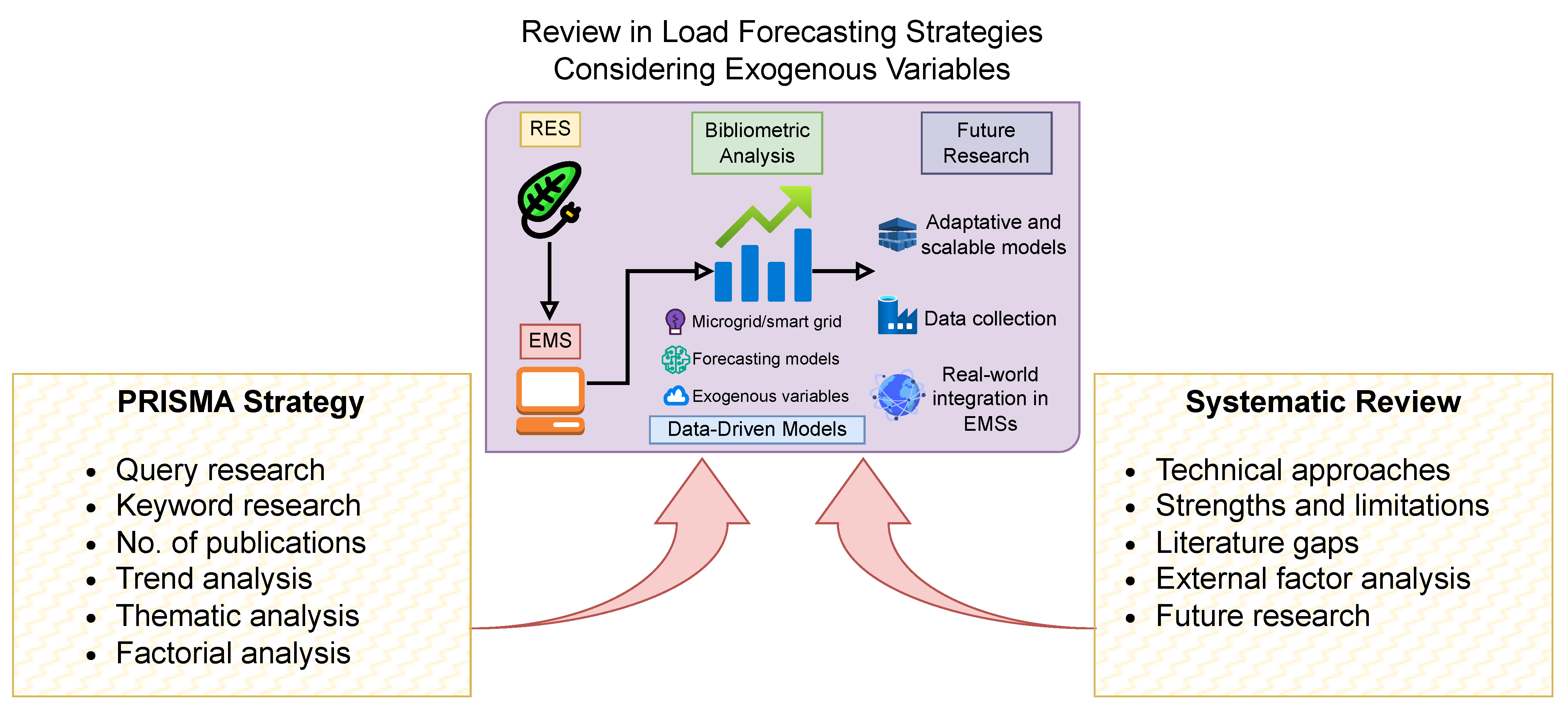
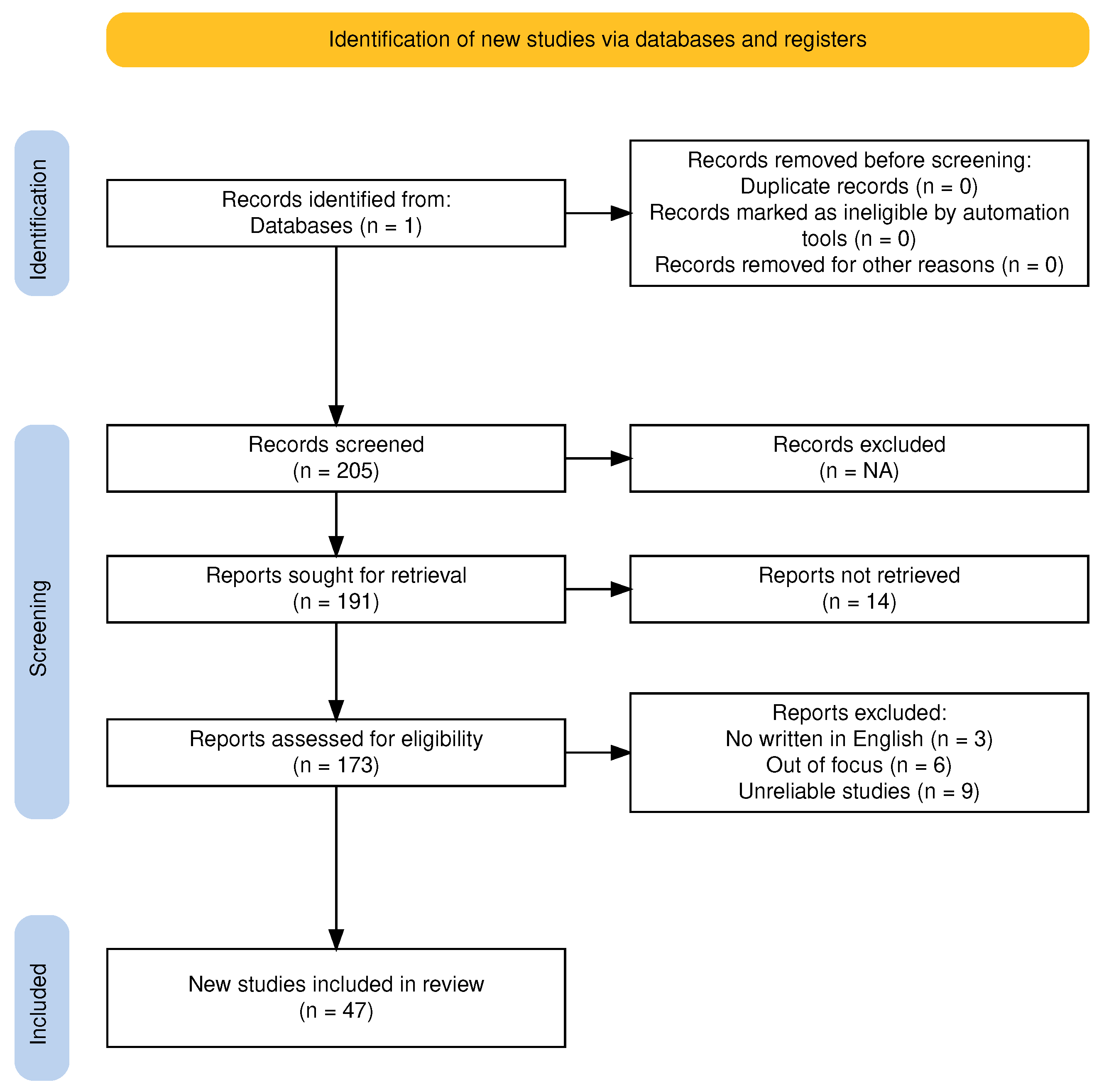
3. Bibliometric Analysis

A bibliometric analysis is a method for examining scientific literature that enables the assessment of academic output using indicators derived from publications within a specific research field, e.g., citation counts, thematic areas, authors, or journals. This tool is highly effective for identifying research trends, knowledge gaps, and influential contributors in the field, as it allows researchers to narrow the scope of their study using selection criteria such as authorship, journals, and topics of interest. This type of analysis contributes to the development of a robust and evidence-based theoretical framework, offering a more accessible visualization of the research field, including related concepts and sub-branches within a broader area of study, while also serving as a foundation for subsequent critical analyses and synthesis, rather than being limited to the preparation of review papers alone.

This section presents a bibliometric analysis using the bibliometrix library, which provides the necessary functions for statistical analyses of the selected references, and the biblioshiny library, which provides an interactive web interface for viewing and analyzing the results of these analyses. These tools are available in the R programming language, and the R GUI is used to launch the user interface by simply importing the “bibliometrix” library and invoking the biblioshiny() module. For this analysis, Figure 2 presents a PRISMA-inspired diagram that transparently illustrates the process of identifying, screening, and selecting studies. More than 200 scientific publications were extracted from the Scopus database by searching for terms in titles, keywords, and abstracts. We have chosen the Scopus database because it is well-known, provides user-friendly tools, and excels at covering diverse source types (e.g., books, conferences, preprints). In this regard, Keywords such as “smart grid”, “microgrid”, and “electrical microgrid” were used to define the scenario of interest in the advanced search Scopus tool. Additionally, relevant applications were identified using keywords such as “load forecasting”, “demand forecasting”, “demand prediction”, “load prediction”, and “electrical load forecasting”. To extract the methods used for load forecasting, we also employed keywords such as “pattern recognition”, “statistical model”, and “artificial intelligence”. To focus exclusively on studies that propose a load forecasting method, the term “review” was excluded from the search query. We also limited our selection to publications dated between 2015 and 2024. Additionally, we excluded some studies that were not written in English, outside the research focus, or unreliable (e.g., those with poor formatting or published in low-impact journals or conferences). Besides, we selected subject areas, including computer science, engineering, and energy, based on conference papers, journal articles, and books. This approach ensured that the articles aligned with the research field of interest. The final selection comprises 173 studies derived from the systematic screening process, supplemented by 47 additional records identified through manual search and snowballing to ensure a comprehensive state-of-the-art review, totaling 220 references.

Our bibliometric analysis is broken down into three components: (i) a trend analysis of topics, (ii) a thematic map revealing the relationships between different topics, and (iii) a factorial analysis to categorize the various topics based on their degree of similarity. The primary objective of this analysis is to examine the distribution of research topics, their interconnections, and the prominence of specific keywords or concepts.

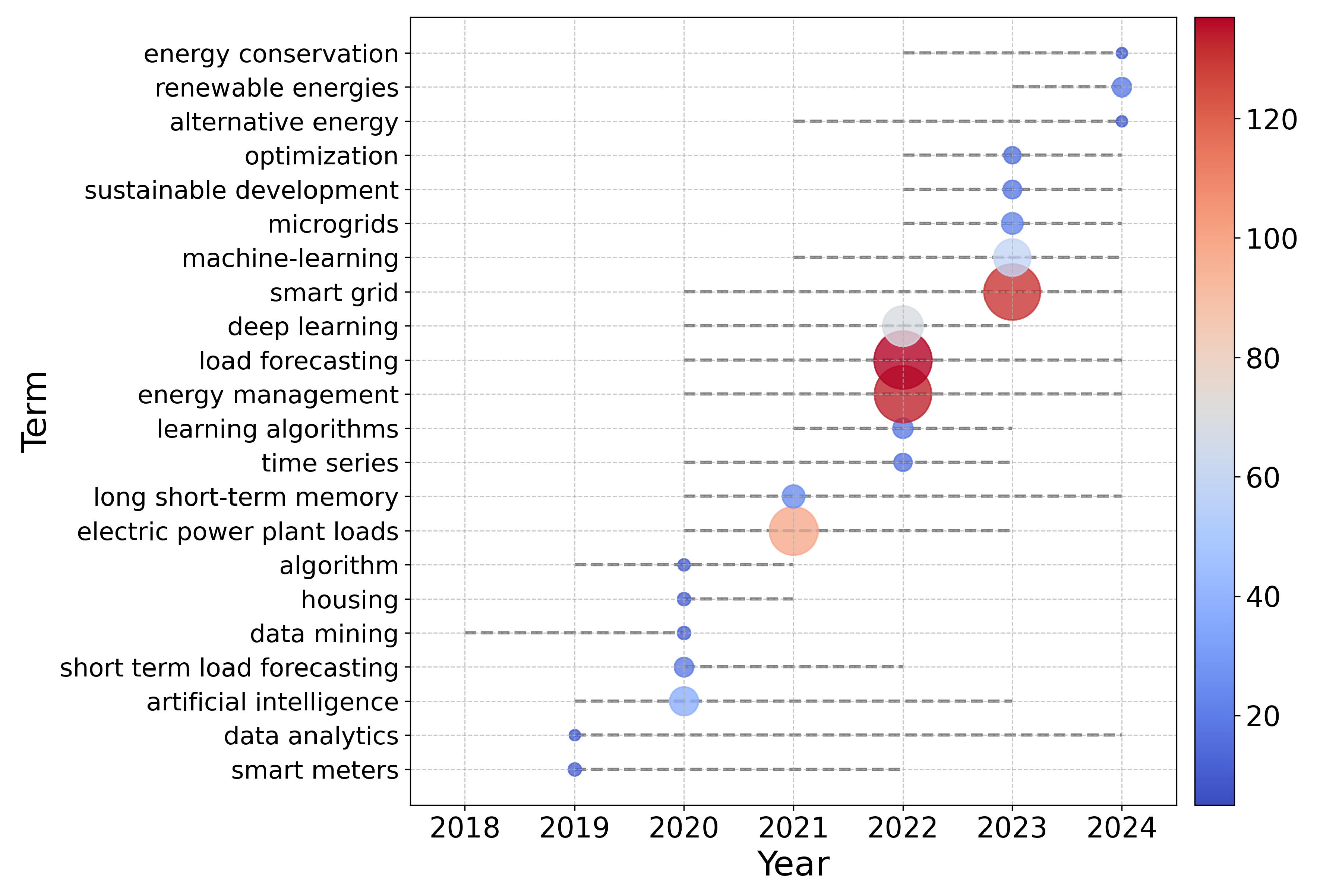
3.1. Trend Topics Analysis

The trend topics bubble chart shown in Figure 3 provides a clear visualization of the evolving research landscape in energy and technology from 2018 to 2024. This visualization is based on the most frequently used keywords, selected based on a minimum document count threshold. The x-axis represents the years, while the y-axis lists various terms related to the research field. The bubble size indicates the frequency of occurrence of each term in research publications or its importance in the field, and the color gradient from blue to red represents the intensity or number of occurrences, with red indicating higher values and blue indicating quite the opposite. It is essential to note that each term is placed along the timeline according to the period during which it was most prominent in the literature (not the year it first appeared). For example, if the bubble (peak usage) of a term occurs in 2021, it indicates that its usage or relevance peaked around that time, even though it may have appeared before or after. This visualization highlights how interest in specific topics has shifted over time, enabling the identification of areas that have recently gained traction and those that have become less central. By encapsulating these temporal dynamics, the chart reveals how traditional energy topics and emerging technological concepts have intersected and evolved, providing valuable insights into ongoing and future research directions.

One of the key observations from Figure 3 is the continued relevance of terms such as “energy conservation”, “renewable energies”, “alternative energy”, and “optimization”. These topics have remained important over the years, with notable peaks in recent years, underscoring the sustained focus on sustainable energy solutions. At the same time, terms like “machine learning”, “smart grid”, and “deep learning” gained significant traction around 2021 and 2022, reflecting the growing integration of advanced computational techniques in energy systems. Other prominent terms such as “load forecasting”, “energy management”, and “learning algorithms” highlight the expanding role of analytics and predictive modeling in modern power systems. This trend suggests that the industry is increasingly focused on optimizing energy use through machine learning and related methods. The rise of terms such as “microgrids”, “sustainable development”, and “optimization” further indicates a shift toward more localized and efficient energy solutions. Finally, the presence of terms like “time-series”, “long short-term memory”, and “data mining” underscores the importance of sophisticated analytical tools in recent energy research, reinforcing the field’s move toward intelligent, model-driven approaches for addressing complex energy challenges.

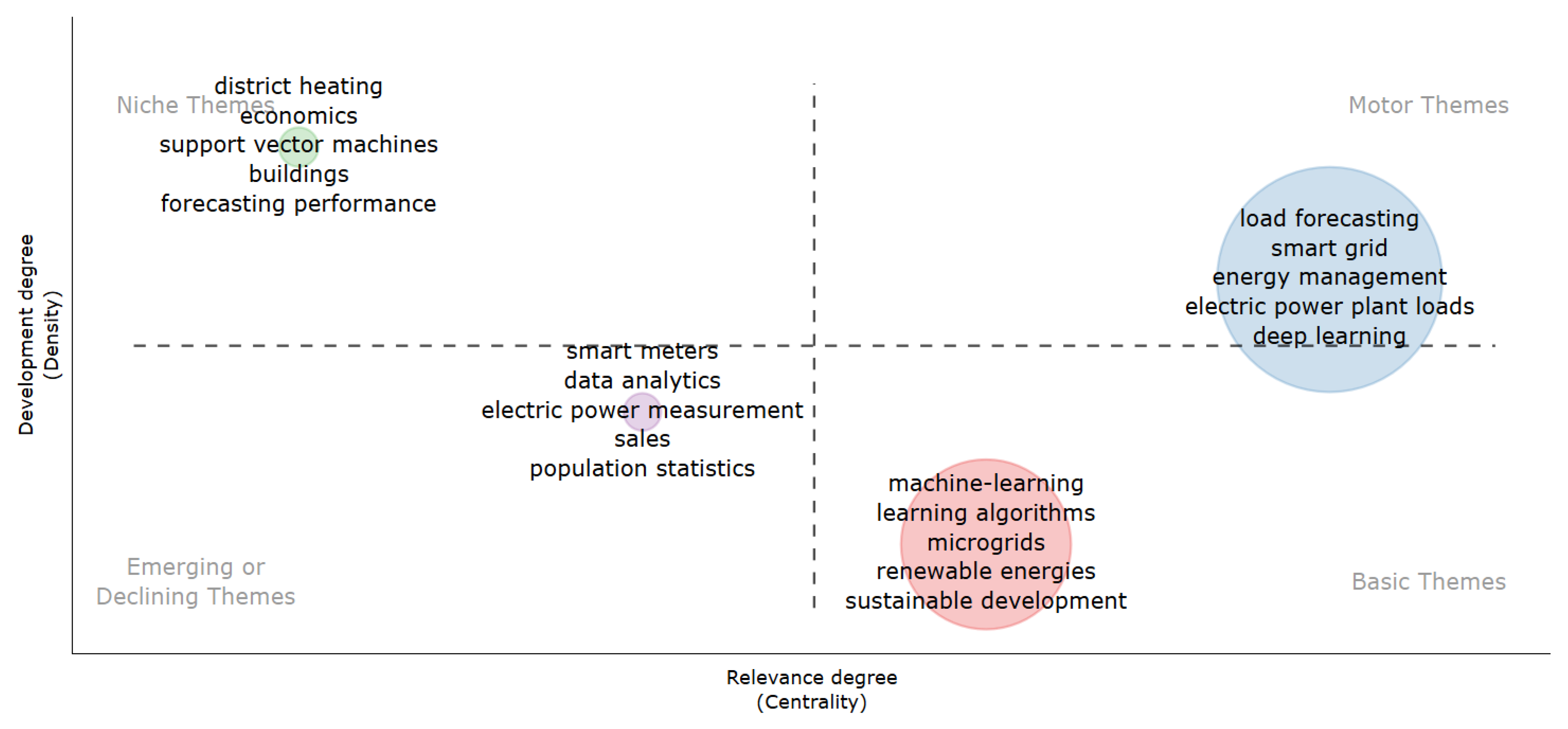
3.2. Thematic Analysis

Thematic maps provide a valuable snapshot of the current research landscape, highlighting areas of intense development and central importance and identifying emerging or foundational topics that require further exploration. This visualization is a good tool for researchers to identify key trends, allocate resources effectively, and pursue impactful research directions. The thematic map for the present work is shown in Figure 4. It offers a comprehensive classification of research topics within the domain, plotted on two axes: the y-axis represents the degree of development (density), and the x-axis represents the degree of relevance (centrality). This visualization is divided into four distinct quadrants, each representing different categories of themes:

(i)

Niche themes, located in the upper left quadrant, exhibit a high degree of development but relatively low relevance. They are specialized and well-developed research areas, yet not central to the overall research field. Notable topics in this quadrant include “district heating”, “economics”, “support vector machines”, “buildings”, and “forecasting performance”. These areas are highly specialized and well-developed, often yielding cutting-edge advances within their respective niches.

(ii)

Motor themes, found in the upper right quadrant, are characterized by both high centrality and high density, which indicates that they are conceptually well developed and strongly connected to other themes in the field, making them the main drivers of the research field. Keywords such as “load forecasting”, “smart grid”, “energy management”, “electric power plant loads”, and “deep learning” exhibit high centrality, meaning they serve as key drivers of progress in the field. Additionally, they present medium-to-high density, which suggests that the number of studies addressing these topics is increasing. This highlights their strategic importance and potential for continued growth within the domain.

(iii)

Emerging or declining themes, located in the lower left quadrant of the thematic map, are characterized by low development and low relevance. This behavior can be interpreted as emerging or declining themes. That is, new themes with few citations but potential for growth correspond to emerging themes. In contrast, more general topics that are not the focus of research and no longer generate citations, but instead represent more conceptual and well-known ideas, correspond to declining themes. The thematic map of load forecasting for electrical microgrids reveals emerging or declining themes, with terms such as “smart meters”, “data analysis”, “electric energy measurement”, “sales”, and “population statistics” appearing with low frequency. Themes such as data analysis and sales are considered declining topics in load forecasting due to the maturity of data-driven methodologies and the emergence of advanced tools. Smart meters and electric energy measurement are emerging topics, with smart meters gaining importance due to their role in data collection and in enabling advanced EMSs in smart grids. Electric energy measurement remains relevant, but it is evolving as newer technologies, such as IoT sensors and smart meters, gain precedence.

(iv)

Basic themes, located in the lower right quadrant, have high relevance but a lower degree of development. They are fundamental to the field and represent well-developed and mature tools that underpin research; however, they are not the main drivers of new explorations in the research field. This quadrant includes topics such as “machine learning”, “learning algorithms”, “microgrids”, “renewable energies”, and “sustainable development”. These areas are fundamental and vital for developing sustainable and intelligent energy systems.

Additionally, the center of the map in Figure 4, straddling the boundaries between the upper and lower quadrants, features topics with moderate development and relevance. As noted above, terms like “smart meters”, “data analytics”, and “electric power measurement” appear near the center of the map, although technically falling in the lower left quadrant. Thus, these themes represent, to some extent, well-rounded areas that balance both development and relevance, indicating their established importance in the research landscape.

3.3. Factorial Analysis

The thematic map is complemented by the dendrogram-based factorial analysis, which helps identify the most relevant current topics, potential future research directions, and relationships between concepts that were not initially evident. In bibliometric analysis, a dendrogram is a visual representation of hierarchical clustering applied to a given set of ideas, like the one shown in Figure 5. The result is groupings based on the distance or dissimilarity between those concepts. The dendrogram is a powerful tool for uncovering underlying structures in bibliometric data, as it helps identify communities among topics. Moreover, the point at which the branches of a particular community merge indicates the degree of similarity among the issues (i.e., lower joins indicate greater similarity). The red line in the Figure 5 helps determine the optimal number of clusters by dividing them into a limited number of groups. Additionally, gaps in the literature can be identified by analyzing concepts that do not belong to the same cluster but would be relevant to the field if they were. This would indicate a lack of integration or interdisciplinarity.

The structure of Figure 5 shows a horizontal axis representing the distance or dissimilarity between clusters, where shorter horizontal lines mean closer relationships between terms or clusters, and a vertical axis listing the clustered words. Words and clusters merge with increasing similarity as we move up the dendrogram. This figure provides valuable insights into the main themes and subthemes within the literature on data-driven load forecasting efforts for smart grids and microgrids. It highlights emerging trends and research hotspots, such as the integration of AI with smart grid technologies, as well as the focus on renewable energy integration. The dendrogram also suggests a gap between electricity load forecasting and its application to real-world EMSs and dispatch systems, as these terms appear in separate branches rather than forming a close cluster. Moreover, computational complexity is absent from the dendrogram, indicating that the community either considers this topic secondary or that it is not yet mature enough to have become a consistent focus of research in real-world applications.

To enhance readability, the dendrogram is divided into several color-coded clusters, each representing groups of semantically related terms and providing insights into the predominant themes:

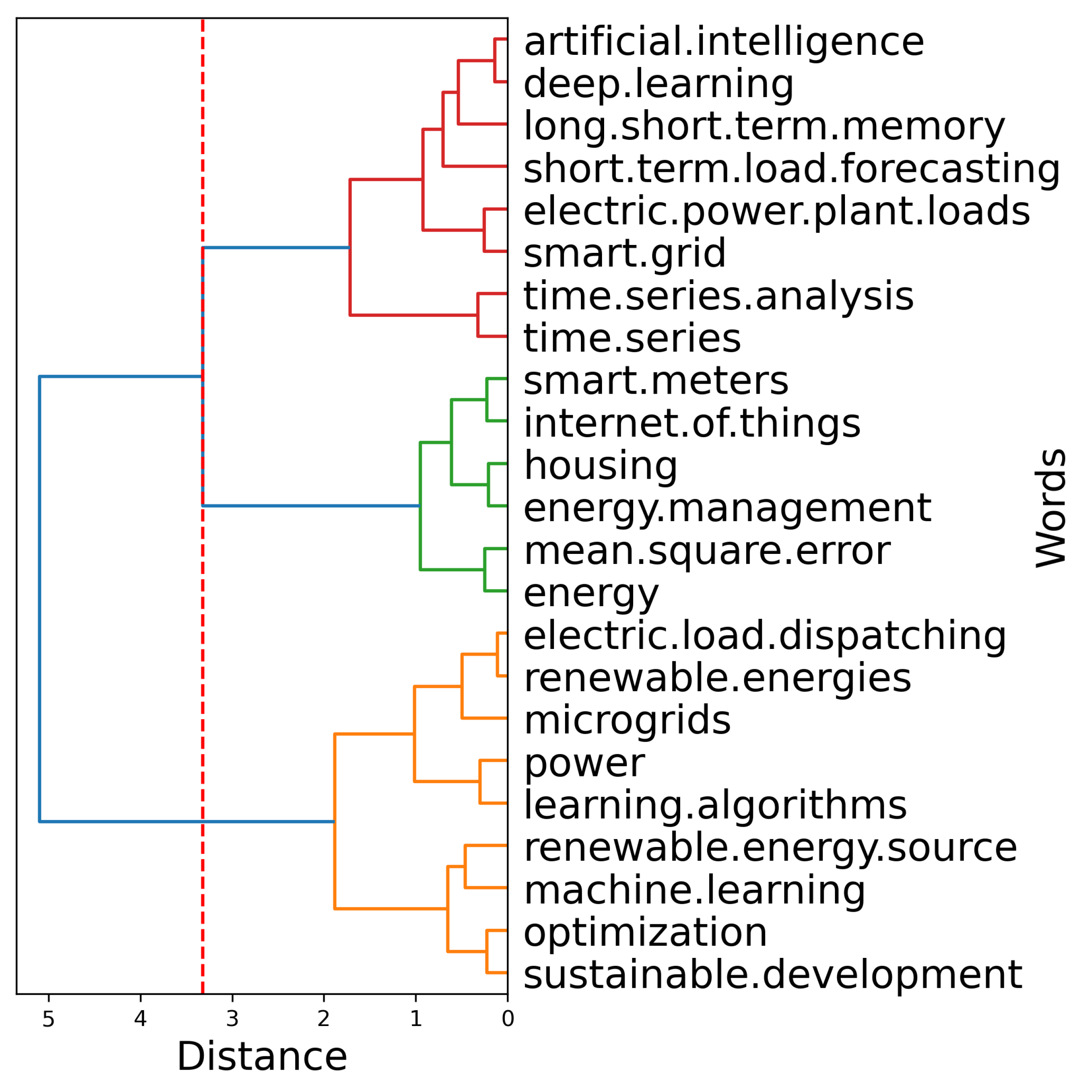
(i)

The red cluster focuses on advanced computational methods and technologies for load forecasting. Keywords such as “artificial intelligence”, “deep learning”, “long-short-term memory”, “short-term load forecasting”, “electric power plant loads”, “smart grid”, “time-series analysis”, “smart meters”, and “internet of things” emphasize an intense research focus on applying ML techniques to improve load forecasting. Additionally, the integration of the smart grid and IoT underscores the importance of combining these technologies with smart grid infrastructure to enhance data collection, prediction accuracy, and control.

(ii)

The green cluster centers on EMSs and evaluation metrics. Keywords such as “housing”, “energy management”, “mean square error”, “energy”, and “electric load dispatching” indicate research on practical aspects of EMSs and the optimization of electric load dispatching. The use of mean squared error suggests a focus on evaluating model forecast accuracy using this statistical measure.

(iii)

The orange cluster addresses RESs, microgrids, and optimization techniques. Keywords such as “renewable energies”, “microgrids”, “power”, “learning algorithms”, “renewable energy source”, “machine learning”, “optimization”, and “sustainable development” indicate the research field focuses on integrating RESs into microgrids and using ML techniques. Terms such as sustainable development and optimization further underscore efforts to achieve sustainable EMS practices through modern data-driven mechanisms.

The hierarchical analysis presented above highlights the relationships between time-series analysis techniques and artificial intelligence in load forecasting for microgrids and smart grids. These groupings of terms, highlighted in red and orange, underscore how accurate and efficient forecasting directly addresses key challenges in modern power systems. For instance, reliable load forecasting helps optimize energy distribution and contributes to the energy transition toward renewable energy. In systems with high shares of renewable energy, forecasting helps mitigate the unpredictability of sources such as solar and wind. Similarly, predictive models are essential for balancing local generation, storage, and load forecasts in electrical microgrid management, especially during transitions between grid-connected and islanded modes. This analysis underscores the importance of investigating load forecasting methodologies, thereby providing a more comprehensive understanding of global approaches to this problem. Consequently, the following section presents load forecasting approaches proposed in the literature, with an emphasis on the use of exogenous variables as predictors of load. This perspective brings a novel approach to this work, as many related studies focus solely on electrical variables, neglecting significant regional climatic or socioeconomic factors that can strongly influence consumption behavior.

3.4. Summary and Implications of the Bibliometric Analysis

The bibliometric analysis reveals several key insights about the current research landscape in load forecasting for smart grids and microgrids:

(i)

Growing prominence of AI-based techniques: Terms such as “machine learning”, “deep learning”, and “long short-term memory” show strong upward trends, confirming a shift from traditional statistical models toward more flexible and adaptable, data-driven approaches.

(ii)

Sustainability as a central theme: Terms such as “renewable energies”, “sustainable development”, and “optimization” highlight the importance of coordinating forecasting activities with more general sustainability goals.

(iii)

Persistent relevance of core concepts: The fact that topics such as “load forecasting”, “smart grid”, and “energy management” are constantly at the forefront shows how fundamental they are to this field.

(iv)

Underexplored areas: The term “computational complexity” is missing in the factorial analysis and thematic maps, which indicates a lack of computational complexity characterization in the development of more sophisticated load forecasting approaches.

(v)

Interdisciplinary integration: Clustering patterns underscore the necessity for cross-disciplinary collaboration by revealing how several domains (including housing, economics, optimization, and IoT) converge in the load forecasting research field.

These findings indicate a promising yet still evolving area of research that is being increasingly adopted to address complex, nonlinear patterns in energy consumption. However, there remain challenges to practical implementation, particularly in long-term forecasting, real-time deployment, and the integration of exogenous variables, such as socioeconomic and environmental data.

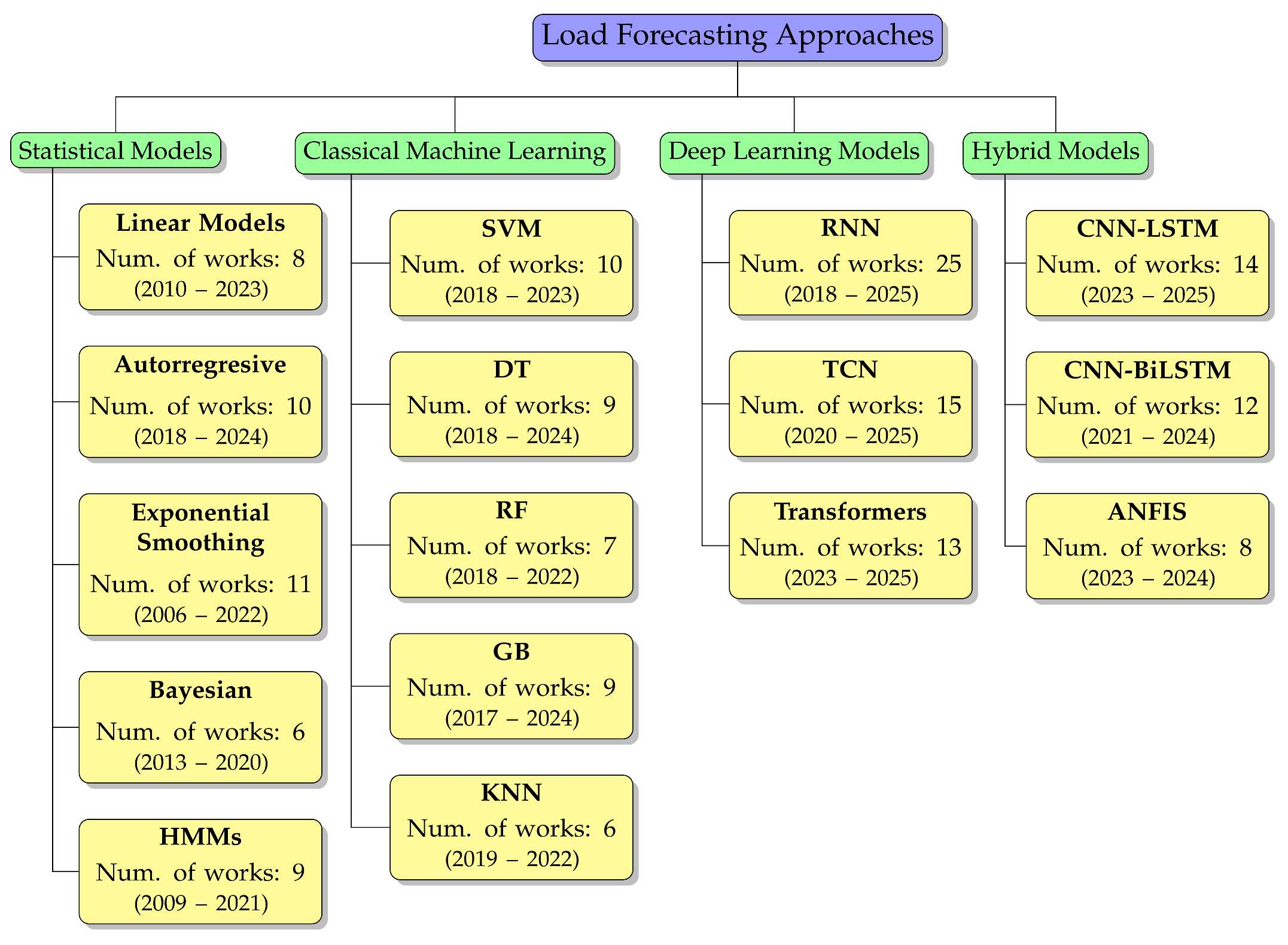
4. Load Forecasting Strategies

Several load forecasting strategies have been explored in the context of electrical microgrids. These strategies range from traditional classical methods to artificial-intelligence-based techniques, including hybrid models. To offer a structured overview of recent works on load forecasting in microgrids, we categorize these efforts into three main subjects, which will serve as subsections for this discussion:

(i)

Traditional statistical models, which include time-series approaches such as ARIMA, exponential smoothing, and linear regression techniques that rely on historical demand data and often assume linear or stationary behavior;

(ii)

Classical machine learning techniques, which introduce more flexible, data-driven algorithms like DT, SVM, and ensemble methods that do not require strong assumptions about the data distribution; and

(iii)

Deep learning and hybrid models, which encompass advanced architectures such as LSTM, CNN, and hybrid systems that combine AI with traditional statistical models to model nonlinear, high-dimensional, and dynamic energy systems more effectively.

In the literature, load forecasting models are commonly evaluated using standard metrics, such as Mean Absolute Percentage Error (MAPE), Root Mean Squared Error (RMSE), and Coefficient of Determination ($R^2$). Rather than delving into their formal definitions, it’s essential to emphasize their practical interpretations. MAPE is particularly useful when comparing results across different systems or regions because it expresses errors as percentages, making it scale-independent. RMSE, on the other hand, is sensitive to large deviations and is more appropriate when the cost of significant forecasting errors is critical, such as in short-term operational planning. Meanwhile, $R^2$ provides an overall measure of how well the model captures the variability in demand, offering insight into the model’s explanatory power but not necessarily its accuracy in operational terms. Together, these metrics complement each other: MAPE facilitates cross-scenario comparisons, RMSE emphasizes the magnitude of errors, and $R^2$ reflects the extent to which the forecasting approach captures demand dynamics.

Throughout this review, we refer to three forecasting horizons: short-term (from a few minutes up to 24 h ahead), medium-term (from one day to several weeks), and long-term (from several weeks to multiple months or even years). Each horizon poses different challenges and requirements regarding model complexity, data input types, and application use cases. This taxonomy enables a comparative analysis of methods across varying levels of complexity, data requirements, and forecasting horizons.

To illustrate these categories, Figure 6 presents a diagram summarizing the number of related works on electric load forecasting strategies, highlighting the four main approaches in the literature, the number of related works for each apporach, and the oldest and latest studie. The first category, traditional statistical models, encompasses linear, probabilistic, and autoregressive models, which are known for their simplicity and computational efficiency. The second category encompasses classical ML models such as KNN, DT, SVM, and various ensemble models, which, according to the literature, effectively capture simple patterns and nonlinear relationships while maintaining high interpretability and low computational costs. However, these techniques contrast with DL methods, which, though computationally demanding and less interpretable, excel at modeling nonlinear relationships and handling large data volumes, offering superior generalization in highly variable contexts. Representative DL techniques include FCNNs, CNNs, and RNNs. Finally, hybrid models are a distinct category, integrating elements from traditional statistical models, classical ML, and DL techniques to leverage their respective strengths. When properly designed, these models can significantly enhance predictive accuracy; however, their complexity makes them particularly susceptible to challenges such as overfitting, which must be carefully addressed during development.

4.1. Traditional Statistical Models

Among traditional statistical models, Linear Regression (LR) and Multiple Linear Regression (MLR) remain foundational baselines in microgrid load forecasting due to their transparency and low computational overhead. Rather than complex feature extraction, these models leverage the direct correlation between load and specific drivers: LR is effective when demand is dictated by a single dominant factor (e.g., temperature), while MLR is essential for capturing the compound effects of diverse exogenous variables, such as humidity and socioeconomic indicators. Some studies that employed linear models to forecast electric load in microgrids or smart grids include [45,46,47,48,49,50,51,52], with performance assessed using the MAPE metric. Notably, in [45], the authors employ a short-term LR model (one-day forecast) to predict global apparent power, achieving a MAPE of less than 6%. Similarly, in [46,47,48,49,50], MLR models using variables such as temperature, wind speed, and relative humidity achieved $R^2$ values ranging from approximately 0.6 to 0.99, and MAPE below 4.5% for short-term predictions. In [51,52], MLR models were implemented for medium-term forecasts, achieving an $R^2$ of up to 0.96 and a MAPE below 4.2%. These models use predictors that include electrical variables, temperature, and seasonality. However, when applied to long-term forecasts, the $R^2$ value decreased to 0.71, indicating reduced performance. The primary advantage of LR models lies in their interpretability and computational efficiency, making them suitable for deployment on resource-constrained edge devices within the microgrid control layer. However, their accuracy tends to decrease when multiple contributing factors interact or when nonlinear relationships dominate, conditions that are increasingly common in modern energy systems due to the stochastic nature of distributed renewable generation. This limitation becomes more evident in long-term load forecasting, where exogenous variables such as demographic shifts, economic trends, and policy changes introduce higher uncertainty and variability. These variables are not only challenging to model accurately but are also measured with lower temporal granularity, which reduces linear models’ ability to maintain reliable performance, especially when they are not sufficiently robust to capture nonlinear behavior.

An essential aspect of the behavior of modern energy systems, particularly when considering exogenous variables such as weather, is their inherent time-dependent nature. Time-series-based techniques, particularly the ARIMA family, continue to serve as essential benchmarks in load forecasting due to their ability to model linear temporal dependencies and trends without the heavy computational requirements of deep neural networks. A few examples of the use of these models in the context at hand can be found in [3,47,53,54,55,56,57,58,59,60,61], where the authors autoregressive frameworks to predict electricity load, achieving varying levels of accuracy depending on the forecasting horizon and the complexity of the data. However, given the highly cyclical nature of microgrid load profiles, driven by human routines and industrial schedules, standard ARIMA models often fall short. In these scenarios, the Seasonal ARIMA (SARIMA) variant becomes indispensable for capturing recurring daily, weekly, or annual fluctuations that basic differencing cannot address. For instance, in [53,54,55,56,57], SARIMA models demonstrated exceptional accuracy in forecasting hourly and daily energy consumption (short-term predictions) when seasonal components are prominent, achieving a MAPE of less than 5%. In contrast, ARIMA models, which do not account for seasonality, achieved an MAPE exceeding 7%. However, the $R^2$ metric was similar across the two models, indicating that although SARIMA improves accuracy in the presence of seasonality, both models effectively capture overall trends.

To further address microgrids’ sensitivity to environmental conditions, the SARIMAX model extends this framework by incorporating exogenous variables. This capability is critical for enhancing resilience, as it allows the model to correlate load changes directly with external drivers such as temperature, humidity, or economic indicators, which is particularly useful for long-term planning. For instance, in [3,60], the authors evaluate SARIMA and SARIMAX models for long-term demand forecasting, achieving a MAPE of up to 6% and errors of approximately 100 MW in both cases. These models demonstrated an $R^2$ coefficient of approximately 0.6 across three study cases.

On the other hand, Exponential smoothing is another family of time-series forecasting techniques that have been explored for load forecasting in smart grids and microgrids. Exponential smoothing is a widely used forecasting method that assigns exponentially decreasing weights to past observations, giving more importance to recent data while still considering historical patterns. This approach is efficient for time-series data with trends and seasonality, as it adapts quickly to changes in underlying patterns [64]. The smoothing parameters (i.e., $\alpha$, $\beta$, $\gamma$) control the rate at which the weights decrease, allowing the model to emphasize recent trends or seasonal patterns. The authors of [62,63,64,65,66,67,68,69,70,71,72] use exponential smoothing techniques that incorporate Holt–Winters seasonal methods and their variations, such as Holt–Winters Taylor (HWT), for predicting short-term and medium-term load demand. Works extensively employ HWT for load forecasting due to its adaptability, computational efficiency, and its ability to capture trends and seasonality in energy consumption data. HWT is particularly suitable for time-series with more complex seasonal patterns, nonlinear trends, and higher variability [62]. Notably, in [62,63], exponential smoothing techniques achieved an MAPE lower than 2% and 13%, respectively, in one-day and one-month forecasts, demonstrating their ability to deliver accurate and reliable predictions when data exhibits single-seasonality patterns, and authors in [72] have demonstrated that applying temperature sensitivity analysis reduces the MAPE in forecasting the maximum load from 8.228% to 1.123%. In addition, the authors in [66] achieved an RMSE of 7% in predicting holidays such as Christmas, New Year’s Day, and National Day, highlighting the robustness of exponential smoothing methods even during atypical consumption periods when demand deviates significantly from regular patterns. On the other hand, in [67], the authors achieved an MAPE error of approximately 3% when predicting load in a city in China.

Finally, probabilistic models, a subset of traditional statistical models that rely primarily on probability theory to quantify uncertainty in predictions or estimations, have also been used for electricity load forecasting. The most commonly used models are Bayesian, Gaussian, and Hidden Markov (HMMs). For instance, Bayesian models use Bayes’ theorem to update the posterior distribution of a hypothesis (e.g., future load demand) as new data become available. This is mathematically expressed as $P(\theta /D)$, i.e., the posterior distribution of the parameters $\theta$ given the data D. These models are compelling for quantifying prediction uncertainty, as they provide point estimates and full probability distributions that capture the range of possible outcomes. In [73,74,75,76,77,78], Bayesian short-term electricity load forecasting methods have been proposed, achieving relatively good results compared to non-probabilistic models using significantly fewer training data points. For instance, in [75], an average accuracy of approximately 80% was achieved using only 10% of the training data. However, as the percentage of training data increases, the performance of other models improves, and they might even outperform Bayesian models. Additionally, in [77], a Bayesian model was compared with an HMM and a Deep Neural Network (DNN). HMMs extend Markov chains by incorporating hidden states [196,197]. While Markov chains model systems where the future state depends only on the current state, HMMs assume that the states are not directly observable [198]. Instead, observations are generated by these hidden states through emission probabilities. Mathematically, an HMM is defined by transition probabilities $P\left(S_t\right|S_{t-1})$ and emission probabilities $P\left(O_t\right|S_t)$, making them suitable for modeling systems with unobserved dynamics, such as electricity demand patterns in smart grids. In [198], the authors show that, in terms of Normalized Root Mean Squared Error (NRMSE), the Bayesian model and HMM had similar errors, which were significantly lower than those of the DNNs. Furthermore, in various studies [79,80,81,82,83,84,85,86,198], HMMs have demonstrated over 90% accuracy in short-term predictions, typically using the temperature as an extra feature in the models. Additionally, a separate study [83] examined the use of HMMs for medium-term (monthly) forecasts, achieving an MAPE of less than 8%. This success was consistent across different datasets and scenarios.

To summarize,

Table 2. Summary of traditional statistical models used for electric load forecasting.

Model Type	Description	Works	Metrics	Forecast Horizon	Strengths	Limitations
LR	Simple linear model: $y={\beta }_0+{\beta }_{1}x+c_0$	[45]	MAPE < 6%	Short	Interpretable, fast	Cannot capture nonlinearities
MLR	Multiple predictors estimated by least squares	[46,47,48,49,50,51,52]	MAPE < 4.5%; $R^2$ up to 0.99	Short–Long	Multi-driver modeling	Degrades in long-term horizons
ARIMA	autorregresive + integrative + moving-average (p,d,q)	[3,47,53,54,55,56,57,58,59,60,61]	MAPE approx 7%	Short–Medium	Captures autocorrelation and trends	Limited with strong seasonality
SARIMA	ARIMA with seasonal terms	[53,54,55,56,57]	MAPE < 5%	Short	Good for periodic data	No exogenous terms by default
SARIMAX	SARIMA plus exogenous variables	[3,60]	MAPE approx 6%	Medium–Long	Models external drivers	Needs high-quality exogenous data
Holt–Winters (HWT)	Exponential smoothing with level/trend/seasonality (alpha, beta, gamma)	[62,63,64,65,66,67,68,69,70,71]	MAPE 2–13%	Short–Medium	Adaptive and efficient	Weaker for multi-seasonality
Bayesian models	Probabilistic inference giving posterior distributions	[73,74,75,76,77,78]	approx. 80% acc with 10% training data	Short	Good with sparse data; uncertainty quantification	Sensitive to priors; may be outperformed with large data
HMMs	Hidden states with transition and emission probabilities	[79,80,81,82,83,84,85,86]	Accuracy > 90% in some short-term studies; MAPE < 8%	Short–Medium	Models latent regimes; robust to noise	State design critical; needs data for stable transitions

shows traditional statistical models that have been fundamental in demand forecasting, particularly in scenarios where researchers prioritize simplicity, interpretability, and computational efficiency [69]. Their performance, evaluated using metrics such as MAPE and $R^2$, demonstrates reliability for predicting structured data in stable environments, especially for short-term forecasts [66,67]. In particular, when data availability is reduced, probabilistic models, such as Bayesian models, perform robustly. However, these methods face significant limitations when handling nonlinear and high-dimensional data [54,56,57]. This analysis underscores the need for more advanced techniques, including those that incorporate modern artificial intelligence techniques [55,65], which enable models to capture nonlinear relationships, outlier behaviors, and complex patterns within the system.

4.2. Classical Machine Learning Models

Classical ML models learn patterns and relationships directly from data through iterative optimization processes without relying on explicit rules or predefined equations [199]. Unlike traditional statistical models, which often assume a specific functional form (e.g., linear relationships) and require heavy manual feature engineering, classical ML models can automatically adapt to the data structure, making them highly flexible for capturing complex, nonlinear relationships. This adaptability makes ML particularly suitable for tasks where the underlying data patterns are poorly understood or highly dynamic, such as load forecasting in smart grids [200]. While traditional statistical models excel in scenarios with well-defined assumptions and structured data, classical ML models thrive in more complex environments where the relationships between variables are intricate and cannot be easily modeled by simple equations [201].

Several classical ML-based load forecasting models have been proposed in recent years [87,88,89,90,91,92,93,94,96]. For example, in [87,88,89,90,91,92,93], the authors suggest using an SVM-based model for load forecasting. The SVM-based regression, also called the Support Vector Regressor (SVR), adapts the SVM model to regression tasks by optimizing a linear function $f\left(x\right)$ while tolerating minor errors within an $ϵ$-insensitive margin. Deviations beyond $ϵ$ are penalized using slack variables ${\xi }_i$ and ${\xi }_i^{*}$, which measure excess errors above and below the margin, respectively. The trade-off between model complexity and error tolerance is controlled by the hyperparameter C. Nonlinearity is handled via kernel functions, preserving the core principles of SVM while predicting continuous outputs [202]. Standard kernel functions include the linear, polynomial, and Radial Basis Function (RBF) kernels, each suited to different types of data patterns. Proper tuning of these hyperparameters (e.g., selecting an appropriate kernel function and optimizing the regularization parameter) is crucial for achieving high accuracy and robustness in SVM models [8]. When applied to load forecasting, SVR-based models achieve an MAPE of less than 4% for short-term predictions, outperforming time-series and linear models when meteorological and time-related features are included [89,91,93]. Additionally, an accuracy of approximately 90% was achieved for weekly load and price predictions [87]. Another set of explorations using SVR-based methods was presented in [94,96], which achieved RMSE and MAPE of approximately 1208 MW and 3.99%, respectively.

Another family of classical ML models is DT, including ensemble techniques such as RF and GB. This family of models has also been used to forecast load, as shown in [87,88,90,94,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111]. Beyond their predictive capability, DTs are particularly valued in microgrid management for their “white-box” nature, offering explicit interpretability that allows operators to trace the logic behind a load forecast, a critical feature for trust in automated decision-making [99,100]. To address the high variance and overfitting risks of single trees, Random Forest (RF) is employed as a robust ensemble method. By aggregating predictions from multiple independent estimators, RF significantly improves generalization on noisy datasets, which is common in low-voltage smart metering infrastructure [97]. In load forecasting, DT has been shown in [87,88,90,97,98] to achieve errors below 3.4% by incorporating weather data into short-term forecasts. Additionally, in some cases, DT has achieved lower MAE than SVM, reducing the total error by approximately 25%. On the other hand, authors of [98,101,102,103,104] report prediction errors for medium-term and long-term forecasts ranging from 3% to 19% using RF models, depending on the implemented feature extraction techniques and the used dataset. Notably, in [104], the authors achieved an MAPE of up to 1.7% using several weather variables (e.g., hourly temperature, humidity, wind speed, and sea-level pressure). This highlights the crucial role of data quality and exogenous variables, such as regional climate, in the performance of these models.

Gradient-boosting (GB) architectures have emerged as the dominant tree-based approach for scenarios requiring high precision on structured data, effectively bridging the gap between traditional statistical methods and deep learning. In [101,104,105,106,107,108,109,110,111], the authors use GB models and their variations to predict energy demand, demonstrating that sequential error correction yields superior accuracy in capturing complex, non-linear relationships compared to parallel ensemble methods. Some GB variants, such as AdaBoost, have achieved only a 3% lower MAPE than RNNs for medium-term predictions. These models incorporated variables like relative humidity, precipitation, surface pressure, temperature at 2 m, and wind speed and direction at 10 and 50 m. XGBoost, another variant of GB, has demonstrated MAPE values of approximately 1% for short-term predictions, comparable to RF in the same study for hourly forecasts. However, compared to RF, which offers robustness through simpler averaging, GB is operationally more demanding, being more sensitive to hyperparameter tuning and more prone to overfitting if not carefully managed. This trade-off implies that, while GB can theoretically achieve the lowest bias, rigorous validation protocols are required to ensure generalizability in real-world microgrid deployments.

Leaving aside tree-based models, another approach for load forecasting is the K-Nearest Neighbor (KNN) algorithm. KNN is a classical ML model technique that classifies new data points using the most similar labeled data points. The algorithm assigns a value based on the k nearest neighbors of the point under evaluation. It can classify the data or estimate a value based on the average of the neighbors. The choice of k significantly impacts the results of the algorithm [95]. For example, a small k value may yield high variance but low bias, whereas a larger k value may yield high bias but low variance. Authors in [91,95,96,112,113,114] achieved an average error, measured in kWh, lower than that of Individual Load Profiles (ILPs) when using KNN-based methods for load forecasting. ILPs are detailed representations of an individual household’s or building’s electricity consumption over time. These profiles illustrate the varying amounts of electricity used at different times of the day, providing insight into consumption patterns and each user’s energy needs. In [95,112,113], the use of the KNN algorithm achieved a MAPE of less than 17% for short-term load forecasting, reducing the error to as low as 3% for 1-h to 12-h predictions with an accuracy exceeding 95%. Additionally, in [112], a variation of KNN known as an Enhanced K-Nearest Neighbor (EKNN) demonstrated 12% greater accuracy than the classic KNN algorithm. Lastly, in [91,96], the authors achieved an MAPE below 6% and an $R^2$ up to 0.8 for medium-term forecasts.

Classical ML models have proven to be more versatile and practical tools for load forecasting in modern microgrids than traditional statistical models, particularly for short-term and medium-term forecasting horizons [95,112].

Table 3. Summary of classical machine learning models applied to electric load forecasting.

Model Type	Description	Works	Metrics	Forecast Horizon	Strengths	Limitations
SVR	SVM for regression with epsilon-insensitive loss and kernels (C, epsilon)	[87,88,89,90,91,92,93,94,96]	MAPE < 4% (short); weekly acc  90%; RMSE  1208 MW	Short, weekly	Good nonlinear fit; robust with tuning	Sensitive to kernel/hyperparams; poor scaling
DT	Single decision tree; interpretable splits	[87,88,90,97,98,99,100]	Errors < 3.4% (short with weather)	Short	Interpretable; fast	Prone to overfitting; less stable
RF	Ensemble of trees; averages predictions	[98,101,102,103,104,105,106,107,108,110,111]	MAPE 3–19% (medium-long); best  1.7% reported	Short–Medium	Robust baseline; handles mixed features	May be outperformed by tuned boosting; inference cost
GB/XGBoost	Sequential boosting of trees; focus on residual errors	[101,104,105,106,107,108,109,110,111]	XGBoost: MAPE  1% (short examples)	Short–Medium	Often top accuracy; flexible loss	Sensitive to tuning; risk of overfitting
KNN/EKNN	Instance-based; average of k nearest neighbors	[91,95,96,112,113]	MAPE < 17% typical; down to  3% for 1–12 h; EKNN +12% acc	Short–Medium	Simple; interpretable	Prediction cost grows with data; sensitive to metric

summarizes the insights in the previous section by showing how models such as SVM, DT, RF, and GB have achieved relatively low errors, especially when incorporating not only electrical variables but also relevant exogenous variables, as these models can capture dynamic data structures with nonlinear relationships [91,93,95]. Additionally, the importance of data quality and hyperparameter selection highlights the crucial role of feature engineering in enhancing model performance. However, as data volume and complexity increase, classical ML models face limitations in capturing more abstract and long-term patterns, which drives the exploration of DL approaches to enhance data representation and predictive capabilities in more challenging scenarios [30].

4.3. Advanced Load Forecasting Methods

Advanced load forecasting approaches could be broken down into two classes: DL and hybrid models. Firstly, DL models are a subset of ML algorithms that use neural network architectures with three or more computational layers to adaptively learn from training data and generate predictions [115]. In contrast, classical ML models (such as SVM, DT, or LR) often rely on manual feature engineering and lack layered architectures altogether, while shallow neural networks (e.g., basic perceptrons) may use one or two layers [117,203]. A DNN comprises multiple interconnected layers of nodes, where each successive layer refines the input data representation to improve prediction accuracy or classification performance. This hierarchical computation, known as forward propagation [115,116], begins with the input layer (which receives raw data) and culminates in the output layer (which produces final predictions, either continuous estimates or discrete classifications). The inverse process, backpropagation [203], optimizes model parameters by propagating prediction errors backward through the network and adjusting weights and biases using algorithms like gradient descent. Together, these mechanisms enable iterative refinement of DL models, enhancing their predictive performance over time [117,203].

In second place, hybrid models, which integrate DL with complementary techniques such as classical ML or traditional statistical models, have emerged to address scenarios where standalone DL architectures face limitations. These models leverage DL’s ability to autonomously extract high-dimensional patterns while retaining the interpretability, computational efficiency, or domain-specific strengths of non-DL approaches. For instance, hybrid frameworks might combine CNNs for spatial feature extraction with SVMs for final classification, or pair RNNs with ARIMA models to jointly capture nonlinear and linear temporal dynamics. These combinations often improve robustness and generalizability in complex forecasting tasks.

In electricity demand forecasting, the capacity of the DL models to automatically learn complex nonlinear relationships and temporal dependencies (such as weather effects or consumption patterns [204]) has positioned them as a powerful alternative to classical ML models, which typically require a data preprocessing and feature engineering layer [205]. DL architectures excel at handling the dynamic, high-dimensional nature of smart grid data [206], but hybrid approaches further enhance performance by combining DL’s hierarchical feature learning with complementary techniques. This subsection explores both DL and hybrid models, examining their theoretical foundations, comparative advantages, and applications in load forecasting contexts.

4.3.1. Deep Learning Models

Some examples of the use of DL for load forecasting in microgrids and related application scenarios are [12,36,59,65,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134]. The DL techniques used in these efforts include Fully Connected Neural Networks (FCNNs), CNNs, and RNNs, particularly LSTM networks. These methods have demonstrated superior performance in short-term prediction compared with models such as ARIMA and SVM. Specifically, Refs. [59,65,115,116,117,118,119,120,121,124,134] have reported that FCNNs achieved an MAPE as low as 1.68% in daily predictions, with prediction errors below 300 kWh. However, the authors in [12] obtained MAPE values of 0.8% and 0.62% for a DNN and an ARMA model, respectively, highlighting that a deep architecture does not always outperform a traditional statistical model by a wide margin.

One of the most widely used architectures for load demand forecasting is the LSTM network, a variant of RNNs. LSTM networks have established themselves as the premier architecture for microgrid load forecasting due to their capacity to manage the vanishing gradient problem inherent in standard RNNs, thereby enabling the retention of long-term dependencies in volatile energy time-series [59,123]. In the load forecasting field, the aforementioned approach is particularly valuable because electricity demand exhibits both short-term fluctuations and long-term seasonal patterns, making LSTMs well-suited to capture multiple temporal dependencies that traditional models or simpler DNNs struggle to capture. Numerous studies, e.g., Refs. [12,65,116,120,121,122,123,124,125,126,128,130,131,132,133] have implemented LSTMs for short-term electricity demand forecasting in microgrids, achieving MAPE values as low as 1.4% and $R^2$ scores up to 0.98 for both hourly and monthly predictions. These results were made possible by leveraging large volumes of historical data (including load profiles, weather conditions, and seasonal variations) and tuning key model parameters. In fact, the performance of LSTM models is highly dependent on hyperparameter tuning, such as the number of hidden units, dropout rates, and the choice of optimization algorithms [36,203]. However, even with effective parameterization, there are situations where the performance gains do not warrant the rise in computational complexity. This was demonstrated by the authors in [65], who compared an ARIMA model and an exponential smoothing-based model with an LSTM. The findings revealed that the results for the LSTM and ARIMA models were quite similar. In the context of long-term forecasting (monthly to annual scales), LSTM models have also demonstrated strong performance, with reported MAPE values of approximately 1.77% [36,122,123,134]. Nevertheless, the authors in [120] found that an SVR produces results comparable to those of an LSTM (RMSE between 0.71 and 0.78 kW). However, it was only when utilizing a BiLSTM (RMSE of 0.32 kW) or a combination of CNN-LSTM (RMSE of 0.23 kW) that the performance of the SVR was significantly exceeded, justifying the increase in computational complexity to enhance overall performance.

Another notable RNN variant is the Gated Recurrent Unit (GRU), which offers a streamlined alternative by merging the memory cell and hidden state. This architectural simplification reduces the number of trainable parameters, making GRUs significantly faster to train and less computationally expensive than LSTMs. GRUs are particularly useful when a lower computational cost is needed, such as in real-time forecasting on edge devices employed in decentralized microgrid controllers. Studies using GRU, e.g., Refs. [122,127,128,129,131,132,133] have reported MAPE values up to 2%, only slightly higher than LSTM, while achieving $R^2$ values above 0.9. In this way, LSTM and GRU outperformed other methods, such as ARIMA and FCNN, which typically achieved $R^2$ values of around 0.5 and 0.7, respectively. Particularly, authors in [127] show that incorporating exogenous variables (particularly weather variables) leads to a measurable reduction in forecasting error relative to models trained solely on historical load data. When weather variables were included, the performance of the LSTM-Seq2Seq model improved by approximately 41% in MAE and 18% in $R^2$. However, autoregressive models experience a performance degradation of approximately 18% in MAE and 16% in $R^2$. These results suggest that variables with nonlinear relationships, or pairs of variables, jointly affect demand more than highly correlated variables. On the other hand, this increase in performance can be attributed to DL models’ capacity to handle large datasets. Even authors in [135] provide an ML-DL framework that uses LSTMs for load forecasting and a decision-tree-based method, including DT and RDF, to determine feature importance, resulting in drybulb and electricity price as the variables that most affect demand.

Another DL-based strategy employed in the literature to address the load forecasting problem is the use of CNNs adapted for temporal data. The authors in [26,136,137,138,139,140,141,142,143,144,145,146,147,148,149] have demonstrated that the use of Temporal Convolutional Networks (TCNs) (or 1-dimensional CNNs) can effectively predict short-term and medium-term demand variations [2]. A TCN is a DL architecture that employs dilated convolutions and sliding windows to model temporal patterns in time-series data. For instance, a time-series of demand can be divided into overlapping segments by defining a window size (the number of past data points used at a time) and a stride (the distance the window moves forward to form the next segment). TCNs analyze consumption data in time-series by identifying local trends, recurring cycles, and anomalies, allowing for efficient anticipation of energy demand variations [133,136]. Using dilated convolutions in TCNs enhances training speed and improves the ability to capture long-range patterns without significantly increasing computational complexity [138]. Specifically, studies [26,136,137,138,140,141,142,143,144,146,149] have employed TCN-based approaches for short-term load forecasting, showing that one-step prediction yields a lower MAPE compared to multi-step prediction, with the latter performing approximately 4% worse due to its insufficient receptive field and reliance on only one month of data to predict the following seven days. Notably, in [141], the authors achieved an MAPE of 1.65% and an accuracy exceeding 98% in predicting server network consumption, outperforming models such as ARIMA, FCNNs, and RNNs. Additionally, the impact of voltage on TCN performance has been examined using bus load data, revealing improved performance at lower voltage levels. However, there is limited use of TCNs for medium-term and long-term forecasting because their receptive field (the range of past input data they can effectively consider) is typically constrained. This limitation makes it more challenging for TCNs to capture broader temporal dependencies, which are necessary for accurate predictions over longer horizons. In another set of studies [147,148], the authors forecast load over horizons of one week to one month, considering exogenous variables such as temperature, meteorological data, economic indicators, and demographic information. In these studies, an MAPE of approximately 7% and an RMSE value of around 3 kWh were achieved, compared to models such as LSTM, which obtained an RMSE of approximately 4 kWh. Despite this, TCNs proved more computationally efficient [143,149].

In light of these approaches, recent work has explored hybrid methods that combine the strengths of various statistical, ML, and DL techniques. These models enhance the ability to capture complex patterns and nonlinear relationships and better manage the uncertainty introduced by exogenous variables [207]. For example, hybrid methods that integrate two or more ML and soft computing approaches have shown improved forecasting performance and robustness compared to individual models [37]. We explore such approaches next.

4.3.2. Hybrid Models

Hybrid models refer to forecasting approaches that intentionally combine two or more modeling paradigms to exploit their complementary strengths while compensating for individual weaknesses, thereby enhancing single-model load forecasting [208,209]. In the context of load forecasting, these combinations typically involve statistical methods, machine learning (ML), deep learning (DL), or signal decomposition techniques. Based on the literature, hybrid models can be broadly classified into categories such as (i) statistical methods combined with ML models [189,210], (ii) DL architectures integrated with data decomposition or dimensionality reduction techniques [167,179], and (iii) multi-DL frameworks that merge different neural network structures (e.g., CNN–RNN combinations) [149,163]. Among the hybrid strategies explored in the literature [149,163,164,165,166,167,168,169,170,171,172,173,174,175], models based on CNNs-RNNs and fuzzy models, among others, have demonstrated significant improvements in load forecasting performance, particularly when exogenous variables are integrated into the modeling process [163]. For instance, the CNN-LSTM model is specifically designed for time-series forecasting tasks when the input data has a grid-like or spatial structure. The central concept of CNN-LSTM is to replace matrix-vector multiplication and LSTM memory-cell gating with convolutional operations [149]. As a result, the CNN-LSTM can handle input sequences of arbitrary length while preserving the spatial structure of the data [163]. Numerous studies [163,164,165,166,167,168,169,170,171,172,173,174,175] have demonstrated that the CNN-LSTM model consistently outperforms both CNN and LSTM models in separately way across time horizons ranging from days to a month, achieving MAPE values of approximately 3%, with an error margin of less than 1 MW compared to other methods when utilizing meteorological forecast variables and historical load data. Other research has incorporated additional exogenous variables, such as customer type [165], regional economic conditions [167], and population data [169], thereby providing a more comprehensive dataset for the models. For instance, study [167] reported a MAPE of 1.07% by integrating Principal Component Analysis (PCA) in the data preprocessing phase. This approach is called PCA-CNN-BiLSTM. PCA is a dimensionality reduction technique that transforms correlated variables into uncorrelated principal components, while preserving as much variance as possible, thereby effectively reducing noise and redundancy. In another investigation [171], researchers focused solely on climatological variables (such as humidity, temperature, and other weather variables) alongside load time-series, resulting in an MAPE value as low as 1.05%. Nonetheless, it is observed that performance diminishes slightly for long-term forecasts compared to short-term predictions. For example, in study [169], a MAPE of 4.64% was recorded over a one-year horizon, which remains highly effective, as a MAPE below 5% is considered ideal in load forecasting.

There is another variation of the CNN-LSTM model, known as the CNN-Bidirectional Long Short-Term Memory (CNN-BiLSTM). This approach is explored in a different set of research efforts [176,177,178,179,180,181,182,183,184,185,186,187]. Unlike the standard CNN-LSTM, which processes sequences in one direction by only considering past information, the CNN-BiLSTM features a combination of forward and backward LSTM layers [176]. This combination allows it to connect past and future data more effectively, leading to improved accuracy for medium-term and long-term predictions [177]. In these studies, the MAPE has been slightly enhanced for short-term predictions, achieving an $R^2$ value of 0.9943, which highlights the model’s flexibility (i.e., effectiveness, robustness, adaptability, and a balance between interpretability and predictive capacity). Additionally, in [176], the CNN-BiLSTM was used to predict demand in an area with variable climatic conditions over a medium-term range of approximately five months, using a dataset with six dimensions of features: temperature, wind speed, cloud cover, humidity, daily human activities, and the load time-series. This approach achieved an MAPE close to 1%. Study [179] compared different DNN and hybrid models, demonstrating how the hybrid CNN-LSTM model, along with some of its advancements such as CNN-BiLSTM and Variational Mode Decomposition (VMD)-CNN-BiLSTM, progressively improves the prediction performance of the CNN model in terms of the MAPE metric. In yet another extension of the model, the authors of [176,177,178,180,181,182,185,186] enhanced the CNN-BiLSTM model by incorporating an attention mechanism, resulting in the CNN-BiLSTM-Attention model, which further improved overall performance compared to the CNN-BiLSTM model without attention mechanisms. Additionally, several extensions of CNN-BiLSTM have been proposed to enhance forecasting performance, such as metaheuristic-based adjustments or hybridization strategies applied to the model structure. Examples include Sparrow Search Algorithm (SSA)-CNN-BiLSTM, Improved Sparrow Search Algorithm (ISSA)-CNN-BiLSTM [186,187], and Grey Wolf Optimizer (GWO)-CNN-BiLSTM [183].

Leaving aside convolutional and recurrent-based models, some studies [188,189,190,191,192,193,194,195,211] have explored fuzzy strategies such as the Adaptive Neuro-Fuzzy Inference System (ANFIS) for load forecasting. ANFIS combines the learning ability of neural networks with the rule-based reasoning of fuzzy logic to capture nonlinear relationships, employing a five-layer architecture that integrates these two approaches [190]. The first layer, known as the fuzzy layer, comprises nodes classified as adaptive nodes. The second layer, known as the product layer, has two nodes, and its output is the product of all the inputs from the previous layer. The third layer, the normalization layer, normalizes the weight functions for each node. The fourth layer, referred to as the de-fuzzification layer, also contains adaptive nodes. Finally, the fifth layer is the output layer, which has a single node where all incoming signals are added together [189,190]. ANFIS-based models have achieved MAPE errors ranging from 0.6% to 1.7% for short-term predictions with various modifications. For instance, in [189], a combination of the Whale Optimization Algorithm (WOA) is implemented to adjust the parameters of the ANFIS membership function precisely. At the same time, an RF algorithm is used to calculate correlation coefficients to identify the most essential features. This WOA-ANFIS-RF combination achieves a maximum MAPE of 0.99%, compared to ANFIS, ANFIS-RF, and WOA-ANFIS models, which reached a MAPE of up to 1.67% in prediction. Also, in study [194], ANFIS is employed and compared with a DNN architecture, achieving a slight improvement in MAPE and RMSE metrics under the same scenario conditions. These results demonstrate the model’s ability to handle nonlinear processing and reduce prediction error by leveraging the strengths of each strategy individually [189,195,211].

Several DL models have incorporated attention mechanisms, gaining prominence in the load forecasting field [180,181,185,186]. One of the most famous attention-based models is the Transformer model. Transformers are a specific class of DL models that utilize attention mechanisms to capture long-term dependencies without relying on sequential processing, unlike CNN-LSTM models [150]. These attention mechanisms are crucial in transformers as they enable the model to prioritize different tokens (i.e., the most minor units into which the input sequence is divided, such as numbers, words, or time steps) based on their significance [151,212]. Additionally, transformers consist of large encoder-decoder blocks: the encoder transforms input sequences into continuous representations, while the decoder generates outputs autoregressively, incorporating previously predicted elements to enhance accuracy. Time-series consumption (and other endogenous and exogenous variables) must be transformed into numeric values, known as embeddings, and include their positional information. This allows the model to process the data, maintaining the temporal relationship. Rather than treating all elements equally (as in simpler RNNs) or relying on sequential recall, attention enables the model to “pay attention” to the most relevant parts of the historical demand data. Thus, all of these characteristics make transformers highly effective for sequential data processing in demand forecasting [150,212]. Transformer-based models [150,151,152,153,154,155,156,157,158,159,160,161] have shown significant improvements in load forecasting performance, particularly in handling long-term dependencies and high-dimensional feature spaces [150]. A notable model, the Patch Channel-Mixing Transformer (PCM–Transformer), segments the load sequence and the sequence of multiple factors into subsequences with various resolutions, facilitating more effective feature extraction and a more explicit interaction between channels [150]. This approach has improved forecast accuracy by explicitly modeling the relationship between electrical load and multiple exogenous variables. Enhanced transformer variants, such as the ConvGRU–Transformer, have also been proposed to improve attention mechanisms and extract latent temporal patterns more effectively [151]. Studies have shown that these models outperform LSTMs and CNN-LSTMs in short-term and medium-term load forecasting tasks, consistently achieving MAPE values below 3%, and even below 1% when incorporating meteorological, economic, and demographic data [152,153]. In addition, hybrid probabilistic forecasting approaches, such as the Bayesian Transformer Network (BMDeT), have been introduced, quantifying both aleatoric and epistemic uncertainty and enabling more reliable predictions across multiple energy loads [153]. Another recent advancement, the Hybrid Attention-enabled Transformer (HAT), integrates task-specific attention modules to capture complex coupling relationships between different types of energy loads, further reducing prediction errors and improving uncertainty quantification [155]. In another study [157], the BiLSTM–Transformer model was applied to load forecasting in commercial buildings, achieving notable improvements in accuracy by combining bidirectional sequence modeling with attention mechanisms. Additional modeling techniques have been explored, including Sparse Variational Gaussian Processes (SVGP) [155] and graph-based transformer models (SmartFormer) [156], which aim to improve the robustness, efficiency, and performance of models in multivariate forecasting scenarios. They demonstrate the versatility of transformer models in adapting to various forecasting horizons and effectively integrating exogenous variables. In particular, study [156] provides a comprehensive comparison of various prediction models, ranging from ARIMA to attention-based models, across different datasets. The study demonstrates that the latter improves prediction accuracy by approximately 5% to 10% compared to traditional statistical models, and by about 1% to 3% when compared to reinforcement learning strategies and other hybrid models, such as the vanilla Transformer [159], CrossFormer [160], and MTGNN [161]. Finally, recent work [162] used a Large Language Model (LLM) to improve conventional ARIMA and LSTM models, and the authors quantified the influence of external factors, such as weather conditions, calendar effects, and socio-political events reported on social media. This GPT-based method significantly improves forecasting accuracy, reducing the MAE by 90.7% and the RMSE by 88.5% compared to an initial estimate.

With this in mind, advanced models such as deep learning and hybrid approaches generally outperform traditional statistical and machine learning methods when training and deployment conditions are consistent, particularly under localized settings. However, their adoption is accompanied by several significant limitations that are highly application-dependent. One major challenge is interpretability, as deep models often operate as “black boxes”, making it challenging to identify which variables drive demand variations. Moreover, these models typically require substantial computational resources, large volumes of high-quality training data, and frequent retraining to remain effective under changing system conditions.

From an operational perspective, the growing use of highly complex architectures, including large-scale deep models for energy system optimization, raises an energy-efficiency paradox, whereby the computational cost of training and deployment may offset part of the sustainability gains they aim to enable. Consequently, although deep and hybrid models can deliver notable accuracy improvements, they should not be regarded as universally optimal solutions. Their use must be carefully justified against data availability, computational constraints, interpretability requirements, and the marginal benefits achieved in forecasting accuracy.

To synthesize the advanced load forecasting strategies subsection,

Table 4. Deep Learning and Hybrid Models for Load Forecasting (representative studies).

Model Type	Description	Works	Metrics	Forecast Horizon	Strengths	Limitations
FCNN	Feedforward DNN trained via backpropagation	[59,65,115,116,117,118,119,120,121,124,134]	MAPE ≈ 1.68%; errors < 300 kWh	Short-term	Simple; nonlinear mapping	Needs feature engineering; limited temporal capture
LSTM	RNN with memory cells and gates	[12,65,116,120,121,122,123,124,125,126,128,130,131,132,133]	MAPE 1.4%, $R^2$ 0.98	Short–Long	Captures long-term dependencies	Sensitive to tuning; heavy compute
GRU	Simplified LSTM with fewer gates	[122,127,128,129,131,132,133]	MAPE ≤ 2%, $R^2$ > 0.9	Short–Medium	Fast training; compact structure	Slightly lower accuracy; limited memory depth
TCN/CNN	1D dilated CNN for temporal data	[26,136,137,138,139,140,141,142,143,144,145,146,147,148,149]	MAPE 1.65%; RMSE 3 kWh	Short–Medium	Fast, efficient; good local capture	Limited long-term receptive field
Transformer	Self-attention for long dependencies	[150,151,152,153,154,155,156,157,158,159,160,161]	MAPE < 3%; +5–10% vs. ARIMA	Short–Long	Long-range modeling; parallel	Data-hungry; high compute
CNN-LSTM	CNN feature extraction + LSTM sequence modeling	[163,164,165,166,167,168,169,170,171,172,173,174,175]	MAPE ≈ 3%; PCA-CNN-BiLSTM 1.07%	Short–Medium	Spatial-temporal synergy	Complex; long-term performance drops
CNN-BiLSTM	Bidirectional LSTM for dual temporal context	[176,177,178,179,180,181,182,183,184,185,186,187]	MAPE 1–3%; $R^2$ 0.9943	Medium–Long	Robust; uses past/future data	More complex; high cost
Attention/ Metaheuristic Hybrids	Attention or optimization-enhanced CNN-BiLSTM (SSA, ISSA, GWO)	[183,186,187]	MAPE ↓ by 1–2% vs. base model	Short–Long	Enhanced feature weighting; faster convergence	Higher complexity; tuning overhead
ANFIS	Neuro-fuzzy inference model (5-layer hybrid)	[188,189,190,191,192,193,194,195,211]	MAPE 0.6–1.7%; WOA-ANFIS-RF 0.99%	Short-term	Nonlinear + rule-based; interpretable	Difficult scaling; sensitive to rules
Hybrid Transformers	Probabilistic or multi-branch transformer models	[151,152,153,154,155,156,157]	MAPE < 3%; improved uncertainty quantification	Short–Long	Handles uncertainty; scalable	Very high training cost; low interpretability
Large Language Model	GPT-based adaptive self-tuning mechanism	[162]	MAE ↑ 90.7% and RMSE ↑ 88.5% including exogenous variables	Short-term	Manages extreme scenarios efficiently; scalable framework adaptable to other regions	current validation is restricted to a single regional and operational setting

↓ means that one model has a lower error than another. ↑ indicates that one model performs better than another.

summarizes both DL and hybrid models used in load forecasting.

5. Influence of Exogenous Variables on Load Forecasts in Microgrids

The role of exogenous variables in electricity demand forecasting has been widely used in the literature. Our systematic review confirms this by highlighting how different forecasting models incorporate and respond to such variables [57,194].

Table 5. Summary of studies utilizing external variables, such as weather (blue), socioeconomic (green), and cultural variables (orange), for load forecasting in microgrids: temperature (T); wind speed (WS); humidity (H); solar radiation (SR); atmospheric pressure (AP); cloud cover (CC); precipitation (P); economic activity (EA); population growth (PG); electricity prices (EP); consumption habits (CH); seasonality (S); lifestyle (L).

Work	Weather							Socioeconomic			Cultural			Forecast Horizon
	T	WS	H	SR	AP	CC	P	EA	PG	EP	CH	S	L
Traditional statistical Models
Supapo et al. [46]														short
Kapoor et al. [47]														short
Bracale et al. [49]														short
Saber et al. [50]														short
Hong et al. [51]														short
Hao et al. [52]														mid–long
Fattah et al. [54]														short
Tarmanini et al. [56]														short
Hernández et al. [57]														short
Bensalah et al. [58]														short–mid
Kumar Dubey et al. [60]														short
Kedrowski et al. [61]														short
Abd Jalil et al. [62]														short
Taylor et al. [63]														short
Özger et al. [64]														med
Muneer et al. [65]														short
Shi et al. [66]														short
Abderrezak et al. [68]														short
Souza et al. [70]														short
Woo et al. [71]														short
Nanda et al. [75]														short
Bracale et al. [76]														short
Bessani et al. [77]														short
Henselmeyer et al. [80]														short
Niu et al. [81]														short
Roça et al. [84]														short
Álvarez et al. [86]														short–mid
Classical Machine Learning Models
Ali et al. [87]														short
Liu et al. [89]														short
Jahan et al. [90]														short
Bashawyah et al. [91]														short
Masood et al. [92]														short
Mathumitha et al. [93]														short
Chen et al. [94]														mid–long
Alquthami et al. [96]														short
Hussain et al. [99]														mid
Kim et al. [100]														short–long
Syed et al. [109]														short
Zhang et al. [98]														short
Tiboaca et al. [97]														short
Yaprakdal et al. [101]														mid
Ungureanu et al. [102]														short–mid
Muzumdar et al. [103]														short
Singh et al. [104]														short
Wang et al. [105]														short
Su et al. [106]														short–mid
Masood et al. [107]														short
Prashanthi et al. [108]														short
Bhatia et al. [110]														long
Su et al. [111]														short
Nawaz et al. [95]														short
Khan et al. [112]														short
Ashfaq et al. [113]														short
Aimal et al. [114]														short
Bashawyah et al. [91]														short
Deep Learning Models
Zhu et al. [115]														short
Sayadlou et al. [117]														short
Yaprakdal et al. [135]														mid
Song et al. [116]														short
Yordanos et al. [118]														short
Gonzalez et al. [119]														short
Waheed et al. [122]														short
Krishna et al. [124]														short
Manandhar et al. [125]														short
Hong et al. [12]														short
Fente et al. [126]														short
Gasparin et al. [127]														short
Wen et al. [128]														short–mid
Xia et al. [129]														short
Massaoudi et al. [131]														short
Zuo et al. [136]														short
Gu et al. [137]														short
Levikari et al. [138]														short
Liu et al. [140]														short
Tian et al. [141]														short
Zuo et al. [142]														short
Liu et al. [143]														short
Shi et al. [144]														short
Lu et al. [145]														short
Yue et al. [148]														short–mid
Hybrid Models
Xiong et al. [164]														short
Zhang et al. [166]														short
Han et al. [167]														short
Rubasinghe et al. [169]														short
Sun et al. [171]														short
Zhou et al. [173]														short
Liu et al. [174]														short
Lu et al. [175]														short
Zhang et al. [176]														short
Wang et al. [178]														short
Dai et al. [179]														short
Hao et al. [180]														short
MA et al. [183]														short
Wang et al. [184]														short
Sun et al. [185]														short
Wei et al. [186]														short
Liu et al. [187]														short
Souhe et al. [211]														long
Tindra et al. [188]														short
Yu et al. [189]														short
Stitou et al. [191]														short–mid
Uroševic et al. [192]														short
Figlan et al. [193]														short
Khayat et al. [194]														short
Guan et al. [195]														short
Xing et al. [150]														short
Wang et al. [151]														short
Wang et al. [153]														short
Yu et al. [154]														short
Zhao et al. [155]														short
Saeed et al. [156]														short
Xiong et al. [157]														short
Francis et al. [158]														short
Peijin Li et al. [162]														short

summarizes the studies that have integrated some exogenous variable in their demand forecasting, in addition to the demand time-series itself.

Table 5 shows that weather-related variables are the most commonly used in demand prediction models [57,194]. For example, it is reasonable to assume that temperature is one of the most widely used variables (most 55% of reviewed studies), as multiple studies such as [57,87,89,90,98,109,126,128,176,178,179], to mention a few of them, have demonstrated a correlation value of approximately 0.8 with the energy demand. This is because high temperatures increase electricity demand for cooling systems (such as air conditioners), resulting in consumption peaks, particularly in summer. Similarly, low temperatures increase energy demand for heating systems (such as heaters or stoves). Additionally, temperature has a cultural effect, as colder weather encourages indoor activities such as streaming and gaming. Similar to temperature, humidity is another widely exogenous variable that influences thermal perception and thus tends to behave similarly, impacting electricity demand [57,60,96,104,109,122,150,151,153,154,155,156,184]. Another weather variable frequently used is solar radiation [57,60,96,109,124,184]. Solar radiation can be complex to analyze, as it may either increase or decrease demand. For instance, if alternative generation sources are available and solar radiation is high, demand from other sources may decrease at certain times of day. Moreover, high solar radiation can contribute to heating buildings or homes (reducing heating needs) and may even lower the demand for artificial lighting. However, if radiation levels are too high, they may excessively heat buildings and homes, leading to a sharp increase in air conditioning use. The three exogenous variables mentioned above (temperature, humidity, and solar radiation) are often used in conjunction in forecasting models, as the literature indicates. Another less commonly used climatic variable is cloud cover, which exhibits behavior opposite to that of solar radiation. Physically, clouds block a portion of solar radiation from reaching Earth’s surface; therefore, high cloud cover implies lower surface temperature. This has several implications: if the temperature is high, cloud cover could reduce the need for air conditioning; however, if the temperature is already low, increased cloudiness could lower it further to the point where heating becomes necessary. This illustrates that cloud cover is a complex variable to analyze, similar to solar radiation. Similarly, many other weather variables, such as atmospheric pressure, precipitation, and sunset, influence demand behavior and require careful analysis.

There is another type of exogenous variable, which deals with socioeconomic factors. These variables capture the influence of user behavior on demand. For instance, the country’s economic activity can directly influence energy prices, thereby altering users’ consumption patterns [12,13]. Similarly, the type of activity carried out in a specific region significantly affects energy consumption, e.g., whether the area is residential, commercial, or industrial [12,213]. Additionally, demographic factors and the cost of living are also significant considerations. Population growth and changes in demographic structure (e.g., population aging) directly affect energy demand due to evolving energy needs. Additionally, a population’s purchasing power influences the ownership and use of household appliances and other electrical equipment. Conversely, limited income levels within a population can lead to more conservative consumption patterns. Naturally, these types of variables are highly dependent on the country in which the network is located and tend to change slowly over time, resulting in low measurement granularity. For example, birth rates are not measured as frequently as climatic variables, such as temperature or wind speed, which are commonly recorded every 15 min. For this reason, socioeconomic variables are generally more suitable for medium-term and long-term forecasts [12,56]. However, because most of the studies reviewed focus on short-term predictions, these variables are less widely used than climatic variables. Furthermore, obtaining this information depends on government agencies (which may not make it publicly available), and it cannot be monitored through the grid, unlike climatic variables. All of this makes the use of socioeconomic variables in demand forecasting a current and ongoing challenge.

The final type of exogenous variable identified in the literature concerns cultural factors, such as user consumption habits, lifestyle, and seasonality [214]. The latter, in particular, is categorized here because seasonality is closely linked to the number of holidays and working and non-working days in each country. For example, on working days (weekdays), higher and more consistent demand patterns typically appear in the industrial and commercial sectors. In contrast, on non-working days (weekends), demand in these sectors generally decreases, but it may increase in residential areas [158,215]. Moreover, holidays, even when they fall on weekdays, often show demand patterns similar to those of weekends. This behavior highlights the difficulty of developing a single global demand forecasting model, as such information varies substantially across countries, characterizing network users (e.g., a family in a residential microgrid), and knowing the area in which they reside can have a very positive impact on forecasting accuracy [158]. For instance, Table 5 shows that seasonality is a variable that is almost always included in forecasting models, underscoring its importance for reliable prediction. However, variables such as consumption habits or lifestyle are often challenging to incorporate into demand forecasting models (as shown in Table 5), primarily because of their high modeling complexity, which stems from the fact that all users exhibit these characteristics. This requires monitoring each user individually, which can be overly intrusive, raise privacy concerns, and increase energy consumption through devices that track when and how equipment is used [216], even though this approach is not feasible for an independent system operator.

Demand forecasting models (including traditional statistical models, classical ML models, and more advanced approaches such as DL and hybrid models) have addressed the problem by employing a wide variety of exogenous variables. For instance, most models presented in this work emphasize the use of seasonal variables, such as day of the week, holiday status, and current season. This type of variable is advantageous and essential for demand forecasting, as predictive models aim to capture seasonal patterns in demand, and that’s the reason why over 90% of forecasting models use them, according to the Table 5. Furthermore, Table 5 highlights the extensive use of climatological variables across most forecasting models, ranging from the simplest to the most sophisticated. This highlights the importance of climatological factors in demand prediction, particularly temperature, humidity, and wind speed, which are the most commonly employed variables in most studies. Approximately 50% of studies use at least two of these three types of exogenous variables, while over 75% incorporate at least one of them, and nearly 74% rely specifically on temperature, according to the Table 5. In fact, some studies use temperature as the sole predictor or combine it with a seasonal variable due to the clear linear relationship with the demand. However, most studies have demonstrated that nonlinear models, such as LSTM, outperform traditional statistical models that assume linear relationships among variables. This suggests that other exogenous variables with nonlinear dependencies may affect demand more than highly correlated variables.

On the other hand, socioeconomic variables remain somewhat more confined to traditional statistical models, as artificial intelligence has advanced, making models increasingly robust and better at capturing nonlinearities in demand. As a result, most work on DL and hybrid models is limited to employing only a few climatological variables to forecast demand, leaving aside other factors such as socioeconomic and cultural variables, except for seasonal variables. In addition, certain socioeconomic variables typically exhibit much lower granularity, meaning their data are collected at lower frequencies than demand, which is usually sampled at 15-min, hourly, or even daily intervals, depending on the application and forecasting horizon. When the horizon is short-term, the required granularity must be higher, and weather variables can be monitored with high granularity, while socioeconomic variables are commonly used for mid- and long-term predictions due to their long-term seasonal patterns and the fact that economic and population indicators are measured every year, and it’s not feasible for short-term forecasts. For this reason, Table 5 shows little adoption of socioeconomic variables. Likewise, it becomes evident that cultural variables, particularly consumption habits and lifestyle, are rarely used in forecasting models compared to climatological variables. In this case, granularity is not the problem. Instead, the challenge lies in the need to continuously and individually monitor each user in a personalized way. This can be costly and complex, and may not be well received by users, as it is perceived as intrusive.

In addition to the points mentioned above, predictive models often rely on localized training, i.e., the exogenous variables used to train the model correspond to the same geographical region where the forecasts will be applied. This is important because many exogenous variables are strongly correlated with local demand. In contrast, training with data from different regions is generally not feasible unless strategies such as transfer learning are used to adapt an existing model to a new system within the same area. This approach can reduce costs and implementation time, although a fully generalizable model remains a long way off. This presents a challenge that requires further study to determine how much data from one system can be reused to improve model scalability. Another challenge in the literature is that performance is commonly reported using the same metrics (e.g., MAPE, RMSE, $R^2$) across very different contexts and datasets. As a result, it is challenging to draw meaningful comparisons between models, as similar metric values may correspond to scenarios with varying levels of complexity.

5.1. Remaining Challenges and Future Research Avenues

From a methodological perspective, traditional load prediction approaches have relied on statistics, including probabilistic models and time-series models, such as the ARIMA model and Holt–Winters exponential smoothing, which have proven effective in scenarios with relatively stable consumption patterns [51,52]. However, these methods are limited by the high variability and nonlinearity introduced by exogenous variables [12,127]. The AI-based models described in the earlier sections have demonstrated robustness to these variations, especially when considering the nonlinear behavior of climatic or socioeconomic factors [6,8,217]. The potential of classical ML models, such as SVM, RF, and GB methods, to capture complex relationships between load and exogenous variables demonstrates their applicability to more complex scenarios, thereby increasing their applicability in real microgrids [113,189,202]. In addition, more recently, DL models, particularly RNNs and LSTM networks, have enabled the modeling of long-term temporal dependencies to better adapt to the dynamic nature of electricity demand [149,218].

Despite recent advancements in predictive systems for electrical microgrids, several significant challenges persist that hinder their effective deployment, adaptability, and scalability [57]. Below, we outline the four main gaps identified in this systematic review. The first gap pertains to both bibliometric and literature analysis, while the remaining gaps are based on findings from the literature analysis.

5.1.1. Standardization of Databases

One of the first challenges encountered in our systematic review was the lack of consistency in data collection across databases. For instance, most databases that include exogenous variables tend to feature only climatic variables, excluding socioeconomic and cultural ones [12,156,191]. This, combined with the fact that many data sources are not publicly available, limits the ability to verify the results reported in some studies [65]. Beyond the heterogeneity of variables, differences in data preprocessing, temporal resolution, and evaluation protocols further complicate meaningful comparisons between forecasting models. In this context, the adoption of publicly available benchmark datasets, such as those released within GEFCom or by the IEEE PES Intelligent Systems Subcommittee, represents a concrete step toward improving reproducibility and comparability across studies. It is essential to promote standardization in the collection of data from real-world systems and to encourage the use of shared benchmark datasets to ensure the comparability and scalability of future work in demand forecasting.

5.1.2. Characterization of the Computational Complexity

As identified in the bibliometric analysis using the thematic map and dendrogram, computational complexity is not a primary focus of demand-forecasting research. This observation is further supported by the systematic review, which shows that most studies overlook the computational complexity of forecasting models (e.g., classical ML and DL models often require significant computational resources). In other words, they do not provide a characterization that would allow one to assess the hardware or computational resources required to implement these models in real-world scenarios. This presents a significant challenge, as short-term and very short-term forecasting models are vital for making real-time adjustments or responding to sudden changes in the grid [6,176,219]. This reality becomes especially critical considering that these models are typically required to run on edge devices, which possess limited computational resources compared to the systems utilized during the model development phase. However, the challenge intensifies when forecasting models are integrated into data-driven decision frameworks for energy management, where uncertainty modeling traditionally imposes a high computational burden. To address this, recent advancements establish a critical link between forecasting and control through robust optimization. For instance, authors in [220] propose a data-driven quad-level approach that effectively manages massive renewable integration. By employing a customized column-and-constraint generation algorithm with a pairwise convex-hull uncertainty set, this method reduces the complexity of uncertainty modeling from exponential to quadratic in the number of units. Furthermore, the incorporation of parallel processing and strategic starting points (q-TOAT) prevents premature convergence to local optima, demonstrating that rigorous uncertainty modeling and global optimization can be made computationally feasible for real-time applications.

5.1.3. Challenges in Extending and Generalizing Forecasting Models

Table 5 reveals a lack of long-term forecasting models across most methodological approaches. Most forecasting models focus on short-term and sometimes medium-term horizons, which limits their utility for long-term planning and cost optimization [157,192,194]. At the same time, forecast accuracy varies considerably across studies, even when the same performance metrics are used (e.g., MAPE, MAE, $R^2$), as these can vary substantially with the dataset [3,83]. This divergence arises because models are optimized for specific conditions, such as the region where the grid is located, in which exogenous variables, including temperature, humidity, and socioeconomic strata, can vary significantly. Few works [72,127,135,162] have demonstrated that including exogenous variables improves load predictions in approximately 90% in some cases. However, although several studies recognize that exogenous variables such as weather, socioeconomic factors, and seasonality can improve forecast accuracy, most studies don’t provide direct quantitative comparisons between models that incorporate these variables and those that don’t, but they provide qualitative comparisons in terms of interpretability. Consequently, difficulties arise in generalizing forecasting models across different microgrid contexts [83,130,191]. Therefore, the implementation of forecasting models often requires retraining or adaptation of the dataset, which increases both the cost and complexity of their deployment in real-world scenarios. These findings support the use of standardized datasets to improve reproducibility and comparability across studies.

5.1.4. Practical Implementation of the Load/Demand Forecasting Models in Real-World Scenarios

According to the bibliometric analysis, there is a noticeable disconnect between load forecasting models and topics such as housing, smart meters, and even EMSs. This highlights that forecasting models remain distant from real-world implementations in EMSs. This gap is further supported by a comprehensive literature review, which shows that most studies use a microgrid dataset from somewhere in the world, apply an artificial intelligence technique, and report performance metrics. Generally, these results are good; however, they have limited real-world applicability because they do not assess model generalizability or their direct impact on critical operational tasks, such as energy scheduling, economic dispatch, and resilience enhancement against grid disturbances [220]. A few studies have implemented demand forecasting models in real-world settings to bridge this gap. For instance, in [54], ARIMA was applied at a food manufacturing company, enabling managers to make informed decisions regarding production scheduling. In [59], an EMS based on RNNs was implemented for seven residential buildings, and the solution was successfully replicated in other residential settings. In [74], a Bayesian model was tested on a house in Italy, with variations in the number of loads and forecasts across time horizons (15 min, 24 h, and 48 h). Finally, in [102], an RNN-based model was proposed for the industrial sector to optimize energy flow and generate financial savings. However, the number of works that test models in real-world scenarios and demonstrate their value in closed-loop control systems is minimal. For this reason, future research should, at the very least, aim to implement these forecasting models in the real-world systems from which the data were sourced. Ideally, such work should focus on developing a model that supports the EMS.

Addressing these limitations requires the development of more adaptable models that can generalize across contexts and operate reliably in real-time. In parallel, integrating edge computing and distributed architectures will be essential to ensure low-latency, high-accuracy predictions in resource-constrained environments [55].

6. Conclusions

Forecast load in electrical microgrids and smart grids has become a highly active area of research due to the growth of methodological approaches and practical applications. Forecasting models have evolved from traditional statistical models to DL architectures and hybrid models, with the aim of addressing the increasing complexity of modern energy systems. In this paper, we conducted a bibliometric analysis and a systematic review of forecasting methods, examining how different strategies have been applied and how the field has developed over time.

In particular, the bibliometric analysis carried out revealed some main insights, such as the significant growth in the number of publications on the topic of demand forecasting over the past decade, which confirms the relevance of the field and the interest of the scientific community in the context of the energy transition toward cleaner and greener energy sources. Additionally, there is significant interest in integrating AI/ML-based models, including hybrid models, into EMSs within power grids. Ultimately, the thematic map and factorial analysis revealed a gap in the integration of forecasting models with real-world applications. In other words, most studies rely solely on data and do not test forecasting models in an actual system, or at least in an emulated environment. This finding is further corroborated by the systematic review of the collected studies. All of the above indicate that the field of demand forecasting is in constant growth, although several challenges remain.

Regarding forecasting models, the literature review (see Section 4) indicates that traditional statistical models remain relevant due to their simplicity and efficiency. However, they are increasingly being surpassed by more sophisticated approaches (AI-based models), among which recurrent models and those that incorporate attention mechanisms stand out for their ability to better capture temporal dependencies and nonlinear patterns in demand. These more advanced models have become necessary due to the increasing complexity of modern energy systems. Nevertheless, a clear predominance of short-term forecasting models remains, while medium- and long-term models are comparatively underexplored. This may be attributed to either the inherent complexity of medium- and long-term forecasting or to the particular research interests of the scientific community. In any case, this lack of exploration limits the usefulness of models for infrastructure planning and policy applications, such as renewable energy integration and energy market development.

A key factor for improving predictive accuracy across all forecast horizons is the informed integration of exogenous variables, such as weather, socioeconomic, and environmental data, thereby enhancing the robustness, adaptability, and interpretability of forecasting models. Furthermore, the review highlights the increasing importance of sophisticated models that integrate traditional statistical models with ML models (i.e., classical ML and DL), balancing accuracy, reliability, and interpretability. Despite significant progress, several persistent challenges limit the practical deployment of forecasting models in microgrids. These include the lack of rigorous computational complexity characterization, limited computational efficiency, difficulties in adapting to changes in operational modes, decreased accuracy under extreme conditions, and scalability issues across different geographical and socioeconomic contexts. Additionally, the lack of standardization in data collection and reporting hinders model comparability. Some studies still rely solely on historical electrical data or on a few weather variables, such as temperature and irradiance, while overlooking the influence of other climatic factors and even socioeconomic or regional variables, which are essential for real-world applications. There is also a noticeable gap between model development and operational deployment, partly due to the absence of shared evaluation protocols and accessible, high-quality datasets.

To bridge these gaps, we recommend developing and adopting a standardized smart energy profile protocol (e.g., IEEE P2030.5) to facilitate data exchange across platforms. Additionally, we advocate the use of standardized datasets, such as the Global Energy Forecasting Competitions (GEFCom) or those provided by the IEEE PES Intelligent Systems Subcommittee. These should be used in conjunction with APIs such as Open-Meteo and the National Solar Radiation Database, which can be used to retrieve accurate weather data at hourly or daily resolution, given only the latitude and longitude of the area of interest. We further recommend using resources such as the World Bank Open Data platform or relevant government agencies in the country of interest to extract socioeconomic indicators. This approach will improve interoperability and transparency and ensure the reproducibility and comparability of the works. Collaborative initiatives among academia, industry stakeholders, and policymakers are essential for establishing benchmarks and promoting model reuse through reproducible research practices.

Moreover, future research should move beyond isolated model development and focus on embedding forecasting engines within operational EMSs, enhancing model adaptability under changing conditions, and expanding the socioeconomic representativeness of training datasets. In this context, developing lightweight forecasting architectures, such as optimized or compressed recurrent neural network-based models suitable for deployment on edge devices, represents a promising direction to enable real-time and decentralized energy management. In parallel, establishing cross-regional, transferable prediction frameworks that generalize across diverse climatic, economic, and regulatory contexts and forecast horizons remains an open challenge. Specifically, future research must also validate how predictive inputs enhance decision-making processes, such as scheduling for days, months, and years ahead, and optimize real-time dispatch, while also evaluating their role in improving microgrid resilience against variability and external disruptions. Finally, in addition to the above future research lines related to load forecasting models, other significant issues must be addressed jointly within integrated microgrid management frameworks (such as vulnerability management, state regulations, coordination of DERs, and communication for control and monitoring) in order to develop efficient, secure, reliable, and scalable electrical microgrids.