The Path Towards Decarbonization: The Role of Hydropower in the Generation Mix

Abstract

The evolution of the generation mix towards deep decarbonization poses pressing questions about the role of hydropower and its possible share in the future mix. Most technical–economic analyses of deeply decarbonized systems either rule out hydropower growth due to lack of additional hydro resources or take it into account in terms of additional reservoir capacity. This paper analyzes a generation mix made of photovoltaic, wind, open-cycle gas turbines, electrochemical storage and hydroelectricity, focusing on the optimal generation mix’s reaction to different methane gas prices, hydroelectricity availabilities, pumped hydro reservoir capacities, and mean filling durations for hydro reservoirs. The key feature of the developed model is the sizing of both optimal peak power and reservoir energy content for hydropower. The results of the study point out two main insights. The first one, rather widely accepted, is that cost-effective decarbonization requires the greatest possible amount of hydro reservoirs. The second one is that, even in the case of totally exploited reservoirs, there is a strong case for increasing hydro peak power. Application of the model to the Italian generation mix (with 9500 MWp and 7250 MWp of non-pumped and pumped hydro fleets, respectively) suggests that it is possible to achieve methane shares of less than 10% if the operating costs of open-cycle gas turbines exceed 160 EUR/MWh and with non-pumped and pumped hydro fleets of at least 9200 MWp and 28,400 MWp, respectively.

1. Introduction

Photovoltaic (PV) and wind energy are supposed to form the bulk of the power generation mix of the future to reach a nearly zero emission system. Two main benefits are associated with these two forms of generation: a low levelized cost of electricity (LCOE) relative to other forms of electricity production and negligible CO₂ emissions. In turn, enabling a greater RES integration in an economically affordable way inherently concurs with the fulfillment of one of the outcomes of the Climate Resilience Pathway, namely, building resilient businesses and economies [1].

On the other hand, the main drawbacks are connected to their lack of flexibility. Since generation and consumption must match in any instant to ensure frequency stability and guarantee the power system equilibrium, the lack of flexibility is the main technical limitation to their massive adoption in the power generation mix.

Some forms of dispatchable sources will be needed in a renewable-dominated power system to be coupled with PV and wind, but still the question arises as to how the future energy generation mix will look. Many works have inquired and highlighted important aspects concerning various and still-infant technology to integrate along with PV, wind, and traditional generation technology. Among them are carbon capture and storage (CCS), grid-connected electrochemical storage, concentrating solar power (CSP), compressed air energy storage (CAES), power to gas (hydrogen, ammonia, and methane), and others; demand-side management (DSM) is also often considered, with the aim of increasing the flexibility of the system. Reference [2] considers different scenarios for a 100% renewable European power system, relying mostly on biogas, CSP, DSM, and CCS. Article [3] discusses some scenarios for a 100% renewable electric power system in France, pointing out the key role of DSM, whereas [4] underlines the role of storage technologies for the transition of a fully decarbonized Ukrainian, considering batteries, pumped hydro storage, and gas storage. Some papers rely on large amounts of installed batteries to accommodate PV power production [5,6,7], whereas [8] points out the role of lithium-ion battery and hydrogen storage in the decarbonization of the Chinese power system. As a general remark, these kinds of works usually rely on the assumption that the new technologies’ costs will decrease significantly in the near future to obtain credible power system costs. Moreover, when included in the modeling framework, the available hydropower remarkably increases the performance of the system.

On the other hand, there are some works, even if less numerous, that assess how to integrate traditional generation technology with the massive deployment of PV and wind. Reference [9] investigates the behavior of a system composed of electrochemical batteries, PV, and hydropower using as a case study the eight cascade hydropower plants in the province of Tokat in Turkey, evidencing how the integration of photovoltaic energy is significantly supported by hydroelectric power, while batteries optimize the operation of hydroelectric plants for mutual benefit. The paper [10] shows that the integration of PV and wind into the power system can be achieved by energy storage in the form of pumped-storage hydroelectricity as well as by rapidly up- and down-ramping gas power plants. Reference [8], in addition to showing the role of storage and suggesting the expansion of HV direct current transmission, also presents a model able to simulate the hydroelectricity production of the 41 major existing hydro stations in China based on the HydroBASINS dataset [11] and points out how hydropower can help in ambitious CO₂ emission reductions. Reference [12] shows how very deep decarbonization can be accomplished by hydro reservoirs serving as both short- and long-term energy storage resources, whereas [13] illustrates the value of electricity market integration to deep decarbonization in a strongly committed region, also exploring the enabling role of hydropower in such target. Reference [14] achieves the minimization of future greenhouse gas emissions from electricity production in Brazil by optimizing the daily dispatch of PV, wind, thermal, and hydropower plants. Article [15] shows in Spain the key role of flexible hydro generation in mitigating the risk that supply will be unable to meet load demand but also states that hydro generation may be insufficient to bring an adequate level of security of supply if baseload capacity decreases, thus proposing to legally assign to the power system operator the exploitation of hydro-generating facilities. Reference [16] studies the role of cascade hydropower in fully decarbonized systems, whereas [17] proposes a chance-constrained multi-time aggregate model able to integrate hydro–wind–solar operation, investigating the possibility of exploiting the flexibility of hydropower to increase wind and solar power accommodation and reduce CO₂ emissions. The key role that hydropower flexibility plays in the path toward decarbonization is highlighted in [18], especially in coal-dominated countries with a large amount of hydropower resources, such as China. Different from studies for a single country [19,20], a part of a country [10], or for a small isolated system, the work in [21,22,23] focuses on the possibility that the Norwegian hydropower system can balance variable production in the large neighboring region of Central West Europe. Reference [24] evidences how PV and wind integration in the Australian power system may be achieved by exploiting available potential sites for off-river (closed loop) pumped hydro energy storage, proposing to dramatically expand the pumped hydro generation pool to meet a 100% renewable system, later being criticized for the overestimation of such potential sites [25]. Reference [26] examines the potential for a fully renewable electricity generation mix in New Zealand’s hydro-dominated context, utilizing wind, geothermal, and biomass resources to replace fossil fuels, whereas [27] presents a technical/economic feasibility study of the adequacy of the Sardinian 100% renewable power system, proposing to integrate PV and wind with pumped hydro and biomass plants operated as open-cycle gas turbine (OCGT) plants. In general, all of these works underline the importance of available hydroelectricity, both in the form of pumped hydro and hydro reservoirs, to balance the intermittency of variable renewables as well as other forms of flexibility like combined cycle gas turbine and OCGT plants.

This paper follows this second stream of research, by analyzing a generation mix made of photovoltaic, wind, OCGT, electrochemical storage, and hydroelectricity, in the form of pumped hydro and hydro reservoirs. Non-traditional technologies such as CSP and CAES are not included, since currently they are negligible in terms of installed power due to high investment costs. Hydrogen and other power-to-gas solutions were also not included due to their currently limited installed capacity and comparatively high costs; nevertheless, these technologies are rapidly evolving and may play a larger role in the future, particularly in line with EU policy priorities. Electrochemical storage is included, due to the massive increase in the global installed capacity in the last several years: total installed battery storage capacity in the world stood at around 85 GW at the end of 2023 [28], of which about 65% is for utility-scale systems. In particular, the subject of the work is to investigate the optimal generation mix for a decarbonized power system by analyzing the interplay of PV, wind, OCGT, electrochemical storage, and hydroelectricity. The aim is to understand how the optimal generation mix reacts to changes in hydroelectricity availability and methane gas prices, while also optimizing the rated power of hydro turbines and the volume flow rate of water ducts. This seems a reasonable choice because, if the reservoirs and the lateral inflows are a characteristic of the geography of the system and cannot be exploited beyond a certain threshold, the rated power of the turbines, as well as the number and the diameters of the ducts, in principle can be expanded.

Much of the existing literature still suffers from two main shortcomings. First, hydropower is usually treated as a fixed and exogenous capacity, with no consideration of the possibility of repowering existing plants or optimizing peak power and reservoir sizing. Second, most studies tend to focus on emerging technologies with rapidly decreasing costs (such as batteries or hydrogen), thereby underestimating the strategic role of the existing hydropower fleet. This paper explicitly addresses these gaps by developing an optimization model that relaxes the assumption of fixed hydropower capacity and jointly optimizes reservoir capacity and peak power. By doing so, it provides novel insights into how hydropower can support deep decarbonization, not only through additional reservoirs but also through turbine repowering and increased flexibility of existing assets. The study presented in the paper stems from the doctoral work of one of the co-authors [29] and extends the existing research in several ways:

• Expanding the role of hydropower: The modeling framework explicitly relaxes the usual assumption of fixed hydropower capacity and instead considers the impact of different shares of hydroelectricity in the generation pool as well as the optimization of hydropower plant design parameters. Notably, given a reference load, different parameters of the model concerning the availability of the hydropower inflows and reservoirs in the system are set up and the simulations are repeatedly run. Moreover, the water turbine rating and the volume flow rate of the ducts are not imposed a priori but optimized by the model.
• Investigating the impact of varying methane prices, by analyzing the optimal generation mix under different methane price scenarios, including high and very high prices that reflect potential changes in carbon taxation and market uncertainties due to international tensions.
• Providing insights for policy implications, by investigating the optimal generation mix in all previous scenarios: The paper shows that a strongly decarbonized power system can be achieved with medium–low levels of hydropower availability, coupled with OCGT, wind, and PV, while highlighting the crucial role of hydro reservoirs and the need to maximize their utilization. Moreover, it is evidenced that cost effective decarbonization requires the greatest possible amount of hydro reservoirs and, even in the case of totally exploited resources, there is a strong case for increasing hydro peak power.

The rest of the paper is organized as follows. Section 2 explains all of the hypotheses and assumptions about hydroelectricity necessary to carry out the analysis. In Section 3 the model and data are presented, and Section 4 discusses the results. Finally, Section 5 analyzes the policy implications.

2. Hydropower Model

For this paper, it is crucial to properly model the available hydroelectricity in the power system and make it possible to investigate the optimal generation mix under different parameters. Two equivalent hydropower plants are simulated, a large-scale conventional hydroelectric dam and a pumped hydro storage facility.

The large-scale conventional hydroelectric dam is made of an upper reservoir and a duct–turbine system with a certain water head. The upper reservoir is continuously supplied by a stream of hourly lateral inflows which fill the basin. In turn, the upper reservoir can be unloaded by two means: one is the duct–turbine system, which exploits the potential energy of the water to produce electrical energy, and the other is the spillage system. The main features of interest for this power plant are as follows:

• MFD, mean filling duration, representing the mean time for the upper reservoir to completely fill itself, starting from an empty status, with the stream of lateral inflows.
• Lateral inflow hourly profile.
• Upper reservoir volume or, equivalently, upper reservoir energy content capacity.
• Rated peak power of the duct–turbine system.
• Unload time, which represents the time necessary to completely unload the upper reservoir with the duct–turbine system set at its rated peak power, under the hypothesis of no lateral inflows available.

The equivalent pumped hydro storage facility is made of two reservoirs, upper and lower, and a duct–turbine–pump system, which links the upper and lower basins. Conservatively, any lateral inflow which can potentially fill the upper reservoir water is not included so that the only way the upper reservoir can be inflated is by the pump system which, at the same time, deflates the lower basin. In turn, the upper reservoir is unloaded by the turbine which simultaneously loads the lower reservoir. The model assumes that the upper and lower reservoirs have the same volume capacity and that the rated peak power of the turbine system is the same as that of the pump system. The main parameters of interest, in this context, are as follows:

• Upper and lower reservoir volume or, equivalently, energy content capacity.
• Rated peak power of the duct–turbine–pump system.
• Unload time, which represents the time necessary to completely unload the upper reservoir with the duct–turbine–pump system set at its rated peak power.

The two equivalent hydropower plants are parametrized to study different hydro availabilities in the power system. Concerning the large-scale conventional hydroelectric dam, different thresholds representing the maximum exploitable lateral inflow energy in the system are imposed. At the same time, different MFDs of the actual upper reservoir are simulated, ranging from 100 h up to 2000 h, i.e., at a given lateral inflow availability an increasing energy content capacity of the upper reservoir is considered. This behavior is highlighted by Equations (1)–(3), which describe the large-scale conventional hydroelectric dam in the optimization problem:

$$EUpRes{H}_t = EUpRes{H}_{t-1} + W{H}_t \cdot RESH - Nex{H}_t - Spillag{e}_t, \hspace{0.17em}\forall t > 1$$

(1)

$$0 \le EUpRes{H}_t \le RESH, \hspace{0.17em}\hspace{0.17em}\forall t$$

(2)

$$0 \le RESH \le EUpResHMax$$

(3)

where

• EUpResH_t is the energy content of the upper reservoir at time t.
• Spillage_t is the energy content of the spilled water at time t.
• NexH_t is the net power injection of the large-scale conventional power plant at time t.
• RESH is the available energy content capacity of the upper reservoir.
• WH_t is the hourly lateral inflow in p.u. of the available energy content capacity of the upper reservoir.
• EUpResHMax is the maximum threshold of the upper reservoir energy content capacity.

EupResHMax and WH_t are strictly related to hydro availability, defined as the portion of load demand supplied by the aggregate lateral inflows, and MFD, according to the following equations

$$W{H}_t={\displaystyle \frac{N_T}{MFD}}\cdot {\displaystyle \frac{WHMW{h}_t}{{\displaystyle \sum _{t=1}^{N_T}WHMW{h}_t}}},\hspace{0.17em}\forall t$$

(4)

$$Hydroavailability=\left({\displaystyle \sum _{t=1}^{N_T}W{H}_t}\right)\cdot EupRESHMax$$

(5)

with N_T being the number of time periods and WHMWh_t the hourly lateral inflows expressed in MWh. Note that from (4), the term ${\displaystyle \sum _{t=1}^{N_T}W{H}_t}={\displaystyle \frac{N_T}{MFD}}$ represents how many times the upper reservoir is completely filled during the considered time horizon and, thus, the terms WH_t·RESH in (1) ensure that the hydro energy available in the system within the time horizon is RESH·N_T/MFD. WH_t is inversely proportional to MFD and thus EupResHMax is directly proportional to Hydroavailability and MFD. The parameter EUpResHMax constrains the variable RESH, representing instead the maximal actual upper reservoir energy content capacity chosen by the model. This implies that the model has the possibility not to exploit all of the available hydro resources.

Concerning the equivalent pumped hydro storage facility, the threshold concerning the maximum availability in the power system of the upper and lower reservoir is constrained in a similar manner. The parameter related to the threshold availability of the upper and lower reservoirs of the pumped hydro storage is EUpResPumpMax; the detailed equations can be found in Appendix A. In the model, EupResPumpMax is calculated by the relation

$$EUpResPumpMax=\overline{D}\cdot NHoursPump$$

(6)

with $\overline{D}$ being the mean value of the load demand D and NHoursPump the number of hours that the upper and lower reservoirs with an energy content equal to EUpResPumpMax can supply $\overline{D}$. In the simulation reported in Section 4, different values of NHoursPump are considered, ranging from 0 h (i.e., no pumped hydro storage facility is installed) to 8 h.

The last assumption concerns the annualized costs used in the model. Two different costs for the large-scale conventional hydroelectric dam are set, one related to the annualized cost of damming and building up an upper reservoir, and the other related to the duct–turbine system. The two parameters are CRESH, which is the annualized cost of building one unit of capacity of the hydro reservoir (EUR/MWh), and CPOH, which is the annualized cost of building one unit of hydro peak power (EUR/MWp). The two parameters appear in the objective function in the form CPOH·POH, which is the annualized cost of the hydro peak power for a given choice of POH representing the maximum peak power of the hydroelectric plant, and in the form CRESH·RESH, which is the annualized cost of the upper reservoir capacity. This choice of splitting the cost of energy capacity and peak power seems reasonable because the two activities are independent of each other to a certain degree. In other words, the duct–turbine system can be set almost independently from the size of the upper reservoir and can be expanded even if the upper reservoir is not modified. Moreover, the modeling framework allows us to understand the behavior of the optimal peak hydroelectric power, even in the case of totally exploited reservoirs.

Regarding a large-scale conventional hydroelectric dam, the calculation of CRESH and CPOH arises from the LCOE of hydroelectricity. From [30], the global weighted average LCOE of electricity from hydropower in 2022 was 61 USD/MWh, and for projects commissioned in 2022 LCOE ranged from a low of 16 USD/MWh to a high of 225 USD/MWh. An LCOE equal to 106.20 EUR/MWh is considered, assuming that on average the LCOE is divided equally between the investment costs of damming and the investment cost of the duct–turbine system. Namely, 53.10 EUR/MWh of the LCOE is attributed to the damming and building up the upper reservoir, whereas the other 53.10 EUR/MWh of LCOE is attributed to the duct–turbine system. Given that 1 MWh of capacity of the upper reservoir fills itself 8760/MFD times in a year and yields on average 8760/MFD MWh and given the share of the LCOE equal to 53.10 EUR/MWh for the upper reservoir capacity, the annualized cost per unit of upper reservoir can be approximately inferred as CRESH = 53.10·8760/MFD EUR/MWh. Similarly, assuming that on average a reservoir hydropower plant has an unload time equal to 132 h (arising considering that in Italy, on average, the MFD is 400 h, the production in 2019 for the hydro reservoir was 24.2 TWh, and the nominal peak power of the Italian fleet is 9500 MWp), the reference peak power per unit of upper reservoir energy capacity $RefPeak={\displaystyle \frac{1}{132}}\hspace{0.17em}{\displaystyle \frac{1}{h}}$ can be used. Consequently, the annualized cost of the duct–turbine system can be inferred as CPOH = 53.10·8760/(MFD·RefPeak) EUR/MWp. Both CPOH and CRESH are functions of MFD; in the simulations, MFD is varied in a range between 100 h and 2000 h.

Regarding a large-scale pumped hydro facility, the calculation of CRESPump and CPOPump depends on the levelized cost of storage (LCOS) according to the following relations:

$$CRESPump=0.5\cdot LCOS$$

(7)

$$CPOPump=0.5\cdot LCOS\cdot UnloadTim{e}_{ref}$$

(8)

Following the same reasoning as the large-scale equivalent hydroelectric dam, in (7) and (8), the coefficient 0.5 divides LCOS equally between the investment costs of damming and of the duct–turbine system. Conservatively, LCOS is set to 250 EUR/MWh, and UnloadTime_ref is set to 15 h based on the average value of the Italian pumped hydro fleet. It should be noted that the LCOE assumed for hydropower (106.2 EUR/MWh) and the LCOS for pumped hydro storage (250 EUR/MWh) are on the conservative end of the reported values in the literature. These assumptions were intentionally adopted to test the robustness of the model under unfavorable economic conditions for hydropower. Lower cost assumptions would only reinforce the importance of hydropower in the optimal generation mix.

3. Optimization Model and Data

The model, developed by the authors, is at its core a large-scale linear programming problem yielding the optimal generation mix for a given set of parameters. For its detailed equations and a mathematical explanation, refer to Appendix A.

The model aims at minimizing the annualized costs of generating electricity, constrained upon a detailed representation of the power system demand over the course of 4 years with an hourly resolution. Six technologies are at the disposal of the system: photovoltaic, wind turbines, open-cycle gas turbines, one equivalent large-scale conventional hydroelectric dam, one large-scale pumped hydro facility and one large-scale electrochemical storage (BESS). Load shedding is also incorporated in the model to match demand and production in every time period, heavily penalizing this possibility in the objective function considering a cost of 50,000 EUR/MWh. The objective function is as follows:

$$\min \left(\begin{array}{l}CPV\cdot PVinst+CW\cdot Winst+COCGT\cdot OCGTinst+CPOH\cdot POH+\\ CPOPump\cdot POPump+CRESH\cdot RESH+CRESPump\cdot RESPump+\\ CSOCBess\cdot SOCinst+CPst\cdot Pstinst+\\ {\displaystyle {\sum }_t\left(PMET\cdot NexOCG{T}_t+CLS\cdot L{S}_t+\epsilon \cdot \left(Pc{h}_t+Pdi{s}_t\right)\right)}\end{array}\right)$$

(9)

The annualized costs of photovoltaic installed (CPV·PVinst), of wind energy installed (CW·Winst), of OCGT installed (COCGT·OCGTinst), of BESS installed (CSOCBess·SOCinst + CPst·Pstinst), the operating cost of OCGT (${\displaystyle {\sum }_{t}PMET\cdot NexOCG{T}_t}$), and the cost of load shedding (${\displaystyle {\sum }_{t}CLS\cdot L{S}_t}$) are minimized.

For BESS, the annual investment cost of storage depends on both energy and power ratings, as in [31]; the BESS operating cost is accounted for by the term ${\displaystyle {\sum }_t\epsilon \cdot \left(Pc{h}_t+Pdi{s}_t\right)}$ in the objective function, avoiding simultaneous charging and discharging, as explained in [32]. CSOCBess is set to 56,900 EUR/MWh and CPst is set to 49,800 EUR/MWh, considering investment costs equal to 220,000 EUR/MWh and 190,000 EUR/MW, e is set to 0.01 EUR/MWh (i.e., practically the BESS operating cost is disregarded), the annual discount rate is r = 9%, and the BESS lifespan is set to 5 years.

For hydroelectricity, as explained in Section 2, its annualized cost is split into two terms, one related to the annualized cost of damming and building up a reservoir, and the other related to the duct–turbine system. For the large-scale conventional hydroelectric dam, the annualized cost of building an upper reservoir is indicated by the term CRESH·RESH, whereas the annualized cost of the duct–turbine system is represented by CPOH·POH. The annualized cost of building the upper and lower reservoirs of the conventional pumped hydro facility is indicated by the term CRESPump·RESPump, whereas the annualized cost of the duct–turbine system is represented by CPOPump·POPump.

Equation (10) describes the power system balance between production and demand in each time interval t:

$$NexOCG{T}_t+NexP{V}_t+Nex{W}_t+Nex{H}_t+NexBES{S}_t+NexPum{p}_t+L{S}_t-1.05\cdot D_t=0$$

(10)

The matching between production and demand is ensured on an hourly basis over the set of time periods considered in the modeling framework (4 years overall). Electricity production can be carried out by open-cycle gas turbines (NexOCGT_t), photovoltaic plants (NexPV_t), wind turbines (NexW_t), BESS (NexBESS_t), the large-scale equivalent hydro dam (NexH_t), and the large-scale equivalent pumped hydro facility (NexPump_t). The production of photovoltaic and wind energy can be at most equal to the nominal power installed times a production coefficient relative to the specific time, which is a standard modeling framework for these kinds of sources. This modeling solution allows us to incorporate the curtailment of photovoltaic and wind energy. For both photovoltaic and wind energy, no upper constraint regarding the amount of nominal power that can be installed is imposed.

Concerning hydroelectricity, the production is consistent with the water availability of the upper reservoir in any given time and is consistent with the maximum peak power of the hydro facility. The large-scale conventional hydro can fill the upper reservoir only with lateral inflow, whereas the pumped hydro facility can only fill its upper reservoir with the stream of pumped water coming from its lower reservoir. There is also the possibility to spill water from the upper reservoir of the large-scale hydro dam, as already shown in (1).

OCGTs instead do not have any a priori limitation in their production. Unlike the other production sources, their operating cost is accounted by the term ${\displaystyle {\sum }_{t}PMET\cdot NexOCG{T}_t}$ which basically represents the methane cost in the system. COCGT is about 65,000 EUR/MW, considering an investment cost equal to 730,000 EUR/MW and r = 8%.

Different from the common practice of disregarding unit commitment in long-term planning studies, as explained in [33], for hydroelectricity and OCGTs some ramping constraints are imposed, enforcing that the maximum variation of power injections between two consecutive periods can be at most 30% of their nominal power for OCGTs and pumped hydro, and at most 50% for the large-scale conventional hydroelectric dam. Startup and shutdown costs are neglected.

A reserve constraint is also enforced, which imposes that in each time period the system has at its disposal an upper reserve higher or equal to 10% of the reference load at that time. In the upper reserve pool, the following quantities are incorporated: the curtailed power of wind and photovoltaic if available; the difference between the nominal and the injected power for OCGT; and for BESS and hydroelectricity, the difference between the nominal and injected power with the condition of enough energy stored. This way of modeling the upper reserve availability is in line with [27].

The reference load profile D_t is taken from [34] and refers to Italy during the years 2016–2019, multiplied by 1.05% to roughly consider the joule losses of the system. Any continuous electricity generation sources like run-of-river, geothermal, or nuclear power can be incorporated in the model just subtracting the appropriate quantity from the load. Conservatively, in the analysis presented in the paper these sources are not incorporated. The lateral inflow profile WHMWh_t is computed as a weighted average of the seasonal inflows from three different zones of Italy (north, center, and south) during the years 2016–2019. Production profiles in p.u. for wind energy and photovoltaic are also taken from Italy for the years 2016–2019 from [35]. All data are available in the Supplementary Materials [36].

CPV and CW instead represent the annualized cost per unit of nominal power installed of photovoltaic and wind energy, respectively. The annualized cost is computed from their LCOE—in particular, from the LCOE formulation of photovoltaic and wind energy $\mathrm{LCOE}\cdot \left({\displaystyle \raisebox{1ex}{${\displaystyle {\sum }_{t=1}^n{E}_t}$}\!\left/ \!\raisebox{-1ex}{${\left(1+r\right)}^t$}\right.}\right)={\displaystyle {\sum }_{t=1}^n\frac{I_t+M_t}{{\left(1+r\right)}^t}}$, with r being the discount rate, I_t and M_t the investment and the maintenance cost at year t, respectively, and E_t the electrical energy produced at year t. Note that the term ${\displaystyle {\sum }_{t=1}^n\frac{I_t+M_t}{{\left(1+r\right)}^t}}$ is the net present cost for the amount of photovoltaic or wind power installed yielding E_t over the course of the years. Since the annualized cost is expressed as the equivalent discounted cash flow which repeated over the entire lifespan of the plant yields the same net present cost, the following equation can be written:

$$AC\cdot \left({\displaystyle {\sum }_{t=1}^n\frac{1}{{\left(1+r\right)}^t}}\right)=LCOE\cdot \left({\displaystyle {\sum }_{t=1}^n\frac{E_t}{{\left(1+r\right)}^t}}\right)$$

(11)

with AC being the annualized cost of the project. From the previous equation, it is easy to derive CPV and CW just by substituting the term E_t associated with one unit of nominal power installed and imposing the desired parameters of r and LCOE. For photovoltaic LCOE = 50.5 EUR/MWh, r = 8% and a lifespan equal to 20 years are considered; for wind energy LCOE = 39.8 EUR/MWh, r = 8% and a lifespan equal to 15 years are considered.

At its core, the study in this paper consists of a sequence of simulations, varying the parameters PMET, MFD, EupResHMax, and EUpResPumpMax with PMET which is the gas price scenario, MFD which is the mean filling duration of the large-scale equivalent hydro dam related to WH in p.u., and EUpResHMax and EUpResPumpMax which are the maximum capacity of the upper reservoir of the large-scale equivalent hydro dam and of the equivalent pumped hydro plant, respectively. In this way, the impact of gas price scenarios (variations in PMET) can be assessed, as well as the impact of different hydro availabilities and MFD values (variations in EUpResHMax and WH_t) and the impact of different NHoursPump values (variations in EUpResPumpMax) in the optimal generation mix. The parameter PMET is defined as the operating cost of OCGT, which effectively serves as a proxy for both natural gas fuel cost and carbon policy stringency. While this conflation simplifies the modeling framework, it should be noted that the two drivers have different underlying mechanisms. Therefore, PMET should be interpreted as a synthetic parameter reflecting the overall operating cost of OCGT, rather than a direct forecast of fuel or policy trajectories.

The conservative framework set in the developed model corroborates the outcome of this study. In the authors’ opinion, the results, taken in their context, are credible enough to draw credible contributions. The main conservative hypotheses made in the study are here summarized:

• High costs for hydroelectricity are considered, with 106.2 EUR/MWh LCOE for the large-scale equivalent hydroelectric dam and 250 EUR/MWh LCOS for the large-scale equivalent pumped hydro facility.
• The pumped hydropower plant does not have any lateral inflows and can fill the upper reservoir only with the stream of water coming from the lower reservoir.
• Demand response and demand elasticity have not been considered.
• The ramping constraints for OCGT and hydropower plants are quite restrictive, especially considering that these are flexible sources.
• The grid losses, included in the load and estimated at 5%, are considerably high. Moreover, the static reserve in all periods is included, equal to 10% of the load.
• No contribution to the decarbonization deriving by some sources such as geothermal, nuclear, run-of-river, or waste management is considered, even if each of them can be included just by subtracting the proper quantity from the load.

Finally, there are two main limitations connected to this study. First, the high-voltage electricity grid is not represented to avoid relating the results of the model to a particular case study. By doing so, on one hand the analysis is kept as general as possible, but on the other hand some possible critical congestions that would appear are not considered. Second, the structure of the generation pool is not represented in detail, especially concerning hydroelectricity. Some hydroelectric power plants might have a complex structure made of multiple basins in cascade, clearly depending on the geography of the area, whereas in this study only an equivalent hydropower plant is represented. Again, since the geography of the local areas of the power system is ignored to stay as general as possible and since different hydro availabilities are represented, an equivalent hydropower plant is modeled, which is a choice also pursued by other authors [12,37].

4. Results

In this section, the main results of the study are presented and discussed. The complete set of simulation results is available in the Supplementary Materials [36]. A parametric study is carried out by changing the following quantities:

• The natural gas price varies from a minimum of 40 EUR/MWh to a maximum of 280 EUR/MWh, with a step of 40 EUR/MWh.
• MFD assumes the following values: 100 h, 200 h, 400 h, 500 h, 600 h, 800 h, 1000 h, 1500 h, and 2000 h.
• Hydro availability varies from 0% to 30% of the overall demand with a 5% step.
• NHoursPump varies from 0 h to 8 h with a 1 h step.

The terms “methane price” and “gas price” are both used referring to the operating cost of the OCGT, which in the model is expressed by the parameter PMET, treating “OCGT operating cost” and “methane price” as synonyms. The load shedding and the water spilled from the large-scale hydro dam are not reported, because they are always nil or negligible. Similarly, BESS is quite negligible as well, since it is installed only if NHoursPump = 0 h and PMET ≥ 200 EUR/MWh, and the highest installed rated capacity and power are about one-third and one-fourth of the average load, respectively.

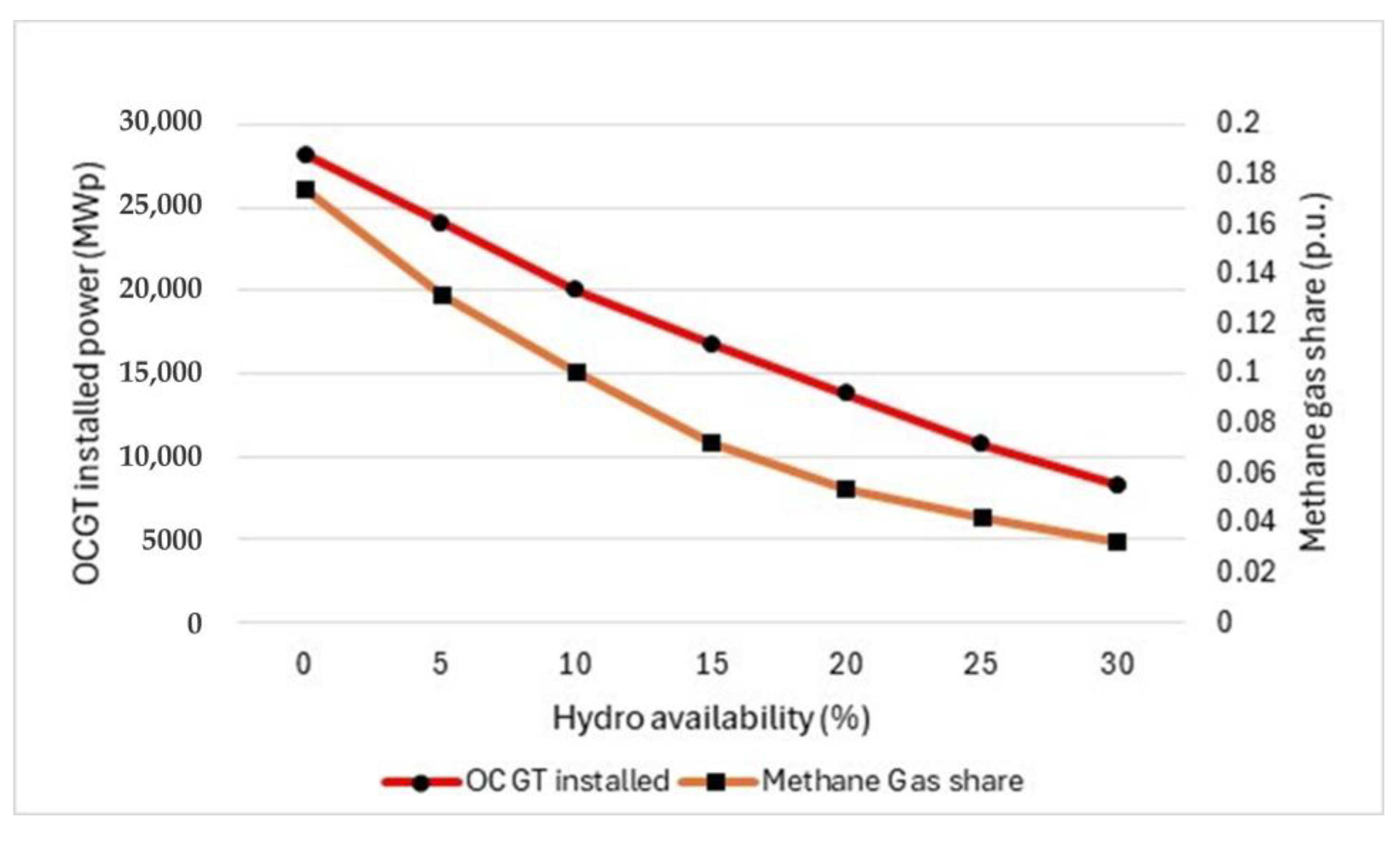
Figure 1 and Figure 2 show the behavior of the OCGT installed and their production share for two fixed gas prices, 120 EUR/MWh and 200 EUR/MWh, MFD = 500 h, NHoursPump = 4 h, and with hydro availability ranging from 0% to 30%.

Table 1. Average generation cost, photovoltaic, and wind peak power installed and curtailed renewable energy in percentage of the renewable potential production at different hydro availabilities. OCGT operating cost is assumed to be 120 EUR/MWh, MFD = 500 h, and NHoursPump = 4 h.

Hydro Availability (%)	AGC (EUR/MWh)	PV (MWp)	Wind (MWp)	Curtailment (%)
0	74.05	92,805	86,469	21.27
5	71.47	91,139	84,959	20.51
10	69.18	88,505	79,774	18.34
15	67.33	85,329	75,991	16.74
20	65.95	80,929	70,436	14.40
25	65.17	71,428	68,196	12.74
30	64.93	60,168	68,021	12.01

and

Table 2. Average generation cost, photovoltaic, and wind peak power installed and curtailed renewable energy in percentage of the renewable potential production at different hydro availabilities. OCGT operating cost is assumed to be 200 EUR/MWh, MFD = 500 h, and NHoursPump = 4 h.

Hydro Availability (%)	AGC (EUR/MWh)	PV (MWp)	Wind (MWp)	Curtailment (%)
0	85.77	103,329	112,559	31.25
5	79.71	102,406	105,920	29.20
10	74.86	99,813	99,440	27.05
15	71.36	92,215	89,227	22.87
20	69.14	81,088	82,899	19.45
25	67.65	68,103	78,446	16.50
30	66.73	59,328	76,578	15.84

instead report the average generation cost (AGC, defined as the ratio between total system costs and total load demand), photovoltaic and wind peak power installed and curtailed, with hydro availability ranging from 0% to 30%, for two fixed gas prices 120 EUR/MWh and 200 EUR/MWh, MFD = 500 h, and NHoursPump = 4 h. The average generation cost is reported because, in a perfectly competitive market, it equals the long-run market price, as established in microeconomic theory [38].

As expected, the larger the hydro availability, the greater the benefit to the system: optimal solutions always make use of the whole available upper reservoir capacity of the large-scale hydro dam. Figure 1 and Table 1 show that it is possible to significantly reduce the OCGT peak power and the methane gas share in the generation mix. At a methane price equal to EUR 120, the OCGT peak power drops from about 28,000 MWp when no hydroelectric power is available at all, to about 8000 MW with a 30% hydro availability. Meanwhile, the methane share in the system drops from 17.4% to 3.3% of the overall demand. Average generation costs experience a remarkable reduction, passing from 74 EUR/MWh to 65 EUR/MWh. Moreover, it can be observed that there is a decreasing trend for both photovoltaic and wind peak power installed; also curtailed renewable energy faces a decreasing trend.

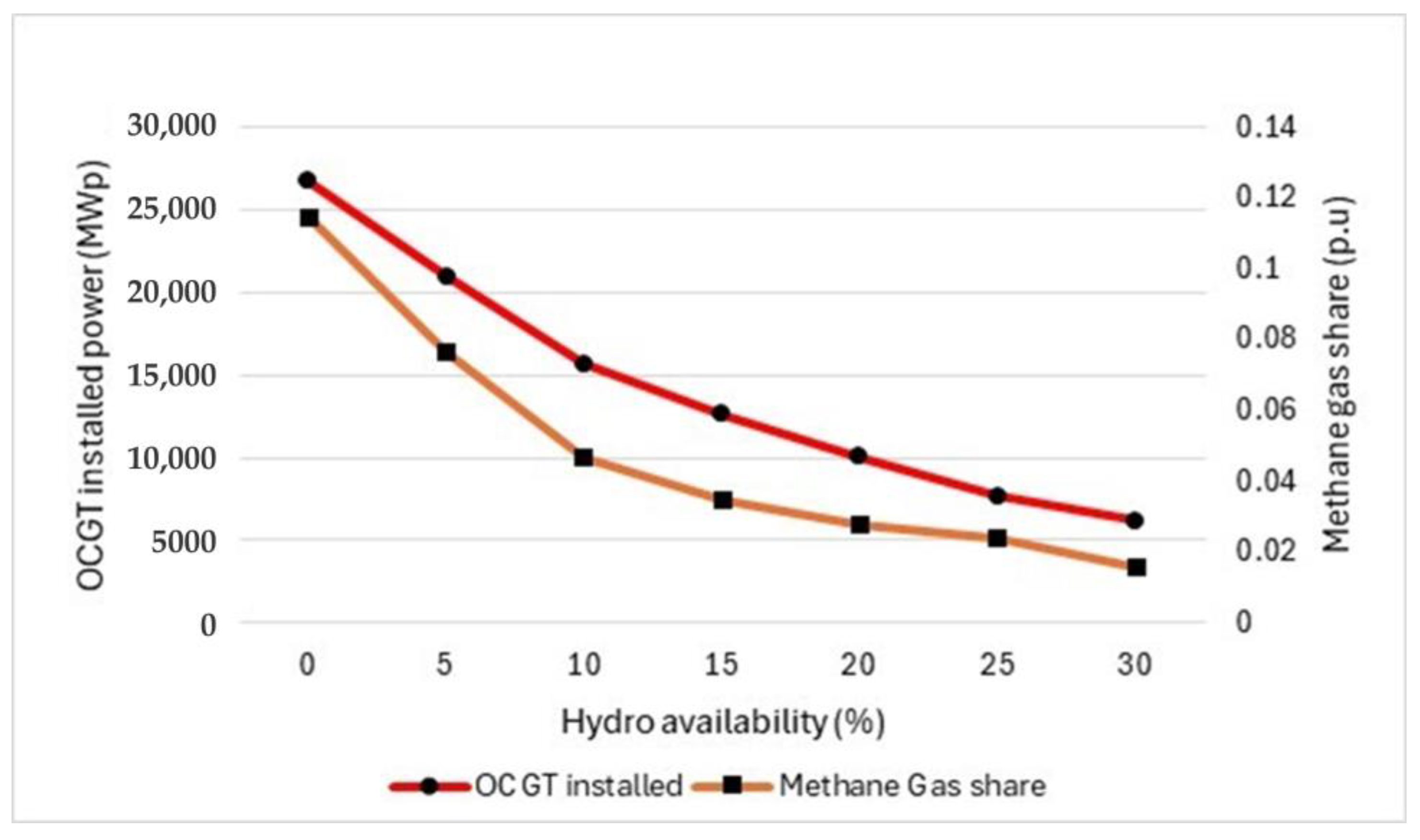
Similar behavior is observed for a methane price equal to 200 EUR/MWh, the results of which are indicated in Table 2 and Figure 2. In this case, the more expensive methane gas induces a larger number of investments in the renewable energy sector, when compared with the scenario at 120 EUR/MWh, with the curtailed renewable energy increasing remarkably. A higher degree of decarbonization is achieved too. This is accomplished under the optimal solution with an overcapacity of the renewable fleet. As in the previous gas price scenario, higher hydro availability remarkably improves the performance of the system.

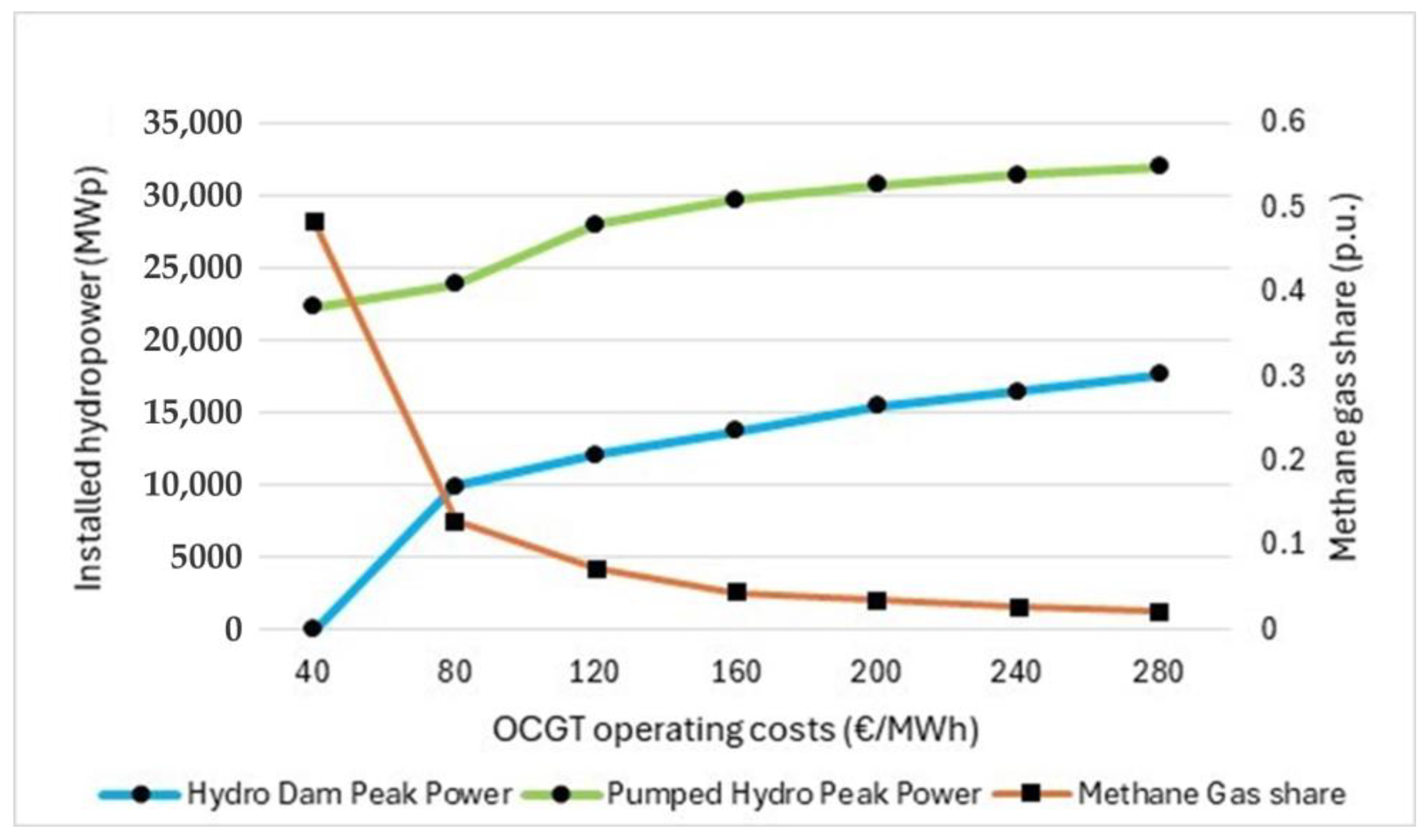
This kind of behavior is repeated for any other fixed gas price, MFD, and NHoursPump scenario. For the sake of brevity, figures or tables with different values of gas price, MFD, and NHoursPump are not reported. Instead, the dynamic of the system is very interesting when, keeping constant hydro availability, MFD, and NHoursPump in the system, a set of OCGT operating costs is simulated. Figure 3 and Figure 4 show the behavior of the nominal peak power for a large-scale hydro dam and for the pumped hydro facility as well as the methane share in the system at different OCGT operating costs.

Table 3. Unload time (ULT) of the large-scale equivalent hydro dam and of the pumped hydro facility, photovoltaic, and wind peak power installed, and curtailed renewable energy at different OCGT operating costs. Hydro availability is supposed to be at 5%, MFD = 500 h, and NHoursPump = 4 h.

Gas Price (EUR/MWh)	ULT Hydro Dam (h)	ULT Pumped Hydro (h)	PV (MWp)	Wind (MWp)	Curtailment (%)
40	/	5.96	50,992	40,208	1.27
80	284.97	5.10	80,503	67,003	12.35
120	206.84	4.39	91,139	84,959	20.51
160	164.97	3.98	99,088	97,156	25.92
200	142.30	3.83	102,406	105,920	29.20
240	125.00	3.77	105,993	114,550	32.34
280	111.41	3.99	108,690	123,991	35.34

and

Table 4. Unload time (ULT) of the large-scale equivalent hydro dam and of the pumped hydro facility, photovoltaic, and wind peak power installed, and curtailed renewable energy at different OCGT operating costs. Hydro availability is supposed to be at 15%, MFD = 500 h, and NHoursPump = 4 h.

Gas Price (EUR/MWh)	ULT Hydro Dam (h)	ULT Pumped Hydro (h)	PV (MWp)	Wind (MWp)	Curtailment (%)
40	/	5.96	50,992	40,208	1.27
80	264.68	5.58	74,437	65,702	11.18
120	217.03	4.75	85,329	75,991	16.74
160	190.30	4.47	89,646	85,536	21.08
200	169.74	4.33	92,215	89,227	22.87
240	158.85	4.24	93,827	93,403	24.67
280	148.25	4.16	95,106	97,482	26.35

instead show the features of the renewable sector at different methane prices, and the corresponding unload time for both the hydro dam and the pumped hydro facility.

Some interesting aspects may be observed. The increasing OCGT operating costs induce a larger number of investments in wind and photovoltaic; at the same time, the hydroelectric sector experiences a strong repowering of its nominal peak power. In other words, despite keeping the upper reservoir capacity constant for the large-scale equivalent dam and for the pumped hydro, both undergo a strong increase in their nominal peak power along with the deeper decarbonization of the generation mix. Clearly, with the greater hydro availability of Figure 4 and Table 4, the decarbonization of the system is significantly more robust compared to Table 3 and Figure 3, where the hydro availability is set to only 5%.

In the simulations, at low gas prices the role of OCGT is predominant; however, despite high simulated values of LCOE and LCOS, hydroelectric resources are always installed and play a decisive role in the generation mix. At higher OCGT costs and, thus, greater degrees of decarbonization, an overcapacity of the renewable fleet can be observed at the optimal solution, which yields a significant amount of curtailment. This kind of behavior is repeated for any other fixed hydro share in the system.

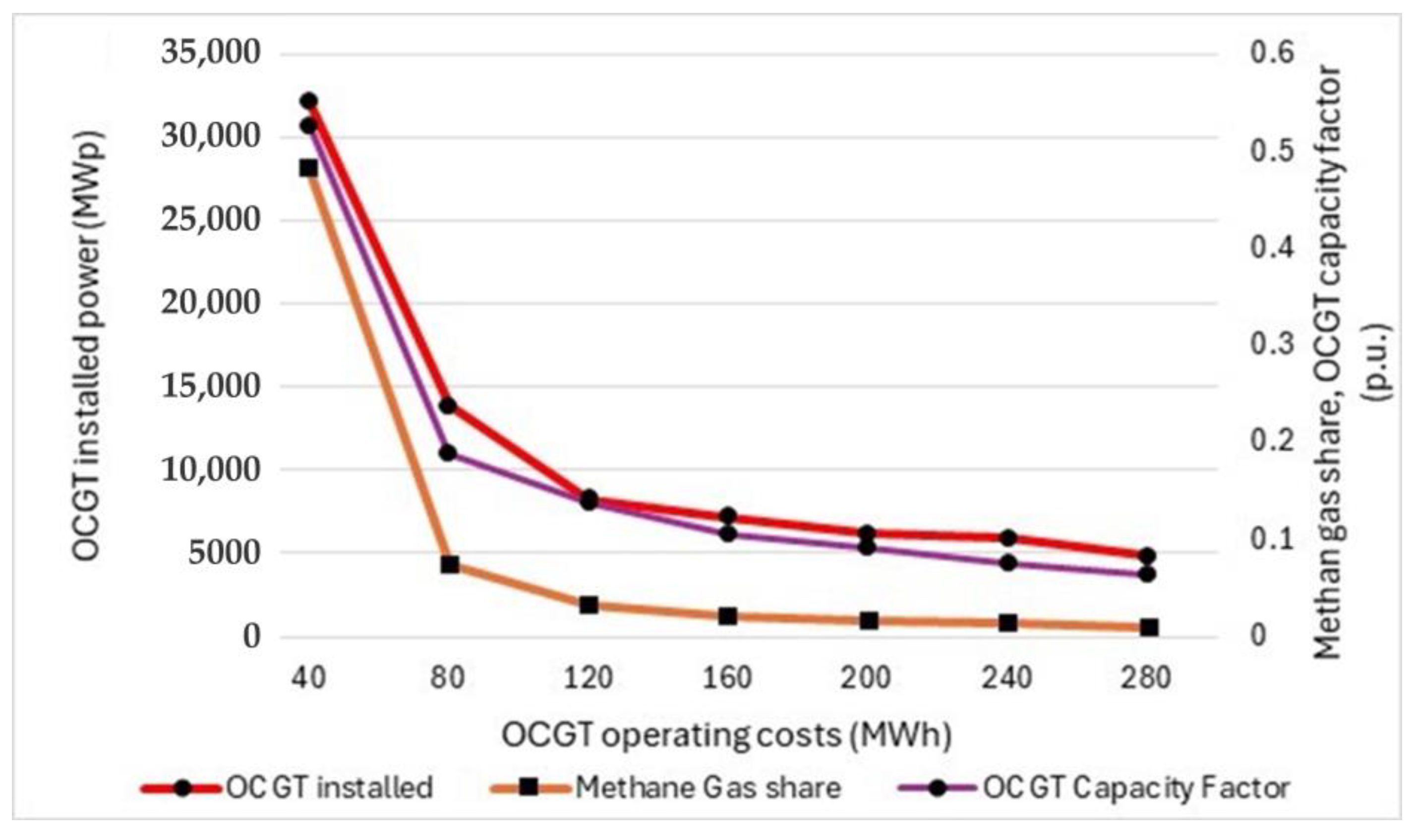
Figure 5 shows the behavior of OCGT with a 30% hydro availability, the highest simulated in the paper (MFD = 500 h; NHoursPump = 4 h). Decreasing trends of installed OCGT power, methane gas share, and OCGT capacity factor can be observed. At a methane gas price equal to 280 EUR/MWh, the gas share is very low, about 0.9%, leading to an overwhelmingly decarbonized power system, but still the installed peak power of OCGT is not negligible (4800 MW) and the capacity factor is 6.2%. It is interesting to note that, despite the remarkable hydro availability and the very high gas price, under the optimal solution the system still relies on a certain amount of OCGT peak power (about 15% of the average load), even if operated at a low capacity factor.

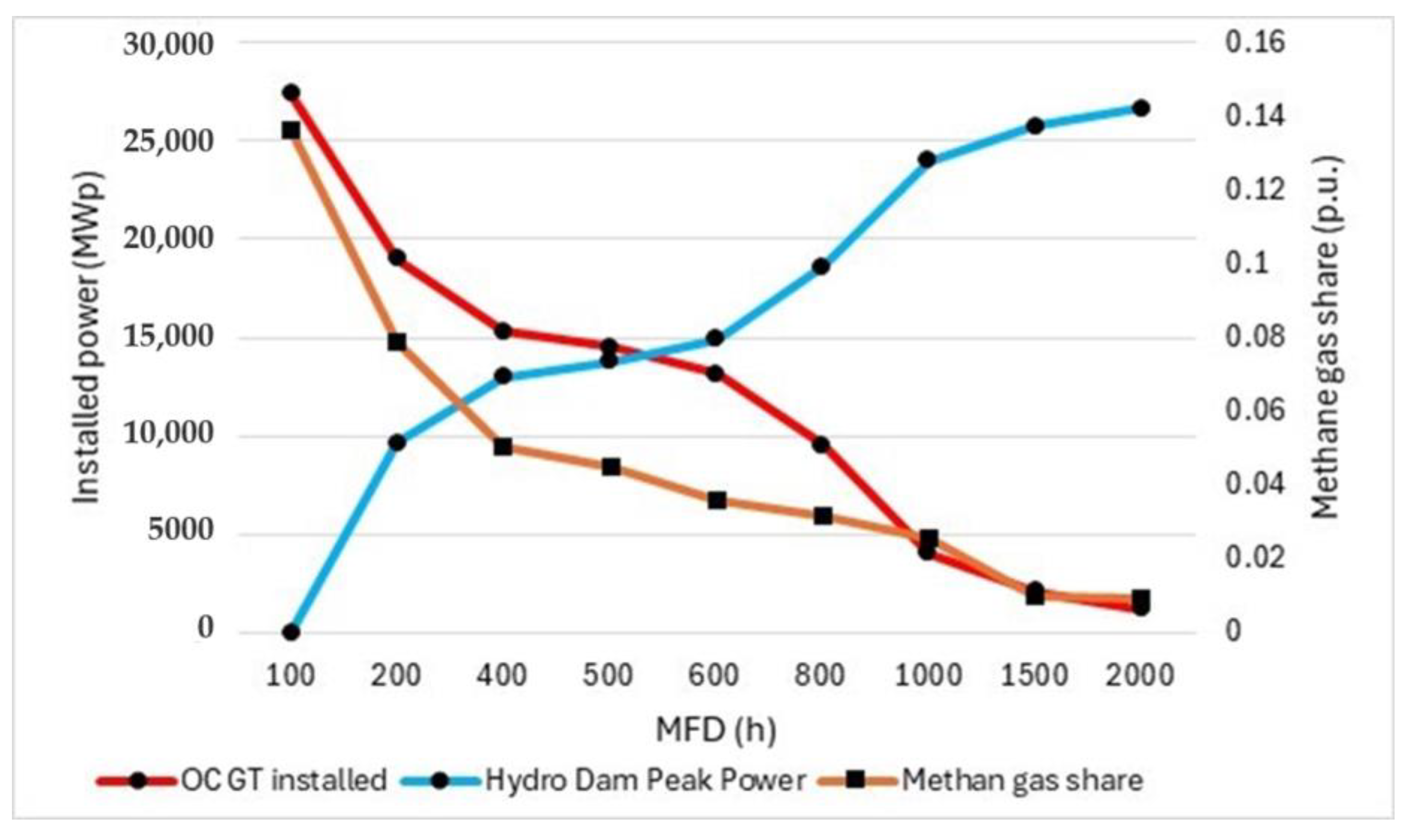
The effect of increasing MFD values on the system generation mix and the degree of decarbonization under the optimal solution is presented in Figure 6. The trend of the nominal peak power for a large-scale hydro dam and for OCGT, as well as the methane share in the system, is shown at different MFD values (hydro availability is 15%, PMET is 160 EUR/MWh, and NHoursPump is 4 h). Increasing MFD values has a positive effect since, despite the same amount of potential hydroelectricity, the system leverages larger reservoirs used to balance the intermittency of variable renewable sources at the expense of OCGT.

Lastly, application in the Italian case is reported. Italy has about a 9% hydro availability of the upper reservoir and, thus, its generation mix can be approximately described by Figure 7.

Excluding run-of river, Italy currently has a nominal peak power for its non-pumped hydro fleet equal to about 9500 MWp and a nominal peak power for the pumped hydro fleet equal to about 7250 MWp [39]. Our results suggest that in the decarbonization process, with a methane gas price higher than 160 EUR/MWh it is possible to reach methane shares of less than 10% with at least 9200 MWp for the large-scale hydro dam and 28,400 MWp for the pumped hydro fleet. It is possible to conclude that it is advisable to strongly invest in the nominal peak power of the pumped hydro fleet, whereas the nominal peak power of the non-pumped hydro is already appropriate.

5. Discussion

Based on the results of the simulations, some insights can be drawn with the aim of facilitating the path towards an overwhelmingly decarbonized power system. First, as expected, the greater the availability of hydro reservoirs the stronger the performance of the power system, from the point of view of both generation costs and the optimal level of decarbonization. Figure 1 and Figure 2 and Table 1 and Table 2 show this aspect clearly. With the other parameters fixed at a certain value, when the hydro availability increases there is a reduction in the methane gas share in the system, which is connected to the optimal decarbonization level of the generation mix under analysis. The average generation cost experiences a significant reduction as well. This first insight has already been pointed to in other works, for example [23], where the advantage of the interconnection to hydro-rich regions has been highlighted. Quite obviously, it can be concluded as well that, from the point of view of power system costs and the optimal level of decarbonization, it is advisable to build the greatest possible number of hydro reservoirs with the greatest possible capacity, as shown in Figure 6. However, one must consider that it might be extremely difficult to build new hydro reservoirs or to make new interconnections to hydro-rich regions. Public opposition to new flooded areas is a binding question and the same is true for new power lines. Indeed, especially in developed countries, the hydropower potential is already exploited to or very close to its maximum possible level. Usually, the best locations for hydropower are already utilized and there might be few places for new hydro facilities.

Despite this aspect, the opinion of the authors is that new investments in hydropower are strongly recommended for unleashing its decarbonizing potential. This is the topic of the second insight and regards the repowering of the duct–turbine system. This aspect is illustrated in Figure 3 and Figure 4 and Table 3 and Table 4. In these figures, despite the upper reservoir availability being kept constant, the nominal peak power experiences a remarkable increase while the generation system undergoes a decarbonization process. It is interesting to observe that both the pumped hydro facility and the large-scale conventional dam are interested in the repowering process. Thus, the second policy conclusion consists of considering investments in the duct–turbine system in the decarbonization process of the generation mix, in order to upgrade the nominal peak power of the hydroelectric fleet. This goal might be accomplished, in the worst-case scenario, by building a new duct–turbine system to operate in parallel with the already existing one, and in more optimistic scenarios just substituting the hydro turbine with an upgraded one. This kind of intervention has a lower environmental impact compared to building new reservoirs, and it is the opinion of the authors that it might meet lower public opposition.

To the authors’ knowledge, no previous works have concretely highlighted this possibility, because the model presented in this paper optimizes the nominal peak power of hydro dams and pumped hydro equivalent plants. Clearly, a deeper study more tailored to the specific studied system is needed in order to better understand the impact of such a decision and this should be the scope of future research.

Moreover, the study described in this paper suggests that a strongly decarbonized power system generation mix is reached even with a somewhat low hydro availability and with a medium–high methane gas price. For example, Figure 7 shows that, fixing the methane gas price at 200 EUR/MWh, already with a hydro availability equal to 9%, the methane gas share in the system is around 6%. This aspect triggers in the authors some reflections and some open questions. In particular, one might suspect that an optimal full decarbonization strategy for a power system with some hydro availability should be based on reducing the methane gas share in the system and, at the same time, making use of carbon-neutral methane gas, like biomethane and synthetic power to methane, which could be competitive with natural gas at such high prices. This point is left for future research.

Two clarifications are warranted. First, while the model is presented in a general form, its input data (load, PV, wind, and hydro inflows) are based on Italian profiles. The results are therefore most directly applicable to systems with similar hydro availability and climatic conditions, and their generalizability to other regions should be approached with caution. Second, the negligible role of BESS across most scenarios is explained by the combination of high assumed battery costs, the large flexibility already provided by hydropower, and the relatively stringent reserve requirements enforced in the model. As battery costs decline further and their deployment expands, their role in complementing hydropower could increase.

Lastly, an additional consideration concerns the risks associated with climate change. In particular, rainfall reduction and altered hydrological regimes could decrease hydropower availability, especially in Southern European countries. While our model parametrically varies hydro availability, it does not explicitly account for long-term changes in inflows due to climate change. This represents a limitation that should be considered in the interpretation of the results and motivates future research on coupling climate impact assessments with system optimization models.

6. Conclusions

This study investigates the role of hydropower in the context of a deeply decarbonized electricity generation mix, highlighting its strategic value when integrated with variable renewable energy sources and open-cycle gas turbines (OCGTs). The proposed optimization framework allows a flexible representation of hydropower resources, explicitly optimizing both reservoir capacity and peak power, unlike traditional approaches that assume fixed hydropower characteristics.

The simulations demonstrate that hydropower—both conventional and pumped—plays a crucial role in reducing reliance on gas-fired generation, even under conservative cost assumptions. Two main insights emerge from the results:

• Hydro reservoir availability is key to cost-effective decarbonization. Increasing hydro availability consistently reduces methane share and average generation cost across all scenarios. However, due to environmental, geographic, and social constraints, expanding reservoir capacity may not always be feasible.
• Repowering hydro peak capacity offers a viable alternative. Even when hydro reservoirs are fully exploited, there is strong economic justification for increasing the peak power of existing hydropower plants. This can be achieved through turbine upgrades or parallel duct systems, with relatively low environmental impact and public opposition.

Importantly, the model shows that even with modest hydro availability (e.g., 9% in the Italian case), methane shares below 10% can be achieved when gas prices exceed 160 EUR/MWh. This suggests that, in addition to increasing renewable penetration, investments in hydropower repowering should be prioritized in national decarbonization strategies.

This study is not without limitations. First, the transmission network is not represented, which prevents the identification of potential congestion effects. Second, hydropower is modeled through an equivalent single-plant representation, which simplifies the real complexity of cascade systems and geographical constraints. Third, conservative cost assumptions for hydropower and storage may underestimate their role in future scenarios. Finally, it should be emphasized that while the gas price usefully captures the sensitivity of the generation mix to open-cycle gas turbine operating costs, it merges fuel price dynamics and carbon policy costs. This modeling simplification limits the precision of direct policy interpretations and should be borne in mind when extrapolating the findings. These limitations suggest caution in directly translating numerical results into operational planning. Future research should therefore build on this work by explicitly modeling transmission constraints, extending the hydropower representation to multiple reservoirs in cascade, and exploring more detailed cost scenarios. Moreover, the integration of carbon-neutral gases such as biomethane or synthetic methane deserves further investigation as a complement to hydropower in achieving full decarbonization. While these directions are beyond the scope of this study, they remain crucial for advancing the understanding of optimal generation mixes in deeply decarbonized systems.

In conclusion, hydropower remains a cornerstone for future resilient and decarbonized power systems. Planning frameworks should move beyond fixed-capacity assumptions and instead consider flexible hydropower expansion strategies, including peak power optimization, to fully leverage its balancing capabilities.