Influence of Surface Complexity and Atmospheric Stability on Wind Shear and Turbulence in a Peri-Urban Wind Energy Site
Abstract
1. Introduction
2. Data Acquisition and Analysis Methodology
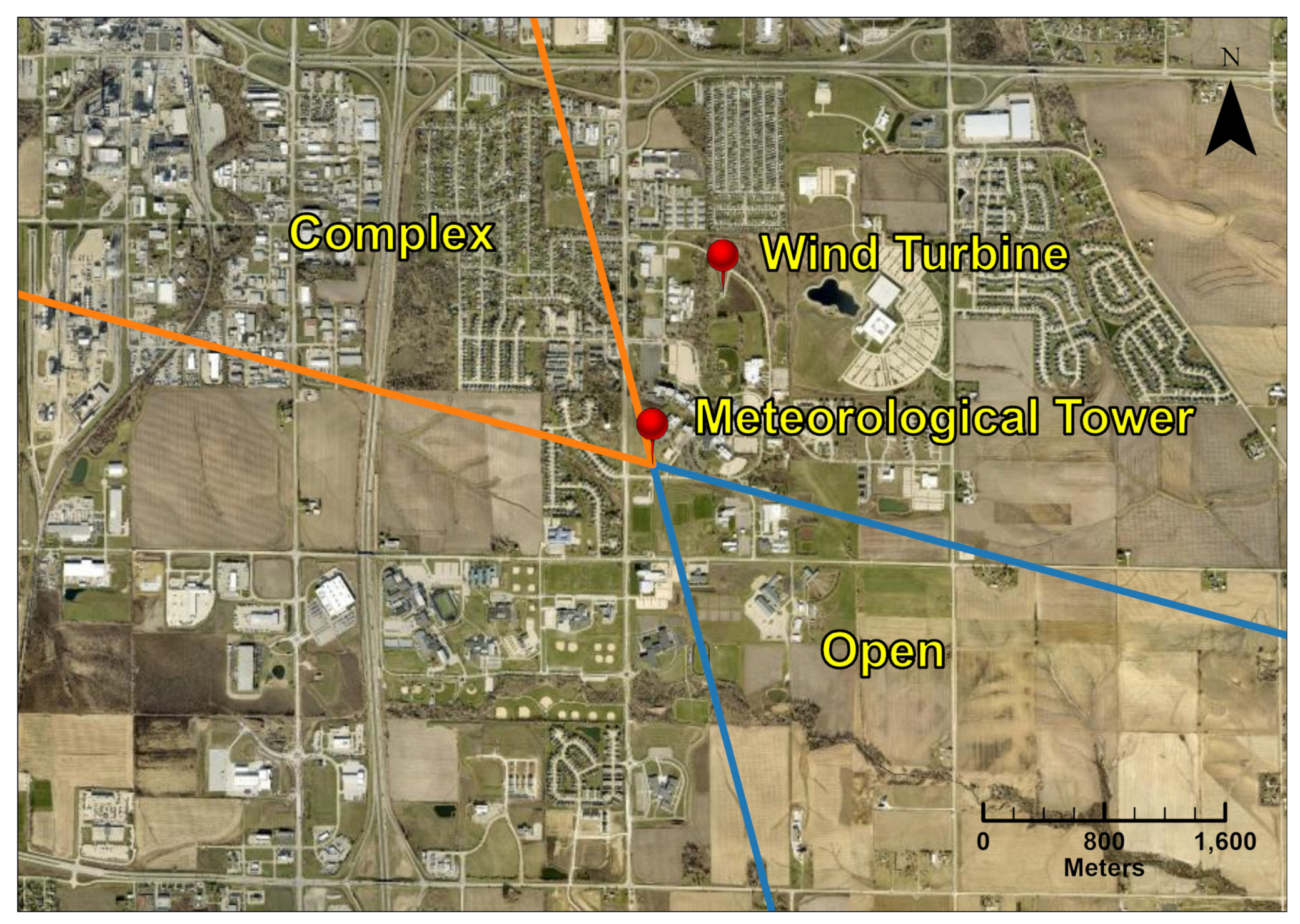
2.1. Field Site, Equipment, and Data Collection
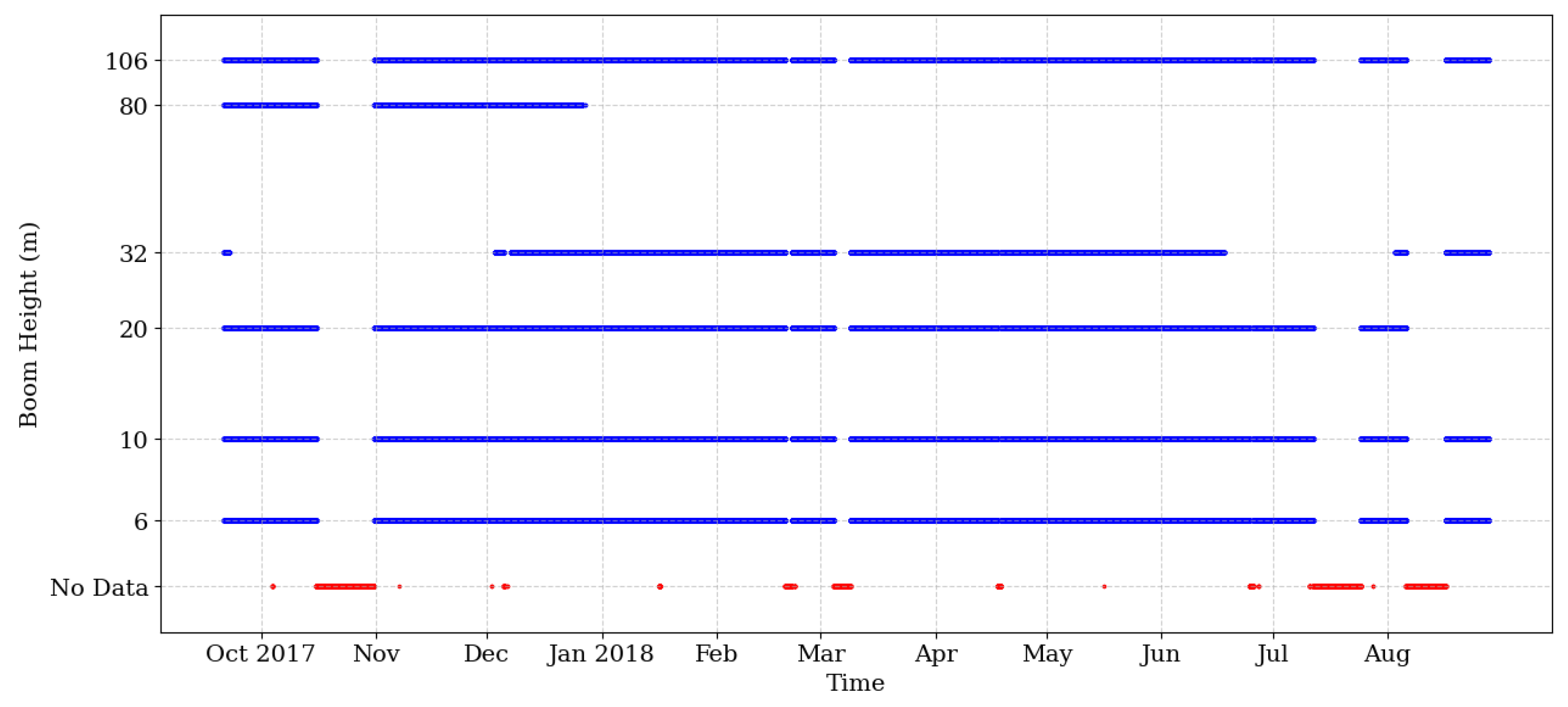
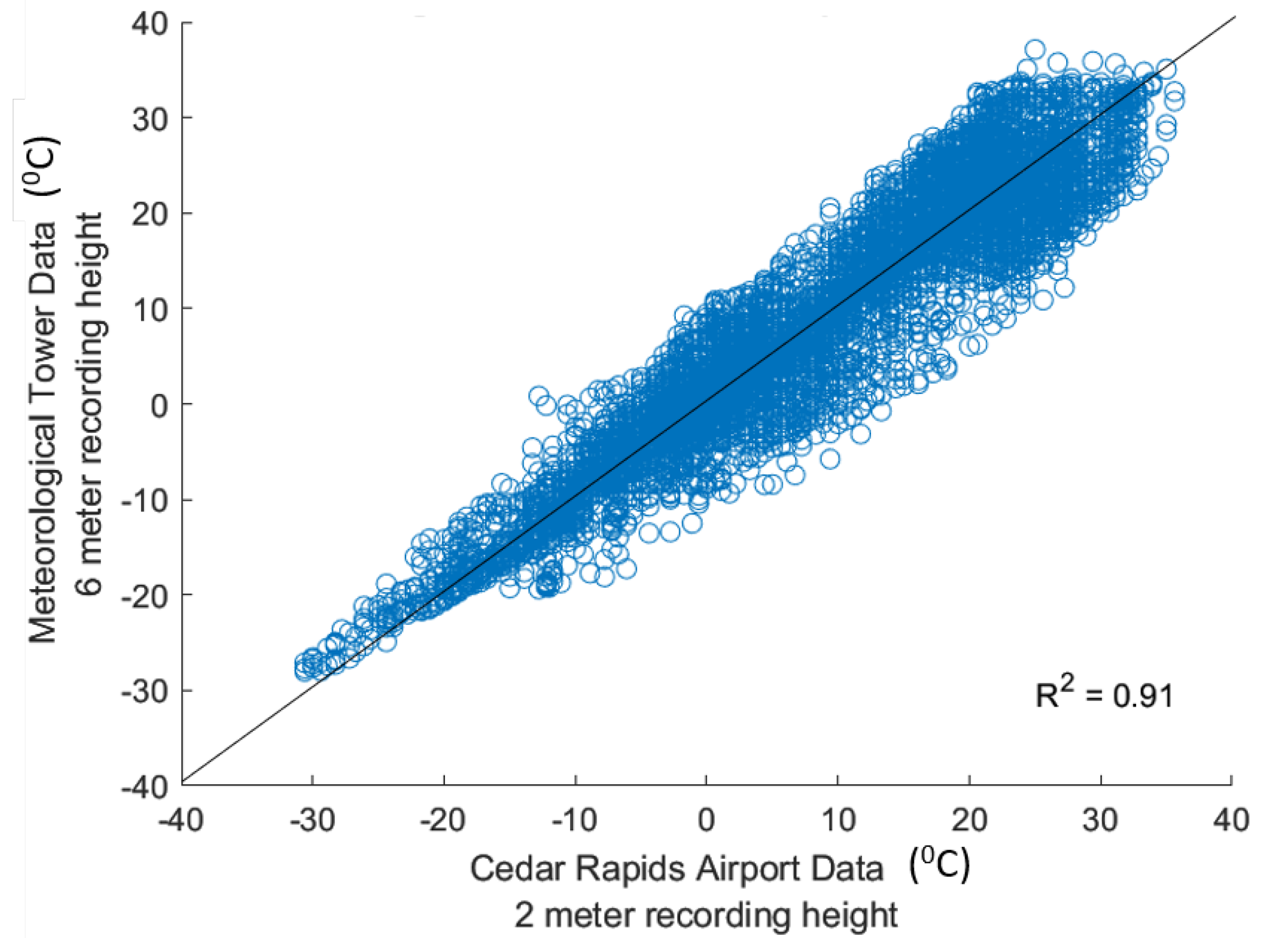
2.2. Data Quality Assessment
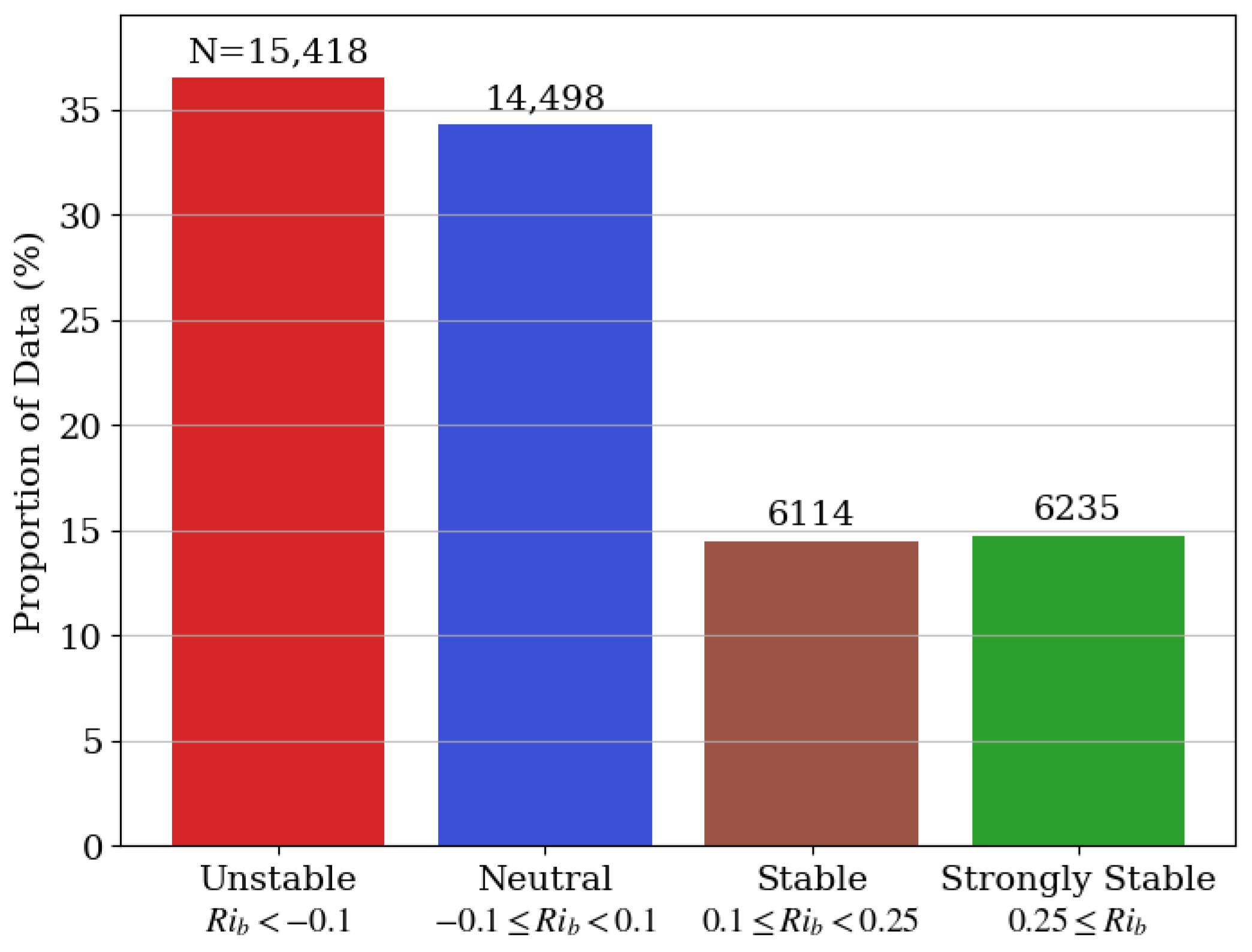
2.3. Classification of Terrain Features and Atmospheric Thermal Stability
2.4. Power-Law Model of Mean Wind Profiles
3. Results and Discussion
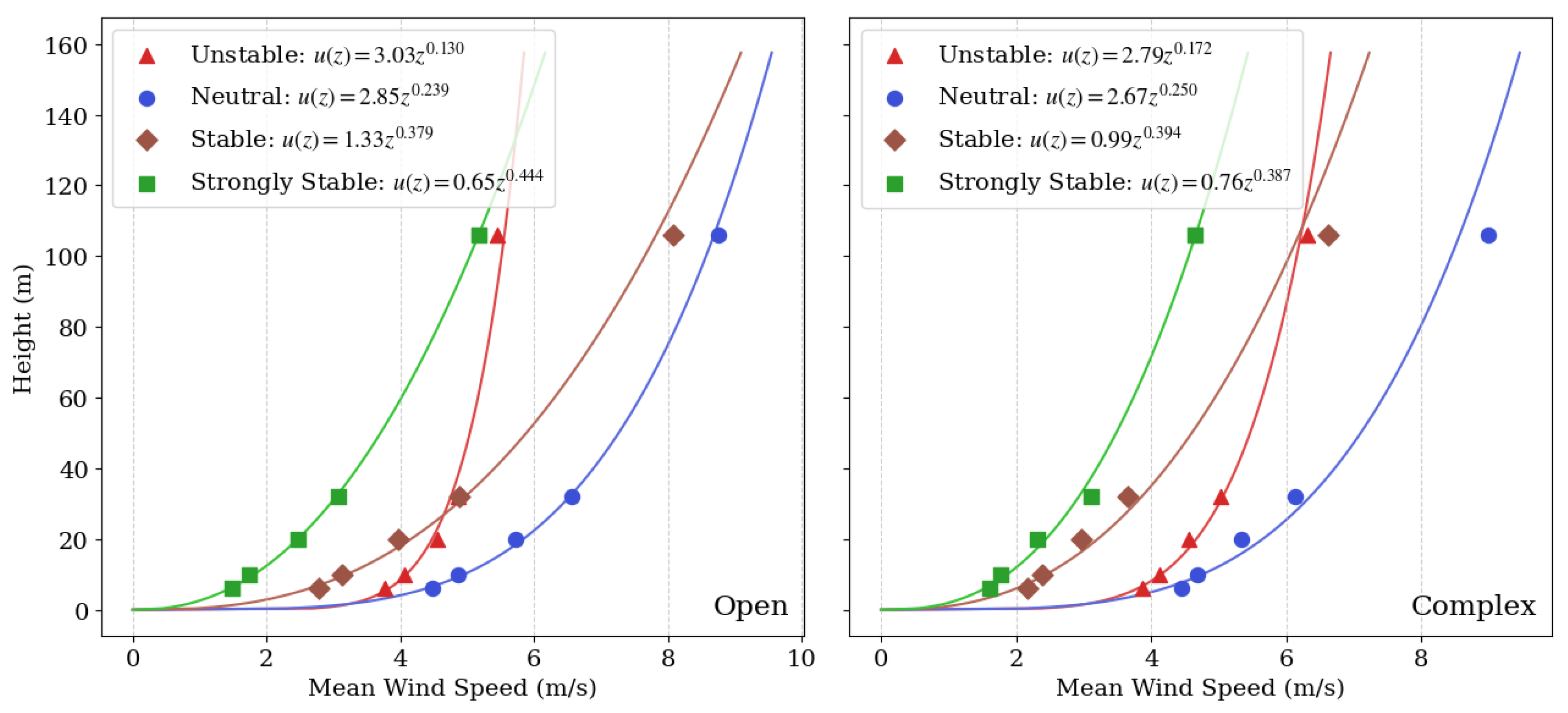
3.1. Variation of Mean Wind Speed Profiles with Height
3.2. Seasonal and Daily Variation of Wind Shear Exponent
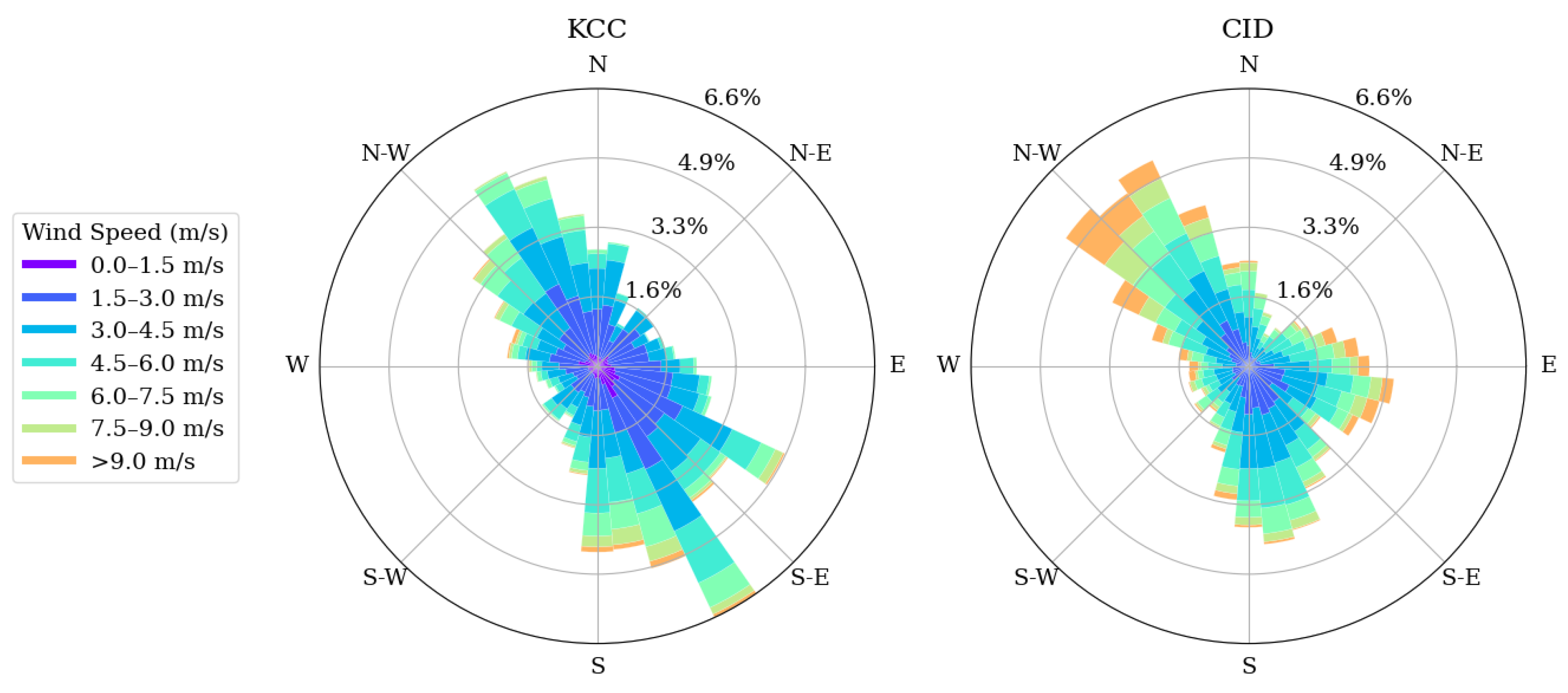
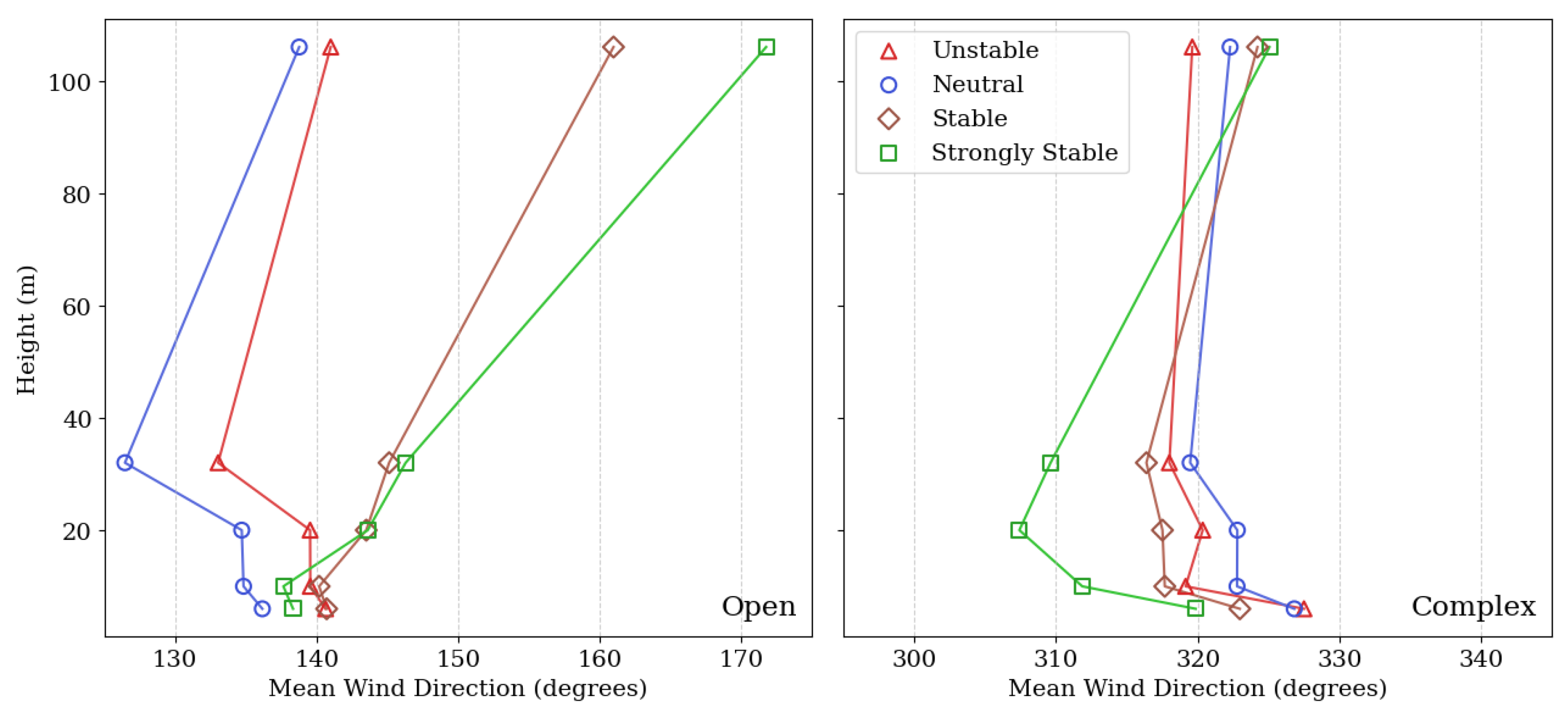
3.3. Variation of Mean Wind Direction with Height
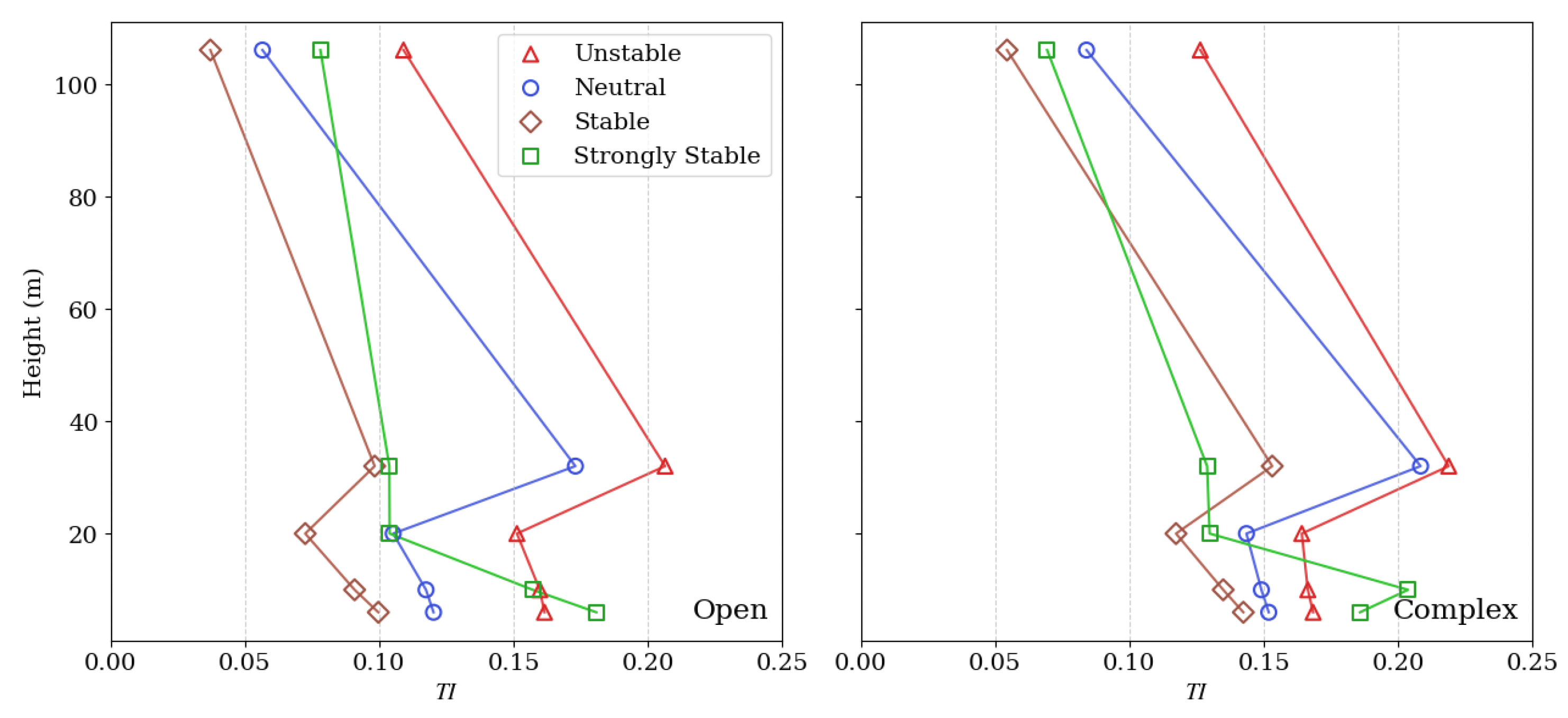
3.4. Variation of Horizontal Wind Turbulence Intensity with Height
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cole, W.J.; Greer, D.; Denholm, P.; Frazier, A.W.; Machen, S.; Mai, T.; Vincent, N.; Baldwin, S.F. Quantifying the challenge of reaching a 100% renewable energy power system for the United States. Joule 2021, 5, 1732–1748. [Google Scholar] [CrossRef]
- Denholm, P.; Arent, D.J.; Baldwin, S.F.; Bilello, D.E.; Brinkman, G.L.; Cochran, J.M.; Cole, W.J.; Frew, B.; Gevorgian, V.; Heeter, J.; et al. The challenges of achieving a 100% renewable electricity system in the United States. Joule 2021, 5, 1331–1352. [Google Scholar] [CrossRef]
- Larson, E. Net-Zero America: Potential Pathways, Infrastructure, and Impacts; Princeton University: Princeton, NJ, USA, 2020. [Google Scholar]
- Banta, R.; Pichugina, Y.; Kelley, N.; Michael Hardesty, R.; Alan Brewer, W. Wind Energy Meteorology: Insight into Wind Properties in the Turbine-Rotor Layer of the Atmosphere from High-Resolution Doppler Lidar. Bull. Am. Meteorol. Soc. 2013, 94, 883–902. [Google Scholar] [CrossRef]
- Dechamps, P. The IEA World Energy Outlook 2022—A brief analysis and implications. Eur. Energy Clim. J. 2023, 11, 100–103. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-farm Flows: A review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Clifton, A.; Barber, S.; Stökl, A.; Frank, H.; Karlsson, T. Research challenges and needs for the deployment of wind energy in hilly and mountainous regions. Wind. Energy Sci. 2022, 7, 2231–2254. [Google Scholar] [CrossRef]
- Zhang, W.; Markfort, C.D.; Porté-Agel, F. Wind-tunnel experiments of turbulent wind fields over a two-dimensional (2d) steep hill: Effects of the stable boundary layer. Bound.-Layer Meteorol. 2023, 188, 441–461. [Google Scholar] [CrossRef]
- Revaz, T.; Porté-Agel, F. Effect of hills on wind turbine flow and power efficiency: A large-eddy simulation study. Phys. Fluids 2024, 36, 95180. [Google Scholar] [CrossRef]
- Markfort, C.D.; Zhang, W.; Porté-Agel, F. Analytical Model for Mean Flow and Fluxes of Momentum and Energy in Very Large Wind Farms. Bound.-Layer Meteorol. 2018, 166, 31–49. [Google Scholar] [CrossRef]
- Riva, A.D.; Hethey, J.; Lüers, S.; Wallasch, A.K.; Rehfeldt, K.; Duffy, A.; Weir, D.E.; Stenkvist, M.; Uihlein, A.; Stehly, T.J.; et al. IEA Wind TCP Task 26—Wind Technology, Cost, and Performance Trends in Denmark, Germany, Ireland, Norway, Sweden, the European Union, and the United States: 2008–2016; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2018. [Google Scholar]
- Bilgili, M.; Alphan, H. Global growth in offshore wind turbine technology. Clean Technol. Environ. Policy 2022, 24, 2215–2227. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Besseau, R.; Jansen, M.; Staffell, I.; Troccoli, A.; Dubus, L.; Schmidt, J.; Gruber, K.; Simões, S.G.; Heier, S. A parametric model for wind turbine power curves incorporating environmental conditions. Renew. Energy 2020, 157, 754–768. [Google Scholar] [CrossRef]
- Vahidzadeh, M.; Markfort, C.D. Modified power curves for prediction of power output of wind farms. Energies 2019, 12, 1805. [Google Scholar] [CrossRef]
- Wagner, R.; Courtney, M.; Gottschall, J.; Lindelöw-Marsden, P. Accounting for the speed shear in wind turbine power performance measurement. Wind Energy 2011, 14, 993–1004. [Google Scholar] [CrossRef]
- Choukulkar, A.; Pichugina, Y.; Clack, C.T.; Calhoun, R.; Banta, R.; Brewer, A.; Hardesty, M. A new formulation for rotor equivalent wind speed for wind resource assessment and wind power forecasting. Wind Energy 2016, 19, 1439–1452. [Google Scholar] [CrossRef]
- Howland, M.F.; Lele, S.K.; Dabiri, J.O. Wind farm power optimization through wake steering. Proc. Natl. Acad. Sci. USA 2019, 116, 14495–14500. [Google Scholar] [CrossRef]
- Kosović, B.; Basu, S.; Berg, J.; Berg, L.K.; Haupt, S.E.; Larsén, X.G.; Peinke, J.; Stevens, R.J.; Veers, P.; Watson, S. Impact of atmospheric turbulence on performance and loads of wind turbines: Knowledge gaps and research challenges. Wind. Energy Sci. Discuss. 2025, 2025, 1–67. [Google Scholar]
- Vahidzadeh, M.; Markfort, C.D. An induction curve model for prediction of power output of wind turbines in complex conditions. Energies 2020, 13, 891. [Google Scholar] [CrossRef]
- Touma, J.S. Dependence of the wind profile power law on stability for various locations. J. Air Pollut. Control. Assoc. 1977, 27, 863–866. [Google Scholar] [CrossRef]
- Fernando, H.J.S. Fluid Dynamics of Urban Atmospheres in Complex Terrain. Annu. Rev. Fluid Mech. 2010, 42, 365–389. [Google Scholar] [CrossRef]
- Kaimal, J.K.; Finnigan, J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Grimmond, C.; Oke, T. Aerodynamic Properties of Urban Areas Derived from Analysis of Surface Form. J. Appl. Meteorol. Climatol. 1999, 38, 1262–1291. [Google Scholar] [CrossRef]
- Giometto, M.G.; Christen, A.; Egli, P.E.; Schmid, M.F.; Tooke, R.T.; Coops, N.C.; Parlange, M.B. Effects of trees on mean wind, turbulence and momentum exchange within and above a real urban environment. Adv. Water Resour. 2017, 106, 154–168. [Google Scholar] [CrossRef]
- Lopez-Villalobos, C.A.; Martinez-Alvarado, O.; Rodriguez-Hernandez, O.; Romero-Centeno, R. Analysis of the influence of the wind speed profile on wind power production. Energy Rep. 2022, 8, 8079–8092. [Google Scholar] [CrossRef]
- IEC 61400-1:2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- IEC 61400-2:2013; Wind Energy Generation Systems—Part 2: Design Requirements for Small Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2013.
- Davenport, A. The Relationship of Wind Structure to Wind Loading. In Proceedings of the National Physical Laboratory, Symposium No. 16, Wind Effects on Buildings and Structures, London, UK, 26–28 June 1963; pp. 54–102. [Google Scholar]
- Drew, D.; Barlow, J.; Cockerill, T. Estimating the potential yield of small wind turbines in urban areas: A case study for Greater London, UK. J. Wind. Eng. Ind. Aerodyn. 2013, 115, 104–111. [Google Scholar] [CrossRef]
- Lange, J.; Mann, J.; Berg, J.; Parvu, D.; Kilpatrick, R.; Costache, A.; Chowdhury, J.; Siddiqui, K.; Hangan, H. For wind turbines in complex terrain, the devil is in the detail. Environ. Res. Lett. 2017, 12, 094020. [Google Scholar] [CrossRef]
- Sathe, A.; Bierbooms, W. Influence of different wind profiles due to varying atmospheric stability on the fatigue life of wind turbines. J. Phys. Conf. Ser. 2007, 75, 12056. [Google Scholar] [CrossRef]
- Honrubia, A.; Vingueras-Rodriguez, A.; Lazaro, E.G.; Rodríguez, D.; Mejias, M.; Lainez, I. The influence of wind shear in wind turbine power estimation. Measurements 2010, 2, 9. [Google Scholar]
- Newman, J.F.; Klein, P.M. The impacts of atmospheric stability on the accuracy of wind speed extrapolation methods. Resources 2014, 3, 81–105. [Google Scholar] [CrossRef]
- Gualtieri, G. Surface turbulence intensity as a predictor of extrapolated wind resource to the turbine hub height. Renew. Energy 2015, 78, 68–81. [Google Scholar] [CrossRef]
- Gualtieri, G. Atmospheric stability varying wind shear coefficients to improve wind resource extrapolation: A temporal analysis. Renew. Energy 2016, 87, 376–390. [Google Scholar] [CrossRef]
- Ahlman, R.M.; Zhang, W.; Markfort, C.D. Effects of terrain and atmospheric thermal stability on wind velocity profiles. In ASTFE Digital Library; Begel House Inc.: Danbury, CT, USA, 2021. [Google Scholar]
- IEC 61400-12-1:2022; Wind Energy Generation Systems—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Albornoz, C.P.; Soberanis, M.E.; Rivera, V.R.; Rivero, M. Review of atmospheric stability estimations for wind power applications. Renew. Sustain. Energy Rev. 2022, 163, 112505. [Google Scholar] [CrossRef]
- Mauritsen, T.; Svensson, G. Observations of stably stratified shear-driven atmospheric turbulence at low and high Richardson numbers. J. Atmos. Sci. 2007, 64, 645–655. [Google Scholar] [CrossRef]
- Murray, F. On the Computation of Saturation Vapor Pressure. J. Appl. Meteorol. 1967, 6, 203–204. [Google Scholar] [CrossRef]
- Gualtieri, G. A comprehensive review on wind resource extrapolation models applied in wind energy. Renew. Sustain. Energy Rev. 2019, 102, 215–233. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Irwin, J. A theortical variation of the wind profile power-law exponent as a function of surface roughness and stability. Atmos. Environ. 1978, 13, 191–194. [Google Scholar] [CrossRef]
- Kelley, C.L.; Ennis, B.L. SWiFT Site Atmospheric Characterization; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2016. [Google Scholar]
- Smith, K.; Randall, G.; Malcom, D.; Kelley, N.; Smith, B. Evaluation of Wind Shear Patterns at Midwest Wind Energy Facilities (NREL/CP-500-32492); American Wind Energy Association (AWEA): Portland, OR, USA, 2002. [Google Scholar]
- Rehman, S.; Al-Abbadi, N.M. Wind shear coefficient, turbulence intensity and wind power potential assessment for Dhulom, Saudi Arabia. Renew. Energy 2008, 33, 2653–2660. [Google Scholar] [CrossRef]
- Clifton, A.; Schreck, S.; Scott, G.; Kelley, N.; Lundquist, J.K. Turbine inflow characterization at the national wind technology center. J. Sol. Energy Eng. 2013, 135, 031017. [Google Scholar] [CrossRef]
- Brock, F.V.; Richardson, S.J. Meteorological Measurement Systems; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Emeis, S. Current issues in wind energy meteorology. Meteorol. Appl. 2014, 21, 803–819. [Google Scholar] [CrossRef]
- Gao, L.; Yang, S.; Abraham, A.; Hong, J. Effects of inflow turbulence on structural response of wind turbine blades. J. Wind. Eng. Ind. Aerodyn. 2020, 199, 104137. [Google Scholar] [CrossRef]
- Träumner, K.; Wieser, A.; Ruck, B.; Frank, C.; Röhner, L.; Kottmeier, C. The suitability of Doppler lidar for characterizing the wind field above forest edges. Forestry 2012, 85, 399–411. [Google Scholar] [CrossRef][Green Version]
- Markfort, C.D.; Porté-Agel, F.; Stefan, H.G. Canopy-wake dynamics and wind sheltering effects on Earth surface fluxes. Environ. Fluid Mech. 2014, 14, 663–697. [Google Scholar] [CrossRef]
- Kanani, F.; Träumner, K.; Ruck, B.; Raasch, S. What determines the differences found in forest edge flow between physical models and atmospheric measurements? An LES study. Meteorol. Z. 2014, 23, 33–49. [Google Scholar] [CrossRef]
- Wang, H.; Takle, E.S.; Shen, J. Shelterbelts and windbreaks: Mathematical modeling and computer simulations of turbulent flows. Annu. Rev. Fluid Mech. 2001, 33, 549–586. [Google Scholar] [CrossRef]
- McClure, S.; Kim, J.J.; Lee, S.J.; Zhang, W. Shelter effects of porous multi-scale fractal fences. J. Wind. Eng. Ind. Aerodyn. 2017, 163, 6–14. [Google Scholar] [CrossRef]
- Peña, A.; Mirocha, J.D. One-year-long turbulence measurements and modeling using large-eddy simulation domains in the Weather Research and Forecasting model. Appl. Energy 2024, 363, 123069. [Google Scholar] [CrossRef]





| Sensor | Make/Model | Quantity | Heights (m) | Sampling Rate (Hz) |
|---|---|---|---|---|
| Barometric Pressure | Setra 278 | 2 | 6, 106 | 1 |
| Temperature Sensor | NRG 110S | 2 | 6, 20 | 1 |
| Wind Vane | NRG 200P | 7 | 6, 10, 20, 32, 80, 106 | 1 |
| Cup Anemometer | A100LK | 7 | 6, 10, 20, 32, 80, 106 | 1 |
| Temp./RH Sensor | Vaisala-HMP 155 | 4 | 10, 32, 80, 106 | 1 |
| Sonic Anemometer | Campbell Scientific-CSAT3B | 4 | 10, 32, 80, 106 | 20 |
| Case | Unstable | Neutral | Stable | Strongly Stable | ||||
|---|---|---|---|---|---|---|---|---|
| Open | Complex | Open | Complex | Open | Complex | Open | Complex | |
| Median value of (Figure 10) | 0.11 | 0.17 | 0.24 | 0.25 | 0.39 | 0.40 | 0.45 | 0.39 |
| Mean value of (Figure 10) | 0.12 | 0.17 | 0.25 | 0.26 | 0.40 | 0.41 | 0.45 | 0.41 |
| (mean profiles in Figure 9) | 0.13 | 0.17 | 0.24 | 0.25 | 0.38 | 0.39 | 0.44 | 0.39 |
| (Oklahoma Mesonet, [35]) | 0.09 | – | 0.13 | – | 0.28 | – | 0.39 | – |
| (tall tower, [35]) | 0.08 | – | 0.16 | – | 0.26 | – | 0.28 | – |
| (TTU 200 m tower, [46]) | 0.05 | – | 0.125 | – | 0.3 | – | – | – |
| Median | −1.01 | −0.38 | 0.00 | −0.02 | 0.17 | 0.16 | 0.48 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Walker, E.; Markfort, C.D. Influence of Surface Complexity and Atmospheric Stability on Wind Shear and Turbulence in a Peri-Urban Wind Energy Site. Energies 2025, 18, 5211. https://doi.org/10.3390/en18195211
Zhang W, Walker E, Markfort CD. Influence of Surface Complexity and Atmospheric Stability on Wind Shear and Turbulence in a Peri-Urban Wind Energy Site. Energies. 2025; 18(19):5211. https://doi.org/10.3390/en18195211
Chicago/Turabian StyleZhang, Wei, Elliott Walker, and Corey D. Markfort. 2025. "Influence of Surface Complexity and Atmospheric Stability on Wind Shear and Turbulence in a Peri-Urban Wind Energy Site" Energies 18, no. 19: 5211. https://doi.org/10.3390/en18195211
APA StyleZhang, W., Walker, E., & Markfort, C. D. (2025). Influence of Surface Complexity and Atmospheric Stability on Wind Shear and Turbulence in a Peri-Urban Wind Energy Site. Energies, 18(19), 5211. https://doi.org/10.3390/en18195211







