Abstract
At the international level, new measures, policies, and technologies are being developed to reduce greenhouse gas emissions and, more broadly, air pollutants. Road transportation is one of the main contributors to such emissions, as vehicles are extensively used in logistics operations, and many fleet owners of fossil-fueled trucks are adopting new technologies such as electric, hybrid, and hydrogen-based vehicles. This paper addresses the Hybrid Fleet Capacitated Vehicle Routing Problem with Time Windows (HF-CVRPTW), with the objectives of minimizing costs and mitigating environmental impacts. A mixed-integer linear programming model is developed, incorporating split deliveries, scheduled arrival times at stores, and a carbon cap-and-trade mechanism. The model is tested on a real case study provided by Decathlon, evaluating the performance of internal combustion engine (ICE), electric (EV), and hydrogen fuel cell (HV) vehicles. Results show that when considering economic and emission trading costs, the optimal fleet deployment priority is to use ICE vehicles first, followed by EVs and then HVs, but considering only total emissions, the result is the reverse. Further analysis explores the conditions under which alternative fuel, electricity, or hydrogen prices can achieve competitiveness, and a further analysis investigates the impact of different electricity generation and hydrogen production pathways on overall indirect emissions.
1. Introduction
With the increasing adoption of electric and hydrogen-powered vehicles in the logistics and transportation sectors, companies worldwide are reevaluating the efficiency and suitability of these alternative fleets. The following question arises: which type of fleet (electric, hydrogen, or diesel) is the most effective, particularly when considering economic, environmental, and social factors? The production and deployment of vehicles with new propulsion technologies are expanding in the industry and logistics companies must carefully weigh the benefits of each technology for their distribution networks. To address this question, two critical criteria (cost efficiency and environmental impact) are consistently considered when evaluating fleet composition for industrial distribution. For this reason a pricing method has been proposed not only to consider the transportation cost but also to take into account green factors in the supply chain using the carbon cap-and-trade mechanism [1]. Figure 1 represents all costs related to a mixed fleet. Different types of vehicles have been considered in this work, and, in order to calculate costs and emissions, it is necessary to quantify the energy consumptions and the resources (power, hydrogen, fuel) required to cover them. Then, costs and emissions to provide such resources should be calculated. The result is that energy consumptions, costs, and emissions are functions of the decision variables (routing, kind of vehicle selected, mass, etc.).

Figure 1.
Hybrid fleet transportation cost breakdown.
In this work, carbon trade emission cost represents a significant part of the overall cost. The emission trading scheme (ETS) operates on two main concepts: allowances and the cap-and-trade system. An allowance grants the right to emit a specific amount of greenhouse gases (GHGs), typically measured as 1 ton of CO2 equivalent (tCO2e), during a certain period. Governments set a cap on total emissions, and companies emitting below their cap earn tradable carbon credits. Companies exceeding the cap must purchase these credits or face penalties. Global examples of ETS include the EU ETS (the largest system), the NZ ETS, the Chicago Climate Exchange, and the Montreal Climate Exchange. The cap-and-trade system encourages businesses to choose between reducing emissions (through supply chain changes) or buying credits. Emission reductions can occur at various supply chain stages, including product design, manufacturing, transportation, and recycling. A structured decision-making approach is essential for cost-effective and sustainable supply chain management while meeting GHG targets [2].
On the other hand, as shown in Figure 1, another category of cost in this study is the transportation cost. This includes expenses related to fuel/energy consumption, depreciation, maintenance, and driver wages for different paths in the distribution system. In particular, fuel consumption depends on various factors, such as the characteristics of the paths/routes, which are similar for all hybrid fleets. In addition, there are factors specific to different vehicle types that vary based on powertrain configurations as well as differences in size and capacity within each category [3].
In this paper, a mathematical optimization problem is proposed, based on a real-world case, to minimize the total distribution cost from the last warehouse to a group of stores pre-assigned to the warehouse. Key features, such as split delivery and scheduling arrival times within specific time windows for each store, are incorporated into the mathematical formulation. The costs addressed in the problem include total transportation costs and CO2 emission trade costs, calculated using a carbon cap-and-trade mechanism. Energy and fuel consumption, as well as carbon emissions, are computed for different vehicle types (internal combustion engine vehicles (ICEs) and, in particular for the case study, diesel engine vehicles (DVs), electric vehicles (EVs), and hydrogen vehicles (HVs)). For each class of vehicles, the costs are considered separately. The mathematical model is implemented for a real case, and the results demonstrate the percentage usage of each fleet type, highlighting the trade-off between transportation and emission costs. These findings are analyzed, and managerial insights derived from the results are discussed. The contribution highlights of the current paper could be listed as the following:
- Development of a mixed-integer linear programming (MILP) model for the Hybrid Fleet Vehicle Routing Problem with Time Windows (HF-VRPTW), incorporating constraints on arrival times and split delivery for stores.
- Integration of carbon cap-and-trade emissions into the model and comparison with other transportation cost components.
- Proposal of a pricing formula for internal combustion engine vehicles (ICEs), electric vehicles (EVs), and hydrogen vehicles (HVs), considering energy and fuel consumption factors.
- Implementation and validation of the mathematical model through a real-world case study, analyzing the daily distribution system of a company (Decathlon).
The remainder of this paper is organized as follows. Section 2 reviews the scientific literature, focusing on studies from the last decade. Section 3 presents the details and the methods for calculating energy consumption and consequently, the CO2 emission and fuel consumption for hybrid fleets. Section 4 presents the problem definition, including all assumptions, emission trading costs, and transportation costs, and then proposes a mathematical model based on a real-world case. Section 5 addresses a real-world case study, incorporating all relevant features and a hybrid fleet for a company’s distribution problem. This section also provides an analysis of the results obtained for case study. Section 6 concludes the paper by summarizing the results and providing managerial insights into the problem and its outcomes.
2. Literature Review
Recent advancements in vehicle routing problem (VRP) research have increasingly focused on integrating environmental and operational efficiency goals, particularly in the context of electric vehicles (EVs) and low-carbon logistics. Reference [4] proposed a VRP model that incorporates dynamic traffic data to minimize carbon emissions while meeting time-sensitive customer demands. Similarly, ref. [5] addressed the challenges of EV-specific constraints, such as range limitations and speed-dependent energy consumption, by integrating en route partial recharging to optimize delivery efficiency. Reference [6] introduced a green VRP model incorporating flexible delivery time windows to reduce travel costs, enhance EV adoption, and improve customer satisfaction, while ref. [7] tackled EV routing in cold chain logistics by balancing operational costs and environmental impacts. Other studies have explored novel dimensions, such as ref. [8]’s inclusion of two-dimensional loading constraints to optimize emissions and loading feasibility, and ref. [9]’s multi-objective EVRP, which balances economic, environmental, and social sustainability goals. Reference [10] in 2025 addressed the three-dimensional loading-capacitated vehicle routing problem (3L-CVRP) by combining vehicle routing and container loading. The study focuses on relocation-ban constraints, which prohibit the repositioning of items during transport. Another paper in 2025 [11] addresses a gap in the existing research by incorporating truck platooning technology into the capacitated vehicle routing problem with time windows (CVRPTW). The objective of their model is to minimize total operational costs, including fixed dispatch and energy costs, while satisfying all delivery time windows.
The diversification of VRP research extends to hybrid fleet scenarios and real-world complexities. For instance, ref. [12] optimized multi-depot green VRP by prioritizing customer satisfaction alongside environmental goals. Reference [13] explored routing for mixed EV and internal combustion engine fleets, focusing on capacity constraints and delivery efficiency. Meanwhile, studies by [14,15] addressed the economic and environmental viability of EVs and the integration of advanced charging technologies. Methodological innovations, such as ref. [16]’s matheuristic approach to solving EVRPTW with time-dependent energy costs, and ref. [17]’s inclusion of payload and speed impacts, highlight the growing sophistication of EVRP models. Additionally, refs. [18,19] emphasized practical constraints, including depot-based recharging infrastructure and hybrid vehicle drive modes, while ref. [20] examined capacitated charging stations with nonlinear constraints. Together, these contributions underscore the field’s commitment to addressing the dual imperatives of sustainability and operational effectiveness in modern logistics.
There are also investigations about the HVs, which are mainly about HVs that use hydrogen as a fuel for internal combustion vehicles, and they try to consider the siting and allocation of the refuel station. An example is provided by [21] where the authors develop a genetic algorithm to solve a VRPTW by considering these kind of HVs. However, since this paper focuses only on hydrogen fuel cell vehicles, from now on the term HVs will only refer to those equipped with fuel cells.
While the VRP is well known, there are not many studies on HVs, especially in the optimal routing framework. One of the papers that consider routing of the HVs is ref. [22], which addresses HVs routing with unmanned aerial vehicles (UAVs) for delivery and pickup services while considering variable drone speeds and customer time windows. The primary objective is to minimize both total cost and makespan by optimizing vehicle–drone coordination, UAV speed adjustments, and time-dependent routing constraints. A new variant of the VRP with drones is introduced, integrating time-dependent HVs speeds, UAV pickup and delivery, and energy consumption dynamics. A mixed-integer programming (MIP) model is formulated to minimize total cost and makespan while ensuring feasibility in large-scale instances and for solving the MIP model the study proposes a multi-objective optimization method based on the Non-Dominated Sorting Genetic Algorithm III with Intelligent Selection (NSGA-III-IS). Instead, authors in [23] present a comprehensive model that integrates hydrogen supply chain logistics with energy system operations, considering factors such as renewable energy availability, hydrogen production, storage, and transportation costs. The study employs a mixed-integer optimization framework to balance economic efficiency and environmental sustainability. However, the emissions for the HVs are modeled as only proportional to the distance and the case study is relatively small.
In order to better categorize and understand the three fleet types considered in this paper, Table 1 is provided, which shows the advantages and disadvantages of different propulsion systems inspired by [24]. Table 1 categorizes the advantages and disadvantages of ICEs, EVs, and HVs across three main aspects: economical, functional, and environmental. Each aspect highlights merits or drawbacks observable for each fleet type.

Table 1.
Merits and drawbacks of the DVs, EVs, and HVs.
Table 2 shows the comparison between the current work and the recent literature. In the taxonomy table, the main focus was on recent papers, mainly after 2022, aiming to compare the current paper with other research in terms of features such as types of decisions made, fleet type and capacity, objectives to be satisfied, solution methods, mathematical model approaches, and some vehicle routing and emission features. This comparison aims to highlight the differences and advantages of the current study compared to others.

Table 2.
Literature review of the last decade on VRP, E-VRP, and HF-VRP.
3. Energy and Fuel Consumption and Emission Calculation of Hybrid Fleet
In this section, the energy required for a certain vehicle (over the logistic network) and the emissions are calculated on the basis of the kind of vehicle (ICEs, EVs, and HVs). These calculations are fundamental to define the optimal routing on the basis of costs and emissions and considering the driving range for each vehicle. In particular, for the case of EVs, the energy consumption is calculated for each link of the network as a function of the specific road and vehicle characteristics; of course, the consumption for the overall route should not exceed the available energy. Moreover, the overall energy consumption is taken from the electrical grid and this implies costs and emissions (in this case, emissions are dependent on the energy mix of the energy production in the considered electrical grid). Similarly, for hydrogen-based vehicles, it is necessary to calculate the power that should be used to feed an electrolyzer to produce the hydrogen required by the vehicle’ s fuel cell. This should be differentiated for each link in the network and each kind of vehicle. For ICEs, energy consumption and emissions are calculated based on fuel consumption per unit distance. Several factors influence this calculation, including vehicle type and efficiency, road characteristics, and emission factors that are to be discussed in the following parts.
3.1. Internal Combustion Engine (ICE)
3.1.1. ICE Energy Consumption
In this section a method based on [27,28] is proposed to calculate the amount of energy consumption and its correlated fuel consumption of ICE vehicles, which could be considered a transportation mean for the current model and distribution system (see (1)). This method computes the total energy consumption represented by [kWh] on arc (i,j), based on a vehicle-specific constant for consumption of ICE truck v on arc (i,j) and an arc-specific (route-specific) constant for ICE truck v consumption on arc (i,j), denoted as [kWh/m] and [kWh/kg∙m], respectively. The first coefficient relates the consumption to the kind of vehicles and to the specific features of the link. The second coefficient takes also into account the weight of the vehicle and of the transported load. More specifically, to calculate (Equation (2)), the following information is considered: the speed of a vehicle over arc as [m/s] (considered independent from the type of the vehicle), the frontal surface area of vehicle v, namely [m2], the coefficient of drag for vehicle v, namely , the air density [kg/m3], and [kWh] that represents the internal power consumption (like air conditioner consumption) of the vehicle v. In order to compute (Equation (3)), some different aspects are considered in which represents the acceleration of the vehicle [m/s2], , and are gravity constant [m/s2], the coefficient of rolling resistance for vehicle v, and the angle of the mean slope of the arc (i,j), respectively. The total weight of a truck in each arc (i,j) must be taken into account to compute the total energy consumed. This weight is given by , where is the weight of the empty truck v [kg] and is the weight of an standard pallet [kg] that could be multiplied by the number of pallets carried out by the vehicle on the considered link (actually, this is one of the main decision variables of the problem, as we will see later).
3.1.2. ICEs Fuel Consumption and Emission
To transform the amount of energy consumption into the amount of fuel consumption denoted as [kg], we apply a simple conversion rule represented by Equation (4). In this equation, [kWh/kg] represents the lower heating value of the fuel used by ICE vehicles and is the overall operating efficiency of the ICE fleet. To derive the amount of emission, represented by [kgCO2], a coefficient of the unit carbon emission of ICE vehicles is needed, denoted as [kg/kW]. By multiplying the amount of energy consumption times the unit of carbon emission over energy consumption, as shown in Equation (5), the CO2 emission of the ICE vehicles can be computed.
3.2. Electric Vehicle
The electricity consumption over a path for electric vehicles depends on the characteristics of the vehicle and the path. Emissions are calculated on the basis of the energy mix that characterizes the electrical grid that feeds the charging stations. To quantify consumptions, it is necessary to define the following parameters and insert them in the overall optimization problem:
- Distance between nodes [m].
- Travel time between the nodes [s].
- The velocity of the EVs [km/h].
- The total weight of truck v, including the curb mass of the truck v, [kg] and the load of the truck ( is the number of pallets and is the average weight of one pallet [kg]).
- The slope of the arc (the gradient of the terrain).
- The efficiency coefficients related to the various energy conversions: the electric vehicles transmission efficiency , the electrical motor efficiency , and the power converter efficiency of each vehicle .
- The regenerative braking power coefficient for each vehicle .
The energy consumption [kWh] can be calculated on the basis of models already introduced in the literature [3,29] as follows:
Equation (6) represents the consumption of EVs over arc (i,j), [kW] is the baseline electricity consumption coefficient for truck v on arc (i,j), which is a function of drag for vehicle v and as the air density [kg/m3], and as the frontal surface area of vehicle v [m2]. represents the internal power consumption of the vehicle v. Equation (8) represents the coefficient for electricity consumption relative to the mass of the cargo on arc (i,j) as [kW/kg]. For each arc in the graph, the terrain’s gradient can be divided into two components, denoted as represents the portion that contributes to recharging the vehicle’s battery when traveling along the arc, while accounts for the portion that causes the battery to discharge ( and ). K and g in Equation (8) are the regenerative braking power coefficient for each vehicle v and the gravity constant [m/s2], respectively.
To compute the amount of emission [kgCO2] incurred by the charging the EVs (located the depot), Equation (9) is used in which [kg/kWh] is the CO2 emission factor of EVs.
3.3. Hydrogen Vehicle
The aim of this section is to compute the energy and hydrogen consumption of the hydrogen fleet. To better understand the function of HVs a brief description of these type of vehicles is presented. Figure 2 depicts the standard configuration of the powertrain in a fuel cell-powered heavy-duty truck. The design exhibits numerous similarities with battery electric vehicles (BEVs). Concerning the propulsion system, the electric motor/generator is directly coupled to the truck chassis via a direct-drive transmission, a differential, and the wheels of the driven axle. The main advantage of this configuration is the possibility of eliminating the conventional multi-speed gearbox, simplifying the vehicle’s drivetrain and enhancing its overall efficiency by minimizing mechanical losses. Moreover, the electric motor enables bidirectional operation, functioning as both a propulsion unit and a generator for regenerative braking, thereby enhancing energy efficiency. The energy storage and generation subsystem comprise a high-voltage battery pack, a fuel cell system, and a hydrogen tank. The battery serves as an energy storage, providing a reserve capacity to take care of sudden power demands or fluctuations, typical of acceleration or regenerative braking. On the hydrogen side, the fuel cell is responsible for converting the hydrogen stored in the tank into electrical energy, offering high energy density and rapid refueling capabilities in comparison to traditional batteries. The hydrogen storage system ensures that there is sufficient onboard energy capacity to support extended driving ranges, which is a key requirement for heavy-duty trucking. The fuel cell system, high-voltage battery pack, and electric motor are interconnected through advanced power electronics, responsible for managing energy flow and conversion, ensuring optimal performance and reliability [30,31].

Figure 2.
The standard configuration of the powertrain in a fuel cell-powered vehicle.
The method of energy consumption of HVs is the same as EVs with different parameter values specified for the HVs. [kWh] represents the total energy consumed by using HV v on are (i,j) in Equation (10) where terms [kW] and [kW/kg] are computed as in Equations (11) and (12), respectively. Since the configuration of fuel cell electric vehicle (FCEV) drivetrain or HVs are the same as EVs, the method computing the energy consumption are similar as well [32].
Knowing that for computing the cost caused hydrogen consumption on hydrogen fleet the amount of hydrogen is needed as well. In order to convert the energy to H2 and compute the total H2 consumption ( [kg]), the lower heating value of the hydrogen fleet [kWh/kg] and the overall operating efficiency of the hydrogen fleet must be used in relationship (13), which provides the H2 consumption in Formula (13) [33]. To produce H2 for the HVs, there are different methods such as the gasification of coals, grid-powered electrolysis, biomass gasification, hydro-powered electrolysis, nuclear-powered electrolysis solar-powered electrolysis, steam reforming of natural gas, and wind-powered electrolysis [34]. All these methods are based on processes that give rise to CO2 emission. To compute the total CO2 emission incurred by using HVs, Equation (14) can be used, in which [kgCO2/kWh] is the coefficient that provides the CO2 emission per unit of energy.
4. Problem Definition
The decision problem is related to the delivery of products from a warehouse or a Distribution Center (DC) to several stores, which are spread over many cities. In particular, it is necessary to define the optimal routes for each vehicle to deliver the products. The considered system is a portion of the overall supply chain of a distribution company, and the association of stores to DCs is considered as given. This means that, if there are various DCs, they correspond to separate problems, each of which must be solved independently from the others.
Any DC receives a set of orders from the (associated) stores on a daily basis. Each order includes the following information: name and position of the stores, a volume of aggregate demand, a deadline by which the demand has to be fulfilled, and a time window for delivery. Each store can order once for each day, but it is possible to satisfy the orders of a single store by more than one visit, when the volume to deliver (i.e., the number of pallets) exceeds the capacity of a single truck. In addition, it may be convenient to split the delivery to a single store by using different trucks, in order to optimize the exploitation of the truck fleet. In any case, the possibility of split deliveries is one of the main features of the considered model. When a split delivery occurs, for a certain store, it is necessary to take into account that this store cannot host more than one truck at the same time. To ensure that this condition is fulfilled, the arrival times of the different trucks arriving at the same store must be scheduled so that the time interval between an arrival time and the subsequent one is greater than or equal to the time interval needed for the first truck unloading.
In the proposed model, despite the demand relevant to a certain store may refer to different classes of products, it is considered as a volume of a single category of items (pallets), each of which has a standard volume.
The deliveries must be accomplished by means of a fleet consisting of trucks belonging to a given set of categories. Each category has (given) specific features, such as propulsion mechanism (ICE, EVs, and HVs), capacity, consumption rate, and emission rate. In the case of using EVs and HVs, we must consider that the total consumption within a given route cannot exceed the capacity of the batteries of the trucks. Some limitations may exist in the association of truck categories to stores, since some stores may be accessible only by some categories of trucks. The number of available trucks, for each category, is considered limited. The duration of truck unload times at each store is univocally determined on the basis of the volume (i.e., the number of pallets) to be unloaded and the kind of the truck. Each truck to which a set of deliveries is assigned for the considered day departs from a DC and ends the trip at the last customer visited in the route. The last store to visit is the final node of the problem because after all deliveries of a day, vehicles are assigned to some other missions, which are totally outside the current problem and thus can be neglected in this model.
The delivery service of a truck within a single day has a maximum duration, different for each category of trucks. The duration of a delivery service (movements + unload operations), hereinafter denoted as a route, can be determined on the basis of the set of stores to be served within the route and the category of truck involved. Then, the problem to be solved is that of determining the set of routes that minimize the overall cost (Section 3.1) to be paid in the considered day, fulfilling completely the demand and the various constraints above mentioned. It should be mentioned that the proportion of vehicle types is not restricted and traffic congestion is neglected in the current model.
Before going through the details of the mathematical model of the described problem, Table 3 provides definitions for various notations, encompassing sets, parameters (representing input and known information), and decision variables (to be determined by solving the optimization problem).

Table 3.
Sets, parameters, and decision variables.
4.1. The Overall Cost Function
The optimization problem considered in this paper is a cost that results from the sum of transportation costs and costs related to CO2 emission trade on the carbon market. In the following subsections, the transportation and emissions costs are detailed separately.
4.1.1. Transportation Cost
The transportation cost depends on a variety of factors, including fuel or energy consumption for each type of vehicle, driver wages, depreciation costs over a specific time horizon, and maintenance costs. These costs vary depending on the type of vehicle, particularly in terms of powertrain, and also may differ across a heterogeneous fleet with varying capacities and sizes. These factors are linearly related to two key elements: the travel time between nodes and the distance between nodes. For instance, driver wages are influenced by both driving and stoppage hours, whereas maintenance costs are primarily affected by the distance traveled. The depreciation of each vehicle is to be calculated for each kilometer of traveling. The fuel consumption here proposed is based on the distance for the ICE fleet and, differently, on the travel time of the routes for EVs and HVs fleet. Considering the issues that have been mentioned, the following Equation (15) shows the total transportation cost, whereas Equations (16)–(18) provide the considered model to express the transportation costs for each of the three fleets considered. All notations have been introduced in Table 3.
4.1.2. Emission Trade Cost (Carbon Cap-and-Trade Mechanism)
In this paper, the cost associated with CO2 emissions is evaluated by using the cap-and-trade mechanism. In this case, the cap-and-trade system sets a limit (cap) on greenhouse gas emissions, allowing companies to either reduce their emissions or purchase tradable carbon credits from others who emit less, incentivizing cost-effective emission reductions. On this basis, Equation (19) is used to evaluate the carbon cap-and-trade emission. In (19), if total emissions exceed the specified capacity of the emitter, a positive value is yielded, which is added to the transportation cost. Conversely, if the emitter produces less CO2 than the pre-assigned capacity, (19) yields a negative value, allowing the remaining capacity to offset transportation costs based on the carbon price in the market. In the carbon cap and trade mechanism, the fluctuating market price of carbon plays an important role. In the same situation, if the carbon unit price is high, companies try not to exceed their emission limits. They may have to transform their fleet to a green one or restrict their production, delivery, and market because the trade-off between production and emissions costs makes them limit their production. Depending on the case, the varying carbon price can produce different results, such as the selection of different fleet types and sizes, as well as different routes derived from the model of this paper. To better understand the total emission separately, the components of the total emission are shown in Equation (20). Then the detailed emission computation based on the energy consumption is showed in Equations (21)–(23) for ICEs, EVs, and HVs, respectively.
Considering the transportation cost in Section 3.1.1 and also the cost caused by carbon emission trade using cap-and-trade mechanism (Section 3.1.2) the total cost could be calculated as Equation (24). A detailed breakdown of the total cost incorporating all factors of pricing is presented in above formulas.
It must be noted that in some terms of the overall cost function a multiplication of decision variables takes place, giving rise to a nonlinearity that will be discussed in the following subsection.
4.2. Mixed Integer Linear Mathematical Model
This section outlines the overall optimization model, the structure of which is derived from [35]. Before introducing the mathematical model, it is necessary to highlight the nonlinearity previously mentioned nonlinearity and to see how this issue can be treated.
Referring to components (21), (22), (23) of the cost functions, we can see a multiplication of the binary decision variables (defining the routes) and the continuous variables (identifying the load of the trucks traveling on the arcs). The nonlinear terms can be linearized before solving the problem. The process of linearization consists of introducing an auxiliary variable in the model. Wherever appears, it can be replaced by the auxiliary variable . Additionally, two extra constraints, Equations (38) and (39), must be added. Equation (38) prevents any artificial inflation of beyond . Equation (39), a big M constraint, is used for linearization to enforce dependencies between decision variables and ensures that can take the value of only when the corresponding binary variable is active . The mentioned procedure transforms the nonlinear relationships into a linear form. After the linearization, the resulting mixed integer linear model for the capacitated vehicle routing problem is the following:
s.t.
The total cost including the transportation economic cost and carbon emission trade cost caused by the trade-off between the total carbon capacity to consume and the actual carbon to be emitted is minimized in (25). Constraints (26) ensure that each trip must initiate from the DC node. To force the demand satisfaction, Constraints (27) guarantee that every customer must be visited at least once, due to the possibility of split delivery. Constraints (28) define an upper bound for the total product volume carried, ensuring it does not exceed the capacity of each truck. Constraints (29) balance the inflow and outflow of the total product to be carried by each truck at customer node j. Considering the demand of the customers, Equation (30) manages flow conservation constraints by taking into account the load of the truck that must be transferred between nodes. At customer nodes, the inflow and outflow of trucks are handled by constraint (31). Constraints (32)–(34) manage the arrivals in the specified time windows for each customer. If split delivery would be needed for a customer, Constraints (35)–(37) schedule non-simultaneous truck permanence by considering at least unloading time as the difference between two arrival times. Constraints (38) and (39) are used for linearization of the model. Constraints (40) and (41) guarantee that if an electric or hydrogen vehicle is chosen for delivery, the energy consumption of the total path for delivery must be less than the capacity of the truck’s battery or the tank of hydrogen. Constraints (42) impose an upper bound for the total CO2 emission over the whole problem horizon. Constraints (43) impose a limitation on the number of visits for each path. This means that each truck cannot exceed the maximum number of delivery allowed by the carrier company in its route. Lastly, Constraints (44) define the type of decision variables in the mathematical model.
5. Application to a Real-World Case Study
In this section, a real-world case study involving Decathlon company is presented. The case study considers the problem of delivering products from a DC to a set of 19 stores in northern Italy, covering parts of Piedmont, Liguria, and Lombardy regions, which are predesignated to receive products from that DC. The data provided by the stores include daily demand volumes, time windows allowed for delivery, and possible constraints relevant to road accessibility (that is, the types of trucks that are allowed to arrive at the store). Conversely, the DC contributes some other information such as truck availability, the maximum number of visits allowed per route, and other data required to build the decision model effectively. Table 4 summarizes the key data inputs necessary for running the model. It is important to note that all inputs and parameters refer to a real case study, apart from some simple modifications. The model analysis considers three distinct fleet types, each different by powertrain configurations. These differences allow comprehensive evaluation of the model’s applicability and performance across diverse possible fleet characteristics.

Table 4.
The real case data and input ([33,34,35,36,37,38], Decathlon Italy).
The input data for the considered instance of the optimization model are shown in Table 3. Then, the problem is coded in Python (version 3.12.6) and solved using the Gurobi Optimizer tool (version 11.0.3) on a PC with a 13th Gen Intel Core i9-13900H processor (2.60 GHz) and 16.0 GB of installed RAM. The results for the CVRPTW problem over one day indicate that, for the considered instance size, the total runtime to reach the optimal solution is between 2 and 10 min. Achieving a solution with a maximum optimality gap of less than 3% typically took less than 1 min. Table 5 presents the energy consumption of different types of trucks, the arrival times, the truck loads after departing from each node, and the split deliveries that occurred at three locations: Grugliasco, Asti, and Alessandria. These split deliveries were necessary to meet the demand of stores at these nodes. To better illustrate the optimal paths, Figure 3 provides a visual representation. For this specific case, the total cost amounted to EUR 4800, and the total distance traveled by all vehicles was 1347 km. The total energy consumed by all the trucks was 5567 kwh and total CO2 consumed by the trucks was 1392 kg as well. A total of 21 trucks were available, comprising 7 DVs, 7 EVs, and 7 HVs. The results show that the model prioritized the use of DVs first. Once all available DVs were allocated, the model then utilized EVs for deliveries to closer stores. Notably, the model preferred not to use any HVs. The reason behind this choice will be further analyzed in the following sections, considering additional issues.

Table 5.
The real case data and input.
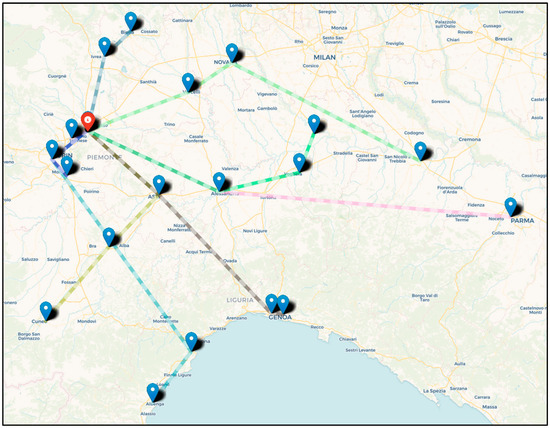
Figure 3.
The optimal route of the one day for a real case (northern Italy).
As it is evident from Table 5, the priority of using different fleet types follows a clear order: DVs are used first, followed by EVs, and finally, HVs have the lowest priority. This indicates that the cost associated with HVs is the highest, followed by EVs and then DVs. To analyze the cost of different truck types, the entire fleet was first considered as EVs and then as HVs. After solving the model under these conditions, the optimal cost for using EVs was found to be EUR 5440, while, for HVs, it was EUR 14137. The significantly higher costs of these two fleet types can be attributed to several factors, including energy or fuel costs, the advanced technology required for their production (which increases vehicle prices and subsequent depreciation costs), and the efficiency of their motors, among other factors. This section of the paper specifically analyzes the impact of fuel prices to determine the extent to which fuel cost reductions would allow EVs and HVs to compete with DVs. To achieve this, the fuel prices for both fleet types were gradually reduced, and after each reduction, the model was rerun to obtain the optimal result. Figure 4 illustrates the effect of hydrogen and electricity price reductions and their intersection nodes with DV costs. The intersection points of EVs and HVs occur when the total optimal routing cost equals EUR 4870, assuming a hydrogen price of EUR 2.2 and an electricity price of EUR 0.12. For EVs to be competitive with DVs, the electricity price would need to decrease to EUR 0.115, while for HVs, the hydrogen price would need to drop to approximately EUR 2.1 (Figure 5). On the other hand, in Figure 6, the change in the fuel price of DVs is investigated to reach the current situation of the HVs and EVs. As it is shown in Figure 6, if the price of gasoil increases slightly above EUR 2, the transportation cost of using DVs would match that of EVs. Furthermore, if the price of gasoil rises to EUR 9, it would also affect the competitiveness of HVs. It is important to note that hydrogen and electricity prices, along with their associated infrastructure, are not the only factors influencing the competitiveness of different fleet types in the market. However, based on the results, they play a significant role in determining fleet viability.
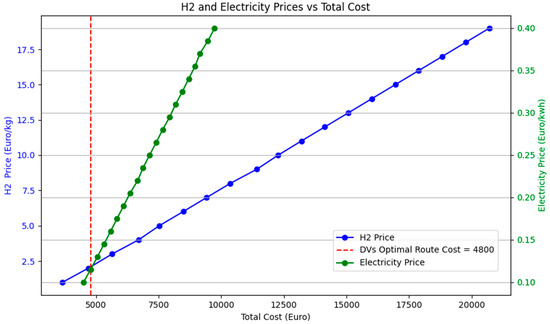
Figure 4.
H2 and electricity prices changes and their consequences transportation cost.
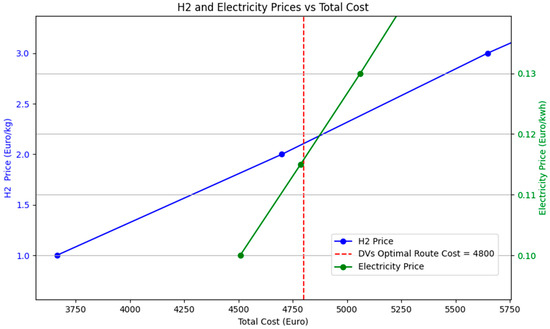
Figure 5.
Intersection points of the transportation cost and H2 and electricity prices.
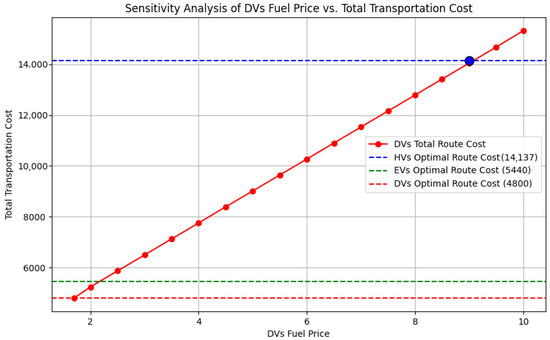
Figure 6.
Intersection points of the transportation cost after increasing the gasoil price.
Although HVs and EVs are generally considered green modes of transportation, their overall emissions depend on the energy sources used for their production and operation. When analyzing the supply chain, the emissions from different power plants that generate electricity or produce hydrogen must be taken into account. This section will examine the various power hydrogen production methods, assess their emissions, and compare them with other fleet-type emissions to provide a comprehensive evaluation of their environmental impact. We start analyzing the H2 production methods and their emissions analysis. Table 6 considers some of the hydrogen production methods with their emissions in different scales. First, the mathematical model for the real sample is solved once by considering DVs as the only available fleet to derive the total emissions of using DVs, and then only the HVs as the available fleet are considered. As mentioned before, there are different ways to produce H2 and for each production method of H2 there is a specified amount of CO2 emission [34]. The model is solved many times to see the total emissions of HVs under varied H2 production to demonstrate the comparison between direct CO2 emission caused by using DVs and indirect CO2 emission caused by using HVs. The results after solving the model for each scenario (Figure 7) explicitly show that, in the worst case of hydrogen production in terms of emission, the total amount of emission with respect to usable hydrogen for HVs is much less than the total amount of emission caused by DVs in the routes. It should be considered that the production of gasoil itself has emissions that are neglected in this computation. Figure 7 also shows the comparison of HVs production emissions with the EVs general emissions caused by the production of electricity and demonstrates that EVs and HVs can have rivalry in terms of CO2 emission based on the electricity and hydrogen production method.

Table 6.
Hydrogen production methods and its relevant CO2 emissions [34,39,40,41].
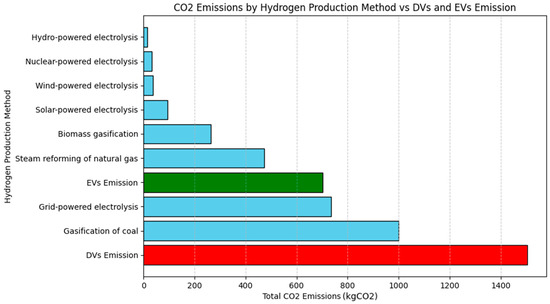
Figure 7.
Different hydrogen production methods and their emission for the optimal routing scenario of the case.
Continuing the previous analysis, different power plants can be investigated in terms of emissions. The amount of emissions per each kWh of energy consumption are reported in Table 7. The total emissions caused by various methods of electricity production are then obtained and shown in Figure 8. This figure also includes a comparison of emissions from EVs under different conditions of electricity production, emissions from DVs, and general emissions from HVs. Figure 8 demonstrates that EVs are significantly greener than DVs in terms of emissions. It should be noted that the emissions from gasoil production are neglected in this analysis. Furthermore, Figure 9 compares the CO2 emissions of hydrogen (in blue) and electricity (in green) production across different methods. While emissions for both energy carriers are expressed in kgCO2/kWh, it should be noted that for hydrogen the reference is its energy content.

Table 7.
Electricity production methods and its relevant CO2 emissions [34,42,43].
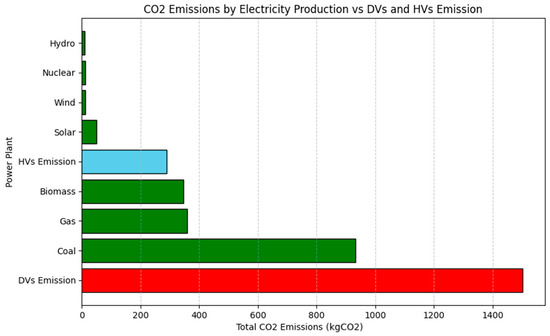
Figure 8.
Different electricity production methods and their emission for the optimal routing scenario of the case.
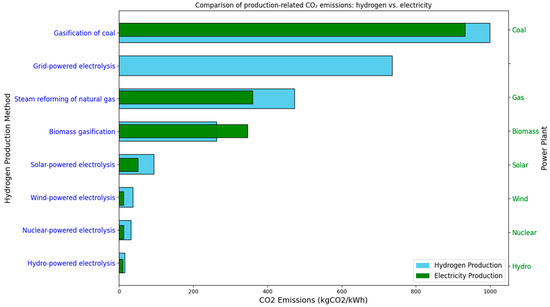
Figure 9.
Comparison of CO2 emissions from hydrogen and electricity production methods.
6. Conclusions and Future Work
This study explores the Hybrid Fleet Capacitated Vehicle Routing Problem with Time Windows (HF-CVRPTW) to determine the optimal fleet composition in industrial distribution, balancing economic and environmental objectives. For the mentioned goal, a MILP model is proposed in which the features of a real case like TW, split delivery, and scheduled arrival time are considered. A method for pricing the total cost by taking into account the economic and emission trade costs is considered. Three different fleet types, ICEs, EVs, and HVs, and their energy consumption are computed. The results reveal that DVs currently offer the lowest operational costs, followed by EVs and HVs, primarily due to the high costs of hydrogen and electricity and advanced technological requirements. However, sensitivity analyses indicate that reductions in electricity and hydrogen prices could significantly alter this hierarchy, making EVs and HVs more competitive. Then it is shown how much the price of hydrogen and electricity should be decreased to have competition with DVs and also between themselves. These findings highlight the critical role of energy pricing in shaping future transportation decisions and underscore the need for policy interventions to enhance the adoption of cleaner technologies.
Beyond economic feasibility, the environmental implications of fleet choices are thoroughly assessed. The study demonstrates that while EVs and HVs are inherently greener alternatives, their actual emissions depend on the energy sources used for electricity and hydrogen production. Comparisons of emissions from different power plants indicate that EVs consistently exhibit lower emissions than DVs, reinforcing their environmental advantage. The analysis also shows that in the worst-case scenario for hydrogen production, HVs still generate lower emissions than DVs. Furthermore, a direct comparison between EVs and HVs suggests that under certain electricity and hydrogen production methods, their emissions may be comparable, emphasizing the importance of cleaner energy generation in maximizing sustainability benefits.
This research provides also valuable insights for decision-makers by quantifying the trade-offs between cost and emissions, supporting a strategic transition toward more sustainable fleet compositions in logistics and industrial transportation. The current study provides real-world insights into supply chain management, with implications that can improve managerial decision-making. Such as fleet usage priority based on economic and emissions trading costs in which the optimal fleet deployment priority, considering total economic and emissions trading costs, is to deploy DVs first, followed by EVs, and then HVs.
This recommendation reflects current technology, infrastructure, and energy prices for the fleet in question. However, when fleet usage is prioritized based on emissions and overall environmental impact, the preferred order of deployment changes. This suggests the use of HVs as the first priority, followed by EVs and then DVs. However, the choice between hydrogen production methods and electricity production technologies, particularly with the exception of biomass, indicates that power plant emissions for electricity production generally result in lower emissions in comparison with hydrogen production or extraction with respect to the current technology.
While this study provides a comparative analysis of electric, hydrogen, and conventional vehicles, it is important to note that the results depend on assumptions regarding energy consumption, vehicle costs, and infrastructure availability. These assumptions may vary significantly across regions and over time. Using the model in different situations with different criteria or parameters can improve the model in future work with more realistic assumptions and data. On the other hand, although EVs and HVs are recommended as greener solutions, their adoption should be considered in light of the current energy supply infrastructure, as well as the prevailing prices and technologies at the time of writing this paper, which makes this approach somewhat optimistic.
The paper takes the perspective of a company’s decision-maker, who must optimize the delivery process on a day-to-day basis, considering current delivery demands, fuel/energy prices, and fleet availability. It does not aim to model higher-level policy optimization, such as setting incentives for certain vehicle types or regulating energy prices.
One of the managerial insights could be competitive conditions in cost management, in which several factors come into play in achieving cost competitiveness among the three fleet types. For EVs and HVs to be cost-competitive with DVs, electricity prices must fall within the range of [EUR 0.1, EUR 0.13], while hydrogen prices must fall within the range of [EUR 2, EUR 2.5]. Assuming vehicle prices and maintenance costs remain constant, these adjustments can equalize total transportation costs across fleet types. The impact of a diesel price increase is another managerial insight that demonstrates conversely, and an increase in the price of gasoil can significantly affect the cost competitiveness between fleet types. A slight rise in the price of diesel up to EUR 2.1in the range of diesel prices could potentially raise the total transportation costs of DVs to match those of EVs, and further increases up to EUR 9could bring them in line with HVs.
Dynamic optimization under uncertainty can be a valuable future research direction, making the model more aligned with real-world conditions. Additionally, separating emissions and transportation costs into two distinct objectives would provide better insights into the impact of emissions on the final decision.
Author Contributions
Conceptualization, M.J.J., L.P., G.F. and M.R.; Methodology, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Software, M.J.J., L.P. and G.F.; Validation, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Formal analysis, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Investigation, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Resources, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Data curation, M.J.J., L.P. and G.F.; Writing—original draft preparation, M.J.J., L.P., G.F. and R.M.; Writing—review and editing, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Visualization, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Supervision, G.F., R.M., M.P. and M.R.; Project administration, M.J.J., L.P., G.F., R.M., M.P. and M.R.; Funding acquisition, M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Restrictions apply to the availability of these data. The data are proprietary to Decathlon Italia S.r.l. and were used under license for the current study. They are available from the corresponding author with the permission of Decathlon Italia S.r.l.
Acknowledgments
This paper and case information constitute a segment of the research conducted for Decathlon company, within the context of the National Resilience and Recovery Plan (PNRR). The authors express their sincere gratitude to Decathlon for their collaboration and for providing crucial case information. In particular, we wish to thank Alessandro Magni and Alberto Mereu for their invaluable contributions. We greatly appreciate the opportunity to address real-world logistics challenges through this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Acronym List
| HF-CVRPTW | hybrid fleet capacitated vehicle routing problem with time windows |
| ICE | internal combustion engine |
| EV | electric vehicle |
| HV | hydrogen vehicle |
| ETS | emission trading scheme |
| GHG | greenhouse gas |
| DV | diesel vehicle |
| MILP | mixed-integer linear programming |
| VRP | vehicle routing problem |
| CVRPTW | capacitated vehicle routing problem with time windows |
| UAV | unmanned aerial vehicle |
| NSGA-III-IS | Non-Dominated Sorting Genetic Algorithm III with Intelligent Selection |
| BEVs | battery electric vehicles |
| DC | Distribution Centre |
References
- Xu, X.; He, P.; Xu, H.; Zhang, Q. Supply Chain Coordination with Green Technology under Cap-and-Trade Regulation. Int. J. Prod. Econ. 2017, 183, 433–442. [Google Scholar] [CrossRef]
- Chaabane, A.; Ramudhin, A.; Paquet, M. Designing Supply Chains with Sustainability Considerations. Prod. Plan. Control 2011, 22, 727–741. [Google Scholar] [CrossRef]
- Ehsani, M.; Gao, Y.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lou, P.; Zhou, Z.; Zeng, Y.; Fan, C. Vehicle Routing Problem with Time Windows and Carbon Emissions: A Case Study in Logistics Distribution. Environ. Sci. Pollut. Res. 2024, 31, 41600–41620. [Google Scholar] [CrossRef]
- Bi, X.; Wang, R.; Jia, Q. On the Speed-Varying Range of Electric Vehicles in Time-Windowed Routing Problems with En-Route Partial Re-Charging. IEEE Trans. Consum. Electron. 2024, 70, 3650–3657. [Google Scholar] [CrossRef]
- Gülmez, B.; Emmerich, M.; Fan, Y. Multi-Objective Optimization for Green Delivery Routing Problems with Flexible Time Windows. Appl. Artif. Intell. 2024, 38, 2325302. [Google Scholar] [CrossRef]
- Li, Y.; Lim, M.K.; Xiong, W.; Huang, X.; Shi, Y.; Wang, S. An Electric Vehicle Routing Model with Charging Stations Consideration for Sustainable Logistics. IMDS 2024, 124, 1076–1106. [Google Scholar] [CrossRef]
- Ferreira, K.M.; De Queiroz, T.A.; Munari, P.; Toledo, F.M.B. A Variable Neighborhood Search for the Green Vehicle Routing Problem with Two-Dimensional Loading Constraints and Split Delivery. Eur. J. Oper. Res. 2024, 316, 597–616. [Google Scholar] [CrossRef]
- Azadi, A.H.S.; Khalilzadeh, M.; Antucheviciene, J.; Heidari, A.; Soon, A. A Sustainable Multi-Objective Model for Capacitated-Electric-Vehicle-Routing-Problem Considering Hard and Soft Time Windows as Well as Partial Recharging. Biomimetics 2024, 9, 242. [Google Scholar] [CrossRef] [PubMed]
- Chi, J.; He, S.; Song, R. Solving Capacitated Vehicle Routing Problem with Three-Dimensional Loading and Relocation Constraints. Comput. Oper. Res. 2025, 173, 106864. [Google Scholar] [CrossRef]
- Hao, Y.; Chen, Z.; Sun, X.; Tong, L. Planning of Truck Platooning for Road-Network Capacitated Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2025, 194, 103898. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, S.; Zhang, C. A Lightweight Genetic Algorithm with Variable Neighborhood Search for Multi-Depot Vehicle Routing Problem with Time Windows. Appl. Soft Comput. 2024, 161, 111789. [Google Scholar] [CrossRef]
- Barletta, C.; Garn, W.; Turner, C.; Fallah, S. Hybrid Fleet Capacitated Vehicle Routing Problem with Flexible Monte–Carlo Tree Search. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2102265. [Google Scholar] [CrossRef]
- Fan, L.; Liu, C.; Dai, B.; Li, J.; Wu, Z.; Guo, Y. Electric Vehicle Routing Problem Considering Energy Differences of Charging Stations. J. Clean. Prod. 2023, 418, 138184. [Google Scholar] [CrossRef]
- Bezzi, D.; Ceselli, A.; Righini, G. A Route-Based Algorithm for the Electric Vehicle Routing Problem with Multiple Technologies. Transp. Res. Part C Emerg. Technol. 2023, 157, 104374. [Google Scholar] [CrossRef]
- Kumar, A.; Aggarwal, A.; Rani, A.; Bedi, J.; Kumar, R. A Mat-Heuristics Approach for Electric Vehicle Route Optimization under Multiple Recharging Options and Time-of-Use Energy Prices. Concurr. Comput. Pract. Exp. 2023, 35, e7854. [Google Scholar] [CrossRef]
- Bruglieri, M.; Paolucci, M.; Pisacane, O. A Matheuristic for the Electric Vehicle Routing Problem with Time Windows and a Realistic Energy Consumption Model. Comput. Oper. Res. 2023, 157, 106261. [Google Scholar] [CrossRef]
- Nolz, P.C.; Absi, N.; Feillet, D.; Seragiotto, C. The Consistent Electric-Vehicle Routing Problem with Backhauls and Charging Management. Eur. J. Oper. Res. 2022, 302, 700–716. [Google Scholar] [CrossRef]
- Seyfi, M.; Alinaghian, M.; Ghorbani, E.; Çatay, B.; Saeid Sabbagh, M. Multi-Mode Hybrid Electric Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102882. [Google Scholar] [CrossRef]
- Froger, A.; Jabali, O.; Mendoza, J.E.; Laporte, G. The Electric Vehicle Routing Problem with Capacitated Charging Stations. Transp. Sci. 2022, 56, 460–482. [Google Scholar] [CrossRef]
- Abibou, S.; El Bourakadi, D.; Yahyaouy, A.; Gualous, H. Hydrogen Vehicle Routing Problem with Time Windows and Vehicle Capacity. In Proceedings of the 2024 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 8 May 2024; pp. 1–6. [Google Scholar]
- Ren, X.; Fan, H.; Ma, M.; Fan, H.; Yue, L. Time-Dependent Hydrogen Fuel Cell Vehicle Routing Problem with Drones and Variable Drone Speeds. Comput. Ind. Eng. 2024, 193, 110330. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Y.; Jiang, J.; Li, Y. Low-Carbon Scheduling of Integrated Hydrogen Transport and Energy System. Int. J. Hydrogen Energy 2024, 52, 655–666. [Google Scholar] [CrossRef]
- Cunanan, C.; Tran, M.-K.; Lee, Y.; Kwok, S.; Leung, V.; Fowler, M. A Review of Heavy-Duty Vehicle Powertrain Technologies: Diesel Engine Vehicles, Battery Electric Vehicles, and Hydrogen Fuel Cell Electric Vehicles. Clean Technol. 2021, 3, 474–489. [Google Scholar] [CrossRef]
- Ashtineh, H.; Pishvaee, M.S. Alternative Fuel Vehicle-Routing Problem: A Life Cycle Analysis of Transportation Fuels. J. Clean. Prod. 2019, 219, 166–182. [Google Scholar] [CrossRef]
- Eslamipoor, R. Direct and Indirect Emissions: A Bi-Objective Model for Hybrid Vehicle Routing Problem. J. Bus. Econ. 2024, 94, 413–436. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The Pollution-Routing Problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Qiu, Y.; Qiao, J.; Pardalos, P.M. A Branch-and-Price Algorithm for Production Routing Problems with Carbon Cap-and-Trade. Omega 2017, 68, 49–61. [Google Scholar] [CrossRef]
- Ferro, G.; Paolucci, M.; Robba, M. Optimal Charging and Routing of Electric Vehicles with Power Constraints and Time-of-Use Energy Prices. IEEE Trans. Veh. Technol. 2020, 69, 14436–14447. [Google Scholar] [CrossRef]
- Bernard, J.; Delprat, S.; Buchi, F.N.; Guerra, T.M. Fuel-Cell Hybrid Powertrain: Toward Minimization of Hydrogen Consumption. IEEE Trans. Veh. Technol. 2009, 58, 3168–3176. [Google Scholar] [CrossRef]
- Pramuanjaroenkij, A.; Kakaç, S. The Fuel Cell Electric Vehicles: The Highlight Review. Int. J. Hydrogen Energy 2023, 48, 9401–9425. [Google Scholar] [CrossRef]
- Waseem, M.; Amir, M.; Lakshmi, G.S.; Harivardhagini, S.; Ahmad, M. Fuel Cell-Based Hybrid Electric Vehicles: An Integrated Review of Current Status, Key Challenges, Recommended Policies, and Future Prospects. Green Energy Intell. Transp. 2023, 2, 100121. [Google Scholar] [CrossRef]
- Ennassiri, Y.; Ferro, G.; Bellotti, D.; Magistri, L.; Robba, M. Optimal Scheduling and Real-Time Control of a Microgrid with an Electrolyzer and a Fuel Cell Systems Using a Reference Governor Approach. Sustain. Energy Grids Netw. 2023, 36, 101218. [Google Scholar] [CrossRef]
- Dulău, L.-I. CO2 Emissions of Battery Electric Vehicles and Hydrogen Fuel Cell Vehicles. Clean Technol. 2023, 5, 696–712. [Google Scholar] [CrossRef]
- Jafari, M.J.; Ferro, G.; Magni, A.; Mereu, A.; Minciardi, R.; Paolucci, M.; Robba, M. Optimizing a Capacitated Vehicle Routing Problem with Scheduled Arrival, Split Deliveries within Time Windows and Emission Consideration. IFAC-Pap. 2024, 58, 180–185. [Google Scholar] [CrossRef]
- Basma, H.; Zhou, Y.; Rodríguez, F. Fuel-Cell Hydrogen Long-Haul Trucks in Europe: A Total Cost of Ownership Analysis; International Council on Clean Transportation: Washington, DC, USA, 2022. [Google Scholar]
- IVECO to Produce and Market Its Heavy-Duty Battery Electric Vehicle and Heavy-Duty Fuel Cell Electric Vehicle Under Its Own Brand|Iveco. Available online: https://www.iveco.com/global/Press/PressReleases/2023/IVECO-to-produce-and-market-its-Heavy-Duty-Battery-Electric-Vehicle-and-Heavy-Duty-Fuel-Cell-Electric-Vehicle (accessed on 5 September 2025).
- Home. Available online: https://theicct.org/ (accessed on 5 September 2025).
- Howarth, R.W.; Jacobson, M.Z. How Green Is Blue Hydrogen? Energy Sci. Eng. 2021, 9, 1676–1687. [Google Scholar] [CrossRef]
- Longden, T.; Beck, F.J.; Jotzo, F.; Andrews, R.; Prasad, M. ‘Clean’ Hydrogen?—Comparing the Emissions and Costs of Fossil Fuel versus Renewable Electricity Based Hydrogen. Appl. Energy 2022, 306, 118145. [Google Scholar] [CrossRef]
- Tenhumberg, N.; Büker, K. Ecological and Economic Evaluation of Hydrogen Production by Different Water Electrolysis Technologies. Chem. Ing. Tech. 2020, 92, 1586–1595. [Google Scholar] [CrossRef]
- Faria, R.; Moura, P.; Delgado, J.; De Almeida, A.T. A Sustainability Assessment of Electric Vehicles as a Personal Mobility System. Energy Convers. Manag. 2012, 61, 19–30. [Google Scholar] [CrossRef]
- Ramachandran, S.; Stimming, U. Well to Wheel Analysis of Low Carbon Alternatives for Road Traffic. Energy Environ. Sci. 2015, 8, 3313–3324. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).