Neutronic and Thermal Coupled Calculations for an HTGR Pebble with Discrete Power Generation Using Serpent and OpenFOAM
Abstract
1. Introduction
2. Methodology of Coupled Calculations for VHTR Pebble
2.1. Thermal Model
2.2. Neutronic Model
2.3. Power Discretization
2.4. Coupled Calculation System
3. Results and Discussion
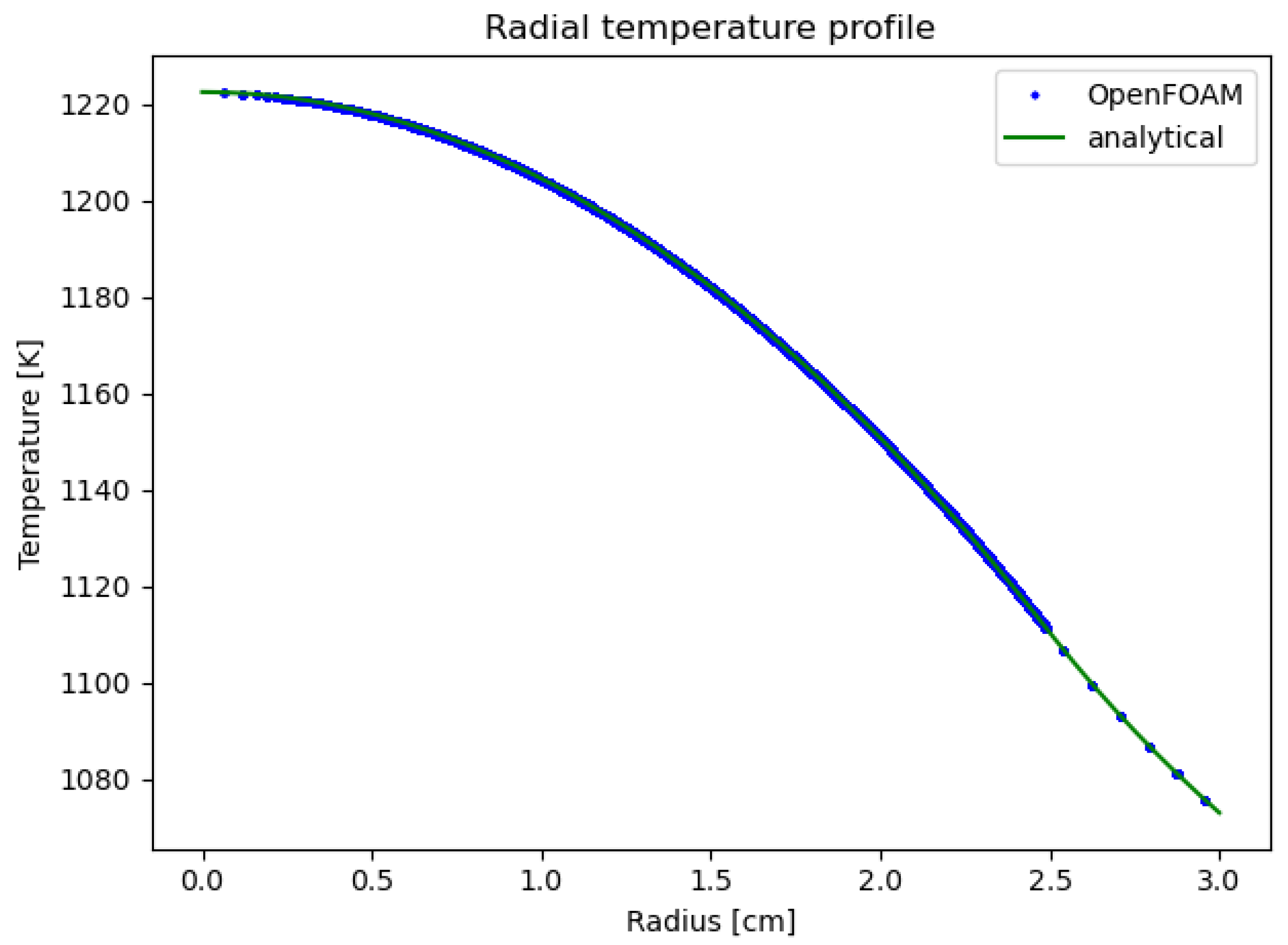
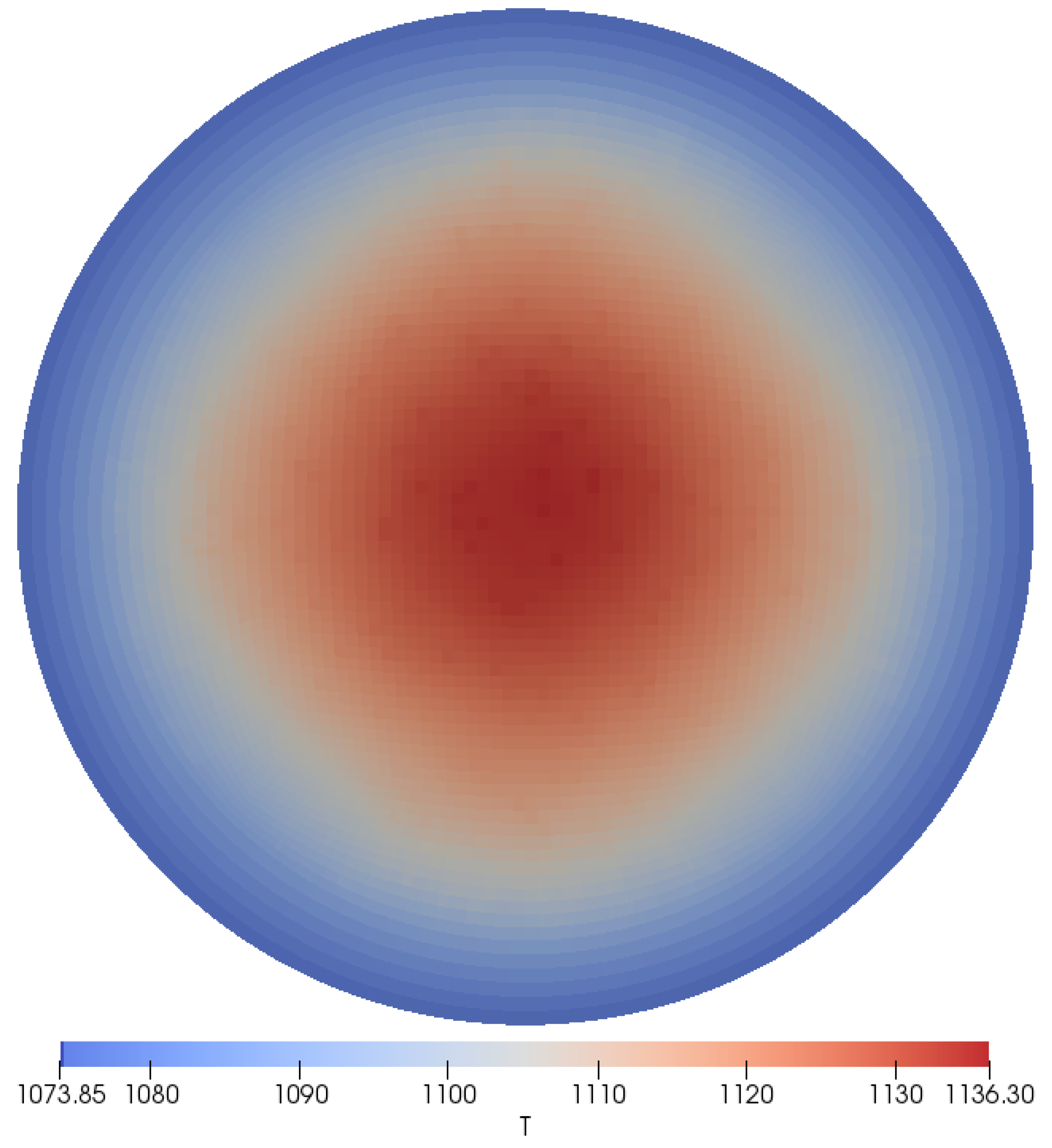
3.1. Thermal Model with Uniform Power Distribution
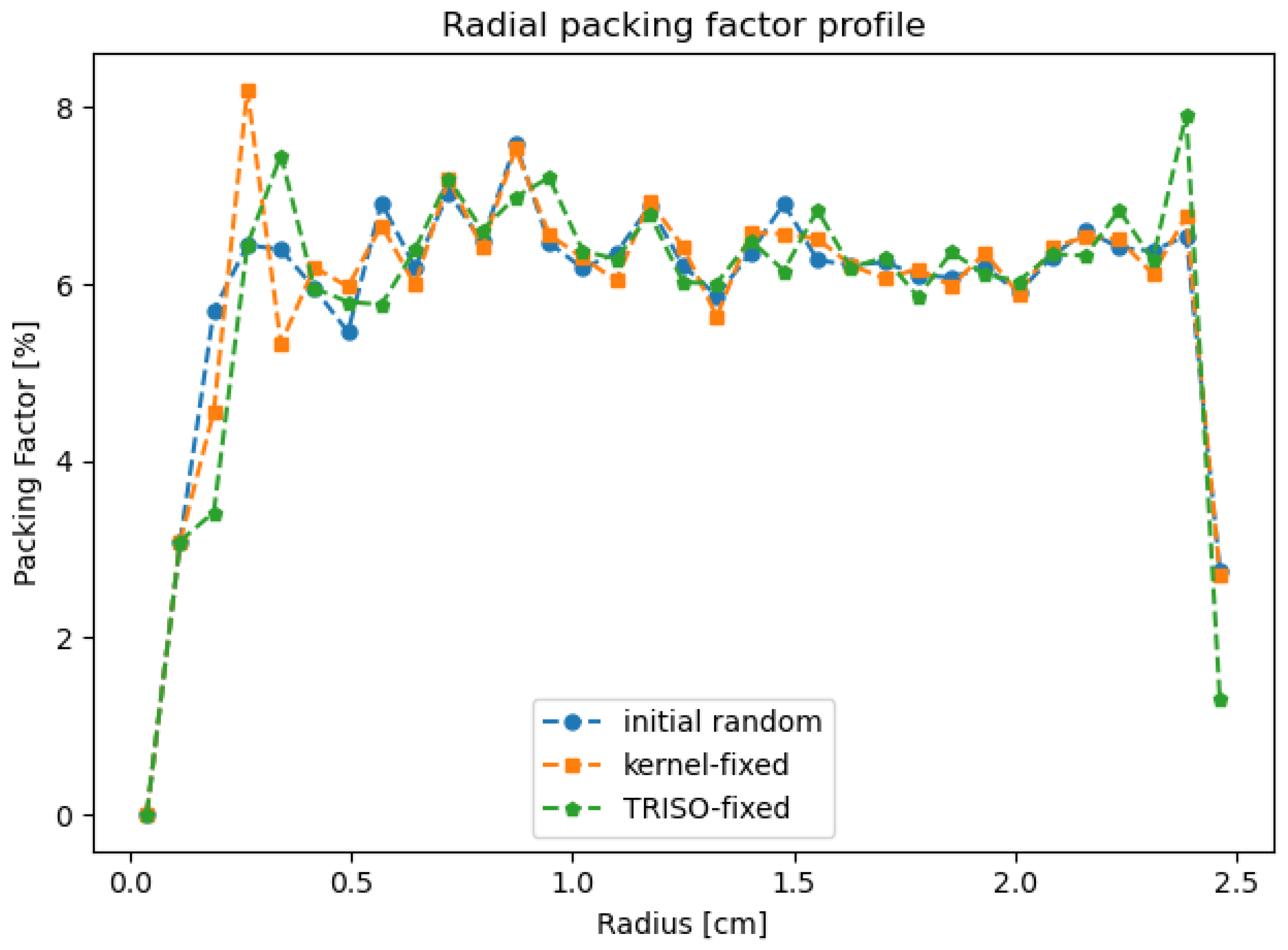
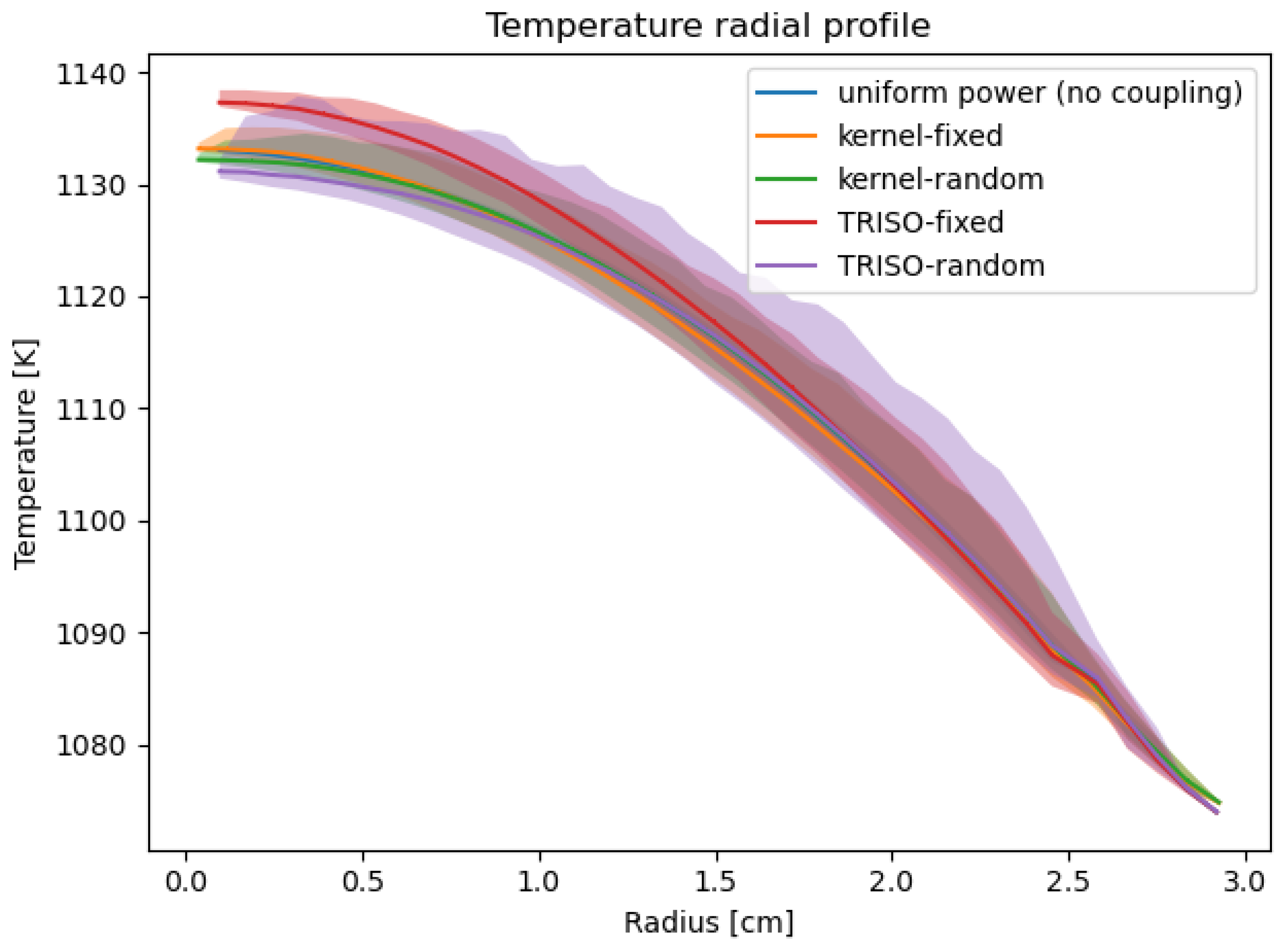
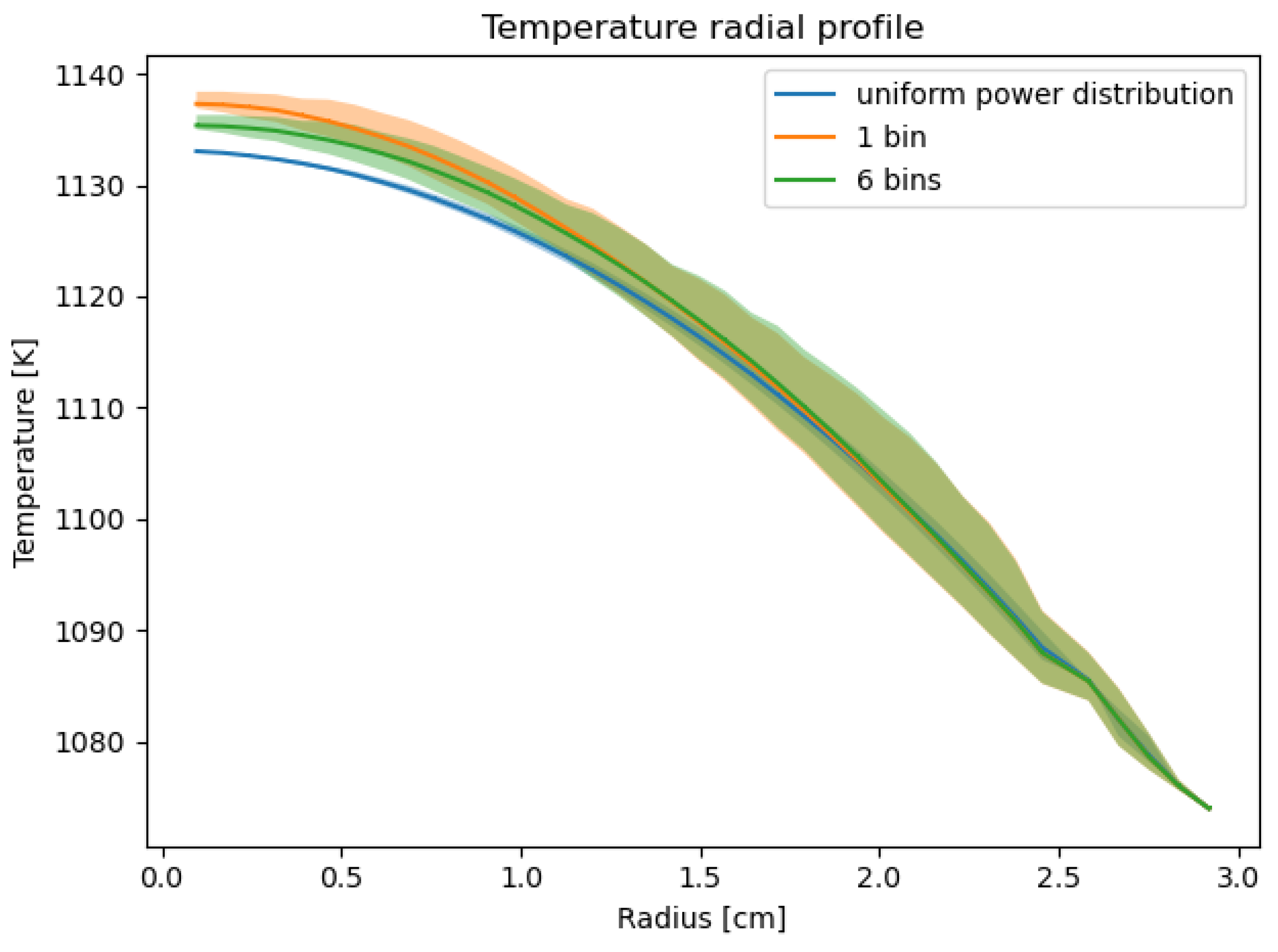
3.2. Coupled Calculations with Power Discretization
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Greek symbols | |
| density | |
| thermal conductivity [] | |
| volume fraction | |
| homogeneous parameters | |
| Latin symbols | |
| q | power density [] |
| Q | power [W] |
| r | radius [cm] |
| specific heat, [] | |
| T | temperature [K] |
| packing factor | |
| infinite neutron multiplication factor | |
| Subscripts | |
| i | i-th element |
| fuel | fuel region |
| shell | shell region |
| UO2 | UO2 fuel kernel |
| buffer | porous carbon buffer |
| IPyC | inner pyrolytic carbon |
| SiC | silicon carbide |
| OPyC | outer pyrolytic carbon |
| C | graphite matrix |
References
- NEA. High-Temperature Gas-Cooled Reactors and Industrial Heat Applications; OECD Publishing: Paris, France, 2022. [Google Scholar] [CrossRef]
- Jia, G.; Zhu, G.; Zou, Y.; Ma, Y.; Dai, Y.; Wu, J.; Tian, J. Economic Analysis of Nuclear Energy Cogeneration: A Comprehensive Review on Integrated Utilization. Energies 2025, 18, 2929. [Google Scholar] [CrossRef]
- Advances in High Temperature Gas Cooled Reactor Fuel Technology; Number 1674 in Entity; International Atomic Energy Agency: Vienna, Austria, 2013.
- Brown, F.B.; Martin, W.R. Stochastic geometry capability in MCNP5 for the analysis of particle fuel. Ann. Nucl. Energy 2004, 31, 2039–2047. [Google Scholar] [CrossRef]
- Rintala, V.; Suikkanen, H.; Leppänen, J.; Kyrki-Rajamäki, R. Modeling of realistic pebble bed reactor geometries using the Serpent Monte Carlo code. Ann. Nucl. Energy 2015, 77, 223–230. [Google Scholar] [CrossRef]
- Wang, J.; Lu, G.; Ding, M. Parametric study of effective thermal conductivity for VHTR fuel pebbles based on a neutronic and thermal coupling method. Ann. Nucl. Energy 2023, 181, 109530. [Google Scholar] [CrossRef]
- Barrachin, M.; Basini, V.; BU, Ü.C.; Dubourg, R.; Feltus., M.A.; Greneche., D.; Guillermier, P.; Hansen, U.; Hanson, D.; Hunn, J.; et al. High Temperature Gas Cooled Reactor Fuels and Materials; Chapter Manufacture of Spherical Fuels; International Atomic Energy Agency: Vienna, Austria, 2010; pp. 34–38. [Google Scholar]
- Mehta, K.S.; Goddard, B.; Wu, Z. Neutronics Analysis on High-Temperature Gas-Cooled Pebble Bed Reactors by Coupling Monte Carlo Method and Discrete Element Method. Energies 2024, 17, 5188. [Google Scholar] [CrossRef]
- Górkiewicz, M.; Cetnar, J. Flattening of the Power Distribution in the HTGR Core with Structured Control Rods. Energies 2021, 14. [Google Scholar] [CrossRef]
- Robert, Y.; Jantzen, L.; Siaraferas, T.; Fiorina, C.; Fratoni, M. Impact of thermal coupling on a pebble bed reactor equilibrium from hyper-fidelity depletion. Proc. Int. Conf. Nucl. Eng. 2023, 30, 1490. [Google Scholar] [CrossRef]
- Pavliotis, G.; Stuart, A. Multiscale Methods: Averaging and Homogenization; Springer: New York, NY, USA, 2008; Volume 53. [Google Scholar] [CrossRef]
- Clifford, I.D. A Hybrid Coarse and Fine Mesh Solution Method for Prismatic High Temperature Gas-Cooled Reactor Thermal-Fluid Analysis. Ph.D Thesis, The Pennsylvania State University, University Park, PA, USA, 2013. [Google Scholar]
- Novak, A.; Andrs, D.; Shriwise, P.; Fang, J.; Yuan, H.; Shaver, D.; Merzari, E.; Romano, P.; Martineau, R. Coupled Monte Carlo and thermal-fluid modeling of high temperature gas reactors using Cardinal. Ann. Nucl. Energy 2022, 177, 109310. [Google Scholar] [CrossRef]
- Novak, A.J.; Carlsen, R.W.; Schunert, S.; Balestra, P.; Reger, D.; Slaybaugh, R.N.; Martineau, R.C. Pronghorn: A Multidimensional Coarse-Mesh Application for Advanced Reactor Thermal Hydraulics. Nucl. Technol. 2021, 207, 1015–1046. [Google Scholar] [CrossRef]
- Novak, A. Multiscale Thermal-Hydraulic Methods for Pebble Bed Reactors. Ph.D Thesis, UC Berkeley, Berkeley, CA, USA, 2020. [Google Scholar]
- Wang, J.; Li, Z.; Ding, M. Study of the neutronic and thermal coupling effect on VHTR fuel pebble using OpenMC and OpenFOAM. Ann. Nucl. Energy 2023, 183, 109643. [Google Scholar] [CrossRef]
- Wang, J.; Wei, B.; Cai, W.; Guo, Z.; Ding, M. A new method of fuel pebble temperature calculation based on neutronic and thermal coupling equivalent model. Ann. Nucl. Energy 2024, 204, 110566. [Google Scholar] [CrossRef]
- Yu, D.; Wang, F.; Mei, H.; Cheng, X.; Duan, C. An improved two-temperature method for computing the temperature distributions within a TRISO-coated particle pebble fuel. Nucl. Eng. Technol. 2025, 57, 103515. [Google Scholar] [CrossRef]
- Strydom, G. Annual Report 2023; Generation IV International Forum: Paris, France, 2024; Chapter System Summaries; p. 35. [Google Scholar]
- OpenFOAM. User Guide Version 10; The OpenFOAM Foundation: London, UK, 2022. [Google Scholar]
- Tuominen, R.; Valtavirta, V.; Peltola, J.; Leppänen, J. Coupling Serpent and OpenFOAM for neutronics—CFD multi-physics calculations. In Proceedings of the PHYSOR 2016: Unifying Theory and Experiments in the 21st Century, Sun Valley, ID, USA, 1–5 May 2016; pp. 255–269. [Google Scholar]
- Górkiewicz, M. Development of Localized Coupled Neutronic and CFD Calculation for HTR Application. Ph.D Thesis, National Centre for Nuclear Research, Świerk, Poland, 2023. [Google Scholar]
- Wu, Z.; Lin, D.; Zhong, D. The design features of the HTR-10. Nucl. Eng. Des. 2002, 218, 25–32. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Wang, D.; Xu, Y.; Sun, Y.; Li, F.; Dong, Y. Current status and technical description of Chinese 2 × 250 MW th HTR-PM demonstration plant. Nucl. Eng. Des.-Nucl Eng. Des. 2009, 239, 1212–1219. [Google Scholar] [CrossRef]
- Folsom, C.; Xing, C.; Jensen, C.; Ban, H.; Marshall, D.W. Experimental measurement and numerical modeling of the effective thermal conductivity of TRISO fuel compacts. J. Nucl. Mater. 2015, 458, 198–205. [Google Scholar] [CrossRef]
- Chiew, Y.C.; Glandt, E.D. Effective conductivity of dispersions: The effect of resistance at the particle surfaces. Chem. Eng. Sci. 1987, 42, 2677–2685. [Google Scholar] [CrossRef]
- Leppänen, J.; Pusa, M.; Viitanen, T.; Valtavirta, V.; Kaltiaisenaho, T. The Serpent Monte Carlo code: Status, development and applications in 2013. Ann. Nucl. Energy 2015, 82, 142–150. [Google Scholar] [CrossRef]
- Leppänen, J.; Valtavirta, V.; Viitanen, T.; Aufiero, M. Unstructured mesh based multi-physics interface for CFD code coupling in the Serpent 2 Monte Carlo code. In Proceedings of the International Conference on Physics of Reactors, PSYHOR 2014: The Role of Reactor Physics Toward Sustainable Future, Kyoto, Japan, 28 September–3 October 2014; Japan Atomic Energy Agency: Tokai-Mura, Japan, 2015; Volume JAEA-Conf 2014-003. [Google Scholar]
- Leppänen, J.; Aufiero, M. Development of an unstructured mesh based geometry model in the Serpent 2 Monte Carlo code. In Proceedings of the Proceedings of the International Conference on Physics of Reactors, PSYHOR 2014: The Role of Reactor Physics Toward Sustainable Future, Kyoto, Japan, 28 September–3 October 2014; Japan Atomic Energy Agency: Tokai-Mura, Japan, 2015; Volume JAEA-Conf 2014-003. [Google Scholar]





| Operational Parameter | Value |
|---|---|
| Power density in fuel region [] | 1615 |
| Thermal conductivity [] | 15 |
| Boundary temperature [K] | 1073 |
| Radius of fuel region [cm] | 2.5 |
| Pebble radius [cm] | 3 |
| Material | Properties |
|---|---|
| UO2 | |
| = 10,970 | |
| buffer | |
| PyC | |
| >SiC | |
| C | |
| −43,449 | |
| Material | Radius [μm] |
|---|---|
| UO2 | 250 |
| buffer | 340 |
| IPyC | 380 |
| SiC | 415 |
| OPyC | 455 |
| Power [W] | Reference T [K] [16] | Kernel-Mesh Homogenized | Kernel-Mesh | TRISO-Mesh Homogenized | TRISO-Mesh | ||||
|---|---|---|---|---|---|---|---|---|---|
| Max. T [K] | ΔT [%] | Max. T [K] | ΔT [%] | Max. T [K] | ΔT [%] | Max. T [K] | ΔT [%] | ||
| 500 | 1100.34 | 1100.19 | −0.01 | 1101.22 | 0.08 | 1100.20 | −0.01 | 1101.21 | 0.08 |
| 800 | 1116.86 | 1116.69 | −0.02 | 1118.35 | 0.13 | 1116.70 | −0.01 | 1118.33 | 0.13 |
| 1057 | 1131.08 | 1130.92 | −0.01 | 1133.13 | 0.18 | 1130.94 | −0.01 | 1133.11 | 0.18 |
| 1400 | 1150.15 | 1150.09 | −0.01 | 1153.04 | 0.25 | 1150.11 | 0.00 | 1153.00 | 0.25 |
| 1700 | 1166.94 | 1167.00 | 0.01 | 1170.61 | 0.31 | 1167.03 | 0.01 | 1170.56 | 0.31 |
| 2000 | 1183.83 | 1184.05 | 0.02 | 1188.33 | 0.38 | 1184.09 | 0.02 | 1188.28 | 0.38 |
| 3000 | 1240.68 | 1241.92 | 0.10 | 1248.52 | 0.63 | 1241.17 | 0.04 | 1248.44 | 0.63 |
| 4000 | 1298.51 | 1301.43 | 0.22 | 1310.47 | 0.92 | 1301.52 | 0.23 | 1310.37 | 0.91 |
| 5000 | 1357.27 | 1362.65 | 0.40 | 1374.28 | 1.25 | 1362.51 | 0.39 | 1374.14 | 1.24 |
| Case | Number of Power Cells | Volume Fraction [%] | Power Fraction [%] | Max. T [K] | +/− | |
|---|---|---|---|---|---|---|
| TRISO-random | 2160 | 0.95 | 18.52 | 1137.82 | 1.74222 | 0.00098 |
| TRISO-Fixed | 10,027 | 4.90 | 98.91 | 1138.40 | 1.74128 | 0.00093 |
| kernel-random | 13,140 | 1.00 | 47.92 | 1134.52 | 1.73992 | 0.00089 |
| Kernel-fixed | 13,264 | 0.94 | 75.60 | 1135.10 | 1.73986 | 0.00096 |
| Number of Bins | Max. T [K] | +/− | |
|---|---|---|---|
| 1 | 1138.40 | 1.74128 | 0.00093 |
| 2 | 1136.10 | 1.74065 | 0.00092 |
| 3 | 1136.29 | 1.74132 | 0.00092 |
| 5 | 1136.28 | 1.74075 | 0.00090 |
| 6 | 1136.30 | 1.73929 | 0.00090 |
| 7 | 1136.27 | 1.74171 | 0.00096 |
| 8 | 1136.23 | 1.74001 | 0.00091 |
| 1 bin | 6 bins | |||||
|---|---|---|---|---|---|---|
| Iteration | Max. [K] | +/− | Max. [K] | +/− | ||
| 1 | 1133.12 | 1.74162 | 0.00097 | 1136.27 | 1.74144 | 0.00093 |
| 2 | 1138.41 | 1.74277 | 0.00090 | 1136.29 | 1.74228 | 0.00099 |
| 3 | 1138.41 | 1.74130 | 0.00098 | 1136.33 | 1.73969 | 0.00084 |
| 4 | 1138.4 | 1.74128 | 0.00093 | 1136.32 | 1.74144 | 0.00103 |
| 5 | 1136.29 | 1.74217 | 0.00090 | |||
| 6 | 1136.30 | 1.73929 | 0.00090 | |||
| Power Deviation [%] | −2 | −1 | −0.5 | −0.1 | Reference | +0.1 | +0.5 | +1 | +2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1-bin | T[K] | 1137.09 | 1137.71 | 1138.09 | 1138.34 | 1138.4 | 1138.44 | 1138.71 | 1139.04 | 1139.71 |
| [%] | −0.115 | −0.061 | −0.027 | −0.005 | - | 0.004 | 0.027 | 0.056 | 0.115 | |
| 6-bins | T[K] | 1135.04 | 1135.64 | 1135.96 | 1136.22 | 1136.3 | 1136.39 | 1136.6 | 1136.92 | 1137.57 |
| [%] | −0.111 | −0.058 | −0.030 | −0.007 | - | 0.008 | 0.026 | 0.055 | 0.112 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Górkiewicz, M.; Sierchuła, J. Neutronic and Thermal Coupled Calculations for an HTGR Pebble with Discrete Power Generation Using Serpent and OpenFOAM. Energies 2025, 18, 5148. https://doi.org/10.3390/en18195148
Górkiewicz M, Sierchuła J. Neutronic and Thermal Coupled Calculations for an HTGR Pebble with Discrete Power Generation Using Serpent and OpenFOAM. Energies. 2025; 18(19):5148. https://doi.org/10.3390/en18195148
Chicago/Turabian StyleGórkiewicz, Michał, and Jakub Sierchuła. 2025. "Neutronic and Thermal Coupled Calculations for an HTGR Pebble with Discrete Power Generation Using Serpent and OpenFOAM" Energies 18, no. 19: 5148. https://doi.org/10.3390/en18195148
APA StyleGórkiewicz, M., & Sierchuła, J. (2025). Neutronic and Thermal Coupled Calculations for an HTGR Pebble with Discrete Power Generation Using Serpent and OpenFOAM. Energies, 18(19), 5148. https://doi.org/10.3390/en18195148





