Machine Learning-Driven Prediction of CO2 Solubility in Brine: A Hybrid Grey Wolf Optimizer (GWO)-Assisted Gaussian Process Regression (GPR) Approach
Abstract
1. Introduction
2. Data and Methods
2.1. Algorithms Used in This Work
- 1
- Gaussian Process Regression (GPR)
- Uses multiple kernel functions (Matern, RBF, etc.)
- Incorporates mineral ion data as input features
- 2
- Optimization with Grey Wolf Optimizer (GWO)
- Automatically adjusts hyperparameters (e.g., length scale)
- Improves model accuracy using a nature-inspired search method
- 3
- Implementation Steps
- Data preprocessing → Kernel selection → GWO optimization → Model validation
- 1
- 70% for training the model
- 2
- 30% for testing the model
2.1.1. Flowchart Used
- Data Preparation
- ▪
- Input Structure: Features (‘X’) include 13 parameters (T, P, and 11 ion concentrations) as columns, with each row representing one sample. Targets (‘T’) are column-oriented CO2 solubility values.
- ▪
- Preprocessing: All features are standardized to equalize their influence on the kernel.
- Train-Test Split (70–30%)Randomly split data into training (70%) and testing (30%) sets.
- Hyperparameter OptimizationPopulation Setup:‘n_wolves = 30’: Balances exploration and computational cost.‘n_iterations = 50’: Determined via early stopping if fitness plateaus (<0.1% R2 improvement over 5 iterations).Hyperparameter Bounds:
- ▪
- Length scales (‘[0.001, 100]’): Wide range accommodates diverse feature sensitivities
- ▪
- Sigma (signal variance) (‘[0.001, 10]’): Reflects expected magnitude of solubility variations.
These bounds ensure a wide search space while preventing numerical instability in GPR.- ▪
- Kernel Selection: Evaluates 8 kernels (e.g., Matern 3/2, ARD Squared Exponential) during GWO iterations.
- GWO Core Mechanics
- ▪
- Leader Hierarchy: Alpha (best), Beta, and Delta wolves guide updates.
- ▪
- Position Update:
A = 2*a*rand ()—a; % Exploration coefficient (a decreases linearly from 2 to 0)C = 2*rand (); % Random perturbationnew_position = (alpha_pos—A*abs (C*alpha_pos—current_pos))/3 + … % Beta/Delta terms - GPR Training with Optimized Kernel
- ▪
- Kernel Configuration:
ARD (Automatic Relevance Determination): Each feature gets a unique length scale (optimized by GWO). - Prediction & Evaluation
- ▪
- Predict on training/test sets.
- ▪
- Metrics: R2, MAE, RMSE.
- Output
- ▪
- Optimal hyperparameters.
- ▪
- Performance metrics and plots
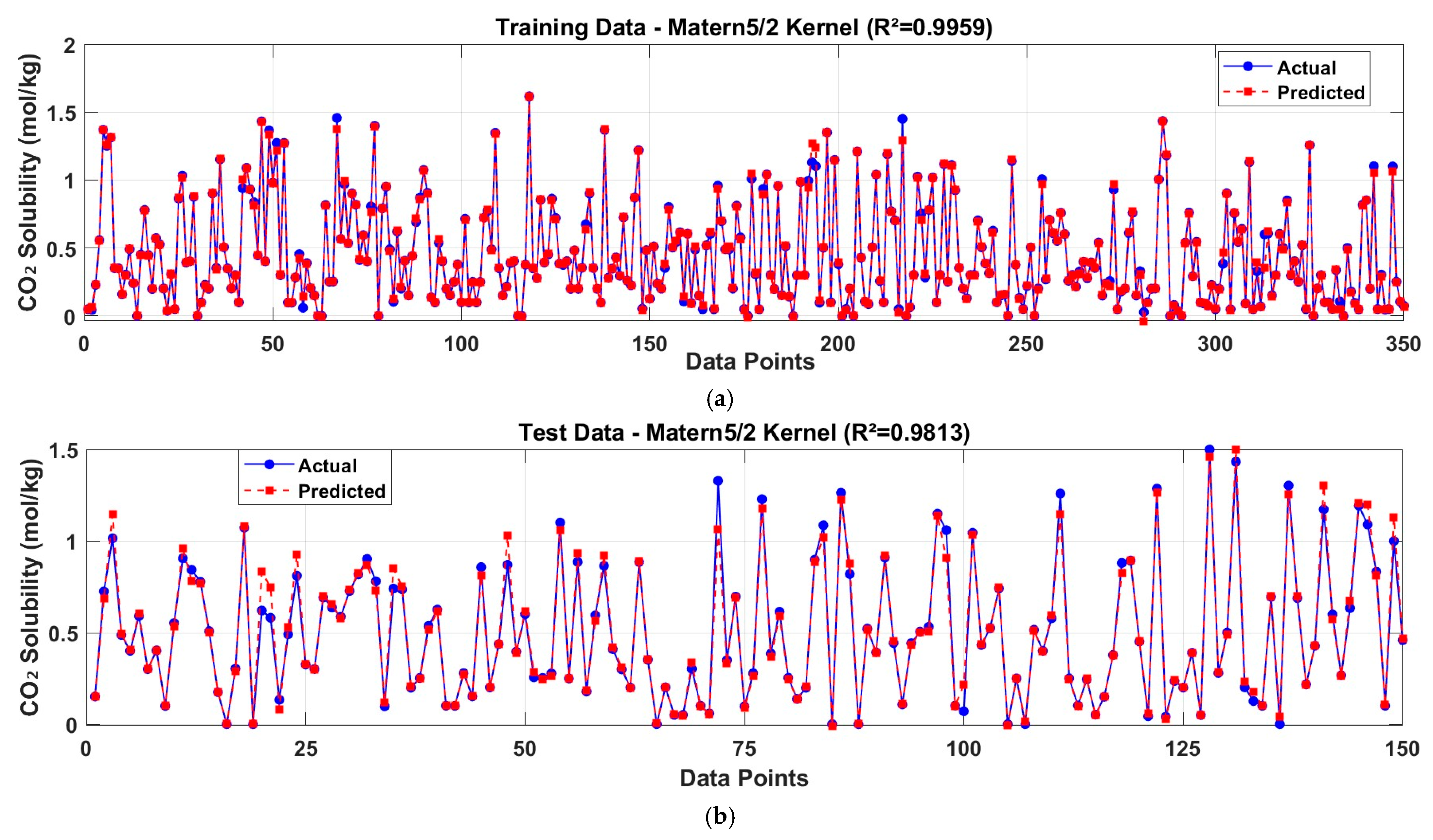
2.1.2. GPR Kernel Parameters
2.1.3. Physics-Informed GPR Model
2.2. Data Collection
3. Results and Discussion
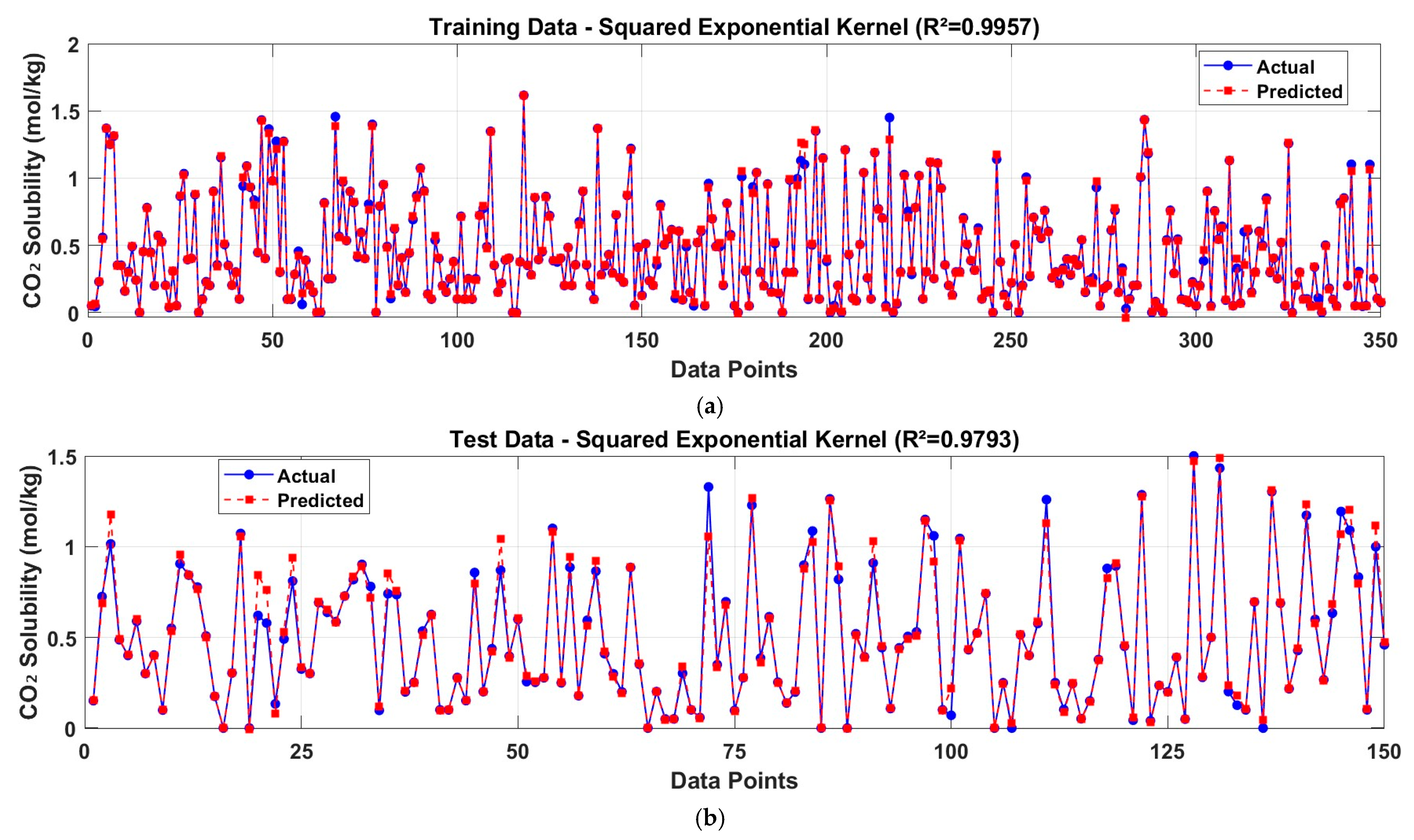
- Length Scale: 66.141
- Sigma: 3.782
- Training R2 = 0.9957
- Test R2 = 0.9793
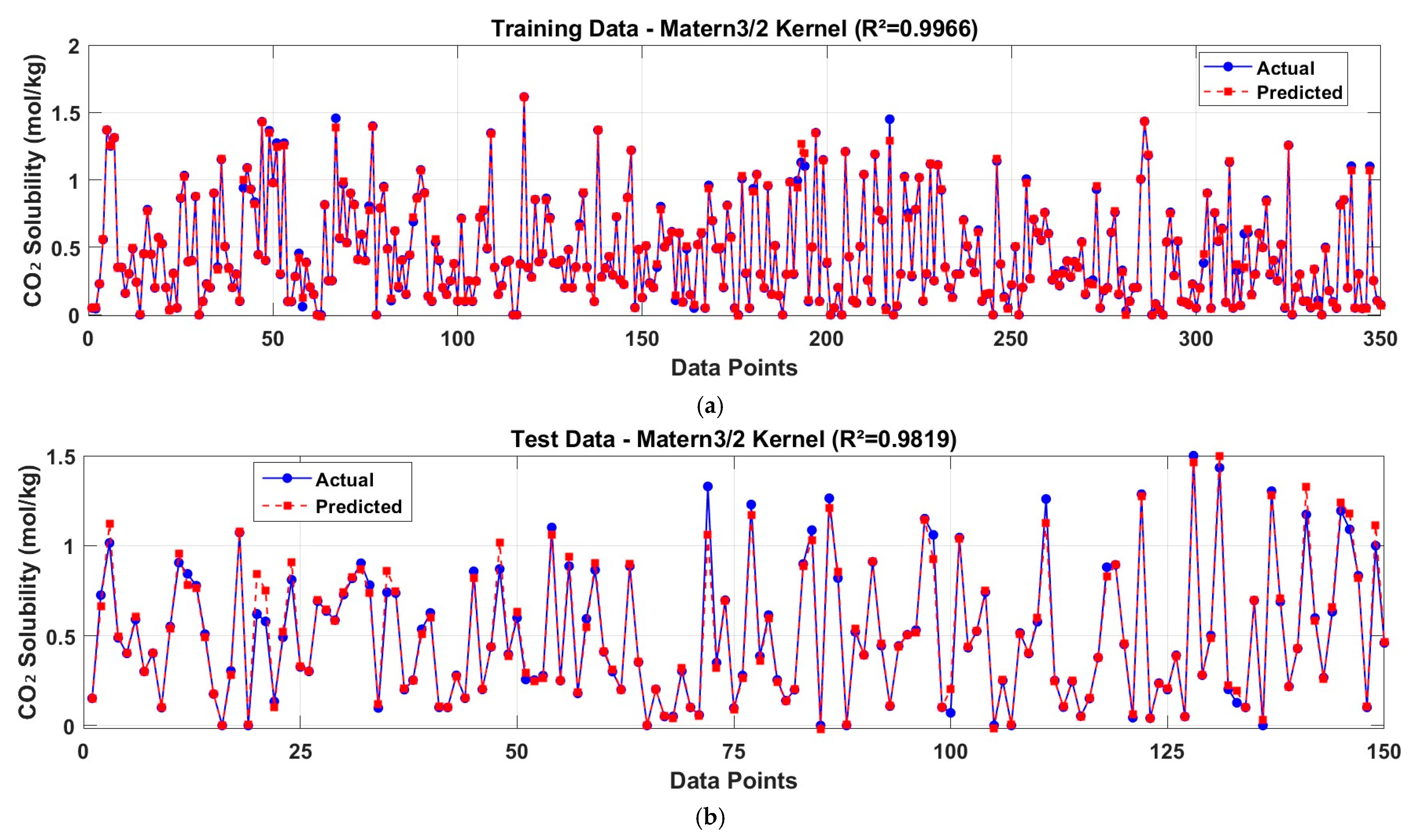
- Length Scale: 57.208
- Sigma: 9.865
- Training R2: 0.9966
- Test R2: 0.9819
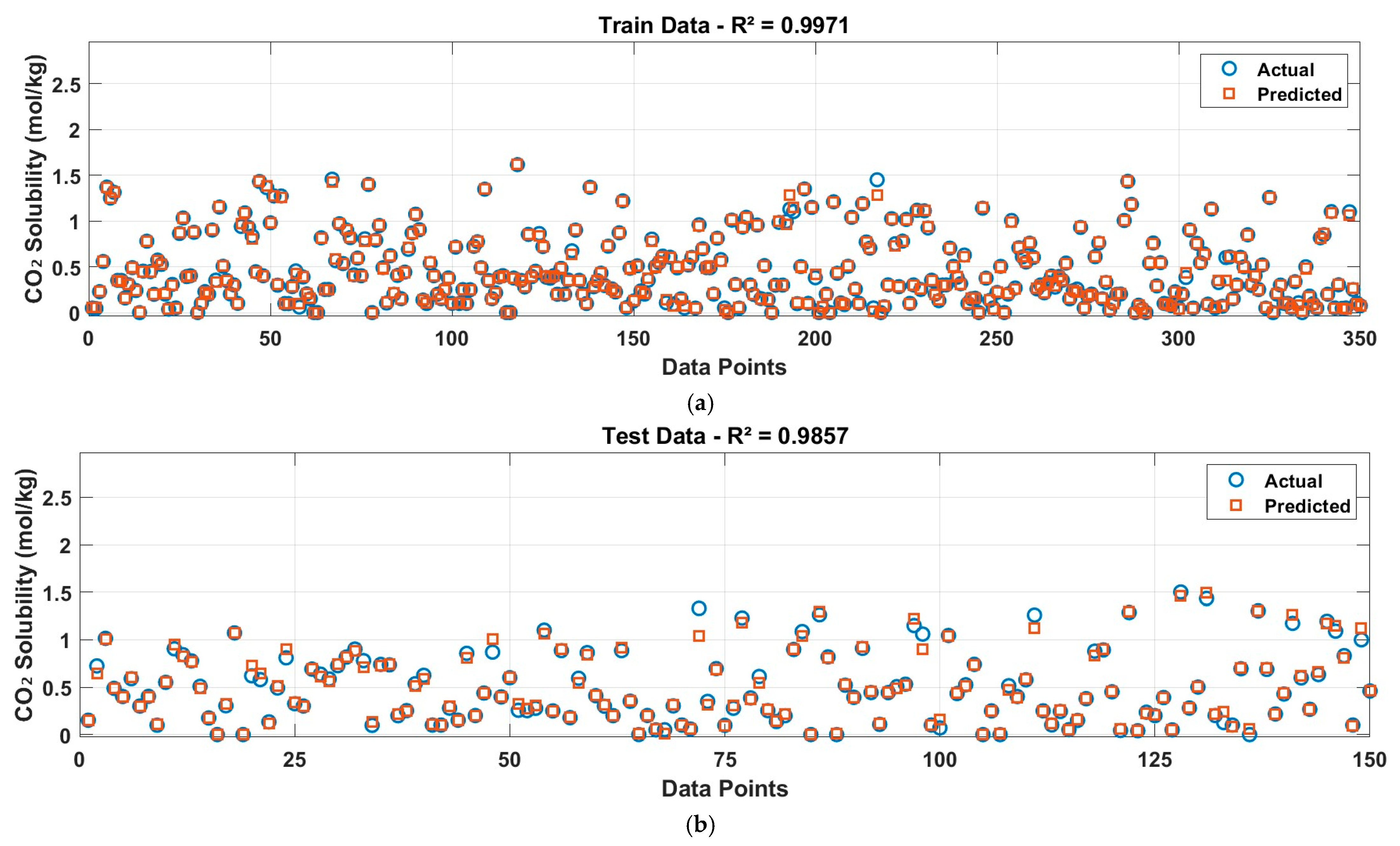
- Length scales: 31.346, 17.390, 3.762, 53.374, 41.885, 17.647, 3.070, 63.066, 54.515, 20.266, 45.695, 36.488, 9.548
- Signal variance (σ): 4.590
- Training R2: 0.9971 (99.71% accuracy)
- Test R2: 0.9960 (99.60% accuracy)

- (1)
- Interpretability requirements (some kernels provide clearer feature importance)
- (2)
- Flexibility needs (certain kernels handle complex patterns better)
- (3)
- Practical implementation constraints
4. Conclusions
5. Future Research Directions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Izadpanahi, A.; Kumar, N.; Tassinari, C.; Ali, M.; Ahmad, T.; Pinto, M.A. A Review of Carbon Storage in Saline Aquifers: Key Obstacles and Solutions. Geoenergy Sci. Eng. 2025, 250, 213806. [Google Scholar]
- Izadpanahi, A.; Blunt, M.; Kumar, N.; Ali, M.; Tassinari, C.; Pinto, M.A. A review of carbon storage in saline aquifers: Mechanisms, prerequisites, and key considerations. Fuel 2024, 369, 131744. [Google Scholar]
- Ismail, I.; Gaganis, V. Carbon Capture, Utilization, and Storage in Saline Aquifers: Subsurface Policies, Development Plans, Well Control Strategies and Optimization Approaches—A Review. Clean Technol. 2023, 5, 609–637. [Google Scholar]
- Gunatilake, T.; Zappone, A.; Zhang, Y.; Zbinden, D.; Mazzotti, M.; Wiemer, S. Quantitative Modeling and Assessment of CO2 Storage in Saline Aquifers: A Case Study in Switzerland. Carbon Capture Sci. Technol. 2025, 14, 100360. [Google Scholar]
- Ratnakar, R.; Chaubey, V.; Dindoruk, B. A novel computational strategy to estimate CO2 solubility in brine solutions for CCUS applications. Appl. Energy 2023, 342, 121134. [Google Scholar]
- Pradhan, S.; Bhattacherjee, R.; Aichele, C.; Bikkina, P. Determination of CO2 solubility in brines and produced waters of various salinities for CO2 EOR and storage applications. Chem. Eng. J. 2025, 507, 160401. [Google Scholar]
- Bhattacherjee, R.; Botchway, K.; Pashin, J.; Chakraborty, G.; Bikkina, P. Machine learning-based prediction of CO2 fugacity coefficients: Application to estimation of CO2 solubility in aqueous brines as a function of pressure, temperature, and salinity. Int. J. Greenh. Gas Control. 2023, 128, 103971. [Google Scholar]
- Sadeghi, A.; Salami, H.; Taghikhani, V.; Robert, M. A comprehensive study on CO2 solubility in brine: Thermodynamic-based and neural network modeling. Fluid Phase Equilibria 2015, 403, 153–159. [Google Scholar]
- Zou, X.; Zhu, Y.; Lv, J.; Zhou, Y.; Ding, B.; Liu, W.; Xiao, K.; Zhang, Q. Toward Estimating CO2 Solubility in Pure Water and Brine Using Cascade Forward Neural Network and Generalized Regression Neural Network: Application to CO2 Dissolution Trapping in Saline Aquifers. ACS Omega 2024, 9, 4705–4720. [Google Scholar]
- Jeon, P.R.; Lee, C.H. Artificial neural network modelling for solubility of carbon dioxide in various aqueous solutions from pure water to brine. J. CO2 Util. 2021, 47, 101500. [Google Scholar]
- Yang, S.; Wang, D.; Dong, Z.; Li, Y.; Du, D. ANN prediction of the CO2 solubility in water and brine under reservoir conditions. AIMS Geosci. 2025, 11, 201–227. [Google Scholar]
- Mohammadian, E.; Liu, B.; Riazi, A.; Huang, J. Evaluation of Different Machine Learning Frameworks to Estimate CO2 Solubility in NaCl Brines: Implications for CO2 Injection into Low-Salinity Formations. Lithosphere 2022, 1615832. [Google Scholar] [CrossRef]
- Du, X.; Thakur, G.C. Development of Advanced Machine Learning Models for Predicting CO2 Solubility in Brine. Energies 2025, 18, 1202. [Google Scholar]
- Karaei, A.M.; Honarvar, B.; Azdarpour, A.; Mohammadian, E. On prediction of carbon dioxide solubility in aqueous systems of NaCl using LSSVM algorithm. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 2801–2810. [Google Scholar]
- Hashemi, S.H.; Torabi, F. Machine Learning-Based Prediction of Scale Inhibitor Efficiency in Oilfield Operations. Processes 2025, 13, 1964. [Google Scholar]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar]
- Ulapane, N.; Thiyagarajan, K.; Kodagoda, S. Hyper-Parameter Initialization for Squared Exponential Kernel-based Gaussian Process Regression. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 1154–1159. [Google Scholar]
- Available online: https://www.mathworks.com/help/stats/kernel-covariance-function-options.html (accessed on 6 July 2025).
- Kanagawa, M.; Hennig, P.; Sejdinovic, D.; Sriperumbudur, B. Gaussian Processes and Kernel Methods: A Review on Connections and Equivalences. arXiv 2018, arXiv:1807.02582. [Google Scholar] [CrossRef]
- Beckers, T. An Introduction to Gaussian Process Models. arXiv, 2021; arXiv:2102.05497. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Chapter 4:Covariance Functions. In Gaussian Processes for Machine Learning; MIT Press: Cambridge, UK, 2006. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2960–2968. [Google Scholar]
- Li, K.Q.; Yin, Z.Y.; Zhang, N.; Liu, Y. A data-driven method to model stress-strain behaviour of frozen soil considering uncertainty. Cold Reg. Sci. Technol. 2023, 213, 103906. [Google Scholar]
- Li, K.Q.; Yin, Z.Y.; Zhang, N.; Li, J. A PINN-based modelling approach for hydromechanical behaviour of unsaturated expansive soils. Comput. Geotech. 2024, 169, 106174. [Google Scholar]
- Rumpf, B.; Nicolaisen, H.; Maurer, G. Solubility of carbon dioxide in aqueous solutions of ammonium chloride at temperatures from 313 K to 433 K and pressures up to 10 MPa. Berichte Bunsenges. Für Phys. Chem. 1994, 98, 1077–1081. [Google Scholar]
- El-Maghraby, R.M.; Pentland, C.H.; Iglauer, S.; Blunt, M.J. A fast method to equilibrate carbon dioxide with brine at high pressure and elevated temperature including solubility measurements. J. Supercrit. Fluids 2012, 62, 55–59. [Google Scholar]
- Zhao, H.; Dilmore, R.; Allen, D.E.; Hedges, S.W.; Soong, Y.; Lvov, S.N. Measurement and modeling of CO2 solubility in natural and synthetic formation brines for CO2 sequestration. Environ. Sci. Technol. 2015, 49, 1972–1980. [Google Scholar]
- Li, Z.; Dong, M.; Li, S.; Dai, L. Densities and Solubilities for Binary Systems of Carbon Dioxide + Water and Carbon Dioxide + Brine at 59 °C and Pressures to 29 MPa. J. Chem. Eng. Data 2004, 49, 1026–1031. [Google Scholar] [CrossRef]
- Poulain, M.; Messabeb, H.; Lach, A.; Contamine, F.; Cézac, P.; Serin, J.P.; Dupin, J.C.; Martinez, H. Experimental Measurements of Carbon Dioxide Solubility in Na–Ca–K–Cl Solutions at High Temperatures and Pressures up to 20 MPa. J. Chem. Eng. Data 2019, 64, 2497–2503. [Google Scholar]
- Rumpf, B.; Maurer, G. An Experimental and Theoretical Investigation on the Solubility of Carbon Dioxide in Aqueous Solutions of Strong Electrolytes. Berichte Bunsenges. Für Phys. Chem. 1993, 97, 85–97. [Google Scholar]
- Cruz, J.L.; Neyrolles, E.; Contamine, F.; Cézac, P. Experimental Study of Carbon Dioxide Solubility in Sodium Chloride and Calcium Chloride Brines at 333.15 and 453.15 K for Pressures up to 40 MPa. J. Chem. Eng. Data 2021, 66, 249–261. [Google Scholar]
- Stewart, P.B.; Munjal, P. Solubility of Carbon Dioxide in Pure Water, Synthetic Sea Water, and Synthetic Sea Water Concentrates at -50 to 250 C. and 10- to 45-Atm. Pressure. J. Chem. Eng. Data 1970, 15, 67–71. [Google Scholar]
- Tang, Y.; Bian, X.; Du, Z.; Wang, C. Measurement and prediction model of carbon dioxide solubility in aqueous solutions containing bicarbonate anion. Fluid Phase Equilibria 2015, 386, 56–64. [Google Scholar]





| Studied Ions | Machine Learning Algorithm Used | References |
|---|---|---|
| Na+, Cl− | Linear Regression (LR), Support Vector Machine (SVM), Decision Tree (DT), Random Forest (RF), Extreme Gradient Boosting (XGB) | [7] |
| Na+, Cl− | Artificial Neural Network (ANN) | [8] |
| Na+, K+, Ca2+, Mg2+, Cl−, HCO3−, SO42− | Cascade Forward Neural Network (CFNN), Generalized Regression Neural Network (GRNN) | [9] |
| Na+, K+, Mg2+, Ca2+, Cl−, SO42−, HCO3− | Feed-forward Back-propagation Neural Network (BPNN) | [10] |
| Na+, Cl− | Multilayer Perceptron (MLP) | [11] |
| Na+, Cl− | XGBoost (XGB), K-Nearest Neighbor (KNN), Multilayer Perceptron (MLP), Genetic Algorithm (used to derive an empirical equation) | [12] |
| Na+, Cl− | Decision Tree (DT), Random Forest (RF), XGBoost, Multilayer Perceptron (MLP), Support Vector Regression with Radial Basis Function Kernel (SVR-RBF) | [13] |
| Na+, Cl− | Least Squares Support Vector Machine (LSSVM) optimized by Particle Swarm Optimization (PSO) | [14] |
| Na+, K+, Mg2+, Ca2+, Cl−, SO42−, HCO3−, Br−, Fe2+, Sr2+, NH4+ | A Multi-Kernel Gaussian Process Regression (GPR) Framework Optimized by Grey Wolf Algorithm and Physics-Informed GPR Model | This work |
| Kernel Functions | Mathematical Formula | Hyperparameter | References |
|---|---|---|---|
| Squared Exponential | σl, σf | [18,19,20,21] | |
| Matern 3/2 | σl, σf | [18,19,20,21] | |
| Matern 5/2 | σl, σf | [18,19,20,21] | |
| Rational Quadratic | σl, σf, α | [18,20,21] | |
| ARD Squared Exponential | θm = log σm, for m = 1,2, …, d θd+1 = log σf | [18,20,22] | |
| ARD Matern 3/2 | r = | θm = log σm, for m = 1,2, …, d θd+1 = log σf | [18] |
| ARD Matern 5/2 | r = | θm = log σm, for m = 1,2, …, d θd+1 = log σf | [18,22] |
| ARD Rational Quadratic Kernel | θm = log σm, for m = 1,2, …, d θd+1 = log σf | [18] |
| Brine Composition | Pressure (MPa) | Temperature (K) | CO2 Solubility (mol/kg) | References |
|---|---|---|---|---|
| NH4Cl + H2O | 0.48–9.69 | 313.15–433.15 | 0.09–1.1519 | [25] |
| NaCl + KCl + H2O | 0.34–9 | 306.15–343.15 | 0.045–1.105 | [26] |
| NaCl + KCl + MgCl2 + CaCl2 + Na2SO4 + SrCl2 + NaBr + H2O | 10–17.5 | 323.15–423.15 | 0.326–0.956 | [27] |
| Formation Brine Sample: Ca, Na, Mg, K, Fe, Cl, SO4 | 1.76–20.87 | 332.15 | 0.24–0.958 | [28] |
| Salt Solution: Na, K, Ca, Cl | 1.01–19.93 | 323–423 | 0.1305–0.8517 | [29] |
| Al2(SO4)3 + H2O Na2SO4 + H2O | 0.185–9.868 | 313–433 | 0.049–0.7272 | [30] |
| NaCl + CaCl2 + H2O | 6.06–40.05 | 333.15–453.15 | 0.3–1.37 | [31] |
| NaCl + CaCl2 + MgSO4 + MgCl2 + KCl +NaHCO3+ NaBr + H2O | 0.101325–4.5596 | 268.15–298.15 | 0.025–1.4573 | [32] |
| Formation Brine Sample: Ca, Na, Mg, K, Fe, Cl, SO4, HCO3 | 8–40 | 308.15–408.15 | 0.46–1.6155 | [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hashemi, S.H.; Torabi, F.; Tontiwachwuthikul, P. Machine Learning-Driven Prediction of CO2 Solubility in Brine: A Hybrid Grey Wolf Optimizer (GWO)-Assisted Gaussian Process Regression (GPR) Approach. Energies 2025, 18, 4205. https://doi.org/10.3390/en18154205
Hashemi SH, Torabi F, Tontiwachwuthikul P. Machine Learning-Driven Prediction of CO2 Solubility in Brine: A Hybrid Grey Wolf Optimizer (GWO)-Assisted Gaussian Process Regression (GPR) Approach. Energies. 2025; 18(15):4205. https://doi.org/10.3390/en18154205
Chicago/Turabian StyleHashemi, Seyed Hossein, Farshid Torabi, and Paitoon Tontiwachwuthikul. 2025. "Machine Learning-Driven Prediction of CO2 Solubility in Brine: A Hybrid Grey Wolf Optimizer (GWO)-Assisted Gaussian Process Regression (GPR) Approach" Energies 18, no. 15: 4205. https://doi.org/10.3390/en18154205
APA StyleHashemi, S. H., Torabi, F., & Tontiwachwuthikul, P. (2025). Machine Learning-Driven Prediction of CO2 Solubility in Brine: A Hybrid Grey Wolf Optimizer (GWO)-Assisted Gaussian Process Regression (GPR) Approach. Energies, 18(15), 4205. https://doi.org/10.3390/en18154205







