Abstract
The use of power smoothing for renewable energy resources is attracting increasing attention. One widely used resource that could benefit from this technique is the grid-tied photovoltaic (PV) system. Solar energy production typically follows a Gaussian bell curve, with peaks at midday. This paper confirms this pattern by using the bell curve as a reference; however, climate variations can significantly alter this pattern. Therefore, this study aimed to smooth the power supplied to the grid by a PV system. The proposed controller manages the charge and discharge processes of the energy storage system (ESS) to ensure a smooth Gaussian bell curve output. It adjusts the parameters of this curve to closely match the generated energy, absorbing or supplying fluctuations to maintain the desired profile. This system also aims to provide accurate predictions of the power that should be supplied to the grid by the PV system, based on the capabilities of the ESS and the overall system performance. Although experimental results were not included in this analysis, the system was implemented in SIMULINK using real-world data. The controller utilizes a hybrid ESS comprising a vanadium redox battery (VRB) and supercapacitors (SCs). The design and operation of the controller, including curve tuning and ESS charge–discharge management, are detailed. The simulation results demonstrate excellent performance and are thoroughly discussed.
1. Introduction
The exponential growth of renewable energy resources and their increasing contribution to the grid has been accompanied by rapid fluctuations in the power they generate, which significantly impact grid stability. Electricity generated by these resources is subject to natural variability; for instance, in PV systems, the output fluctuates based on factors such as cloud cover, temperature, and solar irradiation. ESSs are widely used to mitigate the intermittency of renewable energy sources, especially in grid-connected systems [1]. Their primary function is to smooth the power output through peak-cutting and valley-filling [2]. Batteries are commonly used as ESSs, but reducing their size presents both technical and financial challenges [3]. To address these challenges, using an effective controller for power smoothing is essential, especially under unpredictable weather conditions.
Various methods have been developed to control the charging and discharging processes in order to ensure predictable and stable delivery of power from renewable resources. Techniques such as low-pass filters, moving averages [4,5], fuzzy logic [6], neural network-based predictive systems [7], and deep reinforcement learning [8] have been explored for this purpose. This paper proposes a novel method that involves fine-tuning the Gaussian bell curve to provide a robust solution. The proposed method functions as a dynamic filtering mechanism throughout the day and adjusts in real time based on key ESS parameters, such as the state of charge (SOC). Additionally, the controller actively manages the ESS to prevent overcharging or excessive discharging.
It should be noted that previous studies have utilized Gaussian filters to smooth generated energy [9]. However, this paper adopts a different approach by focusing on the Gaussian bell curve, which represents the Gaussian distribution. The study in [10] also focuses on the Gaussian distribution of PV and wind energy, aligning closely with the concept presented in this paper.
While earlier smoothing methods sought to predict the next set of data without considering the broader context, this paper examines the behavior of PV-generated energy across the entire day. It provides a comprehensive perspective on predicting daily energy production by analyzing variations at different hours. The tuning process further enhances the reliability of the proposed approach. The method introduced in this paper is both simple and effective. Although it aligns with the objectives of previous research, it differs significantly in its approach by analyzing the energy output of a PV system over an entire day and establishing a reference framework.
This paper adopts a comprehensive perspective to present an effective solution, as demonstrated by the results. The chosen system is detailed in Section 2, while PV data collected from two sources are discussed in Section 3. The concept of using a Gaussian bell curve for power smoothing using ESS explained in Section 4. The process of deriving and tuning the Gaussian bell curve for parameter adjustments is outlined in Section 5. Section 6 describes the controller developed for the entire system, and the results are presented and analyzed in Section 7. Section 8 provides a comparison of the curves achieved in this study with theoretically fitted curves.
2. System Description
The proposed network comprises the electricity grid, a renewable energy resource, and an energy storage system (ESS). The ESS is designed to smooth the energy supplied to the grid by the renewable energy resource, specifically, a PV solar system. It is a hybrid system consisting of a vanadium redox battery (VRB) and supercapacitors (SCs). It achieves energy smoothing by absorbing sudden increases in energy generated by the PV system, and by supplying energy to the grid to counteract sudden decreases caused by the PV system. This system has been previously utilized and discussed in [11].
Figure 1 presents a block diagram of the system. The VRB used is the E22 Energy Storage Solutions 400 kWh model, designed for four-hour operation. The SC system is the MAXWELL TECHNOLOGIES BMOD0165 P048 BXX model, manufactured by Maxwell Technologies Shanghai Trading Co. Ltd., Shanghai, China. This SC consists of 14 cells in series at 660 V DC and 35 sets in parallel, resulting in a total of 14 × 35 (490 cells) and a capacity of 26 kVA. The equivalent models implemented in Simulink are described in [11]. A hybrid system comprising a VRB and SCs is often utilized as a hybrid storage solution. VRBs offer a high energy density, which is suitable for long-term charging and discharging, while SCs offer a high power density, enabling rapid response times. This paper introduces modifications focused on the controller. Using a VRB as an ESS offers numerous advantages [7], with an effective efficiency range in the SOC window of 20–85%. Incorporating SCs to construct a hybrid system enhances the ESS’s ability to eliminate fluctuations in the power supply from renewable energy resources, making this one of the most effective solutions [7,12].
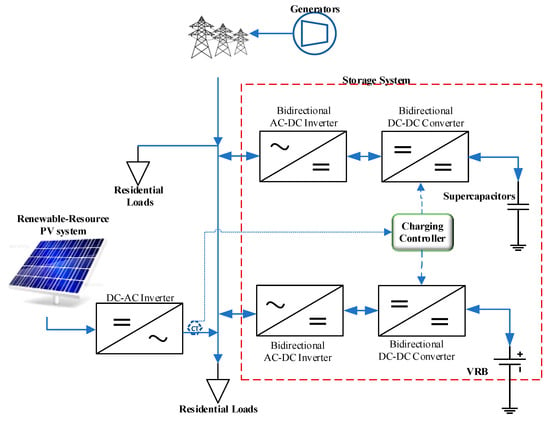
Figure 1.
A block diagram of the system.
3. PV Data
The data tested in this study were obtained from two sources. The first dataset was collected from a 30 MW PV plant in Malaysia between 30 June 2021 and 8 July 2021. It was gathered using a Fluke meter connected to the output of a 2 MW plant inverter, as described in [11]. The collected power data are shown in Figure 2. The second dataset was sourced from a project conducted by UK Power Networks, with data recorded at 1 min intervals during the summer of 2014 [13]. A portion of this dataset is presented in Figure 3a. The data shown in Figure 3a represent the output of UK Power Networks scaled by a factor of 660 to align with the output collected in Malaysia. The original data collected over two days, as described in [11], are displayed in Figure 3b. This figure highlights the difference between a sunny and a cloudy day.
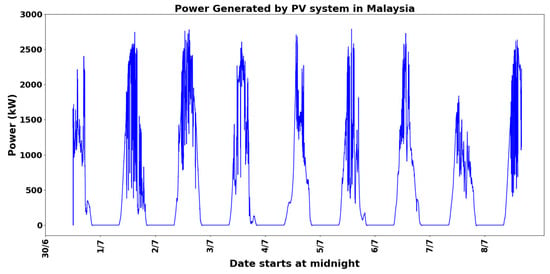
Figure 2.
The PV output collected from 2 MW PVs in Malaysia between 30 June 2021 and 8 July 2021.
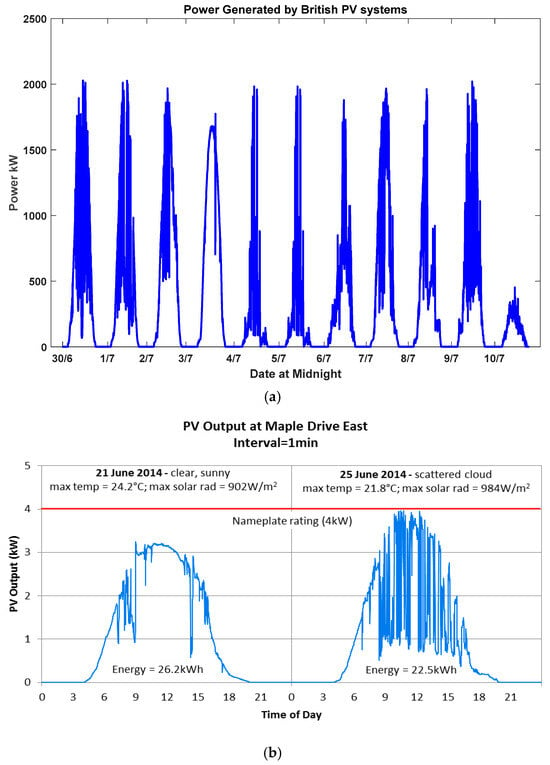
Figure 3.
(a) The PV output collected from UK Power Networks between 30 June 2014 and 10 July 2014. (b) The PV output power at Maple Drive East collected from UK Power Networks on a clear sunny day vs. a scattered cloudy day, as described in [13].
4. Power Smoothing Using ESS
Grid integration with ESS offers numerous advantages, primarily enhancing stability when combined with renewable energy sources. It improves power quality and bolsters economic efficiency [14]. The ESS can balance the supplied power and demand in a grid connected to renewable energy sources. A significant challenge is storing enough energy for later use to compensate for sudden drops in energy supply while simultaneously being able to absorb peak power demands. Although weather patterns are difficult to predict, the total incoming power from renewable resources, such as photovoltaic (PV) systems, is more manageable. The purpose of this research is to effectively manage the energy storage levels in the ESS, ensuring it is prepared to absorb and supply the necessary energy for grid stability.
The expected power output varies based on geographical and climatic conditions at specific locations on Earth. This paper employs data averaging from recent days to create a curve that closely approximates the incoming power for a given day, utilizing a Gaussian bell curve as a model. Just as managing expenditure and savings is crucial for a company’s long-term success, maintaining a certain equilibrium is essential in this context. Therefore, adjusting and fitting parameters is necessary to achieve this balance. These parameters define the shape of the curve, with the charging and discharging processes analogous to spending and saving.
There is no specific reference signal to which this curve can be compared with the proposed curve. However, the effective management of charging and discharging, without increasing the size of the ESS, can be achieved by keeping the SOC within its designated limits.
5. Gaussian Smoothing
The characteristic power generated by a PV system during the day generally resembles a bell curve, which is similar to a Gaussian distribution [15]. This pattern reflects the natural radiation spectrum throughout the day, which increases after sunrise, peaks at midday, and then decreases until sunset [16,17]. The total power supplied throughout the day can be smoothed to follow a Gaussian function [12], defined as follows:
where a is the height of the curve’s peak, b is the position of the center of the peak, and c controls the width of the “bell”, as shown in Figure 4. The parameters in Equation (1) can be adjusted or tuned to achieve a curve that closely matches the generated power. For simplicity, b (the position of the center of the peak) can be assumed to be constant, as it typically corresponds to midday (noon). Meanwhile, a and c can be tuned to achieve the desired curve. The times of sunset and sunrise vary according to the season, latitude, and longitude. This affects a and c in the bell curve, with a corresponding to radiation and c depending on the location and the time of year. As illustrated in Figure 4, altering c changes the width of the bell curve, while adjusting a modifies the height of the peak. The error observed in the morning and afternoon—corresponding to the tails of the curve—is significantly influenced by changes in c (the width). This error mathematically corresponds to times of day far from the time represented by b. Conversely, adjustments to a (the peak height) have a substantial effect on the error during periods of high radiation, which correspond to times closer to b. Based on these observations, it can be concluded that the error can be used to tune a and c, proportionally to the time of day relative to b for a, and inversely for c. To simplify this, the change factor Cfact in a and c due to the error can be derived as follows:
where Time is the time in minutes from midnight, and b is the time in minutes corresponding to the peak radiation (as defined in Equation (1)). To explain the effect of Cfact it is a factor less than one that has a large value at the tails of the day and decreases to zero near noon. Therefore, if the error is multiplied by Cfact it will have significant weight which necessitates modifying c. Conversely, (1 − Cfact) is used to modify a. The error is calculated as the difference between the total power (or discrete current values, assuming that the voltage remains nearly constant) and the total area under the Gaussian bell curve. The control system adjusts a and c by incrementally adding or subtracting small values to minimize this error. Another important factor to consider is the SOC of the battery. Adjustments to a and c must ensure that the SOC remains at around 0.5, as this will minimize the adverse effects of a fully charged or completely discharged battery. The updated values of a and c can be derived as follows:
where Ppv is the power generated by the PV system at the start of the day, AreaBell represents points on the generated bell curve, and k is a factor used to minimize the step change k = 0.1. The values a0 and c0 are the averages of their respective variables over the previous several days. Each day starts with the assumption that a = a0 and c = c0, with the tuning process starting at 5:00 am, as the power summation before that time is negligible.
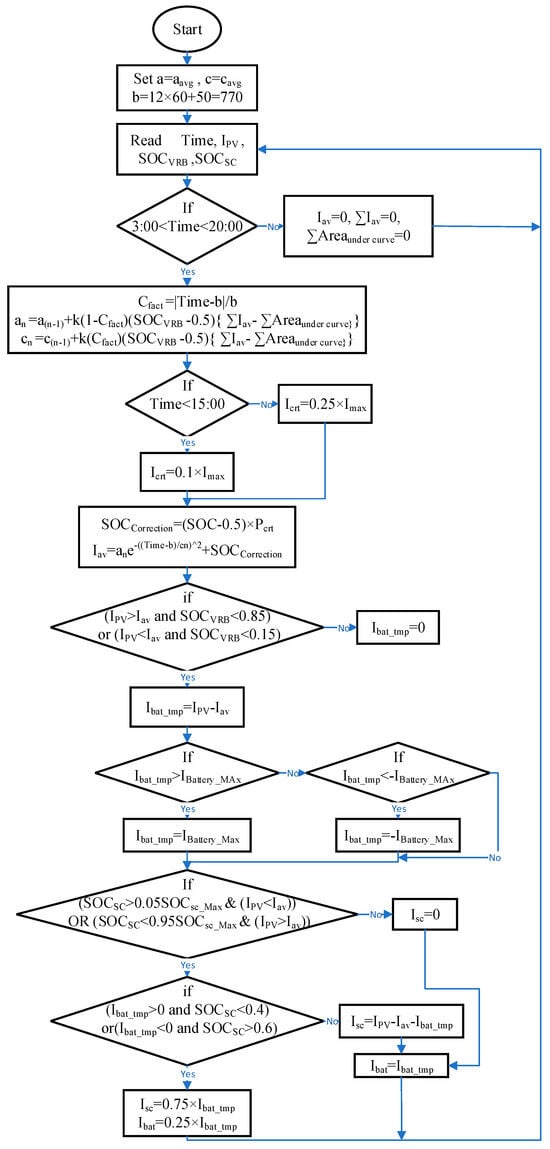
Figure 4.
A flowchart of the control process.
The above equations provide a reliable approximation of the smoothed average power of the PV system. However, in practical applications, two additional factors must be considered to make the smoothing process more effective. Firstly, the power generated in the morning does not follow a bell curve. Instead, it remains near zero before increasing rapidly with the onset of sunshine. A similar phenomenon occurs at sunset, where the power drops sharply. This problem is addressed by ensuring that zero power is assumed outside of the sunshine period, defined as the hours of 5:00–20:00. Secondly, changes in PV-generated power can exhibit significant, abrupt variations, which could drive the SOC to its limits (either fully charged or fully discharged). To mitigate this, approximately ±10% of the total power is added to the bell curve. Thus, Equation (1) becomes the following:
The expression of is as follows:
where Pcrt = 0.05 × Pmax (Pmax: the maximum power generated by the PV system); this level can be maintained until 15:00. After this time, it can be increased by up to 10%, so Pcrt = 0.1 × Pmax if the SOC deviates significantly from 50%. This adjustment helps the battery to maintain approximately half of its charge, ensuring that it begins the next day with an effective charge level. It is important to note that if the battery is intended to serve as a power source during peak consumption hours, SOCcorrection (SOC − 0.8) Pcrt should be used during the final hours of the day to maintain the battery’s charge level at around 50%. Additionally, the battery can be charged to 50% during the early hours of the day in such scenarios.
6. Control Process
The implemented controller is designed to reduce imitation fluctuations in PV-generated power by providing an expected average power that is aligned as closely as possible with the actual generated power. This approach enables the energy storage system (ESS) to absorb surplus power and supply additional power to smooth out fluctuations, thereby maintaining network stability. Achieving an accurate estimation of the average power generated by the PV minimizes the size and cost of the ESS required for smoothing.
The controller performs three main functions: generating the optimal expected average power (based on the methodology described in the previous section), managing the charging and discharging of the battery to achieve power smoothing, and controlling the selection of charging and discharging between the VRB and SC to prevent overcharging or excessive discharging.
The controller achieves this functionality by monitoring the PV-generated current and the state of charge (SOC) of the VRB and SC. These parameters determine the current that needs to be absorbed or generated by the VRB and SC, as shown in the flowchart in Figure 4. The system was simulated using SIMULINK by incorporating the collected data described in Section 3 as a PV current source. To optimize the simulation efficiency, an average inverter model was used. The SOC of the SC was calculated as described in [11].
The relationship between the charging and discharging processes of the VRB and the SC is illustrated in the flowchart shown in Figure 4. When the state of charge of the VRB (SOCVRB) is low and the state of charge of the SC (SOCSC) is high, the controller will prioritize charging the VRB to over 50% during the charging process, with the remaining charge directed to the SC. Conversely, during the discharging process, the controller will discharge the SC more than the VRB. This pattern is reversed when the states of charge are swapped.
7. Simulation Results
The new controller, outlined in the flowchart in Figure 4, was implemented within the system shown in Figure 5. This controller regulates the charging process for both the VRB and the SC. The parameters (a), (b), and (c) in Figure 4 were estimated based on the average values of previous test data. The system stores the average values of parameters (a) and (c) from the previous ten days, while (b) is kept constant. The averaged parameters can also be obtained through alternative methods, such as analyzing historical data, calculating radiation based on geographical location [18], or employing machine learning techniques in the future based on training [19]. Two cases of collected data are shown. The simulation was performed using MATLAB Simulink R2024a with adherence to the methods described in Section 3 to ensure that the results would closely reflect real-world applications. The simulation utilized averaged bidirectional inverters for both the VRB and SC, functioning as three-phase current sources to replicate the current observed in practice.
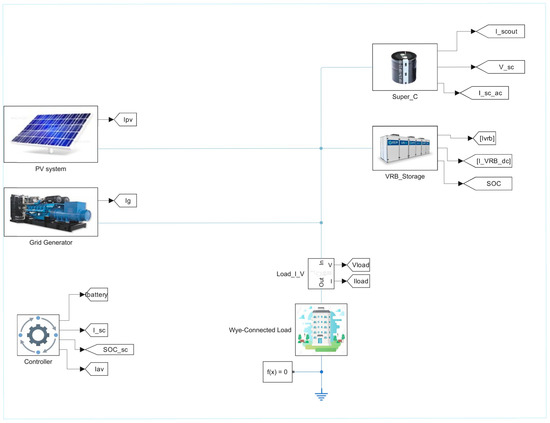
Figure 5.
A Simulink block diagram for the system.
These assumptions were made to expedite the simulation process. While minor losses and transient cases may occur, they are not expected to significantly impact the overall results. The simulation results for the PV data collected from Malaysia, as shown in Figure 2, were simulated and are displayed in Figure 6. The figure illustrates the following: the original current generated by the PV system; the current absorbed or supplied by the VRB; the current absorbed or supplied by the SC; the current supplied to the system, which exhibits an almost Gaussian bell shape; and the SOC of both the VRB and SC. The results illustrate a smooth output closely resembling a Gaussian bell curve. The controller successfully maintains the SOC of the VRB at around 0.5, which aligns with the range recommended in [2,20] between 20 and 85%. It is evident that the VRB is charged and discharged sequentially to smooth the power supplied to the grid. Guided by the reference signal generated by the controller, the dissipated power aligns with the expected curve, enhancing the grid stability. Figure 7 displays the controller’s output for the data collected by UK Power Networks. This figure shows the original current generated by the PV system, the currents associated with the VRB and the SC, the current supplied to the grid, and the SOC of both the VRB and SC. The results are similar to those presented in [11]; however, on 23 June 2014, the battery reached full charge. Figure 8 focuses on the data collected in Malaysia on 30 June, providing detailed insights into how the ESS absorbed the current that exceeded the expected curve. The ESS effectively supplied a sufficient current to meet the proposed curve. Additionally, Figure 8 highlights instances of unsmoothing caused by full discharging of the SC and the VRB’s inadequacy in filling the supply gap. The tuning parameters (a, c) are displayed in Figure 9. Each day starts with the average values from the previous 10 days, as previously discussed. Adjustments are made throughout the day according to the flowchart in Figure 4.
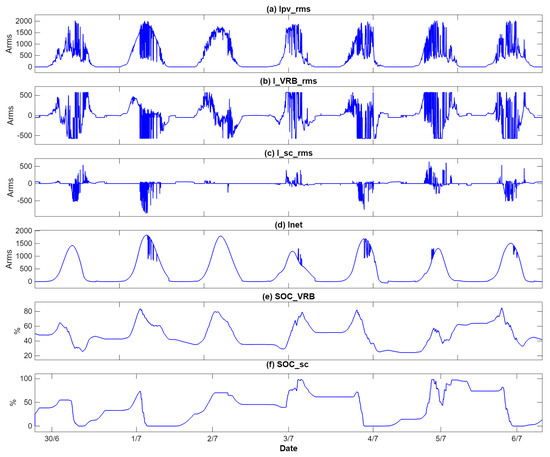
Figure 6.
The simulation results for the data collected in Malaysia from 30 June to 8 July. (a) Ipv is the PV-generated current, (b) IBatt is the current absorbed or supplied by the VRB, and (c) Isc is the current absorbed or supplied by the SC. (d) The current supplied to the grid, (e) the SOCBatt of the VRB, and (f) the SOCsc of the SC.
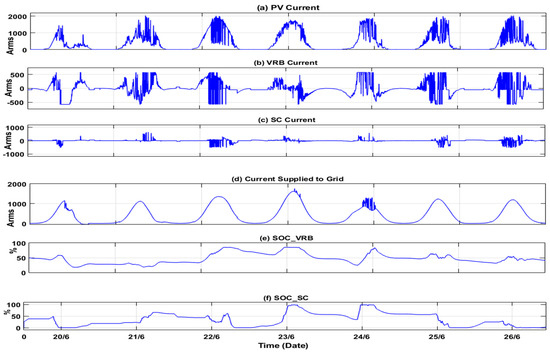
Figure 7.
The simulation results for the data collected in the UK on 20 June–25 June: (a) Ipv represents the PV-generated current, (b) IBatt represents the current absorbed or supplied by the VRB, and (c) Isc represents the current absorbed or supplied by the SC. (d) The current supplied to the grid, (e) the SOCBatt of the VRB, and (f) the SOCsc of the SC.
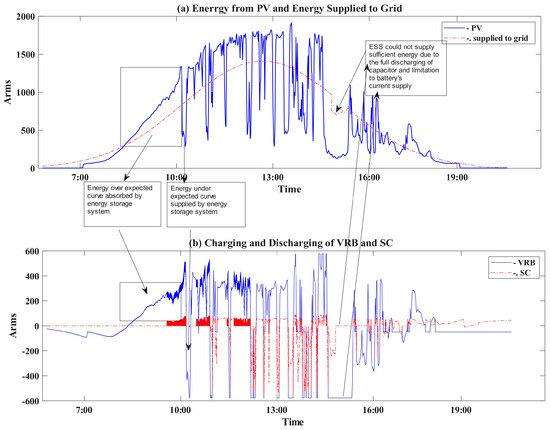
Figure 8.
Details of the charging and discharging process to provide smoothing. (a) The data collected in Malaysia on 29 June and the current supplied to the grid. (b) The charging and discharging of the VRB and SC.
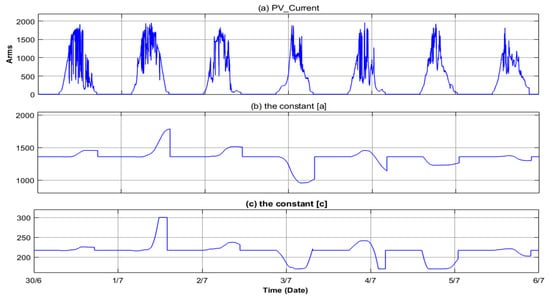
Figure 9.
The simulation results for the data collected in Malaysia from 1 July to 6 July, (a) PV supplied current, (b) the change in constant a of the Gaussian bell, and (c) the change in constant c of the Gaussian bell.
8. Comparison of Results
The parameters (a), (b), and (c) can be determined using statistical and probability fitting, as well as using the methods described in [21,22]. In this study, the primary goal was to enable real-time predictions.
The method proposed in this paper relies on statistical analysis, with the primary objective of generating curves that smoothly represent the power output from the (PV) system. The challenge with these curves is to balance the power or current above the curve with that below. In an ESS, this means that the charging power should be nearly equal to the discharging power. Currently, there is no ideal curve that can serve as a reference for comparison. The achievement of a state of equilibrium between charging and discharging can be easily verified by monitoring the SOC. Maintaining the SOC at around 50% indicates that the charging and discharging processes are nearly equal.
Comparing results with a known reference enhances their reliability. The data presented in Figure 2 were subjected to Gaussian fitting in MATLAB, and the result referred to as a reference curve. Additionally, the calculated averages of (a) and (c) were used to generate a Gaussian curve in Simulink, also termed a reference curve. The current supplied to the grid, as shown in the real-time simulation illustrated in part d of Figure 6, represents the achieved curve.
Figure 10 illustrates the comparison between these curves. Part A shows the curve generated through fitting in MATLAB, the curve generated using the averaged parameters for a specific date, and the curve generated in Simulink of the power supplied to the grid using this system. It is evident that the three curves exhibit significant similarity. The differences between the achieved curve and the ideal reference curve in certain areas are attributed to smoothing or minor fluctuations caused by full charging or discharging, as previously shown in Figure 9.
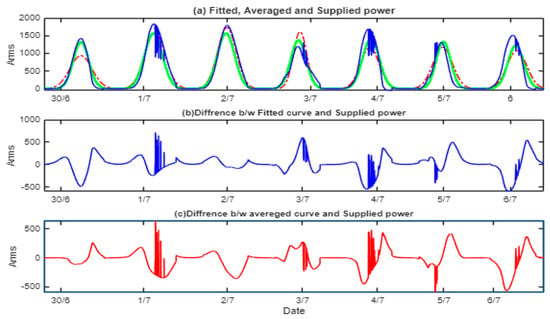
Figure 10.
A comparison of the different curves (a) the curve generated in MATLAB through fitting (red dash), the generated curve using the averaged parameters for a specific date (green), and the curve generated in Simulink of the power supplied to the grid using this system (blue). (b) the error between the fitted and averaged curve. (c) the error between the fitted curve and the supplied power.
The comparison of Figure 9 with the results presented in Figure 10 indicates that parameter c increases when irradiation occurs after midday, remaining above the expected curve, as illustrated in 1/7 in those figures. However, it reaches a minimum when irradiation decreases, as shown in 3/7, which is a typical outcome in the actual curve fitting. Additionally, parameter a demonstrates a nearly identical response with reduced reflection.
9. Conclusions
The proposed method successfully achieved a smooth Gaussian bell shape of the power delivered to the grid. The controller dynamically adjusted the Gaussian bell parameters (a, c) to generate a reference signal that minimized the likelihood of the battery becoming fully charged or completely discharged. This method effectively smoothed the energy supplied to the grid, maintaining the SOC at approximately 50%, which optimizes the battery’s efficiency and prolongs its lifespan. This equilibrium between charging and discharging is essential for achieving the desired smoothing effect. The hybrid system effectively absorbed current fluctuations. Although the system was only simulated and it neglected some transient cases, it utilized real instrument parameters (VRB and SC) and real collected data. Furthermore, the simulation was conducted using MATLAB Simulink, a highly trusted piece of simulation software. The Gaussian tuning method provides a highly effective solution for power smoothing by optimally controlling the energy storage system in conjunction with the PV plant.
In addition, the approach of tuning the Gaussian bell shape using parameters has the potential to address a wide range of challenges in other applications that rely on natural Gaussian curves.
Author Contributions
Methodology, A.I.A.; software and simulation, A.I.A.; validation, A.I.A. and N.A.R.; formal analysis, A.I.A.; investigation, A.I.A.; resources, A.I.A. and J.S.; writing—original draft preparation, A.I.A.; writing—review and editing, A.I.A., N.A.R. and J.S.; supervision, N.A.R. and J.S.; funding acquisition, A.I.A. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work is supported financially by the Ministry of Higher Education Malaysia via Fundamental Research Grant Scheme FP103-2018A (FRGS/1/2018/TK10UM/02/4), UM Power Energy Dedicated Advanced Centre (UMPEDAC) and the Higher Institution Centre of Excellence (HICoE) Program Research Grant, Ministry of Higher Education Malaysia, Universiti Malaya Research Grant UM.0001452/HRU.OP (Energy Applications Optimization for Renewable Energy and Building Usage). The authors would also like to thank Collaborative Research in Engineering, Science & Technology Center (CREST)-PV122-2024 for their continuous support in this research.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of hotovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar]
- Li, J.; Hu, D.; Mu, G.; Wang, S.; Zhang, Z.; Zhang, X.; Lv, X.; Li, D.; Wang, J. Optimal control strategy for large-scale VRB energy storage auxiliary power system in peak shaving. Int. J. Electr. Power Energy Syst. 2020, 120, 106007. [Google Scholar]
- Laajimi, M.; Go, Y.I. Energy storage system design for large-scale solar PV in Malaysia: Techno-economic analysis. Renew. Wind. Water Sol. 2021, 8, 3. [Google Scholar]
- Syed, M.A.; Abdalla, A.A.; Al-Hamdi, A.; Khalid, M. Double Moving Average Methodology for Smoothing of Solar Power Fluctuations with Battery Energy Storage. In Proceedings of the 2020 International Conference on Smart Grids and Energy Systems (SGES), Perth, Australia, 23–26 November 2020; pp. 291–296. [Google Scholar]
- Atif, A.; Khalid, M. Saviztky–Golay Filtering for Solar Power Smoothing and Ramp Rate Reduction Based on Controlled Battery Energy Storage. IEEE Access 2020, 8, 33806–33817. [Google Scholar]
- Li, X.; Li, N.; Jia, X.; Hui, D. Fuzzy logic based smoothing control of wind/PV generation output fluctuations with battery energy stor- age system. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar]
- Etxeberria, A.; Vechiu, I.; Baudoin, S.; Camblong, H.; Kreckelbergh, S. Control of a Vanadium Redox Battery and supercapacitor using a Three-Level Neutral Point Clamped converter. J. Power Sources 2014, 248, 1170–1176. [Google Scholar]
- Kolodziejczyk, W.; Zoltowska, I.; Cichosz, P. Real-time energy purchase optimization for a storage-integrated photovoltaic system by deep re- inforcement learning. Control. Eng. Pract. 2021, 106, 104598. [Google Scholar]
- Desta, A.A.; Courbin, P.; Sciandra, V.; George, L. Gaussian-Based Smoothing of Wind and Solar Power Productions Using Batteries. Int. J. Mech. Eng. Robot. Res. 2017, 6, 154–159. [Google Scholar]
- Addisua, A.; Georgeb, L.; Courbina, P.; Sciandra, V. Smoothing of renewable energy generation using Gaussian-based method with power constraints. In Proceedings of the 9th International Conference on Sustainability in Energy and Buildings, Chania, Crete, Greece, 5–7 July 2017. [Google Scholar]
- Alyan, A.; Rahim, N.A.; Jeyraj, S. Energy Storage System Sizing for a Grid-Tied Pv System: Case Study in Malaysia. Preprints 2025, 2025061910. [Google Scholar] [CrossRef]
- Guo, H. A Simple Algorithm for Fitting a Gaussian Function [DSP Tips and Tricks]. IEEE Signal Process. Mag. 2011, 28, 134–137. [Google Scholar]
- Photovoltaic (PV) Solar Panel Energy Generation Data. Data Collected as Part of the Project Run by UK Power Networks, July, 2024. Available online: https://data.london.gov.uk/dataset/photovoltaic–pv–solar-panel-energy-generation-data (accessed on 13 May 2025).
- Poullikkas, A. A comparative overview of large-scale battery systems for electricity storage. Renew. Sustain. Energy Rev. 2013, 27, 778–788. [Google Scholar]
- Jaramillo, O.; Aguilar, J.; Robles-Pérez, M.; Borunda, M. Simple Analytical Approach to Estimating Solar Flux Distribution in a Multifaceted Solar Furnace Concentrator. Processes 2025, 13, 1383. [Google Scholar] [CrossRef]
- Zhou, B.; Li, H.; Wang, C.; Wang, D.; Ma, X. Energy Distribution and Working Characteristics of PIPVT Dual-Energy Module. Sustainability 2024, 16, 9151. [Google Scholar] [CrossRef]
- Ramírez-Rivera, F.; Guerrero-Rodríguez, N. Ensemble Learning Algorithms for Solar Radiation Prediction in Santo Domingo: Measurements and Evaluation. Sustainability 2024, 16, 8015. [Google Scholar]
- de Luis-Ruiz, J.M.; Salas-Menocal, B.R.; Pereda-García, R.; Pérez-Álvarez, R.; Sedano-Cibrián, J.; Ruiz-Fernández, C. Optimal Location of Solar Photovoltaic Plants Using Geographic Information Systems and Multi-Criteria Analysis. Sustainability 2024, 16, 2895. [Google Scholar] [CrossRef]
- González-Plaza, E.; García, D.; Prieto, J.-I. Monthly Global Solar Radiation Model Based on Artificial Neural Network, Temperature Data and Geographical and Topographical Parameters: A Case Study in Spain. Sustainability 2024, 16, 1293. [Google Scholar] [CrossRef]
- Ceraolo, M.; Lutzemberger, G.; Poli, D. State-of-Charge Evaluation Of Supercapacitors. J. Energy Storage 2017, 11, 211–218. [Google Scholar]
- Peña, V.; Jauch, M. Properties of the generalized inverse Gaussian with applications to Monte Carlo simulation and distribution function evaluation. Stat. Probab. Lett. 2025, 220, 110359. [Google Scholar]
- Zhu, Y.; Yao, W. A conditional probability density function model for fatigue damage estimation in broadband non-Gaussian stochastic processes. Int. J. Fatigue 2025, 197, 108958. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).