Recent Advances in Numerical Modeling of Aqueous Redox Flow Batteries
Abstract
1. Introduction
2. Key Processes and Physicochemical Phenomena in ARFBs
2.1. Flow Battery Structure
2.2. Porous Electrode Structure and Performance
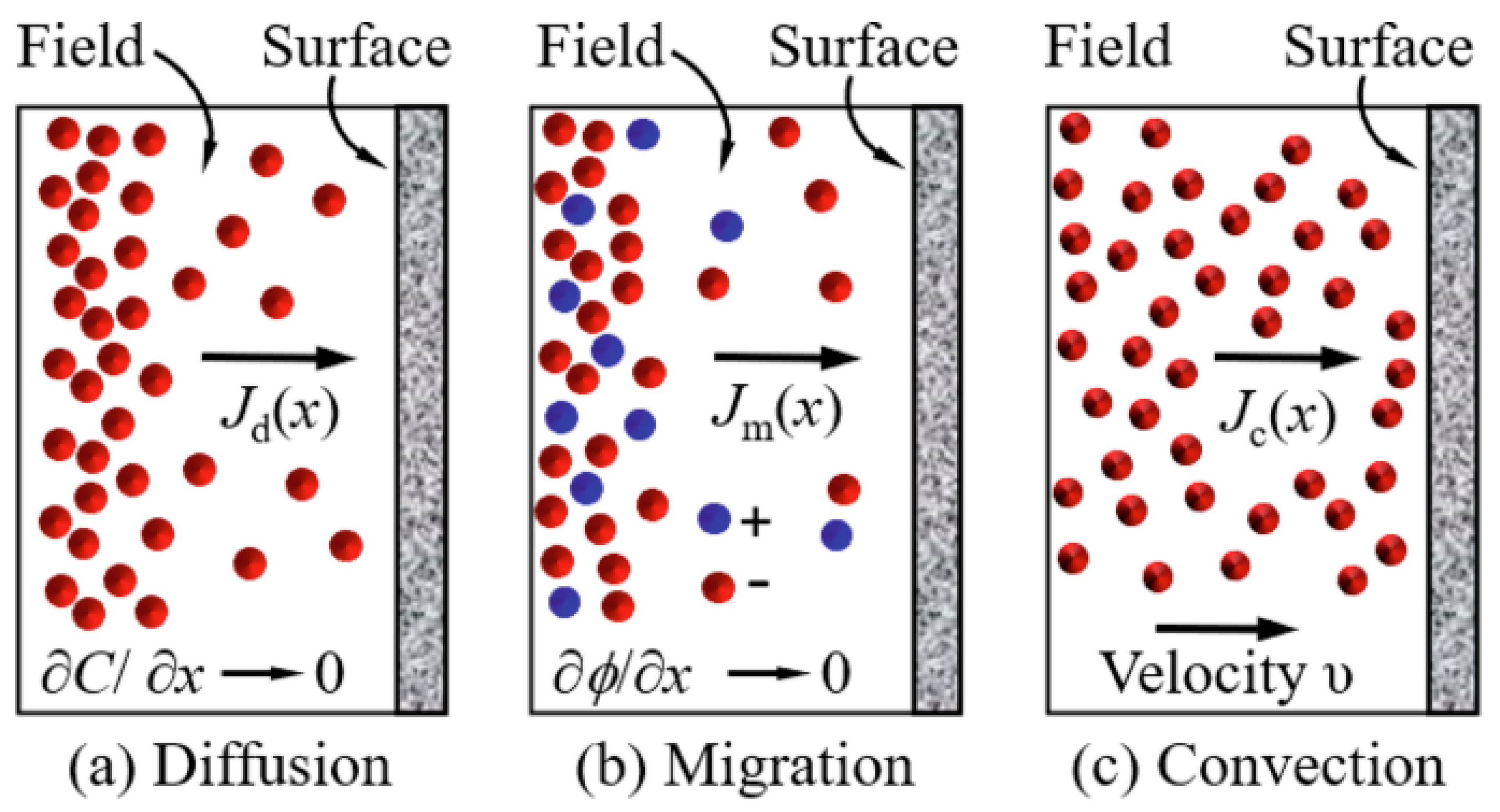
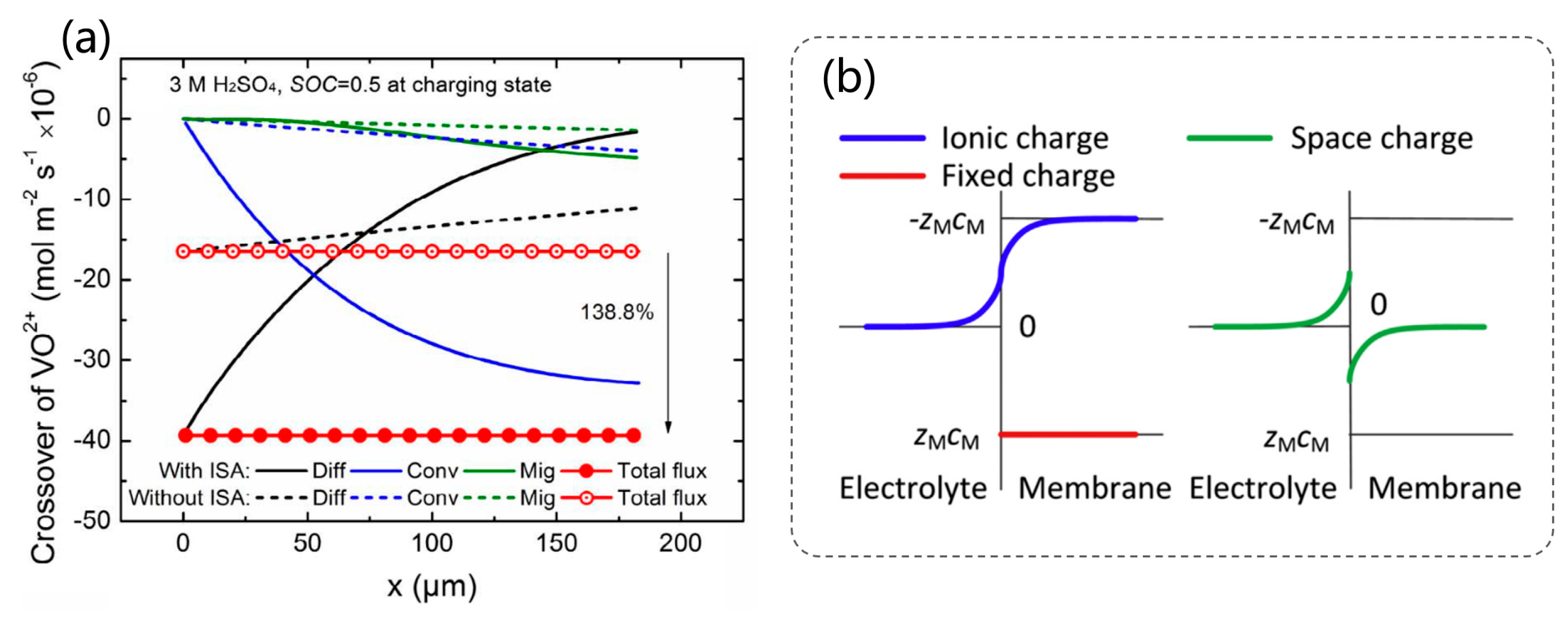
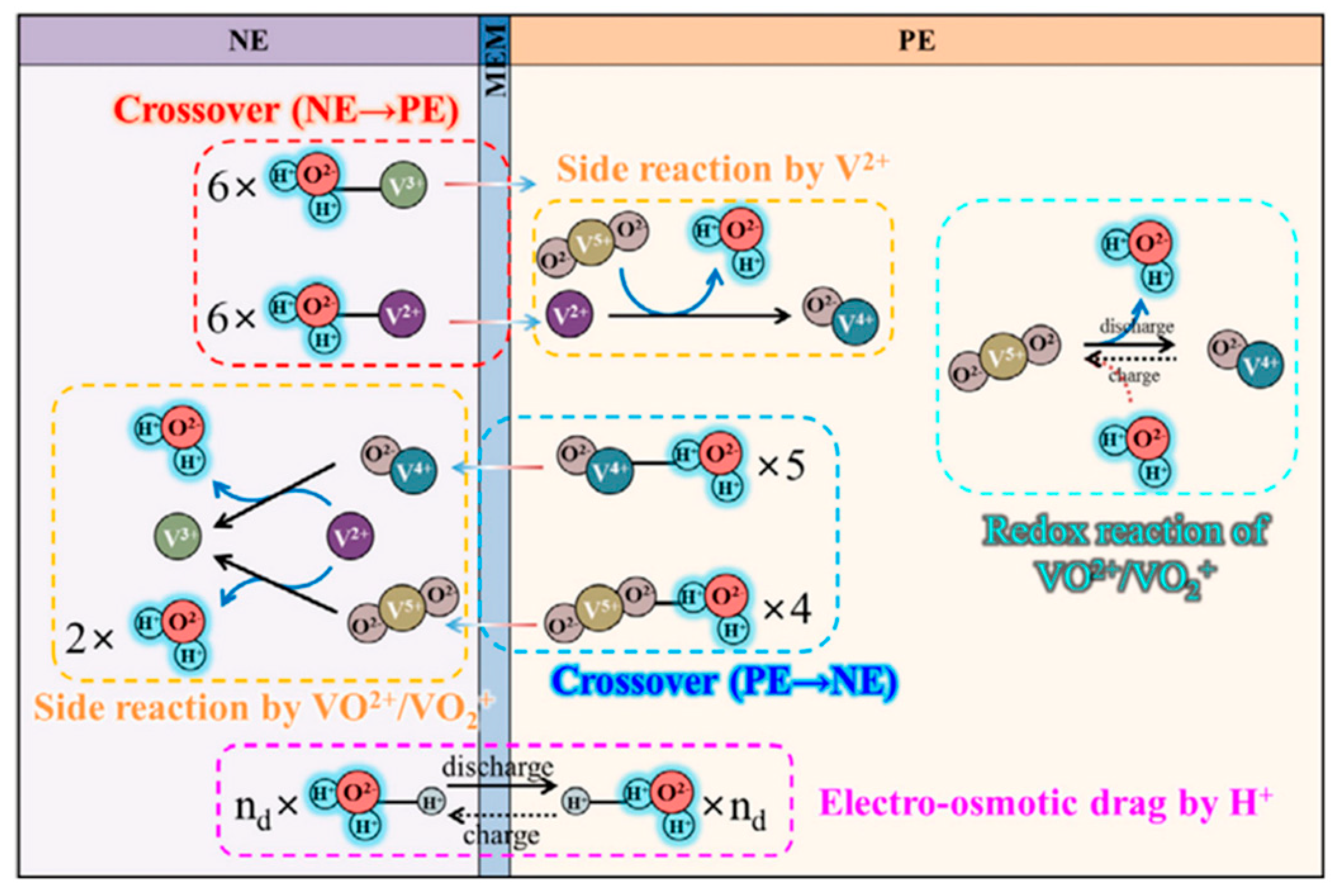
2.3. Mass Transport Processes
2.4. Electrode Reaction Kinetics
2.5. Transport Theory in Membranes
3. Modeling Approaches and Scales for Aqueous Redox Flow Batteries
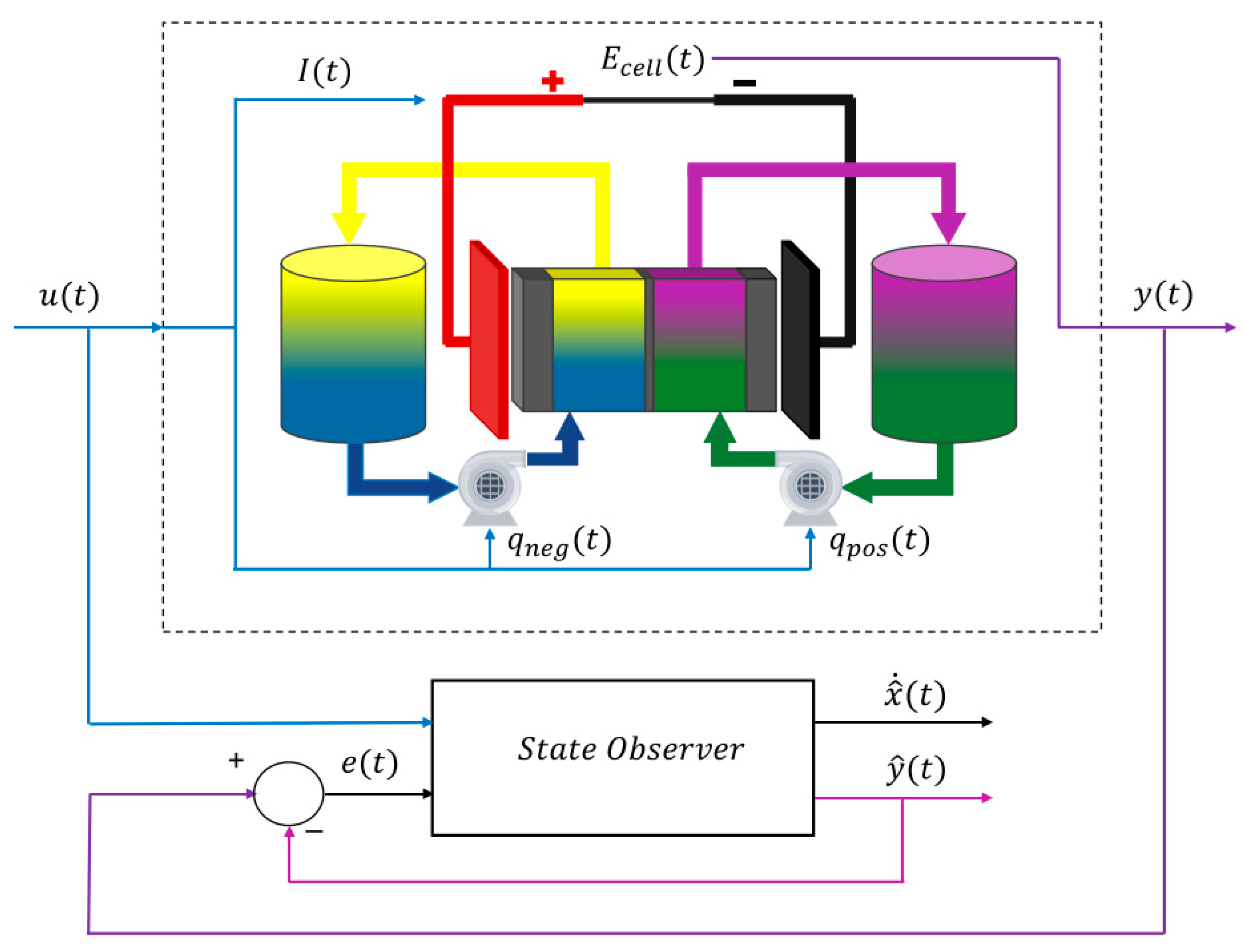
3.1. Lumped Parameter Models
3.2. Microscale Modeling
3.3. Multi-Scale Modeling
4. Modeling of Other Typical Aqueous Redox Flow Batteries
4.1. Zinc-Based Flow Batteries
4.2. Hydrogen Bromide Flow Battery
5. Key Challenges and Future Opportunities
6. Summary
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ARFB | aqueous redox flow battery |
| HBRFB | hydrogen–bromine redox flow battery |
| LBM | lattice Boltzmann methods |
| PNM | pore network modeling |
| PINNs | physics-informed neural networks |
| SOC | state of charge |
| SOH | state of health |
| VRFB | all-vanadium redox flow battery |
| ZFB | zinc-based flow battery |
| ZIFB | zinc–iron flow battery |
References
- Hou, Z.; Chen, X.; Liu, J.; Huang, Z.; Chen, Y.; Zhou, M.; Liu, W.; Zhou, H. Towards a High Efficiency and Low-Cost Aqueous Redox Flow Battery: A Short Review. J. Power Sources 2024, 601, 234242. [Google Scholar] [CrossRef]
- Ahmad, A.; Aldawood, T.A.; Mansha, M.; Ali, S.; Tahir, M.N.; Khan, M.; Khan, I.A.; Khan, S.A. Optimized and Cost-Effective Elemental-Sulfur Sodium Polysulfide/Sodium Bromide Aqueous Electrolytes for Redox Flow Batteries. J. Power Sources 2024, 614, 235013. [Google Scholar] [CrossRef]
- Park, G.; Jeong, H.; Lee, W.; Han, J.W.; Chang, D.R.; Kwon, Y. Scaled-up Aqueous Redox Flow Battery Using Anthraquinone Negalyte and Vanadium Posilyte with Inorganic Additive. Appl. Energy 2024, 353, 122171. [Google Scholar] [CrossRef]
- Xi, D.; Alfaraidi, A.M.; Gao, J.; Cochard, T.; Faria, L.C.I.; Yang, Z.; George, T.Y.; Wang, T.; Gordon, R.G.; Liu, R.Y.; et al. Mild PH-Decoupling Aqueous Flow Battery with Practical PH Recovery. Nat. Energy 2024, 9, 479–490. [Google Scholar] [CrossRef]
- Belongia, S.; Wang, X.; Zhang, X. Progresses and Perspectives of All-Iron Aqueous Redox Flow Batteries. Adv. Funct. Mater. 2024, 34, 2302077. [Google Scholar] [CrossRef]
- Wu, J.; Nie, R.; Yu, L.; Nie, Y.; Zhao, Y.; Liu, L.; Xi, J. Next-Generation Ultrathin Lightweight Electrode for PH-Universal Aqueous Flow Batteries. Small 2024, 20, e2405643. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Xiao, J.; Tang, W.; He, Y.; Tan, P.; Haranczyk, M.; Wang, D.Y. A Novel Benchmarking Approach to Assess Fire Safety of Liquid Electrolytes in Lithium-Ion Batteries. Adv. Energy Mater. 2024, 14, 2401241. [Google Scholar] [CrossRef]
- He, Y.; Cui, Y.; Yu, J.; Shang, W.; Tan, P. Advancing Flow Batteries: High Energy Density and Ultra-Fast Charging via Room-Temperature Liquid Metal. Adv. Energy Mater. 2024, 15, 2405066. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Song, C.; Platt, A.; Zhao, N.; Wang, H.; Li, H.; Fatih, K.; Jang, D. A Review of All-Vanadium Redox Flow Battery Durability: Degradation Mechanisms and Mitigation Strategies. Int. J. Energy Res. 2019, 43, 6599–6638. [Google Scholar] [CrossRef]
- Wang, Y.; Mu, A.; Wang, W.; Yang, B.; Wang, J. A Review of Capacity Decay Studies of All-Vanadium Redox Flow Batteries: Mechanism and State Estimation. ChemSusChem 2024, 17, e202301787. [Google Scholar] [CrossRef]
- Michel Myures, X.; Suresh, S.; Arthanareeswaran, G. Construction of Thermal, Chemical and Mechanically Stable Ion Exchange Membranes with Improved Ion Selectivity for Vanadium Redox Flow Batteries Applications. J. Power Sources 2024, 591, 233818. [Google Scholar] [CrossRef]
- He, Y.; Shang, W.; Ni, M.; Huang, Y.; Zhao, H.; Tan, P. In-Situ Observation of the Gas Evolution Process on the Air Electrode of Zn-Air Batteries during Charging. Chem. Eng. J. 2022, 427, 130862. [Google Scholar] [CrossRef]
- Muralidharan, V.; Jayasubramaniyan, S.; Lee, H.W. Surpassing Water-Splitting Potential in Aqueous Redox Flow Batteries: Insights from Kinetics and Thermodynamics. EES Catal. 2024, 2, 522–544. [Google Scholar] [CrossRef]
- Chace, W.S.; Tiano, S.M.; Arruda, T.M.; Lawton, J.S. Effects of State of Charge on the Physical Characteristics of V(IV)/V(V) Electrolytes and Membrane for the All Vanadium Flow Battery. Batteries 2020, 6, 49. [Google Scholar] [CrossRef]
- Jing, M.; Wei, Z.; Su, W.; He, H.; Fan, X.; Qin, Y.; Liu, J.; Yan, C. Improved Electrochemical Performance for Vanadium Flow Battery by Optimizing the Concentration of the Electrolyte. J. Power Sources 2016, 324, 215–223. [Google Scholar] [CrossRef]
- Wei, Z.; Qu, G.; Huang, Z.; Wang, Y.; Li, D.; Yang, X.; Zhang, S.; Chen, A.; Wang, Y.; Hong, H.; et al. Gradient Distribution of Zincophilic Sites for Stable Aqueous Zinc-Based Flow Batteries with High Capacity. Adv. Mater. 2024, 36, e2414388. [Google Scholar] [CrossRef]
- Zou, W.; Jung, H.; Jung, S. Modeling and Performance Optimization of Vanadium Redox Flow Batteries. J. Energy Storage 2025, 121, 116601. [Google Scholar] [CrossRef]
- Seepana, M.M.; Samudrala, S.; Suresh, P.V.; Vooradi, R. Unit Cell Modelling and Simulation of All Vanadium Redox Flow Battery. Chem. Prod. Process Model. 2018, 13, 1–11. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Non-Isothermal Modelling of the All-Vanadium Redox Flow Battery. Electrochim. Acta 2009, 55, 78–89. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Modelling the Effects of Oxygen Evolution in the All-Vanadium Redox Flow Battery. Electrochim. Acta 2010, 55, 3192–3205. [Google Scholar] [CrossRef]
- Jiang, H.J.; Underwood, T.C.; Bell, J.G.; Ranjan, S.; Sasselov, D.; Whitesides, G.M. Mimicking Lighting-Induced Electrochemistry on the Early Earth. Proc. Natl. Acad. Sci. USA 2024, 121, e2400819121. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.W.; Duan, Z.N.; Bai, J.Q.; Wang, Y. Numerical Study of the Performance of All Vanadium Redox Flow Battery by Changing the Cell Structure. J. Energy Storage 2020, 29, 101370. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, B.W.; Bai, B.F.; Zhao, T.S. A Transient Electrochemical Model Incorporating the Donnan Effect for All-Vanadium Redox Flow Batteries. J. Power Sources 2015, 299, 202–211. [Google Scholar] [CrossRef]
- Esan, O.C.; Shi, X.; Pan, Z.; Huo, X.; An, L.; Zhao, T.S. Modeling and Simulation of Flow Batteries. Adv. Energy Mater. 2020, 10, 2000758. [Google Scholar] [CrossRef]
- Yuan, Z.; Yin, Y.; Xie, C.; Zhang, H.; Yao, Y.; Li, X. Advanced Materials for Zinc-Based Flow Battery: Development and Challenge. Adv. Mater. 2019, 31, e1902025. [Google Scholar] [CrossRef]
- Shi, X.; Wu, Q. Recent Understanding on Pore Scale Mass Transfer Phenomena of Flow Batteries: Theoretical Simulation and Experimental Visualization. Curr. Opin. Electrochem. 2025, 49, 101603. [Google Scholar] [CrossRef]
- Chakrabarti, B.K.; Kalamaras, E.; Singh, A.K.; Bertei, A.; Rubio-Garcia, J.; Yufit, V.; Tenny, K.M.; Wu, B.; Tariq, F.; Hajimolana, Y.S.; et al. Modelling of Redox Flow Battery Electrode Processes at a Range of Length Scales: A Review. Sustain. Energy Fuels 2020, 4, 5433–5468. [Google Scholar] [CrossRef]
- Prifti, H.; Parasuraman, A.; Winardi, S.; Lim, T.M.; Skyllas-Kazacos, M. Membranes for Redox Flow Battery Applications. Membranes 2012, 2, 275–306. [Google Scholar] [CrossRef]
- Yang, T.F.; Chen, Y.K.; Lin, C.Y.; Yan, W.M.; Rashidi, S. Effects of Flow Field Designs on Performance Characteristics of Vanadium Redox Flow Battery. J. Taiwan Inst. Chem. Eng. 2025, 171, 106043. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Y.; Huang, Z.; He, Z.; Liu, Y.; Huang, Q.; Guo, Z. Numerical Analysis of the Design Optimization Obstruction to Guide Electrolyte Flow in Vanadium Flow Batteries. J. Energy Storage 2024, 101, 113802. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, R.; Zhou, H.; Ma, Q.; Zhang, W.; Su, H.; Yang, W.; Xu, Q. Effect of Ultrasonic Field on the Performance of an Iron-Vanadium Flow Battery with Non-Aqueous Deep Eutectic Solvent Electrolyte. Int. J. Energy Res. 2022, 46, 17616–17629. [Google Scholar] [CrossRef]
- Duan, Z.N.; Zhang, G.B.; Zhang, J.F.; Qu, Z.G. Experimental Investigation on the Performance Characteristics of Flow Fields in Redox Flow Batteries Under Various Electrode Parameters. Front. Therm. Eng. 2022, 2, 931160. [Google Scholar] [CrossRef]
- Shao, M.; Zhang, B. A 2D Thermal Model of Stacked Vanadium Redox Flow Batteries for Efficient Thermal Management. Energy Technol. 2024, 12, 2300873. [Google Scholar] [CrossRef]
- Yu, Z.; Jia, X.; Cai, Y.; Su, R.; Zhu, Q.; Zhao, T.; Jiang, H. Electrolyte Engineering for Efficient and Stable Vanadium Redox Flow Batteries. Energy Storage Mater. 2024, 69, 103404. [Google Scholar] [CrossRef]
- Puleston, T.; Trovò, A.; Marini, G.; Serra, M.; Costa-Castelló, R.; Guarnieri, M. Design and Experimental Validation of an Optimal Remixing Procedure for Vanadium Flow Batteries Affected by Faradaic Imbalance. J. Power Sources 2024, 624, 235487. [Google Scholar] [CrossRef]
- Forner-Cuenca, A.; Brushett, F.R. Engineering Porous Electrodes for Next-Generation Redox Flow Batteries: Recent Progress and Opportunities. Curr. Opin. Electrochem. 2019, 18, 113–122. [Google Scholar] [CrossRef]
- Hu, H.; Han, M.; Liu, J.; Zheng, K.; Zou, Z.; Mu, Y.; Yu, F.; Li, W.; Wei, L.; Zeng, L.; et al. Strategies for Improving the Design of Porous Fiber Felt Electrodes for All-Vanadium Redox Flow Batteries from Macro and Micro Perspectives. Energy Environ. Sci. 2025, 18, 3085–3119. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Lin, D.; Wang, Q.; Liu, C.; Chu, P.; Leung, P. Electrospun Carbon Nanofiber Composite Electrode with Gradient Porous Structure for Rapid Ion Transport in an All-Vanadium Redox Flow Battery. Energy Technol. 2024, 12, 2400825. [Google Scholar] [CrossRef]
- Wang, P.; Zhao, Y.; Ban, Y.; Zheng, M. A Review of Porous Electrode Structural Parameters and Optimization for Redox Flow Batteries. J. Energy Storage 2024, 97, 112859. [Google Scholar] [CrossRef]
- Tai, Z.; Hanawa, K.; Ju, D.; Luo, W.; Lyu, R.; Ishikawa, K.; Sato, S. Effects of Carbon Fiber Compression Ratio and Electrolyte Flow Rate on the Electrochemical Performance of Vanadium Redox Batteries. J. Chem. 2021, 1, 6646256. [Google Scholar] [CrossRef]
- Zheng, Y.; Qu, D.; Yang, F.; Chen, D. Study on Performance Improvement of Vanadium Redox Flow Batteries Focused on Electrode Fabrication Parameters and Compression Strategies. J. Energy Storage 2025, 109, 115142. [Google Scholar] [CrossRef]
- Wolf, A.; Noack, J.; Krause, M.J.; Nirschl, H. Enhancing Flow Batteries: Topology Optimization of Electrode Porosity and Shape Optimization of Cell Design. Energy Technol. 2024, 12, 2400244. [Google Scholar] [CrossRef]
- Muñoz-Perales, V.; van der Heijden, M.; de Haas, V.; Olinga, J.; Vera, M.; Forner-Cuenca, A. Understanding the Role of Electrode Thickness on Redox Flow Cell Performance. ChemElectroChem 2024, 11, e202300380. [Google Scholar] [CrossRef]
- He, Q.; Li, Z.; Bello, I.T.; Xu, Q.; Xia, L.; Wang, C.; Zhao, S.; Zhao, T.; Ni, M. A Comprehensive Modelling Study of All Vanadium Redox Flow Battery: Revealing the Combined Effects of Electrode Structure and Surface Property. J. Energy Storage 2023, 66, 107427. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effect of Electrode Compression and Operating Parameters on the Performance of Large Vanadium Redox Flow Battery Cells. J. Power Sources 2019, 427, 231–242. [Google Scholar] [CrossRef]
- Kim, M.; Yoo, H.; Lee, G.; Choi, J. Enhanced VRB Electrochemical Performance Using Tungsten as an Electrolyte Additive. Electrochim. Acta 2017, 246, 190–196. [Google Scholar] [CrossRef]
- Devi, N.; Singh, P.; Chen, Y.S. Binder-Free CNT-Modified Excellent Electrodes for All-Vanadium Redox Flow Batteries. Nanomaterials 2024, 14, 767. [Google Scholar] [CrossRef]
- Zhang, B.W.; Lei, Y.; Bai, B.F.; Zhao, T.S. A Two-Dimensional Model for the Design of Flow Fields in Vanadium Redox Flow Batteries. Int. J. Heat Mass Transf. 2019, 135, 460–469. [Google Scholar] [CrossRef]
- Kumar, S.; Jayanti, S. Effect of Flow Field on the Performance of an All-Vanadium Redox Flow Battery. J. Power Sources 2016, 307, 782–787. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; El Sawy, E.; Maslovara, S.; Yasri, N.; Birss, V.; Roberts, E.P.L. Investigation of the Impact of the Flow Mode in All-Vanadium-Redox-Flow Battery Using Macroporous and Mesoporous Carbon Electrodes. Mater. Today Commun. 2024, 40, 109773. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Hao, L. Three-Dimensional Modeling Study of All-Vanadium Redox Flow Batteries with the Serpentine and Interdigitated Flow Fields. J. Electroanal. Chem. 2022, 918, 116460. [Google Scholar] [CrossRef]
- Messaggi, M.; Canzi, P.; Mereu, R.; Baricci, A.; Inzoli, F.; Casalegno, A.; Zago, M. Analysis of Flow Field Design on Vanadium Redox Flow Battery Performance: Development of 3D Computational Fluid Dynamic Model and Experimental Validation. Appl. Energy 2018, 228, 1057–1070. [Google Scholar] [CrossRef]
- Perez, N. Mass Transport. In Materials Science: Theory and Engineering; Springer Nature: Cham, Switzerland, 2024; pp. 265–301. ISBN 978-3-031-57152-7. [Google Scholar]
- Zago, M.; Casalegno, A. Physically-Based Impedance Modeling of the Negative Electrode in All-Vanadium Redox Flow Batteries: Insight into Mass Transport Issues. Electrochim. Acta 2017, 248, 505–517. [Google Scholar] [CrossRef]
- Yin, C.; Gao, Y.; Guo, S.; Tang, H. A Coupled Three Dimensional Model of Vanadium Redox Flow Battery for Flow Field Designs. Energy 2014, 74, 886–895. [Google Scholar] [CrossRef]
- Lala, A.M.S.; El-Sayed, N.A.A. Controls of Pore Throat Radius Distribution on Permeability. J. Pet. Sci. Eng. 2017, 157, 941–950. [Google Scholar] [CrossRef]
- Khazaeli, A.; Vatani, A.; Tahouni, N.; Panjeshahi, M.H. Numerical Investigation and Thermodynamic Analysis of the Effect of Electrolyte Flow Rate on Performance of All Vanadium Redox Flow Batteries. J. Power Sources 2015, 293, 599–612. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A Simple Model for the Vanadium Redox Battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Krowne, C.M. Nernst Equations and Concentration Chemical Reaction Overpotentials for VRFB Operation. J. Electrochem. Soc. 2023, 170, 100534. [Google Scholar] [CrossRef]
- Mai, Z.; Zhang, H.; Zhang, H.; Xu, W.; Wei, W.; Na, H.; Li, X. Anion-Conductive Membranes with Ultralow Vanadium Permeability and Excellent Performance in Vanadium Flow Batteries. ChemSusChem 2013, 6, 328–335. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, R.; Leirós, J.; Boaventura, M.; Mendes, A. Insights into All-Vanadium Redox Flow Battery: A Case Study on Components and Operational Conditions. Electrochim. Acta 2018, 267, 80–93. [Google Scholar] [CrossRef]
- Yang, X.G.; Ye, Q.; Cheng, P.; Zhao, T.S. Effects of the Electric Field on Ion Crossover in Vanadium Redox Flow Batteries. Appl. Energy 2015, 145, 306–319. [Google Scholar] [CrossRef]
- Knehr, K.W.; Kumbur, E.C. Role of Convection and Related Effects on Species Crossover and Capacity Loss in Vanadium Redox Flow Batteries. Electrochem. Commun. 2012, 23, 76–79. [Google Scholar] [CrossRef]
- Hao, L.; Wang, Y.; He, Y. Modeling of Ion Crossover in an All-Vanadium Redox Flow Battery with the Interfacial Effect at Membrane/Electrode Interfaces. J. Electrochem. Soc. 2019, 166, A1310–A1322. [Google Scholar] [CrossRef]
- Lei, Y.; Zhang, B.W.; Zhang, Z.H.; Bai, B.F.; Zhao, T.S. An Improved Model of Ion Selective Adsorption in Membrane and Its Application in Vanadium Redox Flow Batteries. Appl. Energy 2018, 215, 591–601. [Google Scholar] [CrossRef]
- Xiong, R.; Xiong, B.; Zhang, Q.; Shi, S.; Su, Y.; Zhang, D. Capacity Fading Model of Vanadium Redox Flow Battery Considering Water Molecules Migration. Int. J. Green Energy 2022, 19, 1613–1622. [Google Scholar] [CrossRef]
- Sukkar, T.; Skyllas-Kazacos, M. Water Transfer Behaviour across Cation Exchange Membranes in the Vanadium Redox Battery. J. Memb. Sci. 2003, 222, 235–247. [Google Scholar] [CrossRef]
- Shin, J.; Jeong, B.; Chinannai, M.F.; Ju, H. Mitigation of Water and Electrolyte Imbalance in All-Vanadium Redox Flow Batteries. Electrochim. Acta 2021, 390, 138858. [Google Scholar] [CrossRef]
- Oh, K.; Moazzam, M.; Gwak, G.; Ju, H. Water Crossover Phenomena in All-Vanadium Redox Flow Batteries. Electrochim. Acta 2019, 297, 101–111. [Google Scholar] [CrossRef]
- Bromberger, K.; Kaunert, J.; Smolinka, T. A Model for All-Vanadium Redox Flow Batteries: Introducing Electrode-Compression Effects on Voltage Losses and Hydraulics. Energy Technol. 2014, 2, 64–76. [Google Scholar] [CrossRef]
- Chen, L.; He, Y.L.; Tao, W.Q.; Zelenay, P.; Mukundan, R.; Kang, Q. Pore-Scale Study of Multiphase Reactive Transport in Fibrous Electrodes of Vanadium Redox Flow Batteries. Electrochim. Acta 2017, 248, 425–439. [Google Scholar] [CrossRef]
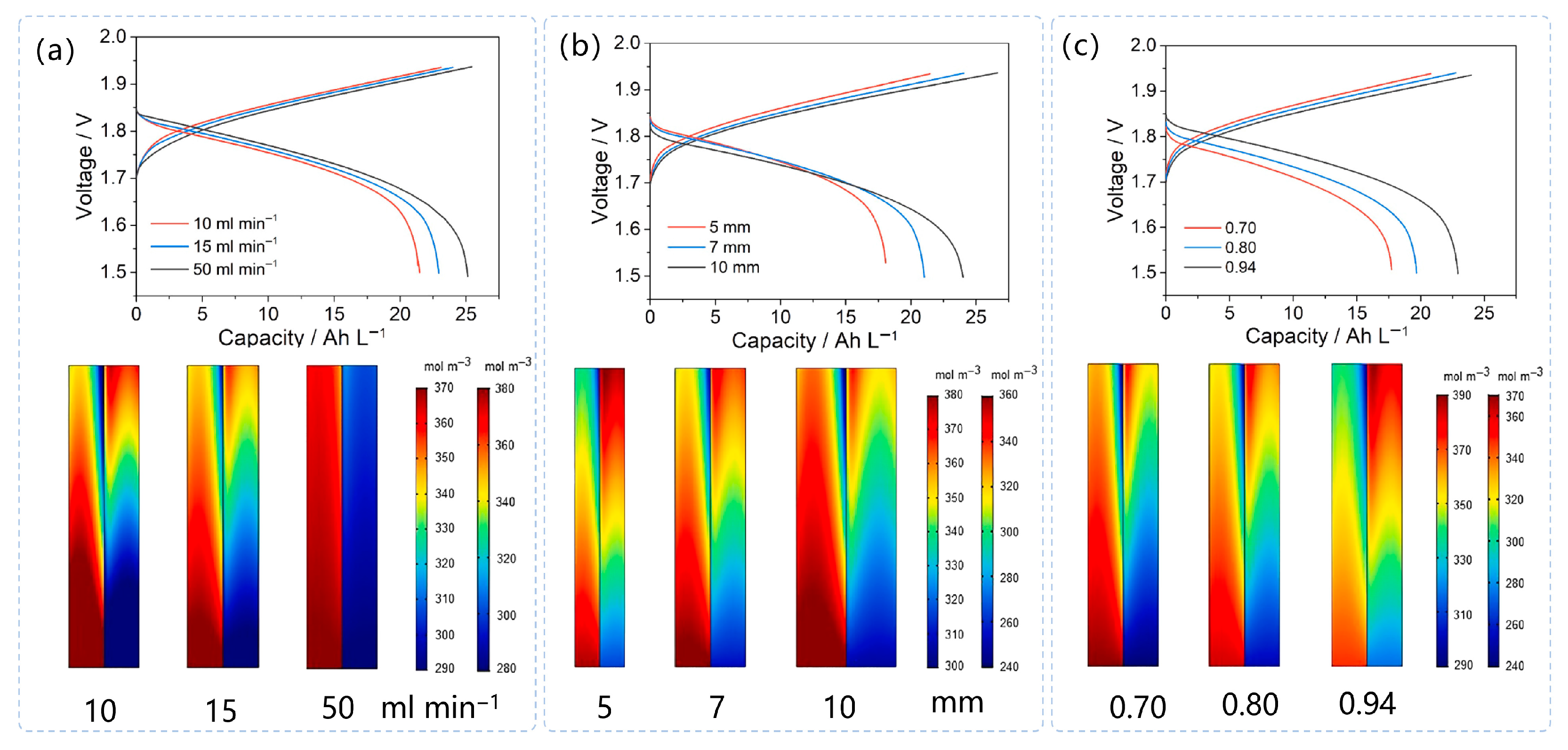
- Delgado, N.M.; Monteiro, R.; Abdollahzadeh, M.; Ribeirinha, P.; Bentien, A.; Mendes, A. 2D-Dynamic Phenomenological Modelling of Vanadium Redox Flow Batteries—Analysis of the Mass Transport Related Overpotentials. J. Power Sources 2020, 480, 229142. [Google Scholar] [CrossRef]
- Li, Y.; Sun, L.; Cao, L.; Bao, J.; Skyllas-Kazacos, M. Dynamic Model Based Membrane Permeability Estimation for Online SOC Imbalances Monitoring of Vanadium Redox Flow Batteries. J. Energy Storage 2021, 39, 102688. [Google Scholar] [CrossRef]
- Barton, J.L.; Brushett, F.R. A One-Dimensional Stack Model for Redox Flow Battery Analysis and Operation. Batteries 2019, 5, 25. [Google Scholar] [CrossRef]
- Zhong, L.; Chu, F. A Novel Biomimetic Lung-Shaped Flow Field for All-Vanadium Redox Flow Battery. Sustainability 2023, 15, 13613. [Google Scholar] [CrossRef]
- Lee, S.B.; Mitra, K.; Pratt, H.D.; Anderson, T.M.; Ramadesigan, V.; Chalamala, B.R.; Subramanian, V.R. Open Data, Models, and Codes for Vanadium Redox Batch Cell Systems: A Systems Approach Using Zero-Dimensional Models. J. Electrochem. Energy Convers. Storage 2019, 17, 011008. [Google Scholar] [CrossRef]
- Pugach, M.; Kondratenko, M.; Briola, S.; Bischi, A. Zero Dimensional Dynamic Model of Vanadium Redox Flow Battery Cell Incorporating All Modes of Vanadium Ions Crossover. Appl. Energy 2018, 226, 560–569. [Google Scholar] [CrossRef]
- Pathak, A.; Kumar Sharma, A.; Kumar Gupta, A. Systematic Lumped Modeling of All-Vanadium Redox Flow Batteries. J. Electrochem. Soc. 2022, 169, 100533. [Google Scholar] [CrossRef]
- Puleston, T.; Clemente, A.; Costa-Castelló, R.; Serra, M. Modelling and Estimation of Vanadium Redox Flow Batteries: A Review. Batteries 2022, 8, 121. [Google Scholar] [CrossRef]
- Clemente, A.; Montiel, M.; Barreras, F.; Lozano, A.; Costa-Castello, R. Vanadium Redox Flow Battery State of Charge Estimation Using a Concentration Model and a Sliding Mode Observer. IEEE Access 2021, 9, 72368–72376. [Google Scholar] [CrossRef]
- Chen, Y.; Bao, J.; Xu, Z.; Gao, P.; Yan, L.; Kim, S.; Wang, W. A Hybrid Analytical and Numerical Model for Cross-over and Performance Decay in a Unit Cell Vanadium Redox Flow Battery. J. Power Sources 2023, 578, 233210. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S. Fundamental Models for Flow Batteries. Prog. Energy Combust. Sci. 2015, 49, 40–58. [Google Scholar] [CrossRef]
- Qiu, G.; Joshi, A.S.; Dennison, C.R.; Knehr, K.W.; Kumbur, E.C.; Sun, Y. 3-D Pore-Scale Resolved Model for Coupled Species/Charge/Fluid Transport in a Vanadium Redox Flow Battery. Electrochim. Acta 2012, 64, 46–64. [Google Scholar] [CrossRef]
- Wlodarczyk, J.K.; Schärer, R.P.; Friedrich, K.A.; Schumacher, J.O. Upscaling of Reactive Mass Transport through Porous Electrodes in Aqueous Flow Batteries. J. Electrochem. Soc. 2024, 171, 020544. [Google Scholar] [CrossRef]
- Guo, A.; Zhang, P.; Ma, Y.; Yuan, S. Molecular Dynamics Simulation of the Electrochemical Impact of Aminomethanesulfonic Acid on VO2+ in Vanadium Flow Batteries. Mater. Today Chem. 2025, 47, 102815. [Google Scholar] [CrossRef]
- Fu, Y.; Bao, J.; Zeng, C.; Chen, Y.; Xu, Z.; Kim, S.; Wang, W. A Three-Dimensional Pore-Scale Model for Redox Flow Battery Electrode Design Analysis. J. Power Sources 2023, 556, 232329. [Google Scholar] [CrossRef]
- Misaghian, N.; Sadeghi, M.A.; Lee, K.M.; Roberts, E.P.L.; Gostick, J.T. Utilizing Pore Network Modeling for Performance Analysis of Multi-Layer Electrodes in Vanadium Redox Flow Batteries. J. Electrochem. Soc. 2023, 170, 070520. [Google Scholar] [CrossRef]
- Xiao, L.; Luo, M.; Zhu, L.; Duan, K.; Bevilacqua, N.; Eifert, L.; Zeis, R.; Sui, P.-C. Pore-Scale Characterization and Simulation of Porous Electrode Material for Vanadium Redox Flow Battery: Effects of Compression on Transport Properties. J. Electrochem. Soc. 2020, 167, 110545. [Google Scholar] [CrossRef]
- van der Heijden, M.; van Gorp, R.; Sadeghi, M.A.; Gostick, J.; Forner-Cuenca, A. Assessing the Versatility and Robustness of Pore Network Modeling to Simulate Redox Flow Battery Electrode Performance. J. Electrochem. Soc. 2022, 169, 040505. [Google Scholar] [CrossRef]
- Pan, S.; Fang, W.; Yan, J.; Zhang, S.; Zhang, H. Multiscale Coupled Electron-Ion Transport in Semi-Solid Lithium Flow Batteries. Energy Environ. Sci. 2025, 18, 5868–5896. [Google Scholar] [CrossRef]
- Hamid, M.A.; Smith, K.C. A Bottom-up, Multi-Scale Theory for Transient Mass Transport of Redox-Active Species through Porous Electrodes beyond the Pseudo-Steady Limit. J. Power Sources 2023, 565, 232756. [Google Scholar] [CrossRef]
- Yu, Y.; Zuo, Y.; Zuo, C.; Liu, X.; Liu, Z. A Hierarchical Multiscale Model for Microfluidic Fuel Cells with Porous Electrodes. Electrochim. Acta 2014, 116, 237–243. [Google Scholar] [CrossRef]
- Bao, J.; Murugesan, V.; Kamp, C.J.; Shao, Y.; Yan, L.; Wang, W. Machine Learning Coupled Multi-Scale Modeling for Redox Flow Batteries. Adv. Theory Simul. 2020, 3, 1900167. [Google Scholar] [CrossRef]
- Luo, Y.; Lv, W.; Zheng, M. A Multi-Scale Model for Local Polarization Prediction in Flow Batteries Based on Deep Neural Network. J. Energy Storage 2023, 68, 107842. [Google Scholar] [CrossRef]
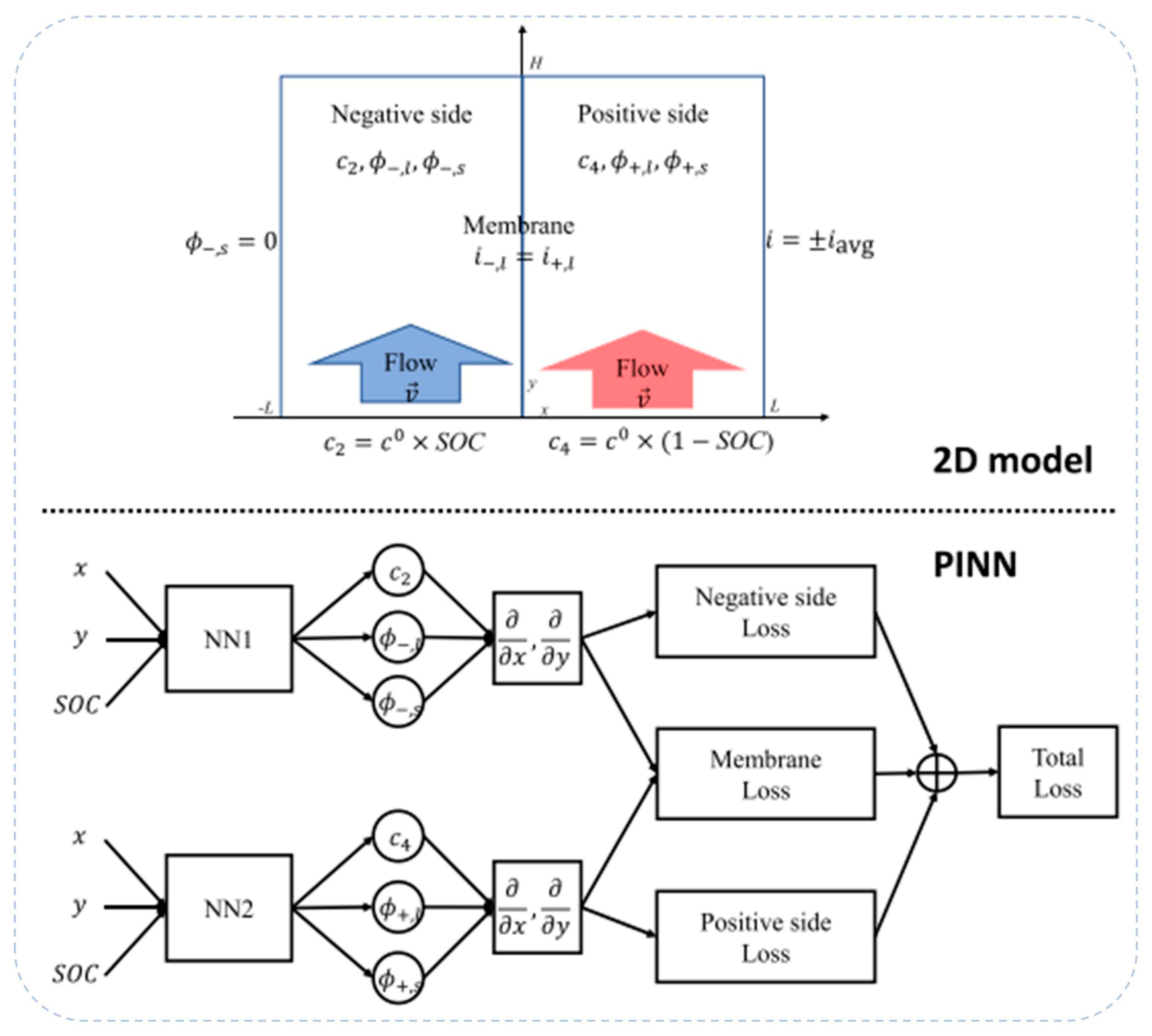
- Chen, W.; Fu, Y.; Stinis, P. Physics-Informed Machine Learning of Redox Flow Battery Based on a Two-Dimensional Unit Cell Model. J. Power Sources 2023, 584, 233548. [Google Scholar] [CrossRef]
- Korolev, D.; Schmidt, T.; Natarajan, D.K.; Cassola, S.; May, D.; Duhovic, M.; Hintermüller, M. Hybrid Machine Learning Based Scale Bridging Framework for Permeability Prediction of Fibrous Structures. arXiv 2025, arXiv:2502.05044. [Google Scholar]
- Bukola, S.; Li, Z.; Zack, J.; Antunes, C.; Korzeniewski, C.; Teeter, G.; Blackburn, J.; Pivovar, B. Single-Layer Graphene as a Highly Selective Barrier for Vanadium Crossover with High Proton Selectivity. J. Energy Chem. 2021, 59, 419–430. [Google Scholar] [CrossRef]
- Lutz, C.; Hampel, S.; Ke, X.; Beuermann, S.; Turek, T.; Kunz, U.; Guilherme Buzanich, A.; Radtke, M.; Fittschen, U.E.A. Evidence for Redox Reactions during Vanadium Crossover inside the Nanoscopic Water-Body of Nafion 117 Using X-Ray Absorption near Edge Structure Spectroscopy. J. Power Sources 2021, 483, 229176. [Google Scholar] [CrossRef]
- Prieto-Díaz, P.A.; Trovò, A.; Marini, G.; Rugna, M.; Vera, M.; Guarnieri, M. Experiment-Supported Survey of Inefficient Electrolyte Mixing and Capacity Loss in Vanadium Flow Battery Tanks. Chem. Eng. J. 2024, 492, 152137. [Google Scholar] [CrossRef]
- Wan, Y.H.; Sun, J.; Jiang, H.R.; Fan, X.Z.; Zhao, T.S. A Highly-Efficient Composite Polybenzimidazole Membrane for Vanadium Redox Flow Battery. J. Power Sources 2021, 489, 229502. [Google Scholar] [CrossRef]
- Mans, N.; Krieg, H.M.; van der Westhuizen, D.J. The Effect of Electrolyte Composition on the Performance of a Single-Cell Iron–Chromium Flow Battery. Adv. Energy Sustain. Res. 2024, 5, 2300238. [Google Scholar] [CrossRef]
- Zeng, Y.K.; Zhou, X.L.; An, L.; Wei, L.; Zhao, T.S. A High-Performance Flow-Field Structured Iron-Chromium Redox Flow Battery. J. Power Sources 2016, 324, 738–744. [Google Scholar] [CrossRef]
- Bai, E.; Sun, C.; Zhu, H.; Liu, Z.; Xu, C.; Xie, X.; Wu, S. Amino–Functionalized Multi–Walled Carbon Nanotube/SPEEK Hybrid Proton Exchange Membrane for Iron–Chromium Redox Flow Battery. Batter. Supercaps 2024, 7, e202400007. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, X.; Xu, W.; Duan, Y.; Zhang, H.; Li, X. Negatively Charged Nanoporous Membrane for a Dendrite-Free Alkaline Zinc-Based Flow Battery with Long Cycle Life. Nat. Commun. 2018, 9, 3731. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yan, H.; Hao, H.; Song, Y.; Li, Y.; Liu, Q.; Tang, A. Synergetic Modulation on Solvation Structure and Electrode Interface Enables a Highly Reversible Zinc Anode for Zinc-Iron Flow Batteries. ACS Energy Lett. 2022, 7, 2331–2339. [Google Scholar] [CrossRef]
- Saadi, K.; Kuettinger, M.; Fischer, P.; Zitoun, D. Hydrogen-Bromine Redox-Flow Battery Cycling with Bromine Complexing Agent: On the Benefits of Nanoporous Separator Versus Proton Exchange Membrane. Energy Technol. 2021, 9, 2000978. [Google Scholar] [CrossRef]
- Fajardo, D.A.O.; Mul, G.; Lammertink, R.G.H. Effect of Hydrogen Pressure on The Mass Transfer Characteristics of Hydrogen-Bromine Flow Battery Electrodes Effect of Hydrogen Pressure on The Mass Transfer Characteristics of Hydrogen-Bromine Flow Battery Electrodes. J. Electrochem. Soc. 2024, 171, 090525. [Google Scholar] [CrossRef]
- Wu, M.; Nan, M.; Liu, S.; Zhong, C.; Qiao, L.; Zhang, H.; Ma, X. Multi-Dimensional Bi@C Electrocatalyst for Cr3+/Cr2+ Redox Reaction Boosting High-Performance Iron-Chromium Flow Batteries. Sci. China Chem. 2025, 68, 2735–2743. [Google Scholar] [CrossRef]
- Niu, Y.; Heydari, A.; Qiu, W.; Guo, C.; Liu, Y.; Xu, C.; Zhou, T.; Xu, Q. Machine Learning-Enabled Performance Prediction and Optimization for Iron-Chromium Redox Flow Batteries. Nanoscale 2024, 16, 3994–4003. [Google Scholar] [CrossRef]
- Mansha, M.; Ayub, A.; Khan, I.A.; Ali, S.; Alzahrani, A.S.; Khan, M.; Arshad, M.; Rauf, A.; Akram Khan, S. Recent Development of Electrolytes for Aqueous Organic Redox Flow Batteries (Aorfbs): Current Status, Challenges, and Prospects. Chem. Rec. 2024, 24, e202300284. [Google Scholar] [CrossRef]
- Lim, Y.; Shin, M.; Lee, J.J.; Kim, C.; Kwon, Y. High Performance Alkaline Zinc-Iron Flow Battery Achieved by Adoption of Advanced Organic Additive. Chem. Eng. J. 2025, 508, 161090. [Google Scholar] [CrossRef]
- Xie, C.; Duan, Y.; Xu, W.; Zhang, H.; Li, X. A Low-Cost Neutral Zinc–Iron Flow Battery with High Energy Density for Stationary Energy Storage. Angew. Chem.-Int. Ed. 2017, 56, 14953–14957. [Google Scholar] [CrossRef]
- Karaeyvaz, M.C.; Duman, B.; Fıçıcılar, B. An Alternative HCMS Carbon Catalyst in Bromine Reduction Reaction for Hydrogen-Bromine Flow Batteries. Int. J. Hydrogen Energy 2021, 46, 29512–29522. [Google Scholar] [CrossRef]
- Küttinger, M.; Brunetaud, R.; Włodarczyk, J.K.; Fischer, P.; Tübke, J. Cycle Behaviour of Hydrogen Bromine Redox Flow Battery Cells with Bromine Complexing Agents. J. Power Sources 2021, 495, 229820. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Duan, Y.; Yuan, Z.; Li, X. Effect of Electrolyte Additives on the Water Transfer Behavior for Alkaline Zinc-Iron Flow Batteries. ACS Appl. Mater. Interfaces 2020, 12, 51573–51580. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Zhang, K.; Li, N. Modeling and Simulation of Single Flow Zinc–Nickel Redox Battery Coupled with Multi-Physics Fields. Batteries 2024, 10, 166. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Y.; Dong, C.; Xiao, F.; Huang, J.; Chen, J.; Liang, G.; Cheng, H.M. A Zn-Dendrite Dissolving Membrane to Increase the Cycling Life of Zinc Bromine Flow Batteries. Adv. Funct. Mater. 2025, 2500909, 1–6. [Google Scholar] [CrossRef]
- Xiong, Q.; Huang, M.; Ren, T.; Wu, S.; Wang, W.; Xiang, Z.; Wan, K.; Fu, Z.; Liang, Z. Homogeneous Complexation Strategy to Manage Bromine for High-Capacity Zinc–Bromine Flow Battery. Adv. Energy Mater. 2024, 15, 2403347. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Yu, W.; He, Q.; Ni, M.; Yang, S.; Zhang, S.; Tan, P. Cost Evaluation and Sensitivity Analysis of the Alkaline Zinc-Iron Flow Battery System for Large-Scale Energy Storage Applications. J. Energy Storage 2021, 44, 103327. [Google Scholar] [CrossRef]
- Gong, K.; Ma, X.; Conforti, K.M.; Kuttler, K.J.; Grunewald, J.B.; Yeager, K.L.; Bazant, M.Z.; Gu, S.; Yan, Y. A Zinc-Iron Redox-Flow Battery under $100 per KW h of System Capital Cost. Energy Environ. Sci. 2015, 8, 2941–2945. [Google Scholar] [CrossRef]
- Kim, Y.; Yun, D.; Jeon, J. Performance Improvement of Aqueous Zinc-Iron Flow Batteries through Organic Ligand Complexation of Fe(II)/Fe(III). Electrochim. Acta 2020, 354, 136691. [Google Scholar] [CrossRef]
- Zhang, Y.; Henkensmeier, D.; Kim, S.; Hempelmann, R.; Chen, R. Enhanced Reaction Kinetics of an Aqueous Zn–Fe Hybrid Flow Battery by Optimizing the Supporting Electrolytes. J. Energy Storage 2019, 25, 100883. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, W.; Liu, Y.; Zeng, Y.; He, Q.; Tan, P.; Ni, M. Mathematical Modeling and Numerical Analysis of Alkaline Zinc-Iron Flow Batteries for Energy Storage Applications. Chem. Eng. J. 2021, 405, 126684. [Google Scholar] [CrossRef]
- Chang, N.; Yin, Y.; Yue, M.; Yuan, Z.; Zhang, H.; Lai, Q.; Li, X. A Cost-Effective Mixed Matrix Polyethylene Porous Membrane for Long-Cycle High Power Density Alkaline Zinc-Based Flow Batteries. Adv. Funct. Mater. 2019, 29, 1901674. [Google Scholar] [CrossRef]
- Yuan, Z.; Duan, Y.; Liu, T.; Zhang, H.; Li, X. Toward a Low-Cost Alkaline Zinc-Iron Flow Battery with a Polybenzimidazole Custom Membrane for Stationary Energy Storage. iScience 2018, 3, 40–49. [Google Scholar] [CrossRef]
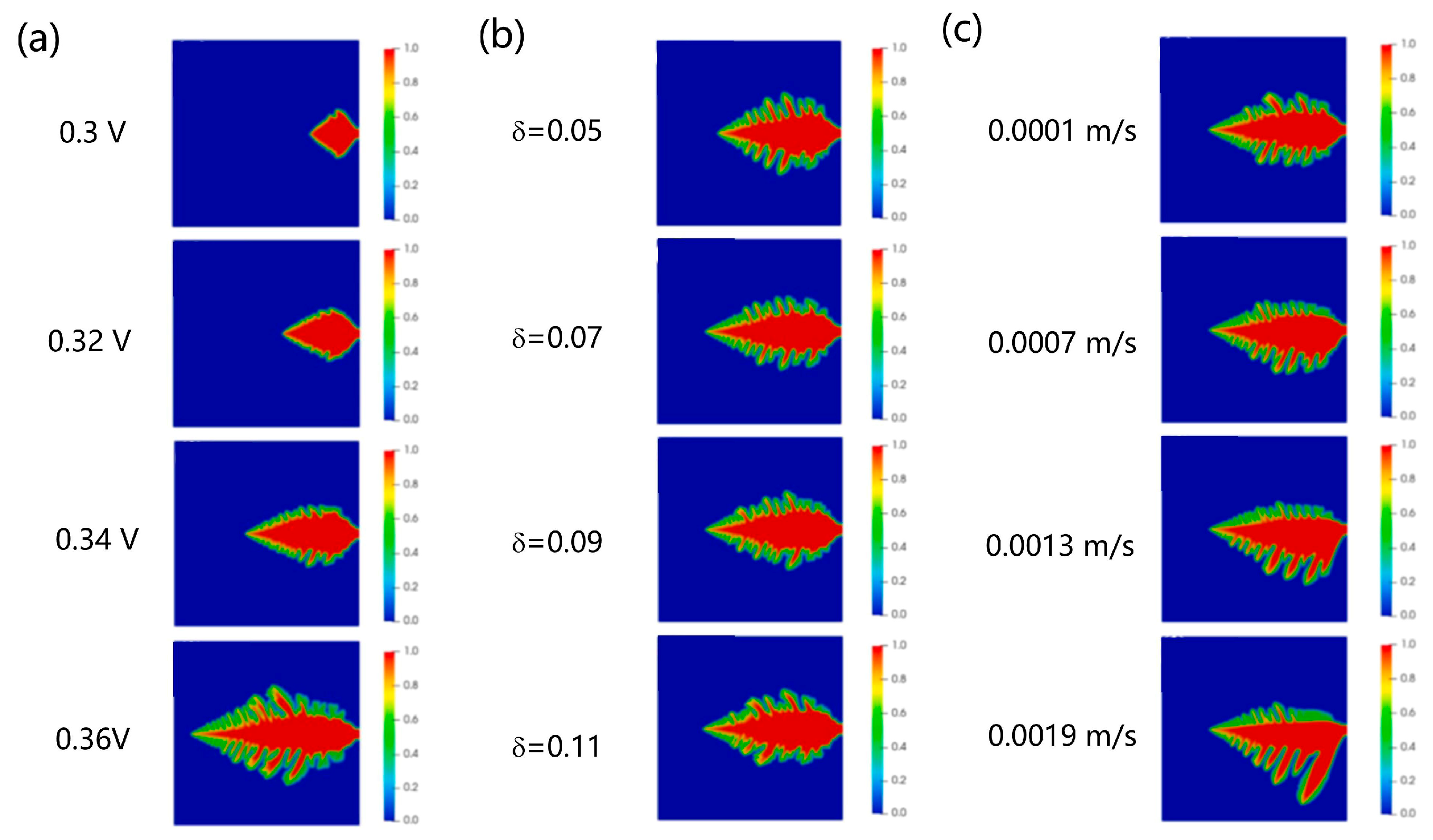
- Jian, Q.; Sun, J.; Li, H.; Guo, Z.; Zhao, T. Phase-Field Modeling of Zinc Dendrites Growth in Aqueous Zinc Batteries. Int. J. Heat Mass Transf. 2024, 223, 125252. [Google Scholar] [CrossRef]
- Wang, L.; Yao, S.; Ying, C.; Yao, H.; Yang, J. Numerical Simulation of Factors in Charge of Dendrite Growth in Zinc-Nickel Single Flow Batteries. Electrochim. Acta 2024, 475, 143622. [Google Scholar] [CrossRef]
- Society, E. Phase Field Simulation for Dendrite Growth in Energy Storage Batteries Phase Field Simulation for Dendrite Growth in Energy Storage Batteries. J. Electrochem. Soc. 2025, 172, 070515. [Google Scholar]
- Gao, L.; Guo, Z. Phase-Field Simulation of Li Dendrites with Multiple Parameters Influence. Comput. Mater. Sci. 2020, 183, 109919. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, M.; Xia, Y.; Wang, X.; Liu, Y.; Yao, Y.; Zhang, H.; Li, Y.; Lu, S.; Qin, W.; et al. A Stable and High-Capacity Redox Targeting-Based Electrolyte for Aqueous Flow Batteries. Joule 2019, 3, 2255–2267. [Google Scholar] [CrossRef]
- Guo, L.; Guo, H.; Huang, H.; Tao, S.; Cheng, Y. Inhibition of Zinc Dendrites in Zinc-Based Flow Batteries. Front. Chem. 2020, 8, 557. [Google Scholar] [CrossRef]
- Wittman, R.M.; Sacci, R.L.; Zawodzinski, T.A. Alkaline Zinc Passivation Mechanism Is Controlled by Hydroxide Concentration Alkaline Zinc Passivation Mechanism Is Controlled by Hydroxide Concentration. J. Electrochem. Soc. 2025, 172, 040514. [Google Scholar] [CrossRef]
- Xie, W.; Zhu, K.; Yang, H.; Yang, W. Advancements in Achieving High Reversibility of Zinc Anode for Alkaline Zinc-Based Batteries. Adv. Mater. 2024, 36, 2306154. [Google Scholar] [CrossRef]
- Rana, A.; Roy, K.; Heil, J.N.; Nguyen, J.H.; Renault, C.; Tackett, B.M.; Dick, J.E. Realizing the Kinetic Origin of Hydrogen Evolution for Aqueous Zinc Metal Batteries. Adv. Energy Mater. 2024, 14, 2402521. [Google Scholar] [CrossRef]
- Subramaniam, T.; Idris, M.B. Mitigating Hydrogen Evolution Reaction and Corrosion of Zinc in Electrically Rechargeable Zinc-Air Batteries Using Nanofluid Electrolytes. J. Energy Storage 2024, 81, 110457. [Google Scholar] [CrossRef]
- Wang, P.; Peng, T.; Ban, Y.; Zheng, M. Hierarchical Pore Structure Composite Electrode by Electrospinning for Dendrite-Free Zinc-Based Flow Battery. Adv. Funct. Mater. 2024, 34, 2409036. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, R.; Hu, Z.; Wang, Y.; Zhang, K.; Wang, Y.; Han, X.; Zhang, A.; Wu, C.; Bai, Y. Blocking the Passivation Reaction via Localized Acidification and Cation Selective Interface towards Highly Stable Zinc Anode. Energy Storage Mater. 2024, 70, 103449. [Google Scholar] [CrossRef]
- Yu, X.; Chen, M.; Li, Z.; Tan, X.; Zhang, H.; Wang, J.; Tang, Y.; Xu, J.; Yin, W.; Yang, Y.; et al. Unlocking Dynamic Solvation Chemistry and Hydrogen Evolution Mechanism in Aqueous Zinc Batteries. J. Am. Chem. Soc. 2024, 146, 17103–17113. [Google Scholar] [CrossRef]
- Oh, K.; Kang, T.J.; Park, S.; Tucker, M.C.; Weber, A.Z.; Ju, H. Effect of Flow-Field Structure on Discharging and Charging Behavior of Hydrogen/Bromine Redox Flow Batteries. Electrochim. Acta 2017, 230, 160–173. [Google Scholar] [CrossRef][Green Version]
- Wlodarczyk, J.K.; Baltes, N.; Friedrich, K.A.; Schumacher, J.O. Mass Transport Limitations in Concentrated Aqueous Electrolyte Solutions: Theoretical and Experimental Study of the Hydrogen–Bromine Flow Battery Electrolyte. Electrochim. Acta 2023, 461, 142640. [Google Scholar] [CrossRef]
- Küttinger, M.; Riasse, R.; Wlodarczyk, J.; Fischer, P.; Tübke, J. Improvement of Safe Bromine Electrolytes and Their Cell Performance in H2/Br2 Flow Batteries Caused by Tuning the Bromine Complexation Equilibrium. J. Power Sources 2022, 520, 230804. [Google Scholar] [CrossRef]
- Chinannai, M.F.; Ju, H. Effects of Water Transport on Performance Behaviors of Hydrogen Bromine Redox Flow Batteries. J. Energy Storage 2022, 49, 104151. [Google Scholar] [CrossRef]
- Chinannai, M.F.; Ju, H. Analysis of Performance Improvement of Hydrogen/Bromine Flow Batteries by Using Bromate Electrolyte. Int. J. Hydrogen Energy 2021, 46, 13760–13774. [Google Scholar] [CrossRef]
- Küttinger, M.; Wlodarczyk, J.K.; Daubner, D.; Fischer, P.; Tübke, J. High Energy Density Electrolytes for H2/Br2redox Flow Batteries, Their Polybromide Composition and Influence on Battery Cycling Limits. RSC Adv. 2021, 11, 5218–5229. [Google Scholar] [CrossRef]
- Saadi, K.; Hardisty, S.S.; Tatus-Portnoy, Z.; Zitoun, D. Influence of Loading, Metallic Surface State and Surface Protection in Precious Group Metal Hydrogen Electrocatalyst for H2/Br2 Redox-Flow Batteries. J. Power Sources 2022, 536, 231494. [Google Scholar] [CrossRef]
- Braff, W.A.; Bazant, M.Z.; Buie, C.R. Membrane-Less Hydrogen Bromine Flow Battery. Nat. Commun. 2013, 4, 2346. [Google Scholar] [CrossRef]
- Hua, L.; Lu, W.; Li, T.; Xu, P.; Zhang, H.; Li, X. A Highly Selective Porous Composite Membrane with Bromine Capturing Ability for a Bromine-Based Flow Battery. Mater. Today Energy 2021, 21, 100763. [Google Scholar] [CrossRef]
- Hugo, Y.A.; Kout, W.; Sikkema, F.; Borneman, Z.; Nijmeijer, K. In Situ Long-Term Membrane Performance Evaluation of Hydrogen-Bromine Flow Batteries. J. Energy Storage 2020, 27, 101068. [Google Scholar] [CrossRef]
- Küttinger, M.; Saadi, K.; Faverge, T.; Samala, N.R.; Grinberg, I.; Zitoun, D.; Fischer, P. Influence of Strong Bromine Binding Complexing Agent in Electrolytes on the Performance of Hydrogen/Bromine Redox Flow Batteries. J. Energy Storage 2023, 70, 107890. [Google Scholar] [CrossRef]
- Cantu, B.B.M.; Fischer, P.; Zitoun, D.; Tübke, J.; Pinkwart, K. In Situ Measurement of Localized Current Distribution in H2-br2 Redox Flow Batteries. Energies 2021, 14, 4945. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, Q.; Ma, Z. Effects of Trace Amount of Copper, Nickel and Bismuth on Hydrogen Evolution Reaction of the Carbon Felt Electrode in a Hydrochloride-Based Flow Battery. J. Energy Storage 2024, 103, 114329. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Z.; Tan, H.; Zheng, S.; Fan, B.; Zhang, Y. Suppression of the Hydrogen Evolution Reaction of Iron–Chromium Flow Batteries by Organic Compounds Containing the Imidazole Group. J. Electroanal. Chem. 2025, 978, 118874. [Google Scholar] [CrossRef]
- AbdelMessih, Y.; El-Deib, A.; Elkaramany, E. An Electrochemical Thermal Model for Vanadium Redox Flow Battery Lifetime Estimation under Dynamic Loading Conditions. Mater. Renew. Sustain. Energy 2025, 14, 41. [Google Scholar] [CrossRef]
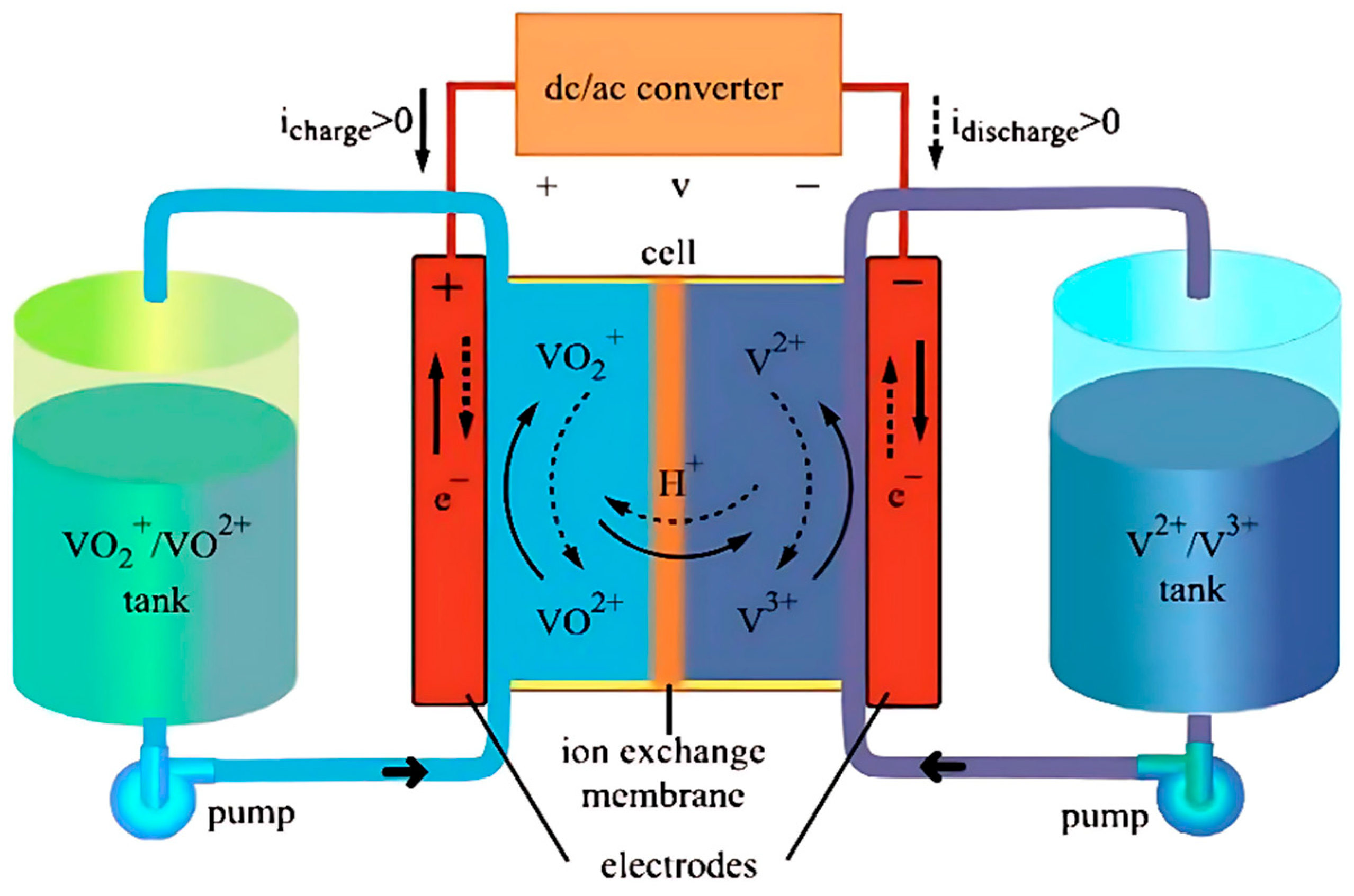
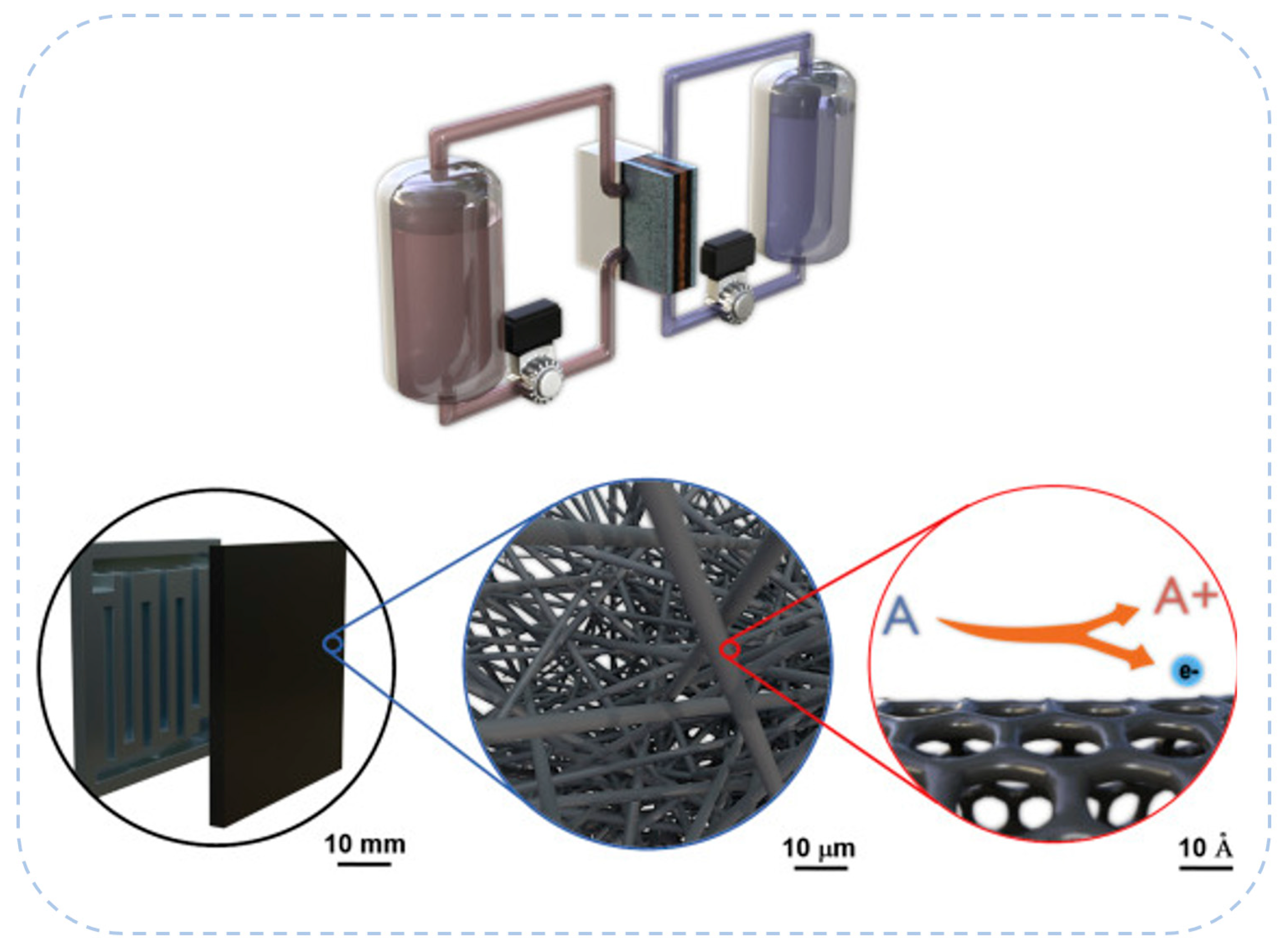
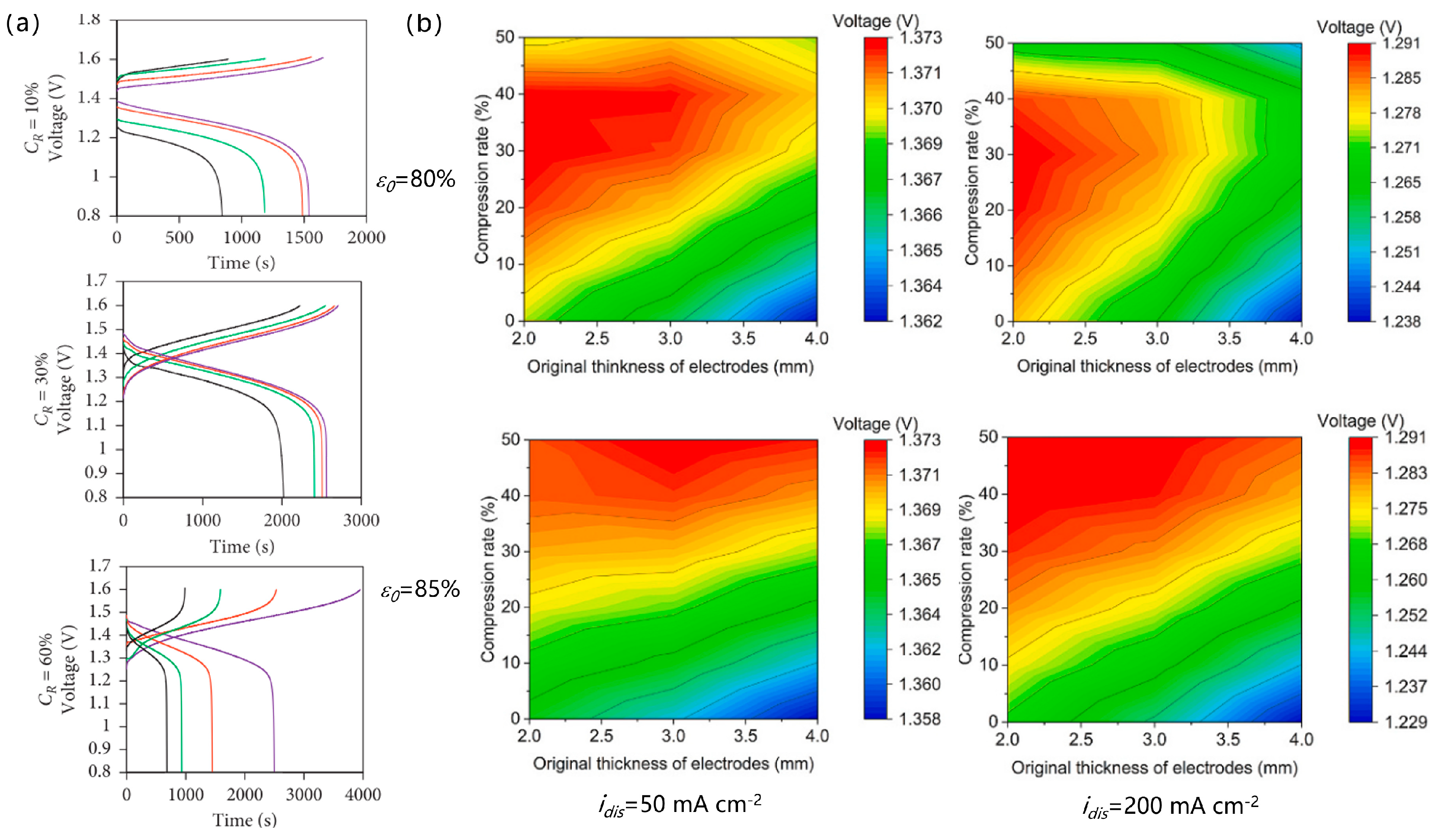

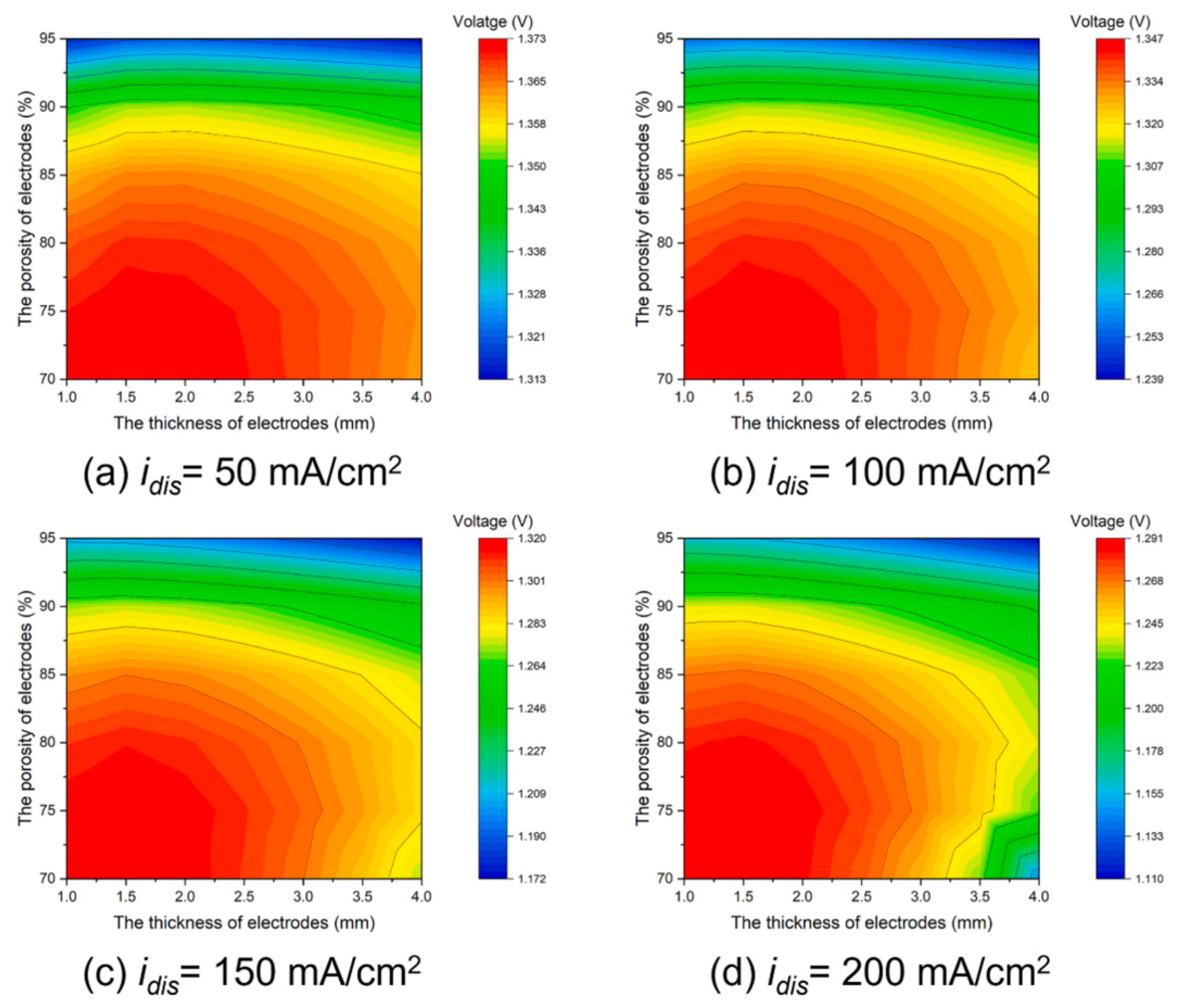









| Battery System | Reaction Characteristics | Modeling Features |
|---|---|---|
| VRFB | Liquid–liquid | Mass conservation equation; Nernst–Planck equation; Charge conservation equation; Butler–Volmer equation |
| ZFB | Liquid–liquid | Similar modeling equations as in VRFB, with additional consideration of porous electrode gap variation; For studying zinc dendrite issues involving solid–liquid phase transitions, embed Butler–Volmer kinetics into the Allen–Cahn equation to form a non-equilibrium reaction phase-field model |
| HBFB | Liquid–gas | Similar modeling approach to VRFB, but the presence of two-phase flow at the hydrogen electrode requires all related physical quantities to be evaluated using multiphase flow theory |
| Model Type | Description | Modeling Scale | Modeling Methods |
|---|---|---|---|
| Lumped parameter models | Treat the battery as one or more integrated reaction units, assuming that key variables (e.g., concentration, potential, temperature) are spatially uniform and vary only with time. | Macroscale | Finite element method; Finite volume method |
| Microscale modeling | Focuses on fundamental physical and electrochemical processes at the electrode–electrolyte interface and within the pore structure of porous electrodes. | Pore scale | Finite element method; Finite volume method; LBM; PNM; |
| Multi-scale modeling | Integrates microscale features such as electrode pore structure and transport properties into macroscale models to enhance accuracy and applicability. | Pore scale + Macroscale | PNM; LBM; PINN; Deep neural networks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; He, Y. Recent Advances in Numerical Modeling of Aqueous Redox Flow Batteries. Energies 2025, 18, 4170. https://doi.org/10.3390/en18154170
Liu Y, He Y. Recent Advances in Numerical Modeling of Aqueous Redox Flow Batteries. Energies. 2025; 18(15):4170. https://doi.org/10.3390/en18154170
Chicago/Turabian StyleLiu, Yongfu, and Yi He. 2025. "Recent Advances in Numerical Modeling of Aqueous Redox Flow Batteries" Energies 18, no. 15: 4170. https://doi.org/10.3390/en18154170
APA StyleLiu, Y., & He, Y. (2025). Recent Advances in Numerical Modeling of Aqueous Redox Flow Batteries. Energies, 18(15), 4170. https://doi.org/10.3390/en18154170








