Abstract
Under China’s ‘Dual Carbon’ strategy, the power sector plays a central role in achieving carbon neutrality. This study develops a bi-level game-optimization model involving the government, power producers, and technology suppliers to explore the dynamic coordination between shadow carbon pricing and emission trajectories. The upper-level model, guided by the government, focuses on minimizing total costs, including emission reduction costs, technological investments, and operational costs, by dynamically adjusting emission targets and shadow carbon prices. The lower-level model employs evolutionary game theory to simulate the adaptive behaviors and strategic interactions among power producers, regulatory authorities, and technology suppliers. Three representative uncertainty scenarios, disruptive technological breakthroughs, major policy interventions, and international geopolitical shifts, are incorporated to evaluate system robustness. Simulation results indicate that an optimistic scenario is characterized by rapid technological advancement and strong policy incentives. Conversely, under a pessimistic scenario with sluggish technology development and weak regulatory frameworks, there are substantially higher transition costs. This research uniquely contributes by explicitly modeling dynamic feedback between policy and stakeholder behavior under multiple uncertainties, highlighting the critical roles of innovation-driven strategies and proactive policy interventions in shaping effective, resilient, and cost-efficient carbon pricing and low-carbon transition pathways in the power sector.
Keywords:
dual carbon; bi-level game-optimization model; shadow carbon pricing; emission trajectories; game theory MSC:
91-10
1. Introduction
Achieving global carbon neutrality has become a central objective of contemporary climate policy, with the power sector, one of the largest sources of carbon emissions, playing a pivotal role in the transition to low-carbon energy systems [1,2]. The sector’s high dependence on fossil fuels, coupled with complex stakeholder structures and investment cycles, presents persistent challenges to effective decarbonization. One of the most urgent issues is how to scientifically formulate carbon pricing mechanisms and rationally plan emission reduction pathways that account for economic efficiency, technological feasibility, and institutional coordination [3,4,5].
Among the various policy instruments, shadow carbon pricing has emerged as a critical internal planning tool used by governments and regulatory agencies to reflect the social cost of carbon and guide strategic decisions, particularly in long-term investment planning and project evaluation. Unlike market-based carbon prices derived from cap-and-trade systems or carbon taxes, shadow carbon prices are administratively determined values used in policy assessments, cost–benefit analyses, and infrastructure planning. They aim to simulate the effect of an ideal carbon price in contexts where explicit markets may be underdeveloped or absent [6,7]. Prior studies show that well-designed shadow pricing mechanisms can promote the early adoption of green technologies, reduce long-term abatement costs, and improve market adaptability [8,9]. However, the effectiveness of shadow carbon pricing is highly sensitive to uncertainties in technological progress, policy enforcement intensity, the strategic behavior of market agents, and global geopolitical shifts [10,11]. Existing research on carbon pricing and emission trajectory optimization primarily falls into two categories: economic optimization models and static game-theoretic frameworks. The former includes cost–benefit analyses, integrated assessment models (IAMs), and energy system simulations to estimate optimal carbon prices and emission pathways [12,13]. The latter focuses on strategic interactions among firms and regulators, often using Nash equilibrium or Stackelberg models to explore policy incentives and compliance behavior [14,15]. While these approaches have contributed valuable insights, they frequently neglect the dynamic feedback between policy design and behavioral adaptation and seldom incorporate multiple sources of uncertainty that characterize real-world decarbonization transitions [16,17]. In response to these limitations, recent studies have increasingly adopted evolutionary game theory to model the dynamic strategy adjustments of heterogeneous agents under bounded rationality and policy feedback [18,19]. Replicator dynamics have been applied to study how power producers adapt to carbon pricing or how technology providers respond to innovation subsidies [20]. Nevertheless, integrated frameworks that combine dynamic policy optimization, shadow carbon pricing, and stakeholder strategy evolution remain scarce, especially under multi-dimensional uncertainty.
Recent years have seen a surge of research on carbon pricing mechanisms and low-carbon transition strategies, with many works employing optimization and game-theoretic models to capture the dynamic and strategic interactions among stakeholders in the power sector [13,14,16,17,18,19]. Studies such as [10,11] have examined the effectiveness of carbon pricing in diverse market environments, while others have integrated evolutionary game theory or bi-level programming to better reflect adaptive behavior and regulatory feedbacks [4,20]. Despite these advances, relatively few works have systematically addressed the joint optimization of shadow carbon pricing and emission pathways under multiple sources of uncertainty, especially in rapidly transforming energy systems. In recent years, research on carbon pricing mechanisms has advanced significantly, especially with growing recognition of the complex uncertainties facing low-carbon transitions. In particular, several recent studies have proposed dynamic carbon pricing models that explicitly incorporate various sources of uncertainty, such as technological innovation, policy variability, and external market shocks. For example, Zakaria et al. [21] analyzed stochastic optimization approaches for uncertainty modeling in renewable energy applications. Similarly, Dominique and Tian [22] explored the financial impacts of carbon pricing policies under the framework of Knightian uncertainty. Zhong and Sun [23] used a game-theoretic approach to analyze pricing and low-carbon strategies, taking into account dual fairness concerns and different competitive behaviors. These recent contributions underscore the need for integrated modeling approaches that can account for dynamic feedback and multi-level uncertainties in carbon pricing and emission pathway planning. The present study focuses on China, which plays a pivotal role in global climate mitigation due to its status as the world’s largest emitter of and its significant influence on global energy trends. China’s “Dual Carbon” strategy, which targets carbon peaking before 2030 and carbon neutrality before 2060, represents one of the most ambitious national policy agendas for low-carbon transition [1,2,24]. The Chinese power sector is not only the largest in the world but also features unique regulatory, institutional, and technological characteristics—including a developing carbon market [25], strong government intervention, and large-scale deployment of both conventional and renewable energy resources. These features make China an important and timely case for modeling the interplay between shadow carbon pricing and low-carbon transitions. Building upon these advances, our study introduces a bi-level game-optimization model that not only incorporates government, producers, and technology suppliers as adaptive agents but also systematically examines the effects of disruptive technologies, policy shifts, and international dynamics on shadow carbon pricing. This extension aims to address current research gaps by providing a more comprehensive analytical framework for resilient and adaptive carbon policy in the power sector. In the upper-level model, the government serves as a Stackelberg leader and determines dynamic carbon price adjustments and annual emission targets through optimization, aiming to minimize the combined cost of emission reduction, technological investments, and pricing volatility. In the lower-level model, a tripartite evolutionary game based on replicator dynamics is developed to capture the adaptive behaviors of power producers, regulatory agencies, and technology suppliers responding to government incentives and market feedback. Moreover, this research incorporates three key uncertainty scenarios into the simulation framework, (i) disruptive technological breakthroughs, (ii) major shifts in domestic policy, and (iii) international geopolitical fluctuations, thereby enabling a more comprehensive and realistic evaluation of the shadow carbon pricing mechanism’s robustness and adaptability. By systematically analyzing system dynamics under varying conditions, this study seeks to inform both academic modeling efforts and policy design for resilient low-carbon transitions in the power sector.
2. Model Description
This study aims to deeply analyze the dynamic coordination and optimization mechanisms between shadow carbon pricing and the dual carbon pathway in the power sector’s journey toward carbon neutrality. At present, due to the influence of multiple uncertainties, including technological development, policy regulation, and international environment, the low-carbon transition of the power industry faces a complex dynamic game landscape. Understanding how to scientifically determine shadow carbon pricing and optimize the carbon emission pathway has become a core issue in promoting the sustainable development of the sector. Therefore, this study constructs a bi-level game-optimization model involving three key stakeholders (government, power producers, and technology providers) to clarify the dynamic feedback mechanisms and evolutionary patterns among them. By introducing three types of uncertainty scenarios—disruptive technological breakthroughs, major policy interventions, and international landscape shifts—the model analyzes the impact of external disturbances on the evolution of carbon pricing and the carbon neutrality pathway. The aim is to provide more robust and efficient carbon pricing strategies and transition planning support for policymakers.
Model Structure and Assumptions
To achieve internal carbon neutrality within the power sector, this study develops a bi-level game-optimization model. The upper level is led by the government, which plans the carbon emission pathway and regulates the shadow carbon price for the industry. The lower level comprises a tripartite evolutionary game system involving power producers (coal and renewable), regulatory agencies, and technology providers. These agents adjust their strategies based on replicator dynamics. The upper and lower levels form a closed-loop feedback system through carbon pricing and actual emission outcomes. The model is built under the following core assumptions:
A1: Power producers decide whether to adopt low-carbon technologies; the government chooses between strict or lenient regulatory policies; and technology providers decide whether to promote disruptive low-carbon technologies.
A2: All agents aim to maximize their own payoffs, and their behavioral adjustments follow replicator dynamics.
A3: The government-set shadow carbon price acts as an internal guiding mechanism in the absence of full market pricing and influences the revenue structure of firms.
A4: The upper-level planning influences the evolutionary process at the lower level, while the strategy distribution at the lower level determines actual emissions and feeds back into the upper level.
A5: During system operation, three typical types of uncertainty—technological breakthroughs, policy changes, and international dynamics—may exert external disturbances.
Specifically, the upper level is a pathway–carbon pricing optimization layer, whose objective function aims to minimize the total cost of emission reduction:
where denotes the carbon emission target set by the pathway planning, represents the cost of carbon emission reduction, denotes the investment cost for low-carbon technologies, and indicates the operational cost of the power system. The parameter is the penalty coefficient for carbon price fluctuations. denotes the shadow carbon price (in this paper, shadow carbon pricing refers to a non-market-based internal carbon pricing mechanism set by the government to guide decision-making in the power sector, particularly in the absence of or alongside formal carbon markets), is the reference value for the expected stable shadow carbon price, is the ideal carbon pathway the government aims to set, and is the penalty coefficient for deviation from the pathway target. In particular, the use of the squared deviation is a standard approach in pathway optimization and control, as it provides a smooth, differentiable penalty function that emphasizes larger deviations while maintaining unit consistency [16,23]. This form also aligns with the treatment of widely used variance and quadratic loss functions and ensures that the cost of deviating from the ideal trajectory is weighted appropriately within the total cost function.
Specifically, the carbon emission reduction cost typically exhibits increasing marginal cost characteristics, i.e., the stricter the emission target (the lower the ), the higher the cost required to achieve that target [16,23]. It is commonly modeled using a quadratic loss function to reflect the nonlinear increase in marginal abatement cost under policy pressure. The technology investment cost also increases as the emission target tightens, but at a relatively slower rate compared to emission reduction costs, making it suitable for representation with a linear or low-order polynomial function [13,17]. The operational cost includes both the direct generation load cost and the system flexibility cost induced by emission reduction [4,19]. As a result, it incorporates both positive terms (e.g., increased ancillary service costs due to higher renewable penetration) and potentially negative terms (e.g., reduced fuel costs due to decreased coal power output) and is thus appropriately modeled using a linearly weighted form. Based on the above considerations, the specific formulations of the three cost functions (, , and ) are given as follows.
where are cost parameters and represents the baseline carbon emissions (i.e., emissions without policy interventions). The functional forms of the cost terms in Equation (2) are constructed based on a combination of theoretical expectations and stylized facts from the existing literature. Specifically, the cost of adopting green technologies for firms is modeled as a convex function to reflect increasing marginal costs associated with scaling up green investments and overcoming technological barriers, a structure supported by prior studies in environmental economics and energy transition modeling. Similarly, the R&D cost function for technology suppliers adopts a nonlinear increasing form, consistent with empirical findings that show diminishing returns and rising expenditures at higher levels of innovation intensity. The government’s policy cost functions incorporate both fixed regulatory costs and marginal subsidy outlays, which are common in models simulating policy implementation and fiscal impacts.
To ensure the feasibility of upper-level optimization decisions and compliance with policy requirements, the planning of the carbon emission trajectory and the regulation of the shadow carbon price are standardized and constrained. First, to control the total carbon emissions of the power sector over the entire planning horizon, a carbon budget constraint is established as follows:
where denotes the upper limit of the total cumulative carbon emissions permitted for the power sector over the entire planning horizon . This value is typically determined by national “Dual Carbon” goals (such as “carbon peaking by 2030 and carbon neutrality by 2060”) in conjunction with the sectoral emission allocation targets set for the energy industry. This constraint reflects the long-term cumulative emission ceiling established by national or regional authorities—for instance, the total carbon budget corresponding to achieving carbon neutrality before 2060. It ensures that the carbon emission trajectory planned during the model’s optimization process does not exceed the overall emission cap, serving as a foundational condition for realizing the dual carbon strategy objectives.
Secondly, to maintain consistency between the annual carbon emission control path and the actual emission outcomes, the following carbon path consistency constraint is introduced:
where is the tolerance term that allows for a permissible margin of deviation during policy implementation. This constraint reflects the guiding role of the target pathway in influencing behavioral responses while allowing for certain deviations between planned and actual behavior, thereby enhancing the model’s feasibility and robustness.
Finally, to ensure the policy formulation is both practically reasonable and mathematically well-posed, the following non-negativity constraints are imposed:
and
For the lower-level tripartite evolutionary game layer, let x represent the proportion of power enterprises choosing low-carbon strategies, y the proportion of government agencies implementing strict regulation, and z the proportion of technology providers promoting disruptive technologies. The replicator dynamic equations for the tripartite game are as follows [18,20]:
where denotes the payoff for enterprises adopting low-carbon technologies, and represents the average expected payoff of the enterprise group. Similarly, denotes the payoff for the government under strict regulation, and is the average expected payoff for the government. denotes the payoff for technology suppliers promoting disruptive technologies, and is the average payoff of all suppliers.
The payoff for power enterprises adopting low-carbon technology is
For enterprises not adopting low-carbon technologies, the payoff is
where is the revenue from electricity sales using low-carbon technologies, is the cost per unit of electricity with low-carbon technologies, is the emissions reduced through low-carbon technologies, and is the government subsidy for adopting low-carbon strategies. are the revenue and cost under high-carbon technologies, and is the carbon emissions generated by high-carbon technologies.
The average expected payoff of the enterprise group is
The government’s payoff under strict regulation is
Under weak regulation, the government’s payoff is
where is the emission target set for year t, is the actual emissions resulting from enterprise and technology behaviors, reflects the government’s emphasis on achieving emission reduction goals, is the enforcement cost under strict regulation, and is the basic administrative cost under weak regulation.
The government’s average expected payoff is
The payoff for suppliers promoting disruptive technologies is
For maintaining traditional technologies, the payoff is
where is the revenue from market sales of the new technology (potentially influenced by adoption rate and carbon price), is the R&D and deployment cost of disruptive technologies, is the government subsidy for new technology, and are the revenue and cost for traditional technologies.
The average expected payoff for technology suppliers is
In addition, actual carbon emissions are determined by the strategy combination at the lower level:
The shadow carbon price is dynamically adjusted based on emission deviation:
where is the maximum carbon reduction potential, is the emission reduction efficiency of technology, is the pathway deviation adjustment coefficient reflecting the government’s sensitivity to deviations from the emission target, and is the behavioral deviation adjustment coefficient reflecting the government’s responsiveness to deviations in enterprise adoption behavior.
Note that variables such as renewable penetration rate, capacity utilization rate, PV storage size, and plant scale can all serve as important system constraints. However, the primary objective of the present study is to develop and demonstrate the feasibility of a bi-level game-optimization framework for shadow carbon pricing and low-carbon transition in the power sector. To maintain analytical tractability and focus on the core mechanisms of policy–behavior feedback and dynamic carbon pricing, we have deliberately employed a simplified set of constraints, primarily involving carbon budgets and emission pathway consistency. Figure 1 provides a visual overview of the research process, including data processing, parameter setting, simulation procedures, and result analysis.
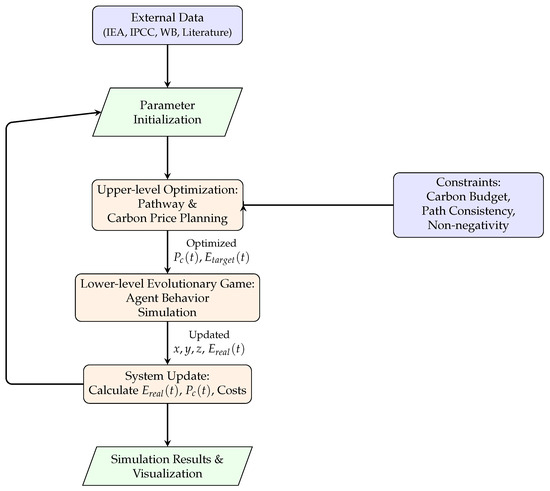
Figure 1.
Flowchart of the data processing, upper-level pathway–carbon pricing optimization, and lower-level evolutionary game simulation process.
3. Simulations
3.1. Simulation of Agent Behavior Evolution
To analyze the behavioral evolution of the three types of agents in the power sector under incentive mechanisms, all parameter values used in the simulation are presented in Table 1, together with their descriptions and sources. Where possible, parameters were selected based on published literature, official policy reports, or widely accepted empirical benchmarks in the fields of energy economics and carbon policy. For example, values for , , , and reflect typical cost and revenue levels reported in recent studies on green and traditional power technologies (see, e.g., [1,2]). Policy-sensitive parameters such as and are aligned with prevailing subsidy schemes and incentive programs found in national and international policy documents. Where no direct empirical source was available, values were chosen to reflect reasonable baseline conditions as established in prior modeling work. Specifically, we employed Python 3.11 for model implementation, simulation, and visualization.

Table 1.
Model parameters, values, units, and justification.
Figure 2 illustrates that under the current policy framework and economic parameter settings, there exists an inherent evolutionary drive among the three major agents in the power sector toward a low-carbon transition (0 denotes the base year). Here, (blue line) denotes the proportion of power producers adopting low-carbon strategies; (orange line) represents the proportion of government regulators implementing stringent oversight; and (green line) indicates the proportion of technology suppliers promoting disruptive technologies. The initial state is set as , indicating that at the outset, governmental regulatory intent is moderately strong, while green behaviors among producers and technology providers are still in their early development. The monotonically increasing trend of over time suggests that the total benefits of adopting low-carbon technologies—including carbon pricing revenues and government subsidies—exceed those of conventional high-carbon options. This evolution aligns with real-world trends in China, where leading energy enterprises (e.g., Huaneng, Huadian) have accelerated investments in clean energy following the implementation of the national “dual carbon” goals. The model assumes , indicating that low-carbon technologies are economically more attractive under carbon price incentives and policy subsidies. Meanwhile, the proportion of government actors choosing stringent regulation, , shows a decreasing trend over time. This reflects the diminishing marginal returns of regulatory enforcement. As power producers () and technology suppliers () increase their adoption of low-carbon and disruptive technologies, the system’s overall emissions steadily decline, reducing the deviation from the government’s emission target . In the evolutionary game, the marginal benefit of strict regulation decreases while the enforcement cost remains constant, causing the relative benefit of strong versus weak regulation to decline and thereby reducing . The upward trend in indicates that disruptive technologies are gradually gaining market dominance, giving technology providers sufficient incentives for R&D and diffusion. This mirrors real-world developments such as the rise of “PV + storage” and “wind-powered hydrogen production,” which have received strong government support and market traction. Since , it implies that disruptive strategies are more competitive when subsidies and demand pull are present. Therefore, as long as carbon pricing and subsidy mechanisms are properly designed, the system can spontaneously evolve toward the “dual carbon” targets through strategic interactions. This confirms that with institutional guidance, market behavior can be synergistically aligned with low-carbon development trajectories.
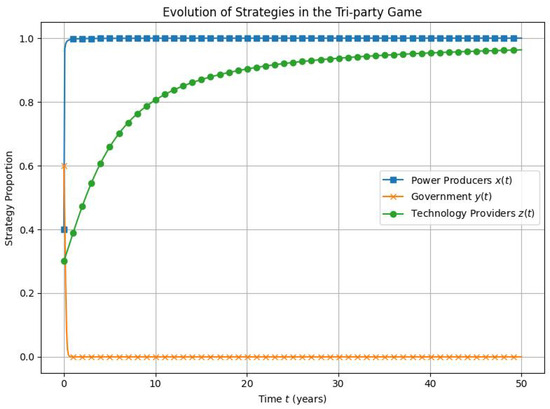
Figure 2.
Evolution of strategies in the tri-party game. This figure shows that under the current policy framework and economic parameter settings, there exists an inherent evolutionary drive among the three major agents in the power sector toward a low-carbon transition.
Figure 3 illustrates the temporal evolution of both the shadow carbon price and the total emission reduction cost J over a 30-year planning horizon. The blue curve shows that the shadow carbon price increases steadily over time, starting from approximately 150 yuan/t and reaching 300 yuan/t by year 30. This upward trend suggests that, under the simulated scenario, increasingly stringent carbon emission targets or lagging abatement progress require higher internalized carbon prices to incentivize further emission reductions. Such a pattern may reflect a tightening policy environment, higher marginal abatement costs, or slower adoption of low-carbon technologies. Notably, the final shadow carbon price remains within the plausible policy range reported in recent empirical studies and aligned with global benchmarks. In contrast, the red dashed line indicates that the total cost of emission reduction decreases monotonically throughout the simulation period. The initial cost is relatively high, exceeding 13.7 thousand yuan, but steadily declines to around 12.0 thousand yuan by the end of the planning horizon. This trend can be attributed to the cumulative effect of technology learning, economies of scale, and increased adoption of low-carbon technologies over time, which drive down both technological and operational costs. The divergence between rising carbon prices and falling total costs highlights the non-linear relationship between carbon pricing policies and overall system expenditures: while carbon prices increase to maintain pressure on emissions, system-wide optimization and technological progress enable cost reductions. The results underscore the importance of dynamic, adaptive carbon pricing mechanisms in supporting the low-carbon transition. Rising shadow carbon prices serve as a strong incentive for continuous emission reductions, particularly as low-hanging fruit is exhausted and marginal costs increase. Simultaneously, system-wide learning effects and innovation drive down the total cost burden, enabling a more economically efficient pathway toward deep decarbonization. These findings reinforce the critical role of both robust policy instruments and technological advancement in achieving long-term emission targets in the power sector.
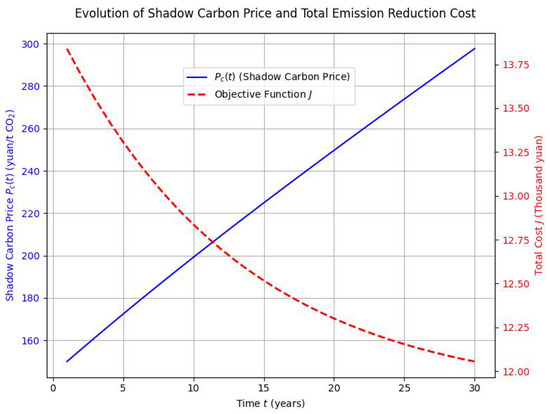
Figure 3.
Evolution of shadow carbon price and the total cost of emission reduction. This graph illustrates the temporal trends of shadow carbon price and total carbon abatement cost during the tripartite evolutionary game in the power sector as corporate and technological behaviors evolve.
3.2. Simulation of Three Key External Disruption Scenarios
To enhance the applicability and robustness of the proposed model in the context of real-world policy formulation and technological transition, this study incorporates three key types of external disruption scenarios into the bi-level game-optimization framework. These scenarios are defined as “Disruptive Technological Breakthroughs,” “Major Policy Interventions,” and “Changes in the International Landscape.” Specifically, we construct three composite scenarios—S1 (Optimistic), S2 (Baseline), and S3 (Pessimistic)—each representing different combinations of the aforementioned uncertainty dimensions (see parameter settings in Table 2). In Scenario S1, we assume successful breakthroughs in disruptive technologies, proactive implementation of policy mechanisms, and a relatively relaxed international environment. Scenario S2 reflects a continuation of current trends under existing policy and market conditions. In Scenario S3, we simulate the combined effects of technological stagnation, weak policy incentives, and rising international pressure from carbon restrictions. By simulating and analyzing these three scenarios, we systematically evaluate the stability and robustness of the shadow carbon pricing mechanism and the evolution of strategic behavior under multifaceted uncertainty. The following table presents specific adjustments in key parameter values under different types of uncertainty perturbations to construct these simulation scenarios.

Table 2.
Key parameter variations under three scenarios.
Figure 4 presents the dynamic evolution of both the shadow carbon price and actual emissions across three policy–technology scenarios (S1, S2, S3), each reflecting different levels of technological progress and government support. The upper panel illustrates the trajectory of the shadow carbon price, while the lower panel compares actual emissions against the emission reduction target (dashed line). In the optimistic scenario (S1), where technology adoption and policy incentives are strong, actual emissions decline rapidly over time. Within just a few years, emissions drop below the policy target, demonstrating the effectiveness of coordinated policy support and technological advancement. As the emissions gap closes, the shadow carbon price exhibits a steady downward trend, falling from 200 yuan/t at the outset to just above 100 yuan/t by year 30. This decline reflects a “policy dividend” from early action: once mitigation is on track, price pressure on firms can be relaxed, reducing overall compliance costs and signaling the success of the dual-carbon strategy. In the baseline scenario (S2), which assumes moderate innovation and only partial policy support, the results are less encouraging. Emissions decrease more slowly and plateau above the target level for the entire period. As a result, the shadow carbon price quickly escalates to the policy-imposed ceiling of 300 yuan/t and remains fixed at this maximum. This persistent price cap signals ongoing difficulty in bridging the mitigation gap and points to the risk of cost escalation if technological diffusion stalls or policy design is insufficiently adaptive. The pessimistic scenario (S3), characterized by weak innovation and low incentives, produces the least favorable outcomes. Emissions remain nearly flat, barely deviating from the baseline and failing to approach the target at any stage. The shadow carbon price reaches the upper cap even faster than in S2, reflecting severe policy stress and the system’s inability to generate sufficient behavioral or technological response. This result highlights the limits of price-based mechanisms alone and suggests that under adverse conditions, additional non-market or administrative measures may be necessary to achieve emission reduction goals. Comparing all three scenarios, the analysis underscores that the trajectory and effectiveness of shadow carbon pricing are highly sensitive to the underlying pace of technological progress and the strength of supporting policies. Aggressive early investment in clean technology and robust policy design not only accelerate emission reductions but also allow for a gradual relaxation of carbon price signals, reducing long-term compliance costs. Conversely, weak policy support and technological inertia lead to persistently high carbon prices and missed mitigation targets, raising economic and political challenges for the transition. In summary, these results reinforce the importance of coupling adaptive carbon pricing with proactive technology and policy intervention. Without such alignment, the carbon price will remain high, and the system will struggle to meet ambitious dual carbon targets. The findings provide clear evidence for policymakers: sustained investment in technology, combined with credible and flexible policy frameworks, is essential for an effective, efficient, and politically sustainable low-carbon transition.
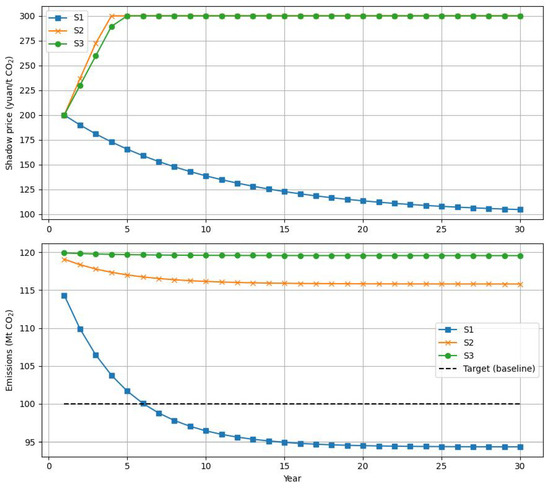
Figure 4.
Evolution of shadow carbon price and the total cost of emission reduction. The system’s behavioral evolution in terms of shadow carbon price (top) and actual carbon emission trajectory (bottom).
4. Conclusions
This study investigates the dynamic coordination between shadow carbon pricing and the dual-carbon transition pathway in the context of carbon neutrality in the power sector. A government-led bi-level game-optimization model is developed, integrating a replicator dynamics-based evolutionary game among three key stakeholders: power producers, regulatory authorities, and technology providers. This framework captures the closed-loop feedback between policy planning and strategic behavioral adaptation. Moreover, the analysis incorporates three representative uncertainty scenarios: disruptive technological breakthroughs, major policy interventions, and shifts in the international landscape, to explore the system’s responses to external shocks. The main findings are as follows: (1) Under the current policy framework, both power producers and technology suppliers increasingly adopt low-carbon strategies, while government regulatory intensity gradually declines. This reflects a co-evolutionary mechanism in which strategic interactions lead to collective improvements. As the adoption rate of low-carbon technologies rises, the shadow carbon price and total emission reduction costs both decline and eventually stabilize, indicating effective policy–behavior coordination. (2) External disturbances significantly affect the evolution of carbon pricing and emission trajectories. In the optimistic scenario, synergistic effects from technological breakthroughs and strong policy enforcement drive rapid reductions in both shadow carbon prices and emissions, highlighting high-efficiency and low-cost decarbonization. The baseline scenario presents a steady decline in carbon prices and emissions, reflecting the stability of the current policy environment. In contrast, the pessimistic scenario, characterized by slow technological progress, weak policy intervention, and heightened international pressure, results in higher transition costs and more challenging emission reductions. (3) These results underscore the critical importance of aligning technological innovation and policy instruments to achieve dual-carbon goals in the power sector. It is recommended that governments simultaneously enhance R&D investment and policy incentives while maintaining the flexibility to respond dynamically to external shocks. This approach can improve the resilience and robustness of the emission reduction trajectory.
Despite its contributions, this study has several limitations. First, the modeling and simulations rely primarily on stylized assumptions and literature-based parameters, rather than empirical data, which may affect the direct applicability of the results to real-world settings. Second, the model simplifies certain system constraints, such as renewable energy penetration, plant scale, and storage integration, which are relevant for more granular policy analysis. Third, behavioral heterogeneity and regional differences among stakeholders are not fully captured. In addition, the model does not incorporate market fluctuations, consumer demand dynamics, or comprehensive policy portfolios that may also influence the low-carbon transition process. Future research should focus on empirical calibration and validation of the model using real-world data from different regions and power systems. Expanding the model to include more detailed operational constraints, broader types of uncertainties, and heterogeneous agent behaviors would further enhance its practical relevance. Moreover, incorporating consumer-side responses and market mechanisms could provide a more comprehensive understanding of low-carbon transitions. Finally, scenario-based policy simulation and sensitivity analysis are recommended to inform adaptive and resilient decision-making for carbon neutrality pathways. In summary, this study provides theoretical and methodological support for the design of shadow carbon pricing mechanisms and the planning of carbon neutrality pathways. It contributes to more scientific, adaptive, and resilient decision-making in the low-carbon transformation of the power sector.
Author Contributions
G.S.: Writing—original draft, Writing—review and editing, Conceptualization, Methodology, Software, Visualization; P.X.: Writing—original draft, Writing—review and editing, Conceptualization, Methodology, Software, Visualization; B.Y.: Writing—review and editing, Conceptualization, Methodology; H.Z.: Writing—review & editing, Conceptualization, Methodology; P.X.: Writing—review and editing, Conceptualization, Methodology; C.W.: Writing—review and editing, Conceptualization, Methodology; Y.G.: Writing—original draft, Writing—review and editing, Conceptualization, Methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the State Grid Corporation Headquarters Science and Technology Project of China (1400-202426279A-1-1-ZN); State Grid Energy Research Institute Young Talents Project of China. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Data Availability Statement
No data was used for the research.
Conflicts of Interest
Guangzeng Sun, Bo Yuan, Han Zhang, Peng Xia, Cong Wu and Yichun Gong are employed by State Grid Energy Research Institute Co., Ltd. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- IEA. Net Zero by 2050: A Roadmap for the Global Energy Sector; IEA: Paris, France, 2021. [Google Scholar]
- IPCC. Climate Change 2023: Mitigation of Climate Change; Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Edenhofer, O.; Pichs-Madruga, R.; Sokona, Y.; Minx, C.; Farahani, E.; Kadner, S.; Seyboth, K.; Adler, A.; Baum, I.; Brunner, S.; et al. Climate Change 2014: Mitigation of Climate Change; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Zhang, S.; Chen, W. Assessing the energy transition in China towards carbon neutrality with a probabilistic framework. Nat. Commun. 2022, 13, 87. [Google Scholar] [CrossRef] [PubMed]
- Newbery, D.; Pollitt, M.; Ritz, R.; Strielkowski, S. Market design for a high-renewables European electricity system. Renew. Sust. Energ. Rev. 2018, 91, 695–707. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Revisiting the social cost of carbon. Proc. Natl. Acad. Sci. USA 2017, 114, 1518–1523. [Google Scholar] [CrossRef] [PubMed]
- Bertram, C.; Johnson, N.; Luderer, G.; Riahi, K.; Isaac, M.; Eom, J. Carbon lock-in through capital stock inertia associated with weak near-term climate policies. Technol. Forecast. Soc. Change 2015, 90, 62–72. [Google Scholar] [CrossRef]
- Aldy, J.E.; Pizer, W.A.; Akimoto, K. Comparing emissions mitigation efforts across countries. Clim. Policy 2017, 17, 501–515. [Google Scholar] [CrossRef]
- Fuss, S.; Lamb, W.F.; Callaghan, M.W.; Hilaire, J.; Creutzig, F.; Amann, T.; Beringer, T.; de Oliveira Garcia, W.; Hartmann, J.; Khanna, T.; et al. Negative emissions—Part 2: Costs, potentials and side effects. Environ. Res. Lett. 2018, 13, 063002. [Google Scholar] [CrossRef]
- Baranzini, A.; Van den Bergh, J.C.; Carattini, S.; Howarth, R.B.; Padilla, E.; Roca, J. Carbon pricing in climate policy: Seven reasons, complementary instruments, and political economy considerations. WIREs Clim. Change 2017, 8, e462. [Google Scholar] [CrossRef]
- Best, R.; Burke, P.J.; Jotzo, F. Carbon pricing efficacy: Cross-country evidence. Environ. Resour. Econ. 2020, 77, 69–94. [Google Scholar] [CrossRef]
- Tol, R.S.J. The economic impacts of climate change. J. Econ. Perspect. 2009, 23, 29–51. [Google Scholar] [CrossRef]
- Calvin, K.; Bond-Lamberty, B.; Clarke, L.; Edmonds, J.; Eom, J.; Hartin, C.; Kim, S.; Kyle, P.; Link, R.; Moss, R.; et al. The SSP4: A pathway of inequality and climate change. Glob. Environ. Change 2017, 42, 284–296. [Google Scholar] [CrossRef]
- Benchekroun, H.; Long, N. Game theoretic modeling in environmental and resource economics. In Handbook of Regional Science; Fischer, M., Nijkamp, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Tu, Z.; Liu, B.; Jin, D.; Wei, W.; Kong, J. The effect of carbon emission taxes on environmental and economic systems. Int. J. Environ. Res. Public Health 2022, 19, 3706. [Google Scholar] [CrossRef] [PubMed]
- Heuberger, C.F.; Staffell, I.; Shah, N.; Dowell, N. Impact of myopic decision-making and disruptive events in power systems planning. Nat. Energy 2018, 3, 634–640. [Google Scholar] [CrossRef]
- Pietzcker, R.; Ueckerdt, F.; Carrara, S.; de Boer, H.; Despres, J.; Fujimori, S.; Johnson, N.; Kitous, A.; Scholz, Y.; Sullivan, P.; et al. System integration of wind and solar power in integrated assessment models: A cross-model evaluation of new approaches. Energy Econ. 2017, 64, 583–599. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, X.; Wang, C.; Liu, L.; Hu, J.; Zheng, Z.; Tang, S.; Zheng, H.; Dong, J. Evolutionary dynamics in stochastic nonlinear public goods games. Commun. Phys. 2024, 7, 377. [Google Scholar] [CrossRef]
- Li, F.; Guo, Y.; Dong, T.; Liu, B.; Geng, X. Tripartite evolutionary game analysis on corporate carbon reduction decisions considering dual supervision under carbon trading. Comput. Ind. Eng. 2024, 187, 109786. [Google Scholar] [CrossRef]
- Nowak, M.A. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Zakaria, A.; Ismail, F.; Lipu, H.; Hannan, M. Uncertainty models for stochastic optimization in renewable energy applications. Renew. Energy 2020, 145, 1543–1571. [Google Scholar] [CrossRef]
- Dominique, C.; Tian, Y. Corporate credit risk modeling under carbon pricing uncertainty: A Knightian uncertainty approach. Sustain. Futures 2024, 8, 100283. [Google Scholar] [CrossRef]
- Zhong, Y.; Sun, H. Game theoretic analysis of prices and low-carbon strategy considering dual-fairness concerns and different competitive behaviours. Comput. Ind. Eng. 2022, 169, 108195. [Google Scholar] [CrossRef]
- Xu, J.; Li, L.; Zhang, B.; Hao, M.; Mei, F. Dual carbon goals’ enhances policy integration: Analysing recent changes in China’s national climate policy. J. Asian Public Policy 2024, 1–18. [Google Scholar] [CrossRef]
- Zhang, D.; Karplus, V.J.; Cassisa, C.; Zhang, X. Emissions trading in China: Progress and prospects. Energy Policy 2014, 75, 9–16. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).