Abstract
This paper presents an adaptive wireless droop control scheme that uses an adaptive virtual resistance to regulate the DC voltage and control the active power. The proposed methodology is implemented to address the power mismatch problem in a fixed-droop control for multi-terminal HVDC (MT-HVDC or MTDC) systems. Each inverter calculates available power and adjusts its output power accordingly while adapting the virtual resistance to mimic the behavior of a mesh system that is based on loading effects. The main objective of this methodology is to increase the reliability of the MTDC system by eliminating the need for fast communication links and ensuring proper power sharing between inverters. Additionally, this communication-free scheme includes a power management algorithm that controls power sharing during peak hours of the inverters among the rectifiers as per mutual agreements between the operators to mitigate the risk of a system overload and optimize the power sharing. A simulation of a five-terminal mesh MTDC system has been verified by using PSCAD/EMTDC to validate the performance and effectiveness of the proposed method. The results show the flexibility and feasibility of the proposed control method in three different modes.
1. Introduction
In recent years, governments around the world have been engaged in reducing greenhouse gas emissions, which has led to rapid penetration of renewable energy resources in the power grids [1]. As a result, there is a pressing need to efficiently integrate these renewable energy resources into the existing grid setup. MT-HVDC systems present one of the solutions for this integration. They are described as multiple sources or loads connected to a common DC power transmission network. This has emerged as a promising solution for accommodating the increasing share of renewable energy generation and facilitating its effective long-distance power transmission and control [2]. Renewable energy resources connect with their respective voltage-source converters (VSCs) in MT-HVDC systems. The advantages of forming VSC-MT-HVDC systems are their ability to control active and reactive power independently [3] and their black-start capability, which enables such systems to be restored and operated without reliance on an external power source.
The VSC-MT-HVDC systems feature the ability to reverse power flow without requiring polarity reversal [4,5]. Researchers have also concentrated on stability [6,7], power-sharing imbalance, voltage deviation [8], and protection [9]. MT-HVDC enables the interconnection of multiple AC systems or the division of a single AC system into isolated power grids [8]. In general, these features make it suitable for integrating grid-connected wind farms, weak grids, and urban grids.
The control and operation of MT-HVDC grids pose several technical challenges. In particular, accurate power sharing between parallel VSC terminals is required to maintain DC voltage stability and avoid severe transient disturbances during load changes or shifting power flows [10]. One of the main challenges is the existence of a communication link between the terminals to ensure proper power sharing and improved stability for the grid, which affects system reliability. As a result, it has become essential to control power sharing without any dependence on communication links.
A power allocation strategy for a black start in VSC-MT-HVDC is discussed in [11]. This strategy allows multiple healthy AC grids to provide the required power and minimize the frequency fluctuations across the grids in order to achieve better stability and safe operation. This is achieved when there is some level of communication between the AC grids to determine the correct proportion of black start power that is provided to the blacked-out grid. Hence, dependence on communication makes this system prone to a single point of failure.
Another commonly used control methodology for VSC-MT-HVDC systems is master–slave control. In this methodology, the master converter controls the DC bus voltage, and the slave VSCs control the active power [12]. The main drawback of this method is the limited level of reliability because of the need for a fast communication link to achieve better voltage regulation and proper power sharing amongst the converters. Another concern in systems of significant size is the need for a high-rated master converter, which can increase the initial cost of the system as well.
Droop control strategies, such as voltage margin control (VMC) and voltage droop strategy [13,14,15,16], are also introduced to avoid relying on communication. The VMC method operates similarly to master–slave control. However, when an outage occurs in the main converter, the system transitions to one of the reserved converters, where, in cases of voltage oscillation, the terminal with the higher voltage reference takes over the role of the main converter to continue providing DC voltage regulation. Conversely, in cases of voltage drop, the terminal with a lower voltage reference takes over, as shown in Figure 1. These transactions rely on local measurements like DC voltage and active power. However, the main drawback of this method is the voltage oscillation due to its controller structure.
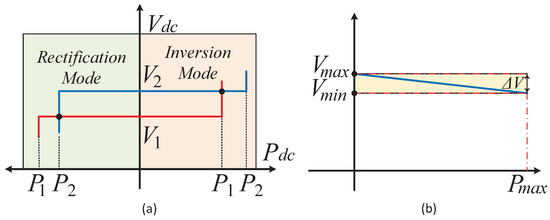
Figure 1.
(a) Voltage margin control in [13,14,15,16] (b) droop control characteristics [17].
The voltage droop method is based on the active power-frequency droop concept in AC systems. It distributes voltage regulation among multiple converters by sharing active power according to their droop characteristics, but achieving precise power sharing among terminals is challenging. Due to the non-linear relationship between voltage and real power, an increase in power requires the voltage to decrease to balance the power in the grid, as shown in Figure 1. Additionally, the available power for sharing is limited by the predefined droop controller coefficient. The droop gain is commonly determined based on the converter’s rating. However, increasing the droop gain can potentially impose greater responsibility on the converter to regulate voltage, thereby placing constraints on power sharing among MT-HVDC converters. Furthermore, variations in droop gain between converters may lead to power mismatch issues [17].
Another control scheme to avoid relying on fast communication is called priority control. This scheme prioritizes one converter station as the “master” for DC voltage regulation, which operates at constant voltage, and the other slaves in droop control. However, when there is a power outage or a voltage disturbance in the system, the slave converters transition from constant power mode to droop control mode, controlling both voltage and active power [18]. The main drawback of this method is the necessity for high power ratings on all converters, which can potentially increase capital costs. Furthermore, the design and expansion of these converters for larger systems can be complex [19].
To overcome the limitations of conventional control methods, research studies have proposed adaptive droop control as an alternative approach. Adaptive droop control involves dynamically adjusting droop coefficients in response to the present circumstances. It is implemented to address various technical challenges, such as power flow regulation [16,17,18,19,20,21], optimizing cost [22,23], and frequency support [6,24]. Adaptive droop with communication is proposed to further enhance power sharing and DC voltage dynamics. In [11], an optimal power flow secondary supervisory centralized controller is described. It calculates and sends the optimal droop parameters to the primary controller. To provide more accurate power sharing without exceeding the DC voltage limit, the authors in [25] propose that both no-load voltage reference and droop gain be updated at the same time. To achieve cost reduction in active power generation, a cost-based adaptive droop is proposed in [23]. This utilizes a modified economic dispatch algorithm that determines the cost-based droop gain while meeting the power balance and generation constraints. However, communication failures can significantly impact the reliability of a system.
An alternative secondary communication-based control method, known as pilot voltage, is utilized to achieve precise power sharing and direct changes in active power to converters with appropriate capacity. This control method involves setting a reference pilot voltage for each converter station. The actual output voltage of each converter is then regulated by adjusting its pilot voltage value, preventing overloads in MT-HVDC grids following converter outages or variations. However, this control scheme needs fast communication to transfer the measurements of the DC voltages of different converter stations. In [26], a control strategy is proposed that relies on a common connection point for all converters instead of local measurement to control the voltage. The main drawback of this method is that it could potentially cause ineffective power sharing in cases of disturbance. The authors in [27] propose an adaptive pilot voltage droop control scheme that provides both DC voltage regulation and frequency support in MT-HVDC grids. This is achieved by adjusting the reference operating point of voltage droop control, ensuring adequate power sharing and efficient voltage regulation among converter stations. In [28], the droop coefficients change adaptively based on the available power to share the burden of a power mismatch.
A distributed control methodology that focuses on communication only between neighboring converters to increase the system’s resilience by eliminating single points of failure is proposed in [24,29]. The authors in [29] make use of a secondary distributed controller added to the primary controller to correct the power mismatch by observing the voltage deviation and estimating the value of voltage based on the local measurement and the neighboring estimation. To provide frequency support, the authors in [24] propose an adaptive droop control method using a distributed consensus algorithm for frequency support and power sharing. This consists of a primary control layer, a consensus stage, and a coordination by optimization stage that minimizes the cost associated with generation, frequency variation, and converter losses.
Alternative solutions to address the limitations associated with communication loss in centralized control systems are also examined in the literature. Autonomous control implements a supplementary decentralized controller to provide a backup mechanism that operates independently in the event of communication loss. This guarantees that the rectifier does not exceed its rated capacity, thereby preventing overloading issues. To maintain system operation, an autonomous supplemental controller for proportional power distribution and voltage regulation is proposed in [30]. However, communication is needed to update the model and could have a severe impact on the system in the case of communication loss. In the absence of communication, the system switches to the autonomous controller, ensuring equal power sharing and system stability.
Similarly, another study in [21] presents a novel control strategy that operates effectively without communication between converters, maintaining DC voltage by autonomously sharing the appropriate power between the converter stations. To enhance economic efficiency in MT-HVDC systems, the authors in [22] propose an autonomous control strategy for power sharing. This strategy involves integrating a local controller within each inverter to determine the necessary power intake, enabling power sharing based on availability or a predetermined percentage agreed upon by the system operator. However, the operating cost will increase in the event of a communication loss.
To address the power mismatch in droop control, the virtual impedance method is a commonly used control technique. The virtual impedance method provides a tool to control the power flow of the droop control by inserting another constant impedance that can adaptively change based on a communication link. In [31], the power mismatch of both reactive and active power is utilized and then transmitted via a communication link into an integral controller. This controller generates a resistive and inductive virtual impedance to ensure proper power sharing. Furthermore, Ref. [32] investigates the virtual impedance technique by inserting a virtual node impedance, which adjusts the injected power based on the DC voltage level, thereby optimizing power-sharing capabilities. While the virtual impedance method can provide a great enhancement to power-sharing accuracy, the control methodologies in [31,32] can exhibit issues when dealing with large-scale systems.
A comprehensive comparison between the study presented in this paper and recent literature is summarized in Table 1. The evaluation is based on several desired features that are crucial to achieving optimal system performance. These include the capability of possessing available power, the speed of communication links, the impact of communication failures during operation, the ability to ensure equal power sharing in the event of a power shortage, and the reliability of the controller that is incorporated. Each of these features is colored green, yellow, or red in Table 1 to represent desired, semi-desired and undesirable features of a particular control scheme in comparison to the proposed work in this paper. This comprehensive comparison provides valuable insights into the performance and effectiveness of different approaches, aiding in the determination of the most suitable solution for a given criterion.

Table 1.
Comparison of features covered by the proposed work with recent literature.
In summary, the primary contribution of this research paper is the proposal of a novel methodology that utilizes an adaptive wireless droop (AWD) with adaptive virtual resistance. This methodology is capable of adaptively controlling power sharing based solely on local measurements, and it can adapt the varying virtual resistance of mesh MT-HVDC to compensate for variable loading conditions and eliminate power-sharing errors. Furthermore, this strategy also manages power flow during rush hours. This further optimizes the results and maintains system stability. The key contributions that are addressed in this paper are summarized below:
- There are limited non-communication-based power-sharing methods, particularly in achieving precise and equal power sharing among both rectifiers and inverters.
- Most of the previous studies on power sharing in the MT-HVDC grid are based on radial systems. However, evaluating the MT-HVDC grid based on a mesh system with multiple converters can more closely emulate a real MT-HVDC operation.
- Previous works on power management did not consider the peak demand of different connected inverters.
2. MT-HVDC Architecture
The AWD control strategy is implemented in a mesh MT-HVDC system, as shown in Figure 2. The system consists of two rectifier stations that control voltage and three inverters that wirelessly regulate power sharing using the AWD method. The mesh MT-HVDC system is selected to showcase the capabilities of both methods in various mesh configuration scenarios. The system in Figure 2 is based on [26], considering that the resistance may vary between different transmission lines, to establish the system’s feasibility across diverse configurations. The wind turbine as a renewable energy resource is considered purely by choice, and it does not restrict readers from including other energy sources to replace it.
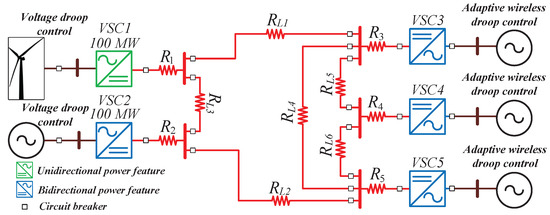
Figure 2.
Architecture of mesh MT-HVDC system.
In Figure 2, the MT-HVDC system consists of five VSC converters. The first two terminals are considered to be wind farms in order to supply power to the grid, and they are assigned to control the DC voltage in the terminals using the traditional droop method. The remaining terminals will wirelessly control power sharing inside the MT-HVDC system using the AWD method, as well as establish policies and agreements between each other in rush hours to optimize power sharing.
Section 4 presents four cases that verify and test the proposed method. These cases include the normal operation mode for three scenarios, where there is no priority for a particular converter over the others. Furthermore, a rush hour case is also analyzed, whereby a priority is specified for particular converters. In this case, the system’s ability to handle the agreements between converters for power sharing is evaluated.
3. Proposed Control Methodology
3.1. AWD Based on Adaptive Virtual Resistance
The proposed AWD in a mesh MT-HVDC system is divided into two parts: the adaptive virtual resistance algorithm and the adaptive wireless droop method. Even though AWD is based on the same droop control that is used in an earlier work by the authors in [34], the AWD in this work will adaptively change the virtual resistance based on the loading effect to mimic the mesh MT-HVDC system behavior and minimize the error in power sharing. Figure 3 illustrates the control structure that implements the proposed AWD control strategy. The indicated AWD control loop provides the required power reference for the outer control loop to set the desired power for an inverter.
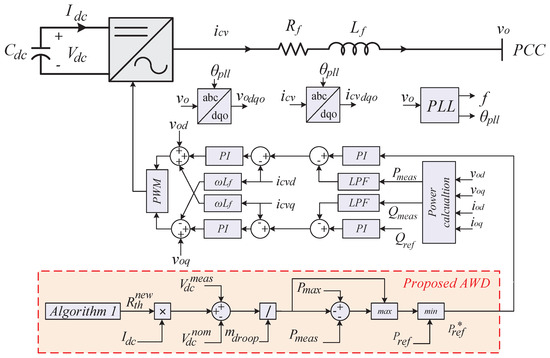
Figure 3.
Control structure using the proposed AWD control strategy and AVRUA algorithm for inverters.
3.1.1. The Adaptive Virtual Resistance Update Algorithm (AVRUA)
The first step in the implementation of AWD in any mesh system is to calculate the Thevenin resistance from the point of view of each converter. This involves simplifying the electrical circuit by removing the rectifier and inverter components, leaving only the external resistors for analysis. The goal is to determine the value of with respect to the perspective of each remaining inverter and rectifier connection point. Due to the complex design of the system, directly calculating these values proves to be a challenging task. Thus, experimental methods are used to obtain this.
Once the initial value is obtained, the rectifier and inverter components are brought back into the circuit. However, it is important to consider additional factors that can affect the total resistance of the system. These factors involve the internal resistances within the inverter and rectifier themselves, the non-linear behavior of the terminals that handle power flow, and the variations in the amount of power drawn by each terminal. These factors can lead to fluctuations in effective resistance. To compensate for these effects, a correction factor is applied. This correction factor is multiplied by the initial value. It accounts for the impact of the internal resistances of each component of the inverter, rectifier, and terminal behavior on the overall resistance. This also allows the system to have a dynamic that is regulated based on its current operating state. This approach offers a worthy advantage in achieving accurate power sharing between the inverters without relying on a complex communication system. In this paper, is calculated as
where refers to the newly measured virtual resistance in (2). The voltage and current measurements for equal power sharing are denoted as and . In order to minimize the errors in power sharing due to different DC-line resistances, the model uses Kirchhoff’s laws to determine the threshold currents and voltages for each inverter as a power range, given by , where i is the inverter index. This is, however, limited by the maximum rating of all rectifier terminals given by . The calculated resistance of components is represented by , and the updated voltage and current are noted by and .
Essentially, (2) tells us that as the system’s power increases, the overall will decrease, and vice versa. This dynamic adjustment contributes to significantly enhanced power sharing amongst the inverters and allows for better prediction of the mesh system’s requirements. However, to consider applying this equation, the total power consumption of the system must exceed the total available power of the system. If the available power overtakes the total consumption power, the equation will not be needed, as all available power can be delivered to the load.
The development of the proposed formula in (2) is based on the pseudocode shown in Algorithm 1. Maintaining accurate calculations is crucial for the system. This is achieved by continuously updating the equation with the latest values. This continuous update helps to prevent any imbalances in power flow that could otherwise occur during the power-sharing process.
| Algorithm 1 AVRUA algorithm |
|
3.1.2. Adaptive Wireless Droop Algorithm
A functioning MT-HVDC system is primarily reliant on the effective management of DC voltage and power-sharing control. The DC voltage across the entire MT-HVDC system fluctuates based on the load conditions. Therefore, a terminal operating in inversion mode determines the amount of power it can consume or request by measuring the local DC voltage at each terminal. This localized measurement of DC voltage provides valuable information regarding the power availability and consumption capabilities of individual terminals within the MT-HVDC system when it is operating in an inverted mode. Consequently, if there is a breakdown in communication, the reliability of a communication-based controller is reduced to ensure the smooth operation of the system in Figure 2. Based on this principle, the AWD control strategy is developed by considering the differences in virtual resistances to better suit the mesh system operation, as given by
The superscript i in the mathematical expression (3) is an indicator of a terminal operating in inversion mode; and indicate the maximum and minimum of a DC voltage variation allowable limits; the maximum active power is represented by ; and are the voltages measured and the entire MT-HVDC voltages; and Thevenin resistance and the virtual resistance value are denoted by and , respectively.
The Thevenin resistance in (3) is conducted when a conflict arises between the inverters due to imbalances in power consumption, i.e., the total power consumption is above the total power available. In this scenario, the power available and the calculated Thevenin resistance, , in (2) exhibit an inverse relationship. When the available power increases, the new Thevenin resistance, , also decreases to offer a dynamic change in the available power equation, , in an effort to mimic the mesh system behavior. But when an inverter requests less power than what is available, it utilizes the available power. The remaining power is then distributed among the other inverters based on their respective power demands. Moreover, equal power sharing among inverters occurs when each inverter requests an amount of power that is equal to or greater than the power agreement between inverters. In such cases, the system ensures that power is evenly distributed among all inverters to maintain power balance and stability within the MT-HVDC system.
3.2. Power Management and Control Methodology
The objective of the power management control scheme is to optimize power-sharing capability by introducing policies and agreements among the terminals and by adaptively changing the power at all terminals based on the system state. This can be either a normal power state or a rush hour state.
The process of calculating power in the rush hour state, , involves a comprehensive examination of various power-related factors, necessitating the comparison of different parameters. This evaluation starts by inputting the power agreement between the terminals () and the power reference () values.
The concept of arises when multiple inverters simultaneously request an increase in power. This situation can lead to a power conflict where the available resources are insufficient to meet the demands of all the inverters. To prevent such conflicts and ensure system stability, power agreements come into play. This process facilitates a form of negotiation or arbitration to ensure smooth operation and sufficient power sharing within the system. The system continues to measure each inverter’s current power status via . During rush hours, specifically when the value surpasses , the system encounters distinct scenarios. Firstly, if the total current power consumption remains below the total available power, the system maintains its current power output. Conversely, if the total current power consumption exceeds the total available power, the system adjusts its output to align with the value. This ensures the system does not overload and potentially experience critical failures. At this stage, each inverter has to calculate the total current power consumption, , given by:
where n represents the total number of rectifiers, and are the maximum and minimum allowable voltages, respectively, and is the maximum available power in the system.
To enhance the security and reliability of the system, especially during the transition from measured power to power levels, a strategic time delay mechanism is integrated. This deliberate delay ensures a gradual increase in power output, effectively mitigating the risk of sudden spikes in current. By meticulously managing these transitions, the system aims to maintain stability and minimize the potential impact of transient states on its performance and longevity. In the proposed method scheme, the operational modes of each unit will depend on the power reference for the inverter section and the selection of policies and agreements set by the transmission system operator. The description of operational states in each power unit is explained next.
3.2.1. Normal Power State
In this state, the rectifiers are set to distribute power to the load, ranging between the maximum power output () and zero. Within this operational mode, as all inverters are functioning under normal conditions, each individual inverter is tasked with calculating the available power for the system. It must then decide, based on this calculation, whether to fulfill the requested power demand, utilize the power it has available, or, in the event of insufficient power availability, resort to an equal power-sharing condition. Furthermore, using the AVRUA algorithm in Algorithm 1, each inverter is required to update its Thevenin resistance, , if necessary.
3.2.2. Rush Hour Mode
The rush hour in the system is defined as the time at which a terminal can have priority in taking power over the other terminals, which gives the system a greater ability to control power sharing by specifying time periods to give preference to any inverter within the system. This mechanism can be helpful during peak load. Additionally, it can also prevent any potential blackouts or overloads.
4. Simulation Results and Discussion
The objective of the simulations is to validate the proposed AWD methodology for both the inverters and rectifiers. The simulation results are obtained using PSCAD/EMTDC. Some simulations are run for 20 s and 54 s. The time step for these simulations is set as s. In the simulations, the proposed method is evaluated under six different cases. Table 2 shows the specifications and parameters of the MT-HVDC system.

Table 2.
MT-HVDC system parameters.
4.1. Case 1: Power Available
Figure 4a shows the simulation result of the proposed AWD in the scenario where inverter 3 requests power above the agreement while inverters and request power within the limits of their agreements. Figure 4b shows the DC-link voltage for this scenario.
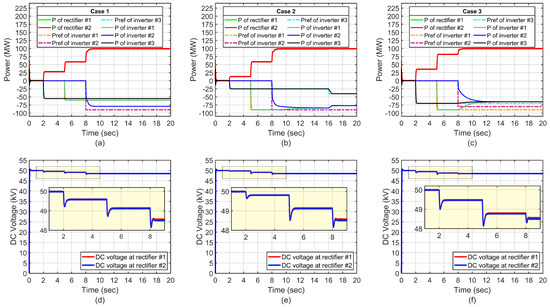
Figure 4.
Simulation results showing available power and power references for rectifiers and inverters in (a,c,e) and associated DC−link voltages in (b,d,f) for cases 1–3.
Initially, at s, the power flow in the system is equivalent to the system losses since none of the inverters request any power. During this period, the MT-HVDC system’s DC voltage is 50 kV. At s, inverter begins to request 60 MW of power, which is available at the rectifier station, while the remaining inverters are still inactive. Consequently, both rectifiers initiate the delivery of available power to the inverter while maintaining equal power sharing between themselves. Consequently, the DC-link voltage decreases to approximately 49.5 kV.
At s, inverter requests 55 MW of power, which is available at the rectifier station. This request is fulfilled if there are no other requests from the remaining inverters. At the same time, the DC-link voltage decreases to approximately 49.1 kV in accordance with the characteristics of the droop controller.
At s, inverter requests 90 MW of power, which is not available at the rectifier station. Consequently, the system will initiate a recalculation based on the flowchart in Figure 5. This determines the revised available power that can be allocated, which is 80 MW to inverter . At the same time, the DC voltage further decreases to 48.5 kV. This recalculation enables the system to adjust and allocate the maximum power possible to meet the inverter’s request.
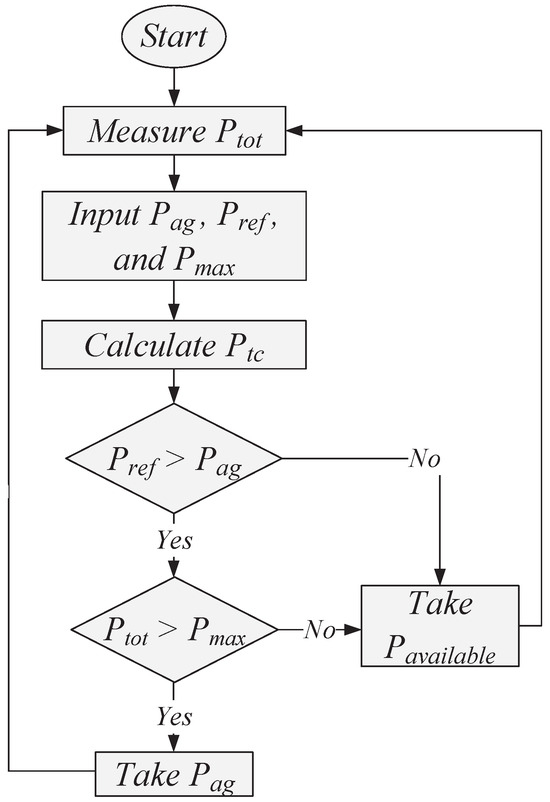
Figure 5.
Flowchart to determine power allocation.
4.2. Case 2: Equal Power Sharing Between Two Inverters
Figure 4c shows the simulation results for the cases of inverters and requesting power above their agreement, which is not available at the rectifier station, while inverter requests power within the limits of the agreement. Figure 4d shows the DC-link voltage for this scenario.
At s, inverter begins to request 25 MW of power, which is available at the rectifier station, while the remaining inverters are still inactive. Furthermore, both rectifiers deliver the available power to the inverters while maintaining equal power sharing between themselves. Meanwhile, the DC-link voltage decreases to approximately 49.5 kV.
At s, inverter requests 90 MW of power, which is available at the rectifier station. Therefore, the rectifier station grants this request in the absence of any other requests from the remaining inverters. At the same time, the DC-link voltage decreases to approximately 49.1 kV accordingly.
At s, inverter requests 90 MW of power, which is not available at the rectifier station. Since the two inverters request more power than their power agreement, the system initiates a recalculation based on the flowchart in Figure 5 and shares available power equally between inverters and . This is observed in Figure 4c. At the same time, the DC-link voltage also decreases to 48.5 kV.
At s, inverter increases its request to 40 MW. In this scenario, the system recalculates the available power to distribute it equally between inverters and .
4.3. Case 3: Equal Power Sharing Between All Inverters
Figure 4e shows the simulation results for the scenario where all inverters request power above their agreements, which is not available at the rectifier station. Figure 4f shows the DC-link voltage for this scenario.
At s, inverter requests 90 MW of power, which is available at the rectifier stations, and this request is granted.
At s, inverter requests 90 MW. In this scenario, the power request exceeds the power agreement, and the system shares the available power equally between the inverters, with the DC-link voltage decreasing to approximately 48.8 kV.
At s, all the inverters requested power above their power agreement. To avoid overloading the system, a recalculation is initiated based on Figure 5 to share the available power equally among all inverters. At the same time, the DC-link voltage decreases to approximately 48.5 kV.
4.4. Case 4: Rush Power Management State
Figure 6 shows the simulation results for the system during rush hour intervals. The rush hour intervals for inverters #1–3 are from 0–20 s, 20–40 s, and 40–55 s, respectively. The power reference for the inverters across the rush hour intervals is shown in Figure 6. Figure 7 shows the DC-link voltage variations for these scenarios.
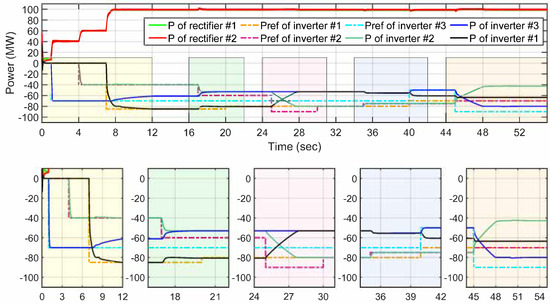
Figure 6.
Rush power management of MT-HVDC system for case #4 with power references for inverters.
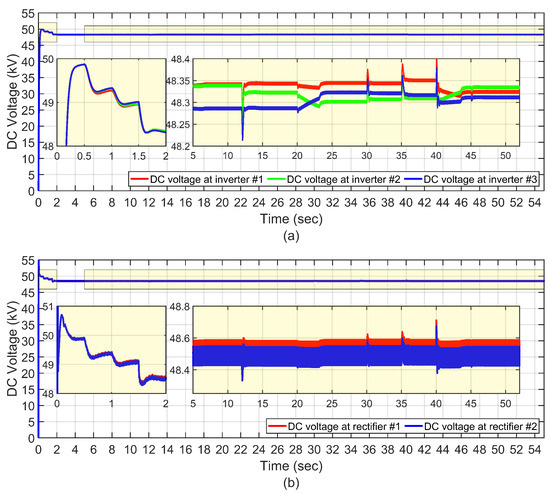
Figure 7.
DC link voltage variations in (a,b) are for rush power management of MT-HVDC system under various conditions as described in case #4.
It is observed from Figure 6 that the inverter having priority will result in a lower voltage drop, resulting in greater available power based on (3). The AVRUA algorithm’s function, illustrated in Figure 5, in conjunction with the droop concept, aims to establish a non-communications line by determining the voltage drop of each inverter. The measured voltage and current, along with the varying virtual resistance, offer a great deal of precise power sharing.
At , the priority inverter increases its power until it reaches the requested power of 85 MW. On the other hand, inverter has to shed power to the priority inverter and take the available power. This is shown more vividly in the zoomed-in subplot of Figure 6 for this time interval.
At s, inverter increases its power request from 40 MW to 90 MW. Consequently, the priority inverter has to decrease its power to the power agreement level. As long as all requests from other inverters are less than the agreed power at each terminal, the priority inverter can take the remaining power without requiring any communication links. In this particular scenario, both inverters #2 and adjust their output power to the agreed power level. This is shown in the zoomed-in subplot of Figure 6 for this time interval.
At s, inverter has priority, resulting in a lower voltage droop for it. Furthermore, given inverter ’s priority, the voltage drops for the other two inverters due to a reevaluation of Thevenin resistance, . This is shown in the zoomed-in subplot of Figure 6 for this time interval.
At s, the rush hour inverter changes from inverter to inverter , marking a shift in priority. During this interval, the requested power for inverters #1–3 is 80 MW, 90 MW, and 70 MW, respectively. As a result of all requested power being higher than the agreement power levels, the system initiates the process of switching the priority from one inverter to another and adjusts the power for all inverters to the power agreement accordingly. The zoomed-in subplot of Figure 5 illustrates this process for this time interval.
At s, the priority switches from inverter to inverter , resulting in a seamless transition based on the voltage drop.
At s, while remaining in the rush hour interval, inverter starts to reduce its power request to 60 MW. Inverter receives the requested power, and the remaining available power will be shared equally, as mentioned in the previous cases.
At s, inverter reduces its requested power to 50 MW, which is below the agreed power level. In this scenario, the priority inverter will take over the remaining power until inverter reaches the requested power. Furthermore, inverter calculates the available power and determines its output power based on Figure 5. This is shown in the zoomed-in subplot of Figure 6 for this time interval.
At s, the priority inverter switches from inverter to inverter . During this interval, the requested power of inverters #1–3 is 70 MW, 70 MW, and 90 MW, respectively. In this case, there is an agreement between inverter #1 and #2 to divide the remaining power after the priority inverter has taken its requested power. Hence, inverter receives of the power, while inverter receives . Additionally, since the requested power exceeds the agreement power for all inverters, the inverters adjust their power to the agreement power level, as shown in Figure 6.
At s, the priority switches to inverter #3. In this case, the inverters and dynamically change and set the voltage value according to the agreed power.
4.5. Case 5: Proposed Controller in Rectification Mode
Figure 8a,b show the simulation results for the proposed AWD controller in rectification mode. Before 8 s, the simulation results portray a similar scenario to that in case 2. During this time, the inverters receive the requested power from the rectifier stations in the system. At 15 s, it is observed that inverter becomes a rectifier, as seen by the positive flow of power in the system. As a result, the remaining rectifiers in the system must reduce their power accordingly to match the demands of the remaining inverters, i.e., inverters and . This mode inversion by inverter results in a jump in the DC-link voltage, as is observed at 15 s in Figure 8b. This case illustrates the effectiveness of the proposed control strategy in handling multiple rectifiers and inverters in the system with mode inversion during operation without resulting in instabilities.
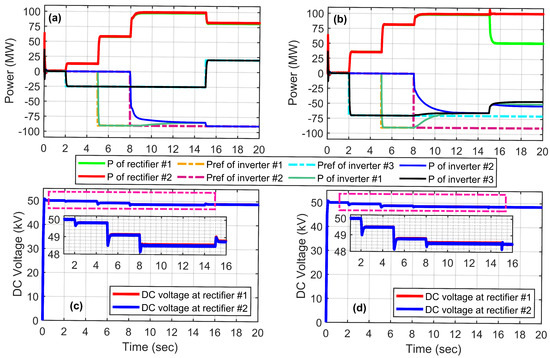
Figure 8.
Simulation results showing available power and power references for rectifiers and inverters in (a,b) and associated DC-link voltages in (c,d) for cases #5 and 6.
4.6. Case 6: Generation from One Rectifier Reduces by 50%
Figure 8b,d show the simulation results for the proposed controller dealing with a reduction in generation from the rectifier station. Before 8 s, the simulation portrays a similar scenario to that in case 3. At 15 s, rectifier reduces its power by . This case represents the random nature of power generation from the renewable energy resources in the system, like wind or PV stations. The power sharing between the inverters will then have to be recalculated based on the new Thevenin resistance presented to the rectifiers when looking into the mesh system. Considering Equations (1) and (2), it is clear that a change in the current, , results in a new value for and hence a new Thevenin equivalent, . The proposed AWD controller takes this updated in Figure 3 to generate the correct power references for inverters #1–3. The power sharing between the inverters will not be equal in this case as each inverter has different line resistances, , as illustrated in Figure 2. The unequal power sharing between inverters is clearly evident in the zoomed version of Figure 8b.
4.7. Quantitative Error Analysis
Two main evaluation metrics are used to measure the performance of the proposed Adaptive Weighted Droop (AWD) control methodology, i.e., voltage deviation (VD%) and power-sharing error (PSE%). Voltage deviation (VD%) measures the percentage deviation between the measured DC voltage at each inverter and the nominal voltage expected at the rectifier station, as determined by the droop control equation. It is defined as
Power-sharing error (PSE%) shows how far off the actual output power of each inverter is from the reference value that the adaptive virtual resistance under allocation (AVRUA) mechanism set for it.
The results of these calculations are summarized in Table 3, which reports the maximum voltage deviation and average power-sharing error under six different operational scenarios:

Table 3.
Quantitative analysis of the proposed AWD control methodology.
These findings validate the robustness of AWD under varied conditions, including scenarios with unequal inverter requests, power scarcity, and load priority dynamics.
In particular, Case 6 demonstrates the system’s ability to recalibrate under generation loss, while Cases 4 and 5 show the effectiveness of adaptive prioritization and mode switching. The relatively low error values across all cases indicate that the adaptive virtual resistance logic significantly enhances the precision and fairness of power distribution.
To further analyze system behavior, time-domain plots of voltage and power trajectories can be introduced, showcasing the controller’s rapid response and stabilization within milliseconds following sudden load changes or inverter reconfiguration. This dynamic stability is the key advantage over traditional fixed droop or communication-reliant methods.
5. Conclusions
This research paper presents an adaptive wireless droop control scheme with adaptive virtual resistance for power sharing in an MT-HVDC grid. The novel aspect of this work is the communication-free control approach that adjusts the virtual resistance to mimic the behavior of a mesh system. This addresses the power mismatch issues associated with conventional fixed droop control and improves the system’s reliability. The proposed AWD control scheme with adaptive virtual resistance demonstrates several advantages over previous works in this field.
Future work in this line includes additional power management strategies to enhance system efficiency and stability. Additionally, further studies will focus on optimizing the AVRUA algorithm to enhance its accuracy and responsiveness in mimicking the behavior of larger-scale mesh MT-HVDC systems. These future research directions aim to advance the understanding and practical implementation of adaptive control strategies for efficient power sharing management in MT-HVDC grids.
Author Contributions
Conceptualization, H.A.; methodology, H.A., A.A.-Z., F.A.-S. and S.A.R.; software, H.A., A.A.-Z. and F.A.-S.; validation, H.A. and S.A.R.; formal analysis, S.A.R.; investigation, H.A.; resources, H.A., A.A.-Z. and F.A.-S.; data curation, H.A.; writing—original draft preparation, S.A.R.; writing—review and editing, S.A.R. and H.A.; visualization, H.A.; supervision, H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Syed A. Raza was employed by the TAE Technologies Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Attya, A.; Domínguez-García, J.; Bianchi, F.; Anaya-Lara, O. Enhancing frequency stability by integrating non-conventional power sources through multi-terminal HVDC grid. Int. J. Electr. Power Energy Syst. 2018, 95, 128–136. [Google Scholar] [CrossRef]
- Abdelwahed, M.; El-Saadany, E. Power Sharing Control Strategy of Multiterminal VSC-HVDC Transmission Systems Utilizing Adaptive Voltage Droop. IEEE Trans. Sustain. Energy 2017, 8, 605–615. [Google Scholar] [CrossRef]
- Beerten, J.; Belmans, R. Modeling and control of Multi-terminal VSC HVDC systems. Energy Procedia 2012, 24, 123–130. [Google Scholar] [CrossRef]
- Liang, J.; Ekanayake, J.; Livermore, L. MTDC VSC Technology and its applications for wind power. In Proceedings of the 45th International Universities Power Engineering Conference UPEC2010, Cardiff, UK, 31 August–3 September 2010. [Google Scholar]
- Molinas, M.; Haileselassie, T.; Undeland, T. Multi-Terminal VSC-HVDC System for Integration of Offshore Wind Farms and Green Electrification of Platforms in the North Sea. In Proceedings of the Nordic Workshop on Power and Industrial Electronics, Espoo, Finland, 9–11 June 2018; pp. 1–8. [Google Scholar]
- Wang, W.; Barnes, M.; Marjanovic, O. Stability limitation and analytical evaluation of voltage droop controllers for VSC MTDC. CSEE J. Power Energy Syst. 2018, 4, 238–249. [Google Scholar] [CrossRef]
- Latorre, H.; Ghandhari, M. Improvement of power system stability by using a VSC-HVDC. Int. J. Electr. Power Energy Syst. 2011, 33, 332–339. [Google Scholar] [CrossRef]
- Yadav, O.; Kishor, N.; Negi, R. Power imbalance sharing among the power converters in MTDC system. Int. J. Electr. Power Energy Syst. 2019, 109, 584–596. [Google Scholar] [CrossRef]
- Ara, R.; Khan, U.; Bhatti, A.; Lee, B. A Reliable Protection Scheme for Fast DC Fault Clearance in a VSC-Based Meshed MTDC Grid. IEEE Access 2020, 8, 88188–88199. [Google Scholar] [CrossRef]
- Liu, Y.; Green, T.; Wu, J.; Rouzbehi, K.; Raza, A.; Xu, D. A New Droop Coefficient Design Method for Accurate Power-Sharing in VSC-MTDC Systems. IEEE Access 2019, 7, 47605–47614. [Google Scholar] [CrossRef]
- Feng, W.; Shi, Q.; Cui, H.; Li, F. Optimal power allocation strategy for black start in VSC-MTDC systems considering dynamic impacts. Electr. Power Syst. Res. 2021, 193, 107023. [Google Scholar] [CrossRef]
- Rudion, K.; Orths, A.; Eriksen, P. Offshore power system operation planning considering energy market schedules. IEEE Trans. Sustain. Energy 2013, 4, 725–733. [Google Scholar] [CrossRef]
- Nakajima, T.; Irokawa, S. A control system for HVDC transmission by voltage sourced converters. In Proceedings of the IEEE Power Engineering Society Summer Meeting. Conference Proceedings (Cat. No.99CH36364), Edmonton, AB, Canada, 18–22 July 1999; pp. 1113–1119. [Google Scholar] [CrossRef]
- Luo, F.; Zhao, X.; Liu, J.; Wang, B.; Zhao, H.; Li, C. A Control Strategy of VSC-MTDC Transmission System Based on Voltage Margin. In Proceedings of the IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Torres, F.; Martinez, S.; Roa, C.; Lopez, E. Comparison between voltage droop and voltage margin controllers for MTDC systems. In Proceedings of the IEEE ICA-ACCA 2018-IEEE International Conference on Automation/23rd Congress of the Chilean Association of Automatic Control: Towards an Industry 4.0-Proceedings, Concepcion, Chile, 17–19 October 2018. [Google Scholar] [CrossRef]
- Alshammari, K. Optimal Power-Sharing Control for MTDC Systems. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- Rouzbehi, K.; Miranian, A.; Candela, J.; Luna, A.; Rodriguez, P. A generalized voltage droop strategy for control of multiterminal DC grids. IEEE Trans. Ind. Appl. 2015, 51, 607–618. [Google Scholar] [CrossRef]
- Alyami, H. master–slave with Droop Control for MTDC Grids. In Proceedings of the 2nd IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Cagliari, Italy, 1–3 September 2020; pp. 119–124. [Google Scholar] [CrossRef]
- Bianchi, F.; Domínguez-García, J.; Gomis-Bellmunt, O. Control of multi-terminal HVDC networks towards wind power integration: A review. Renew. Sustain. Energy Rev. 2016, 55, 1055–1068. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Li, W. Autonomous DC Line Power Flow Regulation Using Adaptive Droop Control in HVDC Grid. IEEE Trans. Power Deliv. 2021, 36, 3550–3560. [Google Scholar] [CrossRef]
- Kumar, A.; Padhy, B. A Novel Adaptive Droop Control Strategy for Improved Power Sharing and DC Voltage Control in MTDC grids. In Proceedings of the 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alsiraji, H.; El-Saadany, E. Cooperative autonomous control for active power sharing in multi-terminal VSC-HVDC. Int. J. Process Syst. Eng. 2014, 2, 303. [Google Scholar] [CrossRef]
- Song, S.; McCann, R.; Jang, G. Cost-Based Adaptive Droop Control Strategy for VSC-MTDC system. IEEE Trans. Power Syst. 2021, 36, 659–669. [Google Scholar] [CrossRef]
- Ambia, M.; Meng, K.; Xiao, W.; Al-Durra, A.; Dong, Z. Adaptive Droop Control of Multi-Terminal HVDC Network for Frequency Regulation and Power Sharing. IEEE Trans. Power Syst. 2021, 36, 566–578. [Google Scholar] [CrossRef]
- Abdelwahed, M.; Elsaadany, E. Adaptive droop based power sharing control algorithm for offshore multi-terminal VSC-HVDC transmission. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), London, ON, Canada, 26–28 October 2015; pp. 67–72. [Google Scholar] [CrossRef]
- Mohammadi, F.; Nazri, G.; Saif, M. An improved droop-based control strategy for MT-HVDC systems. Electronics 2020, 9, 87. [Google Scholar] [CrossRef]
- Kirakosyan, A.; El-Saadany, E.; Moursi, M.E.; Al-Hosani, K. DC Voltage Regulation and Frequency Support in Pilot Voltage Droop-Controlled Multiterminal HVDC Systems. IEEE Trans. Power Deliv. 2018, 33, 1153–1164. [Google Scholar] [CrossRef]
- Chaudhuri, N.; Chaudhuri, B. Adaptive Droop Control for Effective Power Sharing in Multi-terminal DC (MTDC) Grids. IEEE Trans. Power Syst. 2012, 28, 21–29. [Google Scholar] [CrossRef]
- Zhang, Y.; Shotorbani, A.; Wang, L.; Li, W. Distributed voltage regulation and automatic power sharing in multi-Terminal HVDC grids. IEEE Trans. Power Syst. 2020, 35, 3739–3752. [Google Scholar] [CrossRef]
- Zhang, Y.; Shotorbani, A.; Wang, L.; Li, W. A Combined Hierarchical and Autonomous DC Grid Control for Proportional Power Sharing With Minimized Voltage Variation and Transmission Loss. IEEE Trans. Power Deliv. 2022, 37, 3213–3224. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, J.; Huang, L.; Wang, H.; Shu, J. Adaptive droop control for accurate power sharing in islanded microgrid using virtual impedance. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2383–2388. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, F.; Wang, Z.; Ji, Y.; Shu, J.; Chen, Z.; Wang, C. Mode-switching strategy of droop control for VSC-MTDC systems considering maximum DC voltage regulation capability. CSEE J. Power Energy Syst. 2022, 10, 903–912. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, Z.; Deng, Y. An Improved Droop Control Method for VSC- MTDC Considering Power Mismatch Allocation. In Proceedings of the 4th IEEE Workshop on the Electronic Grid (eGRID), Xiamen, China, 11–14 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Alrajhi, H. An Adaptive Wireless Power Sharing Control for Multiterminal HVDC. Comput. Syst. Sci. Eng. 2023, 45, 117–129. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).