Study on High Efficiency Control of Four-Switch Buck-Boost Converter Based on Whale Migration Optimization Algorithm
Abstract
1. Introduction
2. FSBB Converter Working Mode Analysis
3. FSBB Converter Based on WMA Algorithm
3.1. Optimization of FSBB Converter Objective Function Based on WMA Algorithm
3.2. Constraints for FSBB Converter Based on WMA Algorithm
3.2.1. Boundary Condition Limitations
3.2.2. ZVS Implementation Limitations
3.2.3. Ampere-Second Characteristic Limitations
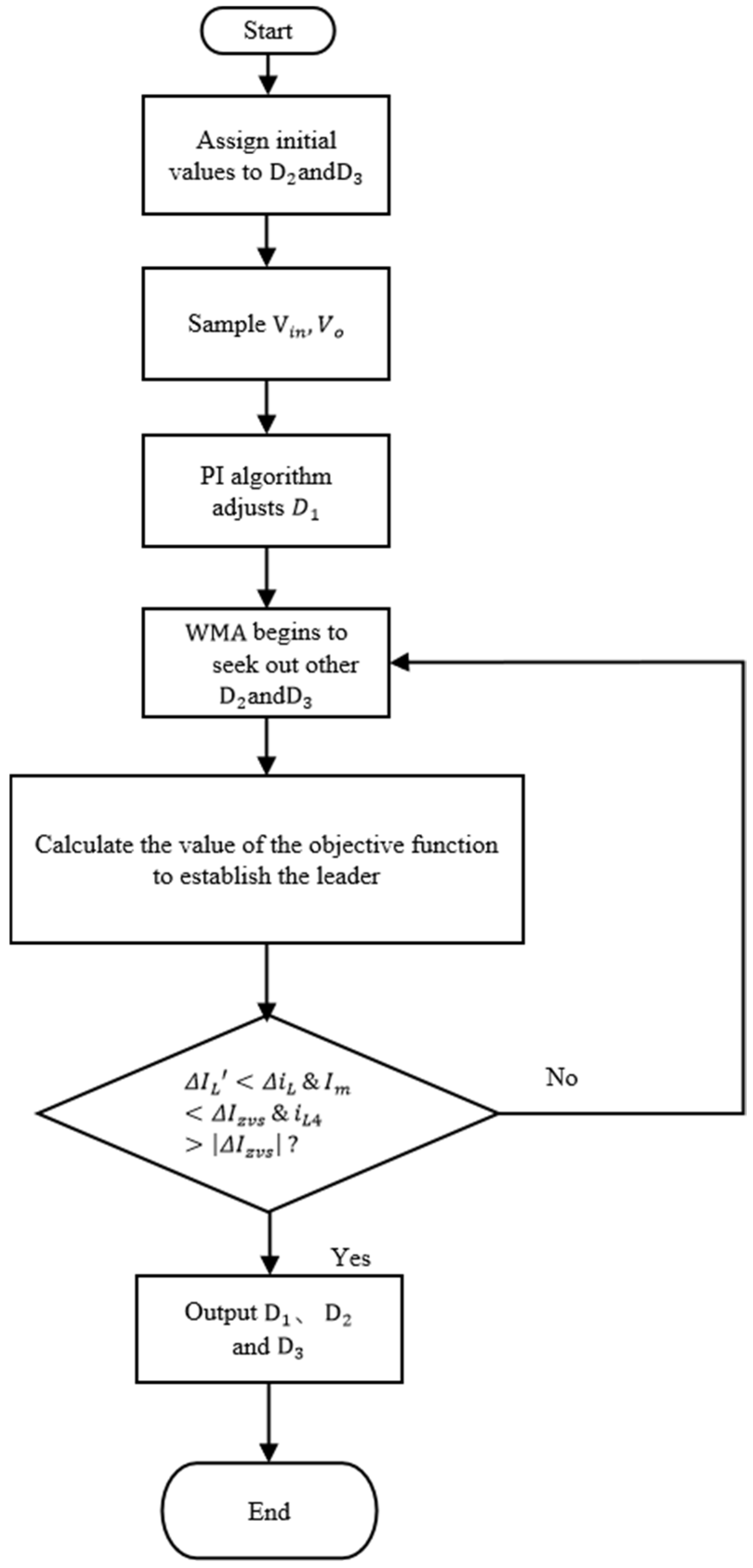
3.3. WMA Optimization Algorithm
3.3.1. Initialization
3.3.2. Adaptation Evaluation
3.3.3. Current Location of Migrating Whales in the Ocean
3.3.4. Less Experienced Whales Move Toward Nearest Neighbors
3.3.5. Less Experienced Whales Are Guided by More Experienced Whales
3.3.6. Discovery and Search of New Territory by Experienced Whales or Leaders
3.4. Comparison of Optimization Algorithms
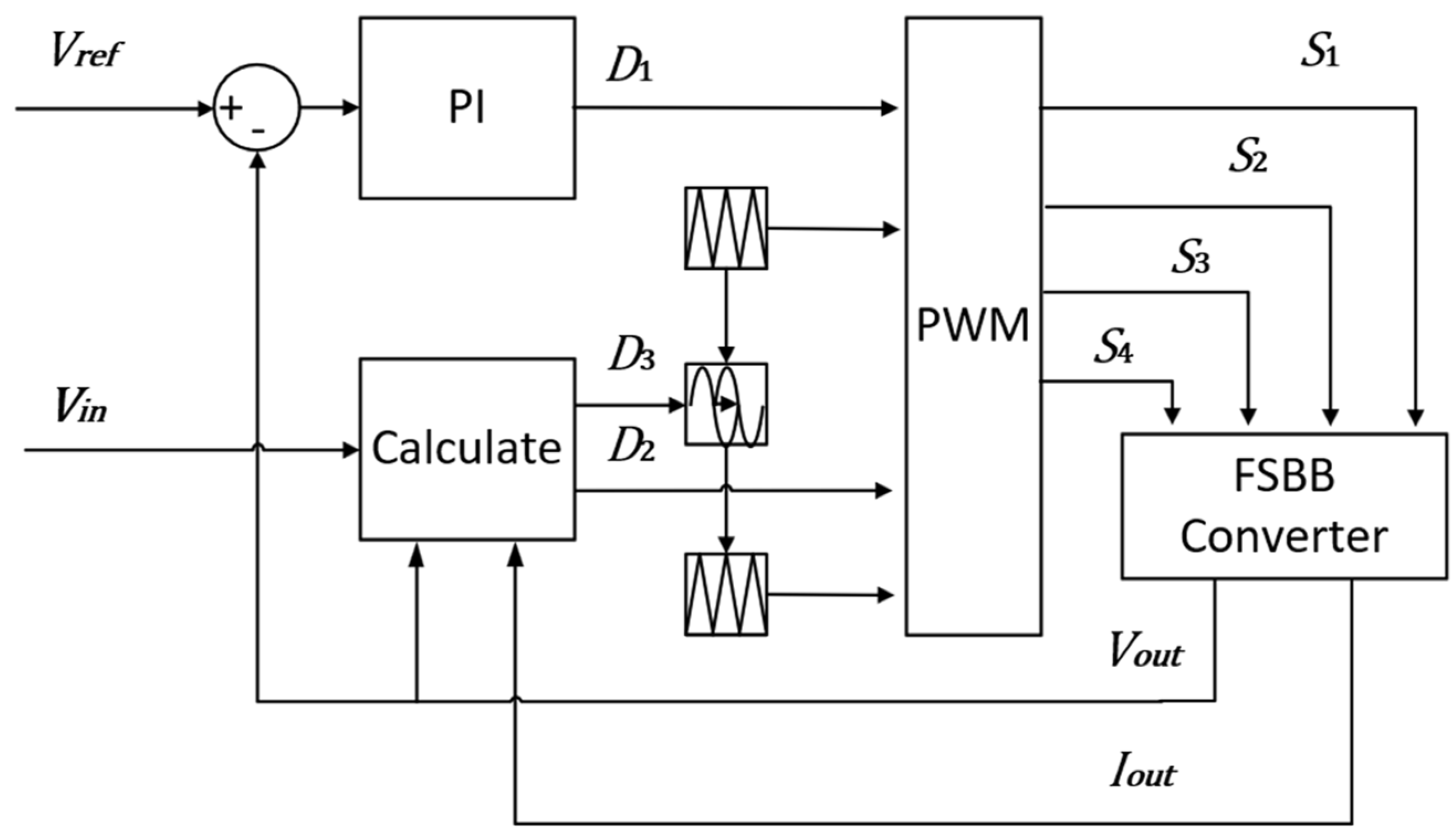
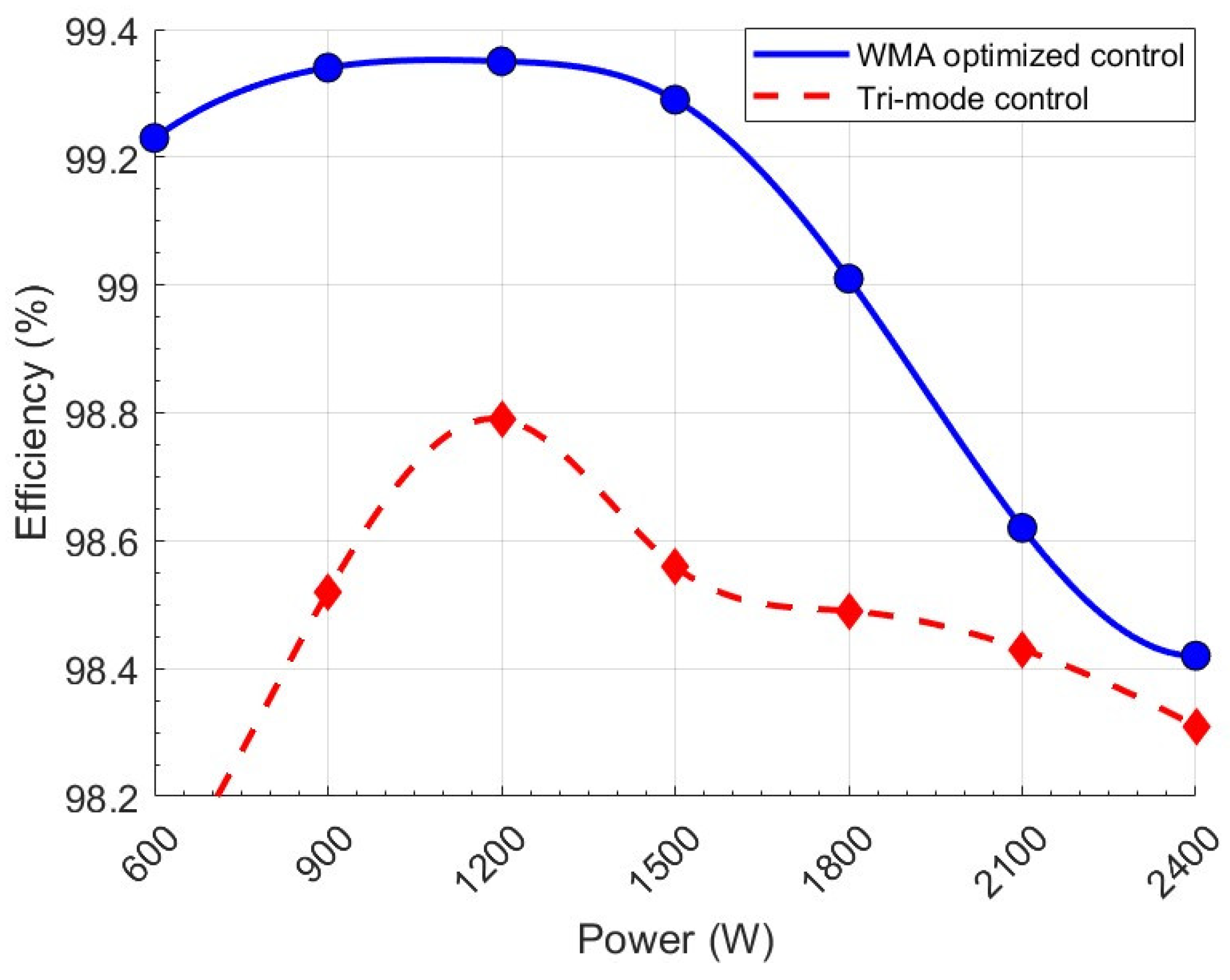
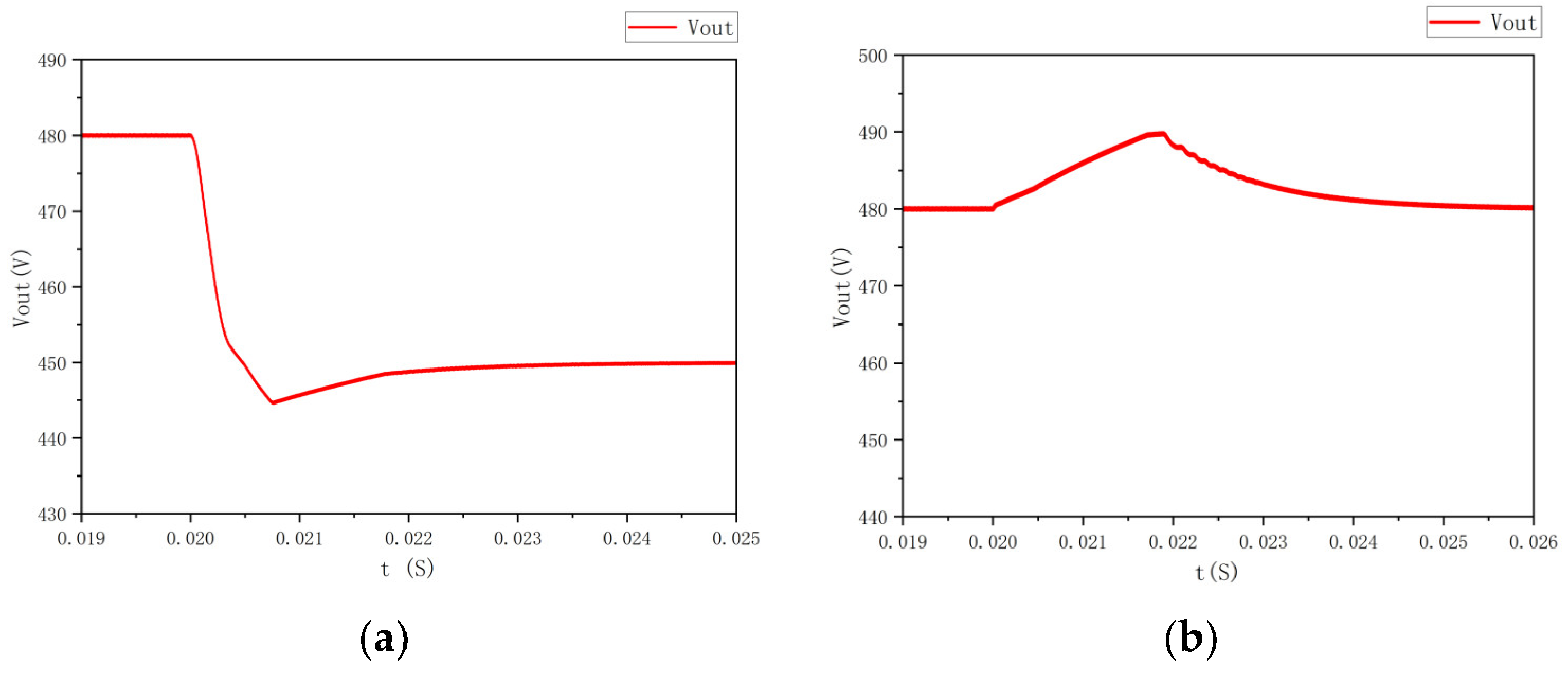
4. Control Strategy and Simulation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Active Inductor Current Balancing for Interleaving Multi-Phase Buck-Boost Converter | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/4802708 (accessed on 13 May 2025).
- An Improved Single-Mode Control Strategy Based on Four-Switch Buck-Boost Converter | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/9124612 (accessed on 13 May 2025).
- Four Switch Buck-Boost Converter for Photovoltaic DC-DC Power Applications | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/5674983 (accessed on 16 April 2025).
- An Interleaving Double-Switch Buck-Boost Converter for PV Grid-Connected Inverter | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/5618019 (accessed on 16 April 2025).
- Analysis of PWM Nonlinearity in Non-Inverting Buck-Boost Power Converters | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/4592538 (accessed on 13 May 2025).
- The MPPT Application of the FSBB Converter with MHz ZVS Digital Control | IEEE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/9959301 (accessed on 13 May 2025).
- Yu, Z.; Kapels, H.; Hoffmann, K.F. High Efficiency Bidirectional DC-DC Converter with Wide Input and Output Voltage Ranges for Battery Systems. In Proceedings of the PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015; pp. 1–8. Available online: https://ieeexplore.ieee.org/document/7149059 (accessed on 23 May 2025).
- An Improved Quadrangle Control Method for Four-Switch Buck-Boost Converter with Reduced Loss and Decoupling Strategy | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/9371427 (accessed on 16 April 2025).
- Four-Mode Control Strategy Based on Four-Switch Buck-Boost Converter. Available online: http://www.jops.cn/EN/10.13234/j.issn.2095-2805.2022.5.11 (accessed on 13 May 2025).
- Zhou, Z.; Li, H.; Wu, X. A Constant Frequency ZVS Control System for the Four-Switch Buck–Boost DC–DC Converter with Reduced Inductor Current. IEEE Trans. Power Electron. 2019, 34, 5996–6003. [Google Scholar] [CrossRef]
- Extreme High Efficiency Non-Inverting Buck-Boost Converter for Energy Storage Systems | VDE Conference Publication | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/7499359 (accessed on 16 April 2025).
- Xia, K.; Li, Z.; Qin, Y.; Yuan, Y.; Yuan, Q. Minimising Peak Current in Boundary Conduction Mode for the Four-Switch Buck–Boost DC/DC Converter with Soft Switching. IET Power Electron. 2019, 12, 944–954. [Google Scholar] [CrossRef]
- A Simplified Real-Time Digital Control Scheme for ZVS Four-Switch Buck–Boost with Low Inductor Current | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/9519164 (accessed on 16 April 2025).
- The Research and Design of High-Efficiency Control Strategy for Four-Switch Buck-Boost Converter. Available online: https://epjournal.csee.org.cn/zgdjgcxb/en/article/doi/10.13334/j.0258-8013.pcsee.231719 (accessed on 16 April 2025).
- A Constant Frequency ZVS Modulation Scheme for Four-Switch Buck–Boost Converter with Wide Input and Output Voltage Ranges and Reduced Inductor Current | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/9818858 (accessed on 16 April 2025).
- Liu, F.; Xu, J.; Chen, Z.; Yang, P.; Deng, K.; Chen, X. A Multi-Frequency PCCM ZVS Modulation Scheme for Optimizing Overall Efficiency of Four-Switch Buck–Boost Converter with Wide Input and Output Voltage Ranges. IEEE Trans. Ind. Electron. 2023, 70, 12431–12441. [Google Scholar] [CrossRef]
- Ghasemi, M.; Deriche, M.; Trojovský, P.; Mansor, Z.; Zare, M.; Trojovská, E.; Abualigah, L.; Ezugwu, A.E.; Mohammadi, S. kadkhoda An Efficient Bio-Inspired Algorithm Based on Humpback Whale Migration for Constrained Engineering Optimization. Results Eng. 2025, 25, 104215. [Google Scholar] [CrossRef]
- JADE: Adaptive Differential Evolution with Optional External Archive | IEEE Journals & Magazine | IEEE Xplore. Available online: https://ieeexplore.ieee.org/document/5208221 (accessed on 16 April 2025).
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
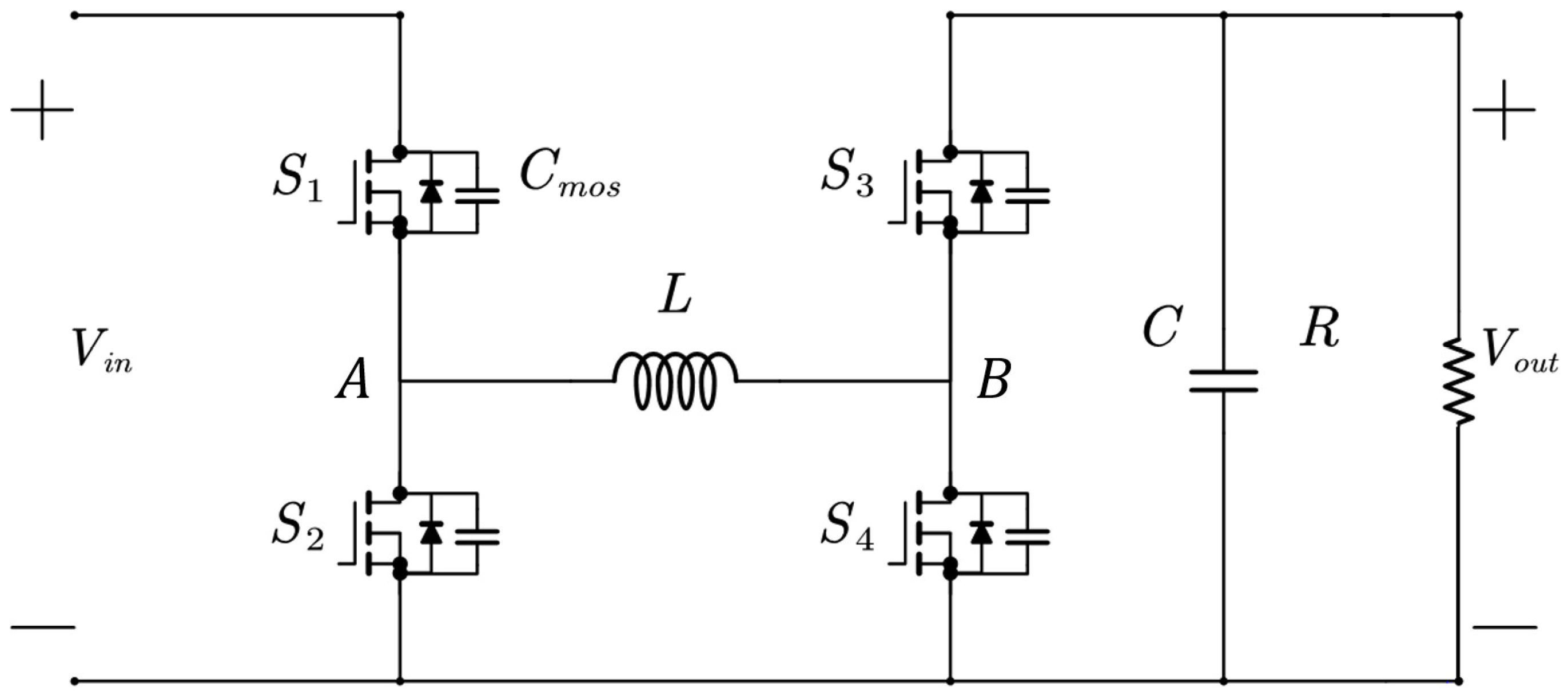
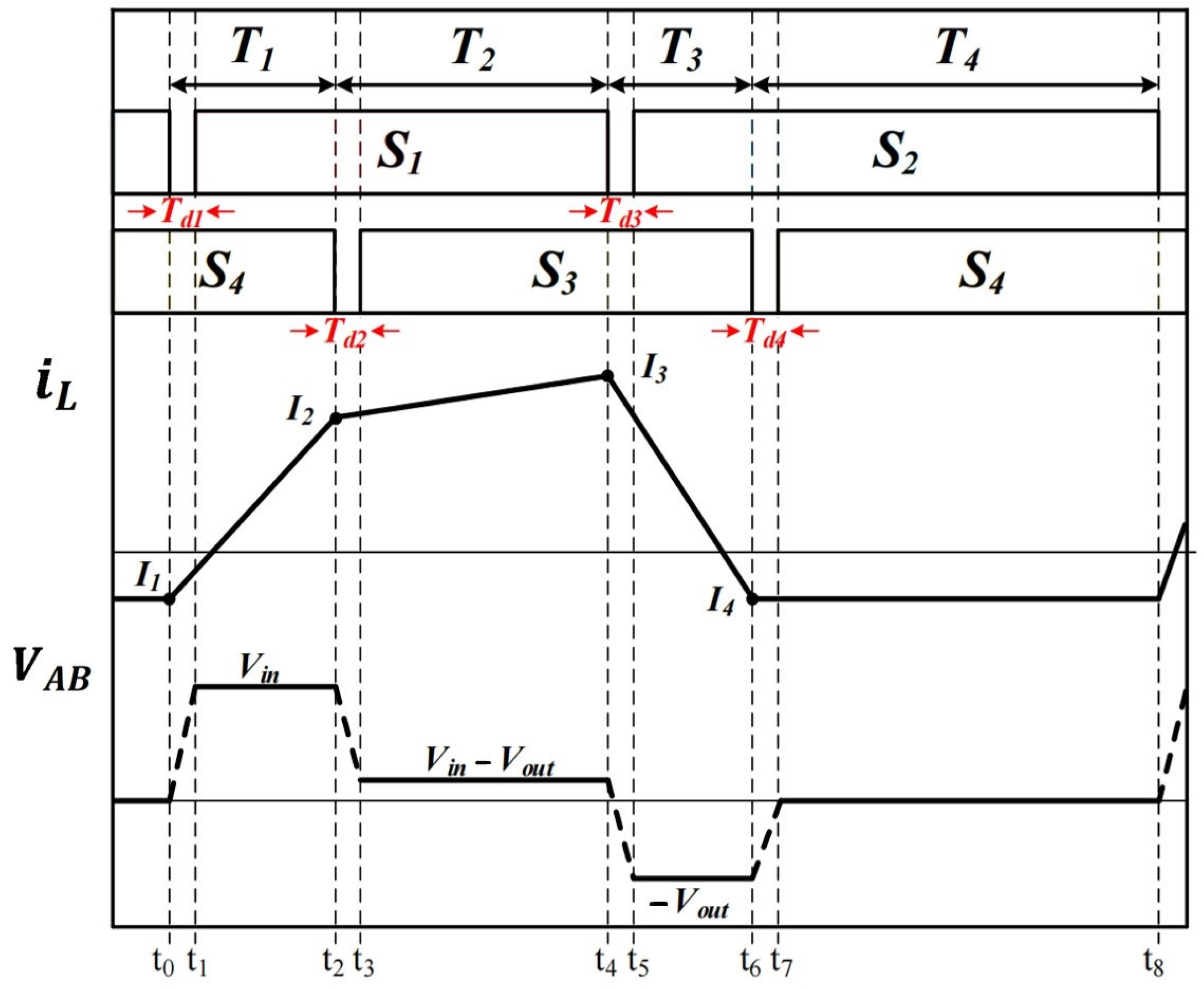
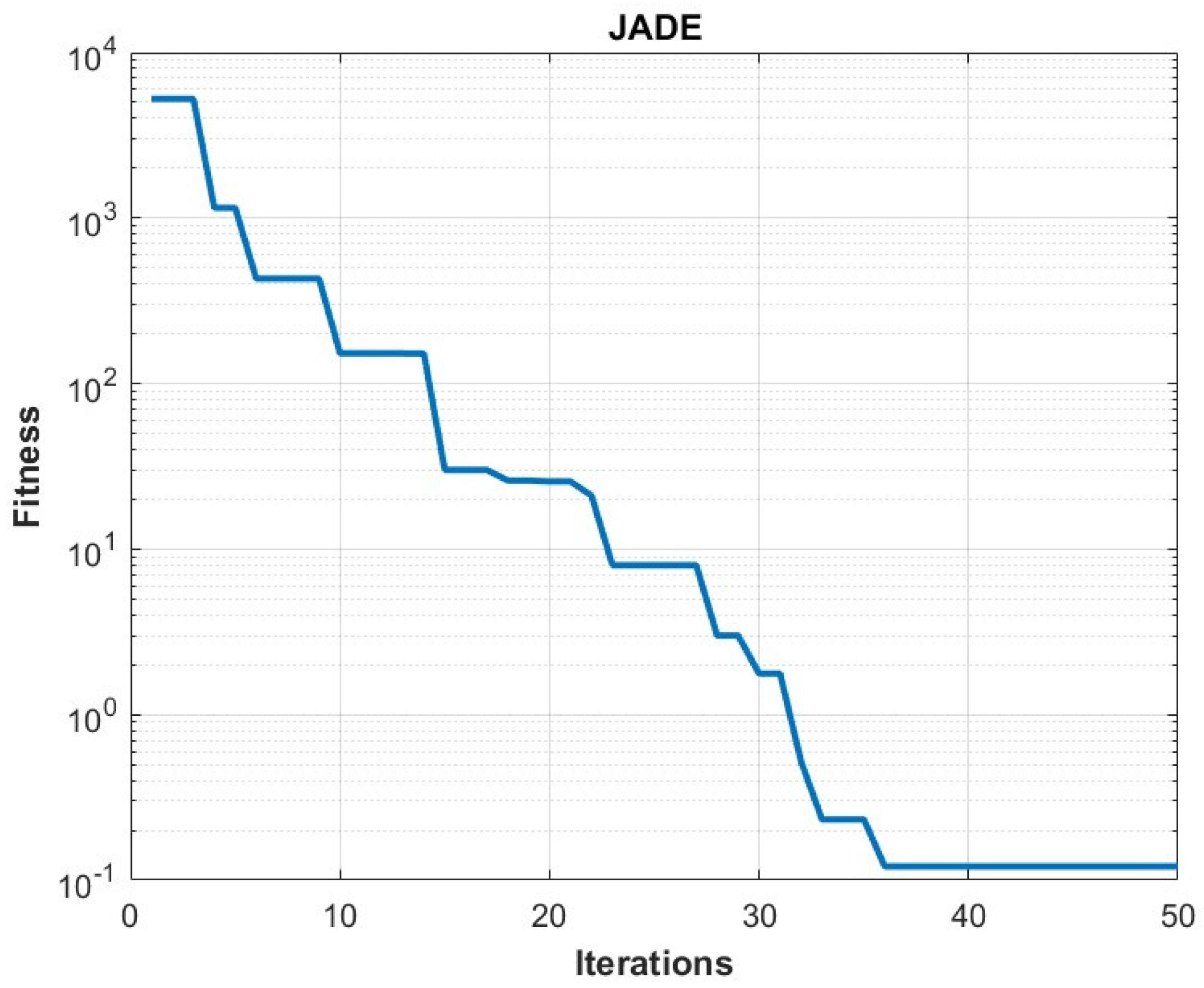
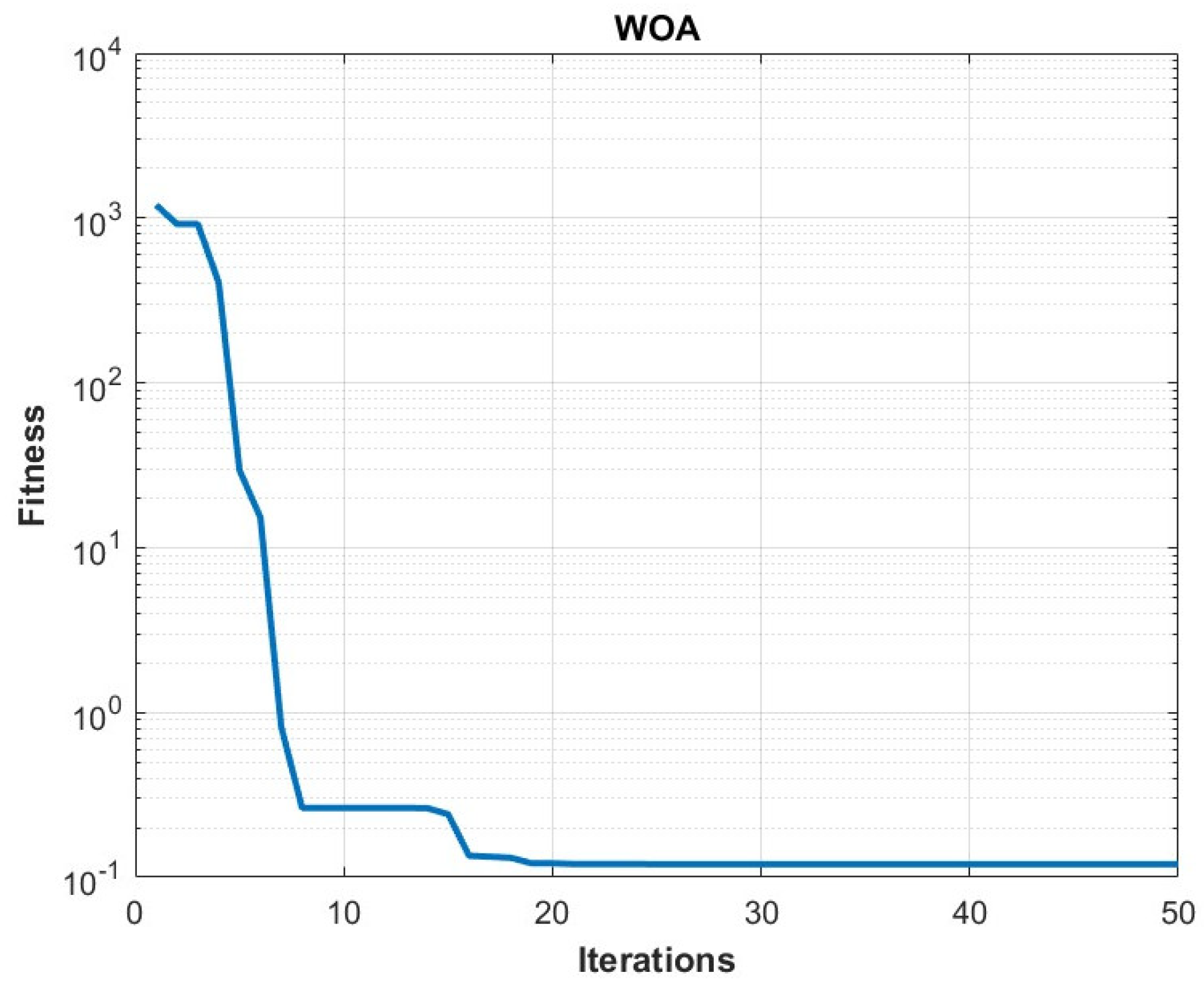
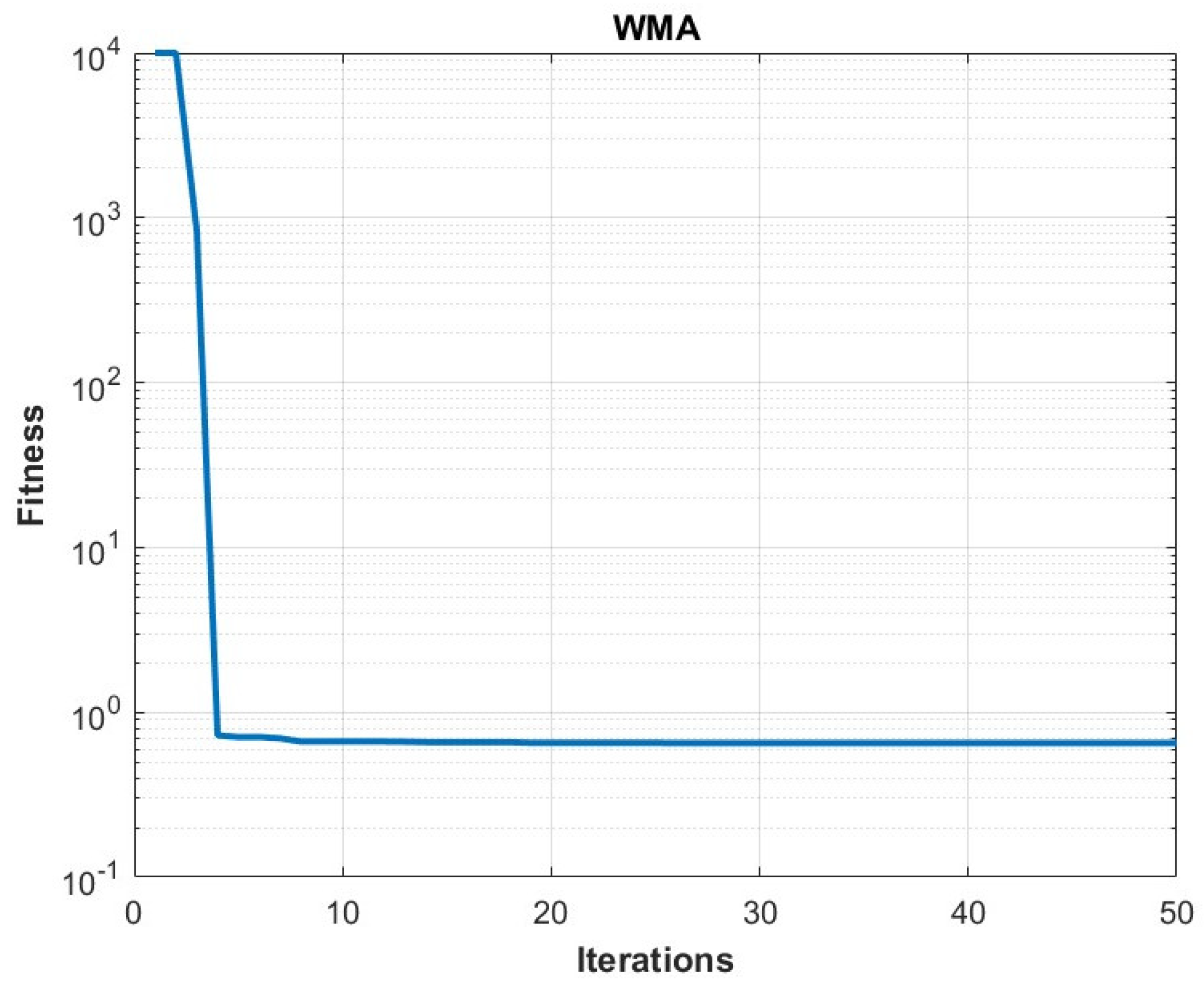
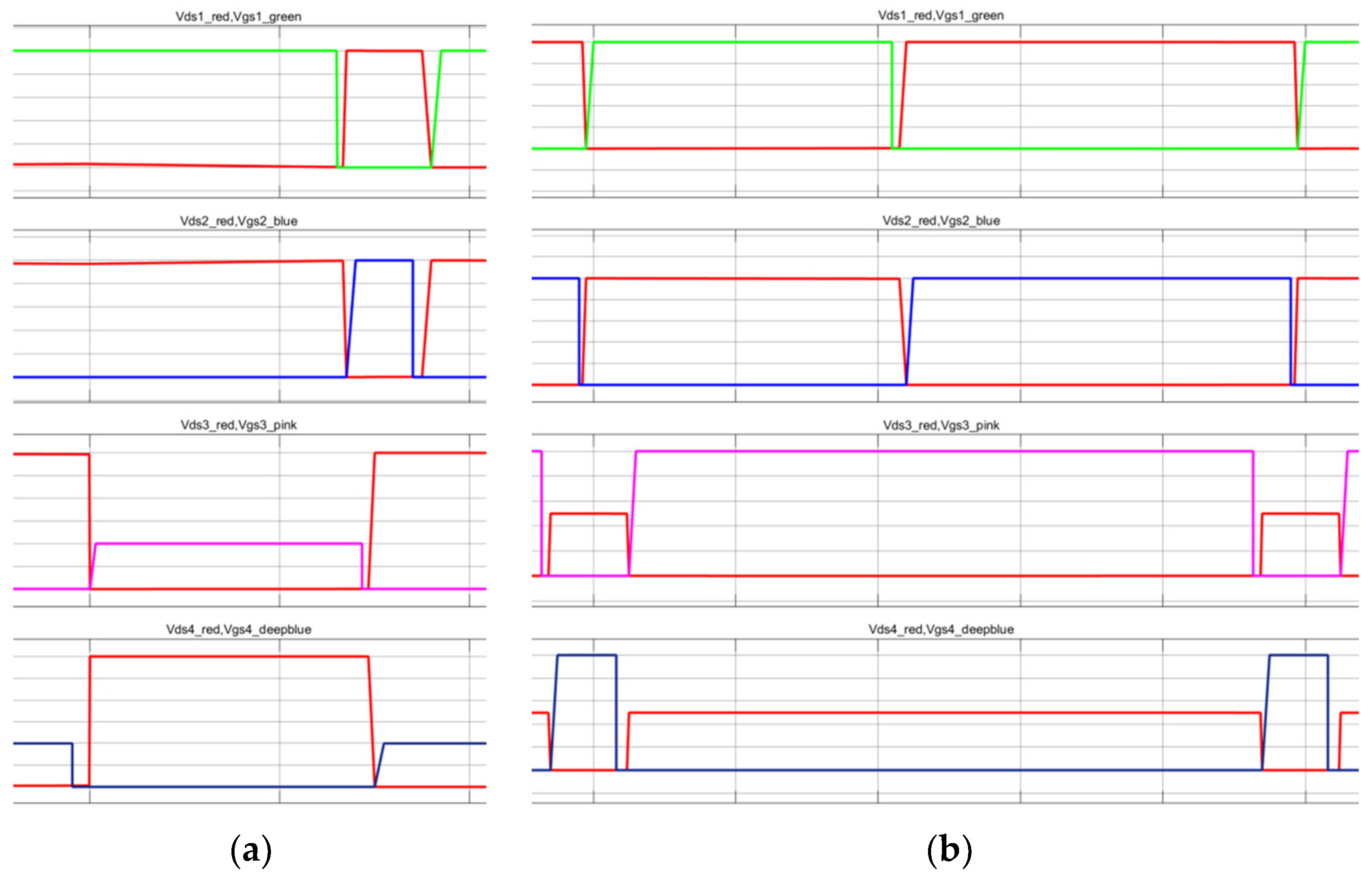
| Circuit Parameters | Value | Circuit Parameters | Value |
|---|---|---|---|
| Input Voltage (V) | 240 | Inductance | 20 |
| Output Voltage (V) | 720 | Output Capacitance | 100 |
| Output Current () | 10 | Mos Capacitance | 100 |
| Frequency | 100 | Dead time | 200 |
| Number | JADE | WOA | WMA | Number | JADE | WOA | WMA |
|---|---|---|---|---|---|---|---|
| 1 | 49 | 20 | 7 | 6 | 46 | 38 | 11 |
| 2 | 40 | 20 | 12 | 7 | - | 13 | 27 |
| 3 | 46 | 38 | 7 | 8 | 49 | 22 | 16 |
| 4 | 20 | 19 | 6 | 9 | 48 | 21 | 10 |
| 5 | 18 | 16 | 6 | 10 | 19 | 34 | 4 |
| Circuit Parameters | Value | Circuit Parameters | Value |
|---|---|---|---|
| Input Voltage (V) | 240–270 | Inductance | 50 |
| Output Voltage (V) | 120–720 | Output Capacitance | 100 |
| Rated Power | 600–2400 | Mos Capacitance | 100 |
| Frequency | 100 | Dead Time | 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, Z.; Xu, Y.; Bai, J. Study on High Efficiency Control of Four-Switch Buck-Boost Converter Based on Whale Migration Optimization Algorithm. Energies 2025, 18, 2807. https://doi.org/10.3390/en18112807
Hao Z, Xu Y, Bai J. Study on High Efficiency Control of Four-Switch Buck-Boost Converter Based on Whale Migration Optimization Algorithm. Energies. 2025; 18(11):2807. https://doi.org/10.3390/en18112807
Chicago/Turabian StyleHao, Zhencheng, Yu Xu, and Jing Bai. 2025. "Study on High Efficiency Control of Four-Switch Buck-Boost Converter Based on Whale Migration Optimization Algorithm" Energies 18, no. 11: 2807. https://doi.org/10.3390/en18112807
APA StyleHao, Z., Xu, Y., & Bai, J. (2025). Study on High Efficiency Control of Four-Switch Buck-Boost Converter Based on Whale Migration Optimization Algorithm. Energies, 18(11), 2807. https://doi.org/10.3390/en18112807





