Abstract
The aim of this paper is to develop a self-adaptive control methodology capable of optimizing in real-time the operation of PV-powered microgrids by dynamically managing both the output powers of battery energy storage systems (BESSs) and power exchanges with the utility grid. Control actions are evaluated by solving a constrained multi-objective optimization problem that integrates the optimal state-of-charge (SoC) management of BESSs within a broader economic dispatch framework. In this way, the SoC is continuously optimized alongside other economic objectives, such as minimizing operating costs and maximizing revenues from energy sales to the grid, while maintaining the microgrid’s energy balance. This ensures that BESSs operate efficiently within their optimal ranges, preventing premature depletion or overload and thereby safeguarding overall microgrid performance. To enable real-time adaptability, the methodology employs a Lyapunov-based optimization algorithm combined with a sensitivity analysis, ensuring rapid convergence to optimal solutions, even under rapidly changing conditions. Computer simulations performed on a low-voltage PV-BESS-based microgrid under different operating conditions confirm the effectiveness of the proposed methodology in enhancing real-time economic performance, operational efficiency, and microgrid reliability.
1. Introduction
Recent international policies aimed at combating climate change have significantly reshaped the global energy landscape, leading to an increased reliance on renewable energy sources (RESs), especially non-controllable ones such as solar and wind energy [1,2]. Although these sources offer significant environmental benefits, their inherent variability and intermittent nature—driven by weather-dependent factors such as sunlight availability and wind speed—make it challenging to accurately forecast their production or adjust it in real-time to meet demand fluctuations [3]. This unpredictability poses several operational challenges for power grids, as maintaining a stable balance between energy supply and demand becomes increasingly difficult with the growing integration of RESs into distribution networks [4,5,6].
To address these challenges, energy storage systems and, in particular, battery energy storage systems (BESSs), have emerged as a promising solution. Owing to their rapid response capabilities and operational flexibility, these devices can counterbalance the short-term variability of non-dispatchable RESs, ensuring a more stable and resilient energy supply [7,8]. Recognizing their strategic importance in modern energy infrastructures, governments and regulatory authorities have increasingly promoted the adoption of BESSs through incentives, subsidies, and other financial support mechanisms [9]. As a result, large-scale BESS installations are being integrated into distribution networks, fostering the development of renewable-powered Microgrids (MGs) [10].
However, the optimal management of these MGs remains a complex task, requiring optimal coordination among BESSs, RES generation, and electricity demand to maximize economic benefits while ensuring system reliability. To address this problem, several control strategies have been developed over the last decade [11,12]. Among these, one of the most popular strategies is 24 h ahead operational planning, which aims to minimize operating costs, maximize the use of RES, and improve MG reliability by taking advantage of forecasts of energy production, consumption, and market prices. This planning process relies on advanced optimization techniques, such as model predictive control (MPC) [13,14,15,16], machine learning-based forecasting [17,18], genetic algorithms (GA) [19], linear programming (LP) [20,21], and mixed-integer linear programming (MILP) [22]. Despite their effectiveness, these strategies often suffer from forecast inaccuracies, which can compromise their performance. To mitigate the impact of forecast inaccuracies, hybrid approaches integrating feed-forward neural networks (FFNN) with error analysis [23] and methodologies based on information gap decision theory (IGDT) [24] have been proposed. Despite these advancements, their effectiveness decreases when forecast errors exhibit significant variability.
To overcome this drawback, two-stage optimization models have been proposed. These methods divide decision-making into a day-ahead planning phase which relies on initial forecasts, and an intraday adjustment phase where the initial schedule is continuously refined as updated information becomes available. Advanced techniques, such as MILP [25], neural network (NN) [26], machine learning (ML) [27], and particle swarm optimization (PSO) [28,29], have been applied to enhance MG responsiveness to fluctuating conditions. Nevertheless, the performance of these approaches still heavily relies on short-term forecast accuracy [30], limiting their robustness in real-world applications.
As a result, there is a growing need for real-time optimization mechanisms that can iteratively adapt MG energy plans based on evolving operating conditions. To address this need, several control strategies have been proposed, including approximate dynamic programming (ADP) [31], adaptive decision-making frameworks based on machine learning [32], and real-time adaptive control methodologies that continuously fine-tune BESS charging and discharging schedules to minimize discrepancies between forecasted and actual production [1,28,33,34]. While these approaches enhance MG stability, they treat the BESS primarily as a passive buffer rather than an active market participant, limiting its ability to optimize MG economic benefits.
A key drawback of these methodologies is their simplistic treatment of the state of charge (SoC) of BESSs, often considering it merely as an inequality constraint, without accounting for its dynamic evolution and strategic role in optimizing MG operations. This rigid approach can lead to the suboptimal utilization of BESSs, as it neglects opportunities to strategically charge or discharge energy in response to market price fluctuations. Moreover, the lack of active SoC management increases the risk of premature depletion or overcharging of the BESSs, ultimately compromising MG reliability and limiting control system flexibility.
To overcome these drawbacks, this paper proposes a novel real-time optimization methodology that integrates dynamic SoC management into an economic dispatch model for PV-based MGs. Although the focus is on PV-powered MGs, the proposed methodology can also be applied to MGs powered by other non-controllable RESs.
Unlike existing real-time methods, the proposed methodology continuously optimizes SoC evolution along with other key operational and economic objectives. By actively coordinating the charging and discharging of the BESS with grid power exchanges in response to ever-changing operating conditions, the methodology transforms the BESS from a passive energy buffer to an active market participant. This integrated approach not only improves the stability of the MG but also maximizes its economic benefits by strategically adjusting power flows to minimize costs and capitalize on favorable market conditions. To ensure rapid adaptability under changing operating conditions, the methodology employs the Lyapunov-based optimization algorithm combined with sensitivity theory, which ensures rapid convergence to optimal solutions and enables continuous fine-tuning of energy management decisions in real time.
The effectiveness of the proposed control methodology has been validated through extensive computer simulations on a low-voltage (LV) PV-BESS-based microgrid modeled to emulate a residential neighborhood in Southern Italy.
2. Mathematical Formulation of the Optimal Control Methodology
This section presents the mathematical formulation of the proposed optimal control methodology for the online operation of MGs powered by PV systems. The objective is to simultaneously minimize the operating costs of the MG, maximize its revenues, and ensure its sustainability by maintaining energy balance and effectively managing the SoC of all available BESSs, while satisfying technical and operational constraints. To achieve a balanced trade-off among these objectives, an integrated approach is adopted that formulates the problem as a multi-objective optimization within a multi-constraint framework. To address this formulation and without loss of generality, consider a grid-connected MG consisting of PV systems along with BESSs and loads.
The following subsections provide a detailed mathematical formulation of the optimization problem, defining the decision variables, objective functions, and constraints that govern the MG operation.
2.1. Decision Variables
The decision variables considered in this method include both the exchanges of power with the main grid and the active power outputs of BESSs within the MG. To effectively manage these variables, the following unified control vector is defined:
which includes the following:
- represents the active power exchanged with the utility grid. It is positive if the MG purchases power from the grid or negative if it sells power to it;
- is the —dimensional column vector of the active power outputs of BESSs, where each component is negative when the corresponding BESS absorbs power (charging) and positive when it releases power (discharging).
2.2. Objective Functions for Multi-Objective Optimization Problem
In this sub-section, the concurrent objectives of the optimization problem are formalized.
2.2.1. Maximization of Microgrid Revenues
One of the main goals of the proposed control strategy is to maximize the MG’s revenue from energy sales to the utility grid. It can be expressed as follows [35]:
where is the time-varying unit price of active power sold to the main grid.
Since the optimization problem is formulated as a minimization, the objective is to minimize the negative of the revenue function, rather than maximizing it directly. Thus, the corresponding cost function is as follows:
2.2.2. Minimization of the Total Microgrid Operating Cost
Another important objective in the optimization process is to minimize the total operating cost of the MG. To comply with this exigency, the following cost function is defined:
where represents the cost of purchasing power from the main grid, while denotes the operating cost of the i-th BESS within the MG.
Details about these cost components are provided below.
Cost Model for Power Purchased from the Utility Grid
The cost of purchasing power from the utility grid can be formalized by the following time-dependent cost model [36]:
where represents the time-varying price paid per unit of power drawn from the main grid.
Cost Model for Battery Energy Storage Systems (BESSs)
The operating cost of each BESS arises from both charging and discharging processes. When a BESS charges, the cost depends on the amount of power absorbed and its source. While power drawn from PV systems is assumed to be cost-free, a cost is incurred when energy is drawn either from the utility grid or from other BESS units within the MG.
If power for charging is purchased from the utility grid, the associated cost is given by the following:
Alternatively, when power is supplied by other BESS units (with j ≠ i), the cost associated with this internal energy exchange can be modeled as follows:
Combining these two contributions, the total charging cost for the i-th BESS can be obtained as follows:
On the other hand, when a BESS unit discharges, the cost—primarily due to inverter losses—is modeled as follows [37]:
where , , and denote the stand-by, voltage-dependent, and current-dependent loss coefficients, respectively.
The total operating cost for the i-th BESS unit can then be modeled as follows:
where and are flag parameters that ensure only the relevant cost term is considered based on the operational state of each BESS. Specifically, if and , the unit is in charging mode and only contributes. Conversely, if and , the unit is in discharging mode and only is considered. When both flags are 0, the BESS is in stand-by mode and no operational costs are incurred.
2.2.3. Optimal State-of-Charge (SoC) Management
Lower operating costs for BESSs might lead the control methodology to prioritize their use, potentially causing these systems to be depleted or overloaded too quickly, which may not be cost-effective for the MG. To prevent both over-charging and over-discharging, the two following objective functions are proposed:
which include the following:
- is the —dimensional column vector of the current SoC of all BESSs;
- is the —dimensional column vector, with each component representing the maximum allowable SoC for each BESS;
- is the —dimensional column vector, with each component representing the minimum allowable SoC for each BESS.
2.2.4. Microgrid Real-Time Power Balance Model
To ensure the optimal operation of the MG, it is essential to balance the energy supply and demand in real-time. To achieve this, the following objective function is considered:
where is the active power output of the h-th PV generator, while is the active power consumed by the k-th load.
2.2.5. The Global Objective Function
To achieve an optimal balance among the above-defined objectives, they are normalized and aggregated into a global objective function using a weighted sum approach.
Denoting with the dimensional column vector of the normalized objective functions, the global objective function can be then expressed as the following weighted quadratic form:
where is a symmetric positive definite matrix, whose components weigh the contribution of each element of the vector to the overall objective function.
2.3. Constraints of the Problem
To ensure that the optimization solution is physically feasible and complies with the technical and operational limits of the MG, the following constraints must be satisfied.
2.3.1. Utility Grid Constraints
To prevent exceeding the tie-line’s capacity during the optimization process, the power exchanged with the utility grid is constrained by the following bounds:
where and are the minimum and maximum allowable power exchanges with the utility grid, respectively.
2.3.2. Battery Energy Storage System Constraints
To ensure that each BESS operates within its allowable active power limits during the optimization process, the following constraints are considered:
where and are the minimum and maximum active power output limits of the i-th BESS.
2.4. Dynamic Optimization for Real-Time Control
To ensure the optimal real-time control of the microgrid, it is essential to adopt an algorithm that can rapidly adapt to changing operating conditions and provide immediate responses. This algorithm must solve the optimization problem defined by Equations (14)–(16) quickly and continuously, updating the solutions in real-time to address variations in MG’s operating conditions. To meet these requirements, the Lyapunov-based optimization algorithm combined with a sensitivity analysis, developed in [38], is employed. According to this method, if the always-positive objective function is treated as a Lyapunov function, the optimization problem is reformulated as the search for an equilibrium point of an artificial dynamic system, where the decision variables serve as state variables. Convergence to this equilibrium point corresponds to the minimization of .
For the system to converge to its equilibrium point, the Lyapunov stability criterion must be satisfied. This requires that the time derivative of the objective function, , to be semi-negative definite, ensuring a monotonic decrease of over time until it reaches its optimal value. To enforce this condition, the dynamics of the decision variables are modeled as follows:
Integrating Equation (17) over time gives the following optimal control laws:
In this expression, the sensitivity matrix quantifies the responsiveness of the objective function to changes in the decision variables. This information enables the control system to adjust rapidly in response to real-time variations in operating conditions. Additionally, saturation blocks are integrated into the control loop to ensure that the control actions remain within safe operational limits, preventing violations of the MG’s technical constraints and maintaining efficient performance.
Figure 1 illustrates the overall control strategy, which integrates the Lyapunov optimization algorithm with the necessary operational constraints and practical implementation considerations.
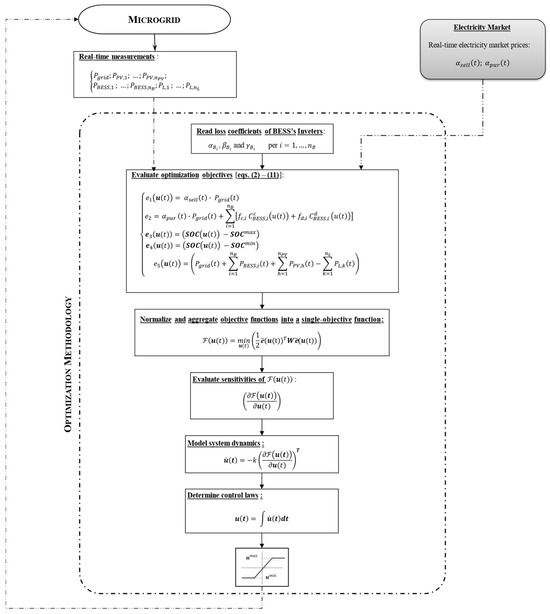
Figure 1.
Flow-chart of the proposed optimization control methodology.
As can be noted, the developed control methodology, powered by real-time measurements from the MG and the electricity market, continuously updates the control laws to quickly adapt to fluctuations in operating conditions. This allows it to promptly react to changes in PV energy generation, load demand, and energy market prices, eliminating the need for short-term predictions and minimizing risks associated with uncertainties in such dynamic environments.
3. Simulation Results
The proposed control methodology was tested on a low-voltage (LV) PV-microgrid (MG), specifically modeled to emulate a residential neighborhood in Southern Italy. It is assumed to consist of households equipped with rooftop photovoltaic (PV) systems, collectively providing a total installed capacity of 120 kWp. To support PV generation, MG is assumed to integrate a 300 kWh battery energy storage system (BESS), capable of regulating power in the range of −50 kW (charge) to +50 kW (discharge). Additionally, the MG includes a connection to the utility grid for bidirectional power exchanges.
All the simulations were carried out using the MATLAB/Simulink R2024a environment [39].
To demonstrate the effectiveness and robustness of the proposed methodology, four different operating scenarios were analyzed, each designed to evaluate the controller’s performance under different environmental and operating conditions:
- Scenario 1—Sunny Summer Workday. This test aims to assess the controller’s ability to optimize MG operations by dynamically managing BESS power output and power exchanges with the utility grid in response to real-time variations in energy demand, PV generation, and market conditions;
- Scenario 2—Partly Cloudy Conditions. In this scenario, the MG operates during a day with partly cloudy weather, leading to fluctuations in solar irradiance and variable PV output. This test assesses the controller’s ability to efficiently manage the uncertainty and variability associated with PV system, simulating a more challenging operating environment than Scenario 1;
- Scenario 3—Prolonged PV Unavailability. This test aims to evaluate the controller’s performance under extreme stress conditions, where the MG experiences a sudden and extended loss of PV generation;
- Scenario 4—Multi-day Performance Evaluation for Real-time Control Feasibility. This scenario aims to evaluate the ability of the proposed control methodology to optimize MG performance under variable operating conditions, such as fluctuations in energy demand, photovoltaic generation, and electricity market prices. This simulation provides insight into the controller’s behavior over an extended period, demonstrating its ability to adapt to real-world conditions that vary over time and effectively manage resources while optimizing economic performance in a variable operational environment.
In all scenarios, the MG was assumed to act as a “price taker” within the energy market, passively responding to market price signals without influencing them.
To ensure that typical fluctuations observed in the Italian electricity market were accurately represented in all the simulations, electricity market prices were modeled for each simulated scenario using real data from the Gestore dei Mercati Energetici S.p.A. (GME), Rome Italy. These price profiles exhibit a low-price valley during the night (between 23:00 and 07:00), a morning peak between 08:00 and 10:00, a drop at midday from 11:00 to 18:00, and an evening increase from 19:00 to 21:00, which coincides with a higher demand for energy. This pricing model was applied to both the sale and purchase of electricity.
3.1. Scenario 1—Sunny Summer Workday
To assess the controller’s ability to optimize the MG’s daily operations in real time, a 24 h simulation was carried out for a typical summer weekday under clear-sky conditions. In this baseline scenario, an ideal PV generation profile shown in Figure 2 was adopted to reflect the optimal solar conditions and simulate the expected energy production during the day. The same figure also reports the daily load demand profile used to emulate the typical consumption behavior of the MG on that day.
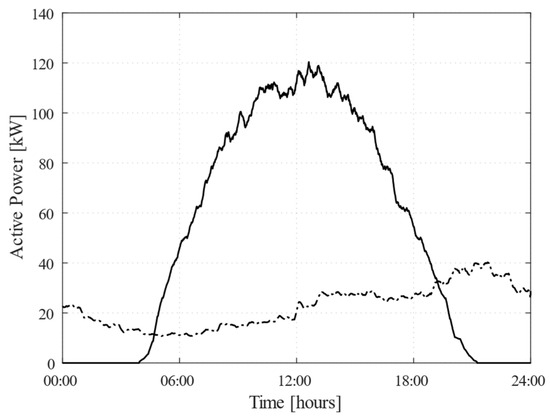
Figure 2.
Daily profiles of PV generation (solid line) and load demand (dotted line).
Based on these inputs and assuming an initial SoC of 60% for the BESS, the developed methodology was applied, and results are reported in Figure 3 and Figure 4. Specifically, Figure 3 shows the time-domain behavior of both the power exchanged with the main grid and the power output from the BESS, while Figure 4 reports the evolution of the BESS SoC.
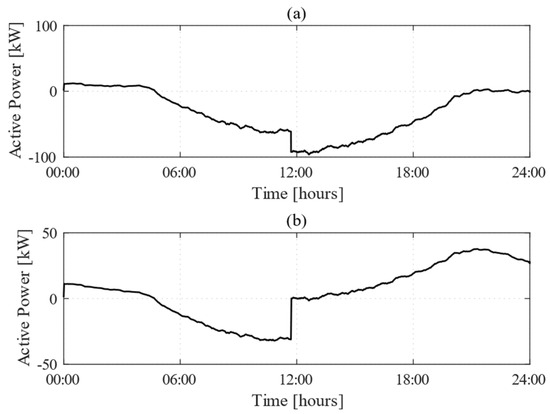
Figure 3.
Time-domain behaviors of (a) tie-line active power flow and (b) BESS power output.
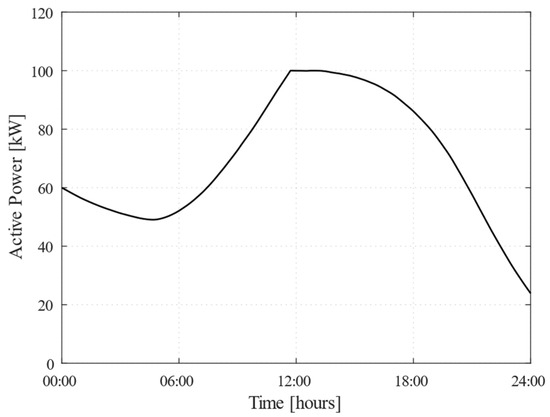
Figure 4.
Time-domain behavior of the state-of-charge (SoC) of the BESS.
During the night and early morning (00:00–05:00), with no PV generation, minimal load demand, and low electricity market prices, the controller opted to purchase power from the main grid rather than relying solely on the BESS to supply the load. This strategy prevented the premature exhaustion of the BESS’s energy reserves, ensuring their availability for periods of higher electricity prices or insufficient PV generation.
As solar radiation increased between 06:00 and 13:00, the PV generation gradually approached its rated output of 120 kW (see Figure 2), while load demand also began to increase, reflecting typical residential energy consumption patterns (Figure 2). In response, the controller prioritized self-consumption, using PV energy to supply the MG’s internal load, while excess energy was either stored in the BESS or exported to the grid. This allowed the controller to maximize energy sales by taking advantage of higher market prices outside valley hours, while ensuring the BESS was charged to handle future fluctuations in load demand and electricity prices. Between 10:00 and 11:30, during the low-price period, the controller prioritized BESS charging to store excess PV-generation, as energy sales were less attractive. As a result, the BESS reached full charge by 11:30, allowing the MG to have sufficient energy reserves to dynamically respond to subsequent fluctuations in load demand, PV generation, and electricity prices. From 11:30 to 14:00, with the BESS fully charged and PV system operating near peak output, the controller prioritized the use of PV power to supply the MG’s load while exporting any surplus to the grid. During this period, the controller refrained from discharging the BESS, as low market prices made energy sales less profitable, thus avoiding the unnecessary depletion of stored reserves. In the afternoon (14:00–17:00), as PV output declined and load demand remained high, the controller unloaded the BESS to increase power exports and maximize revenue by taking advantage of favorable market prices. By regulating the discharge rate of the BESS, it ensured efficient energy usage while optimizing market profits.
During the evening hours (17:00–21:00), when PV output gradually dropped to zero and the second peak in load demand occurred, the controller continued to discharge the BESS to supply the MG’s internal load and export the excess energy to the grid, capitalizing on rising market prices. Finally, from 21:00 to midnight, the controller prioritized using the remaining BESS reserves to supply the MG’s internal load demand, thus avoiding costly purchases of electricity from the main grid. By reducing power imports and stopping additional energy sales, the controller ensured that adequate energy reserves were maintained for the next day. By the end of the day, the BESS SoC decreased from its initial value of 60% to 28.55%, demonstrating the controller’s ability to efficiently manage power flows to maintain a balanced and profitable operation.
To provide a quantitative measure of the effectiveness of the proposed methodology, an economic analysis was performed, and the main results are summarized in Table 1.

Table 1.
Summary of economic analysis.
The analysis reveals that the proposed methodology generated revenues from energy sales of €97.12, while keeping the costs of purchasing energy from the grid low at €4.11. The cost associated with discharging the BESS was minimal, amounting to just €0.89. As a result, the net profit of €92.12 highlights the methodology’s ability to dynamically adapt to real-time operating environments and market conditions, demonstrating its effectiveness in achieving both high operational efficiency and strong economic performance.
3.2. Scenario 2—Partly Cloudy Conditions
Starting from the same initial conditions as Scenario 1, a second one-day simulation was performed for a typical summer weekday in partly cloudy conditions. This scenario was chosen to evaluate the performance of the methodology when faced with fluctuations in PV power generation caused by intermittent cloud cover, which introduces variability and reduces energy output compared to the clear-sky conditions modeled in Scenario 1.
A variable PV generation was used to model these fluctuations, simulating intermittent cloud cover between 06:45 and 18:30. This resulted in reduced PV energy availability, as shown in Figure 5. The same figure also reports the load demand profile used to emulate the MG’s energy requirements for the simulation day. Additionally, a market price similar to that of Scenario 1 was adopted to maintain consistency in economic conditions, thus allowing a more accurate assessment of the impact of PV variability on controller performance.
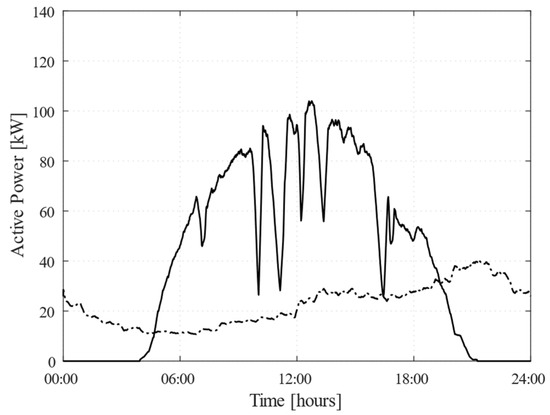
Figure 5.
Daily profiles of PV generation (solid line) and load demand (dotted line).
The optimal control actions obtained, including BESS power output and tie-line power flow, are reported in Figure 6, while Figure 7 shows the evolution of the SoC of the BESS over the simulation period.
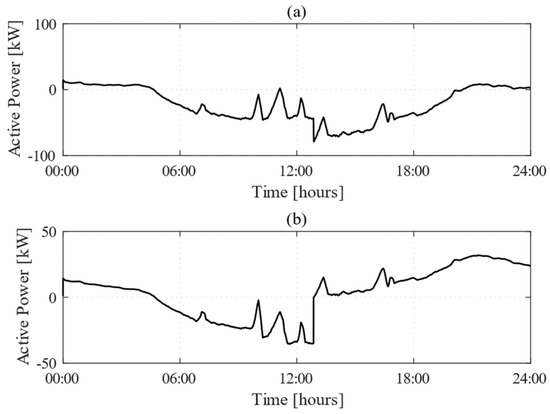
Figure 6.
Time-domain behaviors of (a) tie-line active power flow and (b) BESS active power outputs.
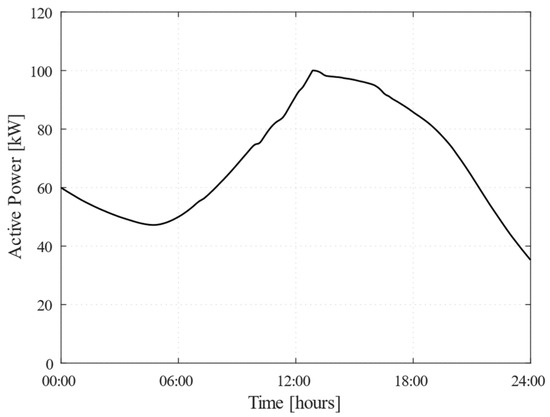
Figure 7.
Time-domain behavior of the state-of-charge (SoC) of the BESS.
From 00:00 to 06:45, the control methodology mirrored the behavior observed in Scenario 1. Energy was purchased from the grid rather than relying solely on the BESS, preserving energy reserves for periods with higher PV generation or more favorable market conditions.
During the period of high PV variability (06:45 to 18:30), the controller dynamically adjusted power flows to maintain the power balance in the MG and optimize economic performance. More specifically, at 06:47, the sudden drop in PV output due to passing clouds caused a rapid power imbalance within the MG. In response, the controller promptly reduced both power exports to the grid and BESS charging power, ensuring that available PV generated power was first used to meet internal MG load demand. Once PV generation recovered, the controller resumed excess power sales to the grid and BESS charging, continuously adapting its strategy based on real-time operating conditions as in Scenario 1. During the morning price dip (10:00–11:30), while PV output continued to fluctuate, the controller prioritized charging the BESS over exporting energy to the grid, as low electricity prices made exports less profitable. This strategy allowed the BESS to be fully charged, ensuring that it was prepared for later periods when higher market prices would provide more favorable profit opportunities. Once the BESS reached full capacity, the controller actively regulated power flows, preventing further energy absorption into the BESS and ensuring that any excess of power generated by the PV systems was exported to the grid.
From 13:00 to 18:00, when PV generation began to decline and market prices gradually increased, the controller progressively increased BESS discharge power to meet the growing load demand and simultaneously export power to the grid, capitalizing on the higher sales prices. By carefully modulating the BESS discharge rate and power exchanges with the grid, the controller ensured an optimal trade-off between energy reserves and revenue generation.
Between 18:00 and 20:30, with PV generation dropping to zero, the controller further increased BESS discharge power to meet the evening peak load demand, while taking advantage of the high-power sales price typically observed during these hours to maximize economic returns.
Finally, from 20:30 until midnight, with PV generation at zero and high load demand, the controller prioritized the use of stored BESS energy to meet internal load demand rather than exporting energy to the grid, as low market prices made export less profitable. This approach avoided costly purchases of electricity from the grid and preserved energy reserves for future opportunities with higher market prices. From Figure 7, it can be seen that the BESS SoC started at 60% at midnight and reached 35.23% at the end of the day, reflecting the controller’s ability to efficiently manage BESS under partially cloudy conditions. The economic analysis of Scenario 2, summarized in Table 2, highlights the financial implications of these operating conditions.

Table 2.
Economic Analysis of Scenario 2.
Compared to Scenario 1, the energy sales revenue decreased to €59.22, mainly due to a reduced surplus of PV energy available for export during the day. In contrast, the costs of purchasing energy from the grid increased to €5.58, as the controller had to rely more on external energy to compensate for fluctuations in PV productions. BESS-related costs remained low, with charging fees at €0.01 and discharged fees at €0.67. As a result, the net profit achieved was €52.96, which, although lower than Scenario 1, underlines the controller’s ability to maintain profitability under more challenging conditions. These results further demonstrate the robustness of the proposed methodology, in particular its ability to adapt to fluctuations in PV generation and market conditions, balancing operational efficiency and financial performance.
3.3. Scenario 3—Prolonged PV Unavailability
Starting from the same initial conditions as Scenario 1, a third one-day simulation was performed for a typical summer weekday, introducing a sudden and prolonged unavailability of PV generation across the microgrid. This stress test was designed to assess the controller’s ability to maintain the stability and profitability of the MG while relying primarily on the BESS.
To simulate this challenging scenario, it was assumed that all PV production would be lost from 11:00 onward, as shown in Figure 8. The same figure also shows the adopted load demand profile, which represents the energy demand of the MG during the day. Additionally, a market price structure consistent with that of Scenario 1 was adopted to ensure comparability of economic conditions and to better assess the impact of PV unavailability on the control methodology performance.
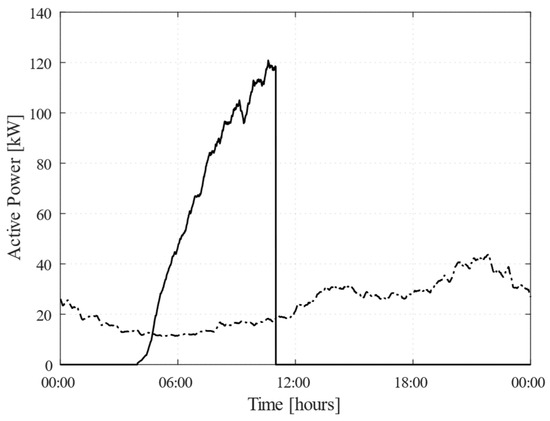
Figure 8.
Daily profiles of PV generation (solid line) and load demand (dotted line).
The time-domain behavior of the control actions, including power exchanges with the main grid and BESS power output, is shown in Figure 9, while Figure 10 illustrates the SoC of the BESS over the simulation period.
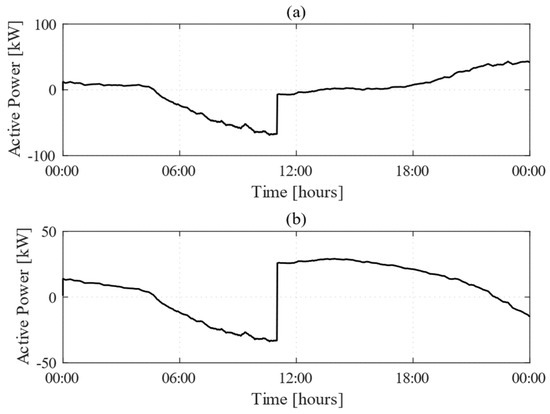
Figure 9.
Time-domain behaviors of (a) tie-line active power flow and (b) BESS active power outputs.
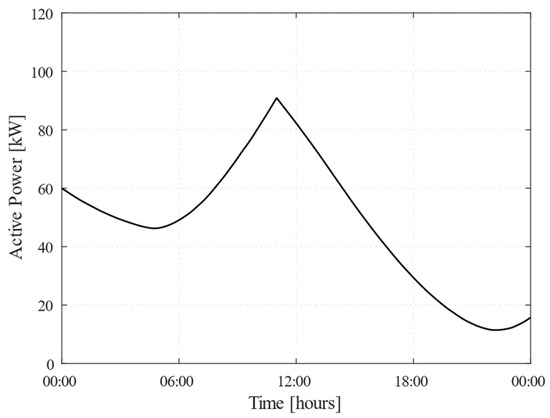
Figure 10.
Time-domain behavior of the state-of-charge (SoC) of the BESS.
From 00:00 to 11:00, the control methodology exhibited a similar behavior to that observed in Scenario 1, optimizing energy flows by purchasing low-cost electricity from the grid during the night, prioritizing PV self-consumption in the morning, and charging the BESS under favorable market conditions. However, the abrupt loss of PV generation at 11:00 led to a sharp rise in the power drawn from the main grid which led to higher grid purchasing costs. To counteract this, the controller promptly regulated the BESS output, reversing its active power from −33 kW (charging) to 26 kW (discharging). This response allowed the MG to remain balanced by meeting internal load demand (18.5 kW) while also exporting surplus energy (7.5 kW) at relatively favorable market prices.
Between 12:00 and 18:00, with PV generation at zero and lower electricity prices, the controller actively managed power flows to balance the MG’s internal demand using the energy stored in the BESS, while simultaneously minimizing the purchase of electricity from the grid. Unlike in the previous scenarios (Scenario 1 and Scenario 2), where the BESS was periodically recharged using excess energy from the PV system, in this scenario, this was not possible due to the lack of PV generation. As a result, the control system had to carefully manage the energy stored in the BESS to prevent its rapid depletion. Consequently, when the BESS SoC dropped below 35% at 17:30, the controller gradually reduced the discharge power to prevent the stored energy from being completely depleted. At the same time, it supplemented energy supply by purchasing small amounts of power from the grid.
During the evening peak (19:00–21:00), when electricity prices were at their highest and load demand was increasing, the controller continued to use the BESS strategically, covering approximately 50% of the MG’s load demand, thus limiting costly purchases from the grid. Despite the SoC reaching critically low levels (22%), the controller’s priority on the use of the energy stored in the BESS ensured economic efficiency while maintaining operational stability. As market prices declined after 22:00, the controller took advantage of lower costs to recharge the BESS, ensuring sufficient reserves for the next day and avoiding unnecessary expenses.
The financial performance under these extreme conditions is summarized in Table 3.

Table 3.
Economic Analysis.
Compared to Scenario 1, energy sales revenues were significantly lower due to the absence of PV generation after 11:00, which reduced the excess energy available for export. The costs of purchasing energy from the grid increased to €23.67, as the controller had to rely more on external energy to compensate for the loss of PV production. However, the costs related to the BESS remained relatively low, particularly for charging (€1.38), demonstrating the controller’s efficiency in managing energy reserves under constrained conditions.
Despite the significantly lower net profit (€7.20), this scenario demonstrates the controller’s ability to maintain economic profitability under severe operating constraints. The total loss of PV generation for more than half of the day posed a significant challenge, but the methodology was able to minimize financial losses through a combination of strategic BESS use and cost-aware grid interactions. Compared to Scenarios 1 and 2, this test demonstrated the robustness of the proposed controller in adapting to extreme variations in PV energy availability. It effectively preserved system stability and ensured cost-effective operation, even under highly adverse conditions.
3.4. Scenario 4—Multi-Day Performance Evaluation for Real-Time Control Feasibility
A five-day summer simulation, from Friday to Tuesday, was performed to evaluate the real-time performance of the proposed controller under continuously changing operating conditions. Unlike previous one-day tests, this scenario used progressively changing initial conditions, where each day’s initial state was determined by the previous day’s final state. This set-up provided a more accurate assessment of the controller’s adaptability to both internal and external changes affecting the MG.
To capture a wide range of operating scenarios, PV generation was modeled to reflect different weather conditions (including clear skies, partly cloudy conditions, cloudy periods, and rainfall), while different load demand profiles were considered for weekdays and weekends (see Figure 11).
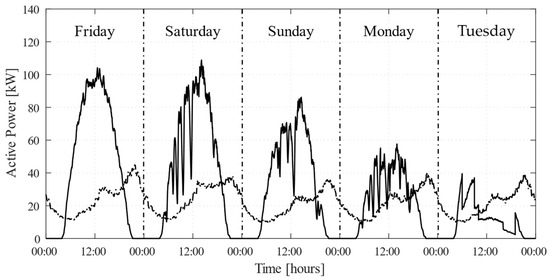
Figure 11.
Time-domain behaviors of PV generation (solid line) and load demand (dotted line).
Additionally, to assess the impact of energy price dynamics on the controller’s performance, different price profiles were used to simulate the typical fluctuations of the Italian electricity market. During weekends, energy prices tend to decline from a nighttime peak (around 23:00) to a minimum around 15:00 and then rise again to an evening peak (between 20:00 and 22:00). In contrast, on weekdays, price profiles follow similar trends to those in the previous scenarios, but with higher peaks and distinct characteristics during periods of low demand.
The simulation results, shown in Figure 12 and Figure 13, demonstrate the controller’s effectiveness in managing power flows between the MG and the main grid, as well as its ability to dynamically adjust BESS charge and discharge rates in response to real-time data. This adaptability enabled the controller to promptly cover fluctuations in PV generation and load demand, thus maintaining power balance within the MG. However, compared to previous scenarios, economic performance showed greater variability, with clear financial trade-offs emerging between stability and profitability.
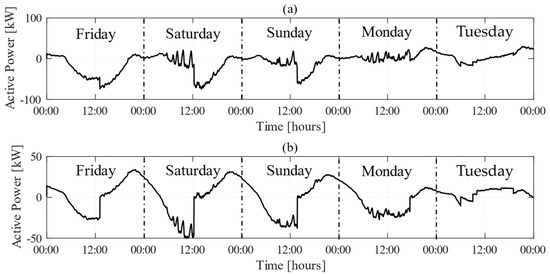
Figure 12.
Time-domain behaviors of (a) tie-line active power flow and (b) BESS active power outputs.
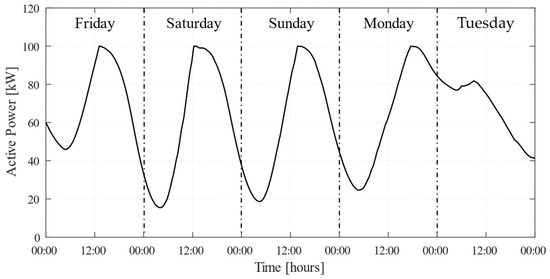
Figure 13.
Time-domain behavior of the state-of-charge (SoC) of the BESS.
During periods of high PV variability, such as those experienced on Saturday and Sunday, two different behaviors were observed. When electricity prices were low and exporting energy to the grid was less profitable, the controller mitigated rapid fluctuations in PV generation by limiting energy exports and, when necessary, purchasing energy from the grid to maximize BESS utilization. Conversely, when electricity prices increase, the controller shifted its priority to BESS discharge, thus addressing power imbalances while capitalizing on higher market prices for power sales.
Similar behavior was observed on Monday, where prolonged overcast conditions resulted in low and highly variable PV generation. In the early morning, when electricity prices were relatively high, the controller satisfied the entire load by discharging the BESS. As PV generation gradually increased, the controller reduced the BESS discharge rate to allow more PV energy to meet internal load. During the midday price dip, when low prices reduced the profitability of power exports, the controller prioritized BESS charging, minimizing exports and relying on grid purchases only when necessary to stabilize PV fluctuations. However, unlike previous days, where peak prices incentivized BESS discharge for both load balancing and grid sales, the controller adopted a more conservative strategy due to the reduced PV availability, thus preserving stored energy.
On Tuesday, marked by persistent rains, the controller initially followed a similar behavior to the previous days, purchasing energy from the grid when PV generation was minimal and prioritizing self-consumption and BESS charging as solar radiation improved. However, following the sudden drop in PV power around 06:00, the controller abruptly stopped the BESS charging due to the high SoC, redirecting the limited PV surplus toward maximizing power sales. Later in the morning, as heavy rains further reduced PV availability, the controller modulated power flows to balance the MG’s internal load demand by drawing on energy stored in the BESS, minimizing grid purchases, similar to the behavior observed in Scenario 3.
Across all five days, during evening hours, when PV generation was zero, the controller consistently increased BESS discharging to meet peak energy demand and capitalize on high energy prices by selling excess energy to the grid. When prices dropped, the controller stopped exporting energy and used the energy stored in the BESS to meet internal consumption, thus avoiding the need to purchase energy from the grid.
At the end of each simulation day, the BESS SoC was as follows: 23.16% on Friday, 37.6% on Saturday, 44.7% on Sunday, 84.4% on Monday, and 42% on Tuesday. These values highlight the controller’s efficiency in managing MG energy flows by adapting to environmental and market fluctuations, but also reveal its limitation in sustaining long-term profitability under persistently unfavorable conditions.
The economic results of Scenario 4 are summarized in Table 4.

Table 4.
Economic Analysis Results.
Compared to previous scenarios, Scenario 4 highlights a deep trade-off between economic performance and operational resilience. While the controller consistently ensured grid stability, its financial outcomes exhibited increased variability due to fluctuating weather conditions and dynamic market price profiles. On Friday, favorable weather and strong PV generation led to high power sales (€61.40) and a net profit of €54.06, very similar to the optimal performance observed in Scenario 1. In contrast, higher PV variability on Saturday, driven by intermittent cloud cover, led to a lower net profit (€31.38), mainly due to reduced PV energy availability. A further decline in PV generation on Sunday due to mostly cloudy conditions resulted in a net profit of €22.53, reflecting limited export opportunities. Persistent cloudy and rainy conditions significantly reduced PV generation on Monday and Tuesday, forcing the controller to rely more on grid purchases while limiting power sales. As a result, both days suffered financial losses, with a negative net profit of –€16.58 and –€15.63, respectively. Despite financial losses of the last two days, the results demonstrate the controller’s robustness in maintaining energy balance and adapting to complex, real-world operating conditions. The results highlight the trade-off between economic optimization and operational resilience, demonstrating the controller’s ability to effectively address different energy challenges.
4. Discussion
The simulation results confirm that the proposed real-time control methodology not only optimizes the performance of the MG but also represents a key innovation. By actively coordinating the charging and discharging of the BESS with grid power exchanges in response to fluctuating electricity market prices, PV generation and load demand, the BESS is transformed from a passive energy buffer into an active market participant. This fundamental change supports the methodology’s ability to improve both the stability and economic performance of the MG.
In Scenario 1, where PV generation was abundant, the controller maximized self-consumption and energy exports, achieving the highest net profit (€92.12). This demonstrates that under favorable conditions, the methodology efficiently minimizes grid reliance while exploiting economic opportunities. In contrast, in Scenario 2, performed under partly cloudy conditions, the controller adapted to variable PV production by adjusting BESS operations and grid exchanges. Although these adjustments maintained system stability, the limited excess PV power available for export resulted in a lower net profit (€52.96). This result illustrates that increasing PV fluctuations have a negative impact on economic returns, highlighting the delicate trade-off between stability and profitability. Scenario 3 presented the most severe challenge, simulating a prolonged loss of PV generation. Despite similar market price conditions to Scenario 1, the absence of PV generation forced the MG to rely predominantly on the BESS and grid imports. The controller reacted by discharging the BESS and optimizing purchases from the grid, but operational flexibility was limited, resulting in only marginal profitability (€7.20). This scenario highlights the economic vulnerability of the MG when PV generation is absent for extended periods and underlines the importance of an active BESS management strategy.
In Scenario 4, a dynamic multi-day environment further emphasized the controller’s adaptive capabilities. Over five consecutive days, with varying weather conditions, load demand, and market price profiles, the controller initially effectively balanced self-consumption and market transactions effectively. However, as adverse conditions persisted, profitability gradually declined and finally turned negative in the final days. Market prices have contributed significantly to this decline. In fact, during periods of high prices, the controller prioritized selling the limited available excess PV power to the grid over BESS charging, thus obtaining short-term profits. Conversely, prolonged low prices discouraged energy exports and encouraged BESS charging, which, while beneficial for energy autonomy, ultimately led to weakening financial performance. These results highlight that, despite the strong short-term adaptability of the controller, long-term profitability is sensitive to prolonged periods of low PV generation and market volatility. Despite these challenges, the MG remained financially sustainable over the observation period. The total energy sales revenue of €138.97, offset by grid purchase costs of €60.32, along with minimum BESS charge costs (€0.10) and discharge costs (€2.79), produced a net profit of €75.76, with an average daily gain of €15.15. This demonstrates that while adverse conditions can temporarily reduce earnings, the proposed real-time control methodology effectively mitigates financial downturns by dynamically adapting to real-time conditions.
These findings also suggest that long-term financial sustainability is influenced by structural factors, such as storage capacity, weather patterns, and market dynamics, that extend beyond the scope of real-time control strategies alone.
In light of these insights, future research should explore further refinements, such as incorporating a penalty function into the optimization model to incentivize achieving an end-of-day target SoC, thereby minimizing the gap between the initial and final SoC, optimizing the BESS size and integrating complementary renewable sources or storage solutions. Such improvements could further strengthen the overall resilience and economic viability of microgrid operations.
5. Conclusions
This paper develops a self-adaptive control methodology to optimize the real-time operation of PV-powered microgrids. By actively managing both BESS power outputs and grid exchanges with the utility grid, the proposed methodology aimed at finding an optimal trade-off between economic and operational objectives. At its core, a multi-objective optimization problem integrates real-time SoC BESS management within an economic optimization problem, ensuring efficient storage utilization, minimizing costs, maximizing energy export revenue, and preventing premature depletion or overload of storage resources. The Lyapunov-based algorithm enhanced with sensitivity theory is adopted to ensure rapid convergence to optimal solutions, enabling the controller to dynamically adapt to changing operating conditions while maintaining MG stability even under challenging scenarios. To assess its performance, several computer simulations were performed on a low-voltage PV-powered MG under different operating conditions, ranging from ideal high PV availability to extreme cases with prolonged PV unavailability. The results demonstrated the controller’s ability to optimally menage BESS power output and grid exchanges with the main grid to maintain stability and optimize economic performance despite rapidly changing operating conditions. Under favorable conditions, the controller maximized revenues by exporting excess power during peak price periods, earning high net profits. In less favorable conditions, where PV output is reduced or absent, the controller adapted by actively managing BESS power output and power exchanges with the grid to minimize operating costs by prioritizing self-consumption and optimal BESS utilization, even at the cost of lower profitability. A key strength of the suggested methodology is its ability to dynamically manage the BESS state-of-charge, preventing premature depletion or overcharging. Although this paper focused on PV/BESS-based microgrids, the proposed methodology can be extended to MGs with a broader mix of renewable energy sources. This aspect will be explored in future work.
Funding
This research received no funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Jin, X.; Mu, Y.; Jia, H.; Wu, J.; Jiang, T.; Yu, X. Dynamic economic dispatch of a hybrid energy microgrid considering building based virtual energy storage system. Appl. Energy 2017, 194, 386–398. [Google Scholar] [CrossRef]
- Shahzad, S.; Jasińska, E. Renewable Revolution: A Review of Strategic Flexibility in Future Power Systems. Sustainability 2024, 16, 5454. [Google Scholar] [CrossRef]
- Bakhtvar, M.; Al Hinai, A.; El Moursi, M.S.; Albadi, M.H. A vision of flexible dispatchable hybrid solar-wind-energy storage power plant. IET Renew. Power Gener. 2021, 15, 2983–2996. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Dicorato, M.; Forte, G.; Trovato, M. PV plants for voltage regulation in distribution networks. In Proceedings of the 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012. [Google Scholar]
- Sinsel, S.R.; Riemke, R.L.; Hoffmann, V.H. Challenges and solution technologies for the integration of variable renewable energy sources—A review. Renew. Energy 2020, 145, 2271–2285. [Google Scholar] [CrossRef]
- Silva, P.; Moreira, A.; Heleno, M.; Marcato, A.L.M. Boundary Technology Costs for Economic Viability of Long-Duration Energy Storage Systems in California. IEEE Trans. Energy Mark. Policy Regul. 2024, 3, 32–45. [Google Scholar] [CrossRef]
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of Renewable Energy Sources in future power systems: The role of storage. Renew. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E. Time domain identification of a simplified model of So–Nick BESS: A methodology validated with field experiments. Electr. Power Syst. Res. 2018, 165, 229–237. [Google Scholar] [CrossRef]
- Gatta, F.M.; Geri, A.; Lauria, S.; Maccioni, M.; Palone, F. Battery energy storage efficiency calculation including auxiliary losses: Technology comparison and operating strategies. In Proceedings of the IEEE PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez-Mata, O. Energy Management Systems for Microgrids: Main Existing Trends in Centralized Control Architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Madrigal-Martínez, M.; Mina-Antonio, J.D.; Iracheta-Cortez, R.; Enríquez-Santiago, J.A.; RodríguezRivera, O.; Martínez-Reyes, G.; Mendoza-Santos, E. A comprehensive review on power-quality issues, optimization techniques, and control strategies of microgrid based on renewable energy sources. Sustainability 2023, 15, 9847. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Zafra-Cabeza, A.; Silva, C.; Grieu, S.; Darure, T.; Estanqueiro, A. Model Predictive Control for Microgrid Functionalities: Review and Future Challenges. Energies 2021, 14, 1296. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M.; Jantzen, J.; Kristensen, M.; Othman, S.B. Energy scheduling of a smart microgrid with shared photovoltaic panels and storage: The case of the Ballen marina in Samsø. Energy 2020, 198, 117188. [Google Scholar] [CrossRef]
- Saleem, M.I.; Saha, S.; Izhar, U.; Ang, L. Optimized energy management of a solar battery microgrid: An economic approach towards voltage stability. J. Energy Storage 2024, 90, 111876. [Google Scholar] [CrossRef]
- Houben, N.; Cosic, A.; Stadler, M.; Mansoor, M.; Zellinger, M.; Auer, H.; Ajanovic, A.; Haas, R. Optimal dispatch of a multi-energy system microgrid under uncertainty: A renewable energy community in Austria. Appl. Energy 2023, 337, 120913. [Google Scholar] [CrossRef]
- Faraji, J.; Ketabi, A.; Hashemi-Dezaki, H.; Shafie-Khah, M.; Catalao, J.P.S. Optimal Day-Ahead Self-Scheduling and Operation of Prosumer Microgrids Using Hybrid Machine Learning-Based Weather and Load Forecasting. IEEE Access 2020, 8, 157284–157305. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, M.K. A novel deep learning-based forecasting model optimized by heuristic algorithm for energy management of microgrid. Appl. Energy 2023, 332, 120525. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, Y. Optimal schedule of grid-connected residential PV generation systems with battery storages under time-of-use and step tariffs. J. Energy Storage 2019, 23, 175–182. [Google Scholar] [CrossRef]
- Escobar, E.D.; Betancur, D.; Isaac, I.A. Optimal power and battery storage dispatch architecture for microgrids: Implementation in a campus microgrid. Smart Grids Sustain. Energy 2024, 9, 27. [Google Scholar] [CrossRef]
- Fan, C.; Lu, M.; Sun, Y.; Liang, D. A novel linear programming-based predictive control method for building battery operations with reduced cost and enhanced computational efficiency. Renew. Energ. 2024, 237 Part C, 121847. [Google Scholar] [CrossRef]
- Shirzadi, N.; Nasiri, F.; El-Bayeh, C.; Eicker, U. Optimal dispatching of renewable energy-based urban microgrids using a deep learning approach for electrical load and wind power forecasting. Int. J. Energy Res. 2021, 46, 3173–3188. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Duffy, M.; Monaghan, R.F.D.; Barrett, E. Residential PV-battery scheduling with stochastic optimization and neural network-driven scenario generation. Energy Rep. 2024, 12, 418–429. [Google Scholar] [CrossRef]
- Bahramara, S.; Sheikhahmadi, P.; Mazza, A.; Chicco, G. Day-ahead self-scheduling from risk-averse microgrid operators to provide reserves and flexible ramping ancillary services. Int. J. Electr. Power Energy Syst. 2022, 142, 108381. [Google Scholar] [CrossRef]
- Islam, M.M.; Nagrial, M.; Rizk, J.; Hellany, A. Dual stage microgrid energy resource optimization strategy considering renewable and battery storage systems. Int. J. Energy Res. 2021, 45, 21340–21364. [Google Scholar]
- Fang, X.; Khazaei, J. A Two-Stage Deep Learning Approach for Solving Microgrid Economic Dispatch. IEEE Syst. J. 2023, 17, 6237–6247. [Google Scholar] [CrossRef]
- Shibl, M.; Ismail, L.; Massoud, A.M. An Intelligent Two-Stage energy dispatch Management System for hybrid power plants: Impact of machine learning deployment. IEEE Access 2023, 11, 13091–13102. [Google Scholar] [CrossRef]
- Yang, H.; Gong, Z.; Ma, Y.; Wang, L.; Dong, B. Optimal Two-stage Dispatch Method of Household PV-BESS Integrated Generation System Under Time-of-use Electricity Price. Int. J. Electr. Power Energy Syst. 2020, 123, 106244. [Google Scholar] [CrossRef]
- Martinez-Rico, J.; Zulueta, E.; de-Argandoña, I.R.; Fernandez-Gamiz, U.; Armendia, M. Multi-objective Optimization of Production Scheduling Using Particle Swarm Optimization Algorithm for Hybrid Renewable Power Plants with Battery Energy Storage System. J. Mod. Power Syst. Clean. Energy 2021, 9, 285–294. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Marcone, F.; Porro, G.; Rasolomampionona, D.D. Economic Dispatch for on-line operation of grid-connected microgrids. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 651–659. [Google Scholar] [CrossRef]
- Lin, Z.Y.; Song, C.Y.; Zhao, J.; Yin, H. Improved approximate dynamic programming for real-time economic dispatch of integrated microgrids. Energy 2022, 255, 124513. [Google Scholar] [CrossRef]
- Meng, F.Y.; Bai, Y.; Jin, J.L. An advanced real-time dispatching strategy for a distributed energy system based on the reinforcement learning algorithm. Renew. Energy 2021, 178, 13–24. [Google Scholar] [CrossRef]
- Zeinal-Kheiri, S.; Mohammadpour Shotorbani, A.; Khardenavis, A.; Mohammadi-Ivatloo, B.; Sadiq, R.; Hewage, K. An adaptive real-time energy management system for a renewable energy-based microgrid. IET Renew. Power Gener. 2021, 15, 2918–2930. [Google Scholar] [CrossRef]
- Shotorbani, A.M.; Zeinal-Kheiri, S.; Chhipi-Shrestha, G.; Mohammadi-Ivatloo, B.; Sadiq, R.; Hewage, K. Enhanced real-time scheduling algorithm for energy management in a renewable-integrated microgrid. Appl. Energy 2021, 304, 117658. [Google Scholar] [CrossRef]
- Lei, X.; Yan, W.-J.; Peng, P.; Ye, T. An optimal purchase and sale power model considering microgrids. Int. Trans. Electr. Energ. Syst. 2015, 25, 246–261. [Google Scholar] [CrossRef]
- Deepak, K.; Sandeep, D.; Yajvender, P.V.; Rintu, K. Impact of optimal sized pump storage unit on microgrid operating cost and bidding in electricity market. J. Energy Storage 2022, 51, 104373. [Google Scholar] [CrossRef]
- Braun, M. Reactive power supply by distributed generators. In Proceedings of the IEEE-Power and Energy Society General Meeting e Conversion and Delivery of Eletrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar]
- Cagnano, A.; Torelli, F.; Alfonzetti, F.; de Tuglie, E. Can PV plants provide a reactive power ancillary service? A treat offered by an on-line controller. Renew. Energy 2011, 36, 1047–1052. [Google Scholar] [CrossRef]
- Matlab/Simulink User’s Guide; MathWorks: Natick, MA, USA, 2024.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).