Dual-Coupled-Inductor-Based High-Step-Up Boost Converter with Active-Clamping and Zero-Voltage Switching
Abstract
1. Introduction
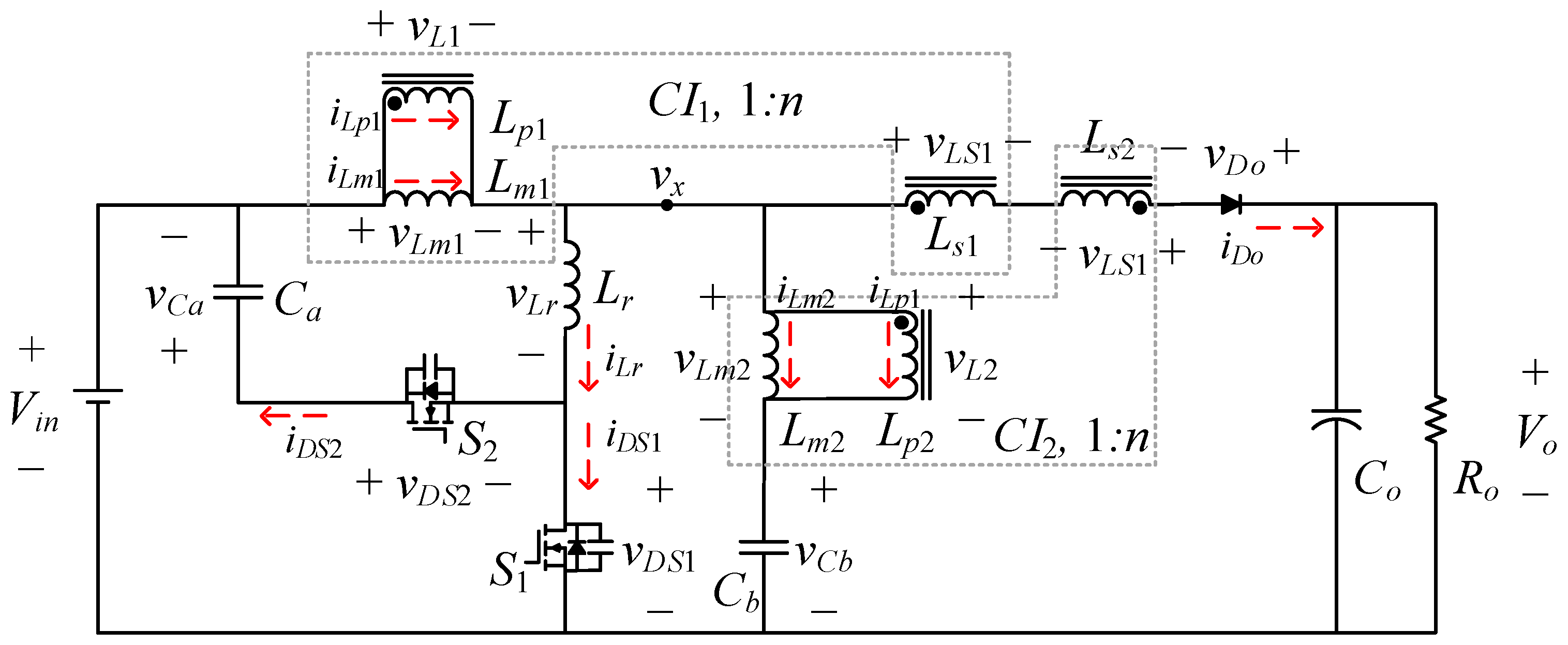
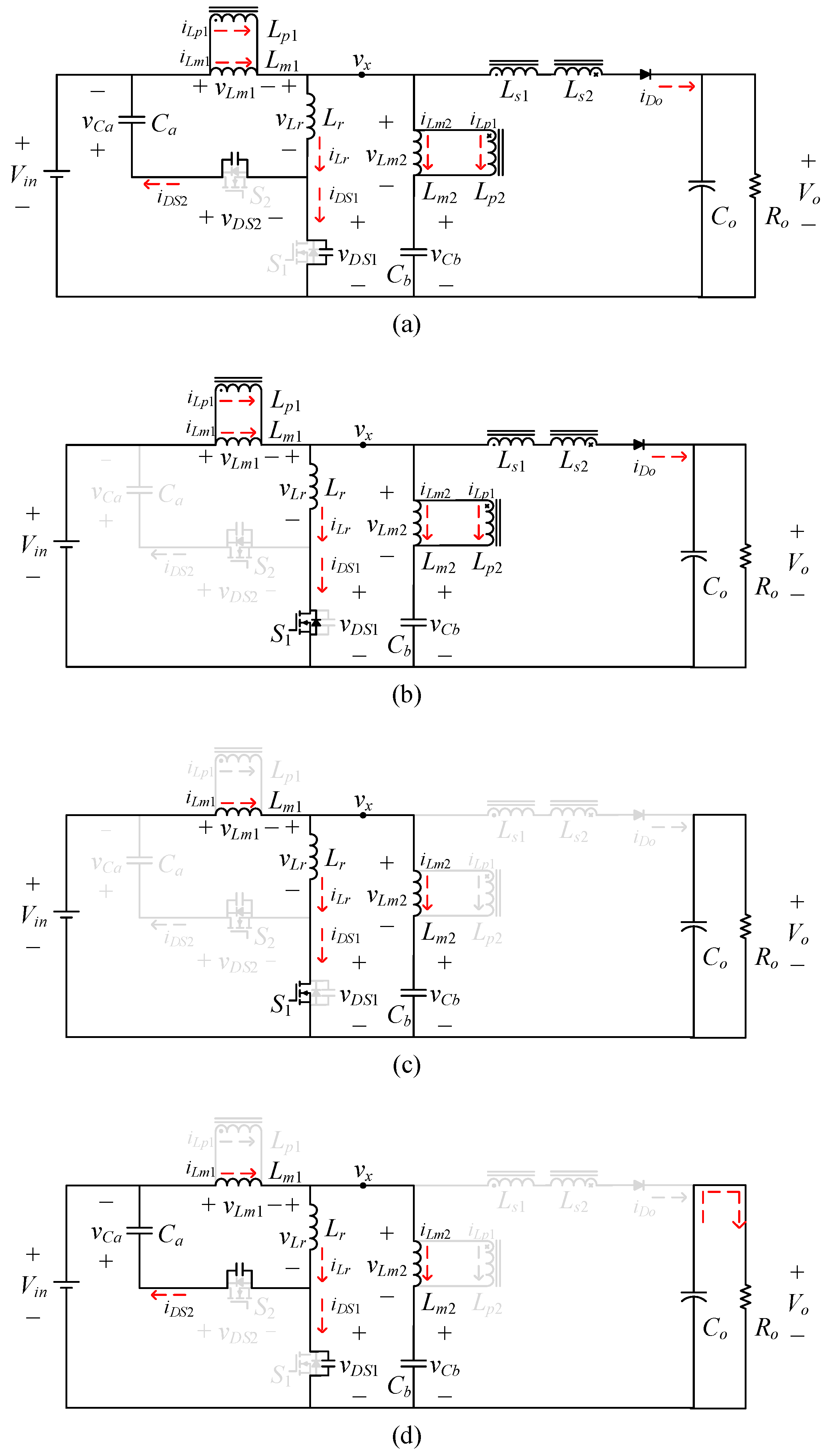
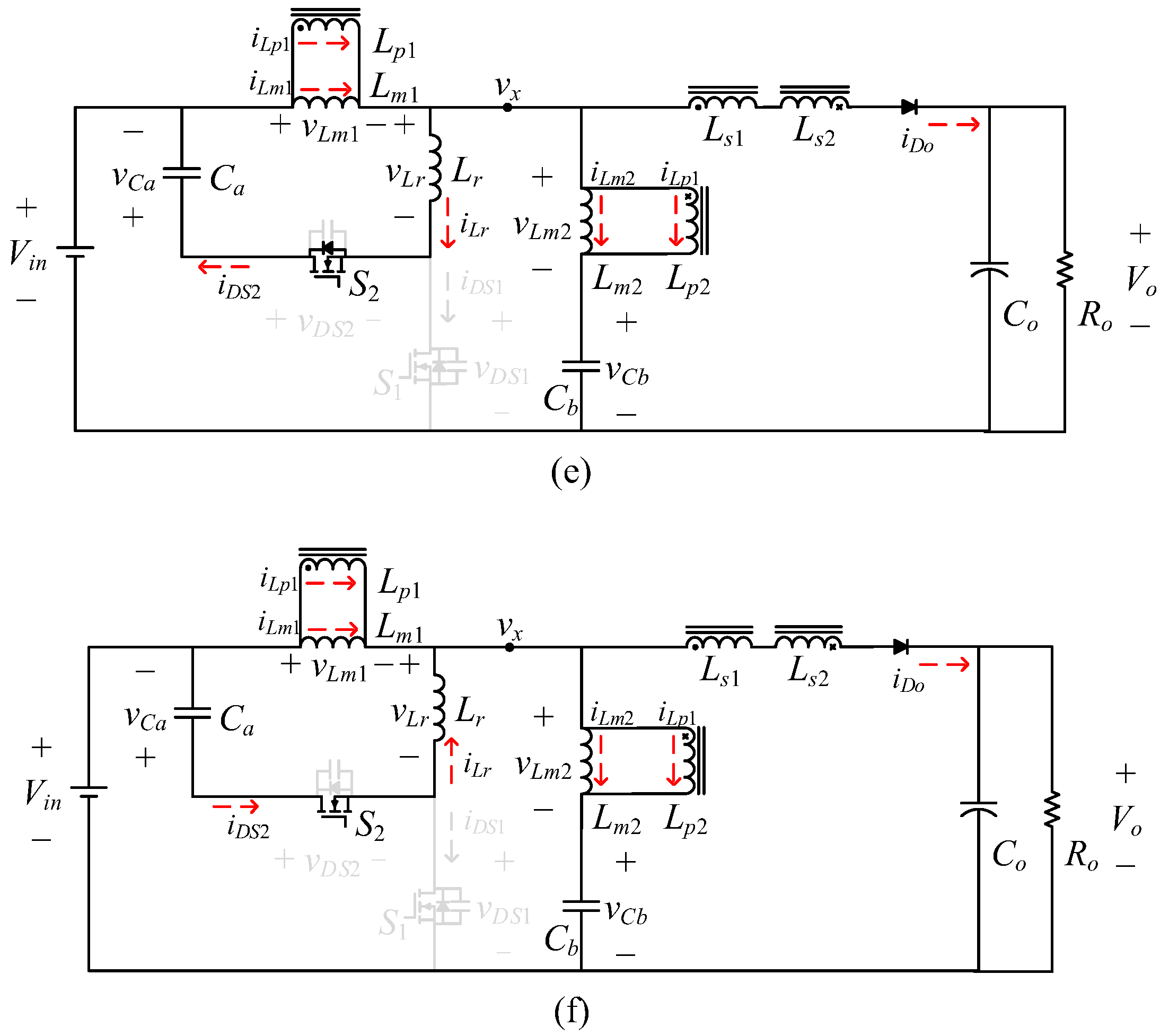
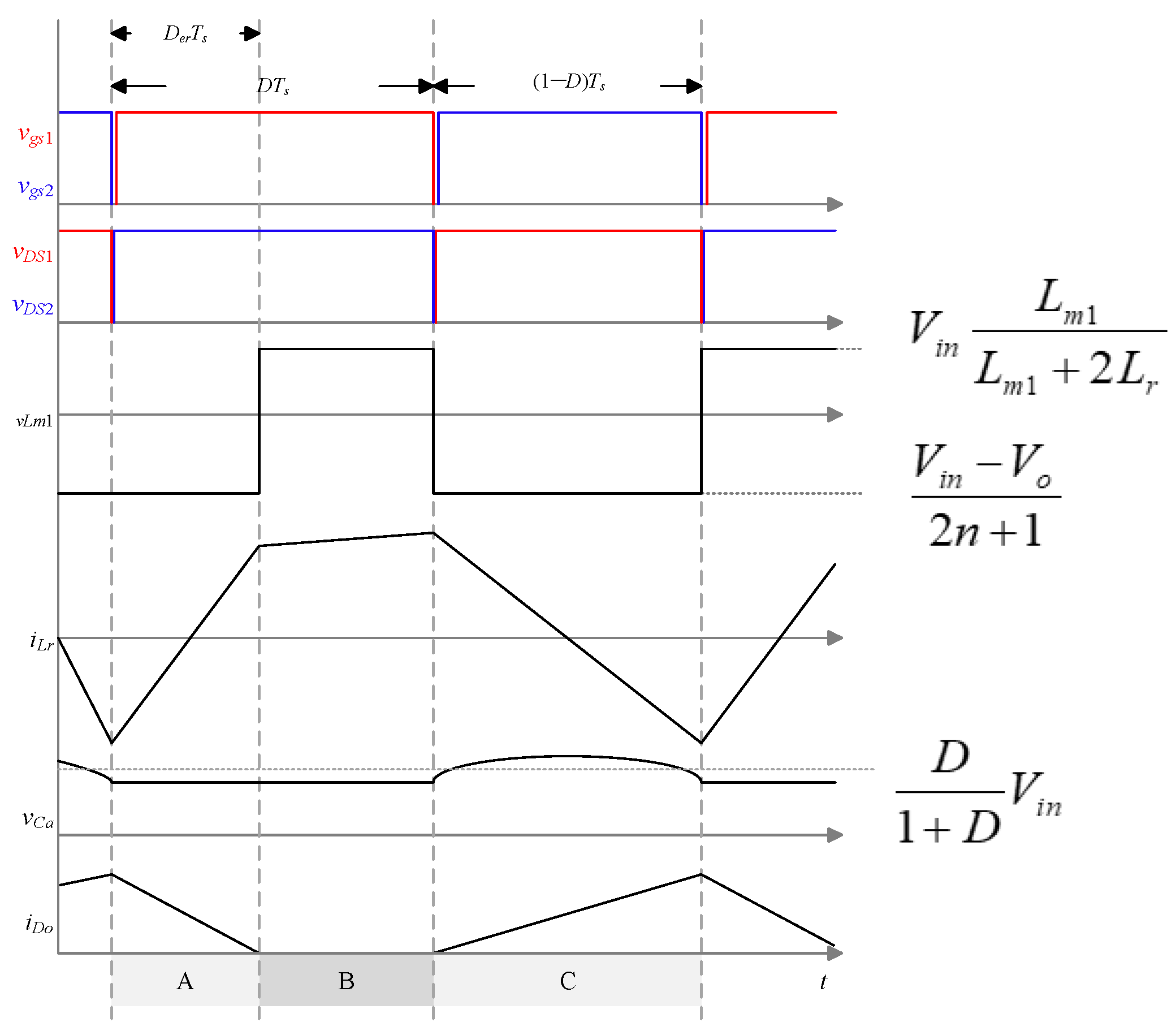
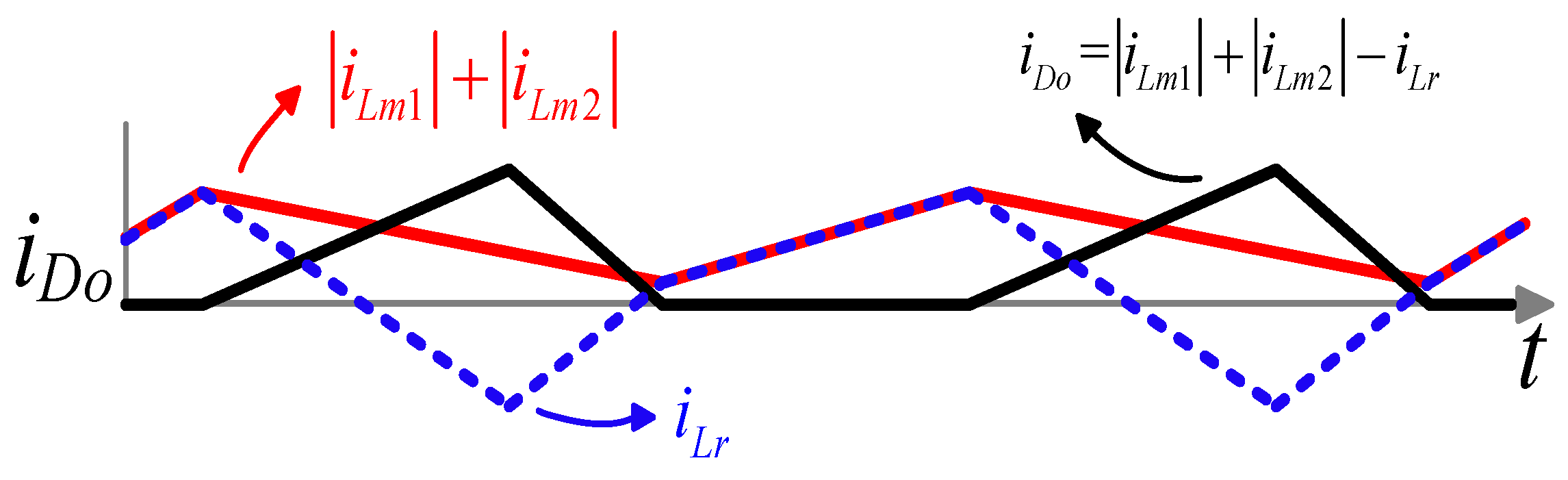
2. Operation of the Proposed Converter
- The turn ratio of the two coupled inductors is the same, which is 1:n.
- The magnetizing inductance of both coupled inductors is the same, which is Lm (Lm1 = Lm2 = Lm).
- The clamping capacitors Ca and Cb and the output capacitor Co are much larger than the output capacitance of power switches Cr1 and Cr2. Their steady-state voltages can be viewed as constant voltage sources, dependent on the input voltage and duty cycle.
- The on times of S1 and S2 are DTs and (1 − D)Ts, respectively, where D is the duty cycle of main switch S1, Ts is the switching period, and the dead time is assumed to be smaller than other conduction times.
- All components are considered ideal such that the conduction losses of all switches and diodes are ignored.
- -
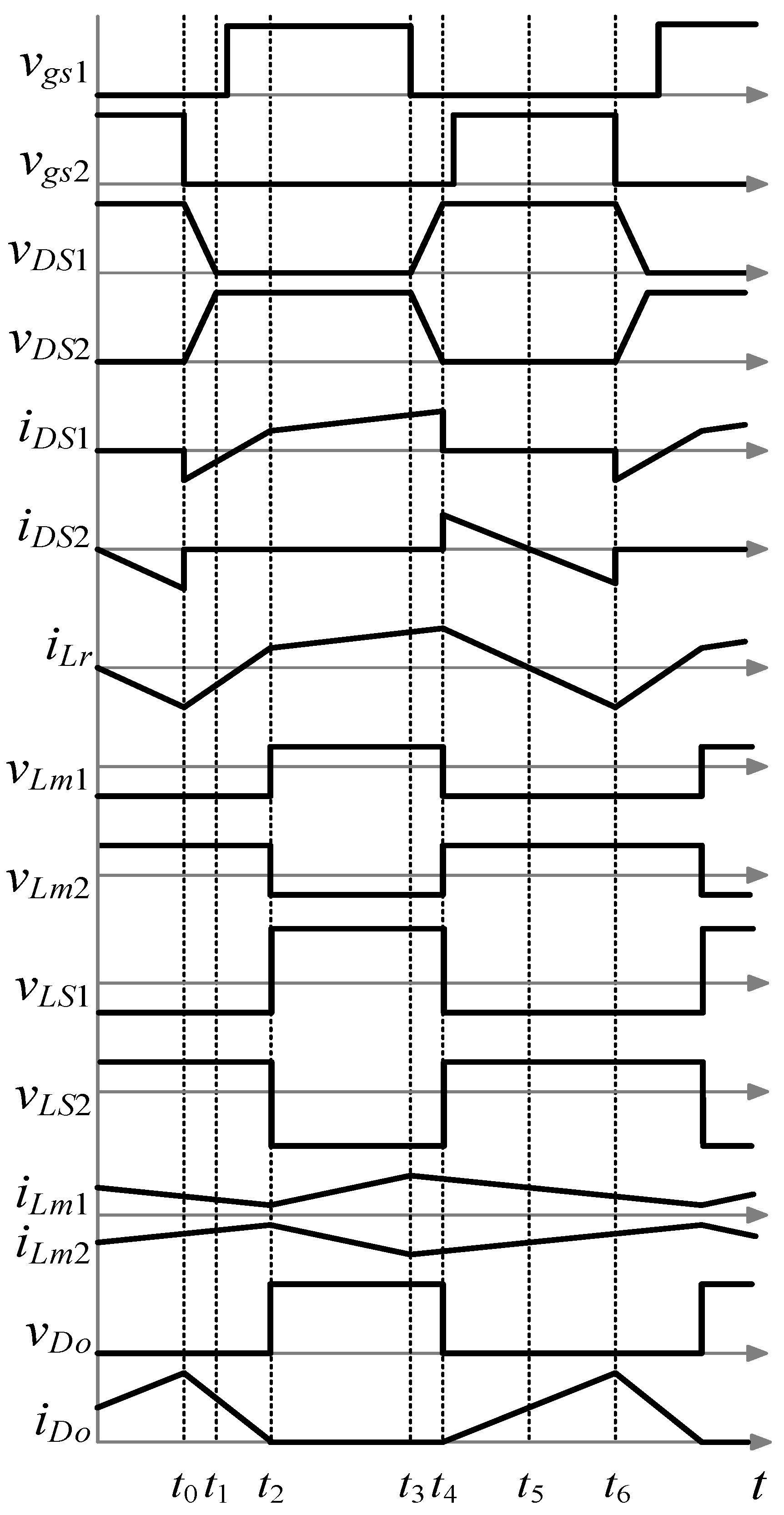
- State 1 (t0–t1)
- -
- State 2 (t1–t2)
- -
- State 3 (t2–t3)
- -
- State 4 (t3–t4)
- -
- State 5 (t4–t5)
- -
- State 6 (t5–t6)
3. Analysis of the Proposed Converter
3.1. Clamped Voltage vCa
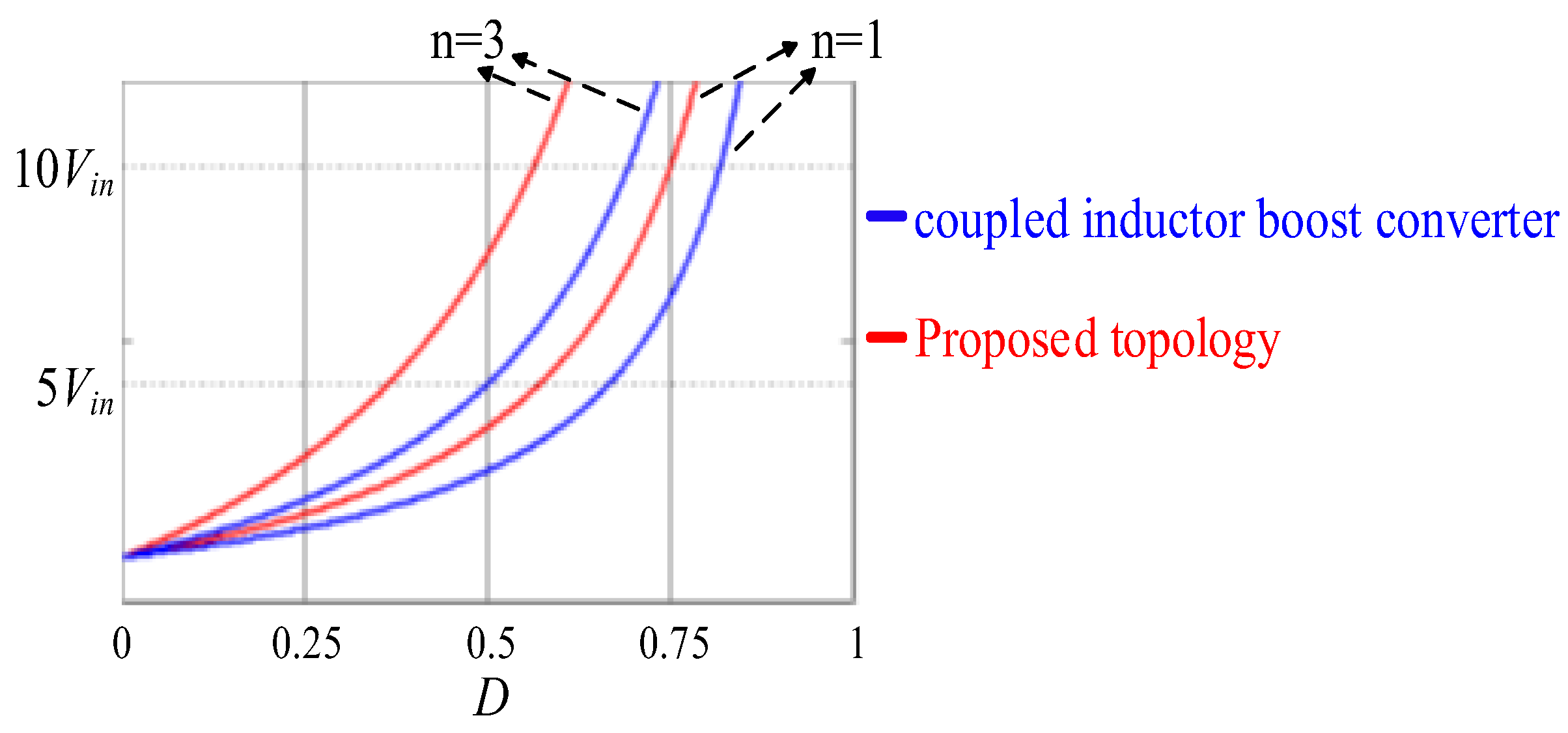
3.2. Voltage Transfer Ratio
3.3. Voltage and Current Stress
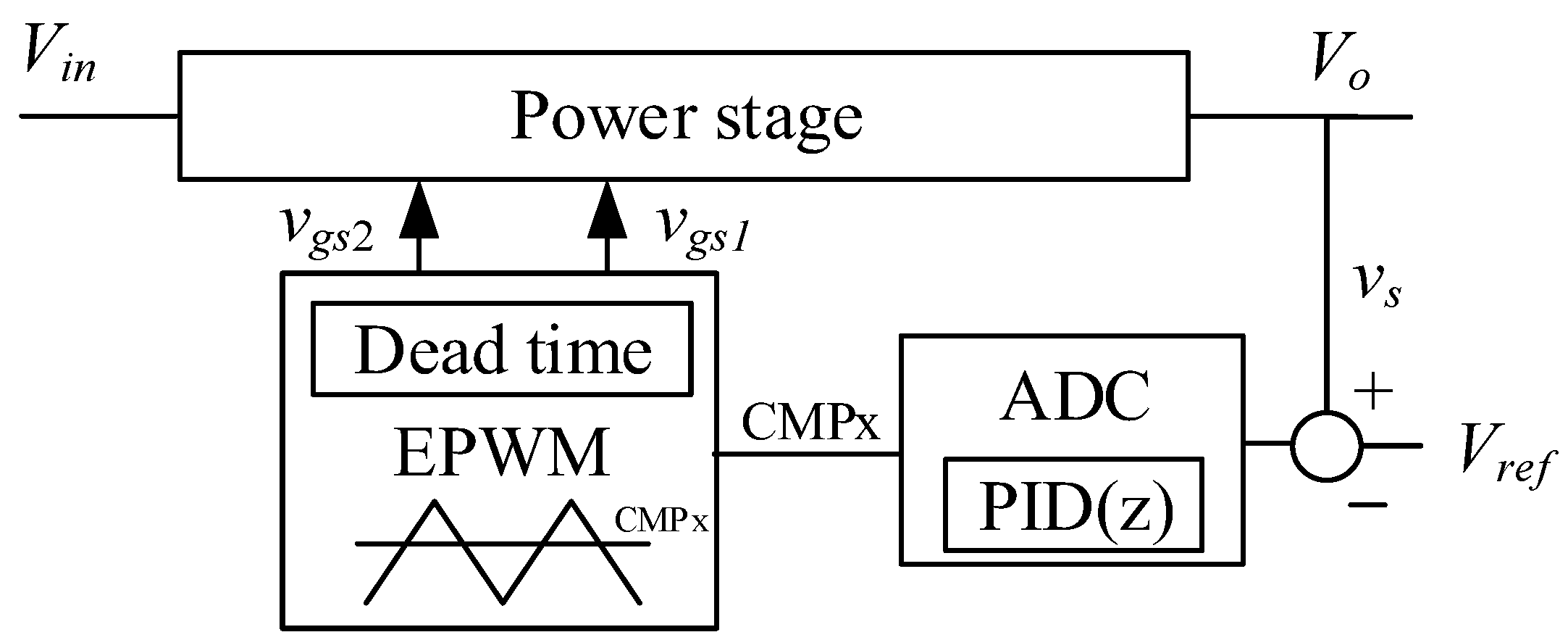
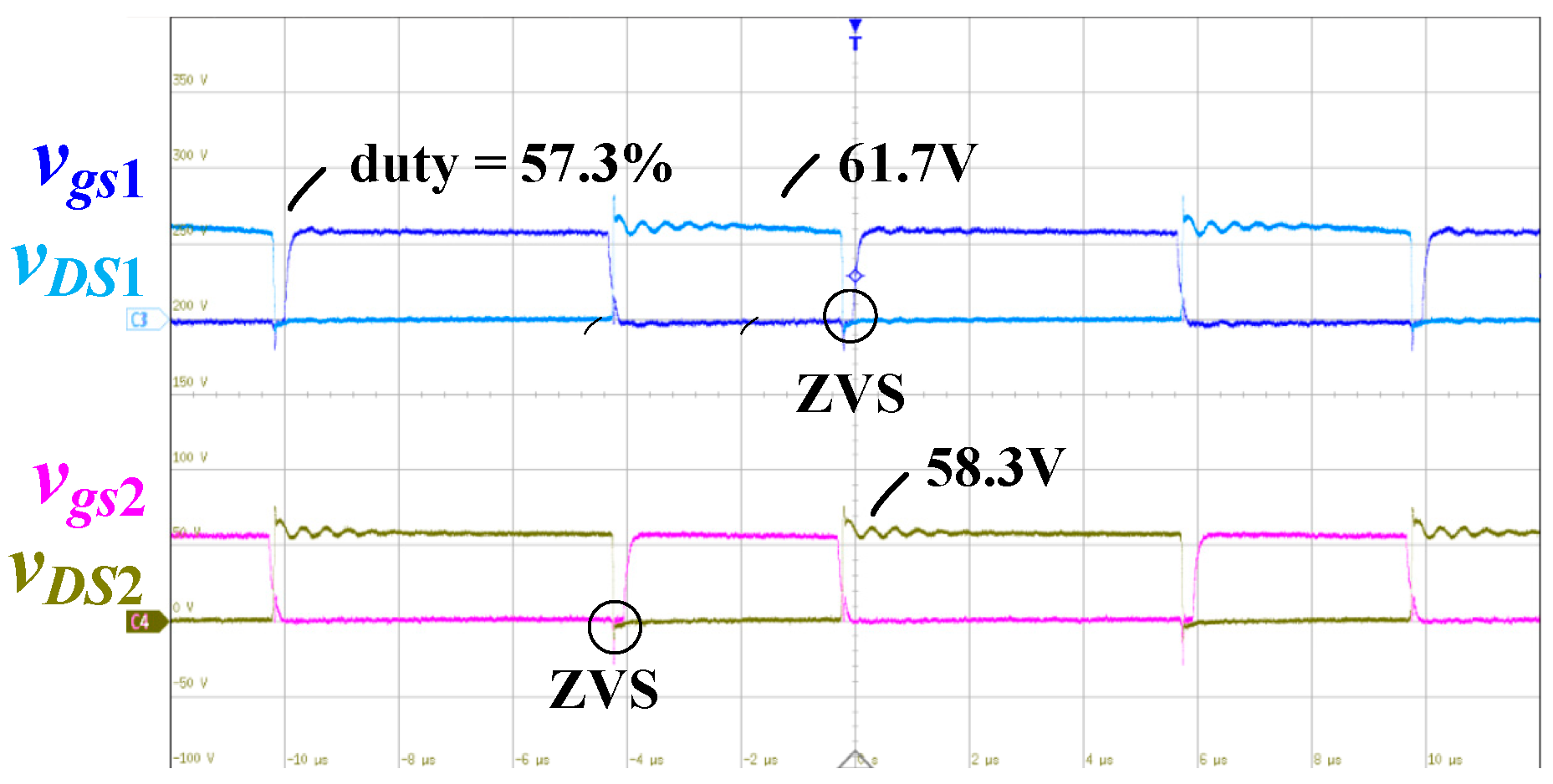
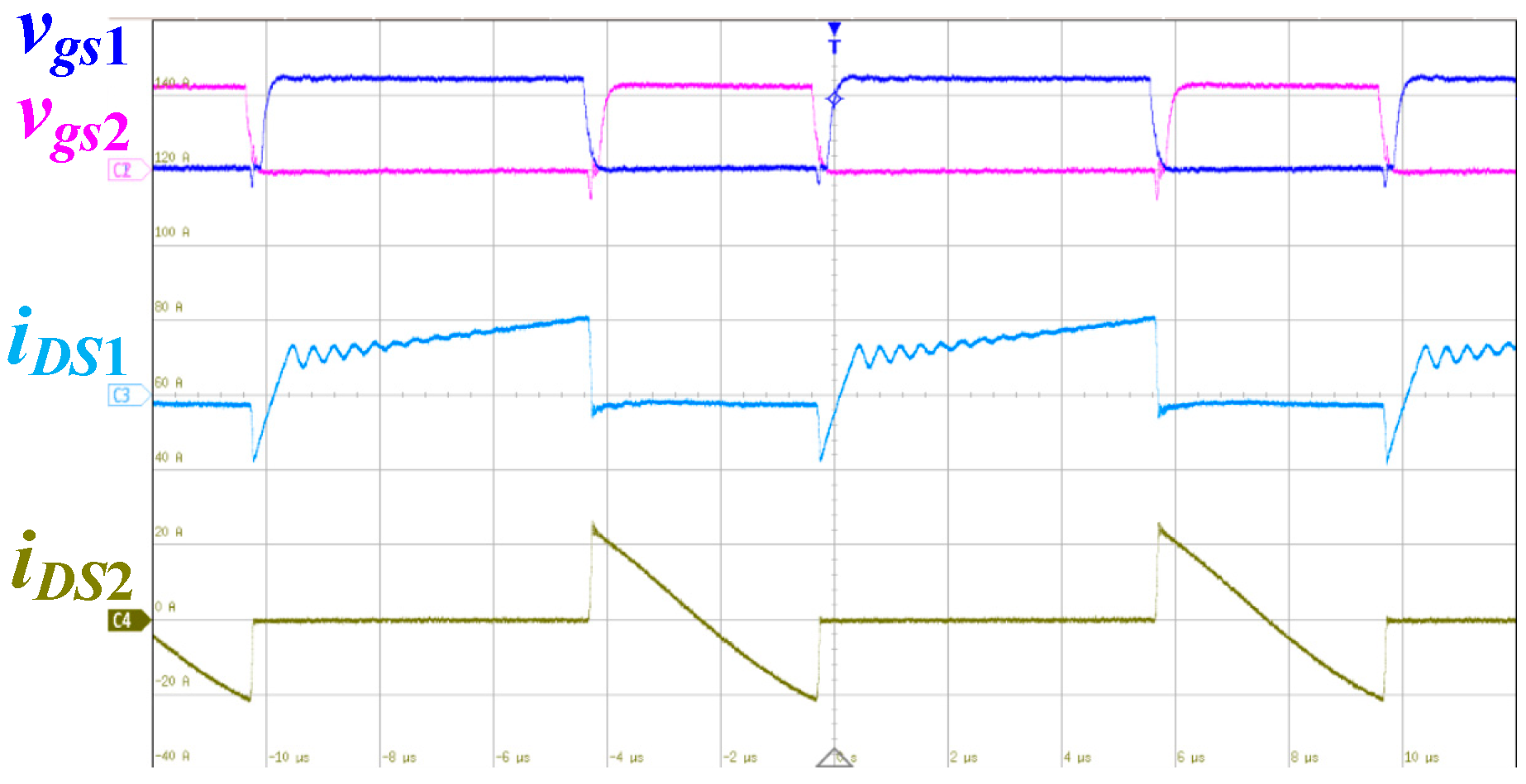
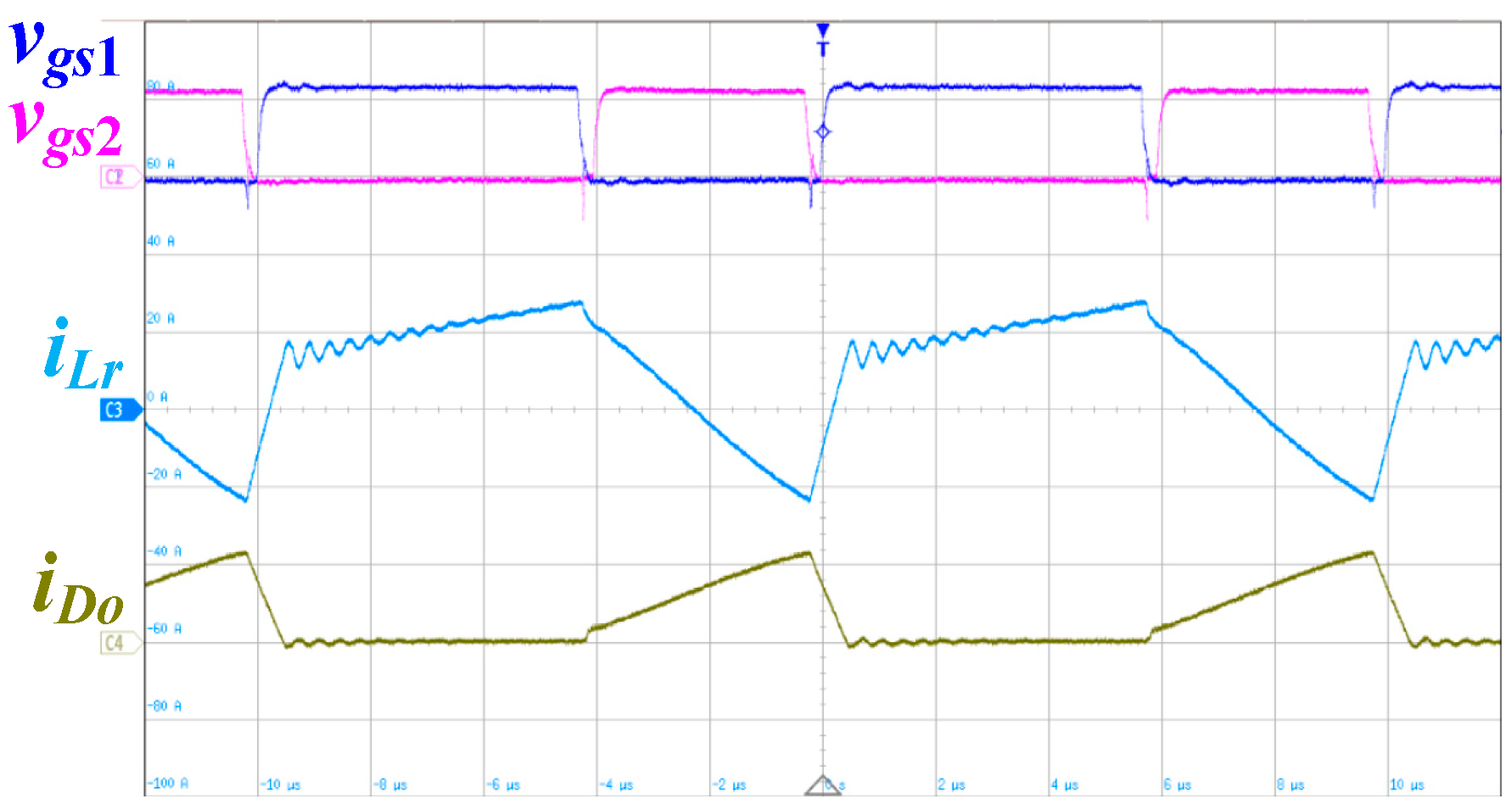
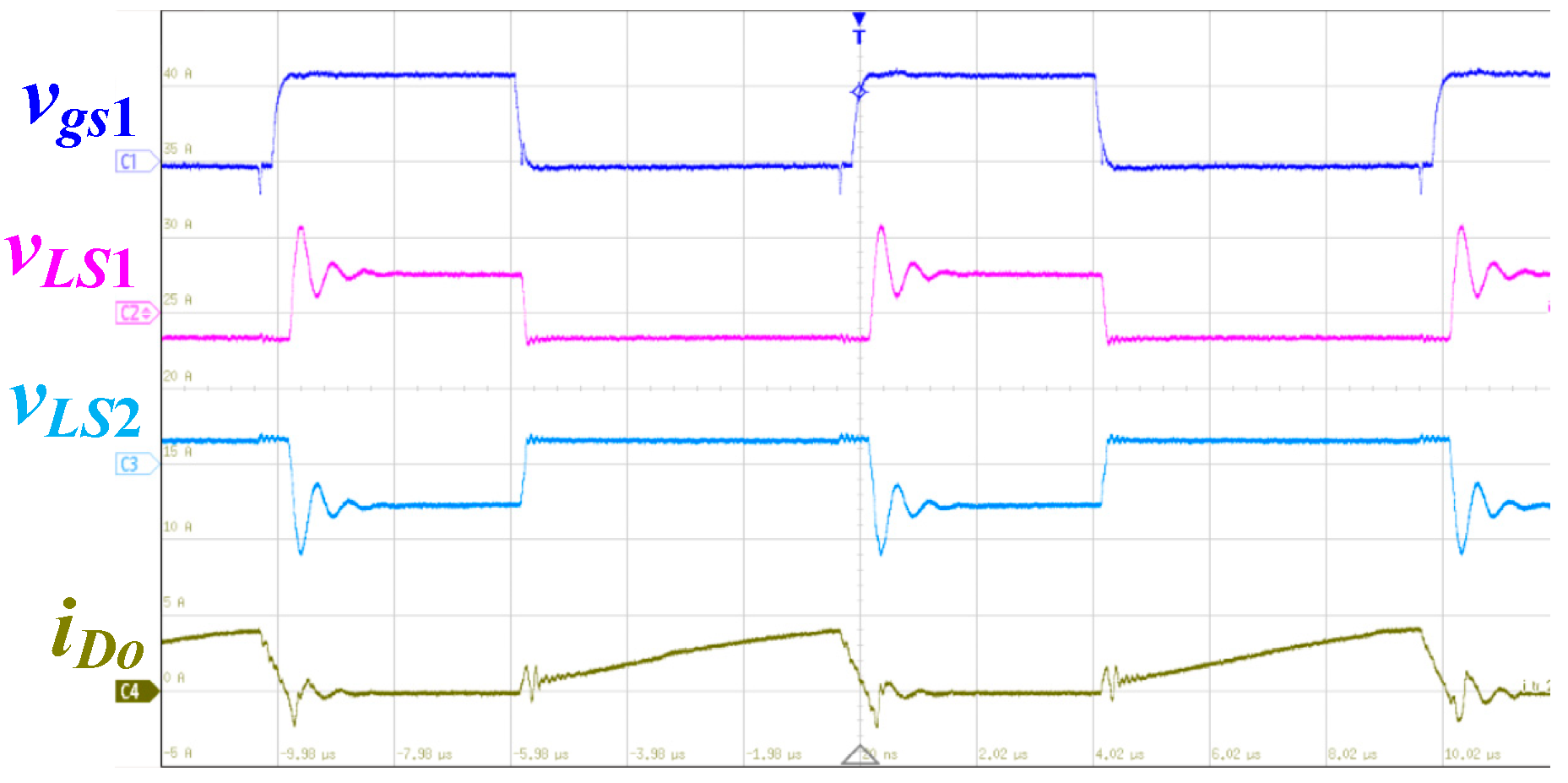
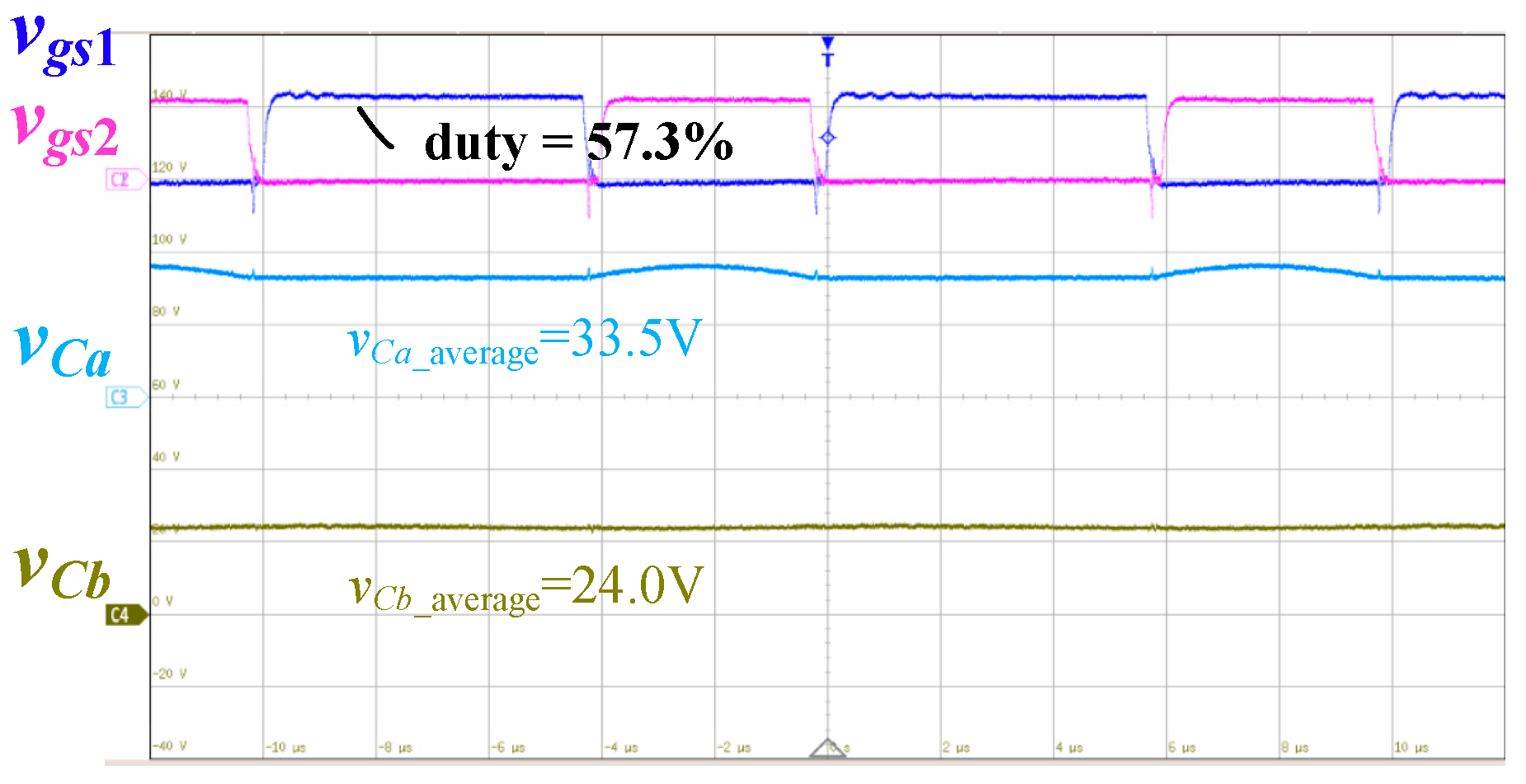
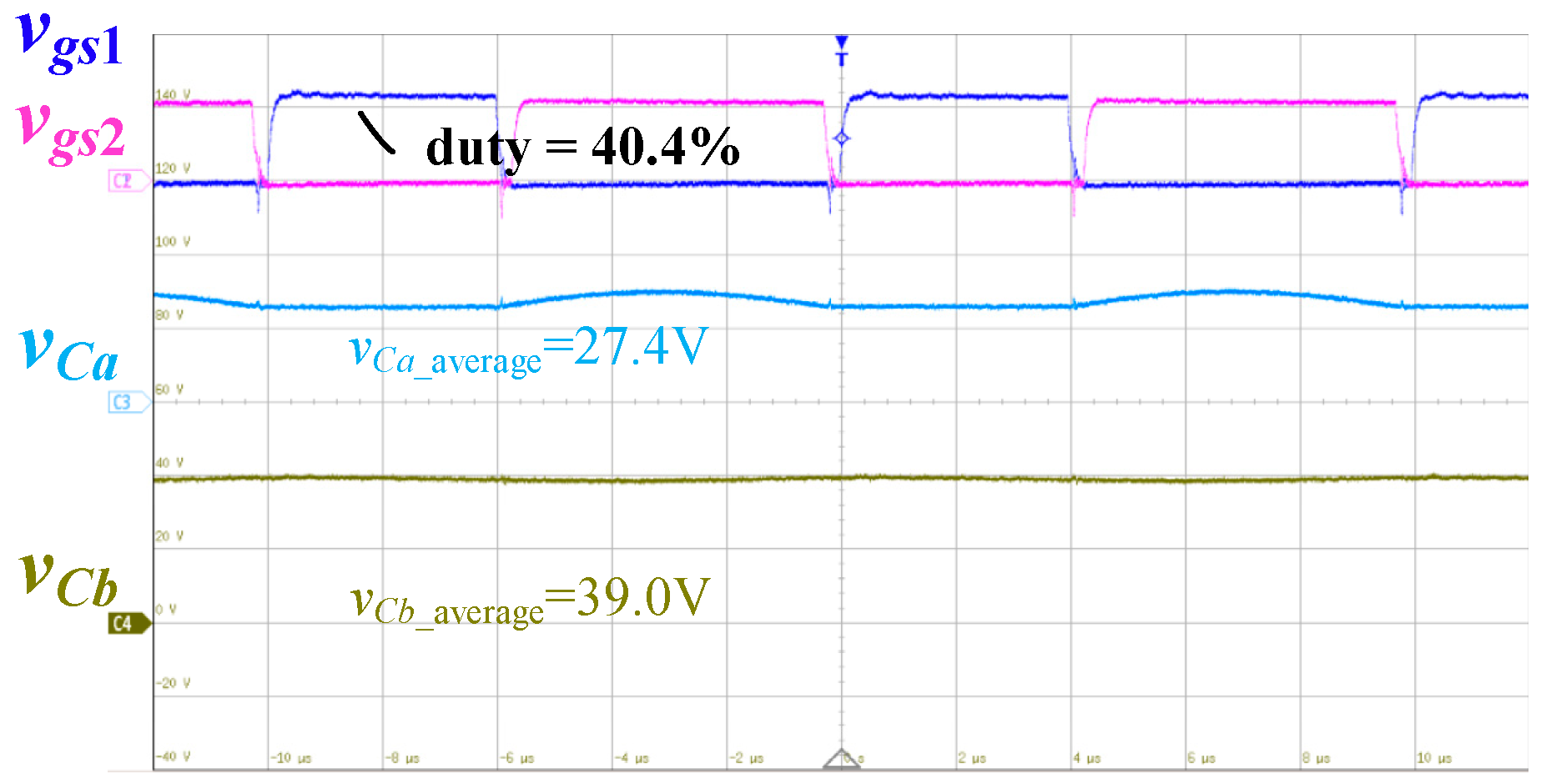
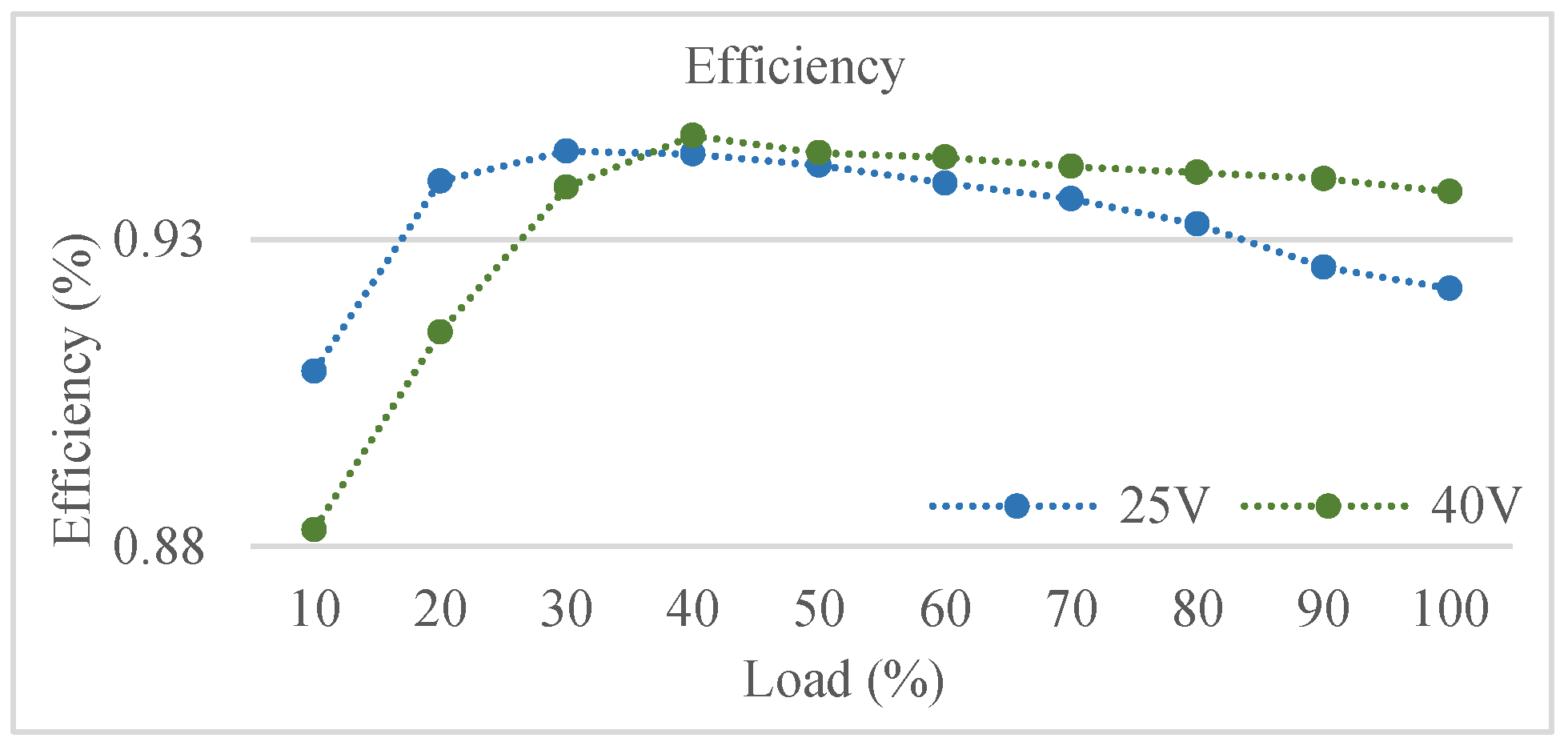
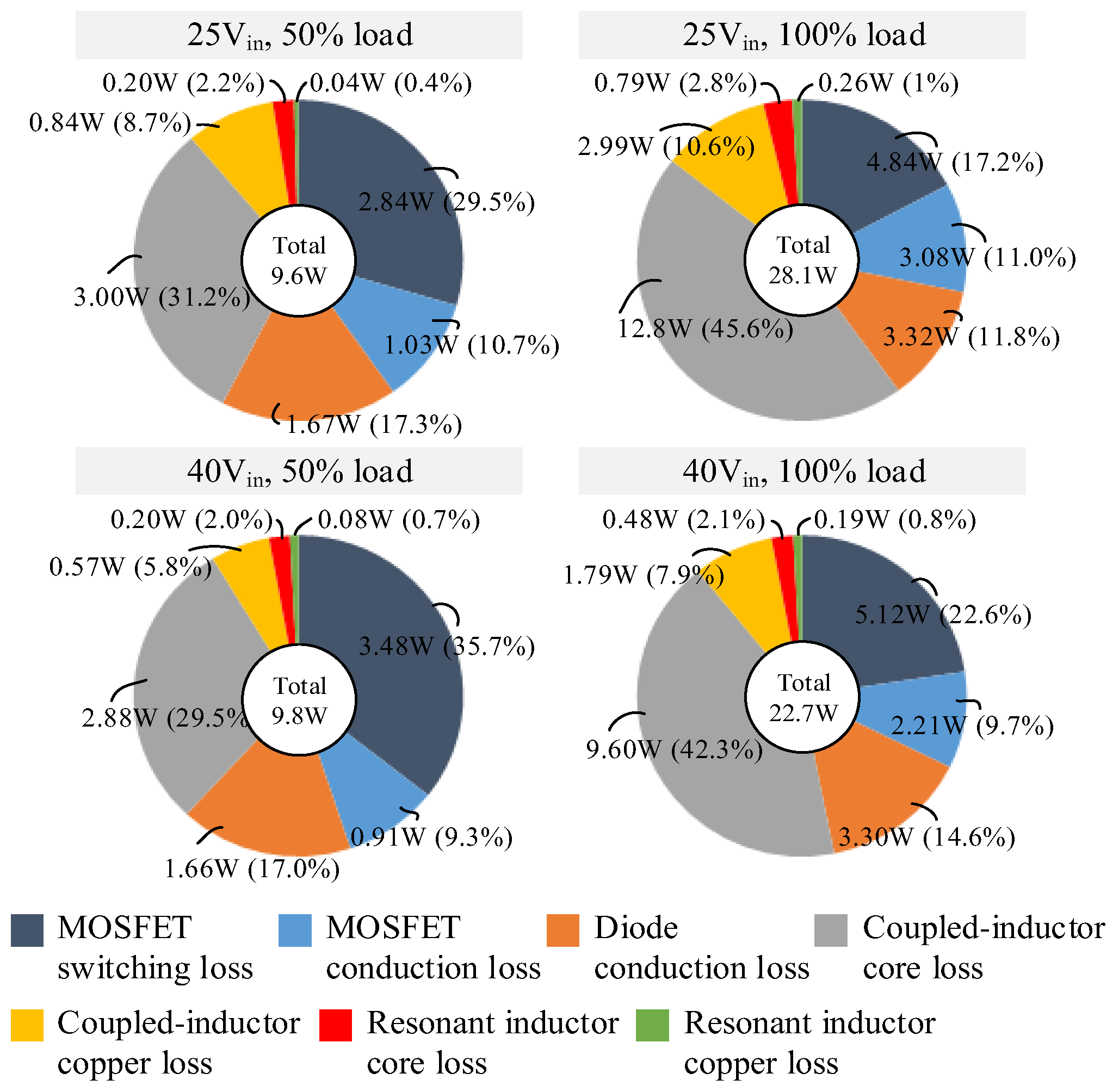
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aghdam, F.H.; Abapour, M. Reliability and cost analysis of multistage boost converters connected to PV panels. IEEE J. Photovolt. 2016, 6, 981–989. [Google Scholar] [CrossRef]
- Agorreta, J.L.; Reinaldos, L.; Gonzalez, R.; Borrega, M.; Balda, J.; Marroyo, L. Fuzzy switching technique applied to PWM boost converter operating in mixed conduction mode for PV systems. IEEE Trans. Ind. Electron. 2009, 56, 4363–4373. [Google Scholar] [CrossRef]
- Liu, J.; Wang, K.; Zheng, Z.; Li, C.; Li, Y. A dual-active-clamp quasi-resonant isolated boost converter for PV integration to medium-voltage DC grids. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 3444–3456. [Google Scholar] [CrossRef]
- Ma, G.; Qu, W.; Yu, G.; Liu, Y.; Liang, N.; Li, W. A zero-voltage-switching bidirectional dc–dc converter with state analysis and soft-switching-oriented design consideration. IEEE Trans. Ind. Electron. 2009, 56, 2174–2184. [Google Scholar]
- Ma, K.W.; Lee, Y.S. A novel uninterruptible dc-dc converter for UPS applications. IEEE Trans. Ind. Appl. 1992, 28, 808–815. [Google Scholar] [CrossRef]
- Kovatchev, E.; Evstatieva, N. Design of a digitally controlled boost converter for automotive headlamp applications. In Proceedings of the 2017 International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 13–15 September 2017; pp. 1–4. [Google Scholar]
- Gacio, D.; Calleja, A.J.; García, J.; Ribas, J.; Rico-Secades, M. Suitable switching converter topologies for automotive signal lamps and headlamps using power LEDs. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–7. [Google Scholar]
- Sreeja, P.; Suresh, L.P. Optimized design of ZVZCS switched non isolated DC-DC boost converter with high voltage gain. In Proceedings of the 2013 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Nagercoil, India, 20–21 March 2013; pp. 500–505. [Google Scholar]
- Barbi, I.; Gules, R. Isolated DC-DC converters with high-output voltage for TWTA telecommunication satellite applications. IEEE Trans. Power Electron. 2003, 18, 975–984. [Google Scholar] [CrossRef]
- Kiran, R.; Kalpana, R. Design and development of modular dual-input DC/DC step down converter for telecom power supply. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Akerlund, J. -48 V DC computer equipment topology-an emerging technology. In Proceedings of the INTELEC-Twentieth International Telecommunications Energy Conference (Cat. No. 98CH36263), San Francisco, CA, USA, 4–8 October 1998; pp. 15–21. [Google Scholar]
- Tofoli, F.L.; Pereira, D.D.C.; de Paula, W.J.; de Sousa Oliveira Júnior, D. Survey on non-isolated high-voltage step-up dc–dc topologies based on the boost converter. IET Power Electron. 2015, 8, 2044–2057. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, D.; Zhao, Z. Input/output current ripple cancellation and RHP zero elimination in a boost converter using an integrated magnetic technique. IEEE Trans. Power Electron 2015, 30, 747–756. [Google Scholar] [CrossRef]
- Vazquez, N.; Estrada, L.; Hernandez, C.; Rodriguez, E. The tapped-inductor boost converter. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 538–543. [Google Scholar]
- Ai, J.; Lin, M. Ultra large gain step-up coupled-inductor DC-DC converter with an asymmetric voltage multiplier network for a sustainable energy system. IEEE Trans. Power Electron 2017, 31, 6896–6903. [Google Scholar] [CrossRef]
- Tintu, V.R.; George, M. Tapped inductor technology based DC-DC converter. In Proceedings of the 2011 International Conference on Signal Processing, Communication, Computing and Networking Technologies, Thuckalay, India, 21–22 July 2011; pp. 747–753. [Google Scholar]
- Lee, J.J.; Cho, B.H. A novel high step-up zero-current-switching tapped-inductor boost converter. In Proceedings of the 8th International Conference on Power Electronics-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011; pp. 1869–1872. [Google Scholar]
- Berkovich, Y.; Axelrod, B. Switched-coupled inductor cell for DC–DC converters with very large conversion ratio. IET Power Electron. 2011, 4, 309–315. [Google Scholar] [CrossRef]
- Li, W.; He, X. Review of non-isolated high-step-up DC/DC converters in photovoltaic grid-connected applications. IEEE Trans. Ind. Electron. 2010, 58, 1239–1250. [Google Scholar] [CrossRef]
- Duarte, C.M.C.; Barbi, I. A Family of ZVS-PWM Active-Clamping DC-to-DC Converters: Synthesis, Analysis, Design, and Experimentation. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 698–704. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, W.; He, X. Single-phase improved active clamp coupled inductor-based converter with extended voltage doubler cell. IEEE Trans. Power Electron. 2012, 27, 2869–2878. [Google Scholar] [CrossRef]
- Hwz, K.I.; Yau, Y.T. High step-up converter based on coupling inductor and bootstrap capacitors with active clamping. IEEE Trans. Power Electron. 2014, 29, 2655–2660. [Google Scholar]
- Zhao, Q.; Lee, F.C. High-efficiency, high step-up DC-DC converters. IEEE Trans. Power Electron. 2003, 18, 65–73. [Google Scholar] [CrossRef]
- Van de Sype, D.M.; De Gusseme, K.; Renders, B.; Van den Bossche, A.R.; Melkebeek, J.A. A single switch boost converter with a high conversion ratio. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, 2005. APEC 2005, Austin, TX, USA, 6–10 March 2005; pp. 1581–1587. [Google Scholar]
- Hsieh, Y.P.; Chen, J.F.; Liang, T.J.; Yang, L.S. Novel high step-up DC–DC converter with coupled-inductor and switched-capacitor techniques. IEEE Trans. Ind. Electron. 2011, 59, 998–1007. [Google Scholar] [CrossRef]
- Liang, T.J.; Chen, S.M.; Yang, L.S.; Chen, J.F.; Ioinovici, A. Ultra-large gain step-up switched-capacitor DC-DC converter with coupled inductor for alternative sources of energy. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 864–874. [Google Scholar] [CrossRef]
- Spiazzi, G.; Mattavelli, P.; Costabeber, A. Effect of parasitic components in the integrated boost-flyback high step-up converter. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 420–425. [Google Scholar]
- Wai, R.J.; Lin, C.Y.; Duan, R.Y.; Chang, Y.R. High-efficiency DC-DC converter with high voltage gain and reduced switch stress. IEEE Trans. Ind. Electron. 2007, 54, 354–364. [Google Scholar] [CrossRef]
- Tseng, K.C.; Lin, J.T.; Huang, C.C. High step-up converter with three-winding coupled inductor for fuel cell energy source applications. IEEE Trans. Power Electron. 2014, 30, 574–581. [Google Scholar] [CrossRef]
- Hu, X.; Gong, C. A high voltage gain DC–DC converter integrating coupled-inductor and diode–capacitor techniques. IEEE Trans. Power Electron. 2013, 29, 789–800. [Google Scholar]
- Deng, Y.; Rong, Q.; Li, W.; Zhao, Y.; Shi, J.; He, X. Single-switch high step-up converters with built-in transformer voltage multiplier cell. IEEE Trans. Power Electron. 2012, 27, 3557–3567. [Google Scholar] [CrossRef]
- Chen, S.M.; Liang, T.J.; Yang, L.S.; Chen, J.F. A cascaded high step-up DC–DC converter with single switch for microsource applications. IEEE Trans. Power Electron. 2010, 26, 1146–1153. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. An efficient high-step-up interleaved DC–DC converter with a common active clamp. IEEE Trans. Power Electron. 2010, 26, 66–78. [Google Scholar] [CrossRef]
- Li, W.; Zhao, Y.; Deng, Y.; He, X. Interleaved converter with voltage multiplier cell for high step-up and high-efficiency conversion. IEEE Trans. Power Electron. 2010, 25, 2397–2408. [Google Scholar] [CrossRef]

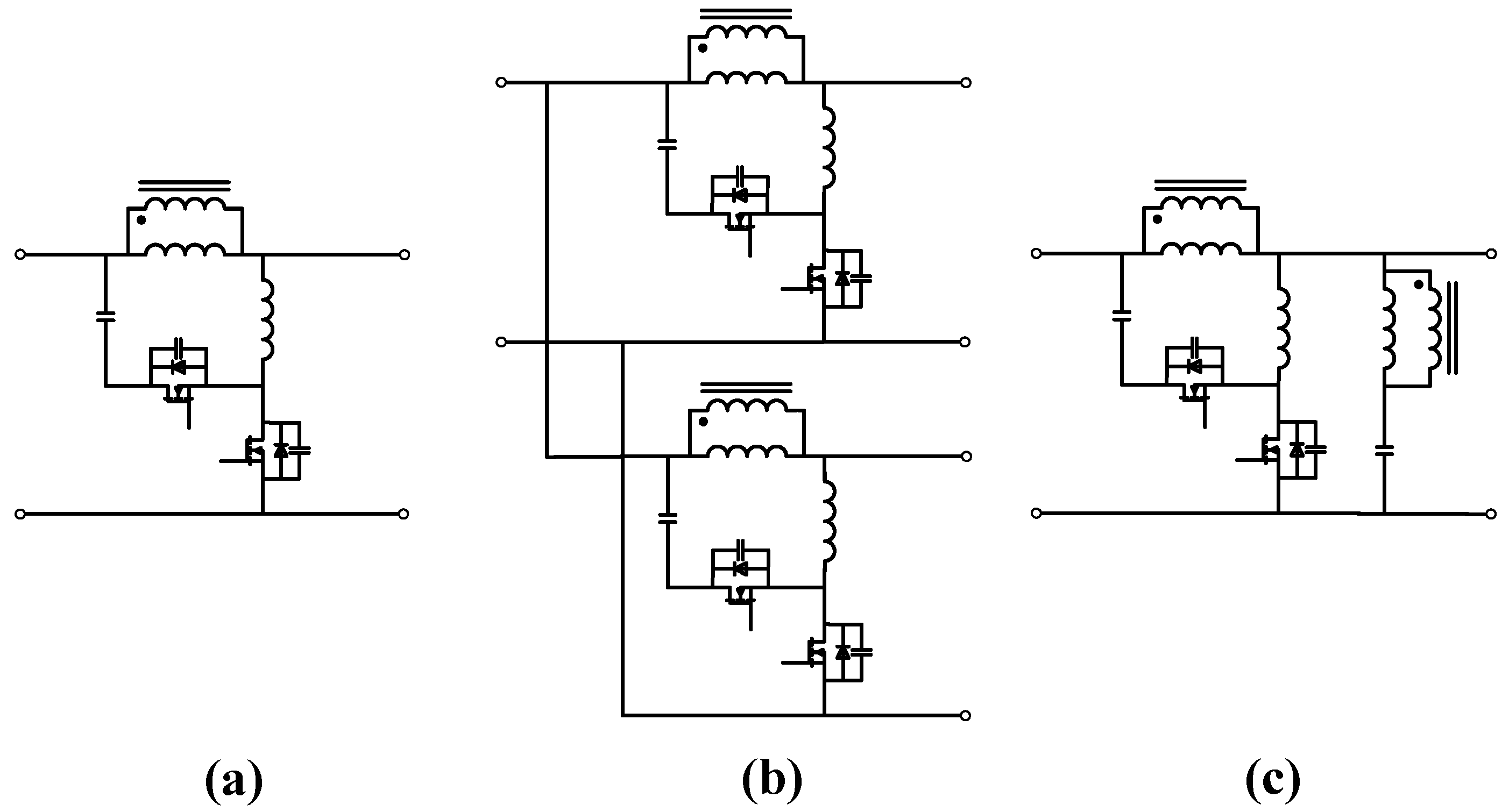





| Topologies | Propose Converter | [21] | [26] | [29] | [34] |
|---|---|---|---|---|---|
| Number of coupled inductors | 2 | 1 | 1 | 1 | 2 |
| Number of switches | 2 | 2 | 2 | 1 | 2 |
| Number of diodes | 1 | 2 | 4 | 4 | 4 |
| Voltage gain | |||||
| Control method | PWM | PWM | PWM | PWM | Interleave |
| Soft-switching performance | ZVS | ZVS | Hard switching | Hard switching | Hard switching |
| Input-current stress | Medium | High | High | High | Medium |
| Diode-voltage stress | High | High | Low | Low | Medium |
| Conduction losses | Low | High | High | High | High |
| Item | Value |
|---|---|
| 25–40 V | |
| 200 V | |
| 1.5 A | |
| 300 W | |
| 100 kHz |
| Item | Value |
|---|---|
| FDP2614 | |
| BYC200-600P | |
| Transformer turn ratio | 1:3 |
| Core material/type | PC 40/PQ35-35 |
| Item | Value |
|---|---|
| Resonant inductor Lr | 1 μH |
| Magnetizing inductance Lm | 15 μH |
| Parasitic capacitor Cr | 500 pF |
| Voltage-stable capacitor Ca | 66 μF |
| Clamping capacitor Cb | 8 μF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.-H.; Chen, C.-T.; Lin, Y.-F. Dual-Coupled-Inductor-Based High-Step-Up Boost Converter with Active-Clamping and Zero-Voltage Switching. Energies 2024, 17, 2018. https://doi.org/10.3390/en17092018
Chen S-H, Chen C-T, Lin Y-F. Dual-Coupled-Inductor-Based High-Step-Up Boost Converter with Active-Clamping and Zero-Voltage Switching. Energies. 2024; 17(9):2018. https://doi.org/10.3390/en17092018
Chicago/Turabian StyleChen, Sheng-Hua, Chuan-Ting Chen, and Yi-Feng Lin. 2024. "Dual-Coupled-Inductor-Based High-Step-Up Boost Converter with Active-Clamping and Zero-Voltage Switching" Energies 17, no. 9: 2018. https://doi.org/10.3390/en17092018
APA StyleChen, S.-H., Chen, C.-T., & Lin, Y.-F. (2024). Dual-Coupled-Inductor-Based High-Step-Up Boost Converter with Active-Clamping and Zero-Voltage Switching. Energies, 17(9), 2018. https://doi.org/10.3390/en17092018






