Online Distribution Network Scheduling via Provably Robust Learning Approach

Abstract

Distribution network scheduling (DNS) is the basis for distribution network management, which is computed in a periodical way via solving the formulated mixed-integer programming (MIP). To achieve the online scheduling, a provably robust learn-to-optimize approach for online DNS is proposed in this paper, whose key lies in the transformation of the MIP-based DNS into the simple linear program problem with a much faster solving time. It formulates the parametric DNS model to construct the offline training dataset and then proposes the provably robust learning approach to learn the integer variables of MIP. The proposed learning approach is adversarial to minor perturbation of input scenario. After training, the learning model can predict the integer variables to achieve online scheduling. Case study verifies the acceleration effectiveness for online DNS.

1. Introduction

To mitigate climate change, the power system supply relies on more renewable generation. However, the volatility and uncertainty of renewable resources pose new challenges to the distribution system management. So the increasing penetration of distributed generation resources in the distribution networks leads to the focus on effective, efficient, and economic operation of a distribution network. Distribution network scheduling (DNS) is the basic scheduling technology of the distribution network management based on optimization research theory. The mathematical form of DNS can be formulated as the mixed-integer programming (MIP) problem and computed repeatedly daily to support the safe and economic operation for distribution system operators [1]. To keep the system safe and economic, DNS is solved for different input scenarios to reach the proper system decisions repeatedly, where the upcoming scenario could be similar to the historical scenario. However, repeatedly solving MIP for DNS could be time-consuming and energy-wasting, because solving similar scenarios of DNS requires solving the corresponding MIP, which is intractable and time-consuming [2,3,4,5]. For MIP, due to the complex features of integer variables, current popular algorithms leverage the idea of branch and bound or benders cut, and the corresponding solution time is unstable. Compared to MIP, linear programming (LP) is more easy to solve due to its continuous variables and convex features, which could be treated as tractable with a stable solution time. The online LP solution is easier than the online MIP solution. So, to achieve the online scheduling via LP, this paper proposes predicting the integer variables of DNS and leveraging the advanced machine learning (ML) methods to learn from the historical solution of DNS for accelerating the similar new DNS scenario solution, which can achieve the online DNS. The key idea behind online scheduling lies in reducing the MIP to LP via ML for the effective distribution network scheduling.

There is growing interest in leveraging ML to advancing the solution of optimization models from the ML area, which is called learn-to-optimize. This area is attracting the interest from both machine learning areas and operation research areas, which can be categorized into two types: (1) learning the values of variables in the optimization models via complex ML models, (2) and learning part of values of variables in the optimization models via complex ML models. The dividing and neural branching neural networks are proposed in Ref. [6] to learn how to branch-and-bound more efficiently by reinforcement learning approaches. The DeepOPF model is proposed in Ref. [7] to learn the ACOPF results more efficiently. End-to-end optimization proxies are proposed in Ref. [8] to achieve a fast economic dispatch. Confidence-Aware Graph Neural Networks are further proposed in Ref. [7] to learn the system reliability for online reliability assessments. However, the above work focuses on the learning of optimization results. We focus on combining learning and optimization for tractable online DNS.

To achieve online DNS in a provably robust way, we propose the provably robust learn-to-optimize (PR-L2O) approach, whose key lies in the transformation of the MIP-based DNS problem into the tractable corresponding convex form, where convex problems are easier than MIP. Concretely, the parametric DNS model is first proposed to map the input DNS scenarios to the values of MIP integer variables, and the DNS training/testing datasets are sampled offline from the above offline model. In the model training process, the provably robust learning approach is utilized to learn and predict the integer variable values in a provably robust way, which is adversarial to the input scenarios difference. The benefits of the provably robust learning method lies in the better generalization to address the vulnerability of machine learning models. After learning, we predict the integer variables of MIP-based DNS and solve the reduced convex problems. Traditional methods solve the complex mixed-integer program of DNS directly, and in comparison, the proposed method utilizes the learning models to identify the values of integer variables in MIP-based DNS and solve the reduced easy linear programming problem.

We summarize the main contributions of this paper into two parts as follows: (1) Based on the MIP-based DNS model, this paper investigates the similarity of integer values in MIP and leverages the historical solutions to facilitate the upcoming solution for online scheduling. (2) Considering the vulnerability of learning model, the provable robust learning approach is proposed to learn the mapping between the scenario and integer variables based on the convex outer bound formulation of the input scenario difference perturbation, the dual network design, and provably robust loss function design. In summary, the proposed PR-L2O approach can achieve the solution acceleration and enhance the benefits of L2O due to data drift between training and testing datasets. The primary objective of this research is leveraging the machine learning models to enhance the solution of distribution network scheduling in a provably robust way. Compared to our previous works [9,10], this paper leverages the provably robust learning [11,12] to achieve the online regulation [13] with better generalization performance. In contrast, [9] focuses on unit commitment, and [10] focuses on online voltage regulation without provably robustness consideration.

The remainder of this paper is organized as follows. Section 2 presents the parametric DNS formulation. Section 3 proposes the PR-L2O approach for online DNS. Section 4 verifies the effectiveness of this paper by numerical simulation. Section 5 summarizes and concludes the total paper.

2. Parametric Distribution Network Scheduling Formulation

This section extends the conventional distribution network scheduling to the parametric distribution network scheduling (P-DNS) problem [14] and discusses the P-DNS solving process [15,16], which achieves the mapping from input scenarios to output decision via MIP in an implicit way [17]. The key of P-DNS lies in achieving the mapping from the parameters (load) to the optimal decisions via solving the corresponding scheduling optimization problems implicitly [18,19,20].

2.1. DNS Model

Traditional DNS models schedule the distributed energy resources with continuous and discrete variables to minimize the system operating cost in an optimized way, which is based on the prediction of uncertain parameters in the distribution network. DNS is usually formulated as a mixed-integer convex program (MICP) mathematically. Furthermore, commercial solvers can solve the formulated MICP problems to obtain the optimal decisions under the various constraints embedded within the advanced algorithms, such as the branch and bound (B&B) algorithm and bender algorithm.

However, the solving of MICP in DNS is intractable due to the complex features of integer variables. To tackle this problem, firstly, we consider formulating a basis DNS model under basic distribution networks with a set G of distributed generators, a set of B buses, and a set of L distribution lines. DNS models optimize the integer variables $s_{i,t}$ and continuous integer power variables $p_{g,t}$ for the T load-ahead scheduling time-step.

$$\begin{array}{cc}\hfill min& \sum _{g\in G}\sum _{t\in T}{f}_g(p_{g,t},s_{g,t})\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill s.t.& (p_{g,t},s_{g,t})\in {\mathcal{G}}_{g}g\in G\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill & \sum _{j\in \mathcal{J}\left(i\right)}{p}_{ij,t}-\sum _{h\in \mathcal{H}\left(i\right)}{p}_{hi,t}=p_{i,t}^{pv}-p_{i,t}^d,\forall i\in {\mathcal{N}}_{\mathcal{B}}\hfill \end{array}$$

(1c)

$$\begin{array}{cc}\hfill & \sum _{j\in \mathcal{J}\left(i\right)}{q}_{ij,t}-\sum _{h\in \mathcal{H}\left(i\right)}{q}_{hi,t}=q_{i,t}^{svr}+q_{i,t}^{cb}+q_{i,t}^{pv}-q_{i,t}^d,\forall i\in {\mathcal{N}}_{\mathcal{B}}\hfill \end{array}$$

(1d)

$$\begin{array}{cc}\hfill & V_{j,t}=V_{i,t}-\frac{r_{ij}{p}_{ij,t}+x_{ij,t}{q}_{ij,t}}{V_0},\forall ij\in {\mathcal{N}}_{\mathcal{L}}\hfill \end{array}$$

(1e)

$$\begin{array}{cc}\hfill & V_{min}\le V_i\le V_{max},i\in {\mathcal{N}}_{\mathcal{B}}\hfill \end{array}$$

(1f)

$$\begin{array}{cc}\hfill & V_{1,t}=V_{base,t}(r^{min}+\sum _s{r}_s{\sigma }_{s,t}^{oltc})\hfill \end{array}$$

(1g)

$$\begin{array}{cc}\hfill & {\sigma }_{m-1,t}^{oltc}\ge {\sigma }_m^{oltc},m\in [2,T_{max}^{oltc}]\hfill \end{array}$$

(1h)

$$\begin{array}{cc}\hfill & T_t^{oltc}=\sum _s{\sigma }_{s,t}^{oltc},T_t^{oltc}\le T_{max}^{oltc}\hfill \end{array}$$

(1i)

$$\begin{array}{cc}\hfill & T_t^{oltc}-T_{t-1}^{oltc}\ge {\sigma }_t^{oltc,in}-{\sigma }_t^{oltc,de}{T}_{max}^{oltc}\hfill \end{array}$$

(1j)

$$\begin{array}{cc}\hfill & T_{t-1}^{oltc}-T_t^{oltc}\le {\sigma }_t^{oltc,in}{T}_{max}^{oltc}-{\sigma }_t^{oltc,de}\hfill \end{array}$$

(1k)

$$\begin{array}{cc}\hfill & \sum _{t\in \mathcal{T}}({\sigma }_t^{oltc,in}+{\sigma }_t^{oltc,de})\le N_{max}^{oltc}\hfill \end{array}$$

(1l)

$$\begin{array}{cc}\hfill & {\sigma }_t^{oltc,in}+{\sigma }_t^{oltc,de}\le 1\hfill \end{array}$$

(1m)

$$\begin{array}{cc}\hfill & q_{i,t}^{cb}=q_{tap}{T}_{i,t}^{cb},i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1n)

$$\begin{array}{cc}\hfill & T_{i,t}^{cb}=\sum _s{\sigma }_{s,t}^{cb},T_t^{cb}\le T_{max}^{cb},i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1o)

$$\begin{array}{cc}\hfill & T_{i,t}^{cb}-T_{i,t-1}^{cb}\ge {\sigma }_{i,t}^{cb,in}-{\sigma }_{i,t}^{cb,de}{T}_{max}^{cb},i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1p)

$$\begin{array}{cc}\hfill & T_{t-1}^{oltc}-T_t^{cb}\le {\sigma }_t^{cb,in}{T}_{max}^{cb}-{\sigma }_t^{cb,de},i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1q)

$$\begin{array}{cc}\hfill & \sum _{t\in \mathcal{T}}({\sigma }_t^{cb,in}+{\sigma }_t^{cb,de})\le N_{max}^{oltc},i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1r)

$$\begin{array}{cc}\hfill & {\sigma }_t^{cb,in}+{\sigma }_t^{cb,de}\le 1,i\in {\mathcal{N}}_{\mathcal{CB}}\hfill \end{array}$$

(1s)

$$\begin{array}{cc}\hfill & {\left(p_i^{pv}\right)}^2+{\left(q_i^{pv}\right)}^2\le {\left(S_i^{pv}\right)}^2,i\in {\mathcal{N}}_{\mathcal{PV}}\hfill \end{array}$$

(1t)

$$\begin{array}{cc}\hfill & q_{i,min}^{svr}\le q_i^{svr}\le q_{i,max}^{svr},i\in {\mathcal{N}}_{\mathcal{SVR}}.\hfill \end{array}$$

(1u)

The key variables are defined for clear delivery. $p_{g,t}$ and $s_{g,t}$ are the power output and status of generation i in time t. Equations (1c)–(1e) formulate the linearized distflow model; Equations (1h)–(1u) formulate the operation of OLTC, CB and PV. The other detailed variables definitions are referred to in Ref. [1]. We unify the integer variables of (1) as $s_{dns}$ for simplicity.

2.2. P-DNS Model

Based on the DNS model, we formulate the parametric DNS (P-DNS) in a general form by (2). The P-DNS model achieves the mapping from the load demand d to the generator continuous power output varibles $p_g$ and binary decision variables $s_{dns}$ via the implicit MIP optimization model of DNS. We denote the system load as input parameters and replaces notation d with $\theta$.

$$\begin{array}{cc}\hfill f\left(\theta \right)=\underset{p,s}{min}& \sum _{g\in G}{f}_g(p_g,s_{dns};\theta )\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill s.t.& f_i(p_g,s_{dns};\theta )\le 0,i=1,\cdots ,m_f\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill & h_j(p_g,s_{dns};\theta )=0,i=0,\cdots ,m_h\hfill \end{array}$$

(2c)

$$\begin{array}{cc}\hfill & p_g\in {\mathbb{R}}^T,s_{dns}\in {\{0,1\}}^T.\hfill \end{array}$$

(2d)

Obviously, the binary variable $s_{dns}$ are more “complicated” but less changing than the continuous variables. Because (2) is reduced to a tractable convex problem with fixed-integer variables. To achieve online regulation, we propose to predict the integer variables of $s_{dns}^{*}$ based on the input parameters $\theta$ to achieve MIP-based DNS solution acceleration, as shown below in (3).

$$\begin{array}{cc}\hfill \hat{c}\left(\theta \right)=\underset{p_g}{min}& \sum _{g\in G}{c}_g(p_g;s_{dns}^{*},\theta )\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill s.t.& f_i(p_g;s_{dns}^{*},\theta )\le 0,i=1,\cdots ,m_f\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill & h_j(p_g;s_{dns}^{*},\theta )=0,i=0,\cdots ,m_h\hfill \end{array}$$

(3c)

$$\begin{array}{cc}\hfill & p_g\in {\mathbb{R}}^T\hfill \end{array}$$

(3d)

$$\begin{array}{cc}\hfill & s_{dns}^{*}\left(\theta \right)=f\left(\theta \right)\hfill \end{array}$$

(3e)

where $s_{dns}^{*}\left(\theta \right)$ refers to values of integer variables in the MIP-based DNS under $\theta$, denoted by policy; the $f(·)$ in (3e) is the learning model, which is called the policy identifier and learned from the historical solution dataset.

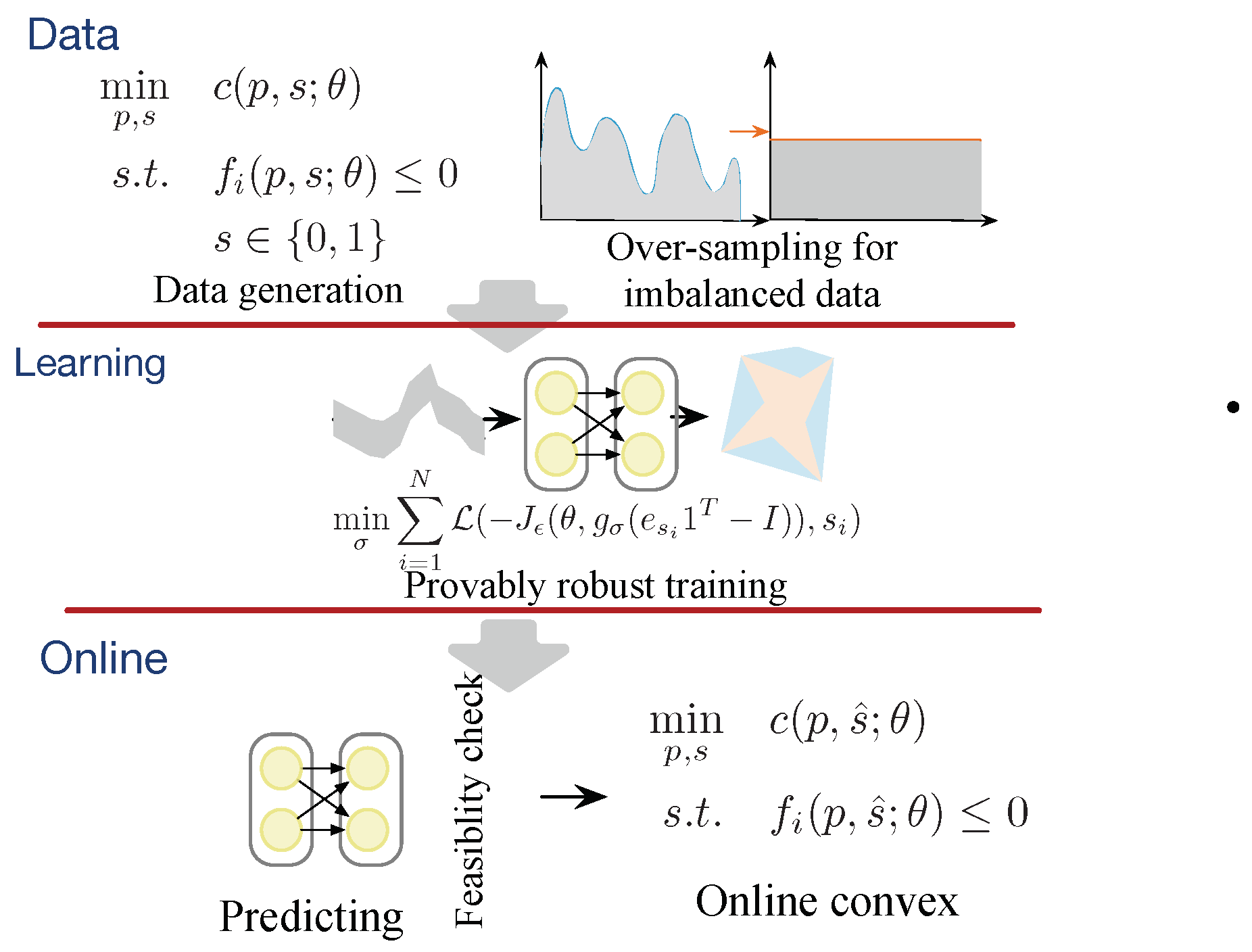
3. Provably Robust Distribution Network Scheduling

Based on the P-DNS formulation, the provably robust learn-to-optimize (PR-L2O) approach is introduced to identify the integer values of P-DNS in MIP-based DNS model, which is composed of data processing, PR-L2O learning and online implementation, as shown in Figure 1.

As shown above, (1) in the data stage, we leverage the P-DNS model of (2) to generate solution instances for different scenarios and construct the corresponding P-DNS dataset; and (2) in the learning stage, we leverage the neural networks to construct the policy identifier and leverage the P-DNS dataset to train the identifier in a provably robust way. In online stage, for an upcoming scenario, the trained identifier predicts the integer values from different groups, and the optimal decisions are obtained from the solving reduced model of (3a). Compared to the solution of MICP, the reduced tractable convex problem is much easier to solve and can satisfy the online solution form. It should be noted that due to vulnerability of machine learning models, the prediction results of machine learning models could be affected by input noise, and learning models should be trained to be adversarially robust to these noises. In our online DNS case, the training set could be similar but different from the upcoming instances. The integer variables from the prediction models should be robust to these minor differences via the proposed provably robust training process, based on the intuition that minor differences between the training and testing instances do not change the values of integer variables. Compared to the solution of the tractable convex problem, the solution of the mixed-integer program is much more complex due to the existence of integer variables. So we propose to utilize the learning models to identify the values of integer variables in MIP-based DNS, which transforms it into a tractable convex problem.

3.1. Provably Robust Learning Approach for Online DNS

Then, we go to the key of online DNS and leverage the provably robust learning approach, whose key lies in learning and predicting the integer variables in the model. The motivation behind the provable learning is that the upcoming scenarios may not be the same as the historical solutions, but they can feature similarity, which can be formulated as the input perturbation difference.

3.1.1. Motivation

Though the machine learning models feature a strong representational capacity, recent machine learning research demonstrates the prevalence of adversarial examples, where an adversarial example is a sample of input data which is modified very slightly in a way that is intended to cause a machine learning classifier to misclassify. It is called the “vulnerability” of machine learning models to the adversarial examples in real-life cases. To address the above vulnerability in learning the integer variables of P-DNS, a provably robust training approach for online DNS is proposed to learn the provably robust learning models, which achieve the provably robust feature. It means that the learning model can be adversarial to input scenario perturbation differences. The key of the perturbation robust model is the robust loss function, which can be derived from the convex outer bound formulation of the learning models under the input perturbation and dual network model.

3.1.2. Neural Networks for Online DNS

We leverage deep learning models to predict the integer variables of P-DNS of (2), where a k-layer neural networks then is formulated in (4) as follows:

$$\begin{array}{cc}\hfill {\hat{z}}_{i+1}& =W_{i,c}{z}_i+b_{i,c},\mathrm{for}i=1,\cdots ,k-1\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill z_i& =\mathrm{ReLU}\left({\hat{z}}_i\right),0,z_1=\theta ,{\hat{s}}_c={\hat{z}}_k\mathrm{for}i=2,\cdots ,k-1\hfill \end{array}$$

(4b)

where $W_{i,c}$ is the linear transformation matrix of layer i; $b_{i,c}$ is the bias of layer i; $z_i$ is the input neuron set of layer i; ${\hat{z}}_i$ is the output neuron set from the linear transformation; $\mathrm{ReLU}(·)$ is the activation function, which is defined as $max(·,0)$; $\theta$ refers to the input scenario of P-DNS; and ${\hat{s}}_c$ refers to the predicted integer variables in P-DNS, compared to the true integer variables of $s_c$.

From a further model, in a function form, the multi-layer neural network of (4) can be formulated in the $\hat{s}=I_{{\sigma }_c}\left(\theta \right)$. So ${\sigma }_c$ represents the set of ${\{W_{i,c},b_{i,c}\}}_{i\in \left[k\right]}$ in (4).

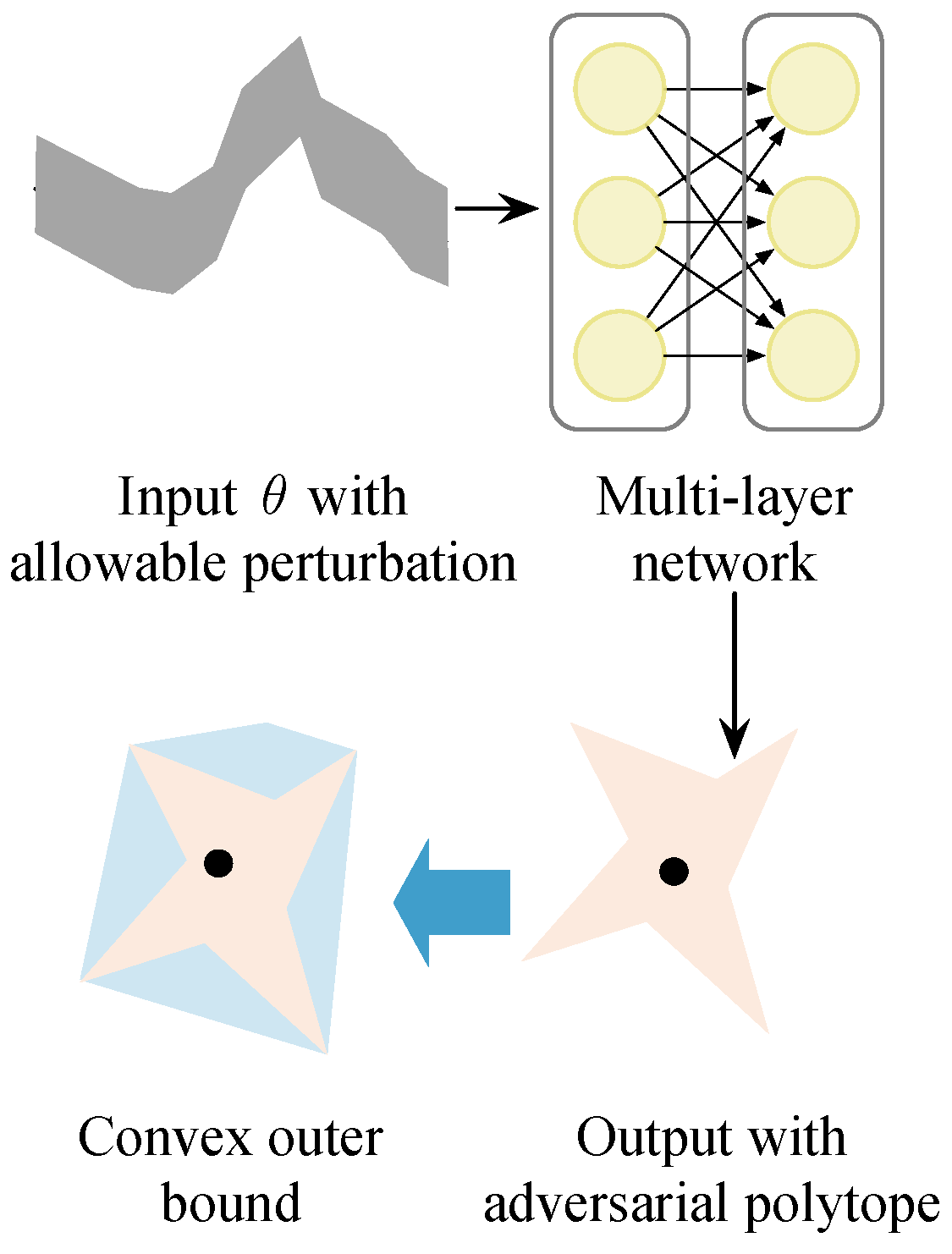
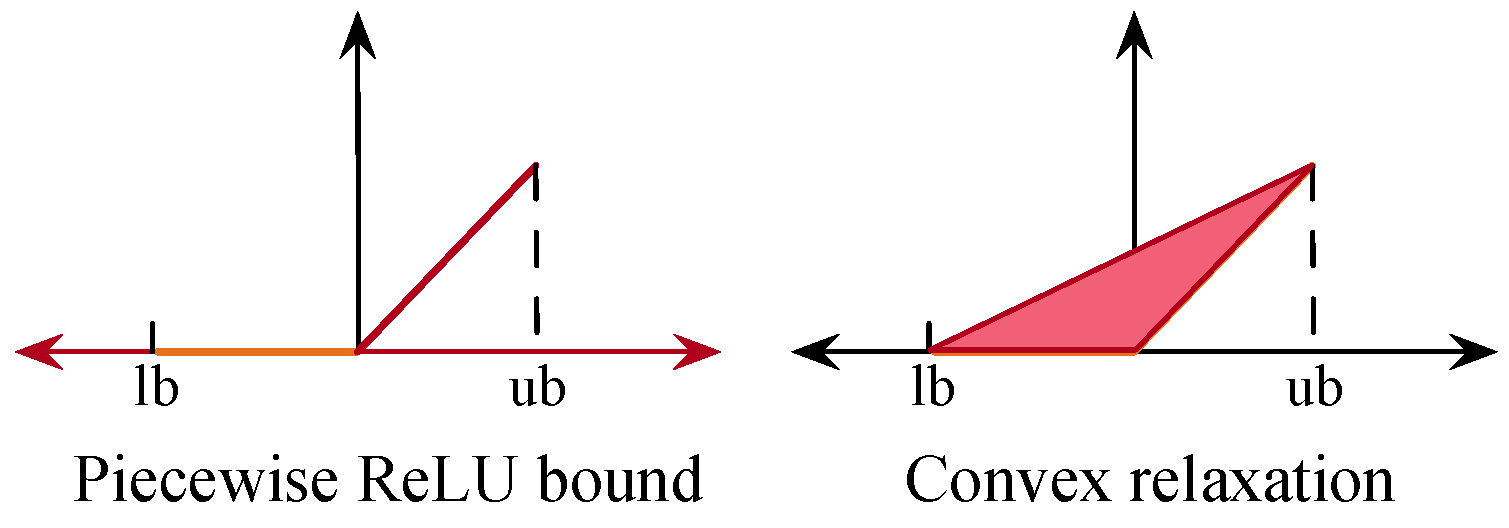
3.1.3. Convex Outer Bound Formulation of the Neural Network

Based on (4), we further perturb the input scenario $\theta$ by $\mathsf{\Delta }$ to construct the DNS input polytope of $\left|\right|\mathsf{\Delta }\left|\right|$ and further construct the output polytope in (5) as follows:

$$\begin{array}{c}\hfill {\mathcal{B}}_{ϵ}\left(\theta \right)=\{I_{\sigma }{(\theta +\mathsf{\Delta }):\left|\right|\mathsf{\Delta }\left|\right|}_{\infty }<ϵ\},\end{array}$$

(5)

where $ϵ$ is defined as the minor perturbation scale value, and ${\mathcal{B}}_{ϵ}\left(\theta \right)$ is the corresponding output adversarial polytope, which is highly non-convex as shown in the pink area of Figure 2.

It should be noted that the DNS input polytope ${\mathcal{B}}_{ϵ}\left(\theta \right)$ is a non-convex set as shown in Figure 2, which is hard to be optimized over for the robust results.

So we construct a convex outer bound over the convex set to approximate ${\mathcal{B}}_{ϵ}\left(\theta \right)$ by ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$, as shown in the extended blue, in Figure 2. Compared to ${\mathcal{B}}_{ϵ}\left(\theta \right)$, the relaxed ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$ occupies more area, indicating higher conservativeness. Not only the pink area but the extended area is considered. The benefits from the above transformation leads to the convex area of the output area. Convex features lead to good optimization quality, which is the basis of provably robust training.

The key of the above ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$ lies in the relaxation of the ReLU function in (4), which is shown in Figure 3. The ReLU activation function of (4) can be bounded by its upper envelope in the red area of Figure 3.

The above transformation formulation in Figure 3 can be further written mathematically in (6).

$$\begin{array}{cc}\hfill z_i& \le \frac{u_i(u_i-{\hat{z}}_i)}{u_i-l_i},\hfill \end{array}$$

(6a)

$$\begin{array}{c}\hfill z_i\ge {\hat{z}}_i,z_i\ge 0,\end{array}$$

(6b)

where $u_i$ is the set of upper bound in layer i, and $l_i$ is the set of lower bound in layer i.

Based on the upper envelope of (6) and the neural network model of (4), the ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$ of (5) can be further formulated via an explicit way in the following (7).

$$\begin{array}{c}\hfill {\hat{z}}_{i+1}=W_i{z}_i+b_i,\mathrm{for}i=1,\cdots ,k+1\end{array}$$

(7a)

$$\begin{array}{c}\hfill z_i\le \frac{u_i(u_i-{\hat{z}}_i)}{u_i-l_i},\mathrm{for}i=1,\cdots ,k+1\end{array}$$

(7b)

$$\begin{array}{c}\hfill z_i\ge {\hat{z}}_i,z_i\ge 0,\mathrm{for}i=1,\cdots ,k+1\end{array}$$

(7c)

$$\begin{array}{c}\hfill z_1=\theta +\mathsf{\Delta },\hat{s}={\hat{z}}_k{,\left|\right|\mathsf{\Delta }\left|\right|}_{\infty }<ϵ\end{array}$$

(7d)

3.1.4. Robust Optimization in Online DNS via Dual Neural Network

Based on the upper envelope of ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$, we leverage the idea of robust optimization to the prediction robustness of prediction models, which means that the worst prediction from the ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$ will not lead to misclassification. The above intuition can be further written as the following linear programming in (8).

$$\begin{array}{c}\hfill \underset{{\hat{z}}_k}{min}{\left({\hat{z}}_k\right)}_{s^{*}}-{\left({\hat{z}}_k\right)}_{s^{tar}}=c_{s^{*}}^T\hat{s}\end{array}$$

(8a)

$$\begin{array}{c}\hfill s.t.{\hat{z}}_k\in {\hat{\mathcal{B}}}_{ϵ}\left(\theta \right)\end{array}$$

(8b)

$$\begin{array}{cc}\hfill & c=e_{s^{*}}-e_{s^{tar}}\hfill \end{array}$$

(8c)

where $e_{(·)}$ represents the category of the strategies. If the objectives under all perturbed predictions are positive, the prediction model can achieve the provably robust under various scenario perturbation difference.

For all possible predictions in ${\hat{\mathcal{B}}}_{ϵ}\left(x\right)$, the corresponding LPs are too many. So we consider the worst prediction by leveraging the dual problem of the original LP from the robust optimization perspective, where dual problems of LPs provide the lower bound of the original LP. The dual problems of multi-layer neural network are formulated as the maximum problem in (9).

$$\begin{array}{cc}\hfill \underset{\alpha }{max}& J_{ϵ}(\theta ,g_{\sigma }(c,\alpha ))\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill s.t.& {\alpha }_{i,j}\in [0,1]\forall i,j\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill \mathrm{where}{J}_{ϵ}(\theta ,v)=& -\sum _{k=1}^{k-1}{v}_{i+1}^T{b}_i-{\theta }^T{\hat{v}}_1-ϵ\left|\right|{\hat{v}}_1{\left|\right|}_1\hfill \end{array}$$

(9c)

$$\begin{array}{cc}\hfill & +\sum _{i=2}^{k-1}\sum _{j\in {\mathcal{L}}_i}{l}_{i,j}{\left[v_{i,j}\right]}_{+}.\hfill \end{array}$$

(9d)

Ref. [11] considers the above dual problems via the dual neural network in $g_{\theta }(c,\alpha )$ and obtain the corresponding lower bound from the output of the dual neural network. So the corresponding dual neural network is formulated in (10).

$$\begin{array}{cc}\hfill v_k& =-c\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill {\hat{v}}_i& =W_i^T{v}_{i+1},\mathrm{for}i=k-1,\cdots ,1\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill v_{i,j}& =\left\{\begin{array}{cc}0\hfill & j\in {\mathcal{L}}_i^{-}\hfill \\ {\hat{v}}_{i,j}\hfill & j\in {\mathcal{L}}_i^{+}\hfill \\ \frac{u_{i,j}}{u_{i,j}-l_{i,j}}{\left[{\hat{v}}_{i,j}\right]}_{+}-{\alpha }_{i,j}{\left[{\hat{v}}_{i,j}\right]}_{-}\hfill & j\in {\mathcal{L}}_i\hfill \end{array}\right.\hfill \end{array}$$

(10c)

We note that ${\mathcal{L}}_i^{-}$, ${\mathcal{L}}_i^{+}$, and ${\mathcal{L}}_i^{+}$ refer to the set of activation functions with negative, both positive, or span zero bounds.

3.1.5. Provably Robust Training of Learning Models for Online DNS

Based on the dual neural network for worst prediction, the provably robust loss function is further designed to train neural networks in the provably robust way, which is called the provably robust neural network and adversarial to input perturbation difference. The key of the provably robust learning model lies in the provably robust learning. The key of provably robust learning lies in the provably robust learning loss function design. The key of the provably robust loss function lies in that it measures the difference between the worst prediction and the true prediction to achieve the robustness, as shown in (11).

$$\begin{array}{c}\hfill \underset{\theta }{min}\sum _{i=1}^N\underset{{\left|\right|\mathsf{\Delta }\left|\right|}_{\infty }<ϵ}{max}\mathcal{L}(f_{\theta }({\theta }_i+\mathsf{\Delta }),s_i).\end{array}$$

(11)

The above problem is a typical robust optimization in the min-max form, which is hard to optimize directly. So we consider the dual form of the inner optimization problem in the form of the minimization problem, leading to the minimization of the whole problem. Based on the above intuition, the corresponding dual minimizing problem of inner maximum problem is formulated in (12) as follows:

$$\begin{array}{c}\hfill \underset{{\left|\right|\mathsf{\Delta }\left|\right|}_{\infty }\le ϵ}{max}\mathcal{L}(f_{\sigma }(\theta +\mathsf{\Delta }),s)\le \mathcal{L}(-J_{ϵ}(\theta ,g_{\sigma }(e_s{1}^T-I)),s).\end{array}$$

(12)

The dual problem in the minimization form formulates the upper bound of the primal maximization problems, leading to the provably robust training approach with conservative guarantee. So, further, the provably robust loss function is further transformed into (13) with a single layer.

$$\begin{array}{c}\hfill \underset{\sigma }{min}\sum _{i=1}^N\mathcal{L}(-J_{ϵ}(\theta ,g_{\sigma }(e_{s_i}{1}^T-I)),s_i).\end{array}$$

(13)

The corresponding dual problem results can be formulated by the dual neural networks of (10). So (13) can be minimized via the current stochastic gradient descent algorithms from the state-of-the-art autograd optimizer. We leverage the dual neural networks to achieve the minimization of provably robust loss by tuning the corresponding neural network parameters. The trained neural networks can predict the integer variable values for online DNS in a provably robust way. Based on the above, the total training process can be summarized by the following process: (1) generate proper dataset with mapping from input scenarios to optimal integer variables; (2) separate the total dataset into the training and testing part; (3) sample mini batches from the total dataset, calculate the robust loss function of (13), derive the corresponding gradients to update the parameters of neural networks; (4) training until convergence; and (5) evaluate the performance of learning models in testing to verify the generality of the proposed approach. The following case study verifies the effectiveness of the proposed approach for online DNS from acceleration and economy perspectives.

4. Case Study

We conduct a case study to verify the effectiveness of the online DNS by simulation on IEEE 123-bus systems from the perspectives of training analysis and online performance analysis. All models are written by Python 3.8; in particular, for the learning part, the neural networks are coded by the Pytorch package to formulate the machine learning models and robust loss function; and, for the optimization part, the corresponding P-DNS models are coded by the Cvxpy package to formulate the distribution network scheduling models. The total learning and optimization parts construct the total online distribution network scheduling models. The organization of this section is composed of the following parts: data sampling, simulation analysis, and discussion.

4.1. Data Sampling

Data are the basis of learning models, and the data sampling technique is the basic technique to learn the proper mapping relationship. For online DNS, we propose to learn the mapping relationship from the input scenarios to the values of integer variables in DNS models. So the uncertain temporal load profile is taken as the parameter of (2) as “X”, and the corresponding MICP of DNS is solved to obtain the values of integer variables, as “Y”. On top of that, we combine the “X” and “Y” to generate offline training dataset for learning models for the training process.

We first formulate the base load profile as $D_{base}\in R^{N_b\times T}$; then, we generate the corresponding whole dataset from the uniform distribution by (14) from the lower bound $0.6d_{base,ij}$ and higher bound $1.4d_{base,ij}$. The whole dataset can be further divided into training and testing datasets.

$$\left\{D\right|d_{ij}\sim U(0.6d_{base,ij},1.4d_{base,ij}),i\in \left[N_b\right]j\in \left[T\right]\},$$

(14)

where $\left[N_b\right]$ is the set of power system buses; $\left[T\right]$ is the set of scheduling time, which could be set as different values for different scheduling types, such as intraday look-ahead scheduling and day-ahead scheduling.

4.2. Experiment Results

We verify the effectiveness of the PR-L2O for online DNS on the case 123-bus system from the training analysis and solution analysis perspectives in this part. The corresponding renewable data can refer to [21].

The proposed provably robust loss (13) is compared with the conventional cross-entropy loss in (15) to verify its robustness.

$$\begin{array}{c}\hfill {\mathcal{L}}^{ce}(\theta ,s)=-\frac{1}{M}\sum _{k=1}^K\sum _{m=1}^M{s}_m^{k}log\left(f_{\sigma }\left(x_m\right)\right)\end{array}$$

(15)

We note that M is the number of training samples, K is the number of possible classes, and $s_m^k$ is the true policy for m instance for k class. We denote the model under (15) as the learn-to-optimize (L2O) model.

4.2.1. Training Analysis

After data processing, Figure 4 compares the changing of robust loss under PR-L2O and L2O; Figure 5 further compares the cross-entropy (CE) loss under PR-L2O and L2O.

Though with higher CE loss, the proposed robust-based learning features high CE. In contrast, though with lower CE, the conventional learning method feature higher robust loss especially with training number growth. This demonstrates the vulnerability of the conventional learning method, which means the prediction results from conventional learning could make the wrong prediction from the minor difference between the training instances and testing instances. This vulnerability could further lead to the suboptimality of reduced models, and the following part further verifies the deficiency.

4.2.2. Online DNS Performance Analysis

After training, the learning models can predict the hard integer variables of P-DNS, and the optimal decisions can be obtained from the reduced tractable convex problems. For the solution time perspective, we compare the solution time of PR-L2O, L2O and B&B. B&B means the solution of complex mixed-integer programming via commercial solvers directly in the following Figure 6.

PR-L2O and L2O features less and more stable solution time, compared with B&B, because B&B is a search algorithm in essence.

After the figure analysis, the mean, variance and maximum solving time are further analyzed in

Table 1. Solution time comparison of B&B, L2O and PR-L2O in the 123-bus system.

Models	B&B	L2O	PR-L2O
Mean	1.207 s	0.0149 s	0.0110 s
Maximum time	1.383 s	0.0182 s	0.0179 s

in the case 123-bus system.

The learning-based methods achieve 77.3 times faster maximum solving time and 109.7 times faster mean solving time than B&B, which satisfies the requirement of online DNS.

The solution optimality of the above three approaches is analyzed in

Table 2. Performance comparison of B&B, L2O and PR-L2O in the 123-bus system.

	B&B	L2O	PR-L2O
Mean gap	0%	0.141%	0.110%
Maximum gap	0%	1.87%	0.72%
Operation cost	$225.610	$224.675	$224.352

. This comparison takes the B&B as the benchmark with zero gaps, which leverages the metrics of the mean and maximum gap for numerical analysis. L2O achieves the mean gap of 0.141%, the maximum gap of 1.87% and average cost of $224.675; the proposed PR-L2O achieves the mean gap of 0.110%, the maximum gap of 0.72%, and average cost of $224.352. From Table 2, PR-L2O achieves a lower mean and maximum gap than L2O. Obviously, the prediction performance of PR-L2O features high benefits with the consideration of provable robustness. More robustness prediction leads to lower operation of online operation. The above demonstrate the generalization performance of the PR-L2O and proper policy identification by considering the input perturbation difference for online regulation. Traditional methods solve the complex mixed-integer program of DNS directly; and in comparison, the proposed method utilizes the learning models to identify the values of integer variables in MIP-based DNS and solve the reduced easy linear programming problem. The proposed approach achieves a high solution speed, verifying the effectiveness of the proposed learn-to-optimize approach.

4.3. Discussion

Based on the above analysis, we have two key results: (1) Predicting the integer variables can accelerate the solving process of the distribution network scheduling by reducing the complex MICP to simple CP, and the solution time is proper for online setting. The results conform to our assumptions. (2) Considering the vulnerability of machine learning models, leveraging the robust loss function in training learning models can enhance the economy of online DNS performances, because the learning models can make more proper decisions by considering the difference between the training scenarios and testing scenarios. The results also conform to our assumptions. In summary, the proposed PR-L2O approach can achieve the solution acceleration and enhance the benefits of L2O due to data drift between training and testing dataset.

5. Conclusions

To achieve the online DNS, this paper proposes the PR-L2O approach to learn and predict the integer variables of the MIP-based DNS problem. To address the vulnerability of the learning model, the PR-DNS training approach is leveraged to train the policy identifier, which is adversarial to the input difference perturbation in a provably robust way. The case study verifies the better performance in the test dataset and acceleration performance of PR-L2O. Future work may consider the further exploration and exploitation of history solution results for enhancing future model solutions in various ways.