Abstract
In response to increasingly stringent emissions regulations and the depletion of conventional fuel sources, integrating carbon-free fuels into the transport sector has become imperative. While hydrogen (H2) presents significant technical challenges, ammonia (NH3) could present a better alternative offering ease of transport, storage, and distribution, with both ecological and economic advantages. However, ammonia substitution leads to high emissions of unburned NH3, particularly at high loads. Combustion chamber retrofitting has proven to be an effective approach to remedy this problem. In order to overcome the problems associated with the difficult combustion of ammonia in engines, this study aims to investigate the effect of the piston bowl shape of an ammonia/diesel dual fuel engine on the combustion process. The primary objective is to determine the optimal configuration that offers superior engine performance under high load conditions and with high ammonia rates. In this study, a multi-objective optimization approach is used to control the creation of geometries and the swirl rate under the CONVERGETM 3.1 code. To maximize indicated thermal efficiency and demonstrate the influence of hydrogen enrichment on ammonia combustion in ammonia/diesel dual fuel engines, a synergistic approach incorporating hydrogen enrichment of the primary fuel was implemented. Notably, the optimum configuration, featuring an 85% energy contribution from ammonia, outperforms others in terms of combustion efficiency and pollutant reduction. It achieves over 43% reduction in unburned NH3 emissions and a substantial 31% improvement in indicated thermal efficiency.
1. Introduction
The continuing reduction in available fossil fuels, and the severe environmental impact of emissions from internal combustion engines (ICE) [1], have preoccupied the global community for decades [2]; today, the need for action is more urgent than ever. One of the most widely discussed solutions is the transition to carbon-free fuels such as ammonia (NH3) [3]. Moreover, given the promising characteristics of dual fuel engine technology [4], using this fuel in these engines is emerging as one of the best alternatives to conventional combustion engines.
In general, ammonia has a well-established storage and distribution infrastructure [5], high octane rating, and high ignition energy [6], which guarantees a high level of safety regarding explosion risk. The real problem with this fuel is its low reactivity, which results in relatively difficult combustion [7], penalizing engine efficiency and aggravating NOx and N2O emissions [8]. It is a major problem that has captured the interest of various researchers in the field.
The subject of exploring the use of ammonia as a primary fuel in ICE is approached in the literature from two main angles: experimental and numerical.
In a conducted experimental investigation, Reiter and King [9] explored the utilization of ammonia as a fuel in a compression-ignition engine. They employed a dual-fuel strategy, where ammonia was introduced into the intake manifold. The results show that an optimum combination of diesel and ammonia achieves maximum engine torque, with an energy replacement of up to 95%. The incorporation of ammonia consistently diminishes CO2 emissions. Furthermore, despite the existence of fuel-bound nitrogen, NOx emissions remain at low levels, provided that the substitution of energy by ammonia does not surpass 60%. In another work, the same authors extended their research using the same experimental procedure [10]. They confirmed the existence of an optimum range of 40–60% diesel energy with 60–40% ammonia energy for constant power and maximum energy efficiency. According to their results, CO and hydrocarbon emissions are generally higher compared to pure diesel, while NOx emissions vary with fuel combinations. This is in line with the results of Guo et al. [11] and Ramachandran et al. [12].
Gross and Kong [13] used dimethyl ether (DME) and ammonia as pilot and primary fuels, respectively. The results show that ammonia causes longer ignition delays, with increased emissions of CO, HC, and NOx. Improvements are observed with increasing injection pressure, and ammonia emissions remain reduced, with extremely low soot emissions. The effect of the nature of the pilot fuel has been extensively explored, where biodiesel is used [14]. The results indicate that 69.4% of the biodiesel’s energy can be replaced by ammonia, although increasing the ammonia flow rate slightly reduces thermal efficiency. Increased ammonia contribution reduces CO2, CO, and HC emissions, but increases NO emissions. In addition, ammonia delays the onset of combustion due to low temperature and resistance to auto-ignition, but combustion time is reduced compared to biodiesel alone.
The percentage of energy replacement of pilot fuel by ammonia was pushed up to 84.2% as reported by Wang et al. [15] in their study. The authors showed that increasing the energy content of ammonia changes the mode of combustion, influencing the duration and auto-ignition delay. Although ammonia reduces CO2, CO, and particulate emissions, it increases NOx and unburned ammonia emissions. The authors found that the best compromise between reducing all emissions can be achieved by replacing diesel with 35.9% ammonia, despite the production of N2O. To optimize the energy yield from ammonia, Chen et al. [16] investigated the application of aqueous ammonia in a dual-fuel engine. Three percentages of ammonia supplementation were studied, showing a reduction in combustion pressure and heat release, but also a significant reduction in NOx (up to 61.75%) and soot (up to 51.04%) emissions due to the replacement of diesel by a carbon-free fuel, despite a reduction in engine performance.
On the other hand, using numerical tools, Li et al. [17] assessed the impact of ammonia as a fuel in ICE, highlighting the risk of increased NOx and N2O emissions. Simulations indicate that high concentrations of N2O can occur during ignition, particularly with high levels of ammonia energy. N2O emissions remain low in fully burned mixtures, with minimal fuel dependence. The concentration of soot decreases as the carbon content in the fuel decreases. Additionally, lower levels of NOx and N2O emissions are observed in fuel-rich regimes and under conditions of complete combustion. According to Xu et al. [18], a 24% replacement by ammonia enabled efficient operation, significantly reducing greenhouse gas emissions despite the challenges of ammonia’s flame propagation speed and increased nitrogen oxide emissions. The recommendations proposed by the authors are focused on enhancing operating conditions and injection strategies, leading to notable reductions in CO emissions. The outcomes include a substantial 60% decrease in total greenhouse gas emissions and an impressive 89% reduction in CO2 emissions when compared to a natural gas/diesel dual fuel engine.
Aiming for higher ammonia utilization rates, numerical results from Xu and Bai [19] show efficient operation where 50% of energy comes from ammonia, with slightly higher NO emissions compared to diesel. The authors found that adding hydrogen improves ammonia combustion, but worsens NO emissions. They also demonstrated that unburned ammonia comes mainly from areas near the cold wall, which is justified by flame extinction [20,21]. The trade-off between reducing all emissions for dual fuel operation with ammonia is confirmed by Rodríguez et al. [22]. Within their study, a multi-criteria analysis is suggested to identify the optimal proportion of ammonia, considering the environmental impact stemming from various pollutants. Due to the substantial adverse effects associated with NOx and N2O emissions, it is determined that a maximum proportion of 20% ammonia in the fuel represents the most suitable choice to mitigate detrimental environmental consequences.
The results confirm without exception the challenge of using ammonia as a primary fuel in dual fuel engines. Its combustion nature, linked to its low flame propagation speed, penalizes engine efficiency and affects emissions of NOx, N2O, and unburned NH3, which are directly linked to incomplete combustion. Because of this obstacle, it is clear that most of the presented work recommends the use of low percentages of ammonia to get around the problems caused by difficult combustion [23].
In order to take advantage of decarbonized combustion with ammonia, other research has tried to find solutions to improve ammonia combustion. Shafiq and Omar [24] employed hydrogen peroxide as an ignition promoter to facilitate the utilization of ammonia. The results showed a significant increase in indicated engine power and torque, as well as a dramatic reduction in NOx emissions. This approach holds the potential to expedite the decarbonization of intensive applications, particularly in the case of trucks. However, further research is necessary to thoroughly evaluate its feasibility and limitations.
The injection strategy for either pilot fuel or ammonia is widely considered in the literature. In a study conducted by Tay et al. [25], primary and secondary heat release peaks are observed with advancing injection timing, which is attributed to the combustion of fuel residues near the cylinder. Replacing diesel with kerosene increases the primary peak of heat release with advancing injection timing.
In a study performed by Shin et al. [26], the impact of ammonia and diesel injection timing was investigated. The results demonstrated that an injection timing of −7 °CA for ammonia and −15 °CA and −10 °CA for diesel led to an 8% improvement in efficiency, a reduction of up to 13.5% in NO emissions, and a decrease of approximately 91% in greenhouse gas emissions compared to conventional diesel operation. Furthermore, the level of unburned ammonia was reduced by 58.4%, indicating a significant enhancement over pre-mixed ammonia combustion. The same authors implemented a similar study [27] to explore diesel injection timing alone, considering ammonia energy fractions from 40% to 90%. Advancing injection timing showed up to 11% more efficient combustion compared with diesel operation, although nitrogen oxide emissions increased with increasing ammonia energy fraction and advancing injection timing. In an alternative approach, Liu et al. [28] studied the possibility of improving ammonia/diesel dual fuel engine efficiency by incorporating a precombustion chamber. The study revealed a notable improvement in thermal efficiency by 7.2% compared to the basic configuration, accompanied by low ammonia emissions.
The presented results still confirm the necessity of using low ammonia levels to avoid any problems linked to the flame propagation speed which characterizes ammonia combustion. In addition, most research focuses on exploring the injection law to improve combustion, utilizing engine configurations very close to the conventional diesel configuration, which has an insufficient effect given the difficult nature of ammonia combustion.
With its significant decarbonization potential, particularly in large engines, ammonia emerges as a promising alternative fuel. However, harnessing its benefits presents challenges due to its unique properties that make combustion difficult. For this reason, a multi-objective approach is essential to optimize the combustion chamber of large dual fuel engines running on high concentrations of ammonia.
The present work aims to adapt the shape of the combustion chamber bowl and the swirl rate in the cylinder to improve internal turbulence, which has a more direct effect on flame propagation speed. This approach is controlled by the creation of an ANN meta-model, linking driving performance and emissions with the swirl rate and geometric parameters controlling the bowl shape, and multi-objective optimization in a parallel fashion, aimed at maximizing indicated thermal efficiency, maximizing combustion efficiency, and minimizing NOx emissions. The various numerical results were used to characterize turbulence in the combustion chamber and explain its influence on combustion enhancement. Once the optimum geometry has been obtained, the influence of enriching the air-ammonia mixture with small percentages of hydrogen is tested, to understand the phenomenology of combustion under these conditions, and consider ways of boosting the ammonia/diesel dual fuel engine to its most optimal operation.
Consequently, the main contributions of the present study can be summarized as follows:
- The implementation of a new configuration for a combustion chamber dedicated to large ammonia/diesel dual fuel engines, featuring high ammonia participation rates. This optimal configuration is the result of a multi-objective optimization aimed at improving engine performance and reducing emissions, while ensuring meticulous control of internal turbulence in the cylinder.
- Demonstrating the effect of hydrogen enrichment on ammonia combustion in ammonia/diesel dual fuel engines, with the aim of exploring the trade-off between improving combustion efficiency with this strategy and controlling NOx emissions.
The sections of this paper first present the characteristics of the engine studied, then describe the proposed modeling and optimization method in general terms and their application to the engine case studied. At the end, the various results are presented and discussed, followed by the main conclusions and outlook.
2. Model Setup
2.1. Test Engine
In this work, a modified CAT 3401 atmospherically aspirated engine [29], originally designed for trucks, is used for both validation purposes and optimization study. It is a single-cylinder, four-stroke, CI diesel engine. The original Caterpillar engine has been modified to enable dual fuel combustion with ammonia and diesel. This was achieved by integrating a gaseous fuel injector block into the intake manifold to introduce ammonia into the engine. Table 1 outlines the primary geometrical characteristics and operational conditions.

Table 1.
Engine features [29].
In all cases studied, the engine operates in dual fuel mode at full load. The primary fuel (ammonia) and the pilot fuel (diesel) provide 85% and 15% of the total energy developed, respectively. Ammonia is introduced in gaseous form through the intake port, while diesel is injected directly into the cylinder.
2.2. Numerical Model
The study utilizes the CFD solver CONVERGETM 3.1 [30] to simulate the complete engine geometry with intake and exhaust sections, as shown in Figure 1. Once the complete cycle has been simulated, the conditions in the combustion chamber at BDC (Bottom Dead Center) will be used to initiate calculations of closed combustion cycles, where the intake and exhaust phases are not calculated.
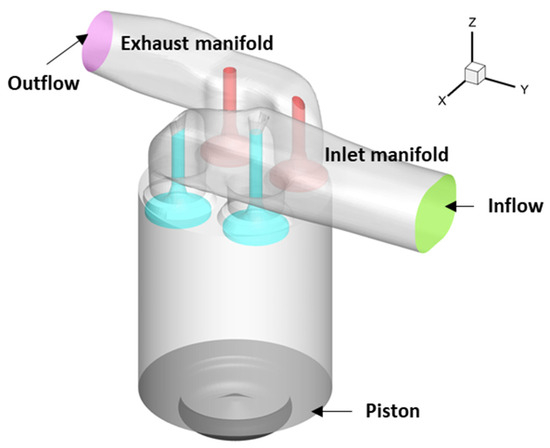
Figure 1.
Computational domain considered in the present study.
For the closed cycles, the code uses a structured cartesian grid with a base cell size of 2 mm and adaptive mesh refinement (AMR). In Figure 2, the different grid refinements using the AMR tool at −14.3, −3.9, and +10.0 °ATDC are illustrated. Local grid refinement has been applied to the piston bowl, cylinder head, cylinder wall, and diesel jet outlet in the combustion chamber to accurately resolve velocity and temperature gradients.
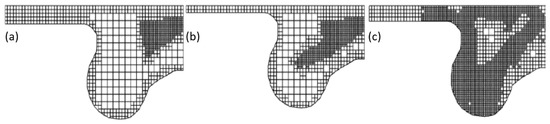
Figure 2.
Different grid refinements by CONVERGETM, (a) −14.3 °ATDC; (b) −3.9 °ATDC; (c) +10.0 °ATDC.
The simulation of the injected primary gas employs the Droplet Discrete Model (DDM) [31], while the KH-RT model is used for the atomization and spray breakup of diesel. For combustion modeling, Heptane (C7H16) represents the physical properties of diesel. The different sub-models used are presented in Table 2.

Table 2.
Sub-models used in the simulation [4].
2.3. Mesh Study
As a first step, a meshing study is carried out. The engine speed for this section is set at 910 RPM based on available results [29]. As shown in Figure 3, this study is based on the convergence of the relative error on indicated work and NOx emissions. This relative error is calculated as the error of the numerical model compared with the experimental results. According to these results, this convergence is achieved for a cell number of 4 × 104, where the error on both parameters is deemed acceptable, taking into consideration its effect on calculation time (8.26% and 6.53% on indicated work and NOx, respectively).
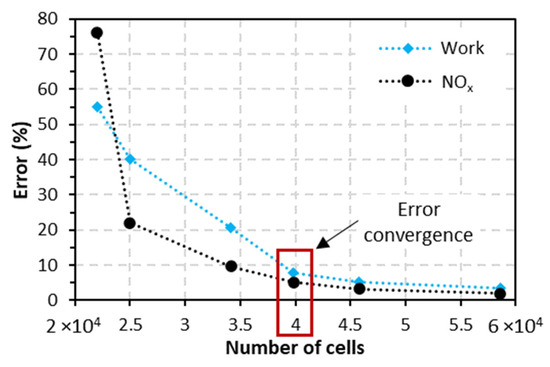
Figure 3.
Effect of maximum number of cells on the relative error of work and NOx emissions.
2.4. Model Validation
After the meshing study, validation of the numerical tool is essential in this work. For the validation case, the engine operates in dual fuel mode at 80% of the full load and a speed of 910 RPM. The primary fuel (ammonia) and the pilot fuel (diesel) provide 85% and 15% of the total energy developed, respectively. Figure 4a shows a comparison between the numerical and experimental pressure signals [29], where agreement between the two is considered acceptable with an error of 4.28%. Figure 4b shows a comparison in terms of indicated thermal efficiency, combustion time, maximum pressure and NOx emissions. The combustion time (or combustion duration) is represented by CA10-CA90, which refers to the crank angle duration between 10% and 90% of the cumulative heat release during the combustion process. The minor differences observed are mainly due to the uncertainties of the physical-chemical models used, which strongly validates the global CFD model used in this work.
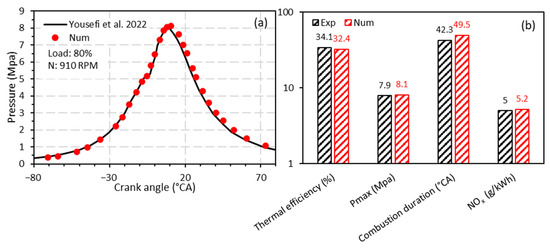
Figure 4.
CFD model validation; (a) in-cylinder pressure profile and (b) engine performance and emissions [29].
3. Approach Description
3.1. Multi-Objective Optimization Technique
Multi-objective optimization is an essential discipline in the field of operations research. This type of optimization aims to find a set of optimal solutions for problems with several conflicting objectives, which asserts the non-existence of a single solution that maximizes or minimizes all objective functions simultaneously. The Non-dominated Sorting Genetic Algorithm II (NSGA-II), used in the present work, is emerging as a powerful method for solving these types of problems, exploiting the principles of genetic evolution.
NSGA-II, developed by Deb et al. [37], extends its predecessor NSGA by incorporating significant improvements for solving problems related to dominated solutions and convergence to the Pareto front encompassing all dominant optimal solutions, as illustrated in Figure 5 for a problem with two objective functions.
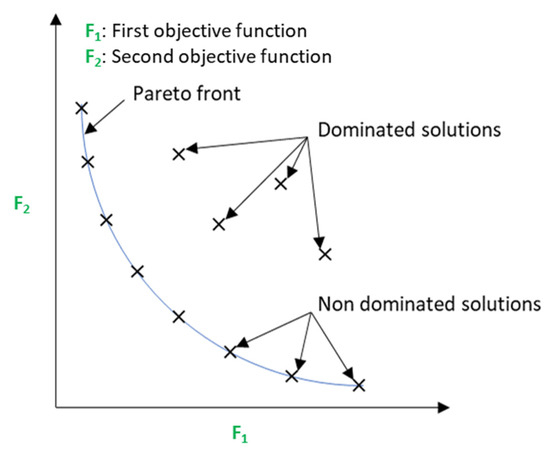
Figure 5.
Bi-objective Pareto front.
A key feature of NSGA-II is its use of non-dominated sorting [38] to rank candidate solutions according to their dominance over other solutions. This creates Pareto fronts, where no solution can be improved in all objectives without degradation in at least one other objective.
NSGA-II also introduces the concept of “crowding distance” [39] to measure the density of solutions in a Pareto front. This helps to promote solution diversity by encouraging the selection of solutions that cover a wider objective space.
The algorithm uses standard genetic operators such as reproduction, crossover, and mutation to create a new generation of candidate solutions [38]. These operators are applied with a probability determined by their impact on solution diversity and quality.
3.2. Adapting the Shape of the Piston
The study presented in this work is based on a parallel optimization algorithm, as shown in Figure 6. In this type of optimization, the model linking the decision variables with the objective functions is created in parallel with the optimization process.
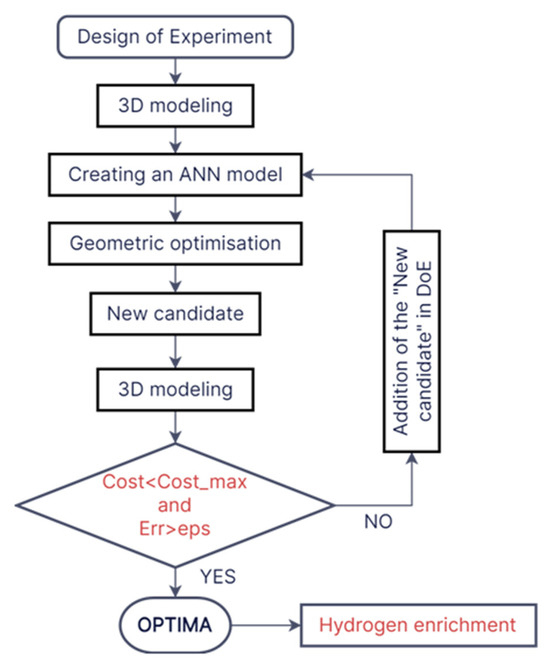
Figure 6.
Flowchart of the proposed approach.
The objective functions and decision variables governing this optimization problem are presented in Table 3.

Table 3.
Optimization problem definition parameters.
At the end of this optimization, a case belonging to the Pareto front is chosen to test the influence of hydrogen enrichment on engine performance and pollutant emissions.
To control the shape of the bowl illustrated in Figure 7a, three geometric parameters have been set (P, b, and d), as shown in Figure 7b. Table 4 summarizes the permitted ranges of variation for the parameters controlling bowl shape and swirl rate.
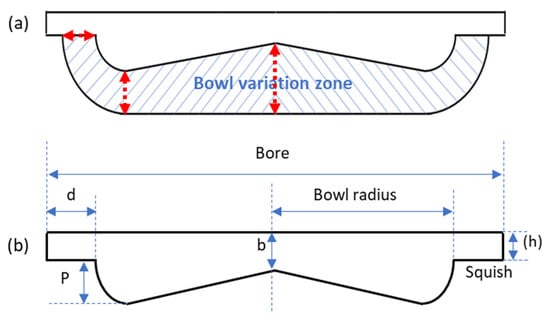
Figure 7.
(a) bowl deformation range and (b) deformation control parameters.

Table 4.
Variation ranges for bowl geometry control parameters.
The optimizer controls the three parameters (P, b, and d), ensuring that geometries can be achieved with the same compression ratio, and controls the swirl rate (S) limited by mechanical conditions directly linked to the creation of the swirl aspect. The final goal is to minimize the NOx rate according to the first objective function, and maximize a weighting between indicated thermal efficiency and combustion efficiency according to a second objective function as defined by Equation (1), ensuring fixed energy input for all optimization cases.
In this optimization problem, the optimizer is controlled by precision variables directly linked to environmental constraints represented by limitations on the allowed rates of CO and HC set at 1.5 g/kWh and 0.13 g/kWh, respectively [29]. These limits represent the emission rates captured when running the same engine in natural gas/diesel dual fuel mode at full load and 1100 RPM.
According to the flowchart proposed in Figure 6, this optimization problem mainly takes place in three essential stages. These stages are based on existing techniques and tools, and are outlined as follows:
- Experimental design generation:
The design of the initial experiment holds significant importance in the field of research. In this investigation, the Latin Hypercube Sampling (LHS) technique is utilized [40]. The principle of this method is based on subdividing the input variable space into n subspaces, with the parameter n representing the size of the experimental design. The main interest of LHS is to address the trade-off between scanning the input variable space and minimizing correlations among these variables [40]. Several optimization algorithms for LHS have been investigated in the literature, underscoring its significance in generating a near-random sample of values [41].
- Meta-model construction using Artificial Neural Network (ANN):
The ANN modeling tool has proven its wide-ranging ability to predict real-time performance and emissions in internal combustion engine applications [42,43,44]. ANN is a computational model inspired by the structure of the human brain, consisting of interconnected nodes called artificial neurons. These neurons are organized in layers and transmit signals through weighted connections. The architecture of an ANN is defined by its layers, the neurons embedded within those layers, the training algorithm employed, and the activation function applied to each layer. These elements collectively contribute to the formation of network architectures [45], as illustrated in Figure 8.
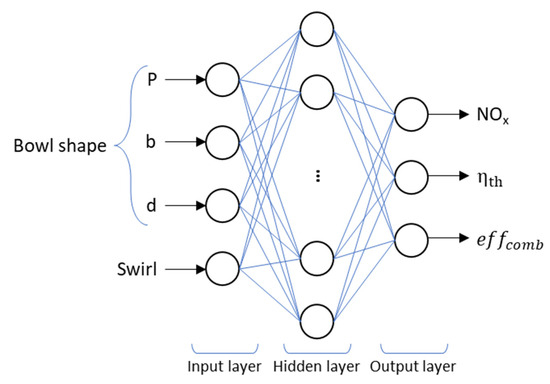
Figure 8.
ANN model architecture.
A prevalent form of artificial neural network (ANN) is the multi-layer perceptron (MLP), categorized as a subset within the realm of feed-forward artificial neural networks (FFNN). The designation “feed-forward” denotes that interconnection amid layers progresses from input layers to output layers. MLPs commonly comprise an input layer, an output layer, and one or two concealed layers. It is imperative, nonetheless, to meticulously ascertain the appropriate count of hidden layers and neurons, as this plays a pivotal role in mitigating the risks of overfitting or underfitting [46].
In an ANN model, signals are transmitted between layers using an activation function, which can be linear or nonlinear. Activation functions commonly utilized include pure-linear, log-sigmoid, and tan-sigmoid, as stipulated by Equations (2) and (3) which define the output (a) of the activation function. The training process for MLP-FFNN is frequently accomplished through backpropagation, with the Levenberg-Marquardt algorithm (LM) being extensively utilized for adjusting weights and biases within the layers [47].
While artificial neural networks (ANN) have showcased considerable prowess in diverse applications, including real-time prediction, it is crucial to acknowledge their limitations, such as their susceptibility to getting trapped in a local optimum. Numerous strategies have been put forth to tackle these constraints and augment the efficacy of conventional ANNs [45].
- Selection of refinement points:
The incorporation of the “experiment space refinement (ESR)” methodology stands as a pivotal phase in guaranteeing the precision of the model. This procedure entails the selection of a refinement point (Pr) through the application of the “max-min distance” criterion, as outlined in Equation (4). The purpose is to systematically investigate uncharted territories within the experimental design. Afterward, the identified refinement point is evaluated using the constructed meta-model and CFD to determine the relative error. If this error (Err) exceeds a critical threshold (eps), the point is reconsidered in the creation of the meta-model via an iterative loop. Otherwise, or if the cost (Cost) reaches its maximum (Cost_max), the iterative loop stops and provides the optimal solution [48].
The vectors and denote the sets corresponding to the experimental design space and the current Pareto front, respectively.
4. Results and Discussion
4.1. Optimization of Bowl Shape and Swirl Rate
Figure 9 shows a history of the last four Pareto fronts according to the global optimization loop presented by the flowchart in Figure 6 which satisfies the two objective functions (F1 and F2) defined by Equation (1).
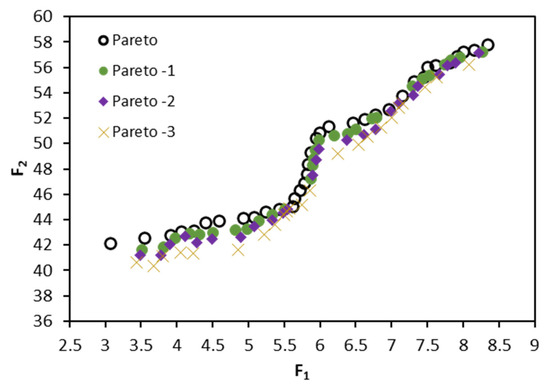
Figure 9.
History of the last four Pareto fronts.
According to these results, the last three Pareto fronts are relatively close to the final one. This implies that the maximum perturbations allowed relative to the final front are relatively large, as shown by the results in Table 5. In other words, if perturbations are applied to the decision variables (P, b, d, and S), the objective functions will be shifted to local optimums that are close to the global optimum represented by the final Pareto front, which confirms the robustness of this model.

Table 5.
Maximum perturbation of the last Pareto fronts to the final front.
Figure 10 shows the final Pareto front summarizing all non-dominated cases according to this optimization, where the two limiting cases of this front are indicated as follows: Case 1, for which the optimizer focuses on maximizing indicated thermal efficiency and combustion efficiency. Case 2, for which the optimizer focuses on minimizing NOx emissions.
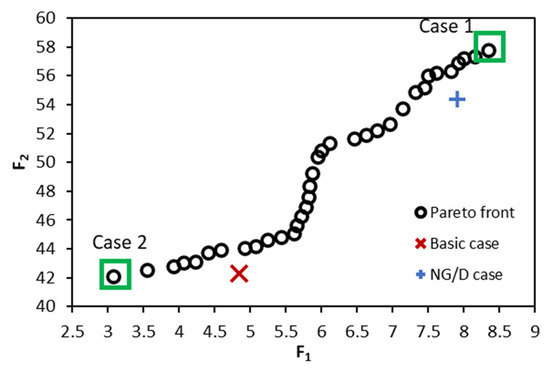
Figure 10.
Final Pareto front.
Table 6 compares four reference cases defined as follows:

Table 6.
Comparison of reference operation cases.
- Case 1 and Case 2: the two extreme cases of the Pareto front, where the optimizer fully favors maximizing the weighting between indicated thermal efficiency and combustion efficiency for Case 1, and fully favors minimizing NOx emissions for Case 2.
- Base case: this case represents operation with the original geometry of the combustion chamber (without bowl modification).
- NG/D case: this case represents operation with the basic geometry, using natural gas as the primary fuel instead of ammonia. It should be noted that the natural gas energy share in this case is 85%, similar to the other cases.
According to these results, Case 1 represents an indicated thermal efficiency improvement of 30% and 12% compared with the base case and NG/D case, respectively. This improvement had a direct impact on NOx levels in this case (Case 1), which increased by 65% and 5% compared with the base case and NG/D case, respectively. These results confirm that the choice of a good compromise between objective functions is necessary for driving performance according to need.
To better analyze the results and the effect of bowl shape and swirl rate on combustion development in the cylinder, the flame front is illustrated in Figure 11 for the base case and Case 1 as a function of crank angle. The combustion rate , defined by Equation (5), is also shown, as well as the enhancement in combustion rate for Case 1 compared to the Basic case for different crank angle.
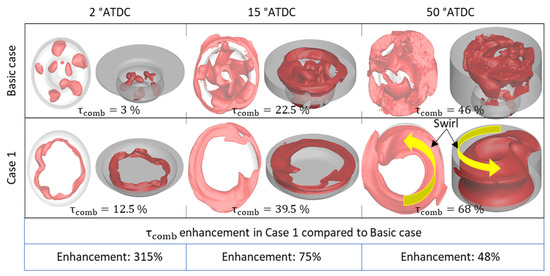
Figure 11.
Effect of geometry and swirl rate on combustion development.
According to these results, Case 1 is characterized by better mixture preparation, which is explained by the considerable improvement in start-up combustion. In Case 1, flame advancement is more structured, which means that all zones in the cylinder are swept, unlike the Basic case, where the flame remains trapped in the bowl due to its shape. The effect of the swirl is seen on the flame front at the end of combustion (50 °ATDC), where the flame propagates away from the revolution axis in Case 1.
Figure 12 shows the velocity field perpendicular to the revolution axis of the cylinder at 2 °ATDC in Case 1 and the Basic case, giving an idea of the Squish intensity. According to the analysis of the results, the Squish is greater in Case 1, implying faster flame propagation. The Squish is directed towards the side walls in Case 1, which explains the uniform propagation of the combustion flame towards the outside of the revolution axis.
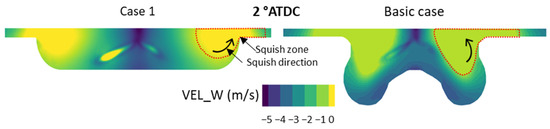
Figure 12.
Effect of geometry and swirl rate on velocity perpendicular to the axis of revolution.
According to the results found, the bowl shape affects the Squish in the cylinder, further improving ammonia combustion. The optimizer seeks to find an optimum combination of swirl and squish via the bowl shape for better combustion efficiency by pushing the flame outside the injector towards the side walls and bringing the unburnt ammonia inside the bowl.
4.2. Effect of Hydrogen Addition
The main aim of this section is to demonstrate the effectiveness of hydrogen enrichment on ammonia combustion in an ammonia/diesel dual fuel engine. This improved combustion is guaranteed by the enhanced reactivity of the gas mixture in the combustion chamber.
In this section, Case 2 is chosen for testing the influence of hydrogen enrichment because of its lower efficiency, which justifies its relatively low NOx level compared with the other operating cases.
In this analysis, different fractions of the energy supplied by ammonia are provided by hydrogen addition, namely: 5%, 10%, and 15%. This implies a distribution of the energy shared (Esh) for each fuel, as shown in Table 7.

Table 7.
Distribution of energy shared.
Figure 13a illustrates the distribution of total energy between indicated work, exhaust losses, heat transfer, and incomplete combustion for the different cases studied. Figure 13b illustrates the influence of hydrogen enrichment on NOx emissions.
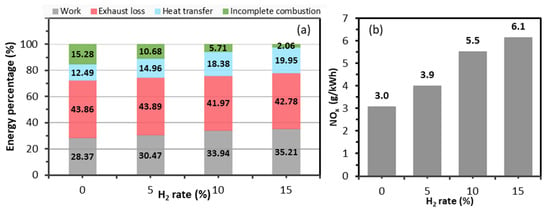
Figure 13.
Effect of hydrogen enrichment on (a) energy distribution and (b) NOx emissions.
According to the results, the addition of hydrogen offers major advantages in terms of combustion efficiency due to the increase in pressure (Figure 14a) and temperature (Figure 14b), which is explained by the decrease in the energy of incomplete combustion as shown in Figure 13a. These conditions directly affect indicated thermal efficiency, and for this reason, the indicated work increases by around 25% between the case with 15% hydrogen enrichment and the case without enrichment.
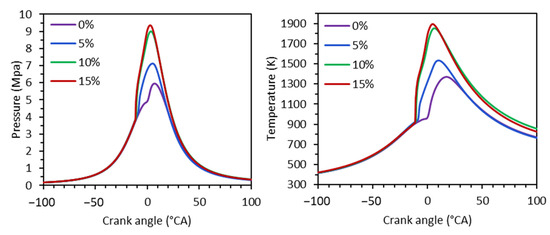
Figure 14.
Effect of hydrogen enrichment on (a) in-cylinder pressure and (b) temperature profiles.
According to Figure 13b, the increase in hydrogen content is accompanied by an increase in NOx rate as a result of improved combustion and higher temperatures.
Figure 15 shows the flame front for Case 2 and Case 2 with 15% hydrogen enrichment (Case 2/15%H2) as a function of crank angle.
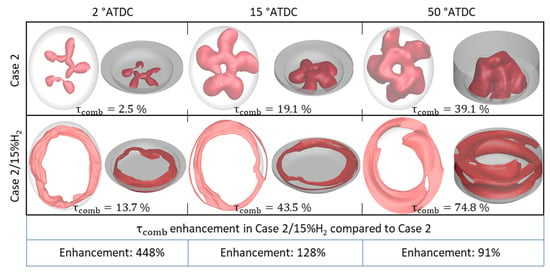
Figure 15.
Effect of hydrogen enrichment on combustion development.
Based on the findings, the flame propagation speed demonstrates an increase as hydrogen enrichment increases. This observation justifies the evolution of the flame front as a function of crank angle in Figure 15. The introduction of hydrogen makes the mixture less resistant to ignition, attributable to the distinctive flame propagation velocity associated with hydrogen, as detailed in Table 8. This suggests that an NH3-H2 mixture is marked by a relatively high flame propagation velocity.

Table 8.
Fuels properties.
Table 9 shows the characteristics of Case 2 with 15% hydrogen enrichment (Case 2/15%H2).

Table 9.
Performance and emissions specific to Case 2 with hydrogen enrichment.
A comparison of the results in Table 9 with Table 6 reveals that Case 2/15%H2 offers an indicated thermal efficiency improvement of 32% and 13% compared with the base case and NG/D case, respectively. This efficiency improvement is accompanied by an increase in NOx of around 26% compared with the base case, and a reduction of over 22% compared with the NG/D case.
The results show that with hydrogen enrichment, the trade-off between improved performance and combustion efficiency and NOx reduction is achieved.
5. Conclusions
The study presented in this paper represents a qualitative advance in the field of large dual fuel engines running on ammonia as the primary fuel. In this context, a multi-objective optimization coupled with parallel meta-modeling is applied to the engine, characterized by an energy participation rate of 85% for ammonia. This approach aims to develop an engine dedicated to ammonia diesel dual fuel operation. The main points raised by this work are as follows:
- Using multi-objective optimization techniques, this work targets the search for an optimal piston bowl shape and Swirl rate that collectively enhance indicated thermal efficiency, combustion efficiency, and minimize NOx emissions for ammonia/diesel dual fuel operation. This approach confirms the significant impact of piston shape and Swirl rate on combustion dynamics, shaping flow fields within the combustion chamber to promote efficient flame development and facilitate the complete consumption of introduced ammonia, thereby advancing overall engine performance.
- The optimum configuration outperformed the others in terms of combustion efficiency and reduction of pollutants emitted, with a reduction of over 43% in unburned NH3 and a significant improvement in indicated thermal efficiency of over 31%.
- Enhancing fuel reactivity by incorporating small proportions of hydrogen is crucial for ensuring the smooth operation of the ammonia/diesel dual fuel engine, especially under limiting operating conditions in terms of high load and significant ammonia percentage. A 15% hydrogen enrichment on the non-adapted ammonia/diesel dual fuel engine improves indicated thermal efficiency and combustion efficiency by 28% and 50%, respectively.
Given the influence of the pilot fuel injection timing on the combustion process in dual fuel engines in general, optimizing the pilot injection law for the new bowl configuration, dedicated to operation with ammonia, is a promising avenue for further work. This will allow the exploration of the effect of the interaction of the injection law with the new bowl shape on engine performance and emissions, in the search for the optimal ammonia/diesel dual fuel engine configuration.
Author Contributions
Conceptualization, Y.S.; methodology, Y.S. and K.L.; software, Y.S.; validation, Y.S., L.T. and M.C.; formal analysis, Y.S. and K.L.; investigation, Y.S.; resources, K.L. and M.C.; data curation, C.L.; writing—original draft preparation, Y.S.; writing—review and editing, Y.S. and L.T.; visualization, K.L.; supervision, K.L., L.T. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Convergent Science provided CONVERGE licenses and technical support for this work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AMR | adaptive mesh refinement |
| ATDC | after top dead center |
| ANN | artificial neural network |
| BDC | bottom dead center |
| combustion efficiency | |
| combustion rate | |
| CFD | computational fluid dynamics |
| D | diesel |
| DME | dimethyl ether |
| DDM | droplet discrete model |
| Esh | energy shared |
| ESR | experiment space refinement |
| FFNN | feed-forward artificial neural networks |
| ICE | internal combustion engine |
| LHS | latin hypercube sampling |
| LM | levenberg-Marquardt |
| MLP | multi-layer perceptron |
| NG | natural gas |
| NSGA | non-dominated sorting genetic algorithm |
| NTC | no-time-counter |
| Fi | objective function |
| Pr | refinement point |
| indicated thermal efficiency | |
| TDC | top dead center |
| VEL_W | velocity parallel to cylinder’s axis of revolution |
References
- Kim, W.; Park, C.; Bae, C. Characterization of Combustion Process and Emissions in a Natural Gas/Diesel Dual-Fuel Compression-Ignition Engine. Fuel 2021, 291, 120043. [Google Scholar] [CrossRef]
- Sehili, Y.; Loubar, K.; Tarabet, L.; Cerdoun, M.; Lacroix, C. Development of Predictive Model for Hydrogen-Natural Gas/Diesel Dual Fuel Engine. Energies 2023, 16, 6943. [Google Scholar] [CrossRef]
- Ma, F.; Guo, L.; Li, Z.; Zeng, X.; Zheng, Z.; Li, W.; Zhao, F.; Yu, W. A Review of Current Advances in Ammonia Combustion from the Fundamentals to Applications in Internal Combustion Engines. Energies 2023, 16, 6304. [Google Scholar] [CrossRef]
- Sehili, Y.; Loubar, K.; Lounici, M.S.; Tarabet, L.; Cerdoun, M.; Lacroix, C. Development of Knock Prediction Technique in Dual Fuel Engines and Its Mitigation with Direct Water Injection. Fuel 2024, 358, 130297. [Google Scholar] [CrossRef]
- Al-Aboosi, F.Y.; El-Halwagi, M.M.; Moore, M.; Nielsen, R.B. Renewable Ammonia as an Alternative Fuel for the Shipping Industry. Curr. Opin. Chem. Eng. 2021, 31, 100670. [Google Scholar] [CrossRef]
- Mounaïm-Rousselle, C.; Brequigny, P. Ammonia as Fuel for Low-Carbon Spark-Ignition Engines of Tomorrow’s Passenger Cars. Front. Mech. Eng. 2020, 6, 70. [Google Scholar] [CrossRef]
- Westlye, F.R.; Ivarsson, A.; Schramm, J. Experimental Investigation of Nitrogen Based Emissions from an Ammonia Fueled SI-Engine. Fuel 2013, 111, 239–247. [Google Scholar] [CrossRef]
- Kane, S.P.; Northrop, W.F. Thermochemical Recuperation to Enable Efficient Ammonia-Diesel Dual-Fuel Combustion in a Compression Ignition Engine. Energies 2021, 14, 7540. [Google Scholar] [CrossRef]
- Lee, D.; Song, H.H. Development of Combustion Strategy for the Internal Combustion Engine Fueled by Ammonia and Its Operating Characteristics. J. Mech. Sci. Technol. 2018, 32, 1905–1925. [Google Scholar] [CrossRef]
- Lhuillier, C.; Brequigny, P.; Contino, F.; Rousselle, C. Performance and Emissions of an Ammonia-Fueled SI Engine with Hydrogen Enrichment; SAE International: Warrendale, PA, USA, 2019. [Google Scholar]
- Guo, L.; Zhu, J.; Fu, L.; Li, Z.; Liu, F.; Wang, Z.; Liu, X.; Dong, Q. Effects of Pre-Injection Strategy on Combustion Characteristics of Ammonia/Diesel Dual-Fuel Compression Ignition Mode. Energies 2023, 16, 7687. [Google Scholar] [CrossRef]
- Ramachandran, E.; Krishnaiah, R.; Perumal Venkatesan, E.; Saleel, C.A.; Shaik, S. Investigation on Ammonia—Biodiesel Fueled RCCI Combustion Engine Using a Split Injection Strategy. ACS Omega 2023, 8, 30990–31001. [Google Scholar] [CrossRef]
- Gross, C.W.; Kong, S.-C. Performance Characteristics of a Compression-Ignition Engine Using Direct-Injection Ammonia—DME Mixtures. Fuel 2013, 103, 1069–1079. [Google Scholar] [CrossRef]
- Nadimi, E.; Przybyła, G.; Emberson, D.; Løvås, T.; Ziółkowski, Ł.; Adamczyk, W. Effects of Using Ammonia as a Primary Fuel on Engine Performance and Emissions in an Ammonia/Biodiesel Dual-Fuel CI Engine. Int. J. Energy Res. 2022, 46, 15347–15361. [Google Scholar] [CrossRef]
- Nadimi, E.; Przybyła, G.; Lewandowski, M.; Adamczyk, W. Effects of Ammonia on Combustion, Emissions, and Performance of the Ammonia/Diesel Dual-Fuel Compression Ignition Engine. J. Energy Inst. 2023, 107, 101158. [Google Scholar] [CrossRef]
- Al-Dawody, M.F.; Al-Obaidi, W.; Aboud, E.D.; Abdulwahid, M.A.; Al-Farhany, K.; Jamshed, W.; Eid, M.R.; Raizah, Z.; Iqbal, A. Mechanical Engineering Advantages of a Dual Fuel Diesel Engine Powered by Diesel and Aqueous Ammonia Blends. Fuel 2023, 346, 128398. [Google Scholar] [CrossRef]
- Pedersen, K.A.; Lewandowski, M.T.; Schulze-Netzer, C.; Pasternak, M.; Løvås, T. Ammonia in Dual-Fueled Internal Combustion Engines: Impact on NO x, N2O, and Soot Formation. Energy Fuels 2023, 37, 17585–17604. [Google Scholar] [CrossRef]
- Xu, L.; Xu, S.; Bai, X.-S.; Repo, J.A.; Hautala, S.; Hyvönen, J. Performance and Emission Characteristics of an Ammonia/Diesel Dual-Fuel Marine Engine. Renew. Sustain. Energy Rev. 2023, 185, 113631. [Google Scholar] [CrossRef]
- Xu, L.; Bai, X.-S. Numerical Investigation of Engine Performance and Emission Characteristics of an Ammonia/Hydrogen/n-Heptane Engine under RCCI Operating Conditions. Flow Turbul. Combust. 2023, 1–18. [Google Scholar] [CrossRef]
- Cai, K.; Liu, Y.; Chen, Q.; Qi, Y.; Li, L.; Wang, Z. Combustion Behaviors and Unregular Emission Characteristics in an Ammonia—Diesel Engine. Energies 2023, 16, 7004. [Google Scholar] [CrossRef]
- Sun, X.; Li, M.; Li, J.; Duan, X.; Wang, C.; Luo, W.; Liu, H.; Liu, J. Nitrogen Oxides and Ammonia Removal Analysis Based on Three-Dimensional Ammonia-Diesel Dual Fuel Engine Coupled with One-Dimensional SCR Model. Energies 2023, 16, 908. [Google Scholar] [CrossRef]
- Rodríguez, C.G.; Lamas, M.I.; Rodríguez, J.D.D.; Abbas, A. Multi-Criteria Analysis to Determine the Most Appropriate Fuel Composition in an Ammonia/Diesel Oil Dual Fuel Engine. J. Mar. Sci. Eng. 2023, 11, 689. [Google Scholar] [CrossRef]
- Tornatore, C.; Marchitto, L.; Sabia, P.; De Joannon, M. Ammonia as Green Fuel in Internal Combustion Engines: State-of-the-Art and Future Perspectives. Front. Mech. Eng. 2022, 8, 72. [Google Scholar] [CrossRef]
- Shafiq, O.; Tingas, E.-A. Computational Investigation of Ammonia-Hydrogen Peroxide Blends in HCCI Engine Mode. Int. J. Engine Res. 2023, 24, 2279–2294. [Google Scholar] [CrossRef]
- Tay, K.L.; Yang, W.; Chou, S.K.; Zhou, D.; Li, J.; Yu, W.; Zhao, F.; Mohan, B. Effects of Injection Timing and Pilot Fuel on the Combustion of a Kerosene-Diesel/Ammonia Dual Fuel Engine: A Numerical Study. Energy Procedia 2017, 105, 4621–4626. [Google Scholar] [CrossRef]
- Shin, J.; Park, S. Numerical Analysis and Optimization of Combustion and Emissions in an Ammonia-Diesel Dual-Fuel Engine Using an Ammonia Direct Injection Strategy. Energy 2024, 289, 130014. [Google Scholar] [CrossRef]
- Shin, J.; Park, S. Numerical Analysis for Optimizing Combustion Strategy in an Ammonia-Diesel Dual-Fuel Engine. Energy Convers. Manag. 2023, 284, 116980. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Q.; Im, H.G. Enhancing Ammonia Engine Efficiency through Pre-Chamber Combustion and Dual-Fuel Compression Ignition Techniques. J. Clean. Prod. 2024, 436, 140622. [Google Scholar] [CrossRef]
- Yousefi, A.; Guo, H.; Dev, S.; Lafrance, S.; Liko, B. A Study on Split Diesel Injection on Thermal Efficiency and Emissions of an Ammonia/Diesel Dual-Fuel Engine. Fuel 2022, 316, 123412. [Google Scholar] [CrossRef]
- Richards, K.; Senecal, P.; Pomraning, E. CONVERGE 3.0, Convergent Science; Convergent Science: Madison, WI, USA, 2021. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Dukowicz, J.K. A Particle-Fluid Numerical Model for Liquid Sprays. J. Comput. Phys. 1980, 35, 229–253. [Google Scholar] [CrossRef]
- Han, Z.; Reitz, R.D. Turbulence Modeling of Internal Combustion Engines Using RNG κ-ε Models. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI 3.0 Mechanism; Version 3.0; Gas Research Institute, University of California: Berkeley, CA, USA, 1999; Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 2 January 2024).
- Beale, J.C.; Reitz, R.D. Modeling Spray Atomization with the Kelvin-Helmholtz/Rayleigh-Taylor Hybrid Model. At. Sprays 1999, 9, 623–650. [Google Scholar]
- Hiroyasu, H.; Kadota, T. Models for Combustion and Formation of Nitric Oxide and Soot in Direct Injection Diesel Engines. SAE Trans. 1976, 85, 513–526. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-Objective Optimization Using Genetic Algorithms: A Tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Fortin, F.-A.; Parizeau, M. Revisiting the NSGA-II Crowding-Distance Computation. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam The Netherlands, 6–10 July 2013; pp. 623–630. [Google Scholar]
- Helton, J.C.; Davis, F.J. Latin Hypercube Sampling and the Propagation of Uncertainty in Analyses of Complex Systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Damblin, G.; Couplet, M.; Iooss, B. Numerical Studies of Space-Filling Designs: Optimization of Latin Hypercube Samples and Subprojection Properties. J. Simul. 2013, 7, 276–289. [Google Scholar] [CrossRef]
- Tosso, H.G.; Jardim, S.A.B.; Bloise, R.; Santos, M.M.D. Spark Ignition Engine Modeling Using Optimized Artificial Neural Network. Energies 2022, 15, 6587. [Google Scholar] [CrossRef]
- Veza, I.; Afzal, A.; Mujtaba, M.A.; Hoang, A.T.; Balasubramanian, D.; Sekar, M.; Fattah, I.M.R.; Soudagar, M.E.M.; EL-Seesy, A.I.; Djamari, D.W.; et al. Review of Artificial Neural Networks for Gasoline, Diesel and Homogeneous Charge Compression Ignition Engine. Alexandria Eng. J. 2022, 61, 8363–8391. [Google Scholar] [CrossRef]
- Yang, R.; Yan, Y.; Sun, X.; Wang, Q.; Zhang, Y.; Fu, J.; Liu, Z. An Artificial Neural Network Model to Predict Efficiency and Emissions of a Gasoline Engine. Processes 2022, 10, 204. [Google Scholar] [CrossRef]
- Mokashi, I.; Afzal, A.; Khan, S.A.; Abdullah, N.A.; Azami, M.H.B.; Jilte, R.D.; Samuel, O.D. Nusselt Number Analysis from a Battery Pack Cooled by Different Fluids and Multiple Back-Propagation Modelling Using Feed-Forward Networks. Int. J. Therm. Sci. 2021, 161, 106738. [Google Scholar] [CrossRef]
- Abujazar, M.S.S.; Fatihah, S.; Ibrahim, I.A.; Kabeel, A.E.; Sharil, S. Productivity Modelling of a Developed Inclined Stepped Solar Still System Based on Actual Performance and Using a Cascaded Forward Neural Network Model. J. Clean. Prod. 2018, 170, 147–159. [Google Scholar] [CrossRef]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Department of Civil and Environmental Engineering, Duke University: Durham, NC, USA, 2019; Volume 19. [Google Scholar]
- Sehili, Y.; Loubar, K.; Tarabet, L.; Mahfoudh, C.; Lacroix, C. Meta-Model Optimization of Dual-Fuel Engine Performance and Emissions Using Emulsified Diesel with Varying Water Percentages and Injection Timing; SAE International: Warrendale, PA, USA, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).