A Transmission and Distribution Cooperative Congestion Scheduling Strategy Based on Flexible Load Dynamic Compensation Prices
Abstract
1. Introduction
- The congestion management architecture and the process of transmission and distribution coordination are identified;
- The dynamic compensation prices of flexible loads are obtained based on load satisfaction;
- The model of the transmission network layer and distribution network layer is established, and the bi-level optimal congestion scheduling model of transmission and distribution coordination is obtained;
- Based on the modified IEEE-39 experimental system, the effectiveness of the proposed strategy is verified using a simulation.
2. Transmission and Distribution Collaborative Congestion Management Architecture and Process
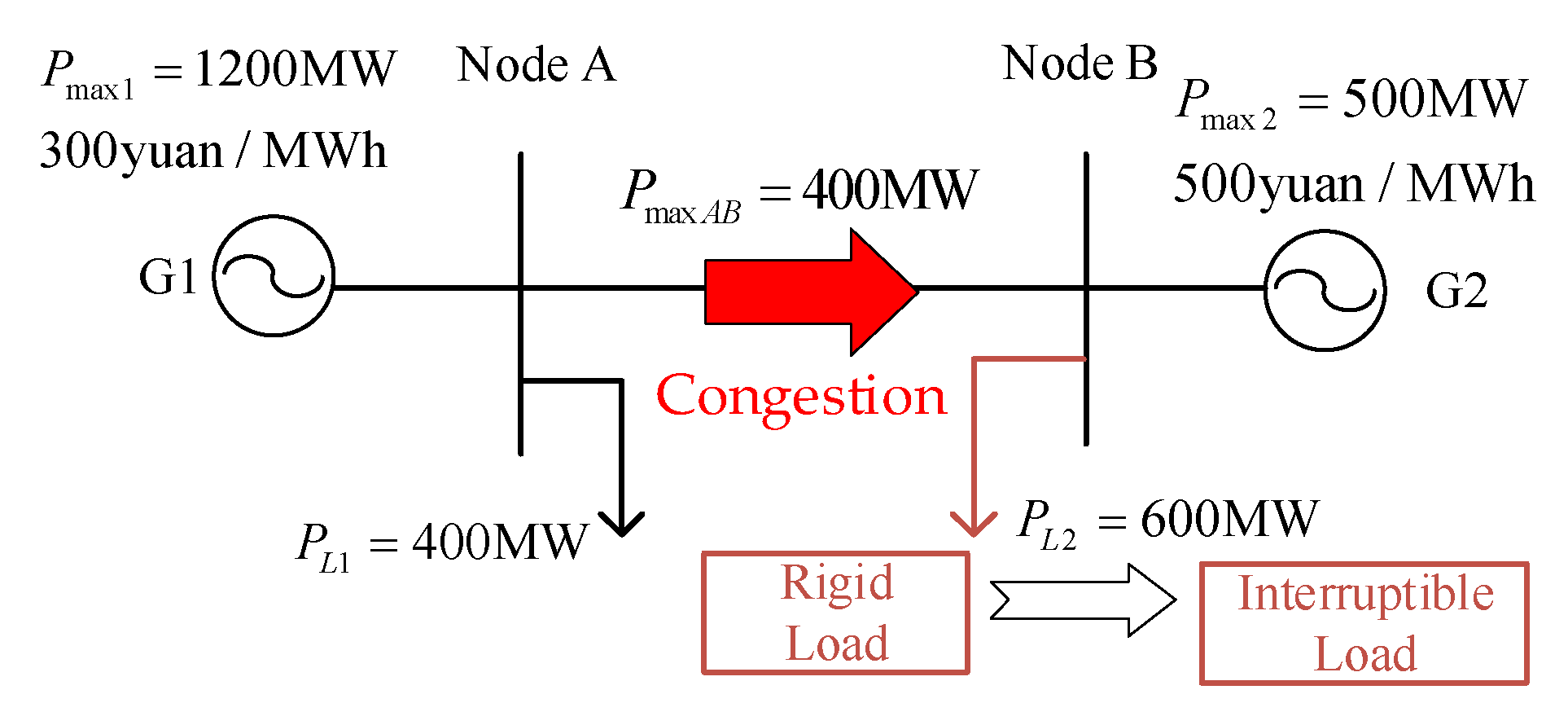
2.1. Congestion Problem and Compensation Price
2.2. Dynamic Integration of Distribution Network Flexibility Resources
2.3. Congestion Management Architecture and the Process Considering Flexible Resource Participation
3. Congestion Scheduling Model Based on Transmission and Distribution Coordination
3.1. Transmission Network Layer Model
3.2. Active Distribution Network Layer Model
3.3. Solution Method and Process
- We set the basic parameters of the algorithm, initialized the particle position and velocity, and modified the particle position according to the constraint conditions. We then calculated the particle fitness, after which each particle was evaluated and the individual optimal position and the global optimal position were obtained;
- We updated the position and velocity of the particles, modified the particle position according to the constraint conditions, after which the particle fitness function value was calculated and the historical individual optimal position and global optimal position of the particle were updated;
- Lastly, we determined whether the number of iterations reached the maximum number of iterations. If the maximum number of iterations is reached, the result is output, otherwise, it returns 2.
4. Example Analysis
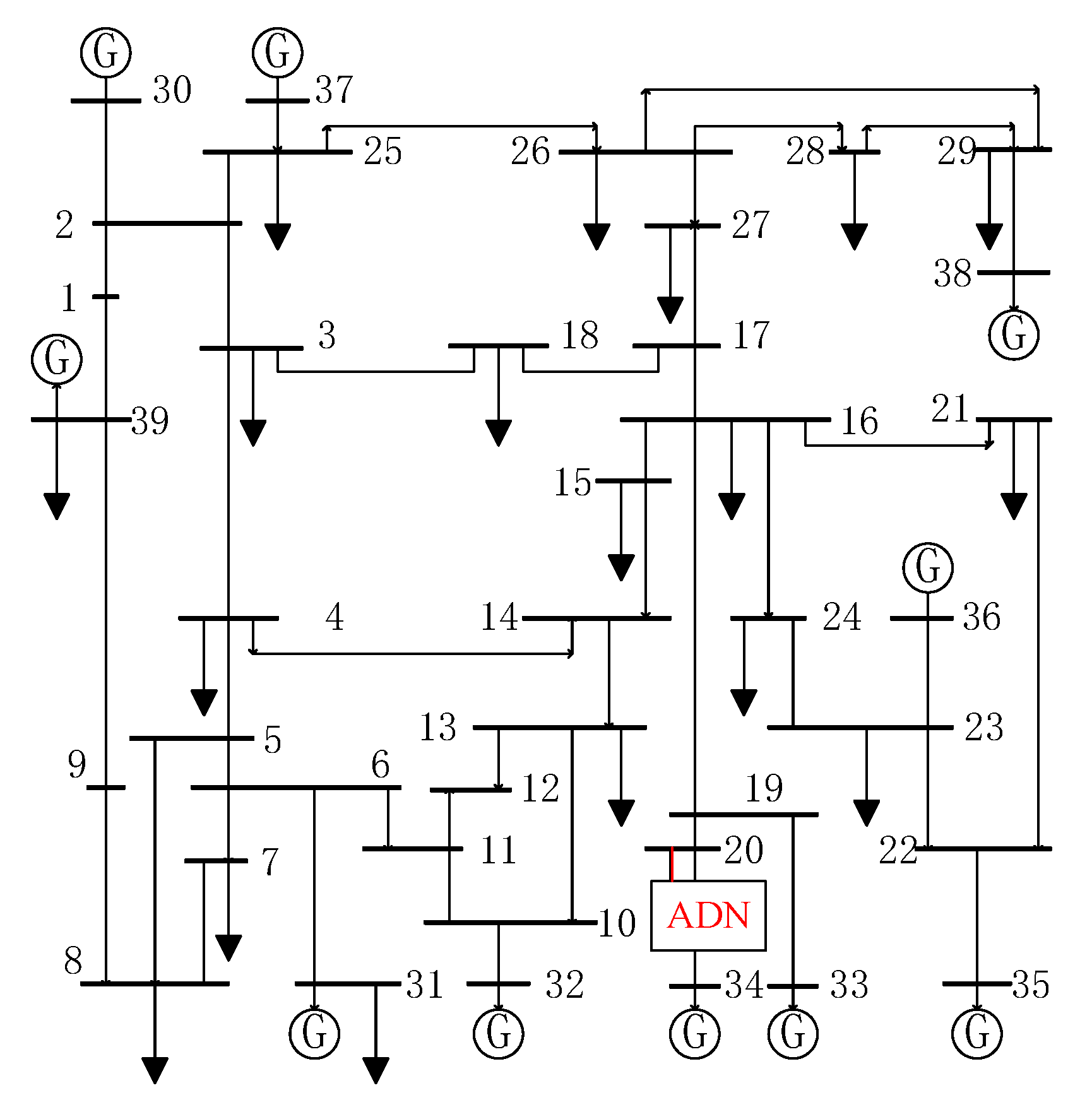
4.1. Simulation Scenario Setting
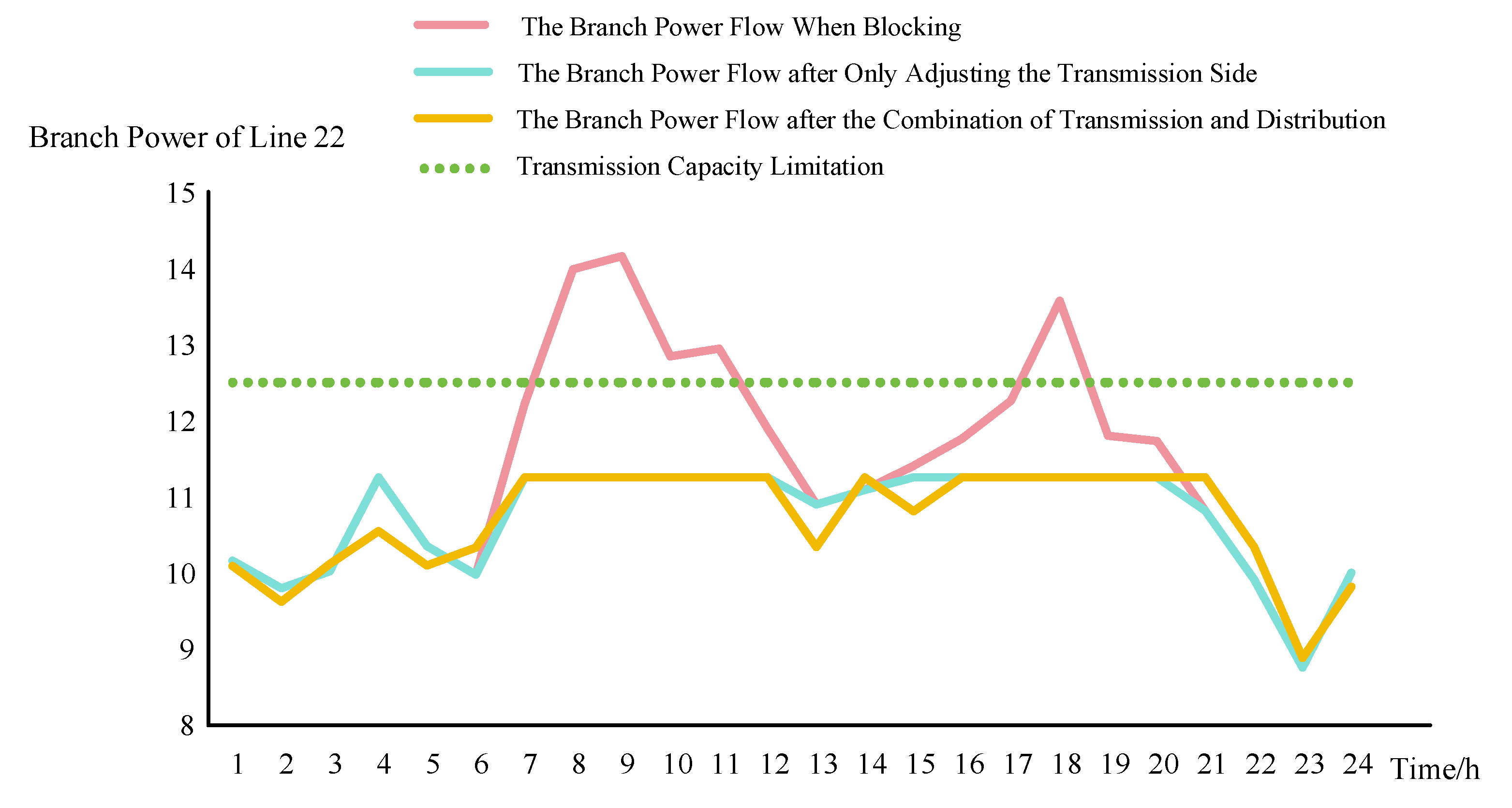
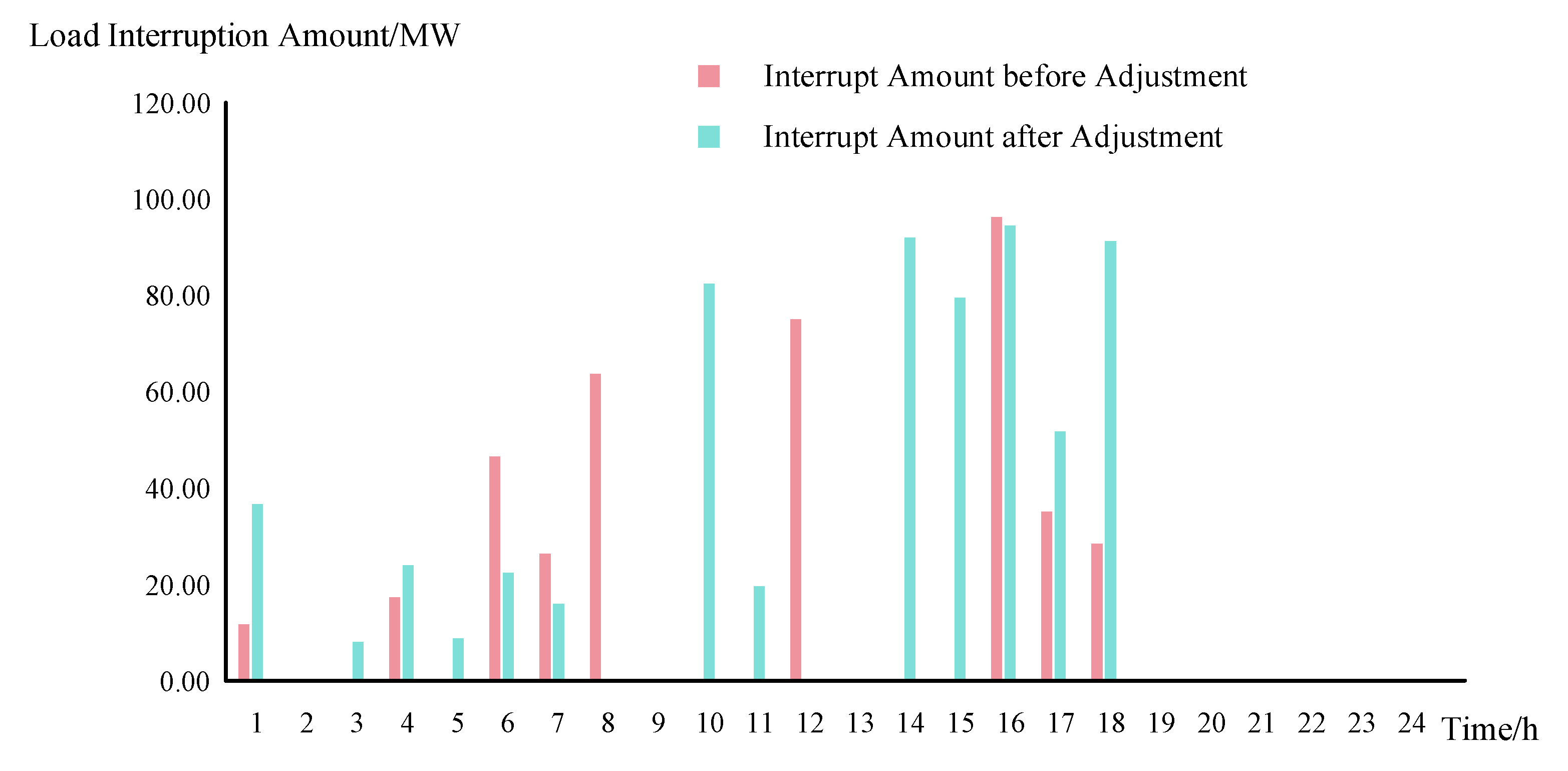
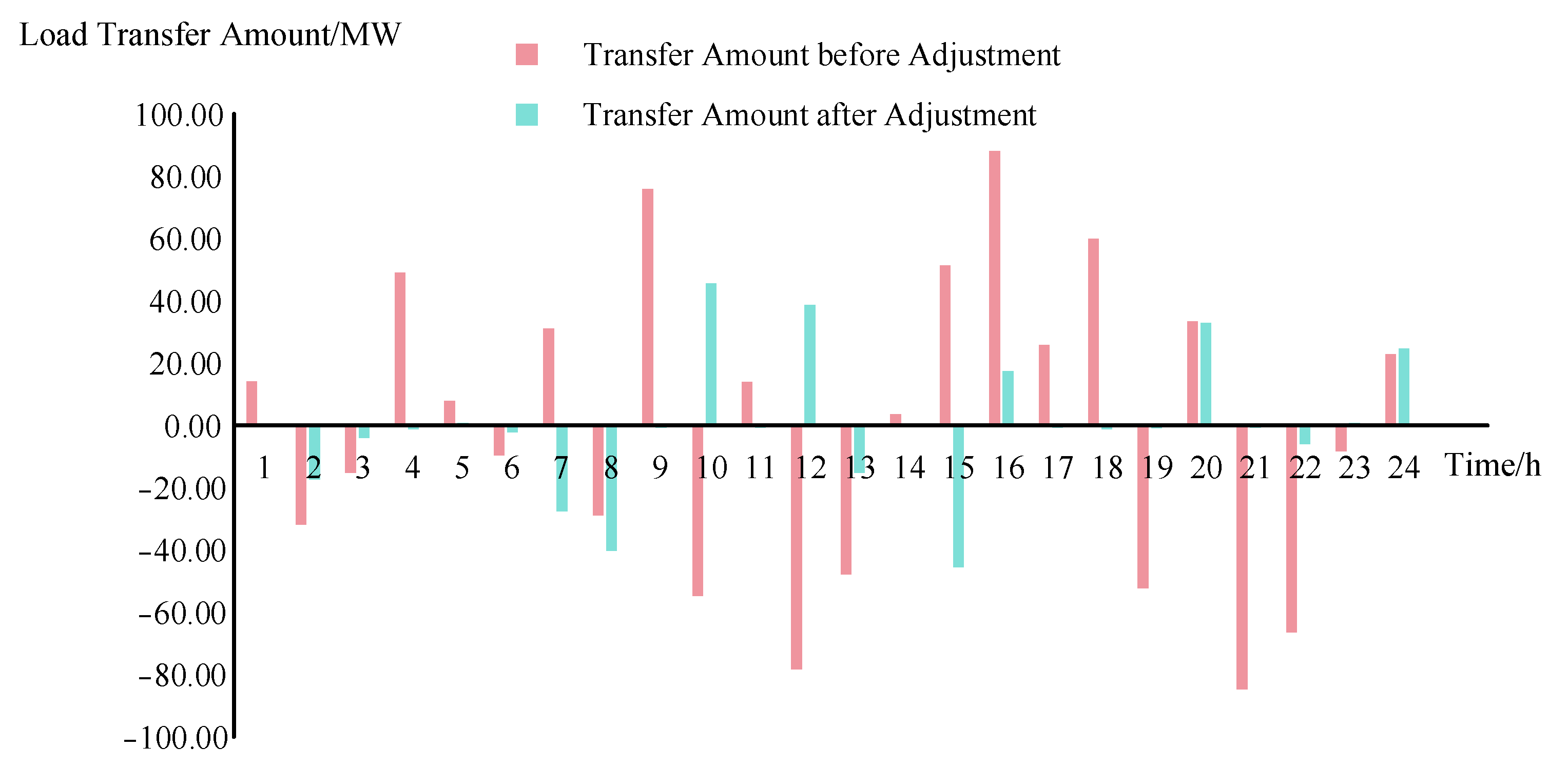
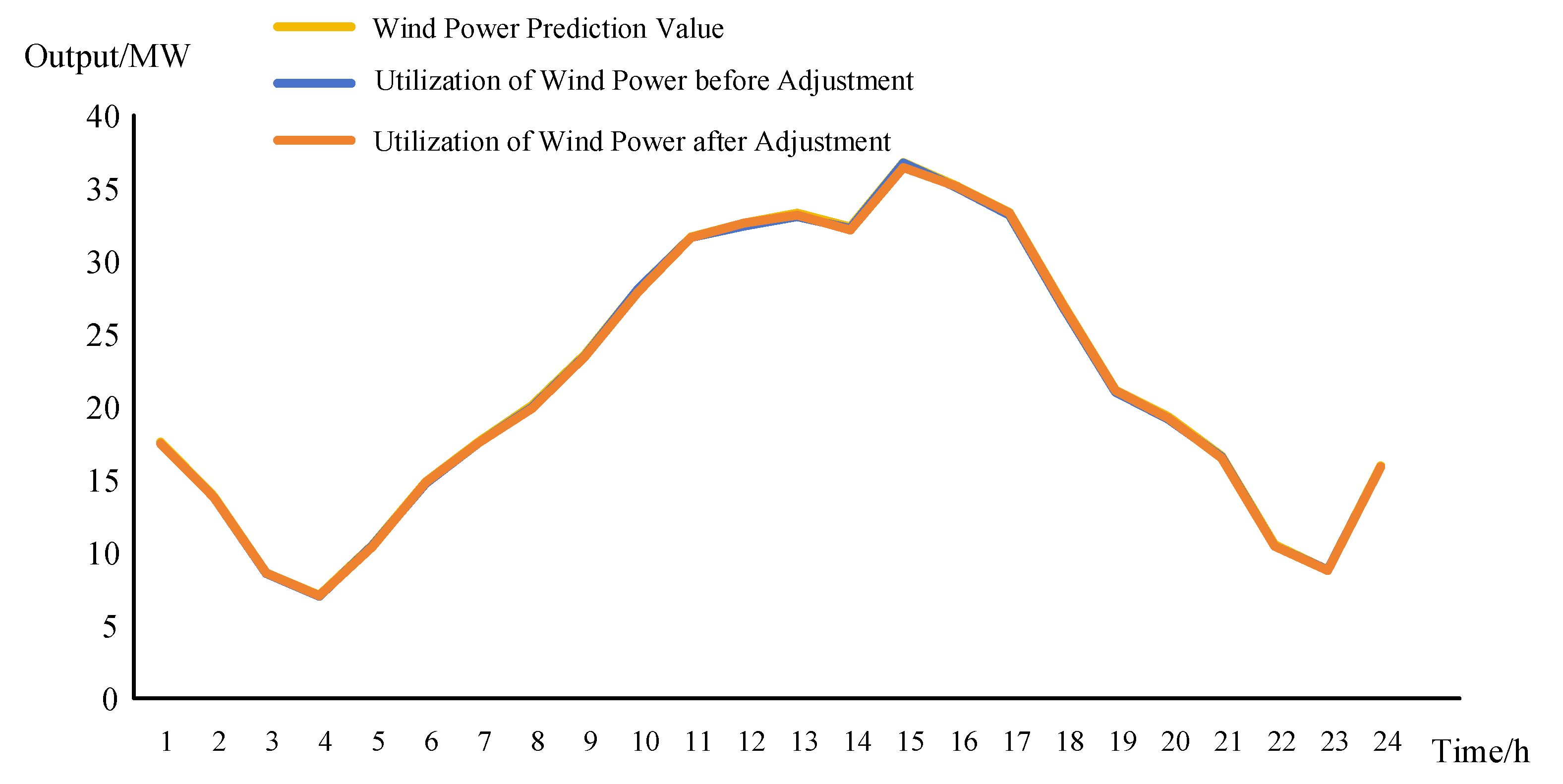
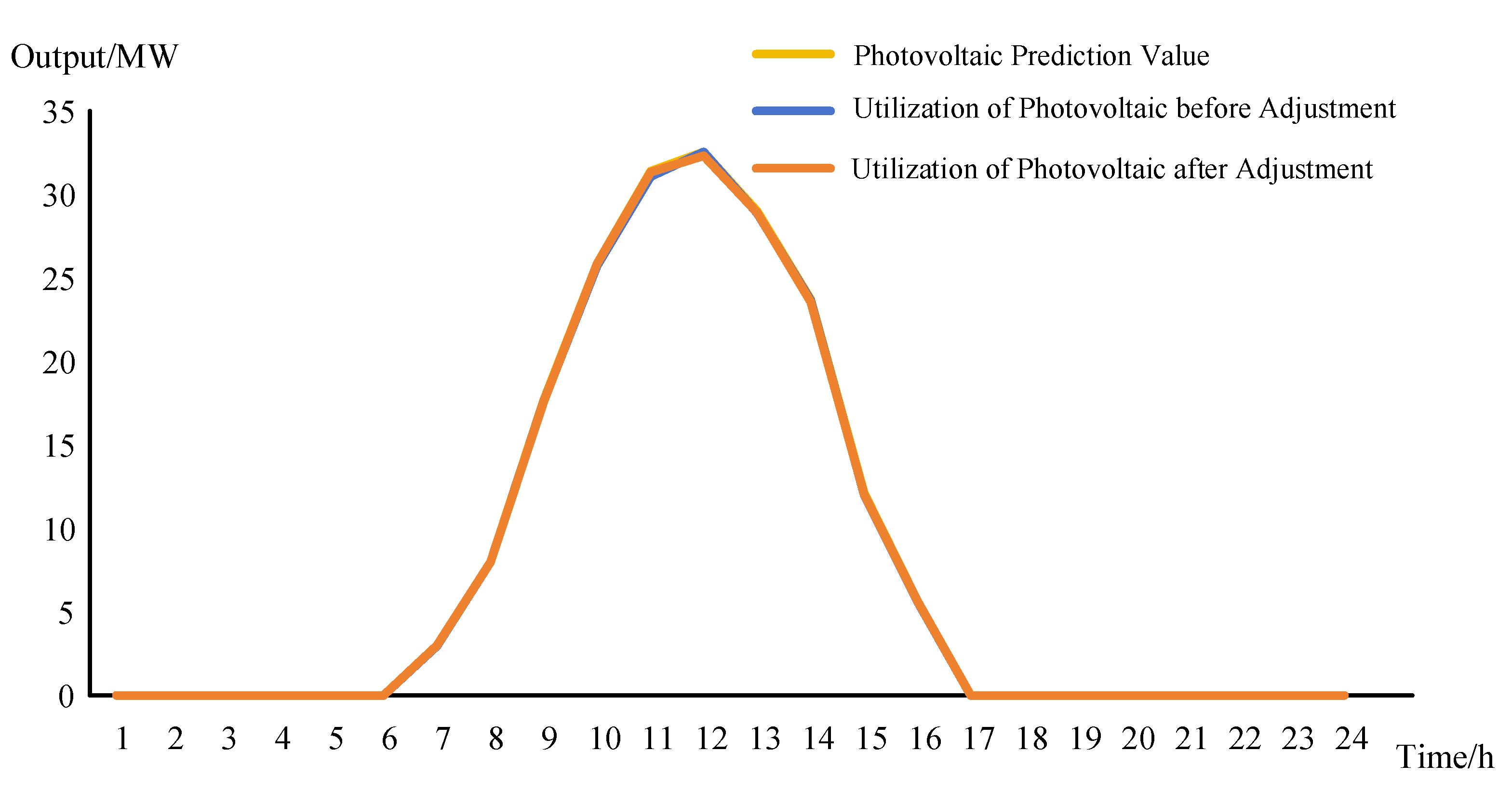
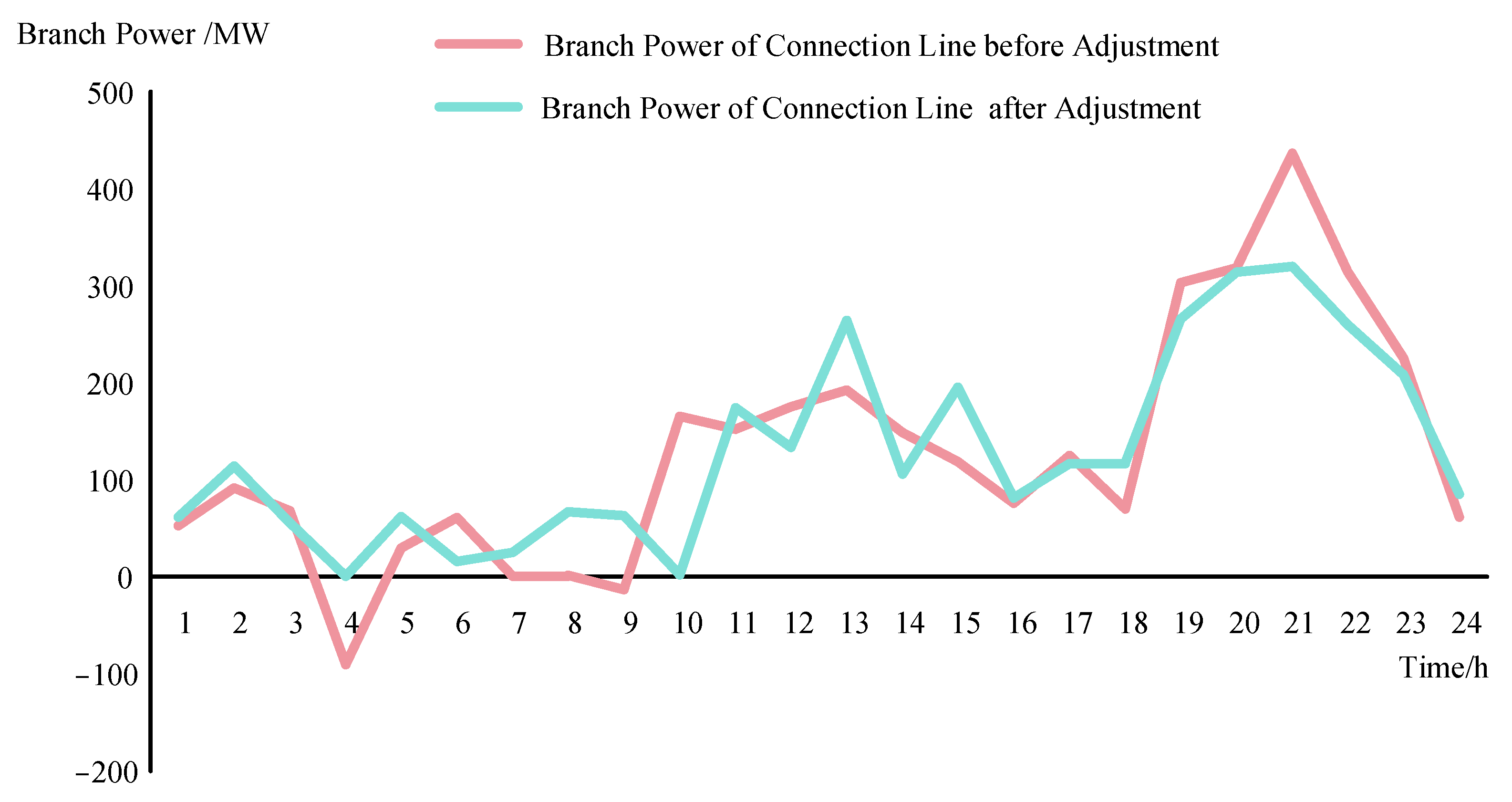
4.2. Comparative Analysis of the Distribution Network before and after Participation
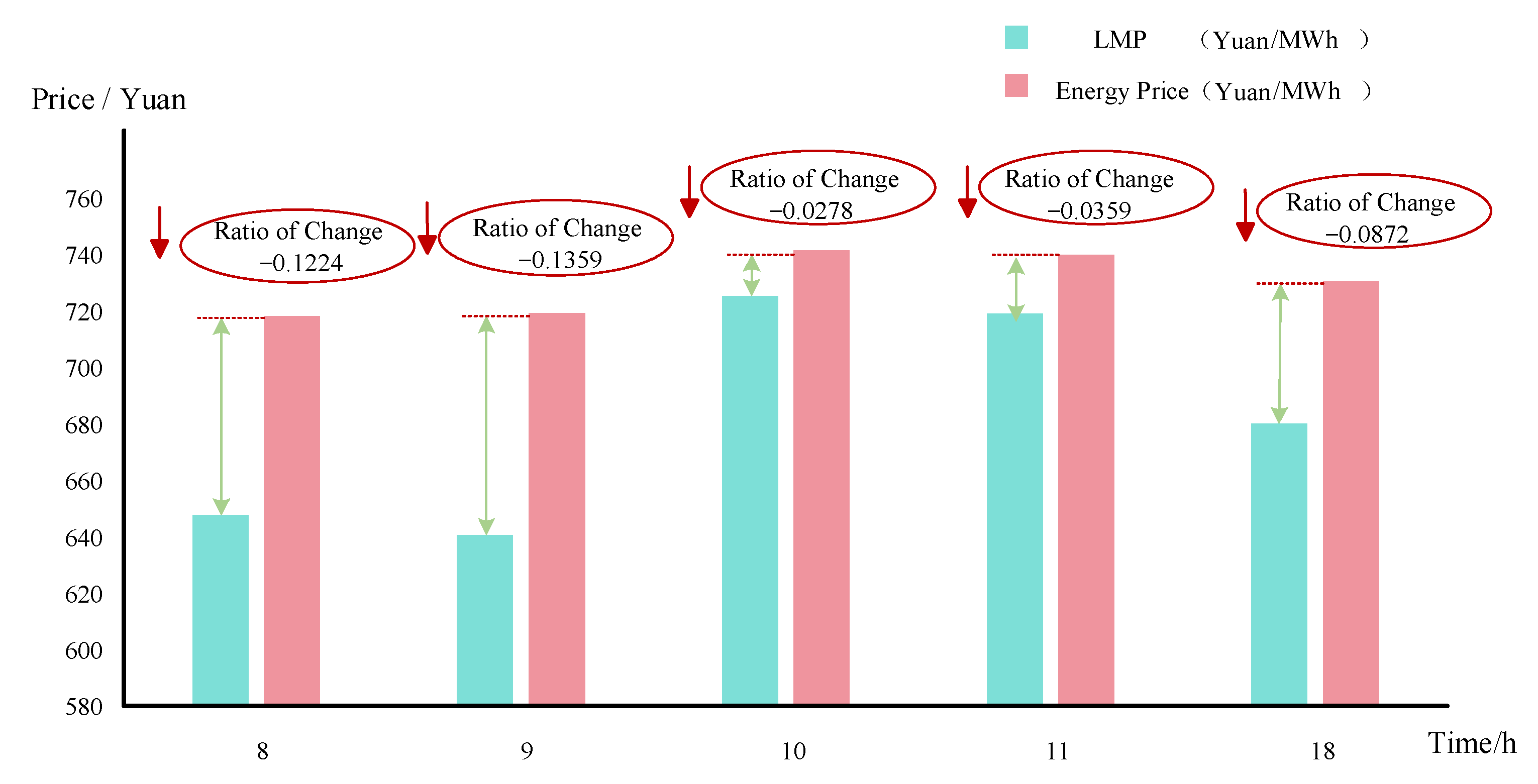
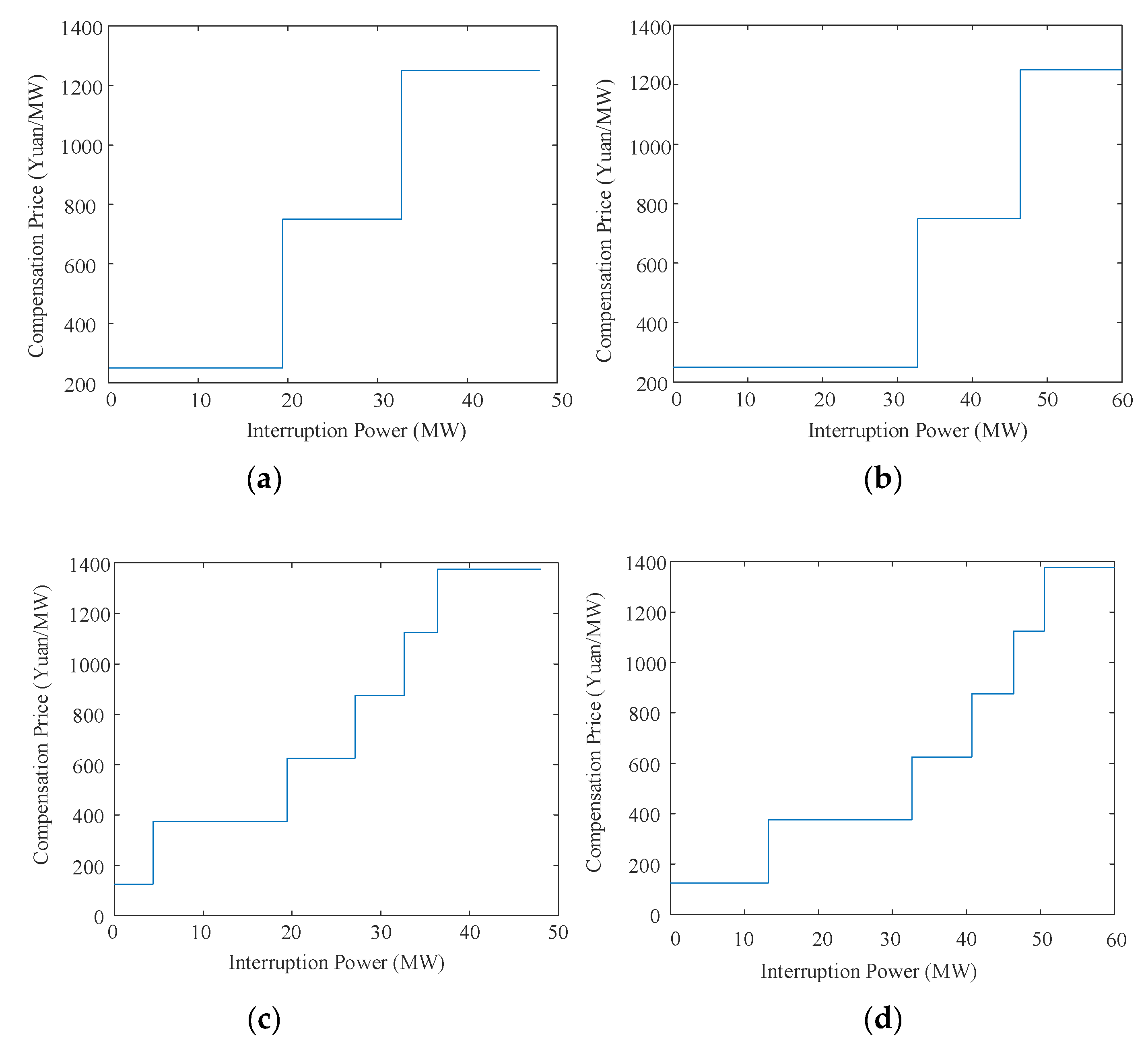
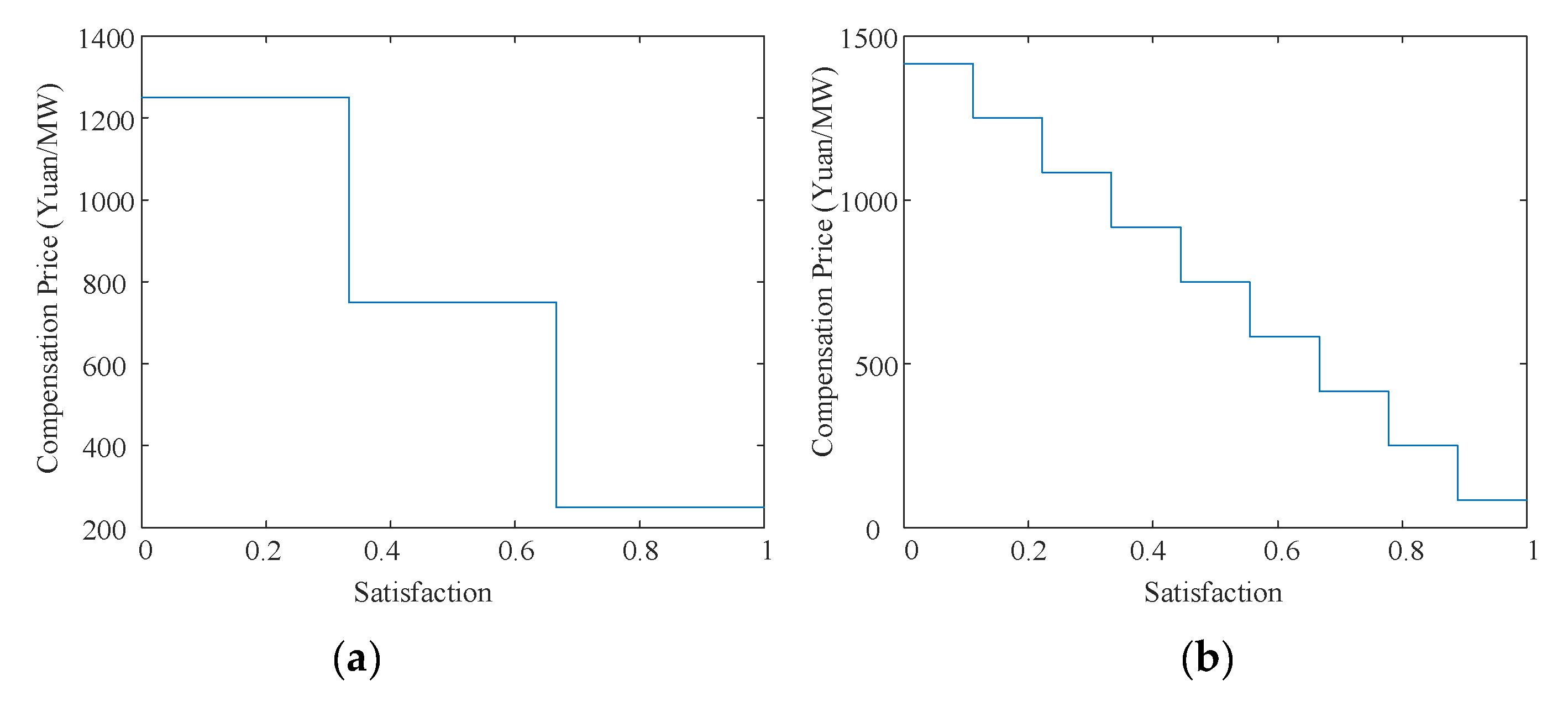
4.3. Flexible Load Satisfaction and Compensation Price Analysis
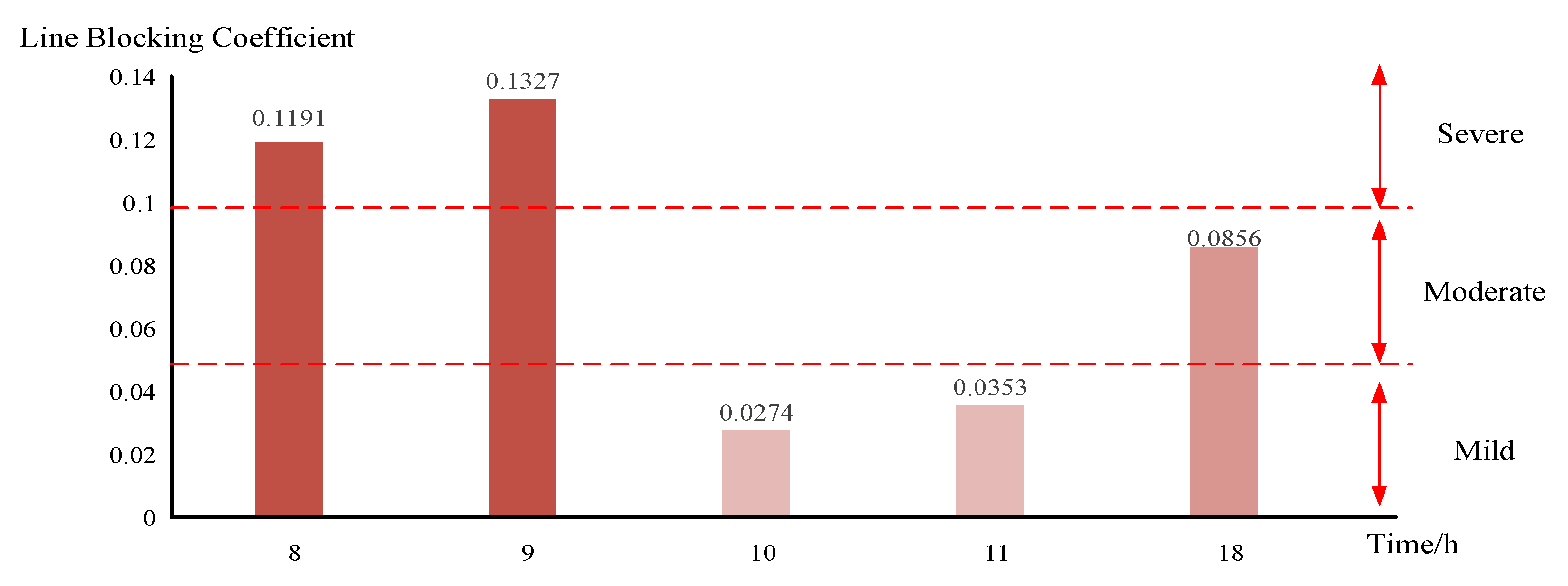
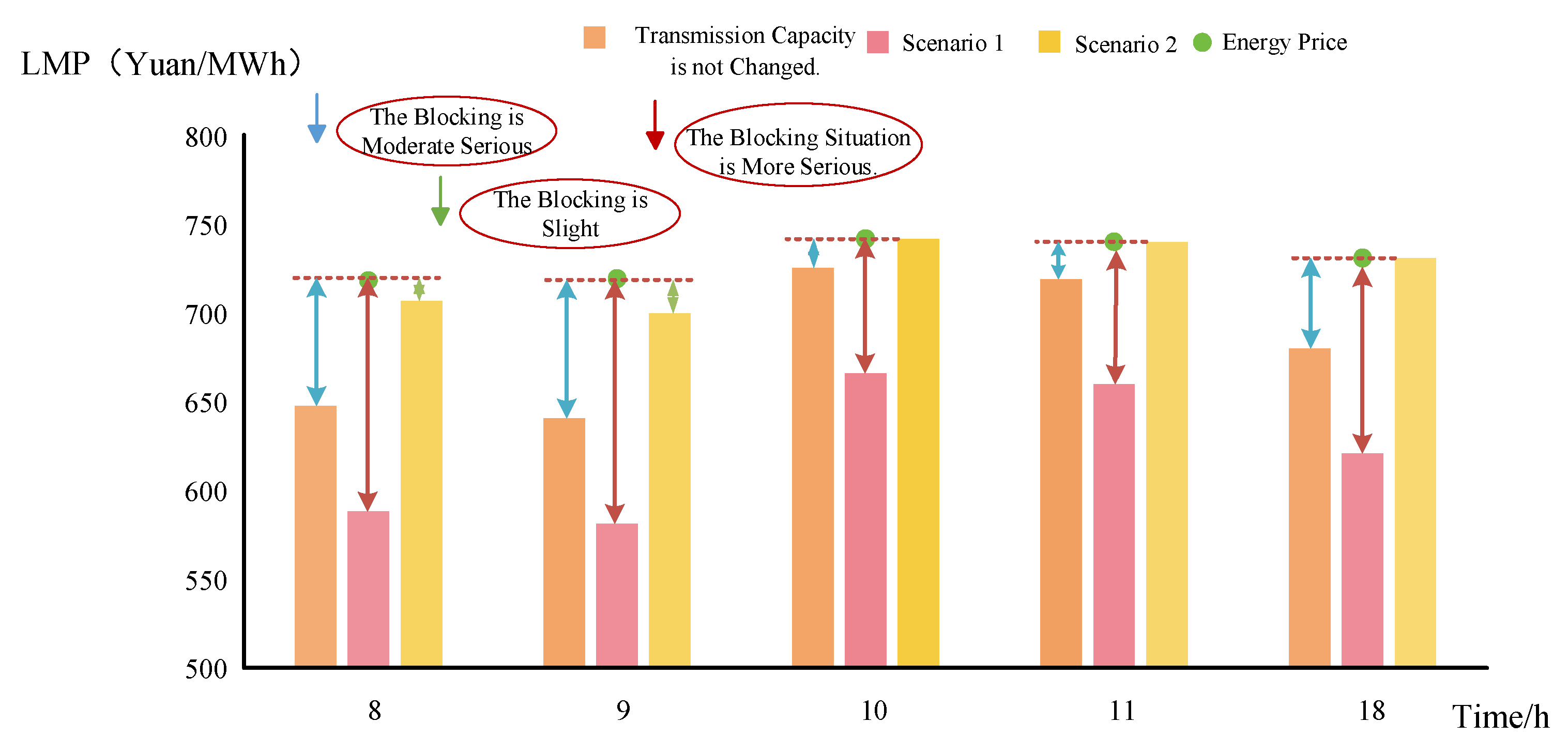
4.4. Comparative Analysis under Different Degrees of Congestion
5. Conclusions
- Considering the satisfaction characteristics of flexible loads in a distribution network layer model, the dynamic collaborative compensation method was adopted to fully mobilize the enthusiasm of the demand response and effectively improve the flexibility of transmission network scheduling;
- The transmission network layer model was based on the node price method in the congestion management mechanism. The electricity price signal was used to guide the generation and consumption of electricity so that the distribution network could respond to transmission congestion mitigation and effectively solve the transmission congestion problem;
- Through the transmission and distribution coordination method, the flexible resources in the distribution network were encouraged to participate in transmission congestion management and the transmission congestion cost was effectively reduced.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Di Persio, L.; Fraccarolo, N. Investment and Bidding Strategies for Optimal Transmission Management Dynamics: The Italian Case. Energies 2023, 16, 5950. [Google Scholar] [CrossRef]
- Du, P. Research on Key Technologies of Transmission Network Congestion Management Based on Transmission and Distribution Coordination. Ph.D. Thesis, SouthEast University, Nanjing, China, 2022. [Google Scholar]
- Huang, Y.; Liu, X.; Zhang, Z.; Yang, L.; Lin, Z.; Dan, Y.; Sun, K.; Lan, Z.; Zhu, K. Multi-Stage Transmission Network Planning Considering Transmission Congestion in the Power Market. Energies 2020, 13, 4910. [Google Scholar] [CrossRef]
- Guo, Q. Source-Storage-Network Joint Planning Method to Deal with Insufficient Flexibility and Transmission Congestion. Master’s Thesis, Northeast Electric Power University, Jilin, China, 2023. [Google Scholar]
- Lei, J. A New Method to Solve the Problem of Transmission Congestion by Using Interruptible Load. Master’s Thesis, North China Electric Power University, Beijing, China, 2023. [Google Scholar]
- Sahoo, A.; Hota, P.K.; Sahu, P.R.; Alsaif, F.; Alsulamy, S.; Ustun, T.S. Optimal Congestion Management with FACTS Devices for Optimal Power Dispatch in the Deregulated Electricity Market. Axioms 2023, 12, 614. [Google Scholar] [CrossRef]
- Huang, P. Research on Selection Method of Transmission Congestion Management Mechanism. Master’s Thesis, North China Electric Power University, Beijing, China, 2019. [Google Scholar]
- Wu, J. Research on Transmission Congestion Management Considering Uncertainty of Wind Power and Demand Response. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Hou, W.; Man Li, R.Y.; Sittihai, T. Management Optimization of Electricity System with Sustainability Enhancement. Sustainability 2022, 14, 6650. [Google Scholar] [CrossRef]
- Hu, Y.; Xun, P.; Kang, W.; Zhu, P.; Xiong, Y.; Shi, W. Power System Zone Partitioning Based on Transmission Congestion Identification Using an Improved Spectral Clustering Algorithm. Electronics 2021, 10, 2126. [Google Scholar] [CrossRef]
- Tan, Q. Research on Transmission Congestion Management under Electricity Market Conditions. Master’s Thesis, Guangxi University, Nanning, China, 2019. [Google Scholar]
- Laaksonen, H.; Khajeh, H.; Parthasarathy, C.; Shafie-khah, M.; Hatziargyriou, N. Towards Flexible Distribution Systems: Future Adaptive Management Schemes. Appl. Sci. 2021, 11, 3709. [Google Scholar] [CrossRef]
- Baczyńska, A.; Niewiadomski, W. Power Flow Tracing for Active Congestion Management in Modern Power Systems. Energies 2020, 13, 4860. [Google Scholar] [CrossRef]
- Yasmin, R.; Amin, B.M.R.; Shah, R.; Barton, A. A Survey of Commercial and Industrial Demand Response Flexibility with Energy Storage Systems and Renewable Energy. Sustainability 2024, 16, 731. [Google Scholar] [CrossRef]
- Ruppert, M.; Baumgartner, N.; Märtz, A.; Signer, T. Impact of V2G Flexibility on Congestion Management in the German Transmission Grid. World Electr. Veh. J. 2023, 14, 328. [Google Scholar] [CrossRef]
- Ratshitanga, M.; Orumwense, E.F.; Krishnamurthy, S.; Melamu, M. A Review of Demand-Side Resources in Active Distribution Systems: Communication Protocols, Smart Metering, Control, Automation, and Optimization. Appl. Sci. 2023, 13, 12573. [Google Scholar] [CrossRef]
- Li, Y. An Intraday Spot Market Congestion Optimal Scheduling Model for Promoting Renewable Energy Consumption. Master’s Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar]
- Zhao, J.; Yang, T.; Yao, J. Transmission and Distribution Cooperative Transmission Congestion Management in Power Spot Market. Autom. Electr. Power Syst. 2020, 44, 107–114. [Google Scholar]
- Huang, K.; Liang, J. Transmission and Distribution Coordination Mitigation Congestion Model and Solution in Electricity Spot Market. J. Taiyuan Univ. Technol. 2023, 54, 193–202. [Google Scholar]
- Zhang, F.; Pei, X.; Wang, B. Coordinated Scheduling and Congestion Management of Active Distribution Network and Transmission Network. Electr. Meas. Instrum. 2020, 57, 46–53+65. [Google Scholar]
- Zhou, Q. Optimal Dispatch of Demand Response Active Distribution Network Based on User Behavior Difference. Master’s Thesis, North China Electric Power University, Beijing, China, 2022. [Google Scholar]
- Jin, Y.; Wang, Z.; Jiang, C. Coordinated Scheduling of Active Distribution Network and Main Network. Electr. Power Constr. 2016, 37, 38–44. [Google Scholar]
- Zhang, T.; Tian, F.; Yang, H. Optimal Scheduling of Integrated Energy Considering Demand Response and Uncertainty. Proc. CSU-EPSA 2023, 1–10. [Google Scholar]
- Li, Z.; Su, S.; Jin, X.; Xia, M.; Chen, Q.; Yamashita, K. Stochastic and Distributed Optimal Energy Management of Active Distribution Network with Integrated Office Buildings. CSEE J. Power Energy Syst. 2022, in press. [Google Scholar] [CrossRef]







| Scene | Congestion Cost (Ten Thousand Yuan) | Transmission Network Cost (Ten Thousand Yuan) | Distribution Network Cost (Ten Thousand Yuan) |
|---|---|---|---|
| Original Scheme | - | 4985.93 | 404.26 |
| Scene 1 | 1.95 | 4987.88 | - |
| Scene 2 | 1.37 | 4986.08 | 335.63 |
| Scene | Power Generation Adjustment on the Transmission Side (MW) | Purchase Power Adjustment on the Distribution Side (MW) |
|---|---|---|
| Scene 1 | 1000.25 | - |
| Scene 2 | 1627.49 | 1004.37 |
| Scene | Congestion Cost (Ten Thousand Yuan) | Transmission Network Cost (Ten Thousand Yuan) | Distribution Network Cost (Ten Thousand Yuan) |
|---|---|---|---|
| Dynamic Step | 1.37 | 4986.08 | 335.63 |
| Fixed Step | 4.48 | 4990.41 | 337.24 |
| Scenario | Whether the Distribution Network is Involved | Congestion Cost (Ten Thousand Yuan) | Transmission Network Cost (Ten Thousand Yuan) | Distribution Network Cost (Ten Thousand Yuan) | Total Cost of Transmission and Distribution Network (Ten Thousand Yuan) |
|---|---|---|---|---|---|
| Transmission Capacity is Not Changed. | Yes | 1.37 | 4986.08 | 335.63 | 5321.71 |
| No | 1.95 | 4987.88 | 404.26 | 5392.14 | |
| Scenario 1 | Yes | 4.50 | 4990.44 | 324.56 | 5315.00 |
| No | 6.08 | 4992.01 | 404.26 | 5396.27 | |
| Scenario 2 | Yes | 0.057 | 4985.99 | 337.34 | 5323.33 |
| No | 0.068 | 4986.00 | 404.26 | 5390.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Jin, T.; Gao, Z.; Hu, S.; Dou, Y.; Lu, X. A Transmission and Distribution Cooperative Congestion Scheduling Strategy Based on Flexible Load Dynamic Compensation Prices. Energies 2024, 17, 1232. https://doi.org/10.3390/en17051232
Sun H, Jin T, Gao Z, Hu S, Dou Y, Lu X. A Transmission and Distribution Cooperative Congestion Scheduling Strategy Based on Flexible Load Dynamic Compensation Prices. Energies. 2024; 17(5):1232. https://doi.org/10.3390/en17051232
Chicago/Turabian StyleSun, Hui, Tian Jin, Zhengnan Gao, Shubo Hu, Yanan Dou, and Xueli Lu. 2024. "A Transmission and Distribution Cooperative Congestion Scheduling Strategy Based on Flexible Load Dynamic Compensation Prices" Energies 17, no. 5: 1232. https://doi.org/10.3390/en17051232
APA StyleSun, H., Jin, T., Gao, Z., Hu, S., Dou, Y., & Lu, X. (2024). A Transmission and Distribution Cooperative Congestion Scheduling Strategy Based on Flexible Load Dynamic Compensation Prices. Energies, 17(5), 1232. https://doi.org/10.3390/en17051232





