Position Sensorless Vector Control System for Lawnmower Permanent Magnet Synchronous Motor Based on Extended Kalman Filter
Abstract
1. Introduction
- 1.
- A sensorless position vector control system based on the EKF was designed for a specifically powered lawnmower PMSM.
- 2.
- To evaluate the performance of the control system, experiments with no load, acceleration, deceleration, and different loads as well as simulated typical lawnmower working conditions were designed; these verified the control system’s robustness and performance.
- 3.
- In this study, a vector control system based on the EKF was successfully applied to a lawnmower motor and achieved stable and efficient control, providing practical experience and data support for the field of lawnmower motor control.
2. Mathematical Model of Permanent Magnet Synchronous Motors
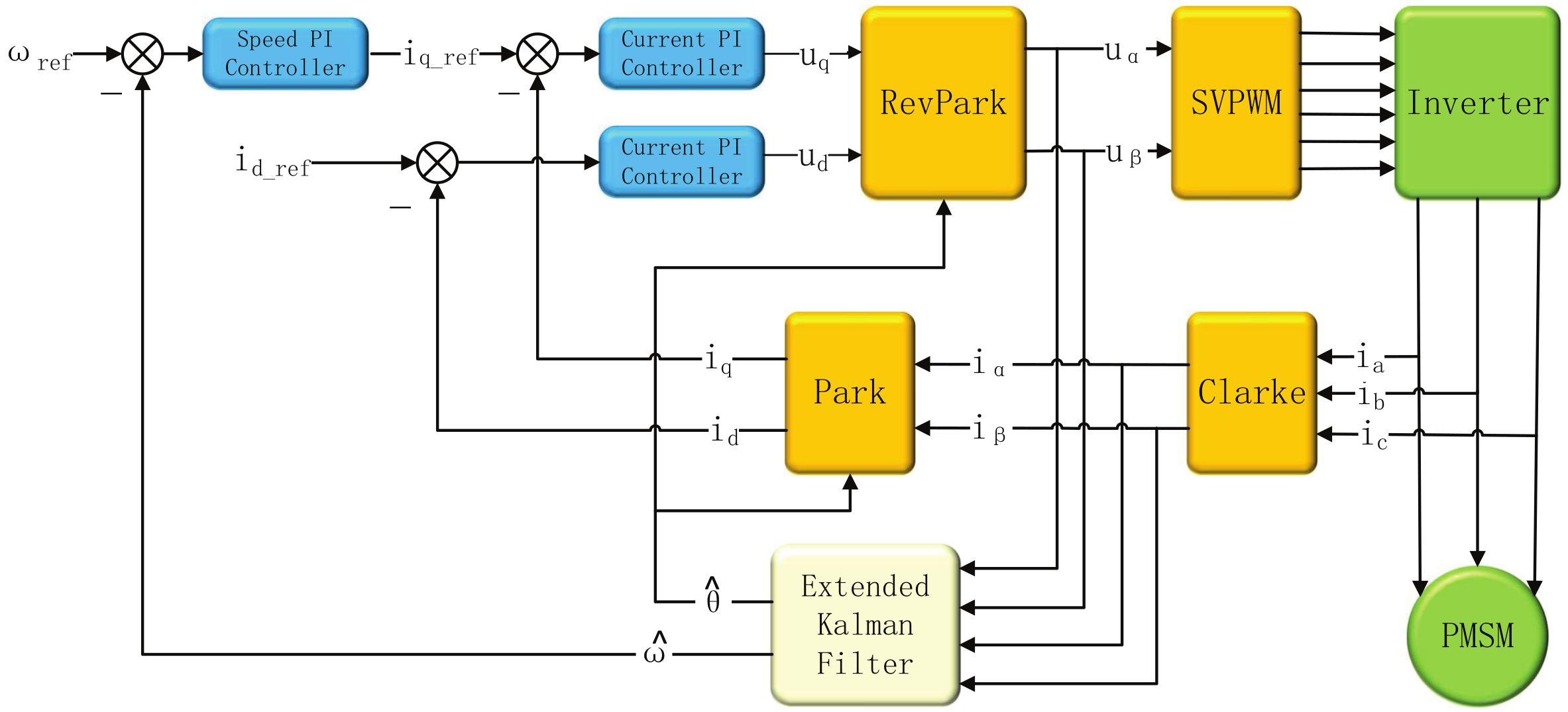
3. Sensorless Vector Control System for Permanent Magnet Synchronous Motors
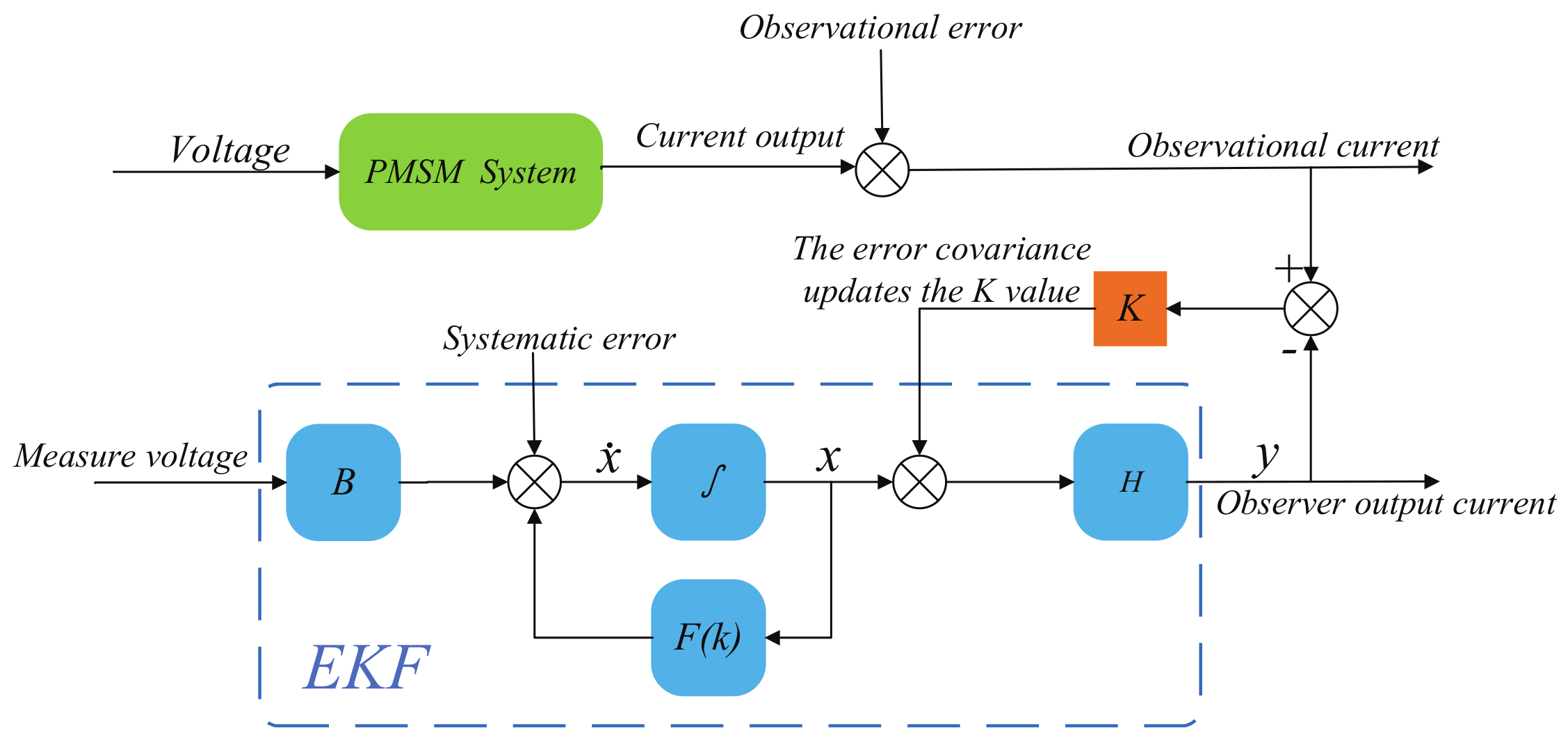
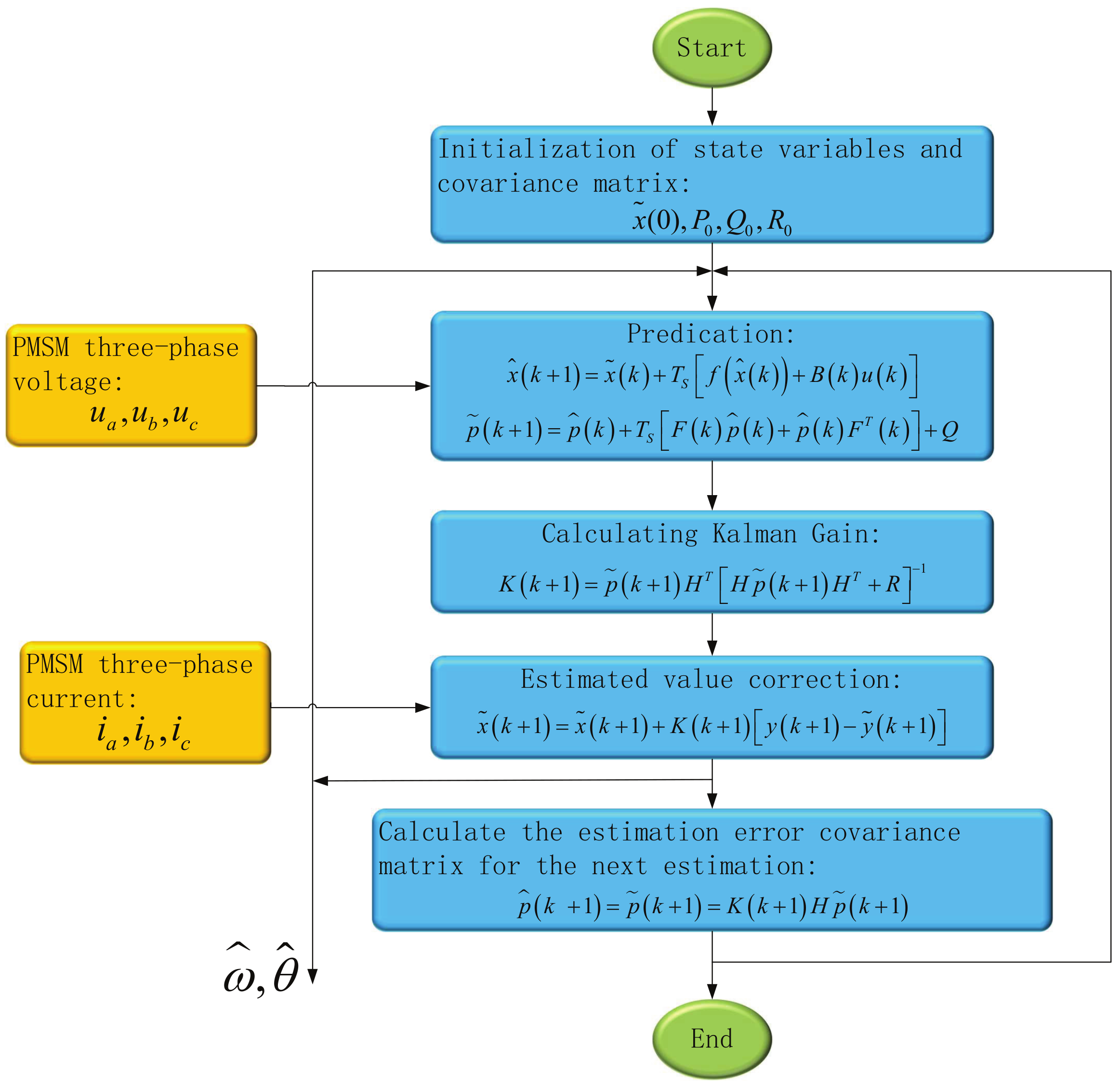
3.1. Implementation of the Extended Kalman Filter
- 1.
- Estimating the state vector: based on the state estimate at the previous moment and the input value , estimating the state vector at the next moment can be undertaken using the following expression:where denotes the sampling period, denotes the state estimate, and denotes the prediction.
- 2.
- Then, the corresponding output can be computed to obtain the following:In this step, the EKF algorithm predicts the measured value at the next moment based on the predicted value of the state and, thus, uses this predicted value in the update step to update the state estimate.
- 3.
- The error covariance matrix can then be computed to obtain the following:The process noise covariance matrix Q describes the uncertainty and noise in the system dynamics, which are usually estimated based on empirical knowledge from system models and practical applications.When has the following expression,the following results are obtained:
- 4.
- The gain matrix of the EKF is computed and obtained as follows:The gain matrix is used to measure the difference between the predicted value and the actual measurement and to correct the state estimate based on this difference.
- 5.
- The feedback correction of the predicted state vector results in the optimized state estimate as follows:This stage is the corrected prediction, which is designed to correct the predicted state values to more closely match the actual observations. In this stage, the previously predicted states are compared with the actual observations, and the observations are used to correct the state estimates and to make them more accurate. In the equation, represents the observed value used to correct the state estimate at the moment . Usually, the observed value can be measured by the detection equipment, and in this paper, according to Equation (5), represents the current value at the moment , which is specifically collected by the hardware sampling circuit and converted by the processing program.
- 6.
- The covariance matrix of the estimation error needs to be pre-calculated for the next estimation as follows:
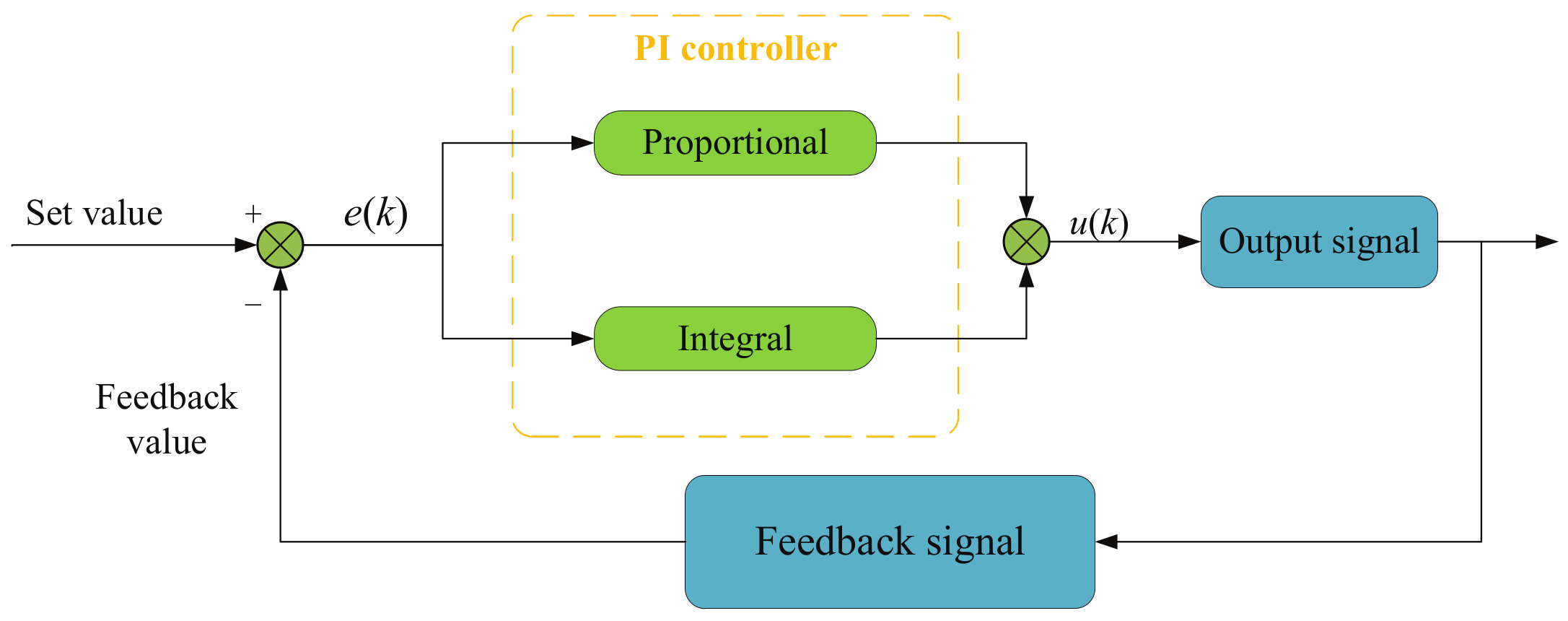
3.2. Vector Control Strategy Based on the Extended Kalman Filter
4. Experimentation
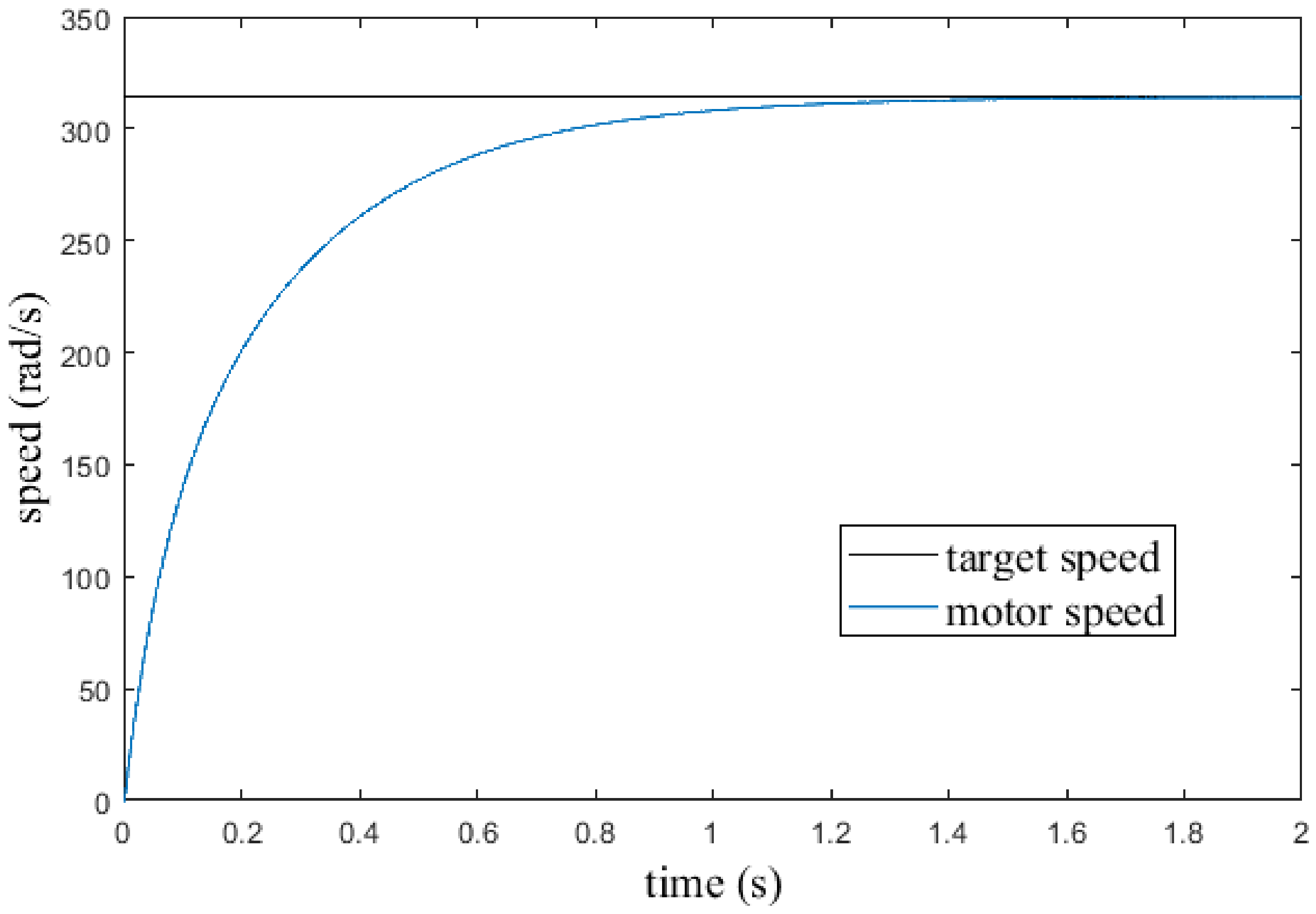
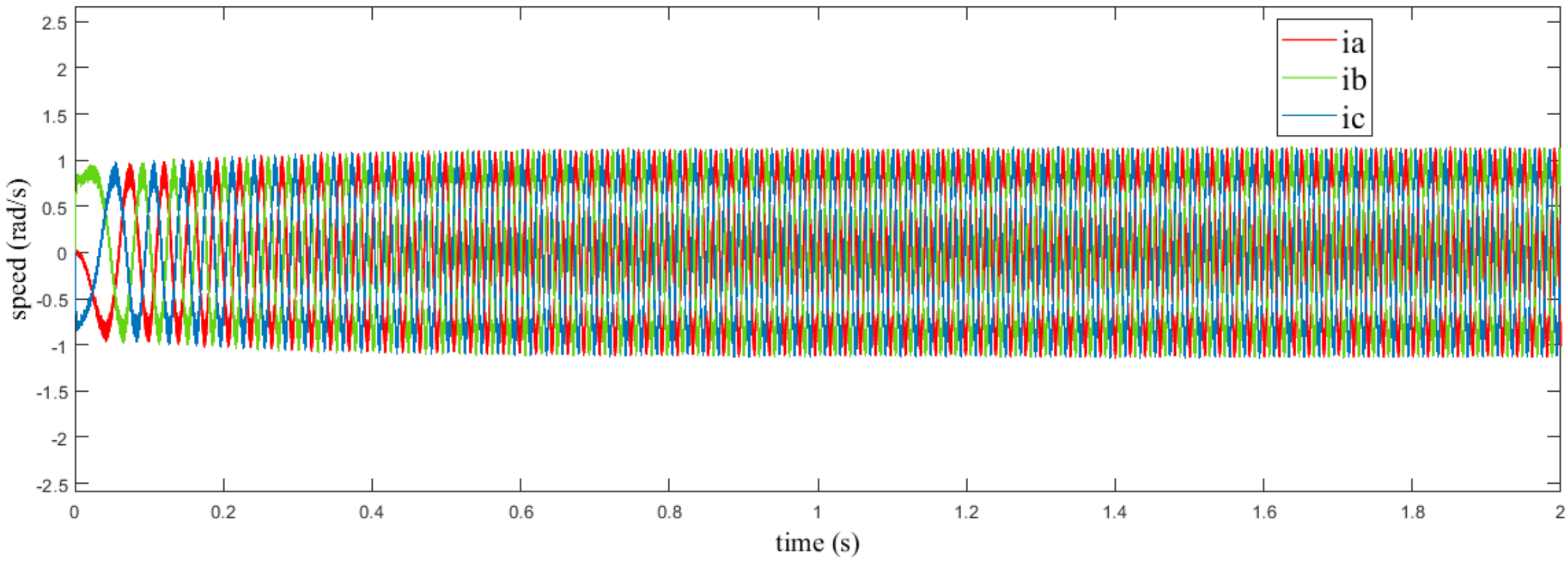
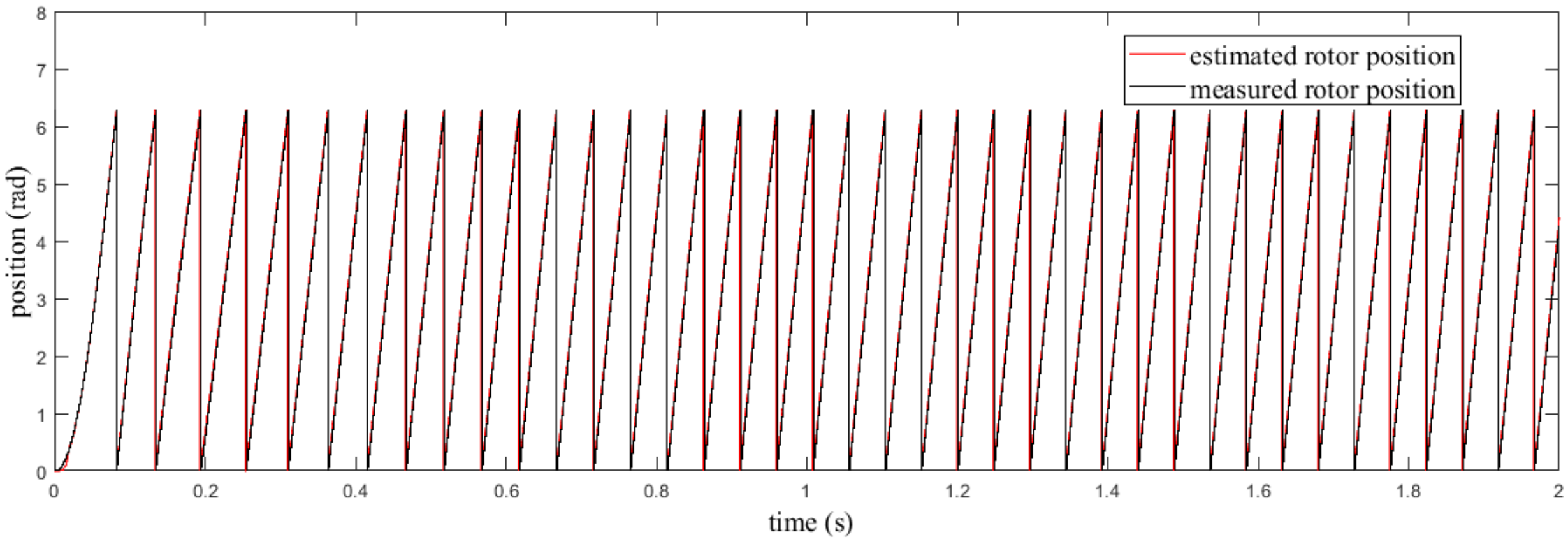
4.1. Simulation Results
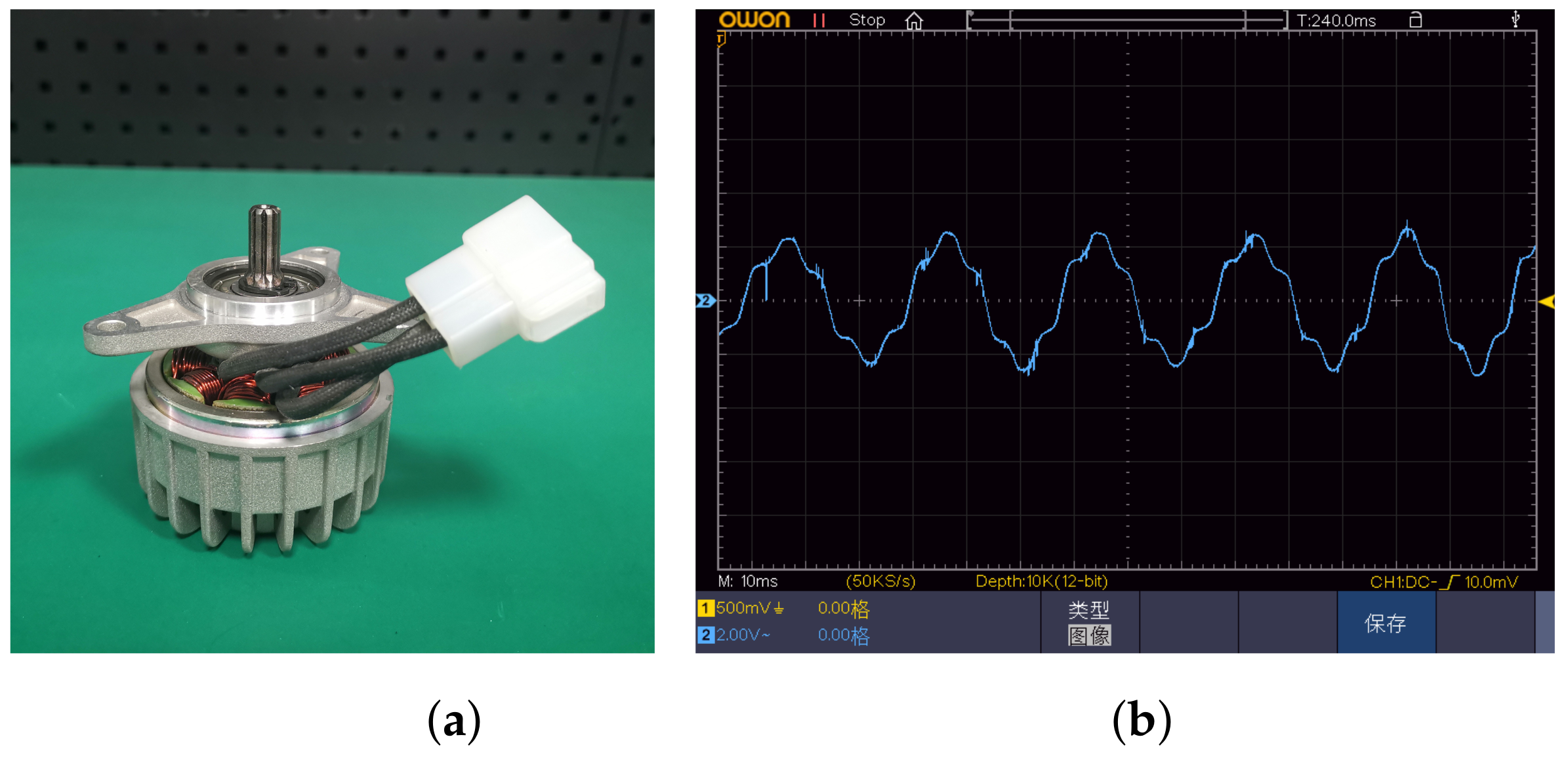
4.2. Hardware Platform
4.3. Parameter Selection
4.3.1. Parameters of the Current Loop PI Controller
4.3.2. Parameters of the Speed Loop PI Controller
4.3.3. Parameters of the Covariance Matrix
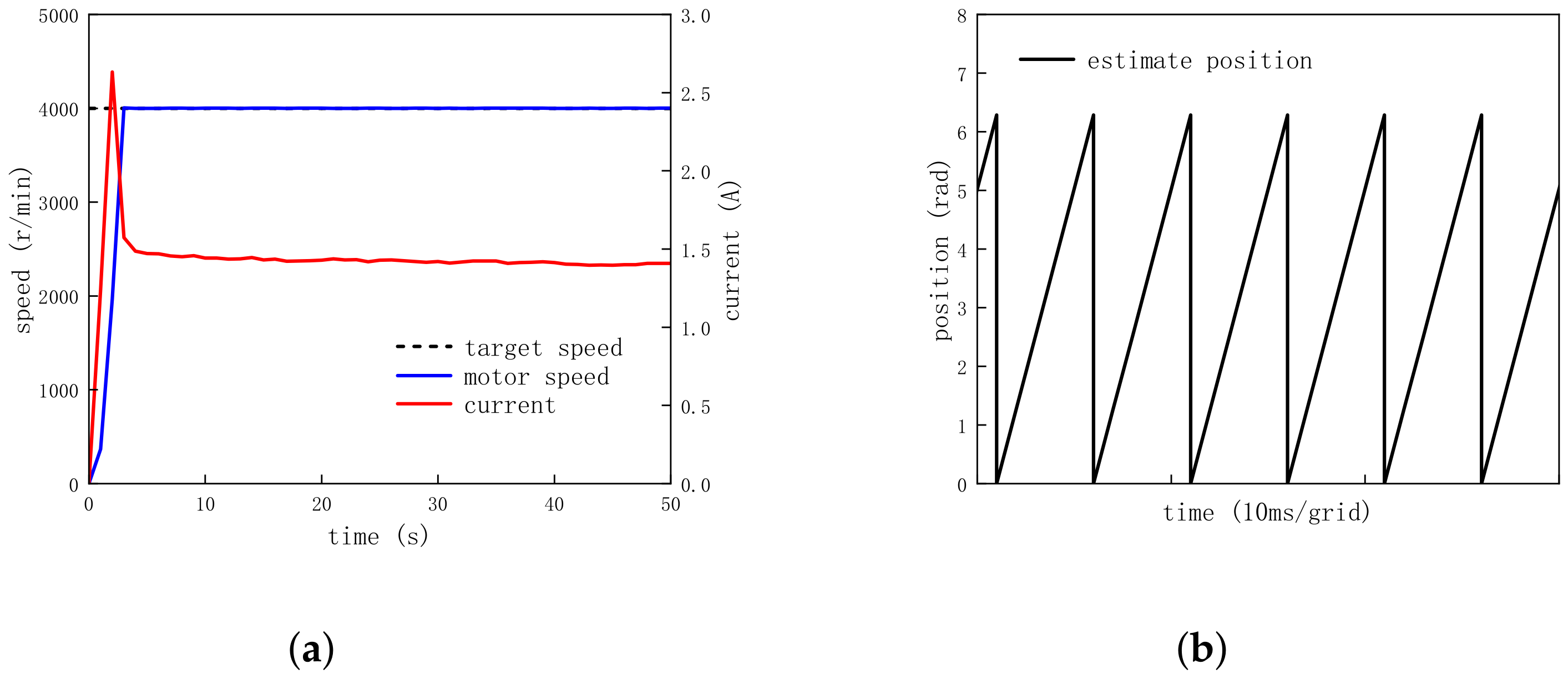
4.4. No-Load Operation
- 1.
- No-load operation;
- 2.
- Acceleration and deceleration operation;
- 3.
- Different load operation;
- 4.
- Simulation of the typical working conditions of the lawnmower.
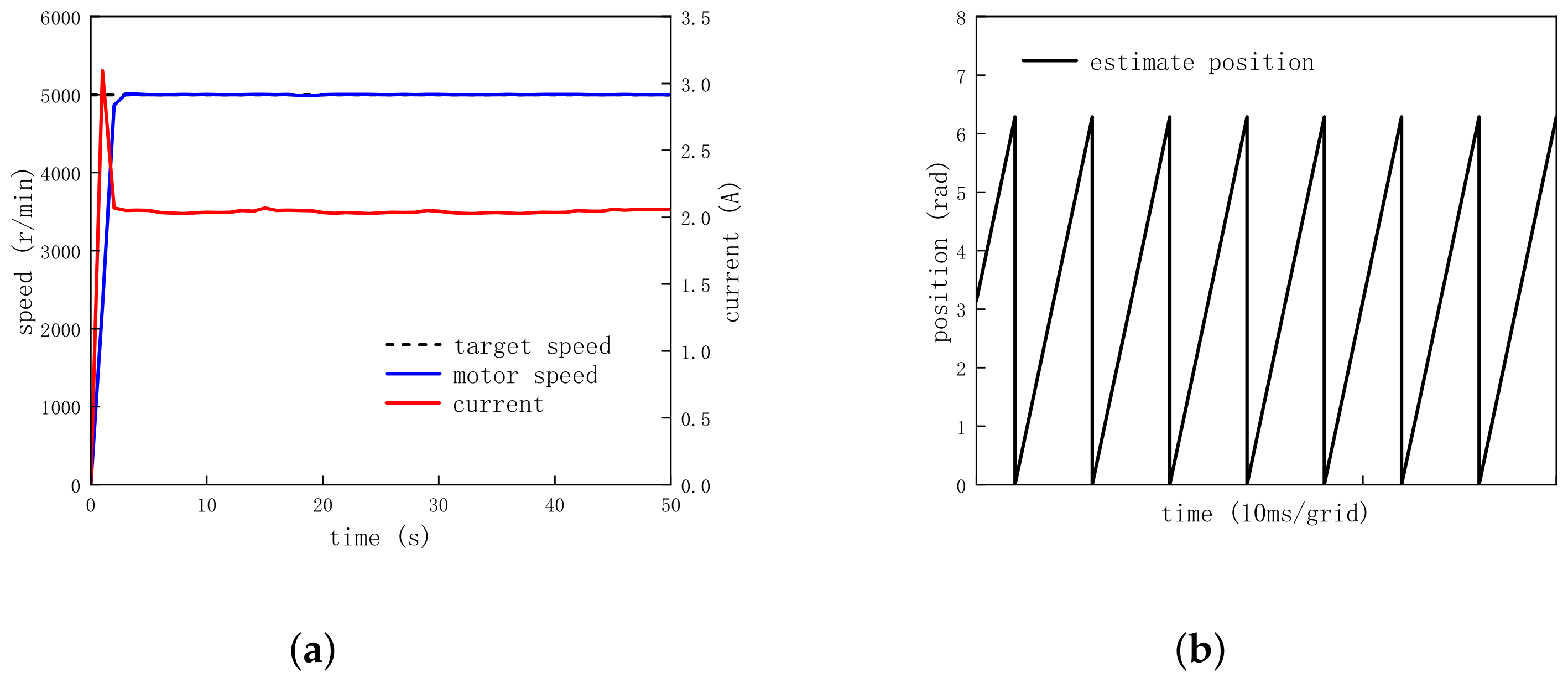
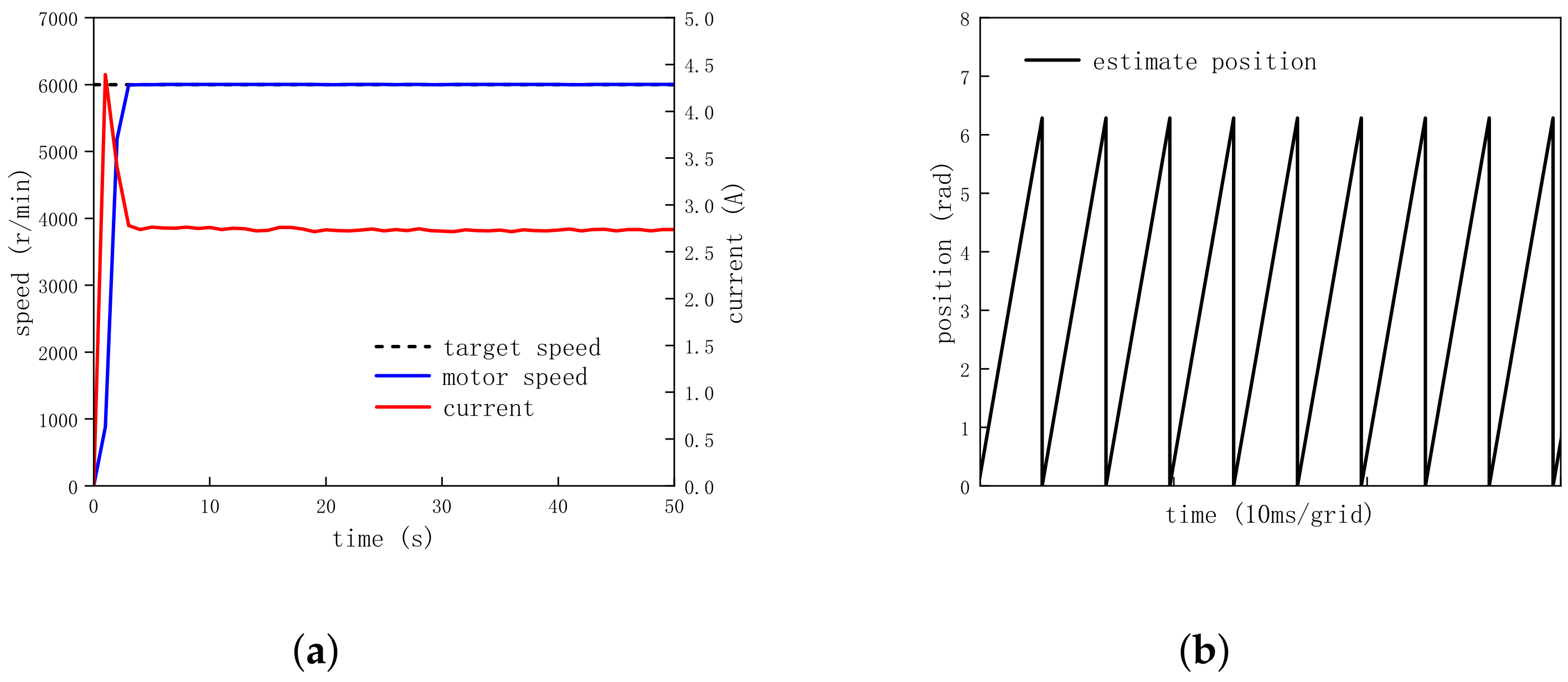
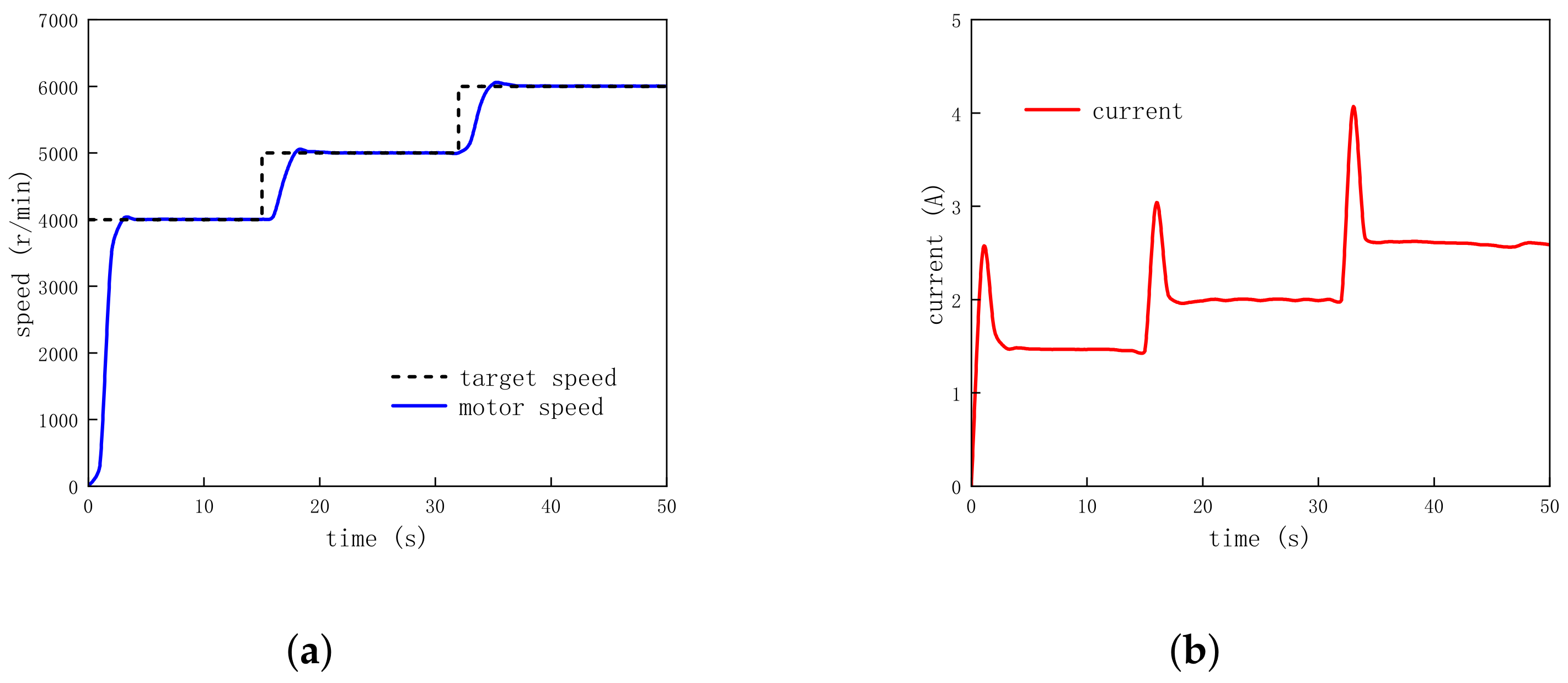
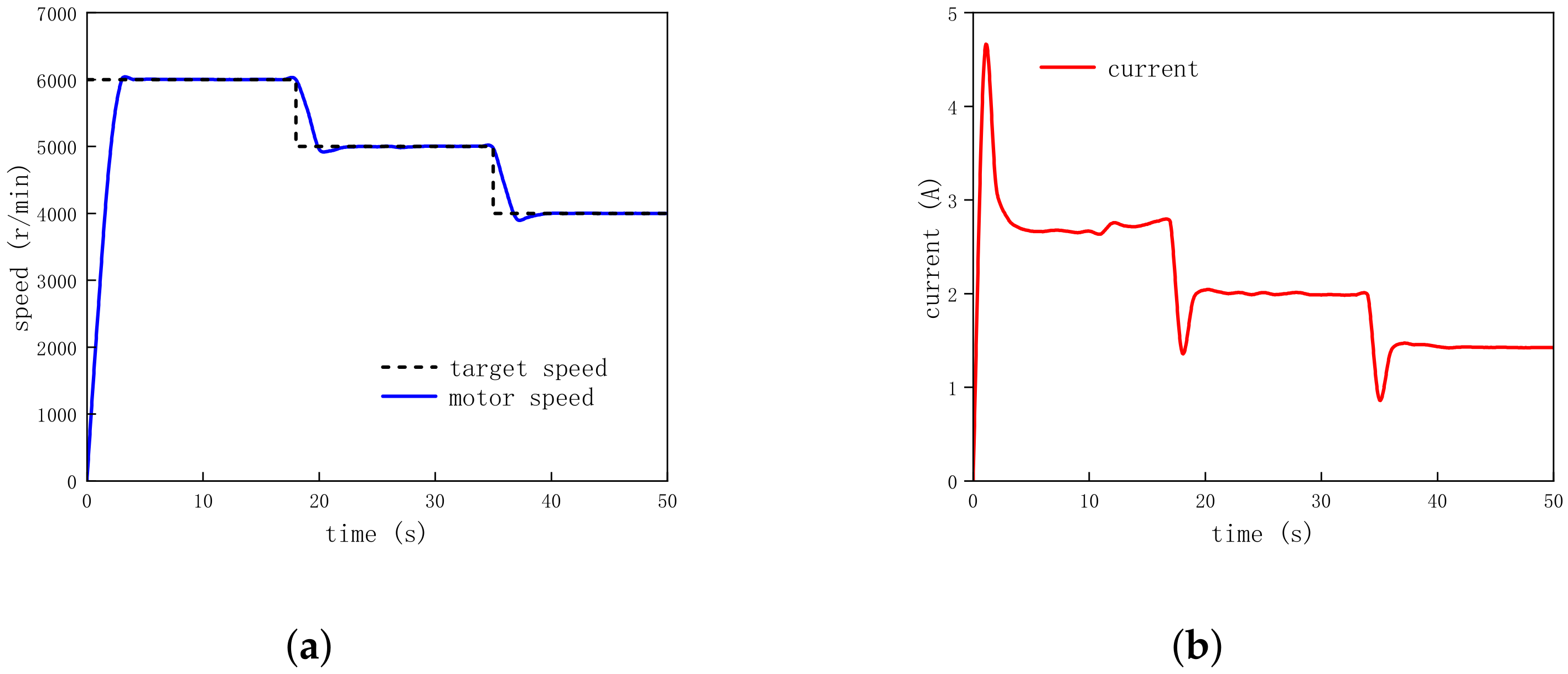
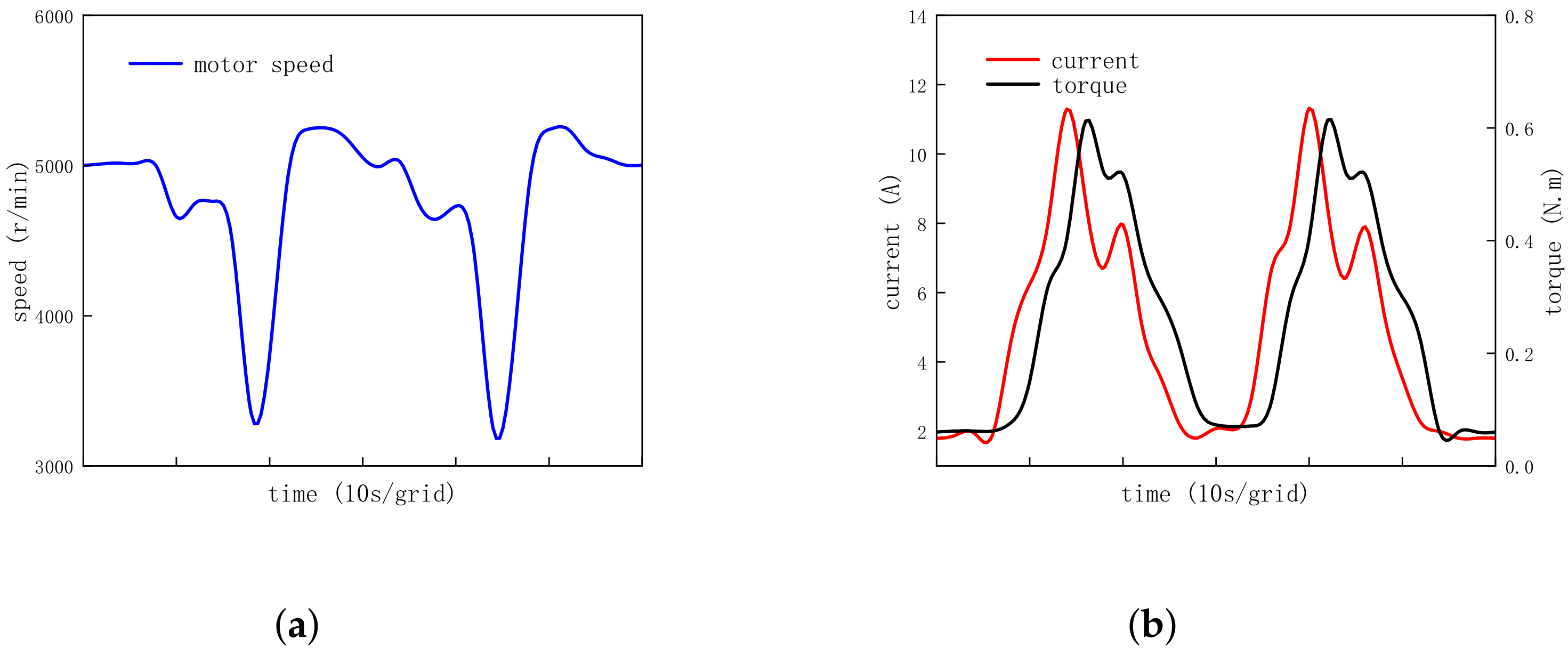
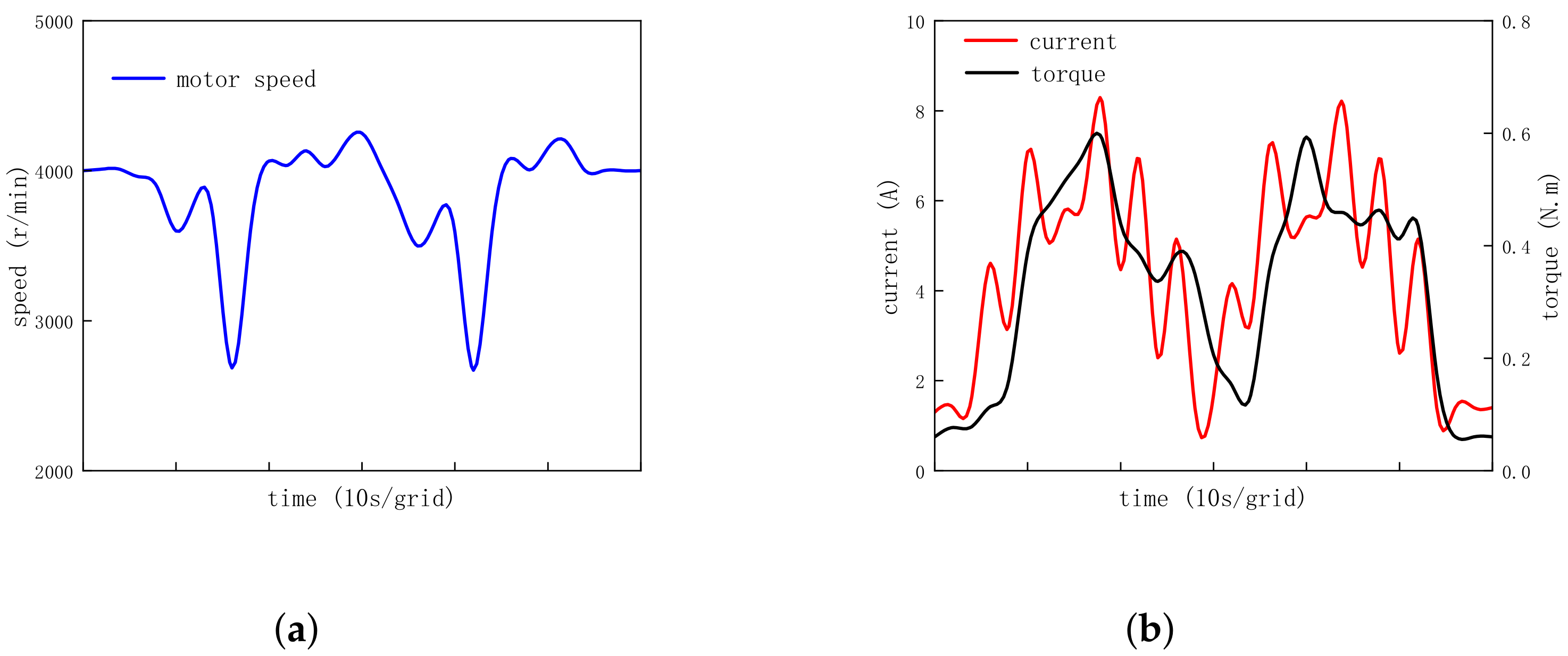
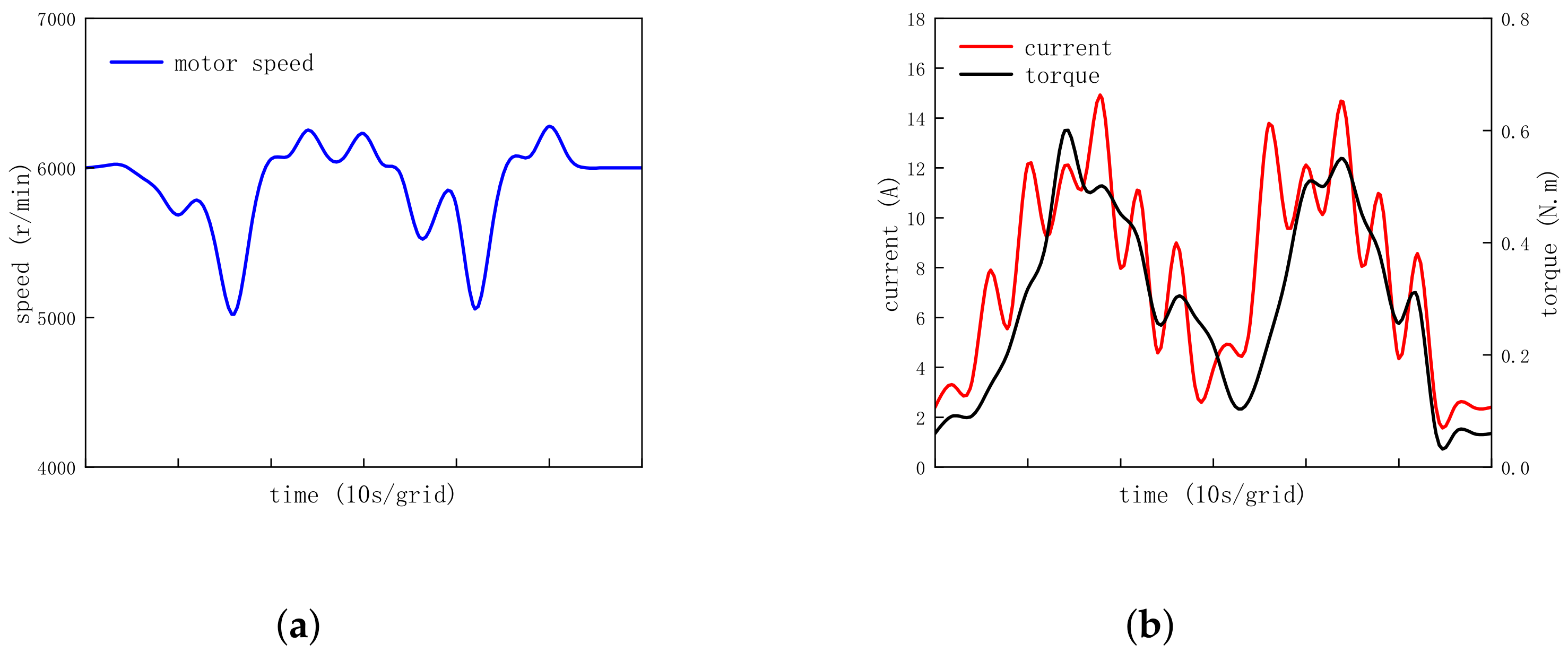
4.5. Acceleration and Deceleration Operation
- 1.
- Set the target speed from 4000 r/min to 5000 r/min and then to 6000 r/min for the acceleration operation;
- 2.
- Set the target speed from 6000 r/min to 5000 r/min and then to 4000 r/min for the deceleration operation.
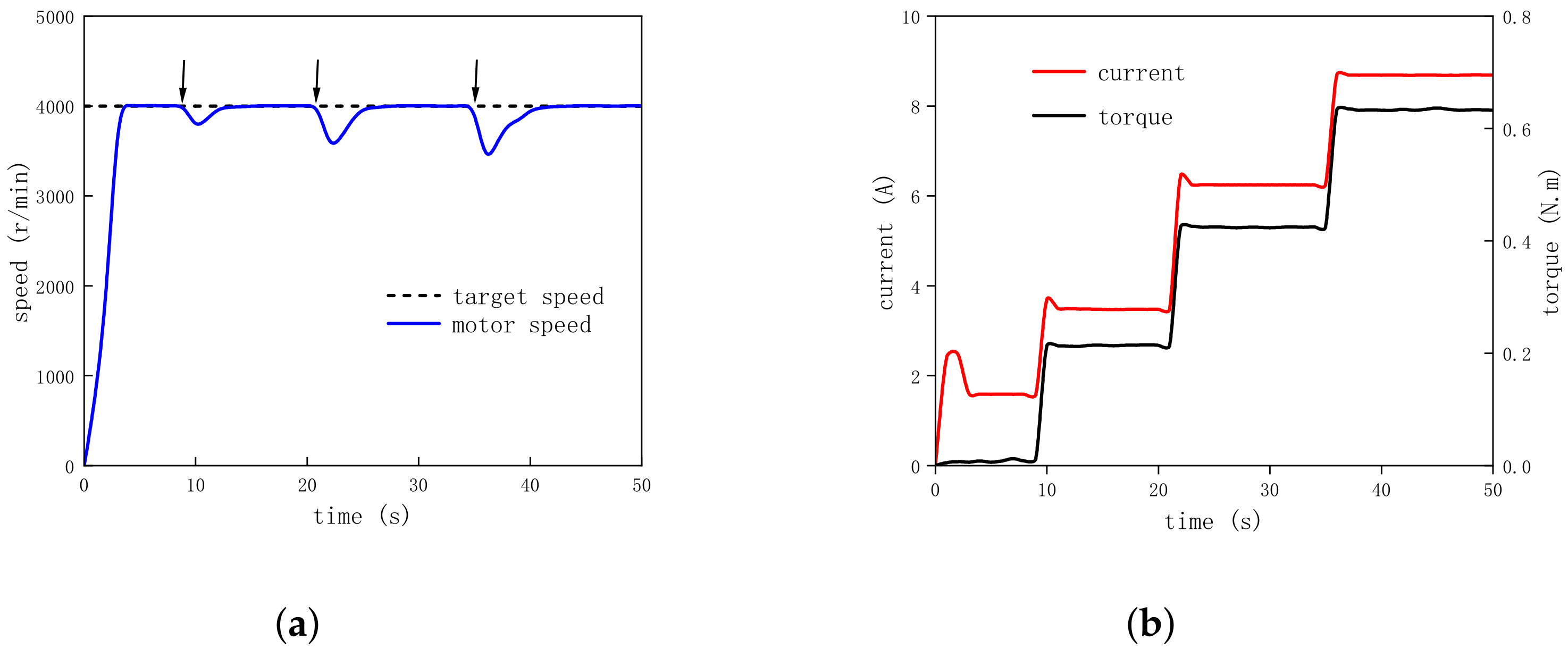
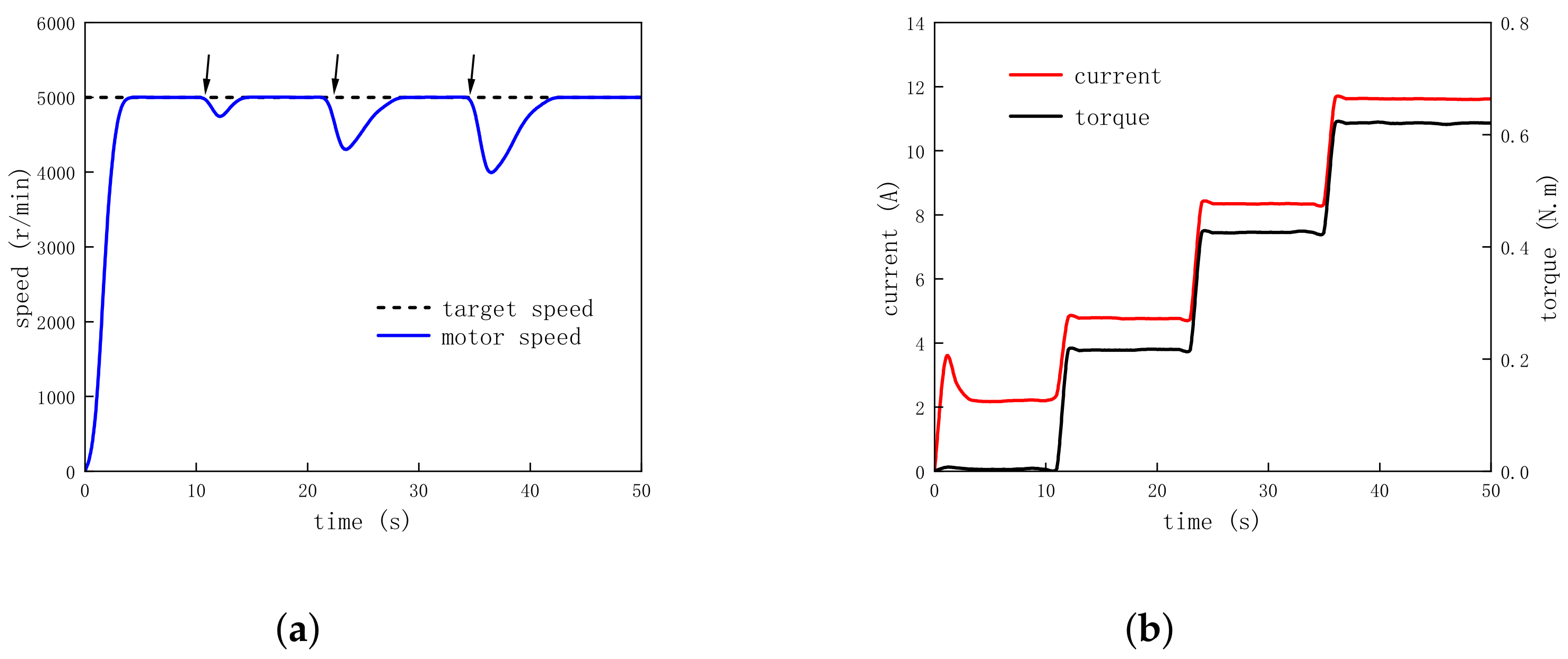
4.6. Different Load Operations
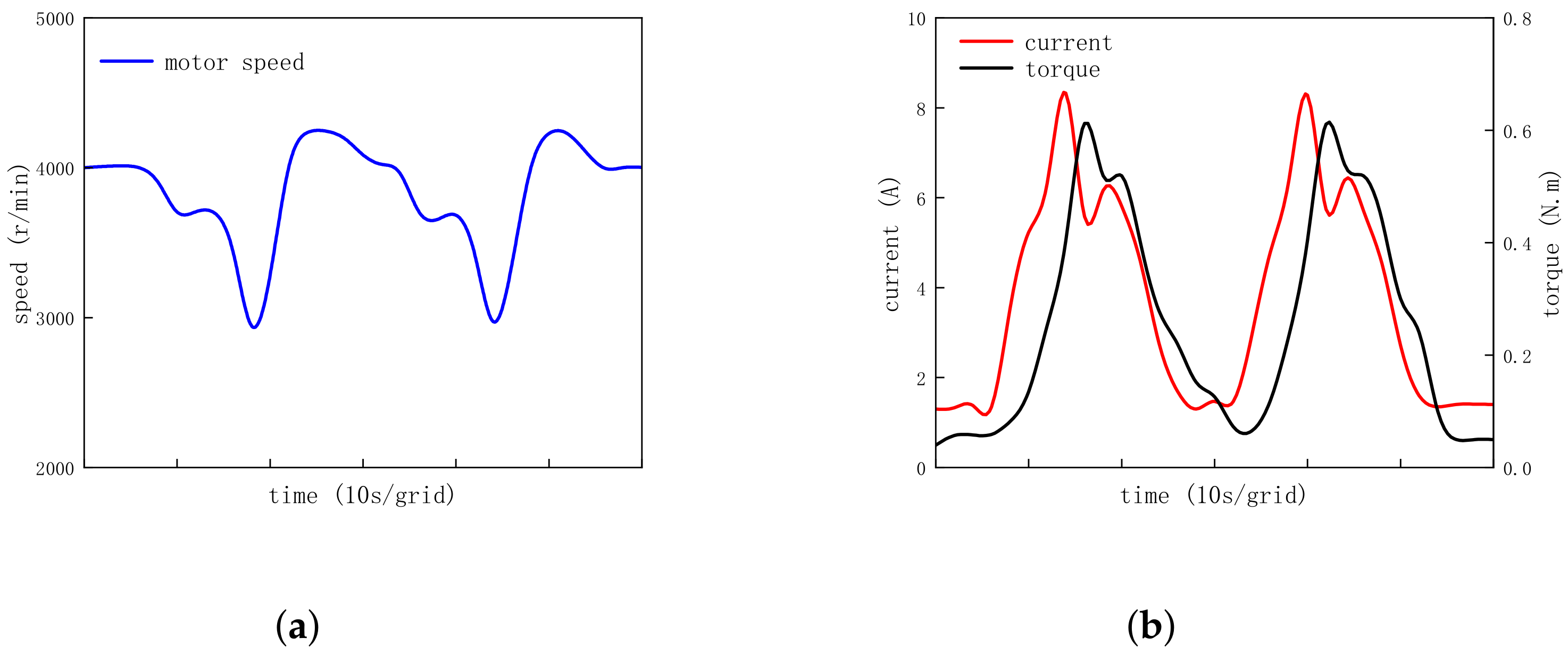
4.7. Simulation of the Typical Working Conditions of a Lawnmower
- 1.
- Lawnmower work in areas of uniform lawn density with smooth load variations;
- 2.
- Lawnmower work in areas of mixed lawn density with random load variations.
4.7.1. Smooth Load Variation Operation
4.7.2. Random Load Variation Operation
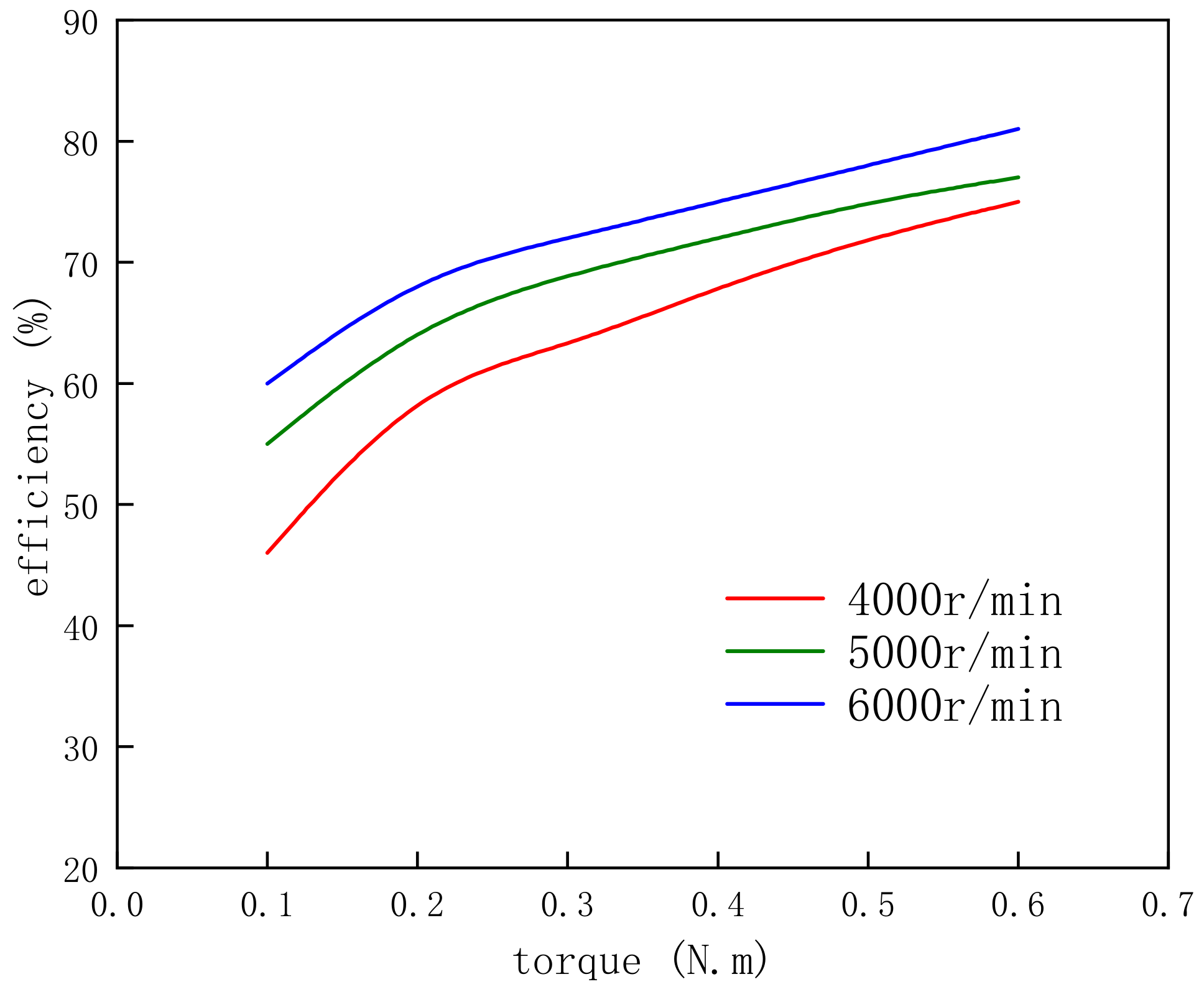
4.8. Motor Efficiency Monitoring
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, C.Q.; Ng, P.K.; Liew, K.W. The Conceptual Synthesis and Development of a Multifunctional Lawnmower. Inventions 2021, 6, 38. [Google Scholar] [CrossRef]
- Ibrahim, B.; Brahmaiah, V.S.; Sharma, P. Design of smart autonomous remote monitored solar powered lawnmower robot. Mater. Today Proc. 2020, 28, 2338–2344. [Google Scholar] [CrossRef]
- Saji, A.; Bastian, G.G.; Muhammad Jaseel, K.; Sajeevan, S. Design and Implementation of Intelligent Lawn-Mower Robot. Int. J. Innov. Sci. Res. Technol. 2018, 3, 477–480. [Google Scholar]
- Daniyan, I.; Balogun, V.; Adeodu, A.; Oladapo, B.; Peter, J.K.; Mpofu, K. Development and performance evaluation of a robot for lawn mowing. Procedia Manuf. 2020, 49, 42–48. [Google Scholar] [CrossRef]
- Dutta, P.P.; Baruah, A.; Konwar, A. A technical review of lawn mower technology. ADBU J. Eng. Technol. 2016, 4, 179–182. [Google Scholar]
- Tahir, T.; Khalid, A.; Arshad, J.; Haider, A.; Rasheed, I.; Rehman, A.U.; Hussen, S. Implementation of an IoT-Based Solar-Powered Smart Lawn Mower. Wirel. Commun. Mob. Comput. 2022, 2022, 1–12. [Google Scholar] [CrossRef]
- Wirtz, J.; Patterson, P.G.; Kunz, W.H.; Gruber, T.; Lu, V.N.; Paluch, S.; Martins, A. Brave new world: Service robots in the frontline. J. Serv. Manag. 2018, 29, 907–931. [Google Scholar] [CrossRef]
- Ahn, H.; Park, H.; Kim, C.; Lee, H. A Review of State-of-the-art Techniques for PMSM Parameter Identifi-cation. J. Electr. Eng. Technol. 2020, 15, 1177–1187. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Chen, C. Review of sensorless control techniques for PMSM drives. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1543–1552. [Google Scholar] [CrossRef]
- Türker, T.; Buyukkeles, U.; Bakan, A.F. A robust predictive current controller for PMSM drives. IEEE Trans. Ind. Electron. 2016, 63, 3906–3914. [Google Scholar] [CrossRef]
- Linares-Flores, J.; Garcia-Rodriguez, C.; Sira-Ramirez, H.; Ramirez-Cardenas, O.D. Robust backstepping tracking controller for low-speed PMSM positioning system: Design, analysis, and implementation. IEEE Trans. Ind. Inform. 2015, 11, 1130–1141. [Google Scholar] [CrossRef]
- Bida, V.M.; Samokhvalov, D.V.; Al-Mahturi, F.S. PMSM vector control techniques—A survey. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow and St. Petersburg, Russia, 29 January–1 February 2018; pp. 577–581. [Google Scholar]
- Wang, T.; Huang, J.; Ye, M.; Chen, J.; Kong, W.; Kang, M.; Yu, M. An EMF observer for PMSM sensorless drives adaptive to stator re-sistance and rotor flux linkage. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 1899–1913. [Google Scholar] [CrossRef]
- Bao, D.; Pan, X.; Wang, Y.; Wang, X.; Li, K. Adaptive synchronous-frequency tracking-mode observer for the sensor-less control of a surface PMSM. IEEE Trans. Ind. Appl. 2018, 54, 6460–6471. [Google Scholar] [CrossRef]
- Yan, H.; Wang, W.; Xu, Y.; Zou, J. Position sensorless control for PMSM drives with single current sensor. IEEE Trans. Ind. Electron. 2022, 70, 178–188. [Google Scholar] [CrossRef]
- Novak, Z.; Novak, M. Adaptive PLL-based sensorless control for improved dynamics of high-speed PMSM. IEEE Trans. Power Electron. 2022, 37, 10154–10165. [Google Scholar] [CrossRef]
- Xuan Mung, N.; Nguyen, N.P.; Pham, D.B.; Dao, N.N.; Hong, S.K. Synthesized landing strategy for quadcopter to land pre-cisely on a vertically moving apron. Mathematics 2022, 10, 1328. [Google Scholar] [CrossRef]
- Volpato Filho, C.J.; Xiao, D.; Vieira, R.P.; Emadi, A. Observers for high-speed sensorless pmsm drives: Design methods, tuning challenges and future trends. IEEE Access 2021, 9, 56397–56415. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Zhang, G.; Xu, D. Comparative investigation of pseudorandom high-frequency signal injection schemes for sensorless IPMSM drives. IEEE Trans. Power Electron. 2016, 32, 2123–2132. [Google Scholar] [CrossRef]
- Wang, S.; Yang, K.; Chen, K. An improved position-sensorless control method at low speed for PMSM based on high-frequency signal injection into a rotating reference frame. IEEE Access 2019, 7, 86510–86521. [Google Scholar] [CrossRef]
- Chen, D.; Lu, K.; Wang, D. An If Startup method with compensation loops for pmsm with smooth transition. IEEJ J. Ind. Appl. 2020, 9, 263–270. [Google Scholar] [CrossRef]
- Nair, S.V.; Hatua, K.; Prasad, N.D.; Reddy, D.K. A Quick I-F Starting of PMSM Drive With Pole Slipping Preven-tion and Reduced Speed Oscillations. IEEE Trans. Ind. Electron. 2020, 68, 6650–6661. [Google Scholar] [CrossRef]
- Mesloub, H.; Boumaaraf, R.; Benchouia, M.T.; Goléa, A.; Goléa, N.; Srairi, K. Comparative study of conventional DTC and DTC_SVM based control of PMSM motor—Simulation and experimental results. Math. Comput. Simul. 2020, 167, 296–307. [Google Scholar] [CrossRef]
- Song, X.; Fang, J.; Han, B.; Zheng, S. Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error. IEEE Trans. Power Electron. 2015, 31, 1438–1449. [Google Scholar] [CrossRef]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Chi, X.; Wang, C.; Wu, Q.; Yang, J.; Lin, W.; Zeng, P.; Li, H.; Shao, M. A ripple suppression of sensorless FOC of PMSM electrical drive system based on MRAS. Results Eng. 2023, 20, 101427. [Google Scholar] [CrossRef]
- Li, M.; Lv, K.; Wen, C.; Zhao, Q.; Zhao, X.; Wang, X. Sensorless control of permanent magnet synchronous linear motor based on sliding mode variable structure MRAS flux observation. Prog. Electromagn. Res. Lett. 2021, 101, 89–97. [Google Scholar] [CrossRef]
- Yang, H.; Yang, R.; Hu, W.; Huang, Z. FPGA-based sensorless speed control of PMSM using enhanced perfor-mance controller based on the reduced-order EKF. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 9, 289–301. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wang, Y.; Yan, L. An improved delay-suppressed sliding-mode observer for sensorless vec-tor-controlled PMSM. IEEE Trans. Ind. Electron. 2019, 67, 5913–5923. [Google Scholar] [CrossRef]
- Niedermayr, P.; Alberti, L.; Bolognani, S.; Abl, R. Implementation and experimental validation of ultra-high-speed pmsm sensorless control by means of extended kalman filter. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 3337–3344. [Google Scholar] [CrossRef]
- Toso, F.; Da Ru, D.; Alotto, P.; Bolognani, S. A moving horizon estimator for the speed and rotor position of a sensorless PMSM drive. IEEE Trans. Power Electron. 2018, 34, 580–587. [Google Scholar] [CrossRef]
- Anwer, A.M.O.; Omar, F.A.; Bakir, H.; Kulaksiz, A.A. Sensorless control of a PMSM drive using EKF for wide speed range supplied by MPPT based solar PV system. Elektron. Ir Elektrotechnika 2020, 26, 32–39. [Google Scholar] [CrossRef]
- Do, T.D.; Xuan-Mung, N.; Nguyen, N.P.; Lee, J.W.; Lee, Y.S.; Lee, S.T.; Hong, S.K. Multi-sensor-based Target Pose Estimation for Autonomous Precision Perching of Nano Aerial Vehicles. In Proceedings of the 2022 22nd International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 27 November–1 December 2022; pp. 1565–1571. [Google Scholar]





| Item | Value | Unit |
|---|---|---|
| DC supply voltage | 24 | V |
| Flux linkage | 0.024 | Wb |
| Stator resistance | 0.03 | ohm |
| Stator inductance | 0.08 | mH |
| Number of pole pairs | 3 | / |
| Item | Value | Unit |
|---|---|---|
| Rated voltage | 36 | V |
| Rated power | 500 | W |
| Rated torque | 0.6 | N·m |
| Number of pole pairs | 3 | / |
| Torque coefficient | 0.036 | Nm/A |
| Line-to-line resistance | 0.055 | ohm |
| Line-to-line inductance | 0.16 | mH |
| Target Speed (r/min) | Peak Current at Startup (A) | Current During Stable Operation (A) |
|---|---|---|
| 4000 | 2.63 | 1.42 |
| 5000 | 3.12 | 2.05 |
| 6000 | 4.45 | 2.74 |
| Load Value (N·m) | Load Duration (s) | Implementation Period |
|---|---|---|
| 0.1 | 2 | |
| 0.2 | 2 | |
| 0.3 | 2 | |
| 0.4 | 2 | |
| 0.5 | 2 | |
| 0.6 | 2 | 2 |
| 0.5 | 2 | |
| 0.4 | 2 | |
| 0.3 | 2 | |
| 0.2 | 2 | |
| 0.1 | 2 |
| Load Value (N·m) | Load Duration (s) | Implementation Period |
|---|---|---|
| 0.3 | 2 | |
| 0.1 | 2 | |
| 0.5 | 2 | |
| 0.2 | 2 | |
| 0.6 | 2 | |
| 0.3 | 2 | 2 |
| 0.5 | 2 | |
| 0.2 | 2 | |
| 0.4 | 2 | |
| 0.1 | 2 | |
| 0.3 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, D.; Wang, D.; He, D.; Zhang, P. Position Sensorless Vector Control System for Lawnmower Permanent Magnet Synchronous Motor Based on Extended Kalman Filter. Energies 2024, 17, 1230. https://doi.org/10.3390/en17051230
Shan D, Wang D, He D, Zhang P. Position Sensorless Vector Control System for Lawnmower Permanent Magnet Synchronous Motor Based on Extended Kalman Filter. Energies. 2024; 17(5):1230. https://doi.org/10.3390/en17051230
Chicago/Turabian StyleShan, Dongri, Di Wang, Dongmei He, and Peng Zhang. 2024. "Position Sensorless Vector Control System for Lawnmower Permanent Magnet Synchronous Motor Based on Extended Kalman Filter" Energies 17, no. 5: 1230. https://doi.org/10.3390/en17051230
APA StyleShan, D., Wang, D., He, D., & Zhang, P. (2024). Position Sensorless Vector Control System for Lawnmower Permanent Magnet Synchronous Motor Based on Extended Kalman Filter. Energies, 17(5), 1230. https://doi.org/10.3390/en17051230






