Characterization of the Macroscopic Impact of Diverse Microscale Transport Mechanisms of Gas in Micro-Nano Pores and Fractures
Abstract
1. Introduction
2. Mechanism and Model
2.1. Transport Mechanism of Gas
2.1.1. Bulk Gas
Flow Pattern
Continuous Flow
Slippage Flow
Knudsen Diffusion
Transition Flow
2.1.2. Adsorption Gas
2.2. Changing Mechanism of Reservoir
2.2.1. Stress Sensitive Effect
2.2.2. Matrix Shrinkage Effect
2.2.3. Effect of Adsorption Layer
2.3. Transport Model of Gas
3. Model Validation
4. Analysis and Discussion
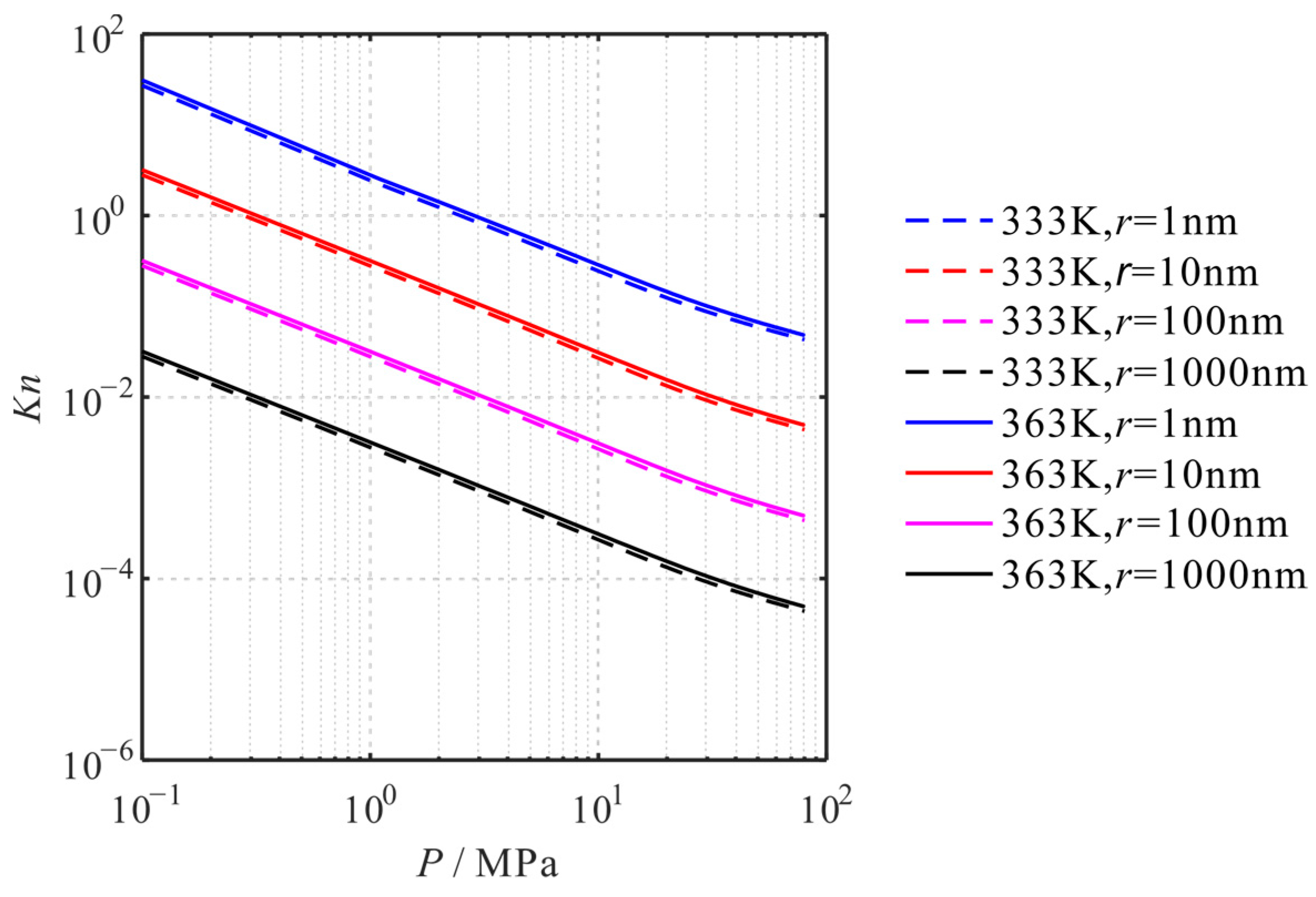
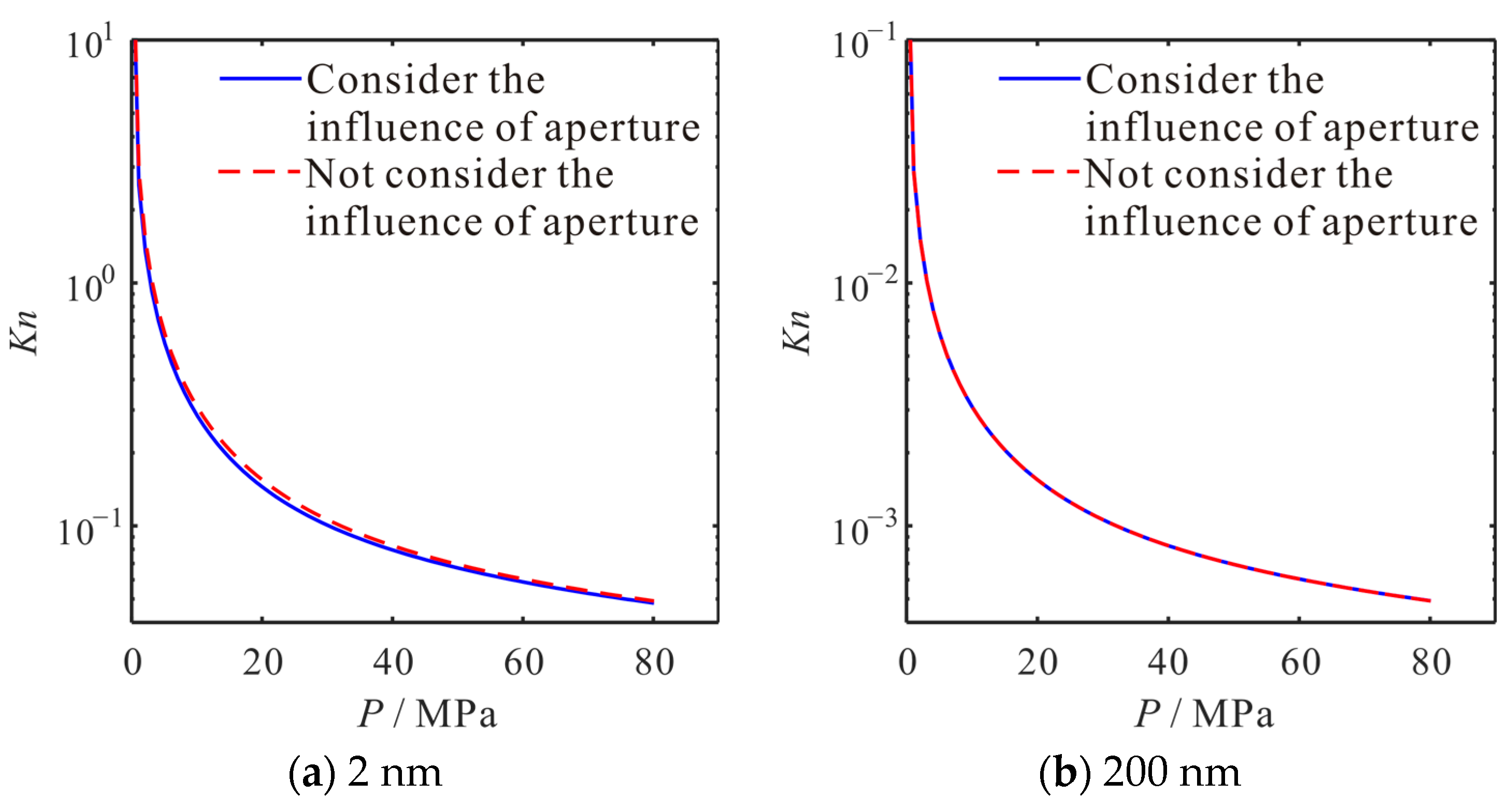
4.1. Influence for Knudsen Number
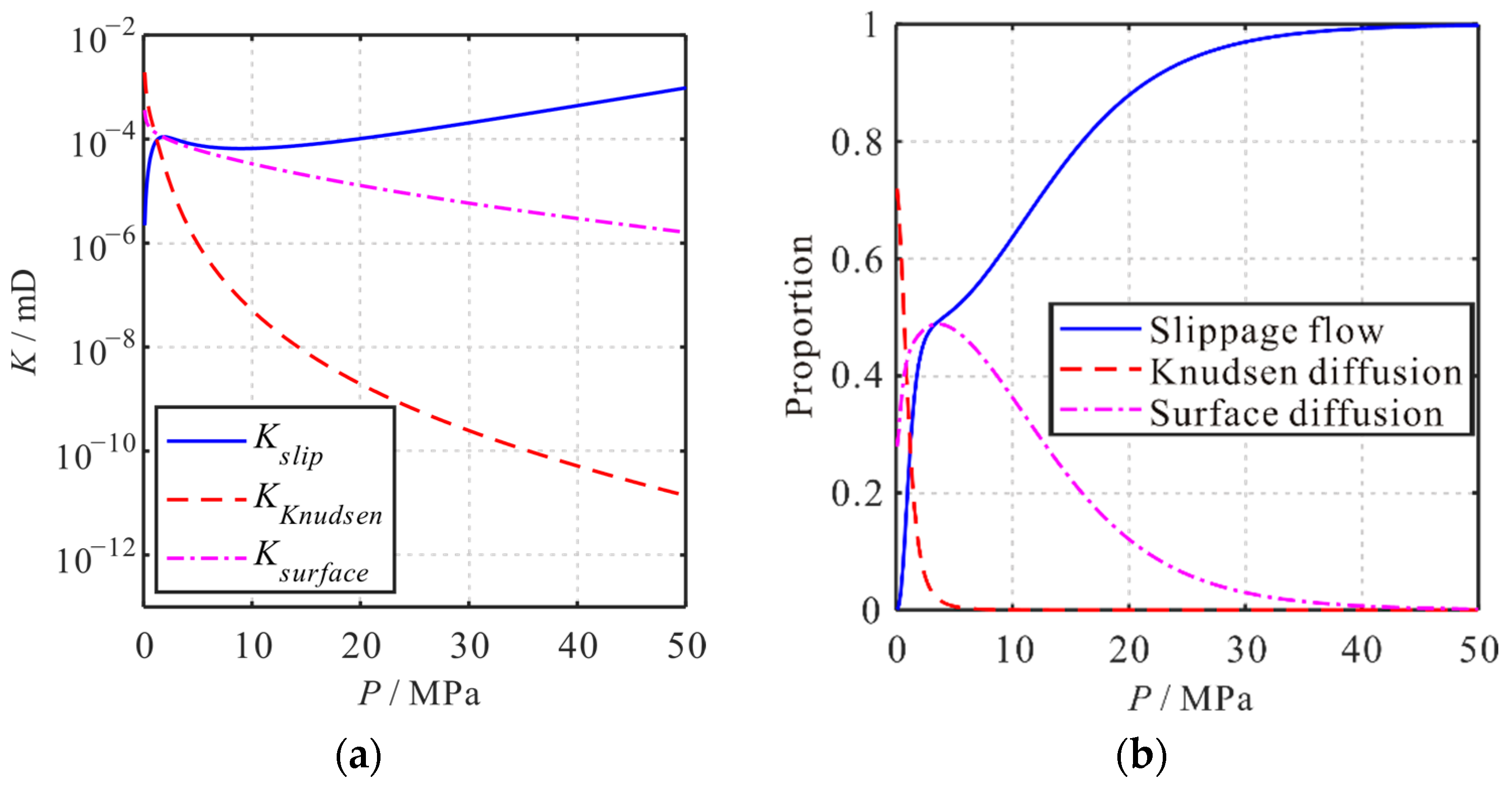
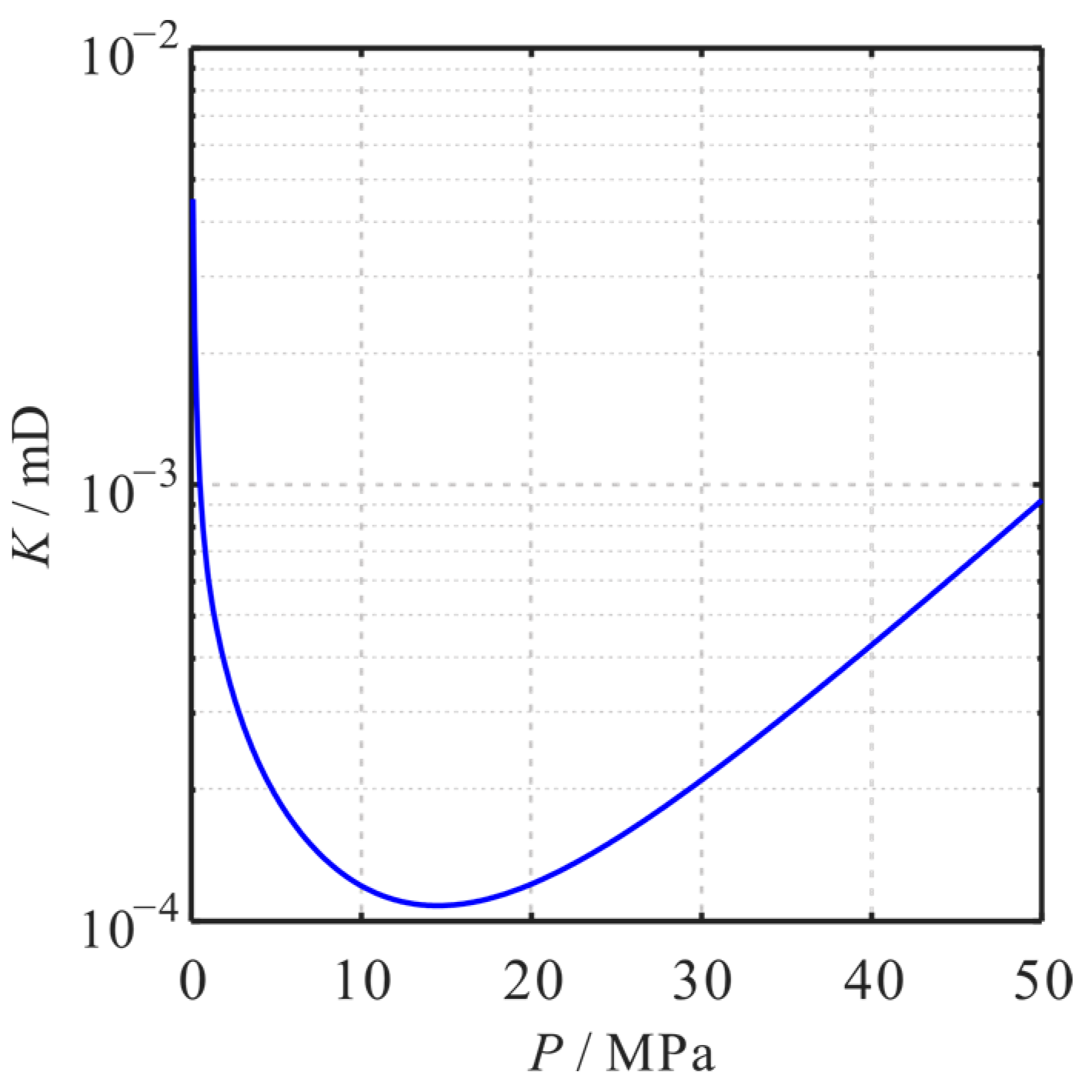
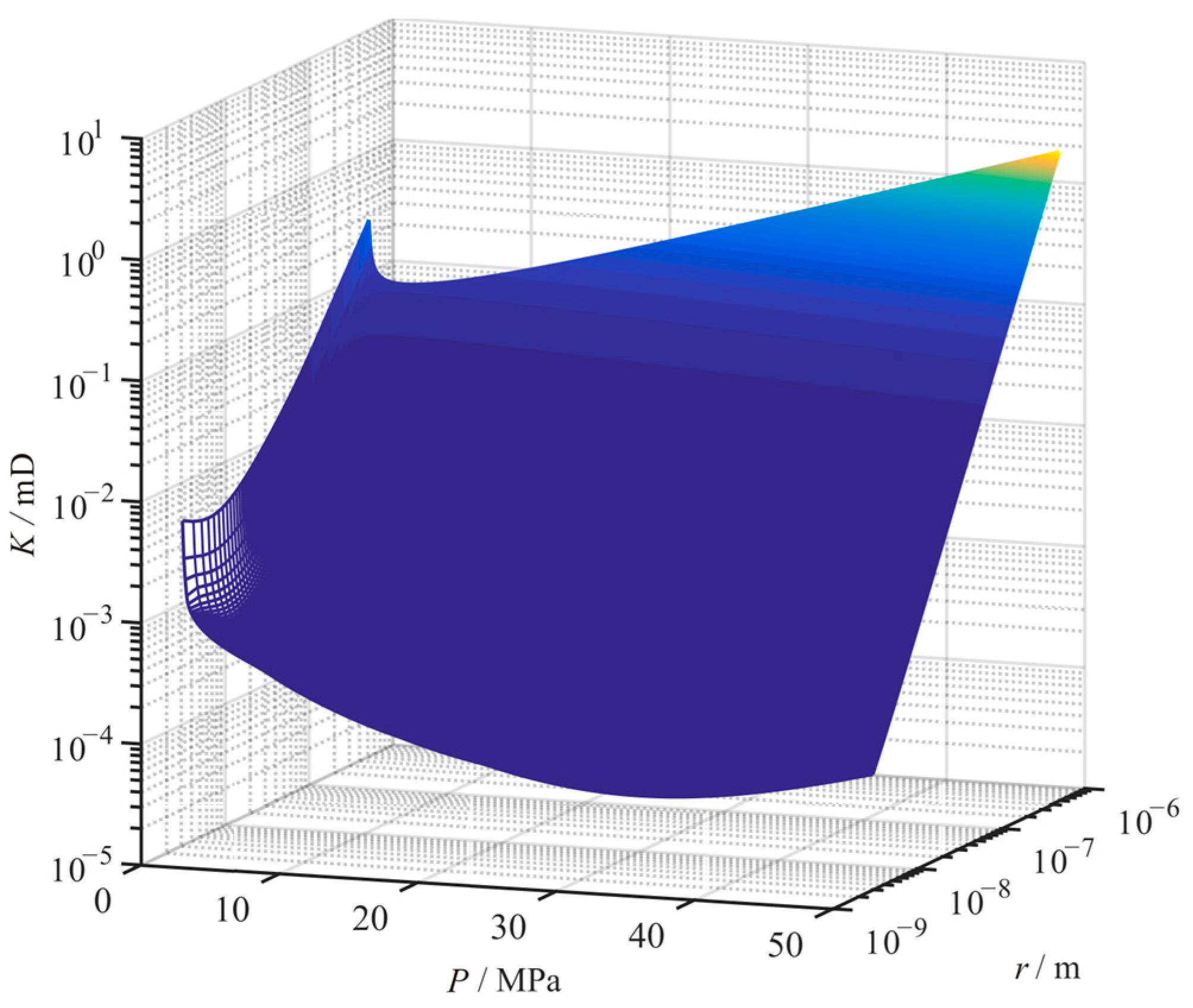
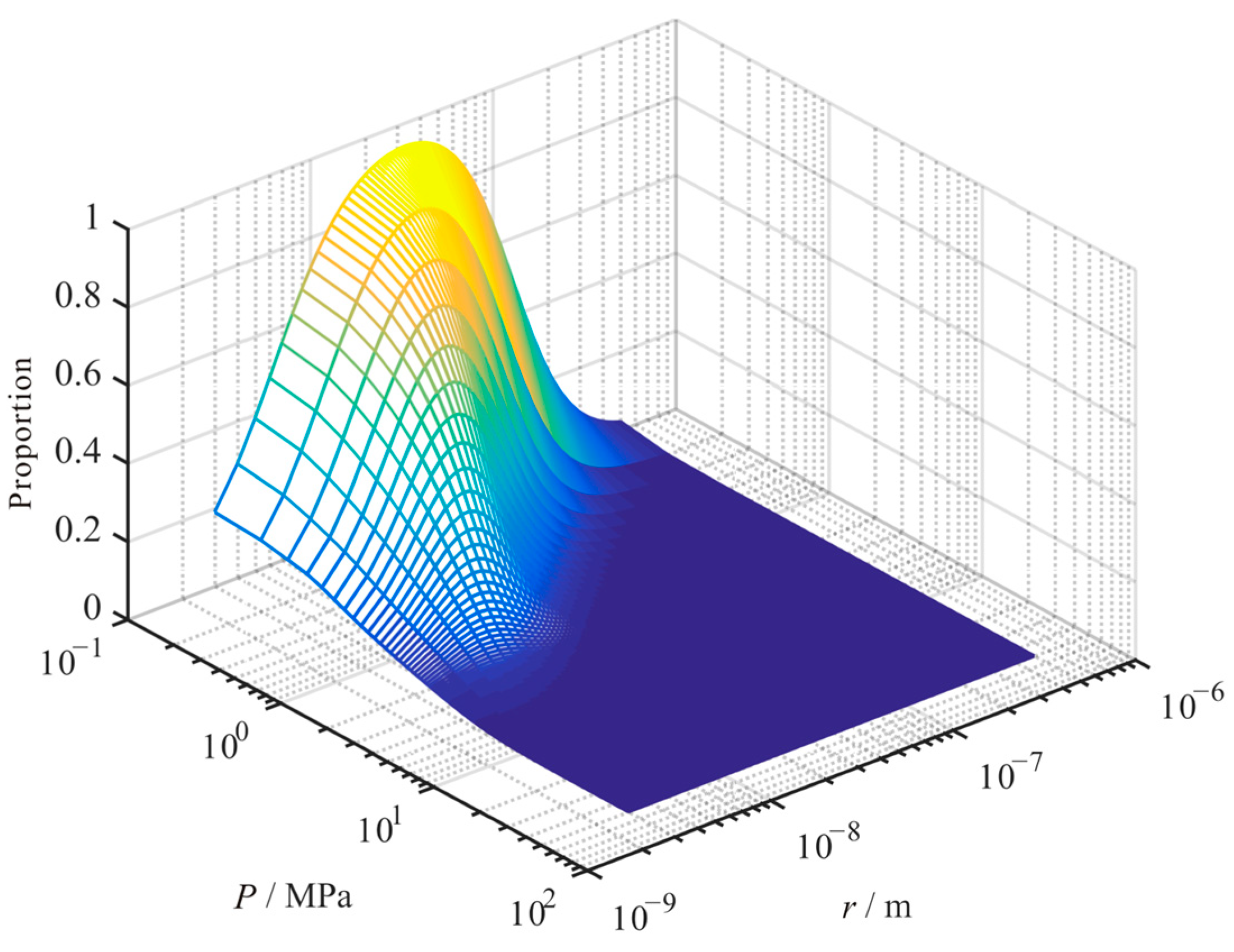
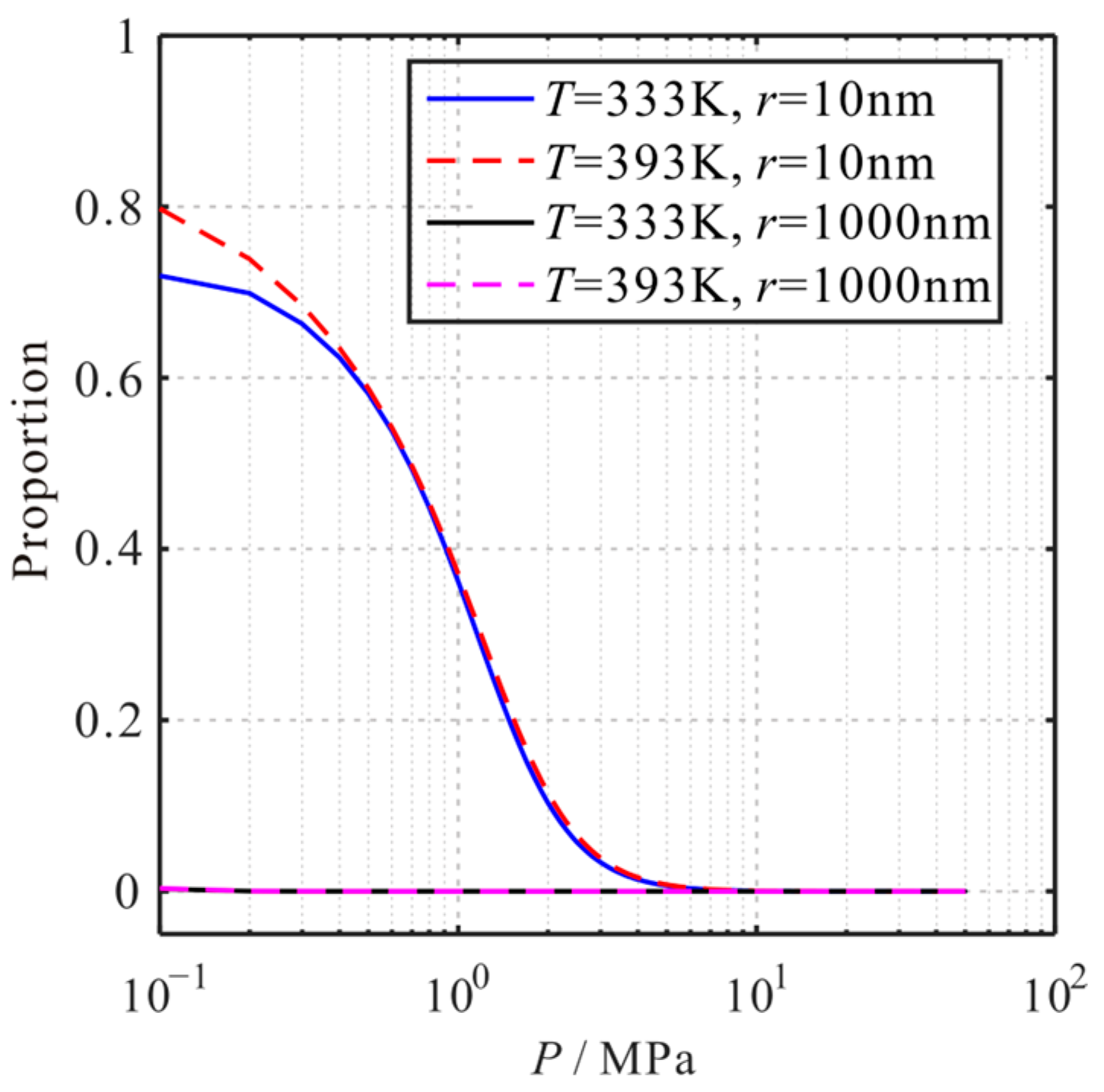
4.2. Influence of Pressure
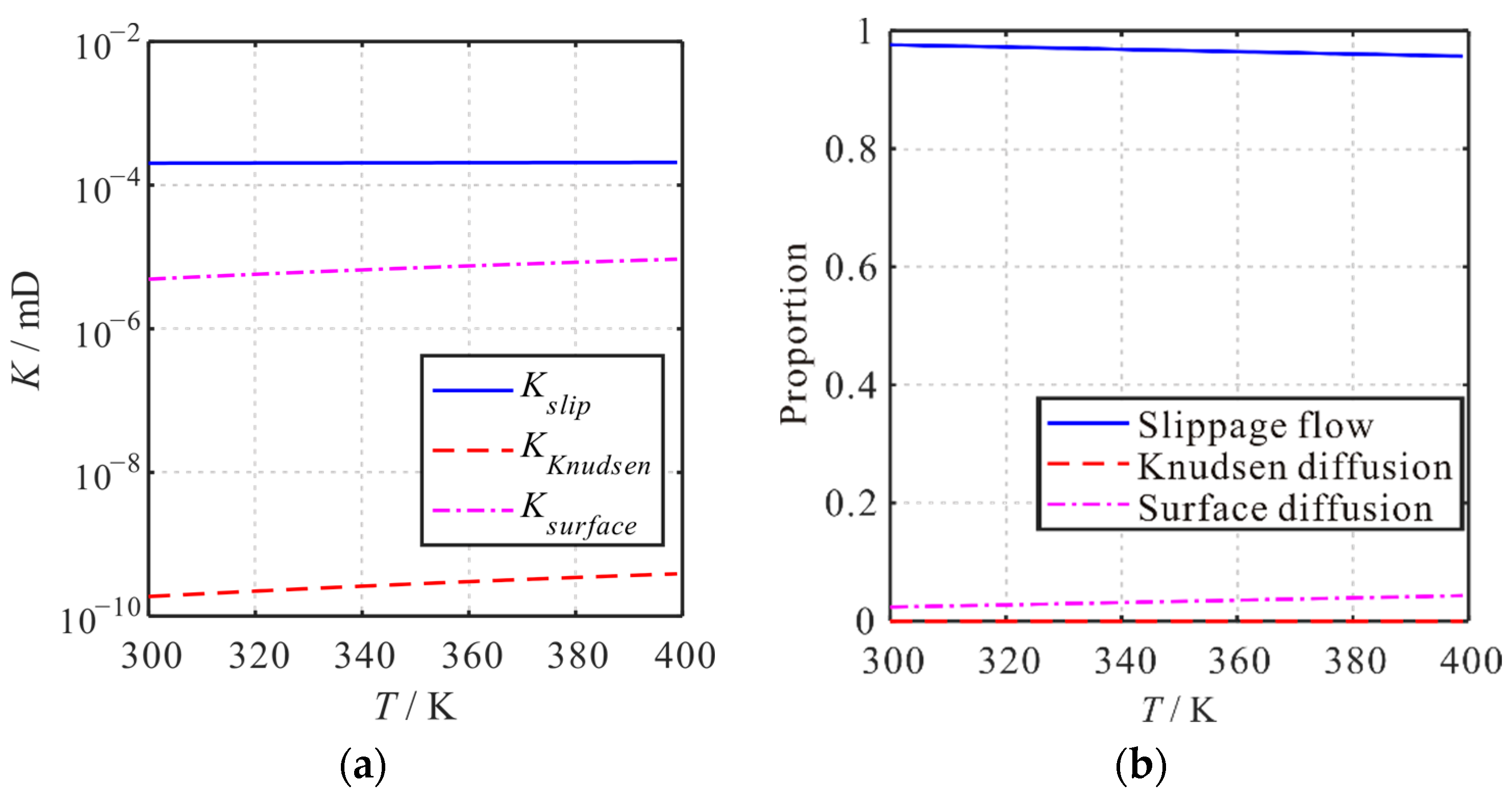
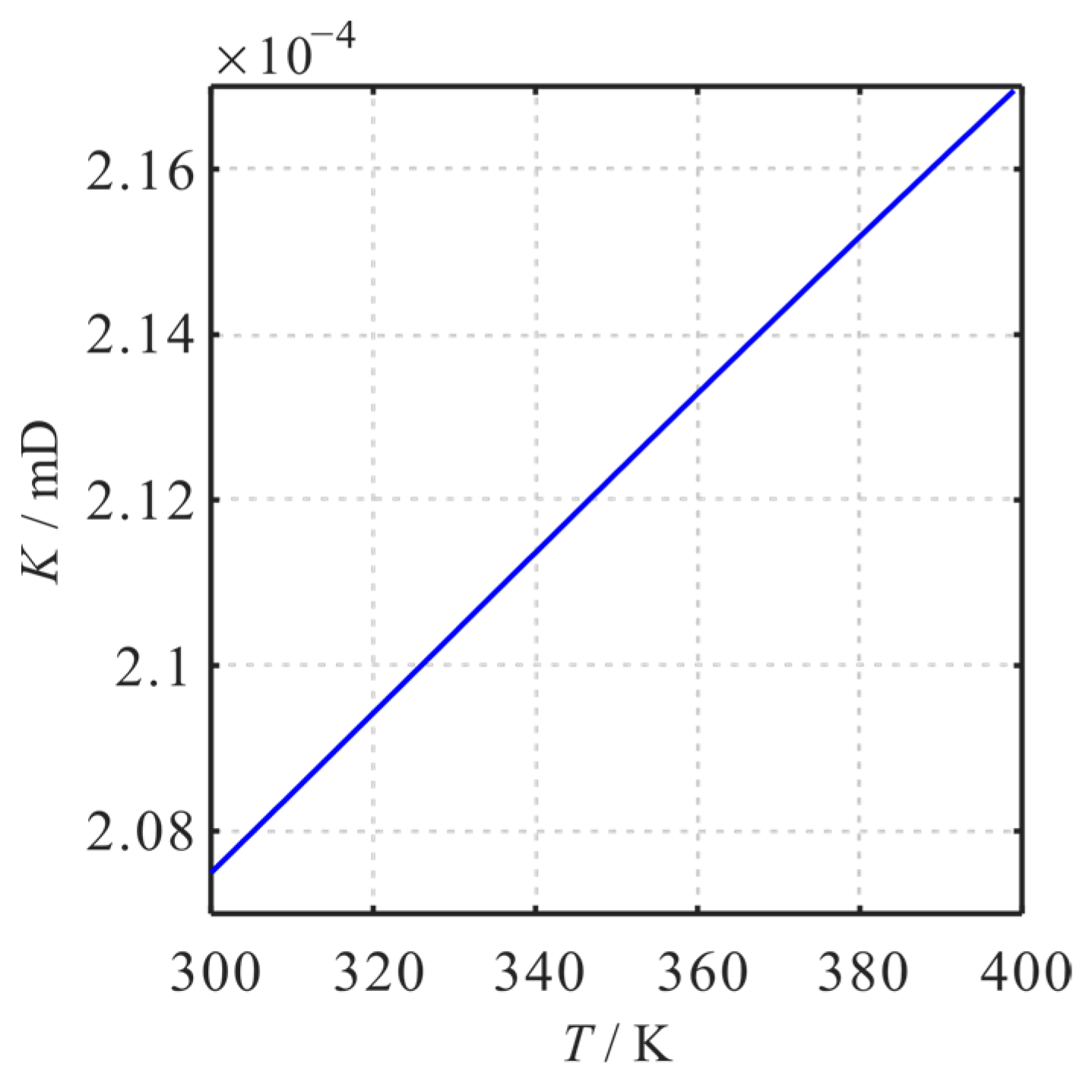
4.3. Influence of Temperature
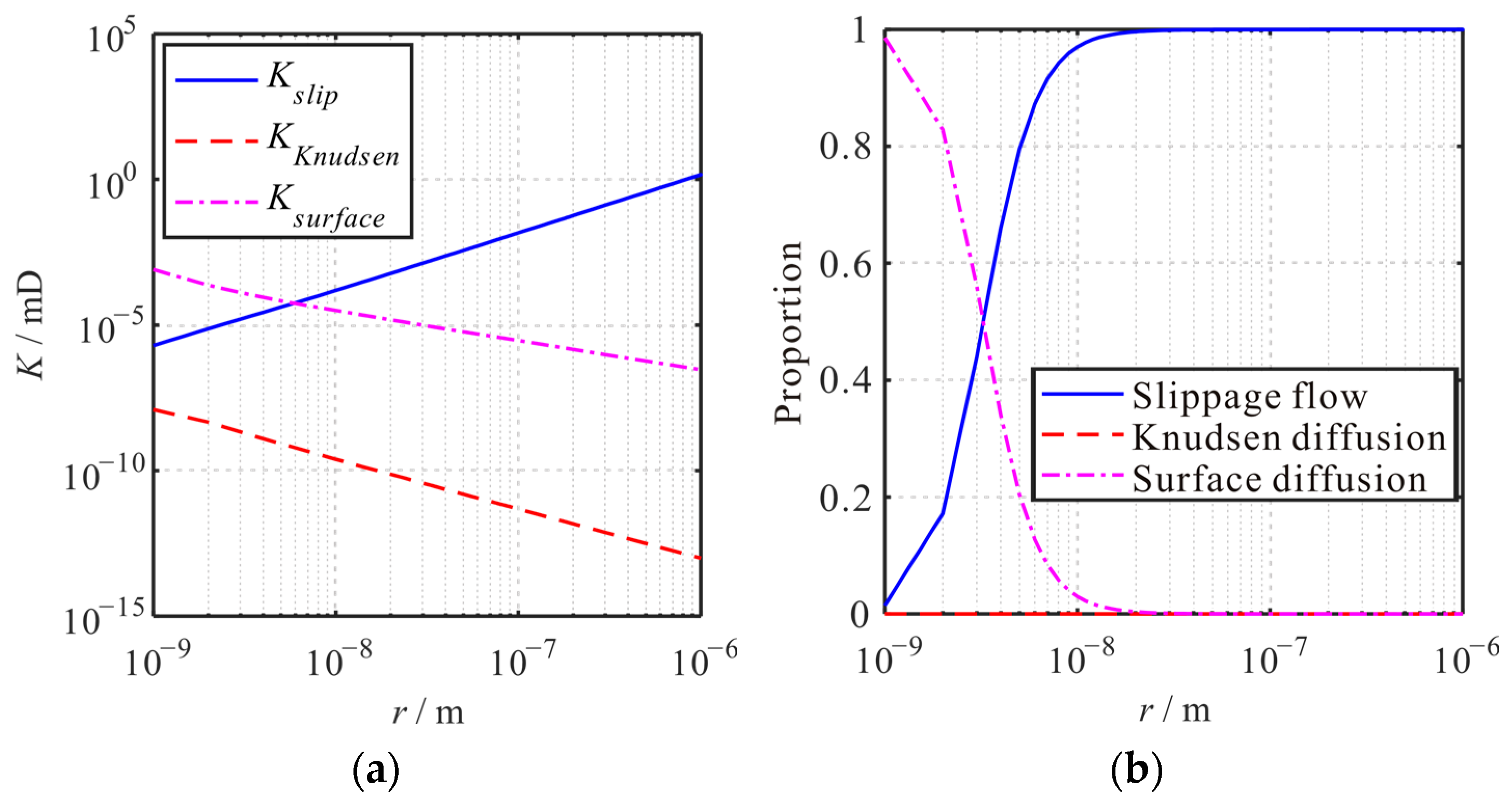
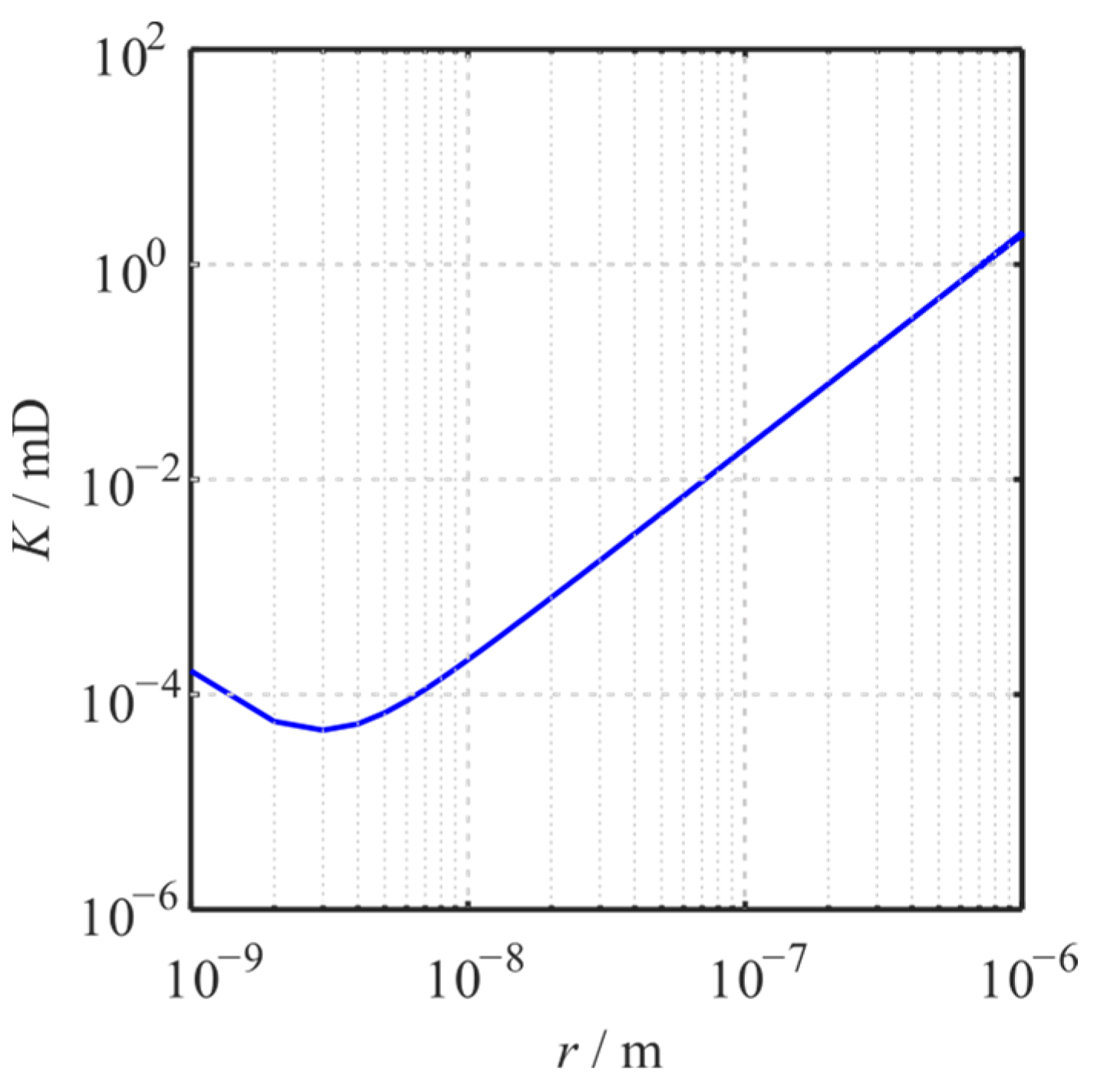
4.4. Influence of Pore Size
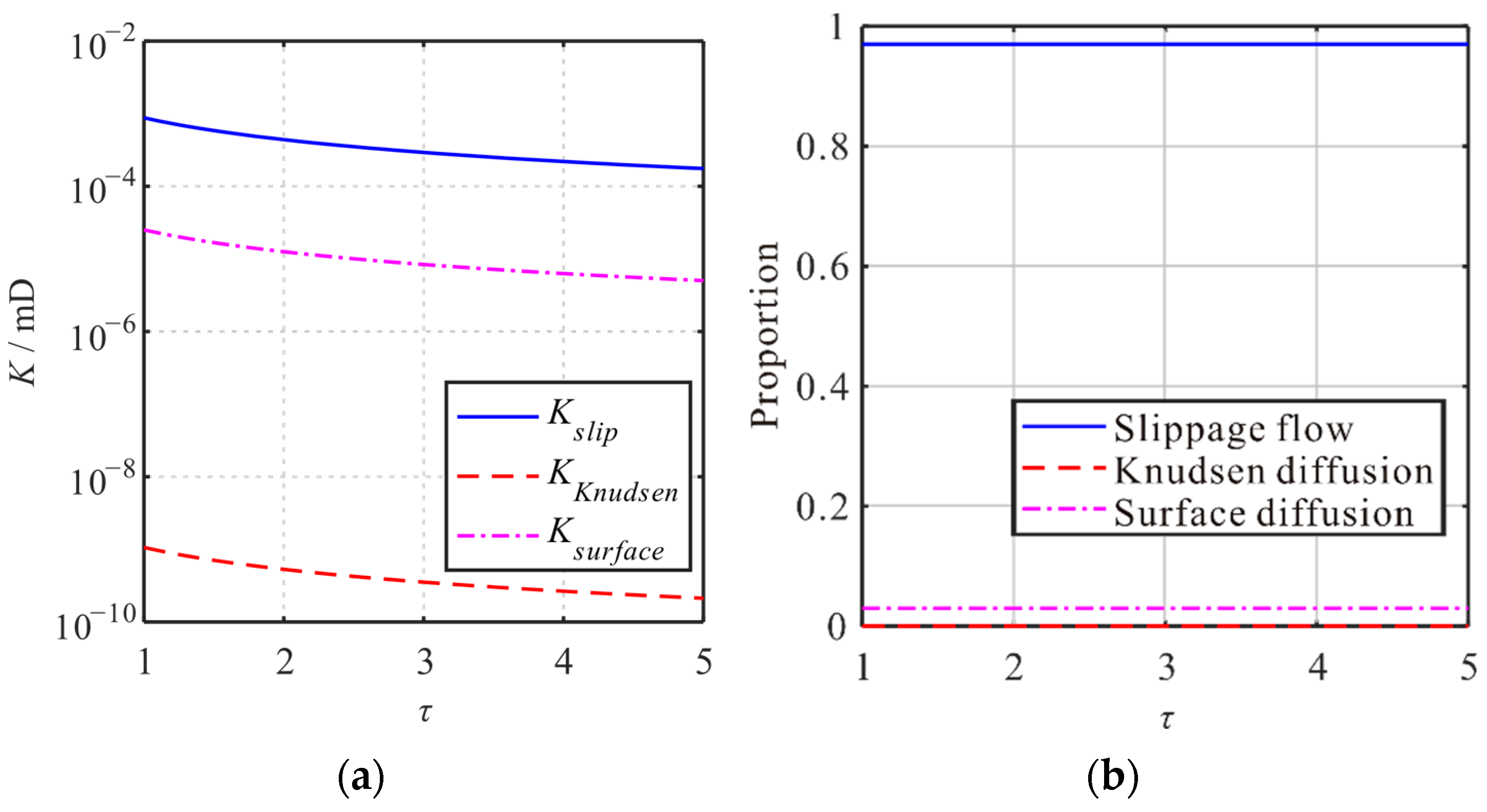
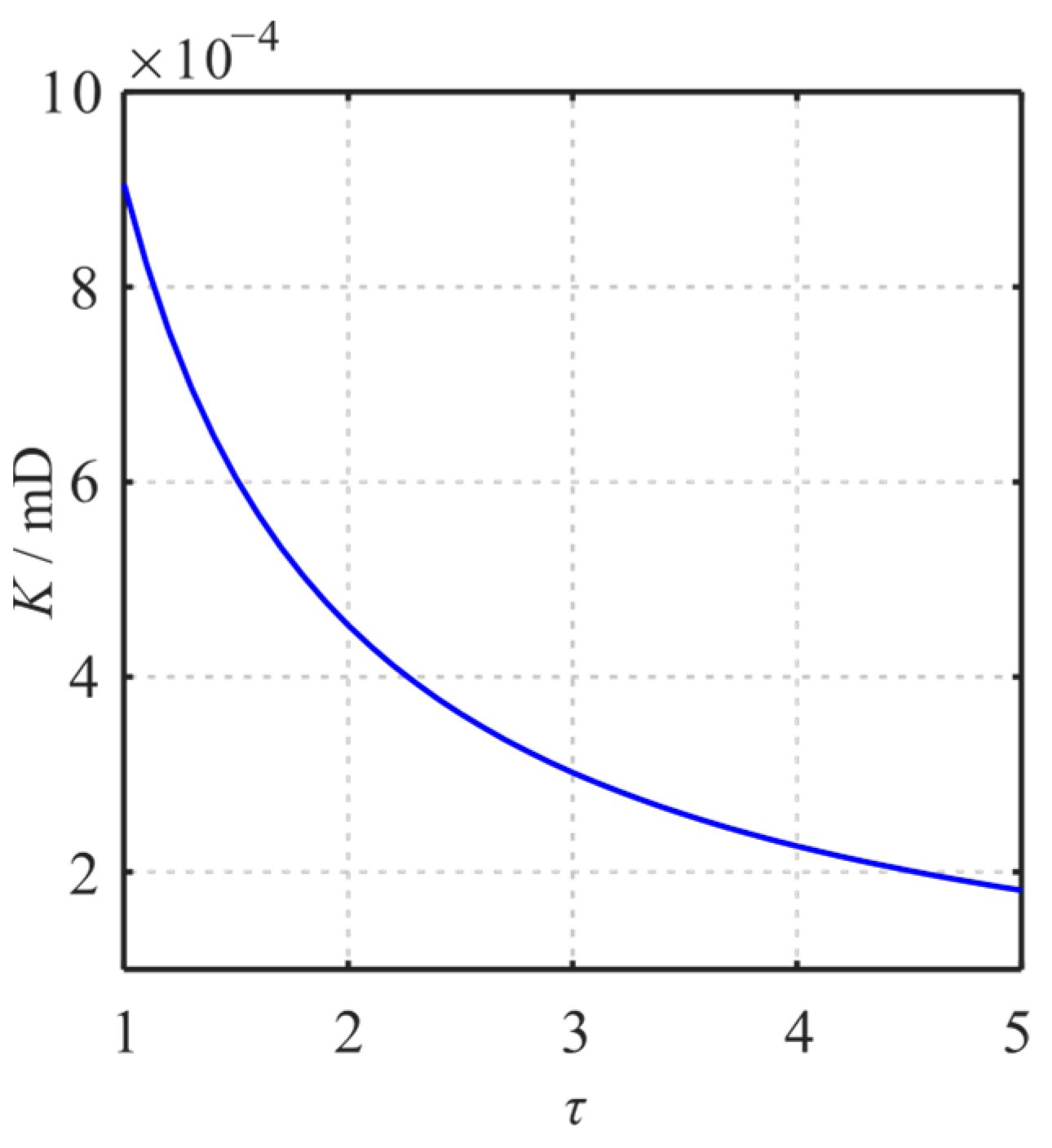
4.5. Influence of Tortuosity
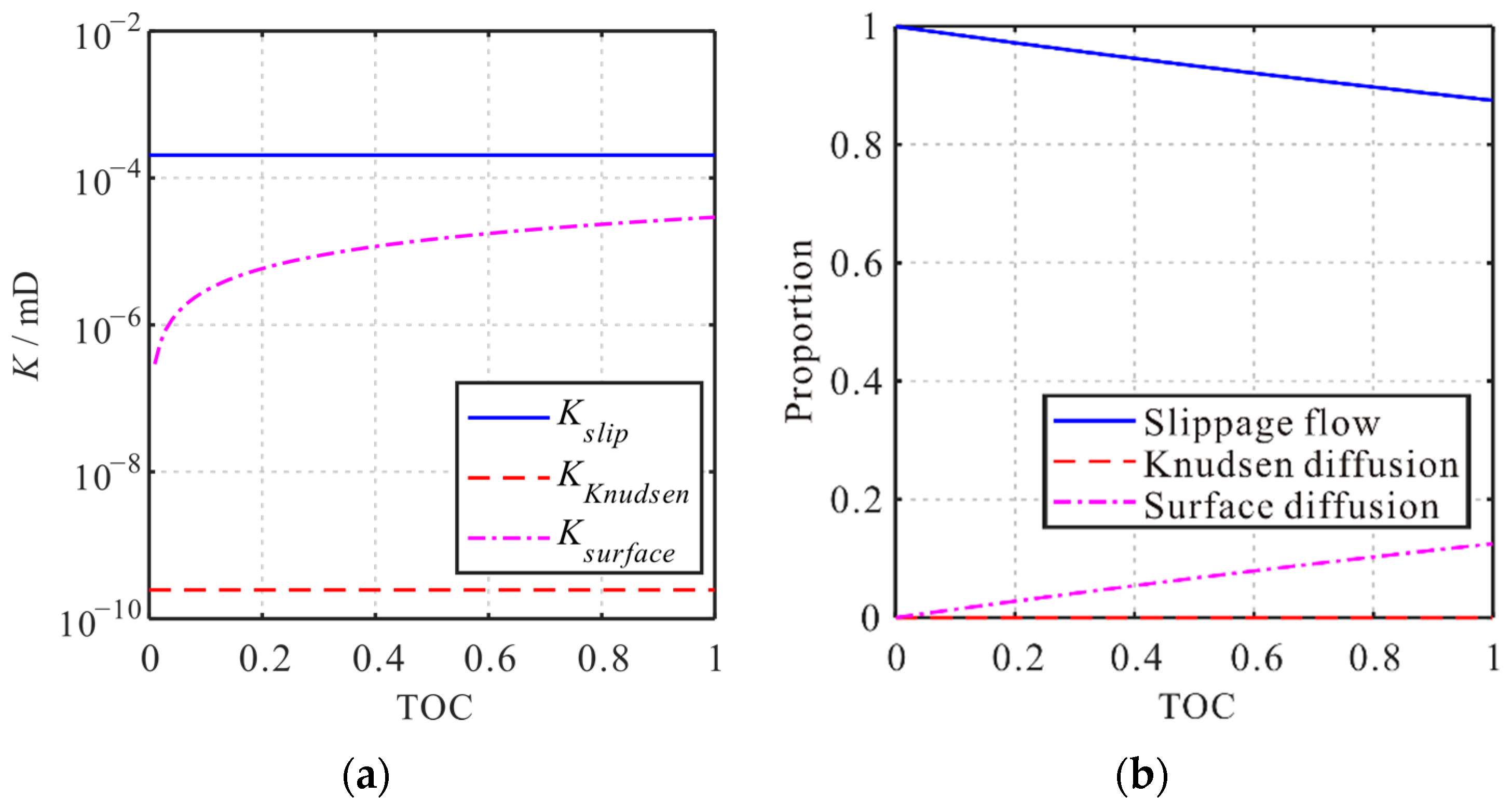
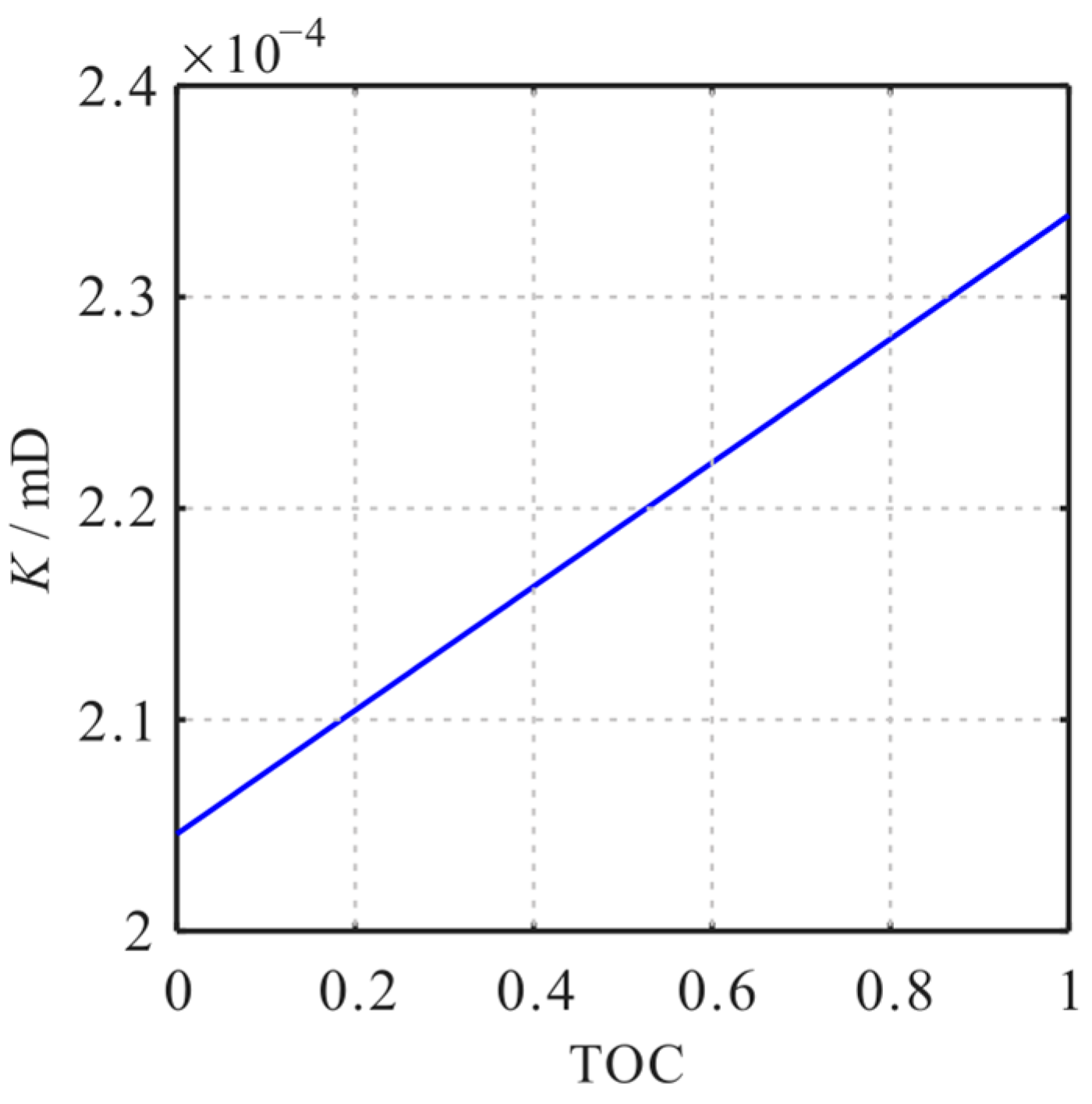
4.6. Influence of Total Organic Carbon (TOC)
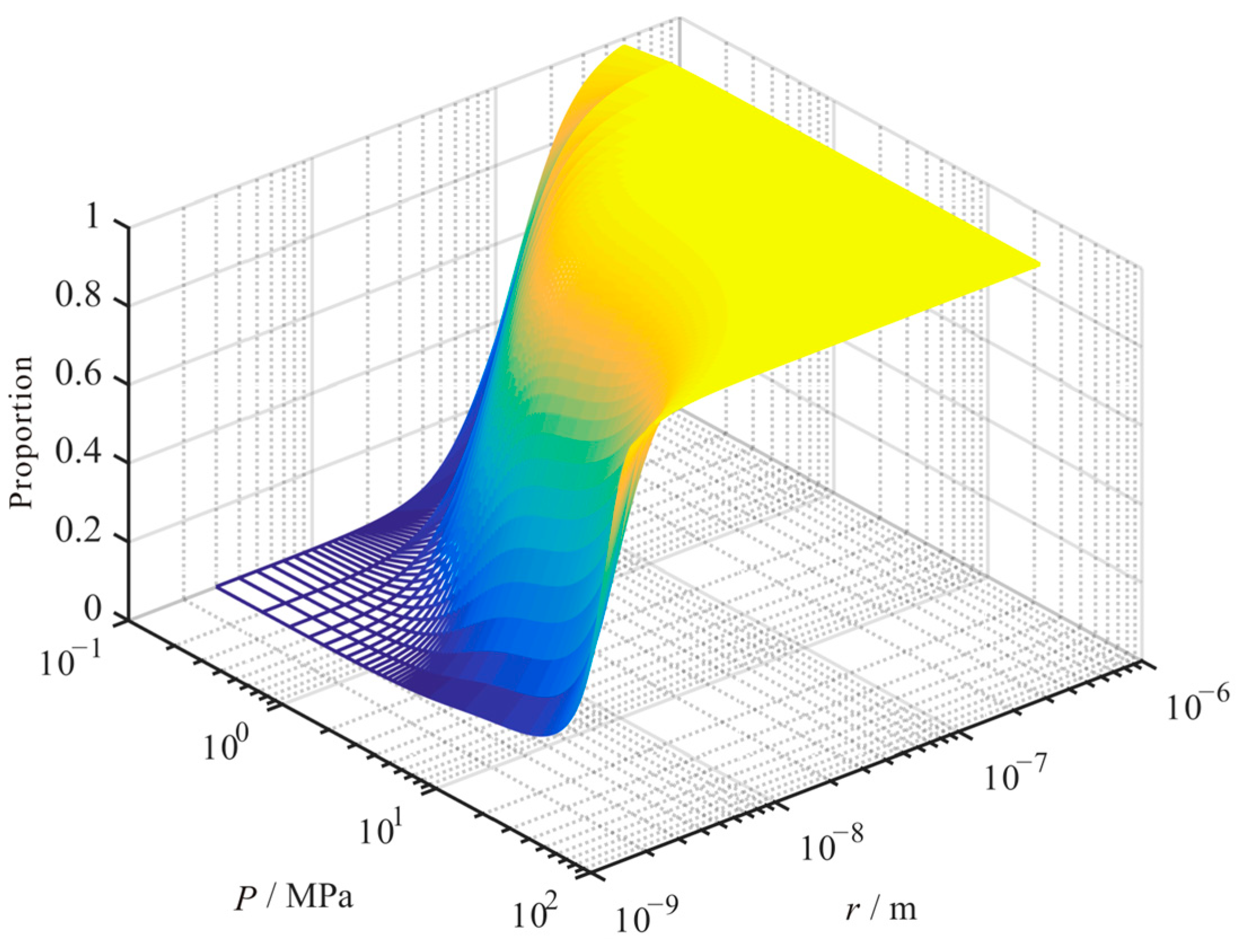
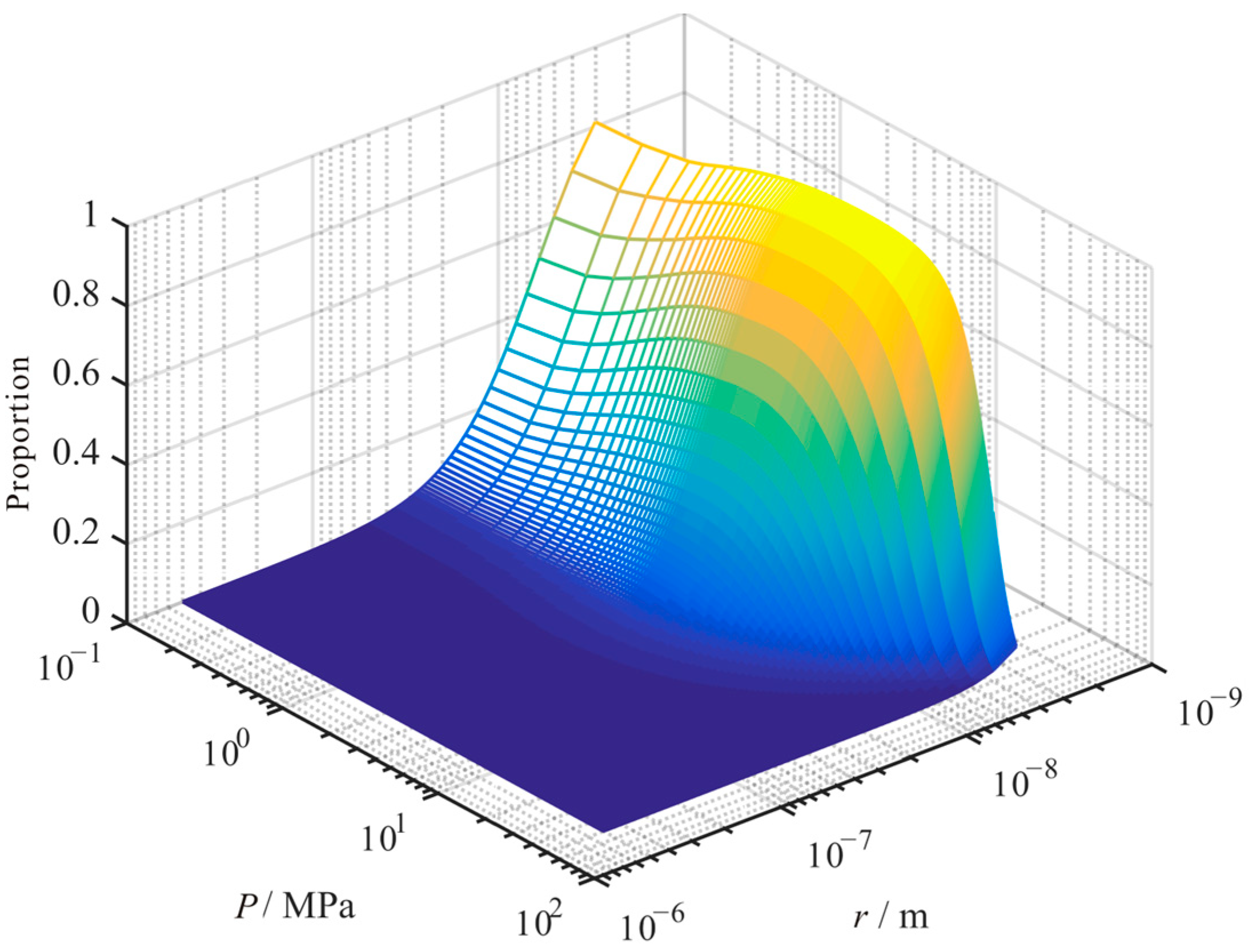
4.7. Combined Influence
5. Conclusions
- (1)
- Considering the slippage flow, Knudsen diffusion, transition flow, surface diffusion, and reservoir changing mechanism, the apparent permeability model of the shale reservoir matrix is verified by the experimental data. This model can accurately fit the changes in reservoir matrix permeability in the process of shale gas development.
- (2)
- The calculation of the Knudsen number should consider the impact of changes in reservoir and gas properties. Considering these influences, the Knudsen number decreases. Moreover, this decrease in the Knudsen number is more obvious under the conditions of low pressure and small pore size.
- (3)
- The apparent permeability of the shale reservoir matrix is significantly influenced by pressure, temperature, pore size, and TOC. As the pressure or pore size decreases, the apparent permeability decreases first and then increases. With the increase in temperature or TOC, the apparent permeability increases. With the increase in tortuosity, the apparent permeability of the reservoir matrix decreases.
- (4)
- The contribution proportion of the three transport mechanisms to the apparent permeability of the shale matrix is significantly influenced by pressure, temperature, pore size, and TOC. With the decrease in pressure, the proportion of slippage flow decreases, and the proportion of Knudsen diffusion increases. Moreover, the proportion of surface diffusion increases first and then decreases. With the increase in temperature, the proportion of Knudsen diffusion and surface diffusion increases, and the proportion of slippage flow decreases. With the increase in pore size, the proportion of slippage flow increases, and the proportion of surface diffusion decreases. The proportion of Knudsen diffusion increases first and then decreases. With the increase in TOC, the proportion of slippage flow decreases, and the proportion of surface diffusion increases. Moreover, the proportion of Knudsen diffusion decreases.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, K.; Chen, Z. Review of gas transport in nanopores in shale gas reservoir. Sci. Bull. 2016, 1, 91–127. [Google Scholar]
- Zhang, Q.; Liang, F.; Pang, Z.; Jiang, S.; Zhou, S.; Zhang, J. Lower threshold of pore-throat diameter for the shale gas reservoir: Experimental and molecular simulation study. J. Pet. Sci. Eng. 2019, 173, 1037–1046. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, Z.; Tang, X.; He, S.; Wang, Y.; Chang, J. Critical conditions and capabilities of shale gas diffusion and seepage types in the Longmaxi Format. Acta Geol. Sin. 2023, 97, 210–220. [Google Scholar]
- Yang, X.; Zhou, W.; Liu, X.; Yan, Y. A multiscale approach for simulation of shale gas transport in organic nanopores. Energy 2020, 210, 118547. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Guo, J. Characterization of gas transport in shale: A multi-mechanism permeability modeling approach. Chem. Eng. J. 2022, 438, 135604. [Google Scholar] [CrossRef]
- Wu, K.; Li, X.; Chen, Z. Micro-scale effects of gas transport in organic nanopores of shale gas reservoirs. Nat. Gas Ind. 2016, 36, 51–64. [Google Scholar]
- Florence, F.A.; Rushing, J.; Newsham, K.E.; Blasingame, T.A. Improved permeability prediction relations for low permeability sands. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 April 2007. [Google Scholar]
- Cipolla, C.; Lolon, E.; Mayerhofer, M. Reservoir Modeling and Production Evaluation in Shale-Gas Reservoirs. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 7–9 December 2009. [Google Scholar] [CrossRef]
- Sheng, M.; Li, G.; Huang, W.; Tian, S. Shale gas transient flow model with effects of surface diffusion. Acta Pet. Sin. 2014, 35, 347–352. [Google Scholar]
- Yin, Y.; Qu, Z.; Zhang, J. An analytical model for shale gas transport in kerogen nanopores coupled with real gas effect and surface diffusion. Fuel 2017, 210, 569–577. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, J.; Tan, X. Apparent gas permeability model of shale matrix coupling stress sensitivity and water saturation. Nat. Gas Geosci. 2021, 223, 861–870. [Google Scholar]
- Wu, K.; Li, X.; Chen, Z. Real gas transport through nanopores of shale gas reservoir. Sci. Sin. Technol. 2016, 46, 68–78. [Google Scholar] [CrossRef][Green Version]
- Ertekin, T.; King, G.A.; Schwerer, F.C. Dynamic gas slippage: A unique dual-mechanism approach to the flow of gas in tight formations. SPE Form. Eval. 1986, 1, 43–52. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Nobakht, M.; Kaviani, D.; Ertekin, T. Production analysis of tight-gas and shale-gas reservoirs using the dynamic-slippage concept. SPE J. 2012, 17, 230–242. [Google Scholar] [CrossRef]
- Javadpour, F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). J. Can. Pet. Technol. 2009, 48, 16–21. [Google Scholar] [CrossRef]
- Swami, V.; Settari, A. A Pore Scale Gas Flow Model for Shale Gas Reservoir. In Proceedings of the American Unconventional Resources Conference, Pittsburgh, PA, USA, 5–7 June 2012. [Google Scholar]
- Li, D.; Zhang, Y.; Sun, X.; Zhao, F.; Cui, X.; Qiao, W.; Su, Y. A new model for assessing apparent permeability of shale gas at real gas condition considering surface diffusion. J. China Univ. Pet. (Ed. Nat. Sci.) 2018, 42, 82–90. [Google Scholar]
- Tian, S.; Wang, T.; Li, G.; Sheng, M.; Liu, Q.; Zhang, S. An analytical model for shale gas transport in circular tube pores. Int. J. Heat Mass Transf. 2018, 127, 321–328. [Google Scholar] [CrossRef]
- Huang, T.; Tan, W.; Zhuang, Q.; Wang, G.; Yin, T. Coupling model for nanopore gas transport in shale reservoir. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2019, 41, 118–126. [Google Scholar]
- Song, H.; Li, B.; Chen, S.; Li, J.; Gao, Z. Evolution mechanism of dynamic apparent permeability of shale reservoirs. J. China Univ. Min. Technol. 2022, 248, 873–885. [Google Scholar]
- Villazon, G.; Sigal, R.F.; Civan, F.; Devegowda, D. Parametric Investigation of Shale Gas Production Considering Nano-Scale Pore Size Distribution. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Zheng, D.; Ozbayoglu, E.; Miska, S.; Zhang, J. Experimental Study of Anisotropic Strength Properties of Shale. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar]
- Zheng, D.; Ozbayoglu, E.; Miska, S.; Zhang, J. Combined Experimental and Well Log Study of Anisotropic Strength of Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 16–18 October 2023. [Google Scholar]
- Liu, J.; Bai, X.; Elsworth, D. Evolution of pore systems in low-maturity oil shales during thermal upgrading—Quantified by dynamic SEM and machine learning. Pet. Sci. 2024, in press. [Google Scholar] [CrossRef]
- Javadpour, F.; Fisher, D.; Unsworth, M. Nanoscale gas flow in shale gas sediments. J. Can. Pet. Technol. 2007, 46, 55–61. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, X.; Guo, C.; Wei, M. A model for multiple transport mechanisms through nanopores of shale gas reservoirs with real gas effect-adsorption-mechanic coupling. Int. J. Heat Mass Transf. 2016, 93, 408–426. [Google Scholar] [CrossRef]
- Shi, J.; Lei, Z.; Li, Y.; Wei, Y.; Tao, W. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting. In Proceedings of the SPE Unconventional Reservoir Conference, Calgary, AB, Canada, 5–7 November 2013. [Google Scholar]
- Raghavan, R.; Chin, L.Y. Productivity changes in reservoirs with stress-dependent permeability. SPE Reserv. Eval. Eng. 2004, 7, 308–315. [Google Scholar] [CrossRef]
- Fu, X.; Li, D.; Qin, Y.; Jiang, B.; Wang, W.; Li, G. Experimental Research of Influence of Coal Matrix Shrinkage on Permeability. J. China Univ. Min. Technol. 2002, 31, 129–131. [Google Scholar]
- Cao, C.; Li, T.; Zhang, L.; Gao, C.; Wang, H. Shale gas dual porosity-dual permeability model with matrix shrinking. Nat. Gas Geosci. 2015, 26, 2381–2387. [Google Scholar]
- Wang, S.; Elsworth, D.; Liu, J. A mechanistic model for permeability evolution in fractured sorbing media. J. Geophys. Res. 2012, 117, 6205–6221. [Google Scholar] [CrossRef]
- Dong, Y.; Zhao, Q.; Lu, C.; Lu, C.; Gan, Y.; Chen, G. High-pressure isothermal adsorption model for supercritical methane in shale. In Proceedings of the 2022 International Field Exploration and Development Conference, IFEDC, Xi’an, China, 16–18 November 2022; Springer Science and Business Media Deutschland GmbH: Singapore, 2022. [Google Scholar]
- Shi, R.; Liu, J.; Derek, E. Mechanistic Analysis of Shale Permeability Evolution Data. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
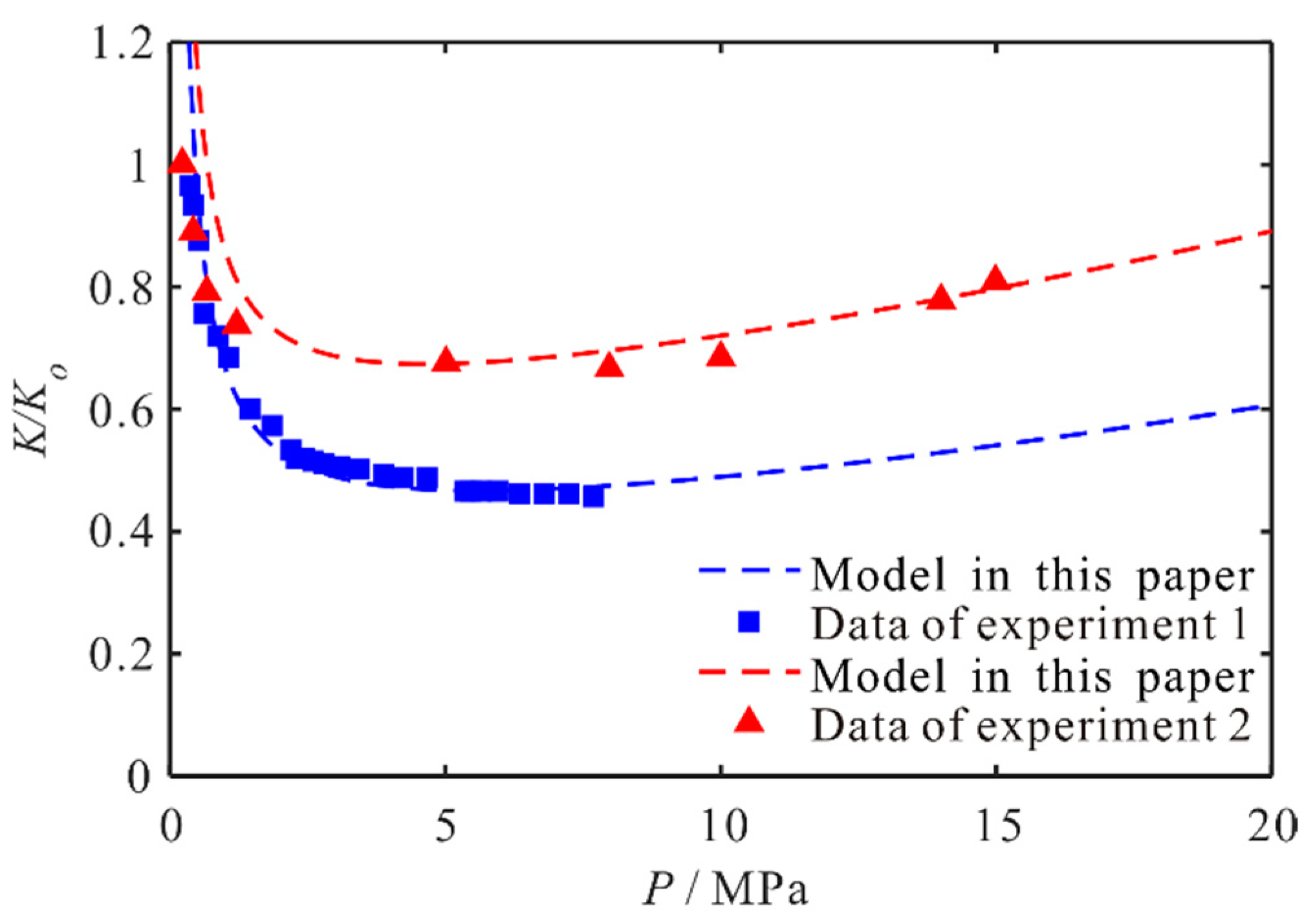



| Fitting Parameters (Experiment 1) | Values | Fitting Parameters (Experiment 2) | Values |
|---|---|---|---|
| Initial pressure Po (MPa) | 40 | Initial pressure Po (MPa) | 25 |
| Porosity ϕ (f) | 0.015 | Porosity ϕ (f) | 0.05 |
| Rock compressibility factor Cp (MPa−1) | 0.013 | Rock compressibility factor Cp (MPa−1) | 0.012 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Temperature T (K) | 300 | Fluid viscosity μ (mPa·s) | 0.0175 |
| Porosity ϕ (f) | 0.05 | Molecular molar mass M (kg/mol) | 0.028 |
| Tortuosity τ (f) | 4.3 | The ratio of molecular diameter to local pore diameter σ (f) | 0.5 |
| Fracture width h (nm) | 50 | Fractal dimension of pore wall Df (f) | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Song, L.; Lai, F.; Zhao, Q.; Lu, C.; Chen, G.; Chong, Q.; Yang, S.; Wang, J. Characterization of the Macroscopic Impact of Diverse Microscale Transport Mechanisms of Gas in Micro-Nano Pores and Fractures. Energies 2024, 17, 1145. https://doi.org/10.3390/en17051145
Dong Y, Song L, Lai F, Zhao Q, Lu C, Chen G, Chong Q, Yang S, Wang J. Characterization of the Macroscopic Impact of Diverse Microscale Transport Mechanisms of Gas in Micro-Nano Pores and Fractures. Energies. 2024; 17(5):1145. https://doi.org/10.3390/en17051145
Chicago/Turabian StyleDong, Yintao, Laiming Song, Fengpeng Lai, Qianhui Zhao, Chuan Lu, Guanzhong Chen, Qinwan Chong, Shuo Yang, and Junjie Wang. 2024. "Characterization of the Macroscopic Impact of Diverse Microscale Transport Mechanisms of Gas in Micro-Nano Pores and Fractures" Energies 17, no. 5: 1145. https://doi.org/10.3390/en17051145
APA StyleDong, Y., Song, L., Lai, F., Zhao, Q., Lu, C., Chen, G., Chong, Q., Yang, S., & Wang, J. (2024). Characterization of the Macroscopic Impact of Diverse Microscale Transport Mechanisms of Gas in Micro-Nano Pores and Fractures. Energies, 17(5), 1145. https://doi.org/10.3390/en17051145





