A Comprehensive Review on Voltage Stability in Wind-Integrated Power Systems
Abstract
1. Introduction
2. Overview of Voltage Stability
2.1. Types of Voltage Stability
2.1.1. Large Disturbance Voltage Stability
2.1.2. Small Disturbance Voltage Stability
2.1.3. Long-Term Voltage Stability
2.1.4. Short-Term Voltage Stability
2.2. Voltage Stability Assessment
- Jacobian matrix and System variable-based Voltage Stability Indices.
- Bus, line, and overall Voltage Stability Indices.
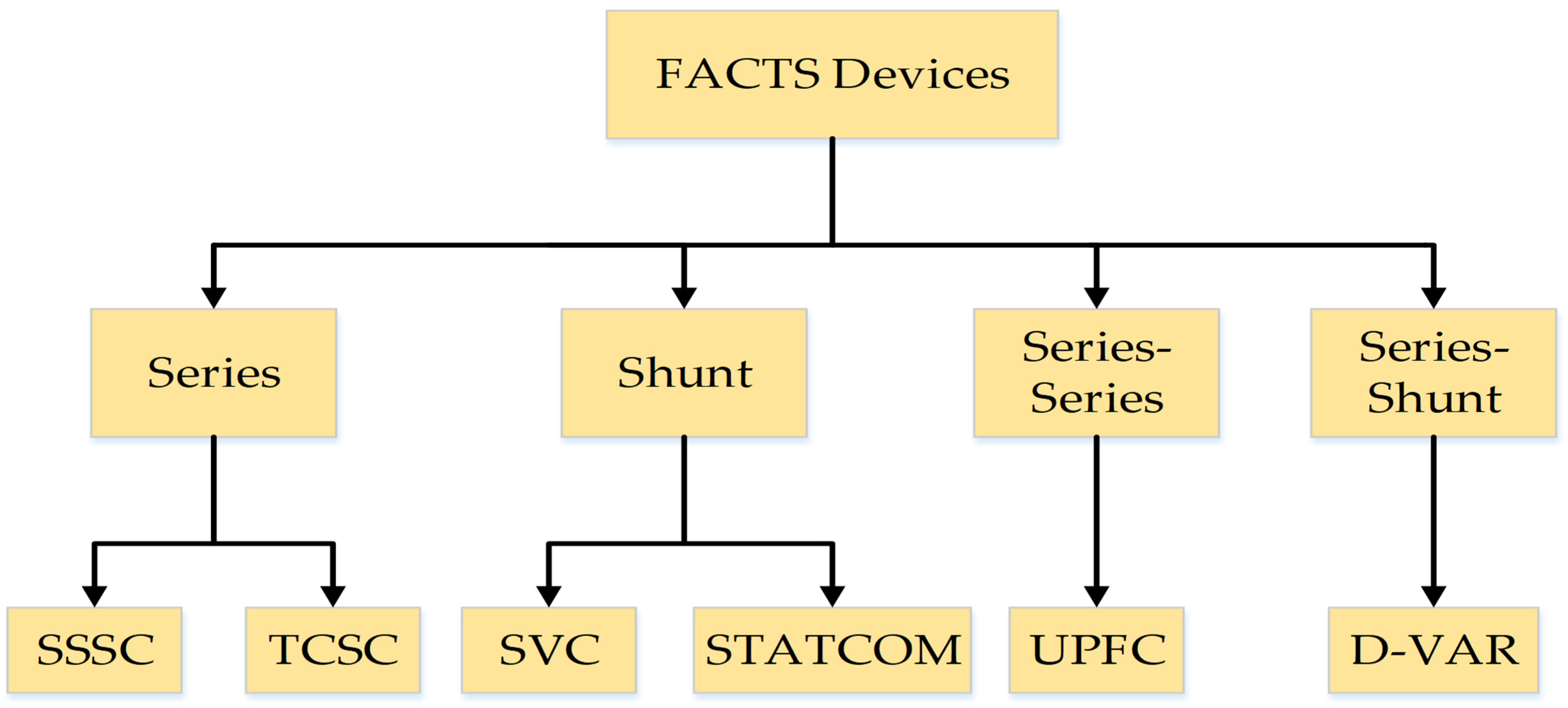
2.3. Voltage Stability Improvement by FACTS Devices
2.4. Identification of Weakest Bus
- ❖
- voltage sensitivity factor;
- ❖
- reactive power margin;
- ❖
- L-Index.
3. Wind-Integrated Power Systems
3.1. Grid Codes
- active power control;
- frequency control;
- voltage regulation;
- frequency variations;
- overvoltage conditions;
- fault ride-through;
- voltage regulation and power factor;
- power quality.
3.2. Wind Farm Integration
3.3. Weak Grids
- the AC system impedance may be high relative to DC power at the point of common coupling (PCC);
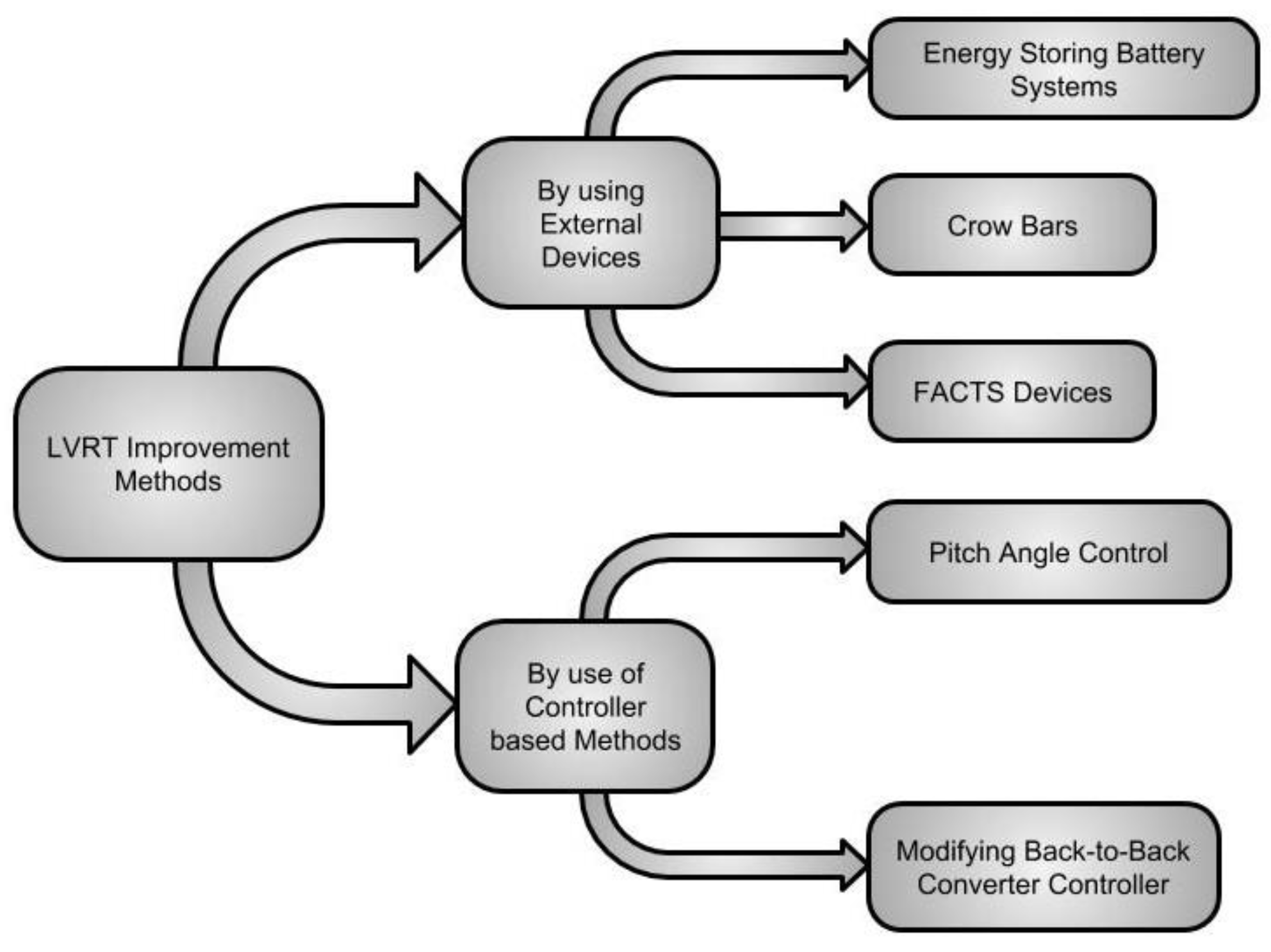
3.4. Low Voltage Ride-through
- it gives more realistic results as compared to the ones found in the laboratory;
- to ensure the LVRT capability of all the installed wind turbines;
- to counter-check the capability of wind turbines after major events in a system’s maintenance.
3.5. High Voltage Ride-through
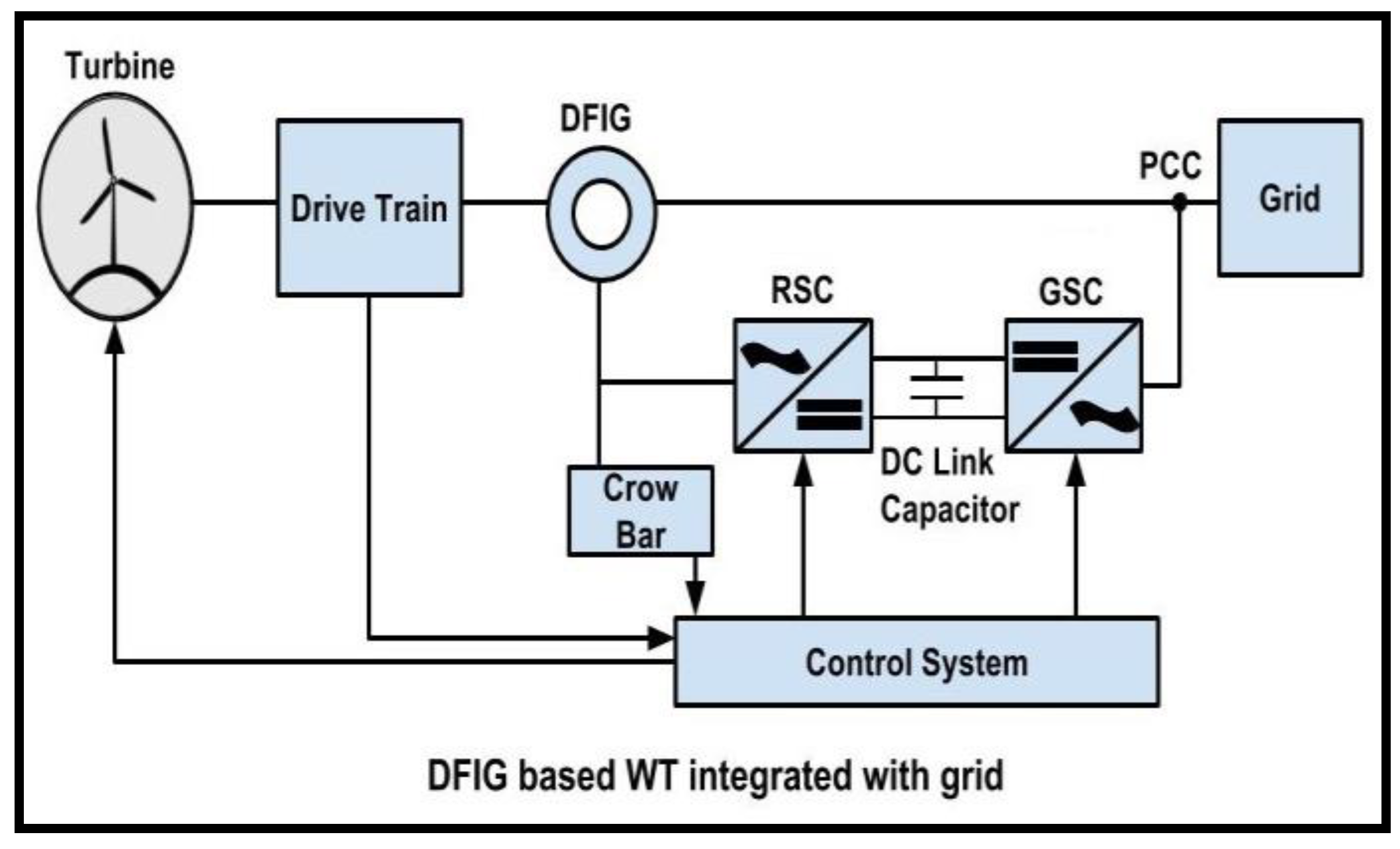
3.6. Role of DFIG in Voltage Stability Improvements
- independent control capability for active and reactive powers;
- constant frequency operation at variable speed for robust four quadrants’ reactive power control;
- handles 20–30% of total system power that eventually lowers power losses;
- operate at a higher range of wind speed
- lower mechanical stress and acoustical noise;
- high energy efficiency;
- lower cost due to low rating power electronic converters.
3.7. Penetration Level of Wind Energy
- frequency deviation range = ±0.2 Hz;
- maximum predicted load disturbance = 0.04 pu.
3.8. The Optimal Location for Wind Farm
- gusts-free availability of wind;
- regular smooth winds with least variations;
- strong air currents due to thermal gradients;
- distance from the power system;
- land cost and roads to approach the site.
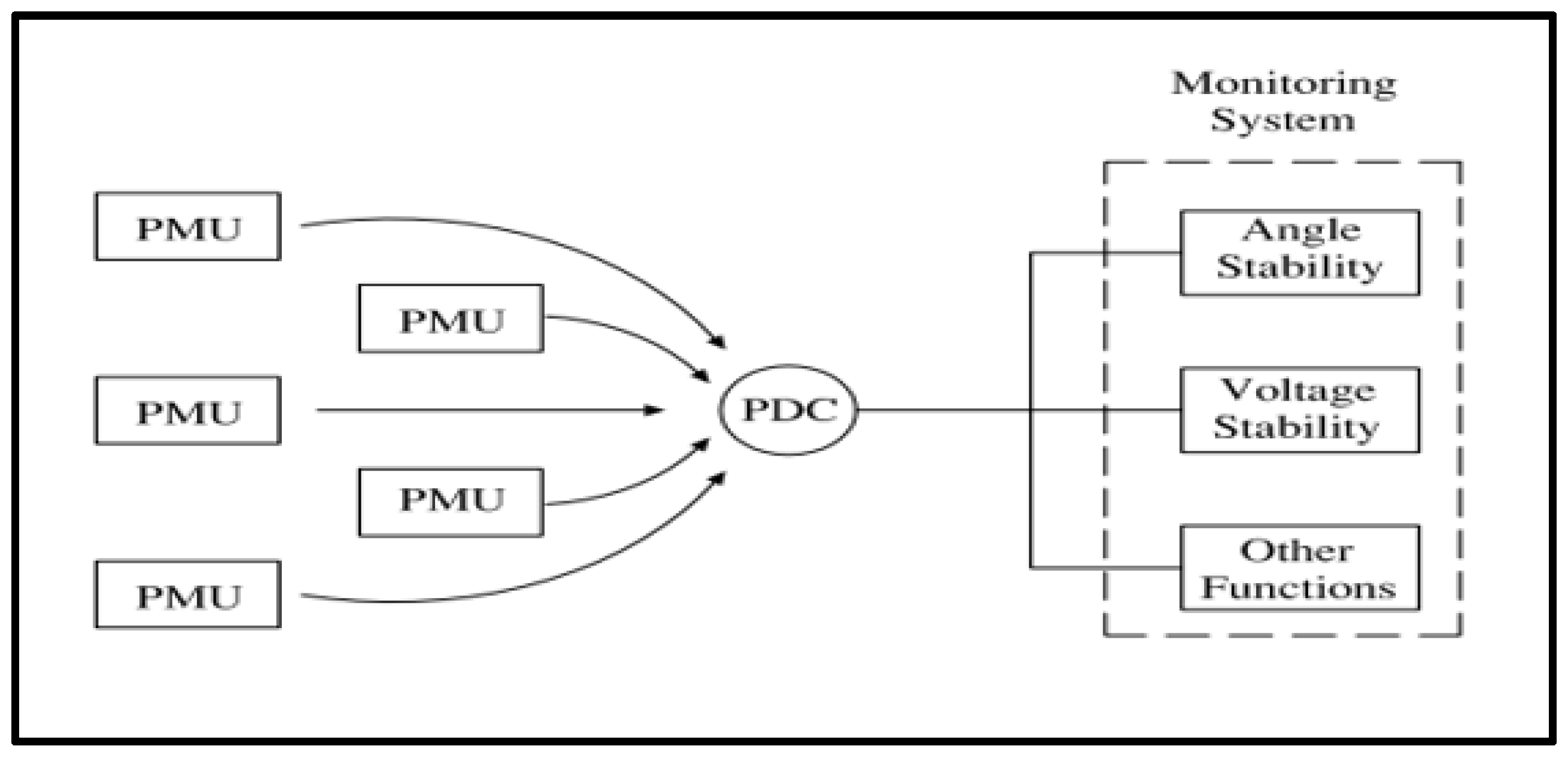
3.9. Wide Area Monitoring (Measurement) Systems
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villacreses, G.; Gaona, G.; Martínez-Gómez, J.; Jijón, D.J. Wind farms suitability location using geographical information system (GIS), based on multi-criteria decision making (MCDM) methods: The case of continental Ecuador. Renew. Energy 2017, 109, 275–286. [Google Scholar] [CrossRef]
- Meegahapola, L.; Littler, T.; Perera, S. Capability curve based enhanced reactive power control strategy for stability enhancement and network voltage management. Int. J. Electr. Power Energy Syst. 2013, 52, 96–106. [Google Scholar] [CrossRef]
- Goh, H.H.; Chua, Q.S.; Lee, S.W.; Kok, B.C.; Goh, K.C.; Teo, K.T.K. Evaluation for Voltage Stability Indices in Power System Using Artificial Neural Network. Procedia Eng. 2015, 118, 1127–1136. [Google Scholar] [CrossRef]
- Ahmed, M.; EL-Shimy, M.; Badr, M.A. Advanced modeling and analysis of the loading capability li mits of doubly-fed induction generators. Sustain. Energy Technol. Assess. 2014, 7, 79–90. [Google Scholar]
- Khezri, R.; Bevrani, H. Voltage performance enhancement of DFIG-based wind farms integrated in large-scale power systems: Coordinated AVR and PSS. Int. J. Electr. Power Energy Syst. 2015, 73, 400–410. [Google Scholar] [CrossRef]
- Tohidi, S.; Tavner, P.; McMahon, R.; Oraee, H.; Zolghadri, M.R.; Shao, S.; Abdi, E. Low voltage ride-through of DFIG and brushless DFIG: Similarities and differences. Electr. Power Syst. Res. 2014, 110, 64–72. [Google Scholar] [CrossRef]
- Rahimi, M. Coordinated control of rotor and grid sides converters in DFIG based wind turbines for providing optimal reactive power support and voltage regulation. Sustain. Energy Technol. Assess. 2017, 20, 47–57. [Google Scholar] [CrossRef]
- Liu, X. Quality of Optical Channels in Wireless SCADA for Offshore Wind Farms. IEEE Trans. Smart Grid 2012, 3, 225–232. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Tang, C.Y.; Jiang, J.N. Calibration of a Wind Farm Wind Speed Model with Incomplete Wind Data. IEEE Trans. Sustain. Energy 2014, 5, 343–350. [Google Scholar] [CrossRef]
- Ericsson, G.N. Cyber Security and Power System Communication—Essential Parts of a Smart Grid Infrastructure. IEEE Trans. Power Deliv. 2010, 25, 1501–1507. [Google Scholar] [CrossRef]
- Macdonald, H.; Hawker, G.; Bell, K. Analysis of wide-area availability of wind generators during storm events. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; pp. 1–6. [Google Scholar]
- Baghaee, H.R.; Jannati, M.; Vahidi, B.; Hosseinian, S.H.; Rastegar, H. Improvement of voltage stability and reduce power system losses by optimal GA-based allocation of multi-type FACTS devices. In Proceedings of the 2008 11th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 22–24 May 2008; pp. 209–214. [Google Scholar]
- Deb, G.; Chakraborty, K.; Deb, S. Voltage stability analysis using reactive power loading as indicator and its improvement by FACTS device. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–5. [Google Scholar]
- Ross, M.; Borodulin, M.; Kazachkov, Y. Using D-SMES devices to improve the voltage stability of a transmission system. In Proceedings of the 2001 IEEE/PES Transmission and Distribution Conference and Exposition. Developing New Perspectives (Cat. No.01CH37294), Atlanta, GA, USA, 2 November 2001; Volume 2, pp. 1144–1148. [Google Scholar]
- Ruan, J.Y.; Lu, Z.X.; Qiao, Y.; Min, Y. Analysis on Applicability Problems of the Aggregation-Based Representation of Wind Farms Considering DFIGs’ LVRT Behaviors. IEEE Trans. Power Syst. 2016, 31, 4953–4965. [Google Scholar] [CrossRef]
- Wen, G.; Chen, Y.; Zhong, Z.; Kang, Y. Dynamic Voltage and Current Assignment Strategies of Nine-Switch-Converter-Based DFIG Wind Power System for Low-Voltage Ride-Through (LVRT) under Symmetrical Grid Voltage Dip. IEEE Trans. Ind. Appl. 2016, 52, 3422–3434. [Google Scholar] [CrossRef]
- Rashid, G.; Ali, M.H. Nonlinear Control-Based Modified BFCL for LVRT Capacity Enhancement of DFIG-Based Wind Farm. IEEE Trans. Energy Convers. 2017, 32, 284–295. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- de Leon, J.A.D.; Taylor, C.W. Understanding and solving short-term voltage stability problems. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Chicago, IL, USA, 21–25 July 2002; Volume 2, pp. 745–752. [Google Scholar]
- Nikolaidis, V.C. Emergency Zone 3 Modification as a Local Response-Driven Protection Measure Against System Collapse. IEEE Trans. Power Deliv. 2016, 31, 2114–2122. [Google Scholar] [CrossRef]
- Johnson, M.; Vaziri, M.; Vadhva, S. Understanding slow voltage instability. In Proceedings of the 2012 IEEE 13th International Conference on Information Reuse & Integration (IRI), Las Vegas, NV, USA, 8–10 August 2012; pp. 502–508. [Google Scholar]
- Duan, J.; Huang, J. The Mechanism of Voltage Instability Analysis Considering Load Characteristic. Energy Power Eng. 2013, 5, 1497–1502. [Google Scholar] [CrossRef]
- Sauer, P.W.; Lesieutre, B.C.; Pai, M.A. Maximum loadability and voltage stability in power systems. Int. J. Electr. Power Energy Syst. 1993, 15, 145–153. [Google Scholar] [CrossRef]
- Williams, B.R.; Schmus, W.R.; Dawson, D.C. Transmission voltage recovery delayed by stalled air conditioner compressors. IEEE Trans. Power Syst. 1992, 7, 1173–1181. [Google Scholar] [CrossRef]
- Tirtashi, M.R.S.; Samuelsson, O.; Svensson, J. Dynamic and static analysis of the shunt capacitors control effect on the long-term voltage instability. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- de Mello, F.P.; Feltes, J.W. Voltage oscillatory instability caused by induction motor loads. IEEE Trans. Power Syst. 1996, 11, 1279–1285. [Google Scholar] [CrossRef]
- Van Cutsem, T. Voltage instability: Phenomena, countermeasures, and analysis methods. Proc. IEEE 2000, 88, 208–227. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Mangione, S. Voltage collapse proximity indicators for radial distribution networks. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; pp. 1–6. [Google Scholar]
- Amjady, N.; Ansari, M.R. Small disturbance voltage stability assessment of power systems by modal analysis and dynamic simulation. Energy Convers. Manag. 2008, 49, 2629–2641. [Google Scholar] [CrossRef]
- Atputharajah, A.; Saha, T.K. Power system blackouts—Literature review. In Proceedings of the 2009 International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 28–31 December 2009; pp. 460–465. [Google Scholar]
- Brayley, H.; Redfern, M.A.; Bo, Z.Q. The Public Perception of Power Blackouts. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 15–18 August 2005; pp. 1–5. [Google Scholar]
- Kamali, S.; Amraee, T. Blackout prediction in interconnected electric energy systems considering generation re-dispatch and energy curtailment. Appl. Energy 2017, 187, 50–61. [Google Scholar] [CrossRef]
- Wang, P.; Qin, W.; Han, X.; Ding, Y.; Du, X. Reliability assessment of power systems considering reactive power sources. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar]
- Xu, C.; Li, P.; Li, X.; Chen, D.; Zhang, Y.; Lei, B. Small disturbance voltage stability considering thermostatically controlled load. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 862–866. [Google Scholar]
- Chen, H.; Chen, J.; Shi, D.; Duan, X. Power flow study and voltage stability analysis for distribution systems with distributed generation. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 8. [Google Scholar]
- Veloza, O.P.; Santamaria, F. Analysis of major blackouts from 2003 to 2015: Classification of incidents and review of main causes. Electr. J. 2016, 29, 42–49. [Google Scholar] [CrossRef]
- Haque, M.H. Determination of steady-state voltage stability limit of a power system in the presence of SVC. In Proceedings of the 2001 IEEE Porto Power Tech Proceedings (Cat. No.01EX502), Porto, Portugal, 10–13 September 2001; Volume 2, p. 6. [Google Scholar]
- Haque, M.H. Use of V–I characteristic as a tool to assess the static voltage stability limit of a power system. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 1–7. [Google Scholar] [CrossRef]
- Tripathy, M.; Mishra, S. Optimizing Voltage Stability Limit and Real Power Loss in a Large Power System using Bacteria Foraging. In Proceedings of the 2006 International Conference on Power Electronics, Drives and Energy Systems, New Delhi, India, 12–15 December 2006; pp. 1–6. [Google Scholar]
- Ramalingam, K.; Indulkar, C.S. Determination of Steady State Voltage Stability limit using PQ curves for voltage sensitive loads. In Proceedings of the 2008 Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi, India, 12–15 December 2008; pp. 1–5. [Google Scholar]
- Koessler, R.J. Voltage instability/collapse—An overview. In Proceedings of the IEE Colloquium on Voltage Collapse (Digest No: 1997/101), London, UK, 24 April 1997; pp. 1/1–1/6. [Google Scholar]
- Tiranuchit, A.; Thomas, R.J. A posturing strategy against voltage instabilities in electric power systems. IEEE Trans. Power Syst. 1988, 3, 87–93. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, W. Power system static voltage stability limit and the identification of weak bus. In Proceedings of the TENCON ’93. IEEE Region 10 International Conference on Computers, Communications and Automation, Beijing, China, 19–21 October 1993; Volume 5, pp. 157–160. [Google Scholar]
- Yokoyama, A.; Kumano, T.; Sekine, Y. Static voltage stability index using multiple load-flow solutions. Elect. Eng. Jpn. 1991, 111, 69–79. [Google Scholar] [CrossRef]
- Obadina, O.O.; Berg, G.J. Determination of voltage stability limit in multimachine power systems. IEEE Trans. Power Syst. 1988, 3, 1545–1554. [Google Scholar] [CrossRef]
- Le, H.T.; Santoso, S.; Nguyen, T.Q. Augmenting Wind Power Penetration and Grid Voltage Stability Limits Using ESS: Application Design, Sizing, and a Case Study. IEEE Trans. Power Syst. 2012, 27, 161–171. [Google Scholar] [CrossRef]
- Wannoi, C.; Khumdee, A.; Wannoi, N. An Optimum Technique for Renewable Power Generations Integration to Power System Using Repeated Power Flow Technique Considering Voltage Stability Limit. Procedia Comput. Sci. 2016, 86, 357–360. [Google Scholar] [CrossRef]
- Tripathy, M.; Mishra, S. Bacteria Foraging-Based Solution to Optimize Both Real Power Loss and Voltage Stability Limit. IEEE Trans. Power Syst. 2007, 22, 240–248. [Google Scholar] [CrossRef]
- Balachennaiah, P.; Suryakalavathi, M.; Nagendra, P. Optimizing real power loss and voltage stability limit of a large transmission network using firefly algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 800–810. [Google Scholar] [CrossRef]
- Duan, J.; Zhu, S. The Effect of OLTC on Static Voltage Stability Limit. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Raviprakasha, N.S.; Ramar, K. Maximum power transfer in AC transmission lines limited by voltage stability. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; Volume 2, pp. 776–781. [Google Scholar]
- Liu, H.; Jin, L.; McCalley, J.; Kumar, R.; Ajjarapu, V.; Elia, N. Planning reconfigurable reactive control for voltage stability limited power systems. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; p. 1. [Google Scholar]
- NERC Transmission Transfer Capability Task Force. Available Transfer Capability Definitions and Determination; North American Electric Reliability Council: North Princeton, NJ, USA, 1996. [Google Scholar]
- Jain, T.; Singh, S.N.; Srivastava, S.C. Dynamic available transfer capability computation using a hybrid approach. IET Gener. Transm. Distrib. 2008, 2, 775–788. [Google Scholar] [CrossRef]
- Shaaban, M.; Li, W.; Liu, H.; Yan, Z.; Ni, Y.; Wu, F. ATC calculation with steady-state security constraints using Benders decomposition. IEE Proc.-Gener. Transm. Distrib. 2003, 150, 611–615. [Google Scholar] [CrossRef]
- Li, W.; Chen, T.; Xu, W. On impedance matching and maximum power transfer. Electr. Power Syst. Res. 2010, 80, 1082–1088. [Google Scholar] [CrossRef]
- Indulkar, C.S.; Viswanathan, B.; Venkata, S.S. Maximum power transfer limited by voltage stability in series and shunt compensated schemes for AC transmission systems. IEEE Trans. Power Deliv. 1989, 4, 1246–1252. [Google Scholar] [CrossRef]
- Basu, K.P. Power transfer capability of transmission line limited by voltage stability: Simple analytical expressions. IEEE Power Eng. Rev. 2000, 20, 46–47. [Google Scholar] [CrossRef]
- Jadhav, H.T.; Roy, R. A comprehensive review on the grid integration of doubly fed induction generator. Int. J. Electr. Power Energy Syst. 2013, 49, 8–18. [Google Scholar] [CrossRef]
- Wei, X.; Chow, J.H.; Fardanesh, B.; Edris, A.A. A dispatch strategy for a unified power-flow controller to maximize voltage-stability-limited power transfer. IEEE Trans. Power Deliv. 2005, 20, 2022–2029. [Google Scholar] [CrossRef]
- Wei, X.; Cjow, J.H.; Edris, A.A.; Fardanesh, B. A dispatch strategy for multiple unified power flow controllers to maximize voltage-stability limited power transfer. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 1, pp. 865–870. [Google Scholar]
- Tobón; Esteban, J.; Ramirez, J.M.; Gutierrez, R.E.C. Tracking the maximum power transfer and loadability limit from sensitivities-based impedance matching. Electr. Power Syst. Res. 2015, 119, 355–363. [Google Scholar] [CrossRef]
- El-Metwally, M.M.; El-Emary, A.A.; El-Azab, M. Effect of load characteristics on maximum power transfer limit for HV compensated transmission lines. Int. J. Electr. Power Energy Syst. 2004, 26, 467–472. [Google Scholar] [CrossRef]
- Ramar, K.; Raviprakasha, M.S. Design of compensation schemes for long AC transmission lines for maximum power transfer limited by voltage stability. Int. J. Electr. Power Energy Syst. 1995, 17, 83–89. [Google Scholar] [CrossRef]
- Gayathri; Reddy, K.; Maruteswar, G.V. Frequency and Voltage Stability Assessment Applied to Load Shedding. Int. J. Eng. Trends Technol. 2015, 19, 106–115. [Google Scholar] [CrossRef]
- Meegahapola, L.; Littler, T. Characterisation of large disturbance rotor angle and voltage stability in interconnected power networks with distributed wind generation. IET Renew. Power Gener. 2015, 9, 272–283. [Google Scholar] [CrossRef]
- Glavic, M.; Van Cutsem, T. Detecting with PMUs the onset of voltage instability caused by a large disturbance. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Guedes, R.B.L.; Silva, F.H.J.R.; Alberto, L.F.C.; Bretas, N.G. Large disturbance voltage stability assessment using extended Lyapunov function and considering voltage-dependent active loads. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 2, pp. 1760–1767. [Google Scholar]
- Yong, T.; Shiying, M.; Wuzhi, Z. Mechanism Research of Short-Term Large-Disturbance Voltage Stability. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–5. [Google Scholar]
- Huadong, S.; Xiaoxin, Z. A Quick Criterion on Judging Short-Term Large-Disturbance Voltage Stability Considering Dynamic Characteristic of Induction Motor Loads. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–6. [Google Scholar]
- Kumar, G.N.; Kalavathi, M.S. Reactive power compensation for large disturbance voltage stability using FACTS controllers. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; pp. 164–167. [Google Scholar]
- Zheng, X.Y.; He, R.M.; Ma, J. A new load model suitable for transient stability analysis with large voltage disturbances. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 1898–1902. [Google Scholar]
- Najafi, H.R.; Robinson, F.V.P.; Dastyar, F.; Samadi, A.A. Small-disturbance voltage stability of distribution systems with wind turbine implemented with WRIG. In Proceedings of the 2009 International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 18–20 March 2009; pp. 191–195. [Google Scholar]
- Wang, W.; Ni, J.; Ngan, H.W. Small-Disturbance Voltage Stability Study on Shaanxi Power System. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 15–18 August 2005; pp. 1–5. [Google Scholar]
- Amjady, N.; Ansari, M.R. Small disturbance voltage stability evaluation of power systems. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–9. [Google Scholar]
- Rumiantsev, V.V.; Oziraner, A.S. Stability and Stabilization of Motion with Respect to Part of the Variables; Moscow Izdatel Nauka: Moscow, Russia, 1987. [Google Scholar]
- Wang, L.; Girgis, A.A. On-line detection of power system small disturbance voltage instability. IEEE Trans. Power Syst. 1996, 11, 1304–1313. [Google Scholar] [CrossRef]
- Xu, C.; Liang, J.; Yun, Z.; Zhang, L. The Small-disturbance Voltage Stability Analysis through Adaptive AR Model Based on PMU. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 15–18 August 2005; pp. 1–5. [Google Scholar]
- Khoshkhoo, H.; Shahrtash, S.M. On-line small disturbance voltage stability assessment in power systems based on wide area measurement. In Proceedings of the 2011 10th International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011; pp. 1–5. [Google Scholar]
- Preece, R.; Milanović, J.V. Risk-Based Small-Disturbance Security Assessment of Power Systems. IEEE Trans. Power Deliv. 2015, 30, 590–598. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control, 1st ed.; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Farmer, R.G. Power System Dynamics and Stability. In The Electric Power Engineering Handbook; Grigsby, L.L., Ed.; CRC Press LLC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Londero, R.R.; Affonso, C.M.; Vieira, J.P.A.; Bezerra, U.H. Impact of different DFIG wind turbines control modes on long-term voltage stability. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–7. [Google Scholar]
- Liu, J.H.; Chu, C.C. Long-Term Voltage Instability Detections of Multiple Fixed-Speed Induction Generators in Distribution Networks Using Synchrophasors. IEEE Trans. Smart Grid 2015, 6, 2069–2079. [Google Scholar] [CrossRef]
- Wang, Y.; Chan, K.W.; Mei, S.; Zhang, Y. A novel criterion on judging long-term voltage stability. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 1542–1547. [Google Scholar]
- Löf, P.-A.; Hill, D.J.; Arnborg, S.; Andersson, G. On the analysis of long-term voltage stability. Int. J. Electr. Power Energy Syst. 1993, 15, 229–237. [Google Scholar] [CrossRef]
- Assis, T.M.L.; Nunes, A.R.; Falcao, D.M. Mid and Long-Term Voltage Stability Assessment using Neural Networks and Quasi-Steady-State Simulation. In Proceedings of the 2007 Large Engineering Systems Conference on Power Engineering, Montreal, QC, Canada, 10–12 October 2007; pp. 213–217. [Google Scholar]
- Freitas, W.; Vieira, J.C.M.; da Suva, L.C.P.; Affonso, C.M.; Morelato, A. Long-term voltage stability of distribution systems with induction generators. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 3, pp. 2910–2913. [Google Scholar]
- Xu, T.; Taylor, P.C. Voltage Control Techniques for Electrical Distribution Networks Including Distributed Generation. IFAC Proc. Vol. 2008, 41, 11967–11971. [Google Scholar] [CrossRef]
- Liu, S.; Liu, M.; Xie, M. MPC-based Load Shedding for Long-term Voltage Stability Enhancement Using Trajectory Sensitivities. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–5. [Google Scholar]
- Perez, A.; Jóhannsson, H.; Vancraeyveld, P.; Östergaard, J. Suitability of voltage stability study methods for real-time assessment. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Zheng, W.; Liu, M. Long Term Voltage Stability Enhancement Using Direct Dynamic Optimization Method. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Stewart, V.; Camm, E.H. Modeling of stalled motor loads for power system short-term voltage stability analysis. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 2, pp. 1887–1892. [Google Scholar]
- Dong, Y.; Xie, X.; Zhou, B.; Shi, W.; Jiang, Q. An integrated high side var-voltage control strategy to improve short-term voltage stability of receiving-end power systems. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; p. 1. [Google Scholar]
- Tiwari, A.; Ajjarapu, V. Addressing short term voltage stability problem—Part I: Challenges and plausible solution directions. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Vournas, C.D.; Potamianakis, E.G. Induction Machine Short-term Voltage Stability and Protection Measures. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 993–998. [Google Scholar]
- Dong, Y.; Xie, X.; Shi, W.; Zhou, B.; Jiang, Q. Demand-Response Based Distributed Preventive Control to Improve Short-term Voltage Stability. IEEE Trans. Smart Grid 2017, 9, 4785–4795. [Google Scholar] [CrossRef]
- Hossain, M.J.; Pota, H.R.; Ugrinovskii, V. Short and Long-Term Dynamic Voltage Instability. IFAC Proc. Vol. 2008, 41, 9392–9397. [Google Scholar] [CrossRef]
- Han, T. Surrogate Modeling Based Multi-objective Dynamic VAR Planning Considering Short-term Voltage Stability and Transient Stability. IEEE Trans. Power Syst. 2017, 33, 622–633. [Google Scholar] [CrossRef]
- Wehenkel, L.; Pavella, M. Preventive vs. emergency control of power systems. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; Volume 3, pp. 1665–1670. [Google Scholar]
- Xu, Y.; Zhang, R.; Zhao, J.; Dong, Z.Y.; Wang, D.; Yang, H.; Wong, K.P. Assessing Short-Term Voltage Stability of Electric Power Systems by a Hierarchical Intelligent System. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1686–1696. [Google Scholar] [CrossRef]
- Kawabe, K.; Tanaka, K. Analytical Method for Short-Term Voltage Stability Using the Stability Boundary in the P-V Plane. IEEE Trans. Power Syst. 2014, 29, 3041–3047. [Google Scholar] [CrossRef]
- Arya, L.D.; Choube, S.C.; Shrivastava, M. Technique for voltage stability assessment using newly developed line voltage stability index. Energy Convers. Manag. 2008, 49, 267–275. [Google Scholar] [CrossRef]
- Reis, C.; Andrade, A.; Maciel, F.P. Line stability indices for voltage collapse prediction. In Proceedings of the 2009 International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 18–20 March 2009; pp. 239–243. [Google Scholar]
- Ismail, N.A.M.; Zin, A.A.M.; Khairuddin, A.; Khokhar, S. A comparison of voltage stability indices. In Proceedings of the 2014 IEEE 8th International Power Engineering and Optimization Conference (PEOCO2014), Langkawi, Malaysia, 24–25 March 2014; pp. 30–34. [Google Scholar]
- Musirin, I.; Rahman, T.K.A. Novel fast voltage stability index (FVSI) for voltage stability analysis in power transmission system. In Proceedings of the Student Conference on Research and Development, Shah Alam, Malaysia, 17 July 2002; pp. 265–268. [Google Scholar]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A comprehensive review of the voltage stability indices, Renewable and Sustainable. Energy Rev. 2016, 63, 1–12. [Google Scholar]
- Cupelli, M.; DoigCardet, C.; Monti, A. Voltage stability indices comparison on the IEEE-39 bus system using RTDS. In Proceedings of the 2012 IEEE International Conference on Power System Technology (POWERCON), Auckland, New Zealand, 30 October–2 November 2012; pp. 1–6. [Google Scholar]
- Cupelli, M.; DoigCardet, C.; Monti, A. Comparison of line voltage stability indices using dynamic real-time simulation. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Lof, P.A.; Andersson, G.; Hill, D.J. Voltage stability indices for stressed power systems. IEEE Trans. Power Syst. 1993, 8, 326–335. [Google Scholar] [CrossRef] [PubMed]
- Oukennou, A.; Sandali, A. Assessment and analysis of Voltage Stability Indices in electrical network using PSAT Software. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 705–710. [Google Scholar]
- Moghavvemi, M.; Omar, F.M. Technique for contingency monitoring and voltage collapse prediction. IEE Proc.-Gener. Transm. Distrib. 1998, 145, 634–640. [Google Scholar] [CrossRef]
- Balamourougan, V.; Sidhu, T.S.; Sachdev, M.S. Technique for online prediction of voltage collapse. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 453–460. [Google Scholar] [CrossRef]
- Kamel, M.M.M.; Karrar, A.A.; Eltom, A.H. Development and Application of a New Voltage Stability Index for On-Line Monitoring and Shedding. IEEE Trans. Power Syst. 2017, 33, 1231–1241. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Lu, J. A new node voltage stability index based on local voltage phasors. Electr. Power Syst. Res. 2009, 79, 265–271. [Google Scholar] [CrossRef]
- Verbic, G.; Gubina, F. A new concept of voltage-collapse protection based on local phasors. IEEE Trans. Power Deliv. 2004, 19, 576–581. [Google Scholar] [CrossRef]
- Chattopadhyay, T.K.; Banerjee, S.; Chanda, C.K. Impact of distributed generator on voltage stability analysis of distribution networks under critical loading conditions. In Proceedings of the 2014 1st International Conference on Non Conventional Energy (ICONCE 2014), Kalyani, India, 16–17 January 2014; pp. 288–291. [Google Scholar]
- Yazdanpanah-Goharrizi, A.; Asghari, R. A novel line stability index (NLSI) for voltage stability assessment of power systems. In Proceedings of the 7th WSEAS International Conference on Power Systems, Beijing, China, 15–17 September 2007; pp. 164–167. [Google Scholar]
- Tiwari, R.; Niazi, K.R.; Gupta, V. Line collapse proximity index for prediction of voltage collapse in power systems. Int. J. Electr. Power Energy Syst. 2012, 41, 105–111. [Google Scholar] [CrossRef]
- Eminoglu, U.; Hocaoglu, M.H. A voltage stability index for radial distribution networks. In Proceedings of the 2007 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007; pp. 408–413. [Google Scholar]
- Feltes, C.; Engelhardt, S.; Kretschmann, J.; Fortmann, J.; Koch, F.; Erlich, I. High voltage ride-through of DFIG-based wind turbines. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–8. [Google Scholar]
- Moghavvemi, M.; Faruque, O. Real-time contingency evaluation and ranking technique. IEE Proc.-Gener. Transm. Distrib. 1998, 145, 517–524. [Google Scholar] [CrossRef]
- Mohamed, A.; Jasmon, G.B.; Yusoff, S. A static voltage collapse indicator using line stability factors. J. Ind. Technol. 1989, 7, 73–85. [Google Scholar]
- Althowibi, F.A.; Mustafa, M.W. Power system network sensitivity to Voltage collapse. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012; pp. 379–383. [Google Scholar]
- Gong, Y.; Schulz, N.; Guzmán, A. Synchrophasor-Based Real-Time Voltage Stability Index. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October–1 November 2006; pp. 1029–1036. [Google Scholar]
- Pérez-Londoño, S.; Rodríguez, L.F.; Olivar, G. A Simplified Voltage Stability Index (SVSI). Int. J. Electr. Power Energy Syst. 2014, 63, 806–813. [Google Scholar] [CrossRef]
- Nizam, M.; Mohamed, A.; Hussain, A. Dynamic Voltage Collapse Prediction in Power Systems Using Power Transfer Stability Index. In Proceedings of the 2006 IEEE International Power and Energy Conference, Putra Jaya, Malaysia, 28–29 November 2006; pp. 246–250. [Google Scholar]
- Subramani, C.; Dash, S.S.; Bhaskar, M.A.; Jagadeeshkumar, M.; Sureshkumar, K.; Parthipan, R. Line outage contingency screening and ranking for voltage stability assessment. In Proceedings of the 2009 International Conference on Power Systems, Kharagpur, India, 27–29 December 2009; pp. 1–5. [Google Scholar]
- Smon, I.; Verbic, G.; Gubina, F. Local voltage-stability index using tellegen’s Theorem. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; p. 1. [Google Scholar]
- Albuquerque, M.A.; Castro, C.A. A contingency ranking method for voltage stability in real time operation of power systems. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 1, p. 5. [Google Scholar]
- Kanimozhi, R.; Selvi, K. A novel line stability index for voltage stability analysis and contingency ranking in power system using fuzzy based load flow. J. Electr. Eng. Technol. (JEET) 2013, 8, 694–703. [Google Scholar] [CrossRef]
- Wiszniewski, A. New Criteria of Voltage Stability Margin for the Purpose of Load Shedding. IEEE Trans. Power Deliv. 2007, 22, 1367–1371. [Google Scholar] [CrossRef]
- Althowibi, F.A.; Mustafa, M.W. Line voltage stability calculations in power systems. In Proceedings of the 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 396–401. [Google Scholar]
- Hawisa, K.; Ibsaim, R.; Daeri, A. Voltage instability remedy using FACTS, TCSC compensation first A. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2016; pp. 104–107. [Google Scholar]
- Jena, R.; Swain, S.C.; Panda, P.C.; Roy, A. Analysis of voltage and loss profile using various FACTS devices. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, Odisha, 3–5 October 2016; pp. 787–792. [Google Scholar]
- Hridya, K.R.; Mini, V.; Visakhan, R.; Kurian, A.A. Analysis of voltage stability enhancement of a grid and loss reduction using series FACTS controllers. In Proceedings of the 2015 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 9–11 December 2015; pp. 1–5. [Google Scholar]
- Roselyn, J.P.; Devaraj, D.; Dash, S.S. Multi-Objective Genetic Algorithm for voltage stability enhancement using rescheduling and FACTS devices. Ain Shams Eng. J. 2014, 5, 789–801. [Google Scholar] [CrossRef]
- Wibowo, R.S.; Yorino, N.; Eghbal, M.; Zoka, Y.; Sasaki, Y. FACTS Devices Allocation with Control Coordination Considering Congestion Relief and Voltage Stability. IEEE Trans. Power Syst. 2011, 26, 2302–2310. [Google Scholar] [CrossRef]
- Nascimento, S.D.; Gouvêa, M.M. Voltage Stability Enhancement in Power Systems with Automatic Facts Device Allocation. Energy Procedia 2017, 107, 60–67. [Google Scholar] [CrossRef]
- Tiwari, R.; Niazi, K.R.; Gupta, V. Optimal location of FACTS devices for improving performance of the power systems. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Tiwari, P.K.; Sood, Y.R. Optimal location of FACTS devices in power system using Genetic Algorithm. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 1034–1040. [Google Scholar]
- Saravanan, M.; Slochanal, S.M.R.; Venkatesh, P.; Abraham, P.S. Application of PSO technique for optimal location of FACTS devices considering system loadability and cost of installation. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; Volume 2, pp. 716–721. [Google Scholar]
- Yu, D.; Li, M.S.; Ji, T.Y.; Wu, Q.H. Optimal voltage control of power systems with uncertain wind power using FACTS devices. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 937–941. [Google Scholar]
- Rao, N.S.; Amarnath, J.; Rao, V.P. Effect of FACTS devices on enhancement of Voltage Stability in a deregulated power system. In Proceedings of the 2014 International Conference on Circuits, Power and Computing Technologies [ICCPCT-2014], Nagercoil, India, 20–21 March 2014; pp. 642–650. [Google Scholar]
- Lakkireddy, J.; Rastgoufard, R.; Leevongwat, I.; Rastgoufard, P. Steady-state voltage stability enhancement using shunt and series FACTS devices. In Proceedings of the 2015 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2015; pp. 1–5. [Google Scholar]
- Rathi, A.; Sadda, A.; Nebhnani, L.; Maheshwari, V.M.; Pareek, V.S. Voltage stability assessment in the presence of optimally placed D-FACTS devices. In Proceedings of the 2012 IEEE 5th India International Conference on Power Electronics (IICPE), Delhi, India, 6–9 December 2012; pp. 1–6. [Google Scholar]
- Muthu, V.U.; Bhaskar, M.A.; Arthur, A.; Kumar, T.; Surya, S.K. Modeling of wind energy based SSSC for voltage stability enhancement. In Proceedings of the 2014 International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 13–14 February 2014; pp. 1–6. [Google Scholar]
- Bhatt, P. Short term active power support from DFIG with coordinated control of SSSC and SMES in restructured power system. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014; pp. 1–6. [Google Scholar]
- Shankar; Udhaya, C.; Thottungal, R.; Mythili, S. Voltage stability improvement and power oscillation damping using Static Synchronous Series Compensator (SSSC). In Proceedings of the 2015 IEEE 9th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 9–10 January 2015; pp. 1–6. [Google Scholar]
- Hridya, K.R.; Mini, V.; Visakhan, R.; Kurian, A.A. Comparative study of voltage stability enhancement of a grid and loss reduction using STATCOM and SSSC. In Proceedings of the 2015 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 9–11 December 2015; pp. 1–4. [Google Scholar]
- Besharat, H.; Taher, S.A. Congestion management by determining optimal location of TCSC in deregulated power systems. Int. J. Electr. Power Energy Syst. 2008, 30, 563–568. [Google Scholar] [CrossRef]
- Joshi, N.N.; Mohan, N. Application of TCSC in wind farm application. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2006, Taormina, Italy, 23–26 May 2006; pp. 1196–1200. [Google Scholar]
- Mohammadpour, H.A.; Ghaderi, A.; Mohammadpour, H.; Ali, M.H. Low voltage ride-through enhancement of fixed-speed wind farms using series FACTS controllers. Sustain. Energy Technol. Assess. 2015, 9, 12–21. [Google Scholar] [CrossRef]
- Adjoudj, L.; Lakdja, F.; Gherbi, F.Z.; OuldAbdsallem, D. Synthesis integrating wind generation and FACTS of network. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014; pp. 1–6. [Google Scholar]
- Berrouk; Rachedi, B.A.; Lemzadmi, A.; Bounaya, K.; Zeghache, H. Applications of shunt FACTS controller for voltage stability improvment. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014; pp. 1–6. [Google Scholar]
- Yorino, N.; El-Araby, E.E.; Sasaki, H.; Harada, S. A new formulation for FACTS allocation for security enhancement against voltage collapse. IEEE Trans. Power Syst. 2003, 18, 3–10. [Google Scholar] [CrossRef]
- Elhassan, Z.; Li, Y.; Tang, Y. Simplified voltage control of paralleling doubly fed induction generators connected to the network using SVC. Int. Trans. Electr. Energy Syst. 2015, 25, 2847–2864. [Google Scholar] [CrossRef]
- Tang, B.; Fan, H.; Wang, X.; Yang, X.; Huang, C. The dynamic simulation research on application of SVC in the south Hebei power grid. In Proceedings of the CICED 2010 Proceedings, Nanjing, China, 3–6 September 2010; pp. 1–4. [Google Scholar]
- Kehrli, A.; Ross, M. Understanding grid integration issues at wind farms and solutions using voltage source converter FACTS technology. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 3, p. 1828. [Google Scholar]
- SreeLatha, K.; Kumar, M.V. STATCOM for enhancement of voltage stability of a DFIG driven wind turbine. In Proceedings of the 2014 Power and Energy Systems: Towards Sustainable Energy, Bangalore, India, 13–15 March 2014; pp. 1–5. [Google Scholar]
- Zhu, K.; Jiang, D.; Lian, X. Cascade STATCOM application in voltage stability of grid-connected wind farm. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 174–177. [Google Scholar]
- Jalali, A.; Aldeen, M. Placement and operation of STATCOM-storage for voltage stability enhancement of power systems with embedded wind farms. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 948–953. [Google Scholar]
- Rao, R.S.; Rao, V.S. A generalized approach for determination of optimal location and performance analysis of FACTs devices. Int. J. Electr. Power Energy Syst. 2015, 73, 711–724. [Google Scholar]
- Papantoniou, A.; Coonick, A. Simulation of FACTS for wind farm applications. In Proceedings of the IEE Colloquium on Power Electronics for Renewable Energy (Digest No: 1997/170), London, UK, 16 June 1997; pp. 8/1–8/5. [Google Scholar]
- Alharbi, Y.M.; Yunus, A.M.S.; Siada, A.A. Application of UPFC to improve the LVRT capability of wind turbine generator. In Proceedings of the 2012 22nd Australasian Universities Power Engineering Conference (AUPEC), Bali, Indonesia, 26–29 September 2012; pp. 1–4. [Google Scholar]
- Chen, Y.-L. Weak bus-oriented optimal multi-objective VAr planning. IEEE Trans. Power Syst. 1996, 11, 1885–1890. [Google Scholar] [CrossRef]
- Rong, Y.; Zheng, X.; Niu, H. Power system static voltage stability analysis including large-scale wind farms and system weak nodes identification. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 2747–2753. [Google Scholar]
- Qin, W.; Zhang, W.; Wang, P.; Han, X. Power system reliability based on voltage weakest bus identification. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–6. [Google Scholar]
- Acharjee, P.; Mallick, S.; Thakur, S.S.; Ghoshal, S.P. Detection of maximum loadability limits and weak buses using Chaotic PSO considering security constraints. Chaos Solitons Fractals 2011, 44, 600–612. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Chang, C.-W.; Liu, C.-C. Efficient methods for identifying weak nodes in electrical power networks. IEE Proc.-Gener. Transm. Distrib. 1995, 142, 317–322. [Google Scholar] [CrossRef]
- Aziz, T.; Saha, T.K.; Mithulananthan, N. Identification of the weakest bus in a distribution system with load uncertainties using reactive power margin. In Proceedings of the 2010 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010; pp. 1–6. [Google Scholar]
- Canizares, C.A.; De Souza, A.C.Z.; Quintana, V.H. Comparison of performance indices for detection of proximity to voltage collapse. IEEE Trans. Power Syst. 1996, 11, 1441–1450. [Google Scholar] [CrossRef]
- Chen, Y.L. Weak bus oriented reactive power planning for system security. IEE Proc.-Gener. Transm. Distrib. 1996, 143, 541–545. [Google Scholar] [CrossRef]
- Li, H.; Song, Y.H. Identification of weak busbars in large scale power system. In Proceedings of the International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 3, pp. 1700–1704. [Google Scholar]
- Acharjee, P. Identification of Maximum Loadability Limit under security constraints using Genetic Algorithm. In Proceedings of the 2011 International Conference on System Science and Engineering, Macao, China, 8–11 June 2011; pp. 234–238. [Google Scholar]
- Prada, R.B.; Palomino, E.G.C.; Pilotto, L.A.S.; Bianco, A. Weakest bus, most loaded transmission path and critical branch identification for voltage security reinforcement. Electr. Power Syst. Res. 2005, 73, 217–226. [Google Scholar] [CrossRef]
- Zahedi, A. Current status and future prospects of the wind energy. In Proceedings of the 2012 10th International Power & Energy Conference (IPEC), Ho Chi Minh City, Vietnam, 12–14 December 2012; pp. 54–58. [Google Scholar]
- Global Wind Statistics 2016. Available online: https://gwec.net/global-wind-report-2016/ (accessed on 27 July 2023).
- Jalboub, M.K.; Rajamani, H.S.; Abd-Alhameed, R.A.; Ihbal, A.M. Weakest bus identification based on modal analysis and Singular Value Decomposition techniques. In Proceedings of the 2010 1st International Conference on Energy, Power and Control (EPC-IQ), Basrah, Iraq, 30 November–2 December 2010; pp. 351–356. [Google Scholar]
- Chanda, S.; Das, B. Identification of weak buses in a power network using novel voltage stability indicator in radial distribution system. In Proceedings of the India International Conference on Power Electronics 2010 (IICPE2010), New Delhi, India, 28–30 January 2011; pp. 1–4. [Google Scholar]
- Divya, B.; Devarapalli, R. Estimation of sensitive node for IEEE-30 bus system by load variation. In Proceedings of the 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, 6–8 March 2014; pp. 1–4. [Google Scholar]
- Global Wind 2006 Report. Available online: https://gwec.net/wp-content/uploads/2012/06/gwec-2006_final_01.pdf (accessed on 25 July 2023).
- Global Wind Report 2015. Available online: https://gwec.net/global-wind-report-2015/ (accessed on 27 July 2023).
- Azam, A.; Rafiq, M.; Arif, I. The Economics of Wind Energy of Pakistan. In Proceedings of the 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 18–19 October 2016; pp. 1–6. [Google Scholar]
- GWEC. Global Wind Statistics 2012. Available online: https://www.gwec.net/wp-content/uploads/2012/06/Annual_report_2012_LowRes.pdf (accessed on 28 July 2023).
- Global Wind 2013. Available online: https://www.gwec.net/wp-content/uploads/2014/04/GWEC-Global-Wind-Report_9-April-2014.pdf (accessed on 28 July 2023).
- Global Wind Report 2014. Available online: https://www.gwec.net/wp-content/uploads/2015/03/GWEC_Global_Wind_2014_Report_LR.pdf (accessed on 28 July 2023).
- Chang, G.W.; Lu, H.J.; Hsu, L.Y.; Chen, Y.Y. A hybrid model for forecasting wind speed and wind power generation. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Amber, K.P.; Ashraf, N. Energy outlook in Pakistan. In Proceedings of the 2014 International Conference on Energy Systems and Policies (ICESP), Islamabad, Pakistan, 24–26 November 2014; pp. 1–5. [Google Scholar]
- di Marzio, G.; Eek, J.; Tande, J.O.; Fosso, O.B. Implication of Grid Code Requirements on Reactive Power Contribution and Voltage Control Strategies for Wind Power Integration. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 154–158. [Google Scholar]
- Demirol, M.; Çağlar, R.; Demirol, T.N. Wind farm dynamic analysis in terms of Turkish grid codes. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–9. [Google Scholar]
- Sutherland, P.E. Canadian grid codes and wind farm interconnections. In Proceedings of the 2015 IEEE/IAS 51st Industrial & Commercial Power Systems Technical Conference (I&CPS), Calgary, AB, Canada, 5–8 May 2015; pp. 1–7. [Google Scholar]
- Zhang, Y.; Duan, Z.; Liu, X. Comparison of Grid Code Requirements with Wind Turbine in China and Europe. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Armenakis, A. Grid code compliance test for small wind farms connected to the distribution grid in Cyprus. In Proceedings of the 8th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MEDPOWER 2012), Cagliari, Italy, 1–3 October 2012; pp. 1–6. [Google Scholar]
- Fagan, E.; Grimes, S.; McArdle, J.; Smith, P.; Stronge, M. Grid code provisions for wind generators in Ireland. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 2, pp. 1241–1247. [Google Scholar]
- Naser, S.; Anaya-Lara, O.; Lo, K.L. Study of the impact of wind generation on voltage stability in transmission networks. In Proceedings of the 2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 39–44. [Google Scholar]
- Ding, Q.; Qui, Z.; Yang, H.; Qi, Z. Effect of wind turbines integration on voltage stability. In Proceedings of the 2008 China International Conference on Electricity Distribution, Guangzhou, China, 10–13 December 2008; pp. 1–5. [Google Scholar] [CrossRef]
- Hossain, M.J.; Pota, H.R.; Mahmud, M.A.; Ramos, R.A. Impacts of large-scale wind generators penetration on the voltage stability of power systems. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Chi, Y.; Liu, Y.; Wang, W.; Dai, H. Voltage Stability Analysis of Wind Farm Integration into Transmission Network. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–7. [Google Scholar] [CrossRef]
- Nair, A.Y.; Lie, T.T. Integration of wind power into power systems—Voltage stability studies. In Proceedings of the 8th International Conference on Advances in Power System Control, Operation and Management (APSCOM 2009), Hong Kong, China, 8–11 November 2009; pp. 1–6. [Google Scholar]
- Amor, W.O.; Amar, H.B.; Ghariani, M. Grid stability study after the integration of a wind farm. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 678–683. [Google Scholar]
- Zheng, C.; Kezunovic, M. Distribution system voltage stability analysis with wind farms integration. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–6. [Google Scholar]
- Zou, Z.; Zhou, K. Voltage stability of wind power grid integration. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar]
- Nguyen, M.H.; Saha, T.K. Dynamic simulation for wind farm in a large power system. In Proceedings of the 2008 Australasian Universities Power Engineering Conference, Sydney, NSW, Australia, 14–17 December 2008; pp. 1–6. [Google Scholar]
- Meng, K.; Zhang, W.; Li, Y.; Dong, Z.Y.; Xu, Z.; Wong, K.P.; Zheng, Y. Hierarchical SCOPF Considering Wind Energy Integration through Multi-Terminal VSC-HVDC Grids. IEEE Trans. Power Syst. 2017, 32, 4211–4221. [Google Scholar] [CrossRef]
- Toma, R.; Gavrilaş, M. Voltage stability assessment for wind farms integration in electricity grids with and without consideration of voltage-dependent loads. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 14–17 December 2016; pp. 754–759. [Google Scholar]
- Sahni, M.; Khoi, V.; Tabrizi, M.; Prakash, N.; Karnik, N.; Bojorquez, W.; Caskey, M. Control Instability Index (CII) based approach for evaluating weak grid integration of wind generation clusters. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Cai, L.J.; Erlich, I.; Karaagac, U.; Mahseredjian, J. Stable operation of doubly-fed induction generator in weak grids. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Cai, L.J.; Erlich, I. Doubly Fed Induction Generator Controller Design for the Stable Operation in Weak Grids. IEEE Trans. Sustain. Energy 2015, 6, 1078–1084. [Google Scholar] [CrossRef]
- IEEE Std 1204-1997; IEEE Guide for Planning DC Links Terminating at AC Locations Having Low Short-Circuit Capacities. IEEE: Piscataway, NJ, USA, 1997; pp. 1–216.
- Etxegarai, A.; Eguia, P.; Torres, E.; Iturregi, A.; Valverde, V. Review of grid connection requirements for generation assets in weak power grids. Renew. Sustain. Energy Rev. 2015, 41, 1501–1514. [Google Scholar] [CrossRef]
- Lorenzen, S.L.; Nielsen, A.B.; Bede, L. Control of a grid-connected converter during weak grid conditions. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Bindner, H. Power Control for Wind Turbines in Weak Grids: Concepts Development. 1999. Available online: https://www.osti.gov/etdeweb/biblio/365955 (accessed on 8 April 2023).
- Kaur, J.; Yogarathinam, A.; Chaudhuri, N.R. Frequency control for weak AC grid connected to wind farm and LCC-HVDC system: Modeling and stability analysis. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Haider, Z.M.; Mehmood, K.K.; Rafique, M.K.; Khan, S.U.; Lee, S.-J.; Kim, C.-H. Water-filling algorithm based approach for management of responsive residential loads. J. Mod. Power Syst. Clean Energy 2018, 6, 118–131. [Google Scholar] [CrossRef]
- Xu, X.; Mu, G.; Shao, G.; Zhang, H.; Hou, K.; Gao, D.; Tao, J.; Ma, X.; Xiao, Y. The problems and solutions for large-scale concentrated integration of wind power to partially weak regional power grid. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–6. [Google Scholar]
- Zhou, Y.; Nguyen, D.D.; Kjær, P.C.; Saylors, S. Connecting wind power plant with weak grid—Challenges and solutions. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–7. [Google Scholar]
- Chen, X.; Hou, Y. STATCOM control for integration of wind farm to the weak grid. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Huang, S.H.; Schmall, J.; Conto, J.; Adams, J.; Zhang, Y.; Carter, C. Voltage control challenges on weak grids with high penetration of wind generation: ERCOT experience. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Givaki, K.; Xu, L. Stability analysis of large wind farms connected to weak AC networks incorporating PLL dynamics. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; pp. 1–6. [Google Scholar]
- Wang, D.; Hou, Y.; Hu, J. Effect of AC voltage control on the stability of weak AC grid connected DFIG system. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1528–1533. [Google Scholar]
- Dirksen, J.; DEWI GmbH. Wilhelmshaven. Low Voltage Ride-Through (LVRT). DEWI Magazin No 2013, 43. Available online: https://docplayer.org/19386881-Lvrt-low-voltage-ride-through.html (accessed on 16 August 2023).
- Dietmannsberger, M.; Grumm, F.; Schulz, D. Simultaneous Implementation of LVRT Capability and Anti-Islanding Detection in Three-Phase Inverters Connected to Low-Voltage Grids. IEEE Trans. Energy Convers. 2017, 32, 505–515. [Google Scholar] [CrossRef]
- Hossain, M.J.; Pota, H.R.; Kumble, C. Decentralized robust static synchronous compensator control for wind farms to augment dynamic transfer capability. J. Renew. Sustain. Energy 2010, 2, 022701. [Google Scholar] [CrossRef]
- Haider, Z.M.; Mehmood, K.K.; Khan, S.U.; Khan, M.O.; Wadood, A.; Rhee, S.-B. Optimal management of a distribution feeder during contingency and overload conditions by harnessing the flexibility of smart loads. IEEE Access 2021, 9, 40124–40139. [Google Scholar] [CrossRef]
- Chen, L.; Chen, H.; Yang, J.; Zhu, L.; Tang, Y.; Koh, L.H.; Xu, Y.; Zhang, C.; Liao, Y.; Ren, L.; et al. Comparison of Superconducting Fault Current Limiter and Dynamic Voltage Restorer for LVRT Improvement of High Penetration Microgrid. IEEE Trans. Appl. Supercond. 2017, 27, 1–7. [Google Scholar] [CrossRef]
- Song, H.; Zhang, Q.; Qu, Y.; Wang, X. An energy-based LVRT control strategy for doubly-fed wind generator. In Proceedings of the 2016 UKACC 11th International Conference on Control (CONTROL), Belfast, UK, 31 August–2 September 2016; pp. 1–6. [Google Scholar]
- Shukla, R.D.; Tripathi, R.K. Low voltage ride through (LVRT) ability of DFIG based wind energy conversion system-I. In Proceedings of the 2012 Students Conference on Engineering and Systems, Allahabad, India, 16–18 March 2012; pp. 1–6. [Google Scholar]
- Abbey, C.; Joos, G. Effect of low voltage ride through (LVRT) characteristic on voltage stability. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12–16 June 2005; Volume 2, pp. 1901–1907. [Google Scholar]
- Espinoza, N.; Bongiorno, M.; Carlson, O. Novel LVRT Testing Method for Wind Turbines Using Flexible VSC Technology. IEEE Trans. Sustain. Energy 2015, 6, 1140–1149. [Google Scholar] [CrossRef]
- Xiang, D.; Turu, J.C.; Muratel, S.M.; Wang, T. On-Site LVRT Testing Method for Full-Power Converter Wind Turbines. IEEE Trans. Sustain. Energy 2017, 8, 395–403. [Google Scholar] [CrossRef]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. A review of low-voltage ride-through enhancement methods for permanent magnet synchronous generator based wind turbines. Renew. Sustain. Energy Rev. 2015, 47, 399–415. [Google Scholar] [CrossRef]
- Xie, Z.; Shi, Q.; Song, H.; Zhang, X.; Yang, S. High voltage ride through control strategy of doubly fed induction wind generators based on active resistance. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 10–12 May 2012; pp. 2193–2196. [Google Scholar]
- Bollen, M.H.J. Understanding Power Quality Problems: Voltage Sags and Interruptions; Series on Power Engineering; IEEE Press: New York, NY, USA, 2000. [Google Scholar]
- Wessels, C.; Fuchs, F.W. High voltage ride through with FACTS for DFIG based wind turbines. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Mehmood, K.K.; Kim, C.-H.; Khan, S.U.; Haider, Z.M. Unified planning of wind generators and switched capacitor banks: A multiagent clustering-based distributed approach. IEEE Trans. Power Syst. 2018, 33, 6978–6988. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Jung, J.-W. Doubly-fed induction generator based wind turbines: A comprehensive review of fault ride-through strategies. Renew. Sustain. Energy Rev. 2015, 45, 447–467. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, D.; Xiong, P. A coordinated control strategy of DFIG-based WECS for high voltage ride-through enhancement. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 2808–2814. [Google Scholar]
- Mohseni, M.; Masoum, M.A.S.; Islam, S.M. Low and high voltage ride-through of DFIG wind turbines using hybrid current controlled converters. Electr. Power Syst. Res. 2011, 81, 1456–1465. [Google Scholar] [CrossRef]
- Alharbi, Y.M.; Yunus, A.M.S.; Abu-Siada, A. Application of STATCOM to improve the high-voltage-ride-through capability of wind turbine generator. In Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies, Perth, WA, Australia, 13–16 November 2011; pp. 1–5. [Google Scholar]
- Ahmad, A.; Loganathan, R. Development of LVRT and HVRT control strategy for DFIG based wind turbine system. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 316–321. [Google Scholar]
- Zheng, Z.; Yang, G.; Geng, H. High voltage ride-through control strategy of grid-side converter for DFIG-based WECS. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 5282–5287. [Google Scholar]
- Liu, C.; He, J.; Xie, Z. High voltage ride-through of grid-side converter for PMSG based directly driven wind turbines. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 8528–8532. [Google Scholar]
- Mehmood, K.K.; Khan, S.U.; Lee, S.-J.; Haider, Z.M.; Rafique, M.K.; Kim, C.-H. A real-time optimal coordination scheme for the voltage regulation of a distribution network including an OLTC, capacitor banks, and multiple distributed energy resources. Int. J. Electr. Power Energy Syst. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Coughlan, P.; O’sullivan, J.; Kamaluddin, N. High Wind Speed Shutdown analysis. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–5. [Google Scholar]
- Folly, K.A.; Sheetekela, S.P.N. Impact of fixed and variable speed wind generators on the transient stability of a power system network. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–7. [Google Scholar]
- Shehata, E.G. Active and Reactive Power Control of Doubly Fed Induction Generators for Wind Energy Generation under Unbalanced Grid Voltage Conditions. Electr. Power Compon. Syst. 2013, 41, 619–640. [Google Scholar] [CrossRef]
- Ibrahim, A.O.; Nguyen, T.H.; Lee, D.C.; Kim, S.C. A Fault Ride-Through Technique of DFIG Wind Turbine Systems Using Dynamic Voltage Restorers. IEEE Trans. Energy Convers. 2011, 26, 871–882. [Google Scholar] [CrossRef]
- Meegahapola, L.; Littler, T.; Fox, B.; Kennedy, J.; Flynn, D. Voltage and power quality improvement strategy for a DFIG wind farm during variable wind conditions. In Proceedings of the 2010 Modern Electric Power Systems, Wroclaw, Poland, 20–22 September 2010; pp. 1–6. [Google Scholar]
- Yang, L.; Xu, Z.; Ostergaard, J.; Dong, Z.Y.; Wong, K.P. Advanced Control Strategy of DFIG Wind Turbines for Power System Fault Ride Through. IEEE Trans. Power Systems 2012, 27, 713–722. [Google Scholar] [CrossRef]
- Cheng, P.; Nian, H. An improved control strategy for DFIG system and dynamic voltage restorer under grid voltage dip. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1868–1873. [Google Scholar]
- Dong, B.; Asgarpoor, S.; Qiao, W. Voltage analysis of distribution systems with DFIG wind turbines. In Proceedings of the 2009 IEEE Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009; pp. 1–5. [Google Scholar]
- Wang, D.; Hou, Y.; Hu, J. Stability of DC-link voltage control for paralleled DFIG-based wind turbines connected to Weak AC grids. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Banawair, K.S.; Pasupuleti, J. DFIG wind-turbine modeling with reactive power control integrated to large distribution network. In Proceedings of the 2014 IEEE International Conference on Power and Energy (PECon), Kuching, Malaysia, 1–3 December 2014; pp. 298–303. [Google Scholar]
- Abdou, A.F.; Abu-Siada, A.; Pota, H.R. Impact of VSC faults on dynamic performance and low voltage ride through of DFIG. Int. J. Electr. Power Energy Syst. 2015, 65, 334–347. [Google Scholar] [CrossRef]
- Ananth, D.V.N.; Kumar, G.V.N. Fault ride-through enhancement using an enhanced field oriented control technique for converters of grid-connected DFIG and STATCOM for different types of faults. ISA Trans. 2016, 62, 2–18. [Google Scholar] [CrossRef]
- Xiao, S.; Yang, G.; Geng, H. Analysis of the control limit of crowbar-less LVRT methods for DFIG-based wind power systems under asymmetrical voltage dips. In Proceedings of the 2011 IEEE PES Innovative Smart Grid Technologies, Perth, WA, Australia, 13–16 November 2011; pp. 1–7. [Google Scholar]
- Rodriquez, M.; Abad, G.; Sarasola, I.; Gilabert, A. Crowbar control algorithms for doubly fed induction generator during voltage dips. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 1–14 September 2005; p. 10. [Google Scholar]
- Londero, R.R.; Affonso, C.d.M.; Vieira, J.P.A. Long-Term Voltage Stability Analysis of Variable Speed Wind Generators. IEEE Trans. Power Syst. 2015, 30, 439–447. [Google Scholar] [CrossRef]
- Londero, R.R.; Affonso, C.d.M.; Vieira, J.P.A. Effects of operational limits of DFIG wind turbines on long-term voltage stability studies. Electr. Power Syst. Res. 2017, 142, 134–140. [Google Scholar] [CrossRef]
- Kim, J.; Park, G.; Seok, J.K.; Lee, B.; Kang, Y.C. Hierarchical voltage control of a wind power plant using the adaptive IQ-V characteristic of a doubly-fed induction generator. J. Electr. Eng. Technol. 2015, 10, 504–510. [Google Scholar] [CrossRef]
- Hansen, A.D.; Michalke, G.; Sørensen, P.E.; Lund, T.; Iov, F. Co-ordinated voltage control of DFIG wind turbines in uninterrupted operation during grid faults. Wind Energy 2007, 10, 51–68. [Google Scholar] [CrossRef]
- Gkavanoudis, S.I.; Demoulias, C.S. Fault ride-through capability of a DFIG in isolated grids employing DVR and supercapacitor energy storage. Int. J. Electr. Power Energy Syst. 2015, 68, 356–363. [Google Scholar] [CrossRef]
- Liao, Y.; Li, H.; Yao, J.; Zhuang, K. Operation and control of a grid-connected DFIG-based wind turbine with series grid-side converter during network unbalance. Electr. Power Syst. Res. 2011, 81, 228–236. [Google Scholar] [CrossRef]
- Masood, N.A.; Yan, R.; Saha, T.K. Estimation of maximum wind power penetration level to maintain an adequate frequency response in a power system. In Proceedings of the 8th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2014; pp. 587–590. [Google Scholar]
- Le, H.T.; Santoso, S. Analysis of Voltage Stability and Optimal Wind Power Penetration Limits for a Non-radial Network with an Energy Storage System. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Nguyen, N.; Mitra, J. An Analysis of the Effects and Dependency of Wind Power Penetration on System Frequency Regulation. IEEE Trans. Sustain. Energy 2016, 7, 354–363. [Google Scholar] [CrossRef]
- Toma, R.; Gavrilas, M. The impact on voltage stability of the integration of renewable energy sources into the electricity grids. In Proceedings of the 2014 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 16–18 October 2014; pp. 1051–1054. [Google Scholar]
- Jiapaer, A.; Zeng, G.; Ma, S.; Xie, H.; Tong, Y.; Huang, M. Study on capacity of wind power integrated into power grid based on static voltage stability. In Proceedings of the 2012 IEEE 15th International Conference on Harmonics and Quality of Power, Hong Kong, China, 17–20 June 2012; pp. 855–859. [Google Scholar]
- Cocina, V.; Di Leo, P.; Pastorelli, M.; Spertino, F. Choice of the most suitable wind turbine in the installation site: A case study. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1631–1634. [Google Scholar]
- Multazam, T.; Putri, R.I.; Pujiantara, M.; Priyadi, A.; Hery, P.M. Wind farm site selection base on fuzzy analytic hierarchy process method; Case study area Nganjuk. In Proceedings of the 2016 International Seminar on Intelligent Technology and Its Applications (ISITIA), Lombok, Indonesia, 28–30 July 2016; pp. 545–550. [Google Scholar]
- Zhu, J.; Cheung, K. Selection of wind farm location based on fuzzy set theory. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Cetinay, H.; Kuipers, F.A.; Guven, A.N. Optimal siting and sizing of wind farms. Renew. Energy 2017, 101, 51–58. [Google Scholar] [CrossRef]
- Gigoviç, L.; Pamuìar, D.; Božanić, D.; Ljubojević, S. Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: A case study of Vojvodina, Serbia. Renew. Energy 2017, 103, 501–521. [Google Scholar] [CrossRef]
- Bezbradica, M.; Kerkvliet, H.; Borbolla, I.M.; Lehtimäki, P. Introducing multi-criteria decision analysis for wind farm repowering: A case study on Gotland. In Proceedings of the 2016 International Conference Multidisciplinary Engineering Design Optimization (MEDO), Belgrade, Serbia, 14–16 September 2016; pp. 1–8. [Google Scholar]
- Hofer, T.; Sunak, Y.; Siddique, H.; Madlener, R. Wind farm siting using a spatial Analytic Hierarchy Process approach: A case study of the Städteregion Aachen. Appl. Energy 2016, 163, 222–243. [Google Scholar] [CrossRef]
- Putranto, L.M.; Hara, R.; Kita, H.; Tanaka, E. WAMS hybrid configuration for real-time voltage stability monitoring application. In Proceedings of the 2016 17th International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 16–18 May 2016; pp. 1–6. [Google Scholar]
- Zhang, K.; Zhang, S.; Liu, Y. Structure and Applications of a Novel WAMS. Procedia Eng. 2011, 15, 4492–4498. [Google Scholar] [CrossRef]
- Nohac, K.; Tesarova, M.; Nohacova, L.; Veleba, J.; Majer, V. Utilization of Events Measured by WAMS-BIOZE-Detector for System Voltage Stability Evaluation. IFAC-PapersOnLine 2016, 49, 364–369. [Google Scholar] [CrossRef]
- Saha, K.; Meera, K.S.; Shivaprasad, V. Smart grid and WAMS in Indian context—A review. In Proceedings of the 2015 Clemson University Power Systems Conference (PSC), Clemson, SC, USA, 10–13 March 2015; pp. 1–6. [Google Scholar]
- Zhou, Y.; Wang, K.; Xiong, Y.; Zhang, B. Study of Power System Online Dynamic Equivalent Based on Wide Area Measurement System. Energy Procedia 2012, 16, 1768–1775. [Google Scholar]
- Putranto, L.M.; Hara, R.; Kita, H.; Tanaka, E. Risk-based voltage stability monitoring and preventive control using wide area monitoring system. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar]
- Popelka, A.; Jurik, D.; Marvan, P.; Povolny, V. Advanced applications of WAMS. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar]
- Putranto, L.M.; Hoonchareon, N. Wide Area Monitoring System implementation in securing voltage stability based on phasor measurement unit data. In Proceedings of the 2013 10th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 15–17 May 2013; pp. 1–6. [Google Scholar]
- Ahmadi, A.; Beromi, Y.A. Neuro-fuzzy based algorithm for online dynamic voltage stability status prediction using wide-area phasor measurements. In Proceedings of the 2015 30th International Power System Conference (PSC), Tehran, Iran, 23–25 November 2015; pp. 14–20. [Google Scholar]
- Mousavi-Seyedi, S.S.; Aminifar, F.; Afsharnia, S. Application of WAMS and SCADA Data to Online Modeling of Series-Compensated Transmission Lines. IEEE Trans. Smart Grid 2017, 8, 1968–1976. [Google Scholar] [CrossRef]
- Rahmatian, M.; Dunford, W.G.; Palizban, A.; Moshref, A. Transient Stability Assessment of power systems through Wide-Area Monitoring System. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Liu, Y.; Fan, R.; Terzija, V. Power system restoration: A literature review from 2006 to 2016. J. Mod. Power Syst. Clean Energy 2016, 4, 332–341. [Google Scholar] [CrossRef]
- Lei, J.; Li, Y.; Zhang, B.; Liu, W. A WAMS based adaptive load shedding control strategy using a novel index of transient voltage stability. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 8164–8169. [Google Scholar]
- Chen, H.; Jiang, T.; Yuan, H.; Jia, H.; Bai, L.; Li, F. Wide-area measurement-based voltage stability sensitivity and its application in voltage control. Int. J. Electr. Power Energy Syst. 2017, 88, 87–98. [Google Scholar] [CrossRef]
- Hering, P.; Juřík, D.; Janeček, P.; Popelka, A. Applications of Czech PMU/WAMS Systems in Distribution Systems. IFAC-PapersOnLine 2016, 49, 358–363. [Google Scholar] [CrossRef]
- Arias, D.; Vargas, L.; Rahmann, C. WAMS-Based Voltage Stability Indicator Considering Real-Time Operation. IEEE Lat. Am. Trans. 2015, 13, 1421–1428. [Google Scholar] [CrossRef]
- Zhao, J.; Zeng, Y.; Wei, W.; Jia, H. Fast assessment of regional voltage stability based on WAMS. In Proceedings of the APCCAS 2008—2008 IEEE Asia Pacific Conference on Circuits and Systems, Macao, China, 30 November–3 December 2008; pp. 635–638. [Google Scholar]

| Sr. | Index | Proposed by | Expression/Formula | Critical Value | Salient Features | Input variables (of Formula) | References |
|---|---|---|---|---|---|---|---|
| 1 | Fast Voltage Stability Index (FVSI) | Ismail Musiril et al. | FVSI = (4Z2Qj)/Vi2Xij | Critical value ≥ 1 | Used in determining the weakest bus, line criticalness, and maximum load-ability | Z = Line impedance Xij = Line reactance Qj = Receiving end reactive power Vi = Sending end voltage | [106] |
| 2 | Line Stability Index (Lmn) | M. Moghavvemi | If Lmn = 1, system is near to voltage collapse; Lmn < 1 means system is stable; Lmn = 0 means system has no load | Based on ‘’Power flow through a single line.’’ Uses little information like the specific local measurements | = Line reactance | [112,113,114] | |
| 3 | Line Voltage Stability Index (Li) | Arya et al. | Li = AvCos(δ − α) δ = δk − δm | Li < 0.5 | This index halves at voltage collapse | = Receiving end voltage Sending end voltage Phase angle across the line | [103] |
| 4 | Equivalent Node Voltage Collapse Index (ENVCI) | Yang Wang et al. | For strongest bus, ENVCI = 1; for weakest bus, ENVCI = 0 | Useful for online assessment. It is quickly determined by using the voltage phasors | Vn | [115,116,117] | |
| 5 | Novel Line Stability Index (NLSI) | A. Yazdanpanah-Goharrizi et al. | Value close to 1 indicates voltage collapse point | Consider both active and reactive power; accurate results | = Angle difference between sending and receiving buses | [118,119,120] | |
| 6 | Voltage Collapse Point Indicators (VCPIs) | M. Moghavvemi and O. Faruque | = | Lmn = 1 means system is near to voltage collapse; Lmn < 1 means system is stable; Lmn = 0 means system has no load | Based on ‘’Power flow through a single line.’’ This is based on the concept of maximum power transferred through the lines of the network. A higher degree of reliability; higher accuracy; simple; easy to calculate; We do not need the information on other lines in the system for calculation. We need specific local measurements | = Real power transferred to the receiving end Maximum real power that can be transferred Reactive power transferred to the receiving end Maximum reactive power that can be transferred = Real power loss in the line Maximum possible real power loss Reactive power loss in the line Maximum possible reactive power loss | [3,121,122] |
| 7 | LQP index | Mohammad et al. | LQP = 4(X/Vs2)(X/Vs2(Ps2 + QR)) | 1 means the system is near to voltage collapse | Based on line stability factors; fast computation capability; helps to find the cause of voltage collapse | X = Reactance R = Resistance Vi = Input Voltage Pi = Input power Qr = Reactive power at receiving end | [123,124] |
| 8 | VSI_1 | Y. Gong et al. | ) | VSI_1 = 0 System collapse | Provides voltage stability margin of each bus. Also diversifies the most critical load bus | Active load margin Reactive load margin Apparent load margin | [125,126] |
| 9 | Power Transfer Stability Index (PTSI) | M. Nizam et al. | 1 indicates voltage collapse point | Helps in finding dynamic voltage collapse | = Thevenin voltage = Thevenin impedance Maximum load apparent power Load phase angles | [127] | |
| 10 | Line Index (Lij) | C.Subramani et al. | Lij = 0 line is close to voltage collapse | Easily identifies the weak areas of a nearly stressed system | Z = Line impedance X = Line reactance Vi = Sending end voltage Qj = Receiving end reactive power | [128,129] | |
| 11 | LSR | Mario A. Albuquerque and Carlos A. Castro | Lsr = 1 voltage stability indication | Easily used in real time; exactly recognizes the critical contingencies | Apparent power flow Maximum power transfer | [130] | |
| 12 | New Voltage Stability Index (NVSI) | R. Kanimozhi et al. | 1 indicates critical line | This index relates real and reactive powers; high standard voltage instability prediction; relates real and reactive power; exact voltage stability prediction | X = Line reactance P = Real Power Vi = Sending end voltage Qj = Reactive power at receiving end | [131,132] | |
| 13 | ) | F.A. Althowibi et al. | 1 is the point at which voltage collapses | Easily tells the distance from the point of voltage collapse of any line; high speed and accuracy | = Receiving reactive power at bus Sending voltage at system bus Line admittance between bus k and m | [133] |
| Sr | FACT Device | Category | Salient Features | Special Findings | Refs. |
|---|---|---|---|---|---|
| 1 | SSSC | Series |
|
| [147,148,149,150] |
| 2 | TCSC |
|
| [151,152,153,154] | |
| 3 | SVC | Shunt |
|
| [144,155,156,157,158] |
| 4 | STATCOM |
|
| [159,160,161,162] | |
| 5 | UPFC | Combined series shunt |
|
| [163,164,165] |
| 6 | D-Var |
|
| [159] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, F.H.; Khan, M.W.; Rahman, T.U.; Ehtisham, M.; Faheem, M.; Haider, Z.M.; Lehtonen, M. A Comprehensive Review on Voltage Stability in Wind-Integrated Power Systems. Energies 2024, 17, 644. https://doi.org/10.3390/en17030644
Malik FH, Khan MW, Rahman TU, Ehtisham M, Faheem M, Haider ZM, Lehtonen M. A Comprehensive Review on Voltage Stability in Wind-Integrated Power Systems. Energies. 2024; 17(3):644. https://doi.org/10.3390/en17030644
Chicago/Turabian StyleMalik, Farhan Hameed, Muhammad Waleed Khan, Tauheed Ur Rahman, Muhammad Ehtisham, Muhammad Faheem, Zunaib Maqsood Haider, and Matti Lehtonen. 2024. "A Comprehensive Review on Voltage Stability in Wind-Integrated Power Systems" Energies 17, no. 3: 644. https://doi.org/10.3390/en17030644
APA StyleMalik, F. H., Khan, M. W., Rahman, T. U., Ehtisham, M., Faheem, M., Haider, Z. M., & Lehtonen, M. (2024). A Comprehensive Review on Voltage Stability in Wind-Integrated Power Systems. Energies, 17(3), 644. https://doi.org/10.3390/en17030644










