Controller Hardware-in-the-Loop Testbed of a Distributed Consensus Multi-Agent System Control under Deception and Disruption Cyber-Attacks

Abstract

The impact of communication disturbances on microgrids (MGs) needs robust and scalable Information Communication Technology (ICT) infrastructure for efficient MG control. This work builds on advances in the Internet of Things (IoT) to provide a practical platform for testing the impact of various cyber-attacks on a distributed control scheme for a Multi-Agent System (MAS). This paper presents a Controller Hardware-in-the-Loop (CHIL) testbed to investigate the impact of various cyber-attacks and communication disruptions on MGs. A distributed consensus secondary control scheme for a MAS within an MG cyber-physical system (CPS) is proposed. The proposed cyber-physical testbed integrates a real-time islanded AC microgrid on RT-Lab, secondary controllers implemented on single-board computers, and an attacker agent on another single-board computer. Communication occurs via a UDP/IP network between OPAL-RT and controller agents, as well as between the agents. Through meticulous experimentation, the efficacy of the proposed control strategy using the developed platform is validated. Various attacks were modeled and launched including deception attacks on sensors, actuators, and their combinations, as well as disruption attacks. The ramifications of both deception and disruption cyber-attacks on system performance are analyzed.

1. Introduction

In the face of increasing concerns about the environmental impact of fossil fuel-based power plants and the commitment of many countries to achieving net zero carbon emissions by 2050, microgrids have emerged as a practical solution to integrate renewable energy and ensure energy security. The term microgrids refers to a group of distributed generators (DGs), loads, and energy storage systems capable of seamlessly transitioning between islanded and grid-connected modes. The control architecture of microgrids is hierarchically structured, involving primary, secondary, and tertiary control levels [1]. The primary control (PC) often has a droop-based design to stabilize the frequency and voltage and to achieve active/reactive power-sharing using local measurements. The secondary control (SC) is implemented as centralized or distributed [2]. It addresses deviations caused by primary control by restoring frequency and voltage. At the top level, tertiary control (TC) is used to manage the power flow and for optimal dispatch operation. Communication networks become vital as secondary controllers exchange critical information such as voltage, frequency, and active and reactive power among DGs [3]. Some standard communication protocols used in microgrids are DNP3, Modbus, TCP/IP, XML, CAN Bus, IEC 61850 [4], etc. The complex interdependency between cyber and physical systems makes them vulnerable to cyber threats. Therefore, a Controller Hardware-In-the-Loop (CHIL) testbed is developed in the real-time environment using OPAL-RT to analyze the impact of different cyber-attacks on the AC microgrid [5,6,7].

Cyber-physical systems simulation techniques can be classified into three types, i.e., co-simulation, semi-physical simulation, and embedded simulation. The embedded simulation technique aims to design the communication modules in the power system simulation software. However, the difficulty of this technique lies in the communication module design. In the semi-physical simulation method, one of the systems is simulated using simulation software while a real hardware object replaces the other system. This technique presents an increased simulation authenticity and high simulation accuracy. However, real physical devices make it expensive. Finally, the co-simulation technique aims to build a joint simulation platform by using power system and communication network simulation software, and to realize information exchange between both systems. It is divided into real-time co-simulation and non-real-time co-simulation. The physical and communication simulators have different time management mechanisms in the non-real-time co-simulation. Therefore, a time synchronization method should be designed to achieve collaborative simulation between the two simulators. Even though a collaborative study of a CPS can be achieved through non-real-time co-simulation with a good time synchronization method, real-time co-simulation is given more attention. Real-time co-simulation means that the simulation software runs in real time and that the system can be divided into various sub-models for parallel computation purposes. Hardware-based real-time power system simulation platforms are required for real-time co-simulation, such as OPAL-RT and RTDS [8]. CHIL is a specific co-simulation type involving a hardware controller interacting with a simulation [9]. In our study, we built a CHIL testbed using OPAL-RT and implemented multiple secondary controllers using single-board computers. The developed platform is suitable for studying the impact of communication network disturbances, such as time delays, packet loss, limited bandwidth, and cyber-attacks on cyber-physical systems.

Cyber threats present a serious risk to CPS-based microgrids [10]. For instance, a breach in the communication link may result in miscommunication among DERs, deteriorating the power-sharing objectives and MG stability. Compared to conventional cyber security; attacks on CPSs manipulate data transmission and the physical entities within the system. These attacks can be categorized into replay attacks, DoS, and deception attacks. Replay attacks disrupt authentication by intercepting and retransmitting valid messages [11,12], while DoS attackers jam the communication links among agents to prevent data from reaching their destination. DoS attacks are widely discussed in the literature. Deception attacks compromise sensors’ and actuators’ data integrity through injection or modification. These attacks do not necessarily require deep knowledge of system dynamics and may result in catastrophic consequences [13]. Recent cyber-attacks on industrial infrastructure, such as the Stuxnet worm’s attack on Iran’s nuclear power plant and coordinated attacks on power grids in Ukraine and Venezuela, underline the urgent need for robust defensive strategies in CPS security. For instance, the cyber-attack on Ukraine’s power grid in 2015 began with an initial compromise as early as eight months before. Initially, the attacker managed to compromise the information technology (IT) network through spear fishing emails. Once inside the network, variants of BlackEnergy 3 malware were remotely controlled to penetrate the industrial control systems (ICSs) and supervisory control and data acquisition (SCADA) systems responsible for managing the power grid. With control over these systems, the hacker remotely took control and executed commands to manipulate the operation of electrical substations and power distribution equipment. At the same time, the operator was prevented from regaining control of the network using a modified KillDisk firmware attack and customers were prevented from reporting the outages by launching a distributed denial of service (DDoS) attack on call centers. The prolonged impact of the attack underscored the vulnerability of critical infrastructure to cyber-physical threats and highlighted the need for robust defense mechanisms to mitigate such risks effectively [14]. Similarly, Venezuela experienced blackouts caused by cyber-attacks.

Hence, the motivation for this paper arises from the critical need to analyze the impact of different cyber-attacks on microgrids and further develop robust defensive strategies to protect microgrids’ cyber-physical systems.

The contributions of this research paper can be summarized as follows:

-

Development of a novel cyber-physical platform integrating a real-time islanded AC microgrid model running on OPAL-RT, distributed consensus secondary control on Raspberry Pis, and an attacker agent for disruption and deception attacks;

-

Development of a distributed consensus secondary controller for frequency and voltage restoration and accurate power sharing;

-

Implementation of a communication network using graph theory and the Laplacian matrix to enable information exchange among agents and assess network vulnerabilities;

-

Modeling and implementation of disruption and deception attacks on the microgrid communication network using an attacker agent deployed on a Raspberry Pi;

-

Assessment of multi-agent system operation under various scenarios of disruption and deception cyber-attacks.

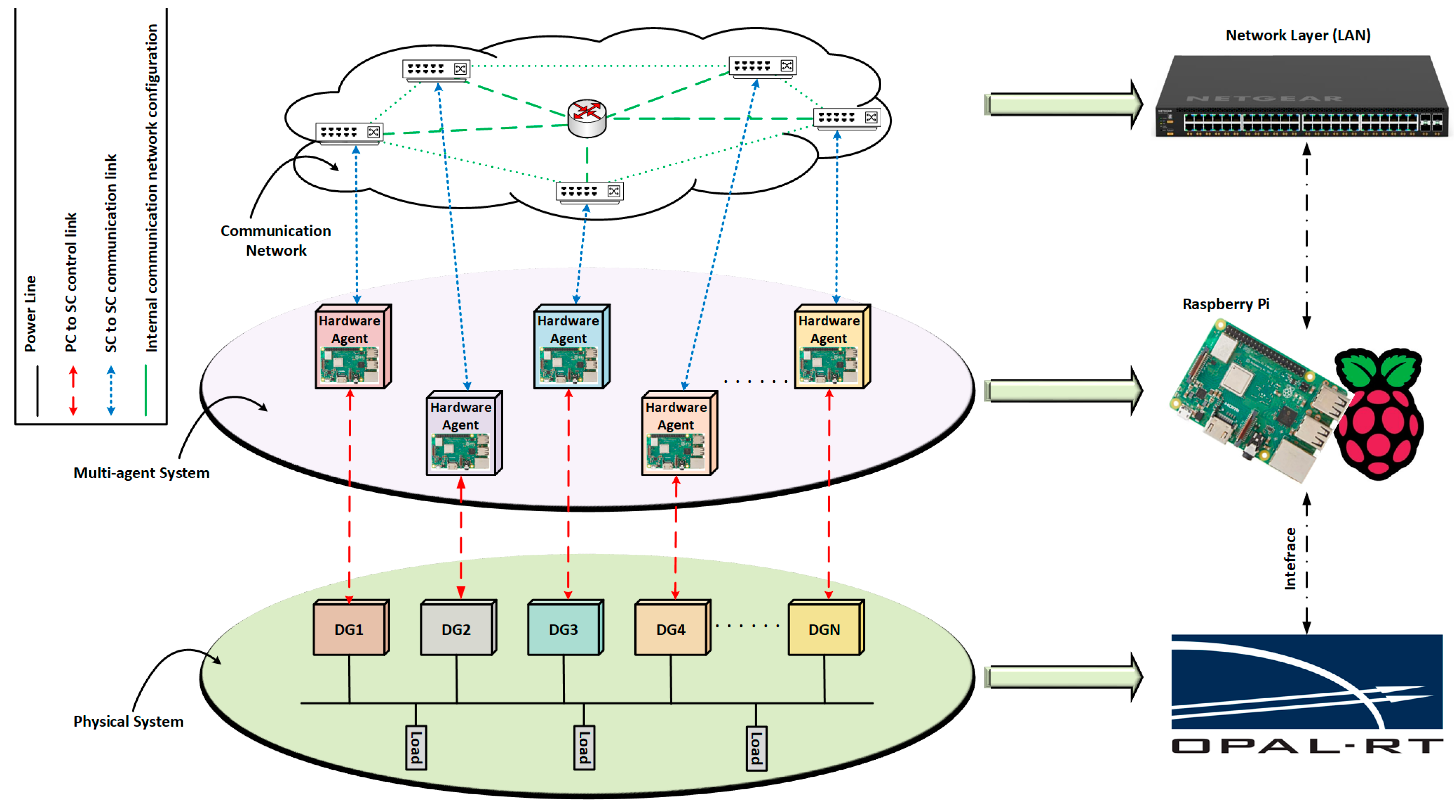
Figure 1 shows a multilayered MAS framework, where each agent receives and shares information with neighboring agents through a communication network. The hardware setup includes an OPAL-RT real-time simulator and independent hardware agents running on Raspberry Pis. The communication between the OPAL-RT and the agents, as well as the communication between the agents, is all through the UDP/IP protocol.

The rest of the paper is organized as follows. Section 2 introduces preliminaries on the primary control, secondary control, and communication network. The cyber-attacks model is explained in Section 3. The testbed setup is presented in Section 4. Section 5 presents experimental results and discussion to validate the testbed setup and show the impact of deception and disruption attacks on the proposed consensus control strategy. Section 6 concludes the research paper.

2. Preliminaries

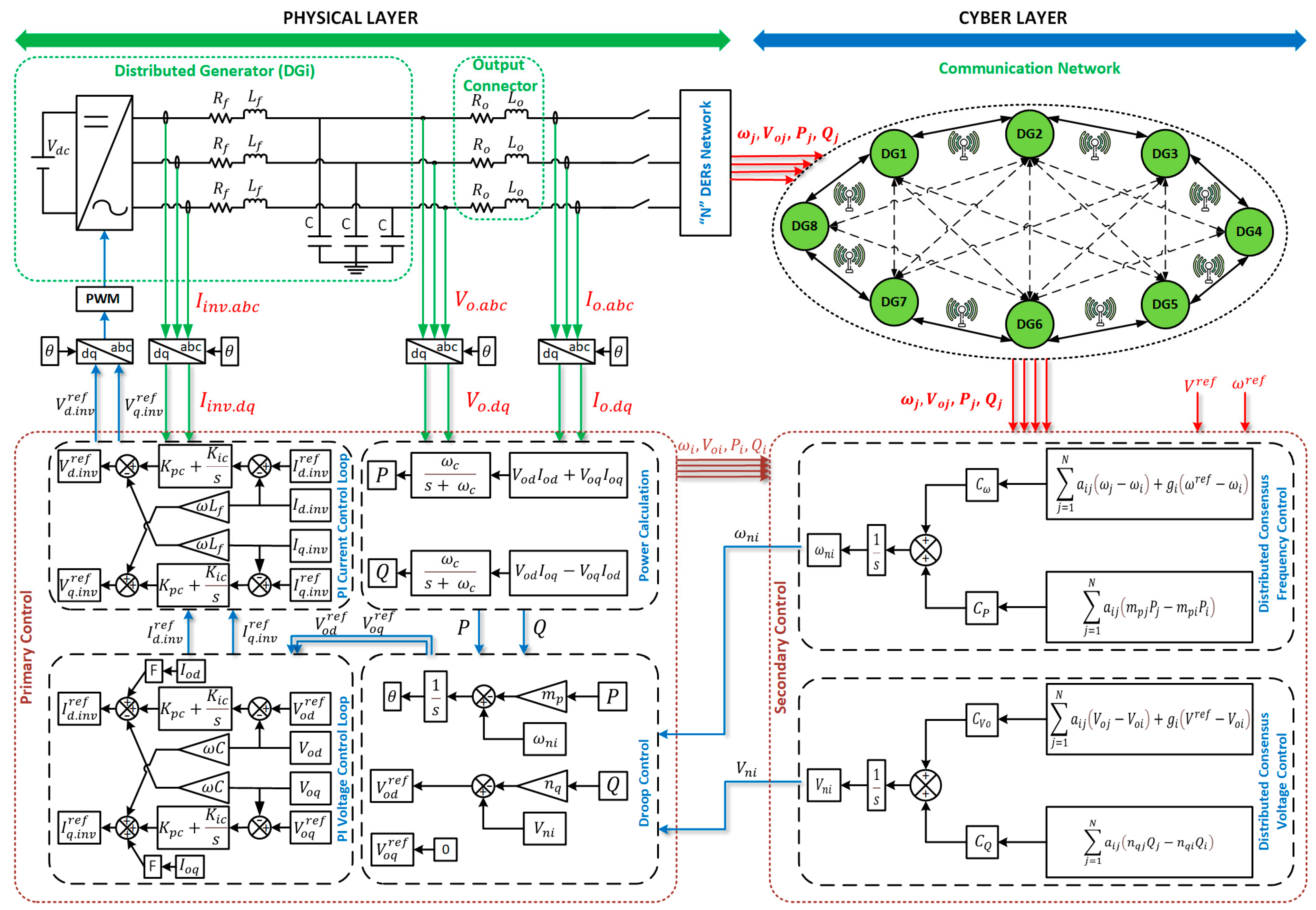
Voltage Source Inverters (VSIs) are usually used to connect DGs to the network. Figure 2 depicts the block diagram of a VSI, its components, the primary and secondary control loops, and the communication network. The primary and secondary control loops are presented in the following.

2.1. Primary Control

The primary control aims to stabilize the microgrid and ensure power sharing. The proportional control loops are employed locally at each inverter to enable plug-and-play functionality and enhance redundancy. While this decentralized control strategy enables power sharing, it also impacts voltage and frequency regulation.

It consists of three control loops: power control loop, voltage control loop, and current control loop.

2.1.1. Power Control Loop

It is widely employed to adjust the frequency and voltage magnitude in the case of inverter-based DGs in islanded MGs. This adjustment is based on droop characteristics associated with both real and reactive power. The concept of droop control is derived from emulating the behavior of synchronous generators in conventional power systems. Rotating machines respond to an increase in demand by decreasing the system frequency, governed by their droop characteristics. Similarly, inverters implement this principle by reducing the reference frequency as the load increases. The reactive power sharing is managed through the implementation of a droop characteristic in the voltage magnitude [15,16,17]. The block diagram of the power control loop is shown in Figure 2.

The active (P) and reactive (Q) power can be calculated from the measured output voltage and current and then passed through low-pass filters as given in Equation (1), where ${\omega }_c$ is the cut-off frequency and $s$ is the Laplace variable.

$$\left\{\begin{array}{c}P=\frac{{\omega }_c}{s+{\omega }_c}(V_{od}{I}_{od}+V_{oq}{I}_{oq}) \\ Q=\frac{{\omega }_c}{s+{\omega }_c}(V_{od}{I}_{oq}-V_{oq}{I}_{od}) \end{array}\right.$$

(1)

The active and reactive power sharing between VSIs is achieved by using an artificial droop, introduced, respectively, in the frequency and the voltage magnitude as given in Equation (2), where ${\omega }_n$ and $V_n$ are the nominal frequency and voltage amplitude, respectively. $\omega$ and $V_o$ are the reference frequency and voltage, respectively [18,19].

$$\left\{\begin{array}{c}\omega ={\omega }_n-m_{p}P\\ V_o=V_n-n_{q}Q\end{array}\right.$$

(2)

The droop coefficients ($m_p$ and $n_q$) are calculated in Equation (3) based on the output power rating. The power control loop provides the voltage reference for the voltage control loop ($V_o^{ref}$). Note that the output voltage reference is chosen to be aligned to the direct axis of the inverter reference frame (d-axis), and the quadrature axis (q-axis) reference is set to zero.

$$m_p=\frac{∆\omega }{P_{max}}\hspace{1em}\hspace{1em},\hspace{1em}\hspace{1em}{n}_q=\frac{∆V_o}{Q_{max}}$$

(3)

2.1.2. Voltage and Current Control Loops

Voltage and current control loops provide the output current and input voltage references ($I_{inv}^{ref} \mathrm{a}\mathrm{n}\mathrm{d} V_{inv}^{ref})$. The block diagram of the internal voltage and current control loops is shown in Figure 2.

2.2. Preliminaries and Communication Network

This section briefly describes graph theory properties. The microgrid is essentially envisioned as a MAS, where the DGs take on the roles of communicating agents or nodes, while the communication links are seen as edges forming a sparse communication network. Each DG can exchange information with its neighboring DGs through this sparse communication network. In our case, the studied system is an islanded microgrid consisting of N DGs, where the communication among them is visually represented by a directed (one-way) or undirected (two-way) communication graph [20,21]. This graph is mathematically represented as $\mathcal{G}=\left(\mathcal{V},E,A\right)$ where $\mathcal{V}=\left\{v_1,v_2,\dots ,v_N\right\}$ is a set of $\mathcal{N}$ nodes, $E\subseteq \mathcal{V}\times \mathcal{V}$ is a set of edges, $A\triangleq \left[a_{ij}\right] \in {\mathbb{R}}^{N\times N}$ is the Adjacency matrix, and it is defined as follows:

$$A\triangleq \left[a_{ij}\right] where { a}_{ij}\triangleq \left\{\begin{array}{c} 0 \forall i=j\\ >0 \forall i\ne j\end{array}\right.$$

(4)

The edge $\left(v_j,v_i\right)$ means that node $j$ transmits information to node $i$. The weight of edge $a_{ij}>0$ if $\left(v_j,v_i\right)\in E$, otherwise $a_{ij}=0$. $N_i=\left\{j|\left(v_j,v_i\right)\in E\right\}$ is the set of neighbors of the $i\mathrm{t}\mathrm{h}$ node where $j$ is called the neighbor of $i$ if $\left(v_j,v_i\right)\in E$. Every node in a graph has an in-degree matrix $D\triangleq diag\left\{d_i\right\}$, defined as follows:

$$D\triangleq diag\left\{d_i\right\} where d_i\triangleq {\sum }_{j\in {\mathcal{N}}_i}{a}_{ij} \forall i=j$$

(5)

where the Laplacian matrix $L\triangleq D-A$ is defined as follows:

$$L\triangleq \left[{\mathcal{l}}_{ij}\right] where {\mathcal{l}}_{ij}\triangleq \left\{\begin{array}{c}{d}_i=\sum _{j\in {\mathcal{N}}_i}{a}_{ij} \forall i=j\\ -a_{ij} \forall i\ne j\end{array}\right.$$

(6)

A weighted graph is called balanced if and only if all the included nodes are balanced such that ${\sum }_{j=1}^{{\mathcal{N}}_i}{a}_{ij}={\sum }_{j=1}^{{\mathcal{N}}_i}{a}_{ji}$. A graph $\mathcal{G}$ is said to be strongly connected (SC) if there is a connection path of edges between each two separate nodes with accurate direction. The graph is said to have a spanning tree if there is a directed path from a root node $i_r$ to every other node in the graph [22].

The adjacency, in-degree and, Laplacian matrices, as well as other parameters, can effectively improve the control algorithm [23]. Equation (7) is always used in control algorithms based on graph theory where any scalar $x_i$ satisfies the consensus principle in continuous time.

$${\dot{x}}_i=u_i={\sum }_{j\in {\mathcal{N}}_i}{a}_{ij}(x_j-x_i)$$

(7)

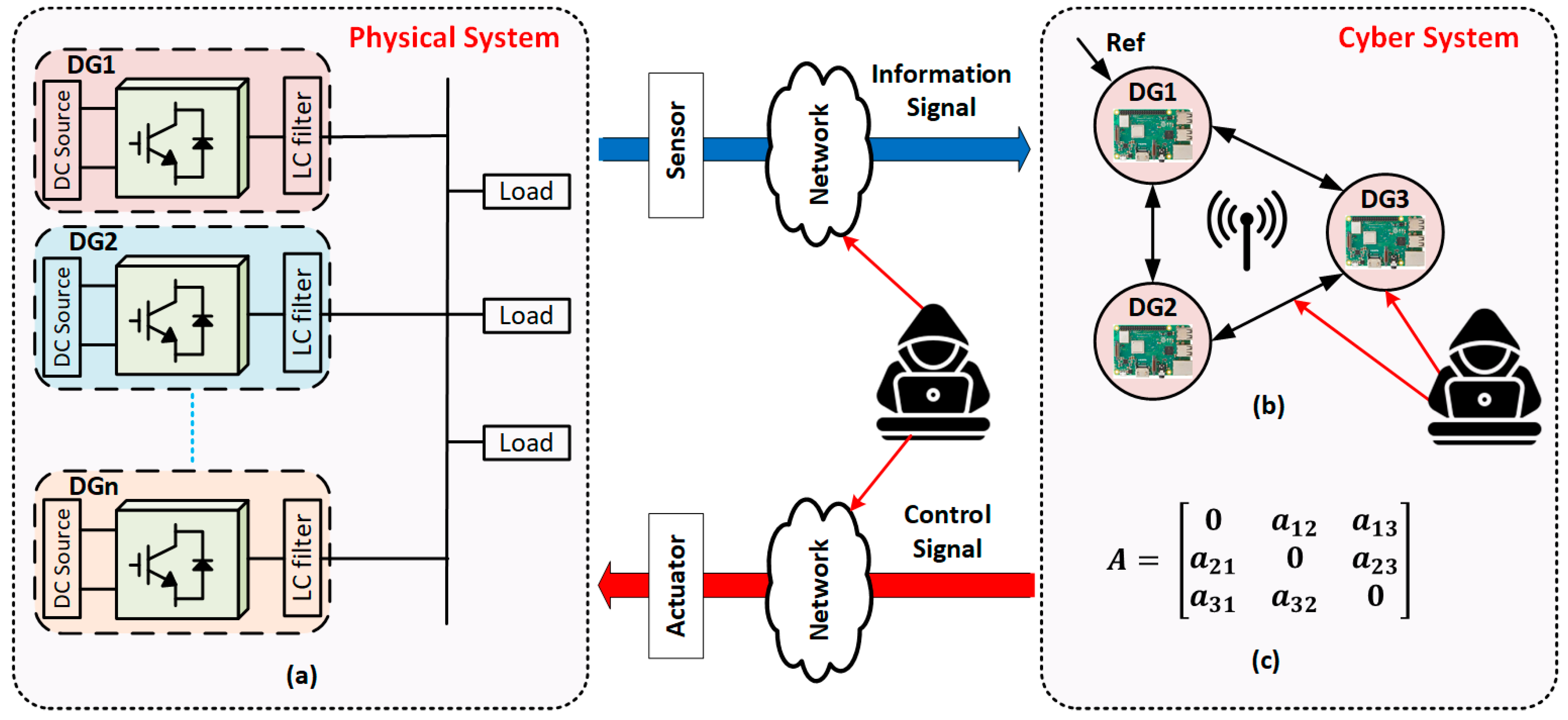
The microgrid model is shown in Figure 3a, its equivalent weighted graph is shown in Figure 3b, and its corresponding adjacency matrix is shown in Figure 3c.

2.3. Distributed Secondary Control

The secondary control objectives include frequency and voltage restoration and contributing to the power sharing. Each DG communicates with its neighboring DGs to exchange information. Differentiating both terms in Equation (2) gives:

$$\left\{\begin{array}{c}{\dot{\omega }}_i={\dot{\omega }}_{ni}-m_{pi}{\dot{P}}_i\equiv u_{\omega i}\\ {\dot{V}}_{oi}={\dot{V}}_{ni}-n_{qi}{\dot{Q}}_i\equiv u_{Voi}\end{array}\right.$$

(8)

The SC sets the nominal set-points ${\omega }_{ni}$ and $V_{ni}$ as follows:

$${\omega }_{ni}=\int \left({{\dot{\omega }}_i+m}_{pi}{\dot{P}}_i\right)dt=\int \left(u_{\omega i}+u_{Pi}\right)dt$$

(9)

$$V_{ni}=\int \left({{\dot{V}}_{oi}+n}_{qi}{\dot{Q}}_i\right)dt=\int \left(u_{Voi}+u_{Qi}\right)dt$$

(10)

The accurate power sharing problem can be expressed as follows: $u_{Pi}=m_{pi}{\dot{P}}_i$ and $u_{Qi}=n_{qi}{\dot{Q}}_i$.

${\omega }_{ni}$ has $u_{\omega i}$ and $u_{Pi}$ as secondary control inputs and $V_{ni}$ has $u_{Voi}$ and $u_{Qi}$ as secondary control inputs, where $u_{\omega i}$ and $u_{Voi}$ are the auxiliary controls.

The proposed distributed SC control objectives are as follows:

• Frequency and voltage restoration:

$$\underset{t\to \mathrm{\infty }}{\lim }\left|{\omega }_i\left(t\right)-{\omega }_{ref}\right|=0 \forall i=\mathrm{1,2},\dots ,N.$$

(11)

$$\underset{t\to \mathrm{\infty }}{\lim }\left|V_{oi}\left(t\right)-V_{ref}\right|=0 \forall i=\mathrm{1,2},\dots ,N.$$

(12)

2.

Accurate Power Sharing:

$$\underset{t\to \mathrm{\infty }}{\lim }\left|m_{pi}{P}_i\left(t\right)-m_{pj}{P}_j\left(t\right)\right|=0 \forall i\ne j.$$

(13)

$$\underset{t\to \infty }{\mathit{lim}}\left|n_{qi}{Q}_i\left(t\right)-n_{qj}{Q}_j\left(t\right)\right|=0 \forall i\ne j.$$

(14)

Achieving these control objectives involves adjusting the control inputs for each agent: $u_{\omega i}$, $u_{Voi}$, $u_{Pi}$, and $u_{Qi}$.

2.3.1. Frequency and Voltage Control

For a microgrid composed of N DGs, the secondary voltage and frequency control for a first order and linear MAS are transformed into the tracking synchronization problem.

$$\left\{\begin{array}{c}{\dot{V}}_{o1}=u_{Vo1}\\ {\dot{V}}_{o2}=u_{Vo2}\\ .\\ .\\ .\\ {\dot{V}}_{oN}=u_{VoN}\end{array}\right.$$

(15)

$$\left\{\begin{array}{c}{\dot{\omega }}_1=u_{\omega 1}\\ {\dot{\omega }}_2=u_{\omega 2}\\ .\\ .\\ .\\ {\dot{\omega }}_N=u_{\omega N}\end{array}\right.$$

(16)

As mentioned earlier, DGs communication is achieved through the designed communication graph shown in Figure 3b. The control signals $u_{\omega i}$ and $u_{Voi}$ are calculated using the DGs’ own information and the neighbors’ information as follows:

$$u_{\omega i}=C_{\omega }\left[{\sum }_{j=1}^N{a}_{ij}\left({\omega }_j-{\omega }_i\right)+g_i\left({\omega }^{ref}-{\omega }_i\right)\right]$$

(17)

$$u_{Voi}=C_{Vo}\left[{\sum }_{j=1}^N{a}_{ij}\left(V_{oj}-V_{oi}\right)+g_i\left(V^{ref}-V_{oi}\right)\right]$$

(18)

$C_{\omega }$ and $C_{Vo}$ represent the control gains; both are greater than zero. The pinning gain $g_i$ is set to 1 if a DG can directly receive set points, otherwise $g_i$ is set to 0.

In a global form, Equations (17) and (18) can be written as:

$$u_{\omega }=C_{\omega }\left[-L\omega +G({\omega }^{ref}{1}_{n\times 1}-\omega )\right]$$

(19)

$$u_{Vo}=C_{Vo}\left[-L{V}_o+G(V^{ref}{1}_{n\times 1}-V_o)\right]$$

(20)

where $u_{Vo}={\left[u_{Vo1},\dots ,u_{VoN}\right]}^T$, $u_{\omega }={\left[u_{\omega 1},\dots ,u_{\omega N}\right]}^T$,$V_o={\left[V_{o1},\dots ,V_{oN}\right]}^T$, $\omega ={\left[{\omega }_1,\dots ,{\omega }_N\right]}^T$, $C_{\omega }=diag\left(C_{\omega 1},\dots ,C_{\omega N}\right)$, $C_{Vo}=diag\left(C_{Vo1},\dots ,C_{VoN}\right)$, and $1_N$ is an all-ones vector of length N.

2.3.2. Active and Reactive Power Sharing

According to the power sharing objective in Equations (13) and (14), the power ratio among DGs will be equalized in steady state.

$$m_{pi}{P}_i\left(t\right)=m_{pj}{P}_j\left(t\right)$$

(21)

$$n_{qi}{Q}_i\left(t\right)=n_{qj}{Q}_j\left(t\right)$$

(22)

Substituting the droop coefficient equations in Equation (3), the real and reactive power among DGs is shared as in Equations (23) and (24).

$$\frac{P_i}{P_j}=\frac{m_{pj}}{m_{pi}}=\frac{\frac{∆\omega }{{Pj}_{max}}}{\frac{∆\omega }{{Pi}_{max}}}=\frac{{Pi}_{max}}{{Pj}_{max}}$$

(23)

$$\frac{Q_i}{Q_j}=\frac{n_{qj}}{n_{qi}}=\frac{\frac{∆V_o}{{Qj}_{max}}}{\frac{∆V_o}{{Qi}_{max}}}=\frac{{Qi}_{max}}{{Qj}_{max}}$$

(24)

The auxiliary controls $u_{Pi}$ and $u_{Qi}$ are chosen based on the DGs’ own information and their neighbors’ information as follows:

$$u_{Pi}=C_P\left[{\sum }_{j=1}^N{a}_{ij}\left({m_{pj}P}_j-{m_{pi}P}_i\right)\right]$$

(25)

$$u_{Qi}=C_Q\left[{\sum }_{j=1}^N{a}_{ij}\left({n_{qj}Q}_j-{n_{qi}Q}_i\right)\right]$$

(26)

In a global form, Equations (25) and (26) can be written as:

$$u_P=-C_{P}L\left(m_{p}P\right)$$

(27)

$$u_Q=-C_{Q}L\left(n_{q}Q\right)$$

(28)

where $u_P={\left[u_{P1},\dots ,u_{PN}\right]}^T$, $u_Q={\left[u_{Q1},\dots ,u_{QN}\right]}^T$, $m_{p}P={\left[m_{p1}{P}_1,\dots ,m_{pN}{P}_N\right]}^T$, $n_{Q}Q={\left[n_{q1}Q,\dots ,n_{qN}{Q}_N\right]}^T$, $C_P=diag\left(C_{P1},\dots ,C_{PN}\right)$, and $C_Q=diag\left(C_{Q1},\dots ,C_{QN}\right)$. Note that L and $a_{ij}$, the Laplacian matrix and the elements of the adjacent matrix A, are defined in the Preliminaries section.

3. Cyber-Attacks Model

3.1. Deception and Disruption Cyber-Attacks

Deception and disruption attacks have been widely discussed in the networked control literature. Disruption attacks, known as DoS or jamming attacks, primarily target data availability, whereas deception attacks target the integrity of packets [24,25]. In deception attacks, intruders may manipulate sensor measurements and control commands within networked agents by accessing physical agents, sensors, controllers, actuators, and/or communication channels. This latter proves challenging to detect and handle especially if the attack sequences are strategically launched. Deception attacks can be classified based on attack types and attack points [26].

3.1.1. Attack Types

-

Linear additive deception attack:

• Characteristics: The attacker injects false data ${\mathfrak{A}}_{ij}\left(t\right)$ into the normal data ${\mathfrak{d}}_{ij}\left(t\right)$ sent by agent $i$;
• Effect: The corrupted data ${\tilde{\mathfrak{d}}}_{ij}\left(t\right)$ received by agent $j$ are the addition of the original data and the injected false data.

  $${\tilde{\mathfrak{d}}}_{ij}\left(t\right)={\mathfrak{d}}_{ij}\left(t\right)+{\mathfrak{A}}_{ij}\left(t\right)$$

  (29)

-

Multiplicative deception attack:

• Characteristics: This attack involves scaling up or down the original data ${\mathfrak{d}}_{ij}\left(t\right)$ by a scaling factor ${\mathfrak{s}}_{ij}\left(t\right)$;
• Effect: The received data ${\tilde{\mathfrak{d}}}_{ij}\left(t\right)$ are a scaled version of the original data, potentially altered in magnitude.

  $${\tilde{\mathfrak{d}}}_{ij}\left(t\right)={\mathfrak{d}}_{ij}\left(t\right){\mathfrak{s}}_{ij}\left(t\right)$$

  (30)

-

Combined additive and multiplicative deception attack:

• Characteristics: This type of attack combines both additive and multiplicative deception. It scales the original data and adds injected false data;
• Effect: The received data ${\tilde{\mathfrak{d}}}_{ij}\left(t\right)$ are a combination of the scaled original data and the injected false data.

  $${\tilde{\mathfrak{d}}}_{ij}\left(t\right)={\mathfrak{d}}_{ij}\left(t\right){\mathfrak{s}}_{ij}\left(t\right)+{\mathfrak{A}}_{ij}\left(t\right)$$

  (31)

-

Replacement attack:

• Characteristics: In a replacement attack, the attacker completely replaces the normal data ${\mathfrak{d}}_{ij}\left(t\right)$ with an arbitrary signal ${\mathfrak{r}}_{ij}\left(t\right)$;
• Effect: The received data ${\tilde{\mathfrak{d}}}_{ij}\left(t\right)$ are entirely replaced by the arbitrary signal, disregarding the original data.

  $${\tilde{\mathfrak{d}}}_{ij}\left(t\right)={\mathfrak{r}}_{ij}\left(t\right)$$

  (32)

-

Impulsive false data attack:

• Characteristics: This attack involves injecting impulsive false data using Dirac impulses $\delta (.)$ at designated time instances ${\left\{t_k\right\}}_{k=1}^{\mathrm{\infty }}$, with destabilizing impulse parameters ${\mathfrak{T}}_k$;
• Effect: The received data ${\tilde{\mathfrak{d}}}_{ij}\left(t\right)$ include the normal data ${\mathfrak{d}}_{ij}\left(t\right)$ along with impulsive false data at designated time instances.

  $${\tilde{\mathfrak{d}}}_{ij}\left(t\right)={\mathfrak{d}}_{ij}\left(t\right)+{\sum }_{k=1}^{\infty }{\mathfrak{T}}_k{\mathfrak{d}}_{ij}\left(t\right)\delta (t-t_k)$$

  (33)

3.1.2. Attack Points

Deception attacks can be classified based on the attack points. Intruders may launch attacks on sensors, actuators, or both. Equations (34) and (35) model attacks on actuators and sensors, respectively [27].

$${\tilde{\mathcal{x}}}_i\left(t\right)={\mathcal{x}}_i\left(t\right)+{\alpha }_i\left(t\right){\mathcal{x}}_i^a\left(t\right)$$

(34)

$${\tilde{\mathcal{u}}}_i\left(t\right)={\mathcal{u}}_i\left(t\right)+{\beta }_i\left(t\right){\mathcal{u}}_i^a\left(t\right)$$

(35)

where, ${\mathcal{x}}_i^a\left(t\right)$ and ${\mathcal{u}}_i^a\left(t\right)$ denote the attack signals injected into the sensor and the actuator of agent $i$, respectively. ${\tilde{\mathcal{x}}}_i\left(t\right)$ and ${\tilde{\mathcal{u}}}_i\left(t\right)$ are the corrupted state and control protocol of agent $i$. ${\alpha }_i\left(t\right)=1$ when agent $i$ is under sensor attack, otherwise ${\alpha }_i\left(t\right)=0$. Similarly, ${\beta }_i\left(t\right)=1$ when agent $i$ is under actuator attack, otherwise ${\beta }_i\left(t\right)=0$.

3.2. Attacks Model

3.2.1. Disruption Attack Model

Various strategies can be employed to conduct a DoS attack such as data packet loss, network flooding, zero input, etc. Let us consider the communication channel between ${DG}_i$ and ${DG}_j$ during $\left[t_1,t_2\right]\subset [0,\mathrm{\infty }]$. The states communicated from the OPAL-RT simulation to the agents as well as between the agents are $x_i\in \left[{\omega }_i,V_{oi},{m_{pi}P}_i,{n_{qi}Q}_i\right]$ and from the agents to the OPAL-RT simulation are $y_i\in \left[u_{\omega i},u_{Voi},u_{Pi},u_{Qi}\right]$. Let $m_{\mu }$ be the number of DoS attacks that might occur during $\left[t_1,t_2\right]\subset [0,\mathrm{\infty }]$ and $I_k=\left[t_a,t_a+{\tau }_a\right]$ is the kth interval in which a DoS attack take place, where $t_a$, $t_a+{\tau }_a$, and ${\tau }_a$ are, respectively, the start, end, and length of DoS attack [7]. The total DoS time intervals of DoS between two DGs can be given as:

$${\mathsf{\Gamma }}_{DoS}^{(i,j)}=\left(t_1,t_2\right)\bigcap \left({\bigcup }_{a=1}^{m_{\mu }}{I}_k^{(i,j)}\right)$$

(36)

In order to achieve stealthiness, which is a property under which attacks are not detected, intruders may impose some additional constraints, for instance on ${\tau }_a$.

3.2.2. Deception Attack Model

Let ${\delta }_i^S$ denotes the potential attacks applied by the adversary on the $ith$ agent sensors. The consensus control in Equations (17) and (18) in the presence of such an attack can be written as follows:

$${\tilde{u}}_{\omega i}=C_{\omega }\left[{\sum }_{j=1}^N{a}_{ij}\left(\left({\omega }_j+{\delta }_{\omega i}^S\right)-{\omega }_i\right)+g_i\left({\omega }^{ref}-{\omega }_i\right)\right]$$

(37)

$${\tilde{u}}_{Voi}=C_{Vo}\left[{\sum }_{j=1}^N{a}_{ij}\left(\left(V_{oj}+{\delta }_{Vi}^S\right)-V_{oi}\right)+g_i\left(V^{ref}-V_{oi}\right)\right]$$

(38)

Similarly let ${\delta }_i^a$ denote the potential attacks applied by the adversary on the $\mathrm{i}\mathrm{t}\mathrm{h}$ agent actuators. The consensus control in Equations (17) and (18) in the presence of such attack can be written as follows:

$${\tilde{u}}_{\omega i}=C_{\omega }\left[{\sum }_{j=1}^N{a}_{ij}\left({\omega }_j-{\omega }_i\right)+g_i\left({\omega }^{ref}-{\omega }_i\right)\right]+{\delta }_{\omega i}^a$$

(39)

$${\tilde{u}}_{Voi}=C_{Vo}\left[{\sum }_{j=1}^N{a}_{ij}\left(V_{oj}-V_{oi}\right)+g_i\left(V^{ref}-V_{oi}\right)\right]+{\delta }_{Vi}^a$$

(40)

The attack signals ${\delta }_{\omega }^a$ and ${\delta }_V^a$ can be designed to cause the microgrid instability while remaining stealthy to adversary-detection systems.

4. Testbed Setup

This section introduces an evaluation framework for the implemented agents featuring the proposed distributed secondary control. It outlines the components of the examined three-bus islanded Microgrid (MG), providing insights into various aspects such as real-time simulation, Multi-Agent System (MAS) control platform, communication network design, and protocols.

As depicted in Figure 4, the Controller Hardware-in-the-Loop (CHIL) experimental testbed comprises two main interconnected parts: (i) the proposed physical system, encompassing AC microgrid elements and local controllers, implemented in the OPAL-RT real-time simulator; (ii) the distributed consensus secondary controller, where hardware agents operate independently on Raspberry Pi devices. Initially, real-time measurements are transmitted from the OPAL-RT simulation to the corresponding external control hardware (Raspberry Pi agents) through the UDP/IP protocol and transmitted to neighboring agents via UDP/IP.

4.1. Real-Time Simulation

The simulated AC microgrid is modeled using MATLAB/Simulink and implemented in OPAL-RT. The developed model for this experiment contains the power system model along with all primary controllers and is implemented in RT-Lab version 2023.1. The primary controllers consist of inner and outer loops for current and voltage control. During each control iteration, the local data packets [${\omega }_i,V_{oi},{m_{pi}P}_i,{n_{qi}Q}_i$] from the primary controllers are transmitted to the corresponding Raspberry Pis via UDP. The control input packets [$u_{\omega i},u_{Voi},u_{Pi},u_{Qi}$] from the secondary controllers are sent back to OPAL-RT via UDP to calculate ${\omega }_{ni}$ and $V_{ni}$ setpoints. The exchange of data between external secondary controllers, the real-time simulator, and neighboring agents occurs through the LAN network. This interconnected system enables the essential communication and coordination for the functioning of the AC microgrid model.

4.2. Cyber Layer-Based Raspberry Pi Agents

The agents designed with the proposed distributed consensus secondary control can update the power network state, perform calculations, and provide control decisions. Each DG is represented by an agent responsible for managing the distributed secondary control algorithm based on predefined control objectives. The secondary agent collects voltage, frequency, active, and reactive power data from local measurements and sends control signals to the primary controller (PC). The communication topology among the Raspberry Pi agents is depicted in Figure 2.

For this implementation, the Raspberry Pi 3 Model B+ is utilized. The control action is programmed within each agent (Rpi) using a Python script, with all agents assigned static IP addresses. Communication ports are established when running the Python script. Each Raspberry Pi opens a communication channel for each device to facilitate data exchange with neighboring agents and establishes a client socket with OPAL-RT. Once the connection is established, the client sends commands to the runtime. The flow of the consensus algorithm implemented in every agent is shown in Figure 5.

4.3. Attack Agent

The attack agents were programmed using Python scripts and implemented in a separate agent. The objective of DoS depends on the targeted agent’s IP address and port. An agent can be flooded with many packets to consume its resources and, therefore, make it out of service. Also, the communication links between DGs or between a DG and the real-time simulator can be attacked, which results in modifying the communication topology.

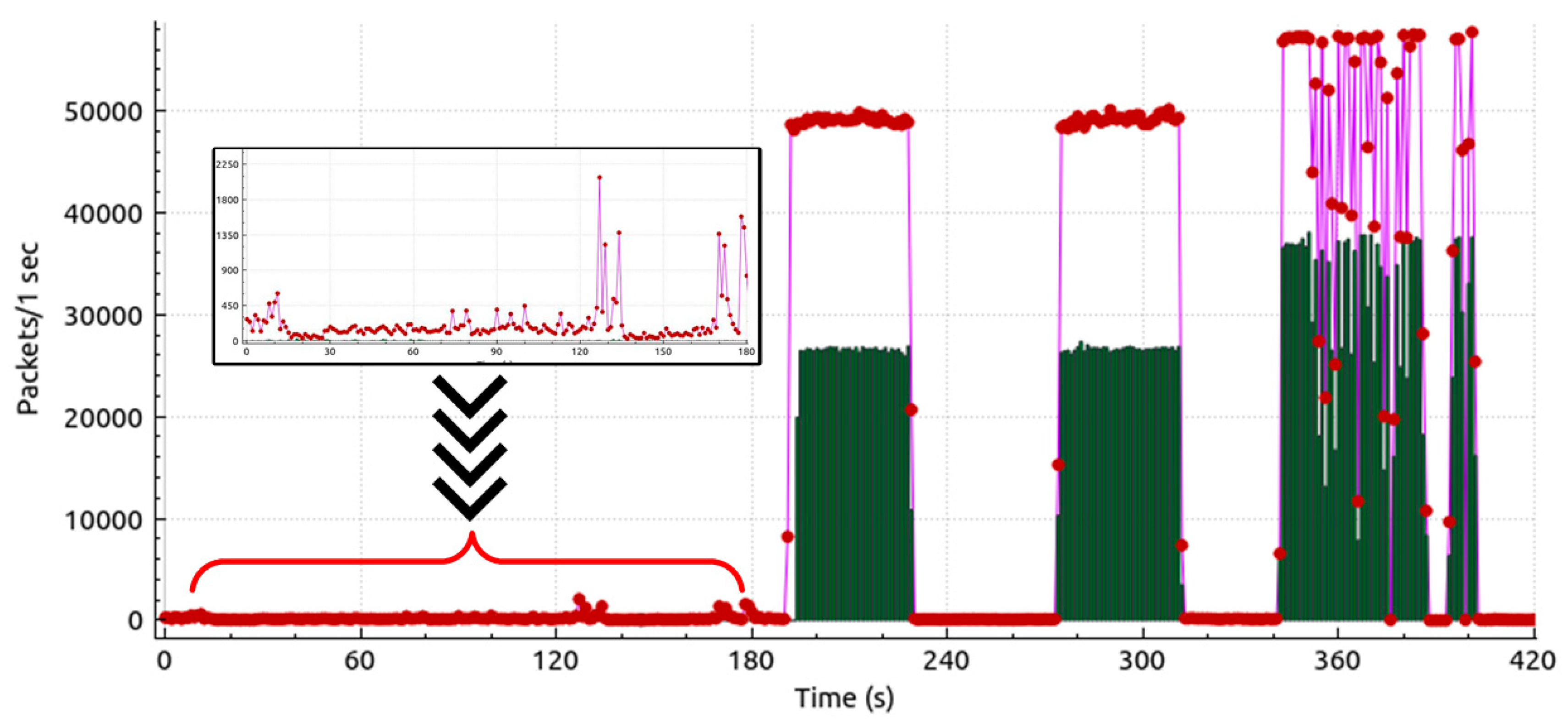
The result of deception and disruption attacks and their impact on the physical system are demonstrated using the CHIL testbed setup. The network traffic during a sequence of DoS attacks with varying packet rates and attack lengths targeting one of the DGs can be shown in Figure 6.

5. Results and Discussion

Extensive real-time digital simulations on OPAL-RT are performed to evaluate the effect of various cyber-attacks on the proposed distributed consensus secondary control of islanded AC MG. Using MATLAB/Simulink, an AC microgrid, structured by three parallel inverters with power ratings of 500 KW, 300 KW, and 200 KW connected to the PCC bus, is modeled. The parameters of distributed secondary controllers are all set to C_ω = 0.2, C_VO = 0.1, C_P = 4, and C_Q = 100. The droop coefficients are all set to m_p = 0.01 and n_q = 0.04.

In this section there are three study cases conducted, including:

-

Performance Under Normal Operation;

-

Performance Under Linear Additive Deception Attacks on Sensor, Actuator, and Combined;

-

Performance Under Disruption Attack.

5.1. Performance under Normal Operation

Under normal operation, the performance of the proposed distributed consensus secondary control strategy in case of load variations is presented in Figure 7. At t = 20 s, droop activation initiated proportional power sharing among the three DGs, maintaining the frequency and voltage around 60.15 Hz and 598 V, respectively. Following a load increase at t = 40 s, the DGs adjusted their power outputs, resulting in a frequency and voltage drop to 59.98 Hz and 694 V, respectively. The activation of the distributed consensus secondary controller at t = 60 s restored frequency and voltage to reference values (60 Hz and 600 V) without disrupting proportional power sharing, indicating stable microgrid operation. Further load variations at t = 80 s, t = 100 s, and t = 120 s prompted additional power output adjustments by the DGs, ensuring continued stability with restored frequency and voltage levels.

5.2. Performance under Deception Attacks

This section evaluates the effect of linear additive deception attacks on sensors, actuators, and both.

5.2.1. Deception Attack on Actuators’ Frequency

In this study case, ${\delta }_1^{a,\omega }$ denotes the actuator attack injections to the frequency control loop of DG #1. The attack signal is ${\delta }_1^{a,\omega }={\delta }_1^{a,\omega 1}$ for $59.8<t\left(s\right)<109.8$ and ${\delta }_1^{a,\omega }={\delta }_1^{a,\omega 2}$ for $109.8<t\left(s\right)<160$ where ${\delta }_1^{a,\omega 1}>{\delta }_1^{a,\omega 2}$.

The simulation scenario for this case is as follows:

-

At t = 20 s, the Droop control is activated;

-

At t = 40 s, the distributed consensus secondary control is activated;

-

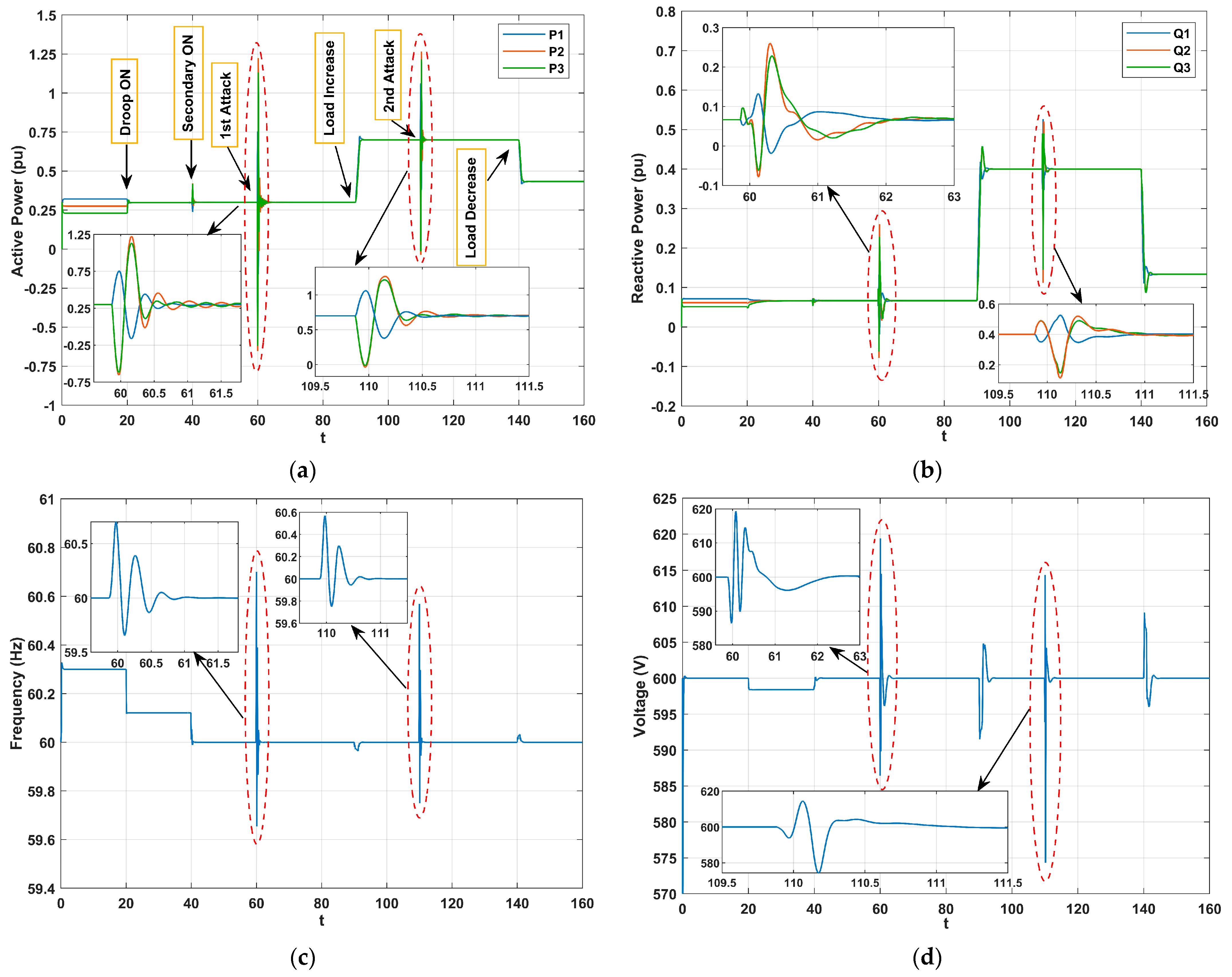
At t = 59.8 s, the first actuator attack is launched;

-

At t = 90 s, the load is increased;

-

At t = 109.8 s, the second actuator attack is launched;

-

At t = 140 s, the load is decreased.

The results are shown in Figure 8. At t = 40 s, when there is no cyber-attack, the frequency and voltage of the islanded microgrid restore to their reference values while the active and reactive power of DGs are accurately sharing. The cyber-attack is initiated at approximately t = 59.8 s, resulting in a notable transient impact on the system. However, both voltage and frequency stabilize, maintaining alignment with the consensus power sharing objectives. Remarkably, despite the ongoing attack, the system recovered. By t = 90 s, even with an increase in load, the microgrid operates as if it were under normal conditions. At t = 109.8 s, the attack signal is slightly reduced. As a result, the system shows behavior similar to that observed during the initial attack. The performed real-time tests demonstrated that the control objectives were achieved successfully with bounded attack signals. However, with unbounded attack signals, the system became unstable. This underscores the vital role of cybersecurity measures in keeping the microgrid stable and dependable.

5.2.2. Deception Attack on Actuators’ Voltage

In this study case, ${\delta }_1^{a,V}$ denotes the actuator attack injections to the voltage control loop of DG #1. The attack signal is ${\delta }_1^{a,V}={\delta }_1^{a,V1}$ for $59.8<t\left(s\right)<109.8$ and ${\delta }_1^{a,V}={\delta }_1^{a,V2}$ for $109.8<t\left(s\right)<160$ where ${\delta }_1^{a,V1}>{\delta }_1^{a,V2}$. The simulation scenario is as follows:

-

At t = 20 s, the droop control is activated;

-

At t = 40 s, the distributed consensus secondary control is activated;

-

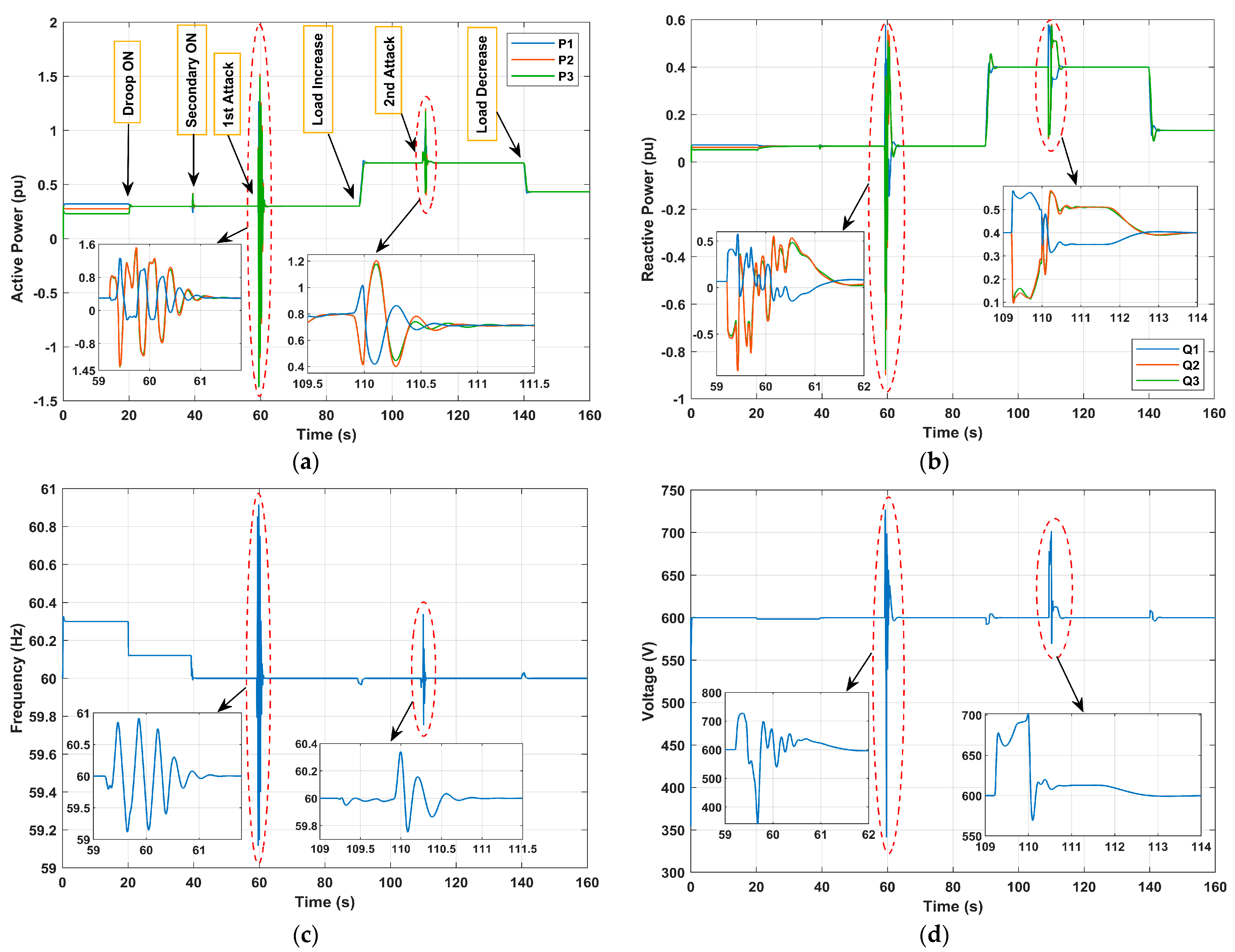
At t = 59.2 s, the first actuator attack is launched;

-

At t = 90 s, the load is increased;

-

At t = 109.2 s, the second actuator attack is launched;

-

At t = 140 s, the load is decreased.

In this experiment, we focused on the vulnerability of the actuator voltage control loop to cyber-attacks within the islanded AC microgrid system. The setup mirrored the first experiment with adjustments made to the voltage control loop instead of the frequency control loop. As depicted in Figure 9, the results showed a similar pattern to the previous experiment.

5.2.3. Deception Attack on Sensors’ Frequency

In this study case, ${\delta }_1^{S,\omega }$ denotes the sensor attack injections to the frequency measurements of DG #1. The attack signal is ${\delta }_1^{S,\omega }={\delta }_1^{S,\omega 1}$ between $60<t\left(s\right)<80$ and ${\delta }_1^{S,\omega }={\delta }_1^{S,\omega 2}$ between $120<t\left(s\right)<140$ where ${\delta }_1^{S,\omega 1}>{\delta }_1^{S,\omega 2}$. The simulation scenario for this case is as follows:

-

At t = 20 s, the droop control is activated;

-

At t = 40 s, the distributed consensus secondary control is activated;

-

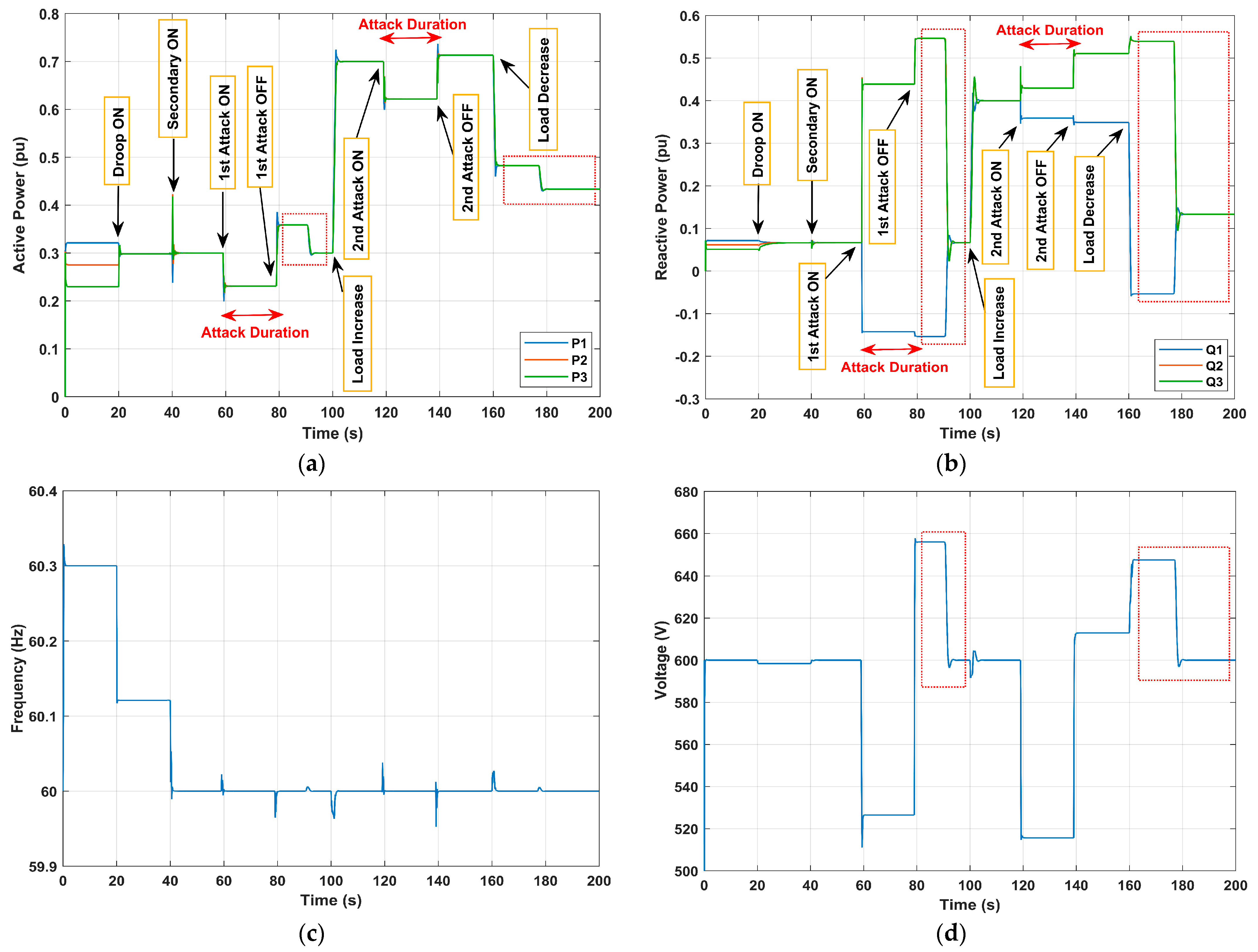
At t = 60 s, the first frequency sensor attack is launched;

-

At t = 80 s, the first attack is removed;

-

At t = 100 s, the total load is increased;

-

At t = 120 s, the second frequency sensor attack is launched;

-

At t = 140 s, the second attack is removed;

-

At t = 160 s, the load is decreased.

The experiment conducted using the test setup demonstrates results when subject to deception attacks on sensor frequency, as shown in Figure 10. Following the activation of droop and secondary controllers, the first attack is launched at t = 60 s. The attack induced a notable impact on the system dynamics; it caused a frequency drop from its rated value. Upon initiation of the attack, the frequency dropped, and the equitable distribution of active power among DGs was impacted. Notably, the attacked DG1’s active power output was minimal while DG2 and DG3 maintained their active power sharing and even increased compared to pre-attack levels. Simultaneously, transient voltage and reactive power disturbances were observed, though quickly mitigated. Upon the removal of the attack at t = 80 s, an instantaneous restoration of the frequency to its nominal value was observed alongside the restoration of active power sharing objectives. Afterwards, a similar behavior was noticed during the second attack at t = 120 s, though with a smaller amplitude, yet still impacting the frequency and active power sharing. These results underscore the importance of understanding the effects of attacks on MG systems and highlight the need for robust defense mechanisms to protect against potential disruptions.

5.2.4. Deception Attack on Sensors’ Voltage

In this study case, ${\delta }_1^{S,V}$ denotes the sensor attack injections to the voltage measurements of DG #1. The attack signal is ${\delta }_1^{S,V}={\delta }_1^{S,V1}$ between $60<t\left(s\right)<80$ and ${\delta }_1^{S,V}={\delta }_1^{S,V2}$ between $120<t\left(s\right)<140$ where ${\delta }_1^{S,V1}>{\delta }_1^{S,V2}$.

The simulation scenario for this case is as follows:

-

At t = 20 s, the droop control is activated;

-

At t = 40 s, the distributed consensus secondary control is activated;

-

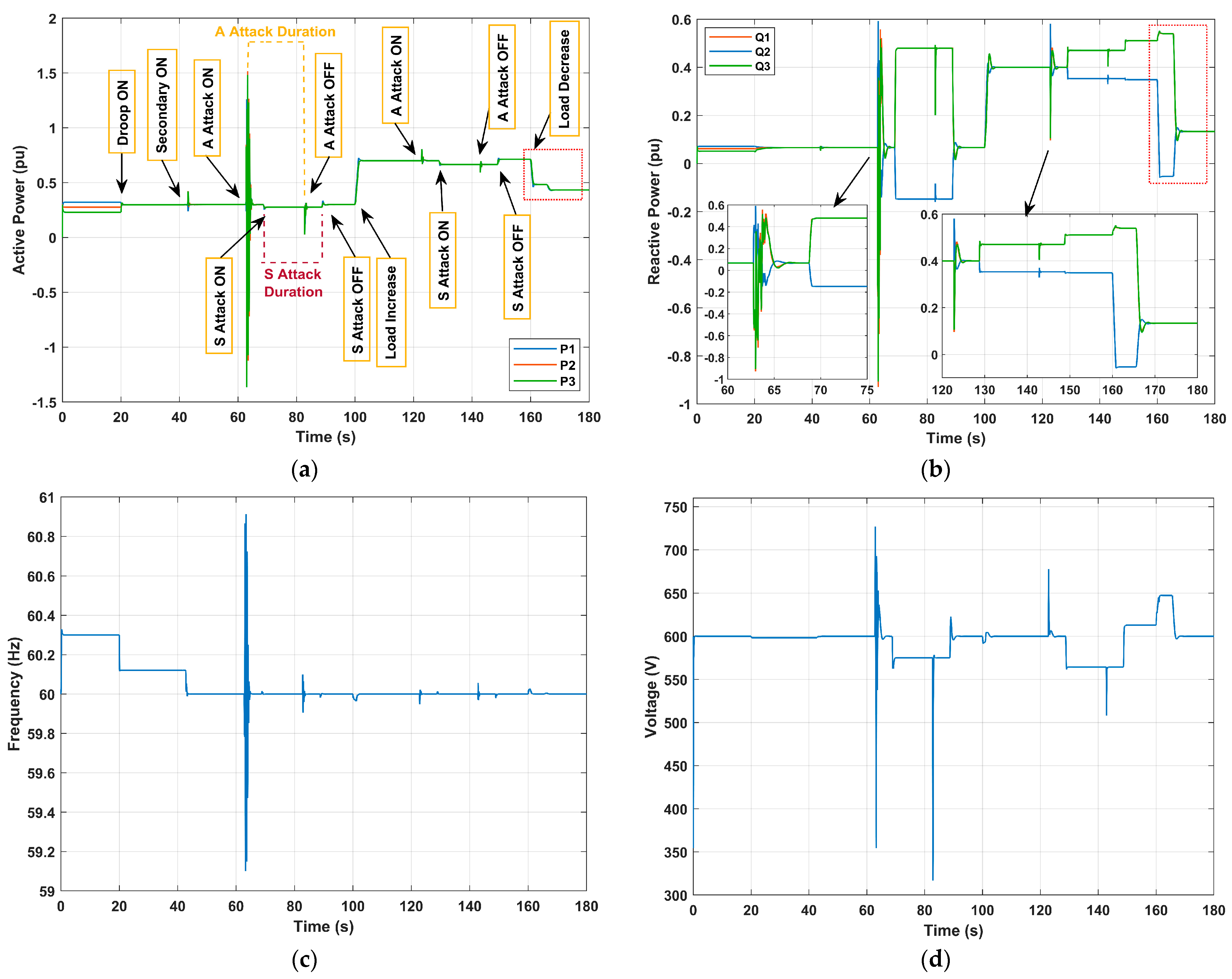
At t = 59 s, the first voltage sensor attack is launched;

-

At t = 79 s, the first attack is removed;

-

At t = 100 s, the total load is increased;

-

At t = 119 s, the second voltage sensor attack is launched;

-

At t = 139 s, the second attack is removed;

-

At t = 160 s, the load is decreased.

The conducted experiment shows the effects of deception attacks on sensor’s voltage measurement within the distributed control framework. Notable consequences were observed upon launching the attack at t = 59 s, where the voltage dropped significantly from its rated value of 600 V to 530 V as shown in Figure 11. The consensus reactive power sharing deteriorated, and there was a decrease in active power sharing compared to pre-attack conditions. However, an unexpected behavior was observed upon ceasing the attack at t = 79 s. Instead of a smooth recovery of the control objectives as seen in the previous experiment, the voltage surged beyond its rated value, accompanied by an increase in both active and reactive power as shown in Figure 11. While the control objectives were eventually restored after approximately 14 s, this deviation highlights the sensitivity of the system to this kind of attack, even with small injected values. After a load increase and the launch of a second attack at t = 119 s, a similar situation was observed, yet with a crucial difference. Despite the attack being stopped at t = 139 s, the system took a longer time to respond. It was not until t = 180 s that the control objectives were eventually restored. This suggests that the severity and duration of the attack directly influence the system’s ability to recover and maintain stability.

5.2.5. Combined Deception Attack on Frequency

In this study case, ${\delta }_1^{a,\omega }$ denotes the actuator attack injections to the frequency control loop of DG #1. The attack signal is ${\delta }_1^{a,\omega }={\delta }_1^{a,\omega 1}$ between $51.6<t\left(s\right)<71.6$ and ${\delta }_1^{a,\omega }={\delta }_1^{a,\omega 2}$ between $111.6<t\left(s\right)<131.6$ where ${\delta }_1^{a,\omega 1}>{\delta }_1^{a,\omega 2}$, and ${\delta }_1^{S,\omega }$ denotes the sensor attack injections to the frequency measurements of DG #1. The attack signal is ${\delta }_1^{S,\omega }={\delta }_1^{S,\omega 1}$ between $57.6<t\left(s\right)<77.6$ and ${\delta }_1^{S,\omega }={\delta }_1^{S,\omega 2}$ between $117.6<t\left(s\right)<137.6$ where ${\delta }_1^{S,\omega 1}>{\delta }_1^{S,\omega 2}$.

The simulation scenario for this case is as follows:

-

At t = 20 s, the droop control is activated;

-

At t = 30.6 s, the distributed consensus secondary control is activated;

-

At t = 51.6 s, the first frequency actuator attack is launched;

-

At t = 57.6 s, the first frequency sensor attack is launched;

-

At t = 71.6 s, the first frequency actuator attack is removed;

-

At t = 77.6 s, the first frequency sensor attack is removed;

-

At t = 100 s, the total load is increased;

-

At t = 111.6 s, the second frequency actuator attack is launched;

-

At t = 117.6 s, the second frequency sensor attack is launched;

-

At t = 131.6 s, the second frequency actuator attack is removed;

-

At t = 137.6 s, the second frequency sensor attack is removed.

-

At t = 160 s, the load is decreased.

This experiment involves both actuator and sensor deception attacks on the frequency control loop of DG #1. It demonstrates a sequence of events where actuator attacks are initiated first, followed by sensor attacks as depicted in Figure 12. The attack signals for both actuator and sensor attacks vary in time intervals and magnitudes. During the attack periods, the system exhibited similar behavior to that observed in experiments 5.2.1 and 5.2.3. Upon removal of the attacks, the system restores to its nominal operating conditions. However, the restoration may not be instantaneous and may depend on the attack’s severity and duration as shown in the next experiment.

5.2.6. Combined Deception Attack on Voltage

In this study case, ${\delta }_1^{a,V}$ denotes the actuator attack injections to the voltage control loop of DG #1. The attack signal is ${\delta }_1^{a,V}={\delta }_1^{a,V1}$ between $62.7<t\left(s\right)<82.7$ and ${\delta }_1^{a,V}={\delta }_1^{a,V2}$ between $122.7<t\left(s\right)<142.7$ where ${\delta }_1^{a,V1}>{\delta }_1^{a,V2}$, and ${\delta }_1^{S,V}$ denotes the sensor attack injections to the voltage measurements of DG #1. The attack signal is ${\delta }_1^{S,V}={\delta }_1^{S,V1}$ between $68.7<t\left(s\right)<88.7$ and ${\delta }_1^{S,V}={\delta }_1^{S,V2}$ between $128.7<t\left(s\right)<148.7$ where ${\delta }_1^{S,V1}>{\delta }_1^{S,V2}$.

The simulation scenario for this case is as follows:

-

At t = 20 s, the droop control is activated;

-

At t = 41.7 s, the distributed consensus secondary control is activated;

-

At t = 62.7 s, the first voltage actuator attack is launched;

-

At t = 68.7 s, the first voltage sensor attack is launched;

-

At t = 82.7 s, the first voltage actuator attack is removed;

-

At t = 88.7 s, the first voltage sensor attack is removed;

-

At t = 100 s, the total load is increased;

-

At t = 122.7 s, the second voltage actuator attack is launched;

-

At t = 128.7 s, the second voltage sensor attack is launched;

-

At t = 142.7 s, the second voltage actuator attack is removed;

-

At t = 148.7 s, the second voltage sensor attack is removed;

-

At t = 160 s, the load is decreased.

This experiment combines scenarios of both experiments 5.2.2 and 5.2.4. Actuator attacks on the voltage control loop are initiated first, followed by sensor attacks. During the attack periods and similar to the individual experiments, deviations from nominal voltage levels occur, impacting the consensus power sharing among DGs. As shown in Figure 13, the recovery of the system after the removal of the attacks at t = 148.7 s depends on severity of the attack.

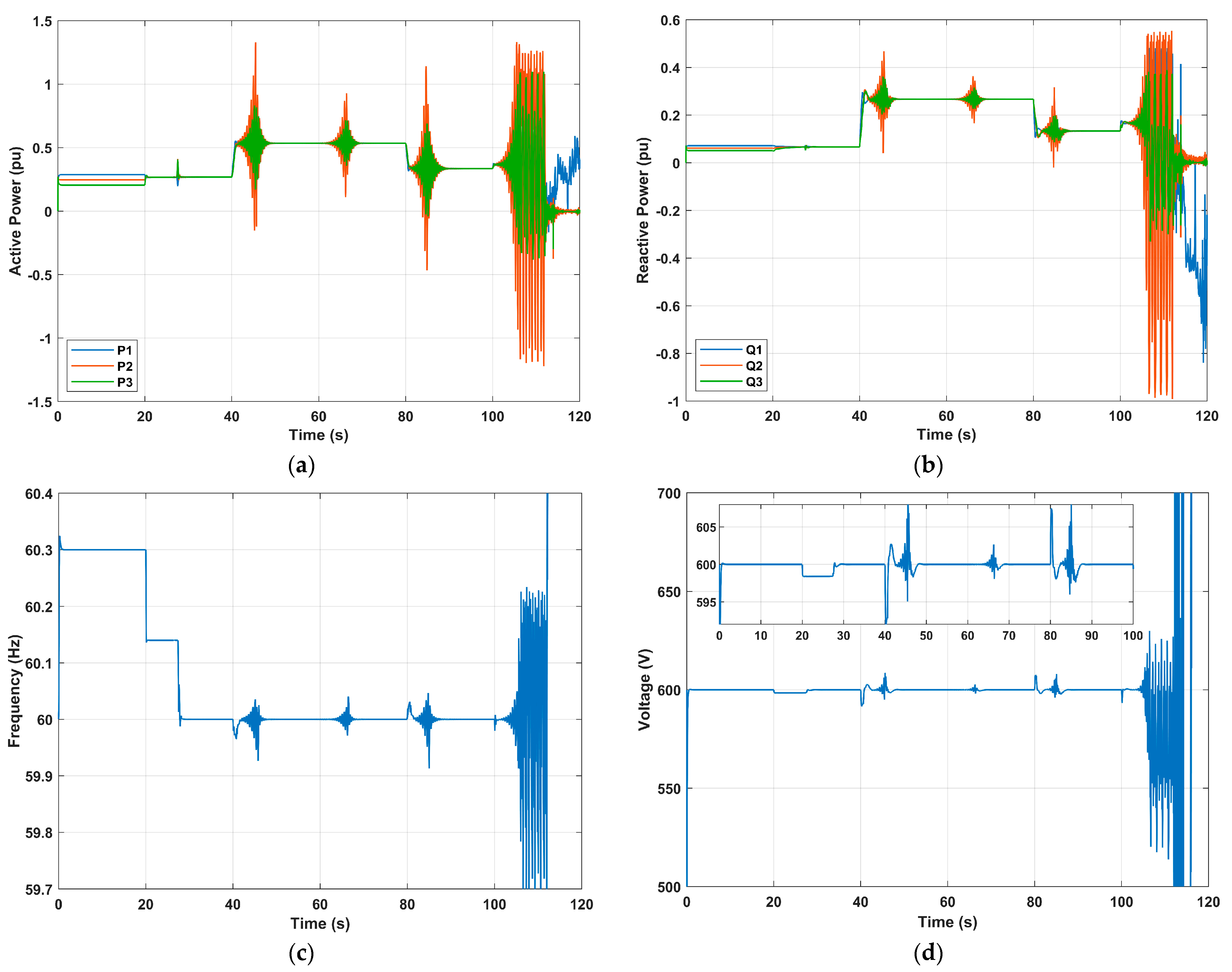
5.3. Performance under Disruption Attacks

The simulation scenario for this case is as follows:

At t = 20 s, the droop control is activated;

At t = 40 s, the total load is increased;

At t = 60 s, the distributed consensus secondary control is activated;

At t = 80 s, the total load is decreased;

At t = 100 s and t = 120 s, the total load is increased.

The DoS attack occurs at t = 20 s, t = 65 s, t = 80 s, and t = 100 s. The attack targeted agent #2 with short lengths (around ${\tau }_a=5 \mathrm{s}$) except the last one (${\tau }_a>10 \mathrm{s}$). Due to local droop control and DG1 reference signal, system frequency and voltage can still be restored to 60 Hz and 600 V as shown in Figure 14. However, it can be noticed that when ${\tau }_a>5 \mathrm{s}$ the DoS attack has a direct impact on the MG stability.

It is worth mentioning that the effectiveness of DoS attacks often depends on the volume of traffic generated and the capacity of the target system to handle it. Attackers may adjust the packet rate based on their own resources and the target capabilities.

6. Conclusions

Considering the growing reliance on interconnected systems, the vulnerabilities of microgrid cyber-physical systems need careful attention. Through the development of a CHIL testbed and the implementation of distributed consensus secondary control strategy, this research not only highlights the potential risks posed by cyber threats but also is a building block for developing concrete solutions to bolster the resilience of microgrids. The proposed platform includes, a real-time islanded AC MG implemented on OPAL-RT, controllers implemented on Raspberry Pis, and a separate Raspberry Pi to launch the attacks. Extensive real-time digital simulations on OPAL-RT are performed to evaluate the effect of various cyber-attacks on the proposed distributed consensus secondary control of the islanded AC MG. The experiments include modeling and launching linear additive deception attacks on sensors, actuators, and their combinations, as well as disruption attacks. The outcomes of our real-time tests vividly illustrated the effects of both bounded and unbounded cyber-attacks on control objectives and system stability. These findings underscore the critical importance of implementing robust cybersecurity measures to uphold the stability and reliability of microgrid cyber-physical systems.