Abstract
Nitrogen oxides (NOxs) are some of the most important hazardous air pollutants from industry. In China, the annual NOx emission in the waste gas of industrial sources is about 8.957 million tons, while power plants remain the largest anthropogenic source of NOx emissions, and the precise control of NOx in power plants is crucial. However, due to inherent issues with measurement and pipelines in coal-fired power plants, there is typically a delay of about three minutes in NOx measurements, bringing mismatch between its control and measurement. Measuring delays in NOx from power plants can lead to excessive ammonia injection or failure to meet environmental standards for NOx emissions. To address the issue of NOx measurement delays, this study introduced a hybrid boosting model suitable for on-site implementation. The model could serve as a feedforward signal in SCR control, compensating for NOx measurement delays and enabling precise ammonia injection for accurate denitrification in power plants. The model combines generation mechanism and data-driven approaches, enhancing its prediction accuracy through the categorization of time-series data into linear, nonlinear, and exogenous regression components. In this study, a time-based method was proposed for analyzing the correlations between variables in denitration systems and NOx concentrations. This study also introduced a new evaluation indicator, part of R2 (PR2), which focused on the prediction effect at turning points. Finally, the proposed model was applied to actual data from a 330 MW power plant, showing excellent predictive accuracy, particularly for one-minute forecasts. For 3 min prediction, compared to predictions made by ARIMA, the R-squared (R2) and PR2 were increased by 3.6% and 30.6%, respectively, and the mean absolute error (MAE) and mean absolute percentage error (MAPE) were decreased by 9.4% and 9.1%, respectively. These results confirmed the accuracy and applicability of the integrated model for on-site implementation as a 3 min advanced prediction soft sensor in power plants.
1. Introduction
Nitrogen oxides, generally known as NOxs, are some of the most important hazardous air pollutants from industry [1,2]. In China, the NOx emission in the waste gas of industrial sources was about 8.957 million tons in 2022 [3]. When emitted into the atmosphere, NOx undergoes a series of photochemical reactions with volatile organic compounds under the UV light of sun radiation to generate irritating photochemical smog [4,5]. NOx also reacts with O2 and H2O to form acid rain [6]. NOx in the stratosphere is believed to be an important ozone depletion substance, damaging the ozone layer protecting our eco-system [7]. With the rapid increase in the growth of the economy and energy demand, the total amount of anthropogenic NOx emitted in the world has increased by three–six times [8], bringing massive hidden dangers to the ecological environment and human health.
Previous research has revealed that the majority of annual ambient NOx emissions could be attributed to fossil fuel combustion, especially coal combustion in power plants [9]. In China, many efforts have been made to control the NOx emission from coal-fired power plants. Over 90% of Chinese coal-fired power plants have completed the installation of selective catalytic reduction (SCR) technology to reduce their NOx emission [10].
However, the existing SCR technology is facing a dilemma that the detection of NOx concentrations cannot keep up with the fluctuation in the NOx concentrations in flue gas due to the sample extraction process which is conducted before the NOx reaches the gas analyzer. The NOx concentration fed to the distributed control system (DCS) is usually several minutes behind the actual NOx variation in the flue gas. Therefore, it is very difficult for the ammonia injection system to quickly respond to the NOx concentration fluctuation to achieve better NOx removal. Most power plants inject excessive ammonia into the SCR reactor to be sure that the NOx finally emitted to the atmosphere is below the government-permitted limit. This strategy will inevitably increase the cost of SCR operation and the chance of ammonia slipping into environment.
To address the inherent delays in traditional NOx measurement, non-contact instantaneous measurement technologies were developed. However, in flue gas environments, dust interference is significant, and laser measurement technology requires precise alignment of the angle of incidence. Their high susceptibility to dust interference can lead to damage to expensive measurement instruments, hence their limited application in power plants.
In situations where improvements in hardware measurement are not feasible, we consider using soft-sensing methods to address the aforementioned issues. An accurate online NOx concentration prediction method for soft sensors is essential in improving the performance of SCR systems, as soft sensors can be used as the feedforward signal for SCR control to make up for the inherent delay problem in the existing NOx measurement, and to control the ammonia injection in advance to achieve the effect of accurate denitrification in the power plant.
NOx prediction can be divided into mechanism-driven and data-driven methods. Many previous efforts have been made to develop NOx mechanism models. Many mechanism models on NOx formation have been proposed using fitting combustion [11,12,13,14] and flow processes [15,16,17]. Thomas Le Bris et al. [18] established computational fluid dynamics simulations for a 600 MW pulverized coal unit, and validated their prediction by NOx reduction via over-fire air. Unfortunately, these mechanism models are too complicated for SCR process control. The formation and transportation of NOx couples chemical reactions and flow processes [19]. The prediction of NOx concentrations at the SCR inlet is either unreliable without the accurate simulation of the in-furnace coal combustion process and downstream flow process [18], or very slow if reaction and flow parameters included. Therefore, it is almost impossible at the moment to build a mechanism model to cope with the requirements of online operation.
By contrast, with the fast development of industrial digitalization [20,21], the massive data generated in power plants every day [2] may contain a lot of information not known to us yet. Fully excavating and making good use of these data might be immensely helpful in regulating the SCR control using a different aspect.
In recent years, the artificial intelligence aided by machine learning and big data technologies has been rapidly applied to the power industry [22,23,24,25,26,27]. Wang et al. [28] proposed a Gaussian process (GP) to fit the NOx emission characteristics with 21 boiler parameters, and identified the optimal parameters to predict boiler combustion and NOx emission. Zhou et al. [29] built an artificial neural network (ANN) model for NOx emission based on 12 sets of experimental data of a 600 MW unit, with the influences of over-firing air, secondary air, nozzle tilt, and coal properties on NOx combustion characteristics being investigated. A modified genetic algorithm (GA) was developed to optimize the combustion conditions for NOx reduction. Adams et al. [30] developed LSSVM and DNN models to predict the SOx and NOx emissions associated with coal conversion in a CFB power plant. Yang et al. [31] treated NOx concentrations as a time-series problem and applied a long-short term memory (LSTM) neural network to model NOx emission. Wang et al. [32] proposed a prediction method of NOx emission and mass flow rate before the SCR of diesel vehicles based on mutual information (MI) and reversed back propagation neural network (BPNN). The above methods demonstrated the effectiveness and potential of industrial data prediction in a data-driven way.
The above literature summarizes relevant studies in the field of industrial NOx emission prediction, primarily employing methods such as artificial neural networks (ANNs), deep neural networks (DNNs), long short-term memory (LSTM) networks, and Gaussian processes. These studies have trained and tested their models on various datasets, achieving a certain level of predictive accuracy.
However, the following limitations remain:
- 1.
- Reliance on single data-driven methods: Most studies rely solely on data-driven machine learning approaches, without considering the physical mechanisms of NOx formation, which may result in limited generalization capabilities of the models;
- 2.
- Poor model interpretability: While deep learning models such as DNN and LSTM demonstrate high predictive accuracy, their “black-box” nature reduces the interpretability and trustworthiness of the models, posing challenges for practical engineering applications;
- 3.
- Inapplicability in real-time operations: The aforementioned deep learning models involve complex convolutional computations, whereas DCS systems in coal-fired power plants are limited to simple operations. As a result, these models are difficult to deploy on-site, rendering them unsuitable for real-time use;
- 4.
- Limited prediction lead time: Some studies do not account for the need to predict NOx emissions ahead of time, thereby failing to provide sufficient adjustment time for process control.
Necessity of this Study:
In light of these limitations, our research aims to integrate mechanistic models with data-driven models to develop a soft-sensing model capable of predicting NOx emissions in coal-fired power plants with physical interpretability and a lead time of 3 min. By combining knowledge of NOx-generation mechanisms with advanced machine learning algorithms, we seek to improve the predictive accuracy and generalization ability of the model, enhance its interpretability, and provide more effective technical support for NOx reduction and control in coal-fired power plants.
This approach not only addresses the shortcomings of purely data-driven models but also ensures that the weak learners used are deployable on-site. Moreover, the ensemble learning method mitigates the risk of gradient explosion and delivers more reliable predictive results, meeting the demands of practical engineering applications for NOx emission control.
In fact, NOx concentration is an industrial variable containing the characteristics of data series and coupling with industrial data itself. The existing research has rarely combined the actual power plant combustion process with the data-driven coupling relationship.
This study aims to bridge this gap by combining the characteristics of industrial time-series data on NOx concentrations with boiler operation parameters related to the formation and transport mechanisms of NOx. The objective of this paper is to propose a forecasting model that can achieve a lead time of up to three minutes, enabling its online application in power plants as an advanced soft measurement sensor which can compensate for the measurement delays of the existing hardware. To develop a robust online 3 min advanced NOx prediction model for power plants, this study will be structured around three main objectives:
Development of a new indicator: We introduced a novel indicator, PR2. This indicator focuses on the model’s predictive accuracy at turning points, filling gaps left by other indicators and providing a specific evaluation of the model’s applicability in industrial settings.
Three-layer integrated prediction method: This study proposed a three-layer integrated framework that categorizes industrial data from a power plant into stable time-series features, volatile time-series features, and external features related to the combustion side. The integrated hybrid prediction algorithm was then developed to accurately forecast NOx concentrations.
A time-based method for analyzing the correlations between variables in the denitration systems and NOx concentrations: By utilizing big data analysis, we investigated the time delays between various exogenous variables related to combustion and the NOx concentrations, as well as the exact measurement delays in an actual power plant.
The predictive model in this paper will be trained offline. To enable deployment in the plant’s DCS system, we integrated a simplified model. Once trained and implemented in the control system, no additional training time or computational resources will be required. The model will simply function as a feedforward signal, as shown in Figure 1, to optimize the control system. The proposed model will be used as the ufeedforward signal in the denitrification control process shown in Figure 1, predicting changes in NOx concentration in advance and enabling timely ammonia injection to ensure precise NH3 concentrations.
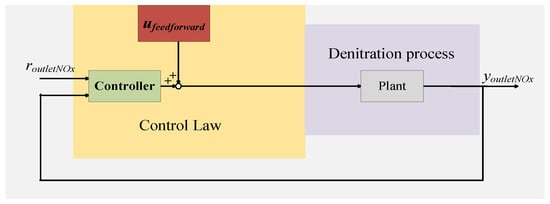
Figure 1.
Denitrification system control diagram.
2. Methodology
2.1. Algorithm with Boosting Strategy
Prediction typically involves addressing a regression problem characterized by uncertain dynamics and external influences within the time-series data. Considering the power plant implementation problem of prediction models, models such as too-complex recurrent neural networks (RNNs) or convolutional neural networks (CNNs) cannot be used in this paper.
Ensemble learning [33] is a method that trains multiple base learners and combines their predictions to obtain improved performance and a better generalization ability. Some studies suggest that ensemble learning often achieves higher predictive accuracy compared to individual machine learning models [34,35,36,37]. Ensemble learning methods can be broadly categorized into: boosting [38], stacking [39], and bagging [40]. In the boosting process, each round of learner training sequentially adjusts the sample weights based on the errors from the previous round, making this method suitable for complex or nonlinear data prediction than others.
Generally, a gradient boosting model is iterated along a gradient descent to find the function combination that best fits a training data set. This study harnessed the idea of gradient boosting models to combine weaker models together. The steps and principles are as follows:
- 1.
- Initialize the model:
- 2.
- Iterative update steps in gradient boosting:
(1) Calculate the predicted residuals:
where represents the residual difference between the actual value and the prediction by the current model for the i-th sample during the t-th iteration. The residuals are used to guide the training of the subsequent weak learner , aiming to correct the prediction errors from the previous model.
(2) Train the weak learner to fit the residual .
(3) Find the best coefficient by minimizing the loss:
where is the coefficient for the weak learner in the t-th iteration, determined by minimizing the overall loss when adding to the model.
(4) Update the model:
- 3.
- Get the final model:
is the final model after T iterations, which is an integrated model built progressively by reducing the residuals of the loss function.
2.2. Weak Learner Selection and Specific Integration Steps
This study integrates both time-series models and external factor regression via machine learning techniques [41]. Time-series forecasting models can be categorized into several types such as exponential smoothing, autoregressive integrated moving average (ARIMA), autoregressive conditional heteroskedasticity (ARCH), support vector regression (SVR), and other machine learning methods.
Through the analysis of NOx data and these models, this study considered that a time-series of consists of four parts: (i) linear component , (ii) nonlinear component , (iii) external component regression , and (iv) namely noise .
The basic expressions corresponding to the three types of methods are as follows.
Linear time-series for statistics part: utilized for the steady portions of the data, these models assume a consistent pattern over time without significant fluctuations:
Nonlinear time-series statistics for fluctuating part: applied to segments of the data exhibiting volatility, these models account for more complex features:
External factor statistical regression: this method incorporates external variables that influence NOx levels, providing a regression analysis that adjusts for these factors. xm is the variable with the largest correlation with NOx generation in the front-end burn, and the flow-side variables are obtained by feature selection.
where is the predicted value at time t, is the real value at time i, is the mth external statistic variable at time i, and are the calculation parameters, and k is the degree of the polynomial.
Figure 2 illustrates the cascading prediction steps of the ensemble learning model proposed in this paper.
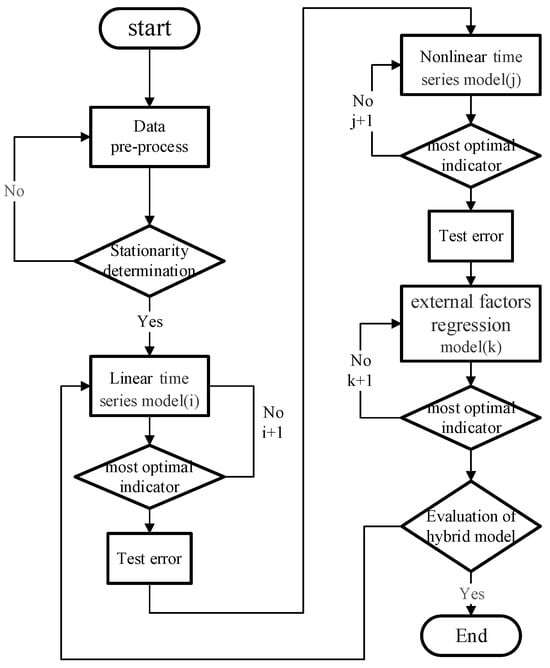
Figure 2.
Flow chart of the model selection.
First, a linear model was trained to predict the real value, and the initial predictions provided by the linear model were used as the starting values. The residuals, which were the differences between the current model’s predictions and the actual values, were then calculated. These residuals were treated as the target variable for training a nonlinear weak learner, and the parameter weights were adjusted to fit the residuals. The new residuals obtained were continuously used as the prediction targets for the regression model, and the regression model was further trained to obtain the optimal parameters. The final prediction of the model was formed by accumulating the initial values and the prediction results of the residuals from each step.
3. Evaluation Indicators and Data Pre-Processing
3.1. Traditional Indicators
- (1)
- The MAE, defined by Equation (1), measures the average magnitude of the errors between the predicted values and actual values. This metric effectively addresses the issue of cancellation between positive and negative errors seen in both absolute and relative error calculations. However, the use of the absolute value in its formulation renders the function non-differentiable. Generally, a lower MAE indicates a more accurate prediction.
- (2)
- The R2 score measures the proportion of variance in the dependent variable that is predictable from the independent variables. It does this by comparing the MSE of our model’s predictions against the MSE of the baseline model, which is the mean of the actual values. An R2 score closer to 1 indicates that our model’s predictions closely match the actual data, signifying a high predictive accuracy.
- (3)
- The MAPE is a statistic that expresses the prediction error as a percentage of the actual values. By focusing on relative rather than absolute values, the MAPE provides an intuitive measure of the size of the errors in relation to the true measurements. This metric is particularly robust as it is less influenced by individual outliers compared to other metrics. Generally, a smaller MAPE indicates a more accurate prediction.
While these traditional indicators are effective for evaluating overall trends in a time-series, they fall short in accurately capturing fluctuations and sudden changes within the process. This limitation highlights the need for a specialized indicator capable of assessing prediction accuracy specifically around change points.
3.2. A New Indicator PR2
In this section, we will introduce a new evaluation indicator, PR2, specifically designed for inflection points. The judgment and calculation process is as follows:
The change point is defined as follows:
First, we define a window of length k and continually slide this window to identify the change point, denoted by t. This involves selecting the data segment from to , allowing us to focus on key transitional periods within the dataset.
We compute the R2 score for each selected window to assess how closely the model’s predictions match the actual observed values in the vicinity of the turning point.
Finally, we average these R2 scores across all identified windows to derive a composite measure reflecting the model’s predictive performance at critical transition points. This averaged value is termed PR2 (part of R2).
Equation of PR2:
A higher PR2 value indicates a model with greater accuracy and better predictive performance. The choice of the k value should be based on the frequency of occurrence of change points in the time-series. As indicated by Equation (12), the choice of k in the PR2 represents the range of the evaluation metric R2. Therefore, the selection of k generally depends on the specific conditions at the inflection points of the data, typically starting at 3 and gradually increasing. In this paper, the data became sparse due to minute-level resampling, so the k value was set as 3 according to the data characteristics of this power plant.
To further explain the effectiveness of the PR2, naive forecast (with 1-lag), ARIMA, and ARIMA with (NF with 1-lag models were used to predict the NOx concentration data of a power plant for 1 min, as shown in Figure 2. Meanwhile, the R2 and PR2 (k = 3) indicators were calculated, and the results are shown in Table 1.

Table 1.
Indicators comparison.
In this study, the naive forecast method [42] is the simplest form of forecasting: it uses the most recent observation as the forecast. Although the naive forecast may not always provide the highest accuracy, it served as a benchmark for other forecasting methods and helped in assessing whether a model was overfitting.
Table 1 indicates that the R2 scores for the three predictive models showed no significant differences across the board. However, the PR2 value of the naive forecast (1-lag) model differed markedly from those of the other two models. This discrepancy is further illustrated in Figure 3, which demonstrates the effectiveness of the newly introduced PR2 indicator. Unlike traditional indicators, the PR2 effectively captured the predictive biases at critical points, offering a more nuanced assessment of the model performance in dynamic scenarios. This ability to pinpoint discrepancies at change points highlighted the PR2’s potential as a valuable tool for enhancing the prediction accuracy in real-time NOx monitoring systems within power plants.
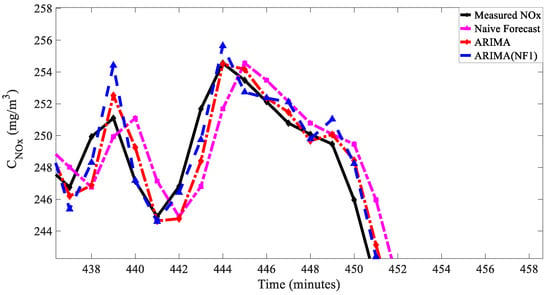
Figure 3.
Prediction accuracy at change points.
3.3. Data Pre-Processing
The sliding window is an important means of time-series prediction [36]. This method realizes the step-by-step prediction of subsequent moments by continuously updating the value of the time-series. The principle is shown in Figure 4.
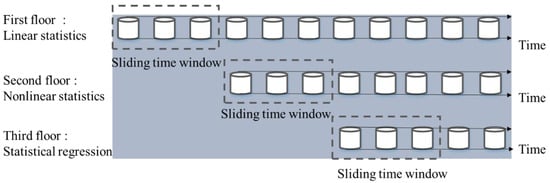
Figure 4.
Schematic diagram of the sliding window method.
At the same time, based on the logic of boosting, this study connected linear statistical models, nonlinear statistical models, and external statistical regression analysis by means of residuals, and used the residuals of the prediction results with the actual values of the former model as the data of the latter model.
The prediction effectiveness of the partially data-driven model was highly dependent on the size of the training set window; the larger the window, the more information that can be learned and the more the accuracy of the model is improved. However, as the window is increased, the redundancy of data information might occur, and unnecessary computational costs might increase.
Experimentally, based on the fact that NOx measurement in general power plants is delayed by 3 min, the ARIMA model was used to predict the 3 min NOx concentration at windows 10, 60, 100, and 200 respectively, as shown in Table 2 and Figure 5.

Table 2.
Comparison of Prediction Results for Different Window Lengths.
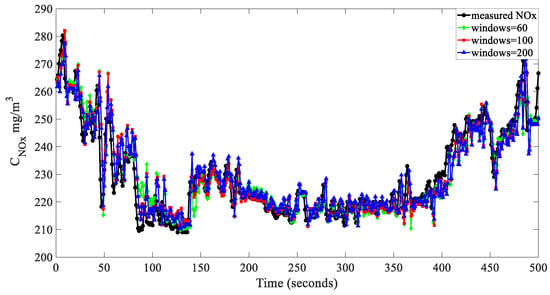
Figure 5.
Comparison of prediction results for different window lengths.
Table 2 primarily examines the impact of different sliding window lengths on the prediction performance. The window length was critical, as it determined the amount of historical data that the model utilized for forecasting. Shorter windows allow quicker adaptation to data changes but increase the susceptibility to noise, while longer windows provide more historical context but may cause insensitivity to recent changes and delayed responses. In this study, the optimal window length was fine-tuned based on the predictive performance.
As shown in Table 2, longer windows generally improved the traditional evaluation indicators, indicating that these models emphasized the overall predictive performance over localized characteristics. However, traditional indicators may not reliably determine the optimal window length. The PR2 indicator, exhibiting varying effects, reached its minimum at a window length of 100, with issues such as insensitivity and lag being identified with the use of longer windows. The PR2 thus offered a more comprehensive model performance assessment. Based on the data characteristics and the study’s industrial forecasting goals, a window length of 100 was deemed optimal and was adopted, with the window being updated every one time point. For external factor analysis, which required a larger training set to capture the variable influences, a sliding window size of 900, updated every 100 time points, was used.
4. Prediction Results
4.1. Feature Selection
In coal-fired power plants, the NOx concentrations involve a variety of complex reaction mechanisms. These mechanisms represent the fundamental characteristics of NOx and are essential for the “interpretability” required by computer models or big data analyses. Due to the complexity of mechanistic models, which often precludes their online application, this paper combined big data time-series features with mechanistic insights to construct a joint NOx prediction model. The incorporation of multivariate mechanistic features significantly enhanced the robustness of the model, avoiding the significant errors and biases typical of simpler univariate models.
In this study, the actual physical process model was mined from the data by the maximal information coefficient (MIC) feature selection of combustion variables involved in the front end. The front-end influence variables included air-side, coal-side, and other variables which had been verified by the MIC to be influential on the NOx concentration. The results of the feature extraction were as follows.
Figure 6 reveals that the variables exhibiting a strong correlation with the NOx concentration include the total coal amount, primary and secondary air flows, , and outlet air temperatures, as well as the SCR inlet and outlet flue gas temperatures. For instance, in Figure 6a, the primarily selected variables relate to air flows, including secondary air flow on the left side of the furnace and on the right side of the furnace. In Figure 6b, the selected variables include the total coal quantity, actual unit load, instantaneous coal feed from the coal feeder, flue gas temperature (variables 123), oxygen content, and pressure difference between the inlet and outlet of the flue gas, which were consistent with existing research on NOx formation mechanisms. These strongly correlated variables selected by both the mechanism model and the data model will participate in the subsequent prediction.
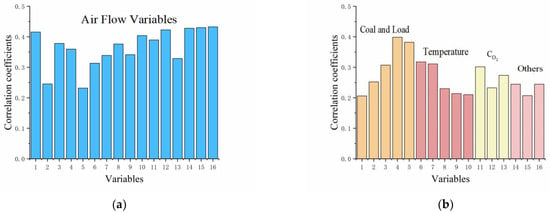
Figure 6.
Initial variables feature selection. (a) represents wind type variables with strong correlation with NOx concentration, (b) represents coal type, temperature, and oxygen variables with strong correlation with NOx concentration.
In addition to traditional feature analysis, this study incorporated time-delayed variables into the model. Each variable was intentionally shifted by varying time delays to examine its correlation with the NOx concentration. This approach not only corroborated the actual measurement delays experienced in the power plant but also aided in determining the realistic time delays for different variables.
Figure 7 revealed that the optimal delay times between the different variables and the NOx concentrations were not the same. Meanwhile, an interesting phenomenon can be observed, that all variables showed optimal delay times around 2–3 min, which corresponded to the previously analyzed potential 3 min delay in NOx measurements at this power plant. This finding confirmed that we can quantitatively describe the temporal delays between the variables and NOx concentrations through data analysis. It also aided in analyzing the measurement delays of NOx at the plant to design an effective advance prediction model. This represented a significant innovation, providing a solid foundation for future NOx prediction in power plants. This method enhanced the predictive accuracy of our NOx concentration model by aligning it more closely with the dynamic operational conditions of the plant.
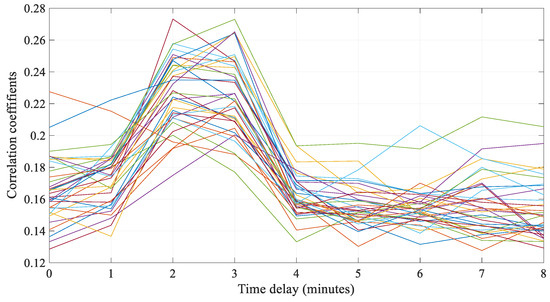
Figure 7.
Feature selection based on time-delay. Each line represents the variables that have a strong correlation with NOx concentration, and this figure shows the trend of these variables in terms of delay time.
4.2. Prediction Results
Due to the long sampling line and the analysis time required for the NOx measurement process in power plants, there is usually a delay of several minutes in the measurement session. The delay time in the power plant in this study was calculated by data and correlation analysis to be approximately 3 min. Therefore, this section will apply the exogenous variables identified through feature selection and a three-tiered prediction approach to forecast real-time data from power plants. The effectiveness of the model’s predictions will be evaluated using the multiple indicators previously discussed and compared. Moreover, since the existing predictive studies typically focus on one-minute single-step predictions, to validate the advantages of the proposed model over the existing methods, this study also conducted single-step one-minute predictions and three-step three-minute predictions.
Figure 8, Figure 9 and Figure 10 and Table 3 below show the forecasting effects of the 1-min linear time series models.
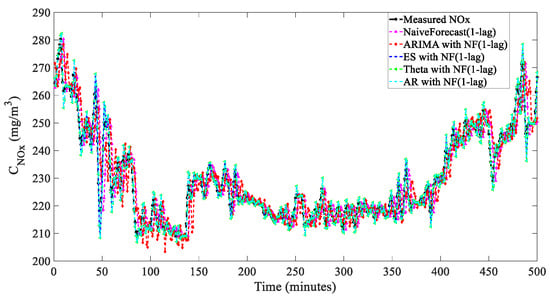
Figure 8.
Predicted value comparison of 1 min linear models.
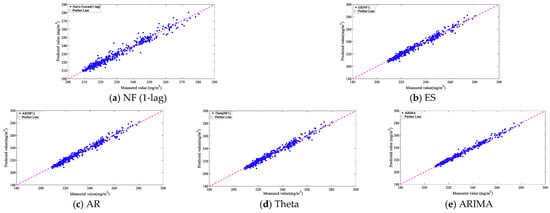
Figure 9.
Prediction effect comparison of 1 min linear models.
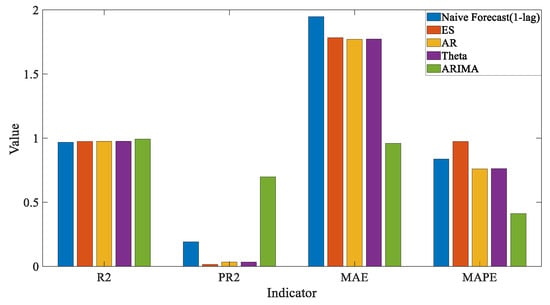
Figure 10.
Indicators comparison of 1 min linear models.

Table 3.
Prediction of NOx Concentration by Linear Time-Series Models.
It can be seen from Table 3 and Figure 10, that, in 1 min prediction, ARIMA (1-lag) had the best prediction among the linear time-series models above. At the same time, the one-minute prediction combined with (NF 1-lag) can greatly improved the effect of the model prediction, and it showed that the data trend was more important in the single-step prediction. Moreover, we can see that the performances of different models on different evaluation indicators were not corresponding. For instance, the Naive Forecast model had a better PR2 value and a worse MAE value when compared with those of AR and Theta models. Therefore, we need to choose a prediction model that better meets our needs. The proposed PR2 might distinguish itself the traditional models when using another aspect.
Then the following Table 4 and Figure 11, Figure 12, Figure 13 and Figure 14 are the three-minute prediction effects of the linear time series model combined with NF (3-lag):

Table 4.
Prediction Effect Comparison of 3 Min linear Combination Models (NF3).
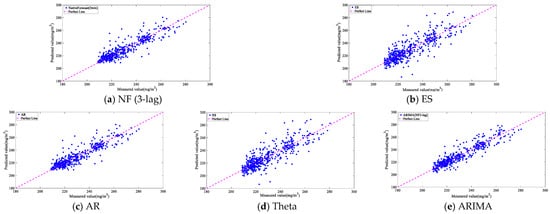
Figure 11.
Prediction effect comparison of 3 min linear combination models (NF3).
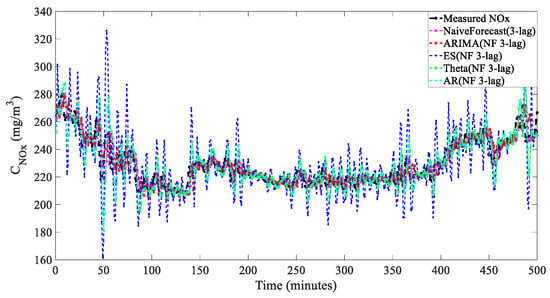
Figure 12.
Predicted value comparison of 3 min linear models (NF3).
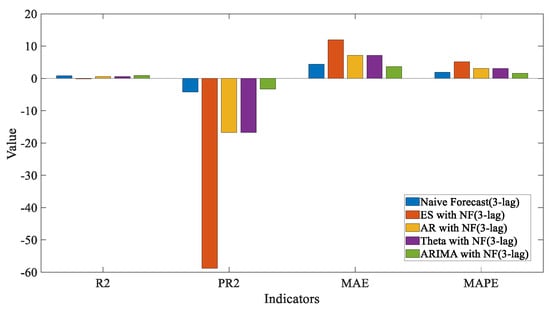
Figure 13.
Indicators comparison of 3 min linear combination models.
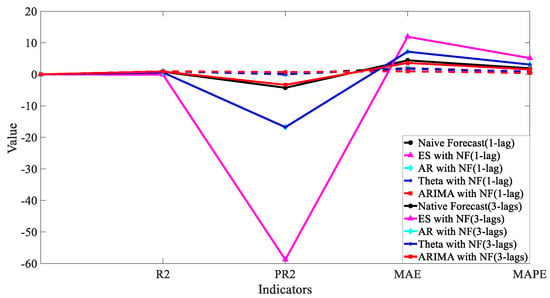
Figure 14.
Comparison of indicators between 1 min (NF1) and 3 min (NF3).
In the 3 min prediction, as shown in Figure 14, the ES (NF3) and AR (NF3) models were diverged. Despite several adjustments to the parameters of both models, the divergence persisted, likely due to the ES and AR models functioning by applying different weighted accumulations to prior NOx concentrations. This mechanism was akin to an open-loop model without feedback. In the three-minute forecasts, the NF-3 (without feedback) combination disrupted the original model, significantly increasing the probability of divergence. For other models, as the forecasting interval extended to three minutes, the amount of useful information contained diminished. The overall performance of the linear time-series forecasting models deteriorated, especially when they were combined with native prediction models. This deterioration may be due to the inaccuracies represented by the three-lag data that the original predictive model cannot rectify. Consequently, we rearranged the three-minutes multi-step forecasts using a linear regression algorithm alone, the results of which are presented below.
Table 5 and Figure 15, Figure 16, Figure 17 and Figure 18 revealed that, with the exception of the ARIMA algorithm, the ES, AR, and Theta methods showed significant improvements in their 3 min prediction performance when not combined with the NF (3-lag) feature. However, despite the ES model’s R2 score improving from −0.126 to 0.64, it still exhibited considerable bias in its predictions. This issue likely stemmed from the intrinsic nature of the ES model as primarily a data smoothing technique, which may not be well-suited for multi-step predictions over a short 3 min interval. Additionally, the ES model’s inherent lag and limited ability to recognize turning points further contribute to its substantial bias in calculations.

Table 5.
Prediction of 3 min NOx Concentration by only Linear Time-Series Model.
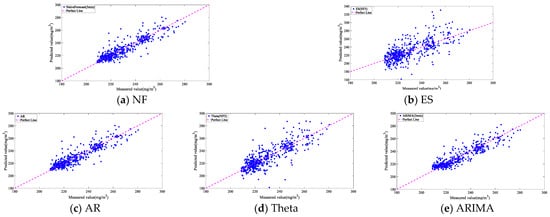
Figure 15.
Prediction effect comparison of 3 min linear models.
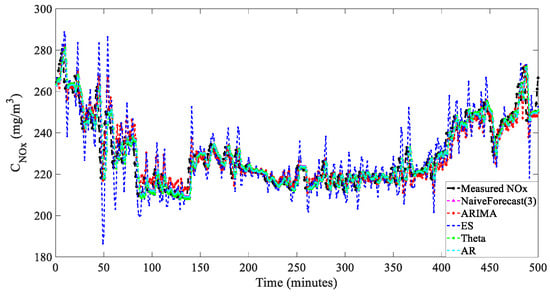
Figure 16.
Predicted value comparison of 3 min only linear models.
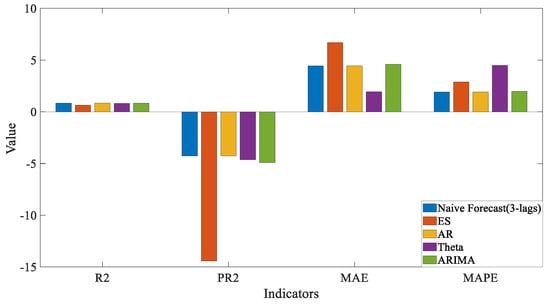
Figure 17.
Indicators comparison of 3 min linear models.
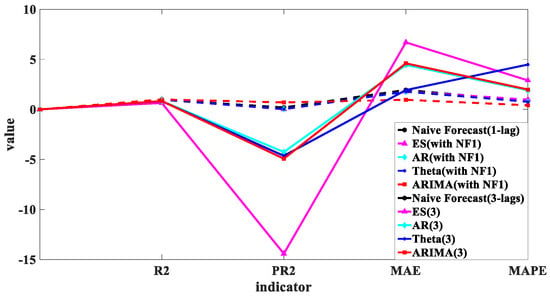
Figure 18.
Comparison of indicators between 1 min (NF1) and 3 min linear models.
In our analysis of linear models, the ARIMA model demonstrated the highest prediction accuracy at one-minute prediction for both turning points and overall average levels. However, as the prediction interval increased to three minutes, the performance of the linear time-series models generally declined. This suggested that most of the predictive information at the one-minute mark can be effectively extracted from the inherent patterns of the time-series itself. ARIMA showed an advantage in modeling short-term predictions where the series is relatively smooth.
For three-minute predictions, there appeared to be a greater need for information about nonlinear or external physical processes. Notably, the ARIMA model maintained its robustness across the different linear prediction models tested, showing little variation in performance whether combined with the NF3-lag feature or not. This indicated that the moving average component of the ARIMA model played a crucial role in stabilizing the predictions. Based on these observations, we selected the ARIMA model as the linear baseline model for integrating subsequent nonlinear and regression models in our predictive framework. This choice was supported by ARIMA’s proven effectiveness in handling predictions and its robust performance under varying conditions.
- (1)
- Prediction of nonlinear time-series models
The application of nonlinear models in our study primarily addressed the local volatility within the time-series that the linear models were unable to manage effectively. The linear models were best-suited for series that display stable expectations and variance. However, if a series exhibits variance changes—as observed in our dataset—models like ARCH and its derivatives were found to be more apt for addressing these fluctuations.
In this study, we employed several nonlinear models, including ARCH, GARCH, and EGARCH, to handle the complexities of the dataset where linear models fall short. To enhance the prediction accuracy, we integrated these nonlinear models with the ARIMA linear model. The hybrid model indicators of ARIMA and the nonlinear models were as follows.
From the data presented in Table 6 and Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24, it was evident that the use of nonlinear models in one-minute, short-term, single-step predictions did not enhance the overall accuracy of the models; instead, it may lead to overfitting. This suggested that, for short prediction intervals, maintaining model simplicity can be more beneficial.

Table 6.
Comparison of 1-min NonLinear Combination Prediction Effects.
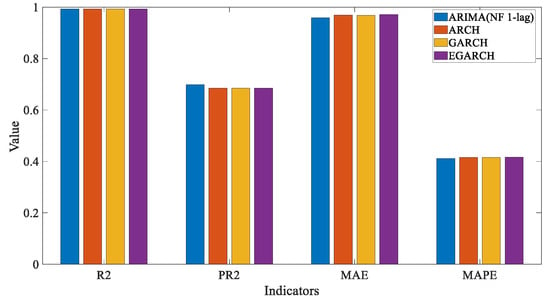
Figure 19.
Indicators comparison of 1 min combined nonlinear models.

Figure 20.
Prediction effect comparison of 1 min combined nonlinear models.

Figure 21.
Prediction effect comparison of 3 min combined nonlinear models.
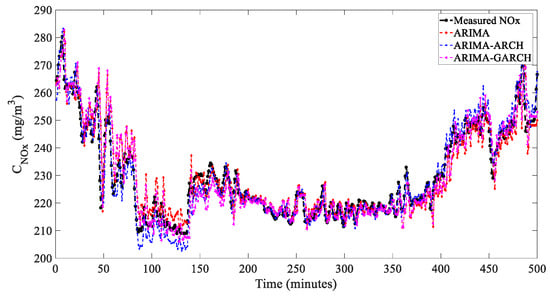
Figure 22.
Predicted value comparison of 3 min combined nonlinear models.
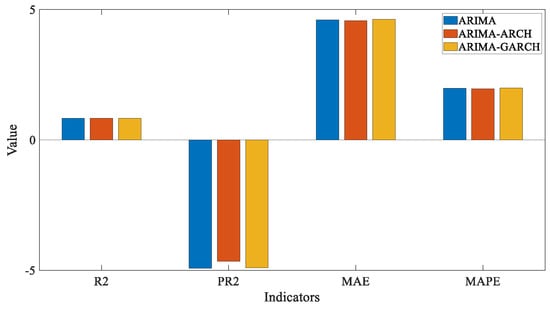
Figure 23.
Indicators comparison of 3 min combined nonlinear models.
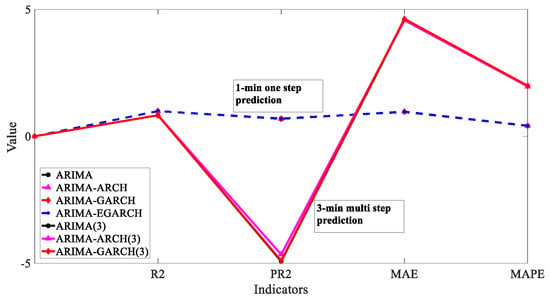
Figure 24.
Comparison of indicators between 1 min (NF1) and 3 min combined nonlinear models.
In the above Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24 and Table 7, detailing the forecasting effect of the combined nonlinear model, it can be seen that the forecasting evaluation indicators such as the R2 and PR2 of the combined model were improved after the addition of the nonlinear model. The PR2 indicator in the pooled ARCH model was improved the most, indicating that ARCH improved the forecasting effect of the combined model through variance compensation. It also confirmed its effectiveness in dealing with local fluctuations.

Table 7.
Comparison of 3 min NonLinear Combination Prediction Effects.
- (2)
- Prediction of multivariate regressive time-series models
In this part, we delineated the models as follows. These models, despite varied mechanisms, shared essential characteristics common to regression models used in statistical learning. This part of the prediction utilizes multivariate regression based on highly correlated variables identified through the feature selection of front-end variables in Section 4.1 The model continued to extract information related to mechanistic models from the operational data, thereby further enhancing the overall predictive performance of the integrated model.
This part of the prediction primarily fitted the weights of different independent variables by reducing residuals and the loss function. Compared to the linear and nonlinear time-series predictions discussed earlier, this prediction was multivariate and included information related to the NOx generation mechanism model. In the power plant experiments, we also adaptively adjusted the weights of these independent variables based on the NOx generation mechanism. Table 8 and Table 9 below show the effect of NOx concentration prediction by combination models for the 1-min and 3-min, respectively.

Table 8.
Prediction of 1 Min NOx Concentration by Integrated Models.

Table 9.
Prediction of 3 Min NOx Concentration by Integrated Models.
As can be seen in Table 8, the combined models are all accurate for 1-min predictions. For the 3-min prediction, there is some difference in the effectiveness of the combined model, and Figure 25 and Figure 26 show the 3-min prediction of the combined model.
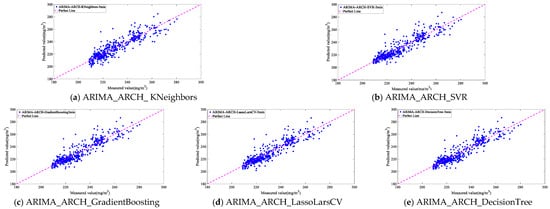
Figure 25.
Prediction effect comparison of 3 min final combined models.
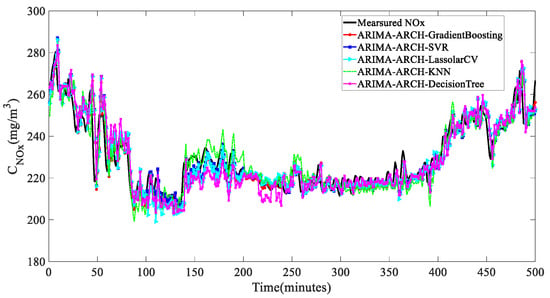
Figure 26.
3 min prediction effects.
The above analysis indicated that, for short-term predictions of one minute, the trend information in the time-series data was relatively important for forecasting. The additional benefits of combining nonlinear or regression models were minimal.
However, for multi-step predictions over three minutes, where the data were resampled at one-minute intervals and then used to predict the concentrations three minutes later, there was an excessive loss of trend information, leading to a decreased forecasting performance. In this case, combining the NOx generation mechanism model with the nonlinear factors of the data will enhance the overall predictive performance.
Our findings highlighted that a composite model, which integrated linear time-series, nonlinear time-series, and exogenous regression models, demonstrates significant advantages in three-minute multi-step forecasts. Notably, in our dataset, the ARIMA_ARCH_GradientBoosting model emerged as the most effective for three-minute predictions. This model adeptly combined the strengths of individual forecasting techniques, optimizing the predictive accuracy and reliability, which are essential for operational efficiency in power plant settings. Therefore, the ARIMA_ARCH_GradientBoosting model will be employed as the proposed model in this study for subsequent tests of generalizability and comparison with the existing literature.
4.3. Generalizability Testing
In applying the prediction models to industrial processes, the most important concern was the generalization of the model. In this study, based on the previous model, predictions were made on an untrained data segment from the same power plant, and the prediction results are shown in Figure 27:
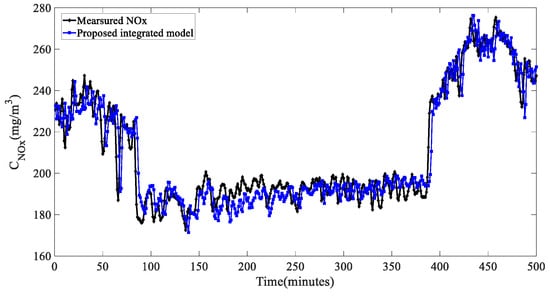
Figure 27.
Generalizability testing.
The results, illustrated in Figure 27, demonstrated that the model effectively predicts NOx levels over a three-minute interval, maintaining a high accuracy even with new data. The smoother characteristics of this data segment yielded an R2 score of 0.9115, which was superior to the previous result of 0.8463 obtained from a different segment. This improvement confirmed the model’s robust generalization performance across varying data conditions.
To compare the three-minute prediction accuracy of the proposed combination boosting model with existing predictino models, this study employed a widely used deep learning approach, the long short-term memory (LSTM) model. The LSTM network is a variant of recurrent neural networks that is specifically designed to process and predict event-related characteristics in time-series data. It is commonly used in fields such as time-series analysis and forecasting. For the LSTM model, we employed a two-layer architecture with 100 and 50 units, respectively, to extract and learn complex time-series relationships. For training, we chose the Adam optimizer with an initial learning rate of 0.01. A dropout rate of 0.2 was implemented to reduce overfitting of the model, and the output layer neurons were selected as 1 and 3 for the single- and three-step predictions, respectively. In single-step forecasting, the LSTM model resulted in an R2 value of 0.9902, a PR2 value of 0.6770, an MAE of 1.0743, and a MAPE of 0.4842. It can be observed that, in single-step prediction using the LSTM model, due to the absence of a residual compensation process, the prediction accuracy at turning points is somewhat inferior. To achieve more precise predictions from the data, the LSTM model can be further optimized through a boosting strategy to enhance its accuracy at turning points. However, since this study was intended for on-site application, one-minute or LSTM predictions can only serve as comparative models and were not suitable for subsequent on-site application. Under these conditions, the prediction model proposed in this paper will possess the strongest adaptability and robustness. Since the ultimate goal of this study is to propose a set of 3 min advance prediction combination models that will be available in the field, we applied the LSTM model to the selected data segments for 3 min prediction; the prediction outcomes are presented below.
Figure 28 shows a comparison between the final proposed combined prediction model and the LSTM model, specifically for time-series prediction, where the R2 of the proposed integrated model was 0.8463, the R2 of the LSTM model was 0.82102, and the PR2 of the LSTM model was −4.4832, which made us realize that deep learning and complex models are not a panacea, and that specific analysis methods for specific data were more meaningful and effective. We believe the superior predictive performance of the model proposed in this paper, compared to related work, is due to continuously optimizing the PR2 metric during the process and the ability to adjust the parameter k in the PR2 based on different data and prediction requirements. Additionally, our familiarity with the NOx formation mechanism allowed us to make specific parameter-weight adjustments in the ARIMA model based on this mechanism.
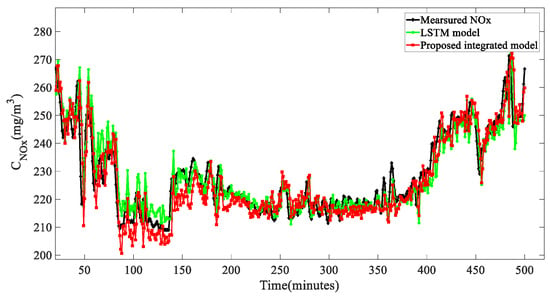
Figure 28.
Prediction effect comparison of 3 min in different models.
More importantly, compared to related studies, the key advantage of the approach proposed in this paper is that it can be implemented on-site. Additionally, it predicts NOx concentrations 3 min ahead, meaning that this is not simply an optimization of a prediction model in the field of computer science, as the reviewer suggested, but rather a practical, deployable model designed to solve real-world problems. Consequently, it is challenging to perform a detailed comparison with existing studies. Furthermore, we introduced the PR2 parameter, tailored to practical applications, and proposed an ensemble learning model based on multiple weak learners, incorporating data characteristics and the conditions of on-site applications. These innovations improve the overall predictive performance, serving as an optimized feedforward for the SCR control systems in power plants.
Additionally, this study opted for a combination of simpler models primarily because such an approach is feasible for implementation in a power plant setting, unlike deep convolutional neural networks which may not be practical on-site. This decision underscores the importance of model applicability in real industrial environments.
4.4. Discussion
In this section, we will analyze the model’s performance in terms of accuracy, robustness, and applicability to real industrial scenarios. We will compare the predictive performance of the proposed model with that of existing studies and the LSTM model.
In one-minute single-step predictions, the trend information in the time-series data dominated the forecast, and incorporating additional models at this stage may cause overfitting, reducing the prediction effectiveness. In contrast, in three-minute multi-step predictions, the trend information was greatly reduced, and the inclusion of the naive forecast model degraded the predictive performance, while incorporating the data’s inherent nonlinearities and the physical generation mechanisms of NOx can enhance the reliability of the predictions.
In this study, the proposed model was applied to actual data from a 330 MW power plant, showing excellent predictive accuracy. For 3 min prediction, compared to predictions made by ARIMA, the fitting degree R2 and the PR2 were increased by 3.6% and 30.6%, respectively, and the MAE and MAPE were decreased by 9.4%, and 9.1%, respectively. It can also be observed that the PR2 evaluation indicator proposed in this paper provided a sharper contrast than traditional indicators. For example, in Table 1, the difference in R2 values between the predictions is minimal, while the difference in the PR2 is significant, indicating that the PR2 offers more distinct prediction results. In Table 2, the traditional prediction indicators were improved with longer window lengths, whereas the PR2 exhibited a turning point, making it easier to select model parameters and window lengths.
Additionally, existing research on NOx prediction has introduced a method combining random forest and just-in-time learning for forecasting NOx concentrations in thermal power plants [43], achieving a maximum R2 of 0.9319 and a MAE of 2.7718. These figures were lower than those reported in our study, with an R2 of 0.9925 and a MAE of 0.4213. This further substantiated the effectiveness of the method proposed in our paper for enhancing predictive accuracy.
In addition, we also conducted predictions using an LSTM model with the same data and, for comparison, the R2 of the proposed model for 3 min prediction is 0.8463, whilst that of the deep learning LSTM model for 3 min prediction is 0.82102. This comparison illustrates that deep learning and complex models are not universally optimal. Tailored analytical methods specific to the data can be more meaningful and effective. More importantly, the field implementation of NOx advance prediction is made possible by the combination of a simple prediction model with a boosting method.
The error analysis can be directly observed in Figure 22, Figure 26, and Figure 28, as well as similar figures. Even though the PR2 parameter was introduced, the model still cannot entirely avoid the inherent shortcomings of prediction models, particularly showing poorer performance when there are large fluctuations in the data. While the introduction of the PR2 parameter offers some improvement over other models in terms of optimization during significant data variations, this remains a common issue in data prediction. Therefore, this is an area for future work, where further advancements in data modeling will allow for more improvements in predictive soft-sensing. On the other hand, since the prediction data in this paper were downsampled to minute-level data, the model’s performance in handling data with jagged fluctuations still requires further improvement.
5. Conclusions and Future Work
To address the issue of delays in online NOx measurement in power plant denitration processes, this study introduced a hybrid boost integration model suitable for on-site implementation at power plants. The forecasting method proposed in this paper aims to achieve a lead time of up to three minutes for forecasts, enabling its online application in power plants as an advanced soft measurement sensor. This advanced forecasting method, when applied in coal-fired power plants, will serve as a feedforward signal in the SCR control system, applied to the ammonia injection valves. It can act as a soft measurement model to compensate for the inherent hardware measurement lag, aligning the control signals with the measurement signals and enhancing the efficiency of precise ammonia injection.
- (1)
- This study introduced a new evaluation indicator, PR2. This indicator focuses on the model’s predictive accuracy at turning points, filling gaps left by other traditional indicators and providing an evaluation different from traditional parameters in data prediction, enhancing the model’s predictive performance;
- (2)
- A time-based method was proposed for analyzing the correlations between variables in denitration systems and NOx concentrations. Using this method, we investigated the time delays between various exogenous variables related to combustion and the NOx concentrations, as well as the exact measurement delays in an actual power plant;
- (3)
- To address the issue of NOx measurement delays, this study introduced a hybrid boosting model suitable for on-site implementation. This model combined generation mechanism and data-driven approaches, enhancing prediction accuracy through the categorization of time-series data into linear, nonlinear, and exogenous regression components. These results confirmed the accuracy and applicability of the integrated model for on-site implementation as a 3 min advanced prediction soft sensor in power plants.
In this paper, we have introduced a novel metric, PR2, tailored specifically for industrial prediction, proposed an ensemble learning model that integrates multiple weak learners and is deployable on-site, and identified the correlation between NOx concentration and upstream combustion and flow-side variables with respect to the time delay. These three innovations represent significant contributions to NOx soft-sensing in coal-fired power plants, as no prior work has addressed these aspects. Importantly, all of our innovations are aimed at solving real-world problems, and the approach outlined in this paper has already been successfully implemented at a power plant.
In the future, given the similarities between many industrial processes and the denitrification stage of coal-fired power plants—such as defined generation mechanisms and limited hardware conditions—the methods proposed in this paper can be directly applied to related industrial processes. Furthermore, the ensemble learning approach introduced here provides valuable insights for using data and weak learners to maximize information extraction and enhance data prediction under constrained industrial conditions. At the same time, the proposed soft-sensing predictive algorithm has already been applied in a real coal-fired power plant, achieving promising results.
Of course, there are still several areas for improvement in this paper. For example, with the further development of mechanistic models and big data technologies, the accuracy of our three-minute-ahead predictions could be improved. Additionally, predicting the NOx concentration across the flue cross-section in the SCR control stage of coal-fired power plants is also an important aspect. However, the plant currently lacks NOx data for its flue cross-section. These issues are expected to be addressed in future developments, which will collectively enhance denitrification efficiency.
Author Contributions
Conceptualization, T.L., R.Z., D.L. and Y.Z.; Methodology, T.L., Y.G., R.Z., S.W., D.L. and Y.Z.; Software, T.L. and Y.G.; Formal analysis, T.L. and S.W.; Writing—original draft, T.L.; Writing—review & editing, T.L. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by “the Fundamental Research Funds for the Central Universities (2022ZFJH04)”.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Yu Gan and Ru Zhang were employed by the company Nanjing Tianfu Software Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Manisalidis, I.; Stavropoulou, E.; Stavropoulos, A.; Bezirtzoglou, E. Environmental and Health Impacts of Air Pollution: A Review. Front. Public Health 2020, 8, 505570. [Google Scholar] [CrossRef] [PubMed]
- Tribus, M.; McIrvine, E.C. Energy and information. Sci. Am. 1971, 225, 179–190. Available online: http://www.jstor.org/stable/24923125 (accessed on 21 January 2021). [CrossRef]
- The Ministry of Ecology and Environment. The Second National Pollution Source Census Bulletin; Ministry of Ecology and Environment: Beijing, China, 2020. [Google Scholar]
- Dimitriades, B. Effects of hydrocarbon and nitrogen oxides on photochemical smog formation. Environ. Sci. Technol. 1972, 6, 253–260. [Google Scholar] [CrossRef]
- Atkinson, R.; Lloyd, A.C. Evaluation of Kinetic and Mechanistic Data for Modeling of Photochemical Smog. J. Phys. Chem. Ref. Data 1984, 13, 315–444. [Google Scholar] [CrossRef]
- Calvert, J.G.; Stockwell, W.R. Acid generation in the troposphere by gas-phase chemistry. Environ. Sci. Technol. 1983, 17, 428A–443A. [Google Scholar] [CrossRef]
- López-Puertas, M.; Funke, B.; Gil-López, S.; von Clarmann, T.; Stiller, G.P.; Höpfner, M.; Kellmann, S.; Fischer, H.; Jackman, C.H. Observation of NOxenhancement and ozone depletion in the Northern and Southern Hemispheres after the October-November 2003 solar proton events. J. Geophys. Res. Space Phys. 2005, 110, A09S43. [Google Scholar] [CrossRef]
- Ehhalt, D.; Prather, M.; Dentener, F.; Derwent, R.; Dlugokencky, E.; Holland, E.; Isaksen, I.; Katima, J.; Kirchhoff, V.; Matson, P.; et al. Atmospheric Chemistry and Greenhouse Gases; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2001. [Google Scholar]
- Luo, L.; Wu, Y.; Xiao, H.; Zhang, R.; Lin, H.; Zhang, X.; Kao, S.-J. Origins of aerosol nitrate in Beijing during late winter through spring. Sci. Total Environ. 2019, 653, 776–782. [Google Scholar] [CrossRef]
- China’s Ministry of Ecology and Environmental Protection. Bulletin of the Second National Pollution Source Census; China’s Ministry of Ecology and Environmental Protection: Beijing, China, 2020. [Google Scholar]
- Stupar, G.; Tucaković, D.; Živanović, T.; Belošević, S. Assessing the impact of primary measures for NOx reduction on the thermal power plant steam boiler. Appl. Therm. Eng. 2015, 78, 397–409. [Google Scholar] [CrossRef]
- Ma, Z.; Deng, J.; Li, Z.; Li, Q.; Zhao, P.; Wang, L.; Sun, Y.; Zheng, H.; Pan, L.; Zhao, S.; et al. Characteristics of NOx emission from Chinese coal-fired power plants equipped with new technologies. Atmos. Environ. 2016, 131, 164–170. [Google Scholar] [CrossRef]
- He, B.; Zhu, L.; Wang, J.; Liu, S.; Liu, B.; Cui, Y.; Wang, L.; Wei, G. Computational fluid dynamics based retrofits to reheater panel overheating of No. 3 boiler of Dagang Power Plant. Comput. Fluids 2007, 36, 435–444. [Google Scholar] [CrossRef]
- Liu, J.; Luo, X.; Yao, S.; Li, Q.; Wang, W. Influence of flue gas recirculation on the performance of incinerator-waste heat boiler and NOx emission in a 500B t/d waste-to-energy plant. Waste Manag. 2020, 105, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Ilbas, M.; Yılmaz, İ.; Kaplan, Y. Investigations of hydrogen and hydrogen–hydrocarbon composite fuel combustion and NOx emission characteristics in a model combustor. Int. J. Hydrog. Energy 2005, 30, 1139–1147. [Google Scholar] [CrossRef]
- Nakamura, K.; Muramatsu, T.; Ogawa, T.; Nakagaki, T. Kinetic model of SCR catalyst-based de-NOx reactions including surface oxidation by NO2 for natural gas-fired combined cycle power plants. Mech. Eng. J. 2020, 7, 20-00103. [Google Scholar] [CrossRef]
- Li, X. Optimization and reconstruction technology of SCR flue gas denitrification ultra low emission in coal fired power plant. IOP Conf. Ser. Mater. Sci. Eng. 2017, 231, 012111. [Google Scholar] [CrossRef]
- Le Bris, T.; Cadavid, F.; Caillat, S.; Pietrzyk, S.; Blondin, J.; Baudoin, B. Coal combustion modelling of large power plant, for NOx abatement. Fuel 2007, 86, 2213–2220. [Google Scholar] [CrossRef]
- Goos, E.; Sickfeld, C.; Mauß, F.; Seidel, L.; Ruscic, B.; Burcat, A.; Zeuch, T. Prompt NO formation in flames: The influence of NCN thermochemistry. Proc. Combust. Inst. 2013, 34, 657–666. [Google Scholar] [CrossRef]
- Rakholia, R.; Le, Q.; Vu, K.; Ho, B.Q.; Carbajo, R.S. AI-based air quality PM2.5 forecasting models for developing countries: A case study of Ho Chi Minh City, Vietnam. Urban Clim. 2022, 46, 101315. [Google Scholar] [CrossRef]
- Pan, L.; Tong, D.; Lee, P.; Kim, H.C.; Chai, T. Assessment of NOx and O3 forecasting performances in the U.S. National Air Quality Forecasting Capability before and after the 2012 major emissions updates. Atmos. Environ. 2014, 95, 610–619. [Google Scholar] [CrossRef]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial intelligence for the modeling and control of combustion processes: A review. Prog. Energy Combust. Sci. 2003, 29, 515–566. [Google Scholar] [CrossRef]
- Tunckaya, Y.; Koklukaya, E. Comparative analysis and prediction study for effluent gas emissions in a coal-fired thermal power plant using artificial intelligence and statistical tools. J. Energy Inst. 2015, 88, 118–125. [Google Scholar] [CrossRef]
- Mazinan, A.H.; Khalaji, A.R. A comparative study on applications of artificial intelligence-based multiple models predictive control schemes to a class of industrial complicated systems. Energy Syst. 2016, 7, 237–269. [Google Scholar] [CrossRef]
- Peres, R.S.; Jia, X.; Lee, J.; Sun, K.; Colombo, A.W.; Barata, J. Industrial Artificial Intelligence in Industry 4.0—Systematic Review, Challenges and Outlook. IEEE Access 2020, 8, 220121–220139. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Zheng, S.; Jiang, A. Optimizing combustion of coal fired boilers for reducing NOx emission using Gaussian Process. Energy 2018, 153, 149–158. [Google Scholar] [CrossRef]
- Zhou, H.; Cen, K.; Fan, J. Modeling and optimization of the NOx emission characteristics of a tangentially fired boiler with artificial neural networks. Energy 2004, 29, 167–183. [Google Scholar] [CrossRef]
- Adams, D.; Oh, D.-H.; Kim, D.-W.; Lee, C.-H.; Oh, M. Prediction of SOx–NOx emission from a coal-fired CFB power plant with machine learning: Plant data learned by deep neural network and least square support vector machine. J. Clean. Prod. 2020, 270, 122310. [Google Scholar] [CrossRef]
- Yang, G.; Wang, Y.; Li, X. Prediction of the NOx emissions from thermal power plant using long-short term memory neural network. Energy 2020, 192, 116597. [Google Scholar] [CrossRef]
- Wang, G.; Awad, O.I.; Liu, S.; Shuai, S.; Wang, Z. NOx emissions prediction based on mutual information and back propagation neural network using correlation quantitative analysis. Energy 2020, 198, 117286. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y.X. A Survey of Ensemble Learning: Concepts, Algorithms, Applications, and Prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
- Liu, Y.; An, A.; Huang, X. Boosting Prediction Accuracy on Imbalanced Datasets with SVM Ensembles. In Advances in Knowledge Discovery and Data Mining; Ng, W.-K., Kitsuregawa, M., Li, J., Chang, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 107–118. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Lu, N.; Lin, H.; Lu, J.; Zhang, G. A Customer Churn Prediction Model in Telecom Industry Using Boosting. IEEE Trans. Ind. Inform. 2014, 10, 1659–1665. [Google Scholar] [CrossRef]
- Duan, T.; Anand, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.; Schuler, A. NGBoost: Natural Gradient Boosting for Probabilistic Prediction. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Volume 119, pp. 2690–2700. [Google Scholar]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. Extending Statistical Boosting. An Overview of Recent Methodological Developments. Methods Inf. Med. 2014, 53, 428–435. [Google Scholar] [CrossRef] [PubMed]
- Naimi, A.I.; Balzer, L.B. Stacked generalization: An introduction to super learning. Eur. J. Epidemiol. 2018, 33, 459–464. [Google Scholar] [CrossRef]
- Kotsiantis, S.B. Bagging and boosting variants for handling classifications problems: A survey. Knowl. Eng. Rev. 2014, 29, 78–100. [Google Scholar] [CrossRef]
- De Gooijer, J.G.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice OTexts. 2021. Available online: https://otexts.com/fpp3/ (accessed on 20 May 2020).
- He, K.; Ding, H. Prediction of NOx Emissions in Thermal Power Plants Using a Dynamic Soft Sensor Based on Random Forest and Just-in-Time Learning Methods. Sensors 2024, 24, 4442. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).