Abstract
Due to the ability to improve the low-inertia characteristics of power systems and offer reliable voltage and frequency support, grid-forming permanent-magnet synchronous-generator wind turbines (PMSG-WTs) based on virtual synchronous-generator (VSG) technology are emerging se the direction for future developments. Previous studies on the small-signal stability of grid-forming PMSG-WTs that connect to the grid usually simplify them into grid-connected grid-side converters (GSC), potentially leading to errors in stability analyses. Therefore, this paper considers the machine-side converter (MSC) control and establishes impedance models for grid-forming PMSG-WTs. Based on the sensitivity calculation of controller parameters using symmetric difference computation based on zero-order optimization, the impact of the internal controller on outside impedance characteristics is quantitatively analyzed. Additionally, an optimization method to enhance the stability of a hybrid wind farm by adjusting the ratio of grid-forming and grid-following wind turbines is proposed.
1. Introduction
The rapid increase in the proportion of the installed capacity for the generation of renewable energy power has led to the progressive weakening of the connected synchronous grids. The frequent occurrence of sub/super-synchronous oscillations caused by interactions between large-scale permanent-magnet synchronous-generator wind turbines (PMSG-WTs) and the grid seriously affects the safe and stable operation of the grid [1,2,3,4]. Compared with traditional geared wind turbines, grid-following PMSG-WTs have the capability to transmit high-quality electrical energy, but they also face drawbacks in high-power-electrified power systems, such as a lack of inertia support, an inability to provide active power support, and an inability to provide voltage and frequency support for distributed devices under islanded operation conditions [5,6].
To address the limitations of grid-following voltage-source converters (VSCs), grid-forming VSCs have emerged. Many scholars have proposed various grid-forming VSC control strategies [7,8,9,10]. Droop control and virtual synchronous generator (VSG) control, which mimic the operating mechanisms of synchronous generators (SGs), have been widely applied. VSG control can not only simulate the primary frequency regulation characteristics of an SG but can also mimic its inertia and damping characteristics, which has attracted increasing attention from scholars [11].
Grid-forming WTs based on VSGs have the capability to either release or absorb rotational kinetic energy from the power grid in response to changes in grid frequency and voltage. This allows for the adjustment of rated power and the reactive power output of the WTs. Within a specific speed range, these turbines can provide inertia and voltage support to the power system. However, the integration of grid-forming WTs not only enhances the frequency and voltage response characteristics but also establishes communication pathways for the interaction between WTs and power grids, thus strengthening the dynamic coupling effect. This may result in a reduction in the system’s oscillation damping levels, leading to the occurrence of wide-band oscillations. When perturbations or oscillations occur in the system, which cause frequency and voltage variations, WTs regulate their power output through VSG control. Improper adjustment of control parameters could alter the system’s damping characteristics and trigger instability. Currently, research on grid-forming PMSG-WTs is relatively limited, focusing primarily on the stability of grid-forming VSCs based on VSG technology [12,13,14]. Studies [15,16,17] have employed harmonic linearization methods to develop impedance models for grid-connected VSCs using VSG technology; such studies have examined the differences between these models and those of grid-following VSCs controlled by phase-locked loops (PLLs). In the mid–low frequency range, grid-forming VSCs exhibit voltage source behavior with lower equivalent output impedance, while grid-following VSCs act as current sources with higher equivalent output impedance. Moreover, grid-forming VSCs mainly display inductive characteristics that align closely with the grid impedance. Building on this foundation, the authors of [18,19] developed impedance models for grid-forming VSCs based on current-control VSGs; they highlighted that voltage-controlled VSGs are more suitable than current-controlled VSGs for grid-connected renewable energy generation in ultra-weak grids from a system stability perspective. Furthermore, the integration of voltage–current dual-loop control with virtual synchronous control has been studied [20,21]; findings show that this leads to changes in the impedance characteristics of grid-forming VSCs and alterations in their inductive impedance behaviors. Finally, the authors of [22] addressed the comprehensive modeling of grid-forming PMSG-WTs, including the machine-side converter (MSC), the grid-side converter (GSC), and DC-link dynamics; they provided methods of mitigating potential instabilities by reshaping GSC impedance characteristics and enhancing DC-link dynamics.
Research on reshaping impedance to suppress oscillations in grid-forming VSCs based on the VSG impedance model, without considering the motor-side converter, is gradually progressing [23,24,25]. However, the authors of [26] demonstrated that, in the presence of a non-inductive grid load, impedance-based small-signal instability is unavoidable under specific conditions for grid-forming VSCs based on VSGs. The authors of [27] qualitatively analyzed the impedance characteristics of grid-forming VSCs based on VSGs in grid-connected systems using Bode plots, pointing out the interaction between grid-forming VSCs based on VSG and series-capacitor-compensated grids. To better adapt grid-forming VSCs based on VSG to variations in the short-circuit ratio of series-capacitor-compensated grids, optimization measures are proposed by introducing impedance-reshaping controllers into the feedback loop of the damping coefficients of grid-forming VSCs based on VSGs [28]. Furthermore, the authors of [29] considered the damping effect of inner-loop control and proposed optimization measures to achieve the decoupled control of the inner and outer loops while ensuring inner-loop tracking control.
In practice, both grid-forming and grid-following VSCs will simultaneously connect to the grid, and the configuration of the two types of converters will affect the system’s oscillation stability [30,31]. From the perspective of grid planning, The authors of [12,32] analyzed the influence of the penetration rate of grid-forming VSCs based on VSGs on the system’s oscillation stability using small-signal models, suggesting a reasonable allocation of output proportions between grid-forming VSCs based on VSGs and grid-following VSCs in microgrids; however, their study does not provide configuration principles for the output proportions of the two types of VSCs. Additionally, the authors of [33] quantitatively analyzed the variation in the oscillation damping in the “grid-forming VSCs based on VSG + grid-following VSCs” hybrid converter system with the proportion of grid-forming VSCs based on VSGs, and provided a critical access ratio for the change from negative to positive oscillation damping, but the obtained critical access ratio is insufficient in ensuring the oscillation stability of the station under all the feasible operating conditions.
In conclusion, studies on grid-forming PMSG-WTs remain limited. Furthermore, the influence of machine-side modeling on the overall impedance characteristics of these models is often overlooked in the literature, potentially leading to errors in stability analyses. As highlighted in [34], MSC control parameters have a significant impact on system stability. Therefore, a comprehensive consideration of the impacts of machine-side converters and generators on impedance characteristics is essential. Additionally, regarding hybrid wind farms with a mix of grid-following and grid-forming WTs, there is currently no consensus on how we can configure the proportion of grid-forming WTs to enhance system stability margins and reduce the risk of oscillations.
To address these issues, this paper adopts a modular multi-harmonic modeling method to establish the impedance models of grid-forming PMSG-WTs, considering machine-side converters with a double closed-loop control structure. Furthermore, the correctness of the impedance models is verified through simulation frequency sweeping. Subsequently, the paper qualitatively analyzes the impact of each controller on the impedance characteristics based on the cut-off frequency and phase margin of the controllers’ open-loop transfer functions. The sensitivity of each controller’s parameters is defined using a zero-order optimization symmetric difference quotient method to quantitatively study their impacts on the impedance characteristics. Moreover, the dominant frequency bands of each controller are identified. Finally, an optimization method to enhance the stability of a hybrid wind farm by adjusting the ratio of grid-forming and grid-following wind turbines is proposed. By leveraging the nearly full frequency damping properties of grid-forming PMSG-WTs, this strategy suggests that configuring an appropriate number of grid-forming WTs can effectively enhance the stability of the model across a wide range of frequencies.
2. Impedance Modeling
2.1. System Structure
Figure 1 presents the circuit topology of a grid-forming PMSG-WT interconnected with an infinite grid, incorporating three main components: a PMSG, a machine-side converter (MSC), and a grid-side converter (GSC). In this context, the MSC is primarily responsible for converting the AC generated by the generator into DC. The GSC, on the other hand, is mainly responsible for converting the DC back into AC and safely and stably delivering it to the power grid.
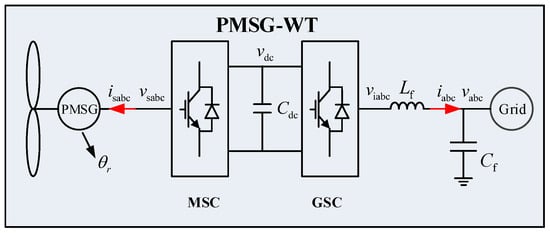
Figure 1.
Circuit topology of PMSG connected to the infinite power grid.
In the realm of virtual synchronous generator models, the Synchronverter model introduced by Professor Qingsheng Zhong [8] has been widely adopted. The Synchronverter model not only incorporates frequency-active power control loops but also features voltage-reactive power control loops, thereby providing dual support for both frequency and voltage and enabling islanded operation. Owing to its unique advantages, the Synchronverter model has rapidly evolved and gained significant recognition among domestic and international scholars, becoming a prevalent virtual synchronous machine model extensively applied in grid-forming technologies.
The VSG control scheme employed in this paper is rooted in the Synchronverter model, similarly partitioned into active power and reactive power controllers. The active power controller takes the actual active power and its set point value as inputs and yields the phase angle of the internal voltage in the VSG as its output. Conversely, the reactive power controller utilizes the actual reactive power, its reference value, the d-axis grid voltage, and the amplitude reference value of the phase voltage as inputs, ultimately delivering the d-axis component of the internal voltage in the VSG as its output.
Grid-forming PMSG-WTs differ from grid-following ones in their control architecture despite sharing identical circuit topologies. Figure 2 illustrates the control block diagram of a grid-forming PMSG-WT utilizing a VSG-based control strategy. Here, the outer loop of GSC employs VSG control, while the inner loop adopts decoupled double-closed-loop control for AC voltage and current. Within the VSG control, , , , and denote the virtual inertia, the active damping coefficient, the reactive inertial coefficient, and the reactive damping coefficient, respectively. The angle for Park transformation and inverse transformation, , and the voltage outer loop references, and , are provided by the VSG control mechanism. In GSC control, and represent the PI controllers for the AC voltage outer loop and the AC current inner loop, respectively, whereas and stand for the current and voltage decoupling coefficients.
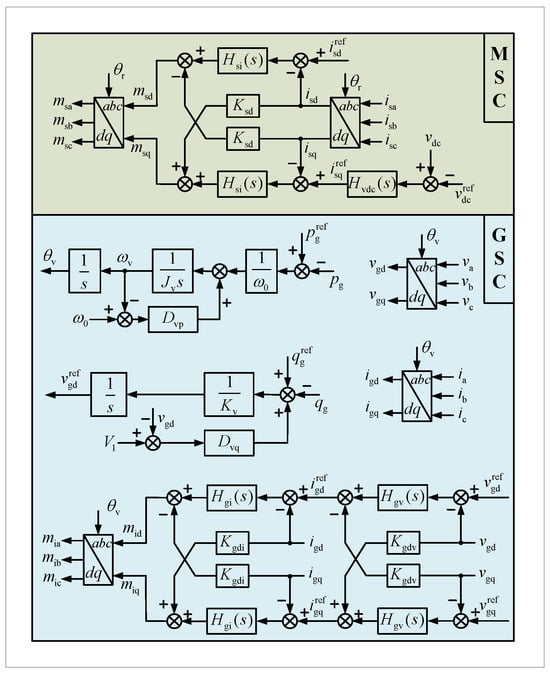
Figure 2.
Control structure diagram of grid-forming PMSG-WTs based on VSG.
In MSC control, the outer loop utilizes constant DC voltage regulation, while the inner loop is governed by current decoupling control. The angle for Park transformation and inverse transformation, , within the MSC control framework, is furnished by the PMSG. Within the MSC control structure, denotes the PI controller for the MSC’s DC voltage loop, signifies the PI controller for the MSC’s current inner loop, and represents the current decoupling coefficient for the MSC.
2.2. GSC Modeling
Under the VSG operating mode, the orientation angle of GSC is determined by VSG and correlates with the output active power. The magnitude of the output voltage is also provided by the VSG and is related to the output reactive power. According to the characteristics of voltages and currents at the GSC terminals and the PCC, the harmonic relationship equations between them are expressed as
where
The active power control loop of VSG is depicted in Figure 2. The output of the active power control loop constitutes the virtual electrical angle, . The harmonics in the voltage and current at the PCC give rise to harmonics in the active power of the GSC, and they enter into the virtual electrical angle under the influence of the active power control loop, thereby introducing harmonics into the Park and inverse Park transformations. Based on the active power control loop of VSG, the harmonic relationship of the virtual electrical angle in the frequency domain can be derived as
where
Harmonics in the virtual electrical angle introduce themselves into the Park and inverse Park transformations. According to the reactive power control loop of the VSG, the harmonic relationship of the reference signal for the AC voltage outer loop can be derived as
Through the current loop and voltage lop, the modulation signals of the GSC controller can be obtained as follows:
In summary, based on the active and reactive power control loops of the VSG, as well as the decoupled dual closed-loop control of AC voltage and current, the specific expression for the harmonic components of the output voltage at the GSC side is derived.
The coefficient matrices are shown in the Appendix A.
2.3. MSC Modeling
In grid-forming PMSG-WTs, MSC in conjunction with the DC bus capacitor maintains the stability of the DC-side voltage. Consequently, the outer loop of MSC employs a DC voltage loop control to regulate the DC-side voltage, while an inner current loop with decoupling control is used to enhance the control characteristics and improve the response time. MSC employs rotor voltage orientation with a stator current frequency denoted as . The control block diagram of MSC’s AC current inner loop decoupling controller is depicted in Figure 3. The explicit representation of the output voltage harmonics is given as follows:
where
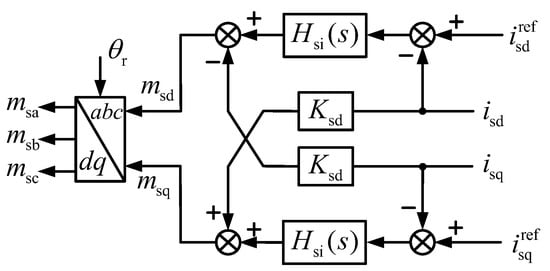
Figure 3.
AC current inner-loop-control diagram of the side converter of grid-forming PMSG-WTs.
Through the impedance derivations, harmonic relationship equations have been established between the AC-side voltage and current and the DC-side voltage of the MSC in grid-forming PMSG-WTs.
2.4. Overall Model
Utilizing symmetrical component analysis and Fourier transforms, the relations between voltage harmonics and current harmonics at PMSG port can be derived in the frequency domain as follows:
where
The DC bus interconnects the machine-side and grid-side models, serving as a pivotal constituent in PMSG units. The active power exchange between the machine-side and grid-side models occurs via the DC bus When the voltage across the DC bus capacitor fluctuates, the capacitor either absorbs or releases a certain amount of active power. Consequently, a harmonic relationship can be established as follows:
where
By integrating the impedance models of the generator, MSC, GSC, and the DC bus in grid-following PMSG-WTs, one can establish the transmission relationships of harmonics within each respective model, culminating in the derivation of the impedance model for grid-forming PMSG-WTs.
From Figure 4, it can be observed that machine-side harmonics influence the DC voltage harmonics through and , subsequently impacting the harmonics of GSC via , thereby affecting the overall impedance characteristics of the system. Under steady-state operating conditions where the capacity and voltage level of WTs remain unchanged, the magnitudes of and are directly related to the DC-side smoothing capacitor , while the value of is solely influenced by the steady-state operating point and remains constant. Hence, it can be deduced that, under unaltered MSC parameters, the role of the machine-side model in shaping the overall system impedance characteristics is exclusively dependent on the DC-side voltage smoothing capacitor.
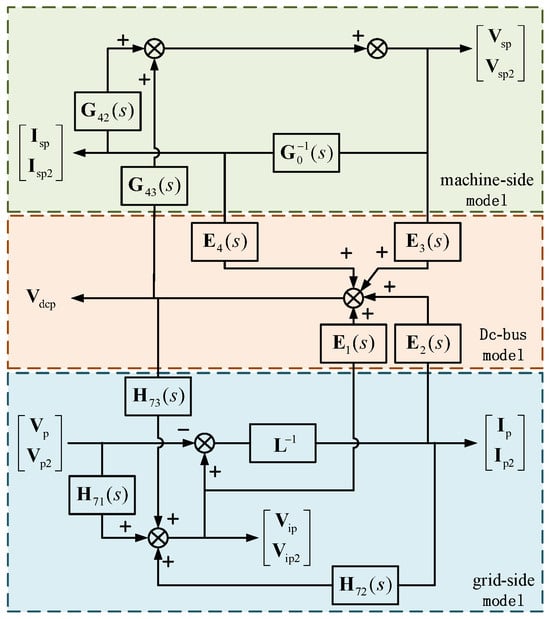
Figure 4.
Harmonic transmission diagram of grid-forming PMSG-WTs.
When the machine-side model’s effect on the total system impedance characteristics is neglected and replaced by a constant voltage source, the internal harmonic relationships within the wind turbine become simplified. The simplified harmonic propagation diagram ensuing from this substitution is depicted in Figure 5.
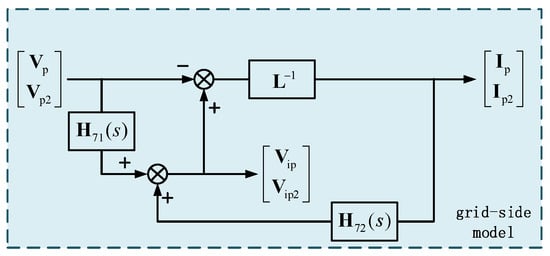
Figure 5.
Harmonic transfer relationship diagram of grid-forming PMSG-WTs without considering the influence of the machine-side factors.
2.5. Model Verification
This study constructs a grid-forming PMSG-WTs model based on the VSG in MATLAB/Simulink, as depicted in Figure 1, which encompasses the PMSG, the MSC, the DC bus, and the GSC. The control strategy detailed in Figure 2 includes VSG control at the grid side, dual closed-loop control of AC voltage and current, as well as DC voltage control and current inner-loop decoupling control at the machine side. The specific values of electrical and control parameters for the grid-forming PMSG-WTs model employing VSG are presented in Table 1 and Table 2, respectively.

Table 1.
Parameter table of grid-forming PMSG-WTs based on VSG.

Table 2.
Control parameter table of grid-forming PMSG-WTs based on VSG.
A frequency-sweeping method was employed to verify the impedance model of the grid-forming PMSG-WTs based on VSG, with the sweep test results depicted in Figure 6. Upon comparison, a satisfactory agreement between the measured and analytical impedance values was observed, thereby validating the accuracy of the constructed impedance analytical model.
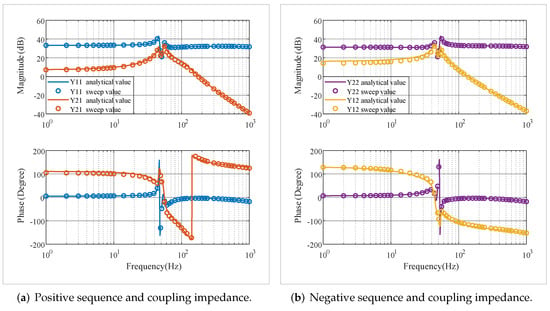
Figure 6.
Sequence impedance verification of grid-forming PMSG-WTs.
3. Impedance Characteristic Analysis
In grid-forming PMSG-WTs, the impedance expressions are highly complex, rendering the calculation of precise partial derivatives challenging. Therefore, this study employs an approach based on quantifying the degree to which various controller parameters in a zero-order approximation of grid-forming PMSG-WTs influence the impedance characteristics. This method enables the qualitative analysis of the dominant frequency bands of individual controllers and the extent of their mutual impacts. The formula for calculating the sensitivity of parameters in grid-forming PMSG-WTs is given as
For the grid-forming PMSG-WTs, the electrical parameters are tabulated in Table 1. With fixed open-loop crossover frequencies of 5 Hz and phase margins of for the VSG active power loop, alongside open-loop crossover frequencies of 5 Hz and phase margins of for the VSG reactive power loop, a proportional gain of 40 and an integral gain of 1 are set for the GSC AC voltage loop controller. The open-loop crossover frequency of GSC AC current inner loop is set to 200 Hz with a phase margin of ; meanwhile, for the MSC DC voltage outer loop, the open-loop crossover frequency is set to 10 Hz and the phase margin is . The open-loop crossover frequency of the MSC AC current inner loop is configured at 60 Hz with a phase margin of . The calculated sensitivities of these control parameters are depicted in Figure 7.
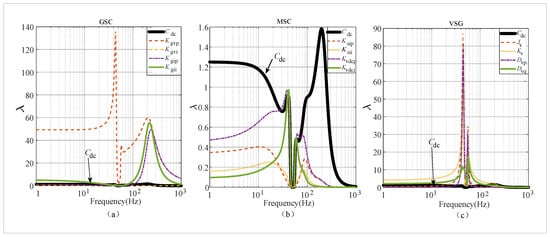
Figure 7.
Parameter sensitivity of each controller for grid-forming PMSG-WTs. (a) GSC controller, (b) MSC controller, (c) VSG controller.
From Figure 7a, it can be deduced that the dominant frequency bands for the active and reactive power control loops in tVSG controller are in the vicinity of the fundamental frequency, with negligible influence on other frequency domains. Moreover, the nearly equal sensitivities of these loops at the fundamental frequency indicate a comparable impact on the overall impedance characteristics. Moving to Figure 7b, it is evident that the AC voltage outer loop in GSC controller exhibits considerable sensitivity across the entire frequency spectrum, suggesting that its influence extends to all frequencies except those close to the fundamental frequency. On the contrary, the influence of the AC current inner loop is mainly concentrated above the fundamental frequency, peaking around the open-loop crossover frequency. From Figure 7c, it is clear that the sensitivities of all controllers within MSC have a relatively minor impact on the overall impedance characteristics. Furthermore, the sensitivities of both the MSC DC voltage outer loop and the AC current inner loop are generally lower than those of the DC bus capacitor. In both Figure 7a,b, the sensitivity of the DC bus capacitor approaches zero compared to other control loops, implying that the controllers within MSC have a lesser influence on the overall impedance characteristics. In grid-forming PMSG-WTs, different controllers exert their primary influence over distinct frequency bands, and the extent to which they affect the impedance characteristic curves varies.
4. Hybrid Wind Farm Oscillation Suppression Strategy
Harnessing the property of grid-forming PMSG-WTs that exhibit damping characteristics across nearly the entire frequency spectrum, these turbines can compensate for the negative damping introduced by grid-following PMSG-WTs when integrated into weak grids. Consequently, in wind farms, the appropriate deployment of grid-forming PMSG-WTs can effectively enhance stability margins and suppress sub- and super-synchronous oscillations. Building upon the preceding discourse, this paper proposes an optimization method to enhance the stability of a hybrid wind farm by adjusting the ratio of grid-forming and grid-following wind turbines as follows:
Step 1: System Initialization. Initialize the system stability margin , grid parameters, and the electrical and control parameters of grid-following PMSG-WTs, and the electrical and control parameters of grid-forming PMSG-WTs. Based on the scale of the wind farm, determine the upper and lower limits for the number of grid-forming WTs to be deployed.
Step 2: Stability Margin Computation. Under different configurations of grid-forming WTs, utilize the sequence impedance models of both grid-forming and grid-following PMSG-WTs, taking into account the machine-grid coupling effects, to compute the sequence impedance of the grid-connected system. Subsequently, derive the open-loop transfer function Nyquist curve from the system’s sequence impedance model and calculate the stability margin for the current configuration, where represents the shortest distance between the Nyquist curve and the point .
Step 3: Impedance Stability Check. Identify the minimum number of grid-forming wind turbines required to satisfy the condition . Validate the system’s safe and stable operation under this optimal configuration through simulation.
Given a 150 MW capacity PMSG wind farm consisting of 100 WTs, with a grid short-circuit ratio set at 2, the proposed oscillation suppression strategy was employed to optimize the number of grid-forming PMSG-WTs. After the optimization, it was determined that a configuration of 24 grid-forming turbines would meet the stability margin requirements for the grid-connected system. To validate this result, time–domain simulations were conducted, and the three-phase current simulation results at the 35 kV collection point of the wind farm are depicted in Figure 8.
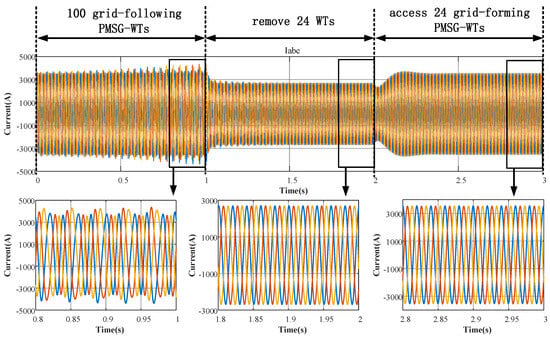
Figure 8.
Oscillation suppression waveform diagram based on configuration optimization.
During full-power generation at 150 MW, the system exhibited inadequate stability margins, leading to the occurrence of sub/super-synchronous oscillations. At 0.7 s, due to the exacerbation of oscillations, some WTs were disconnected from the farm to mitigate these oscillations, consequently causing a reduction in the power output of the wind farm. At 1.0 s, 24 grid-forming PMSG-WTs were interconnected into the wind farm, allowing the farm’s output power to recover to its full capacity of 150 MW. At this juncture, the system stability margin was sufficient, resulting in a stable operation free from sub/super-synchronous oscillations, which aligned with the theoretical analysis. This empirical validation supports the efficacy of the oscillation suppression strategy proposed in this work, which is based on optimizing the number of grid-forming PMSG-WTs.
Moreover, a graphical representation was prepared illustrating the relationship between the varying configurations of grid-forming PMSG-WTs and their associated stability margins under different short-circuit ratios, as shown in Figure 9. The figure reveals that even when the number of grid-forming PMSG-WTs remains constant, alterations in the short-circuit ratio lead to changes in the oscillation vulnerability of the hybrid wind farm. Furthermore, it becomes evident that there is no strict monotonic relationship between the quantity of grid-forming PMSG-WTs and the stability margin; an increase in the number of such turbines does not necessarily guarantee an improvement in the small signal stability of the hybrid grid-connected system.
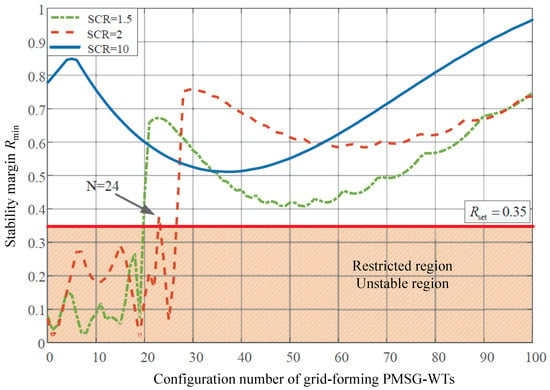
Figure 9.
Relationship between the number of configurations and the stability margin under different short-circuit ratios.
5. Conclusions
In the context of novel power systems, traditional grid-following PMSG-WTs based on PLLs tend to induce sub-synchronous oscillations when connected with weak grids; in contrast, grid-forming PMSG-WTs employing VSG technology not only provide inertial support to the system but also exhibit distinct impedance characteristics compared to grid-following counterparts. Consequently, grid-forming PMSG-WT presents a promising solution for ideal wind farm in the future. This paper employs impedance analysis to conduct an in-depth examination of the oscillation mechanisms in grid-forming PMSG-WTs. An impedance model for grid-connected grid-forming PMSG-WTs is developed, addressing the issue of unclear simplification application ranges in existing modeling practices. This paper further realizes quantitative analysis of the impact of controller parameters on the overall WTs’ impedance characteristics, identifying the principal frequency bands influenced by controllers. Additionally, an optimization method to enhance the stability of a hybrid wind farm by adjusting the ratio of grid-forming and grid-following wind turbines is proposed. By leveraging the nearly full-frequency damping properties of grid-forming PMSG-WTs, this strategy suggests that configuring an appropriate number of grid-forming WTs can effectively enhance its stability across a wide range of frequencies.
Author Contributions
Conceptualization, G.L. and Z.L.; methodology, B.L.; formal analysis, B.L.; investigation, G.L.; resources, Z.L. and R.H.; writing—original draft preparation, B.L.; writing—review and editing, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was Supported in part by the Open Fund of National Key Laboratory of Renewable Energy Grid-Integration (China Electric Power Research Institute) (No. NYB51202301627).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Author Guanghui Li was employed by the company China Electric Power Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The authors declare that this study received funding from China Electric Power Research Institute. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.
Nomenclature:
| virtual inertia | |
| active damping coefficient | |
| reactive inertial coefficient | |
| reactive damping coefficient | |
| output angle of the active power control loop | |
| , | voltage outer loop references |
| AC voltage outer loop | |
| AC current inner loop | |
| current decoupling coefficients conditioner | |
| voltage decoupling coefficients conditioner | |
| rotating angle | |
| rotating angle frequency | |
| PI controller for the MSC’s DC voltage loop | |
| PI controller for the MSC’s current inner loop | |
| current decoupling coefficient for the MSC | |
| stability margin |
Appendix A
References
- Wang, W.; Li, G.; Guo, J. Large-scale renewable energy transmission by HVDC: Challenges and proposals. Engineering 2022, 19, 252–267. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, L.; Rose, J.; Huang, S.H.; Schmall, J.; Wang, X.; Xie, X.; Shair, J.; Ramamurthy, J.R.; Modi, N.; et al. Real-world subsynchronous oscillation events in power grids with high penetrations of inverter-based resources. IEEE Trans. Power Syst. 2022, 38, 316–330. [Google Scholar] [CrossRef]
- Fan, L.; Miao, Z.; Shah, S.; Cheng, Y.; Rose, J.; Huang, S.H.; Pal, B.; Xie, X.; Modi, N.; Wang, S.; et al. Real-World 20-Hz IBR Subsynchronous Oscillations: Signatures and Mechanism Analysis. IEEE Trans. Energy Convers. 2022, 37, 2863–2873. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, P.; Lu, G.; Chen, X. Influence Analysis of Oscillation Harmonics in LCC-HVDC Delivery System Based on Impedance Modeling. IEEE Trans. Circuits Syst. I-Regul. Pap. 2023, 70, 4194–4203. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-synchronization stability of converter-based resources—An overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid forming converters in renewable energy sources dominated power grid: Control strategy, stability, application, and challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Beck, H.P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–6. [Google Scholar]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2010, 58, 1259–1267. [Google Scholar] [CrossRef]
- Rodriguez, P.; Citro, C.; Candela, J.I.; Rocabert, J.; Luna, A. Flexible grid connection and islanding of SPC-based PV power converters. IEEE Trans. Ind. Appl. 2018, 54, 2690–2702. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2009, 25, 809–820. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Guo, J.; Chen, Y.; Wang, L.; Wu, W.; Wang, X.; Shuai, Z.; Guerrero, J.M. Impedance Analysis and Stabilization of Virtual Synchronous Generators with Different DC-Link Voltage Controllers Under Weak Grid. IEEE Trans. Power Electron. 2021, 36, 11397–11408. [Google Scholar] [CrossRef]
- Chen, J.; O’Donnell, T. Parameter Constraints for Virtual Synchronous Generator Considering Stability. IEEE Trans. Power Syst. 2019, 34, 2479–2481. [Google Scholar] [CrossRef]
- Xu, Y.; Nian, H.; Kang, J.; Zhao, J.; Wang, Z.; Zhou, J. Impedance-based Analysis of Potential Stability Risk Between Grid-Forming and Grid-Following Wind Turbine Systems. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 858–862. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, L.; Chen, Y.; Luo, A.; Dong, Y.; Zhou, X.; Xu, Q.; Yang, L.; Guerrero, J.M. Sequence-Impedance-Based Stability Comparison Between VSGs and Traditional Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 46–52. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Z.; Chen, Y.; Wu, W.; Wang, Z.; Lin, G.; Guo, J. Admittance-Based Stability Analysis of Current-Controlled VSG Considering the Frequency Coupling Characteristics. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1191–1202. [Google Scholar] [CrossRef]
- Li, G.; Chen, Y.; Luo, A.; He, Z.; Wang, H.; Zhu, Z.; Wu, W.; Zhou, L. Analysis and Mitigation of Subsynchronous Resonance in Series-Compensated Grid-Connected System Controlled by a Virtual Synchronous Generator. IEEE Trans. Power Electron. 2020, 35, 11096–11107. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Y.; Zhou, L.; Luo, A.; Zhou, X.; He, Z.; Yang, L.; Xie, Z.; Liu, J.; Zhang, M. Sequence Impedance Modeling and Stability Comparative Analysis of Voltage-Controlled VSGs and Current-Controlled VSGs. IEEE Trans. Ind. Electron. 2019, 66, 6460–6472. [Google Scholar] [CrossRef]
- Wang, G.; Lyu, J.; Rao, Y. Small-Signal Stability Analysis of Hybrid Wind Farm with Grid-Following and Grid-Forming Wind Turbine Generators. In Proceedings of the 2023 IEEE PELS Students and Young Professionals Symposium (SYPS), Shanghai, China, 27–29 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, K.; Wang, Y.; Sun, Y.; Xu, P.; Gao, F. Frequency-Coupled Impedance Modeling of Virtual Synchronous Generators. IEEE Trans. Power Syst. 2021, 36, 3692–3700. [Google Scholar] [CrossRef]
- Liu, J.; Xia, Y.; Wei, W.; Feng, Q.; Yang, P. Effect of Control Damping on Small-Signal Stability of Grid-Forming VSCs Considering Interaction Between Inner and Outer Loops. IEEE Trans. Power Electron. 2024, 39, 7685–7695. [Google Scholar] [CrossRef]
- Xu, Y.; Nian, H.; Hu, B.; Sun, D. Impedance Modeling and Stability Analysis of VSG Controlled Type-IV Wind Turbine System. IEEE Trans. Energy Convers. 2021, 36, 3438–3448. [Google Scholar] [CrossRef]
- Shah, C.R.; Molinas, M.; Nilsen, R.; Amin, M. Impedance Reshaping of GFM Converters with Selective Resistive Behaviour for Small-signal Stability Enhancement. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 1619–1626. [Google Scholar] [CrossRef]
- Zhou, W.; Mohammed, N.; Bahrani, B. Voltage and Current Dynamics-Canceled Virtual Synchronous Generators for Stability Guarantee. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Auckland, New Zealand, 21–24 November 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Cheng, L.; Gao, X.; Xu, J.; Blaabjerg, F. A Generic Power Compensation Control for Grid Forming Virtual Synchronous Generator with Damping Correction Loop. IEEE Trans. Ind. Electron. 2023, 71, 10908–10918. [Google Scholar] [CrossRef]
- Shah, C.R.; Molinas, M.; Nilsen, R.; Amin, M. Limitations in Impedance Reshaping of Grid Forming Converters for Instability Prevention. In Proceedings of the 2023 IEEE International Future Energy Electronics Conference (IFEEC), Sydney, Australia, 20–23 November 2023; pp. 526–531. [Google Scholar] [CrossRef]
- Yang, X.; Bao, Y.; Meng, Z.; Xu, C.; Wang, Y.; Xue, H. Restraining Method of Subsynchronous Oscillation in Virtual Synchronous Generator Based on Impedance Reshaping. In Proceedings of the CSEE, Lisbon, Portugal, 29–31 March 2023; pp. 1–13. [Google Scholar]
- Wang, W.; Shi, X.; Wu, G.; Cao, Y. Interaction Between Grid-Forming Converters with AC Grids and Damping Improvement Based on Loop Shaping. IEEE Trans. Power Syst. 2024, 39, 1905–1917. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Kestelyn, X.; Guillaud, X. Analysis of the coupling between the outer and inner control loops of a Grid-forming Voltage Source Converter. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, D.; Hu, P.; Kan, C. Configuration Analysis of Grid-forming Converter Under 100% Renewable Electricity Systems. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 1272–1276. [Google Scholar] [CrossRef]
- Liu, X.; Zou, Z.; Tang, J.; Wang, Z.; Cheng, M. Modeling and Stability Analysis of Converter-based Power Systems. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 3134–3142. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, Z.; Zha, X.; Sun, J.; Li, Y.; Wan, Z. Impedance Stability Analysis and Promotion Strategy of Islanded Microgrid Dominated by Grid-connected and Grid-following Converters. Autom. Electr. Power Syst. 2022, 46, 121–131. [Google Scholar]
- Liu, P.; Xie, X.; Shair, J. Adaptive Hybrid Grid-Forming and Grid-Following Control of IBRs with Enhanced Small-Signal Stability Under Varying SCRs. IEEE Trans. Power Electron. 2024, 39, 6603–6607. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.; Dong, X.; Yu, S.S.; Chen, X.; Oo, A.M.T.; Lian, X.; Shan, Z.; Liu, X. Impedance Modeling and Controllers Shaping Effect Analysis of PMSG Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1465–1478. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).