Parameter Identification of Power Grid Subsynchronous Oscillations Based on Eigensystem Realization Algorithm
Abstract
1. Introduction
2. Synchrophasors Model and Modal Parameter Extraction
2.1. SSO Model with Supersynchronous Component
2.2. Modal Parameter Extraction Problem
3. Parameter Identification of SSO Based on Improved ERA
3.1. The Process of ERA
3.2. Defects of Existing ERA
3.3. The Idea of Improved ERA
3.3.1. Construction of Real Number Field Hankel Matrix
3.3.2. Solution of Modal Parameters
4. Verification
4.1. Verification I: Synthetic PMU Data
4.1.1. Relative Errors under Ideal Conditions
4.1.2. Relative Errors under Noise Conditions
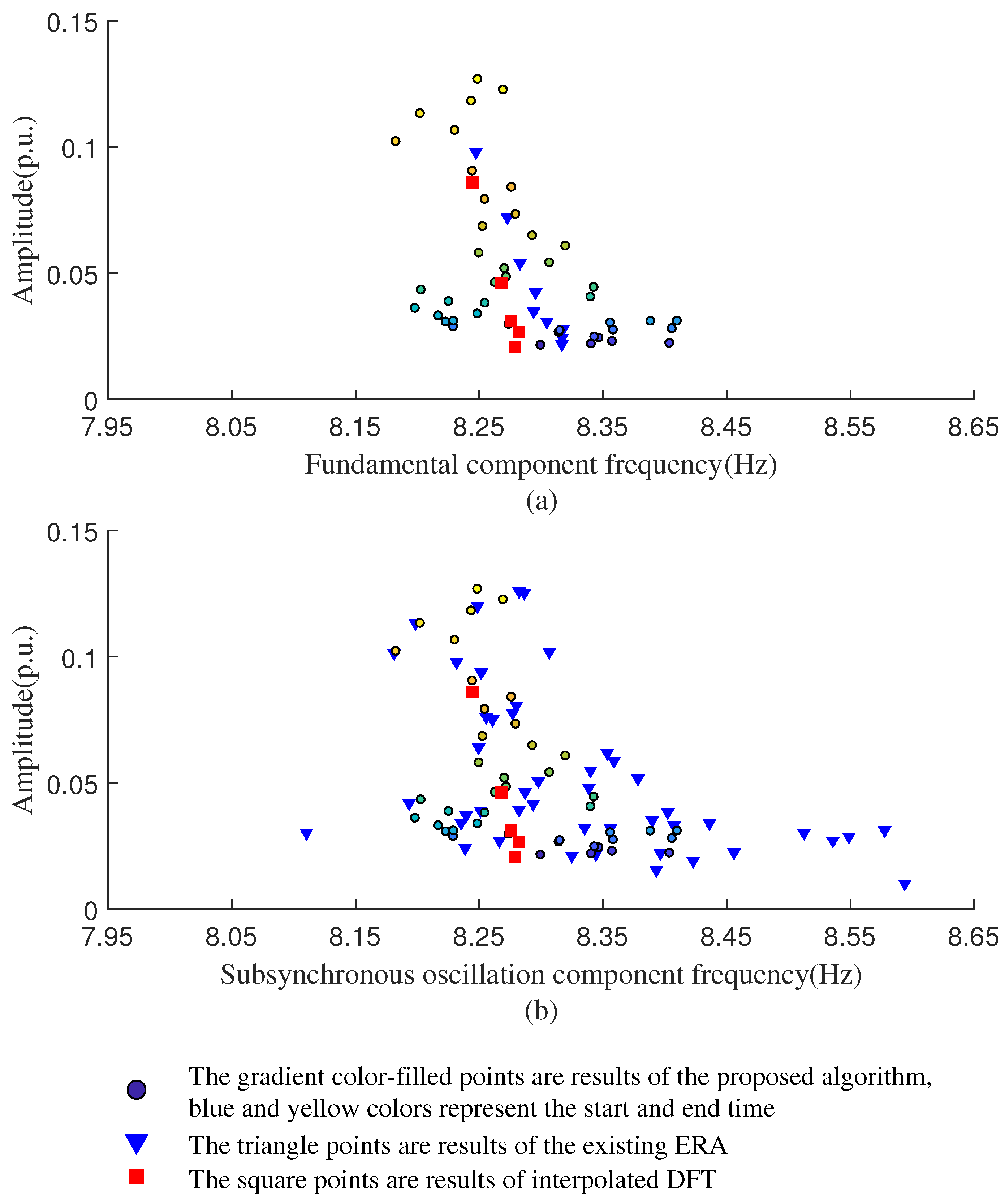
4.2. Verification II: Simulated PMU Data and Actual Measured PMU Data
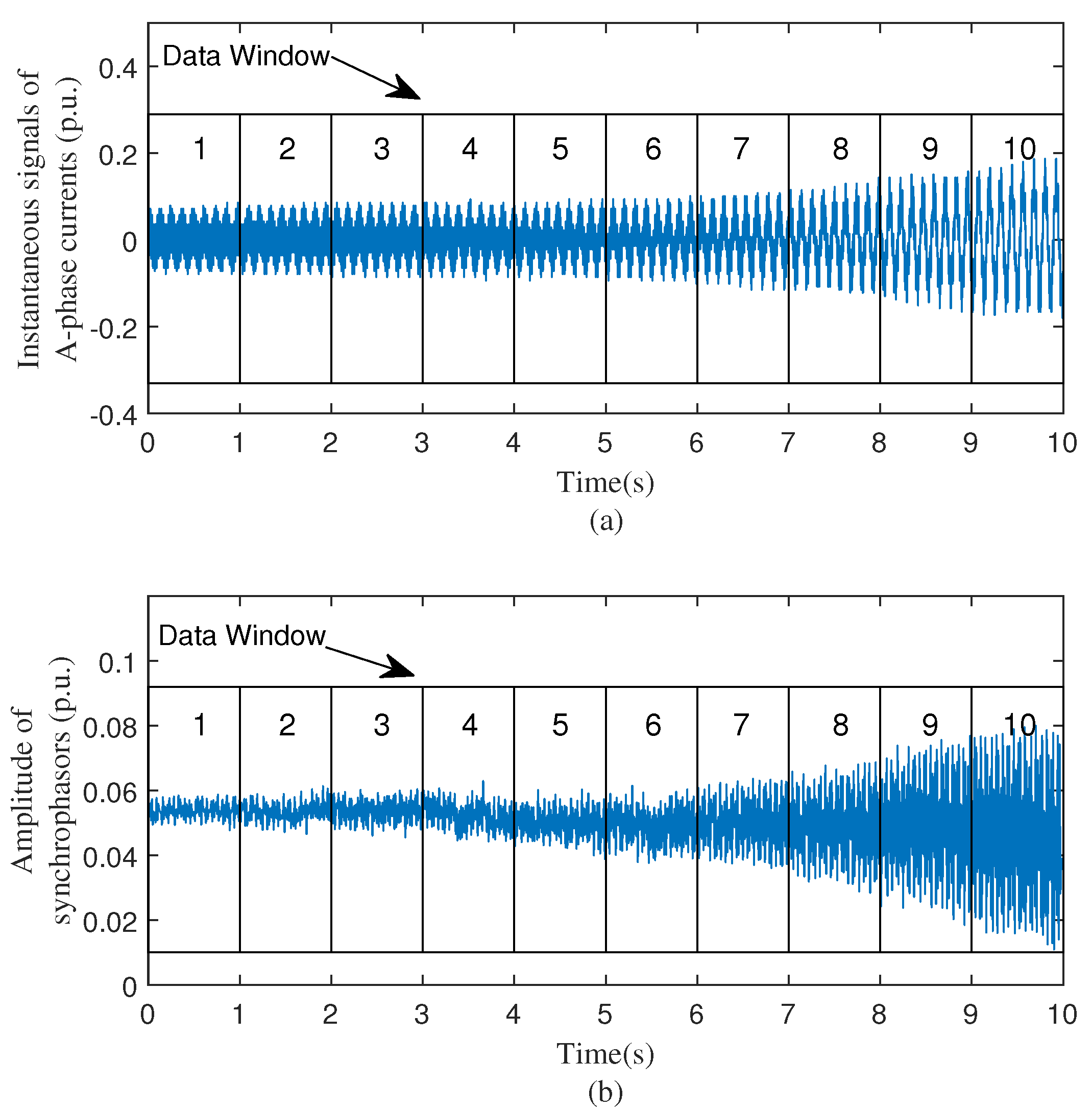
4.2.1. Data Window of Existing ERA: 1 s
4.2.2. Data Window of Existing ERA: 200 ms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Bi, T.; Kong, Y.; Xiao, S.; Zhang, P.; Zhang, T.; Liu, Q. Review of sub-sychronous oscillation with large-scale wind power transmission. J. Electr. Power Sci. Technol. 2012, 27, 10–15. [Google Scholar]
- Wang, B.; Lu, J.; Gong, J.; Hu, M. A method to suppress sub-synchronous oscillation of wind farm composed of doubly fed induction generators with additional rotor side control. Power Syst. Technol. 2013, 37, 2580–2584. [Google Scholar] [CrossRef]
- Li, R.; Lu, Y.; Liu, H.; Han, B. Mechanism analysis on subsynchronous oscillation caused by grid-integration of doubly fed wind power generation system via series compensation. Power Syst. Technol. 2013, 37, 3073–3079. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in Practical DFIG-Based Wind Farms Connected to a Series-Compensated Power System. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- Chen, L.; Wu, S.; Yu, W.; Liu, Z.; Han, Z. A sub/supersynchronous oscillation suppression method for a DFIG-connected grid based on additional damping control on the rotor side converter. Power Syst. Prot. Control 2021, 49, 558–569. [Google Scholar] [CrossRef]
- Khalilinia, H.; Venkatasubramanian, V. Subsynchronous Resonance Monitoring Using Ambient High Speed Sensor Data. IEEE Trans. Power Syst. 2016, 31, 1073–1083. [Google Scholar] [CrossRef]
- Netto, M.; Mili, L. A Robust Prony Method for Power System Electromechanical Modes Identification. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Khazaei, J.; Fan, L.; Jiang, W.; Manjure, D. Distributed Prony analysis for real-world PMU data. Electr. Power Syst. Res. 2016, 133, 113–120. [Google Scholar] [CrossRef]
- Trudnowski, D.; Johnson, J.; Hauer, J. Making Prony analysis more accurate using multiple signals. IEEE Trans. Power Syst. 1999, 14, 226–231. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, L.; Gao, W.; Huang, R. Synchrophasors-Based Identification for Subsynchronous Oscillations in Power Systems. IEEE Trans. Smart Grid 2019, 10, 2224–2233. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Xie, X.; Xiao, X.; Gao, B.; Wang, Y. Interpolated DFT-Based Identification of Sub-Synchronous Oscillation Parameters Using Synchrophasor Data. IEEE Trans. Smart Grid 2020, 11, 2662–2675. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Liu, J.; Gao, W.; He, J. An Improved Interpolated DFT-Based Parameter Identification for Sub-/Super-Synchronous Oscillations With Synchrophasors. IEEE Trans. Power Syst. 2023, 38, 1714–1727. [Google Scholar] [CrossRef]
- Ma, Y.; Cai, D.; Huang, Q. Parameter identification of wind power sub-synchronous oscillation based on Rife-Vincent window and synchrophasor data. Proc. CSEE 2021, 41, 790–802. [Google Scholar] [CrossRef]
- Almunif, A.; Fan, L.; Miao, Z. A tutorial on data-driven eigenvalue identification: Prony analysis, matrix pencil, and eigensystem realization algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12283. [Google Scholar] [CrossRef]
- Crow, M.; Singh, A. The matrix pencil for power system modal extraction. IEEE Trans. Power Syst. 2005, 20, 501–502. [Google Scholar] [CrossRef]
- Hua, Y.; Sarkar, T. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 814–824. [Google Scholar] [CrossRef]
- Sarkar, T.; Pereira, O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials. IEEE Antennas Propag. Mag. 1995, 37, 48–55. [Google Scholar] [CrossRef]
- Juang, J.N.; Pappa, R.S. An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, X.; Xie, X.; Yang, X.; Xiao, X. Identifying Sources of Subsynchronous Resonance Using Wide-Area Phasor Measurements. IEEE Trans. Power Deliv. 2021, 36, 3242–3254. [Google Scholar] [CrossRef]
| Test Set | SNR | Method | |||||||
|---|---|---|---|---|---|---|---|---|---|
| [5, 45] Hz | ∞ | IERA (200 ms) | |||||||
| ERA (200 ms) | |||||||||
| ERA (1 s) | |||||||||
| 40 | IERA (200 ms) | 0.1889 | 0.7619 | 0.0616 | 2.9154 | 2.0477 | 2.1275 | 3.4843 | |
| ERA (200 ms) | 0.6479 | 5.5824 | 0.0961 | 8.0155 | 3.327 | 7.724 | 5.736 | ||
| ERA (1 s) | 0.1322 | 5.8575 | 0.0056 | 1.3558 | 1.5717 | 2.9957 | 1.8074 | ||
| ∞ | IERA (200 ms) | ||||||||
| ERA (200 ms) | |||||||||
| ERA (1 s) | |||||||||
| 40 | IERA (200 ms) | 0.0114 | 0.0561 | 0.0229 | 0.318 | 0.8275 | 0.263 | 0.4533 | |
| ERA (200 ms) | 0.7484 | 5.3621 | 0.0323 | 12.3264 | 8.8875 | 6.9098 | 6.2734 | ||
| ERA (1 s) |
| Test Method | SNR | IERA 200 ms | ERA 200 ms | ERA 1 s |
|---|---|---|---|---|
| [5, 45] | ∞ | |||
| 40 | ||||
| ∞ | ||||
| 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X.; Chen, G.; Liu, Y.; Zhang, F.; Shi, H. Parameter Identification of Power Grid Subsynchronous Oscillations Based on Eigensystem Realization Algorithm. Energies 2024, 17, 2575. https://doi.org/10.3390/en17112575
Zeng X, Chen G, Liu Y, Zhang F, Shi H. Parameter Identification of Power Grid Subsynchronous Oscillations Based on Eigensystem Realization Algorithm. Energies. 2024; 17(11):2575. https://doi.org/10.3390/en17112575
Chicago/Turabian StyleZeng, Xueyang, Gang Chen, Yilin Liu, Fang Zhang, and Huabo Shi. 2024. "Parameter Identification of Power Grid Subsynchronous Oscillations Based on Eigensystem Realization Algorithm" Energies 17, no. 11: 2575. https://doi.org/10.3390/en17112575
APA StyleZeng, X., Chen, G., Liu, Y., Zhang, F., & Shi, H. (2024). Parameter Identification of Power Grid Subsynchronous Oscillations Based on Eigensystem Realization Algorithm. Energies, 17(11), 2575. https://doi.org/10.3390/en17112575






