A Review of Machine Learning Methods in Turbine Cooling Optimization

Abstract

In the current design work, turbine performance requirements are getting higher and higher, and turbine blade design needs multiple rounds of iterative optimization. Three-dimensional turbine optimization involves multiple parameters, and 3D simulation takes a long time. Machine learning methods can make full use of historically accumulated data to train high-precision data models, which can greatly reduce turbine blade performance evaluation time and improve optimization efficiency. Based on the data model, the advanced intelligent combinatorial optimization technology can effectively reduce the number of iterations, find the better model faster, and improve the optimization calculation efficiency. Based on the different cooling parts of turbine blades and machine learning, this research explores the potential of implementing different machine learning algorithms in the field of turbine cooling design.

1. Introduction

Thermal efficiency is one of the key indicators for assessing gas turbine performance. By raising the turbine rotor inlet temperature, it is possible to make a gas turbine’s thermal efficiency and power increase. However, advanced turbine engine inlet temperatures have reached 2000 K, which is considerably larger than the blade material fusion point; consequently, the turbomachinery needs to be cooled. In order to improve the cooling performance of turbine blades, several studies have been conducted, as shown in Figure 1. Xu et al. [1] provided a comprehensive review of the various cooling technologies, including gas film cooling, jet impingement cooling, and rib disturbance cooling. Kong et al. [2] divided the turbine blade into leading edge, mid-chord, and trailing edge regions from the perspective of controlling the cold air flow and focused on reviewing the research progress of the cooling structure of air-cooled turbine blade, as well as the aerodynamic heat transfer characteristics under the rotating state of the turbine, including the vortex impingement cooling, the shape of the film opening, the enhanced heat transfer structure inside the trailing edge with the shape of the separating ribs, and so on.

According to the above literature on turbine cooling, it is obvious that the parameters influencing the cooling of turbine blades are numerous and nonlinear. However, the current study primarily focuses on the utilization of fitting correlation formulas to express the relationship between the working conditions and the cooling efficiency. Nevertheless, the optimization approach based on semi-empirical formulas is inadequate for expressing the nonlinear mapping relationship between variables and cooling efficiency, and its generalizability cannot be guaranteed. For the past few years, machine learning (ML) technology has provided a suitable solution to this kind of nonlinear problem. ML, as a branch of artificial intelligence, improves the model fit by learning the nonlinear mapping relationship between variables and cooling efficiency without explicit programming. ML is usually divided into three types. Supervised learning involves using labeled datasets to train models to be able to predict or classify new data points. Unsupervised learning does not rely on labeled data but looks for hidden structures in the data. Reinforcement learning, on the other hand, uses reward and punishment mechanisms to train models to make optimal decisions in a given environment. Following years of development, ML has been employed in a number of fields, including speech recognition, image recognition, predictive analytics, and self-driving cars. In comparison to conventional programming algorithms, the efficacy of data science-based ML algorithms in addressing issues in these domains has been widely acknowledged by researchers.

The intricate nature of the flow field and the intricate structure of turbomachinery necessitate a significant investment of time to optimize the cooling of turbine structures. However, the outcomes frequently fail to meet expectations. The combination of experimental data and data simulation, with the superior data processing and analysis capabilities of intelligent algorithms, enables the accurate description of the nonlinear relationship between variables and cooling efficiency. This, in turn, allows for a significant reduction in the computational cycle of turbine cooling design while also improving the computational accuracy. A considerable number of studies have been undertaken in the area of optimizing turbine blade cooling structures with intelligent algorithms. In their review of the application of ML in turbomachinery, Liu et al. [3] discussed the use of intelligent optimization algorithms in turbine blade cooling in the film. Wang [4] reviewed various deep learning algorithms application in turbine cooling. Zhang et al. [5] investigated various traditional methods of optimizing the cooling of turbines inside and outside.

Intelligent optimization methods, which have been developed for years, are now widely used in turbine performance optimization and design. Much effort has been put into improving the internal and external cooling structures of turbine blades in recent years, leading to improvements in heat transfer efficiency and a reduction in aerodynamic losses. Therefore, in order to have a clear understanding of this field and to look forward to the future development direction, this paper provides a review of the intelligent algorithms in turbine cooling optimization, and the main research areas include the optimization of internal cooling, external cooling, and composite cooling structures.

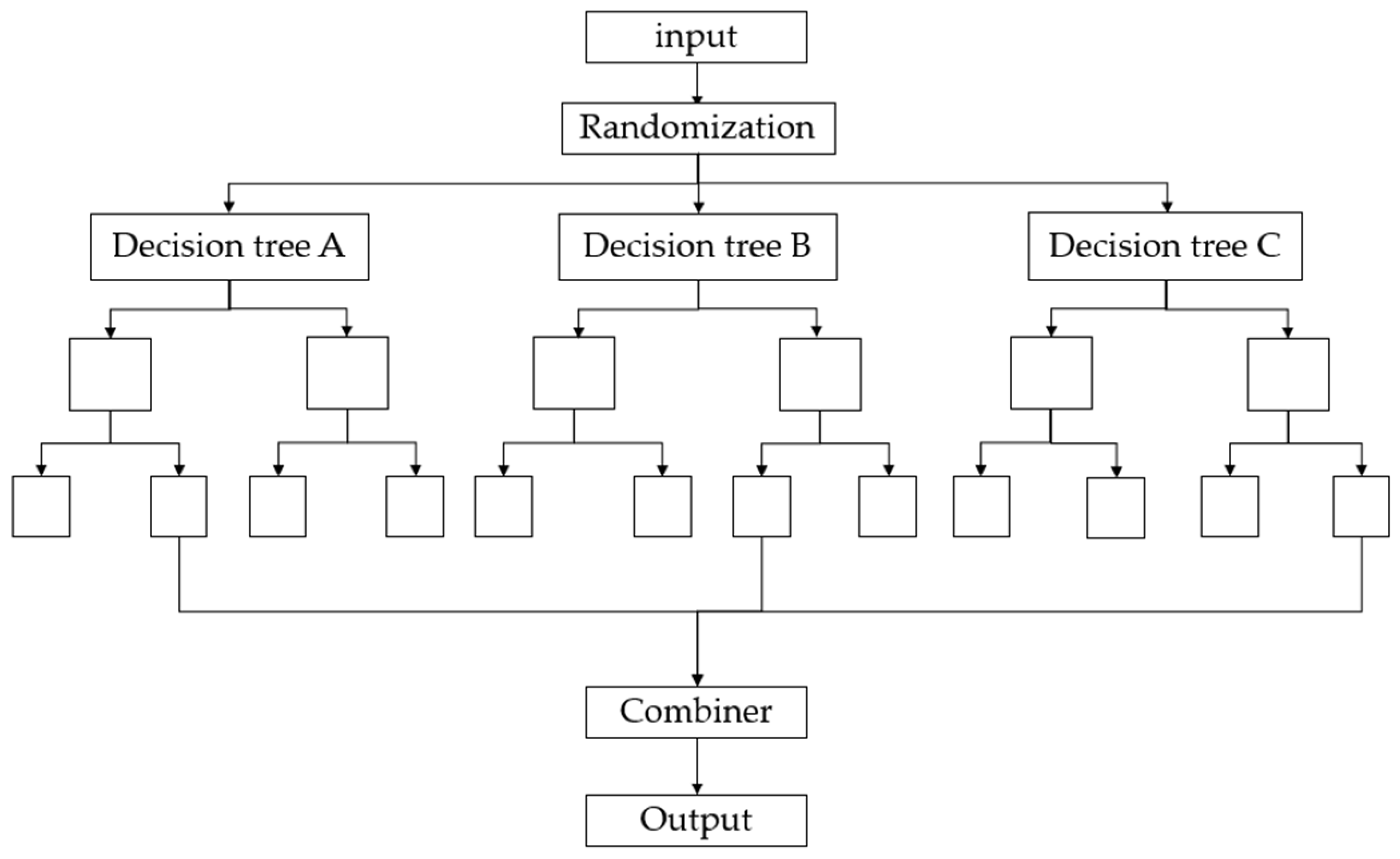
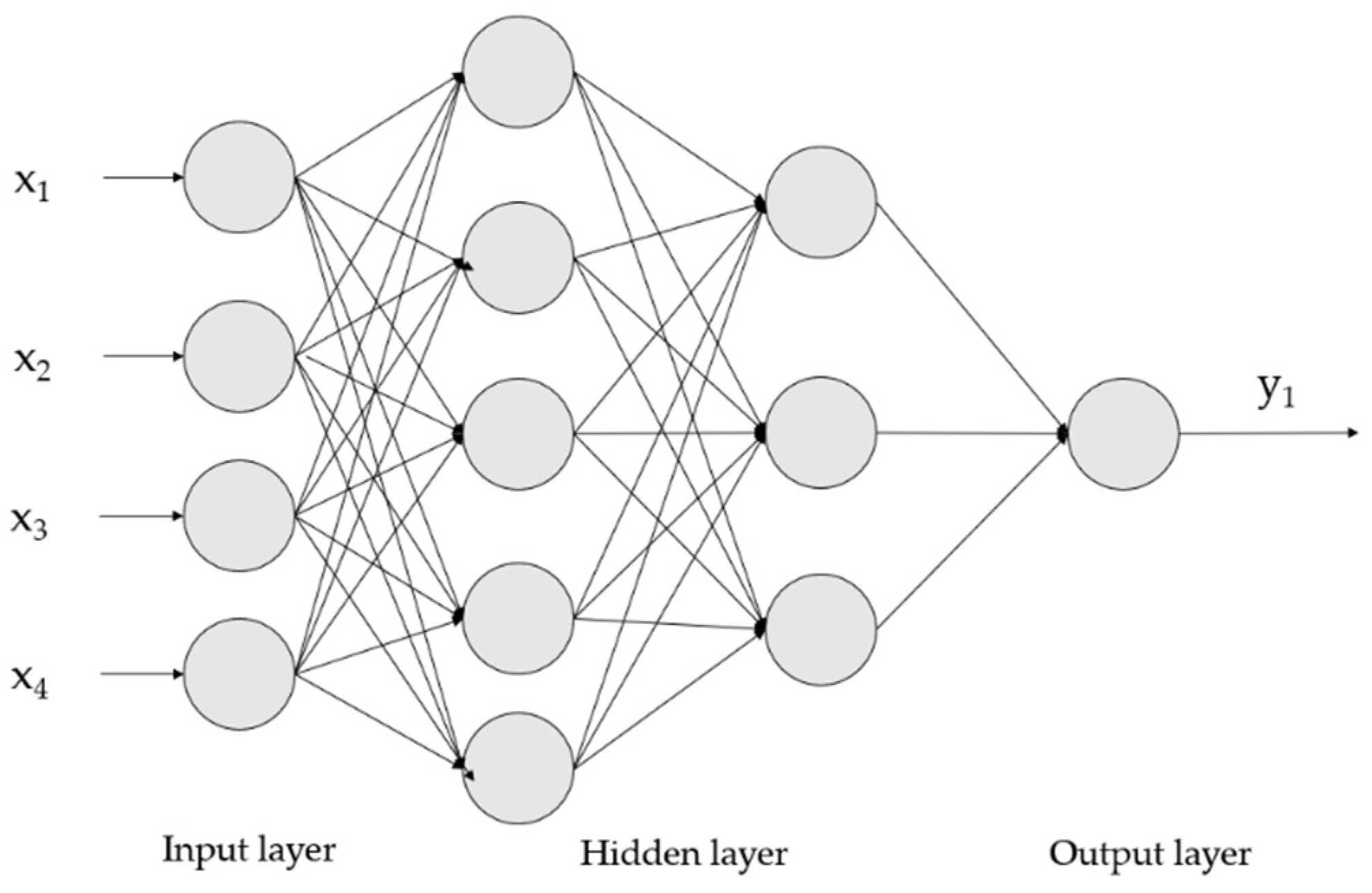
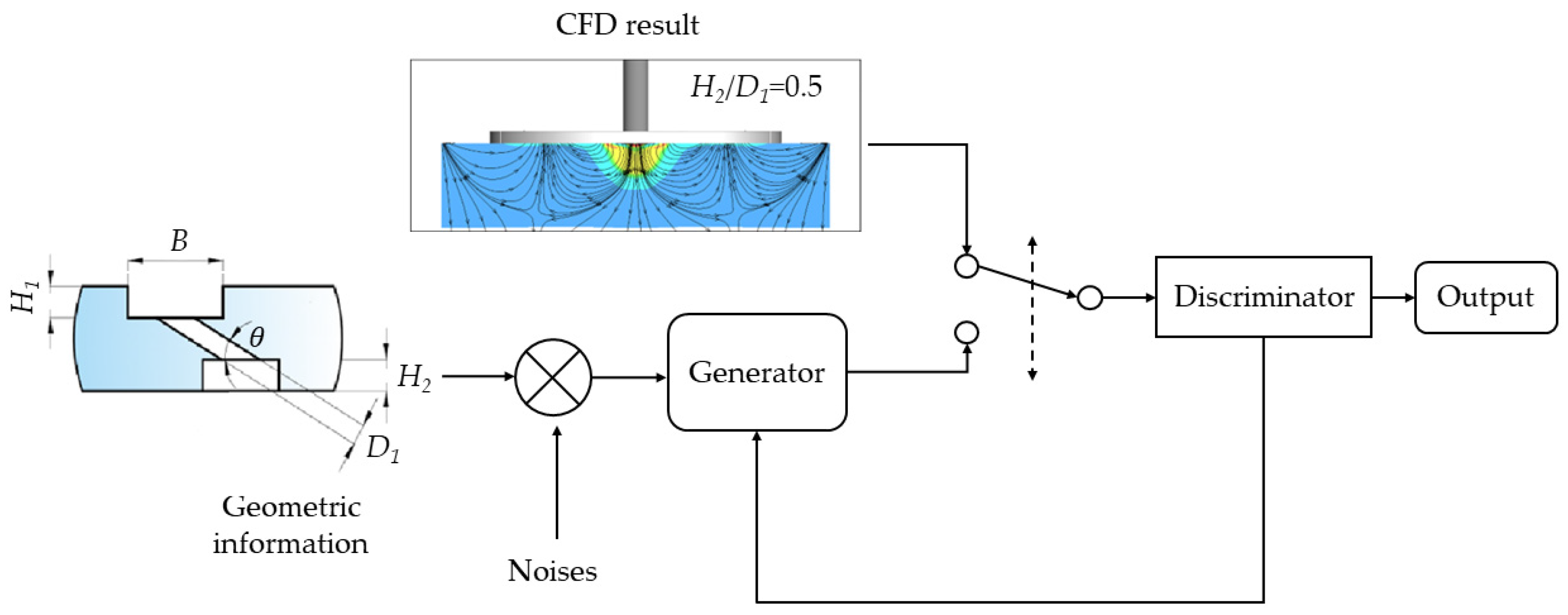
2. Machine Learning Algorithms

2.1. A Review of Machine Learning Algorithms

In the early 1950s, artificial intelligence algorithms commenced to flourish, and researchers postulated that by endowing machines with logical reasoning capabilities, they might attain intelligence. Representative accomplishments at this juncture encompass the Logic Theorist program and the General Problem-Solving program. Nonetheless, as research evolved, artificial intelligence could not be achieved solely through logical reasoning. Subsequently, numerous expert systems were crafted by transferring knowledge to machines. However, due to the intricacy of expert systems, their application spectrum is restricted. Following decades of advancement, artificial intelligence has transitioned into the era of learning machines, and a multitude of connectionisms based on neural networks and inductive learning systems grounded in logic have been developed [6]. Machine learning has now matured into a substantial subject domain, and in diverse application scenarios, the applicable conditions of various ml algorithms are also disparate.

The support vector machine, an implementation of machine learning based on Statistical Learning Theory’s Vapnik–Chervonenkis Dimension methodology and the structural risk minimization tenet, is particularly adept at handling small sample sizes, high-dimensional datasets, and nonlinear phenomena. Hence, its application spectrum spans across areas like pattern recognition, regression modeling, etc. This algorithm is formulated as a constrained quadratic programming issue. Small-scale QP instances can be managed using traditional optimization strategies. Nevertheless, the growth of the training corpus negatively impacts this approach, manifesting in slow training velocity, intricate algorithm structure, and diminished efficiency. The prevailing training strategy currently involves segmenting the original large-scale QP problem into a sequence of smaller QP subproblems, subsequently resolving these subproblems iteratively, thereby approximating the solution of the original QP problem [7]. The quest to enhance efficiency and render SVM more adaptable to large-scale problems remains a focal point of ongoing research.

The decision tree algorithm is a model that elucidates decision rules and classification outcomes in a hierarchical data structure. As an inductive learning algorithm, it transposes unordered datasets into tree-like structures that can predicatively represent unknown data. Where each interior node signifies a test on a feature attribute, each branch signifies the outcome of the test, and each terminal node signifies a decision outcome or category [8]. The merit of the decision tree algorithm is the interpretability of its model, and users can distinctly visualize the decision path from the root node to the terminal node. Moreover, the decision tree algorithm has relatively minimal requirements for data preparation, can manage numerical and categorical data, and possesses a certain tolerance for missing values. However, when decision trees become intricate, the algorithm is susceptible to overfitting. The most renowned representatives of decision tree algorithms are ID3 [9], C4.5 [10], etc. With the demand for large-scale data, a series of algorithms, such as the SLIQ algorithm, SPRINT algorithm, and PUBLIC algorithm, have surfaced.

Random forest (RF) is a technique derived from statistical learning theory. Employing a novel technique termed “bootsrap resampling” to extract diverse samples from the original dataset, a decision tree model is constructed for each sample, thus enhancing the prediction precision and robustness of the model. Its structure is illustrated in Figure 2. The core innovation of the RF algorithm resides in its randomized nature; when training each tree, a random subset of features and samples are selected, thereby mitigating the variance of the model and circumventing overfitting [11]. Presently, random forest is one of the most dynamic research areas in data mining and bioinformatics.

Bayesian algorithm, a probabilistic inference technique grounded on Bayes’ theorem in statistics, is extensively utilized within the domain of machine learning. To circumvent the issues of sample coefficients and combinatorial explosion in the resolution of Bayes’ theorem, the Naive Bayes algorithm introduces attribute conditional independence assumptions, thereby rendering it highly efficacious under numerous conditions [12]. Utilizing generative parameter learning and discriminative parameter learning, Bayes model parameters can be acquired. A prevalent method in generative parameter learning is the frequency evaluation algorithm, which necessitates traversing the training data solely once to acquire the conditional probability table, subsequently enabling the prediction of outcomes. Although this methodology is efficient, the classification accuracy is modest. The discriminative parameter learning method necessitates repetitive iterations; thus, the computational complexity is elevated, but the classification accuracy attained is also substantial.

The essential aspect of accomplishing the cooling design optimization of turbine blades is to construct a model with rapid calculation capability and suitable computational precision, and an efficient method to balance precision and speed is to establish a surrogate model. Traditional surrogate models encompass the Kriging model, response surface analysis model, etc. However, these models can only make differences in the design space in lower dimensions and possess certain constraints on accuracy.

An artificial neural network (ANN) is an algorithm designed for parallel information processing, constructed by emulating the functional characteristics of biological neural networks [13]. Its architectural layout is illustrated in Figure 3. The ANN algorithm tackles intricate pattern recognition and nonlinear challenges by establishing a multilayer network architecture comprising an input layer, a hidden layer, and an output layer. Each layer comprises numerous neurons, interconnected via weight and infusing nonlinear properties via activation functions. Throughout the training process, the ANN recalibrates the weight utilizing the backpropagation algorithm to minimize the discrepancy between the anticipated output and the actual output. The ANN can construct a high-dimensional nonlinear relationship between variables and optimization objectives, thereby compensating for the limitations of traditional surrogate models in modeling dimensions and precision. Nevertheless, the model exhibits poor interpretability and generalization, concurrently necessitating a substantial number of samples. The sample size of straightforward problems can reach hundreds or even thousands.

During the process of turbine blade design optimization, it is crucial to precisely forecast the physical fields within and on the surface of the blade. However, the prediction of these physical fields is essentially an ultra-high-dimensional nonlinear regression challenge, commonly involving more than 10³ data volumes. Traditional ANNs are not equipped to handle this complexity, so many new learning algorithms have emerged, such as deep learning.

Convolutional neural network (CNN) is the first convolutional network widely used in the field of flow heat transfer in recent years, which can effectively predict two-dimensional and even three-dimensional physical fields. CNN uses convolutional layers to extract local features from input data. These convolutional layers slide small filters (kernels) over the input data, calculating the weighted sum of local regions. This convolution operation effectively captures the spatial hierarchical structure of the data while reducing the number of parameters in the fully connected layer, thereby reducing the risk of overfitting and improving the computational efficiency of the model [14]. Recognizing that the maximum likelihood of 2D/3D physics is challenging to articulate, this complicates the formulation of the loss function of CNN models. The Generative Adversarial Network (GAN) [15] generates approximate datasets through the iterative training of two distinct neural networks, namely the generator and discriminator. The objective of the generator is to generate an approximation data instance, and the classifier is utilized to distinguish between the approximation data set and the authentic data set. The two networks are persistently adversarial during the training phase, thereby promoting the enhancement of the data quality generated by the generator. In practical applications, numerous problems in turbine cooling are problems of physical field generation under specified conditions, such as film pore cooling efficiency, blowing ratio, etc. For such generation problems with physical implications, the Conditional Generative Adversarial Network (CGAN) is frequently employed for model construction, and its structural diagram is illustrated in Figure 4. Although convolutional networks exhibit remarkable advantages in acquiring high-dimensional information distribution, lack of versatility is an inevitable drawback at present. After training a specific structure with convolutional networks, it cannot be applied to other analogous problems with regional alterations.

During the optimization process of turbine cooling, flow and heat transfer problems with clear relationships between upstream and downstream are often encountered. When considering the combined effects on blade cooling, the recurrent neural network (RNN) algorithm is commonly used. The core advantage of RNN lies in its recurrent structure, which allows information to be passed between time steps in the network, thus enabling the memory and utilization of previous elements in a sequence. However, traditional RNNs are susceptible to the vanishing or exploding gradient problem, limiting their ability to learn long sequence dependencies. To address this issue, researchers have proposed structures such as Long Short-Term Memory (LSTM) [16] and Gated Recurrent Unit (GRU). Currently, RNNs are only applicable for one-dimensional sequence modeling and have not been extended to high-dimensional distribution modeling. Additionally, the spatial discrete dimensions should not be too small.

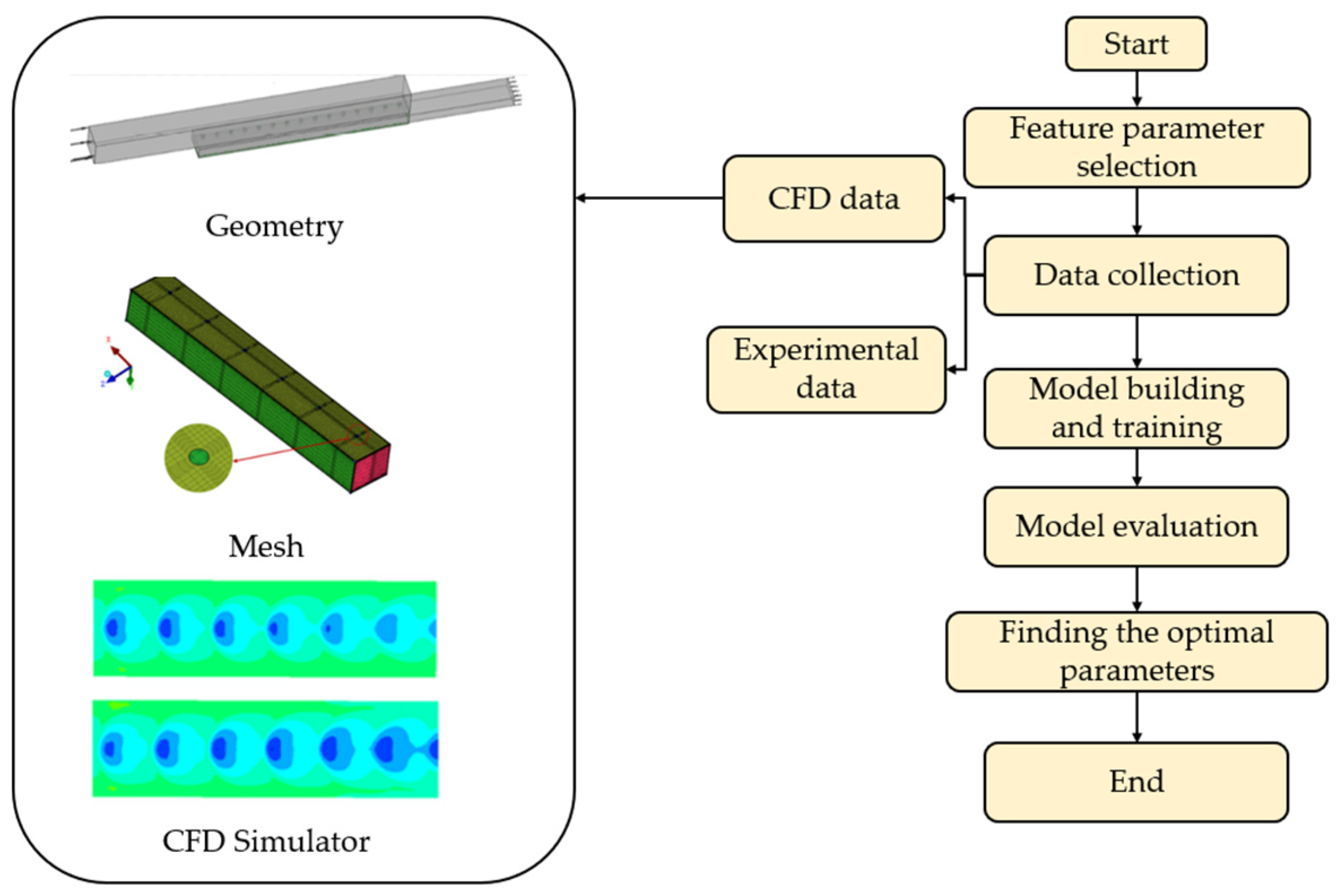
2.2. Optimized Model Building Process Based on ML

The basic construction process of machine learning models in the optimization of turbine blade cooling is shown in Figure 5. The construction of the model first requires the selection of feature parameters. By eliminating irrelevant or redundant features and reducing the number of features, the aim is to improve model accuracy and reduce running time. Based on this, data collection for training models is carried out, usually using a combination of computational fluid dynamics (CFD) and experimental data collection methods. However, the data used for training and prediction are generated through experiments or numerical simulations. In order to minimize computational costs and avoid insufficient ML training, it is necessary to determine an appropriate range for the dataset. Once collected, the data are formatted into a feature matrix as input for ML algorithms. Using suitable intelligent algorithms, the model is trained with training set data by adjusting parameters to improve predictive accuracy. Finally, test set data are used to evaluate the ML model while utilizing optimization algorithms to optimize feature parameters.

The determination of cooling characteristic parameters for blades is currently primarily grounded on design expertise [17]. Nonetheless, when dealing with composite cooling or structural optimization, there exists a myriad of influential parameters for blade cooling performance. Therefore, the utilization of parameter sensitivity analysis can be beneficial in discerning the most pivotal parameters for model prediction and streamlining the model by eliminating redundant input parameters. Moreover, sensitivity analysis can elucidate how output parameters are influenced by multiple input variables. The prevalent sensitivity analysis algorithms utilized in blade cooling optimization encompass the Sobol sequence method and the Monte Carlo algorithm. For optimization algorithm selection, SQP and GA are frequently employed for single-objective optimization, whereas NSGA-II is utilized for multi-objective optimization. The optimal design structure attained through the optimization algorithm can be validated through CFD computation to ensure the precision of the predicted outcomes.

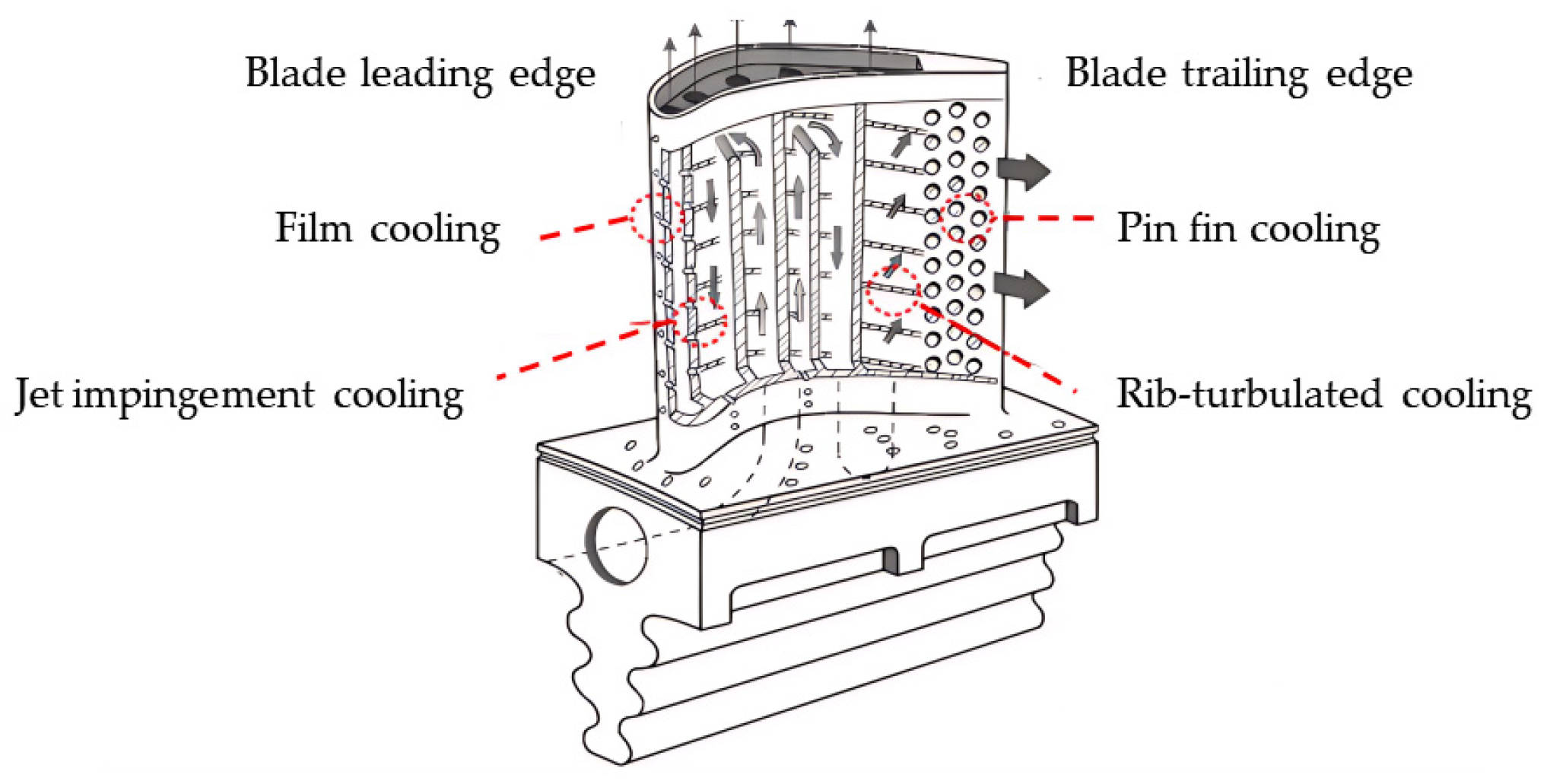
3. Machine Learning in Internal Cooling

The primary purpose of internal cooling is to facilitate the transfer of heat from the cooling air to the inner wall of the internal channel of the blade. Considering that the principle of each cooling method inside the turbine blade is not the same, as well as the position on the blade is not the same, the internal cooling technology of the turbine blade can be divided into three principal categories: jet impingement, rib-turbulated cooling, and pin fin cooling.

3.1. Pin Fin Cooling Optimization

The application of pin fin cooling facilitates the transmit of heat within the channel by utilizing spoiler columns positioned within the walls on either side of the channel. The positioning of the pin fins at the trailing edge of the blades allows for an increase in the turbulence of the cooling airflow, as well as the dissipation of heat from the blade surface by the pin fins. The airflow passing through the pin fins creates a wake that increases the flow disturbance and destroys the wall boundary layer, thus improving the heat transfer efficiency. Meanwhile, the pin fin acts as a heat conductor, and the heat on the blade wall surface is transferred to the pin fins, and then the heat is removed by the cooling airflow. The pin fin cooling principle is shown in Figure 6.

Preliminary work on pin fin cooling in turbine blades commenced in the early 1980s and was predominantly concerned with pin fin arrangement. Metzger [18,19] achieved elevated heat transfer coefficients in staggered rows, providing a power correlation between the average Nusselt number and Reynolds number in this configuration. Subsequently, the performance of various short pin fin arrays in terms of pressure loss and heat transfer was examined. VanFossen [20,21] explored the application of short pin fins at the blade’s trailing edge, investigating the effect of array position on the heat transfer of a single short cylinder. Results indicated that upstream cylinders significantly influenced heat transfer, whereas downstream cylinders had no effect. To gain insight into single-pin fin flow characteristics, Chyu et al. [22,23] utilized a near-surface flow visualization technique to examine the flow near the column and its fixed surface boundary layer. They confirmed that the cubic column array and diamond column array exhibited superior heat transfer effects compared to the circular column array. However, altering the column shape did not alter the overall trend of heat transfer enhancement. Despite the highest mass transfer coefficient of the cubic column, its pressure loss coefficient was also high. Most pin fin shapes struggle to balance heat transfer and pressure loss. Following a stalemate in pin fin shape research, researchers began considering the impact of circular spoiler column geometric parameters on heat transfer. Dogruoz et al. [24] and Chyu et al. [25] arrived at similar conclusions: under constant pin fin diameter, the higher the pin fin within a specific range, the better the local heat transfer effect, but excessive height–diameter ratio resulted in increased pressure loss. Exploring the influence of the pin fin height–diameter ratio on internal flow and heat transfer remains a significant area of interest. Given the advancement of optimization technology and data accumulation, the utilization of data-driven intelligent optimization algorithms for studying pin fins in turbine blades is becoming increasingly prevalent.

To optimize the shape of the pin fins, it is necessary to make a more accurate prediction of the heat transfer coefficients. Kwon et al. [26] conducted ML for channels with different numbers and shapes of pin fins. Using six feature parameters as inputs and 243 sets of data to train the model, a random forest model was constructed with the objective of accurately predicting the local convective heat transfer coefficients in the cooling channel. While a substantial quantity of precise data can ensure the precision of the prediction, the computational resources and time required must be considered. Proxy models are simplified models that are employed to approximate complex systems with the objective of reducing the consumption of computational resources while maintaining an appropriate level of accuracy. These models can rapidly provide approximate results for costly or time-consuming tasks through simplified, data-driven methods, optimization and fitting techniques, and accurate error assessment.

The agent model has the potential to reduce the consumption of computational resources to a certain extent. Consequently, a variety of agent-based models have been employed in the context of turbine blade cooling. For instance, Johnson [27] used a radial basis function neural network (RBF-NN) as an agent model for film cooling. Similarly, Ghosh et al. [28] utilized a combination of a Gaussian process (GP) agent model and a Bayesian-constrained optimization (BO) approach to optimize the geometry of the pin fins. This evidence demonstrates the viability of the agent model in pin fin cooling optimization. The current research on the optimization of the cooling structure of the pin fin is focused on the bumps/pits and the pin fin parameters.

For the aspect of pin shape, Ghosh et al. [29] used the BO method with an agent model to optimize the shape of pin arrays in the trailing edge region of a gas turbine blade with a view to improving the heat transfer efficiency of the pin arrays in the region where the flow develops and reducing the pressure loss. The shape of the pin fins was predicted and optimized by varying the geometrical parameters of the rib columns using CFD simulation and GP regression model. The results indicate that the optimized circular pin fin increases the cooling efficiency by a factor of 1.4 and saves 52% of the computation time compared to a square cross-section. Gaussian stochastic processes (GPs) are linear combinations of arbitrary random variables assumed to have multivariate joint Gaussian probability distributions with the ability to quantify the uncertainty in the prediction. Meanwhile, the team [30] came up with a multi-fidelity Bayesian optimization method to reduce the computational time. The method can significantly reduce the number of high-fidelity simulations that are required and lower the cost of computation.

When optimizing the shape and size of the fins, it is also vital to evaluate the influence of different fin arrangements on cooling performance. A reasonable arrangement of the pin fins can improve the cooling performance on the one hand and the blade strength on the other hand. Liao et al. [31] adopted genetic algorithms to optimize the spacing of the pin fins for square, circular, and teardrop-shaped column fins inline or staggered arrangement to obtain optimal heat transfer efficiency. It was shown that in the inline or staggered rows, the improvement effect of the square fins on the heat transfer performance of the duct was the most obvious, and the improvement effect of the circular fins was the smallest.

The installation of bumps or pits in the cooling channels can increase the secondary flow intensity and thus enhance internal heat transfer. Kim [32] optimized the fork-row elliptical pit cooling channels based on CFD calculations. The ratio of elliptical pit diameters, the ratio of pit depths to mean diameters, and the ratio of flow line spacing between pits to span spacing were taken as input, and the heat transfer efficiency and reduced pressure drop were taken as output. The optimization results show that the optimized structure balances pressure drop and cooling performance.

Topology optimization is a type of structural optimization that involves the free distribution of material in the optimized region for a given load case, constraints, and performance metrics. Yeranee et al. [33] employed a density-based topology optimization method to optimize the cooling channels of the pin fins, strengthening the cooling performance of the pin fin structure. The study employs a minimization of pressure drop loss as the optimization objective while also considering the effect of turbulent flow. Furthermore, the cooling performance of the topology-optimized structure can be raised by integrating ML algorithms with topology optimization. Hu et al. [34] put forward a generative design method based on self-organizing equations. The topology parameters were optimized using a multi-objective Bayesian approach under five performance metrics. The optimization results display that the total Nussle number of the self-organized structure is increased by 43%, and the local Nussle number variance is significantly reduced by 37% compared to the original structure under the same pressure drop conditions.

When a turbine rotor blade operates under rotating conditions, centrifugal force, Coriolis force, and rotational buoyancy exist in the rotating non-isothermal field. The action of these forces results in a significant divergence between the flow and heat transfer characteristics observed in the cooling channel under dynamic conditions and those observed under static conditions. It remains to be seen whether the optimization of pin fin cooling under static lobe conditions using intelligent algorithms exhibits the same superior cooling performance under rotating action. Moon et al. [35] optimized a rectangular channel circular pin fin staggered array under rotating action by using RNS analysis, agent modeling, and multi-objective evolutionary algorithms. In the context of a hydraulic channel diameter with Re = 10,000 and rotations of 0.15, the optimized design of the pin fin array shows an improvement in the pressure drop characteristics with a simultaneous improvement in the heat transfer coefficient.

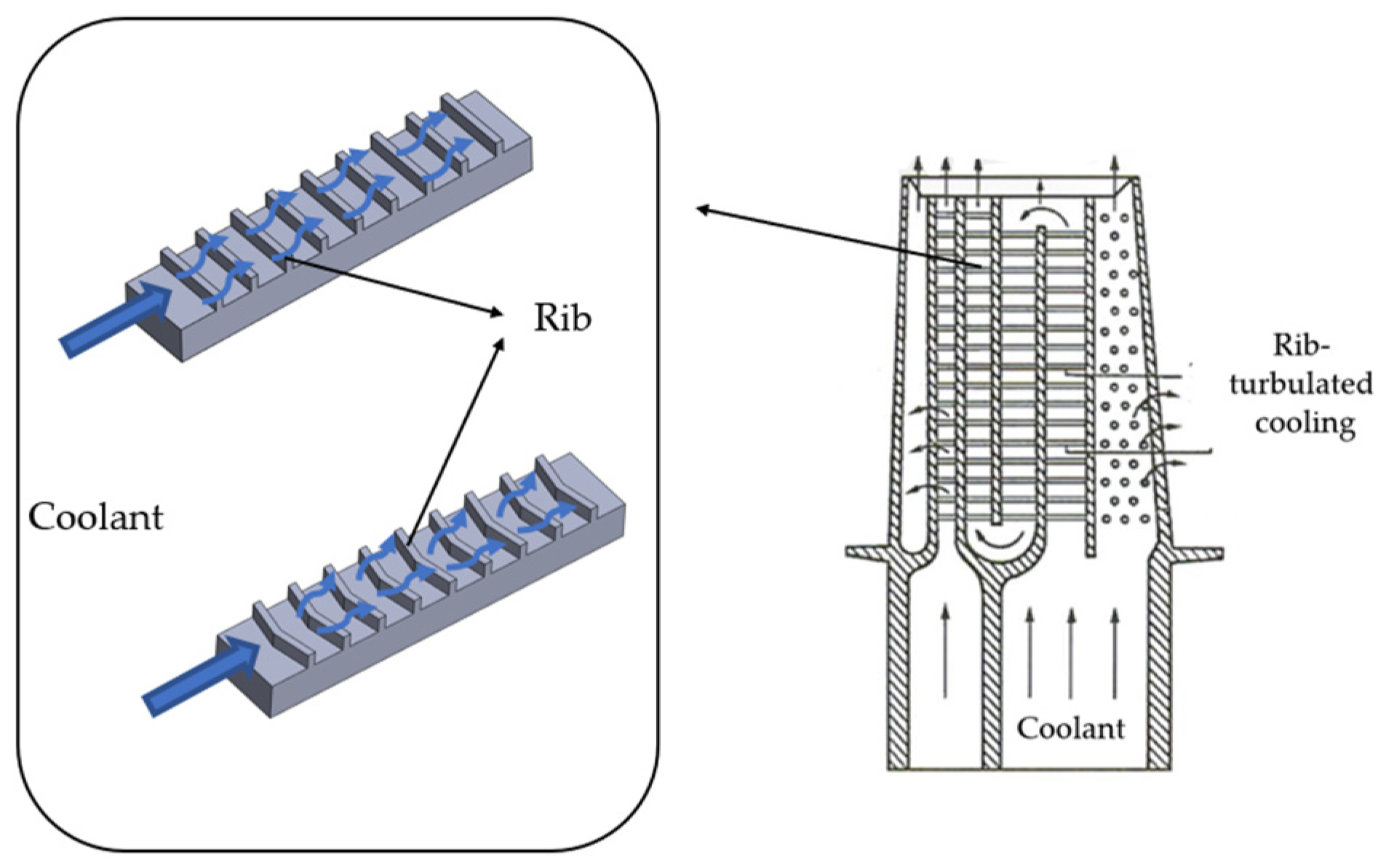
3.2. Rib-Turbulated Cooling Optimization

Establishing a direct channel for cold air circulation within the high-temperature components of a gas turbine was an initial approach for cooling. However, with the advancing sophistication of convective heat transfer theory, researchers incorporated fins within the internal channel to augment heat transfer and maximized the efficient utilization of the internal space of the blade, evolving the ribbed channel cooling technology currently utilized in most blades. On the one hand, this architecture can amplify the channel length of the cold air. In addition, due to the configuration of multiple chambers, the overall temperature level of the blade can be regulated by manipulating the air supply. Concurrently, the augmentation of chambers also amplifies the heat transfer area. The ribbed turbulated cooling is shown in Figure 7. Research on ribbed channels commenced in the 1960s and 1970s. In 1961, Emerson et al. [36] initiated research into the heat transfer efficacy and friction characteristics of the ribbed wall, and the findings indicated that there is a high heat transfer coefficient near the separation point and in the separation area. Since the 1970s, in the cooling design of turbine blades, the methodology of incorporating straight ribs in the internal channel of the blade has been employed to enhance the heat transfer efficiency of the channel wall. Webb and Han et al. [37,38] explored the heat transfer enhancement phenomenon triggered by spoiler ribs in the 1970s utilizing ribbed round tubes and rectangular channels, respectively. When Han et al. examined the heat transfer efficiency of inclined ribs in the channel, they discovered that the heat transfer efficiency of 45° ribs and 90° ribs was comparable, but the pressure drops in the 45° rib channel were significantly lower than that of the 90° rib channel. Han [39] subsequently concluded that in the unrotated ribbed channel, the aspect ratio of the channel space, the Reynolds number of the airflow, and the arrangement of the fins influence the internal heat transfer effect, and initially comprehended the heat transfer enhancement measures for the separation of the airflow induced by the fins. The current focus of research on optimizing ribbed turbulated cooling is on three main areas: size optimization, shape optimization, and topology optimization. These depend on the heat transfer efficiency and pressure drop prediction, which is carried out using ML.

The cooling channels of the turbine blades are designed to increase their thermal efficiency while ensuring blade reliability and durability in high-temperature gas. Higher heat transfer efficiencies mean that heat can be transferred more efficiently from the inside of the blade to the cooling gas stream, thereby protecting the blade from excessive temperatures. However, the increased heat transfer efficiency can increase the pressure loss of the airflow within the duct, resulting in an increased pressure drop. The increase in pressure drop can lead to higher pumping capacity and increase the operating cost of the overall system. The optimized design must therefore strike a balance between improving heat transfer efficiency and controlling pressure drop. Wang [40] researched the matrix cooling structure of a gas turbine blade and explored the effect of geometric scaling on the cooling performance. Through numerical simulations, this study revealed the significant effect of variation of the scaling factor on the heat transfer performance and fluid resistance.

To optimize the size and shape of the fins, bearing in mind that there are many factors that affect the flow and heat transfer performance of the fin channel, it is difficult to integrate the influence of all aspects in a traditional optimization approach. To address this issue, Moon and Kim [41] optimized the geometric parameters of the fan-shaped fins using a multi-objective optimization method combined with a radial basis neural network (RBNN) agent model to improve the heat transfer efficiency and reduce the pressure drop in the duct. Damavandi et al. [42] combined CFD simulation with artificial neural networks (ANNs) and genetic algorithms to optimize an asymmetric V-shaped fin in the combined cooling channel in a multi-objective approach. The method uses two angles (α and β) of the rib root with respect to the transverse axis of the channel and the dimensionless distance from the apex of the asymmetric V-shaped rib to the midline (δ/B) as input variables. Xi et al. [43,44,45,46] optimized the cooling channels of X-type truss array structure by neural network and GA. Through optimization, a significant increase in the average Nussle number and integrated thermal coefficient is achieved, and the optimized cooling channel reduces fluid flow losses while improving heat transfer efficiency.

For channel optimization, Kiyici et al. [47] optimized the turning section of a serpentine cooling channel inside a turbine blade using a mesh deformation tool evolutionary algorithm (EA) optimizer with radial basis function (RBF). At Reynolds number 20,000, the optimized structure shows a 14.4% reduction in pressure drop compared to the original structure. Samad et al. [48,49] adopted a weighted average approximation model for predicting and optimizing cooling channels with pits. The model consists of the response surface model (RSM), KRG model, and RBFNN model. Xi [50] predicted the heat transfer coefficient of the finned channel using a neural network and GA and analyzed and optimized the channel aspect ratio and fin angle. In addition, numerical simulations revealed the mechanism of optimizing the channel to improve the heat transfer efficiency, enhancing the longitudinal secondary flow and suppressing the primary secondary flow. Meanwhile, the team [51] conducted experimental studies on the flow and heat transfer performance of thick-walled rib channels for turbine blades. By using the Sobol method to analyze the global sensitivity of the flow and heat transfer performance of the thick-walled finned channel to the Reynolds number, aspect ratio, and fin angle, a neural network model is obtained. The results indicate that the deviation of the prediction model for the average Nussle number, friction coefficient, and integrated thermal coefficient is within 5% and that the optimum aspect ratios and rib angles are obtained under different Reynolds numbers.

For topology optimization, Kim et al. [52] used topology optimization to minimize the pressure drop in the U-elbow in the internal cooling channel of the turbine. By using topology optimization techniques based on the continuous concomitant method and the most rapid descent method, the U-elbow was optimally modeled in three-dimensional space, and the design space was analyzed using a low-fidelity simulation solver. The optimization results display that the total pressure drop of the optimized structure decreases by 26.8% compared to the initial structure at a Reynolds number of 100,000. Ghosh et al. [53] used topology optimization to optimize the cooling channels inside the gas turbine blade to improve heat transfer efficiency and lower pressure drop. The algorithm optimized the serpentine channel with enhanced heat transfer performance and decreased pressure drop as the objective function. The results show that the optimized serpentine channel improves the heat transfer efficiency by 24% and is able to effectively reduce the separation zone. At present, the topology optimization of fin tube cooling is mainly focused on the internal channel optimization, with less research on the fins in the channel.

Under the effect of rotation, the coolant flowing through the finned cooling channel is subjected to a large Koch force and rotational lift. Under the action of these forces, a secondary flow is induced in the channel, causing an asymmetry in the main flow distribution. The intrinsic rotational force affects the heat transfer by changing the flow field and thus. Moon et al. [54,55] optimized a rectangular ribbed triangular channel under rotation. The rib angle (α), the ratio of rib spacing to hydraulic diameter (P/D_h), and the ratio of rib width to hydraulic diameter (b/D_h) were selected as design variables. Figure 8 is a flowchart of a rectangular ribbed triangle channel optimization. The results show that the target function value of the optimized structure is improved by 21.5%.

3.3. Jet Impingement Optimization

The jet impingement cooling technology was proposed in the 1960s, and the detailed concepts of it were explored by Bradury [56]. In this approach, Sparrow and Wong [57] examined the mass transfer distribution of a single jet impingement. Figure 9 shows the impingement flow distribution of the single-hole jet. The jet stage can be divided into the core area, the development area, and the stable area. When the airflow reaches the target surface, the airflow diffuses around the stagnation point. The heat transfer performance distributes along the radial direction, and the distribution trend is related to the jet distance. Impinging jets are the most useful method for improving the local heat transfer coefficient, but they have a slight adverse impact on the structural strength of turbine blades. It is clear that impingement cooling is the most suitable solution for the front edge of the turbine blade because this part is the place with the thickest blades and the highest heat load. Meanwhile, the strength requirement in the static blade is not as high as that of the rotating blade, so impact jet cooling is also used in the chord area of the static blade. Unlike the single jet hole, the scattering of the jet in the chord region causes the transverse flow. Koopman and Sparrow [58] scrutinized the influence of transverse flow on jet rows. Considering that the shape of the nozzle, the arrangement of the nozzle holes, the shape of the chamber, and the shape of the target surface all affect the distribution of the heat transfer coefficients [59], this part investigates the application of intelligent optimization algorithms in jet impingement cooling.

Considering that the geometrical parameters and permutation of the jet holes affect the average Nussle number of jet impingement, the pumping power of the cooling airflow, and the heat transfer uniformity, Jahromi et al. [60] comprehensively analyzed the effects of the jet hole spacing, the distance of the jet holes to the target surface, and the Reynolds number on the flow field and thermal performance of a single-row jet array. At the same time, a prediction model of Nussle number, cooling airflow pumping power, and temperature uniformity was established using an artificial neural network.

In terms of jet nozzle shape, Chi et al. [61] designed a novel variable-diameter jet hole impact cooling structure for internal cooling of turbine blades. A multi-objective genetic algorithm (GA) was used to optimize the position and diameter of the jet holes to achieve efficient cooling under non-uniform thermal load conditions. The optimization results prove that the new cooling structure offers a more uniform temperature on the blade surface with the same amount of cooling airflow compared to the original design structure. Furthermore, the multi-objective optimization algorithm has been used to obtain a series of optimal cooling structures under different cooling air flow rates, with the wall temperature of the blade surface being very uniform.

For the jet hole arrangement, Chen et al. [62] studied a multi-objective optimization of jet impingement cooling at the front edge of a gas turbine blade. A combination of cyclonic cooling, shock cooling, and double-shock cooling was used, with chamber deformation length, horizontal nozzle position, and tilt/compound angle as design variables. The agent model is trained using data from CFD simulations, and the two designed cooling structures are optimized using genetic algorithms. The optimization results show that the optimized structures result in an enlarged high Nussle number region and a more uniform heat transfer rate distribution. The optimized structure outperforms cyclone cooling in heat transfer efficiency. In the process of structure optimization, the comprehensive effects of jet impact technology and film cooling on the cooling of turbine blade leading edge blades must be considered.

To optimize the target surface shape, micro-textured surfaces for internal jet cooling of gas turbine blades have been optimized. Jacobs et al. [63] designed a micro-textured jet impact target surface (grooves and fins) to improve the internal jet impact cooling efficiency and optimized the target surface structure using a gradient optimization algorithm. The results show that the fin design with enclosing bands performs the best in terms of cooling effect and is able to keep the maximum internal blade temperature below 1219 K. Xu et al. [64] proposed a novel array impact target surface cooling structure. The second-order RSM and the second-generation non-inferiority sequential genetic algorithm (NSGA-II) were used to optimize the multi-objective performance. The optimized structure was subjected to performance tests. The optimal bionic structure is 1.212 mm for slot depth, 1.132 for slot radius ratio, and 12.078 for slot spacing ratio. Currently, the optimization of jet cooling for turbine blades is mainly carried out by the traditional trial-and-error method. There is a clear need for more optimizations of jet holes and target surfaces using topology optimization.

4. Machine Learning in External Cooling

In the 1970s, researchers delved into the mechanism of fluid flow and heat transfer under film cooling. Goldstein [65] pointed out that film cooling involves introducing a secondary airflow (cooling agent or jet) from one or more discrete holes on the surface in a high-temperature environment in order to protect the surface of the injection area and downstream area, as shown in Figure 10. Eckert et al. [66] conducted experimental research on the influence of blowing ratio on film cooling efficiency. They compared their findings with earlier tests, indicating that the effectiveness of film cooling increases as the boundary layer thickness at the injection location decreases. In 1994, Fric and Roshko [67] used flow visualization techniques to reveal the vortex structure in film cooling, pointing out that the presence of kidney-shaped vortices reduces the cooling effectiveness of film cooling. According to Ni et al. [68], the elements that commonly affect the cooling effect of the film may be separated into two groups: the geometric characteristics of the film holes and the aerodynamic parameters of the holes. At present, the blade film cooling study has also begun to use ML.

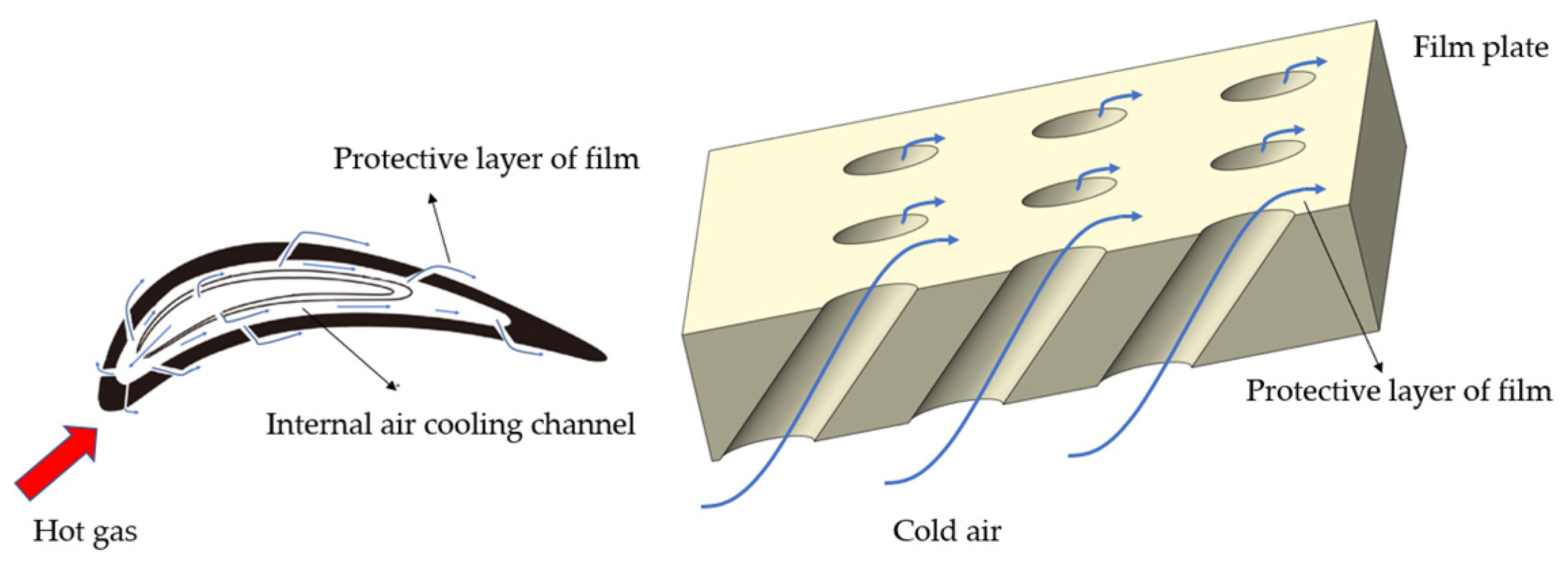
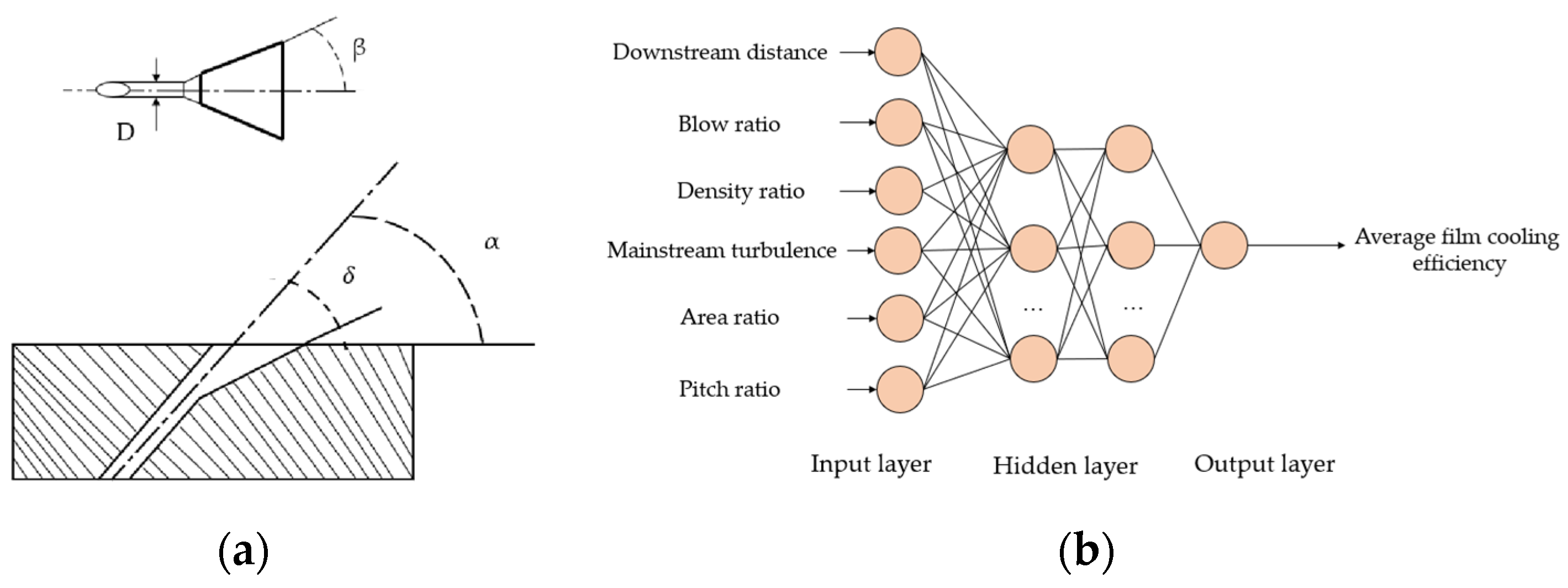
4.1. Film Cooling Performance Prediction

The use of CFD can accurately forecast the film cooling efficiency, but for the simulation and optimization, a long computation cycle cannot be ignored. To overcome the shortcomings of the long cycle time of the traditional CFD optimization structure, semi-empirical formulas for many parameters are used to predict the efficiency [69]. However, it is difficult to maintain the prediction accuracy of the related semi-empirical formulas for the film cooling efficiency. By using ML to construct nonlinear mapping relationships between variables and objective functions, the prediction model’s accuracy can be improved.

Given the significance of blade surface temperature as a reference value for film hole optimization, it is crucial to develop a two-dimensional temperature distribution prediction. Convolutional neural network (CNN) is a type of ANN that employs convolutional computation, which enables it to effectively identify and learn common features across a global scale. Currently, CNNs have been applied in the fields of cooling efficiency distribution, surface temperature distribution, etc. Jin [70] proposed a U-network-based agent model for turbine blade flow field prediction, which can directly predict the static pressurizer temperature distribution on the average cross-section of the blade by taking the three-dimensional blade contour defined by the point cloud as input. Wang [71] used a deconvolution neural network (DNN) and conditional generation adversarial network (CGAN) to forecast the surface temperature of the blade.

In order to forecast the single-hole or single-row hole film cooling effectiveness, according to Zhang et al. [72], it was found that the core influencing factors include mainstream parameters and geometrical structure parameters. Naghashnejad [73] employed the group method of data handling—artificial neural network (GMDH-ANN) to evaluate the impact of one slanted row of cylindrical holes on a flat surface. By using GA for the GMDH neural network, a model can reliably forecast the membrane cooling efficiency within the range of training circumstances for each variable. Qin [74] used BP-NN, constructed a database of 7446 sets of working conditions for training and testing, and then predicted the membrane cooling efficiency. The prediction using this method has greater accurate forecasting than the empirical formula, the applicable range is wider than that of the empirical formula, and the adopted network architecture and design parameters are depicted in Figure 11. Milani [75] utilized a random forest model generating the mapping relationship between input parameters and characteristic parameters of the film flow. It was found that the distributions of the characteristic parameters of the flow field would be significantly different at different blowing ratios, according to the laws, such as excessive blowing ratios leading to blowing the film away from the wall, as found in conventional film cooling. Dolati [76] examined the influence of a plasma exciter on the cylindrical and fan-shaped film hole by combining numerical simulation and GMDH-ANN. The model obtained the area-averaged film cooling efficiency appropriate forecast using the nozzle hole angle, aspect ratio, blowing ratio, and density ratio as neural network input parameters.

It is noteworthy that predictive models predicated on machine learning necessitate an extensive quantity of data for training. If the volume of training dataset data diminishes, the generality of the predictive model will significantly diminish. Concurrently, traditional machine learning algorithms are incapable of being implemented for the prediction of high-dimensional nonlinear regression issues. As demonstrated by Luo et al. [77], the CNN model for film cooling efficiency prediction exhibits a more rapid decline in prediction accuracy if the prediction is beyond the original dataset. This is due to the reduction in the amount of data that can be utilized for training. Consequently, the optimization of traditional ML models through the use of constraint algorithms can reduce the training data and, to some extent, improve the prediction accuracy. Zhu [78] employed the NN prediction method for the distribution of the single-exhaust membrane cooling effect along the transverse direction, utilizing Gaussian function constraints and input variables, including the main stream turbulence degree, density ratio, blowing ratio, film incidence angle, aspect ratio, and dimensionless flow distance. The results demonstrate that the prediction error of the Gaussian function-constrained neural network on the face-averaged cooling efficiency of the test set is only 5.70%, which is 67% lower than that of the direct prediction. In contrast, an analysis of the samples exhibiting larger errors in the two models revealed that the errors were primarily attributable to changes in the state of film separation, reattachment, and complete separation resulting from the relatively large blowing wind, which introduced greater irregularity in the prediction of the average cold efficiency and increased the difficulty of prediction. A study by Li [79] proposed a deep learning-based method for anticipating the cooling performance utilizing a multilayer perceptron model with input parameters, including the film cooling holes’ geometric parameters, the incoming flow parameters, and the flow field location. A comparison of the distribution cloud maps of CFD and the deep model predicting the film cooling efficiency under this condition reveals that the deep model’s overall prediction results exhibit a higher degree of fit. Additionally, the deep learning model’s prediction time is only 1/1000 of that of the CFD, offering a significant advantage in prediction speed. The deep learning model’s superior speed in prediction is evident.

In the context of practical application, the rows of film holes primarily affect the blade film cooling, and the mutual superposition of each film further complicates. Dávalos [80] predicted the turbine blade leading edge area-averaged film cooling efficiency using ANN. After constructing the mapping relationship between the variables and the cooling efficiency, the importance analysis of the input variables was performed, and it was found that the blowing ratio had the largest impact on the cooling performance. Yang [81] constructed a multi-row hole film cooling model in a large parameter space capable of generalization using deep learning. The model employs a recurrent neural network (RNN) with a Long Short-Term Memory (LSTM) algorithm to integrate data from multiple flow lengths and surface areas into a model in the format of a one-dimensional sequence. The model RMS error is reduced by approximately 48% when predicting film cooling efficiency.

However, in many practical application scenarios, the film hole placement is irregular, and how to parametrically describe the relative positions of the film holes becomes a key issue. In this regard, Yang et al. [82,83,84] used a convolutional modeling technique to forecast the diffusion cooling effect at the leading edge. In the study, a set of simulation data of a regular array of film cooling holes was utilized to train an ML model, which was later validated with randomly distributed film cooling holes to confirm the correctness and generalizability of the model. It was found that the convolutional model was able to effectively reconstruct the cooling efficiency distribution over the entire surface and had higher prediction accuracy than the conventional model at high blowdown ratios. David et al. [85] developed a two-dimensional proxy model of film cooling efficiency at the turbine end wall using a CGAN by learning the nonlinear relationship between film hole layout and cooling efficiency while capturing the nonlinear law of film superposition.

4.2. Flat Film Cooling Optimization

In the structural optimization of flat plate film cooling, the main focus is to use intelligent algorithms to optimize the hole types and sizes of various film holes, etc. Wang et al. [86] explored the effect of geometrical parameters on the film cooling performance at different blowing ratios. The study was based on CFD calculations using RBFNN as a surrogate model, and Monte Carlo simulations were used to investigate the statistical properties of the adiabatic film cooling efficiency. Compared with the trench without rounded corners, the air holes with trench rear corners, which are unable to generate separation vortices, are able to effectively alleviate the cold gas detachment downstream of the trench, thus improving the film cooling efficiency. Lee and Kim [87] optimized cylindrical film holes using three basic agent models, RSA, KRG, and RBFNN, and three weighted average agent models. Employing the aspect ratio and hole tilt angle as the design inputs and the space average film cooling efficiency as the target function, 12 experimental sites were selected for testing the performance of various models using Latin hypercube sampling (LHS). Meanwhile, Kim [88,89] used the same approach to optimize the cylindrical notch, curved film hole exit, and curved film cooling holes, respectively. The optimized results improved the film cooling efficiency to different degrees compared to the original film hole.

For other aspects of hole shape, Lee and Kim et al. [90,91] proposed a numerical computation method for fan-shaped hole optimization by combining 3D RANS analysis with the RBFNN method. LHS is used to determine the training data, and sequential quadratic programming (SQP) is utilized to seek the optimum value based on the generated agent model. The improved structure greatly increases the film cooling heat transfer performance compared to the reference structure. Choi et al. [92] employed the Box–Behnken design and RSA methods to optimize the Coanda bump downstream of the rectangular film hole. Lee et al. [93] proposed a leaf-like film hole by borrowing the design method of fan, swept-back fan, and dumbbell-shaped outlets of the film hole. The numerical investigation reveals that the optimized film hole boosts the film cooling efficiency to varied degrees compared to the aforementioned hole types. To improve the thermal efficiency of the new type of film hole, the same optimization method is used with the design parameters of lateral diffusion of diffusion holes, angle of forward expansion holes, length-to-diameter ratio of holes, and spacing-to-diameter ratio of holes. The average film cooling efficiency of the improved structural space was raised by 18.1%.

Considering that the GA can globally search for the optimal design parameters from the proxy model, Zhang et al. [94,95] constructed a high-fidelity model to optimize the cooling efficiency of the sector pore by using the low-fidelity data available in the literature and the high-fidelity data provided by RANS simulation. A combination of GA and SQP was used to optimize the shaped holes using three geometric parameters, namely, diffusion angle, film hole tilt angle, and hole aspect ratio, as input variables. Huang et al. [96] proposed a multi-objective optimization method for circular slotted holes based on CFD analysis and agent model approximation. Obtain the optimal Pareto front using NSGA-II based on the RBFNN model. The above methods are mainly used to optimize the hole type and size by trial-and-error method but are relatively less used for topology optimization in flat plate film cooling.

4.3. Turbine Blade Film Cooling Optimization

In the analysis of factors affecting film cooling efficiency, Wang [97] employed a supervised machine learning multilayer perceptron (MLP) model to investigate the lateral mean film cooling efficiency of a gas turbine blade leading edge model with lateral grooves. The uncertainty inputs for the various geometric factors included the hole position, groove depth and width, and bond angle. The output, under varying blowing ratios, was the lateral average film cooling efficiency. Meanwhile, a nonlinear mapping relationship between the cooling efficiency and the air film cooling parameters was established, and this relationship was used to analyze the air film cooling efficiency using the Monte Carlo algorithm in order to minimize the computing cost. Furthermore, upstream hole spacing had a greater impact on membrane cooling efficiency than downstream hole spacing. Vinogradov et al. [98] performed operational and stochastic uncertainty analyses at the front and top of the blade. Using computational fluid dynamics (CFD) and surrogate modeling techniques, including response surface and Monte Carlo methods, the study quantified the uncertainties and optimized the blade design. The study uses IOSO techniques for robust optimization to obtain a Pareto set that balances cooling effectiveness and aerodynamic efficiency. The study’s findings provide a robust optimal solution that ensures a high level of cooling performance and aerodynamic efficiency for HPT blades with uncertainties in operating parameters and geometric variations.

For the aspect of gas film hole size and hole type, Smith and Dutta [99,100] put forward a nonlinear optimization agent strategy (NORS) based on the ML approach. García [101] combined differential evolution with ANN to optimize the conical gas film holes at the front edge of the gas turbine blade model, which was modeled with hole diameter, hole spacing, hole spacing between columns, hole angle, and main flow velocity as input parameters and area-averaged film cooling efficiency as target parameters. Mostofizadeh [102] developed a CFD-ANN-GA optimization method to choose the film cooling efficiency and the mass flow rate of the coolant as optimization goals.

Compared with the optimization of film hole cooling at the front edge, the greater curvature of the medium string suction surface is highly susceptible to the generation of counterpressure gradients at the surface bends, resulting in the separation of the air film from the blade surface. The air film in the center chord region must be specially optimized. Ayoubi [103,104] used a combination of GA and ANN for the multi-objective optimization of the double-row asymmetrical film holes on the suction surface. The method takes the cone extension angle, complex angle, and aspect ratio of the film hole as independent variables and the film cooling efficiency and aerodynamic loss as target variables. Meanwhile, the team’s earlier study [105] used the same optimization method for the film cooling pores on the VKI rotor. Huang [106,107] used RBFNN to develop an agent model and combined it with GA to improve the structure of the fan-shaped film hole at a specified spot on the surface of the turbine blade. The average adiabatic air film cooling efficiency of the optimized structure area is increased by 18% compared with that of the benchmark reference fan-shaped film hole.

For the optimization of the pressure surface film hole shape and the arrangement, Johnson et al. [108,109] optimized the pressure surface film cooling arrangement of high-pressure turbine blades using a genetic algorithm. Taking the incidence angle, composite angle, film hole size, two-dimensional position of the holes on the blade pressure surface, and air hole arrangement as design variables, the genetic algorithm was combined with Latin hypercube sampling to optimize the size and arrangement of the air film holes. The optimized film hole effectively improves cooling efficiency while reducing the average surface temperature. Lee et al. [110,111] optimized the arrangement of pressure surface film holes for high-pressure turbine nozzles. The study, for the first time, considered the simultaneous cooling and manufacturing differences. A shape function was used to parameterize the hole array with five design variables, and two factors representative of the manufacturing tolerance of the film hole were considered. A KRG proxy model and Monte Carlo were combined to describe the probability over the sampling method and to optimize the design parameters using a GA. The findings demonstrate that the optimized cooling hole design significantly improves the cooling performance’s expectation and variance, especially by lessening the cooling performance’s sensitivity to manufacturing tolerances.

Conjugate heat transfer (CHT) has been neglected in the above studies on the optimization of cooling of pressure surface film hole arrays due to the large amount of computational data and complexity it requires. For this reason, Kim et al. [112] used a three-layer KRG model to optimize the pressure surface film cooling hole arrays of high-pressure turbine blades. Additionally, to increase the overall optimization process efficiency, the layered KRG model and the global optimization method were integrated. The results show that the use of the three-layer KRG model can significantly reduce the calculation time. In addition, the overall cooling efficiency of the optimized array based on film holes under CHT conditions is better than that of the optimized array under adiabatic conditions.

Considering the different structures of the turbine blade regions and the flow characteristics of the high-temperature gas in each region, this is significant in optimizing the overall film cooling effect of the blade to minimize the highest and average temperatures of the blade in the application process. Jiang et al. [113] investigated the multiple rows of cooling holes of a real high-pressure blade for marine applications by using a full three-dimensional optimization platform. The results show that the cooling structure parameters obtained by the numerical optimization method achieve a better cooling effect with a certain aerodynamic loss. Subsequently, the team [114] used the same optimization methodology to improve the configuration of multiple exhaust film cooling holes for C3X gas turbine blades and to optimize the arrangement of exhaust film cooling holes on both the suction and pressure sides. Müller [115] used an evolutionary algorithm to optimize the turbine blade air film cooling. The processes of optimizing air film cooling, shock radiation cooling, and column disruption flow cooling are considered. External surface average temperature, minimum temperature, and maximum temperature are restricted conditions, with cooling air flow mass flow minimum as an optimized target, membrane cavity position, cavity injection angle, number of cavities per cavity, and shock cavity number as design variables. To optimize the strategy, five rows of air membrane holes were arranged at the front edge, and two rows were placed on the pressure side, according to the results.

In the optimization process of film cooling, the effect of rotational action on the cooling efficiency needs to be considered. In dynamic blades, the flow direction of the main flow and the cooling airflow changes due to the rotation-induced Gottingen forces, buoyancy forces, and secondary flows. Moeini et al. [116] optimized the shape of transverse diffusion holes to enhance the effect of film hole cooling under the action of rotation. Under the conditions of rotation speeds of 0, 300, and 500 revolutions, respectively, by changing the incident angle, lateral diffusion angle, and aspect ratio of the hole, the average film cooling efficiency of different areas is obtained, and then the curve fitting method (CFM) is used for approximation to find the optimal combination. The CFM-GA-optimized film hole cooling efficiency was increased at all three speeds compared to that of the reference cylindrical hole.

5. Machine Learning in Composite Cooling

In fact, turbine blade cooling is usually a mutual combination of multiple cooling methods, forming a more complex composite cooling structure. The optimization of turbine blade cooling structure is gradually evolving from the optimization of a single cooling method to the internal and external coupling cooling methods. This section emphasizes the prediction of overall blade cooling efficiency under the influence of composites and the optimization of various composite technologies.

5.1. Prediction of Total Blade Cooling Efficiency

The blade plays a role in a variety of cooling technologies, and the factors affecting the overall cooling efficiency of the blade are many and complex. How to accurately predict the overall cooling efficiency is very important in monitoring the safety of high-temperature turbine blade operating conditions and composite cooling optimization. Zhao et al. [117] innovated a response surface model to investigate the effects of some parameters on cooling efficiency distribution, dimensionless temperature distribution, and temperature non-uniformity of a certain type of blade. The results show that the prediction model has high accuracy. Li et al. [118] proposed a new generalized interpolation correction method based on local gradient and applied it to the double-wall analysis.

However, the advent of ML has led to the proliferation of traditional ML methods across various fields, prompting the emergence of numerous novel learning algorithms, such as deep learning. Wang et al. [119] successfully predicted the heat transfer properties for gas film cooling and rib channels by using a deep learning approach. The model takes the blade profile, cooling channel parameters, film hole parameters, rib parameters, and boundary conditions as input variables and combines approximately 200 high-fidelity CFD simulation data as the training set. In a similar vein, Li et al. [120] presented a supervised graph learning-based approach for rapid and accurate prediction of the performance and temperature field of gas engine blades with complicated cooling channels under different operating conditions. The method is improved on the basis of the Aerodynamic Strength Prediction Graph Neural Network (ASP-GNN). The images of main stream inlet temperature, main stream inlet pressure, rotational speed, etc., are fed into the method and the images of turbine blade aerodynamic performance and temperature field will be output. The ASP-GNN model is capable of achieving high levels of accuracy with a relatively limited training sample size.

5.2. Composite Cooling Optimization

In the present era, the application of novel materials has led to the advent of novel cooling methodologies for blade cooling. One such method is sweating cooling. The cooling medium is sprayed with a number of dispersion holes, forming a film on the blade surface. This prevents direct contact between the hot gases and leaf surfaces. It has been demonstrated that under conditions of limited cooling medium, high cooling efficiency can be achieved through dispersion cooling. Yang et al. [121] developed a theoretical model based on convolution functions to predict local cooling efficiency in the event of blockage of sweating cooling holes. CFD calculations were employed to simulate the case of random pore clogging, with more than 200 data sets utilized to train the model. The results demonstrate that the total clogging ratio exerts a significant influence on the cooling effect. However, a single parameter is insufficient to accurately assess the cooling effect at all locations. In contrast, the sweating pore convolution parameter proposed in this study is more effective than the total clogging ratio in predicting cooling efficiency.

In terms of transpiration cooling structure optimization, Wang et al. [122] numerically investigated and optimized sweating cooling of C3X blades. The designed C3X blade has multiple pore zones with porosity ranging from 0.2 to 0.7. A framework for agent-based optimization was established based on the Darcy–Brinkman–Forchheimer equation and a local heat balance model for flow and heat transfer simulation. This was used to improve the performance of transpiration cooling by combining the KRG method and GA. The optimization results demonstrated that an effective sweating cooling film could be formed by arranging large porosity at the front edge of the blade and the pressure surface. Subsequently, the team [123] developed an optimization based on the ANN agent model and NSGA-II in order to achieve the best balance between cooling performance and minimum aerodynamic losses for c3x sweating cooling. The minimum aerodynamic loss of the minimum area average surface thermometer of the blade was used as optimum objective, and the pores of different regions and the distribution of coolant were taken as the design variables. The results indicate that an increase in the quantity of cooling airflow discharged from the apex of the blade is associated with an improvement in cooling performance. However, it was observed that an increase in the amount of cooling airflow distributed at the apices resulted in a significant increase in aerodynamic loss within the porous medium of the C3X blade. In the pursuit of an a priori balance via the optimal combination of freezing competence and aerodynamic losses, it was determined that the coolant should be distributed in a manner that ensures uniformity at the apices and at the suction and pressure surfaces in the lower part of the apices.

Double-wall cooling is a composite cooling method that integrates internal and external cooling, as shown in Figure 12. This method can enhance the efficiency of blade cooling by combining array impact jet and full-coverage film cooling. Additionally, it can be arranged between the inner and outer wall surfaces with turbulated columns, whereby the cooling airflow impacts the jet from jet pits on the inner wall to the outer wall surface, flows through the turbulated columns, and then out through film holes on the outer surface to form film cooling. The incorporation of turbulated columns also contributes to an increase in structural strength. Kim et al. [124] employed the second-order response surface method for thermal analysis and optimization of shock/film cooling structure. The spacing between the impingement jet and the film hole, the channel height, the mass flux ratio between the crossflow and the impingement jet, and the main flow temperature were employed as design variables. Two jet arrangements (straight and staggered) and two cooling flow directions (same and opposite directions) are investigated by numerical simulation. Based on these considerations, a response surface function is constructed to determine the impact jet system that minimizes the maximum stress calculated within the design range. The outcomes show that the interleaved jet system has the lowest heat stress for the same flow direction and that this stress is only half of the maximum stress of the unimpacted jet cooling system.

In order to develop an impact-disturbing column-film cooling system, Wang et al. [125,126] employed a radial basis neural network to construct the mathematical model and a genetic algorithm to achieve a multi-objective optimization. The model incorporates impact hole diameter, turbulated column diameter, film hole diameter, impact spacing, flow direction hole pitch, and spreading hole pitch as design variables, while integrated cooling efficiency (ICE) and relative pressure loss serve as optimization objectives. The outcomes prove that the optimized structure displays the highest ICE of 0.89 while simultaneously reducing the relative pressure loss to 0.17% within the specified parameter range. In a similar vein, Li [127] used the same optimal strategy for the multi-objective optimization of the strut flame stabilizer. In conjunction with the Sobol method, the effect of geometrical parameters of the double-walled structure and external working conditions of cooling achievements was investigated. The outcomes demonstrate that the optimized structure exhibits enhanced film coverage and superior cooling performance. Conversely, the cooling gas mass flow rate exerts a more pronounced impact and pressure drop than the geometric parameters and temperature ratio.

6. Conclusions and Future Perspectives

Thermal efficiency is a crucial indicator of gas turbine performance. To improve thermal efficiency, it is important to raise the inlet temperature of the turbine. Currently, the maximum turbine inlet temperature has reached 2000 K, far greater than the blade material’s melting point. Therefore, the design and optimization of cooling structures with enhanced cooling performance can mitigate the impact of high-temperature gas on the turbine blades. This study gives a research review on intelligent methods, such as machine learning, in turbine blade cooling optimization. The primary conclusions are as follows:

• In blade cooling optimization studies, agent models like RSA, KRG, RBF, RBNN, ANN, and deep learning algorithms are commonly employed, according to a recent study. However, a significant amount of high-fidelity data is typically required to build the model so as to guarantee the reliability of single-fidelity models, and the data collection procedure is incredibly time-consuming;
• A variety of internal cooling technologies have been optimized for different aspects, including pin fin turbulated cooling, rib-turbulated cooling, impingement jet cooling, and channel cooling. Based on the CHT analysis of the flow and temperature fields, single-fidelity or multi-fidelity models are employed to optimize the cooling structure. However, the current research primarily concentrates on the optimization of static blade states, with fewer studies addressing the optimization of internal blade cooling under rotating conditions;
• Compared with flat film cooling, the optimization of film cooling on turbine blades needs to take into account the shape of film holes and the arrangement of holes. At present, most studies mainly focus on film cooling efficiency and aerodynamic loss as the optimization objectives. On the basis of CFD calculation, combined with a single-fidelity model and optimization algorithm, the cooling performance is optimized. However, there are few studies on conjugate heat transfer analysis, multi-fidelity model, and structural optimization under rotation;
• The majority of current research on transpiration cooling optimization is focused on enhancing blade cooling performance. Nevertheless, the transpiration cooling structure is challenging to manufacture and possesses low strength, and thus, structural strength optimization is less of a priority.

In light of the preceding discussion, the prospective evolution of turbine blade cooling optimization can be pursued in the following domains:

• The combination of high-fidelity data with low-fidelity data to train multi-fidelity agent models can reduce the calculation cost while maintaining the prediction accuracy. Consequently, in the process of optimizing the cooling structure of blades, a multi-fidelity agent model can be employed to predict the target parameters;
• The rotation of the blade will alter the flow field and heat transfer efficacy. In order to ensure the optimization process is more suitable for the actual circumstances, it is vital to consider the influence of rotation when optimizing blade cooling technology. Furthermore, the influence of the CHT on the optimization process is worthy of consideration;
• The application of novel technologies and materials enhances the heat transmission capability of the blade. However, the structural strength and thermal stress act as constraints that impede the deployment of these novel technologies and materials. Consequently, intelligent algorithms must be interdisciplinary and employ multi-objective analysis throughout the optimization process of the cooling structure of the blade;
• In the context of composite structure optimization design, the three primary factors are variable selection, objective function, and constraints. It can be observed that the topology-optimized structure exhibits superior temperature uniformity and a smaller pressure drop. Therefore, the application of topological optimization technology in the design of leaf composite cooling structures and thermal boundary conditions as conditions to obtain optimized structures is very promising.