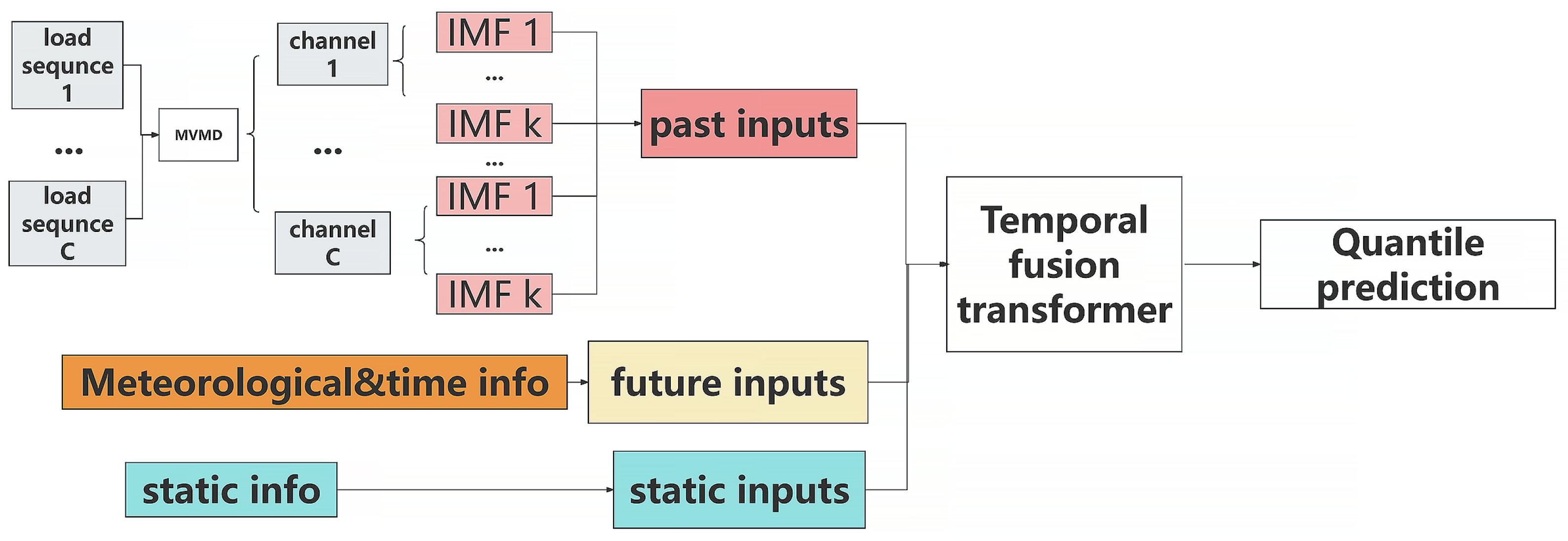
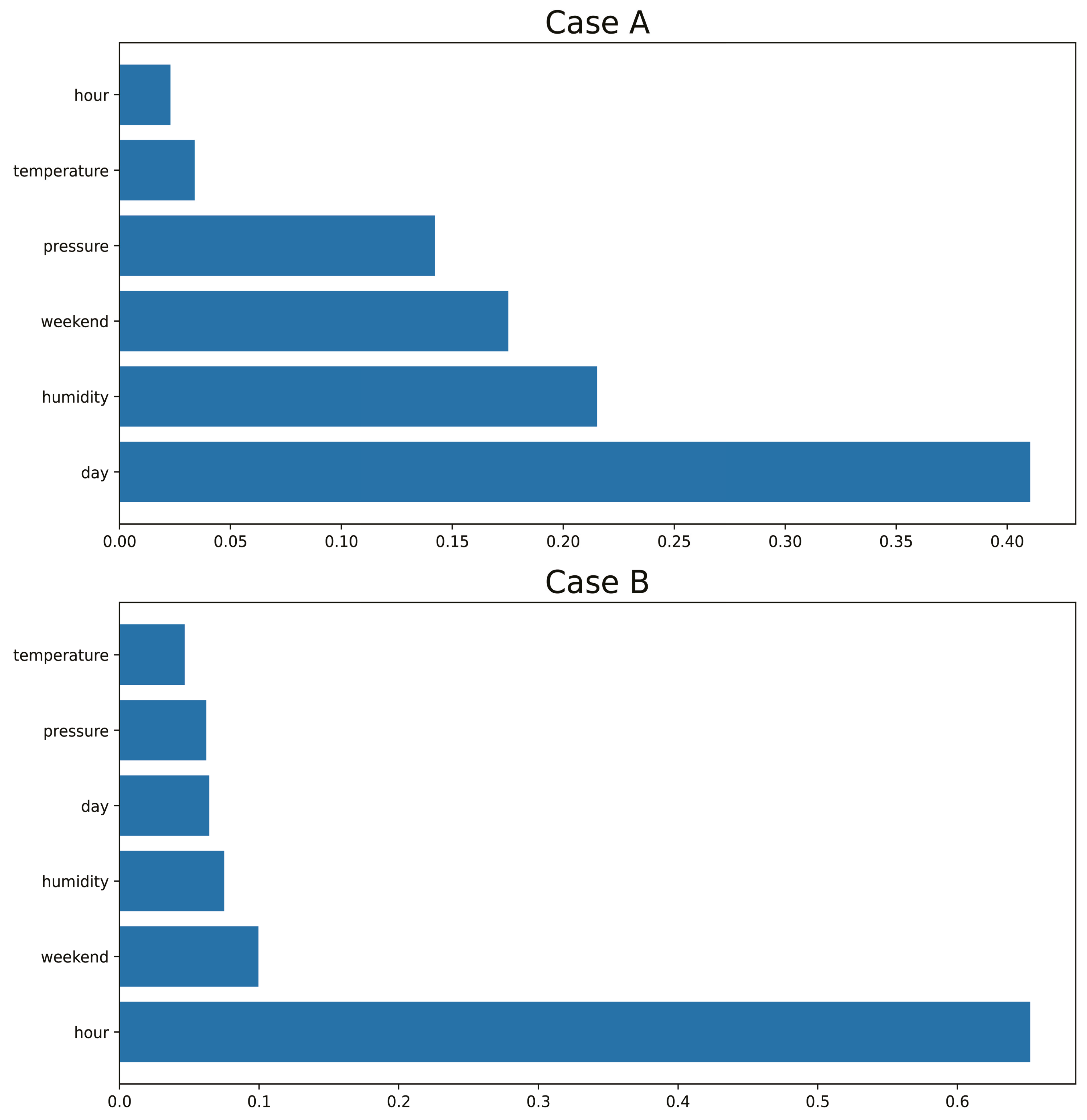
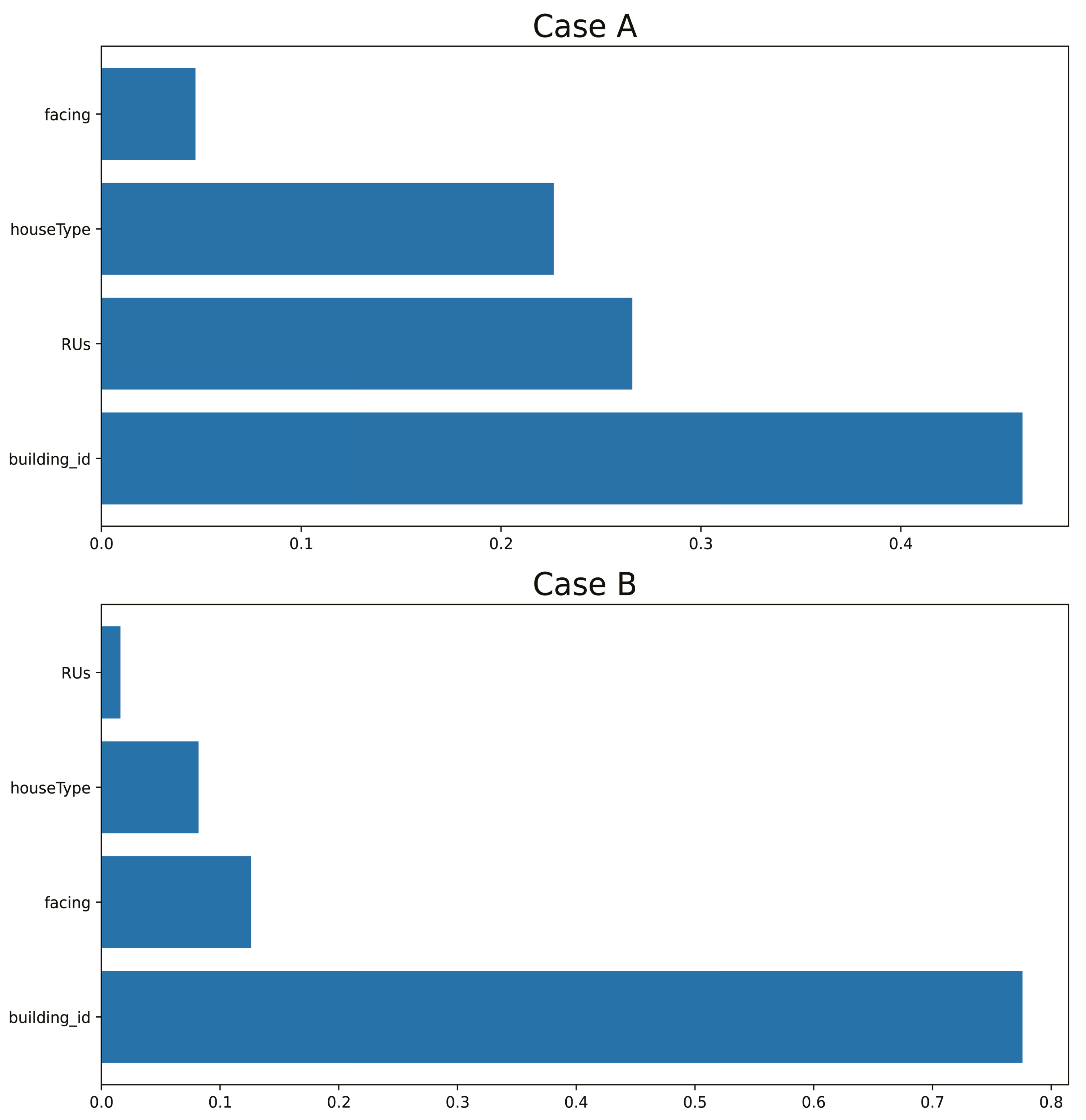
3.3. Entropy Computation Results of MVMD
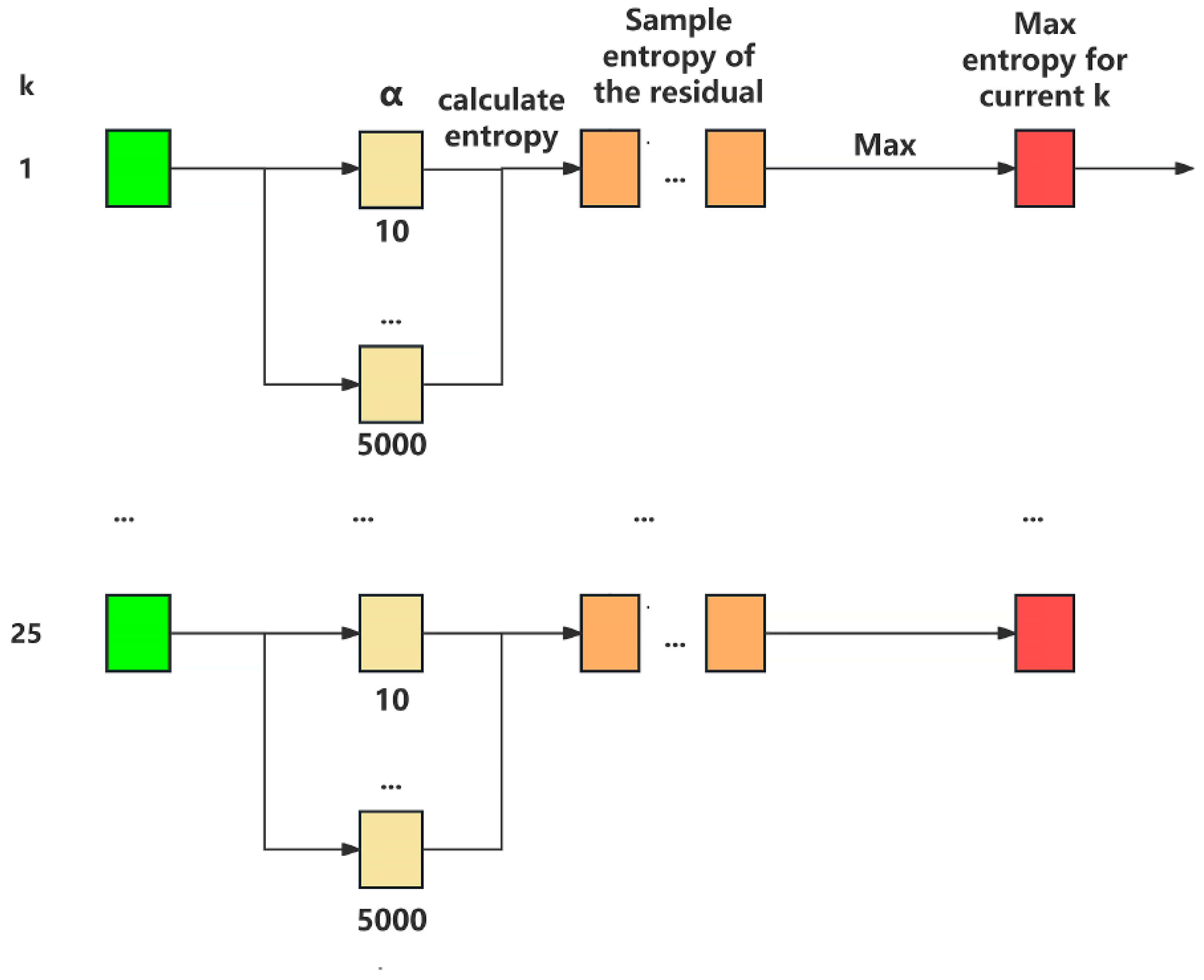
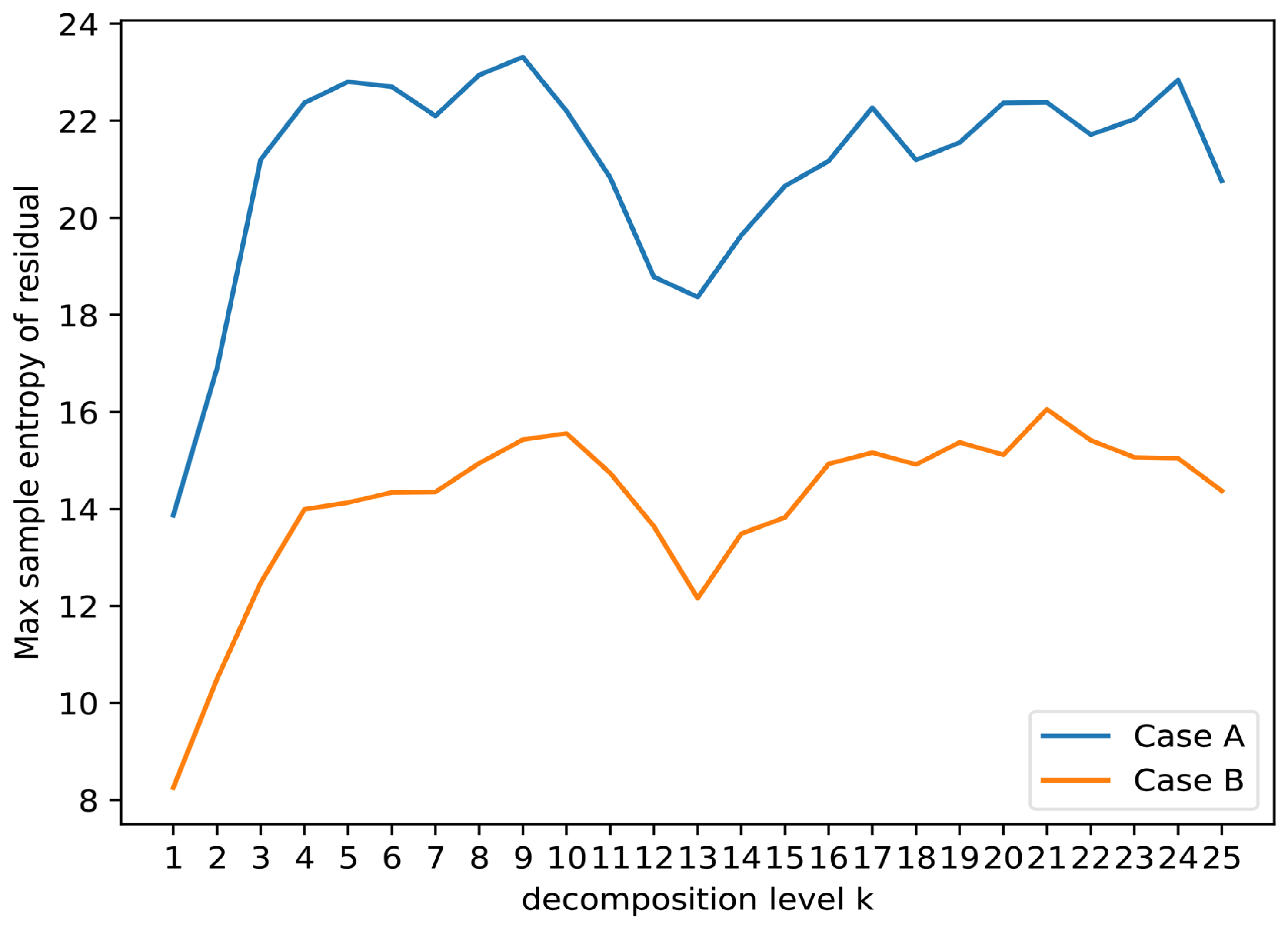
Figure 5 displays the results of residual sample entropy obtained by selecting the optimal penalty factor
for two training set cases (red boxes in
Figure 1). We find that the residual sample entropy of Case B is lower than that of Case A, implying that the signal patterns in Case B are more intricate, resulting in lower residual complexity.
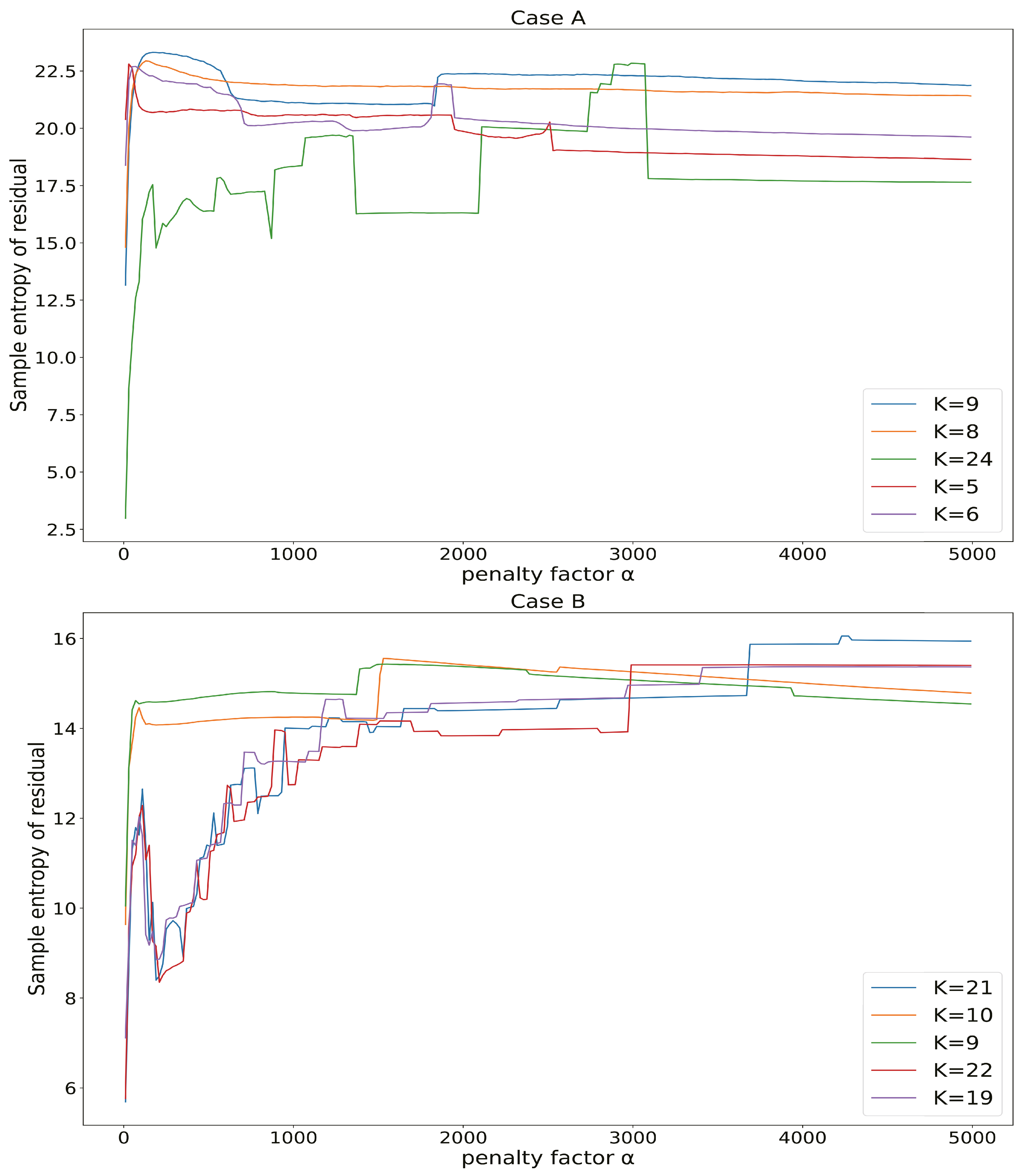
Figure 6 illustrates the impact of different penalty factors on residual sample entropy (yellow boxes in
Figure 1) for the same decomposition level. We selected five decomposition levels for analysis based on their highest residual sample entropy. The introduction of the penalty factor leads to complexity in the pattern of residual sample entropy. Specifically, we observe pronounced fluctuations in residual sample entropy for higher decomposition levels under varying penalty factors, for instance, in Case A, when the decomposition level was set to 24, and in Case B, when the decomposition level was set to 21, 22, and 19. These fluctuations gradually diminish as the penalty factor increases, eventually reaching a relatively stable state. Based on these findings, for Case A, the decomposition level was set to 9, with a corresponding penalty factor of 170. For Case B, the decomposition level was set to 21, with a corresponding penalty factor of 4230. The initial center frequency of MVMD is initialized using a uniform distribution, and the tolerance level is set to 1 × 10
−6.
For the test set and validation set, we similarly obtained their optimal penalty factors based on
Figure 1 while maintaining the same number of decomposition levels as the training set. The penalty factors for the validation set and test set in Case A were set as 1230 and 1240, respectively. For Case B, the penalty factors for the validation set and test set were set as 3410 and 4030, respectively.
3.6. Model Evaluation
For performance comparisons, we employed LSTM [
6], CNN-LSTM, [
7] and BiGRU-CNN [
28]. A distinct model was trained for each building using these methods. In order to ensure consistency with the reference, we adopted the original preprocessing method, which involved representing the time indicator using one-hot encoding. The input for these models consisted of both time indicators and load series, enabling a comprehensive analysis of their predictive capabilities. Additionally, we conducted a comparative analysis with separately trained MVMD-LSTM and MVMD-CNN-LSTM models to further substantiate the efficacy of our method. The implementation of these standalone models followed the methodology outlined in [
29], employing LSTM and CNN-LSTM architectures for the prediction of the IMFs and the subsequent reconstruction of the predicted signals. Concerning the CNN-LSTM-based, LSTM-based, and BiGRU-CNN models, we incorporated one of the lag inputs specified in [
7]. Specifically, we configured it to 12. As a preliminary trial for the TFT and MVMD-TFT models, we utilized 24 lag inputs.
Table 3 displays other configurations of the models.
As our data contain both outliers and stable points, we utilized Equations (11)–(14) to evaluate the performance of the models, where
represents the actual value, and
denotes the predicted value. MAE and MSE are the two most commonly used metrics in predictive problems, with MSE being more sensitive to outliers relative to MAE. MedAE serves as a robust measure of the variability of deviation of the observed values from the predict values. Additionally, we introduce WAPE to measure the percentage difference between actual and predicted values, as our data contain zeros, making this metric an alternative to MAPE. These four metrics provide different perspectives on the model’s performance. All methods exhibit a prediction horizon of 1, meaning that the predicted results correspond to the consumption data for the next hour. We made the original building name more concise by simplifying ‘Residential_’ to ‘R’.
Table 4 illustrates the prediction errors associated with Case A on the test set. The results show that the introduction of MVMD yielded substantial improvements in the performance of the CNN-LSTM, LSTM, and TFT models. A consistent decrease in all metrics shows this enhancement.
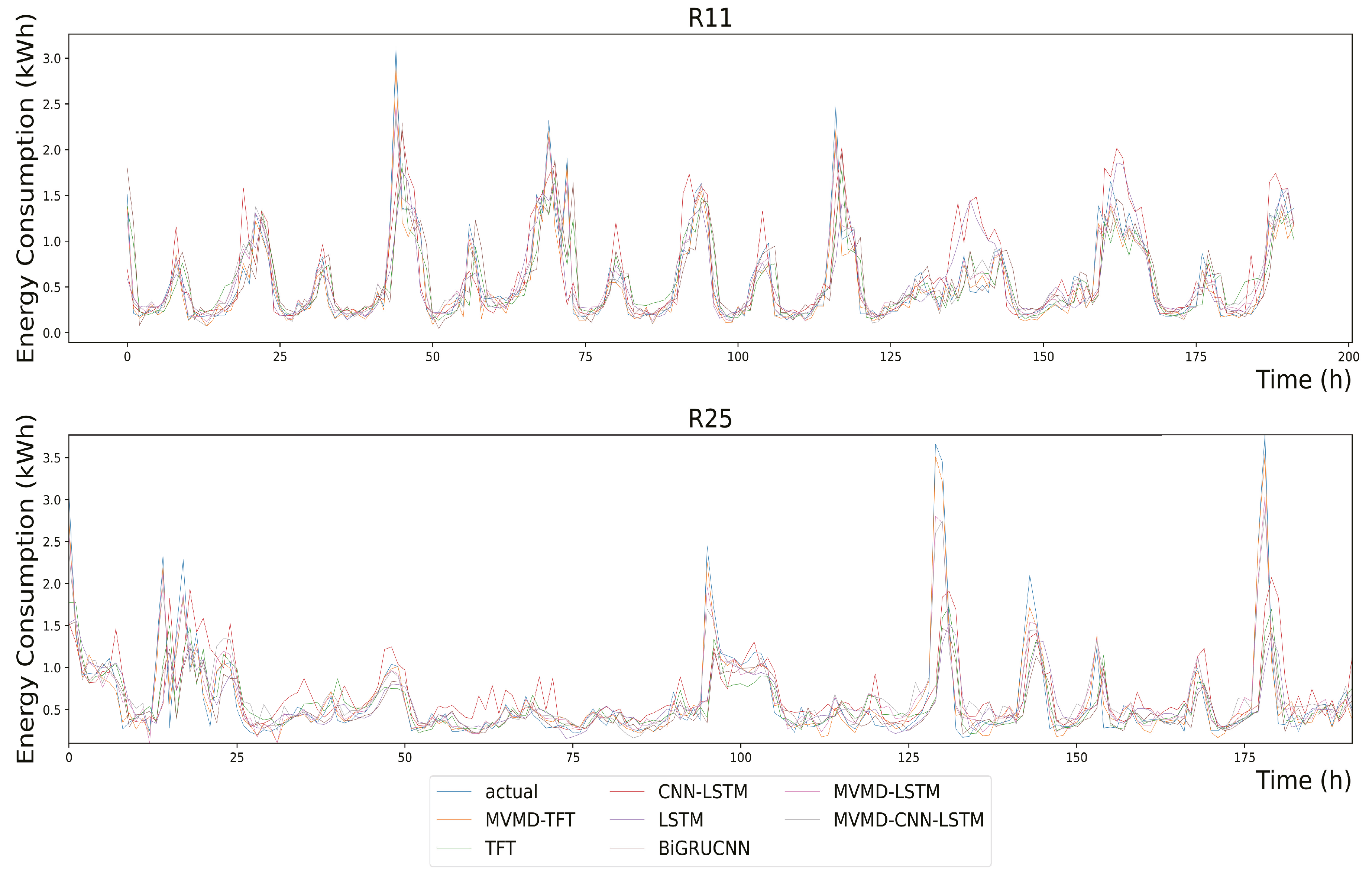
Figure 11 depicts the corresponding prediction outcomes of ‘R11’ and ‘R24’ in
Table 4, where the TFT and MVMD-TFT employ median forecasting.
Table 5 illustrates the four loss function outcomes for Case B on the test set. We can derive similar conclusions to those of Case A when the dataset expands. It is worth noting that certain buildings, such as R13 and R5, demonstrate elevated MSE values that surpass the corresponding MAE values. After undergoing MVMD and subsequent prediction, it is observed that the MSE decreases to a level smaller than that of the MAE. This reveals that the implementation of MVMD preprocessing effectively attenuates the deleterious impact of outliers on predictive outcomes.
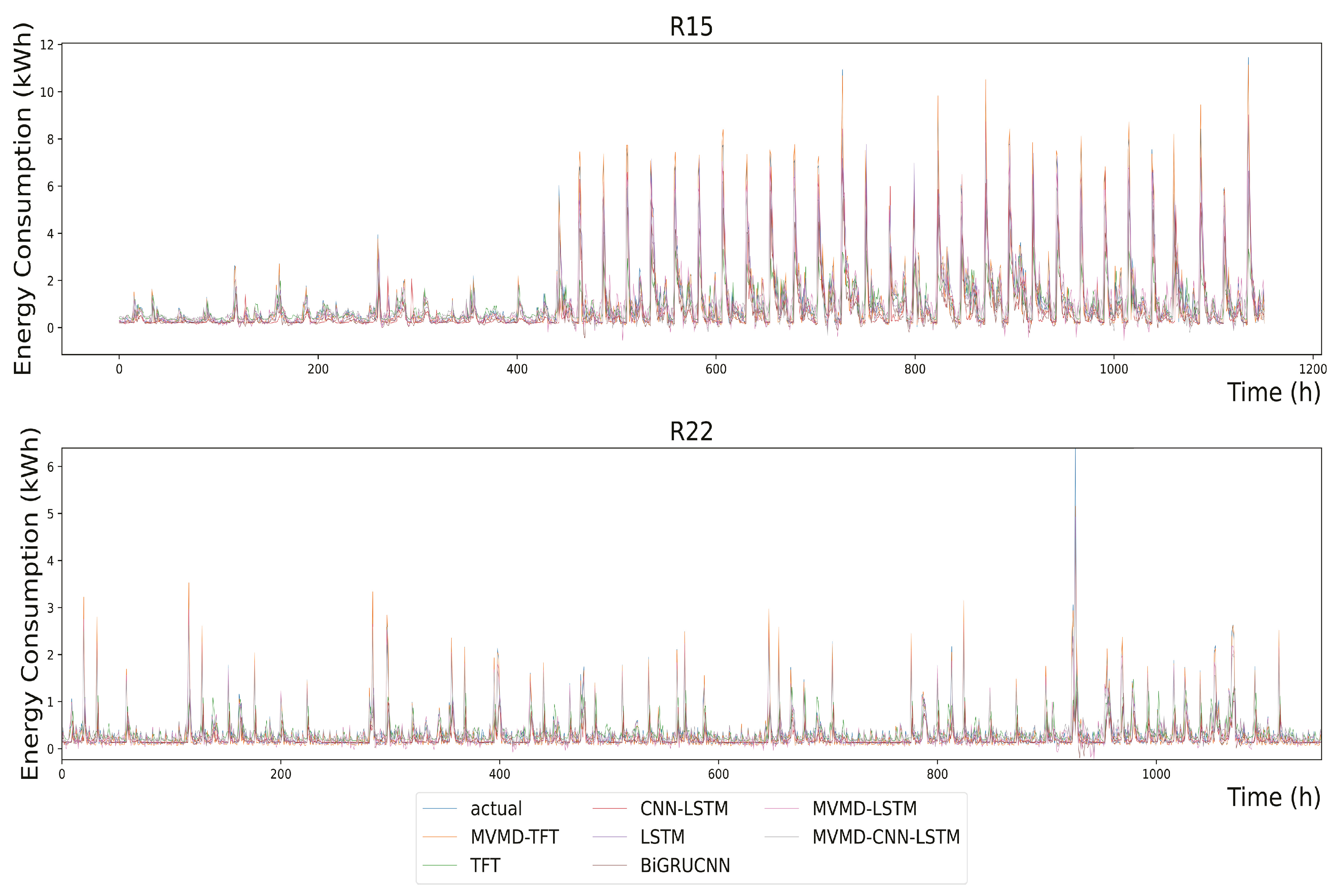
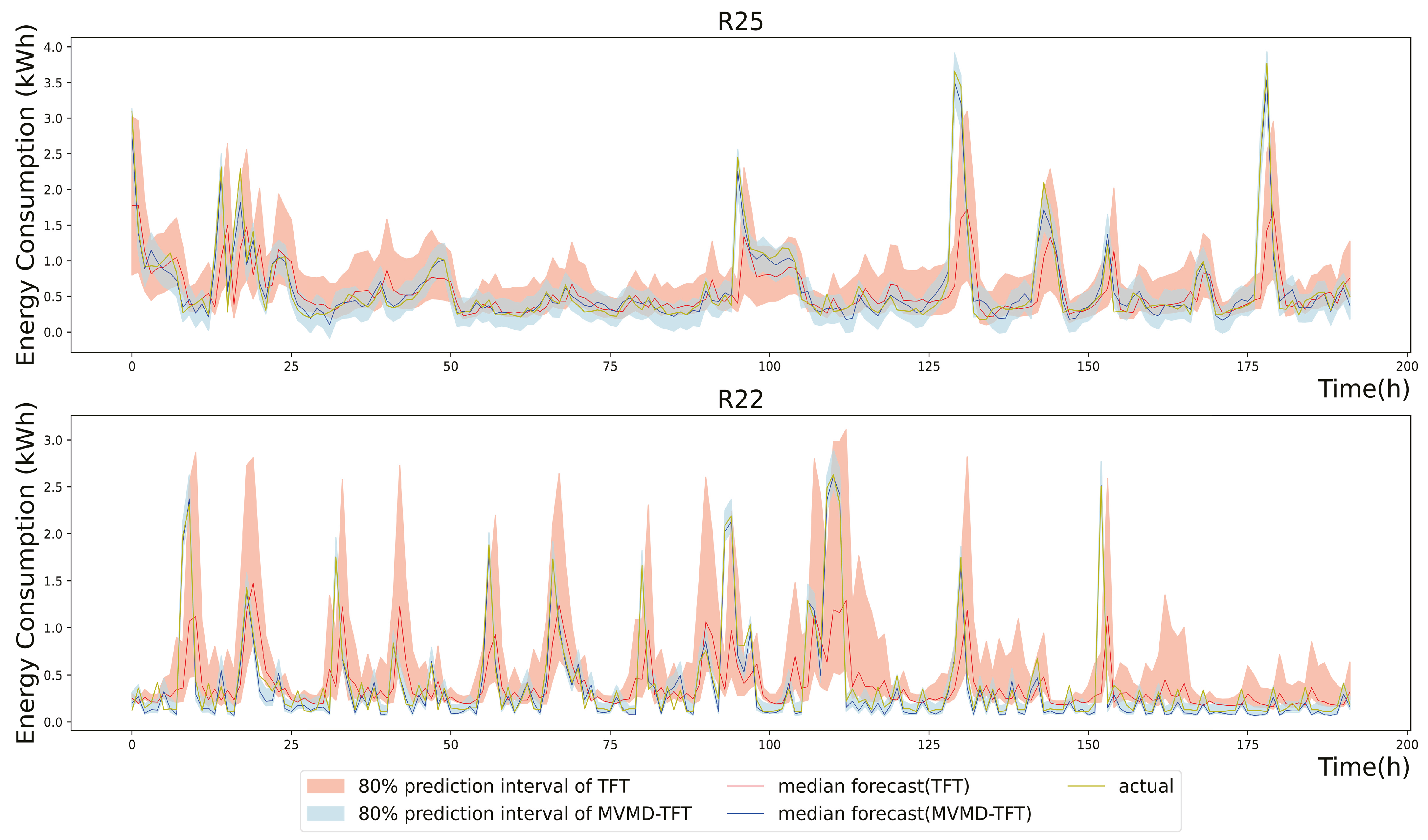
Figure 12 aligns with the predictions of ‘R15’ and ‘R22’ outlined in
Table 4.
The results in
Table 4 and
Table 5 reveal a similarity in the experimental outcomes between the MVMD-based models. In order to establish the statistical significance of the results displayed in
Table 4 and
Table 5, we introduce the Friedman and post-hoc Nemenyi tests [
30] to assess the differences among various models for evaluation. The null hypothesis of the Friedman test is that there is no difference among all comparison methods in the 24 datasets of Case A and Case B. We set the
p-value to be 0.05. If the calculation result of the Friedman test is less than 0.05, the null hypothesis is rejected; otherwise, it indicates a difference between the methods. Furthermore, to assess the performance between pairwise models, we introduced the Nemenyi post-hoc test. This test launches a comparison between a threshold (critical difference) and the difference in average rankings of the performance. If the ranking difference is lower than the threshold, it is considered that there is no significant difference in performance between the pairwise models. On the contrary, there is a significant performance difference between them. The evaluation metric of the Nemenyi test is MAE.
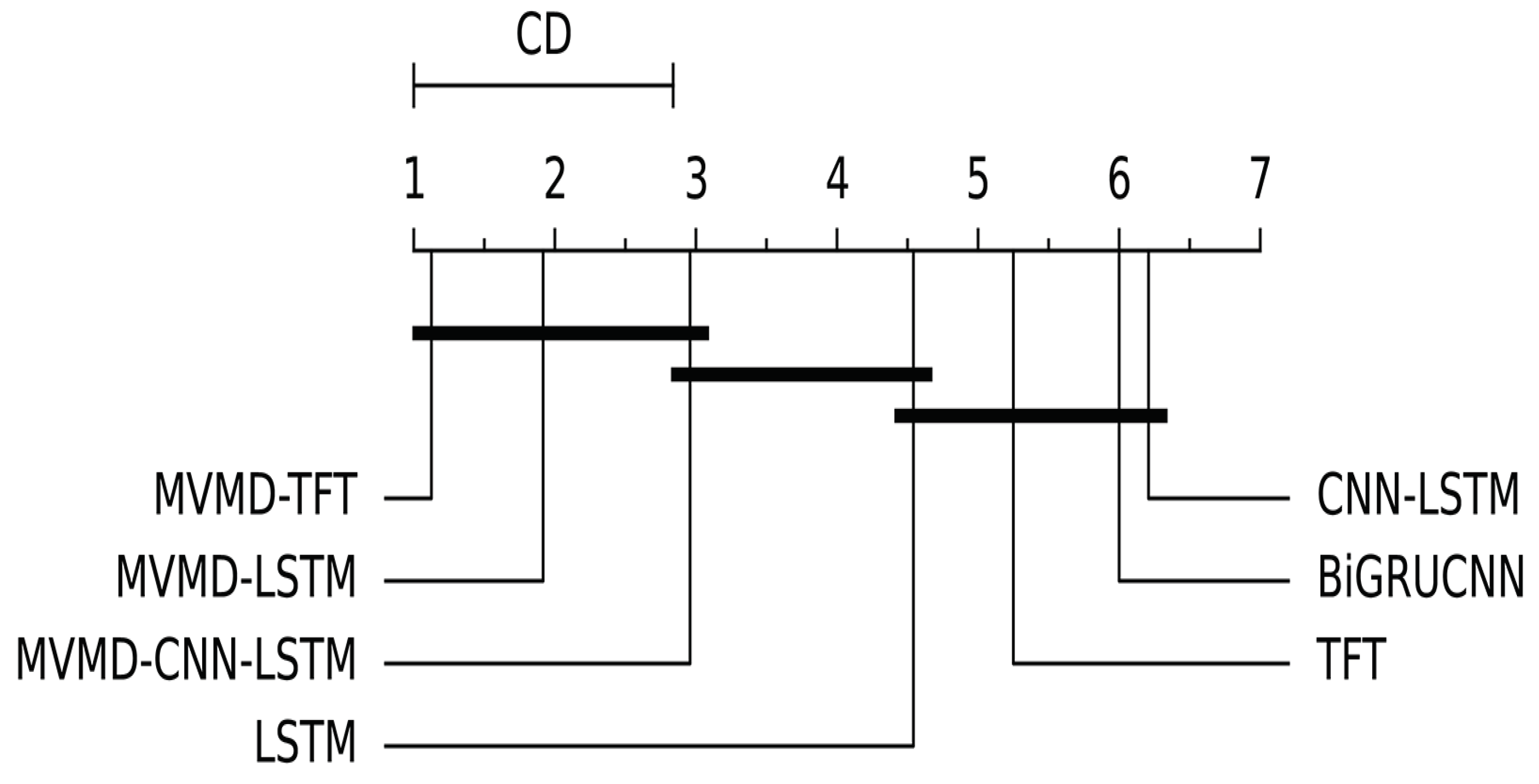
After performing the calculations on 24 datasets, we obtained a p-value of 5.3 × 10−19 for the Friedman test. This is significantly lower than the preset threshold of 0.05, indicating a significant difference in performance among the seven methods.
Figure 13 displays the results of the Nemenyi post-hoc tests, with a calculated CD value of 1.84. The results of the Nemenyi tests indicate that there are no significant differences in the performances of the CNN-LSTM, TFT, LSTM, and BiGRU-CNN. In the case of the MVMD-TFT, it shows differences with all non-MVMD-based methods. Based on the results from
Table 4 and
Table 5, our method achieved an average reduction of 69.9% in MAE for an individually trained CNN-LSTM and BiGRU-CNN, as well as a 67.7% reduction in MAE for an individually trained LSTM. Although no significant performance differences were detected for the MVMD-based methods, the proposed method demonstrated the best performance in the current experiment.
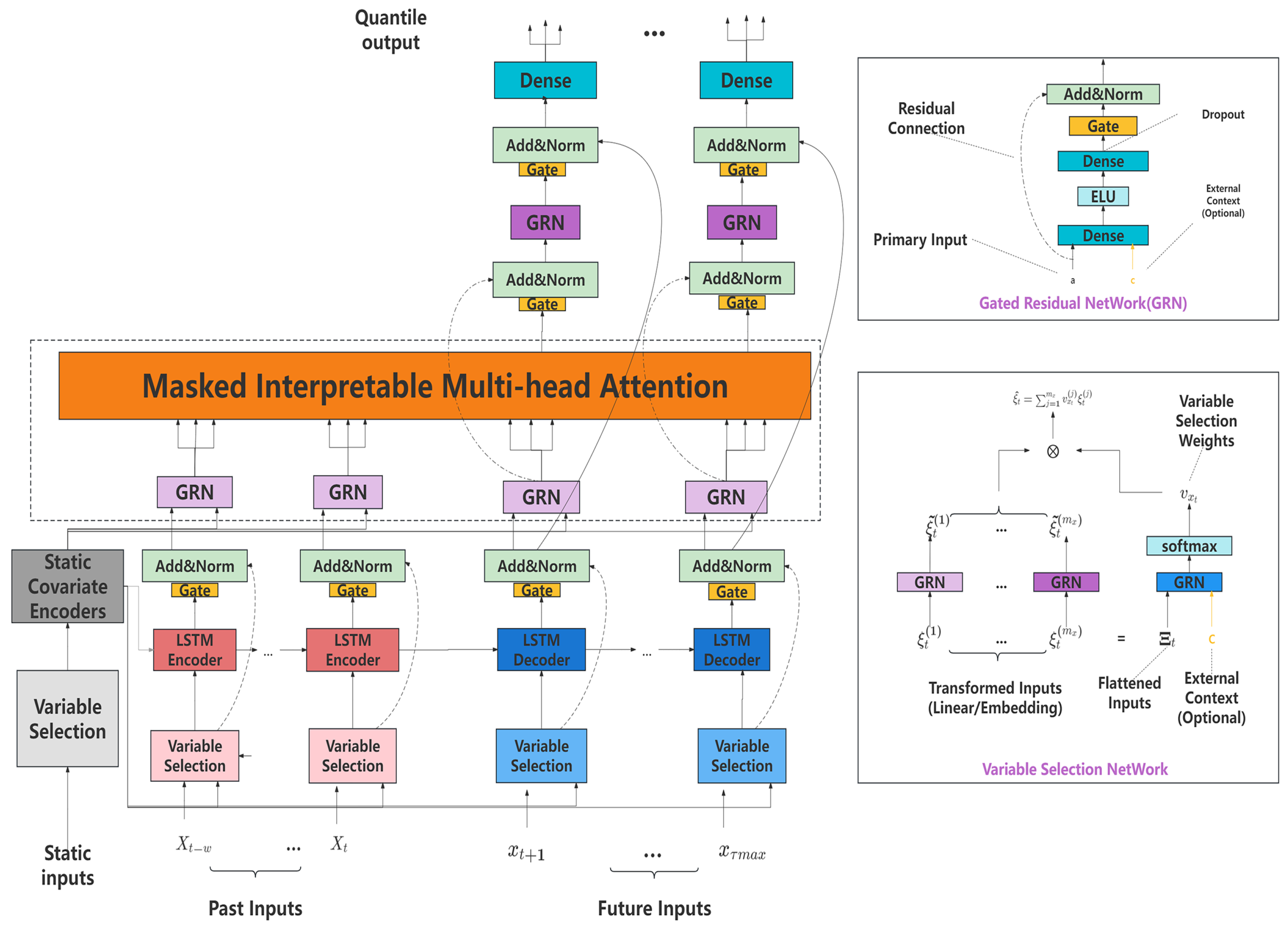
One of the important features of the TFT is that it provides a distribution of possible future outcomes along with point estimates, which is valuable for understanding the uncertainty associated with each prediction. Given that our model utilizes a quantile set of (0.1, 0.5, 0.9), the TFT produces a prediction interval of 80%.
Figure 14 presents both the median prediction results and their associated 80% prediction interval in two chosen buildings where peak values are observed. The results reflect the last 8 days from the entire test set. The proposed model attains a narrower prediction interval than the original method and is more likely to encompass peak values.
In order to perform a thorough assessment of the quantile forecast, we utilized the P50 loss and P90 loss, as specified in [
31] and described in Equation (
15). In the context of the 8-day evaluation, the test set comprises a total of 192 data points. Equation (
15) is applied to compute the
q-Risk value for each data point in the 1-hour-ahead forecast. Consequently, the average quantile loss for the 192 points was derived.
Table 6 showcases the average
q-Risk value for the forecast of the MVMD-TFT and TFT across all points in both cases. The results show that our method yields 75.9% lower P90 loss and 65.8% lower P50 loss on average, providing additional evidence for the effectiveness of our method.
Although our method has successfully produced accurate predictions in two instances, it is burdened by substantial time-related limitations that cannot be ignored. This deficiency is particularly evident in the WOA, where the computational demands of the TFT impose limitations on the selection of optimal initial parameters for the WOA. Consequently, the convergence of the WOA is insufficient, with the magnitude of this flaw becoming increasingly apparent as the dataset size and model complexity grow. Moreover, our method incorporates MVMD, which requires substantial time in data preprocessing to ascertain the most appropriate parameters. The determination of the parameters of the two cases together is approximately seven days. These limitations underscore the need for further improvements in our approach to address the substantial time constraints associated with the optimization process for the TFT and MVMD.