Equivalent Thermal Conductivity of Topology-Optimized Composite Structure for Three Typical Conductive Heat Transfer Models
Abstract
1. Introduction
2. Conductive Heat Transfer Models and Structural Optimization
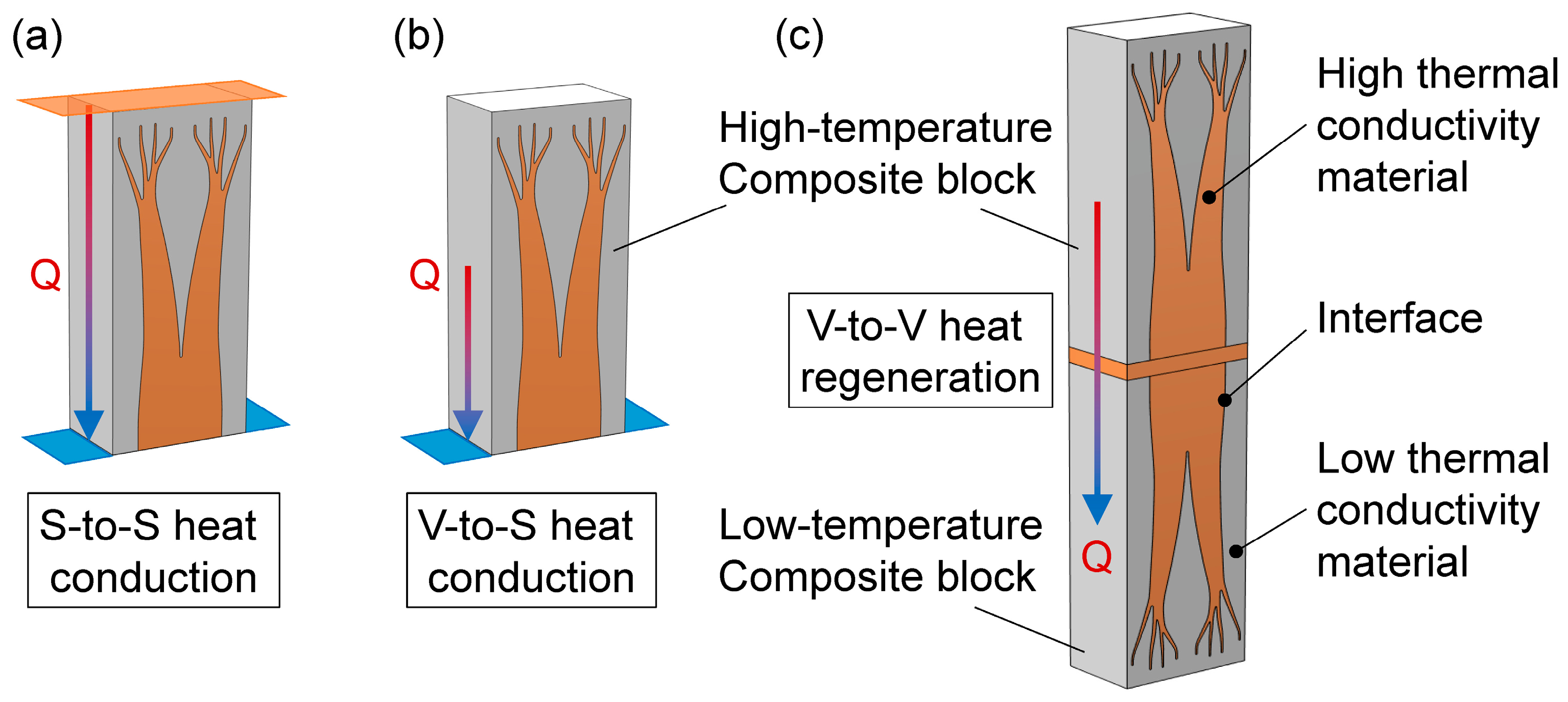
2.1. Surface-to-Surface Heat Transfer Model
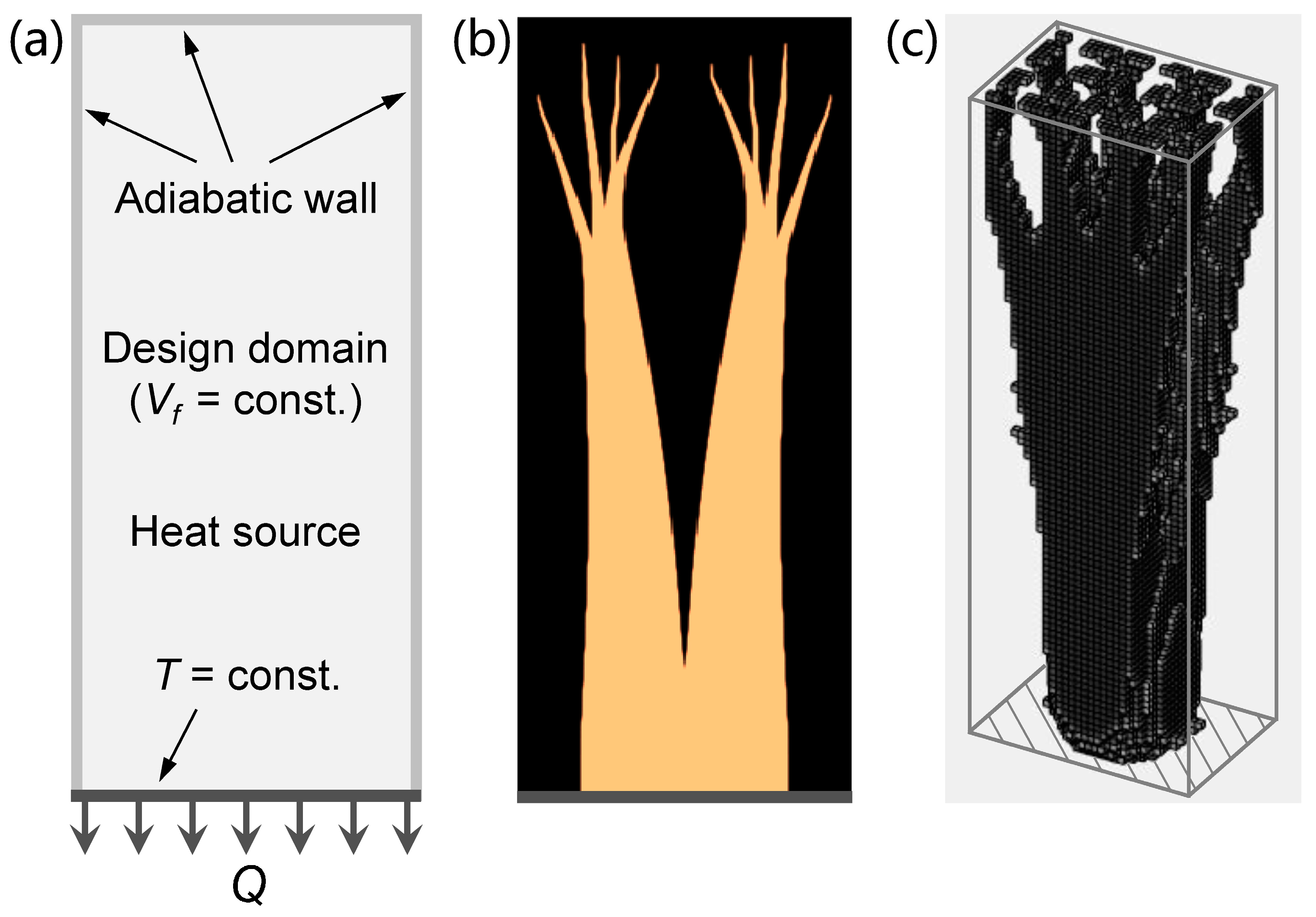
2.2. Volume-to-Surface Heat Transfer Model
2.3. Volume-to-Volume Heat Transfer Model
2.4. Interfacial Thermal Resistance Model
3. Evaluation of Equivalent Thermal Conductivity
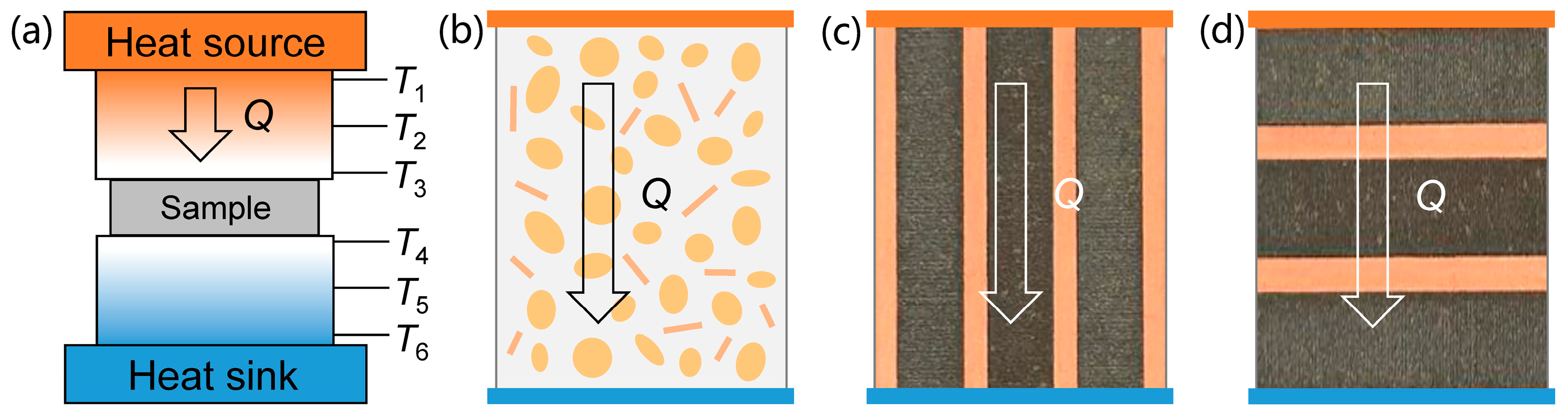
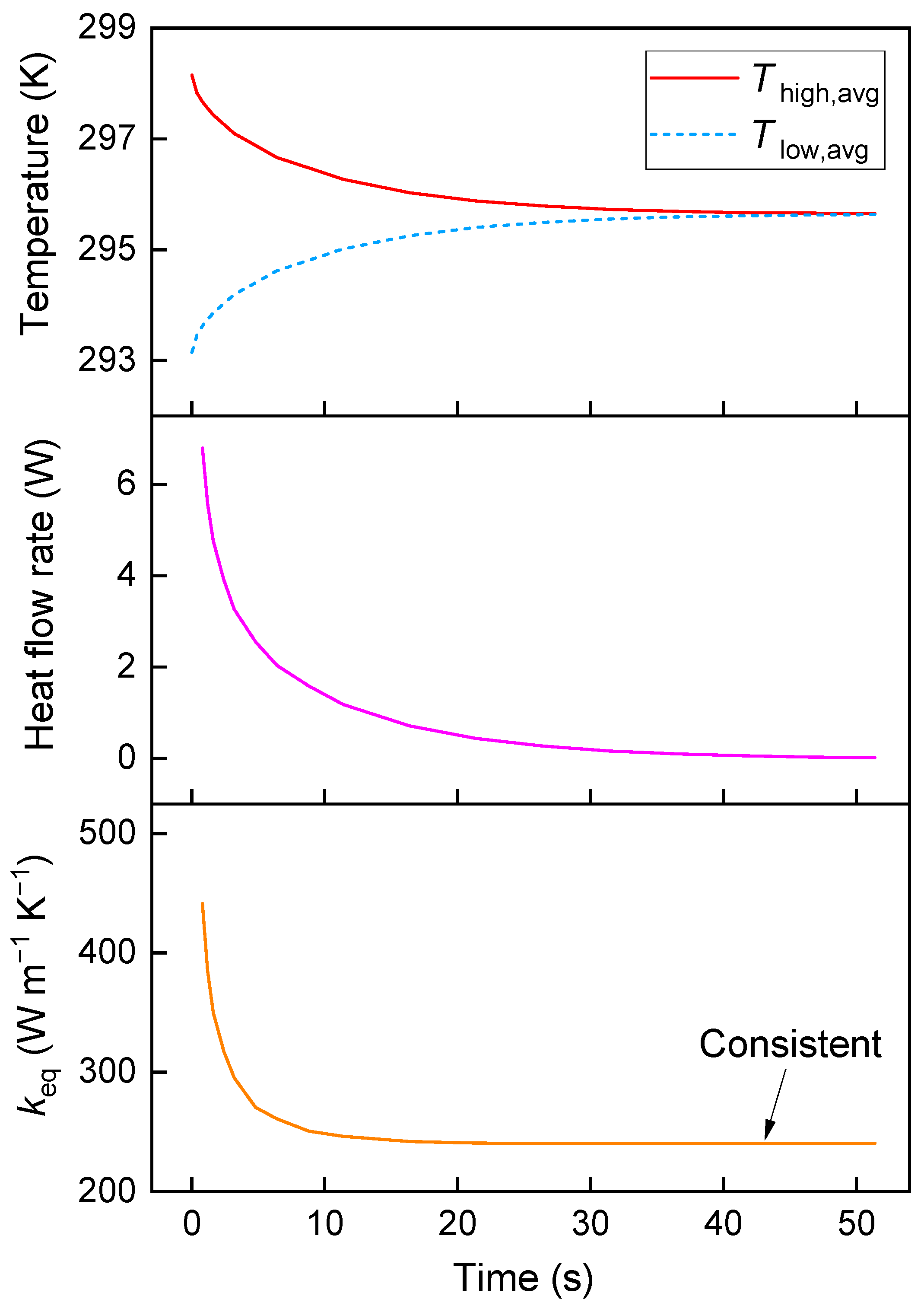
3.1. Definition of Equivalent Thermal Conductivity
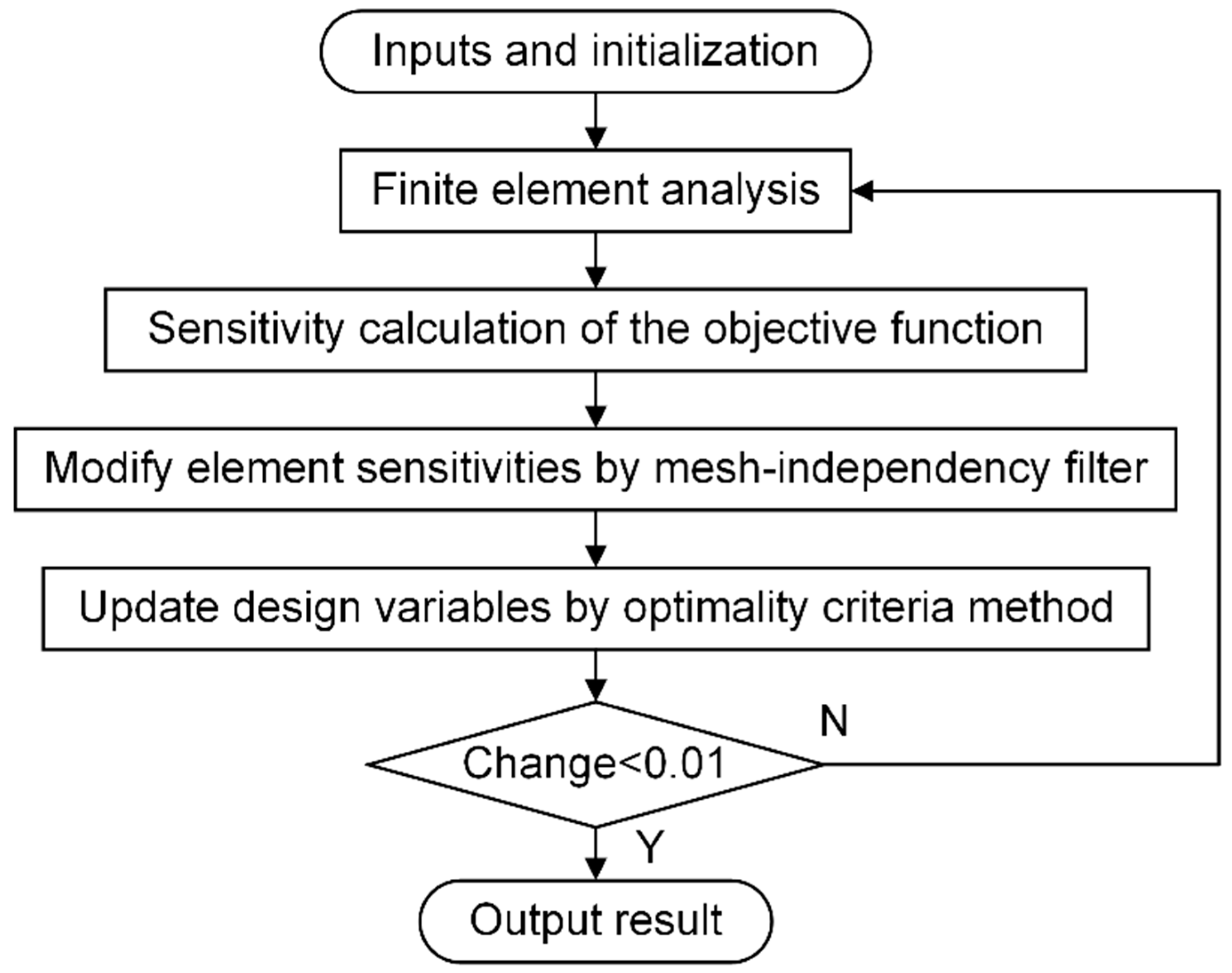
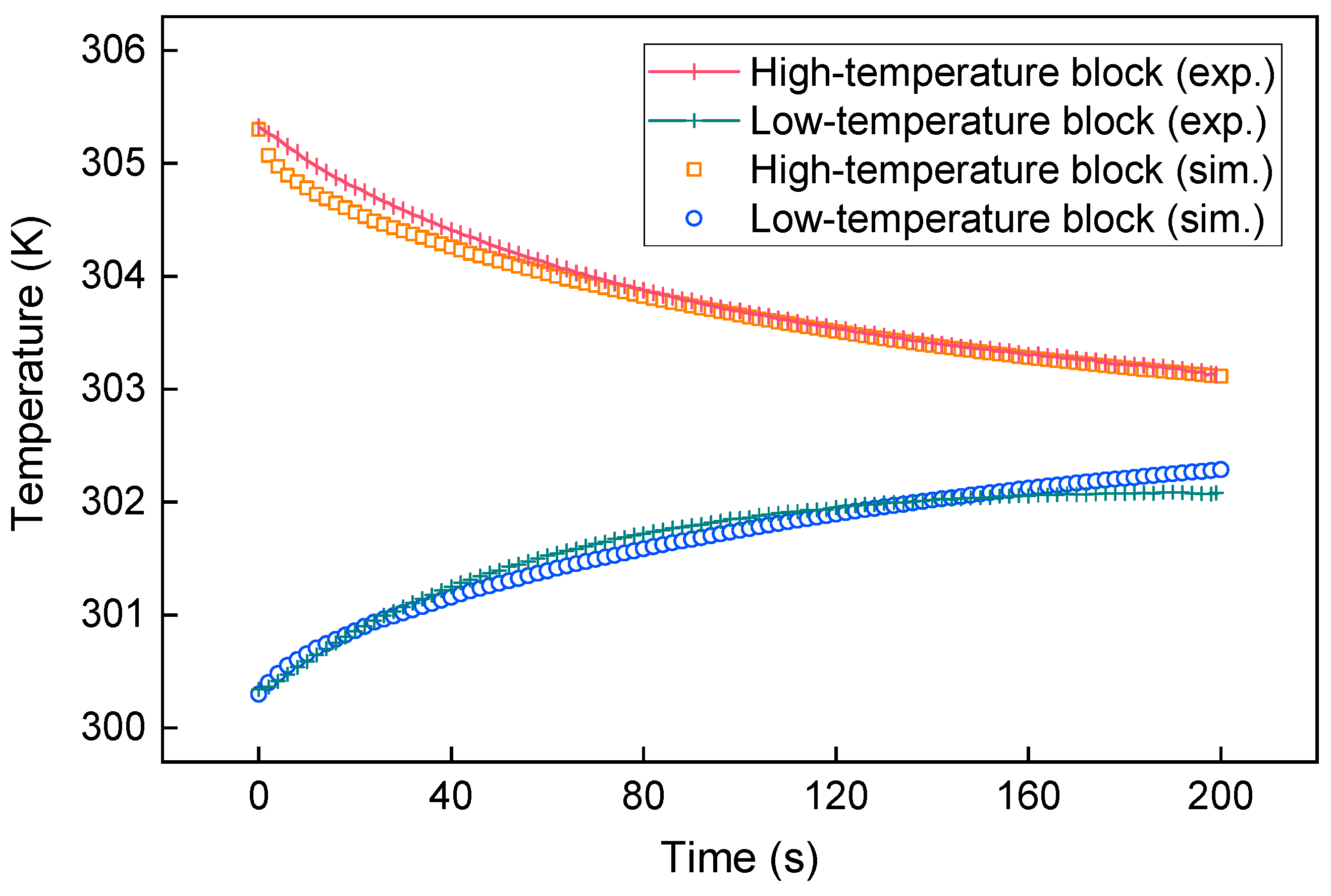
3.2. Simulation Method and Experimental Validation
- For the S-to-S model: a fixed temperature of the upper surface as , a fixed temperature of the lower surface as , an initial volume temperature of the block, and thermally insulated for the whole external surface.
- For the V-to-S model: an initial volume temperature of the single block as , a fixed temperature of the lower surface as , and thermally insulated for the whole external surface.
- For the V-to-V model: an initial volume temperature of the upper block as , an initial volume temperature of the lower block as , and thermally insulated for the whole external surface.
4. Results and Discussion
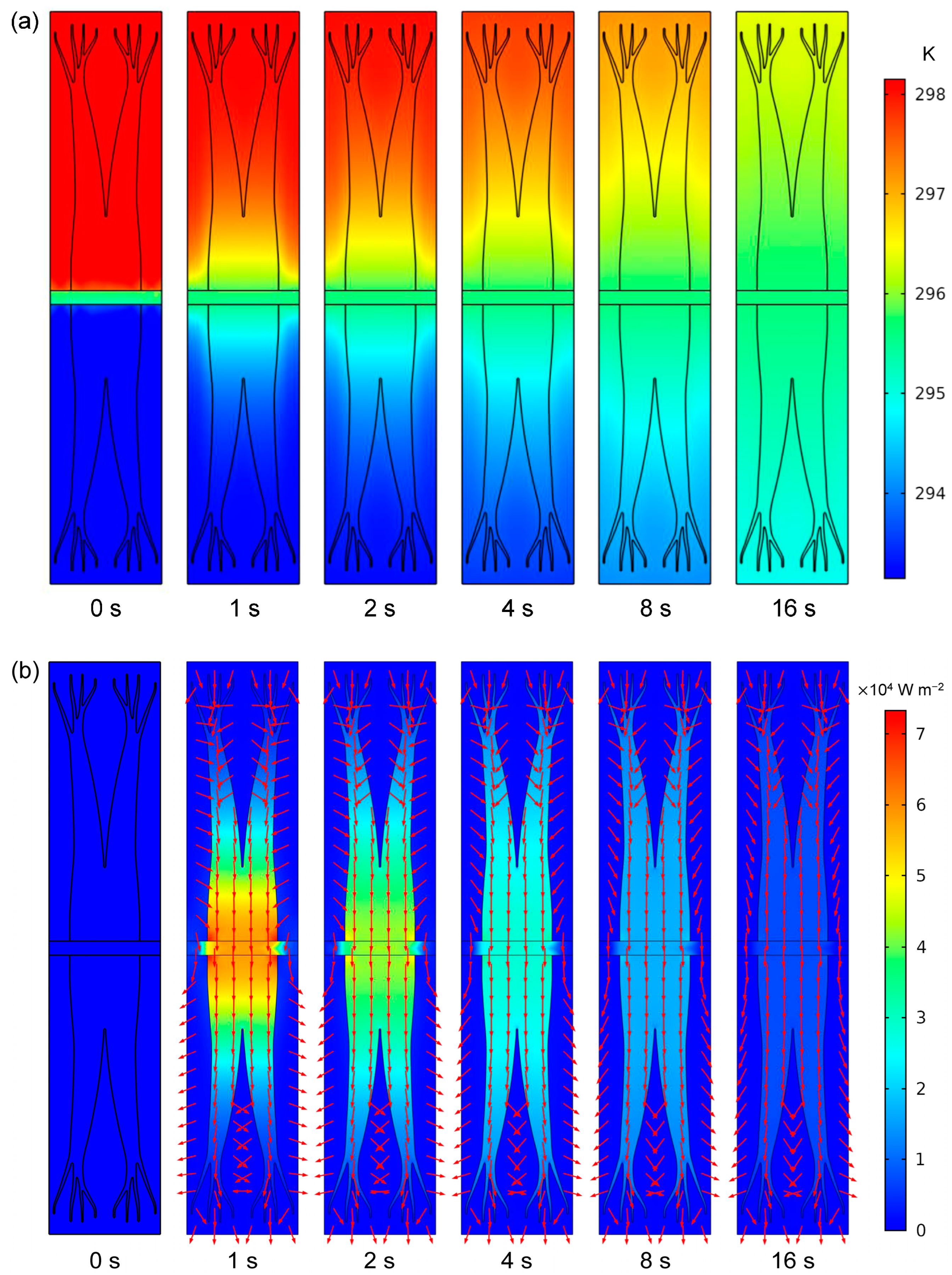
4.1. Results of Equivalent Thermal Conductivity under Three Heat Transfer Models
4.2. Influence of Interfacial Thermal Resistance on Equivalent Thermal Conductivity
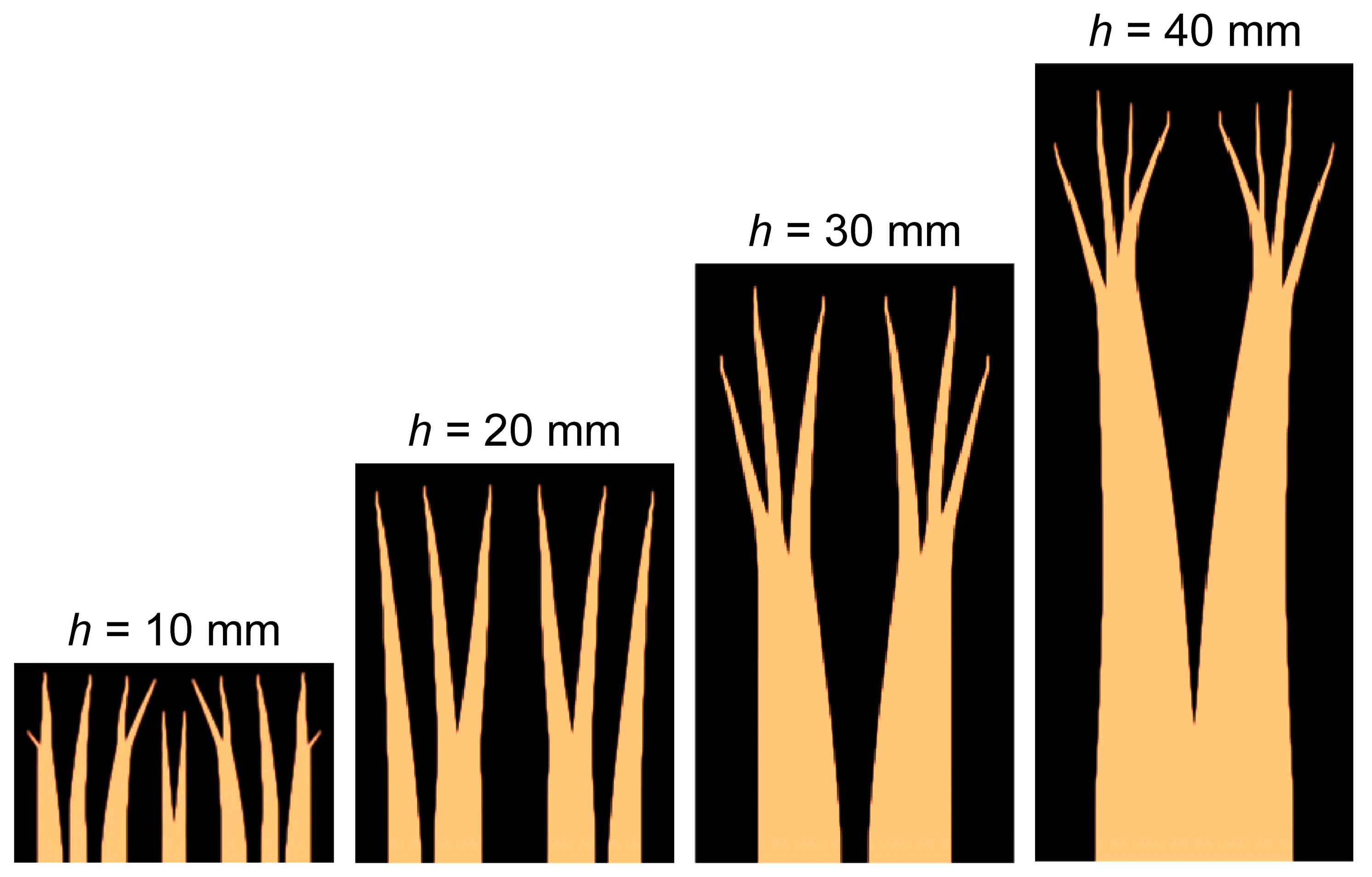
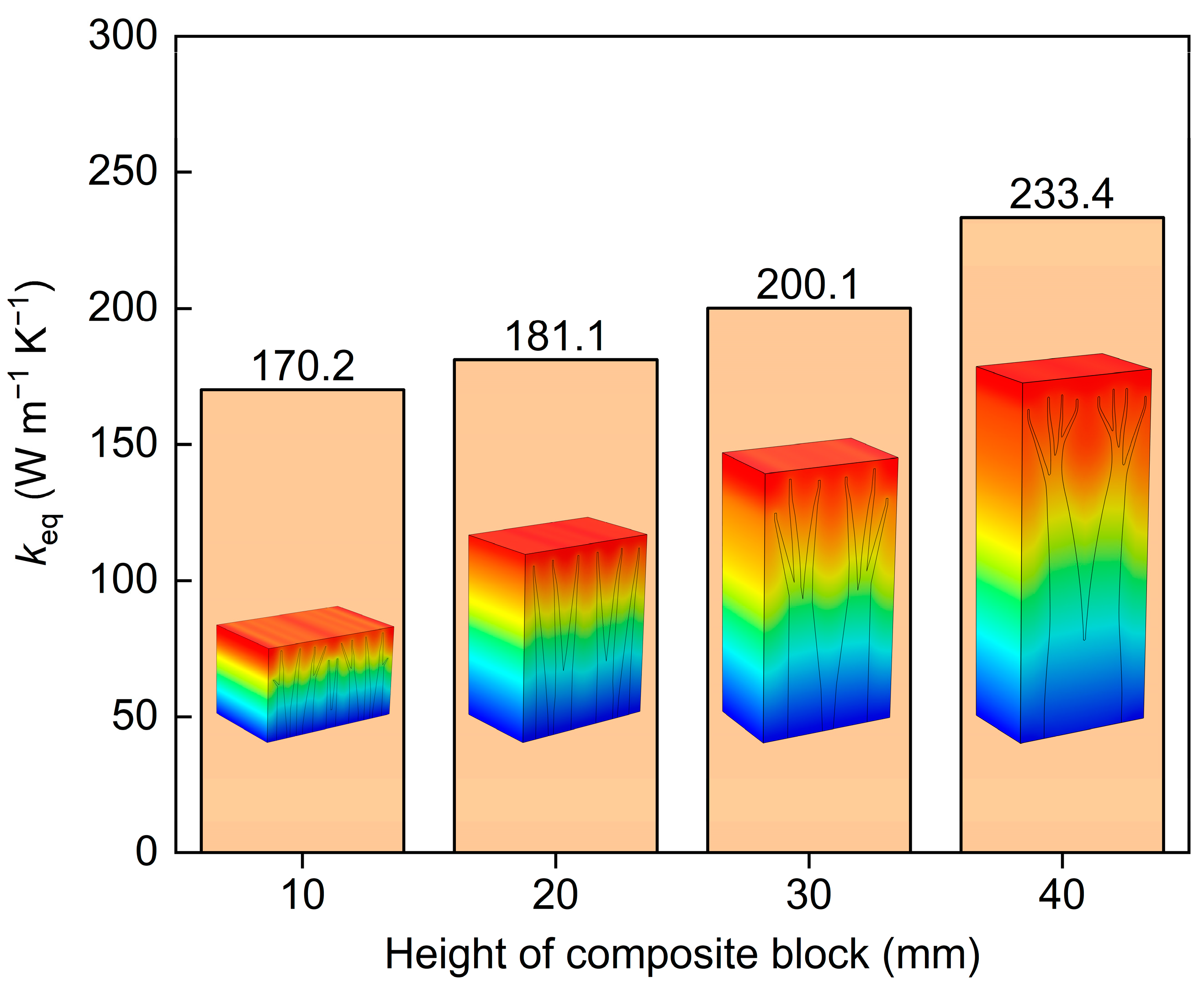
4.3. Influence of Size Effect on Equivalent Thermal Conductivity
5. Conclusions
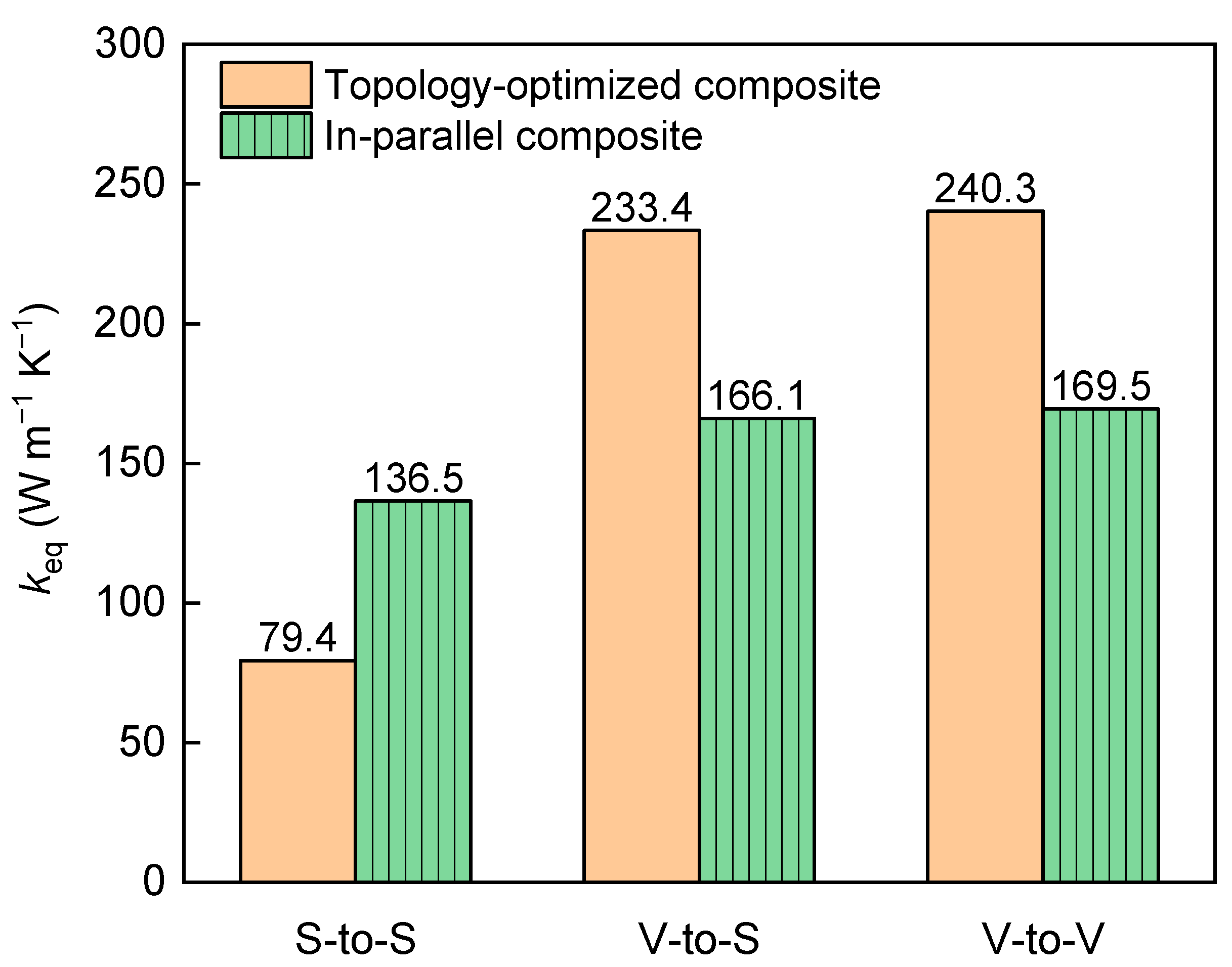
- The composite structure optimized for the V-to-S and V-to-V models has a value of only 79.4 W m−1 K−1 under the S-to-S model. However, the values are 233.4 W m−1 K−1 and 240.3 W m−1 K−1 under the V-to-S and V-to-V models, respectively, which are approximately 41% greater than those of the in-parallel structure. Therefore, the widely used effective thermal conductivity (ETC) for the S-to-S model is not appropriate for evaluating the heat transfer capability of topology-optimized composite structures. The proposed in this study is more suitable for the V-to-S and V-to-V models.
- The influence of the interfacial thermal resistance on is significant, leading to a sharp decrease in . It is important to reduce the interfacial thermal resistance and its influence on the heat transfer enhancement effect of topology-optimized composite structures, and, if necessary, adjust the topology optimization based on the influence of interfacial thermal resistance.
- The size effect has a certain impact on . It is recommended to compare and analyze the of different composite structures under the same optimization objective and specific size.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yüksel, N. The review of some commonly used methods and techniques to measure the thermal conductivity of insulation materials. In Insulation Materials in Context of Sustainability; IntechOpen: Rijeka, Croatia, 2016. [Google Scholar] [CrossRef]
- Sliwa, T.; Leśniak, P.; Sapińska-Śliwa, A.; Rosen, M.A. Effective thermal conductivity and borehole thermal resistance in selected borehole heat exchangers for the same geology. Energies 2022, 15, 1152. [Google Scholar] [CrossRef]
- Yang, G.; Cao, B.Y. Three-sensor 2ω method with multi-directional layout: A general methodology for measuring thermal conductivity of solid materials. Int. J. Heat Mass Transf. 2024, 219, 124878. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Y.; Gariboldi, E.; Li, Y. Computational models of effective thermal conductivity for periodic porous media for all volume fractions and conductivity ratios. Appl. Energy 2023, 349, 121633. [Google Scholar] [CrossRef]
- Zhan, C.; Cui, W.; Li, L. A fractal model of effective thermal conductivity of porous materials considering tortuosity. Energies 2023, 16, 271. [Google Scholar] [CrossRef]
- Hay, B.; Filtz, J.R.; Hameury, J.; Rongione, L. Uncertainty of thermal diffusivity measurements by laser flash method. Int. J. Thermophys. 2005, 26, 1883–1898. [Google Scholar] [CrossRef]
- Chen, B.; Kan, A.; Chen, Z.; Zhang, J.; Yang, L. Investigation on effective thermal conductivity of fibrous porous materials as vacuum insulation panels’ core using Lattice Boltzmann method. Energies 2023, 16, 3692. [Google Scholar] [CrossRef]
- Huang, Q.; Hong, D.; Niu, B.; Long, D.; Zhang, Y. An interpretable deep learning strategy for effective thermal conductivity prediction of porous materials. Int. J. Heat Mass Transf. 2024, 221, 125064. [Google Scholar] [CrossRef]
- Wang, J.; Carson, J.K.; North, M.F.; Cleland, D.J. A new approach to modelling the effective thermal conductivity of heterogeneous materials. Int. J. Heat Mass Transf. 2006, 49, 3075–3083. [Google Scholar] [CrossRef]
- Xiao, T.; Zhang, Q.; Yang, X.; Hooman, K.; Li, G. Influence of solder condition on effective thermal conductivity of two-directional random fibres: Pore-scale simulation. Int. J. Heat Mass Transf. 2023, 202, 123715. [Google Scholar] [CrossRef]
- Baig, M.M.; Hassan, S.F.; Saheb, N.; Patel, F. Metal Matrix Composite in Heat Sink Application: Reinforcement, Processing, and Properties. Materials 2021, 14, 6257. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; He, J.; Wang, K.; Yu, G. Solutions to obstacles in the commercialization of room-temperature magnetic refrigeration. Renew. Sustain. Energy Rev. 2021, 143, 110933. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. The constructal law and the thermodynamics of flow systems with configuration. Int. J. Heat Mass Transf. 2004, 47, 3203–3214. [Google Scholar] [CrossRef]
- Hekimoğlu, G.; Sarı, A.; Gencel, O.; Tyagi, V.V. Thermal conductivity enhancement of silica fume based composite thermal energy storage material using different carbon nanomaterials. Energy Build. 2022, 257, 111789. [Google Scholar] [CrossRef]
- Shchegolkov, A.V.; Nachtane, M.; Stanishevskiy, Y.M.; Dodina, E.P.; Rejepov, D.T.; Vetcher, A.A. The Effect of Multi-Walled Carbon Nanotubes on the Heat-Release Properties of Elastic Nanocomposites. J. Compos. Sci. 2022, 6, 333. [Google Scholar] [CrossRef]
- Meng, F.; Du, W.; Du, X.; Zhu, B.; Liu, K.; Li, S. Simultaneously enhanced thermal conductivity and mechanical performance of carbon nanotube reinforced ZK61 matrix composite. J. Magnes. Alloys 2023. [Google Scholar] [CrossRef]
- Shchegolkov, A.V.; Shchegolkov, A.V. Synthesis of Carbon Nanotubes Using Microwave Radiation: Technology, Properties, and Structure. Russ. J. Gen. Chem. 2022, 92, 1168–1172. [Google Scholar] [CrossRef]
- Feng, G.; Pan, G.; Feng, Y.; Zhang, X.; Qiu, L. Topology optimization of controllable porous microstructure with maximum thermal conductivity. Int. J. Heat Mass Transf. 2024, 220, 124990. [Google Scholar] [CrossRef]
- Zhang, F.; Feng, Y.Y.; Feng, W. Three-dimensional interconnected networks for thermally conductive polymer composites: Design, preparation, properties, and mechanisms. Mater. Sci. Eng. R Rep. 2020, 142, 100580. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, X.; Song, M.; Chen, K. An effective method for hot spot temperature optimization in heat conduction problem. Appl. Therm. Eng. 2023, 227, 120325. [Google Scholar] [CrossRef]
- Greco, A.; Aprea, C.; Maiorino, A.; Masselli, C. A review of the state of the art of solid-state caloric cooling processes at room-temperature before 2019. Int. J. Refrig. 2019, 106, 66–88. [Google Scholar] [CrossRef]
- Li, B.T.; Hong, J.; Tian, X.Y. Generating optimal topologies for heat conduction by heat flow paths identification. Int. Commun. Heat Mass Transf. 2016, 75, 177–182. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Zhang, F.Y.; Ge, Y. Constructal design for composite heat dissipating structure composed of an “arrow”-shaped high conductivity channel and an externally connected “T”-shaped fin. Int. Commun. Heat Mass Transf. 2024, 153, 107341. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization of multi-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Avendano, P.A.; Souza, J.A.; Adamatti, D.F. Construction of conductive pathways using genetic algorithms and constructal theory. Int. J. Therm. Sci. 2018, 134, 200–207. [Google Scholar] [CrossRef]
- Dang, H.; Zhang, Q.; Lu, Y.; Zhang, X.; Ma, W.; Zhang, X. Optimizing the heat source layout of chips using bionic method: Reduction of junction temperature. Int. J. Heat Mass Transf. 2022, 197, 123321. [Google Scholar] [CrossRef]
- Modrek, M.; Viswanath, A.; Khan, K.A.; Ali, M.I.; Al-Rub, R.K. Multi-objective topology optimization of passive heat sinks including self-weight based on triply periodic minimal surface lattices. Case Stud. Therm. Eng. 2023, 42, 102684. [Google Scholar] [CrossRef]
- Ruan, K.; Shi, X.; Guo, Y.; Gu, J. Interfacial thermal resistance in thermally conductive polymer composites: A review. Compos. Commun. 2020, 22, 100518. [Google Scholar] [CrossRef]
- Guo, K.; Qi, W.; Liu, B.; Liu, C.; Huang, Z.; Zhu, G. Optimization of an “area to point” heat conduction problem. Appl. Therm. Eng. 2016, 93, 61–71. [Google Scholar] [CrossRef]
- Cai, H.; Li, X.; Xie, C.; Guo, K.; Liu, H.; Liu, C. Area-to-point heat conduction enhancement using binary particle swarm optimization. Appl. Therm. Eng. 2019, 155, 449–460. [Google Scholar] [CrossRef]
- Zhao, T.; Wu, X.; Guo, Z.Y. Optimal thermal conductivity design for the volume-to-point heat conduction problem based on adjoint analysis. Case Stud. Therm. Eng. 2022, 40, 102471. [Google Scholar] [CrossRef]
- Burger, F.H.; Dirker, J.; Meyer, J.P. Three-dimensional conductive heat transfer topology optimisation in a cubic domain for the volume-to-surface problem. Int. J. Heat Mass Transf. 2013, 67, 214–224. [Google Scholar] [CrossRef]
- Zhao, T.; Sun, Q.H.; Xin, Y.L.; Chen, Q. A generalized Benders decomposition-based algorithm for heat conduction optimization and inverse design. Int. J. Heat Mass Transf. 2023, 211, 124224. [Google Scholar] [CrossRef]
- Zhang, C.; Kong, X.; Wang, X.; Du, Y.; Xiao, G. A predicting model for the effective thermal conductivity of anisotropic open-cell foam. Energies 2022, 15, 6091. [Google Scholar] [CrossRef]
- Feng, G.; Qiu, L.; Feng, Y.; Zhang, X. Topological design of open-cell microstructure with optimal effective thermal conductivity. Int. J. Heat Mass Transf. 2023, 214, 124427. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, P.; Wang, T.; Liu, C. Variabilities and their upper and lower bounds of the equivalent thermal conductivity and resistance defined by the entransy dissipation rate. Int. J. Heat Mass Transf. 2021, 170, 120990. [Google Scholar] [CrossRef]
- Sutheesh, P.M.; Chollackal, A. Thermal performance of multilayer insulation: A review. IOP Conf. Ser. Mater. Sci. Eng. 2018, 396, 12061. [Google Scholar] [CrossRef]
- Almogbel, M.; Bejan, A. Conduction trees with spacings at the tips. Int. J. Heat Mass Transf. 1999, 42, 3739–3756. [Google Scholar] [CrossRef]
- Chen, X.; Yao, W.; Zhou, W.; Zhang, Z.; Li, Y. A general differentiable layout optimization framework for heat transfer problems. Int. J. Heat Mass Transf. 2023, 211, 124205. [Google Scholar] [CrossRef]
- Min, K.; Oh, M.; Kim, C.; Yoo, J. Topological design of thermal conductors using functionally graded materials. Finite Elem. Anal. Des. 2023, 220, 103947. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Lu, B.; Wu, J.; He, J.; Huang, J. Heat transfer optimization of a fully solid state micro-unit regeneration magnetic refrigerator. Int. J. Refrig. 2019, 98, 42–50. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bejan, A.; Zane, J.P. Design in Nature: How the Constructal Law Governs Evolution in Biology, Physics, Technology and Social Organization; The Knopf Doubleday Publishing Group: New York, NY, USA, 2012; ISBN 9780307744340. [Google Scholar]
- Bejan, A. Street network theory of organization in nature. J. Adv. Transp. 1996, 30, 85–107. [Google Scholar] [CrossRef]
- Lei, T.; Alexandersen, J.; Lazarov, B.S.; Wang, F.; Haertel, J.H.; De Angelis, S.; Sanna, S.; Sigmund, O.; Engelbrecht, K. Investment casting and experimental testing of heat sinks designed by topology. Int. J. Heat Mass Transf. 2018, 127, 396–412. [Google Scholar] [CrossRef]
- Subramaniam, V.; Dbouk, T.; Harion, J.-L. Topology optimization of conductive heat transfer devices: An experimental investigation. Appl. Therm. Eng. 2018, 131, 390–411. [Google Scholar] [CrossRef]
- He, J.; Wu, J.; Zhang, H.; Zhang, Y.; Lu, B. Numerical simulation of a fully solid-state micro-unit regeneration magnetic refrigerator with micro Peltier elements. Appl. Therm. Eng. 2021, 186, 116545. [Google Scholar] [CrossRef]
- Węglewski, W.; Pitchai, P.; Chmielewski, M.; Guruprasad, P.J.; Basista, M. Thermal conductivity of Cu-matrix composites reinforced with coated SiC particles: Numerical modeling and experimental verification. Int. J. Heat Mass Transf. 2022, 188, 122633. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, K.; Feng, Y.; Liang, L.; Chi, M.; Zhang, Z.; Chen, X. Recent advances in thermal-conductive insulating polymer composites with various fillers. Compos. Part A Appl. Sci. Manuf. 2024, 178, 107998. [Google Scholar] [CrossRef]
- Song, J.N.; Zhang, Y. Effect of an interface layer on thermal conductivity of polymer composites studied by the design of double-layered and triple-layered composites. Int. J. Heat Mass Transf. 2019, 141, 1049–1055. [Google Scholar] [CrossRef]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of thermal conductivity in composites: Mechanisms, parameters and theory. Prog. Polym. Sci. 2016, 61, 1–28. [Google Scholar] [CrossRef]
- He, J.; Ya, C.; Tang, X.; Ma, L.; Wu, J.; Lu, B. Numerical study of a cascade cycle for the reciprocating solid-state magnetic refrigerator. Appl. Therm. Eng. 2023, 219, 119695. [Google Scholar] [CrossRef]
- Lu, B.; Huang, Y.; Huang, J.; Ma, Z.; Wang, J.; He, J. Influence of the interfacial thermal resistance of a gadolinium-copper bimetal composite on solid-state magnetic refrigeration. Int. J. Refrig. 2023, 153, 90–98. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S.; Isoldi, L.A.; Dos Santos, E.D.; Rocha, L.A. Geometrical evaluation of T-shaped high conductive pathway with thermal contact resistance for cooling of heat-generating medium. Int. J. Heat Mass Transf. 2017, 108, 1884–1893. [Google Scholar] [CrossRef]


| Sensor/Instrument | Type | Range | Accuracy |
|---|---|---|---|
| Thermocouple | calibrated K-type | 200–533 K | ±0.3 K |
| Data acquisition unit | Agilent 34972A | – | ±1 ms/±0.05 K |
| DC power supply | MS3010D | 0–30 V | ±1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, B.; He, J. Equivalent Thermal Conductivity of Topology-Optimized Composite Structure for Three Typical Conductive Heat Transfer Models. Energies 2024, 17, 2558. https://doi.org/10.3390/en17112558
Lu B, He J. Equivalent Thermal Conductivity of Topology-Optimized Composite Structure for Three Typical Conductive Heat Transfer Models. Energies. 2024; 17(11):2558. https://doi.org/10.3390/en17112558
Chicago/Turabian StyleLu, Biwang, and Jing He. 2024. "Equivalent Thermal Conductivity of Topology-Optimized Composite Structure for Three Typical Conductive Heat Transfer Models" Energies 17, no. 11: 2558. https://doi.org/10.3390/en17112558
APA StyleLu, B., & He, J. (2024). Equivalent Thermal Conductivity of Topology-Optimized Composite Structure for Three Typical Conductive Heat Transfer Models. Energies, 17(11), 2558. https://doi.org/10.3390/en17112558






