Numerical Investigation and Experimental Verification of the Thermal Bridge Effect of Vacuum Insulation Panels with Various Cavities
Abstract
1. Introduction
2. Materials and Methods
2.1. Calculation and Analysis of the Thermal Bridge Effect
2.1.1. Thermal Bridge Effect of VIPs
2.1.2. VIP with Cavity
2.1.3. Effective Heat Transfer Coefficient
2.1.4. Analysis of Thermal Bridge Effect
2.2. Experimental Verification
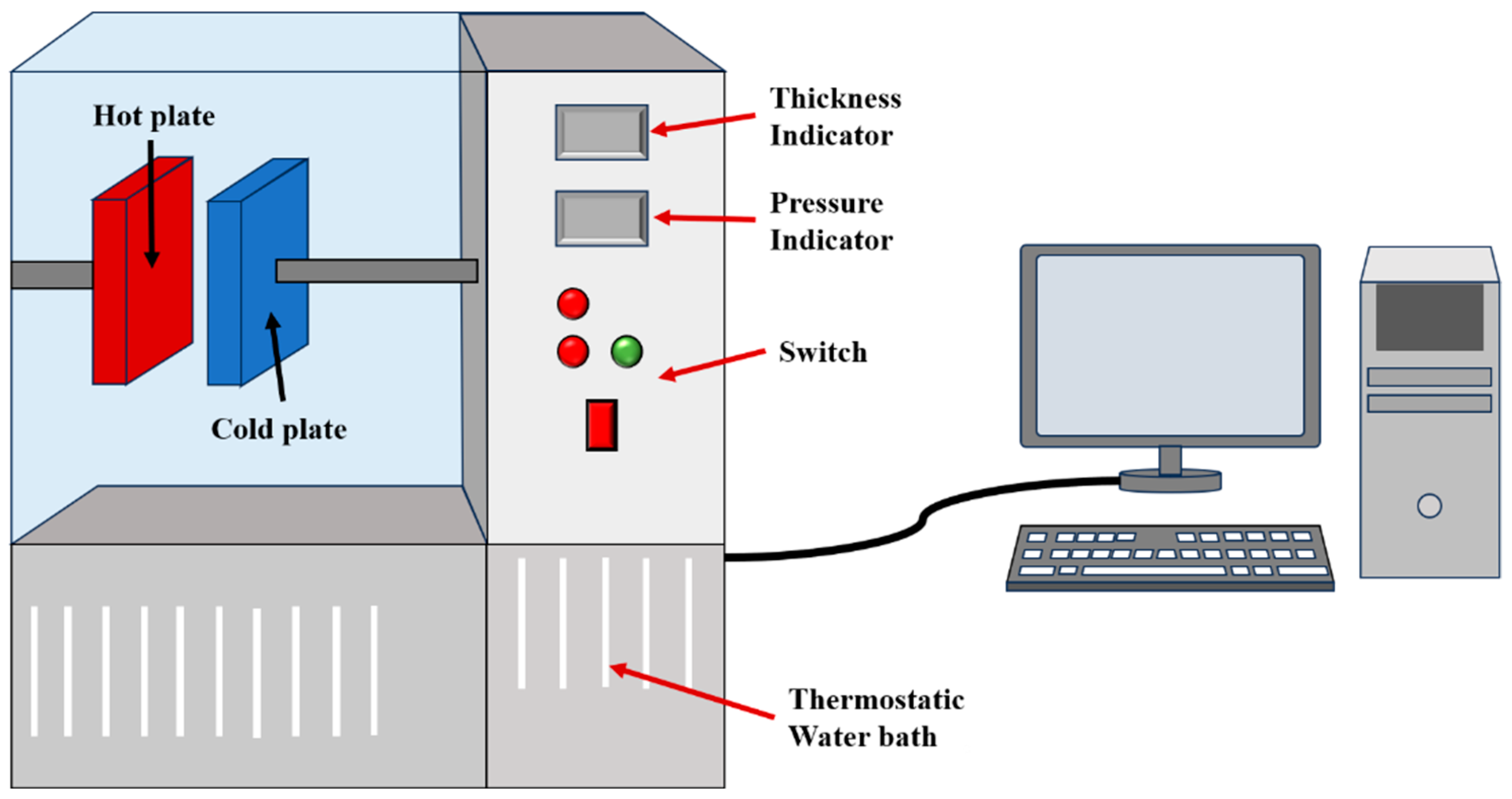
2.2.1. Experimental Apparatus
2.2.2. Preparation of Experimental Materials
2.2.3. Measurement Uncertainties
3. Results and Discussion
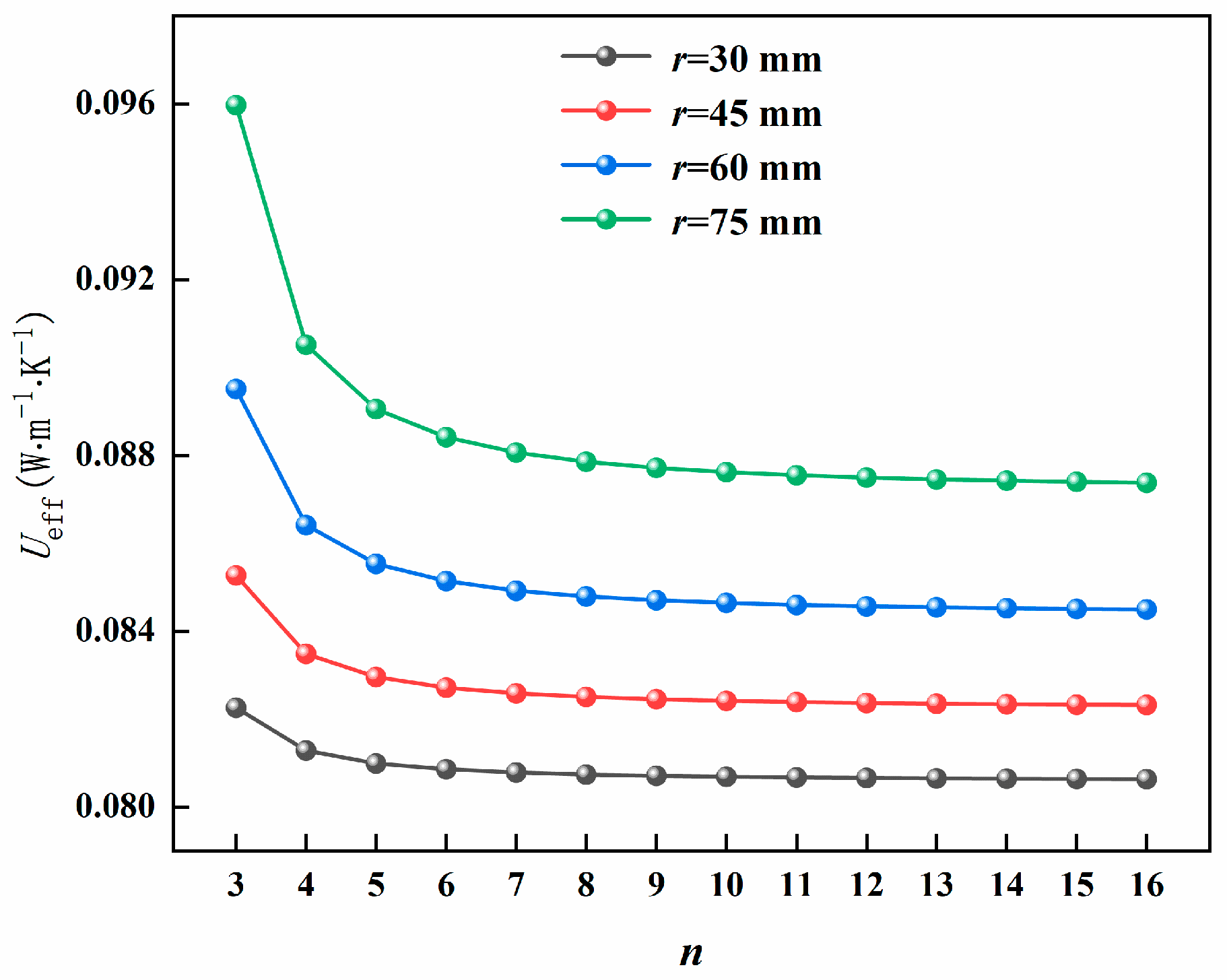
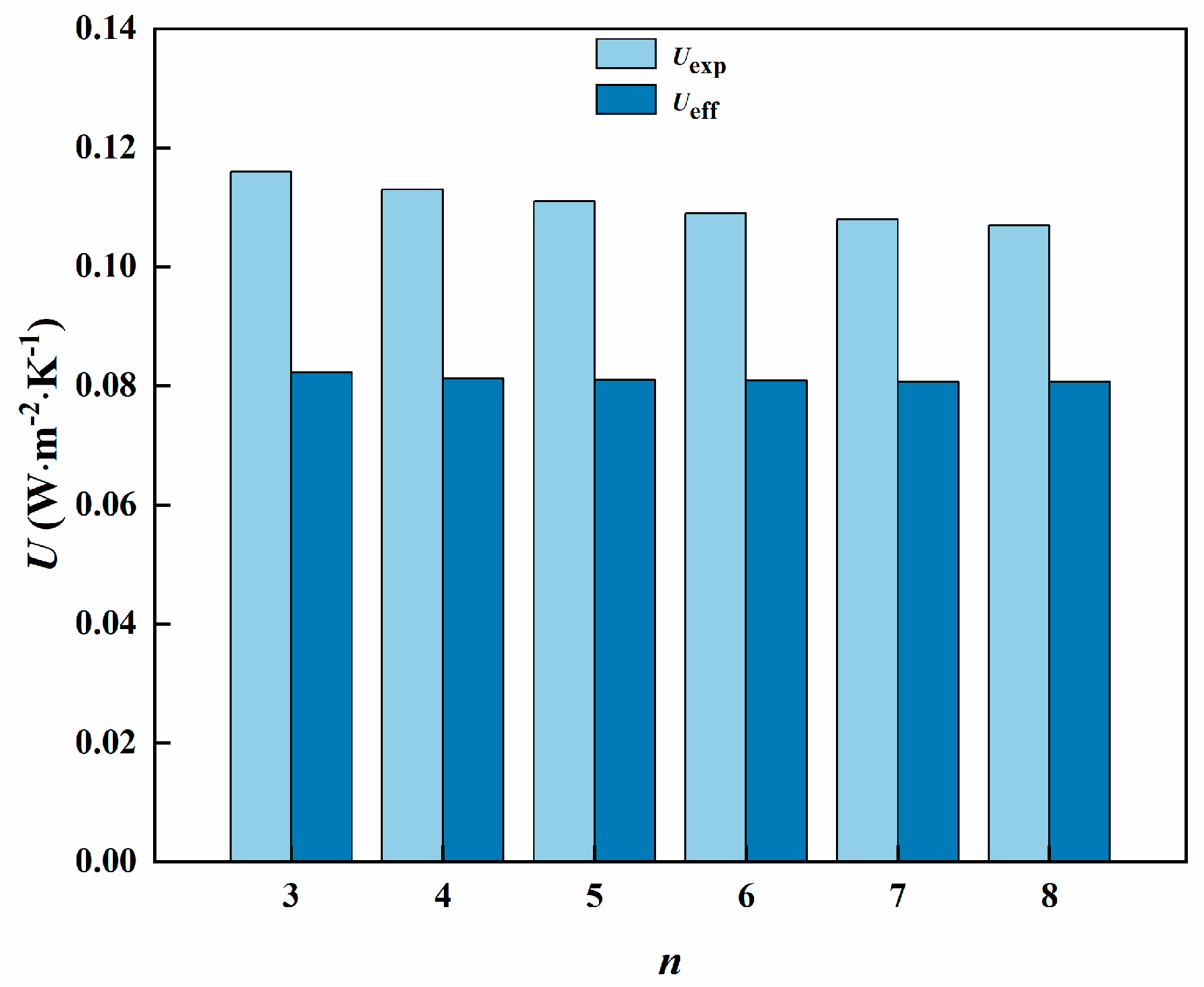
3.1. Influence of the Number of Cavity Sides
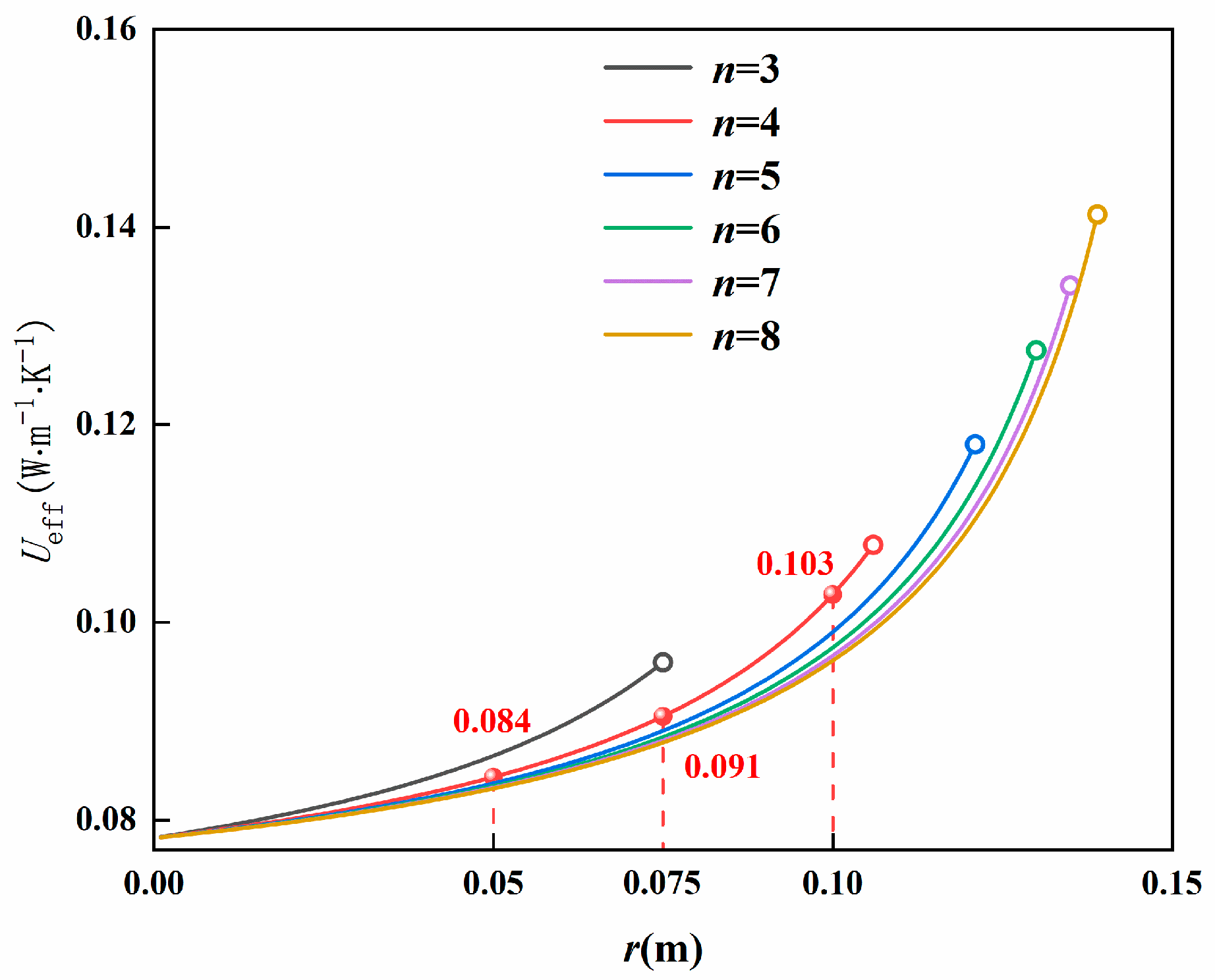
3.2. Influence of the Tangent Circle Radius of the Cavity
3.3. Simulation of the Thermal Bridge Effect
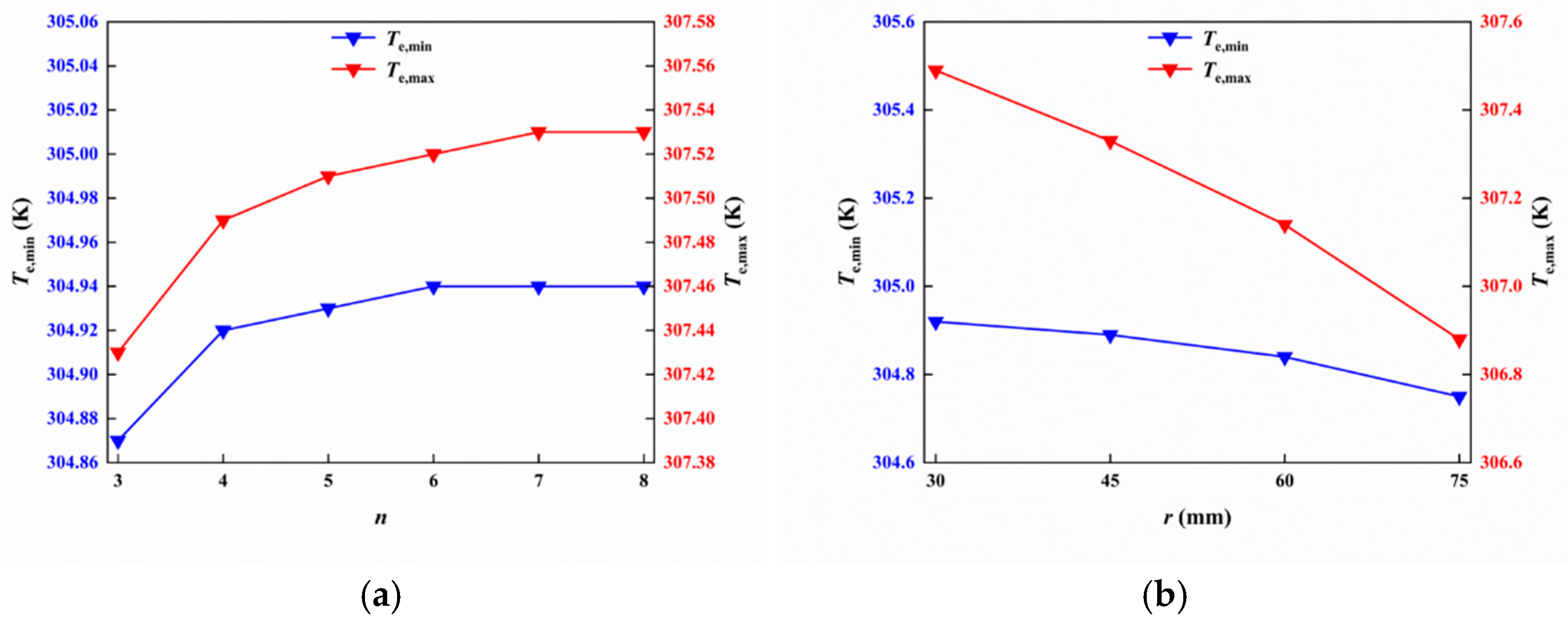
3.3.1. Influence of the Number of Sides of the Cavity
- The materials of the air and the VIP are isotropic;
- The effect of the viscosity of air on the simulation is not considered;
- Air is assumed to be an ideal gas, and its properties are independent of temperature and pressure;
- The side surfaces of the VIP are assumed to be insulated and do not exchange heat with the air.

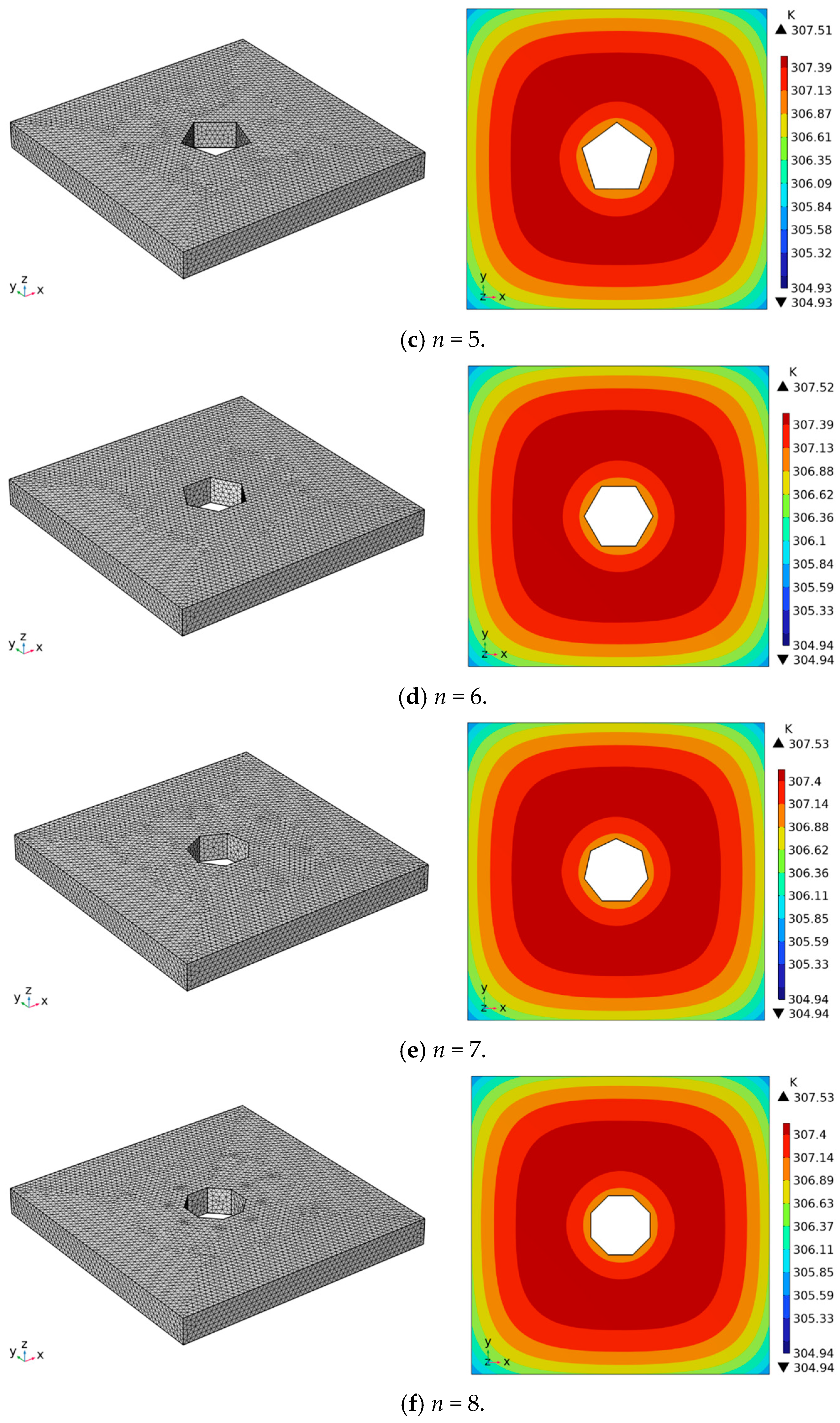
| Shape of the Cavity | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 |
|---|---|---|---|---|---|---|
| Number of domain units | 193,376 | 195,579 | 197,348 | 197,240 | 197,267 | 197,624 |
| Number of surface units | 14,448 | 14,216 | 14,488 | 14,344 | 14,406 | 14,468 |
| Number of edge units | 543 | 520 | 521 | 522 | 525 | 524 |
| Number of freedom degrees for the solution | 272,412 | 275,123 | 277,756 | 277,406 | 277,544 | 278,038 |
| Number of internal freedom degrees included | 29,989 | 29,480 | 30,027 | 29,742 | 29,873 | 29,996 |
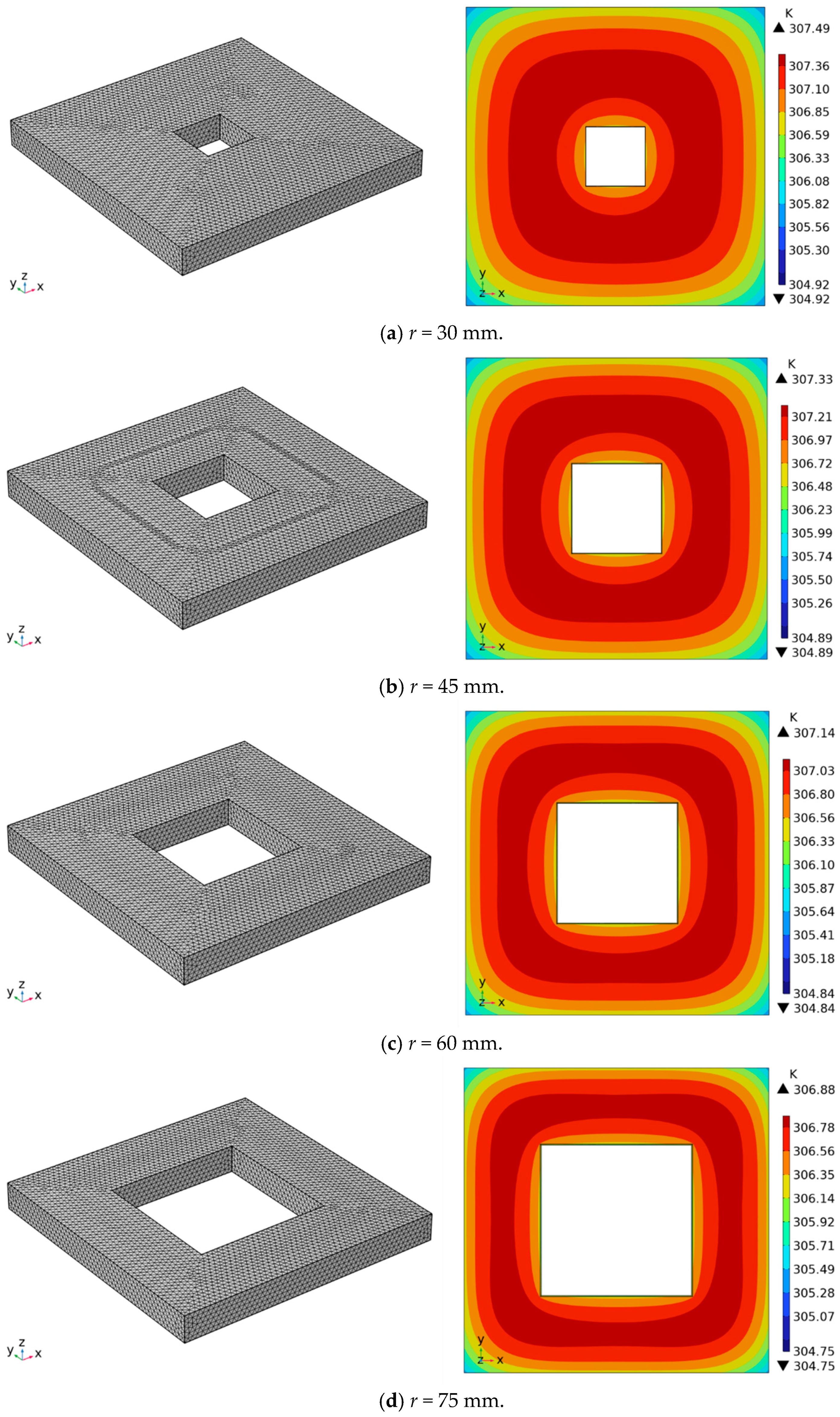
3.3.2. Influence of the Tangent Circle Radius of the Cavity
3.4. Limitations of the Study
4. Conclusions
- The thermal bridge effect when the tangent circle radius r is different or when the number of sides n of the cavity is different was investigated through experiments and numerical calculations. The results show that the influence of n and r on the thermal bridge effect could be verified by experiments and numerical calculations.
- When other boundary conditions are the same, n has a noticeable influence on the thermal bridge effect. When n is 3, the effective heat transfer coefficient is the highest. It was experimentally verified that the effective heat transfer coefficient at n = 3 was 1.9% larger than that at n = 8. The thermal bridge effect decreases with increasing n, and the insulation performance of VIP increases with increasing n. Therefore, in engineering applications, to improve the efficiency of energy utilization, a VIP with more sides to the cavity should be used, and the number of sides should be at least 8 or more.
- When other boundary conditions are the same, r has a noticeable influence on the thermal bridge effect. r is positively correlated with the thermal bridge effect of the VIP. It was experimentally verified that the effective heat transfer coefficient at r = 30 mm was 11.4% smaller than that at r = 75 mm. With an increase in r, the thermal bridge effect of the VIP gradually increases, and the insulation performance of the VIP decreases. Therefore, in engineering applications, the tangent circle radius of the cavity should be as small as possible.
- Through simulation, the thermal bridge effect was investigated when n was different. It was found that the greater the number of sides of the cavity, the higher the maximum and minimum temperatures of the hot surface, and the better the insulation performance of the VIP. The thermal bridge effect at different r values was also investigated. It was found that the larger the r value, the lower the maximum and minimum temperatures of the hot surface, and the poorer the insulation performance of the VIP. To ensure the better insulation performance of the VIP, a cavity should be selected with more sides and a smaller radius of the tangent circle, which is consistent with conclusions 2 and conclusion 3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPHM | Guarded hot plate method |
| TIP | Traditional insulation panel |
| VIP | Vacuum insulation panel |
References
- Tahir, F.; Al-Ghamdi, S.G. Climatic change impacts on the energy requirements for the built environment sector. Energy Rep. 2023, 9, 670–676. [Google Scholar] [CrossRef]
- Pei, Y.; Shen, Z.; Zhou, J.; Yang, B. Experimental and theoretical thermal performance analysis of additively manufactured polymer vacuum insulation panels. Appl. Therm. Eng. 2024, 256, 123957. [Google Scholar] [CrossRef]
- Kaushik, D.; Singh, H.; Tassou, S.A. Vacuum insulation panels for high-temperature applications—Design principles, challenges and pathways. Therm. Sci. Eng. Prog. 2024, 48, 102415. [Google Scholar] [CrossRef]
- Li, X. Farmland rental market participation and residential energy consumption: Evidence from rural areas in China. Energy 2023, 268, 126672. [Google Scholar] [CrossRef]
- Pascual, A.M.; Romero, M.L.; Serra, E.; Guerrero, J.C.; Perez, R. Sustainable insulation panel for buildings made of rice husks and posidonia. Constr. Build. Mater. 2024, 445, 137983. [Google Scholar] [CrossRef]
- Božiček, D.; Peterková, J.; Zach, J.; Košir, M. Vacuum insulation panels: An overview of research literature with an emphasis on environmental and economic studies for building applications. Renew. Sustain. Energy Rev. 2024, 189, 113849. [Google Scholar] [CrossRef]
- Wang, J.; Ma, X.; Sun, Y.; Xie, J. Thermal performance and sustainability assessment of refrigerated container with vacuum insulation panel envelope layer at different design forms. Therm. Sci. Eng. Prog. 2023, 42, 101928. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K. Double envelope vacuum insulation panel to contribute to the long-term thermal insulation performance. Vacuum 2024, 229, 113599. [Google Scholar] [CrossRef]
- Baetens, R.; Jelle, B.P.; Thue, J.V.; Tenpierik, M.J.; Grynning, S.; Uvsløkk, S.; Gustavsen, A. Vacuum insulation panels for building applications: A review and beyond. Energy Build. 2010, 42, 147–172. [Google Scholar] [CrossRef]
- Yuk, H.; Choi, J.Y.; Kim, Y.U.; Chang, S.J.; Kim, S. Historic building energy conservation with wooden attic using vacuum insulation panel retrofit technology. Build. Environ. 2023, 230, 110004. [Google Scholar] [CrossRef]
- Katsura, T.; Miyata, T.; Memon, S.; Radwan, A.; Nagano, K. Experimental analysis of vacuum pressure and gas flow rate in structured-core transparent vacuum insulation panels. Energy Rep. 2023, 9, 1071–1078. [Google Scholar] [CrossRef]
- Kalnæs, S.E.; Jelle, B.P. Vacuum insulation panel products: A state-of-the-art review and future research pathways. Appl. Energy 2014, 116, 355–375. [Google Scholar] [CrossRef]
- Alam, M.; Singh, H.; Limbachiya, M.C. Vacuum Insulation Panels (VIPs) for building construction industry—A review of the contemporary developments and future directions. Appl. Energy 2011, 88, 3592–3602. [Google Scholar] [CrossRef]
- Sun, Q.; Xu, J.; Lu, C.; Zhu, S.; Lin, G.; Fan, M.; Li, J.; Chen, K. Green and sustainable kapok fibre as novel core materials for vacuum insulations panels. Appl. Energy 2023, 347, 121394. [Google Scholar] [CrossRef]
- Gonçalves, M.; Simões, N.; Serra, C.; Flores-Colen, I.; Rottenbacher, K.; Almeida, F.A. Study of the edge thermal bridging effect in vacuum insulation panels: Steady and unsteady-state approaches using numerical and experimental methods. Energy Build. 2022, 258, 111821. [Google Scholar] [CrossRef]
- Sprengard, C.; Holm, A.H. Numerical examination of thermal bridging effects at the edges of vacuum-insulation-panels (VIP) in various constructions. Energy Build. 2014, 85, 638–643. [Google Scholar] [CrossRef]
- Mao, S.; Kan, A.; Wang, N. Numerical analysis and experimental investigation on thermal bridge effect of vacuum insulation panel. Appl. Therm. Eng. 2020, 169, 114980. [Google Scholar] [CrossRef]
- Lorenzati, A.; Fantucci, S.; Capozzoli, A.; Perino, M. Experimental and numerical investigation of thermal bridging effects of jointed Vacuum Insulation Panels. Energy Build. 2016, 111, 164–175. [Google Scholar] [CrossRef]
- Lakatos, Á.; Kovács, Z. Comparison of thermal insulation performance of vacuum insulation panels with EPS protection layers measured with different methods. Energy Build. 2021, 236, 110771. [Google Scholar] [CrossRef]
- Liang, W.; Di, X.; Zheng, S.; Wu, L.; Zhang, J. A study on thermal bridge effect of vacuum insulation panels (VIPs). J. Build. Eng. 2023, 71, 106492. [Google Scholar] [CrossRef]
- Tenpierik, M.; Cauberg, H. Analytical Models for Calculating Thermal Bridge Effects Caused by Thin High Barrier Envelopes around Vacuum Insulation Panels. J. Build. Phys. 2007, 30, 185–215. [Google Scholar] [CrossRef]
- Test Method for Steady-State Thermal Transmission Properties by Means of the Thin-Heater Apparatus. ASTM International: West Conshohocken, PA, USA, 2006. [CrossRef]
- BS EN ISO 10077; Thermal Performance Of Windows, Doors And Shutters—Calculation Of Thermal Transmittance—Part 2: Numerical Method For Frames. BSI: London, UK, 2003. [CrossRef]
- GB/T 39704-2020; Determination of Effective Thermal Conductivity for Vacuum Insulation Panels (VIP). National Standards of the People’s Republic of China: Beijing, China, 2020. (In Chinese)
- Yang, I.; Kim, D. Uncertainty of thermal conductivity measurement at high temperatures using guarded hot plate apparatus. Int. J. Heat Mass Transf. 2022, 198, 123434. [Google Scholar] [CrossRef]
- Yan, X.; Kan, A.; Chen, Z.; Hei, Y.; Chen, H.; Wu, W. A promising approach of caved vacuum insulation panel and investigation on its thermal bridge effect. Int. Commun. Heat Mass Transf. 2023, 148, 107086. [Google Scholar] [CrossRef]
- Planes, E.; Marouani, S.; Flandin, L. Optimizing the heat sealing parameters of multilayers polymeric films. J. Mater. Sci. 2011, 46, 5948–5958. [Google Scholar] [CrossRef]
- Yeo, I.; Jung, H.; Song, T.-H. Gas permeation characteristics through heat-sealed flanges of vacuum insulation panels. Vacuum 2014, 104, 70–76. [Google Scholar] [CrossRef]
- Li, C.-D.; Duan, Z.-C.; Chen, Q.; Chen, Z.-F.; Boafo, F.E.; Wu, W.-P.; Zhou, J.-M. The effect of drying condition of glassfibre core material on the thermal conductivity of vacuum insulation panel. Mater. Des. 2013, 50, 1030–1037. [Google Scholar] [CrossRef]
- Lorenzati, A.; Fantucci, S.; Capozzoli, A.; Perino, M. VIPs Thermal Conductivity Measurement: Test Methods, Limits and Uncertainty. Energy Procedia 2015, 78, 418–423. [Google Scholar] [CrossRef][Green Version]
- Kim, J.H.; Simon, T.W.; Viskanta, R. Journal of Heat Transfer Policy on Reporting Uncertainties in Experimental Measurements and Results. J. Heat Transf. 1993, 115, 5–6. [Google Scholar] [CrossRef]
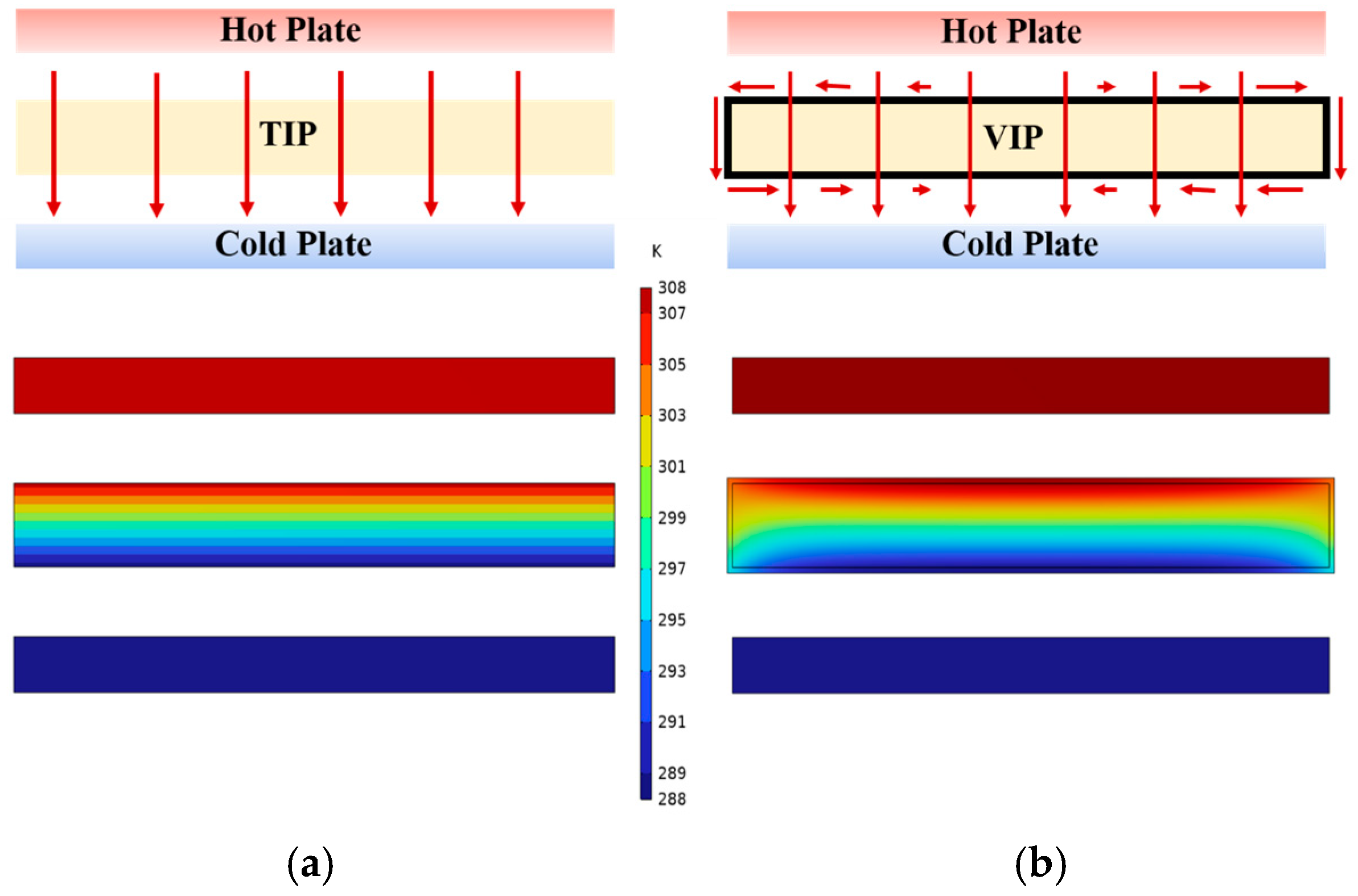





| Parameter | Type | Unit | Value | Resource |
|---|---|---|---|---|
| Ti | Temperature of the cold plate | K | 288 | [22] |
| Te | Temperature of the Hot plate | K | 308 | [22] |
| hi | Heat transfer coefficient of cold surface | W/(m2·K) | 25 | [23] |
| he | Heat transfer coefficient of hot surface | W/(m2·K) | 7.8 | [23] |
| lp | Length of the VIP | m | 0.3 | Experimental measurement |
| wp | Width of the VIP | m | 0.3 | Experimental measurement |
| δp | Thickness of the VIP | m | 0.03 | Experimental measurement |
| λp | Heat transfer conductivity of the barrier film | W/(m·K) | 0.39 | [24] |
| δb | Thickness of the barrier film | m | 8.5 × 10−5 | [24] |
| Ucop | Heat transfer coefficient of the center area of the VIP | W/(m2·K) | 0.002 | Experimental measurement |
| Experimental Group | I | II | III | IV | V | VI | VII | VIII | IX |
|---|---|---|---|---|---|---|---|---|---|
| n | 3 | 4 | 5 | 6 | 7 | 8 | 4 | 4 | 4 |
| r (mm) | 30 | 30 | 30 | 30 | 30 | 30 | 45 | 60 | 75 |
| Components | Type | Error |
|---|---|---|
| Thermocouple | DS18B20 | ±0.18–±0.27 K |
| Thickness sensor | SL-2000 | ±1.2% |
| Measure power | Shunt resistor | 1.00–1.47% |
| Vernier caliper | MNT-150 | ±0.02 mm |
| Size of the Cavity | r = 30 mm | r = 45 mm | r = 60 mm | r = 75 mm |
|---|---|---|---|---|
| Number of domain units | 195,579 | 184,912 | 171,280 | 151,987 |
| Number of surface units | 14,216 | 14,196 | 13,580 | 12,744 |
| Number of edge units | 520 | 560 | 600 | 640 |
| Number of freedom degrees for the solution | 275,123 | 260,884 | 242,138 | 215,331 |
| Number of internal freedom degrees included | 29,480 | 29,520 | 28,368 | 26,776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Kan, A.; Chen, Z.; Yang, C.; Zhang, Y.; Yang, L. Numerical Investigation and Experimental Verification of the Thermal Bridge Effect of Vacuum Insulation Panels with Various Cavities. Energies 2025, 18, 467. https://doi.org/10.3390/en18030467
Huang C, Kan A, Chen Z, Yang C, Zhang Y, Yang L. Numerical Investigation and Experimental Verification of the Thermal Bridge Effect of Vacuum Insulation Panels with Various Cavities. Energies. 2025; 18(3):467. https://doi.org/10.3390/en18030467
Chicago/Turabian StyleHuang, Chao, Ankang Kan, Zhaofeng Chen, Chao Yang, Yuan Zhang, and Lixia Yang. 2025. "Numerical Investigation and Experimental Verification of the Thermal Bridge Effect of Vacuum Insulation Panels with Various Cavities" Energies 18, no. 3: 467. https://doi.org/10.3390/en18030467
APA StyleHuang, C., Kan, A., Chen, Z., Yang, C., Zhang, Y., & Yang, L. (2025). Numerical Investigation and Experimental Verification of the Thermal Bridge Effect of Vacuum Insulation Panels with Various Cavities. Energies, 18(3), 467. https://doi.org/10.3390/en18030467







