Single Three-Phase Inverter for Dual-Frequency Induction Heating
Abstract
1. Introduction
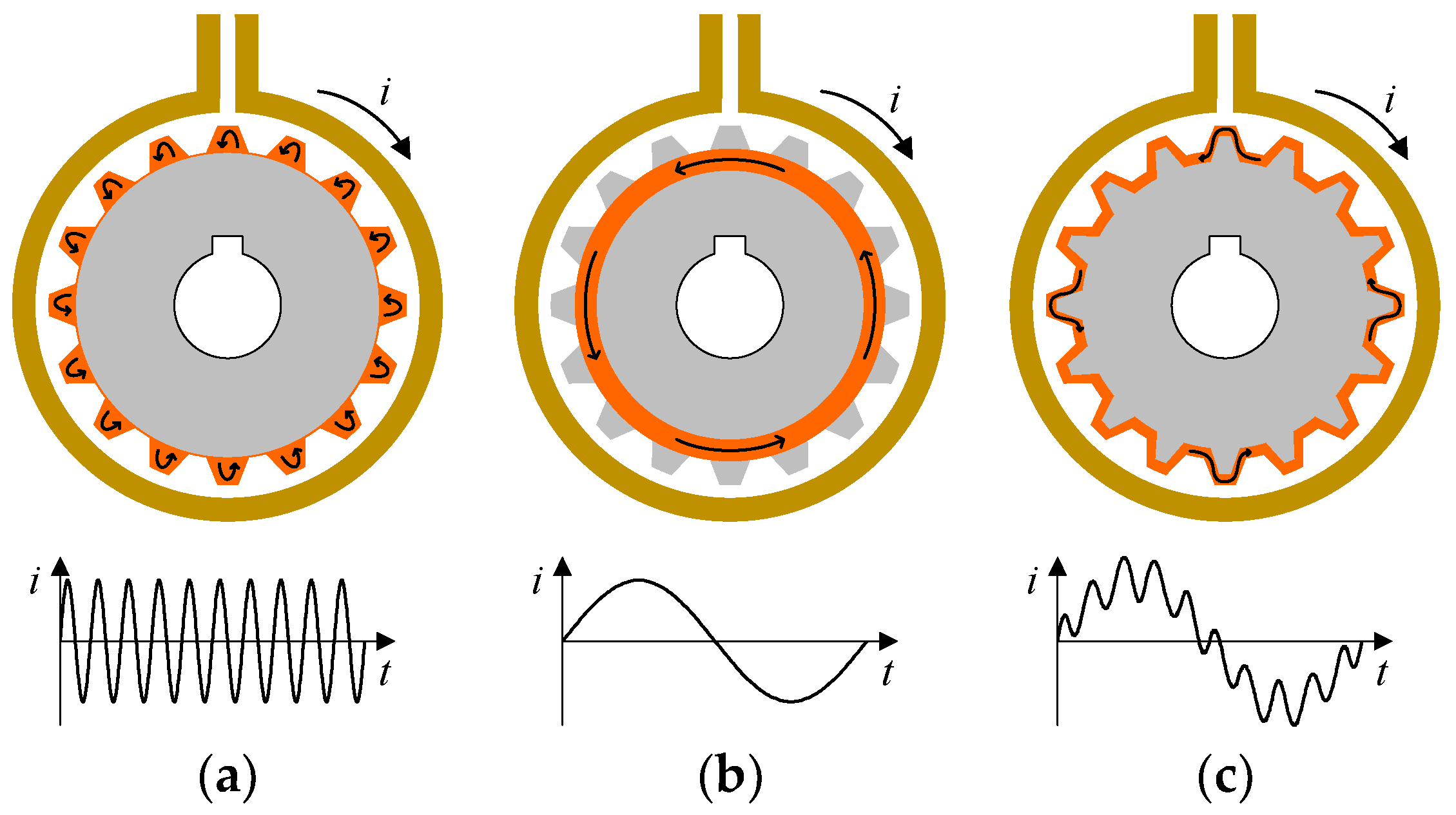
- Conventional single frequency (CSF). It is used for small- and medium-sized gears.
- Pulsing single frequency (PSF). The heating process is divided into two parts. The first one is longer and is a pre-heat. It is performed at a lower power, allowing the heat flow to reach the root without overheating the teeth at the same time. The second one is a post-heat, which is performed at a much higher power and in a much shorter time.
- Pulsing dual frequency (PDF). It is similar to the previous one. Pre-heating is carried out when the inductor is supplied with an MF current. HF current and much higher power are used for post-heating.
- Simultaneous dual frequency (SDF). It is characterized by the fact that the inductor is supplied with a current with two components, HF and MF, simultaneously. The hardening process can be carried out in different ways. It is possible to adjust the on/off times of individual components, as well as their power.
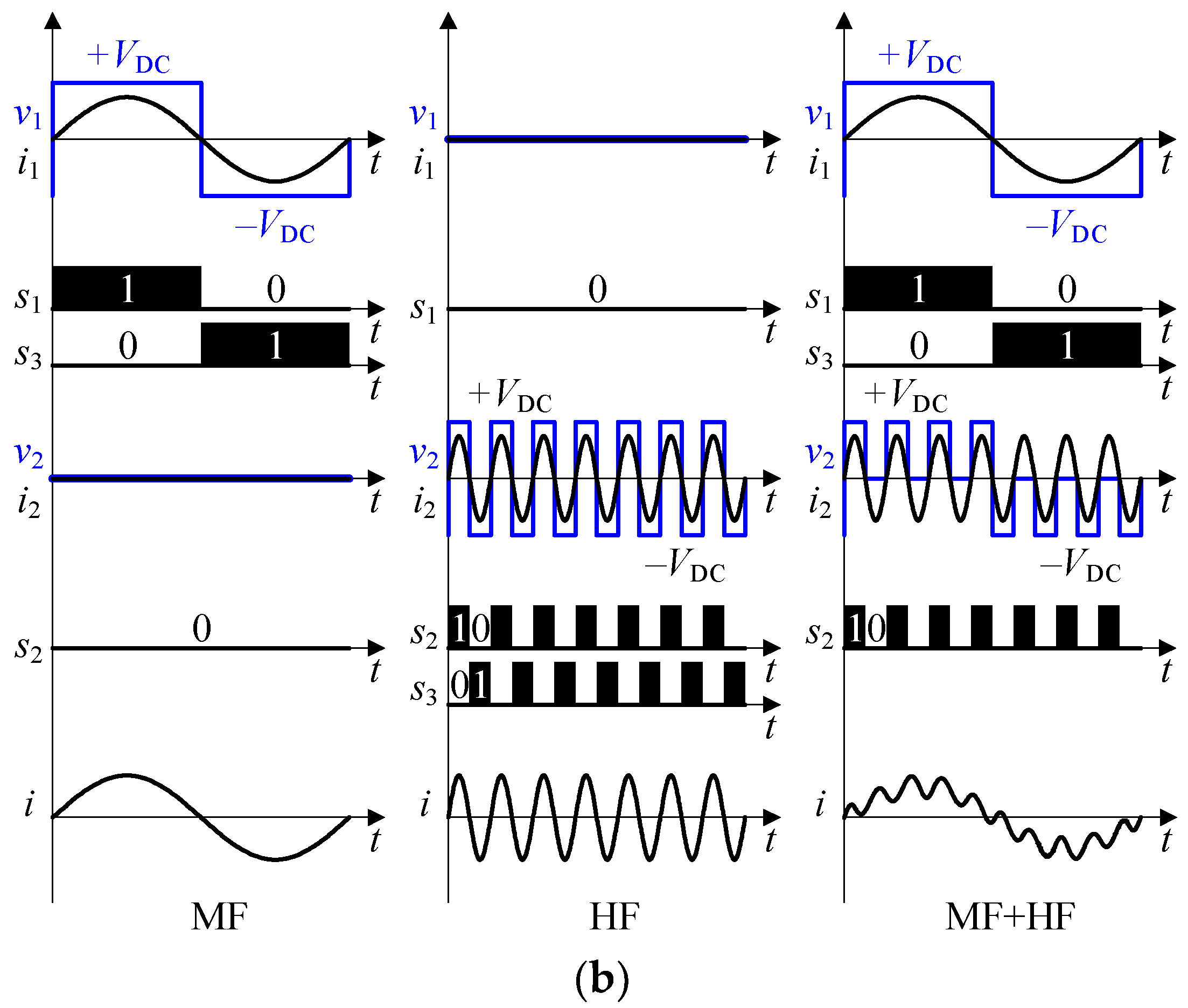
2. Proposed Dual-Frequency Inverter Topologies
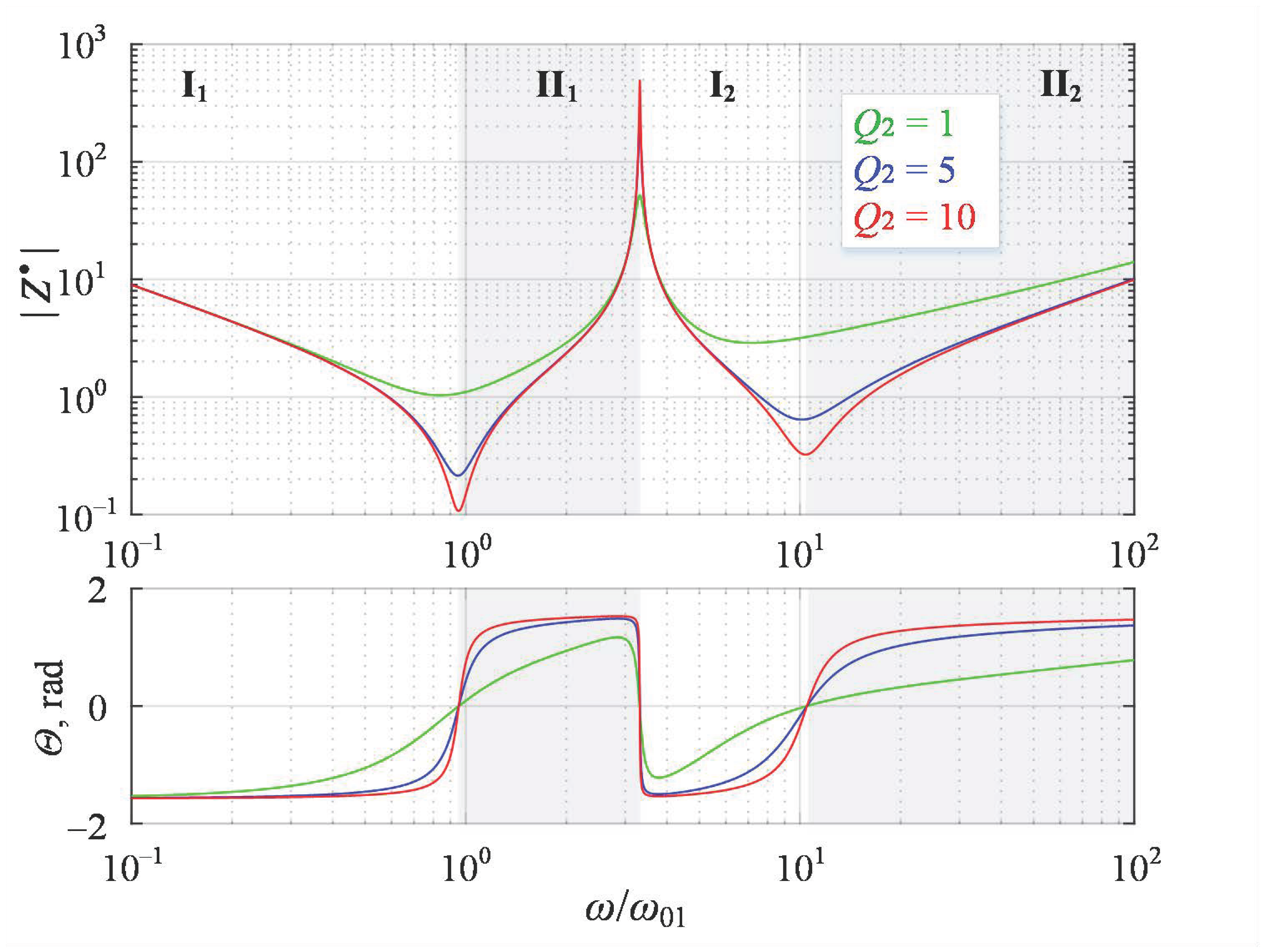
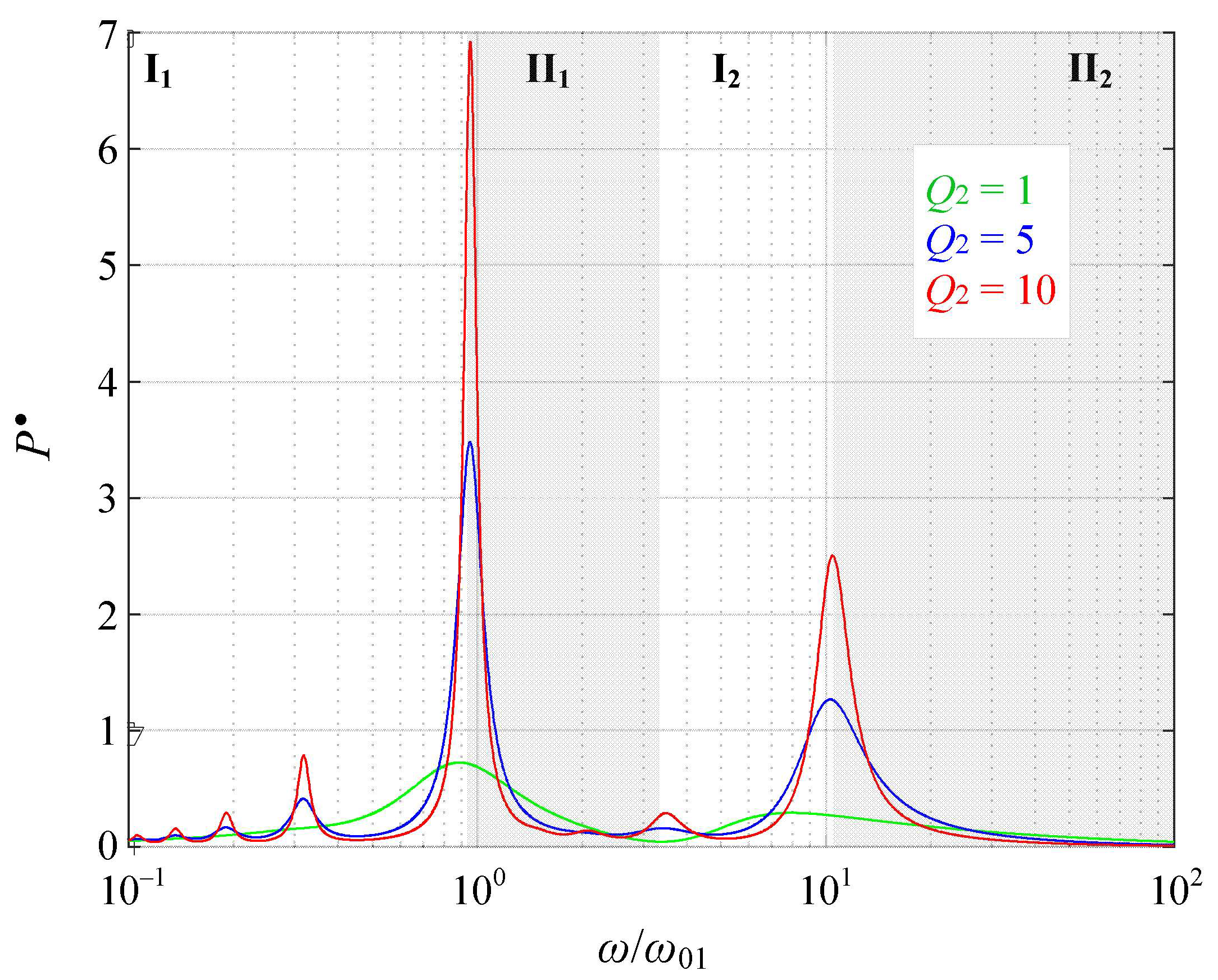
3. Analytical Model of the Inverter Load
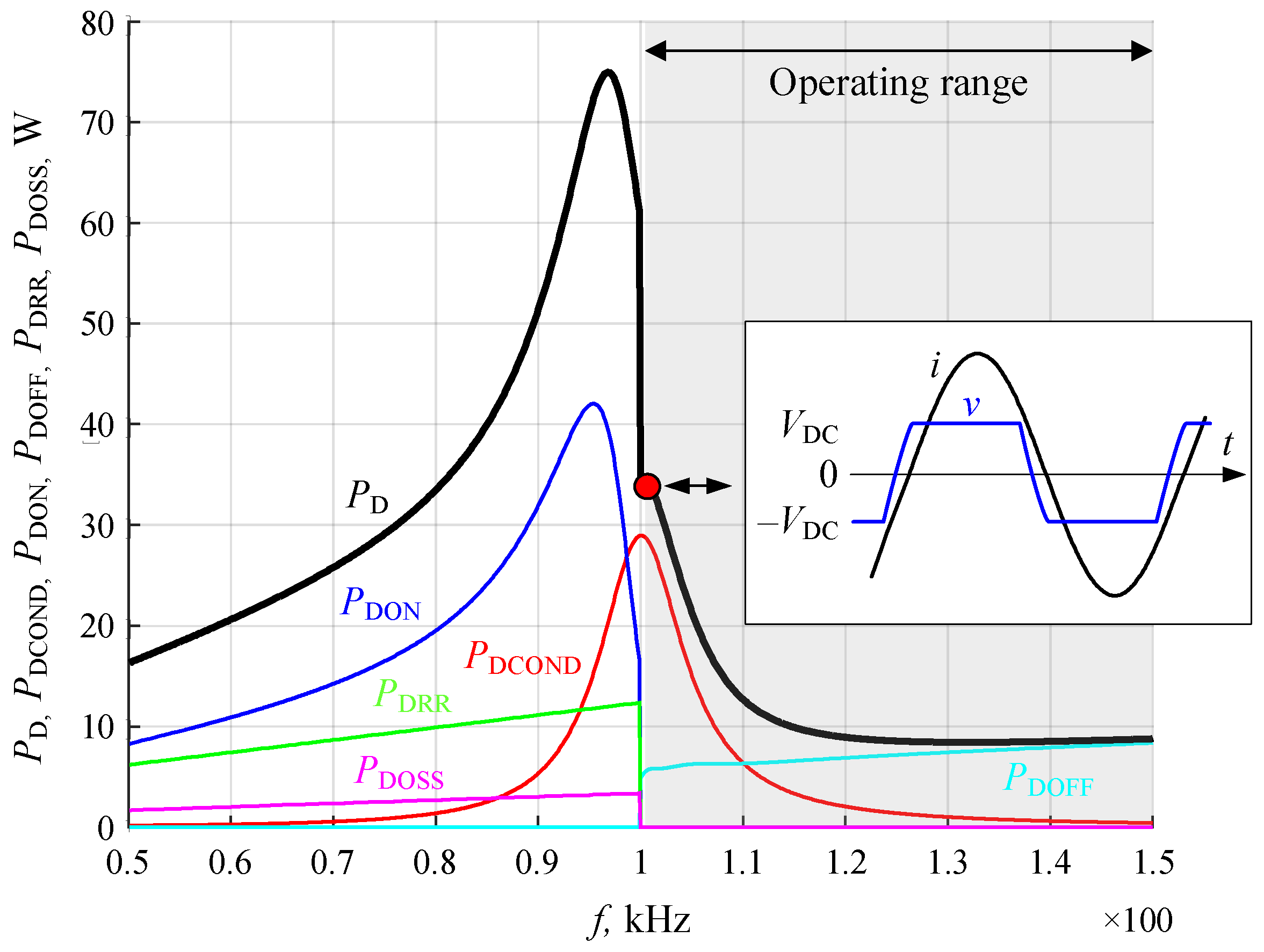
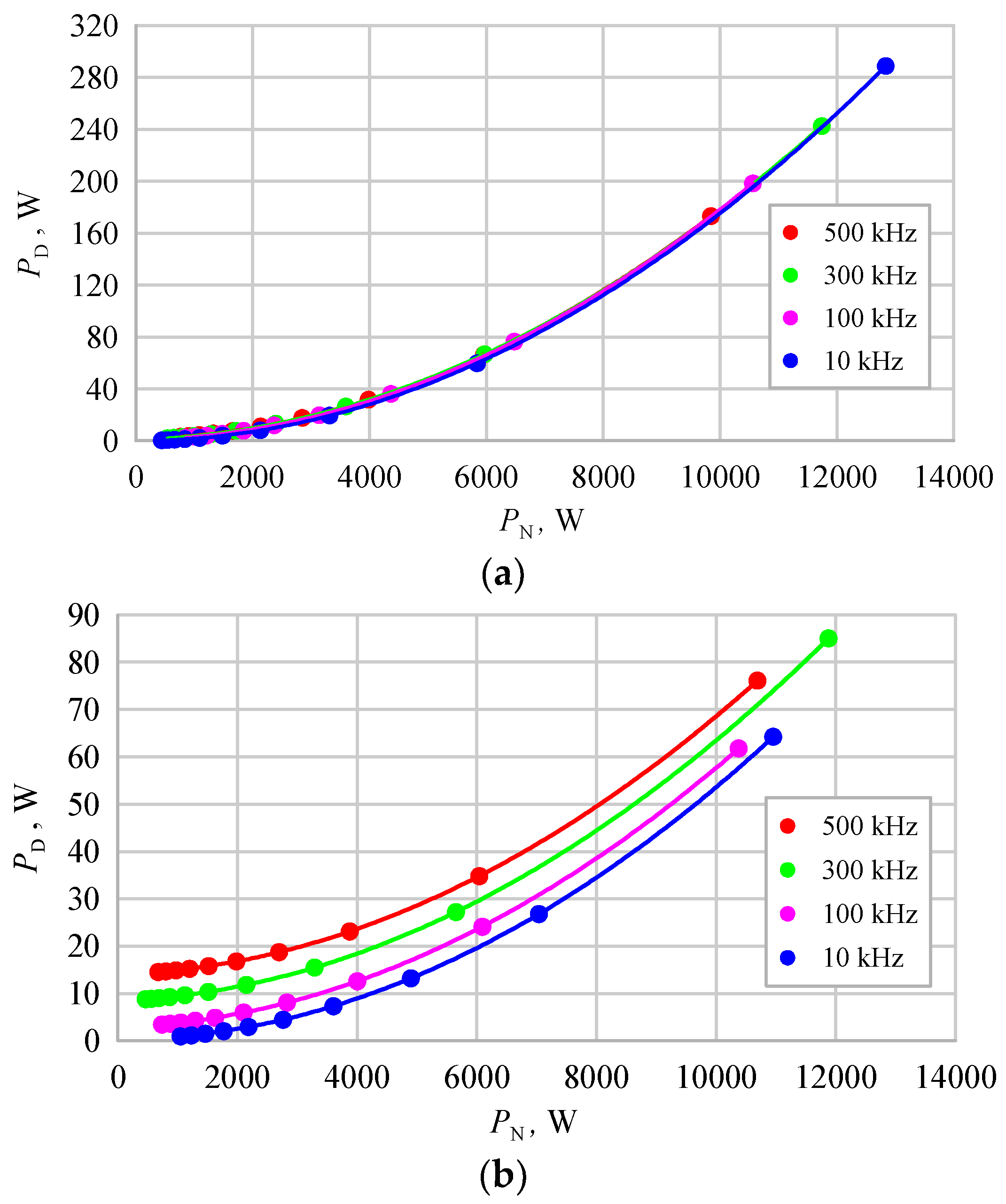
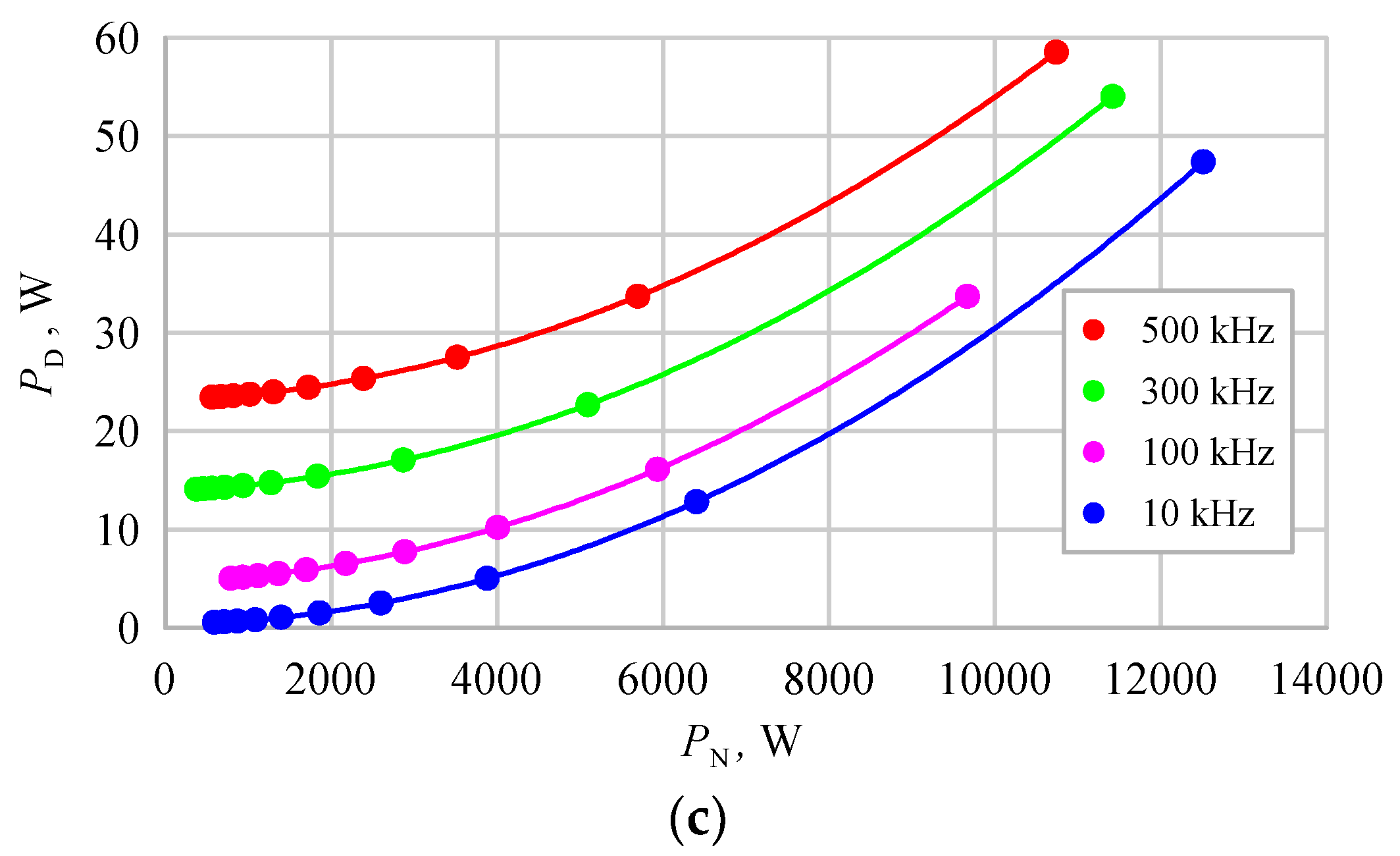
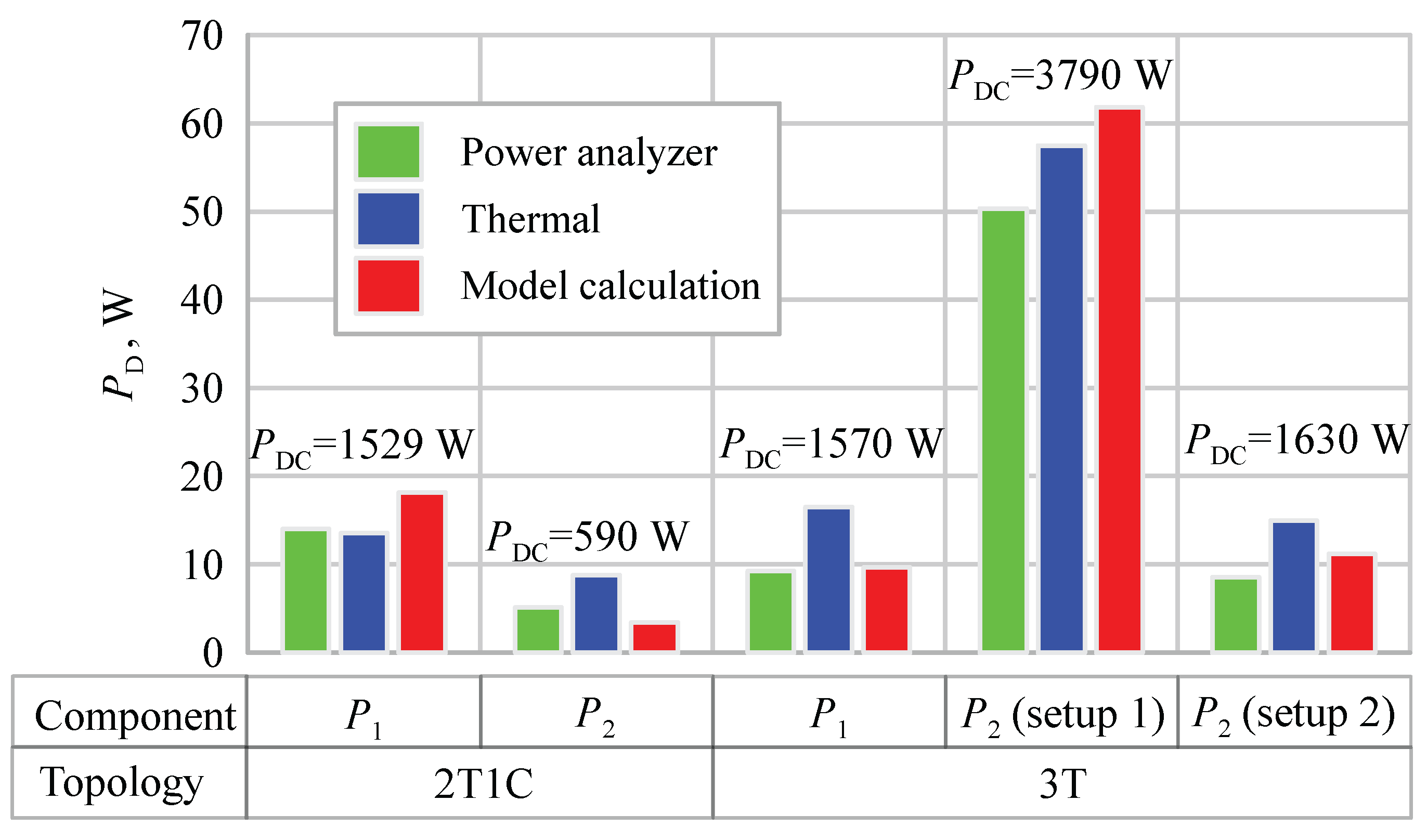
4. Power Losses of Converter
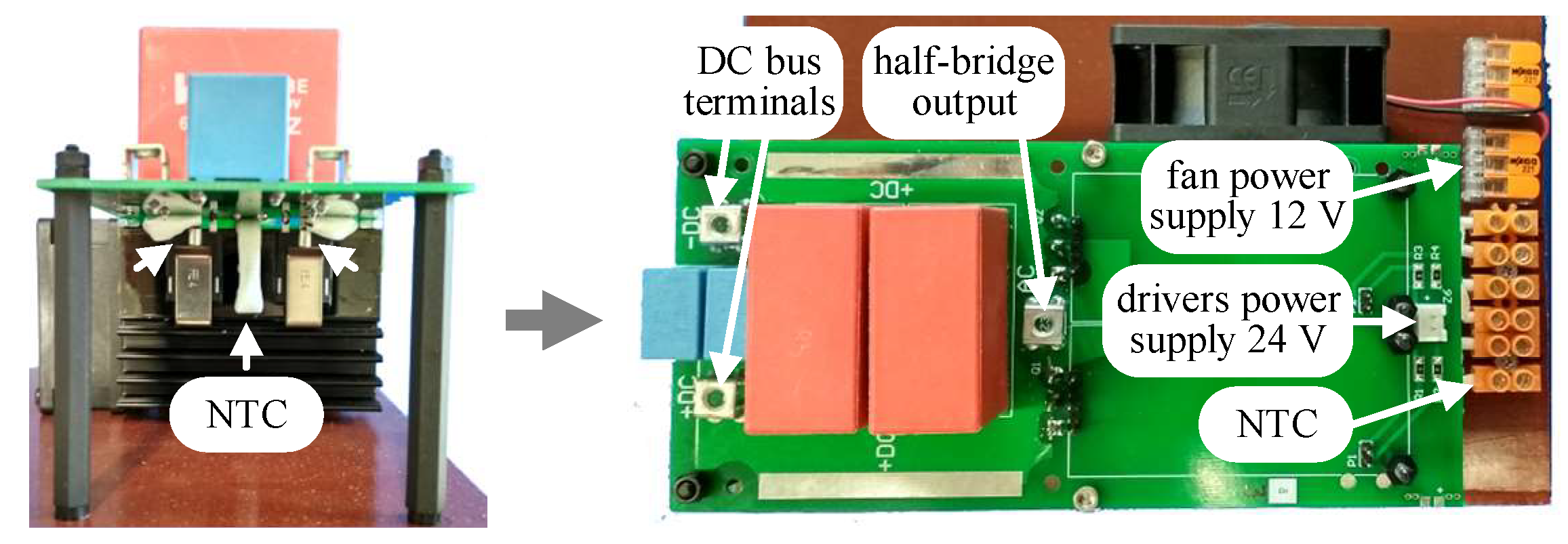
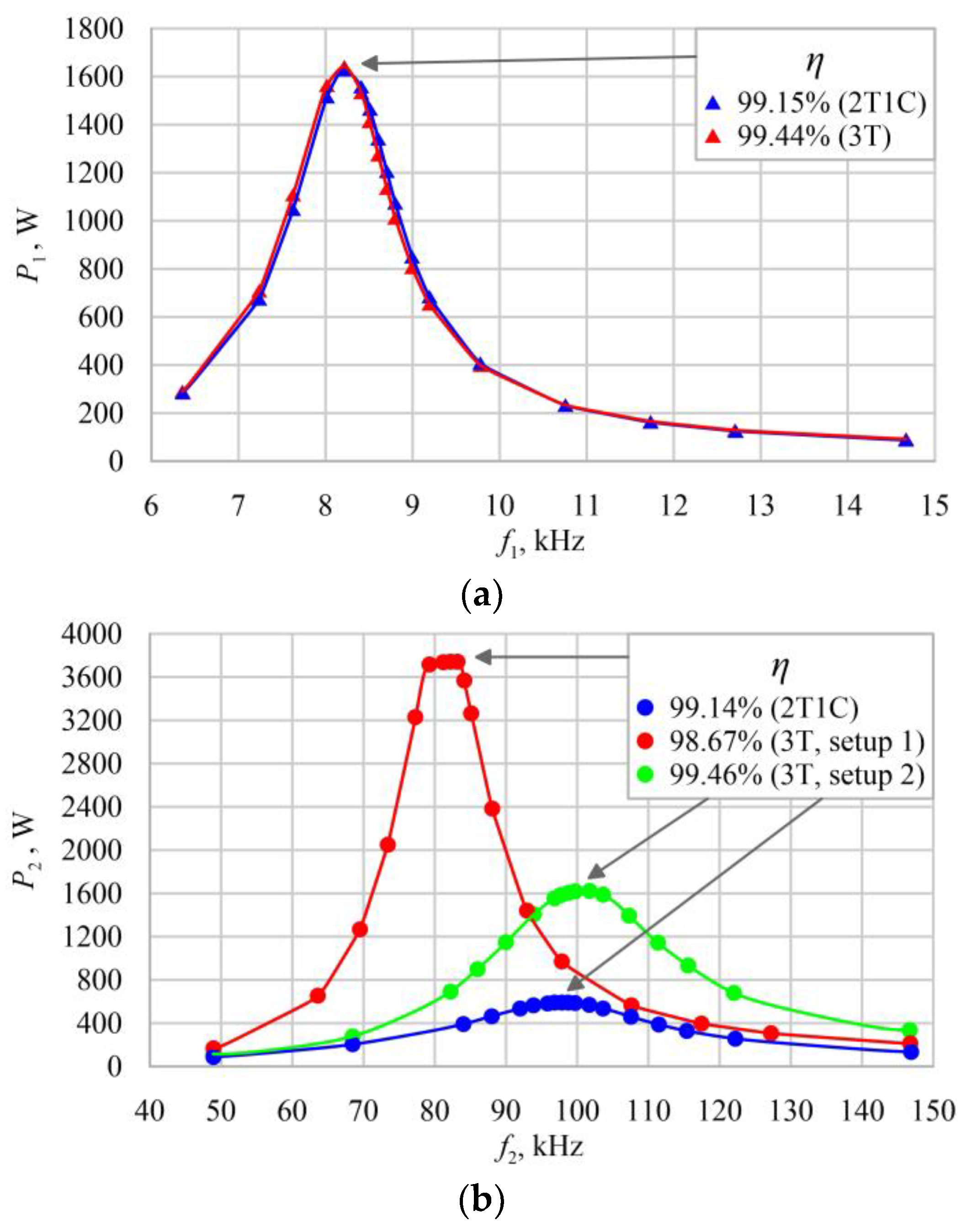
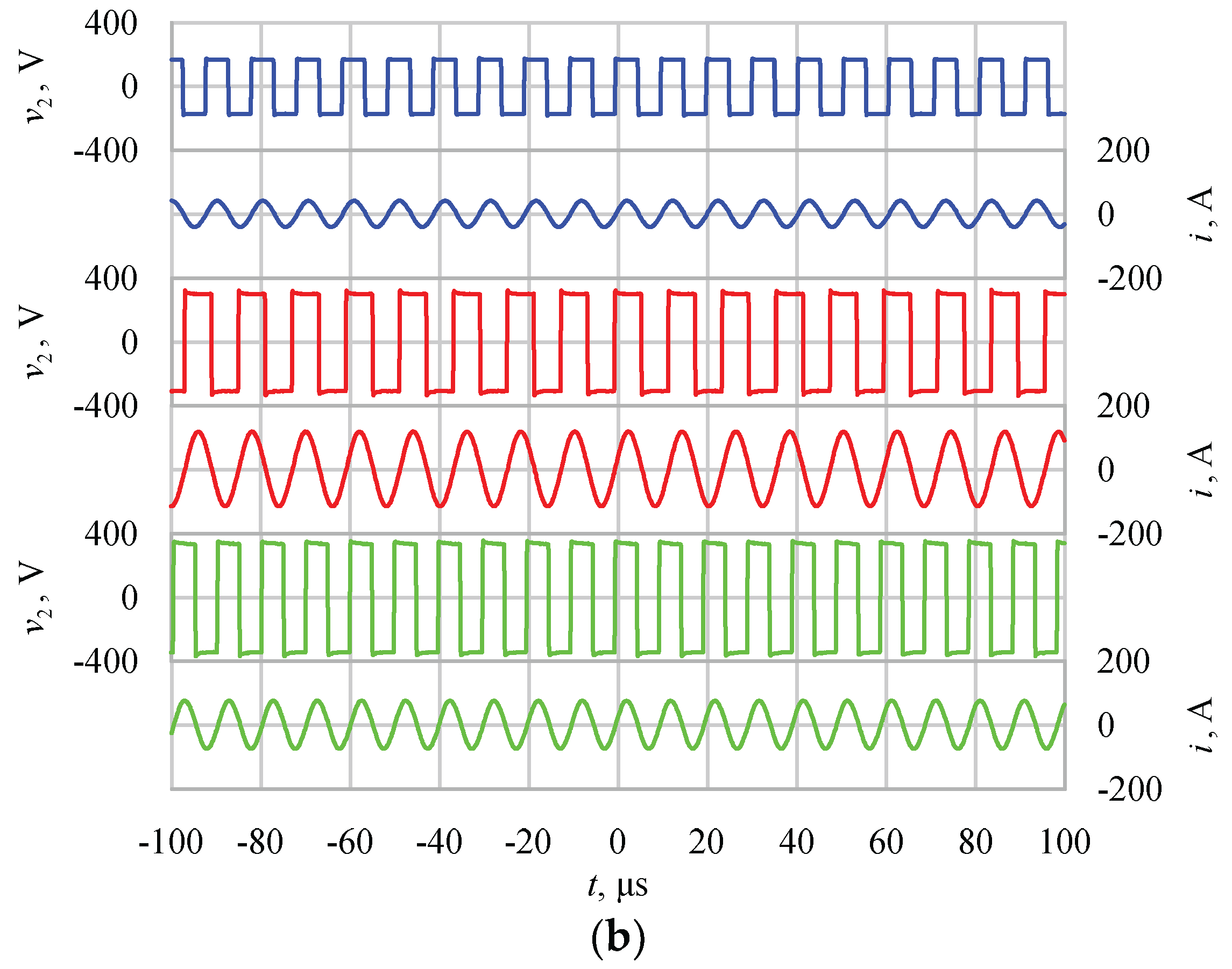
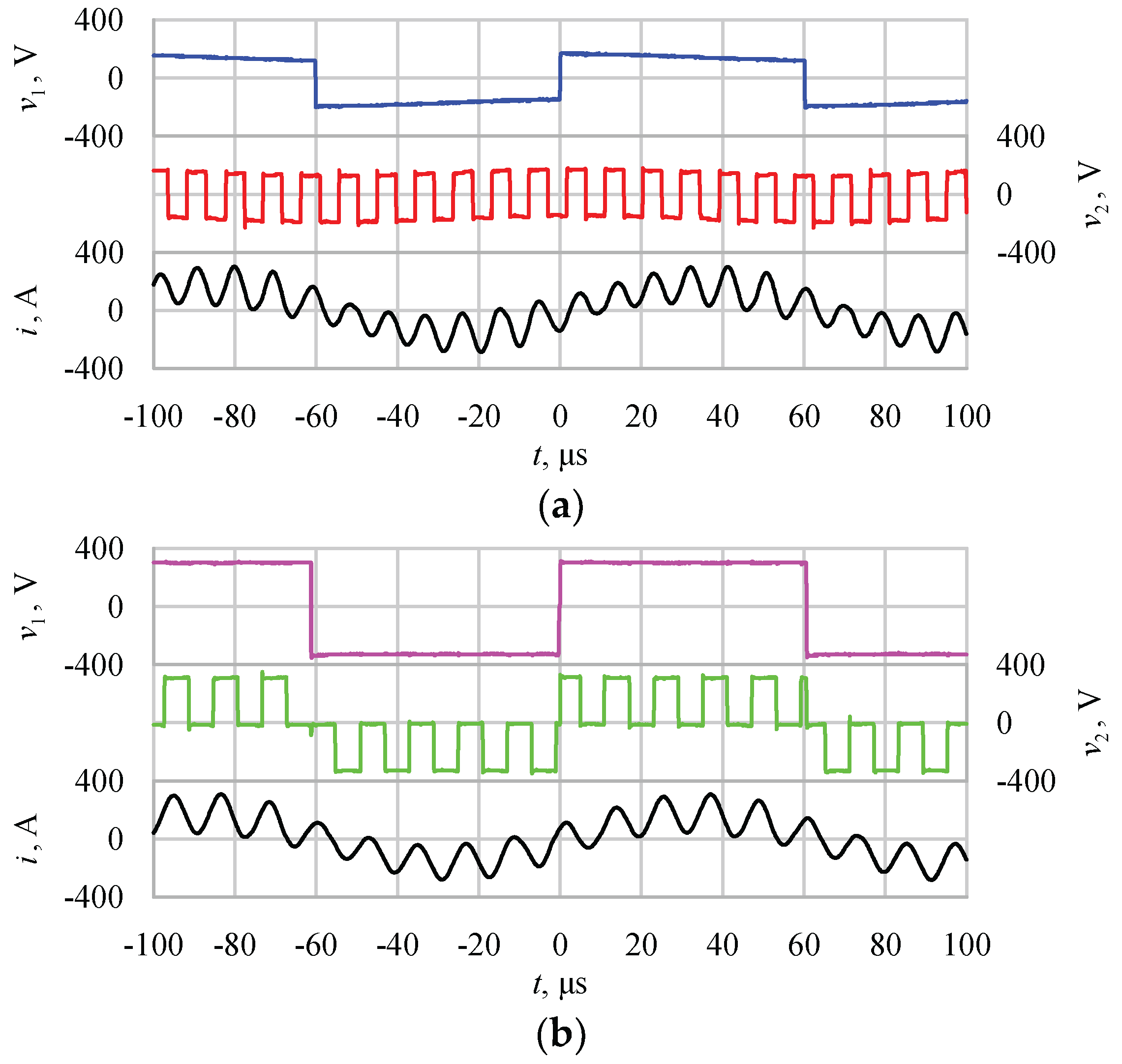
5. Experimental Results
6. Conclusions
7. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mühlbauer, A. History of Induction Heating and Melting; Vulkan-Verlag: Essen, Germany, 2008. [Google Scholar]
- Hofmann, C.; Kroll, M.; Panhale, S.; Wiemer, M.; Kunke, A.; Hiller, K.; Kuhn, H. Inductive Heating Based on VHF-ISM Radio Band Frequencies as Technology Platform for Efficient Heating of Metallic Micro-Scaled Bonding Layers in MEMS Packaging. IEEE Trans. Magn. 2023, 59, 2800905. [Google Scholar] [CrossRef]
- Wang, B.; Mingyin, Y. Research on the Improvement of Lithium-Ion Battery Performance at Low Temperatures Based on Electromagnetic Induction Heating Technology. Energies 2023, 16, 7780. [Google Scholar] [CrossRef]
- Esteve, V.; Jordan, J.; Dede, E.J.; Sanchis-Kilders, E.; Martinez, P.J.; Maset, E.; Gilabert, D. Optimal LLC Inverter Design with SiC MOSFETs and Phase Shift Control for Induction Heating Applications. IEEE Trans. Ind. Electron. 2022, 69, 11100–11111. [Google Scholar] [CrossRef]
- Pascual, A.; Acero, J.; Carretero, C.; Llorente, S.; Burdio, J. Electromagnetic Modeling and Analysis of Multimaterial Cookware for Domestic Induction Heating. IEEE Access 2023, 11, 79275–79284. [Google Scholar] [CrossRef]
- Sezer, C.; Altintas, N. Adaptation of Inductive Power Transfer to Small Household Appliances That Can Operate on Induction Heating Cooktops: Wireless Electric Kettle. Energies 2023, 16, 3544. [Google Scholar] [CrossRef]
- Zungor, F.; Bodur, H.; Ozturk, M.; Obdan, H. Design Methodology of Series Resonant Half Bridge Inverter for Induction Cooker. IEEE Access 2023, 11, 135476–135492. [Google Scholar] [CrossRef]
- Lodi, M.B.; Makridis, A.; Kazeli, K.; Samaras, T.; Angelakeris, M.; Mazzarella, G.; Fanti, A. On the Evaluation of the Hyperthermic Efficiency of Magnetic Scaffolds. IEEE Open J. Eng. Med. Biol. 2023, 5, 88–98. [Google Scholar] [CrossRef] [PubMed]
- Prantner, M.; Parspour, N. Eddy Current Heating of Implanted Devices for Tumor Ablation: Numerical-Analytic Analysis and Optimization. IEEE Access 2023, 11, 52088–52100. [Google Scholar] [CrossRef]
- Chang, C.-J.; Tai, C.-C.; Lin, F.-W.; Kuo, C.-C.; Hung, C.-M. Effects of Flexible Induction Coil Pitch on the Heating Performance of Thermotherapy Needles. IEEE Trans. Instrum. Meas. 2020, 69, 8983–8991. [Google Scholar] [CrossRef]
- Plumed, E.; Lope, I.; Acero, J. Induction Heating Adaptation of a Different-Sized Load With Matching Secondary Inductor to Achieve Uniform Heating and Enhance Vertical Displacement. IEEE Trans. Power Electron. 2021, 36, 6929–6942. [Google Scholar] [CrossRef]
- Pham, H.N.; Fujita, H.; Ozaki, K.; Uchida, N. Estimating Method of Heat Distribution Using 3-D Resistance Matrix for Zone-Control Induction Heating Systems. IEEE Trans. Power Electron. 2012, 27, 3374–3382. [Google Scholar] [CrossRef]
- Egalon, J.; Caux, S.; Maussion, P.; Souley, M.; Pateau, O. Multiphase System for Metal Disc Induction Heating: Modeling and RMS Current Control. IEEE Trans. Ind. Appl. 2012, 48, 1692–1699. [Google Scholar] [CrossRef]
- Pascual, A.; Acero, J.; Llorente, S.; Carretero, C.; Burdio, J.M. Small-Sized Immersible Water Heaters for Domestic Induction Heating Technology. IEEE Access 2023, 11, 51480–51489. [Google Scholar] [CrossRef]
- Rudnev, V.; Loveless, D.; Cook, R.; Black, M. Induction Hardening of Gears: A Review. Part 1. Heat Treat. Met. 2003, 4, 97–103. [Google Scholar]
- Rudnev, V.; Loveless, D.; Cook, R.; Black, M. Induction Hardening of Gears: A Review. Part 2. Heat Treat. Met. 2004, 1, 11–15. [Google Scholar]
- Schwenk, W.; Häussler, A.; Heiliger, A. Einrichtung zum induktiven Erwärmen von Werkstücken. Patent EP1363474B1, 16 April 2003. [Google Scholar]
- Esteve, V.; Jordan, J.; Dede, E.J.; Magraner, J.M.; Cases, C. Inductive Heating Converter Comprising a Resonant Circuit with Simultaneous Multi-Frequency Current Output and at Least Two Inverters. Patent EP2147983A1, 21 July 2008. [Google Scholar]
- Dede, E.J.; Esteve, V.; Jordan, J.; Cases, C.; Magraner, J.M. Inductive Heating Apparatus Comprising a Resonant Circuit with Simultaneous Dual Frequency Current Output and a Single Inverter Circuit with Silicon Carbide. Patent EP2148551A1, 21 July 2008. [Google Scholar]
- Esteve, V.; Pardo, J.; Jordan, J.; Dede, E.J.; Sanchis-Kilders, E.; Maset, E. High Power Resonant Inverter with Simultaneous Dual-Frequency Output. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2005; pp. 1278–1281. [Google Scholar]
- Esteve, V.; Jordan, J.; Dede, E.J.; Sanchis-Kilders, E.; Maset, E. Induction Heating Inverter with Simultaneous Dual-Frequency Output. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006; pp. 1505–1509. [Google Scholar]
- Esteve, V.; Jordan, J.; Sanchis-Kilders, E.; Dede, E.J.; Maset, E.; Ejea, J.B.; Ferreres, A. Comparative Study of a Single Inverter Bridge for Dual-Frequency Induction Heating Using Si and SiC MOSFETs. IEEE Trans. Ind. Electron. 2015, 62, 1440–1450. [Google Scholar] [CrossRef]
- Sarnago, H.; Lucia, O.; Burdio, J.M. Multiresonant Power Converter for Improved Dual-Frequency Induction Heating. IEEE Trans. Power Electron. 2019, 34, 2097–2103. [Google Scholar] [CrossRef]
- Zgraja, J. Dual-Frequency Induction Heating Generator with Adjustable Impedance Matching. IEEE Trans. Ind. Electron. 2019, 66, 8308–8317. [Google Scholar] [CrossRef]
- Kierepka, K.; Frania, K.; Kasprzak, M.; Zimoch, P. Double-Frequency Induction Heating Device with 3-Phase Voltage Inverter with Half Capacitor Bridge. Patent PL241666B1, 25 April 2022. [Google Scholar]
- Kierepka, K.; Frania, K.; Kasprzak, M.; Zimoch, P. Device for Two-Frequency Induction Heating with a 3-Phase Voltage Inverter. Patent PL439134A1, 9 May 2022. [Google Scholar]
- Rudnev, V.; Loveless, D.; Cook, R. Handbook of Induction Heating; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zhang, X.; Feng, Z.; Wang, J.; Yu, S. An Optimized Temperature Sensor Calorimetric Power Device Loss Measurement Method. Energies 2019, 12, 1333. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K. High-Frequency Magnetic Components; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]



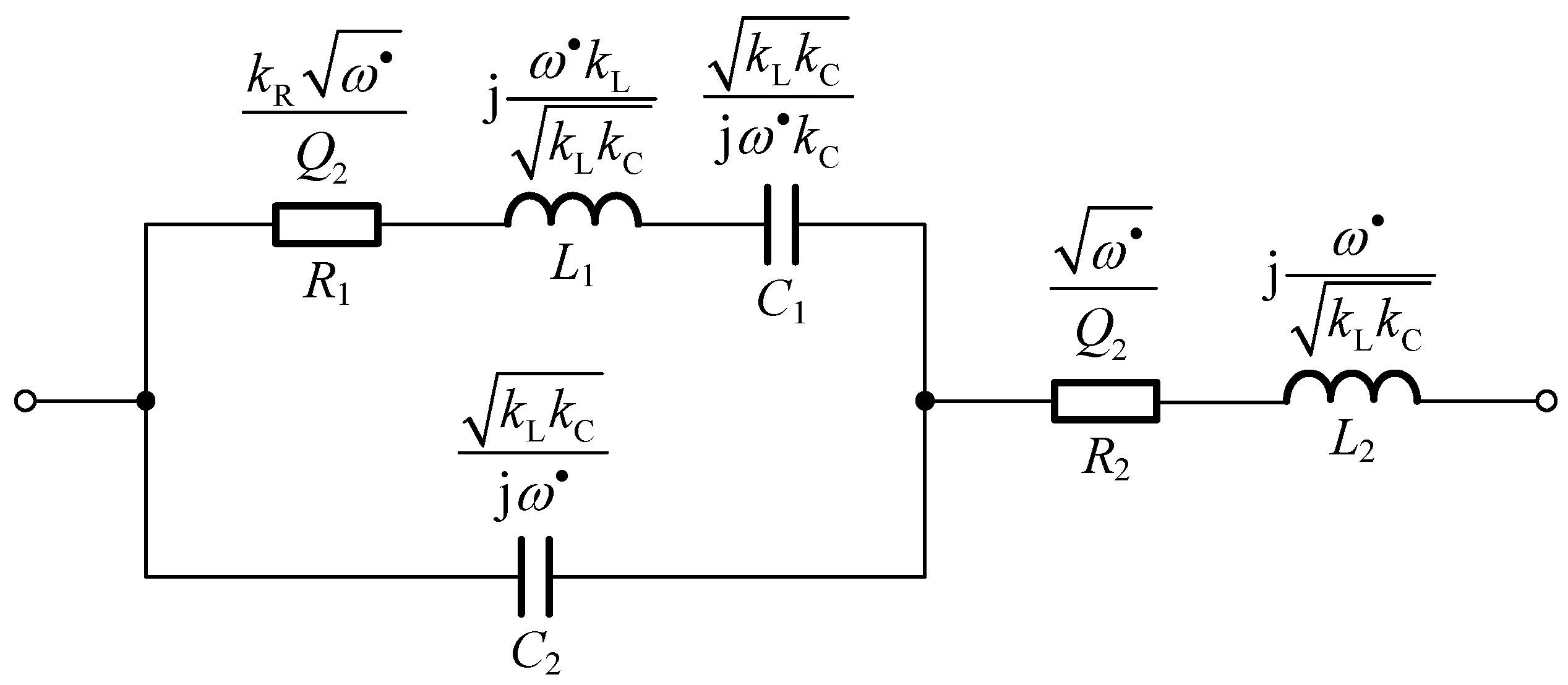





| Patent No. | System Type | Independent Control of HF and MF Components | Load Impedance Matching for the Components HF and MF |
|---|---|---|---|
| EP1363474A2 | complex | Yes | Yes |
| EP2147983A1 | complex | Yes | Yes |
| EP2148551A1 | simple | No | No |
| PL241666B1 | simple | Yes | Yes |
| PL439134A1 | simple | Yes | Yes |
| Symbol | Expression | Unit |
|---|---|---|
| EON, 330 V | 0.2987·i2 − 0.2389·i + 23.355 | µJ |
| EOFF, 330 V | −0.0006·i4 + 0.0421·i3 − 0.7625·i2 + 5.2645·i + 1.5903 | µJ |
| EON, 600 V | 0.5005·i2 + 5.0076·i + 57.282 | µJ |
| EOFF, 600 V | −0.0005·i4 + 0.0368·i 3 − 0.6212·i2 + 3.911·i + 14.017 | µJ |
| EON, 800 V | 0.65·i2 + 8.8939·i + 82.413 | µJ |
| EOFF, 800 V | −0.0004·i4 + 0.0329·i3 − 0.5165·i2 + 2.9084·i + 23.222 | µJ |
| ERR | 76·10−3·VDC | µJ |
| EOSS | 38.32·10−6·VDC2 + 10.94·10−3·VDC + 185.2·10−3 | µJ |
| RDS(on) | 150 | mΩ |
| Setup | Operation Mode | Topology | Tr1 | Tr2 |
|---|---|---|---|---|
| – | pulsing, simultaneous | 2T1C | 11:1 | 8:1 |
| 1 | pulsing, simultaneous | 3T | 22:1 | 8:1 |
| 2 | pulsing | 3T | 22:1 | 11:1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frania, K.; Kierepka, K.; Kasprzak, M.; Zimoch, P. Single Three-Phase Inverter for Dual-Frequency Induction Heating. Energies 2024, 17, 2489. https://doi.org/10.3390/en17112489
Frania K, Kierepka K, Kasprzak M, Zimoch P. Single Three-Phase Inverter for Dual-Frequency Induction Heating. Energies. 2024; 17(11):2489. https://doi.org/10.3390/en17112489
Chicago/Turabian StyleFrania, Krystian, Kamil Kierepka, Marcin Kasprzak, and Piotr Zimoch. 2024. "Single Three-Phase Inverter for Dual-Frequency Induction Heating" Energies 17, no. 11: 2489. https://doi.org/10.3390/en17112489
APA StyleFrania, K., Kierepka, K., Kasprzak, M., & Zimoch, P. (2024). Single Three-Phase Inverter for Dual-Frequency Induction Heating. Energies, 17(11), 2489. https://doi.org/10.3390/en17112489






