Stability Analysis of a Wind Turbine Controlled by Direct Torque Control
Abstract
1. Introduction
2. Mathematical Model of the System
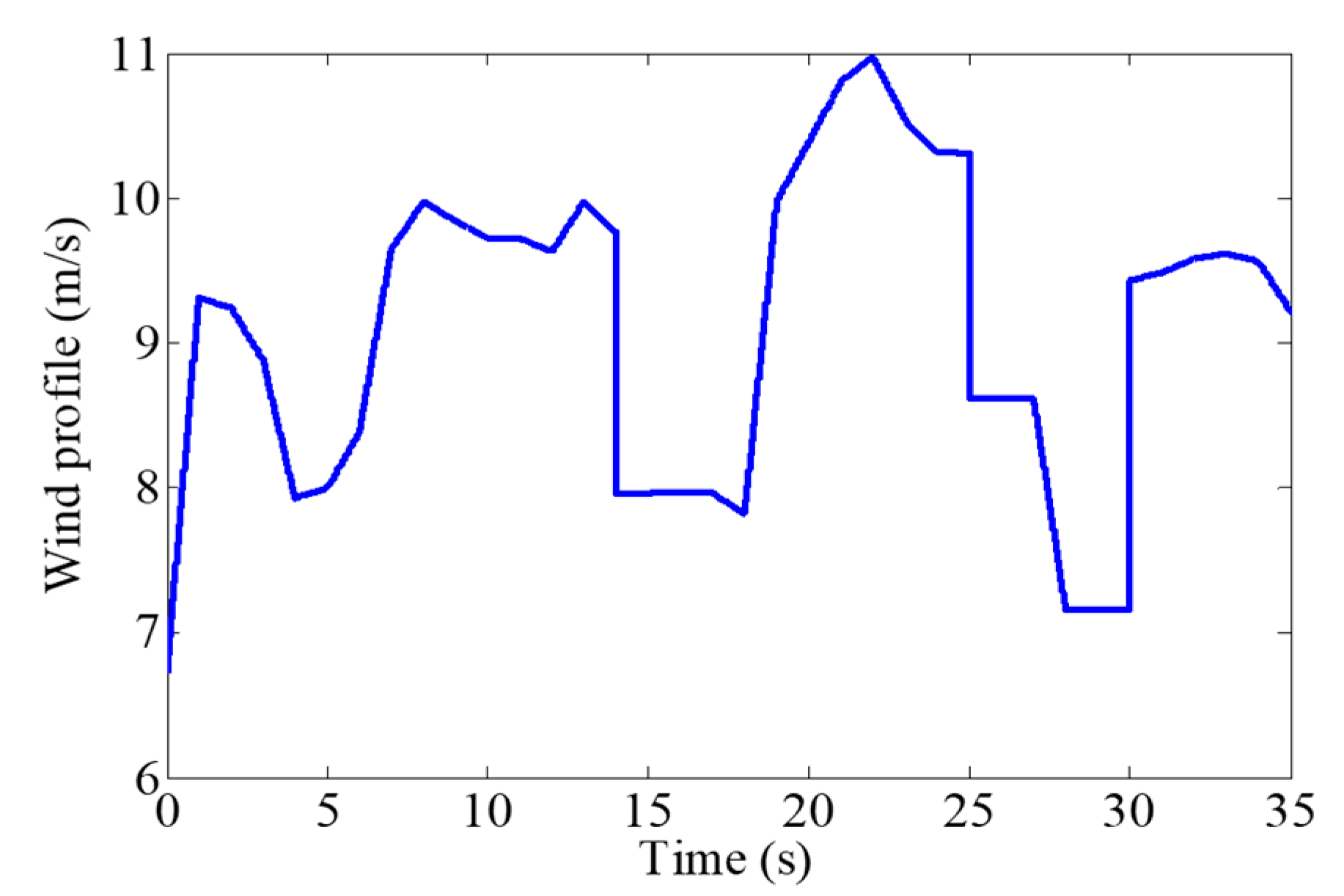
2.1. The Wind Turbine Mathematical Model
2.2. Asynchronous Machine Mathematical Model
2.3. The Mathematical Model of DC Bus Voltage
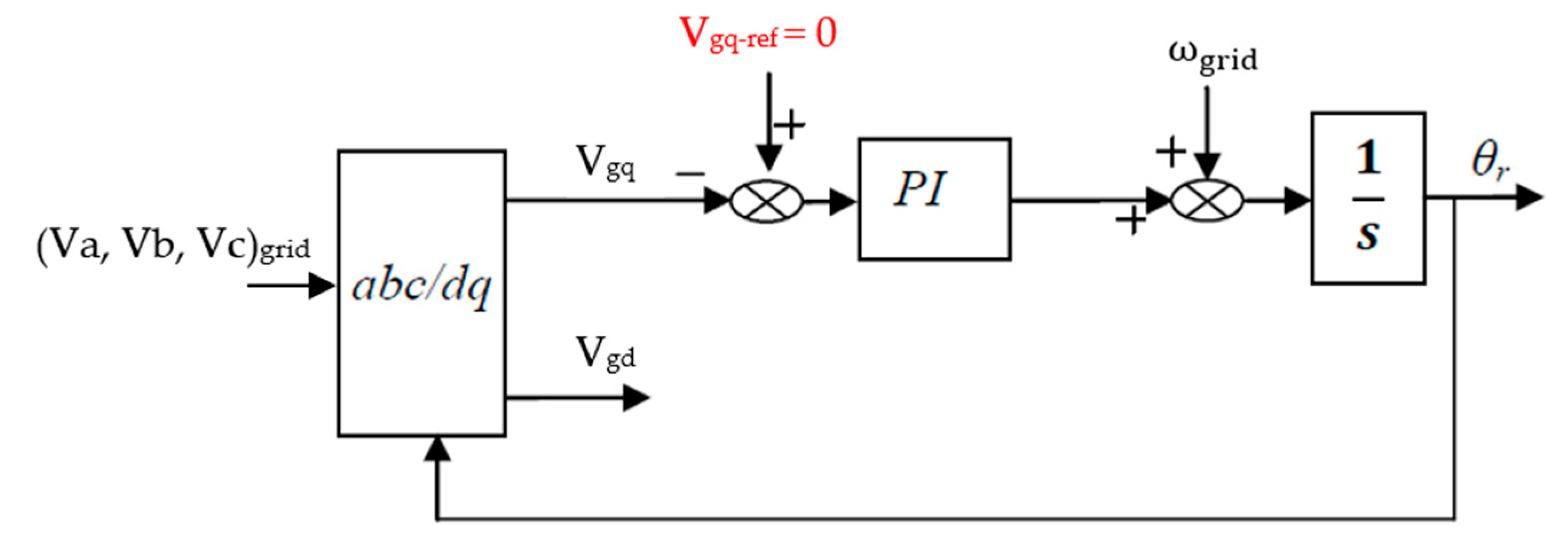
2.4. The Mathematical Model of the Grid
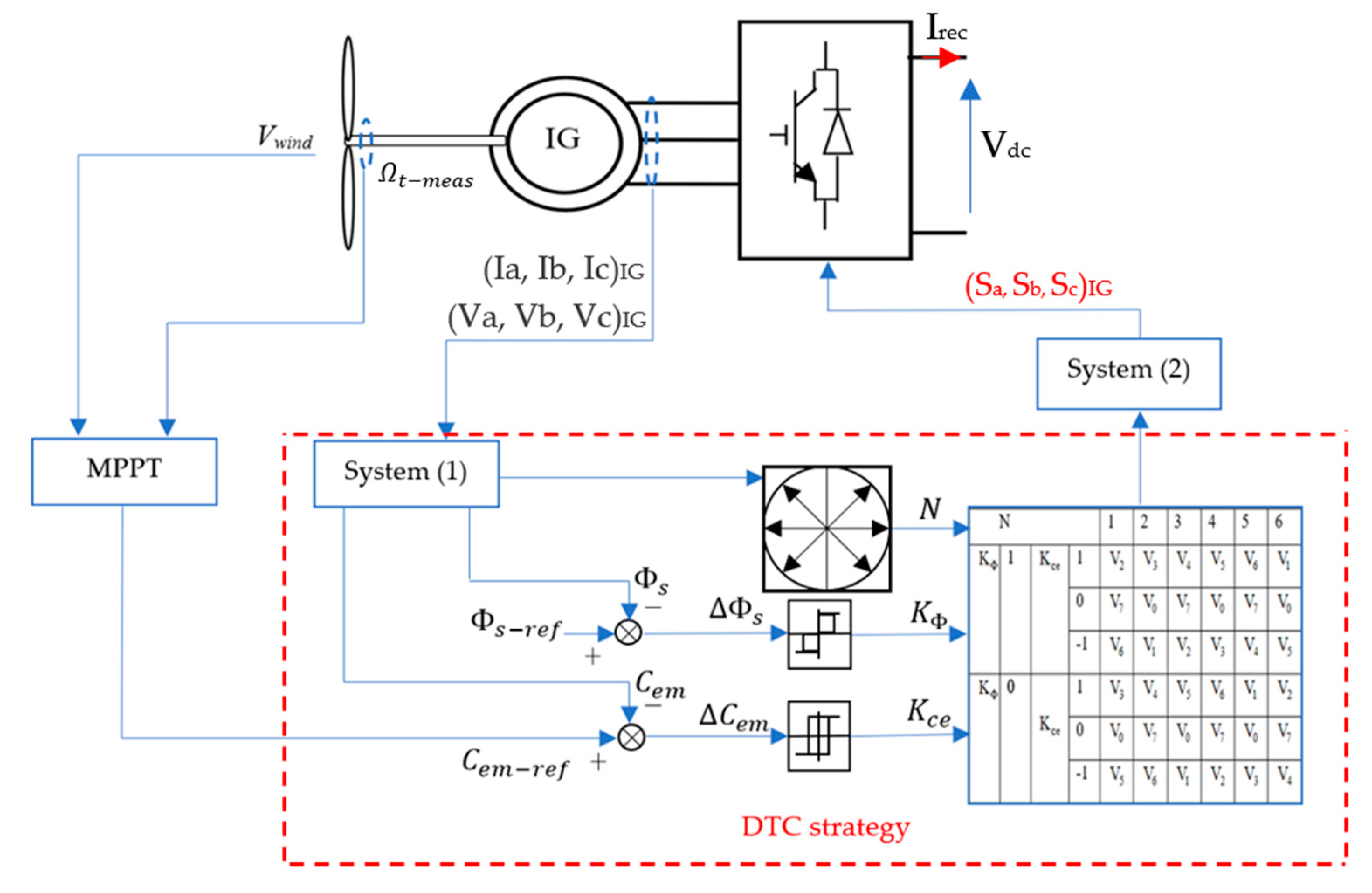
3. The Studied Control Strategy
3.1. DTC Applied to Asynchronous Machine
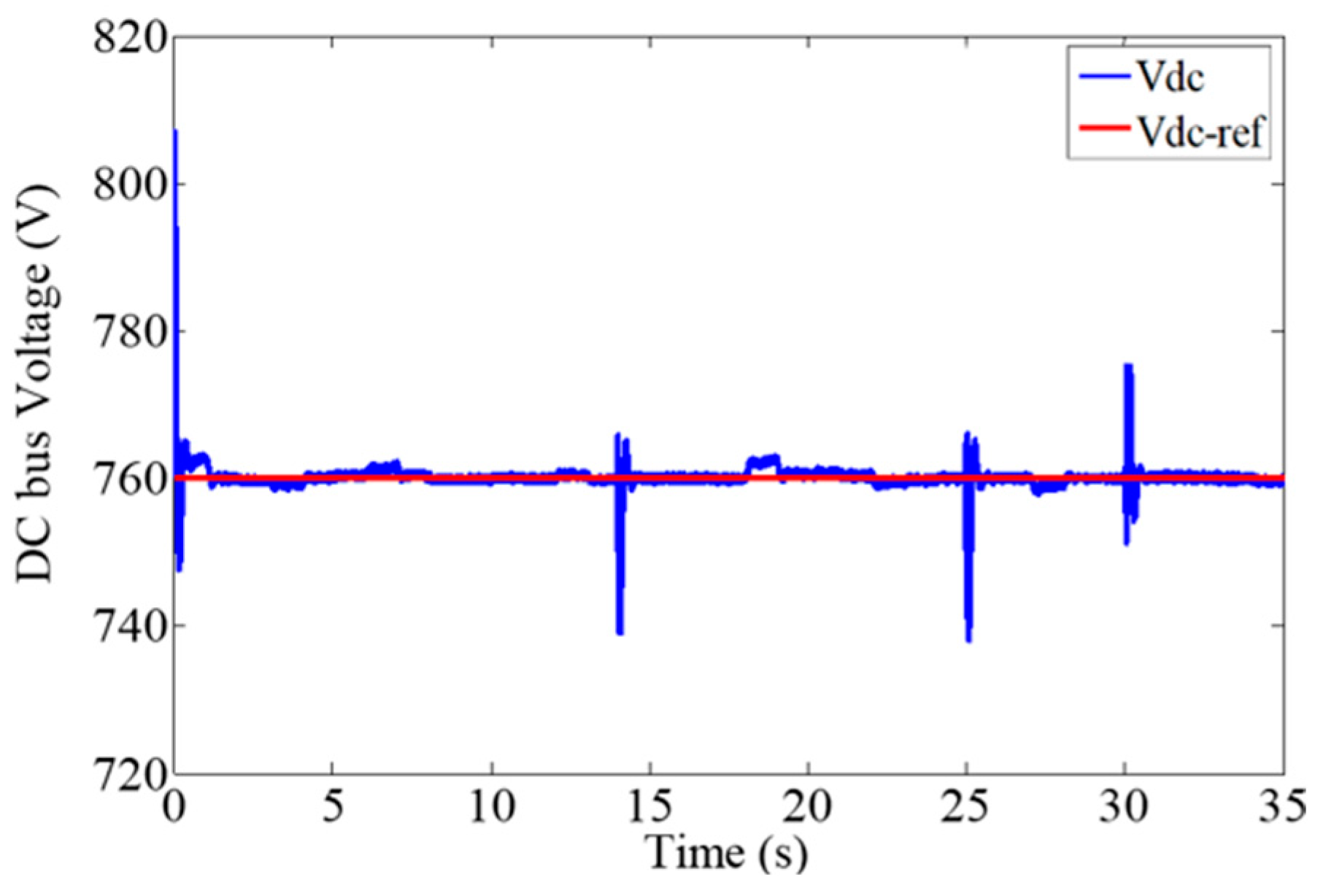
3.2. Control Connection between the Asynchronous Machine and the Grid
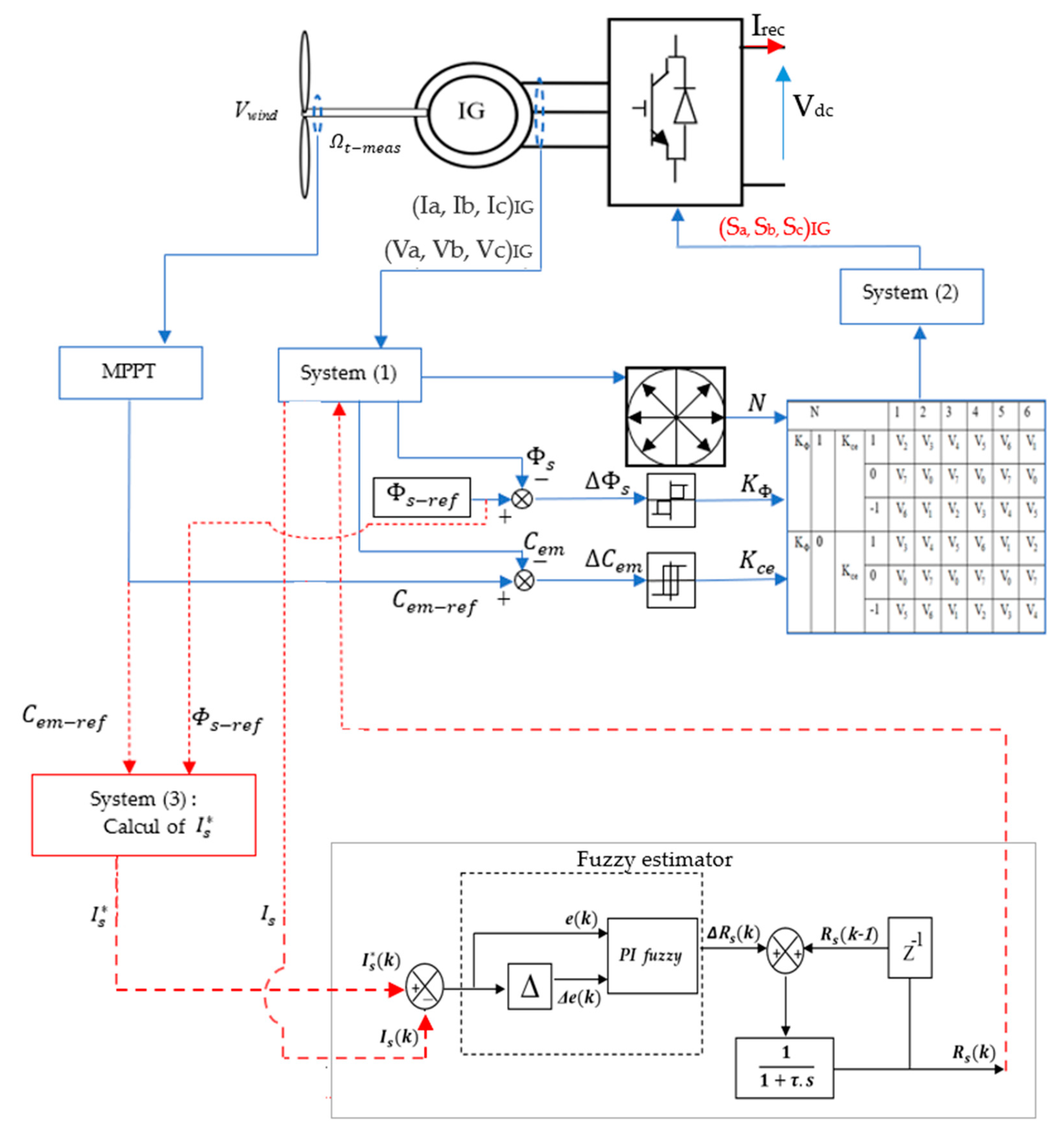
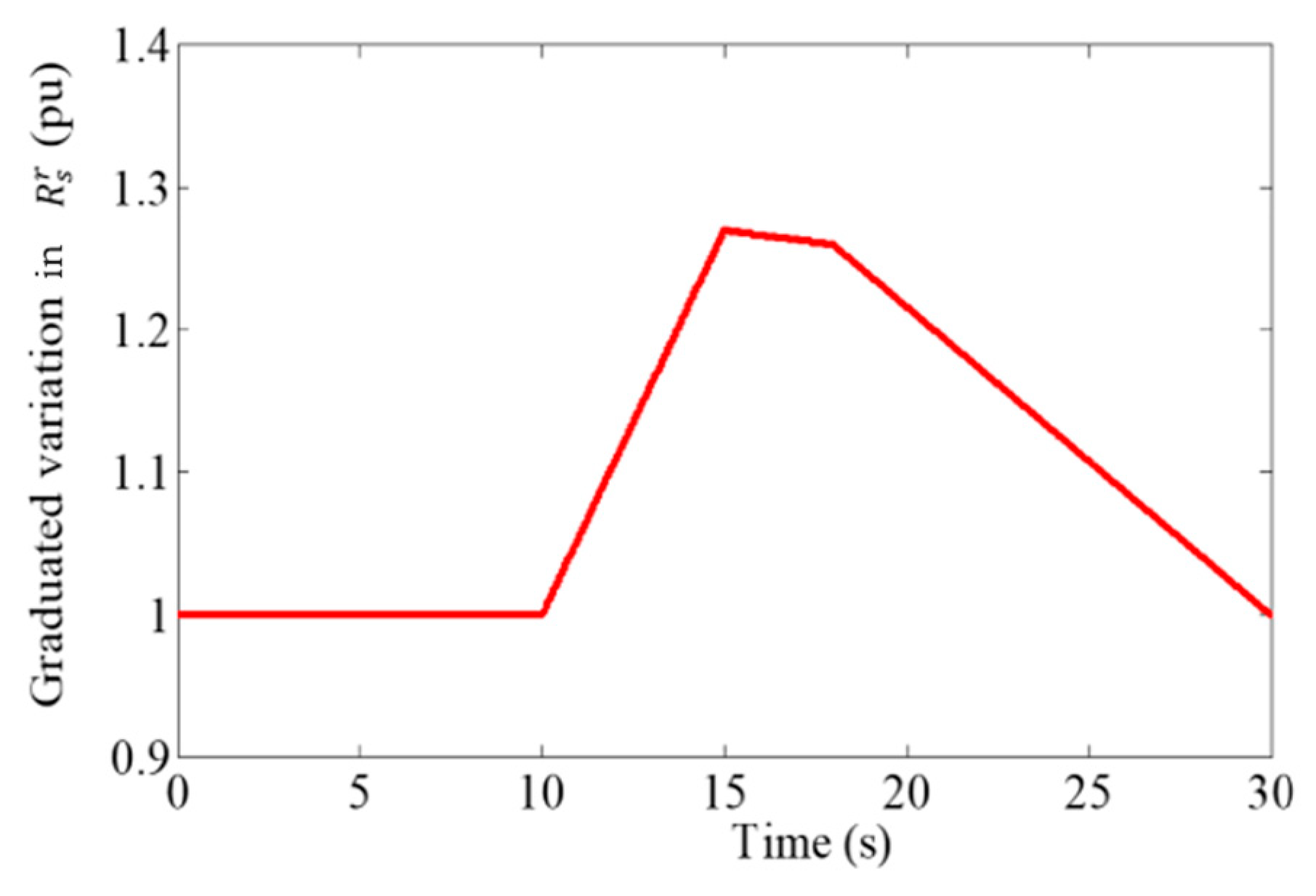
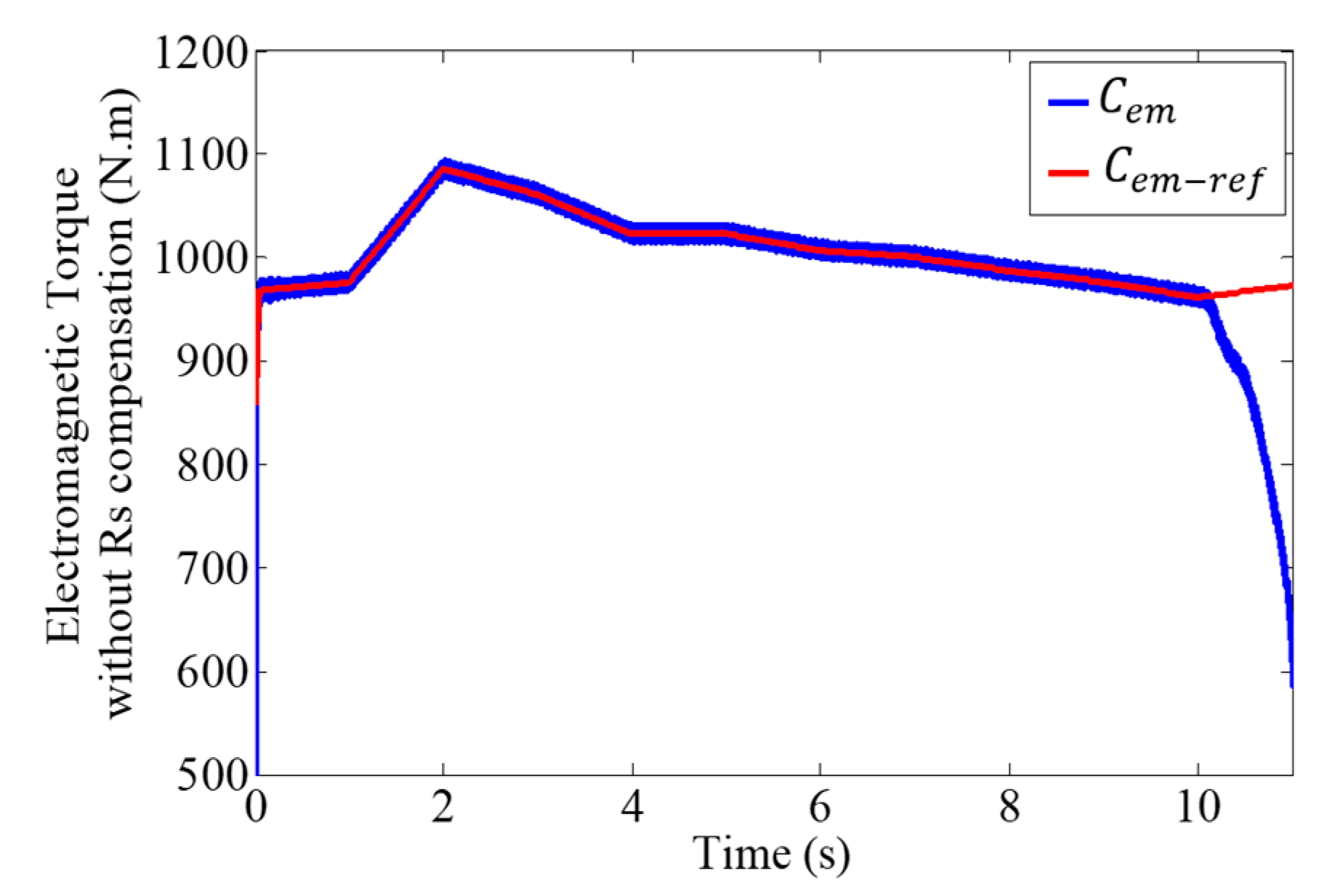
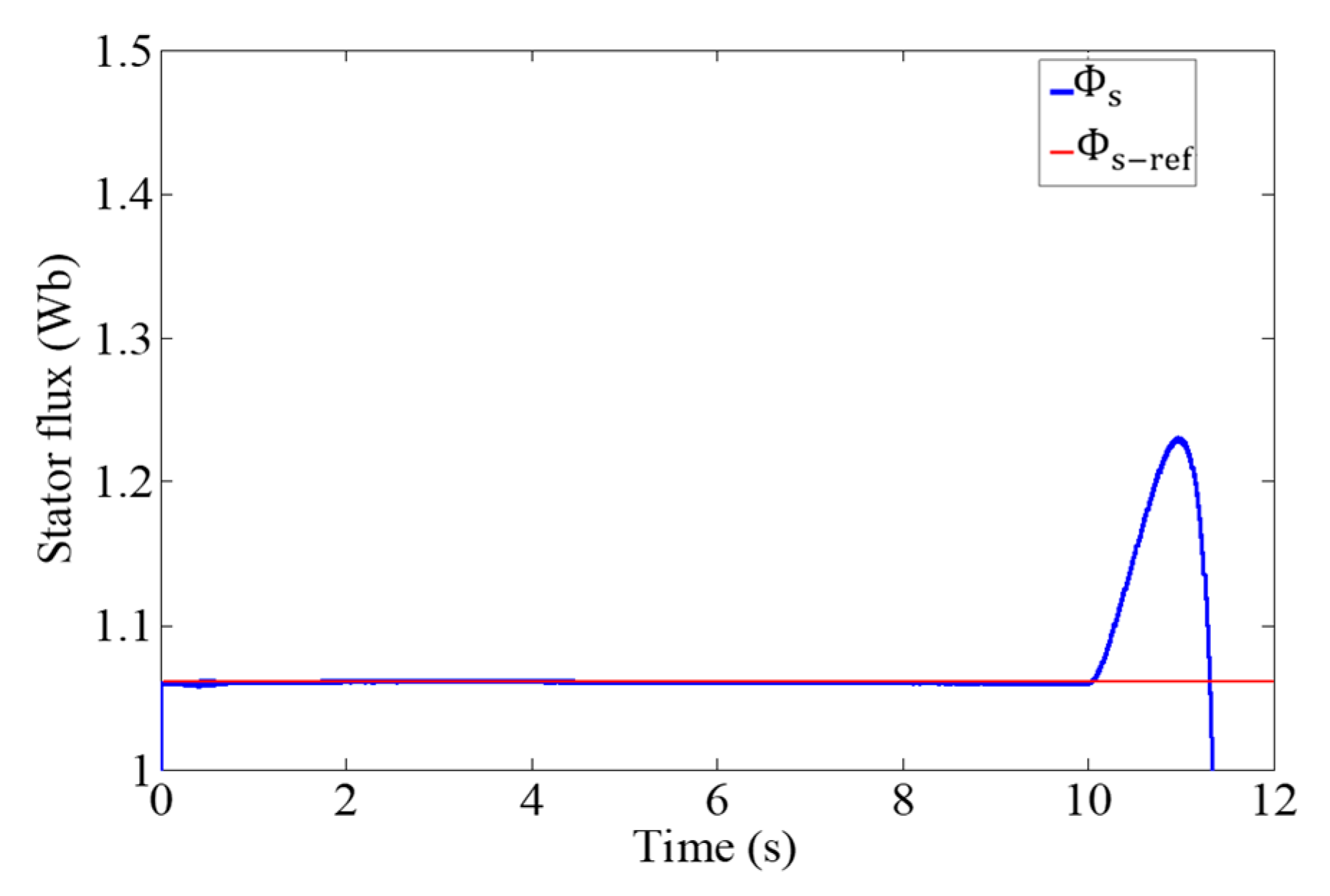
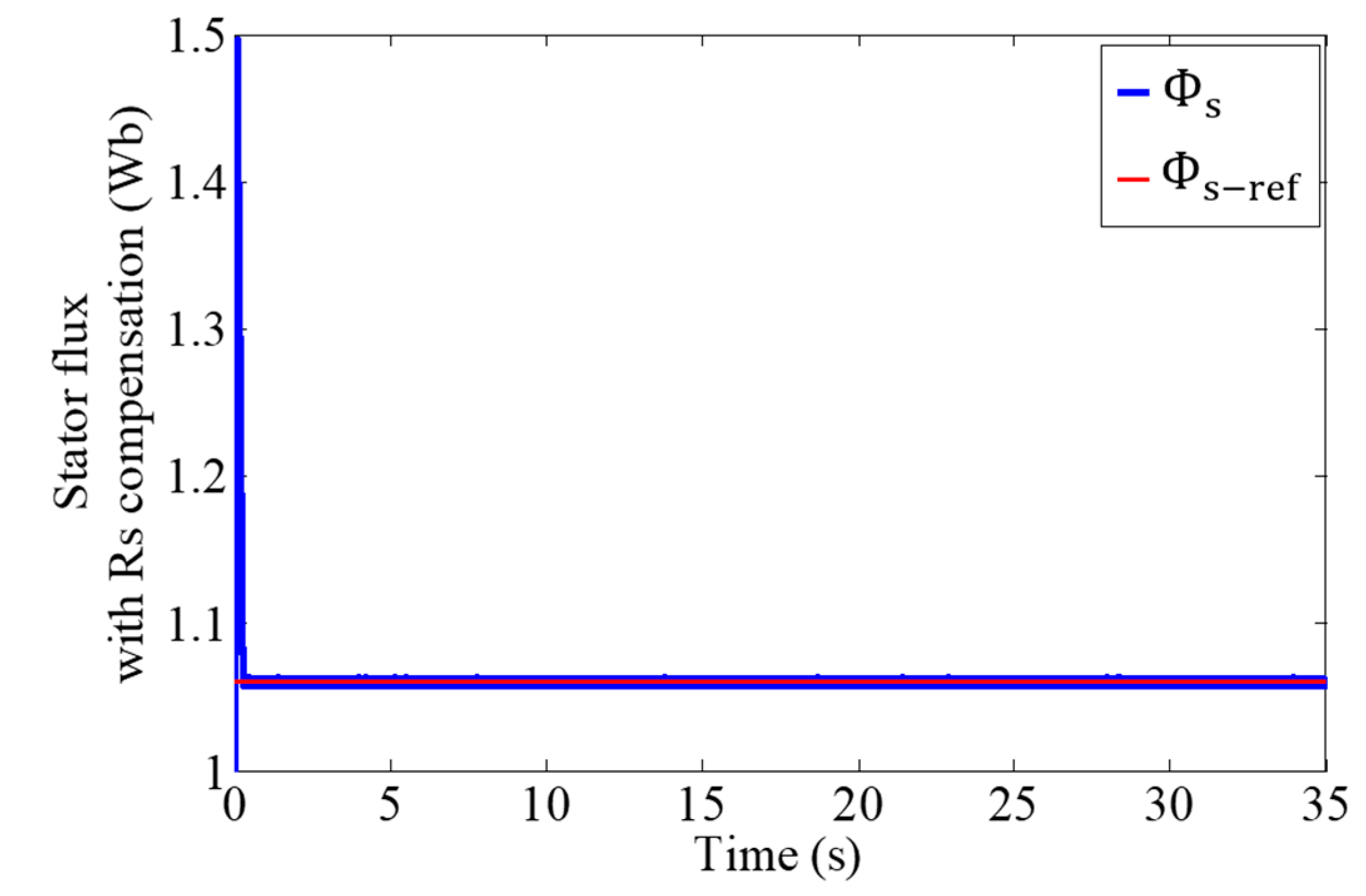
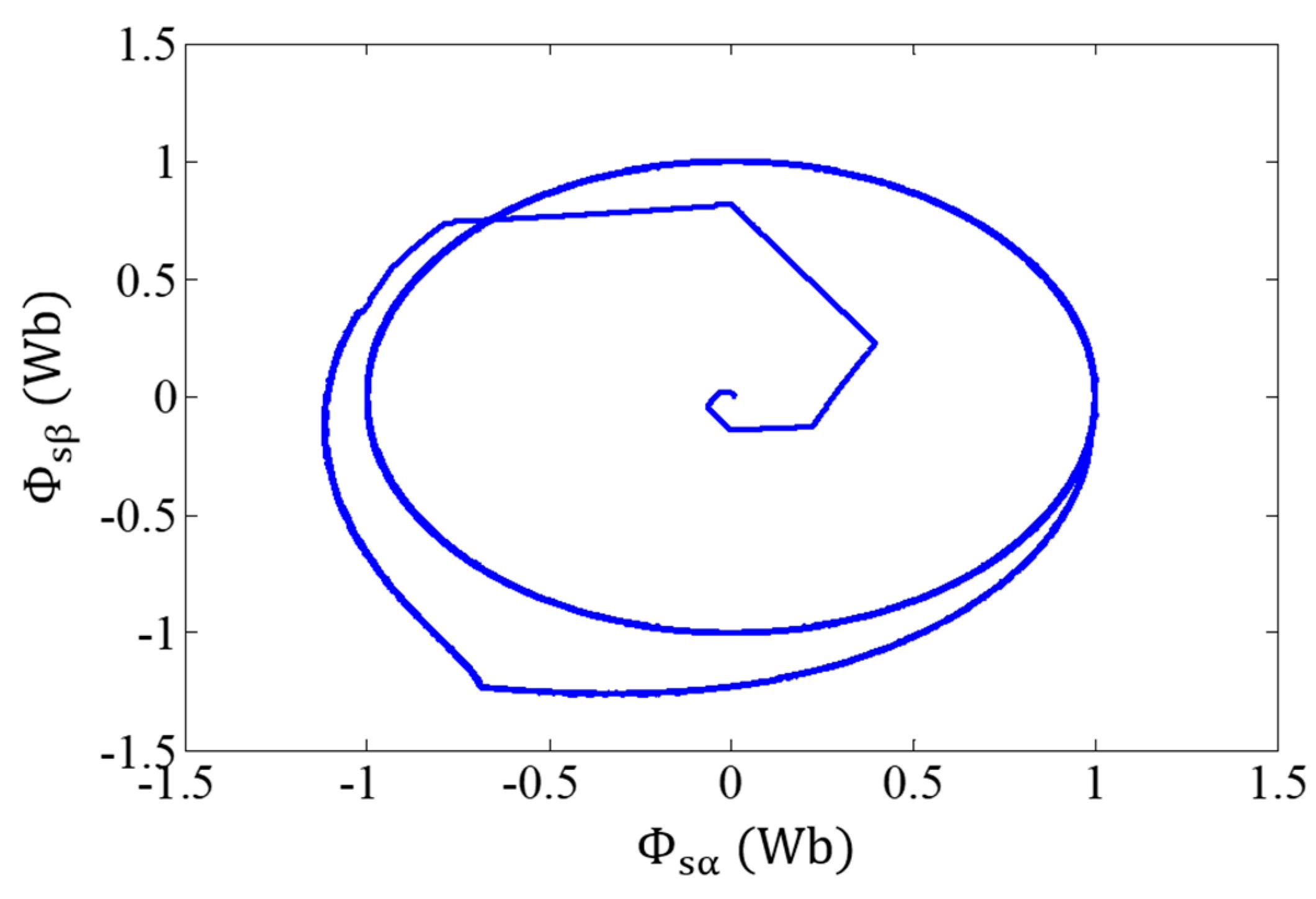
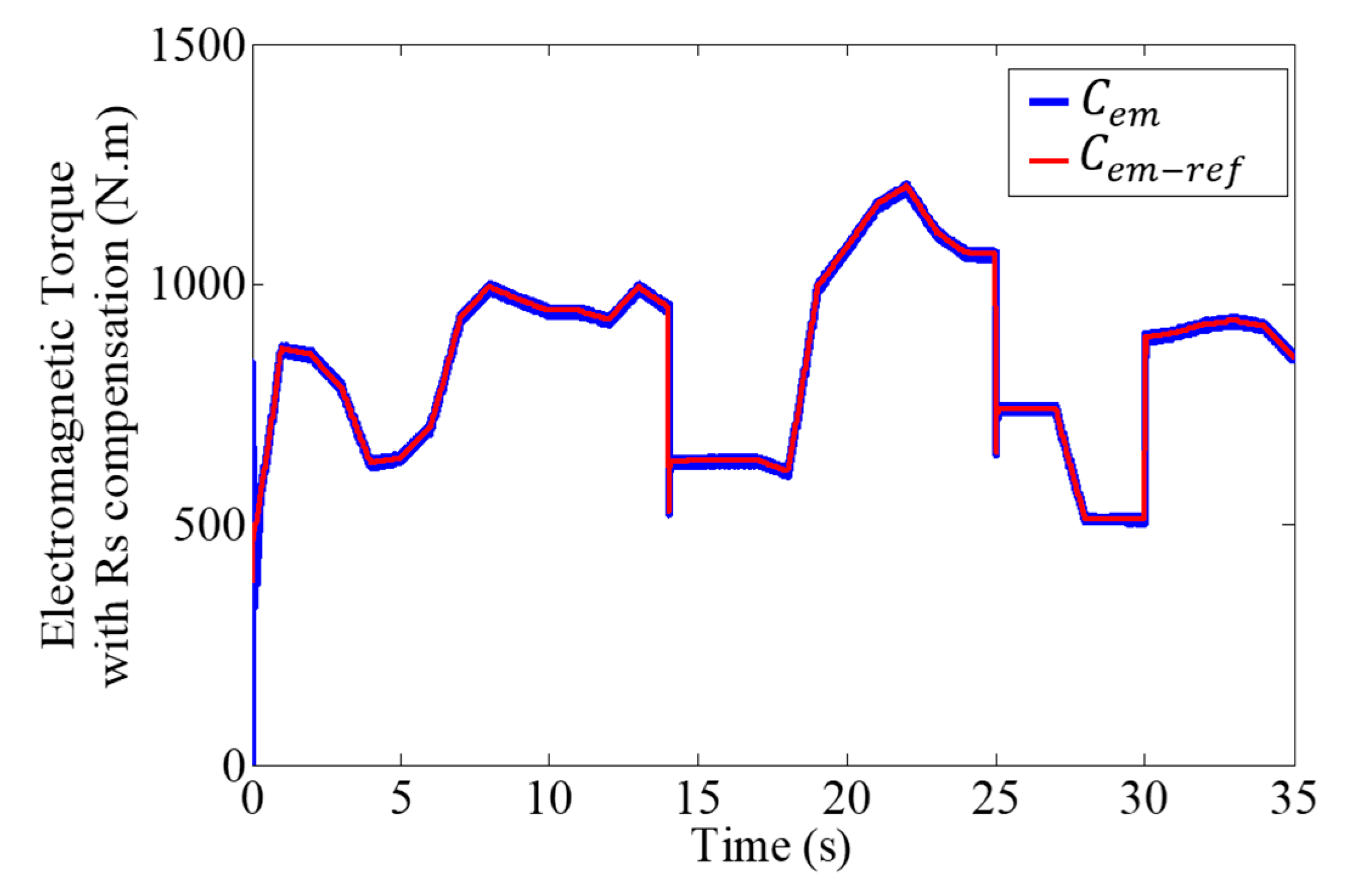
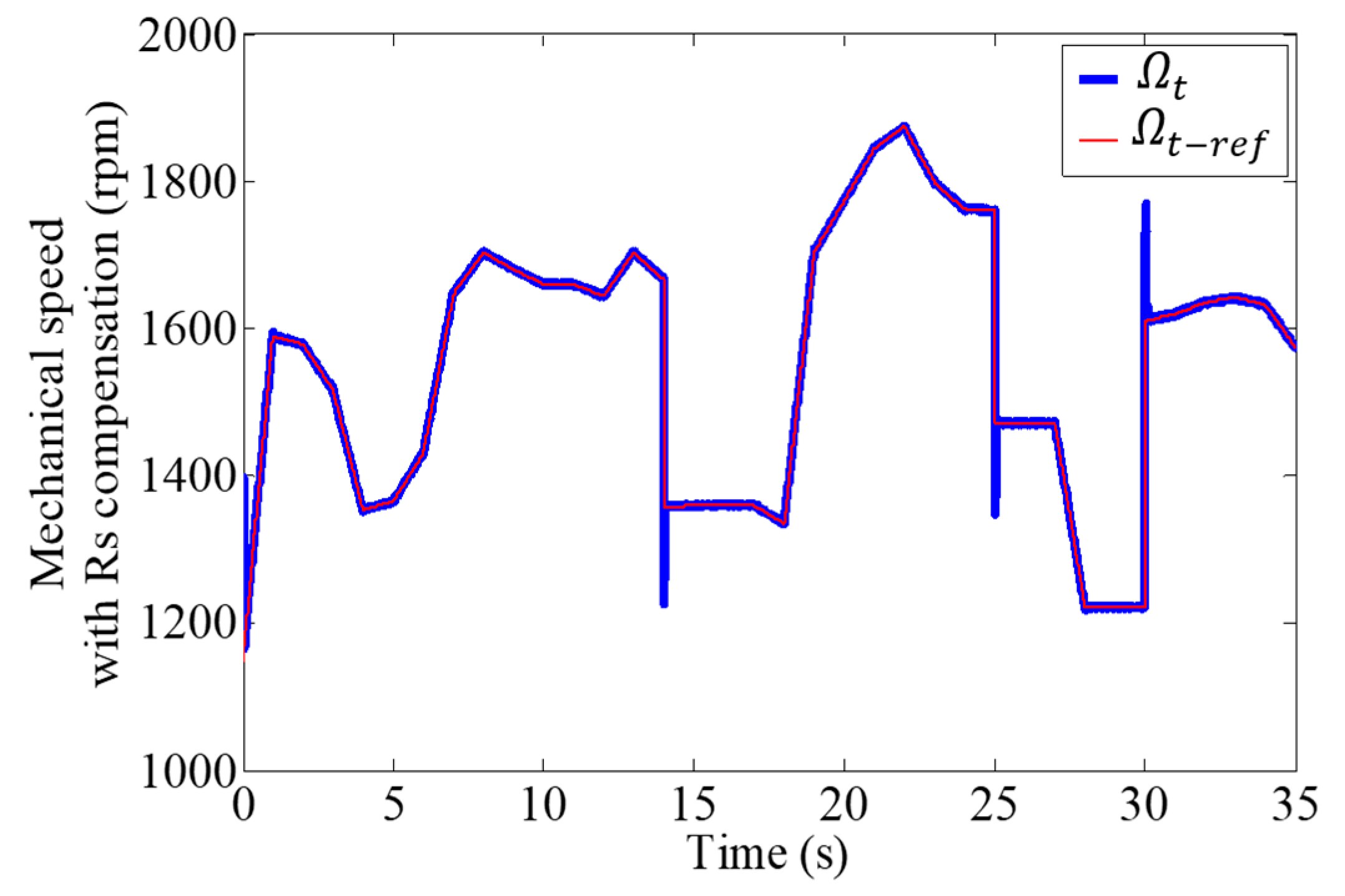
4. Rs Impact on DTC
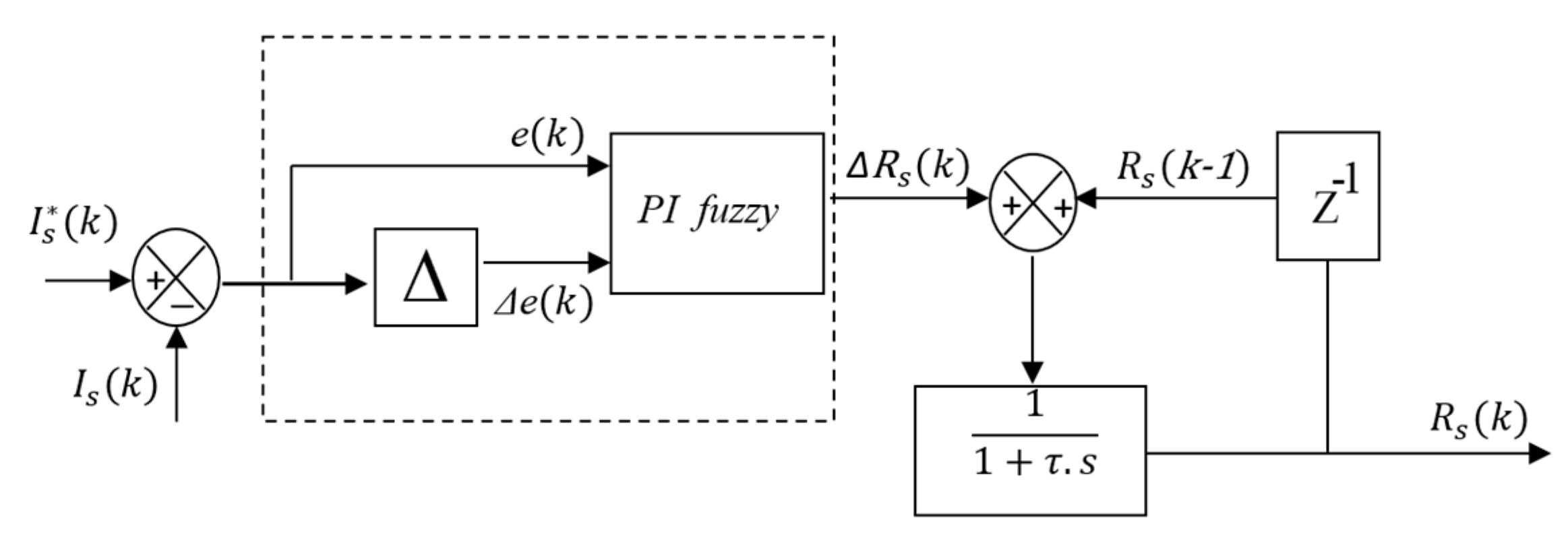
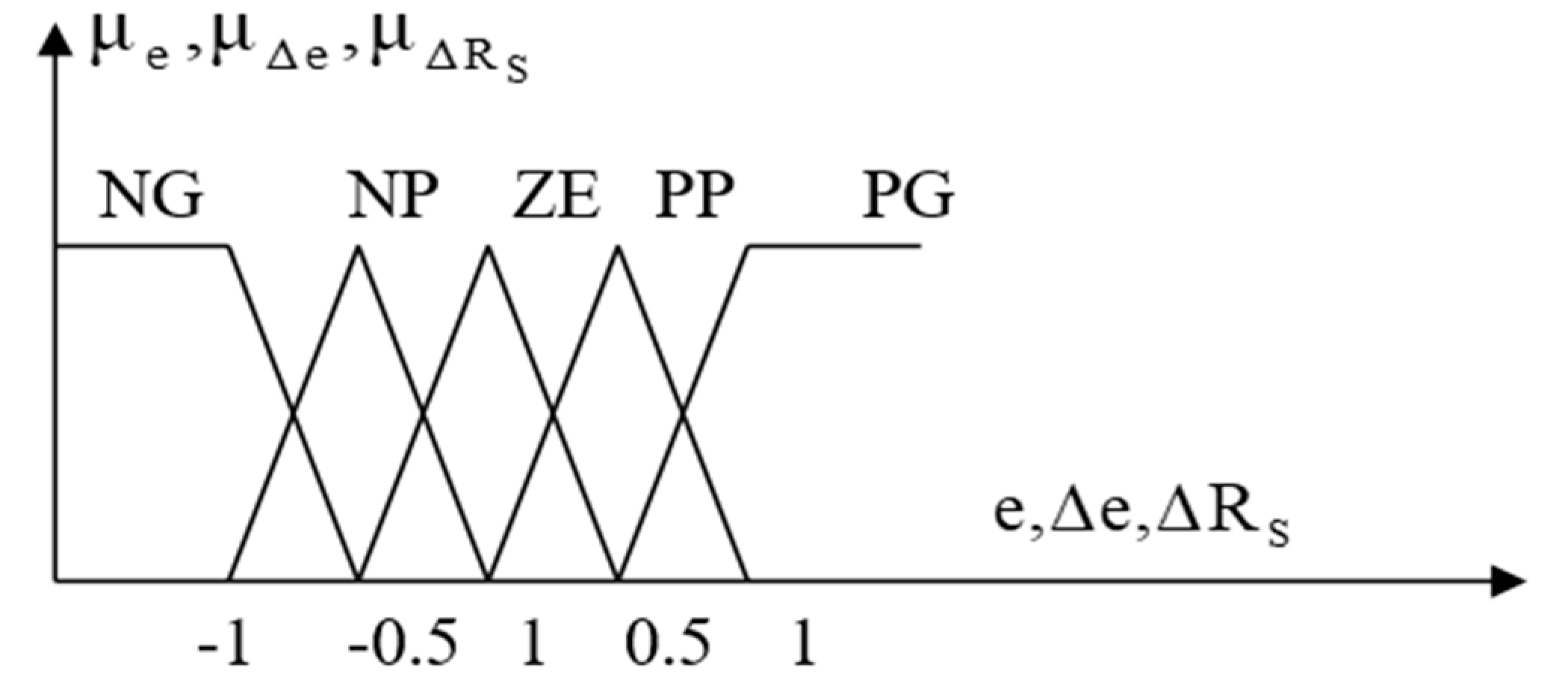
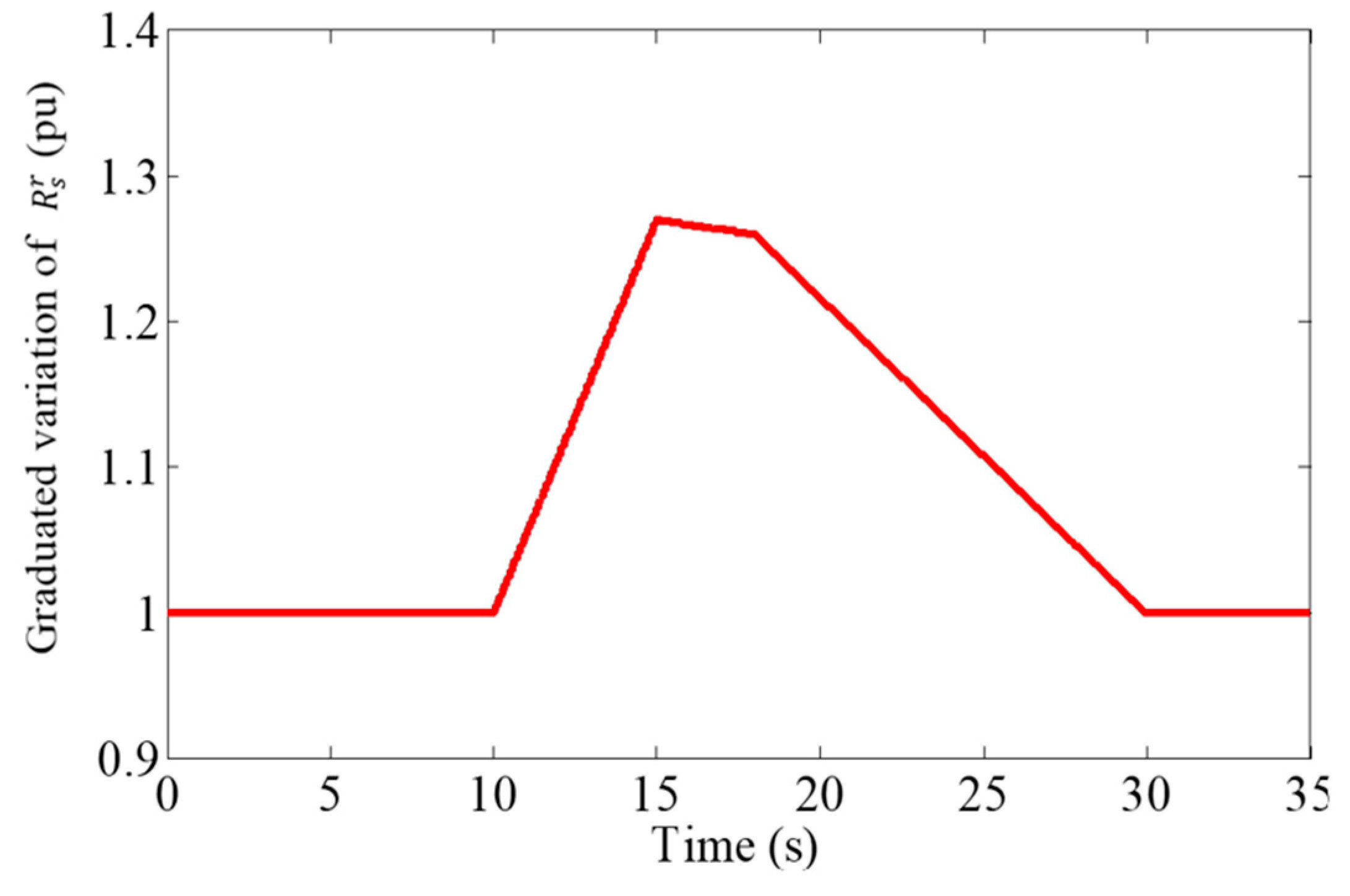
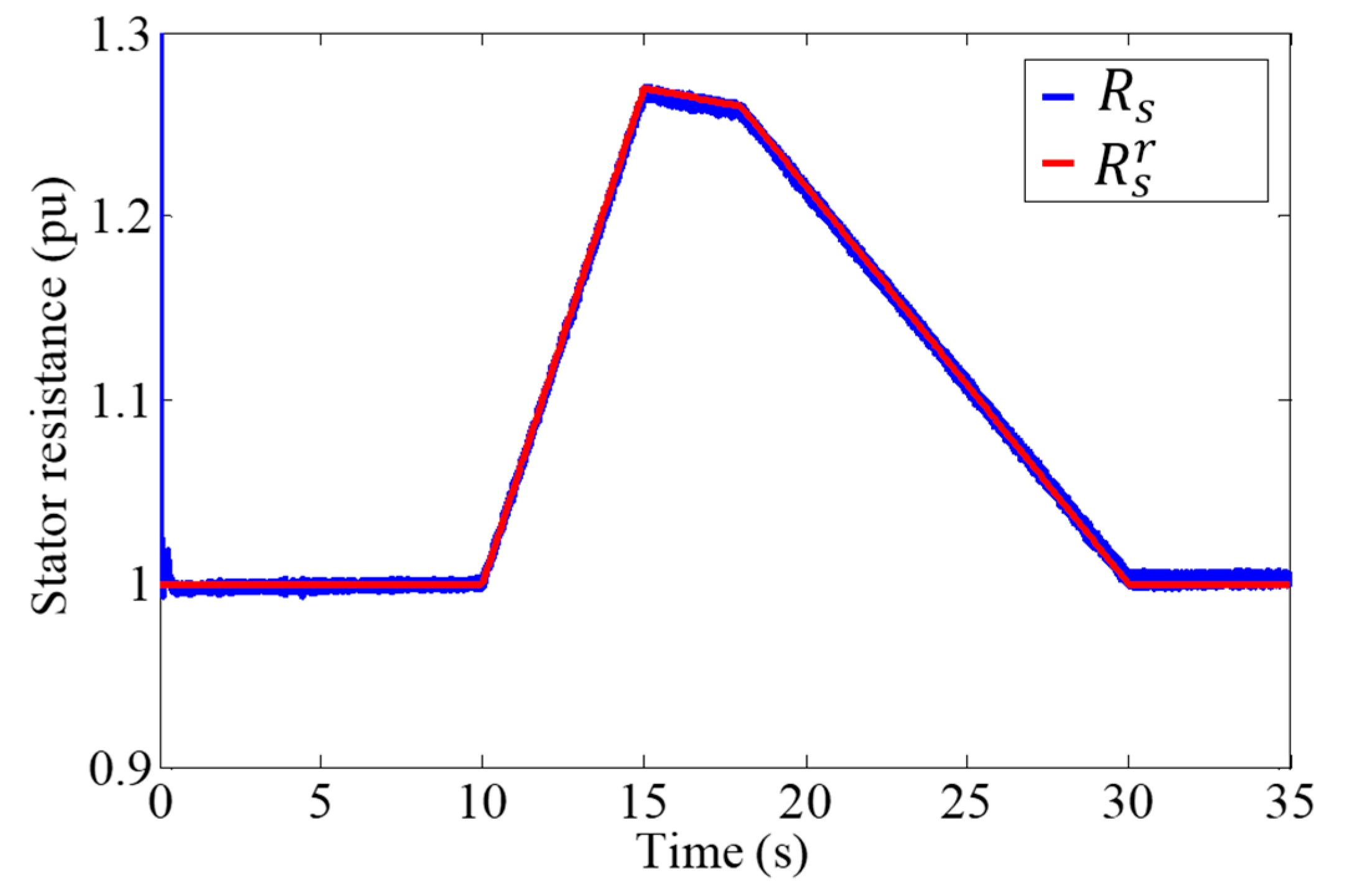
DTC Improved by the Fuzzy Estimator
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
| Symbols | Parameters | Unit (SI) |
|---|---|---|
| ρ | Air density | kg/m3 |
| R | Blade radius | m |
| Vw | Wind speed | m/s |
| λ | Tip speed ratio (TSR) of the rotor blade | N/A |
| β | Blade pitch angle | deg |
| Rs | Stator resistance | Ohm |
| Rr | Rotor resistance | Ohm |
| Lr | Rotor inductance | Henry |
| Ls | Stator inductance | Henry |
| Lm | Mutual inductance | Henry |
| p | Number of pole pairs | N/A |
| ωs | Stator frequency | Hrz |
| ωr | Rotor frequency | Hrz |
| J | Rotor inertia | Kg·m2 |
| Cr | Loading torque | N/m |
| fr | Friction coefficient | Nm/(rad/s) |
| Lg | Inductance component of the filter | Henry |
| Rg | Resistance component of the filter | Ohm |
| Kp-mppt | Parameter of PI controller for MPPT loop. | |
| Ki-mppt | Parameter of PI controller for MPPT loop. | |
| S | Laplace operator |
| Symbols | Parameters | Unit (SI) |
|---|---|---|
| Rs | 0.0089 | Ohm |
| Rr | 0.0137 | Ohm |
| Lr | 0.01267 | Henry |
| Ls | 0.01292 | Henry |
| Lm | 0.01267 | Henry |
| p | 2 | - |
| Lg | 0.0005 | Henry |
| Rg | 0.00001 | Ohm |
| J | 10 | Kg·m2 |
| fr | 0.00001 | Nm/(rad/s) |
| R | 13.5 | m |
| Pmax | 300 | kW |
| Vdc | 760 | V |
| Rs | 0.0089 | Ohm |
References
- García-Sánchez, T.; Gómez-Lázaro, E.; Molina-García, A. A review and discussion of the grid-code requirements for renewable energy sources in Spain. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’14), Cordoba, Spain, 8–10 April 2014; pp. 565–570. [Google Scholar] [CrossRef]
- E.ON Netz GmbH. Requirements for Offshore Grid Connections in the E.ON Netz Network; E.ON Netz GmbH: Bayreuth, Germany, 2008. [Google Scholar]
- Elkodama, A.; Ismaiel, A.; Abdellatif, A.; Shaaban, S.; Yoshida, S.; Rushdi, M.A. Control Methods for Horizontal Axis Wind Turbines (HAWT): State-of-the-Art Review. Energies 2023, 16, 6394. [Google Scholar] [CrossRef]
- Djamel, I. Marine Energy Production: Integration of Offshore Wind Production into a Decentralized Energy Mix. Ph.D. Thesis, Le Havre University, Le Havre, France, 2014. [Google Scholar]
- Meziane, S. Commande Adaptative et Prédictive de la Machine Asynchrone. Ph.D. Thesis, University of Constantine, Constantine, Algeria, 2009. [Google Scholar]
- Sellah, M.; Kouzou, A.; Mohamed-Seghir, M.; Rezaoui, M.M.; Kennel, R.; Abdelrahem, M. Improved DTC-SVM Based on Input-Output Feedback Linearization Technique Applied on DOEWIM Powered by Two Dual Indirect Matrix Converters. Energies 2021, 14, 5625. [Google Scholar] [CrossRef]
- Ortega-García, L.E.; Rodriguez-Sotelo, D.; Nuñez-Perez, J.C.; Sandoval-Ibarra, Y.; Perez-Pinal, F.J. DSP-HIL Comparison between IM Drive Control Strategies. Electronics 2021, 10, 921. [Google Scholar] [CrossRef]
- Sahri, Y.; Tamalouzt, S.; Lalouni Belaid, S.; Bacha, S.; Ullah, N.; Ahamdi, A.A.A.; Alzaed, A.N. Advanced Fuzzy 12 DTC Control of Doubly Fed Induction Generator for Optimal Power Extraction in Wind Turbine System under Random Wind Conditions. Sustainability 2021, 13, 11593. [Google Scholar] [CrossRef]
- Barambones, O. Sliding Mode Control Strategy for Wind Turbine Power Maximization. Energies 2012, 5, 2310–2330. [Google Scholar] [CrossRef]
- Rania, G.M.; Ebrahim, M.A.; Zuhair, M.A.; Ahmed, M.M.R. Optimal Energy Harvesting of Large-Scale Wind Farm Using Marine Predators Algorithm. IEEE Access 2022, 7, 225–238. [Google Scholar] [CrossRef]
- Djamel, I.; Elena, R. Comparative Study Between the Flatness-Based and Field-Oriented Control of a Wind-Energy System. In Proceedings of the International Symposium on Electrical and Electronics Engineering (IEEE-ISEEE), Galați, Romania, 28 October 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Haque, M.E.; Rahman, M.F. Influence of Stator Resistance Variation on Direct Torque Controlled. In Proceedings of the Thirty-Sixth IEEE Industry Applications Conference (IAS), Chicago, IL, USA, 30 September–4 October 2001. [Google Scholar]
- El Ouanjli, N.; Motahhir, S.; Derouich, A.; El Ghzizal, A.; Taoussi, M.; Chebabhi, A. Improved DTC strategy of doubly fed induction motor using fuzzy logic controller. Energy Rep. 2019, 5, 271–279. [Google Scholar] [CrossRef]
- Soedibyo, S.; Feby, A.P.; Ashari, M. Control Design of Wind Turbine System Using Fuzzy Logic Controller for Middle Voltage Grid. Indones. J. Electr. Eng. Comput. Sci. 2015, 3, 476–482. [Google Scholar] [CrossRef]
- Almaged, M.; Mahmood, A.; Alnema, Y.H.S. Design of an Integral Fuzzy Logic Controller for a Variable—Speed Wind Turbine Model. J. Robot. Control. 2023, 4, 762–768. [Google Scholar] [CrossRef]
- Mabrouk, Y.A.; Mokhtari, B.; Allaoui, T. Frequency analysis of stator currents of an induction motor controlled by direct torque control associated with a fuzzy flux estimator. Electr. Eng. Electromech. 2023, 27–32. [Google Scholar] [CrossRef]
- Teggar, T. Comparative Study between Flux Vector Control Orients and Direct Control of the Torque of the machine Asynchronous. Engineering Thesis, University of Ouargla, Ouargla, Algeria, May 2016. [Google Scholar]
- Fathy, A.; Yousri, D.; Rezk, H.; Thanikanti, S.B.; Hasanien, H.M. A Robust Fractional-Order PID Controller Based Load Frequency Control Using Modified Hunger Games Search Optimizer. Energies 2022, 15, 361. [Google Scholar] [CrossRef]
- Djamel, I.; Camara, M.B.; Dakyo, B. Offshore wind farms energy injection in the electrical grid—Lithium battery to mitigate power fluctuations. Int. J. Renew. Energy Res. 2015, 5, 1050–1061. [Google Scholar] [CrossRef]
- Djamel, I. Direct Control of the Torque of an Asynchronous Machine with Fuzzy Estimator of the Stator Resistance. Engineering Thesis, University of Bejaia, Bejaia, Algeria, July 2007. [Google Scholar]
- Mokhtari, B.; Mokrani, L.; Abdessemed, R.; Bendias, M.L. Fuzzy estimator of the stator resistance of an induction motor controlled by neural DTC (Estimateur Flou de la Résistance Statorique d’un Moteur à Induction Commandé par DTC Neuronale). In Proceedings of the International Conference on Electrical and Electronics Engineering (ICEEE), Laghouat, Algeria, 24–26 April 2004. [Google Scholar]
- Mansour, M.; Mansouri, M.N.; Mmimouni, M.F. Study and Control of a Variable-Speed Wind-Energy System Connected to the Grid. Int. J. Renew. Energy Res. 2011, 1, 96–104. [Google Scholar] [CrossRef]
- Jnayah, S.; Moussa, I.; Khedher, A. IM Fed by Three-Level Inverter under DTC Strategy Combined with Sliding Mode Theory. Electronics 2022, 11, 3656. [Google Scholar] [CrossRef]
- Maes, J.; Melkebeek, J.A. Speed-sensorless direct torque control of induction motors using an adaptive flux observer. IEEE Trans. Ind. Appl. 2000, 36, 778–785. [Google Scholar] [CrossRef]
- Martins, C.A.; Roboam, X.; Meynard, T.A.; Carvalho, A.S. Switching frequency imposition and ripple reduction in DTC drives by using a multilevel converter. IEEE Trans. Power Electron. 2002, 17, 286–297. [Google Scholar] [CrossRef]
- de Barros, J.C. Application de la logique floue à la commande optimale du moteur asynchrone. Ph.D. Thesis, Aix-Marseille III University, Marseille, France, 2003. [Google Scholar]
- Elgbaily, M.; Anayi, F.; Alshbib, M.M. A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation. Mathematics 2022, 10, 3842. [Google Scholar] [CrossRef]
- Esparza Sola, T.; Chiu, H.-J.; Liu, Y.-C.; Rahman, A.N. Extending DC Bus Utilization for Induction Motors with Stator Flux Oriented Direct Torque Control. Energies 2022, 15, 374. [Google Scholar] [CrossRef]
- Buja, Y.G.; Menis, R. Steady-State Performance Degradation of a DTC IM Drive Under Parameter and Transduction Errors. IEEE Trans. Ind. Electron. 2008, 55, 1749–1760. [Google Scholar] [CrossRef]
- Mokhtari, B. Intelligent DTC applied to asynchronous machine control. Ph.D. Thesis, University of Batna, Batna, Algeria, July 2014. [Google Scholar]
- Bermúdez, M.; Barrero, F.; Martín, C.; Perales, M. Performance Analysis of Direct Torque Controllers in Five-Phase Electrical Drives. Appl. Sci. 2021, 11, 11964. [Google Scholar] [CrossRef]
- Lai, Y.-S.; Chen, J.-H. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar] [CrossRef]
- Aziz, A.G.M.A.; Abdelaziz, A.Y.; Ali, Z.M.; Diab, A.A.Z. A Comprehensive Examination of Vector-Controlled Induction Motor Drive Techniques. Energies. 2023, 16, 2854. [Google Scholar] [CrossRef]
- Cabrera, L.A.; Elbuluk, M.E.; Husain, I. Tuning the stator resistance of induction motors using artificial neural network. IEEE Trans. Power Electron. 1997, 12, 879–886. [Google Scholar] [CrossRef]
- Lee, B.S.; Krishnan, R. Adaptive Stator Resistance Compensator for High Performance Direct Torque Controlled Induction Motor Drive. In Proceedings of the IEEE IAS Annual Meeting, St. Louis, MO, USA, 12–15 October 1998; pp. 423–430. [Google Scholar] [CrossRef]
- Bayoumi, E.H.E. Multi-resolution analysis wavelet PI stator resistance estimator for direct torque induction motor drive. WSEAS Trans. Circuits Syst. 2013, 12, 211–220. [Google Scholar]
- Zidani, F.; Diallo, D.; Benbouzid, M.E.H.; Nait-Said, R. Direct Torque Control of Induction Motor With Fuzzy Stator Resistance Adaptation. IEEE Trans. Energy Convers. 2006, 21, 619–621. [Google Scholar] [CrossRef]
- Varga, T.; Benšić, T.; Barukčić, M.; Štil, V.J. Optimization of Fuzzy Controller for Predictive Current Control of Induction Machine. Electronics 2022, 11, 1553. [Google Scholar] [CrossRef]
- Kakouche, K.; Oubelaid, A.; Mezani, S.; Rekioua, D.; Rekioua, T. Different Control Techniques of Permanent Magnet Synchronous Motor with Fuzzy Logic for Electric Vehicles: Analysis, Modelling, and Comparison. Energies 2023, 16, 3116. [Google Scholar] [CrossRef]
- Kroičs, K.; Būmanis, A. BLDC Motor Speed Control with Digital Adaptive PID-Fuzzy Controller and Reduced Harmonic Content. Energies 2024, 17, 1311. [Google Scholar] [CrossRef]
- Salma, E.A. Modeling of different wind turbine technologies integrated into a medium voltage network. Ph.D. Thesis, Ecole Central de Lille, Lille, France, 2004. [Google Scholar]

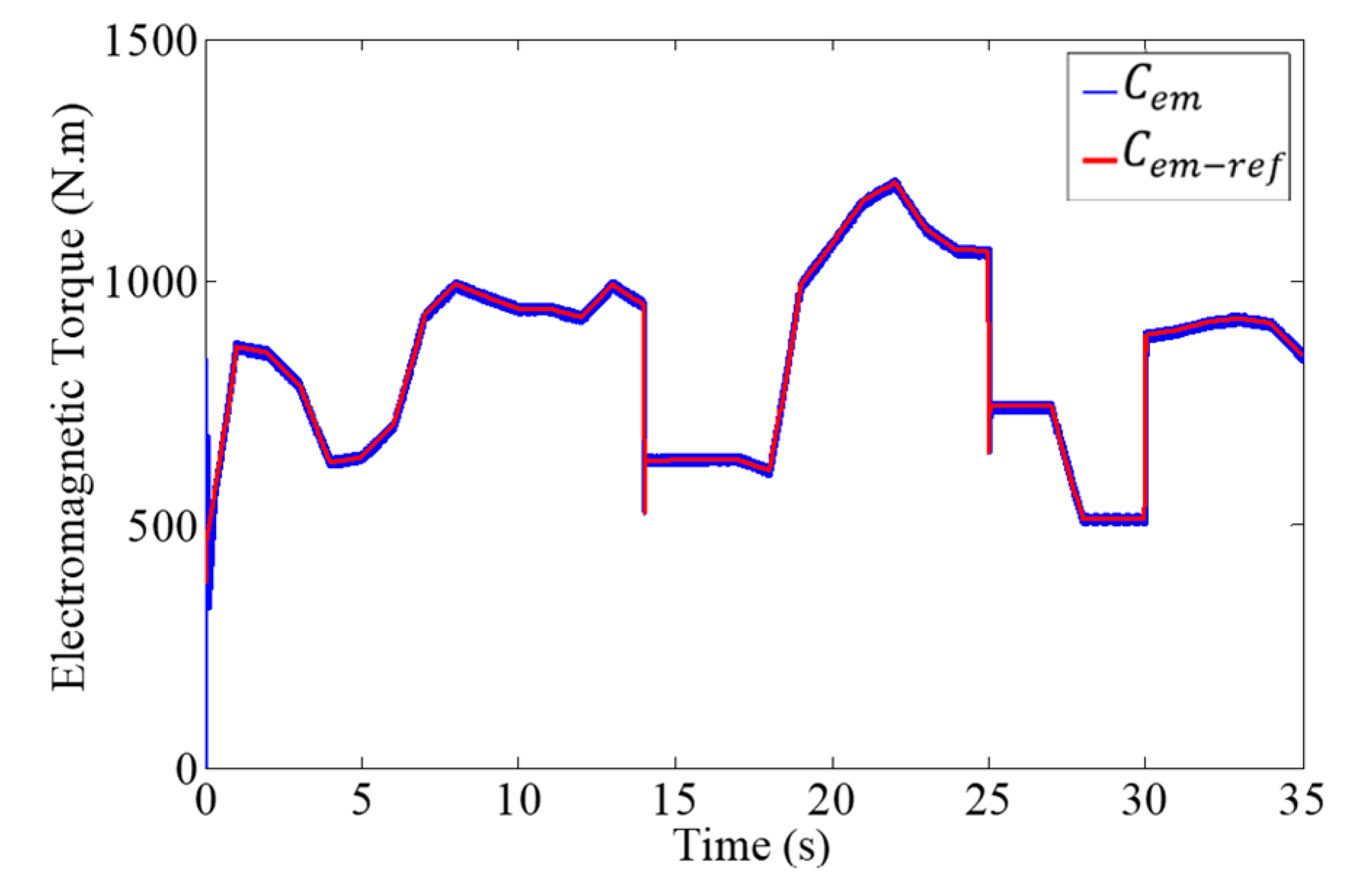

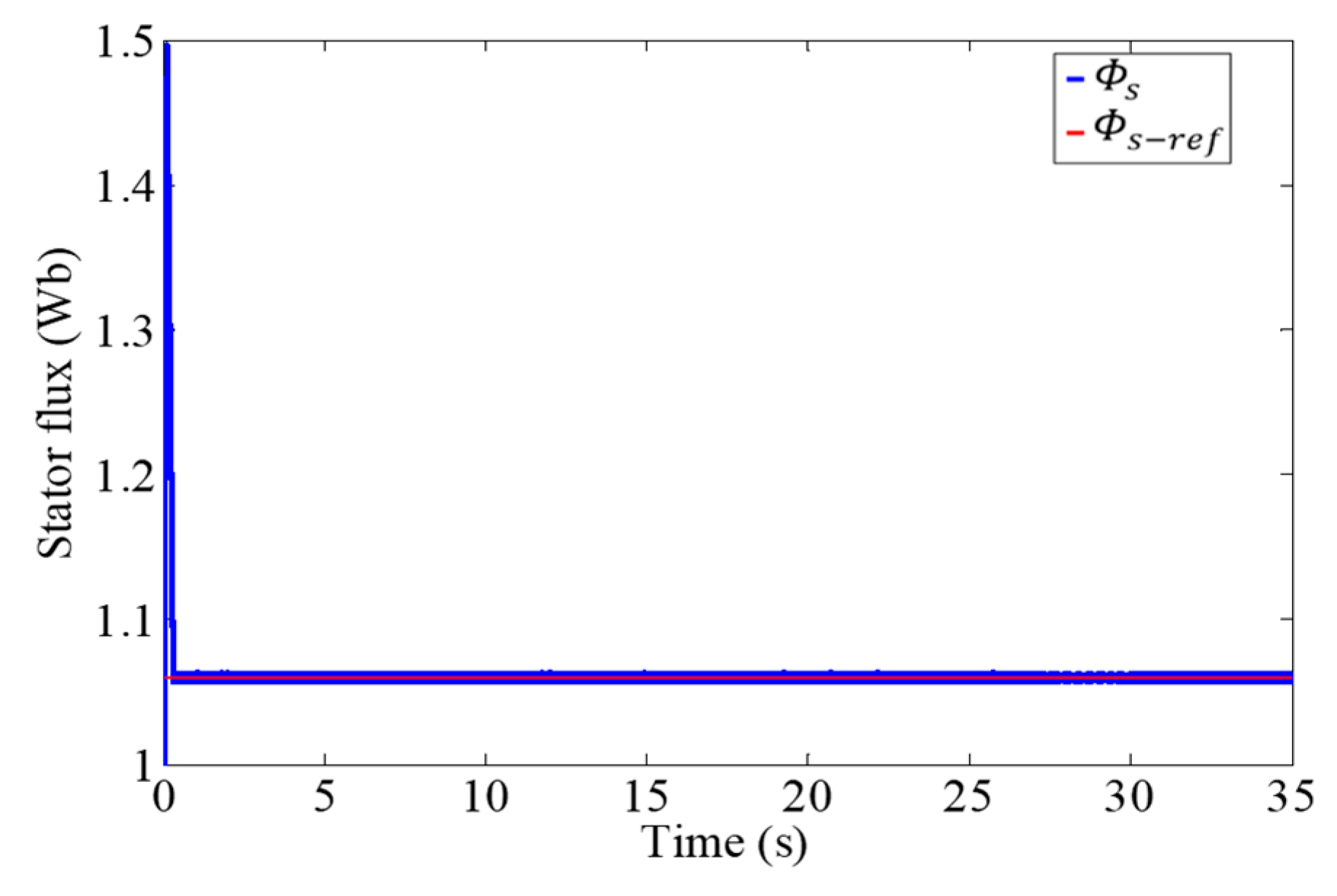
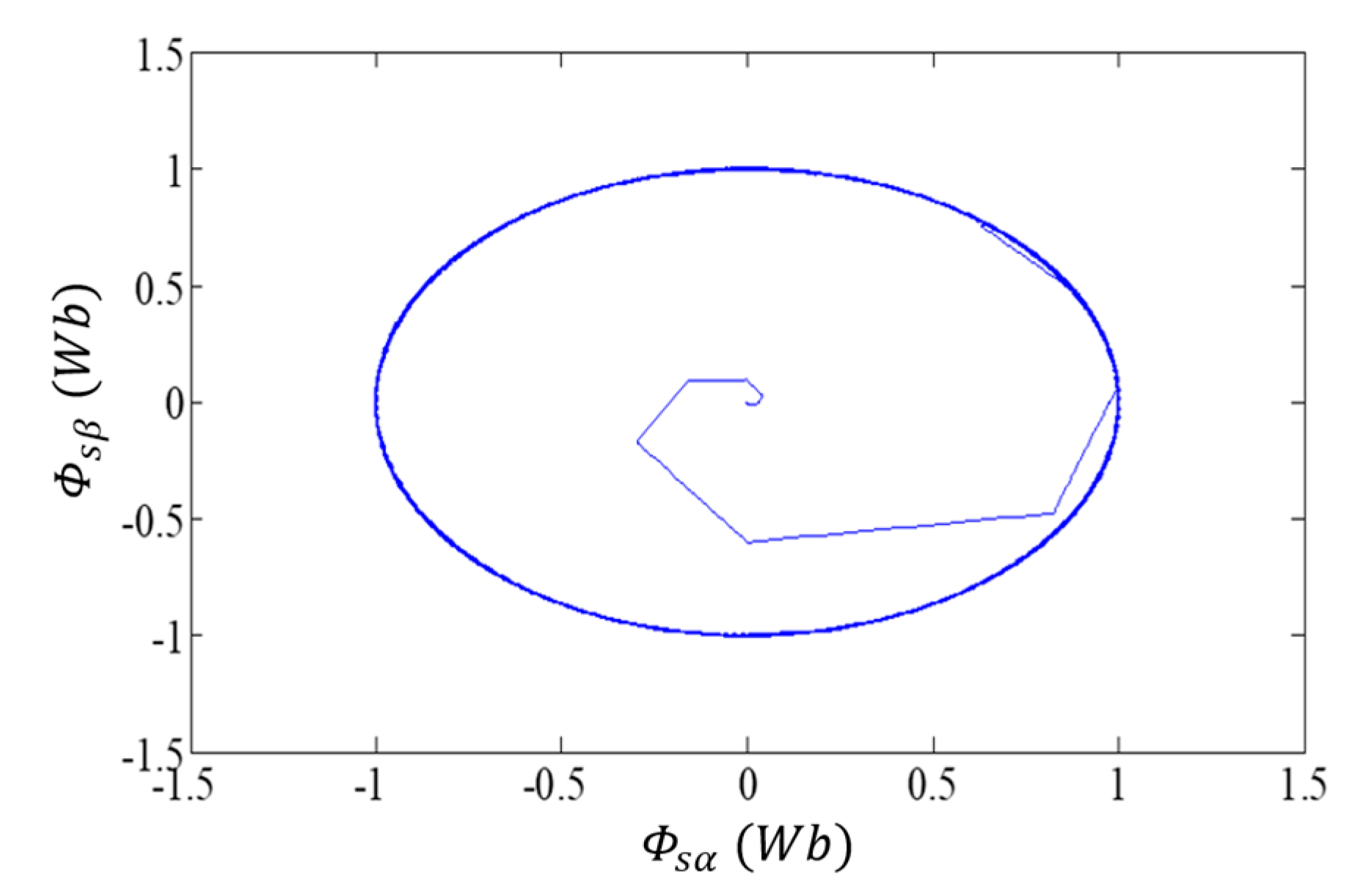

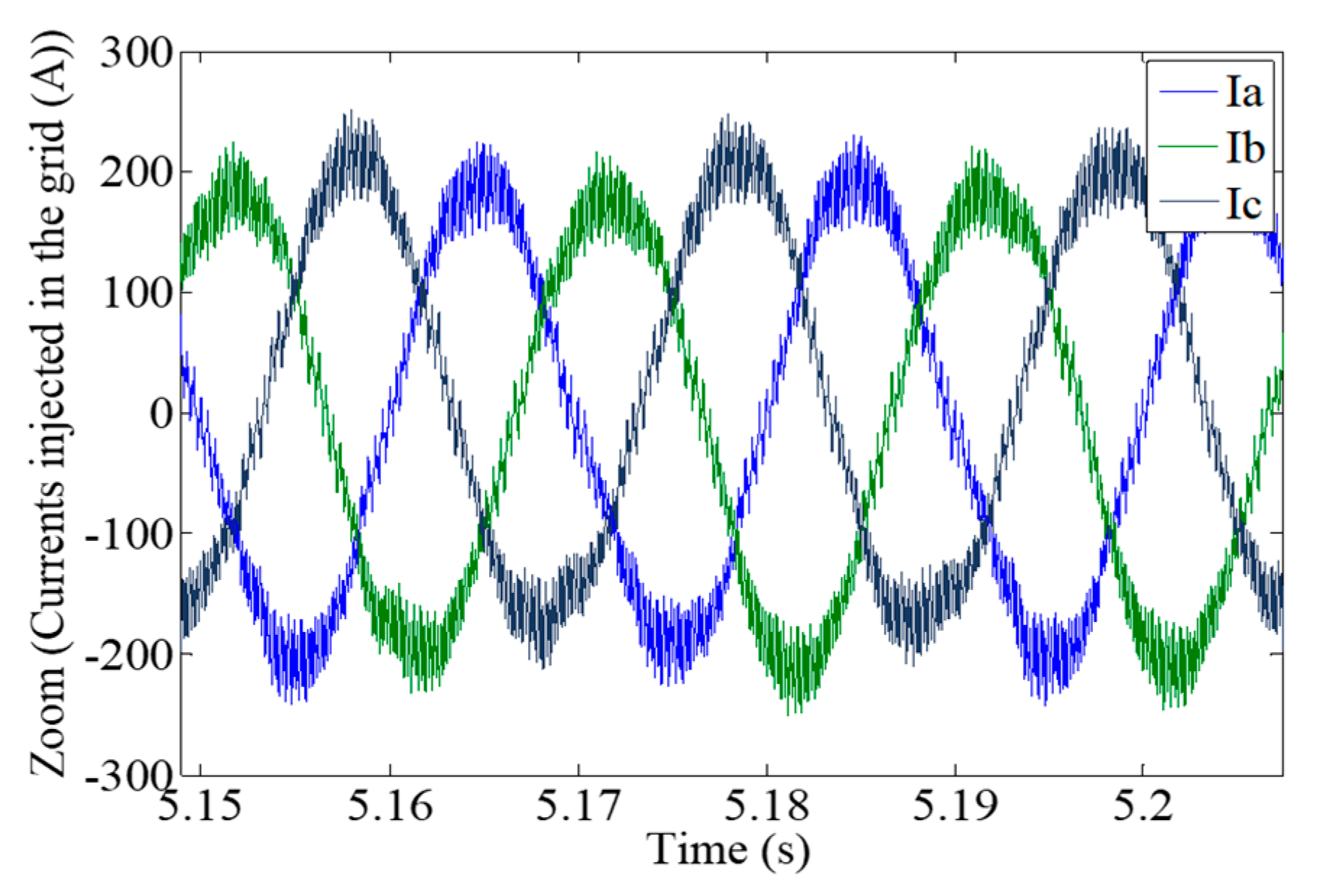

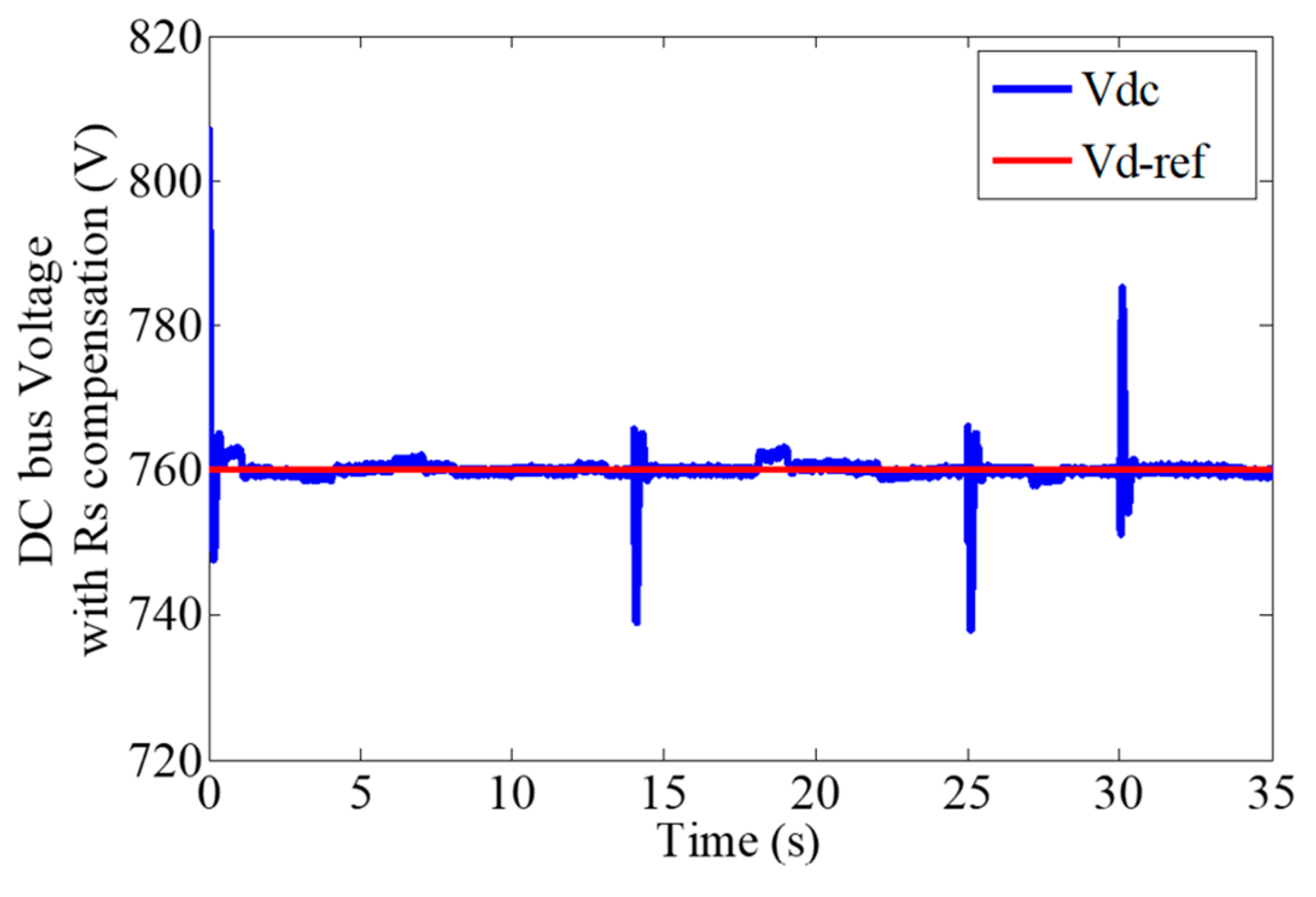
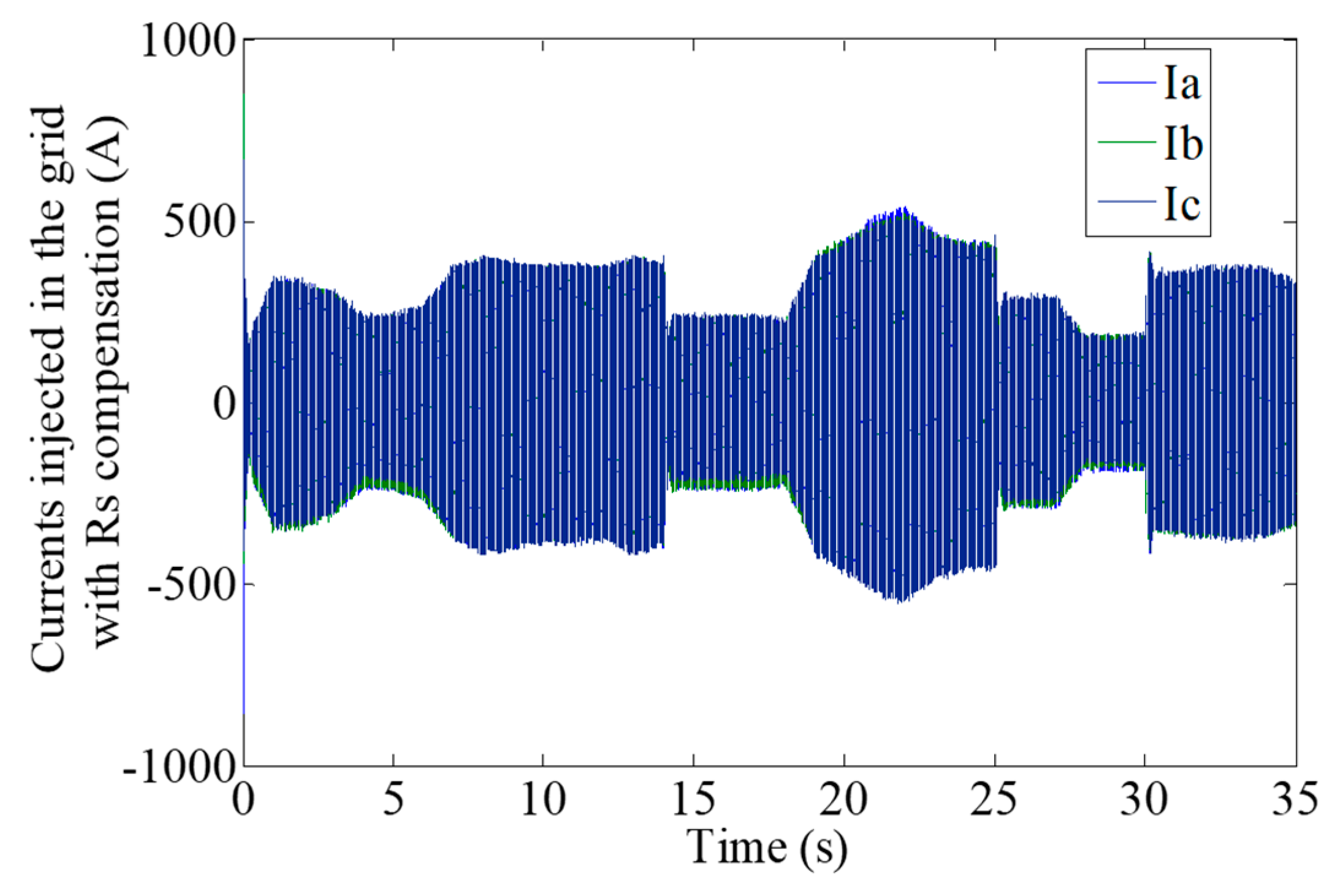
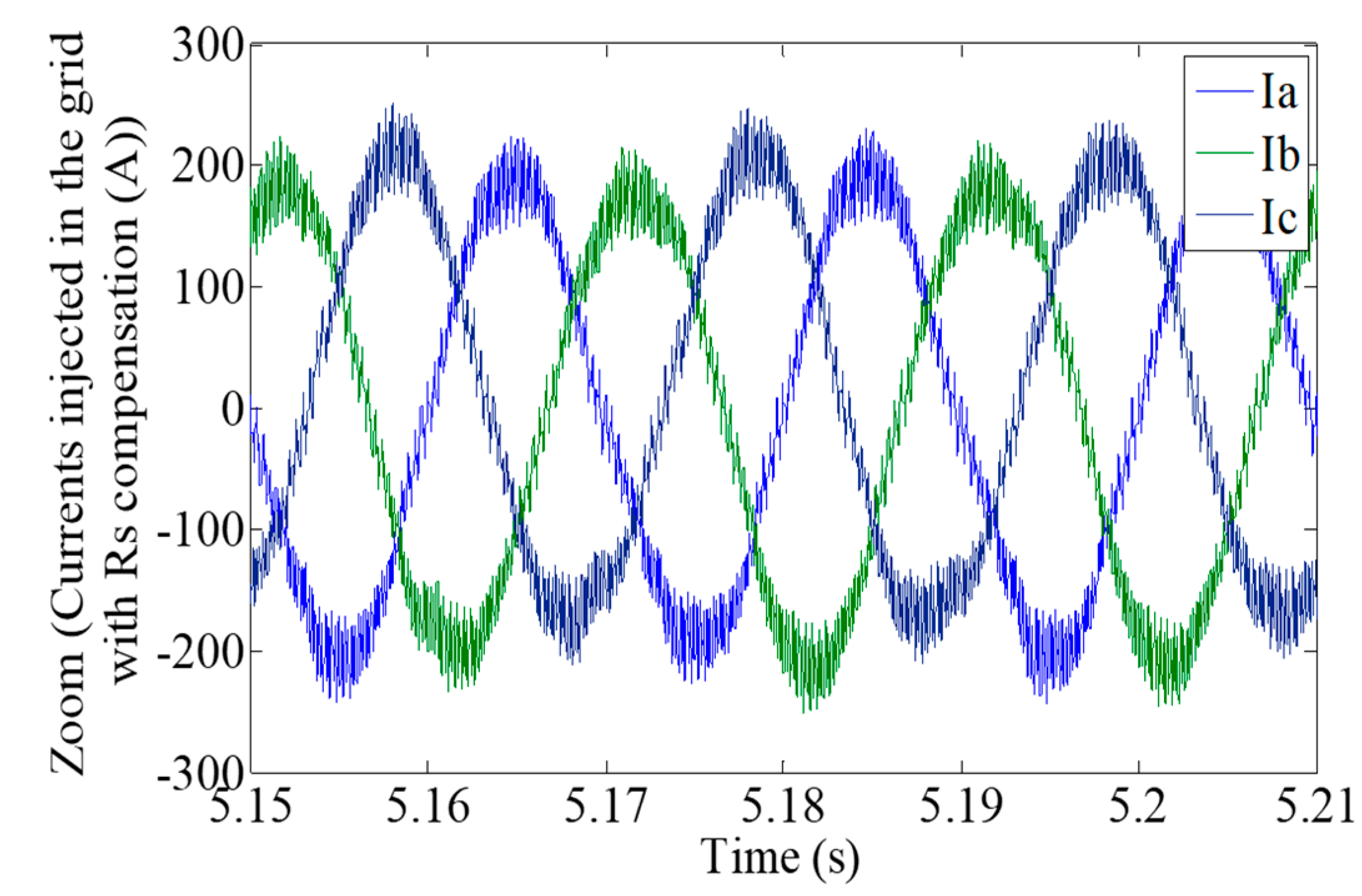
| Vs | V0 | V1 | V2 | V3 | V4 | V5 | V6 | V7 |
|---|---|---|---|---|---|---|---|---|
| (Sa, Sb, Sc)IG | 0 0 0 | 1 0 0 | 1 1 0 | 0 1 0 | 0 1 1 | 0 0 1 | 1 0 1 | 1 1 1 |
| Δe | ||||||
|---|---|---|---|---|---|---|
| PL | PS | ZE | NL | NS | ||
| PL | PL | PL | PL | PS | ZE | |
| PS | PS | PL | PS | ZE | NS | |
| e | ZE | PL | PS | ZE | NS | NL |
| NL | PS | ZE | NS | NL | NL | |
| NS | ZE | NS | NL | NL | NL |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ikni, D.; Raducan, E. Stability Analysis of a Wind Turbine Controlled by Direct Torque Control. Energies 2024, 17, 2488. https://doi.org/10.3390/en17112488
Ikni D, Raducan E. Stability Analysis of a Wind Turbine Controlled by Direct Torque Control. Energies. 2024; 17(11):2488. https://doi.org/10.3390/en17112488
Chicago/Turabian StyleIkni, Djamel, and Elena Raducan. 2024. "Stability Analysis of a Wind Turbine Controlled by Direct Torque Control" Energies 17, no. 11: 2488. https://doi.org/10.3390/en17112488
APA StyleIkni, D., & Raducan, E. (2024). Stability Analysis of a Wind Turbine Controlled by Direct Torque Control. Energies, 17(11), 2488. https://doi.org/10.3390/en17112488