Experimental and Simulation Studies on Stable Polarity Reversal in Aged HVDC Mass-Impregnated Cables
Abstract
1. Introduction
2. Experimental Methods
2.1. Specimen Preparation
2.2. Thermally Accelerated Degradation Tests
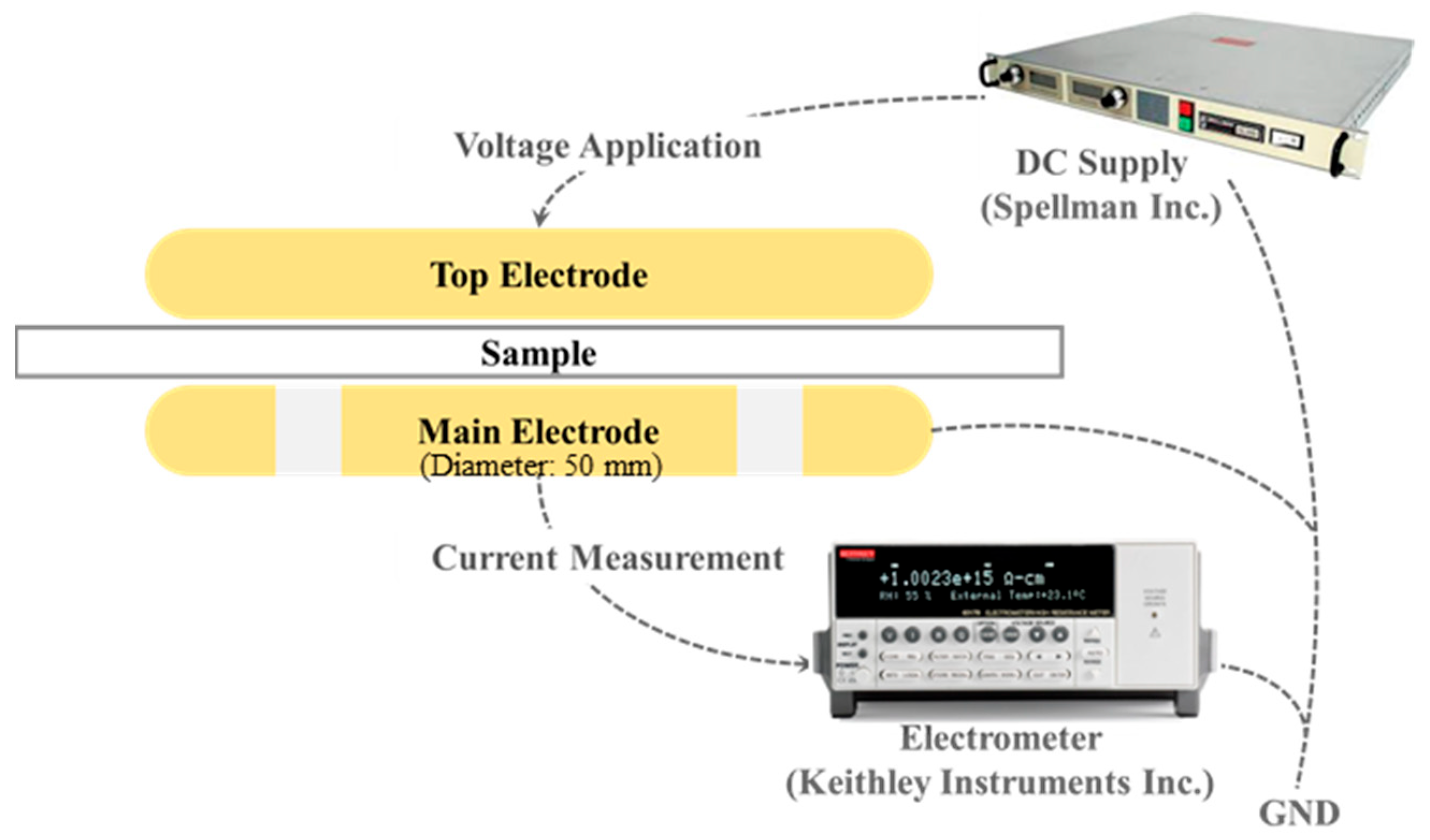
2.3. Measurement of Leakage Current to Determine Electrical Conductivity
3. Experimental Results and Discussion
3.1. Activation Energy and Equivalent Lifetime Calculation
3.2. Electrical Conductivity
4. Simulation Models and Conditions
4.1. DC Electric Field Analysis
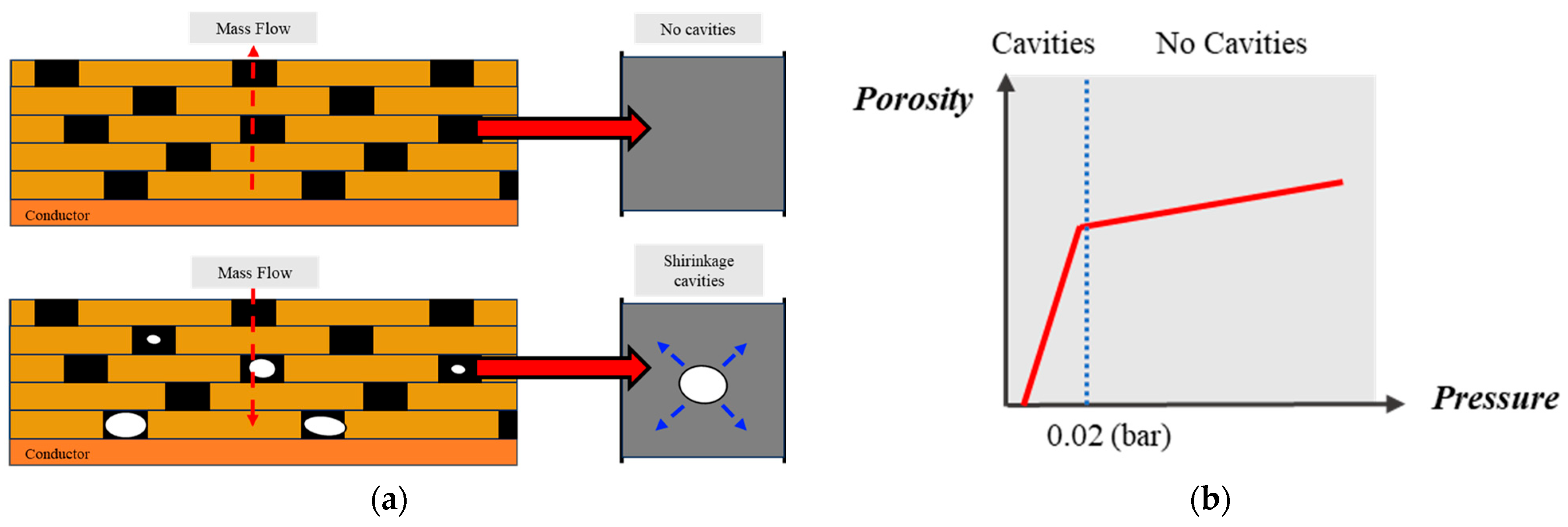
4.2. Pressure Analysis Model for Porous Media
4.3. Geometry and Simulation Conditions
5. Simulation Results and Discussion
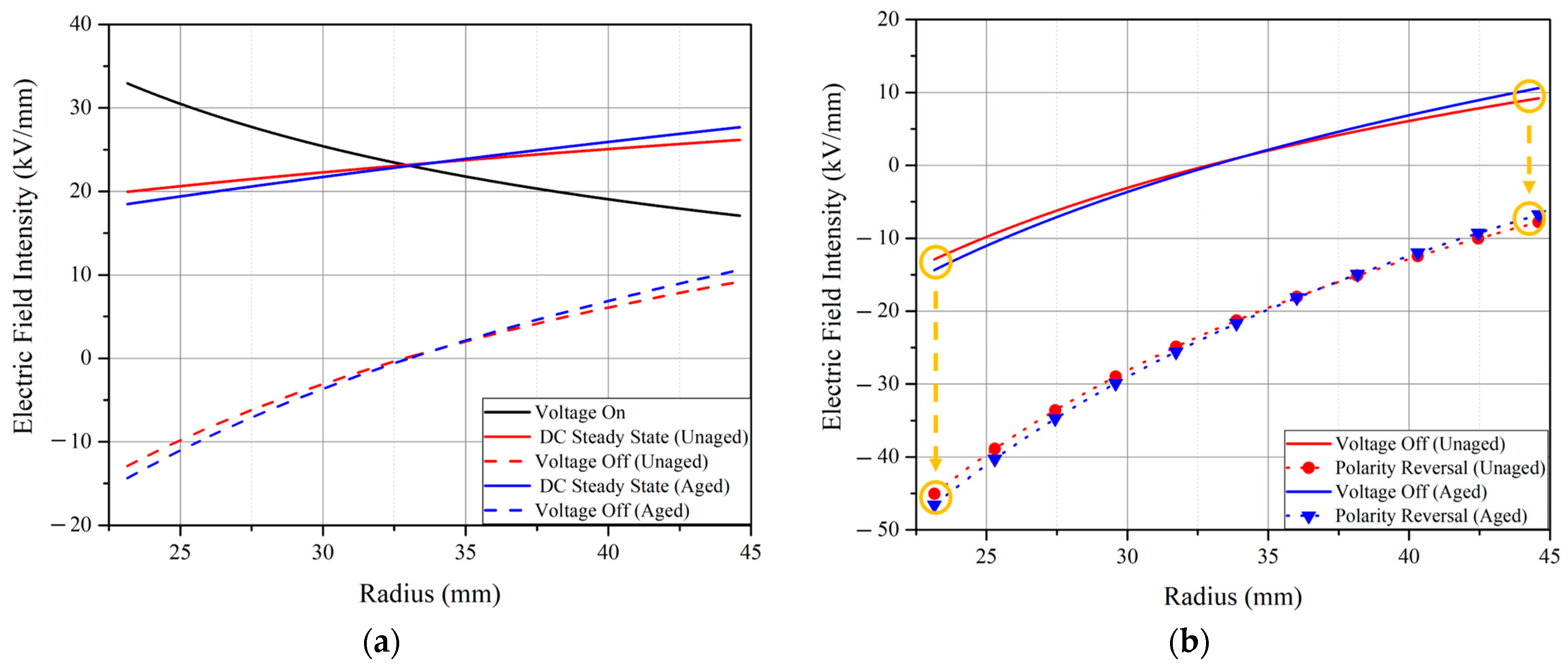
5.1. Time-Varying Electric Field in MI Cable
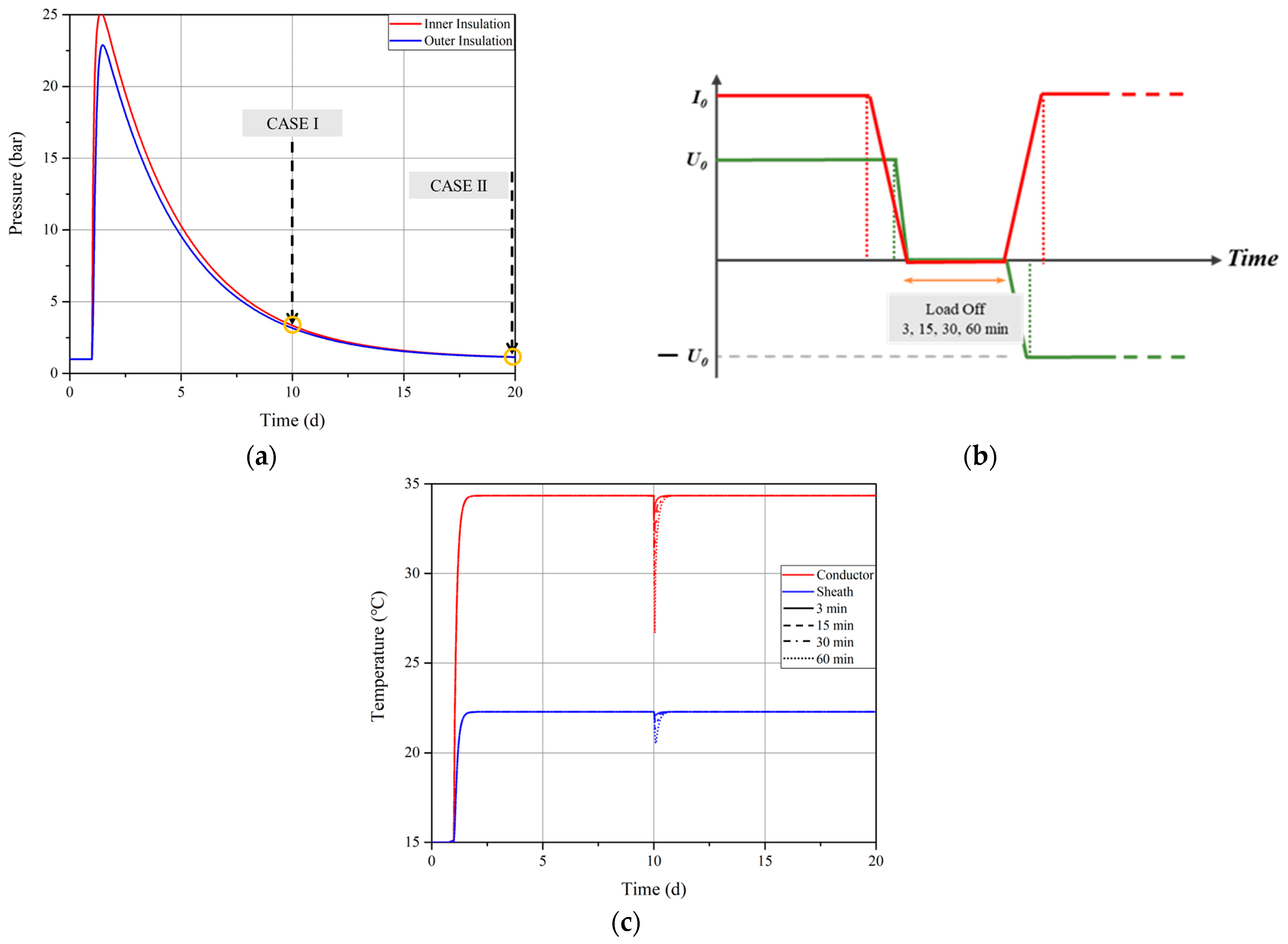
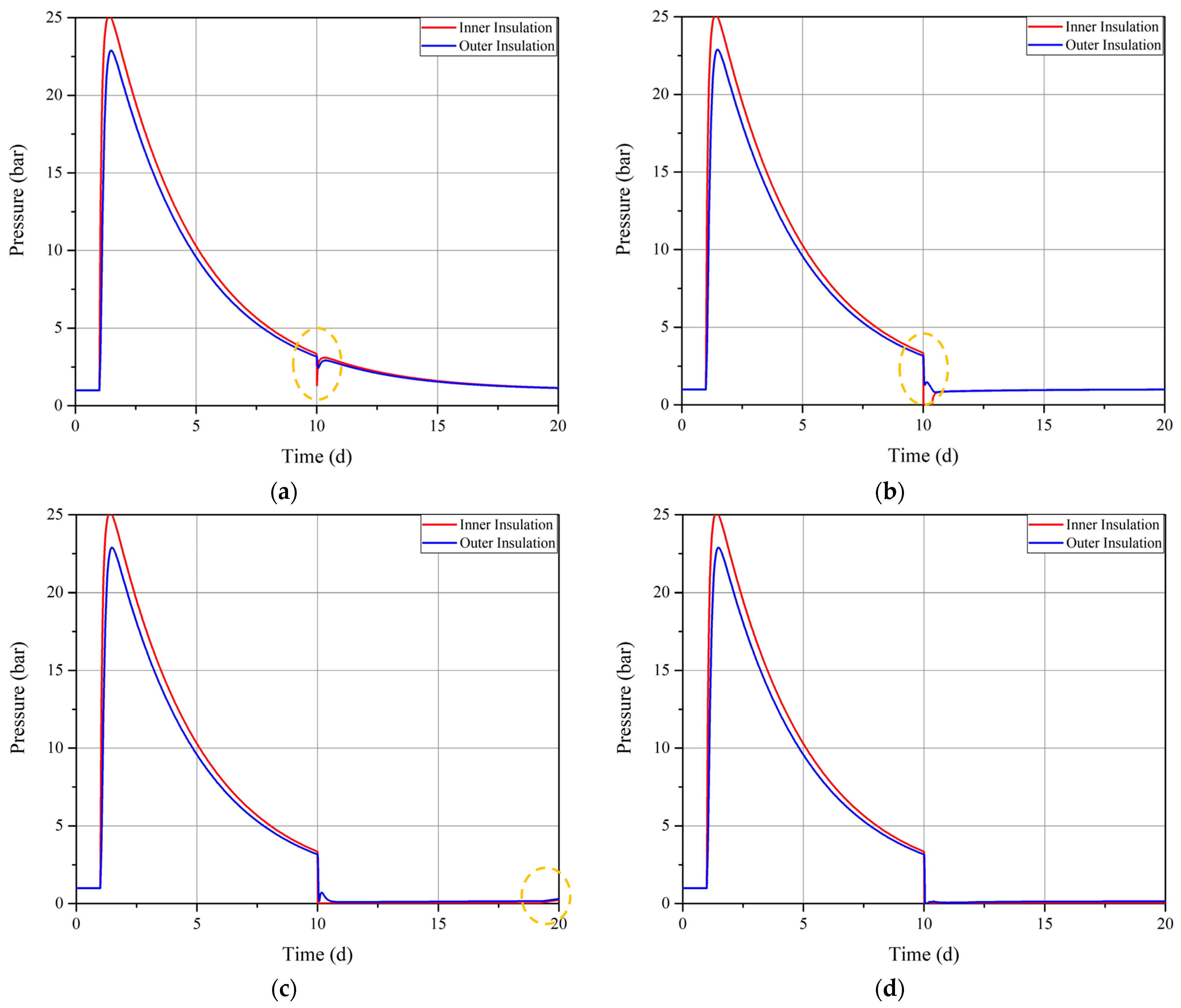
5.2. Internal Pressure Analysis for CASE I
5.3. Internal Pressure Analysis for CASE II
5.4. Adjusting Load Profiles to Prevent Cavitation
6. Conclusions
- It was confirmed that the mass-impregnated paper was resistant to thermal stress and that there was no noticeable change in electrical conductivity even after long-term deterioration.
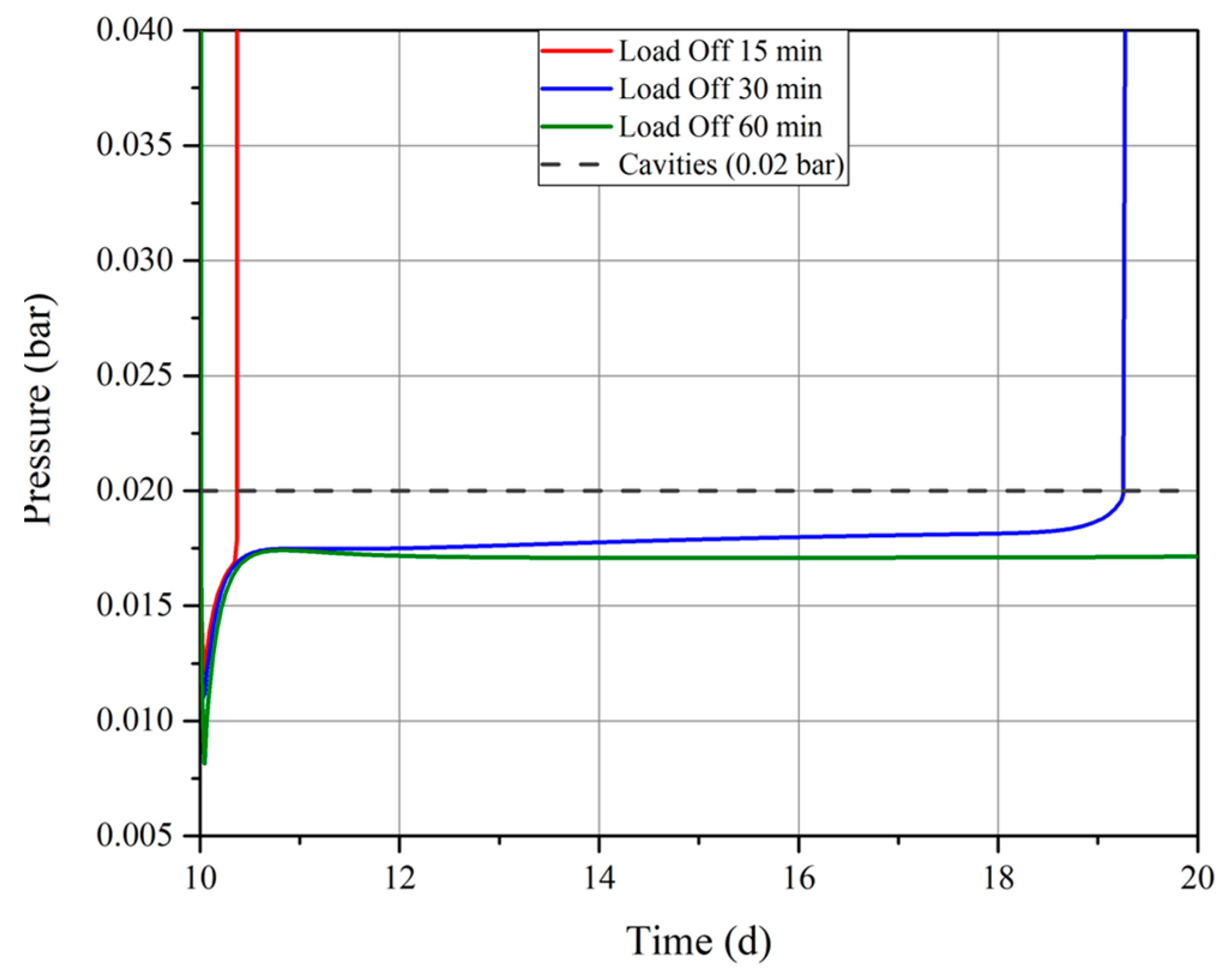
- The time required for cavitation to dissipate increases with the load-off interval. As the temperature drops during this period, the nearby mass contracts and forms cavities, indicating that the duration of load-off is proportional to the extent of cavity formation.
- Sufficient inward migration of the mass is required to fill the shrinkage cavities created during the load-off time, but the cavities formed reduce the available space for the fluid within the porous medium. Consequently, polarity reversal is performed on the cable without adequately filling the cavities created while the cable is cooling.
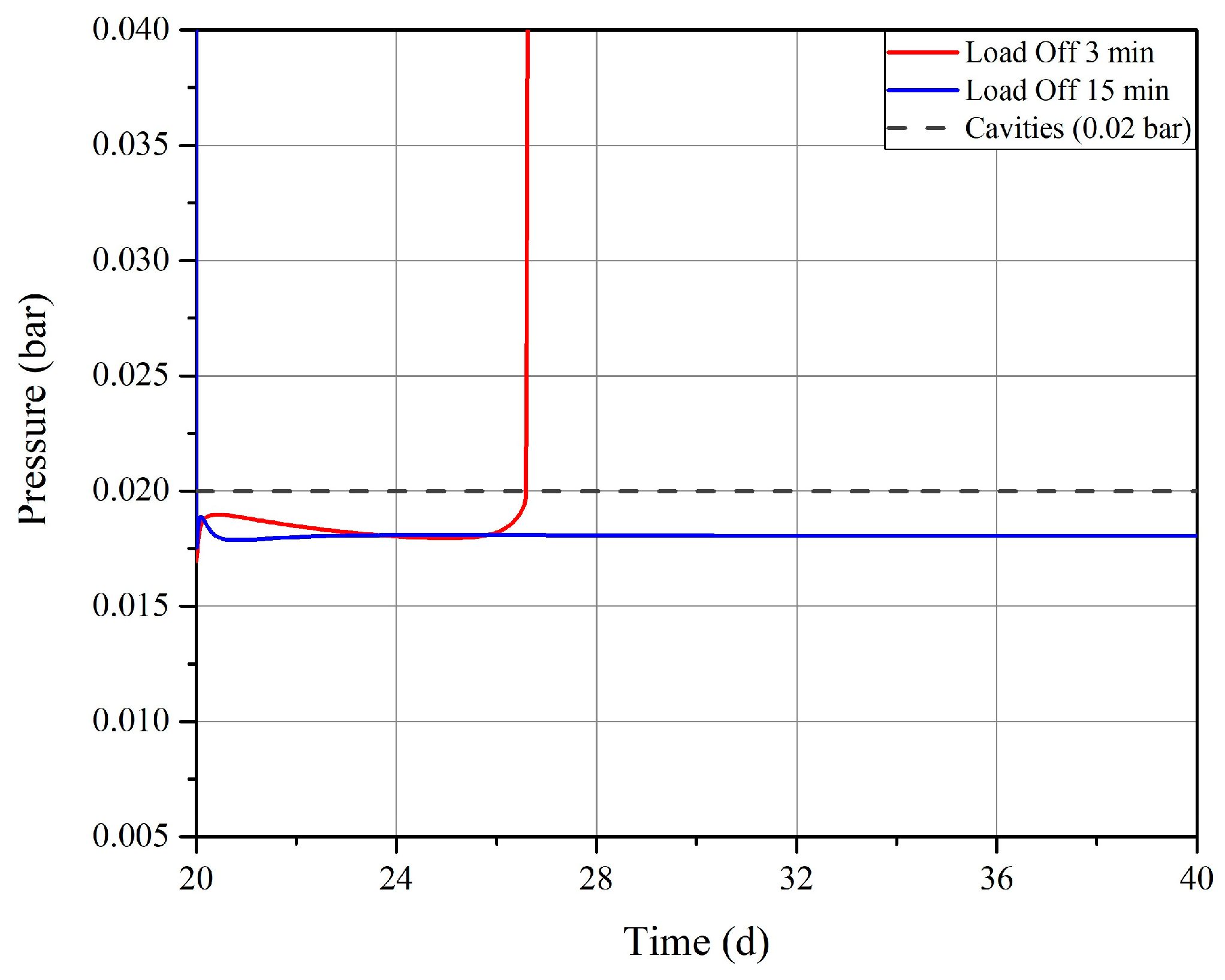
- Adjustments to operational procedures, such as optimizing load conditions to reduce electrical stress and prevent excessive cooling of the cables, have been shown to effectively mitigate the risks associated with polarity reversals.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andersen, B. HVDC transmission-opportunities and challenges. In Proceedings of the 8th IEE International Conference on AC and DC Power Transmission, London, UK, 28–31 March 2006. [Google Scholar]
- Arrillaga, J. High Voltage Direct Current Transmission; Institution of Engineering and Technology (IET): London, UK, 1998. [Google Scholar]
- Meah, K.; Ula, S. Comparative evaluation of HVDC and HVAC transmission systems. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Rudervall, R.; Charpentier, J.; Sharma, R. High voltage direct current (HVDC) transmission systems technology review paper. In Proceedings of the Energy Week 2000, Washington, DC, USA, 7–8 March 2000; pp. 1–19. [Google Scholar]
- Alassi, A.; Bañales, S.; Ellabban, O.; Adam, G.; MacIver, C. HVDC transmission: Technology review, market trends and future outlook. Renew. Sustain. Energy Rev. 2019, 112, 530–554. [Google Scholar] [CrossRef]
- Ardelean, M.; Minnebo, P. HVDC Submarine Power Cables in the World; Joint Research Center: Petten, The Netherlands, 2015. [Google Scholar]
- Evenset, G.; Balog, G. The Breakdown Mechanism of HVDC Mass-Impregnated Cables; International Council on Large Electric Systems (CIGRÉ): Paris, France, 2000. [Google Scholar]
- Albertini, M.; Cotugno, S.; Pietribiasi, D.; Remy, C. HPTE Extruded Cables Polarity Reversals Performance in LCC HVDC Systems. In Proceedings of the 2020 AEIT International Annual Conference (AEIT), Catania, Italy, 23–25 September 2020; pp. 1–6. [Google Scholar]
- Wang, W.; Yan, X.; Li, S.; Zhang, L.; Ouyang, J.; Ni, X. Failure of submarine cables used in high-voltage power transmission: Characteristics, mechanisms, key issues and prospects. IET Gener. Transm. Distrib. 2021, 15, 1387–1402. [Google Scholar] [CrossRef]
- Mazzanti, G. High voltage direct current transmission cables to help decarbonisation in Europe: Recent achievements and issues. High Volt. 2022, 7, 633–644. [Google Scholar] [CrossRef]
- Kwak, E.-S.; Min, J.-H.; Jung, H.-C.; Moon, C.-J. A Study on HVDC and BESS Application for High Penetration of Renewable Energy Sources. J. Korea Inst. Electron. Commun. Sci. 2021, 16, 1339–1348. [Google Scholar]
- Eriksson, A.; Henning, G.; Akke, M.; Axelsson, U. Development work concerning testing procedures of mass-impregnated HVDC cables. In Proceedings of the International Conference on Large High Voltage Electric Systems, Paris, France, 28 August–3 September 1994; pp. 21–206. [Google Scholar]
- Runde, M.; Hegerberg, R.; Magnusson, N.; Ildstad, E.; Ytrehus, T. Cavity formation in mass-impregnated HVDC subsea cables-mechanisms and critical parameters. IEEE Electr. Insul. Mag. 2014, 30, 22–33. [Google Scholar] [CrossRef]
- Runde, M.; Kvien, O.; Förster, H.; Magnusson, N. Cavities in mass-impregnated HVDC subsea cables studied by AC partial discharge measurements. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 913–921. [Google Scholar] [CrossRef]
- Oh, D.-H.; Lee, H.-Y.; Kim, S.-J.; Lee, B.-W. Correlation between partial discharge inception voltage and breakdown voltage characteristics of butt-gap in HVDC mass impregnated PPLP cable. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 518–521. [Google Scholar]
- Hestad, Ø.; Runde, M.; Enoksen, H.; Magnusson, N. Modeling of Internal Pressure Dynamics in Mass-Impregnated Nondraining HVDC Cables. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 1135–1142. [Google Scholar] [CrossRef]
- Runde, M.; Jonsson, E.; Magnusson, N.; Solheim, K.T. Internal pressures and pressure gradients in mass-impregnated HVDC cables during current cycling. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 915–923. [Google Scholar] [CrossRef]
- Runde, M.; Bjerrehorn, E.; Jonsson, E.; Magnusson, N. Internal pressure dynamics of mass-impregnated HVDC subsea cables at different sea depths. CIGRÉ Sci. Eng. 2022, 24, 1–11. [Google Scholar]
- Helal, K.; Abd El-Aal, R.; Dessouky, S.; Backhaus, K.; Speck, J.; Grossmann, S. Partial discharge characteristics of a gas void embedded between oil impregnated papers under the effect of AC and DC voltage. In Proceedings of the 2018 IEEE 2nd International Conference on Dielectrics (ICD), Budapest, Hungary, 1–5 July 2018; pp. 1–4. [Google Scholar]
- Kim, H.-S.; Oh, D.-H.; Kim, Y.-R.; Lee, B.-W. Relation between DC PDIV and DC BDV of Mass Impregnated Polypropylene Laminated Paper Considering the Thermal Aging Characteristics. In Proceedings of the 2020 8th International Conference on Condition Monitoring and Diagnosis (CMD), Phuket, Thailand, 25–28 October 2020; pp. 369–372. [Google Scholar]
- Bystritskaya, E.V.; Monakhova, T.V.; Ivanov, V.B. TGA application for optimising the accelerated aging conditions and predictions of thermal aging of rubber. Polym. Test. 2013, 32, 197–201. [Google Scholar] [CrossRef]
- Dissado, L.A.; Fothergill, J.C. Electrical Degradation and Breakdown in Polymers; Institution of Engineering and Technology (IET): London, UK, 1992; Volume 9. [Google Scholar]
- Setnescu, R.; Badicu, L.; Dumitran, L.; Notingher, P.; Setnescu, T. Thermal lifetime of cellulose insulation material evaluated by an activation energy based method. Cellulose 2014, 21, 823–833. [Google Scholar] [CrossRef]
- Hampton, R. Some of the considerations for materials operating under high-voltage, direct-current stresses. IEEE Electr. Insul. Mag. 2008, 24, 5–13. [Google Scholar] [CrossRef]
- Mauseth, F.; Haugdal, H. Electric field simulations of high voltage DC extruded cable systems. IEEE Electr. Insul. Mag. 2017, 33, 16–21. [Google Scholar] [CrossRef]
- Reddy, C.C.; Ramu, T. On the computation of electric field and temperature distribution in HVDC cable insulation. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1236–1244. [Google Scholar] [CrossRef]
- Jeroense, M.; Morshuis, P. Electric fields in HVDC paper-insulated cables. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 225–236. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, S.; Hu, J.; He, J. Polymeric insulation materials for HVDC cables: Development, challenges and future perspective. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1308–1318. [Google Scholar] [CrossRef]
- Szabo, P.; Hassager, O.; Strobech, E. Modeling of pressure effects in HVDC cables. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 845–851. [Google Scholar] [CrossRef]
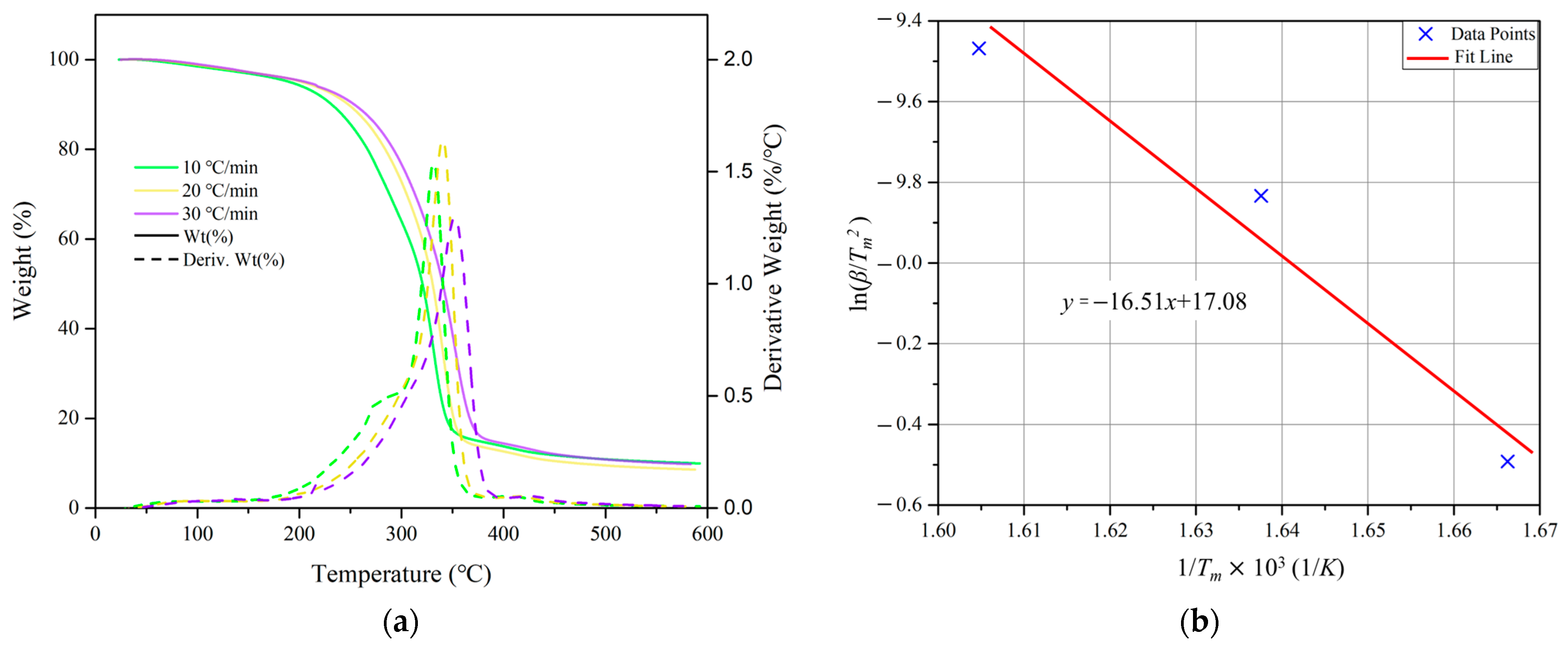




| Heating Rate (°C/min) | Tm (K) | (1/Tm)∙103 (1/K) | ln(β/Tm2) |
|---|---|---|---|
| 10 | 600.15 | 1.66625 | −10.491774 |
| 20 | 610.65 | 1.637599 | −9.833316 |
| 30 | 623.15 | 1.60475 | −9.468377 |
| Cable Components | Radius (mm) |
|---|---|
| Copper conductor | 23.15 |
| Mass-impregnated insulation | 43.7 |
| Lead sheath | 47.9 |
| Polyethylene sheath | 51.2 |
| Steel band | 52 |
| Steel armor | 58 |
| Outer serving | 63 |
| Parameters | Value |
|---|---|
| Parameters of viscosity | |
| μWLF | 2.1 Pa∙s |
| AWLF | 8.15 |
| BWLF | 125 K |
| TWLF | 323 K |
| Density of mass (ρm0) | 939 kg/m3 |
| Pressure-dependent of density (∂ρm/∂p) | 4.7∙10−7 s2/m2 |
| Temperature-dependent of density (∂ρm/∂T) | −0.6 kg/(K∙m3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-J.; Lee, S.; Choi, W.-S.; Lee, B.-W. Experimental and Simulation Studies on Stable Polarity Reversal in Aged HVDC Mass-Impregnated Cables. Energies 2024, 17, 2352. https://doi.org/10.3390/en17102352
Kim S-J, Lee S, Choi W-S, Lee B-W. Experimental and Simulation Studies on Stable Polarity Reversal in Aged HVDC Mass-Impregnated Cables. Energies. 2024; 17(10):2352. https://doi.org/10.3390/en17102352
Chicago/Turabian StyleKim, Sun-Jin, Seol Lee, Woo-Sung Choi, and Bang-Wook Lee. 2024. "Experimental and Simulation Studies on Stable Polarity Reversal in Aged HVDC Mass-Impregnated Cables" Energies 17, no. 10: 2352. https://doi.org/10.3390/en17102352
APA StyleKim, S.-J., Lee, S., Choi, W.-S., & Lee, B.-W. (2024). Experimental and Simulation Studies on Stable Polarity Reversal in Aged HVDC Mass-Impregnated Cables. Energies, 17(10), 2352. https://doi.org/10.3390/en17102352






