Small-Scale Battery Energy Storage System for Testing Algorithms Aimed at Peak Power Reduction
Abstract
1. Introduction
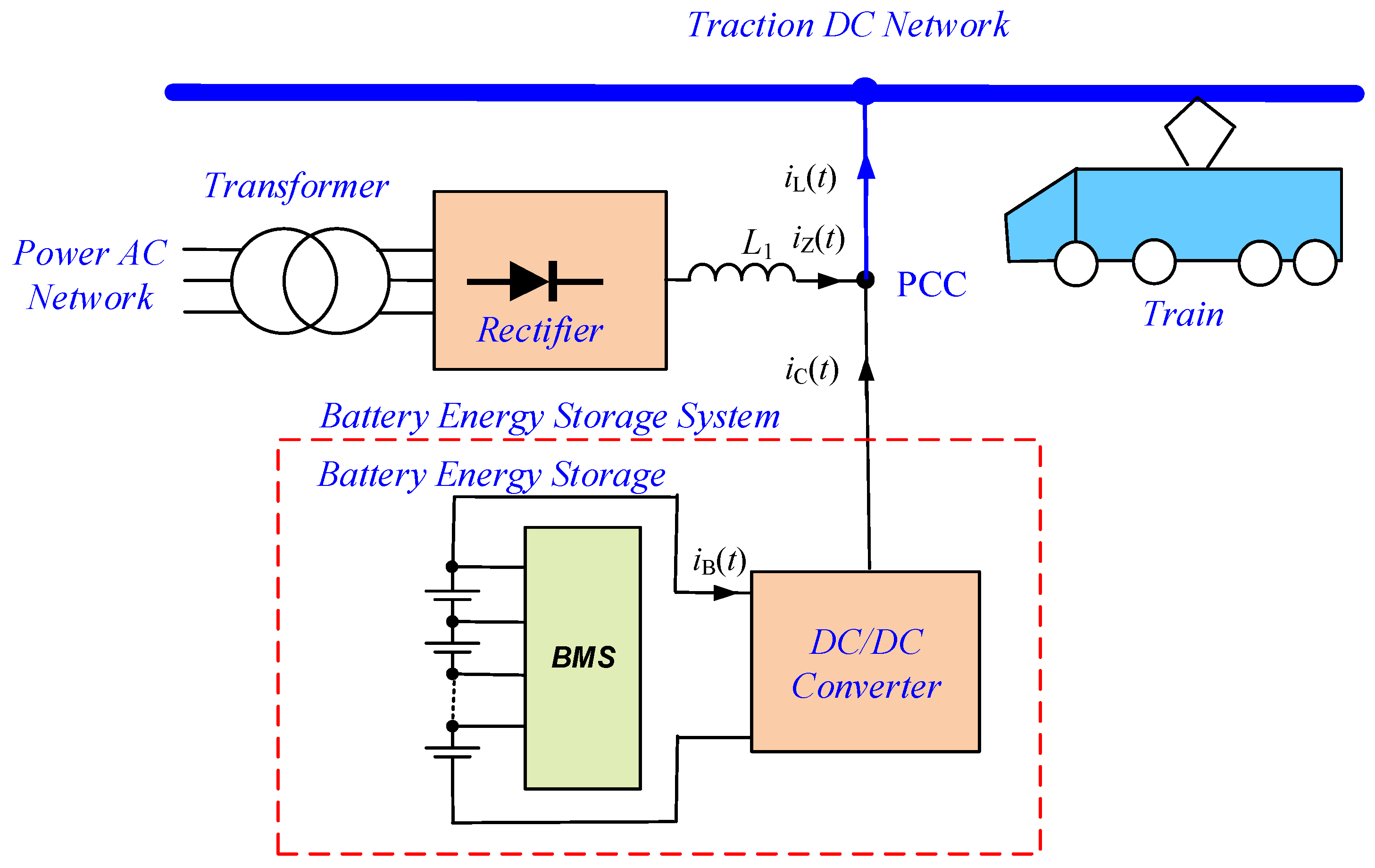
1.1. Role of Battery Energy Storage in the Power System
- The railway operator incurs lower charges because it can reduce the contracted power requirements.
- From the power grid point of view, power fluctuations are reduced and, consequently, voltage sags are reduced.
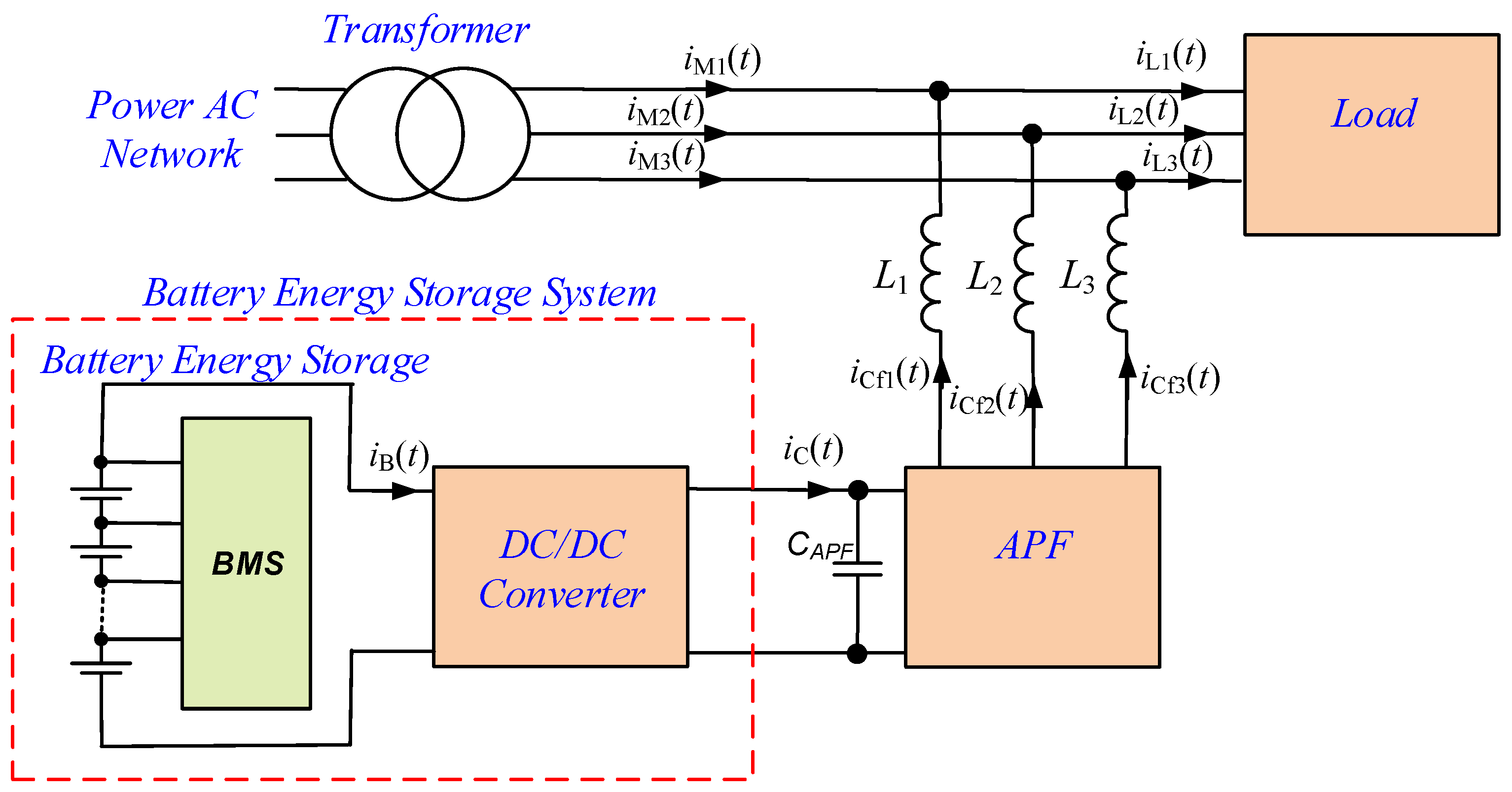
1.2. State-of-the-Art Battery Energy Storage Systems
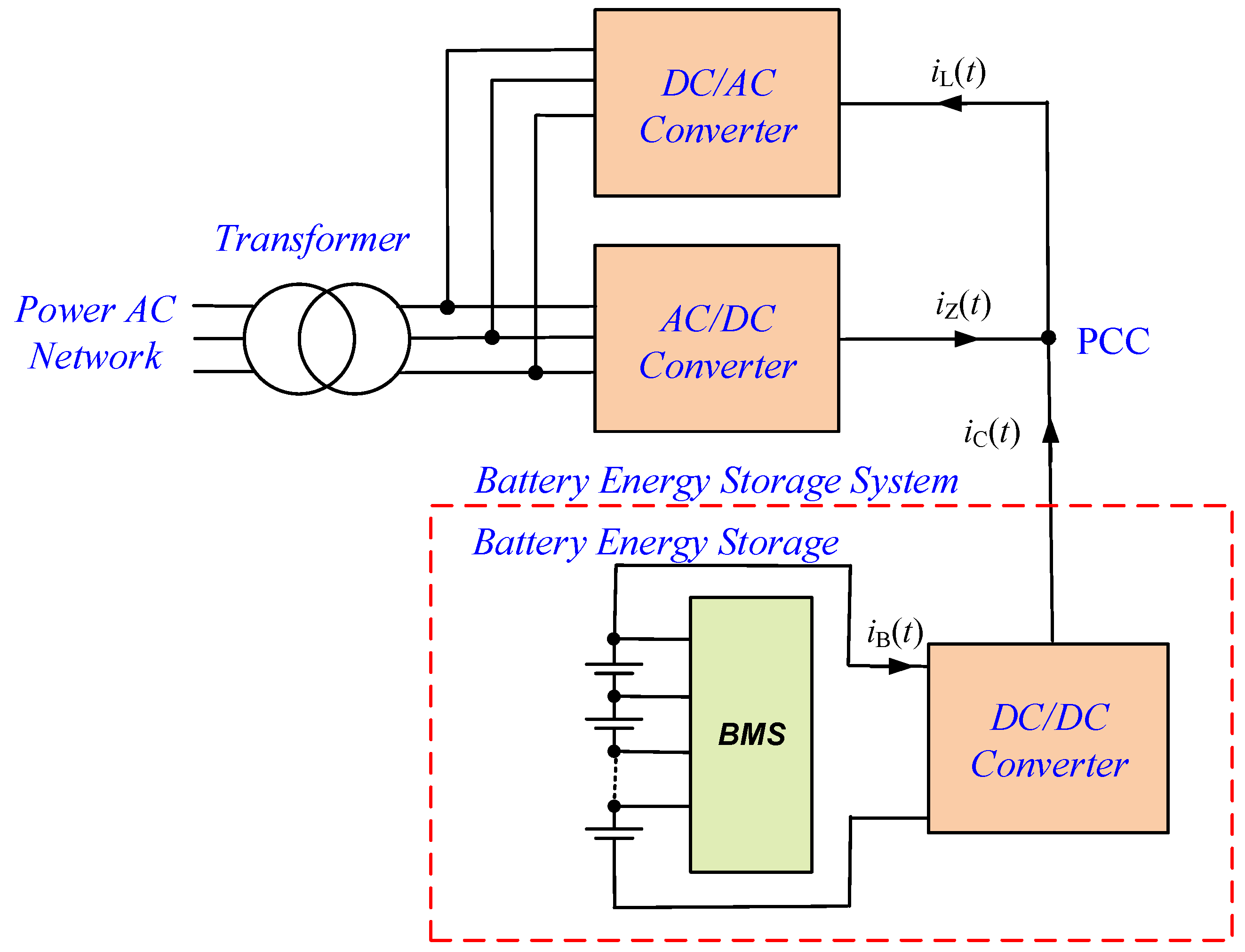
2. DC/DC Converter
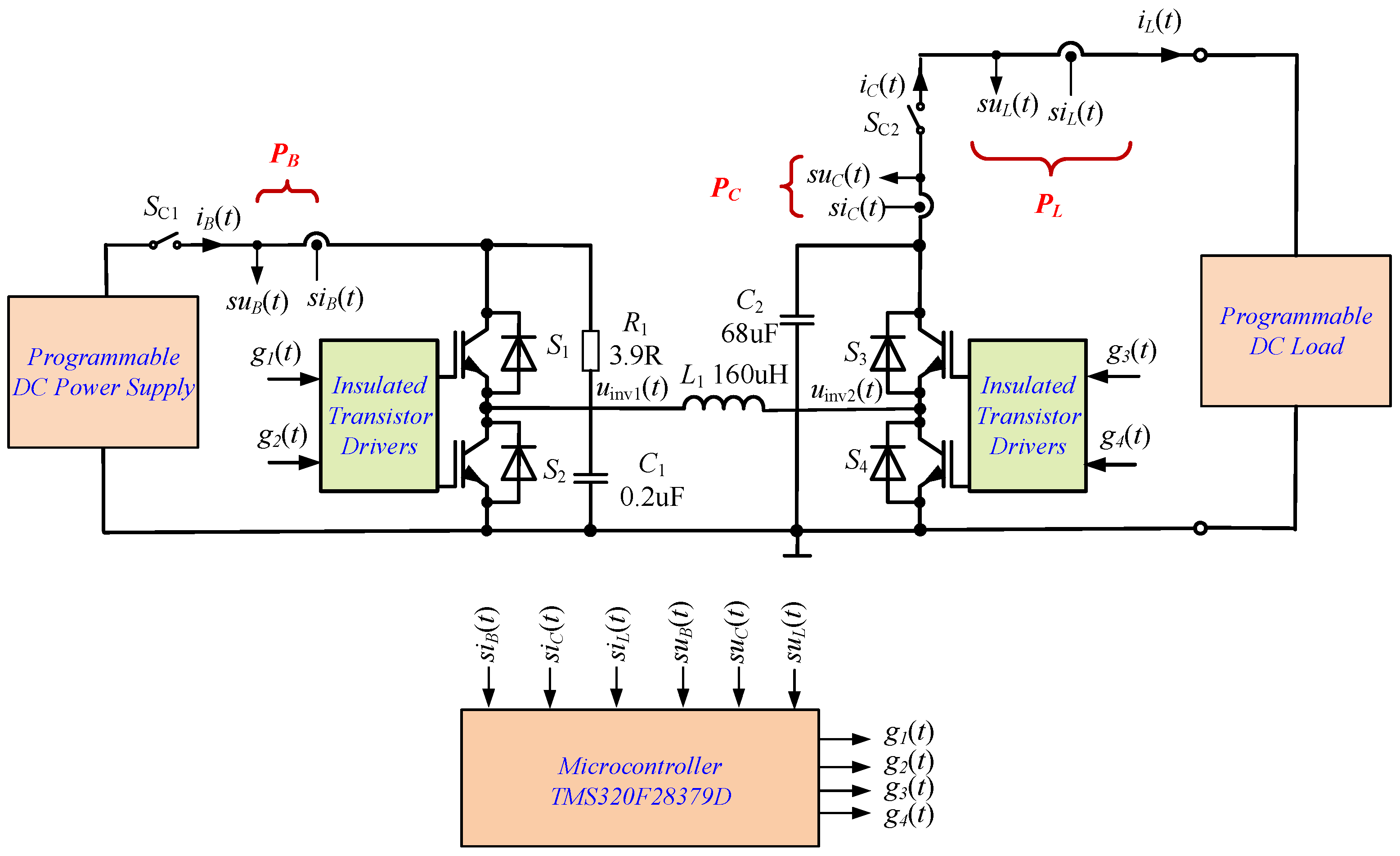
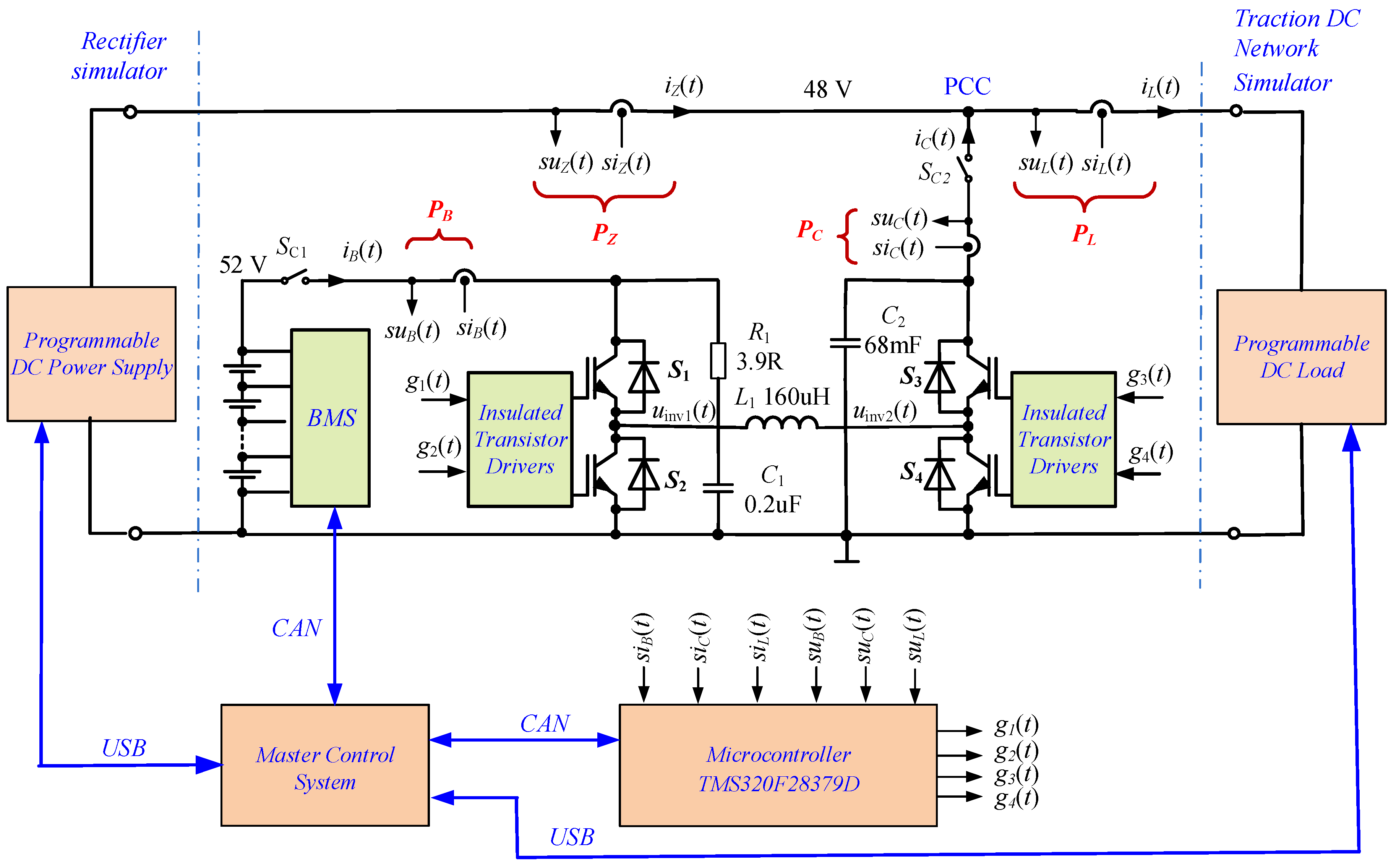
3. Laboratory Model of DC/DC Converter
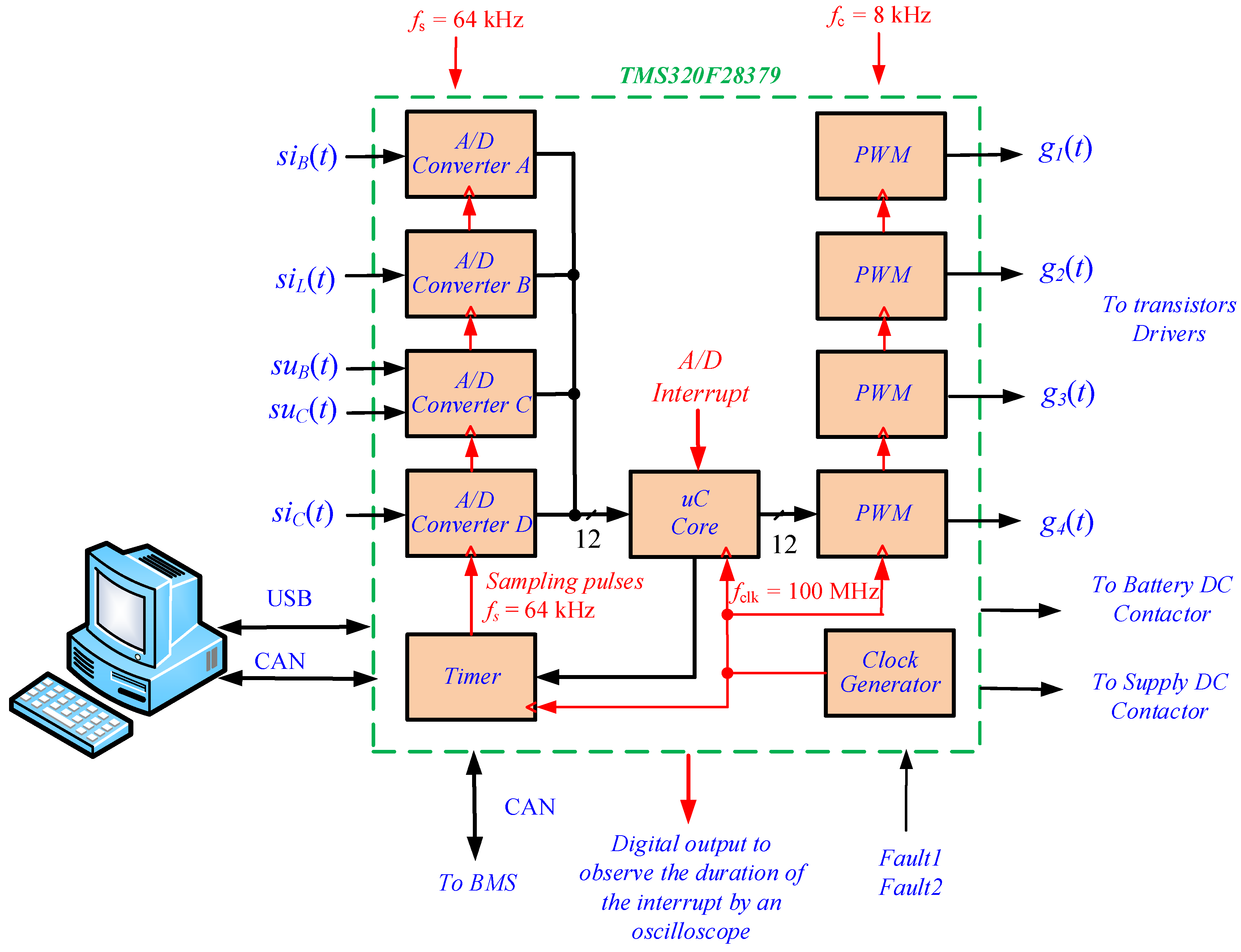
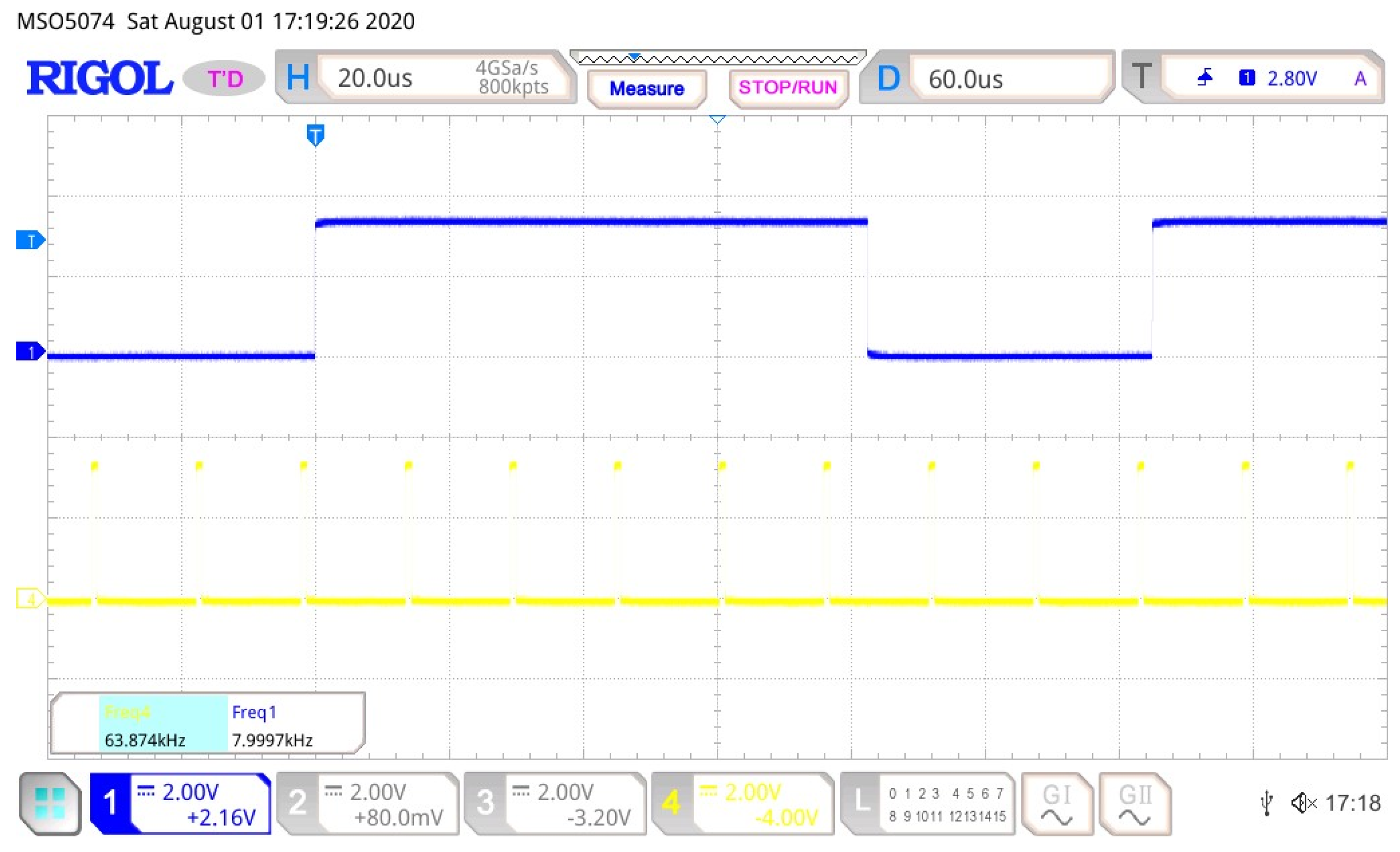
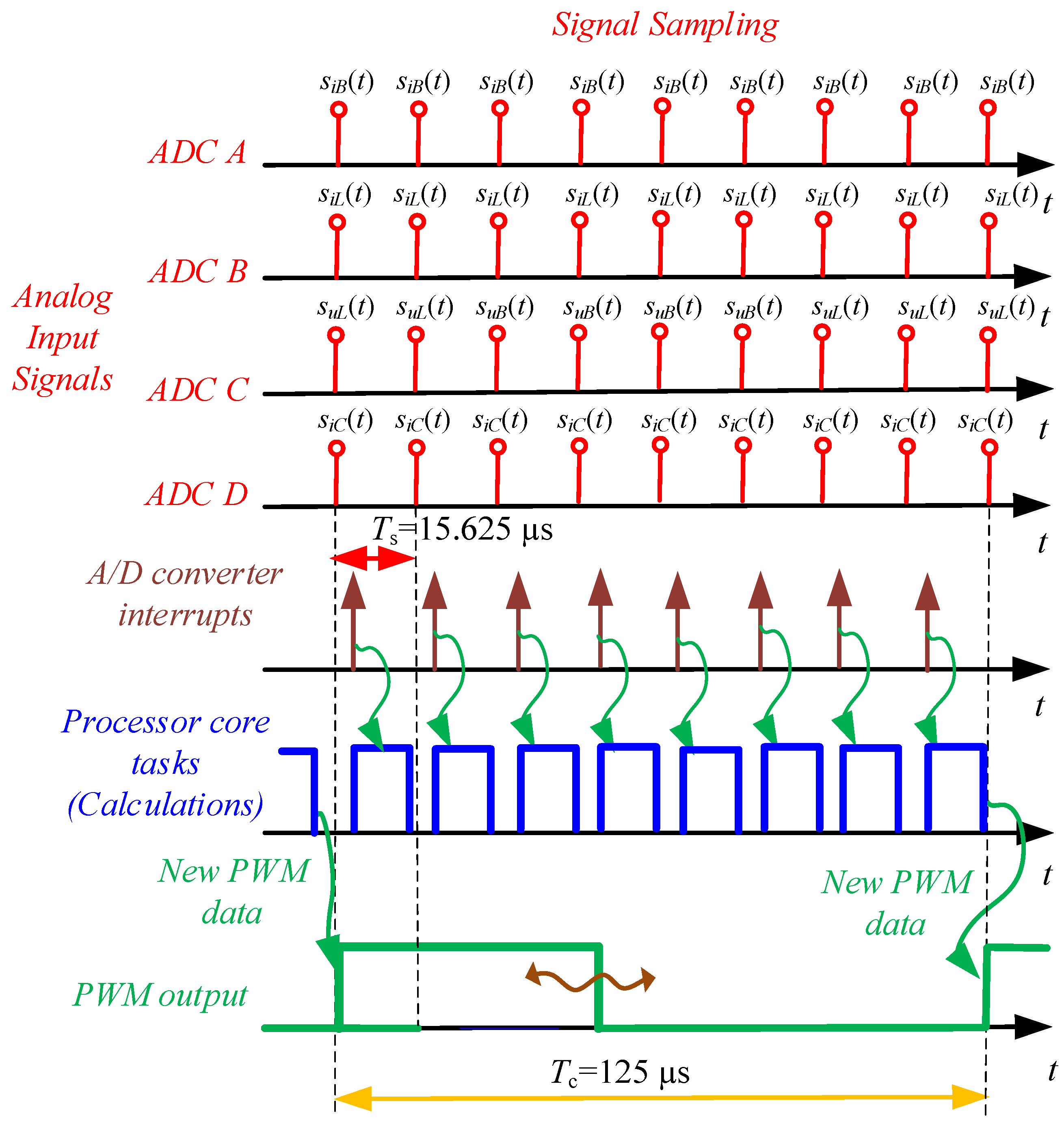
Analog Signal Sampling
4. Laboratory Model of Battery Energy Storage System (BESS)
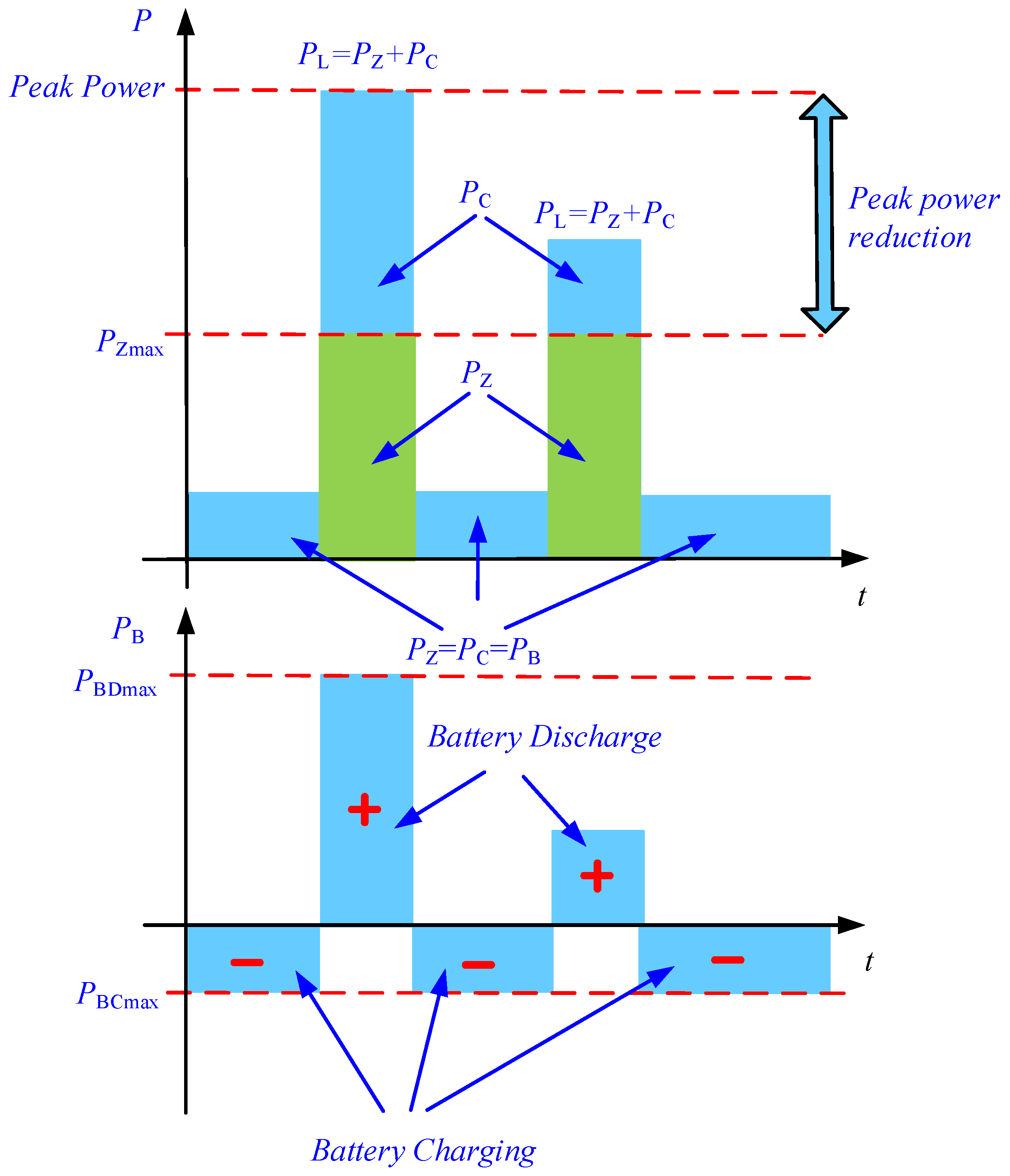
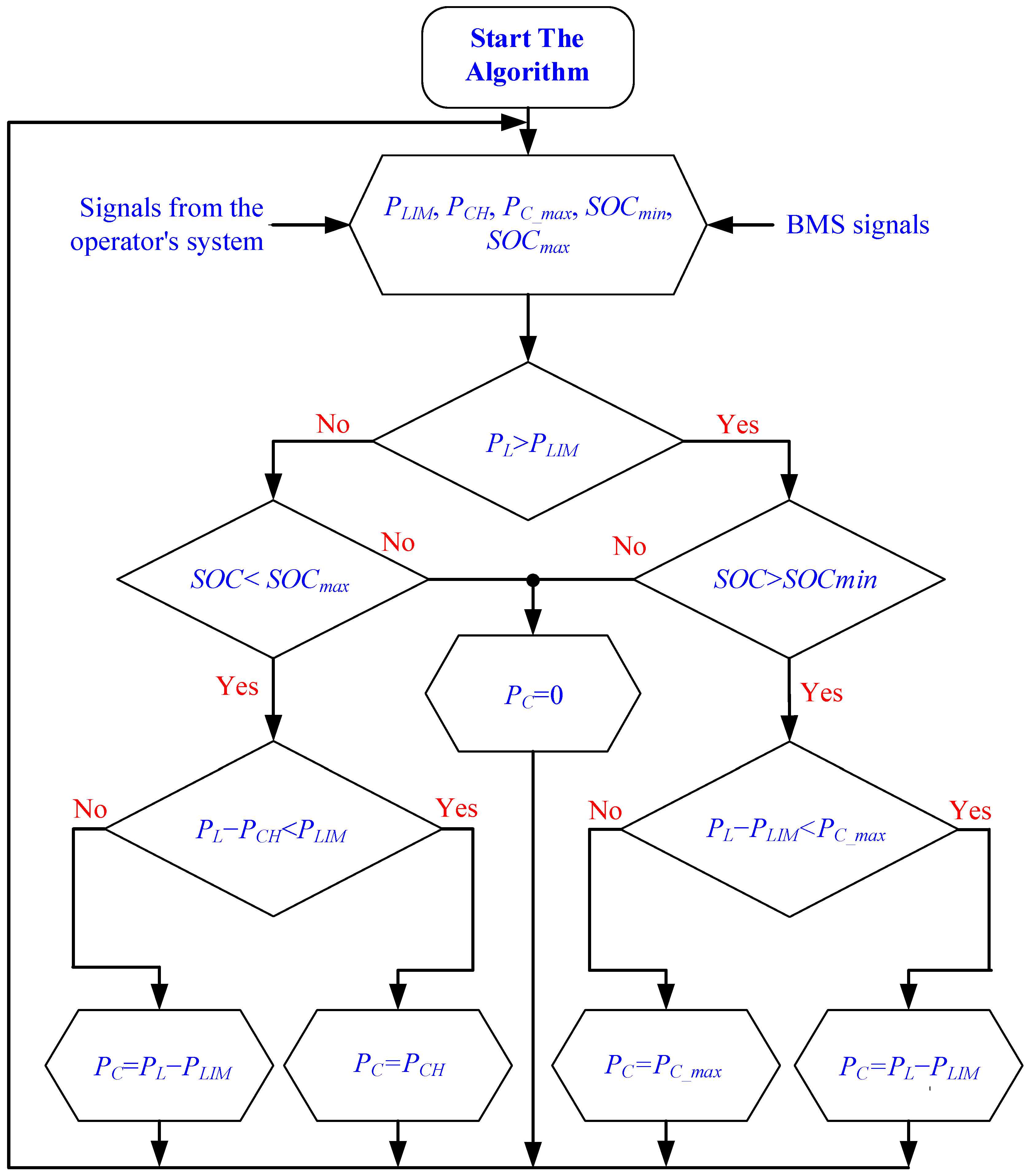
5. The Tested Algorithm
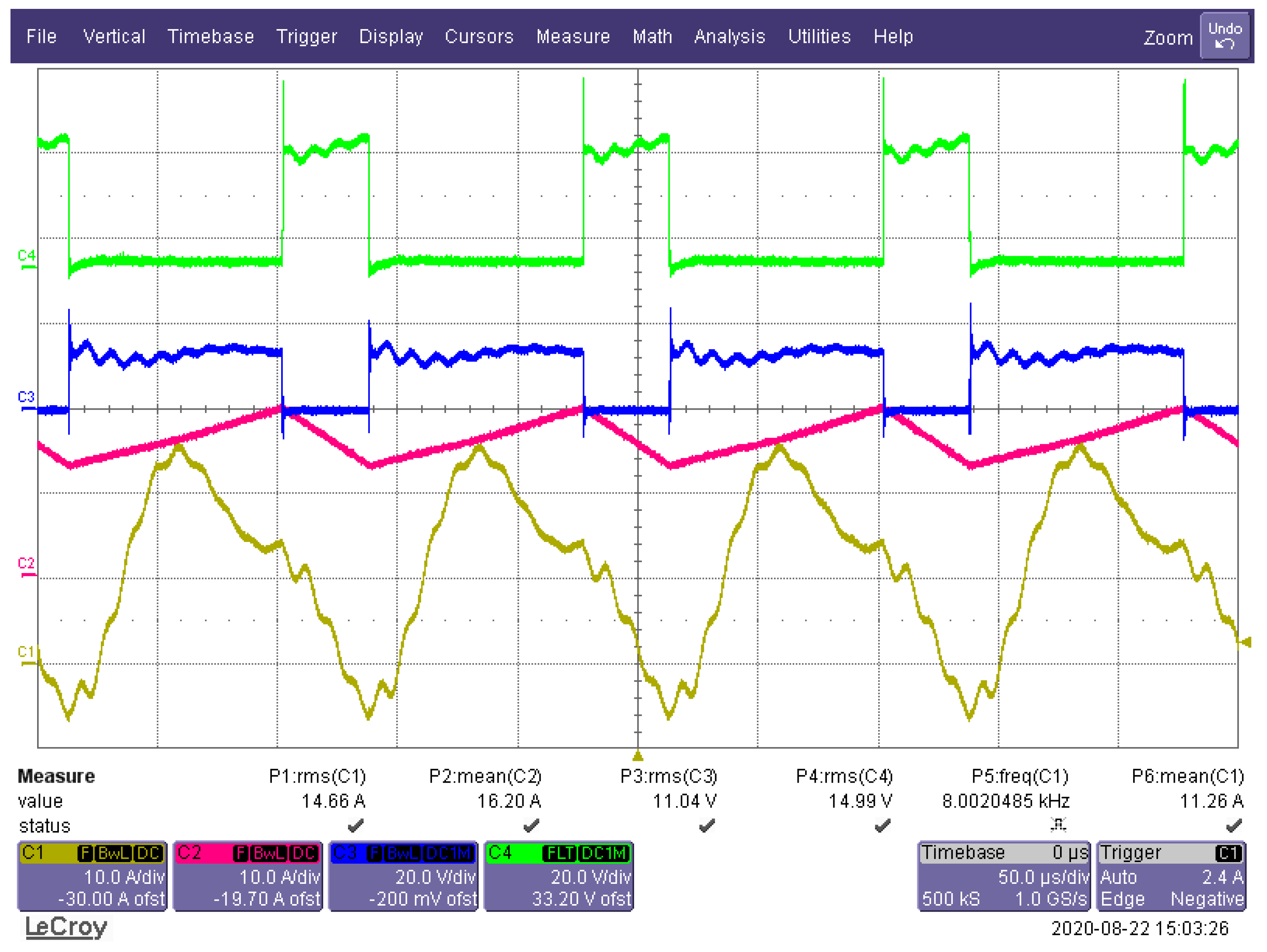
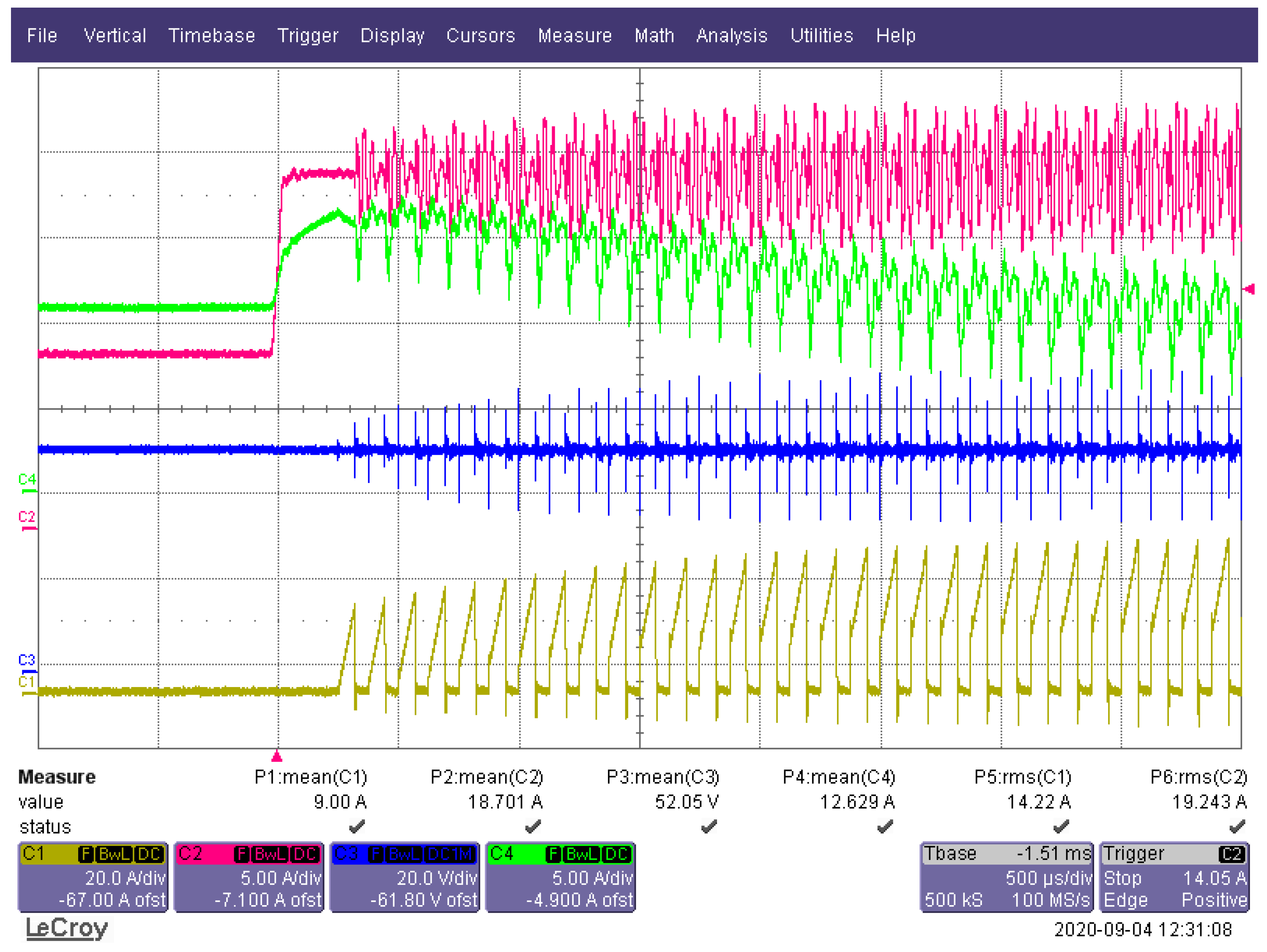
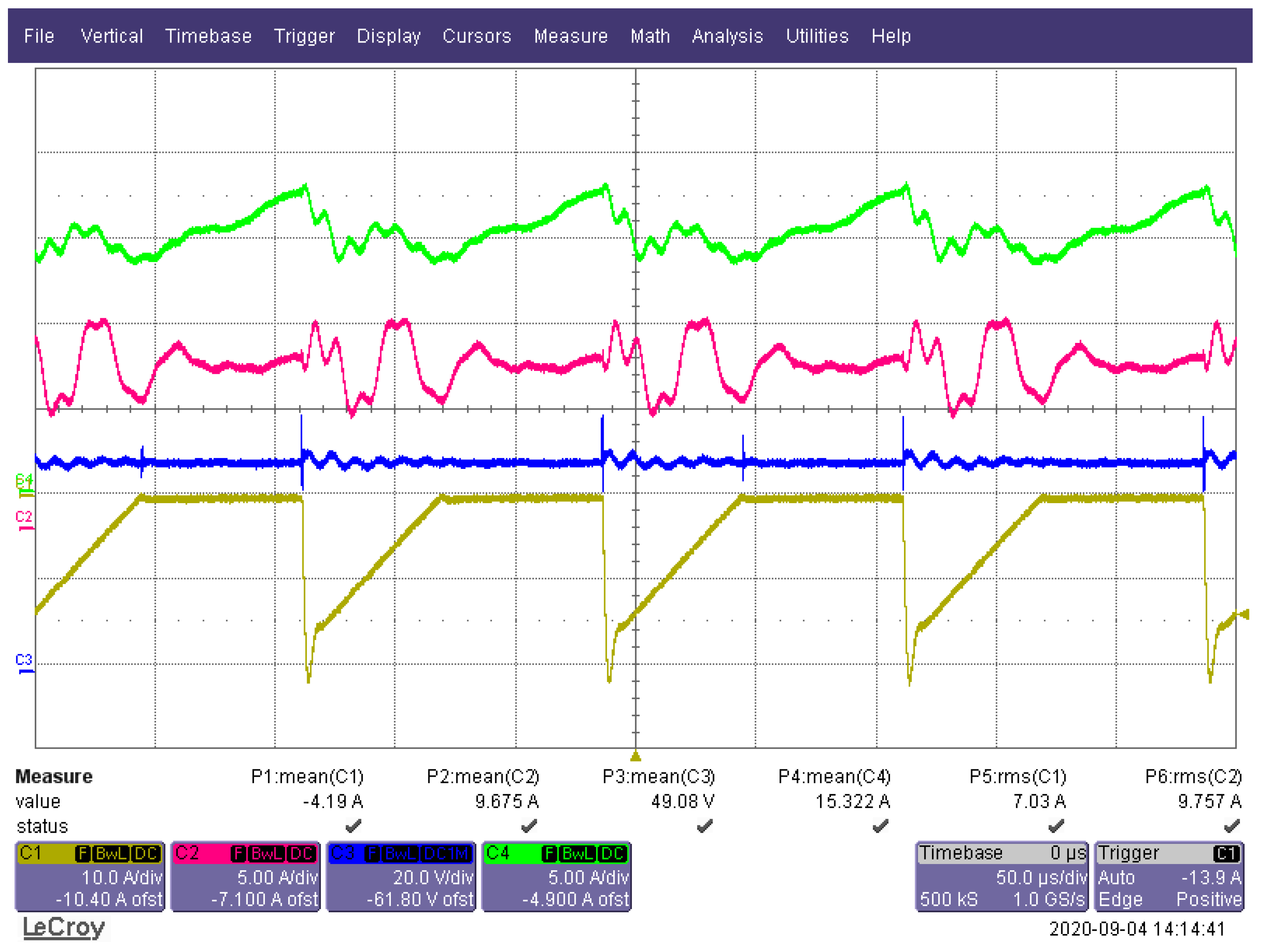
6. Results of Laboratory Tests
7. Discussion and Conclusions
- -
- A reduction in ordered power and electricity charges;
- -
- A decrease in the power and size requirements of transformer stations and transmission lines, as well as a reduction in electricity transmission and transformation losses;
- -
- A reduction in power fluctuation in the power grid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
List of Abbreviations and Symbols
| A/D | Analog-to-digital converter |
| APF | Active power filter |
| BMS | Battery management system |
| BES | Battery energy storage |
| BESS | Battery energy storage system |
| DSP | Digital signal processor |
| DROPT | System of dynamic reduction of traction substation load |
| PLL | Phase lock loop |
| SoC | State of charge |
| SoH | State of health |
| IGBT | Insulated gate bipolar transistor |
| MCU | Microcontroller unit |
| PCC | Point of common coupling |
| PWM | Pulse width modulation |
| SDFT | Sliding discrete Fourier transformation |
| SSDFT | Switching sliding discrete Fourier transformation |
| THD | Total harmonics distortion ratio |
| fc | Transistor switching frequency |
| fs | Sampling frequency |
| iB | Battery current |
| iBDmax | Maximum battery discharging current |
| iBCmax | Maximum battery charging current |
| iL | Load current |
| iC | DC/DC converter current |
| iM | Line current |
| iZ | Supply current |
| PB | Battery energy storage output power |
| PC | DC/DC converter output power |
| PL | Load power |
| si(t) | A signal corresponding to a current (used for iB(t), iL(t), iC(t)) |
| su(t) | A signal corresponding to a voltage (used for uB(t), uC(t)) |
| Tc | Transistor switching period |
| Ts | Sampling period |
| uB | Battery voltage |
| uC | DC/DC converter output voltage |
| uM | Line voltage |
| uZ | Supply voltage |
References
- Hameed, Z.; Hashemi, S.; Ipsen, H.H.; Træholt, C. A business-oriented approach for battery energy storage placement in power systems. Appl. Energy 2021, 298, 117186. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Wang, F.; Miao, Y.; Dong, J. Dual-stage operation strategy of bess for frequency regulation considering planned peak shaving. Energy Rep. 2020, 6, 502–508. [Google Scholar] [CrossRef]
- PKP Energetyka Has Launched Europe’s Largest Traction Energy Storage Facility to Power the Polish Railway. Available online: https://pgeenergetykakolejowa.pl/en/aktualnosc/pkp-energetyka-has-launched-europe-s-largest-traction-energy-storage-facility-to-power-the-polish-railway (accessed on 1 February 2024).
- Szott, M.; Jarnut, M.; Kaniewski, J.; Pilimon, Ł.; Wermiński, S. Fault-Tolerant Control in a Peak-Power Reduction System of a Traction Substation with Multi-String Battery Energy Storage System. Energies 2021, 14, 4565. [Google Scholar] [CrossRef]
- Jarnut, M.; Kaniewski, J.; Protsiuk, V. Energy storage system for peak-power reduction of traction substation. In Proceedings of the Innovative Materials and Technologies in Electrical Engineering (i-MITEL), Sulecin, Poland, 18–20 April 2018. [Google Scholar] [CrossRef]
- Szott, M.; Wermiński, S.; Jarnut, M.; Kaniewski, J. Battery peak-power reduction system of traction substation with two-threshold limitation. Przegląd Elektrotechniczny 2020, 96, 35–39. (In Polish) [Google Scholar] [CrossRef]
- Teshima, M.; Takahashi, H. Lithium ion battery application in traction power supply system. In Proceedings of the 2014 International Power Electronics Conference, Hiroshima, Japan, 18–21 May 2014; pp. 1068–1072. [Google Scholar] [CrossRef]
- Hayashiya, H.; Suzuki, T.; Hino, M.; Hara, D.; Tojo, M.; Shimada, S.; Kudo, K.; Kato, T.; Takahashi, H. Effect evaluation of Li-ion battery for regenerative energy utilization in traction power supply system. In Proceedings of the 17th European Conference on Power Electronics and Applications, EPE’15 ECCE-Europe, Geneva, Switzerland, 8–10 September 2015; pp. 1–9. [Google Scholar]
- Khodaparastan, M.; Dutta, O.; Mohamed, A. Wayside energy storage system for peak demand reduction in electric rail systems. In Proceedings of the IEEE Industry Applications Society Annual Meeting (IAS), Portland, OR, USA, 23–27 September 2018; pp. 1–5. [Google Scholar]
- Fletcher, D.I.; Harrison, R.F.; Nallaperuma, S. Transenergy—A tool for energy storage optimization, peak power and energy consumption reduction in dc electric railway systems. J. Energy Storage 2020, 30, 101425. [Google Scholar] [CrossRef]
- Roch-Dupré, D.; López-López, Á.-J.; Pecharromán, R.-R.; Cucala, A.-P.; Fernández-Cardador, A. Analysis of the demand charge in DC railway systems and reduction of its economic impact with Energy Storage System. Electr. Power Energy Syst. 2017, 93, 459–467. [Google Scholar] [CrossRef]
- Jefimowski, W.; Nikitenko, A. Case study of stationary energy storage device in a 3 kV DC traction system. MATEC Web Conf. 2018, 180, 02005. [Google Scholar] [CrossRef]
- Jefimowski, W. Stationary energy storage system in a 3 kV DC—The conception comparison. MATEC Web Conf. 2018, 180, 02013. [Google Scholar] [CrossRef]
- Gindrat, P.T.R. Is it worth it? sketch appraisal of the relevance of proposals for new rail lines. WIT Trans. Built Environ. 2014, 135, 415–424. [Google Scholar]
- Soler-Nicolau, M.; Mera, J.; López, J.; Cano-Moreno, J. Improving power supply design for high speed lines and 2 × 25 systems using a genetic algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 309–322. [Google Scholar] [CrossRef]
- Meishner, F.; Unlubayir, C.; Sauer, D.U. Model-based investigation of an uncontrolled LTO wayside energy storage system in a 750 V tram grid. Appl. Energy 2023, 331, 120337. [Google Scholar] [CrossRef]
- Lamedica, R.; Ruvio, A.; Palagi, L.; Mortelliti, N. Optimal siting and sizing of wayside energy storage systems in a D.C. railway line. Energies 2020, 13, 6271. [Google Scholar] [CrossRef]
- Cardador, A.; Salcedo-Sanz, S. Optimal location and sizing of energy storage systems in dc-electrified railway lines using a coral reefs optimization algorithm with substrate layers. Energies 2021, 14, 4753. [Google Scholar] [CrossRef]
- Chimplee, S.; Ratniyomchai, T.; Kulworawanichpong, T. Optimal Position of a Wayside Energy Storage Based on Power Loss Minimization in a Railway Station Platform. In Proceedings of the 2020 International Conference on Power, Energy and Innovations (ICPEI), Chiangmai, Thailand, 4–16 October 2020. [Google Scholar] [CrossRef]
- Calderaro, V.; Galdi, V.; Graber, G.; Piccolo, A. Siting and sizing of stationary SuperCapacitors in a Metro Network. In Proceedings of the AEIT Annual Conference, Mondello, Italy, 3–5 October 2013. [Google Scholar] [CrossRef]
- Roch-Dupré, D.; Gonsalves, T.; Cucala, A.P.; Pecharromán, R.R.; López-López, Á.J.; Fernández-Cardador, A. Determining the optimum installation of energy storage systems in railway electrical infrastructures by means of swarm and evolutionary optimization algorithms. Electr. Power Energy Syst. 2021, 124, 106295. [Google Scholar] [CrossRef]
- Guo, T.; Yang, Z.; Lin, F.; Xiong, S. Optimization of peak load shifting control strategy for battery energy storage system used in urban rail transit. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 3901–3906. [Google Scholar]
- Gao, Z.; Fang, J.; Zhang, Y.; Sun, D. Control strategy for wayside supercapacitor energy storage system in railway transit network. J. Mod. Power Syst. Clean Energy 2014, 2, 181–190. [Google Scholar] [CrossRef]
- Qin, Q.; Guo, T.; Lin, F.; Yang, Z. Energy transfer strategy for urban rail transit battery energy storage system to reduce peak power of traction substation. IEEE Trans. Veh. Technol. 2019, 68, 11714–11724. [Google Scholar] [CrossRef]
- Calderaro, V.; Galdi, V.; Graber, G.; Piccolo, A.; Capasso, A.; Lamedica, R.; Ruvio, A. Energy management of auxiliary battery substation supporting high-speed train on 3 kv dc systems. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1224–1229. [Google Scholar]
- Moslem Uddin, M.F.; Romlie, M.F.; Abdullah, M.F.; Tan, C.; Shafiullah, G.M.; Bakar, A.H.A. A novel peak shaving algorithm for islanded microgrid using battery energy storage system. Energy 2020, 196, 117084. [Google Scholar] [CrossRef]
- Hong, Z.; Wei, Z.; Li, J.; Han, X. A novel capacity demand analysis method of energy storage system for peak shaving based on data-driven. J. Energy Storage 2021, 39, 102617. [Google Scholar] [CrossRef]
- Tang, S.; Huang, X.; Yang, N.; Liao, Q.; Sun, K. Optimal Sizing and Energy Management of Hybrid Energy Storage System for High-Speed Railway Traction Substation. J. Electr. Eng. Technol. 2021, 16, 1743–1754. [Google Scholar] [CrossRef]
- Jarnut, M.; Kaniewski, J.; Benysek, G.; Obrycki, P.; Artyszak, D.; Dzienis, W.; Anielak, P. Sposób Sterowania Stacjonarnym Systemem Magazynowania Energii do Zastosowań w Podstacjach Trakcyjnych (Method of Controlling a Stationary Energy Storage System for Use in Traction Substations). Patent No. 240745, 21 April 2022. [Google Scholar]
- Su, N.; Xu, D.; Chen, M.; Tao, J. Study of Bi-Directional Buck-Boost Converter with Different Control Methods. In Proceedings of the IEEE Vehicle Power and Propulsion Conference (VPPC), Harbin, China, 3–5 September 2008. [Google Scholar]
- Liu, K.-B.; Liu, C.-Y.; Liu, Y.-H.; Chien, Y.-C.; Wang, B.-S.; Wong, Y.-S. Analysis and Controller Design of a Universal Bidirectional DC-DC Converter. Energies 2016, 9, 501. [Google Scholar] [CrossRef]
- LAUNCHXL-F28379D Overview, User’s Guide (Rev. C); SPRUI77C; Texas Instruments: Dallas, TX, USA, 2019; Available online: https://www.ti.com/lit/ug/sprui77c/sprui77c.pdf?ts=1708674017951 (accessed on 15 January 2024).
- TMS320F2837xD Dual-Core Microcontrollers—Data Sheet; SPRS880O; Texas Instruments: Dallas, TX, USA, 2021; Available online: https://www.ti.com/lit/ds/sprs880m/sprs880m.pdf (accessed on 15 January 2024).
- Sozański, K. Overview of Signal Processing Problems in Power Electronic Control Circuits. Energies 2023, 16, 4774. [Google Scholar] [CrossRef]
- Sozański, K. Digital Signal Processing in Power Electronics Control Circuits, 2nd ed.; Springer: London, UK, 2017. [Google Scholar]
- Azeredo-Leme, C. Clock jitter effects on sampling: A tutorial. IEEE Circuits Syst. Mag. 2011, 3, 26–37. [Google Scholar] [CrossRef]
- Brannon, B. Sampled Systems and the Effects of Clock Phase Noise and Jitter; Application Note AN-756; Technical Report; Analog Devices, Inc.: Wilmington, MA, USA, 2004. [Google Scholar]
- Brannon, B.; Barlow, A. Aperture Uncertainty and ADC System Performance; Application Note AN-501; Technical Report; Analog Devices Inc.: Wilmington, MA, USA, 2006. [Google Scholar]
- Redmayne, D.; Trelewicz, E.; Smith, A. Understanding the Effect of Clock Jitter on High Speed ADCs; Design Note 1013; Technical Report; Linear Technology, Inc.: Milpitas, CA, USA, 2006. [Google Scholar]
- Mota, M. Understanding Clock Jitter Effects on Data Converter Performance and How to Minimize Them; Technical Report; Synopsis Inc.: Mountain View, CA, USA, 2010. [Google Scholar]

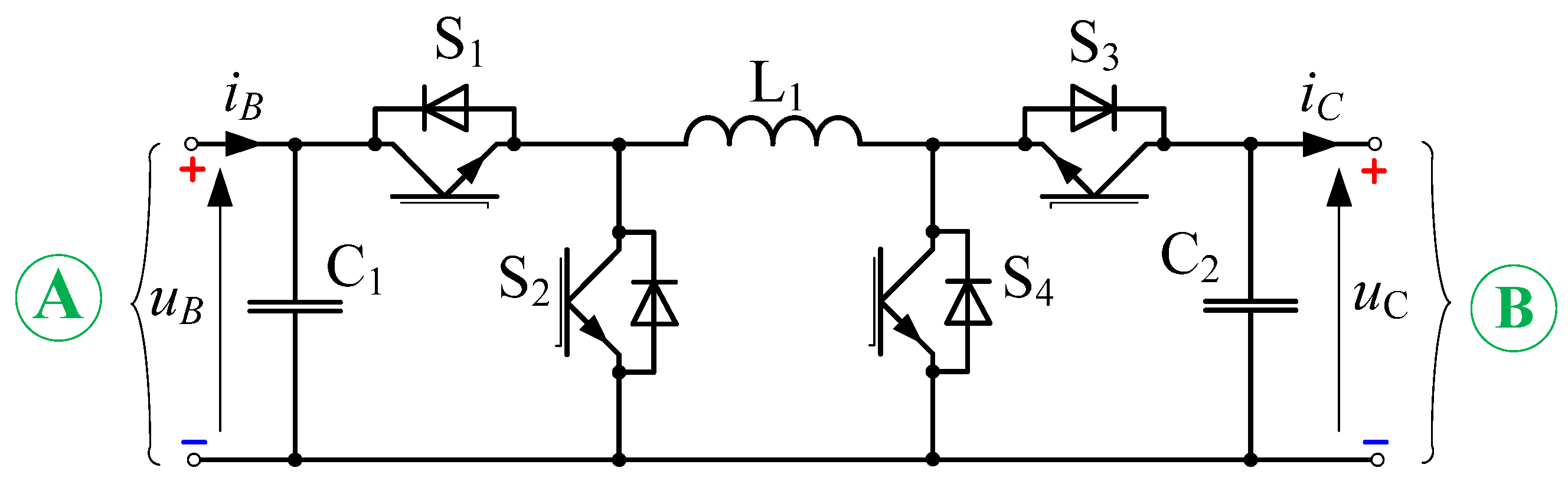
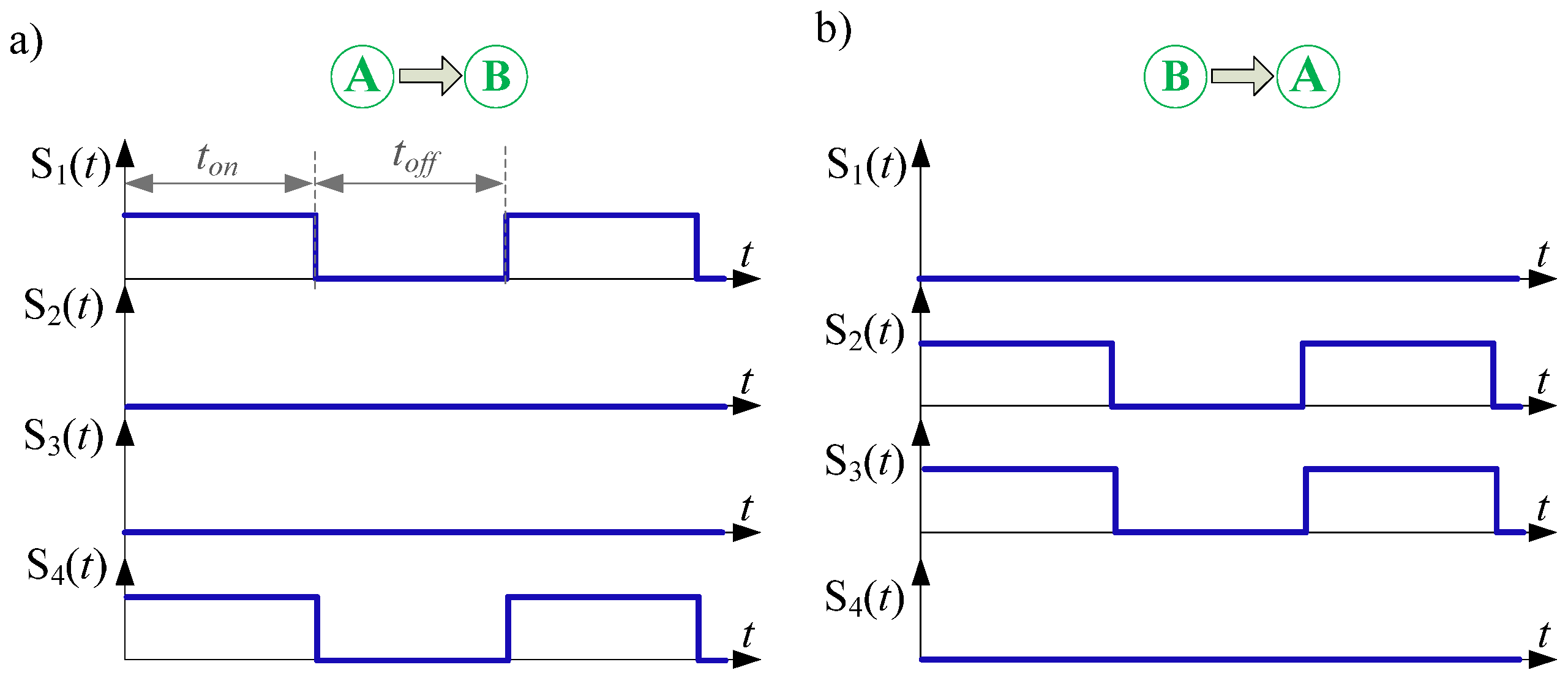
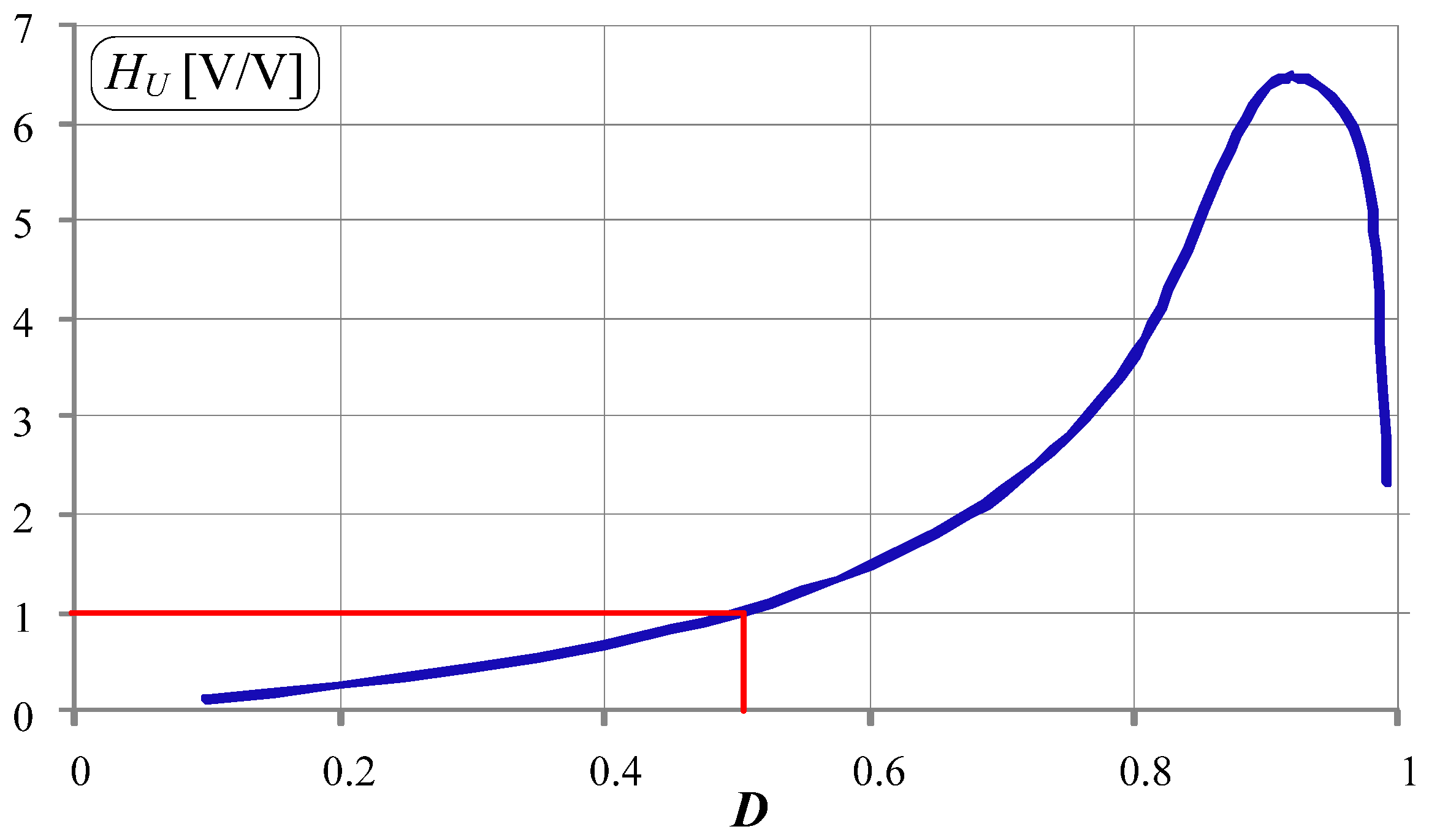
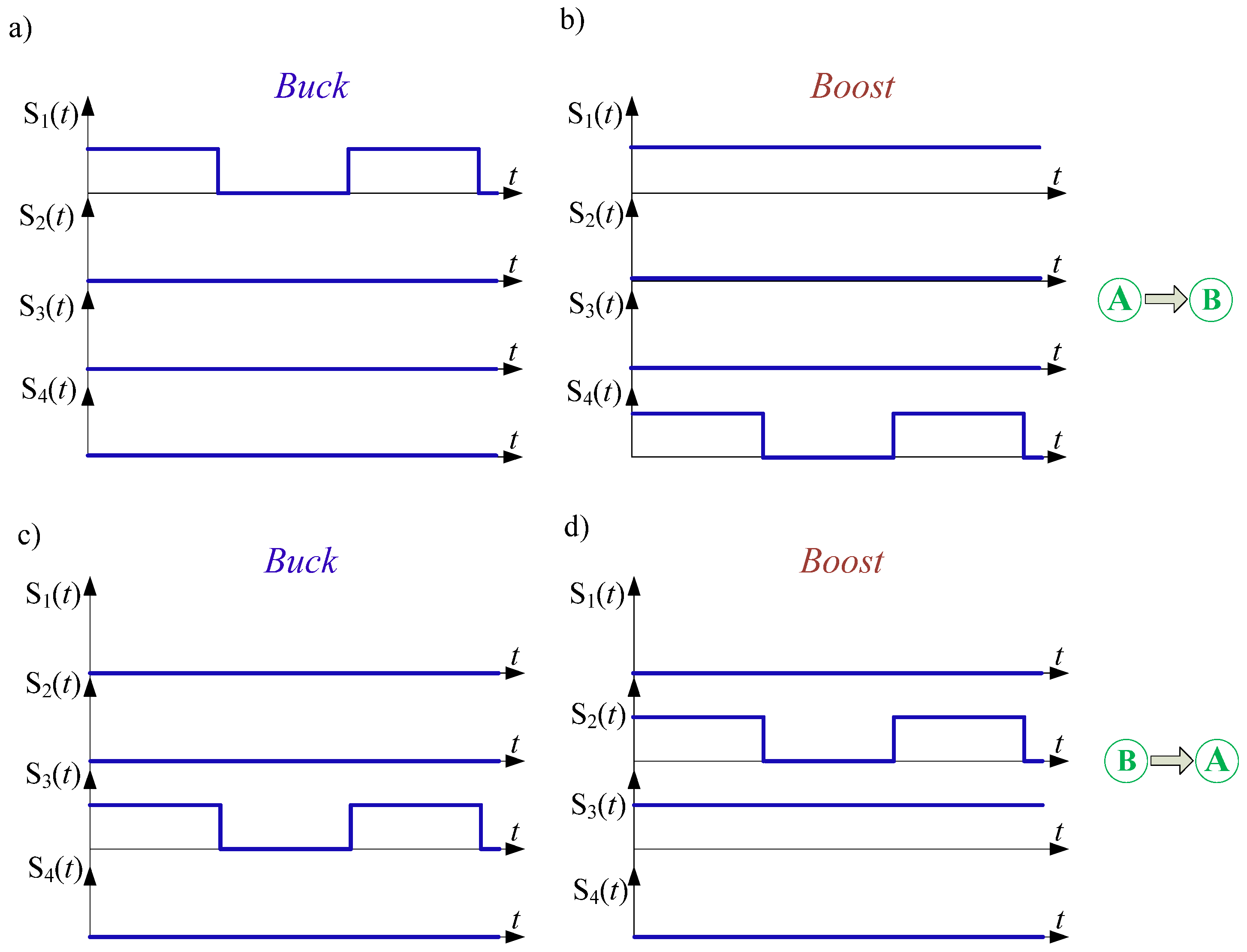
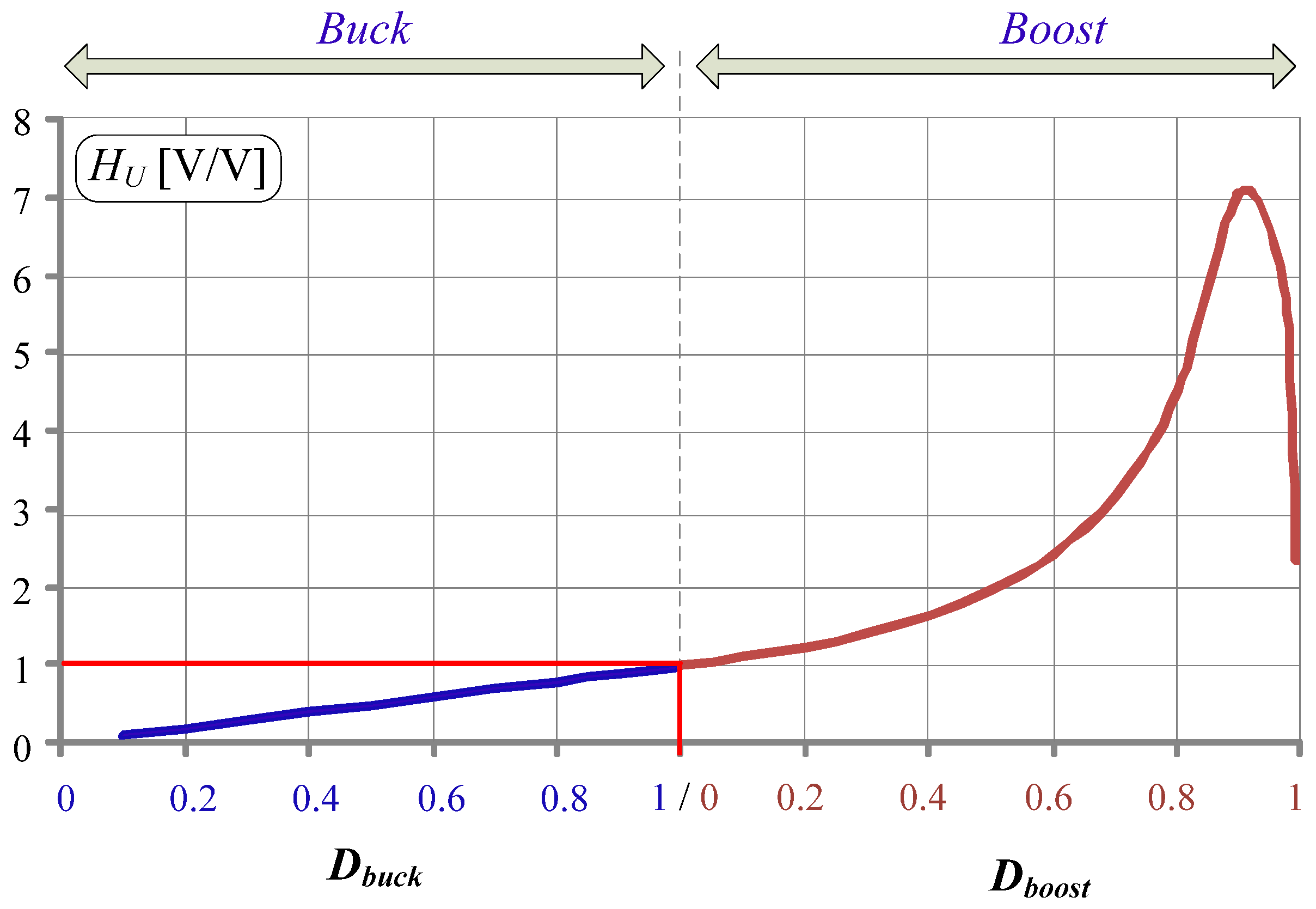
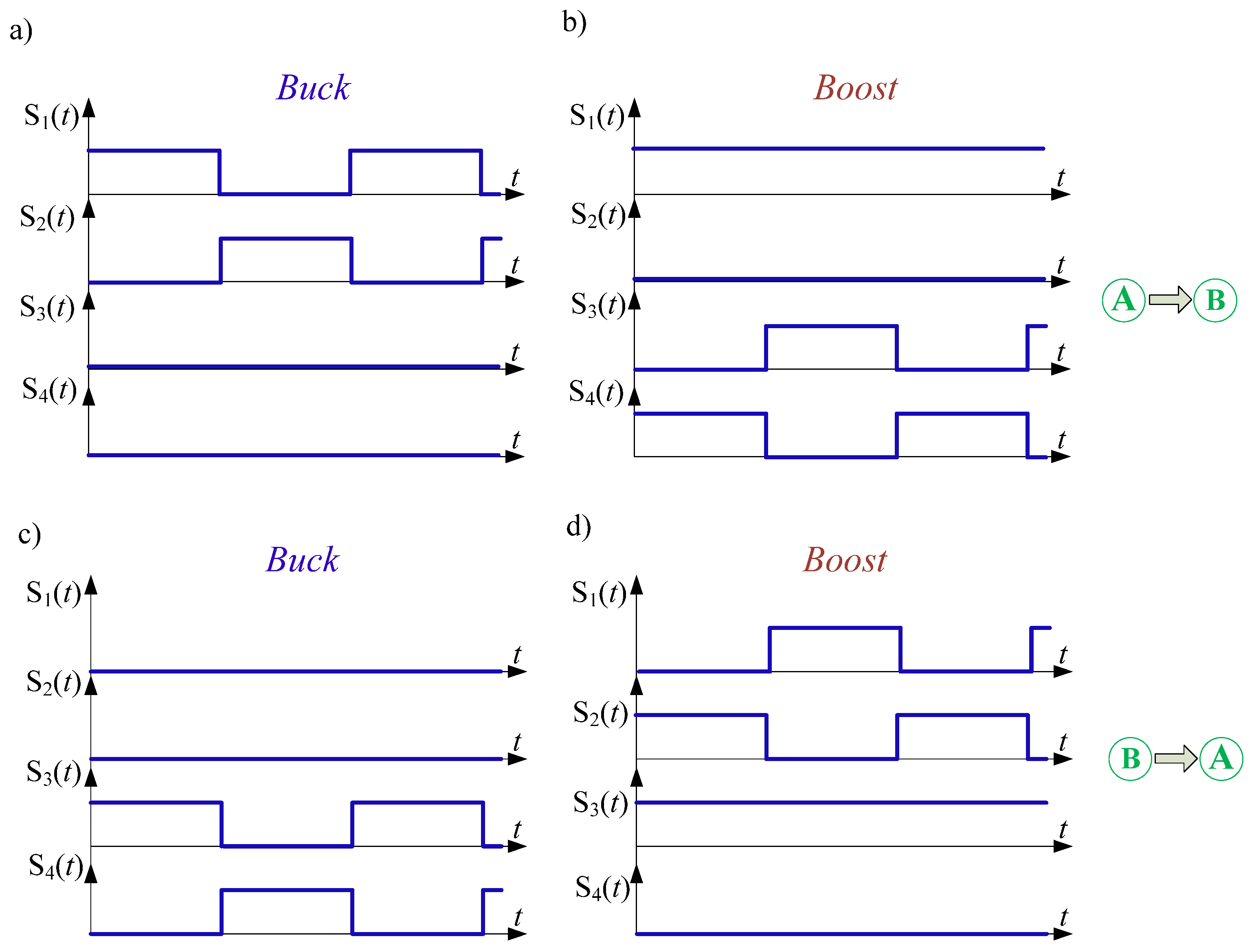
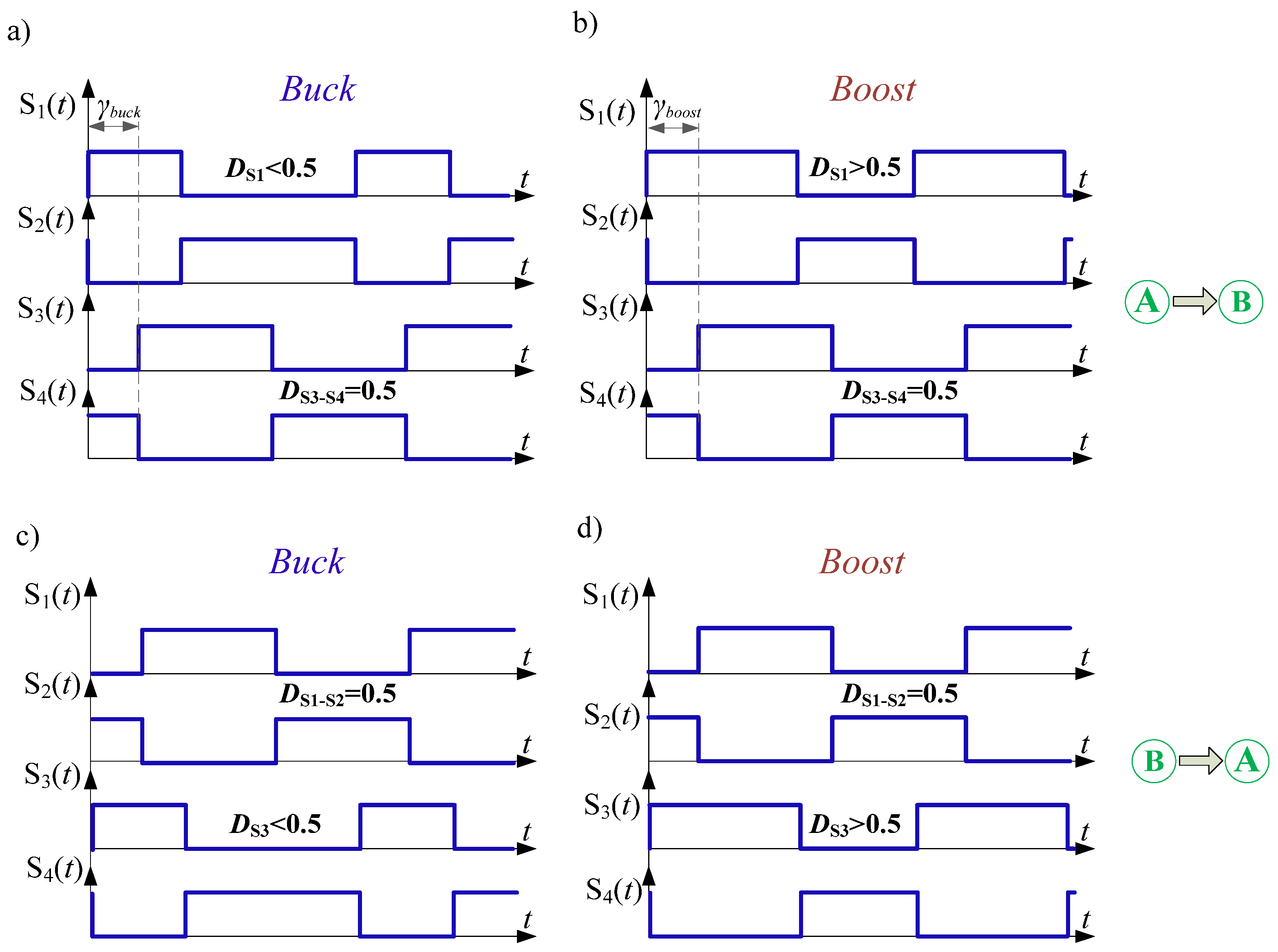
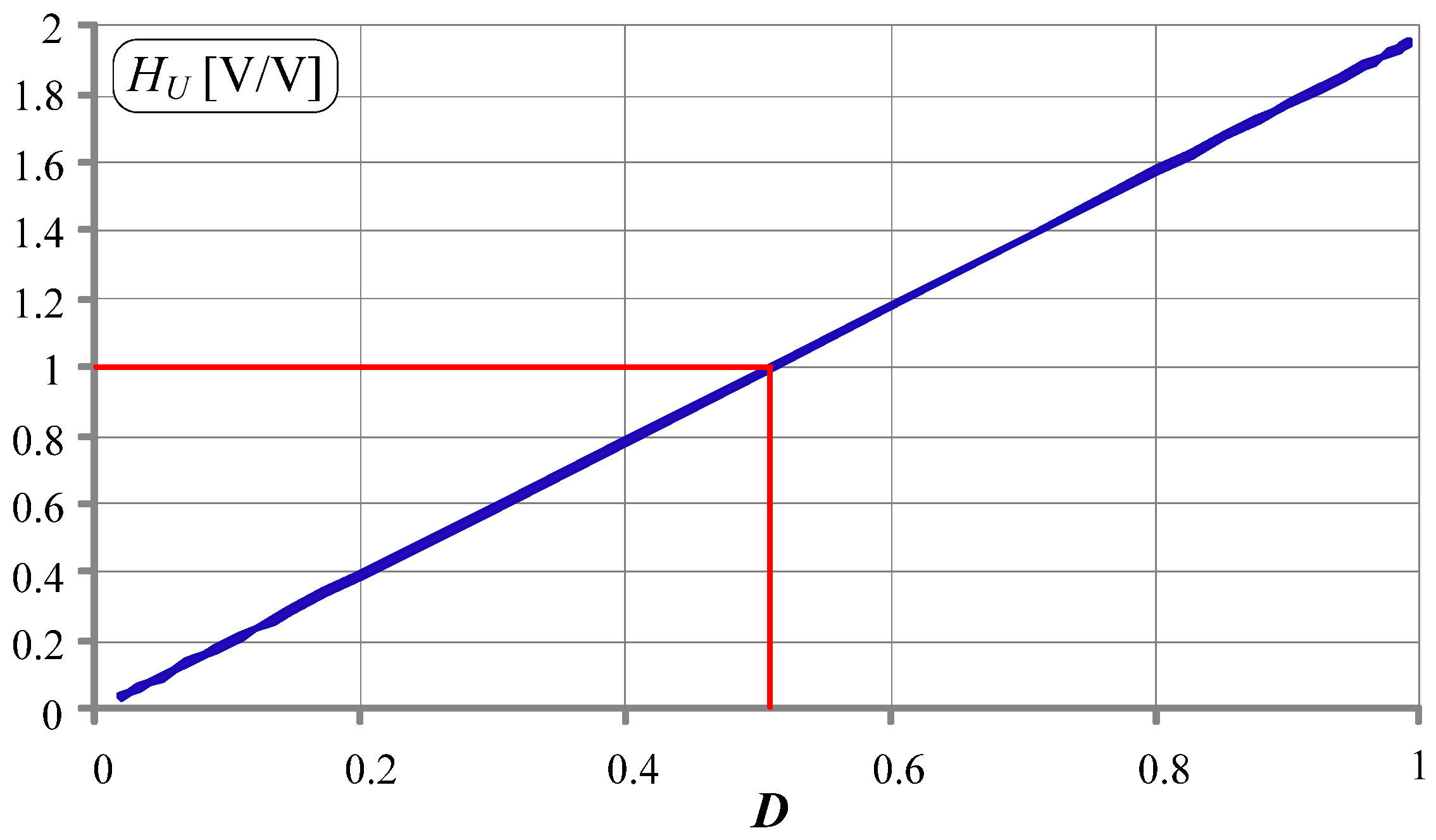




| Energy Flow Direction | Operation Mode | Switches States | Voltage Gain (Voltage Transmittance) | |||
|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | |||
| buck-boost method | ||||||
| A → B | buck-boost | D | 0 | 0 | D | |
| B → A | 0 | D | D | 0 | ||
| buck + boost method | ||||||
| A → B | buck | D | 0 | 0 | 0 | |
| boost | 1 | 0 | 0 | D | ||
| B → A | buck | 0 | 0 | D | 0 | |
| boost | 0 | D | 1 | 0 | ||
| buck + boost method with synchronic switching | ||||||
| A → B | buck | D | 0 | 0 | ||
| boost | 1 | 0 | D | |||
| B → A | buck | 0 | 0 | D | ||
| boost | D | 1 | 0 | |||
| Symbol | Value |
|---|---|
| C1 | 0.2 µF |
| C2 | 68 µF |
| L1 | 160 µH/100 A |
| fc | 8 kHz |
| fs | 64 kHz |
| iBmax, iCmax | 100 A |
| uC | 52 V |
| S1…S4 | IGBT FF100R12RT4 (Infineon, Germany) |
| SC1, SC2 | DC contactor |
| MCU | TMS320F28379D, 100 MHz (Texas Instruments, USA) |
| Battery | 32xHeadway 38120, 3.2 V, 10 AH (Zhejiang Xinghai Energy Technology Co., Ltd., Huzhou, China) |
| Programable DC Power Supply | EA-PSI 9200-210, 0…200 V, 0…210 A, 0…15 kW (EA Elektro-Automatik Group, Germany) |
| Programable DC Load | IT8930A-1200-1200, 1200 V/1200 A/30 kW (ITECH, Taiwan) |
| Sampling Cycle | ADC Channel A | ADC Channel B | ADC Channel C | ADC Channel D |
|---|---|---|---|---|
| 1 | siB(t) | siL(t) | suL(t) | siC(t) |
| 2 | siB(t) | siL(t) | suL(t) | siC(t) |
| 3 | siB(t) | siL(t) | suB(t) | siC(t) |
| 4 | siB(t) | siL(t) | suB(t) | siC(t) |
| 5 | siB(t) | siL(t) | suB(t) | siC(t) |
| 6 | siB(t) | siL(t) | suB(t) | siC(t) |
| 7 | siB(t) | siL(t) | suL(t) | siC(t) |
| 8 | siB(t) | siL(t) | suL(t) | siC(t) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sozański, K.; Wermiński, S.; Kaniewski, J. Small-Scale Battery Energy Storage System for Testing Algorithms Aimed at Peak Power Reduction. Energies 2024, 17, 2217. https://doi.org/10.3390/en17092217
Sozański K, Wermiński S, Kaniewski J. Small-Scale Battery Energy Storage System for Testing Algorithms Aimed at Peak Power Reduction. Energies. 2024; 17(9):2217. https://doi.org/10.3390/en17092217
Chicago/Turabian StyleSozański, Krzysztof, Szymon Wermiński, and Jacek Kaniewski. 2024. "Small-Scale Battery Energy Storage System for Testing Algorithms Aimed at Peak Power Reduction" Energies 17, no. 9: 2217. https://doi.org/10.3390/en17092217
APA StyleSozański, K., Wermiński, S., & Kaniewski, J. (2024). Small-Scale Battery Energy Storage System for Testing Algorithms Aimed at Peak Power Reduction. Energies, 17(9), 2217. https://doi.org/10.3390/en17092217








