Mixed-Mode Ventilation Based on Adjustable Air Velocity for Energy Benefits in Residential Buildings
Abstract
1. Introduction
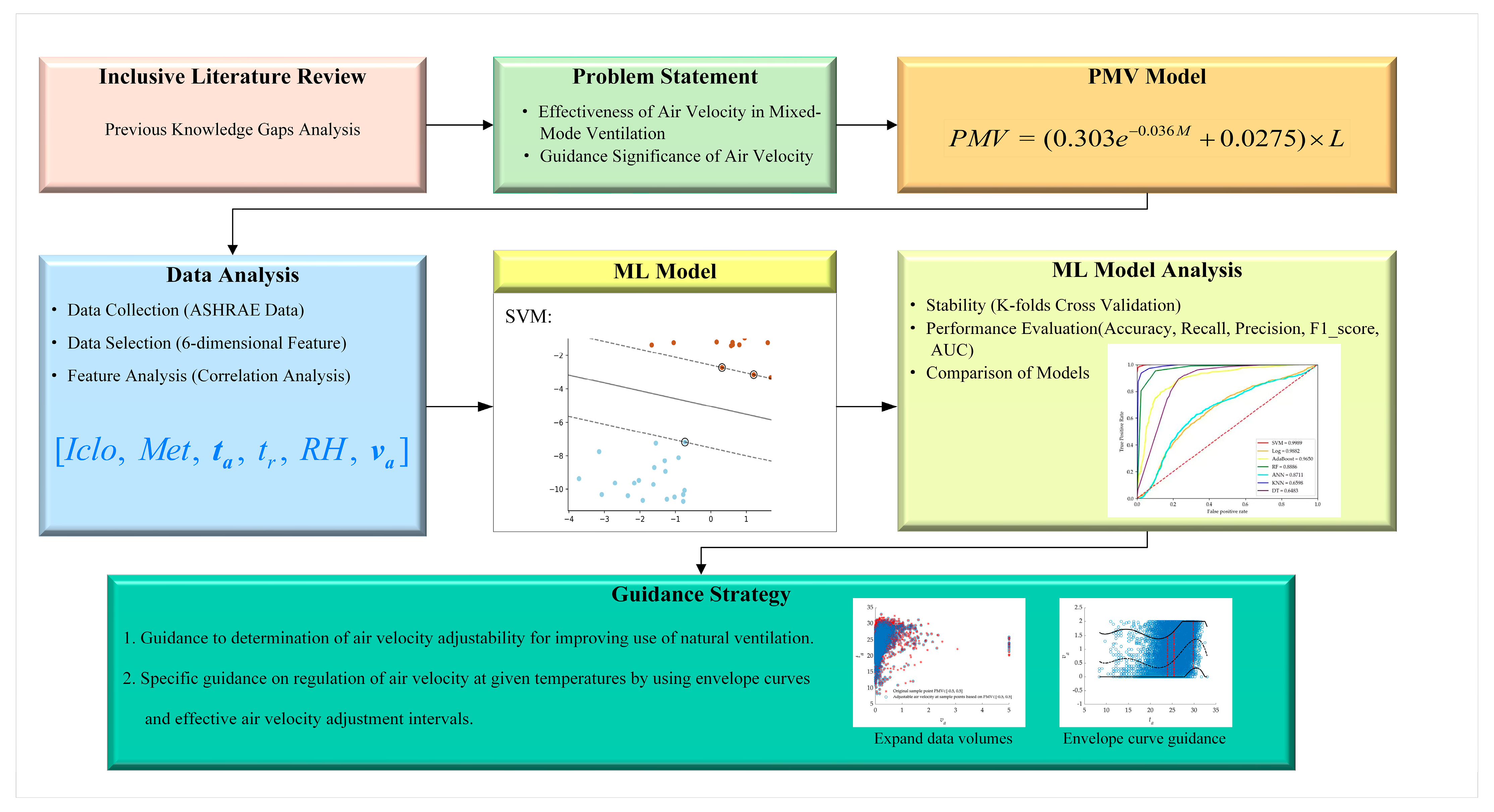
2. Materials and Methodology
2.1. ASHRAE Database and Correlation of Variable Relationships
2.2. Air-Velocity Adjustment Strategy Based on Optimal Comfort Intervals
2.2.1. PMV Model
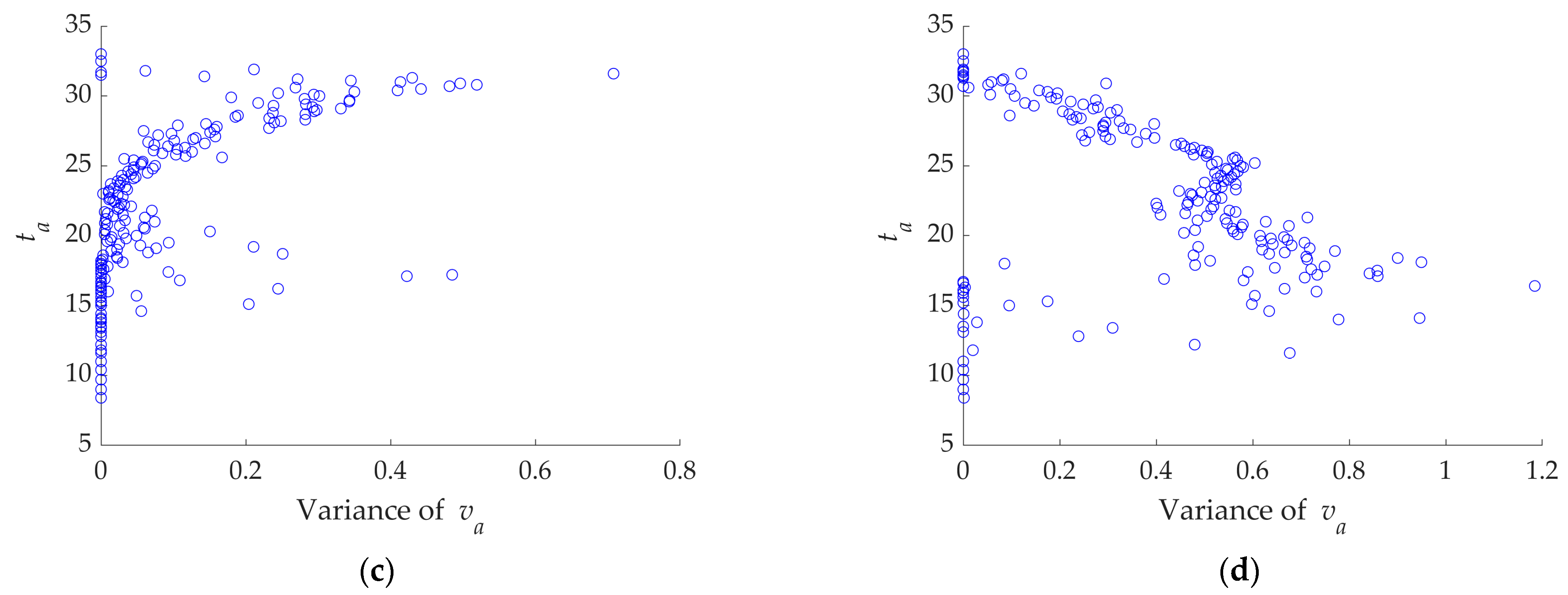
2.2.2. Determination of Air-Velocity Adjustability
| Algorithm 1: Classification algorithm for adjustable air velocity based on optimal comfort interval. |
| Input: Discrete data from ASHRAE_db II dataset |
| Output: Recognition accuracy of adjustable air-velocity case |
| Main framework: |
| Step1: Data preprocessing (outlier elimination, data smoothing, etc.); |
| Step2: Select ta, tr, va, RH, Iclo, M forming a six-dimensional feature vector; |
| Step3: Use SVM for classifying sample points of adjustable air velocity; |
| Step4: Adopt a confidence level to analyze the experimental results; |
| Step5: Return recognition accuracy of classification. |
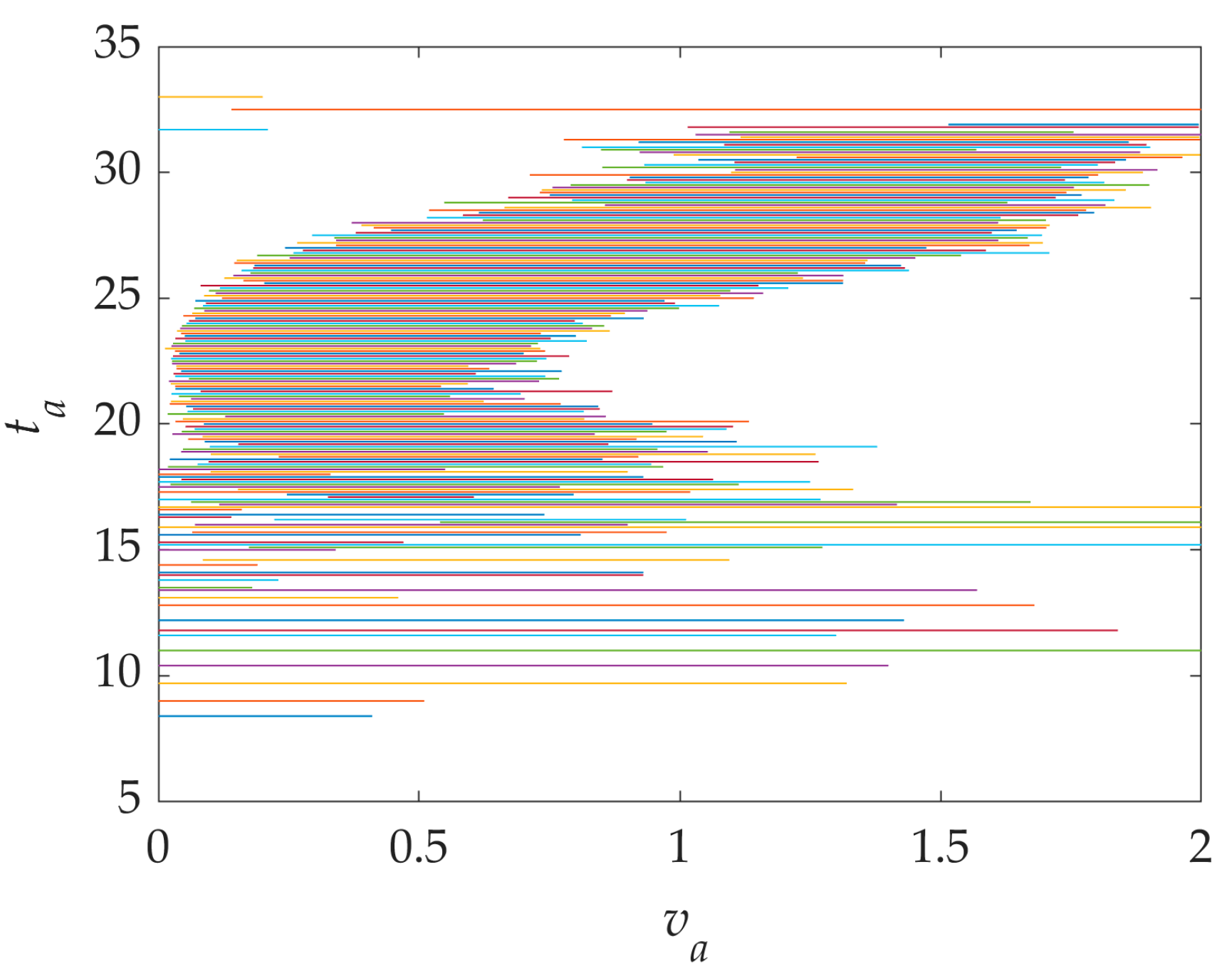
2.2.3. Determination of Adjustable Air-Velocity Intervals
3. Results and Discussions
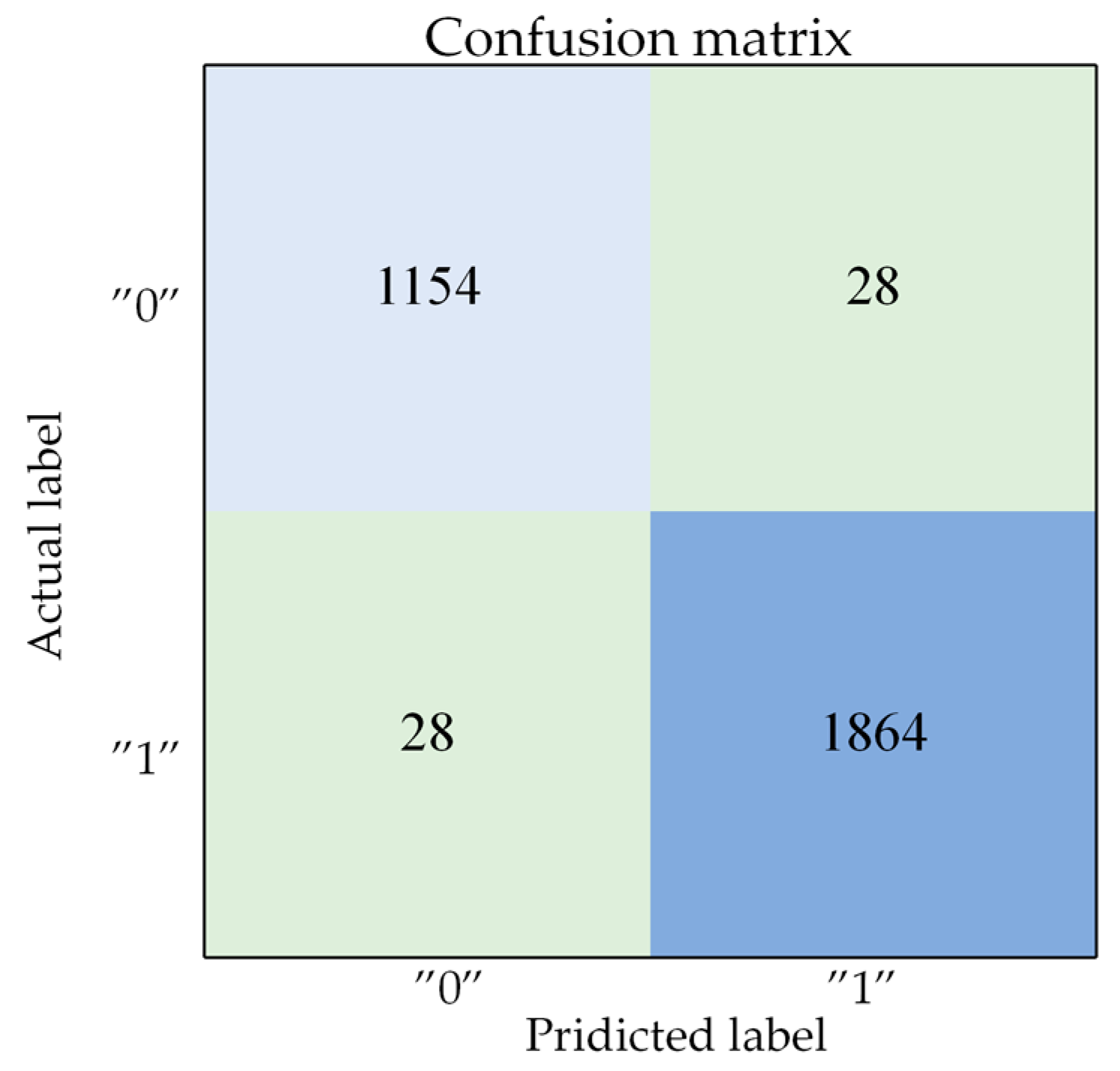
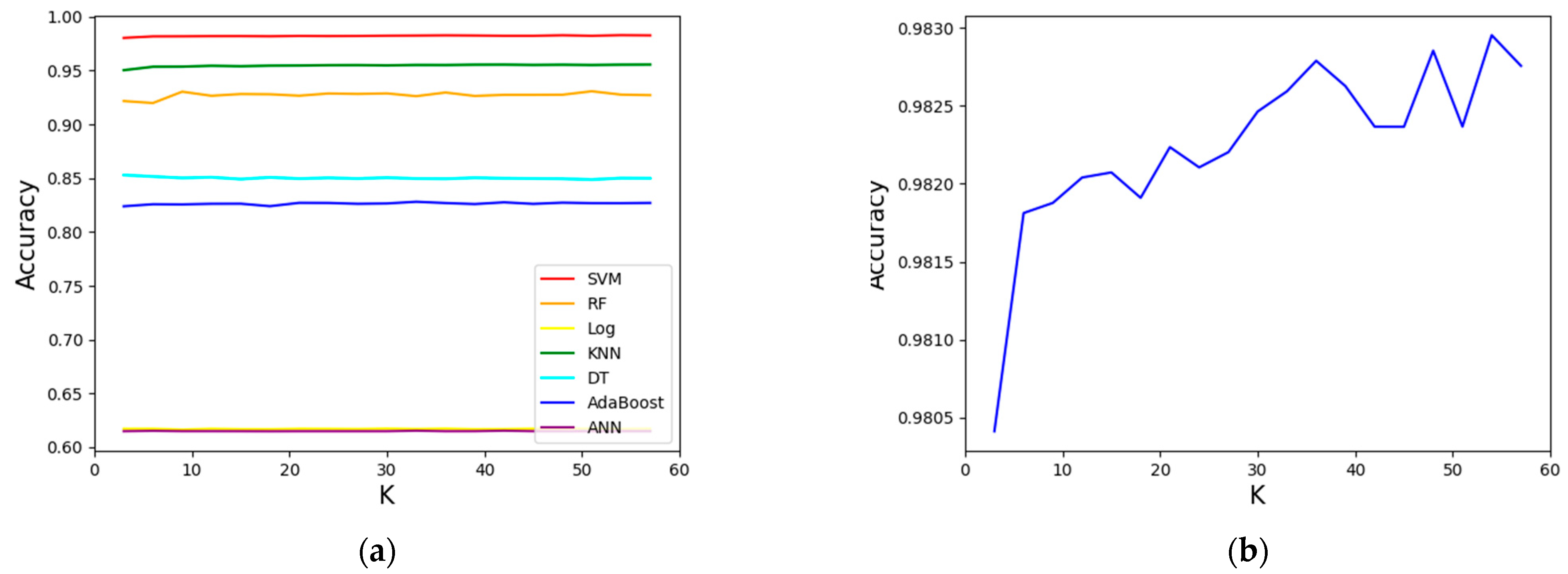
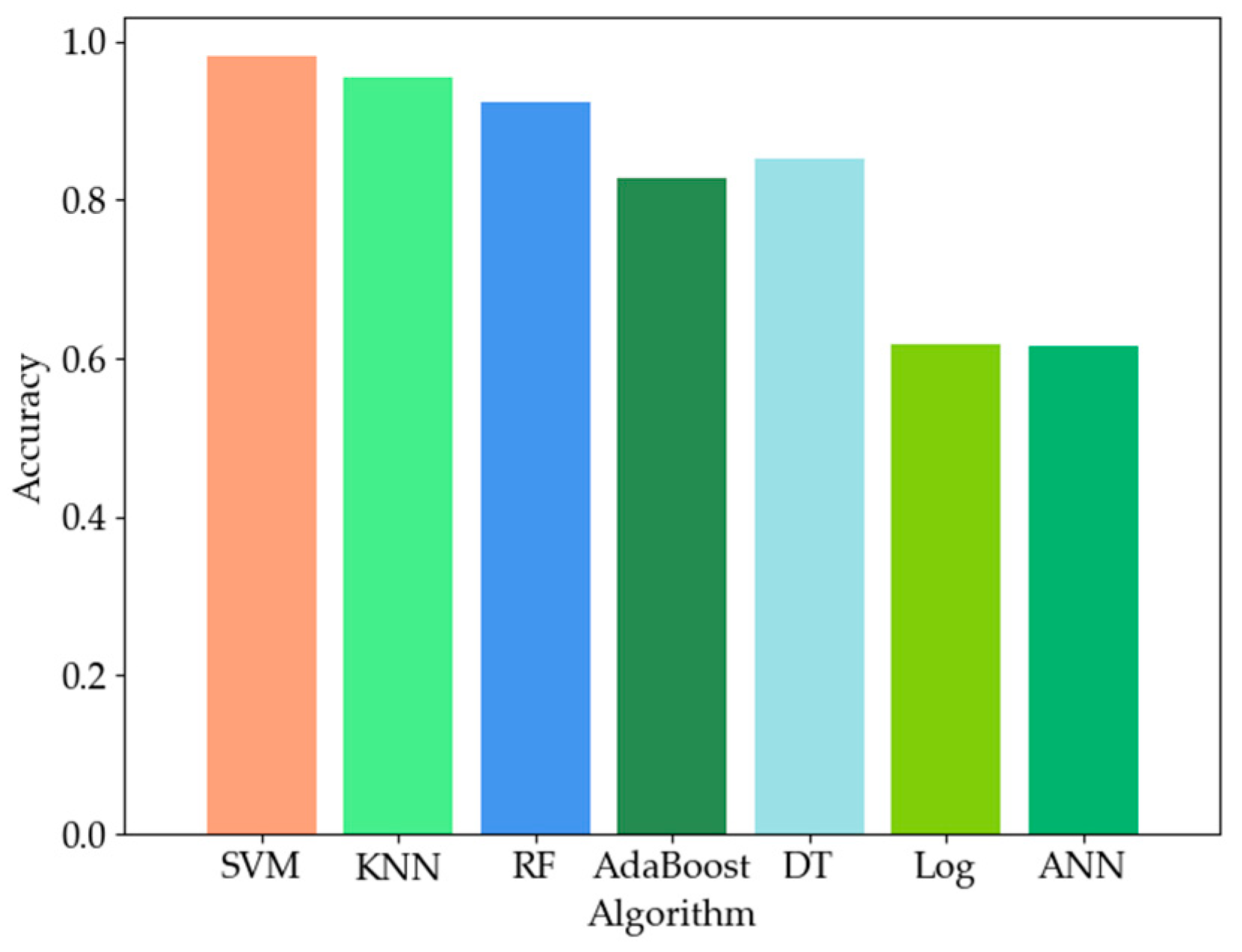
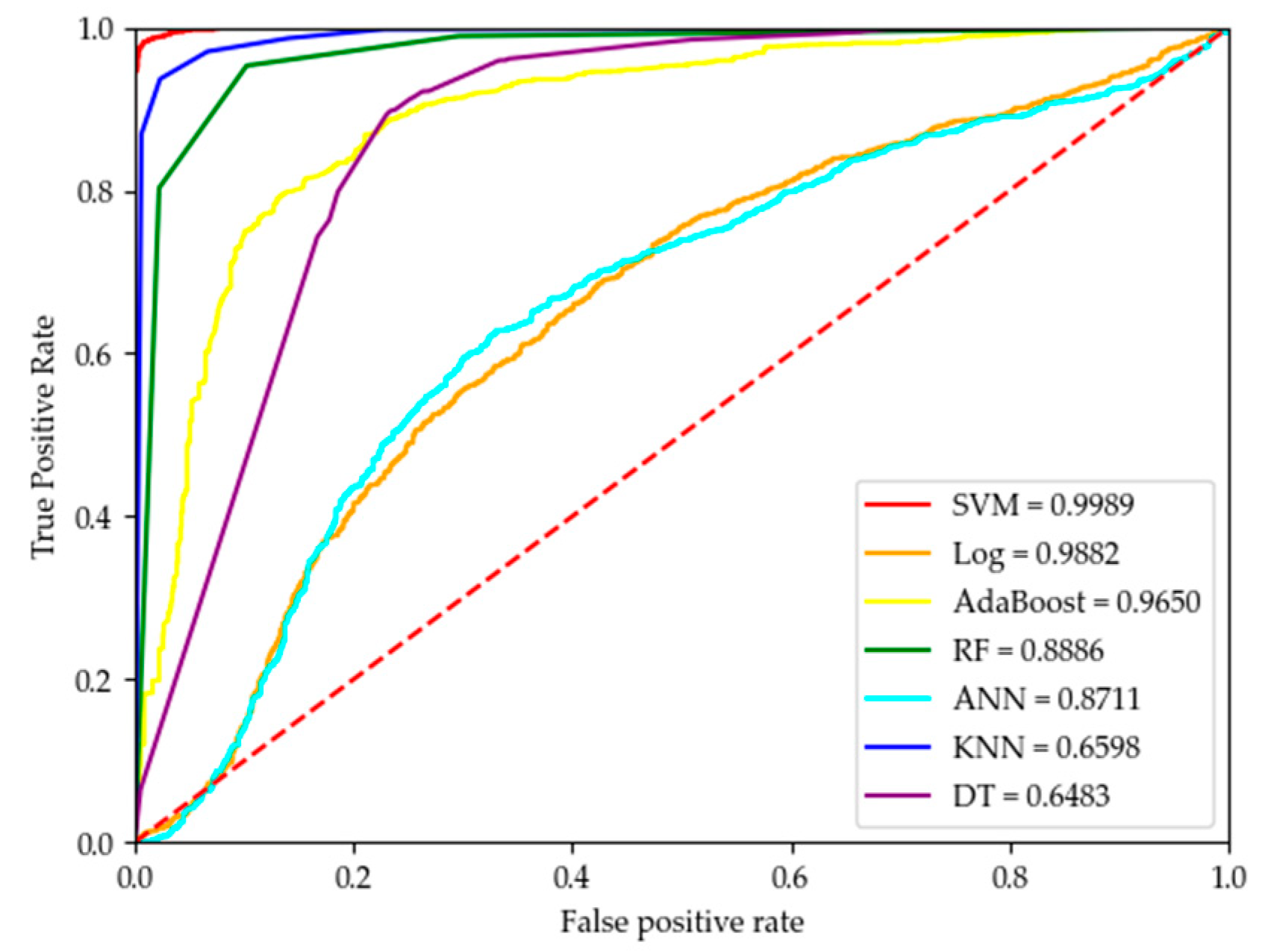
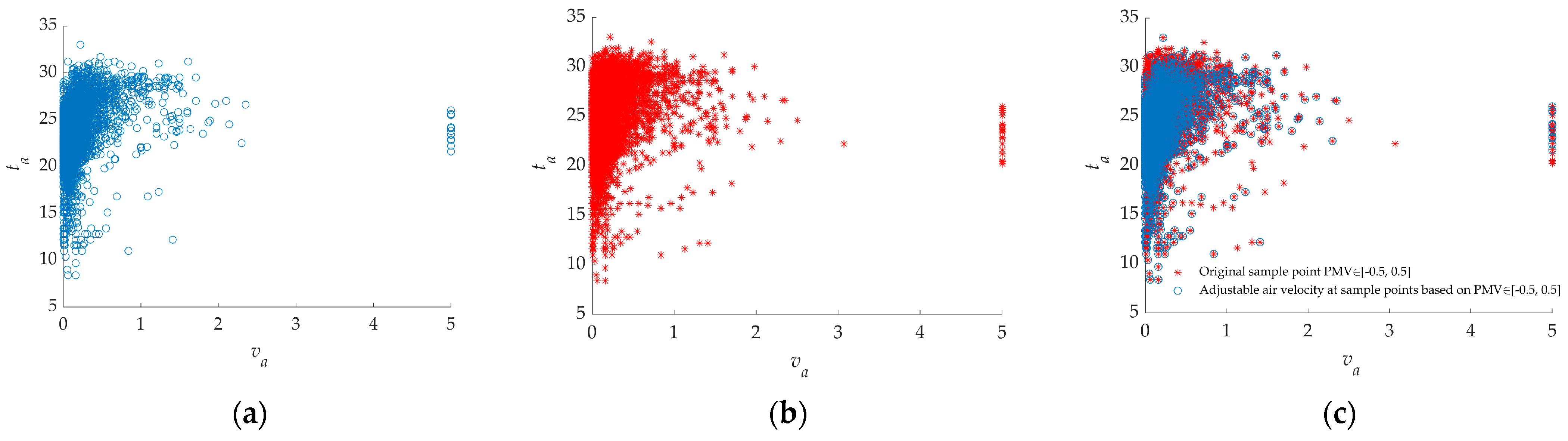
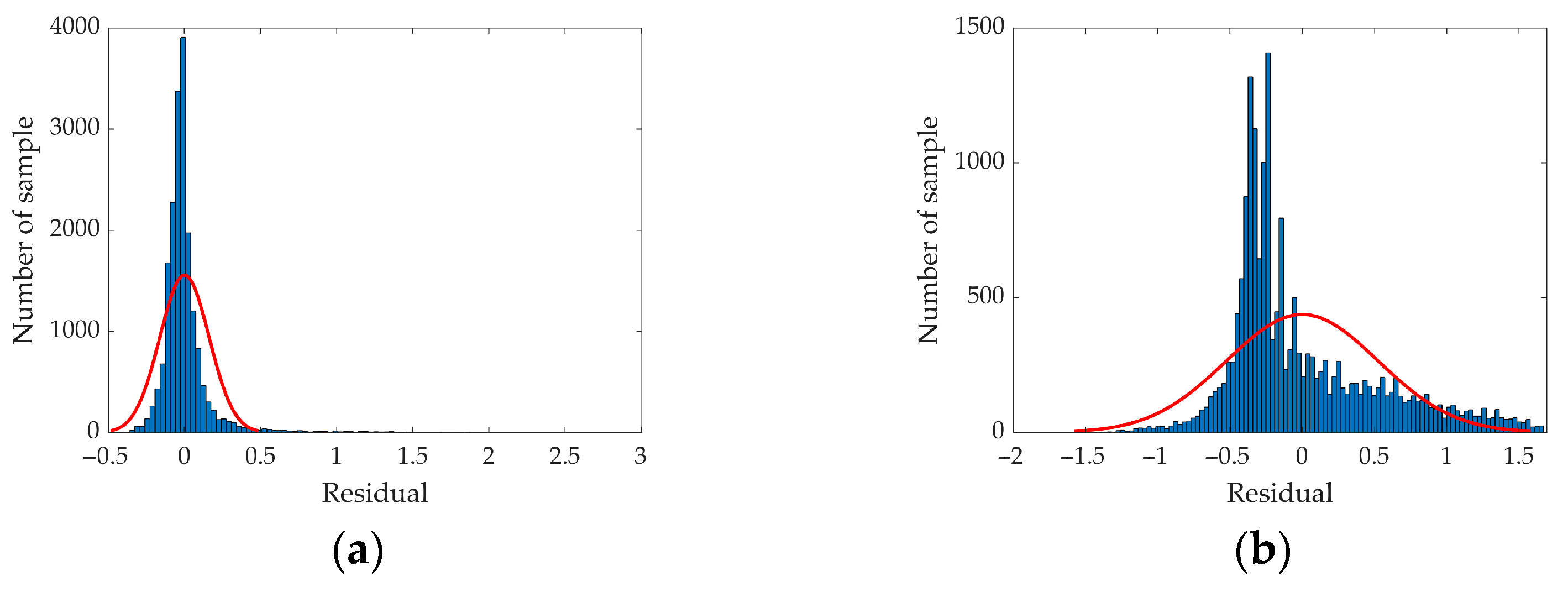
3.1. Verification of Air-Velocity Adjustability Determination
3.2. Calculation Results and Probabilistic Interpretation of Adjustable Air-Velocity Intervals
3.3. Guidance Based on Adjustable Air Velocity
- According to the conclusions in Section 2.2.2 and Section 3.1, an intelligent terminal allows users to determine whether the comfort level can be improved by air-velocity adjustment and also guides the user in determining the timing of air-velocity adjustment. This conclusion changes the timing of air-velocity adjustment from an uncontrolled and subjective user action to a purposeful user action guided by an intelligent terminal.
- 2.
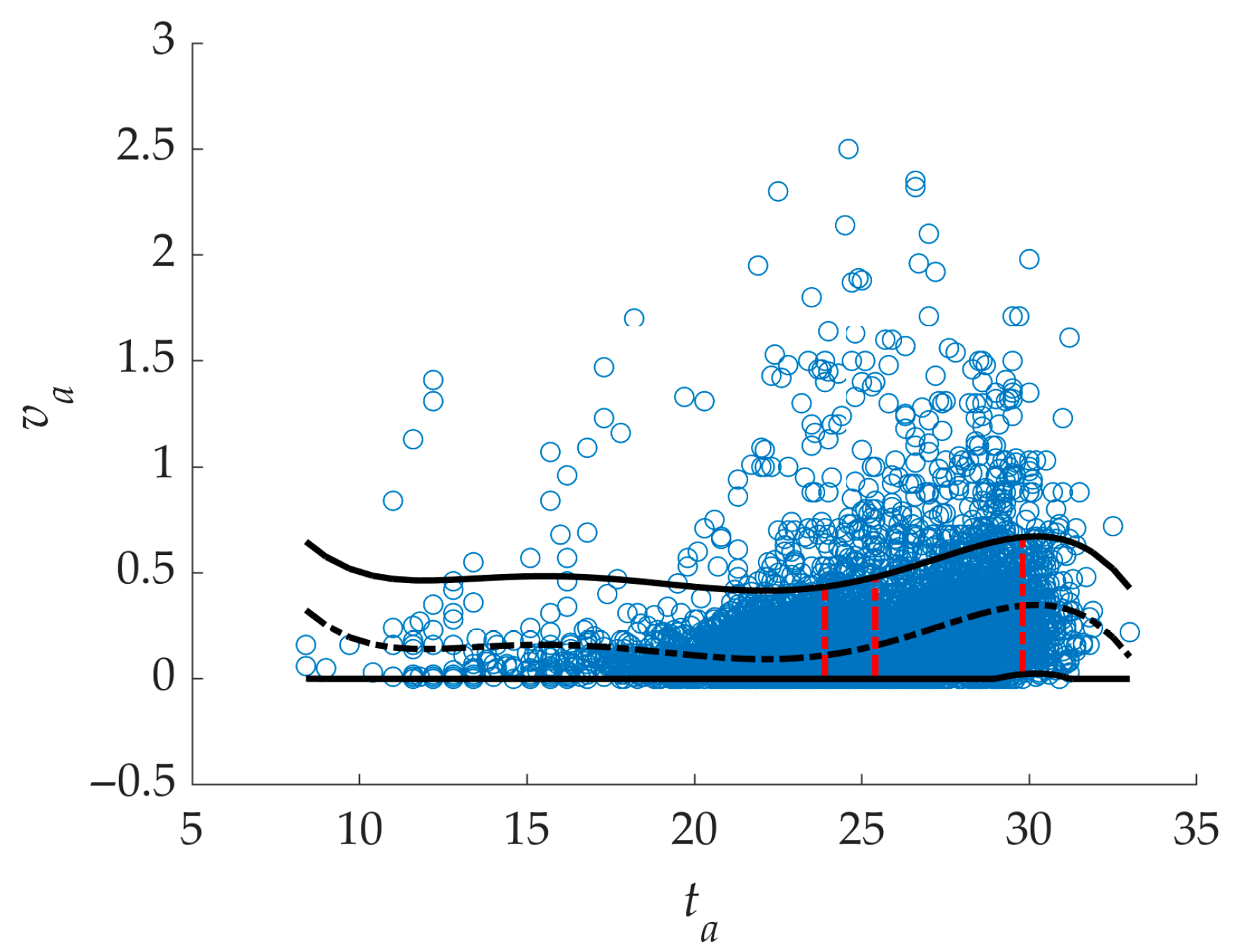
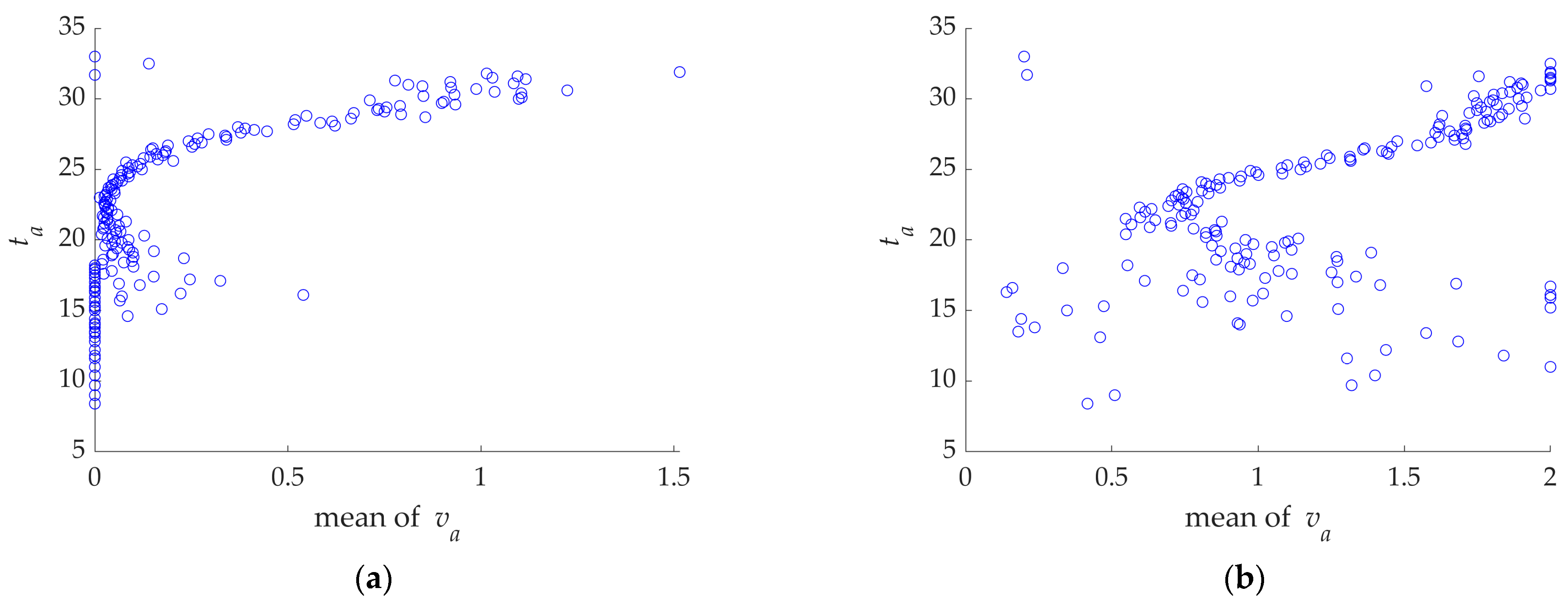
- According to the conclusions in Section 2.2.3 and Section 3.2, there is a guideline range of air velocity for any temperature between 20 °C and 30 °C (the higher the temperature, the higher the need for air-velocity regulation to meet comfort) when the air velocity is adjustable to meet comfort requirements. Figure 13 gives the average air-velocity interval consisting of the mean of the adjustable air-velocity interval left and correct endpoint values for all given temperatures. This figure clearly guides the air-velocity adjustment strategy at the specified temperature.
- 3.
- As shown in Figure 12 and Figure 13, it is difficult to use air-velocity regulation above 30 °C to make the thermal comfort meet demand, which is a guideline for the temperature determination line of whether to activate the HVAC system for cooling in mixed-mode ventilation. This result means taking HVAC systems for cooling above 30 °C and increasing the use of natural ventilation systems below 30 °C, thus reducing the energy consumption of HVAC systems and influencing the energy efficiency of the building.
- 4.
- In addition, as shown in Figure 14, when the temperature is below 20 °C, the lower the temperature, the closer the minimum adjustable air velocity is to 0 m/s. In contrast, the maximum adjustable air velocity is influenced by other factors to a greater extent, indicating that the demand for air-velocity regulation to meet the comfort level is not high under low temperatures. When the air temperature is above 25 °C, the higher the air temperature is, the closer the maximum adjustable air velocity is to 2 m/s. In contrast, other factors influence the minimum adjustable air velocity to a greater extent, suggesting a higher demand for air-velocity regulation to meet the comfort level under high-temperature conditions. These results provide a guiding strategy for adjusting air velocity in the mixed-mode ventilation system, i.e., to enhance indoor thermal comfort by increasing or decreasing ventilation to the guidance range of air velocity at a given temperature.
4. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- González-Torres, M.; Pérez-Lombard, L.; Coronel, J.F.; Maestre, I.R.; Yan, D. A review on buildings energy information: Trends, end-uses, fuels and drivers. Energy Rep. 2022, 8, 626–637. [Google Scholar] [CrossRef]
- Vallati, A.; Matteo, M.D.; Fiorini, C.V. Retrofifit proposals for energy efficiency and thermal comfort in historic public buildings: The case of the engineering faculty’s seat of Sapienza University. Energies 2023, 16, 151. [Google Scholar] [CrossRef]
- Yang, L.; Liu, X.D.; Qian, F. Optimal configurations of high-rise buildings to maximize solar energy generation efficiency of building-integrated photovoltaic systems. Indoor Built Environ. 2019, 28, 1104–1125. [Google Scholar] [CrossRef]
- Yang, L.; Liu, X.D.; Qian, F.; Niu, S.N. Research on the wind environment and air quality of parallel courtyards in a university campus. Sustain. Cities Soc. 2020, 56, 102019. [Google Scholar] [CrossRef]
- Mata, O.; Méndez, J.I.; Ponce, P.; Peffer, T.; Meier, A.; Molina, A. Energy savings in buildings based on image depth sensors for human activity recognition. Energies 2023, 16, 1078. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, J.; Yang, J.; Berardi, U.; Cui, G. An hour-ahead predictive control strategy for maximizing natural ventilation in passive buildings based on weather forecasting. Appl. Energy 2023, 333, 120613. [Google Scholar] [CrossRef]
- Do, H.; Cetin, K.S. Mixed-Mode ventilation in HVAC System for energy and economic benefits in residential buildings. Energies 2022, 15, 4429. [Google Scholar] [CrossRef]
- Wang, J.Q.; Huang, J.J.; Feng, Z.B.; Cao, S.J.; Haghighat, F. Occupant-density-detection based energy efficient ventilation system: Prevention of infection transmission. Energy Build. 2021, 240, 110883. [Google Scholar] [CrossRef] [PubMed]
- Center for the Built Environment (CBE). About Mixed-Mode. Mixed Mode, Cases Studies and Project Database. University of California, Berkeley. Available online: https://cbe.berkeley.edu/mixedmode/aboutmm.html (accessed on 25 January 2022).
- Wanga, L.; Greenberg, S. Window operation and impacts on building energy consumption. Energy Build. 2015, 92, 313–321. [Google Scholar] [CrossRef]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in heating ventilation and air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952. [Google Scholar] [CrossRef]
- Baborska-Narożny, M.; Kostka, M. Seasonal. Air quality in bedrooms with natural, mechanical or hybrid ventilation systems and varied window opening Behavior-Field measurement results. Energies 2022, 15, 9328. [Google Scholar] [CrossRef]
- Arat, S.; Kawakubo, S. Study on productivity of office workers and power consumption of air conditioners in a Mixed-Mode ventilation building during springtime. Build. Environ. 2021, 214, 108923. [Google Scholar] [CrossRef]
- Khoshbakht, M.; Gou, Z.H.; Zhang, F. A pilot study of thermal comfort in subtropical Mixed-Mode higher education office buildings with different change-over control strategies. Energy Build. 2019, 196, 194–205. [Google Scholar] [CrossRef]
- Khadka, S.; Rijal, H.B.; Amano, K.; Saito, T.; Imagawa, H.; Uno, H.; Genjo, K.; Takata, H.; Tsuzuki, K.; Nakaya, T.; et al. Study on winter comfort temperature in mixed mode and HVAC office buildings in Japan. Energies 2022, 15, 7331. [Google Scholar] [CrossRef]
- Jeong, J.; Jeong, J.; Lee, M.; Lee, J.; Chang, S. Data-driven approach to develop prediction model for outdoor thermal comfort using optimized tree-type algorithms. Build. Environ. 2022, 226, 109663. [Google Scholar] [CrossRef]
- Zhong, Y.X.; Knefaty, A.D.; Chen, G.X.; Yao, J.; Zheng, R.Y. Forecast of air-conditioning duration in office buildings in summer using machine learning and Bayesian theories. J. Build. Eng. 2022, 61, 105218. [Google Scholar] [CrossRef]
- Luo, M.H.; Xie, J.Q.; Yan, Y.C.; Ke, Z.H.; Yu, P.R.; Wang, Z.; Zhang, J.S. Comparing machine learning algorithms in predicting thermal sensation using ASHRAE Comfort Database II. Energy Build. 2020, 210, 109776. [Google Scholar] [CrossRef]
- Wang, H.L.; Ding, Z.K.; Tang, R.; Chen, Y.B.; Fan, C.; Wang, J.Y. A machine learning-based control strategy for improved performance of HVAC systems in providing large capacity of frequency regulation service. Appl. Energy 2022, 326, 119962. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Mamlook, R.E.A.; Almuflflih, A.S. Evaluating the impact of external support on green building construction cost: A hybrid mathematical and machine learning prediction approach. Buildings 2022, 12, 1256. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Mamlook, R.E.A.; Almasabha, G.; Almuflflih, A.S.; Alghamdi, S.Y. Prediction liquidated damages via ensemble machine learning model: Towards sustainable highway construction projects. Sustainability 2022, 14, 9303. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Mamlook, R.E.A.; Almuflflih, A.S.; Almakayeel, N. Machine learning-based model for predicting the shear strength of slender reinforced concrete beams without stirrups. Buildings 2022, 12, 1166. [Google Scholar] [CrossRef]
- Cook, M.J.; Shukla, Y.; Rawal, R.; Angelopoulos, C.; Caruggi-De-Faria, L.; Loveday, D.; Spentzou, E.; Patel, J. Integrating low energy cooling and ventilation strategies in Indian residences. Build. Cities 2022, 3, 279–296. [Google Scholar] [CrossRef]
- Ličina, V.F.; Cheung, T.; Zhang, H.; Dear, R.D.; Parkinson, T.; Arens, E.; Zhou, X. Development of the ASHRAE Global Thermal Comfort Database II. Build. Environ. 2018, 142, 502–512. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort: Analysis and Application in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Bo, P.B. Curve Reconstruction from Unorganized Point Cloud. Master’s Thesis, Shandong University, Jinan, China, 2004. [Google Scholar]
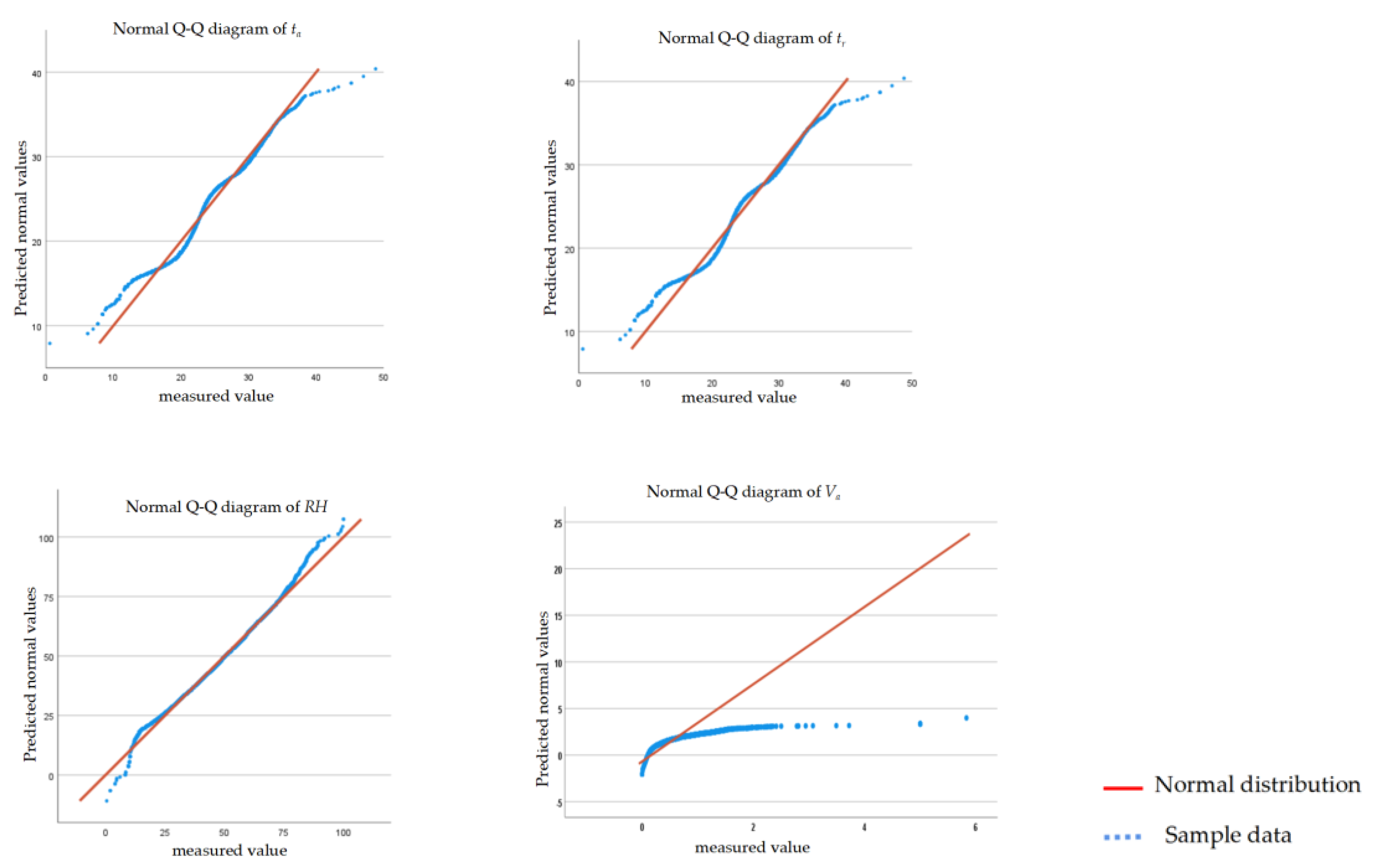
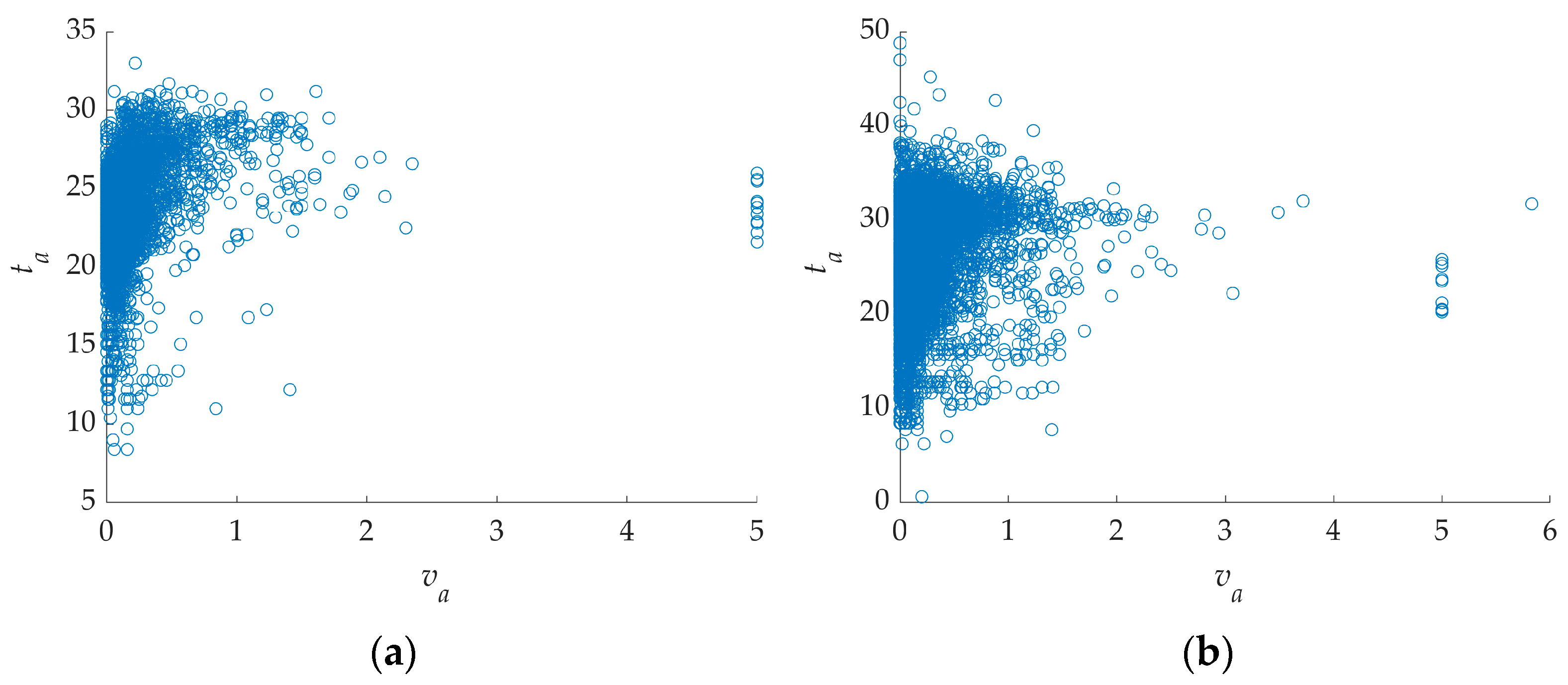


| Variables | Unit | Interval | Mean | Standard Deviation | Median | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| ta | °C | [0.6, 48.8] | 24.15 | 3.96 | 23.50 | 0.06 | 4.44 |
| tr | °C | [1.2, 49.8] | 24.47 | 3.98 | 23.90 | −0.12 | 4.58 |
| va | m/s | [0, 5.83] | 0.16 | 0.24 | 0.10 | 8.44 | 136.73 |
| RH | % | [0.5, 100] | 49.32 | 14.66 | 49.80 | −0.20 | 2.85 |
| Iclo | clo | [0.03, 2.87] | 0.66 | 0.30 | 0.60 | 1.52 | 6.98 |
| M | W/m2 | [0.65, 6.83] | 1.22 | 0.28 | 1.20 | 3.05 | 23.28 |
| PMV | [−3, 3] | 0.03 | 1.07 | −0.01 | 0.13 | 3.44 |
| ta | tr | RH | PMV | |
|---|---|---|---|---|
| ta | 1 | |||
| tr | 0.949 * | 1 | ||
| RH | 0.040 * | 0.075 * | 1 | |
| PMV | 0.784 * | 0.786 * | 0.080 * | 1 |
| Category | Adjustable Case | Non-Adjustable Case |
|---|---|---|
| Mean Recall Accuracy | 0.98520 | 0.97631 |
| Accuracy | Recall | Precision | F1-Score | |
|---|---|---|---|---|
| SVM | 98.16% | 99.14% | 97.85% | 98.49% |
| KNN | 95.42% | 95.81% | 96.78% | 96.29% |
| RF | 92.72% | 93.21% | 95.10% | 94.14% |
| BOOST | 82.82% | 83.81% | 89.34% | 86.49% |
| DT | 85.18% | 83.64% | 94.42% | 88.69% |
| LoG | 61.72% | 62.31% | 95.64% | 75.46% |
| ANN | 61.49% | 61.53% | 99.89% | 76.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Ouyang, J.; Yang, L. Mixed-Mode Ventilation Based on Adjustable Air Velocity for Energy Benefits in Residential Buildings. Energies 2023, 16, 2746. https://doi.org/10.3390/en16062746
Su L, Ouyang J, Yang L. Mixed-Mode Ventilation Based on Adjustable Air Velocity for Energy Benefits in Residential Buildings. Energies. 2023; 16(6):2746. https://doi.org/10.3390/en16062746
Chicago/Turabian StyleSu, Lichen, Jinlong Ouyang, and Li Yang. 2023. "Mixed-Mode Ventilation Based on Adjustable Air Velocity for Energy Benefits in Residential Buildings" Energies 16, no. 6: 2746. https://doi.org/10.3390/en16062746
APA StyleSu, L., Ouyang, J., & Yang, L. (2023). Mixed-Mode Ventilation Based on Adjustable Air Velocity for Energy Benefits in Residential Buildings. Energies, 16(6), 2746. https://doi.org/10.3390/en16062746







