Numerical Investigation of Pelton Turbine Distributor Systems with Axial Inflow
Abstract
1. Introduction
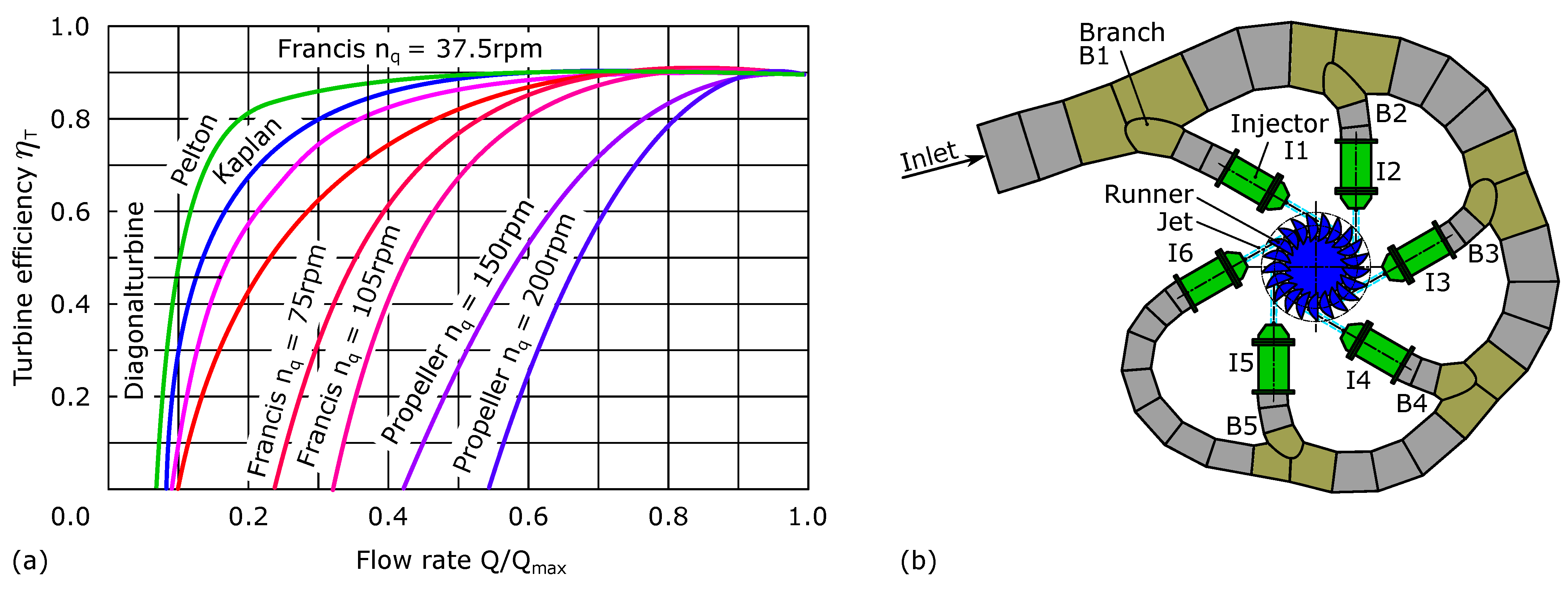
2. Materials and Methods
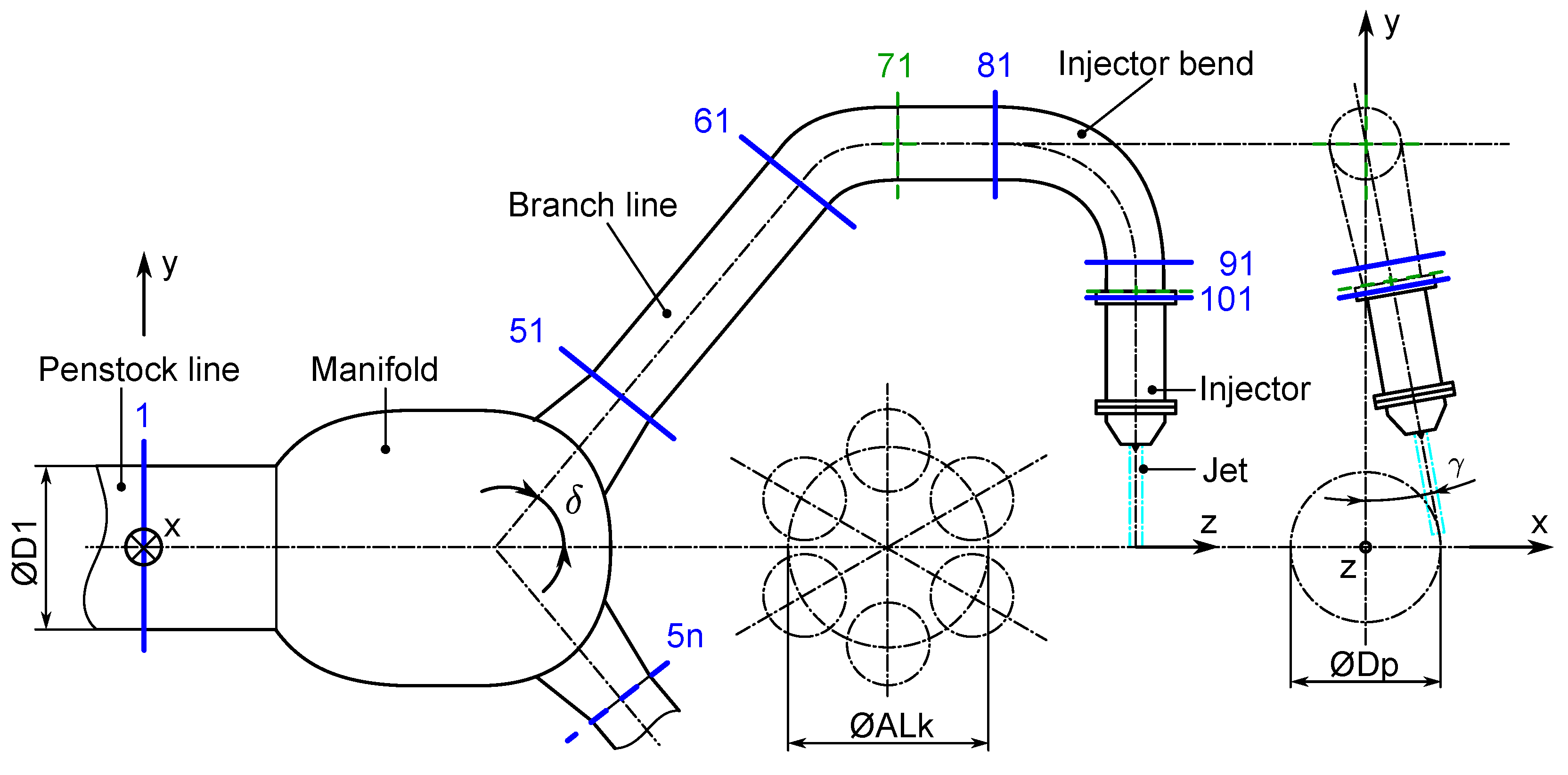
2.1. Pelton Turbine Distributor System with Axial Inflow—AxFeeder
2.2. Description of Investigated Basic Manifold Designs
2.3. Flow Quality in Piping Systems
2.3.1. Total Pressure Drop
2.3.2. Power Loss—Classical Approach
2.3.3. Power Loss—Second Law Analysis
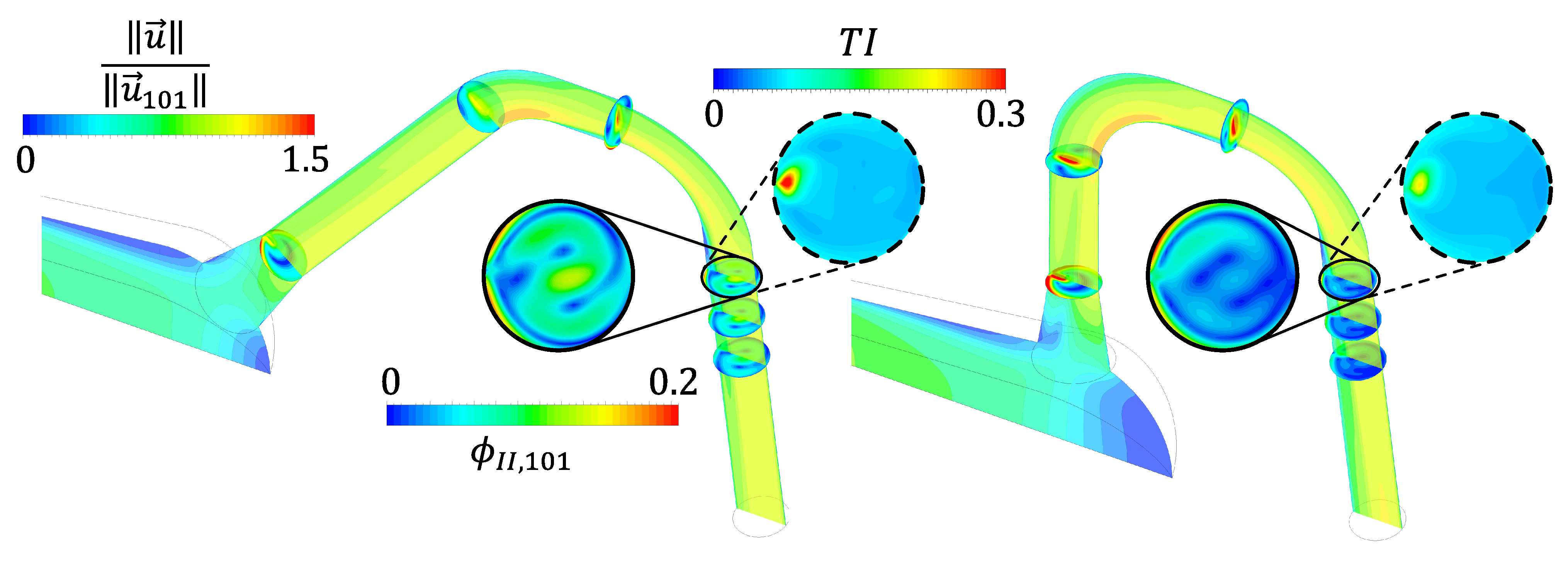
2.3.4. Secondary Flows
2.4. Computational Domain and Simulation Setup
2.5. Grid Refinement Study
3. Results
3.1. Operating Regime
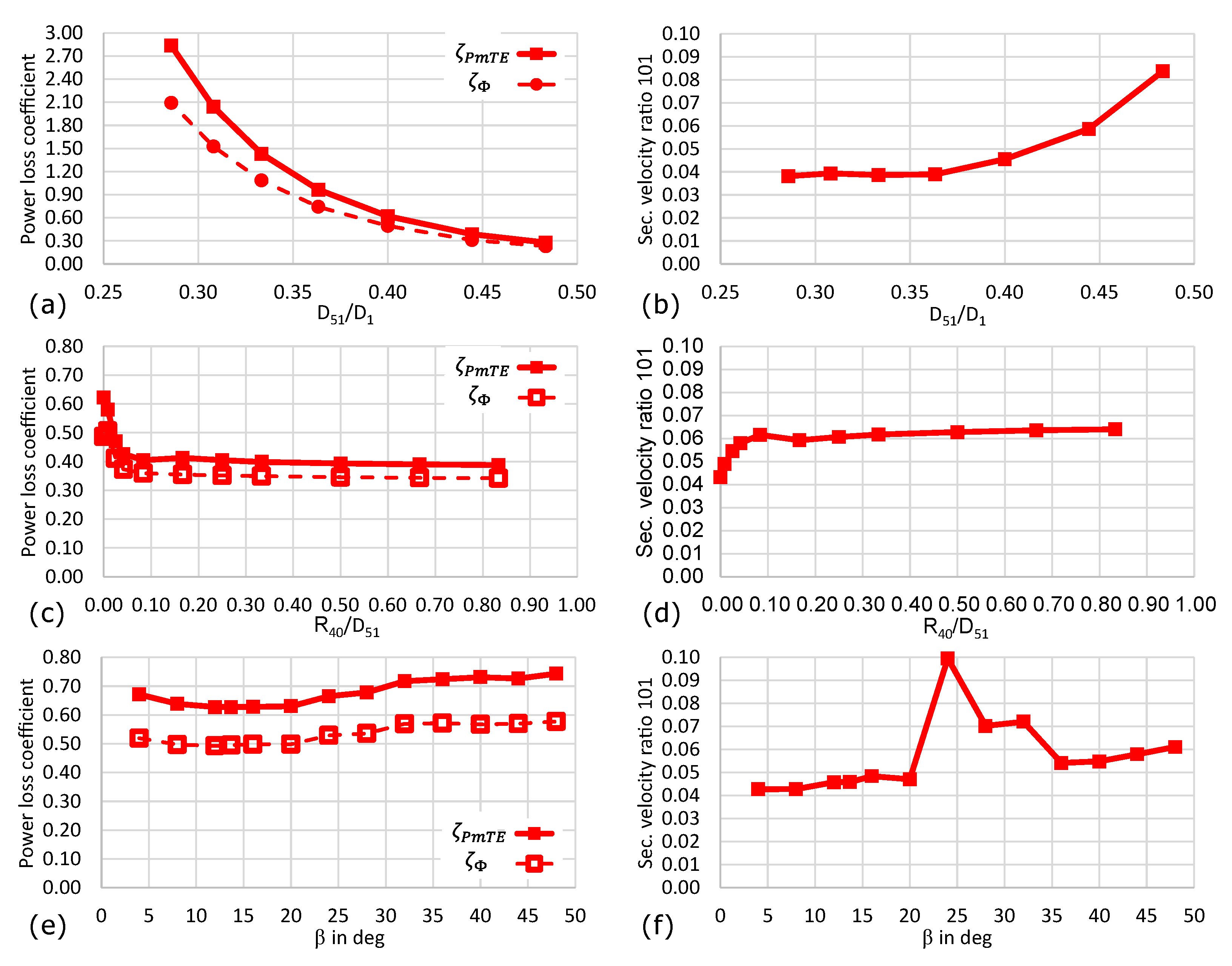
3.2. Parametric Variations of the Basic Model
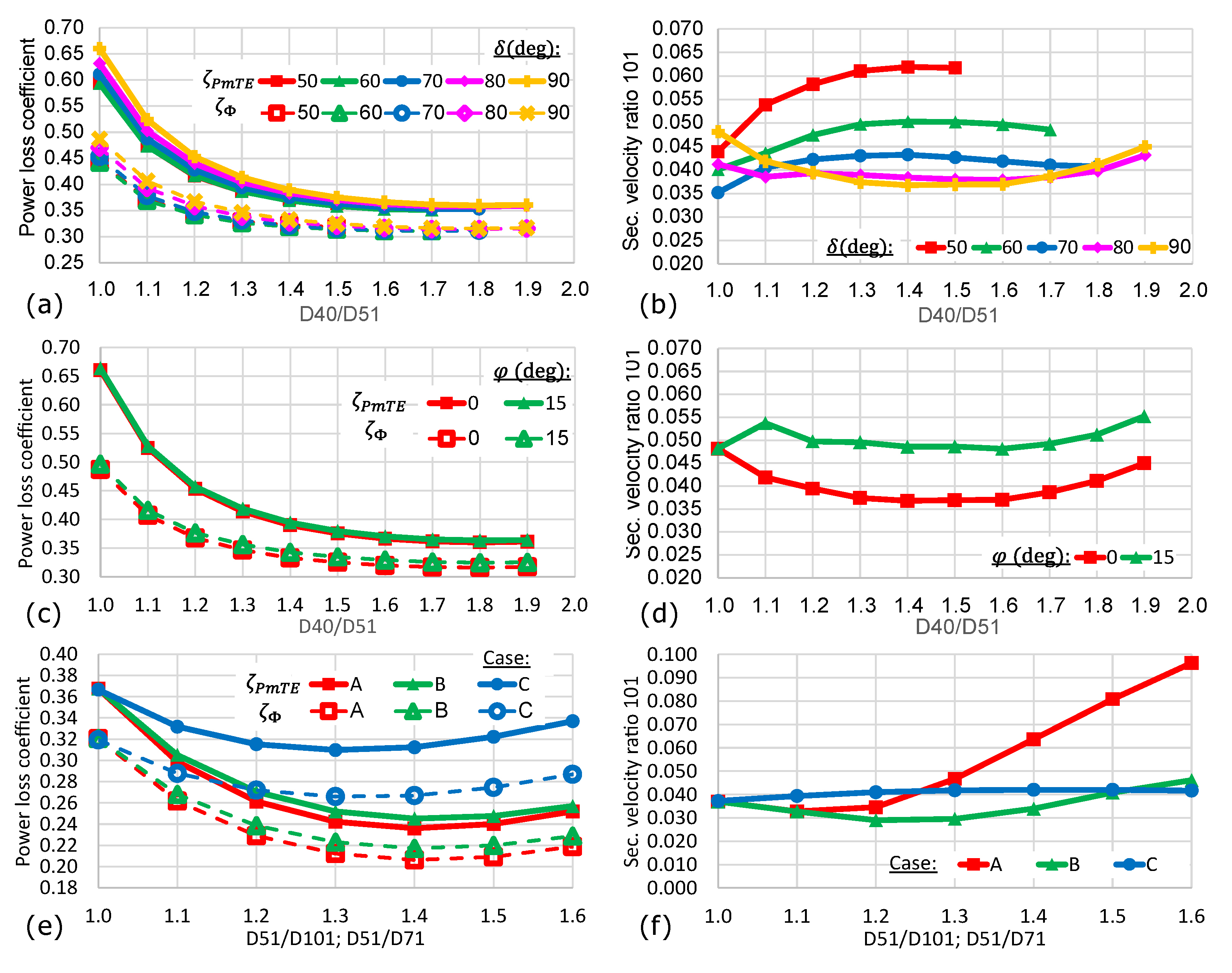
3.3. Parametric Variations of the Basic Model with Conical Frustum
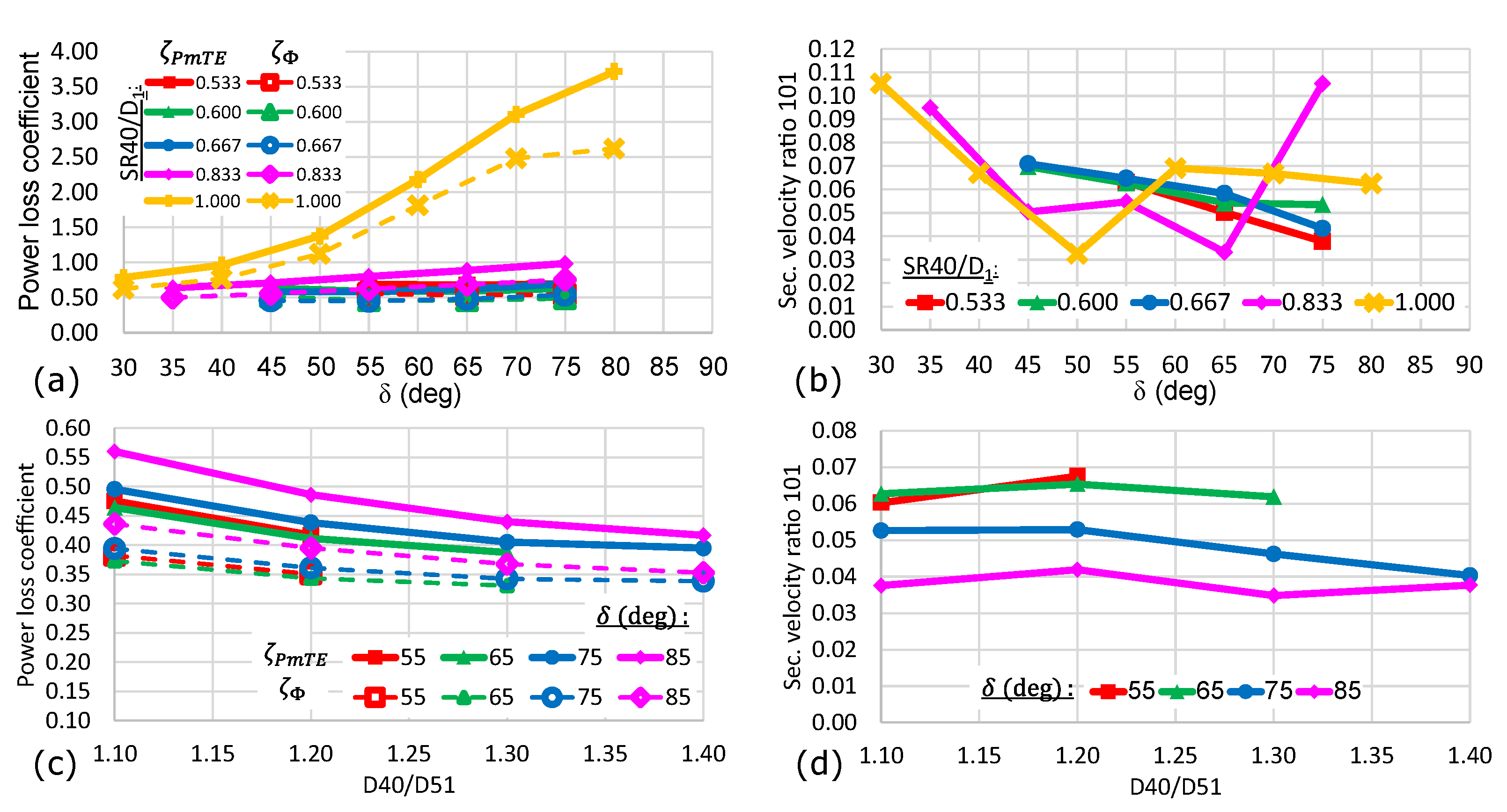
3.4. Parametric Variations of the Distributor Model with Spherical Manifold
3.5. Parametric Variations of the Distributor Model with Cylindrical Manifold
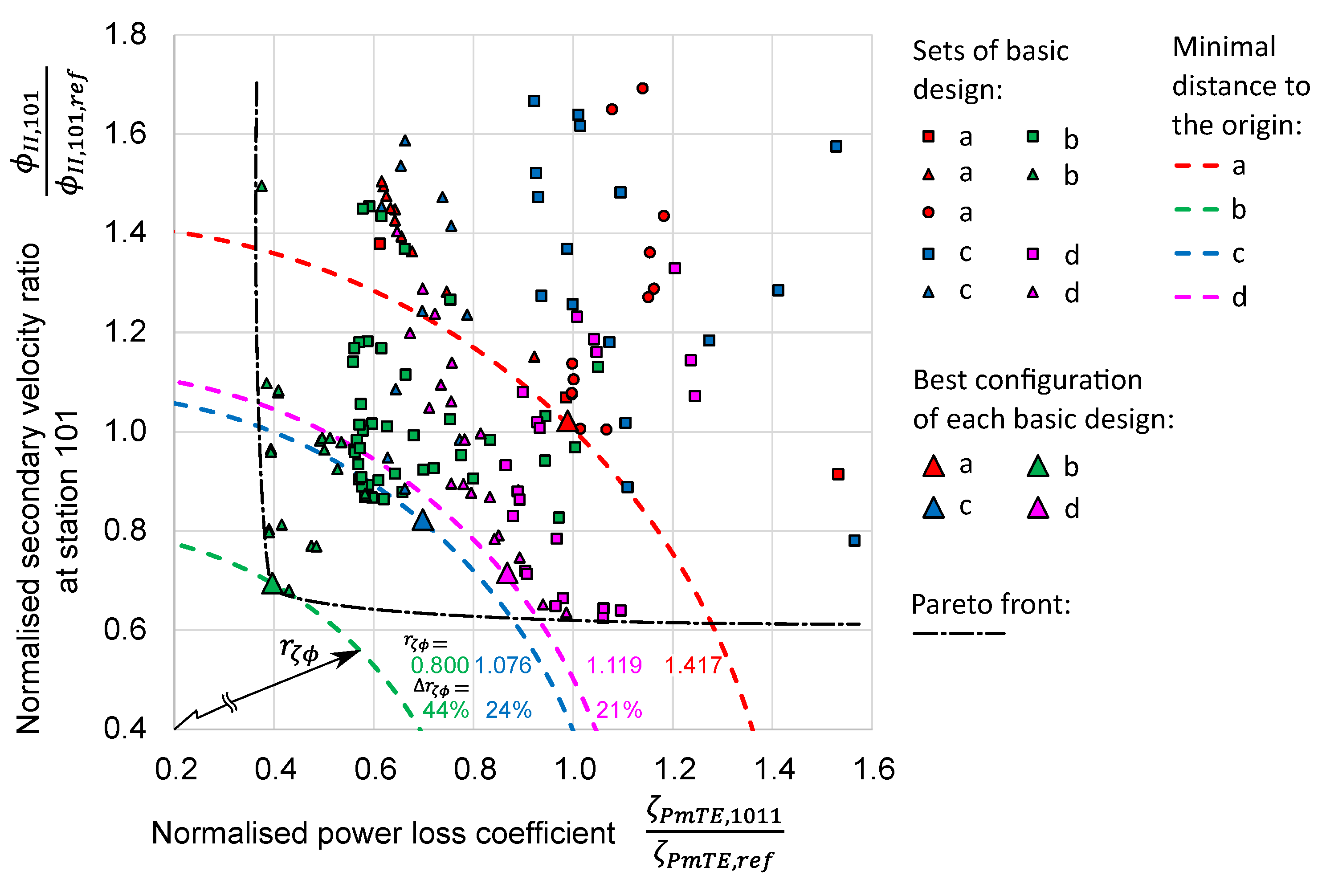
3.6. Comparison of the Four Design Variants
4. Discussion
4.1. Core Findings
- The transition from the penstock to the manifold is crucial, while the model with a spherical manifold becomes susceptible to unsteady flow phenomena if the sphere radius exceeds a certain value, similar unsteady effects were observed for the model with a diffuser-shaped manifold and too-steep diffuser angles .
- The first component of the branch line in the flow direction should be shaped as a conical frustum. It reduces power losses by over a third and decreases the secondary flows for branch lines with steep deviation angles.
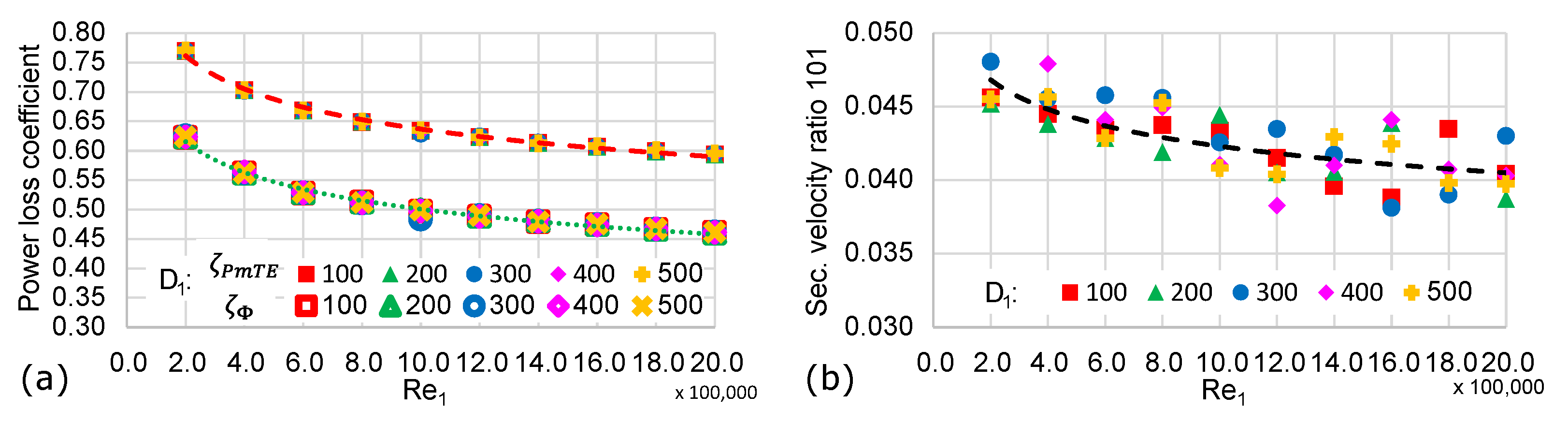
- A steeper deviation angle (ideally ) has multiple advantages: First, the secondary velocity ratio is lowered significantly (see Figure 12). Second, the axial length of the distributor system is shortened, and third, the connection between the manifold and the branch lines becomes easier to manufacture. The slight increase in power losses for steeper deviation angles becomes negligible.
- An injector bend with a converging diameter from station 81 to 91 and a fixed curvature radius allows for a reduction in both quality criteria of up to one-third.
- Only the conical frustum and the converging injector bend reduce power losses and secondary flows simultaneously. The majority of the geometric parameters decrease one but increase the other target quantity. For example, a fillet radius at the connection of the branch lines and the manifold greatly reduces power losses, but amplifies the secondary velocity.
4.2. Additional Insights
4.2.1. On the Secondary Flows at Station 101
4.2.2. On the Power Losses
4.3. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin symbols | ||
| Surface area of station i | m2 | |
| Diameter at which the branch lines are connected to the manifold | ||
| Penstock diameter | ||
| Diameter of pipe segment at station i | ||
| Pitch cycle diameter of the runner | ||
| H | Geodetic head | |
| Total pressure loss coefficient | 1 | |
| k | Turbulence kinetic energy | m2/s2 |
| Length of pipe segment starting from station i | ||
| Mass flow rate at station i | / | |
| Normal vector of surface | 1 | |
| n | Number of branch lines | 1 |
| Specific speed | rpm | |
| Power of kinetic energy | ||
| Power of mechanical total energy | ||
| Power of turbulent dissipation | ||
| Power of viscous dissipation | ||
| p | Pressure | |
| Order of accuracy | 1 | |
| Dynamic pressure | ||
| Total pressure | ||
| Q | Volumetric flow rate | / |
| Reynolds number | 1 | |
| Non-dimensional distance from center point to design point | 1 | |
| Turbulence intensity | 1 | |
| Flow velocity and its components | / | |
| Primary flow velocity | / | |
| Secondary flow velocity | / | |
| V | Integration volume | |
| Non-dimensional wall distance | 1 | |
| Greek symbols | ||
| Deviation angle of first segment of the branch line of design a), see Figure 2 | ||
| Diffuser angle | ||
| Pivot angle of the injector bend | ||
| Difference between quantities | misc. | |
| Deviation angle of the branch line | ||
| Turbulence eddy dissipation | / | |
| Power loss coefficient | 1 | |
| Dissipation power coefficient | 1 | |
| Distributor efficiency | 1 | |
| Turbine efficiency | 1 | |
| Pivot angle of the branch line, see Figure 2 | ||
| Turbulent dissipation | ||
| Viscous dissipation | ||
| Secondary velocity ratio | 1 | |
| Shear stress tensor in index notation | ||
| Turbulence eddy frequency | 1/ | |
| Constants (within the framework of this study) | ||
| g | Gravitational acceleration | 9.807 m/s2 |
| Coefficient of k- SST turbulence model | 0.09 | |
| Dynamic viscosity of water at 25 | 8.009 × 10−4 Pa s | |
| Density of water at 25 | 997 kg/m3 | |
| Common indices | ||
| dyn | Dynamic | |
| i | Station i | |
| KE | Kinetic energy | |
| max | Maximum | |
| min | Minimum | |
| mTE | Mechanical total energy | |
| ref | Reference | |
| T | Turbine | |
| Turb | Turbulent | |
| t | Total | |
| Vis | Viscous | |
| I | Primary | |
| II | Secondary | |
| 101 | Quantity evaluated at station 101 | |
| 1011 | Quantity evaluated as difference of values at stations 1 and 101 | |
| Abbreviations | ||
| FFG | Österreichische Forschungsförderungsgesellschaft | |
| GCI | Grid convergence index | |
| SLA | Second law analysis | |
| SST | Shear stress transport | |
Appendix A
Appendix A.1. Script for Creating Secondary Flow Variables in CFD-Post
| Listing A1: Minimal working example for creating secondary flow variables in CFD-Post. |
 |
References
- Bundesministerium für Nachhaltigkeit und Tourismus. Integrierter Nationaler Energie-und Klimaplan für Österreich; Bundesministerium für Nachhaltigkeit und Tourismus: Wien, Austria, 2019. [Google Scholar]
- Staubli, T.; Abgottspon, A.; Weibel, P.; Bissel, C.; Parkinson, E.; Leduc, J.; Leboeuf, F. Jet quality and Pelton efficiency. In Proceedings of the Hydro-2009, Lyon, France, 26–28 October 2009. [Google Scholar]
- Staubli, T.; Weibel, P.; Bissel, C.; Karakolcu, A.; Bleiker, U. Efficiency increase by jet quality improvement and reduction of splashing water in the casing of Pelton turbines. In Proceedings of the 16th International Seminar on Hydropowerplants, Laxenburg, 24–26 November 2010. [Google Scholar]
- Sick, M.; Drtina, P.; Schärer, C.; Keck, H. Numerical and experimental analyses of Pelton Turbine Flow Part 1: Distributor and Injector. In Proceedings of the 20th IAHR Symposium on Hydraulic Machinery and Systems, Charlotte, NC, USA, 6–9 August 2000. [Google Scholar]
- Peron, M.; Parkinson, E.; Geppert, L.; Staubli, T. Importance of Jet Quality on Pelton Efficiency and Cavitation. In Proceedings of the International Conference on Hydraulic Efficiency Measurements, Milan, Italy, 3–6 September 2008. [Google Scholar]
- Santolin, A.; Cavazzini, G.; Ardizzon, G.; Pavesi, G. Numerical investigation of the interaction between jet and bucket in a Pelton turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 721–728. [Google Scholar] [CrossRef]
- Erlach, J.; Staubli, T. Pelton Turbine with a Supply System. WO 2008/003390 A1, 14 June 2007. [Google Scholar]
- Erlach, J.; Erlach, P. We proudly present the first up to Six Jets Horizontal Pelton Turbine. In Proceedings of the Hidroenergia 2014, European Small Hydropower Association (ESHA) Congress, Istanbul, Turkey, 21–23 May 2014. [Google Scholar]
- Erlach, J.; Erlach, P. Neues Pelton-Konzept—bis zu sechs Düsen in horizontaler Anordnung. WasserWirtschaft 2016, 106, 18–24. [Google Scholar] [CrossRef]
- Giesecke, J.; Heimerl, S.; Mosonyi, E. Wasserkraftanlagen: Planung, Bau und Betrieb; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Han, L.; Duan, X.; Gong, R.; Zhang, G.; Wang, H.; Wei, X. Physic of secondary flow phenomenon in distributor and bifurcation pipe of Pelton turbine. Renew. Energy 2019, 131, 159–167. [Google Scholar] [CrossRef]
- Parkinson, E.; Lestriez, R.; Chapuis, L. Flow Calculations in Pelton Turbines—Part 1: Repartitor and Injector Numerical Analysis. In Proceedings of the 19th IAHR Symposium on Hydraulic Machinery and Systems, Singapore, 9–11 September 1998; pp. 285–293. [Google Scholar]
- Lei, H.; Gaofu, Z.; Ruzhi, G.; Hongda, W.; Wei, L. Physics of bad-behaved flow in 6-Nozzle Pelton turbine through dynamic simulation. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 240, p. 022018. [Google Scholar] [CrossRef]
- Patel, K.; Patel, B.; Yadav, M.; Foggia, T. Development of Pelton turbine using numerical simulation. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2010; Volume 12, p. 012048. [Google Scholar] [CrossRef]
- Shiraishi, T.; Watakabe, H.; Sago, H.; Konomura, M.; Yamaguchi, A.; Fujii, T. Resistance and fluctuating pressures of a large elbow in high Reynolds numbers. J. Fluids Eng. 2006, 128, 1063–1073. [Google Scholar] [CrossRef]
- Dixon, S.L.; Hall, C. Fluid Mechanics and Thermodynamics of Turbomachinery; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Idelchik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; Jaico Publishing House: Mumbai, India, 2005. [Google Scholar]
- Hahn, F.; Semlitsch, B.; Bauer, C. On the numerical assessment of flow losses and secondary flows in Pelton turbine manifolds. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; Volume 1079, p. 012082. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Entropy production calculation for turbulent shear flows and their implementation in CFD codes. Int. J. Heat Fluid Flow 2005, 26, 672–680. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Internal flow losses: A fresh look at old concepts. J. Fluids Eng. 2011, 133, 051201. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Losses due to conduit components: An optimization strategy and its application. J. Fluids Eng. 2016, 138, 031204. [Google Scholar] [CrossRef]
- Schmandt, B.; Herwig, H. Diffuser and nozzle design optimization by entropy generation minimization. Entropy 2011, 13, 1380–1402. [Google Scholar] [CrossRef]
- Herwig, H.; Schmandt, B. How to determine losses in a flow field: A paradigm shift towards the second law analysis. Entropy 2014, 16, 2959–2989. [Google Scholar] [CrossRef]
- Böhle, M.; Fleder, A.; Mohr, M. Study of the losses in fluid machinery with the help of entropy. In Proceedings of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, Honolulu, HI, USA, 10–15 April 2016; pp. 1–9. [Google Scholar]
- Menter, F.R. Improved Two-Equation k-Omega Turbulence Models for Aerodynamic Flows; Technical Report NASA-TM-103975; National Aeronautics and Space Administration: Moffett Field, CA, USA, 1992. [Google Scholar]
- Staubli, T.; Bissel, C. Jet Improvement for Swiss Pelton Plants; Technical Report; swisselectric (defunct as of 2017): Bern, Switzerland, 2009. [Google Scholar]
- CFX 19.2: CFX-Solver Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2023.
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
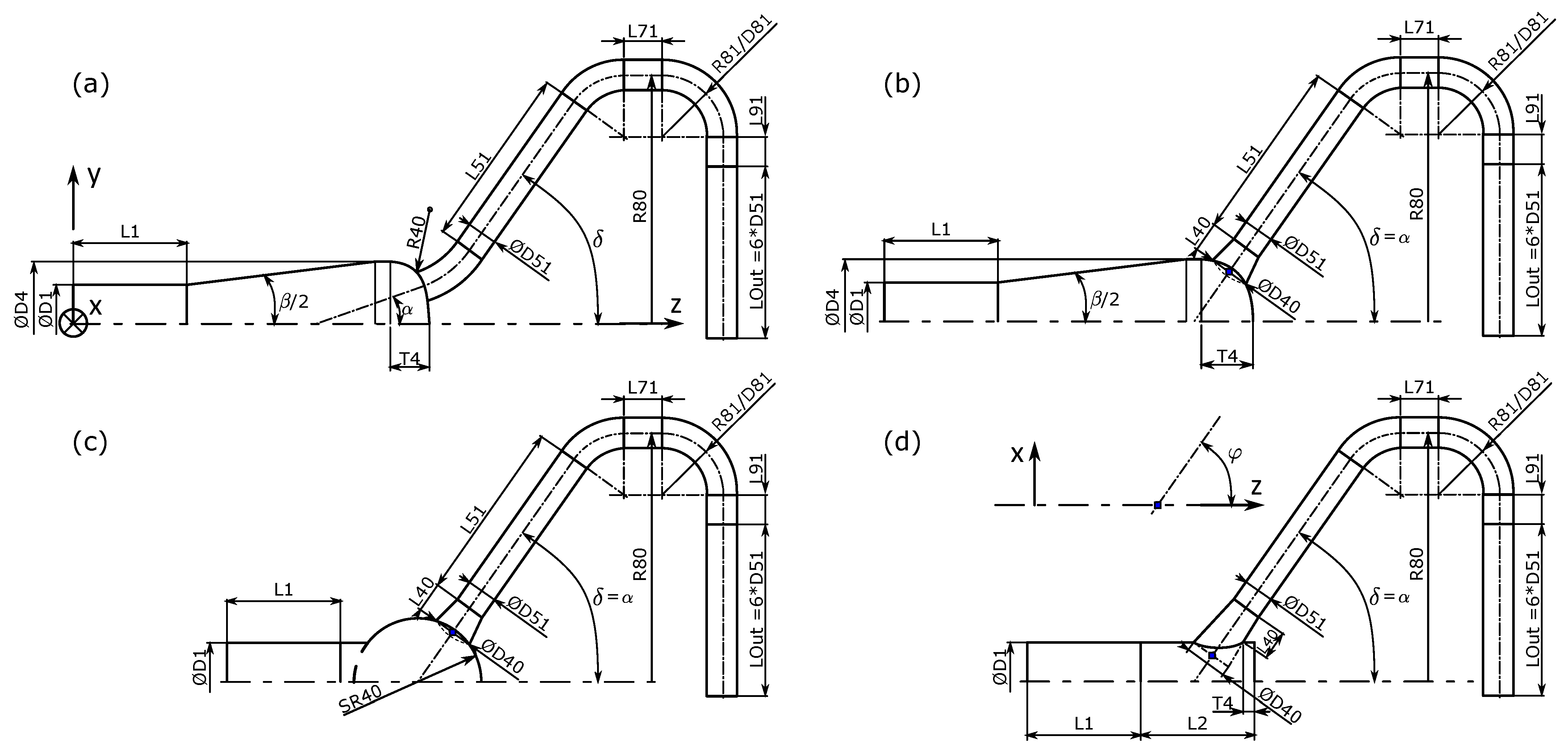


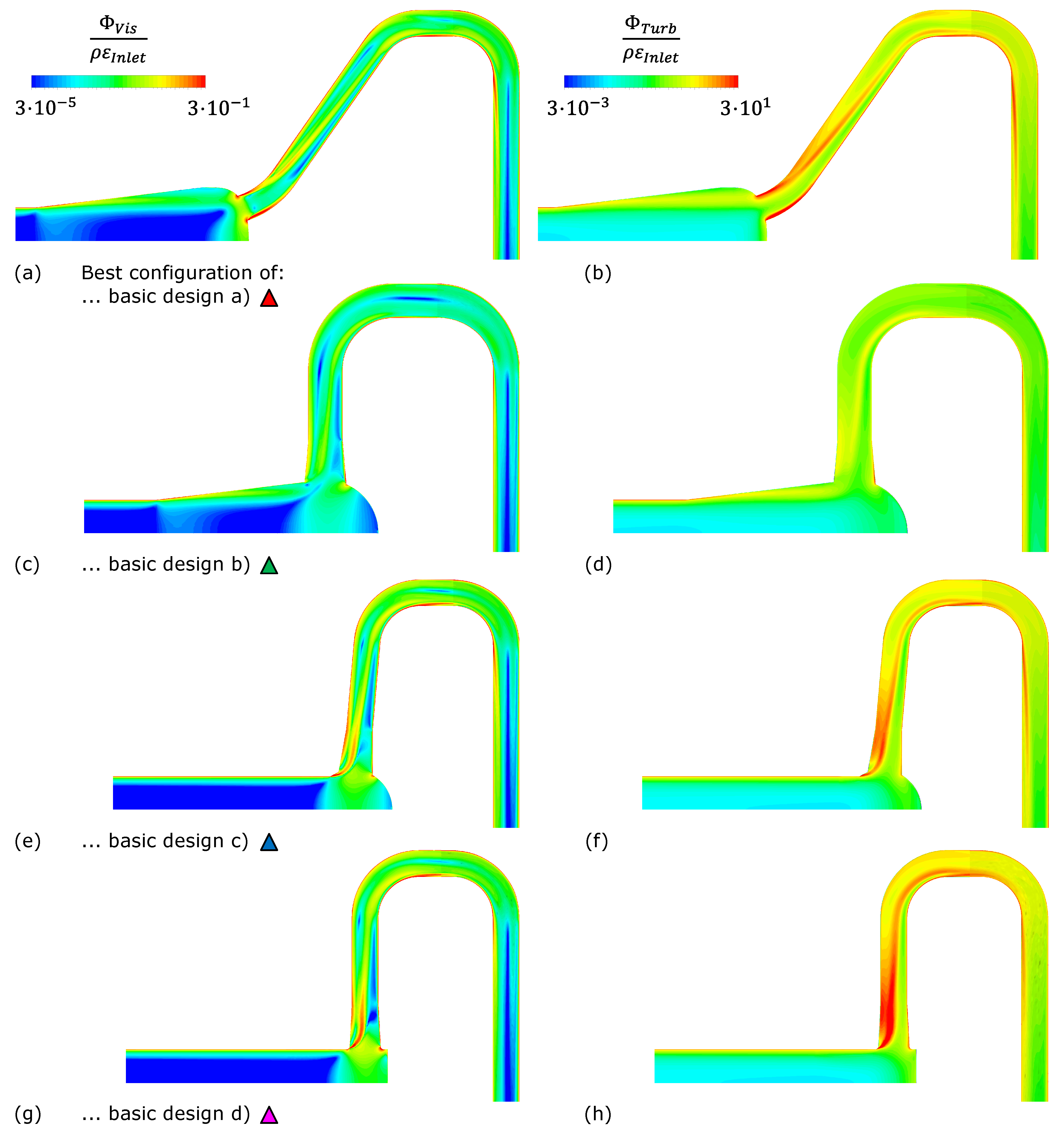
| Basic Design | Varied Parameters | Shown in |
|---|---|---|
| (a) basic model | diameter ratio D51/D1, fillet radius R40/D51, diffuser angle β | Figure 5, Figure 6 and Figure 11 |
| (b) basic model with conical frustum | diameter ratio D40/D51, deviation angle δ, diameter ratios D51/D71 and D51/D101, pivot angle φ | Figure 7, Figures 11 and 12 |
| (c) spherical manifold | sphere radius SR40/D1, deviation angle δ, diameter ratio D51/D101 | Figure 8 and Figure 11 |
| (d) cylindrical manifold | axial position T4/D51, deviation angle δ, fillet radius R40/D51 | Figure 9 and Figure 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hahn, F.J.J.; Maly, A.; Semlitsch, B.; Bauer, C. Numerical Investigation of Pelton Turbine Distributor Systems with Axial Inflow. Energies 2023, 16, 2737. https://doi.org/10.3390/en16062737
Hahn FJJ, Maly A, Semlitsch B, Bauer C. Numerical Investigation of Pelton Turbine Distributor Systems with Axial Inflow. Energies. 2023; 16(6):2737. https://doi.org/10.3390/en16062737
Chicago/Turabian StyleHahn, Franz Josef Johann, Anton Maly, Bernhard Semlitsch, and Christian Bauer. 2023. "Numerical Investigation of Pelton Turbine Distributor Systems with Axial Inflow" Energies 16, no. 6: 2737. https://doi.org/10.3390/en16062737
APA StyleHahn, F. J. J., Maly, A., Semlitsch, B., & Bauer, C. (2023). Numerical Investigation of Pelton Turbine Distributor Systems with Axial Inflow. Energies, 16(6), 2737. https://doi.org/10.3390/en16062737







