Abstract
As the scale of electricity consumption grows, the peak electricity consumption prediction of campus buildings is essential for effective building energy system management. The selection of an appropriate model is of paramount importance to accurately predict peak electricity consumption of campus buildings due to the substantial variations in electricity consumption trends and characteristics among campus buildings. In this paper, we proposed eight deep recurrent neural networks and compared their performance in predicting peak electricity consumption for each campus building to select the best model. Furthermore, we applied an attention approach capable of capturing long sequence patterns and controlling the importance level of input states. The test cases involve three campus buildings in Incheon City, South Korea: an office building, a nature science building, and a general education building, each with different scales and trends of electricity consumption. The experiment results demonstrate the importance of accurate model selection to enhance building energy efficiency, as no single model’s performance dominates across all buildings. Moreover, we observe that the attention approach effectively improves the prediction performance of peak electricity consumption.
1. Introduction
The prediction of electricity consumption in campus buildings is crucial to effectively manage building energy systems and prepare future electricity demand. Although the operational periods of campus buildings in South Korea are reduced during vacations corresponding to peak energy demand seasons, the energy demand of campus buildings has a significant local socioeconomic impact due to their scale [1,2,3]. In the case of the USA, educational buildings account for more than 19% of total energy consumption [4]. Accurate predicting of the electricity consumption in campus buildings helps electricity suppliers plan their distribution in advance. This not only prevents the wastage of electricity production but also helps avoid power outages [5].
Due to substantial variations in electricity consumption trends among campus buildings, influenced by seasonal and structural differences, the selection of the appropriate model is of significant importance to accurately predict electricity consumption. For instance, during the semester seasons, the variability of visitors who randomly change electricity consumption usage is high relatively in a general education building compared to an administrative building [6]. An engineering building accommodates various experimental productions that require significant electricity consumption [7]. Furthermore, the electricity consumption in a large-scale building tends to be relatively high due to the installation of systems, such as lighting and heating, ventilation, and air-conditioning (HVAC) that have substantial electricity demands [8].
There are many methods that have been proposed in prior works to predict electricity consumption according to forecasting horizons such as short-term, medium-term, and long-term [9,10]. Traditional prediction methods such as autoregressive (AR), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) were utilized to predict electricity consumption [11]. However, since traditional prediction methods typically rely on electricity consumption trends, the dynamic fluctuations in electricity consumption pose a challenge when attempting to apply these methods for accurate prediction results.
To overcome these limitations, several researchers have employed a supervised learning (SL) approach, including random forest (RF) [12], support vector regression (SVR) [13,14] and extreme learning [15], artificial neural network [16], and deep neural network [17]. These methods were trained by searching for best parameters that describe the hidden relationships between inputs and outputs and yield the lowest errors for the test instances. Moreover, ensemble learning which combines different algorithms have been applied to improve prediction performances [18,19]. They attempt to predict by using weights to combine different methods and demonstrate better performance than a single prediction model [20]. While SL-based methods improve prediction performances, they usually struggle to observe the hidden sequence patterns due to the limitation of their training mechanism [21].
Several studies have adopted various recurrent neural network approaches due to their excellent training performances by capturing time-series patterns. Rahman et al. [22] proposed a deep recurrent neural network (RNN) model for medium- and long-term electricity consumption predictions. A study utilized long-short-term memory (LSTM), which captures dynamic time-series trends better than RNN for predicting short-term residential consumption prediction [23,24].
Subsequently, several studies proposed electricity consumption predic2tion models by utilizing the combination of a convolutional neural network (CNN) and BiLSTM to enhance prediction performances [25,26]. In [26], the experiment results demonstrate that the proposed model outperforms over existing methods, such as linear regression, LSTM, and CNN-LSTM on the IHEPC dataset. Additionally, several researchers have applied an attention mechanism with LSTM [27,28] and with CNN-LSTM [29], which considers the effects for all the past hidden states. They successfully improve prediction performances, and their performance differences appear based on the characteristics of commercial buildings [30].
Recently, attention approach-based approaches have been utilized to address energy prediction problems. Li et al. [31] proposed RNN with an attention-based method for predicting 24 h ahead the building cooling load prediction. Another study adopted an attention approach to address building energy consumption prediction problems [32]. The results of this research demonstrate the importance of features through the attention approach. Ding et al. [33] proposed LSTM with an attention method to forecast building energy prediction. This study executed a case study of a green building and showed that the LSTM with the attention method is better than the existing methods such as LSTM and light gradient boosting machine (LGBM). The temporal attention approach was utilized to predict electricity power load for providing reliable decisions regarding power systems [34]. The experiment results on the real-world power load dataset obtained from American Electric Power demonstrate that the attention approach is effective in enhancing prediction performance.
Inspired by research results, this study carries out comparison analysis for multiple campus building peak electricity consumption by using deep recurrent neural networks (RNNs). The peak electricity consumption prediction of campus buildings is crucial to effectively facilitate energy management since the electricity consumption demands can be approximately 85% higher than expected [35], and the majority of them are measured in a peak time [36]. Specifically, we investigate the performance differences based on electricity consumption trends and characteristics of campus buildings by using six deep RNN models, which include LSTM, BiLSTM, CNN-LSTM, CNN-BiLSTM, CNN-LSTM with attention (CNN-LSTM-A), and CNN-BiLSTM with attention (CNN-BiLSTM-A).
The main differences of this study compared to previous works are as follows. First, in contrast with [30], we focus on developing models for predicting peak electricity consumption of the campus buildings by using datasets collected in the real world. Second, we employ CNN-LSTM and CNN-BiLSTM with attention approaches to address peak electricity consumption problems. We demonstrate that the attention method helps to improve prediction performance of peak electricity consumption. Third, we emphasize the importance of determining appropriate hyper-parameters through sensitive analysis to enhance prediction performance when training learning-based models.
This paper is organized as follows. Section 2 introduces all the proposed prediction models based on deep RNNs explored in this research. We describe the dataset used in the training and test phases of the prediction models, as well as experiment settings in Section 3. Section 4 provides the results in comparative and sensitivity analyses with the considered prediction models for each campus building. Finally, conclusions and future works are presented in Section 5.
2. Deep RNN Algorithms for Peak Electricity Consumption Prediction
2.1. Features Considered in This Study
In this subsection, we describe the input features and output value used when training and testing deep RNNs-based prediction models. The input features comprise weather, calendar, and trend information. The weather information includes five elements such as temperature (), humidity (%), radiation (), cloudiness (Number), and wind speed ( since those help to capture the impact of the change in peak electricity consumption. As the electricity consumption of campus buildings is related to the special characteristics such as seasonality (Number), rest day (Number), and vacation (Number), we consider these elements as input features. Finally, we consider electricity consumptions (kW) observed before the peak time, since these consumptions are directly associated with the trends of expected peak electricity consumption (kW).
The output value is the peak electricity consumption, which indicates the sequence values observed in hourly increments for a peak time on a day. We remark that the prediction models predict the expected peak electricity consumption in hourly increments for a peak time on a day only considering the input features observed before peak time.
In detail, Table 1 displays and defines the input features and output value observed at time on day as follows. The temperature, humidity, radiation, cloudiness, seasonality, rest day, vacation, and electricity consumption are defined as , , , , , , , and , respectively. These elements collectively form an input vector, denoted as , represented as , , , , , , , . The output value at a time (where ) on day is the electricity consumption, defined as .

Table 1.
The input features and output value observed at time t on day d.
We utilize input features captured from to the previous peak time on day to forecast each peak electricity consumption from the starting peak time to the end peak time on day . Therefore, when a prediction model attempts to predict each peak electricity consumption at time , the input features used and the peak electricity consumption are denoted as , , and , , respectively.
2.2. Peak Electricity Consumption Prediction Models Based on Deep RNN
The six different deep RNNs-based prediction models considered in this study are introduced in this subsection, respectively. First, we describe the LSTM-based peak electricity consumption prediction model. LSTM has been utilized in various domains such as natural language process (NLP) [37], photovoltaic power prediction [38], and visual recognition [39]. The advantage of LSTM structure is its ability to address the long-term dependencies through the use of gate functions and overcome the vanishing gradient problem [40].
Figure 1 illustrates the structure of the LSTM cell for the proposed LSTM-based peak electricity consumption prediction model [38], which consists of three components: a forget gate denoted as , an input gate, and an output gate denoted as , and an output gate denoted as . These gates control how much the short-term- and long-term states observed in previous and current times are memorized. To calculate the long-term state at time on day , denoted as , we define a candidate long-term state as . The previous long-term state, denoted as , interacts with the previous short-term state, denoted as , and to calculate both and .
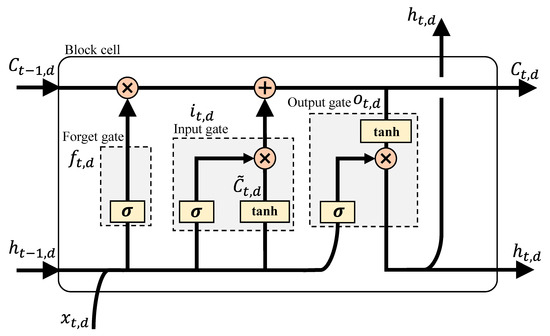
Figure 1.
Cell structure of LSTM-based peak electricity consumption prediction model.
The detailed formulations for the LSTM cell at time on day are defined as Equations (1)–(6).
where , , and are the weight values and , , and are bias parameters of the LSTM cell, which are necessary to be trained through back-propagation. To calculate the output for each gate, we utilize sigmoid function, denoted as . We also employ hyperbolic tangent function, denoted as to calculate internal state and short-term state indicates the element-wise multiplication.
Figure 2 illustrates the architecture of the BiLSTM-based prediction model. Although the structure of BiLSTM is very similar to LSTM structure, it can more carefully consider both the past and future states for a specific time through forward and backward short-term states [41], denoted as and , respectively. controls the degree to which sequential trends memorize between given inputs and outputs, while captures the complex time-series relationships of the past from future sequential patterns. This structure helps to enhance prediction performance by learning periodic dependencies between the input and output values.
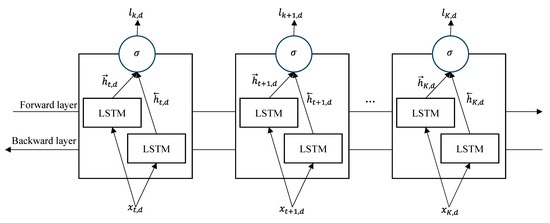
Figure 2.
Architecture of Blest-based peak electricity consumption prediction model.
Next, we introduce the peak electricity consumption prediction models based on the CNN-LSTM and CNN-BiLSTM, respectively. These algorithms were well known for their impressive performance in energy prediction problems [42,43]. Figure 3 illustrates the architecture of the CNN-LSTM-based prediction model, which comprises multiple one-dimension convolutional neural networks (1D-CNNs) and LSTMs. The architecture of CNN-BiLSTM is identical to CNN-LSTM, with the only difference being the incorporation of BiLSTM. Accordingly, we only describe the structure of the CNN-LSTM-based prediction model.
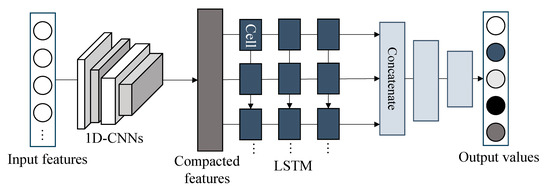
Figure 3.
Architecture of BiLSTM-based peak electricity consumption prediction model.
1D-CNNs are designed with two 1D convolutional layers, each having a specific kernel size. Additionally, a max pooling layer is employed with a particular pixel window and strides after each 1D-CNN. Initially, 1D-CNNs uses , , to extract compacted features representing complex irregular trends of electricity consumption. These compacted features are then used as input values for each LSTM and subsequently passed to fully connected neural networks for predicting , . This implies that the output layer of the fully connected neural network has nodes, with each node’s value representing an hourly peak electricity consumption.
Finally, we describe the attention approach applied for the proposed CNN-LSTM and CNN-BiLSTM prediction models. This approach helps to capture long sequential input features by utilizing the context vector, which controls the importance level of the input states. In this study, we utilize the Luong attention approach [44], which quickly computes the hidden state vector compared to the Bahdanau attention approach [45] by employing local attention. The Luong attention approach utilizes global and local attention phases. During the global attention phase, the context vector is employed to calculate the importance level of each input feature. The context vector aims to capture effectively improved states to accurately predicting by calculating the weighted average over all the source states [40]. The goal of local attention is to understand the importance level of relevant states within a particular window size. This approach offers the advantage of avoiding the computationally expensive nature of soft attention, as suggested in [46], and is easier to learn compared to the hard attention approach.
3. Experiment Settings
3.1. Dataset
The datasets, including the hourly recorded weather information and electricity consumption for each building, were collected in Incheon City, South Korea, from 1 December 2019 to 31 July 2021, resulting in a total of 39,240 instances. For the training of the proposed models, we selected 24,192 instances, while the remaining instances were employed as test instances. We note that the proposed models exclusively utilize input features captured between 06:00 to 09:00 to predict the expected peak electricity consumption between 10:00 to 15:00. Therefore, we extracted the input and output values observed between 06:00 to 15:00 from both the training and test instances to train the proposed models and evaluate their performance.
Table 2 presents the descriptive statistics of electricity consumption for each building. There are three different types of buildings: office, nature science, and general education. The nature science building exhibits lower peak and off-peak electricity consumption compared to the others. Conversely, the peak electricity consumption and its standard deviation in the general education building are higher than in the other buildings. This could be attributed to the higher variability in the number of visitors to the general education building, as well as the larger overall visitor count in comparison to the other buildings. In addition, the fluctuations of the peak electricity consumption for the general education building are high compared to the other buildings.

Table 2.
Descriptive statistics of electricity consumption for each building.
Furthermore, we perform a standard uncertainty analysis, as suggested in [43], on the variables representing weather conditions to describe the difference between seasons. Table 3 displays the standard uncertainty levels for each variable across the four seasons. Humidity and cloudiness are measured on scales of 0–100 and 0–10, respectively, with higher values indicating increased wetness and cloudiness. The results describe that the standard uncertainty level for the variables considered in this study is similar, while the uncertainty levels of temperature and radiation variables are higher in spring and autumn compared to other seasons.

Table 3.
Standard uncertainty level of each variable according to each season.
3.2. Measure Metrics
To analyze the effectiveness of the proposed models for each building, three well-known metrics such as mean absolute error (MAE), root mean square error (RMSE), and coefficient of variance (CV) are adopted and denoted as follows:
where and are the predicted peak electricity consumption at time on day and the mean of the actual peak electricity consumption, respectively. is the total number of observations.
3.3. Training Details
Discovering adequate hyper-parameters of deep RNNs is crucial to obtain high performance for peak electricity consumption. Yet, due to a large search space, it is difficult to decide proper hyper-parameters. Hence, we perform a random search [47] to select best hyper-parameters of all the proposed models, as illustrated in Figure 4.

Figure 4.
The progress of training by selecting best hyper-parameters for each model.
Based on the random search, the hyper-parameters for each prediction model are determined as follows. All prediction models consist of three recurrent layers, each of which has 128, 64, and 32 nodes, along with five fully connected layers consisting of 512, 256, 128, 64, and 32 nodes, respectively. In the case of 1D-CNNs, a kernel size is set to be , and two strides were used in a max pooling layer. Rectified linear units [48] serve as activation function in all layers of all the proposed models. The batch size is set to one to consider time-series properties of input features [49], and we utilized Adam optimizer for training the models. Moreover, we set early stopping epoch to 30 to resolve overfitting problem. At the beginning of training all models, weights were randomly initialized within the range of zero to one.
4. Experiment Results
The performance comparisons between the applied models are carried out in terms of MAE, RMSE, and CV for each building, as presented in Table 4. Furthermore, to demonstrate deep RNN algorithms, we implemented XGBoost, which is a tree-based algorithm and well known to be an effective energy prediction [50]. Bold values imply the best performance which can minimize prediction errors among the considered models.

Table 4.
Comparison results for the proposed models across each campus building.
It is observed that the prediction performance of any single model is not dominant. The results imply the accurate model selection is essential to improve prediction accuracy and manage an efficient energy system for each campus building. Moreover, the proposed models outperform XGB for all buildings, which imply neural networks that can observe sequence trends and improve peak electricity consumption performance.
When fluctuation of electricity consumption is high, the performances of CNN-LSTM and CNN-BiLSTM are better than LSTM and BiLSTM. This means that the CNN helps to capture the high changes in electricity consumption. The prediction performances of CNN-BiLSTM-A tend to be more effective compared to the other models. The results might need to be associated with the fact that BiLSTM and the attention approach contribute to precisely observing sequential patterns between input and output values.
To analyze the performance of the proposed models with respect to different seasons, which exhibit varying trends in electricity consumption, we investigate the RMSE obtained from these models for each building, as shown in Figure 5a–d. Moreover, Figure 6a–c visualize the details of the actual and predicted peak electricity consumption, respectively, of each model across all seasons. The RMSE deviation for all models is notably high when attempting to estimate peak electricity consumption for three campus buildings during spring and autumn, as weather conditions during these seasons exhibit a high level of uncertainty, as shown in Table 3.
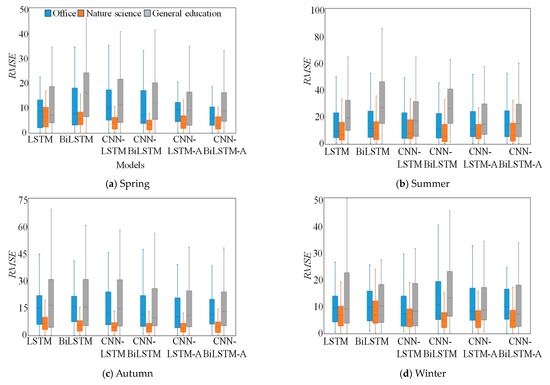
Figure 5.
RMSE observed from the proposed models according to seasons for each building.
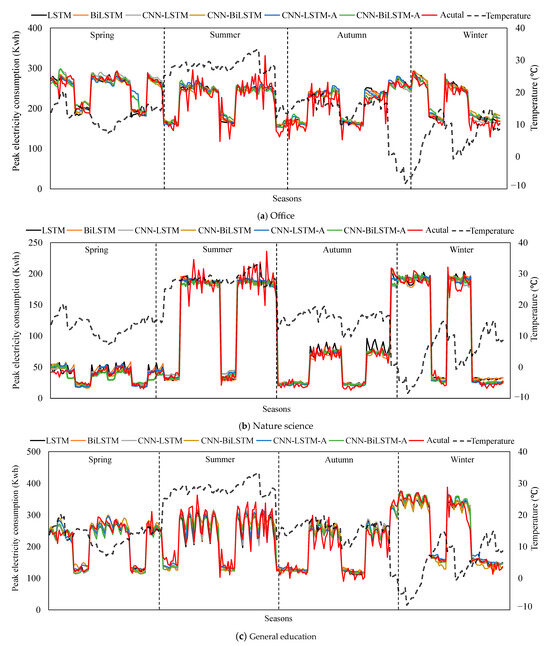
Figure 6.
Visualization of the actual and predicted peak electricity consumption of each model across all seasons in three buildings.
These results suggest that CNN-BiLSTM-A outperforms the other models for office and general education buildings regardless of seasons. These results are related to the fact that the attention approach helps to capture the relevant sequential patterns between inputs and outputs. In contrast, LSTM and BiLSTM show relatively high RMSE compared to the other models. This is due to their simple neural network architecture, which may be less effective for predicting peak electricity consumption. Furthermore, from Figure 5b and Figure 6b, we observe that the prediction deviation of all models is relatively high for the nature science building in summer. This reveals that the performance of all models is ineffective in predicting peak electricity consumption. This inefficiency is attributed to the significant differences between electricity consumption during peak times and before peak times, as well as the high fluctuations in hourly electricity consumption. Nevertheless, CNN-BiLSTM-A consistently exhibits better prediction performance compared to the models. Hence, CNN-BiLSTM-A proves valuable in managing energy systems by accurately predicting peak electricity consumption of campus buildings in the real world.
Finally, we conduct a sensitivity analysis to investigate how changes in peak electricity consumption are influenced by variations in the number of training instances and hyper-parameters since these factors impact the training performance of deep RNN approaches. Table 5 displays the MAE and RMSE of each model according to the number of training instances and loss function. It is evident that the performance of the proposed models tends to improve when large training instances are used during training except for CNN-LSTM-A. The LSTM, BiLSTM, CNN-LSTM, and CNN-BiLSTM models show greater efficiency when utilizing MAE as the loss function than when using MSE. In contrast, CNN-LSTM-A and CNN-BiLSTM-A reduce prediction errors when using MSE rather than MAE. It implies that appropriate hyper-parameter settings can significantly impact prediction performance depending on a specific algorithm. Additionally, the results indicate the importance of selecting the number of training instances when developing deep RNN-based electricity prediction models. Therefore, the operator of the campus building successfully enhances energy systems by developing the electricity consumption prediction model for each building through suitable hyper-parameter settings suggested in Table 5.

Table 5.
The results of the proposed models according to different number of training instances and loss functions.
5. Conclusions
In this study, we implemented six deep RNN approaches-based peak electricity prediction models for peak electricity consumption to identify the most suitable approach across each campus building. These models are trained by using input features consisting of season, calendar, and trend factors, observed before peak electricity consumption time to estimate peak electricity consumption. To determine the most suitable model for peak electricity consumption for each campus building, we perform a comparative analysis in terms of overall and seasonal performances. Theoretical implications from the experiment results demonstrate that the prediction ability between the approaches is different according to the characteristics of a building and trends of electricity consumption. Compared to the previous study [30], our results demonstrate that a suitable model selection is able to significantly support sophisticated management of campus buildings for each building operator.
Moreover, the findings from Figure 5 and Figure 6 suggest that the attention method enhances peak electricity consumption across seasons by effectively capturing seasonal consumption trends. This finding provides managerial implications since an accurate peak electricity consumption can significantly support sophisticated management of campus buildings for each building operator. The sensitive analysis results in Table 5 indicate that the performance of deep RNN algorithms tends to underperform when the number of training instances is lower and varies depending on the number of training instances and hyper-parameters. This implies that sensitive analysis is crucial for improving prediction performance, especially when the training instances are limited in real-world scenarios.
However, this research has some limitations. The dataset used in this study includes electricity consumption records during the COVID-19 pandemic period, which may introduce bias into the prediction results. Future studies may be needed to mitigate potential biases by collecting additional data. Furthermore, the experiment results may have limitations in managing all campus buildings in real-world environments, as they were derived from data collected from only three buildings. In future work, efforts to collect data from all campus buildings and implement new methods to enhance performance are necessary for effectively managing overall building energy systems in real-world environments.
Author Contributions
Conceptualization, D.L. and K.K.; methodology, D.L., J.K. and S.K.; software and validation, J.K. and S.K.; formal analysis and investigation, D.L., J.K. and S.K.; data curation, D.L., J.K. and S.K.; writing—original draft preparation, D.L. and K.K.; writing—review and editing, D.L. and K.K.; project administration and funding acquisition, D.L. and K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Global Post-Doc Fellowship Program (2023) in the Incheon National University.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chung, M.H.; Rhee, E.K. Potential Opportunities for Energy Conservation in Existing Buildings on University Campus: A Field Survey in Korea. Energy Build. 2014, 78, 176–182. [Google Scholar] [CrossRef]
- Alshuwaikhat, H.M.; Abubakar, I. An Integrated Approach to Achieving Campus Sustainability: Assessment of the Current Campus Environmental Management Practices. J. Clean. Prod. 2008, 16, 1777–1785. [Google Scholar] [CrossRef]
- Koester, R.J.; Eflin, J.; Vann, J. Greening of the Campus: A Whole-Systems Approach. J. Clean. Prod. 2006, 14, 769–779. [Google Scholar] [CrossRef]
- U.S. Department of Energy Buildings. Energy Databook. Energy Efficiency & Renewable Energy. 2012. Available online: https://ieer.org/wp/wp-content/uploads/2012/03/DOE-2011-Buildings-Energy-DataBook-BEDB.pdf (accessed on 5 December 2023).
- Liu, C.-L.; Tseng, C.-J.; Huang, T.-H.; Yang, J.-S.; Huang, K.-B. A Multi-Task Learning Model for Building Electrical Load Prediction. Energy Build. 2023, 278, 112601. [Google Scholar] [CrossRef]
- Walter, T.; Price, P.N.; Sohn, M.D. Uncertainty Estimation Improves Energy Measurement and Verification Procedures. Appl. Energy. 2014, 130, 230–236. [Google Scholar] [CrossRef]
- Yang, J.; Santamouris, M.; Lee, S.E.; Deb, C. Energy Performance Model Development and Occupancy Number Identification of Institutional Buildings. Energy Build. 2016, 123, 192–204. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A Review and Analysis of Regression and Machine Learning Models on Commercial Building Electricity Load Forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep Learning for Estimating Building Energy Consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural Networks for Short-Term Load Forecasting: A Review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Huang, S.J.; Shih, K.R. Short-Term Load Forecasting via ARMA Model Identification Including Non-Gaussian Process Considerations. IEEE Trans. Power Syst. 2003, 18, 673–679. [Google Scholar] [CrossRef]
- Sudheer, G.; Suseelatha, A. Short Term Load Forecasting Using Wavelet Transform Combined with Holt-Winters and Weighted Nearest Neighbor Models. Int. J. Electr. Power Energy Syst. 2015, 64, 340–346. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying Support Vector Machines to Predict Building Energy Consumption in Tropical Region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Fan, C.; Xiao, F.; Wang, S. Development of Prediction Models for Next-Day Building Energy Consumption and Peak Power Demand Using Data Mining Techniques. Appl. Energy 2014, 127, 1–10. [Google Scholar] [CrossRef]
- Zhang, R.; Dong, Z.Y.; Xu, Y.; Meng, K.; Wong, K.P. Short-Term Load Forecasting of Australian National Electricity Market by an Ensemble Model of Extreme Learning Machine. IET Gener. Transm. Distrib. 2013, 7, 391–397. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial Neural Network Model for Forecasting Sub-Hourly Electricity Usage in Commercial Buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Yazici, I.; Beyca, O.F.; Delen, D. Deep-Learning-Based Short-Term Electricity Load Forecasting: A Real Case Application. Eng. Appl. Artif. Intell. 2022, 109, 104645. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, Y.; Chen, H.; Wang, J.; Guo, Y.; Ahmad, T. A Novel Energy Demand Prediction Strategy for Residential Buildings Based on Ensemble Learning. Proc. Energy Procedia 2019, 158, 3411–3416. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Srinivasan, R.S. A Novel Ensemble Learning Approach to Support Building Energy Use Prediction. Energy Build. 2018, 159, 109–122. [Google Scholar] [CrossRef]
- Liu, X.; Ding, Y.; Tang, H.; Fan, L.; Lv, J. Investigating the Effects of Key Drivers on Energy Consumption of Nonresidential Buildings: A Data-Driven Approach Integrating Regularization and Quantile Regression. Energy 2022, 244, 122720. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, Y.; Chang, D.; Xie, J.; Ma, Z.; Sun, Q.; Yin, H.; Wennersten, R. Prediction of Short-Term PV Power Output and Uncertainty Analysis. Appl. Energy 2018, 228, 700–711. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting Electricity Consumption for Commercial and Residential Buildings Using Deep Recurrent Neural Networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, N.; Chen, X. A Short-Term Residential Load Forecasting Model Based on Lstm Recurrent Neural Network Considering Weather Features. Energies 2021, 14, 2737. [Google Scholar] [CrossRef]
- Gul, M.J.; Urfa, G.M.; Paul, A.; Moon, J.; Rho, S.; Hwang, E. Mid-Term Electricity Load Prediction Using CNN and Bi-LSTM. J. Supercomput. 2021, 77, 10942–10958. [Google Scholar] [CrossRef]
- Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef]
- Tang, X.; Chen, H.; Xiang, W.; Yang, J.; Zou, M. Short-Term Load Forecasting Using Channel and Temporal Attention Based Temporal Convolutional Network. Electr. Power Syst. Res. 2022, 205, 107761. [Google Scholar] [CrossRef]
- Lin, J.; Ma, J.; Zhu, J.; Cui, Y. Short-Term Load Forecasting Based on LSTM Networks Considering Attention Mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107818. [Google Scholar] [CrossRef]
- Wu, K.; Wu, J.; Feng, L.; Yang, B.; Liang, R.; Yang, S.; Zhao, R. An Attention-Based CNN-LSTM-BiLSTM Model for Short-Term Electric Load Forecasting in Integrated Energy System. Int. Trans. Electr. Energy Syst. 2021, 31, e12637. [Google Scholar] [CrossRef]
- Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust Short-Term Electrical Load Forecasting Framework for Commercial Buildings Using Deep Recurrent Neural Networks. Appl. Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
- Li, A.; Xiao, F.; Zhang, C.; Fan, C. Attention-Based Interpretable Neural Network for Building Cooling Load Prediction. Appl. Energy 2021, 299, 117238. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y. Interpretable Deep Learning Model for Building Energy Consumption Prediction Based on Attention Mechanism. Energy Build. 2021, 252, 111379. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, W.; Hu, T.; Xu, X. Evolutionary Double Attention-Based Long Short-Term Memory Model for Building Energy Prediction: Case Study of a Green Building. Appl. Energy 2021, 288, 116660. [Google Scholar] [CrossRef]
- Jin, X.B.; Zheng, W.Z.; Kong, J.L.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Lin, S. Deep-Learning Forecasting Method for Electric Power Load via Attention-Based Encoder-Decoder with Bayesian Optimization. Energies 2021, 14, 1596. [Google Scholar] [CrossRef]
- Menezes, A.C.; Cripps, A.; Buswell, R.A.; Wright, J.; Bouchlaghem, D. Estimating the Energy Consumption and Power Demand of Small Power Equipment in Office Buildings. Energy Build. 2014, 75, 199–209. [Google Scholar] [CrossRef]
- Brännlund, R.; Vesterberg, M. Peak and Off-Peak Demand for Electricity: Is There a Potential for Load Shifting? Energy Econ. 2021, 102, 105466. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Networks Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Kim, K. PV Power Prediction in a Peak Zone Using Recurrent Neural Networks in the Absence of Future Meteorological Information. Renew. Energy 2021, 173, 1098–1110. [Google Scholar] [CrossRef]
- Donahue, J.; Hendricks, L.A.; Rohrbach, M.; Venugopalan, S.; Guadarrama, S.; Saenko, K.; Darrell, T. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2016; pp. 2625–2634. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Beil, J.; Perner, G.; Asfour, T. Speech Recognition With Deep Recurrent Neural Networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting Residential Energy Consumption Using CNN-LSTM Neural Networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Ullah, F.U.M.; Ullah, A.; Haq, I.U.; Rho, S.; Baik, S.W. Short-Term Prediction of Residential Power Energy Consumption via CNN and Multi-Layer Bi-Directional LSTM Networks. IEEE Access 2019, 8, 123369–123380. [Google Scholar] [CrossRef]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-Based Neural Machine Translation. In Proceedings of the Conference Proceedings-EMNLP 2015: Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.H.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015-Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Xu, K.; Ba, J.L.; Kiros, R.; Cho, K.; Courville, A.; Salakhutdinov, R.; Zemel, R.S.; Bengio, Y. Show, Attend and Tell: Neural Image Caption Generation with Visual Attention. In Proceedings of the 32nd International Conference on Machine Learning, ICML 2015, Lille, France, 6–11 July 2015; pp. 2048–2057. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. 2012, 25, 1–9. [Google Scholar] [CrossRef]
- Li, M.; Zhang, T.; Chen, Y.; Smola, A.J. Efficient Mini-Batch Training for Stochastic Optimization. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 661–670. [Google Scholar] [CrossRef]
- Carrera, B.; Kim, K. Comparison Analysis of Machine Learning Techniques for Photovoltaic Prediction Using Weather Sensor Data. Sensors 2020, 20, 3129. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).