Passive Mixing and Convective Heat Transfer Enhancement for Nanofluid Flow across Corrugated Base Microchannels
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
- The introduction of a novel, interacting microchannel model which generates rotating vortices.
- The generation of vortices across an optimized cross-section and the addition of a novel diverging–converging base corrugation model to promote passive fluid mixing combined with continuous flow disruption.
- The comparison of the results of a nanofluid model proposed by Rea et al. with the KKL model to determine the validity of Rea et al.’s model for geometries compared the one proposed under the study.
2. Materials and Methods
2.1. Methodology
2.2. Assumptions
- Fluid incompressibility in a three-dimensional domain.
- Steady-state heat transfer.
- Negligible radiation heat transfer and viscous heating.
- No slip conditions at the wall.
- No effect of channel surface roughness.
- No effects of natural convection.
2.3. Governing Equations
2.4. Numerical Methods
- Inlet: Tin = 298.15 K and w = win, u = 0, v = 0.
- Outlet: p = 1 atm.
- Solid Liquid Interface: Ts = , ; u = 0, v = 0, w = 0.
- Bottom wall: Dirichlet boundary condition, T boundary [16].
- Other wall surfaces: .
2.5. Parametric Relations
3. Results and Discussion
3.1. Grid Independence
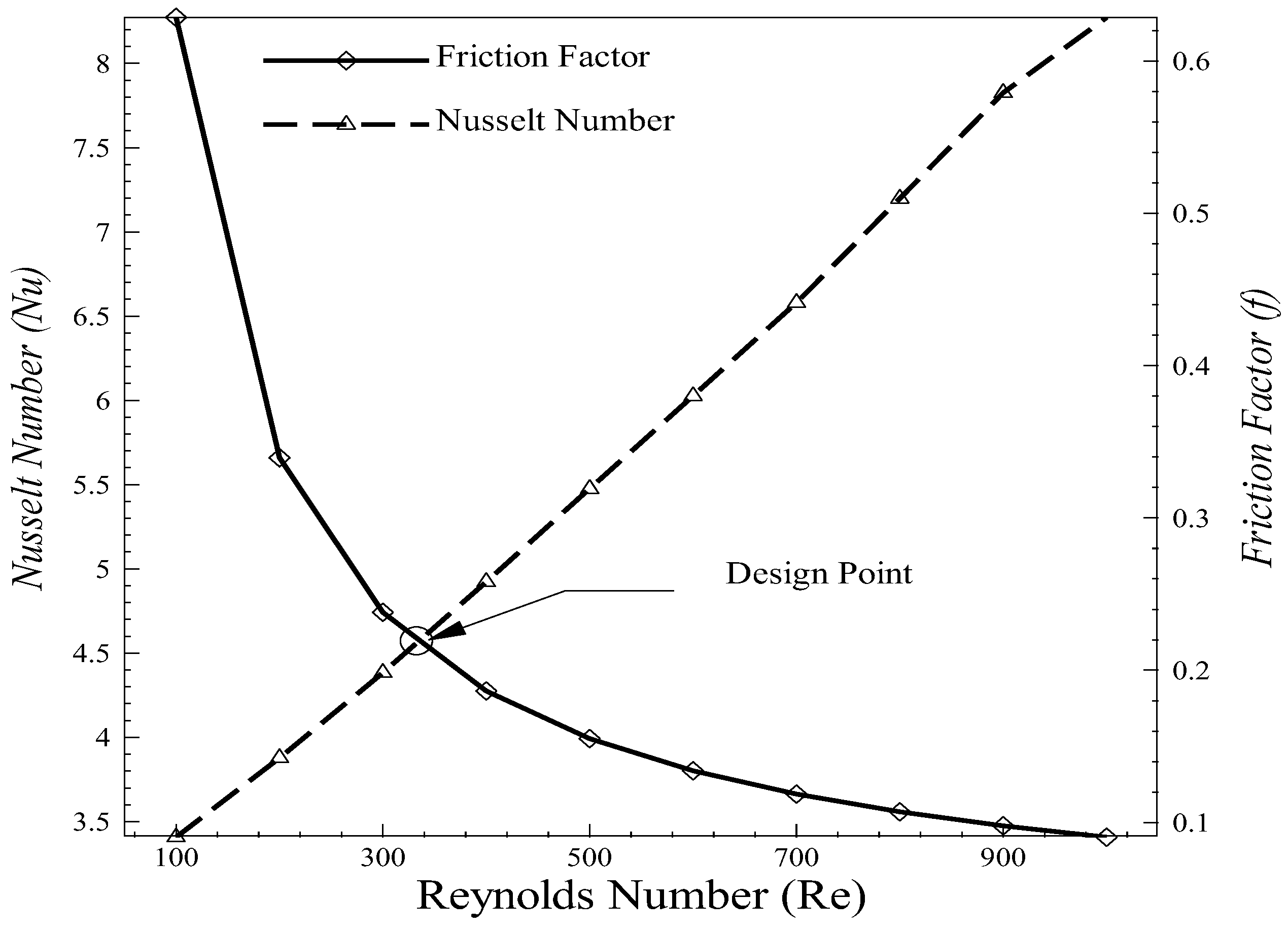
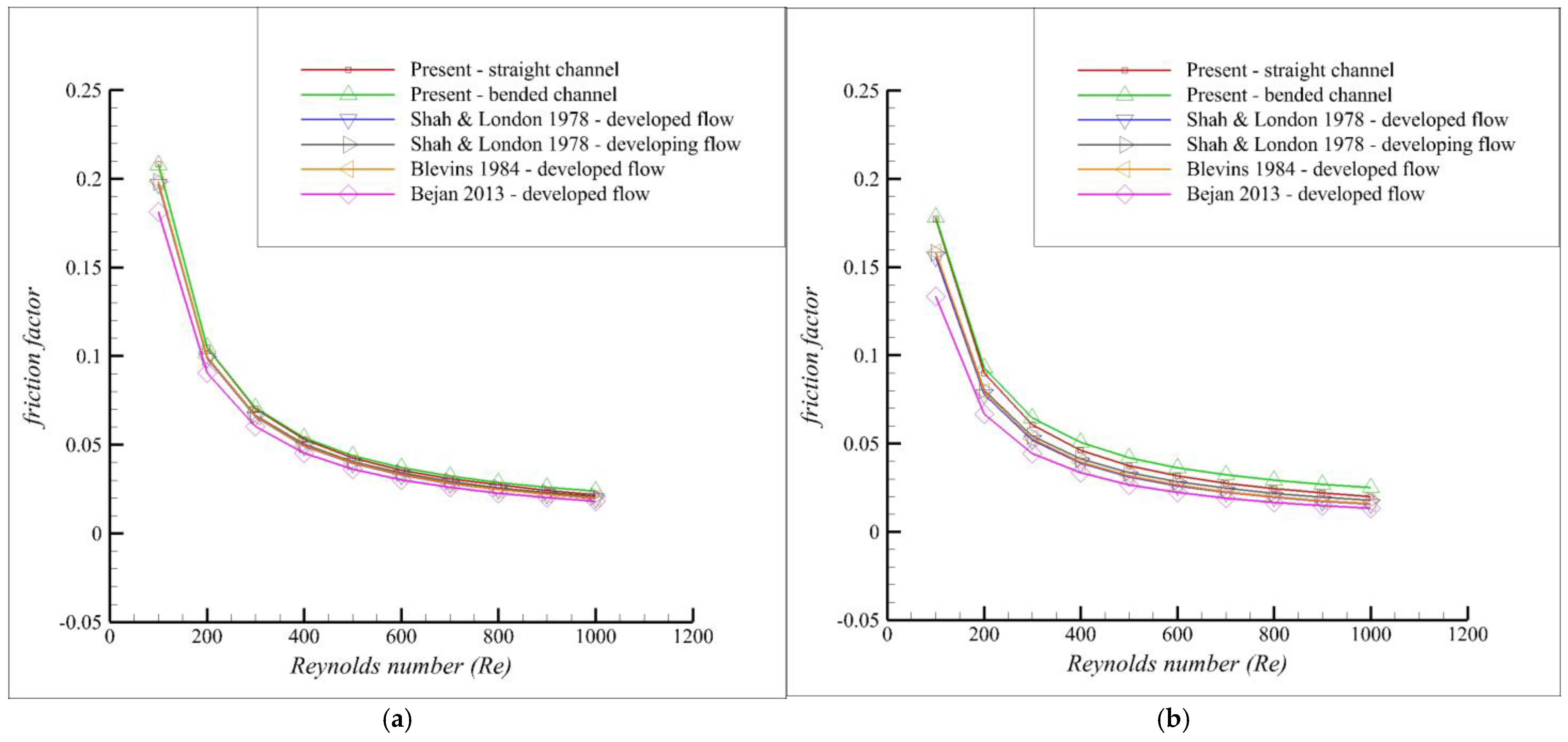
3.2. Validation
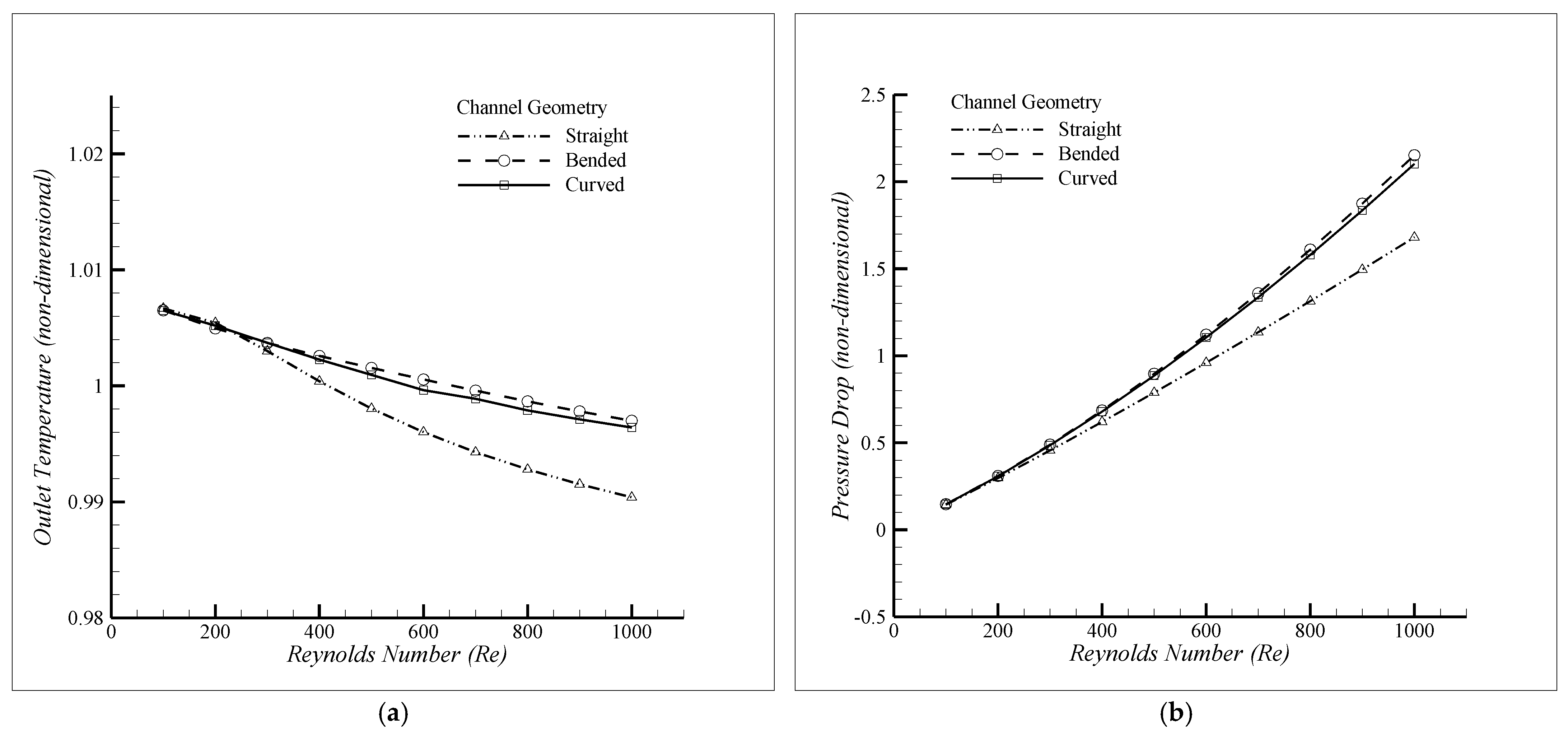
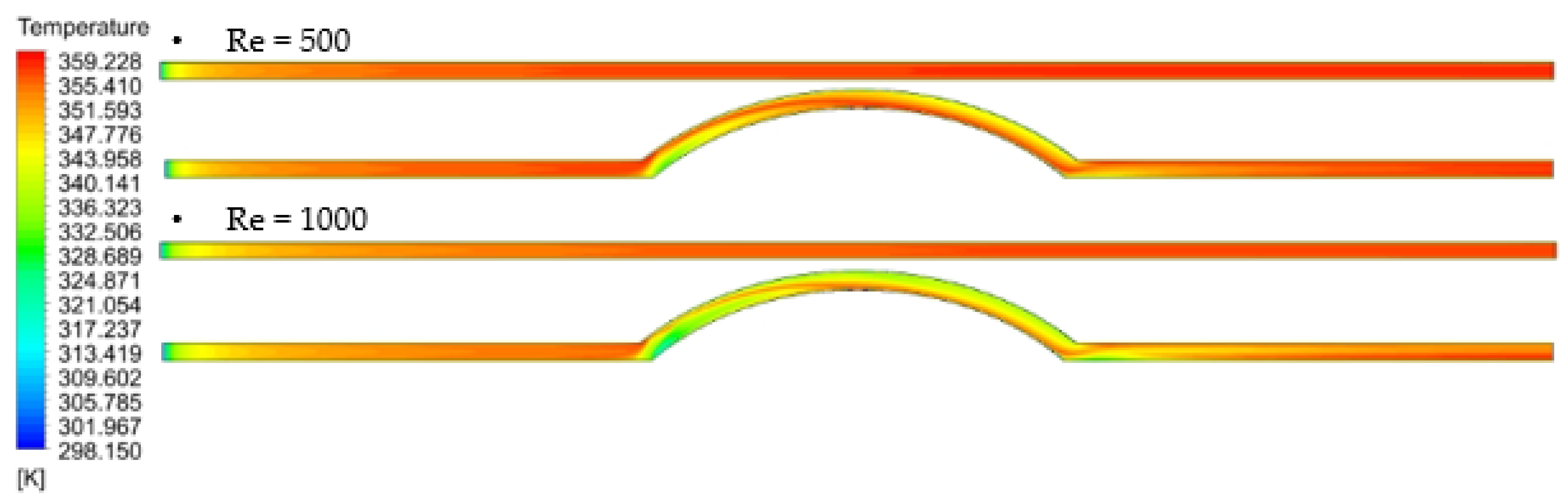
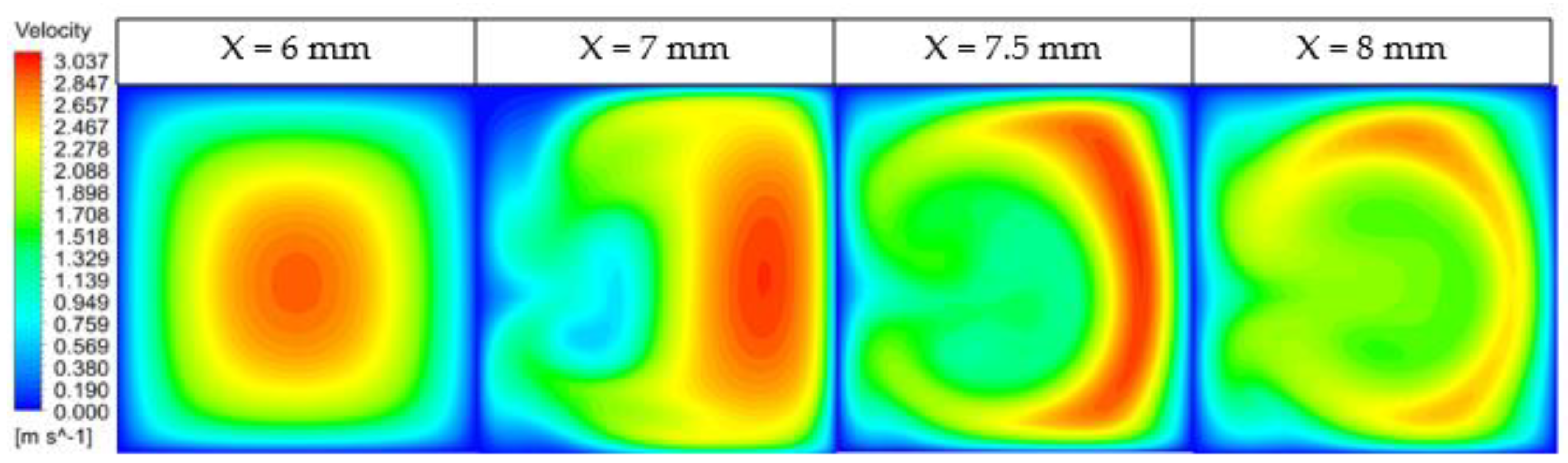
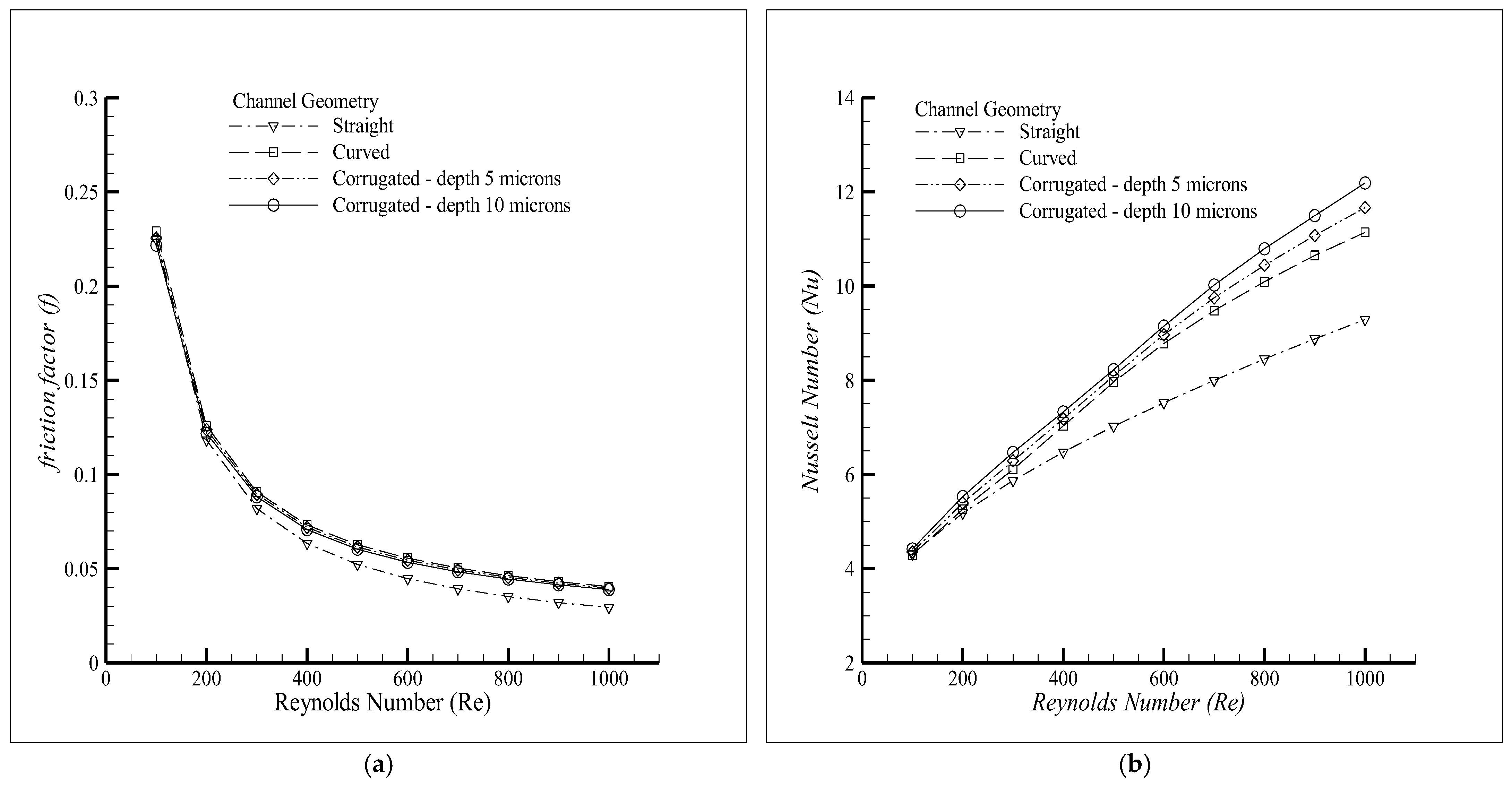
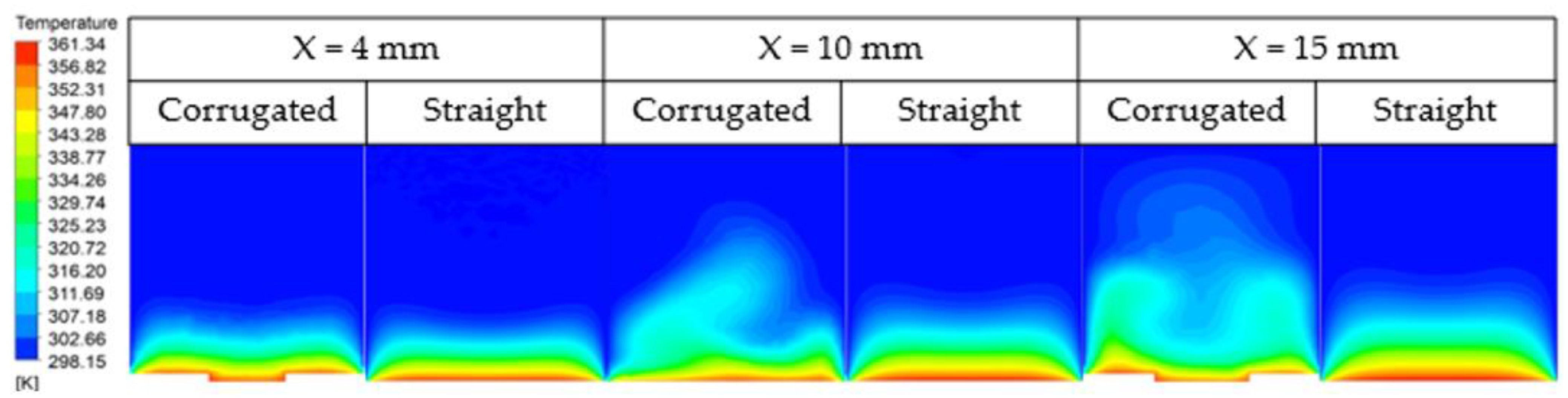
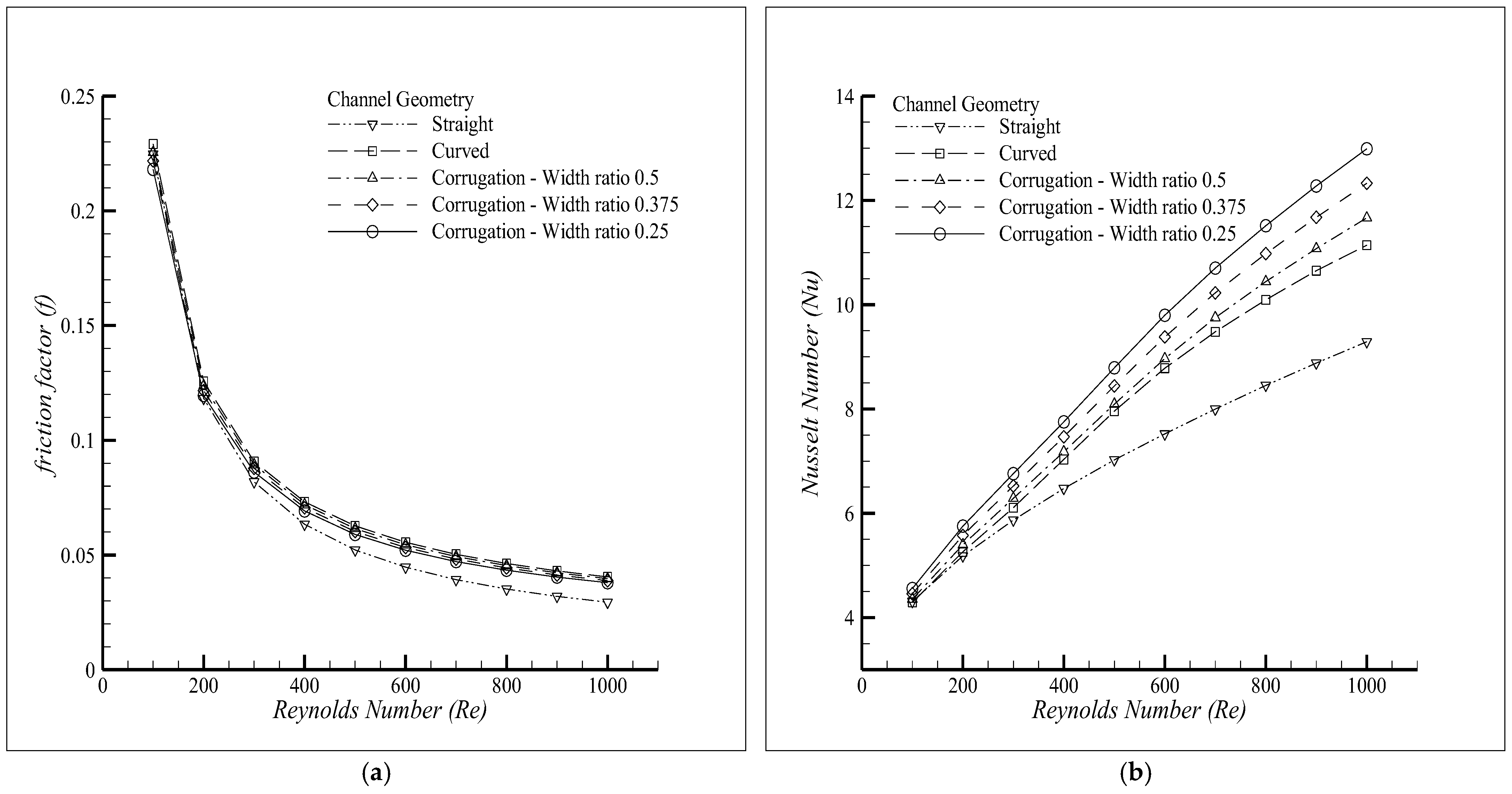
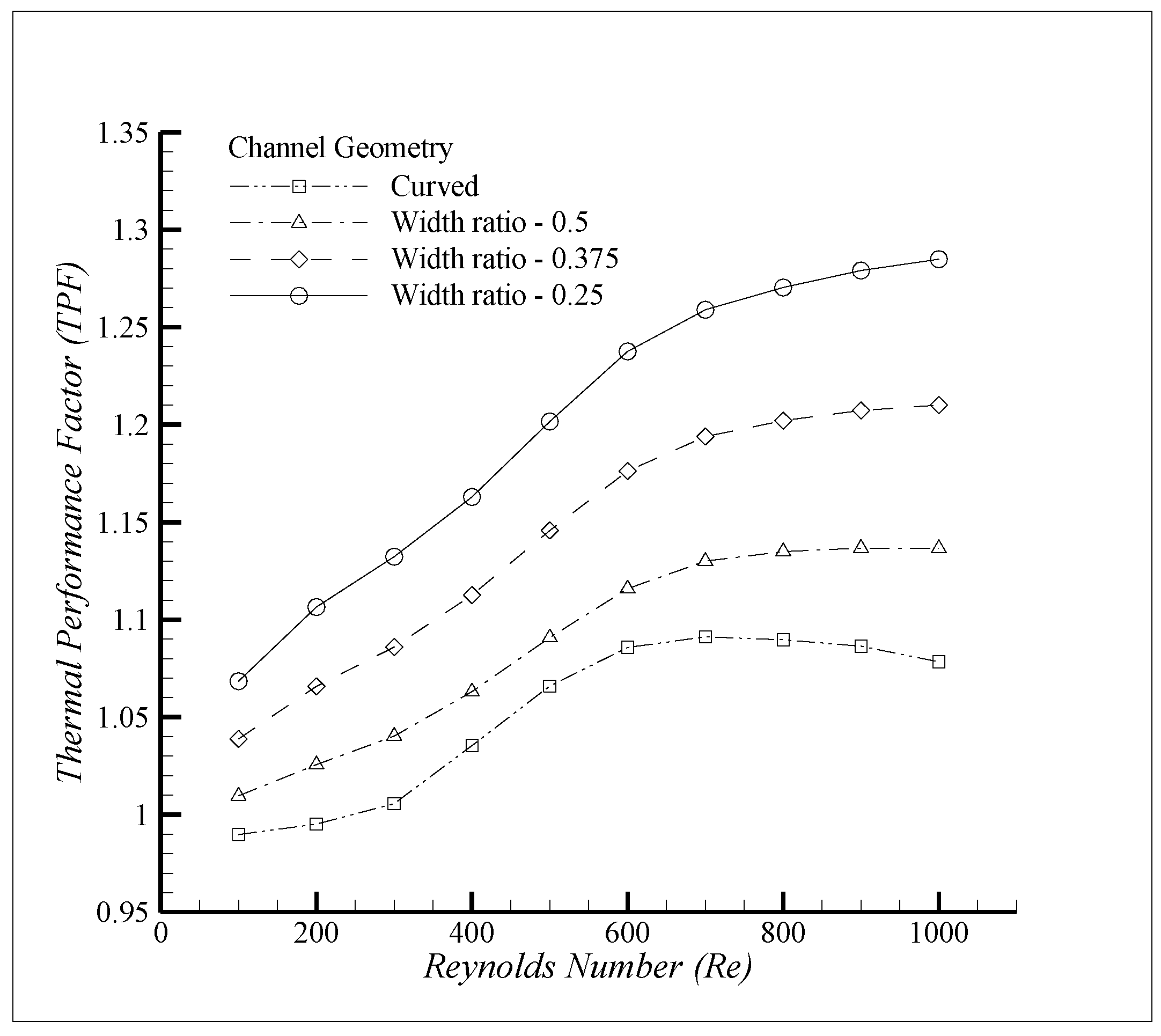
3.3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Re | Reynolds number |
| Nu | Nusselt number |
| T | Temperature |
| FVM | Finite Volume Method |
| microns | Micrometer |
| Cp | Specific heat (J/kg.k) |
| k | Thermal conductivity (W/m.k) |
| ff | Friction factor |
| K | Kelvin |
| Subscript | |
| s | Solid |
| f | Fluid |
| np | Nanoparticle |
| nf | Nanofluid |
| bf | Base fluid |
| al | Aluminum |
| Greek Symbols | |
| ρ | Density (kg/m3) |
| φ | Volume fraction |
References
- Yan, Y.; Xue, Z.; Xu, F.; Li, L.; Shen, K.; Li, J.; Yang, Z.; He, Z. Numerical investigation on thermal-hydraulic characteristics of the micro heat sink with gradient distribution pin fin arrays and narrow slots. Appl. Therm. Eng. 2022, 202, 117836. [Google Scholar] [CrossRef]
- Duan, Z.; Xie, G.; Yu, B.; Jin, P. Multi-objective topology optimization and thermal performance of liquid-cooled microchannel heat sinks with pin fins. Case Stud. Therm. Eng. 2023, 49, 103178. [Google Scholar] [CrossRef]
- Xiang, X.; Yang, J.; Fan, A.; Liu, W. A comparison between cooling performances of water-based and gallium-based micro-channel heat sinks with the same dimensions. Appl. Therm. Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Khalaj, A.H.; Halgamuge, S.K. A Review on efficient thermal management of air- and liquid-cooled data centers: From chip to the cooling system. Appl. Energy 2017, 205, 1165–1188. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of single-phase and two-phase nanofluid heat transfer in macro-channels and micro-channels. Int. J. Heat Mass Transf. 2019, 136, 324–354. [Google Scholar] [CrossRef]
- Emam, M.; Ahmed, M. Cooling concentrator photovoltaic systems using various configurations of phase-change material heat sinks. Energy Convers. Manag. 2018, 158, 298–314. [Google Scholar] [CrossRef]
- Avci, M.; Yazici, M.Y. An experimental study on effect of inclination angle on the performance of a PCM-based flat-type heat sink. Appl. Therm. Eng. 2018, 131, 806–814. [Google Scholar] [CrossRef]
- Xue, Z.; Yan, Y.; Shen, K.; He, Z.; You, J.; Zhang, C. Thermal performance enhancement of a micro-jet heat sink via parametric investigated micro pin fin arrays. Int. J. Therm. Sci. 2024, 196, 108717. [Google Scholar] [CrossRef]
- Kalkan, O. Multi-objective optimization of a liquid metal cooled heat sink for electronic cooling applications. Int. J. Therm. Sci. 2023, 190, 108325. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, P.K. Effects of flow inlet angle on flow maldistribution and thermal performance of water cooled mini-channel heat sink. Int. J. Therm. Sci. 2019, 138, 504–511. [Google Scholar] [CrossRef]
- Li, J.; Yang, L. Recent Development of Heat Sink and Related Design Methods. Energies 2023, 16, 7133. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Lei, L.; Cheng, C.; Xu, J.; Zhou, N. Experimental Study on Heat Transfer Characteristics of Two-Phase Flow in Square and Rectangular Channels. Energies 2022, 15, 8453. [Google Scholar] [CrossRef]
- Khan, M.Z.U.; Younis, M.Y.; Akram, N.; Akbar, B.; Rajput, U.A.; Bhutta, R.A.; Uddin, E.; Jamil, M.A.; Márquez, F.P.G.; Bin Zahid, F. Investigation of heat transfer in wavy and dual wavy micro-channel heat sink using alumina nanoparticles. Case Stud. Therm. Eng. 2021, 28, 101515. [Google Scholar] [CrossRef]
- Tang, K.; Lin, G.; Guo, Y.; Huang, J.; Zhang, H.; Miao, J. Simulation and optimization of thermal performance in diverging/converging manifold microchannel heat sink. Int. J. Heat Mass Transf. 2023, 200, 123495. [Google Scholar] [CrossRef]
- Nunes, J.M.; de Oliveira, J.D.; Copetti, J.B.; Gajghate, S.S.; Banerjee, U.; Mitra, S.K.; Cardoso, E.M. Thermal Performance Analysis of Micro Pin Fin Heat Sinks under Different Flow Conditions. Energies 2023, 16, 3175. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Chapter VII—Rectangular Ducts. In Laminar Flow Forced Convection in Ducts, 1st ed.; Shah, R.K., London, A.L., Eds.; Academic Press: New York, NY, USA, 1978; pp. 196–222. [Google Scholar]
- Sahar, A.M.; Özdemir, M.R.; Fayyadh, E.M.; Wissink, J.; Mahmoud, M.M.; Karayiannis, T.G. Single phase flow pressure drop and heat transfer in rectangular metallic microchannels. Appl. Therm. Eng. 2016, 93, 1324–1336. [Google Scholar] [CrossRef]
- Sun, H.; Fu, H.; Yan, L.; Ma, H.; Luan, Y.; Magagnato, F. Numerical Investigation of Flow and Heat Transfer in Rectangular Microchannels with and without Semi-Elliptical Protrusions. Energies 2022, 15, 4927. [Google Scholar] [CrossRef]
- Wan, Z.; Lin, Q.; Wang, X.; Tang, Y. Flow characteristics and heat transfer performance of half-corrugated microchannels. Appl. Therm. Eng. 2017, 123, 1140–1151. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, Y.; Wang, X.; Tang, Y. Flow boiling characteristics in microchannels with half-corrugated bottom plates. Int. J. Heat Mass Transf. 2018, 116, 557–568. [Google Scholar] [CrossRef]
- Wang, S.-L.; An, D.; Yang, Y.-R.; Zheng, S.-F.; Wang, X.-D.; Lee, D.-J. Heat transfer and flow characteristics in symmetric and parallel wavy microchannel heat sinks with porous ribs. Int. J. Therm. Sci. 2023, 185, 108080. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, T.; Hou, Q.; Song, K.; Hu, W.; Wu, X. Thermal hydraulic performance augmentation by petal-shaped ribs in a two-pass cooling channel. Case Stud. Therm. Eng. 2022, 40, 102542. [Google Scholar] [CrossRef]
- Liu, H.-L.; Fan, C.-C.; He, Y.-L.; Nobes, D.S. Heat transfer and flow characteristics in a rectangular channel with combined delta winglet inserts. Int. J. Heat Mass Transf. 2019, 134, 149–165. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, D.; Xu, F.; He, Z.; Yang, Z. Numerical study on hot spots thermal management in low pressure gradient distribution narrow microchannel embedded with pin fins. Int. J. Heat Mass Transf. 2022, 186, 122518. [Google Scholar] [CrossRef]
- Al-Asadi, M.T.; Mohammed, H.A.; Wilson, M.C.T. Heat Transfer Characteristics of Conventional Fluids and Nanofluids in Micro-Channels with Vortex Generators: A Review. Energies 2022, 15, 1245. [Google Scholar] [CrossRef]
- Ahmad, F.; Cheema, T.A.; Rehman, M.M.U.; Ilyas, M.; Park, C.W. Thermodynamic Analysis of Microchannel Heat Sink With Cylindrical Ribs and Cavities. J. Heat Transf. 2020, 142, 092503. [Google Scholar] [CrossRef]
- Ali, S.; Ahmad, F.; Akhtar, K.; Habib, N.; Aamir, M.; Giasin, K.; Vafadar, A.; Pimenov, D.Y. Numerical investigation of microchannel heat sink with trefoil shape ribs. Energies 2021, 14, 6764. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Liu, W.; Wen, F.; Zhou, X.; Wang, Z. Numerical predictions on heat transfer and flow characteristics in a straight channel with different geometric parameters wavy ribs. Appl. Therm. Eng. 2018, 140, 245–265. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rikhtegar, F.; Sabaghan, A.; Roohi, E. Heat transfer and entropy generation in a microchannel with longitudinal vortex generators using nanofluids. Energy 2016, 101, 190–201. [Google Scholar] [CrossRef]
- Memon, S.A.; Cheema, T.A.; Kim, G.M.; Park, C.W. Hydrothermal investigation of a microchannel heat sink using secondary flows in trapezoidal and parallel orientations. Energies 2020, 13, 5616. [Google Scholar] [CrossRef]
- Tiwari, R.; Andhare, R.S.; Shooshtari, A.; Ohadi, M. Development of an additive manufacturing-enabled compact manifold microchannel heat exchanger. Appl. Therm. Eng. 2019, 147, 781–788. [Google Scholar] [CrossRef]
- Tang, W.; Liu, H.; Zhu, L.; Shi, J.; Li, Z.; Xiang, N.; Yang, J. Fabrication of different microchannels by adjusting the extrusion parameters for sacrificial molds. Micromachines 2019, 10, 544. [Google Scholar] [CrossRef] [PubMed]
- Ashman, S.; Kandlikar, S.G. A review of manufacturing processes for microchannel heat exchanger fabrication. In Proceedings of the ASME 4th International Conference on Nanochannels, Microchannels, and Minichannels, Limerick, Ireland, 19–21 June 2006; pp. 855–860. [Google Scholar]
- Shang, X.-S.; Li, Q.-W.; Cao, Q.; Li, Z.-R.; Shao, W.; Cui, Z. Mathematical modeling and multi-objective optimization on the rectangular micro-channel heat sink. Int. J. Therm. Sci. 2023, 184, 107926. [Google Scholar] [CrossRef]
- Azodinia, M.; Mudabbir, M.; Karimipour, A. Numerical investigation of two-phase Al2O3 nanofluid in a microchannel equipped with bump through slip flow. Eng. Anal. Bound. Elem. 2023, 155, 1028–1034. [Google Scholar] [CrossRef]
- Zeng, X.; Yu, H.; He, T.; Mao, N. A Numerical Study on Heat Transfer Characteristics of a Novel Rectangular Grooved Microchannel with Al2O3/Water Nanofluids. Energies 2022, 15, 7187. [Google Scholar] [CrossRef]
- Tariq, H.; Sajjad, R.; Khan, M.Z.U.; Ghachem, K.; Ammar, A.; Khan, S.U.; Kolsi, L. Effective waste heat recovery from engine exhaust using fin prolonged heat exchanger with graphene oxide nanoparticles. J. Indian Chem. Soc. 2023, 100, 100911. [Google Scholar] [CrossRef]
- Moghanlou, F.S.; Noorzadeh, S.; Ataei, M.; Vajdi, M.; Asl, M.S.; Esmaeilzadeh, E. Experimental investigation of heat transfer and pressure drop in a minichannel heat sink using Al2O3 and TiO2–water nanofluids. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 315. [Google Scholar] [CrossRef]
- Tran, N.; Chang, Y.-J.; Wang, C.-C. Optimization of thermal performance of multi-nozzle trapezoidal microchannel heat sinks by using nanofluids of Al2O3 and TiO2. Int. J. Heat Mass Transf. 2018, 117, 787–798. [Google Scholar] [CrossRef]
- Al-Shamani, A.N.; Sopian, K.; Mohammed, H.; Mat, S.; Ruslan, M.H.; Abed, A.M. Enhancement heat transfer characteristics in the channel with Trapezoidal rib–groove using nanofluids. Case Stud. Therm. Eng. 2015, 5, 48–58. [Google Scholar] [CrossRef]
- Khan, M.Z.U.; Uddin, E.; Akbar, B.; Akram, N.; Naqvi, A.A.; Sajid, M.; Ali, Z.; Younis, Y.; Márquez, F.P.G. Investigation of heat transfer and pressure drop in microchannel heat sink using Al2O3 and ZrO2 nanofluids. Nanomaterials 2020, 10, 1796. [Google Scholar] [CrossRef]
- Heidarshenas, B.; Abidi, A.; Sajadi, S.M.; Yuan, Y.; El-Shafay, A.S.; Aybar, H.Ş. Numerical Study and Optimization of Thermal Efficiency for a Pin Fin Heatsink with Nanofluid Flow by Modifying Heatsink Geometry. Available online: https://ssrn.com/abstract=4631379 (accessed on 1 November 2023).
- Li, C.; Huang, J.; Shang, Y.; Huang, H. Study on the flow and heat dissipation of water-based alumina nanofluids in microchannels. Case Stud. Therm. Eng. 2020, 22, 100746. [Google Scholar] [CrossRef]
- Di Carlo, D.; Royal Society of Chemistry. Inertial microfluidics. Lab Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef] [PubMed]
- Rea, U.; McKrell, T.; Hu, L.-W.; Buongiorno, J. Laminar convective heat transfer and viscous pressure loss of alumina–water and zirconia–water nanofluids. Int. J. Heat Mass Transf. 2009, 52, 2042–2048. [Google Scholar] [CrossRef]
- Peiyi, W.; Little, W. Measurement of friction factors for the flow of gases in very fine channels used for microminiature Joule-Thomson refrigerators. Cryogenics 1983, 23, 273–277. [Google Scholar] [CrossRef]
- Blevins, R.D. Applied Fluid Dynamics Handbook. 1984. Available online: https://api.semanticscholar.org/CorpusID:116954751 (accessed on 1 November 2023).
- Bejan, A. Convection Heat Transfer, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Bergman, T.L.; DeWitt, D.P.; Incropera, F.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; Volume 997. [Google Scholar]
- Li, J.; Kleinstreuer, C. Thermal performance of nanofluid flow in microchannels. Int. J. Heat Fluid Flow 2008, 29, 1221–1232. [Google Scholar] [CrossRef]
- Yong, J.Q.; Teo, C.J. Mixing and Heat Transfer Enhancement in Microchannels Containing Converging-Diverging Passages. J. Heat Transf. 2014, 136, 041704. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Tiwari, S. Heat transfer characteristics of sinusoidal wavy channel with secondary corrugations. Int. J. Therm. Sci. 2019, 145, 105973. [Google Scholar] [CrossRef]
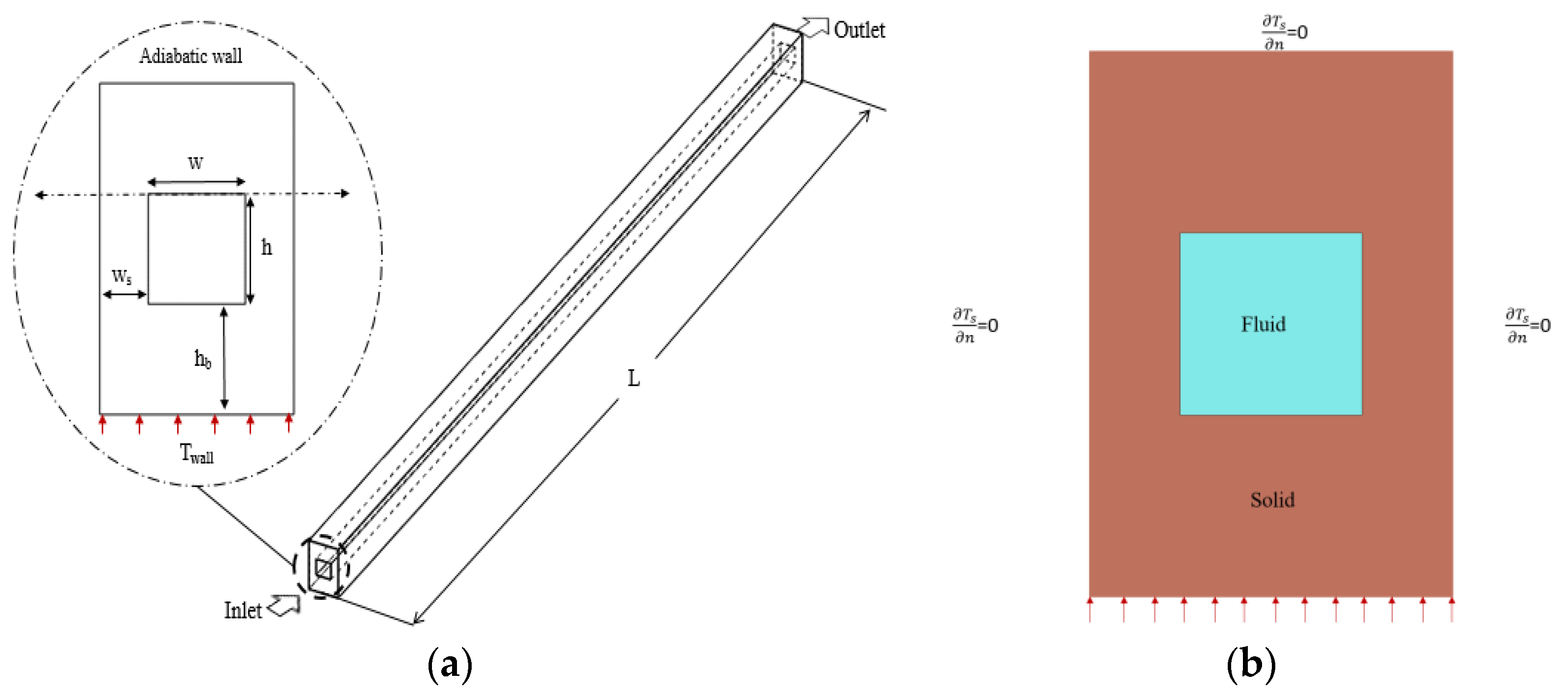
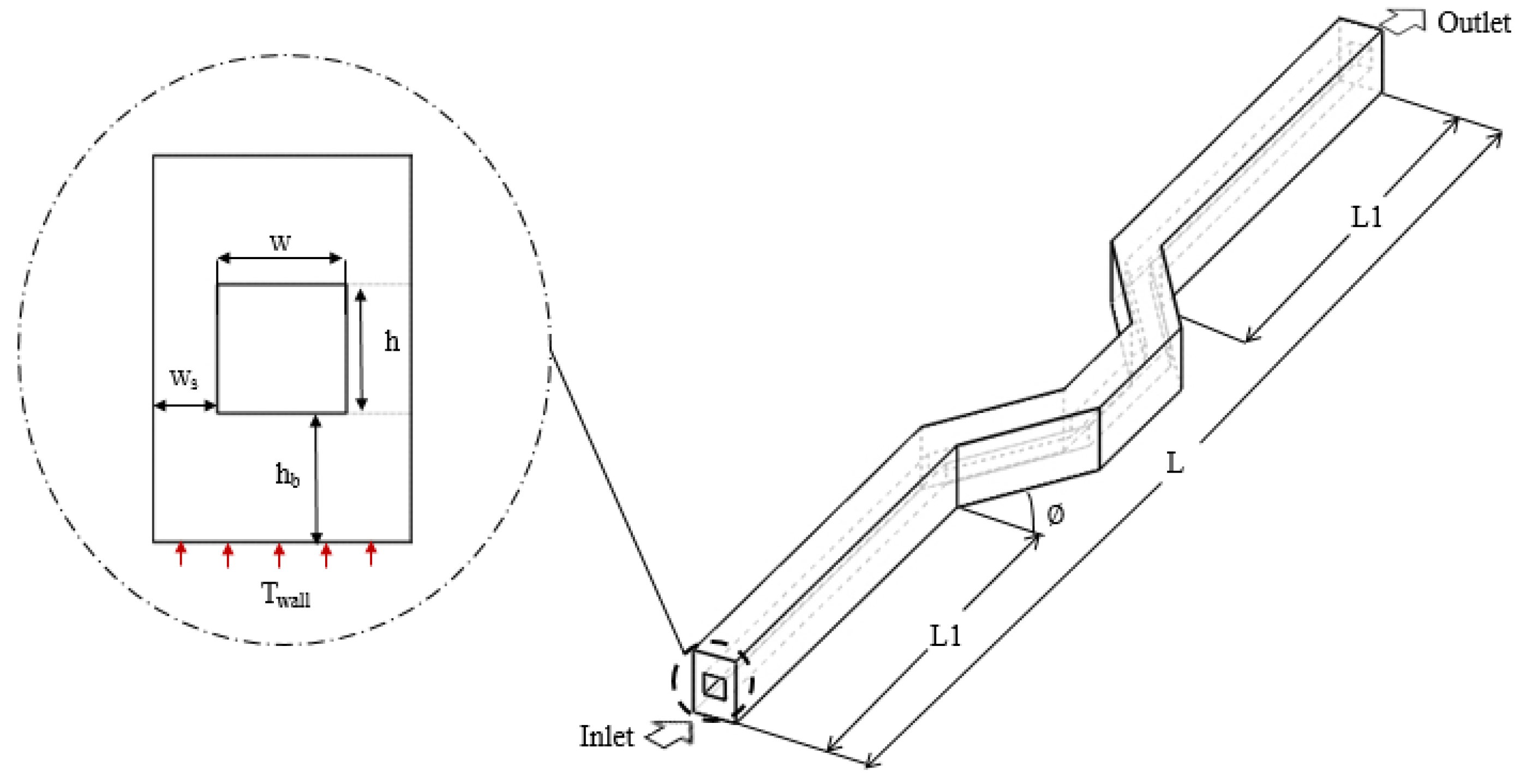

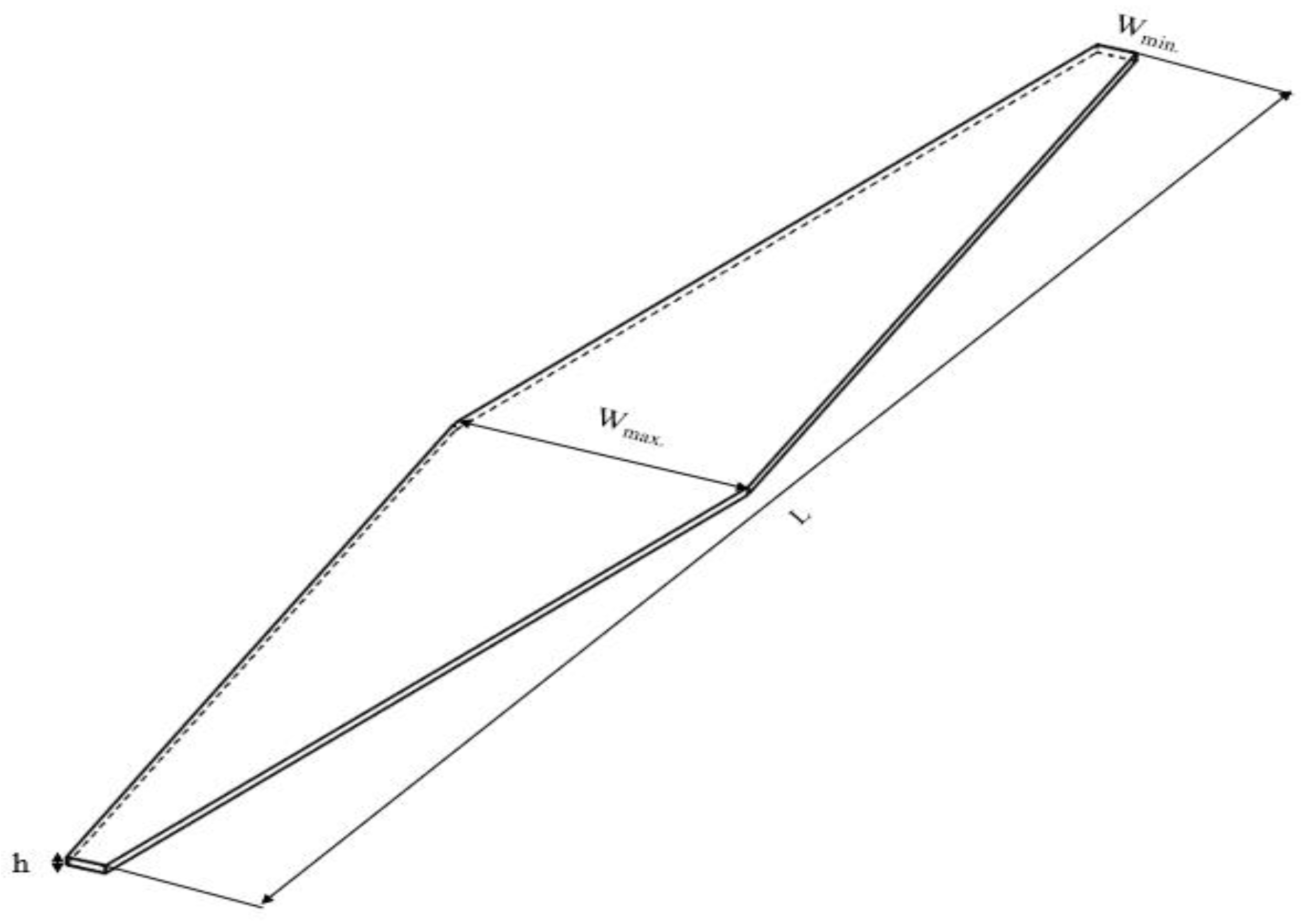



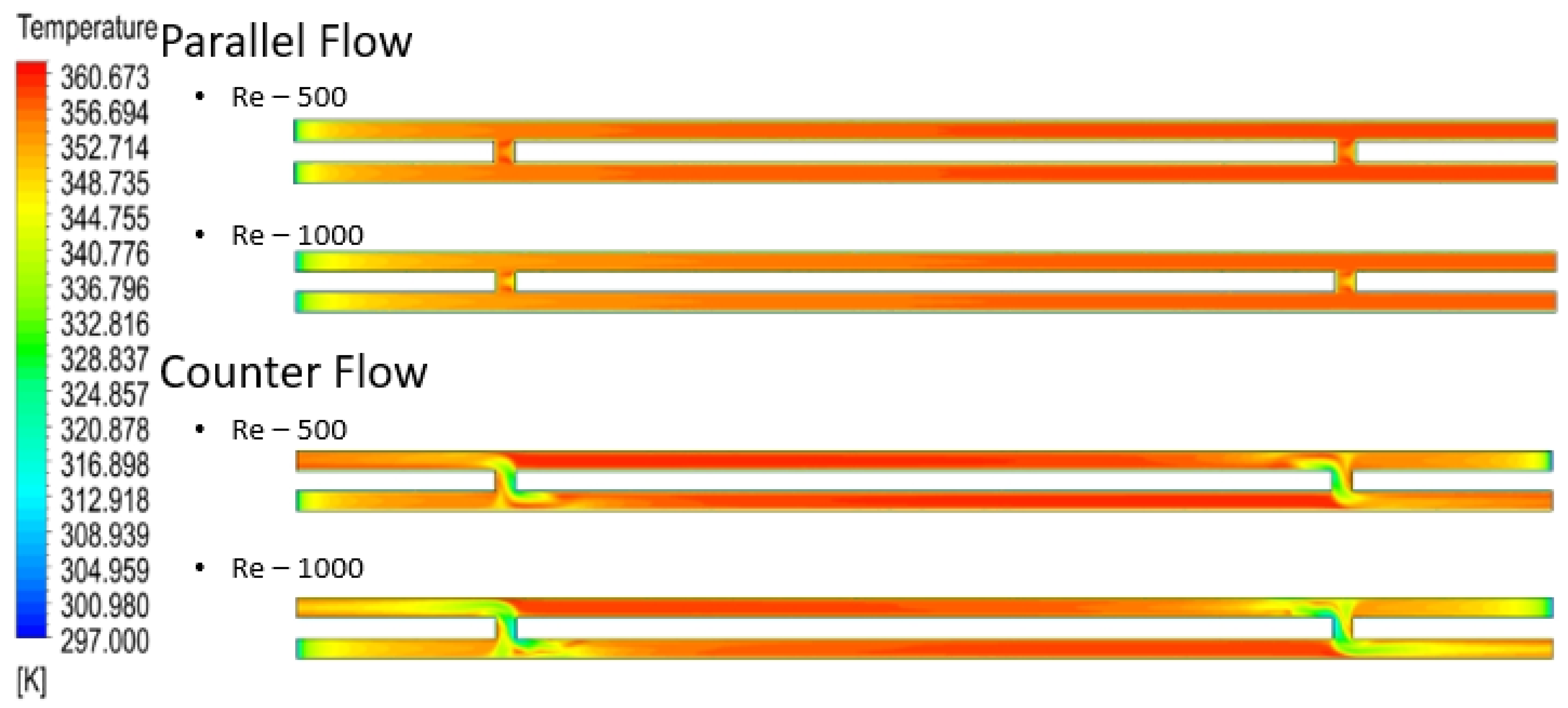
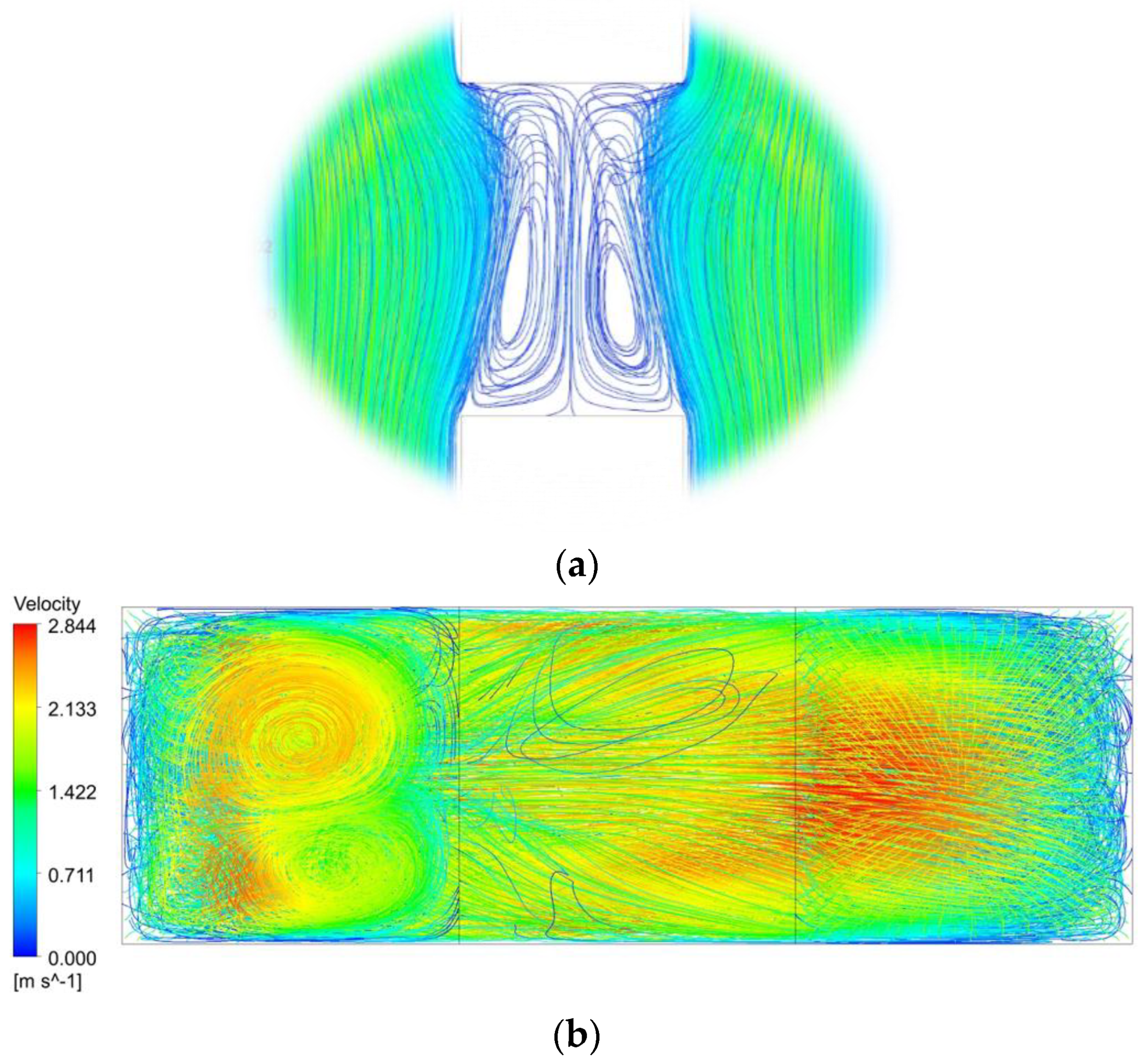

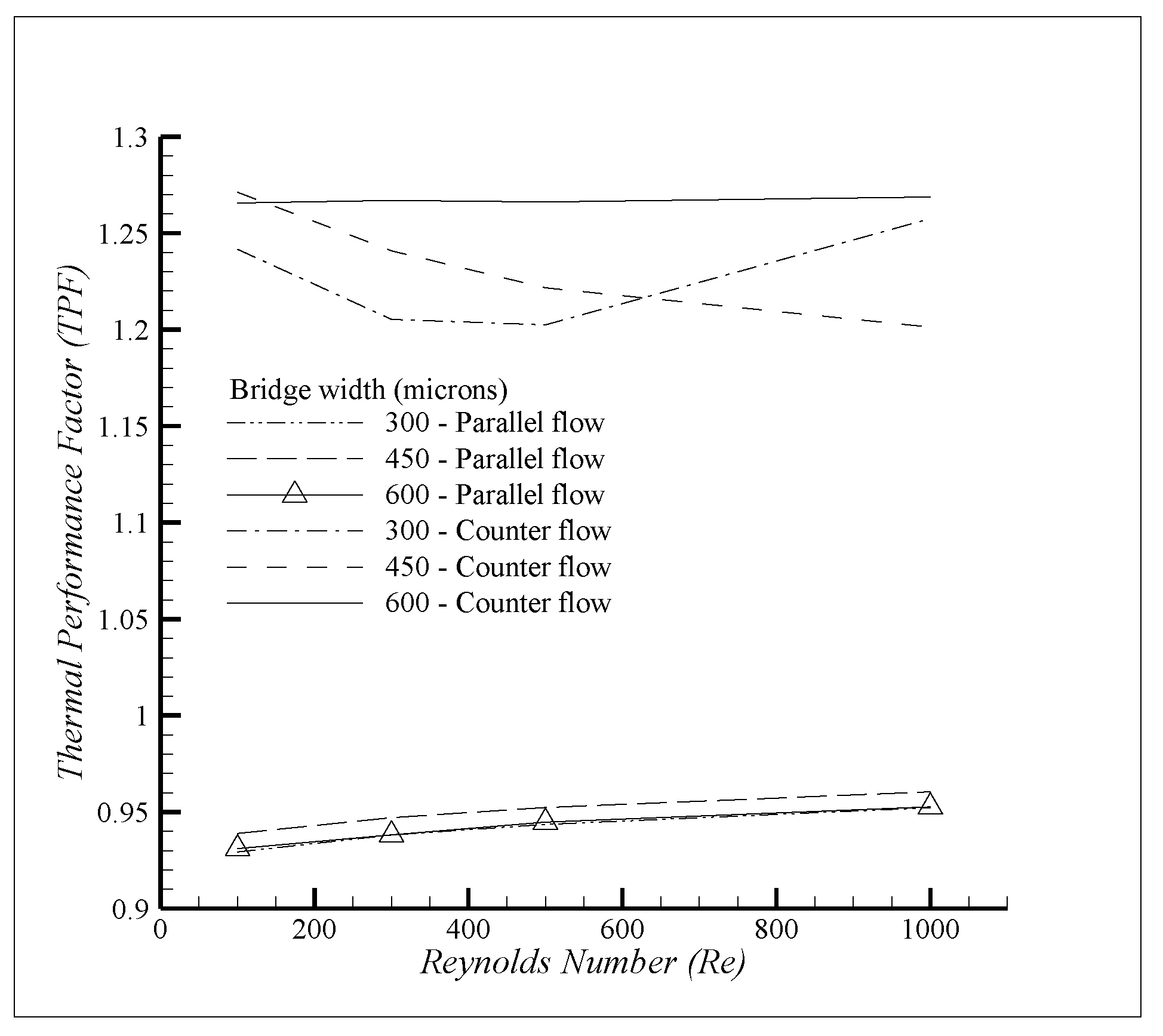

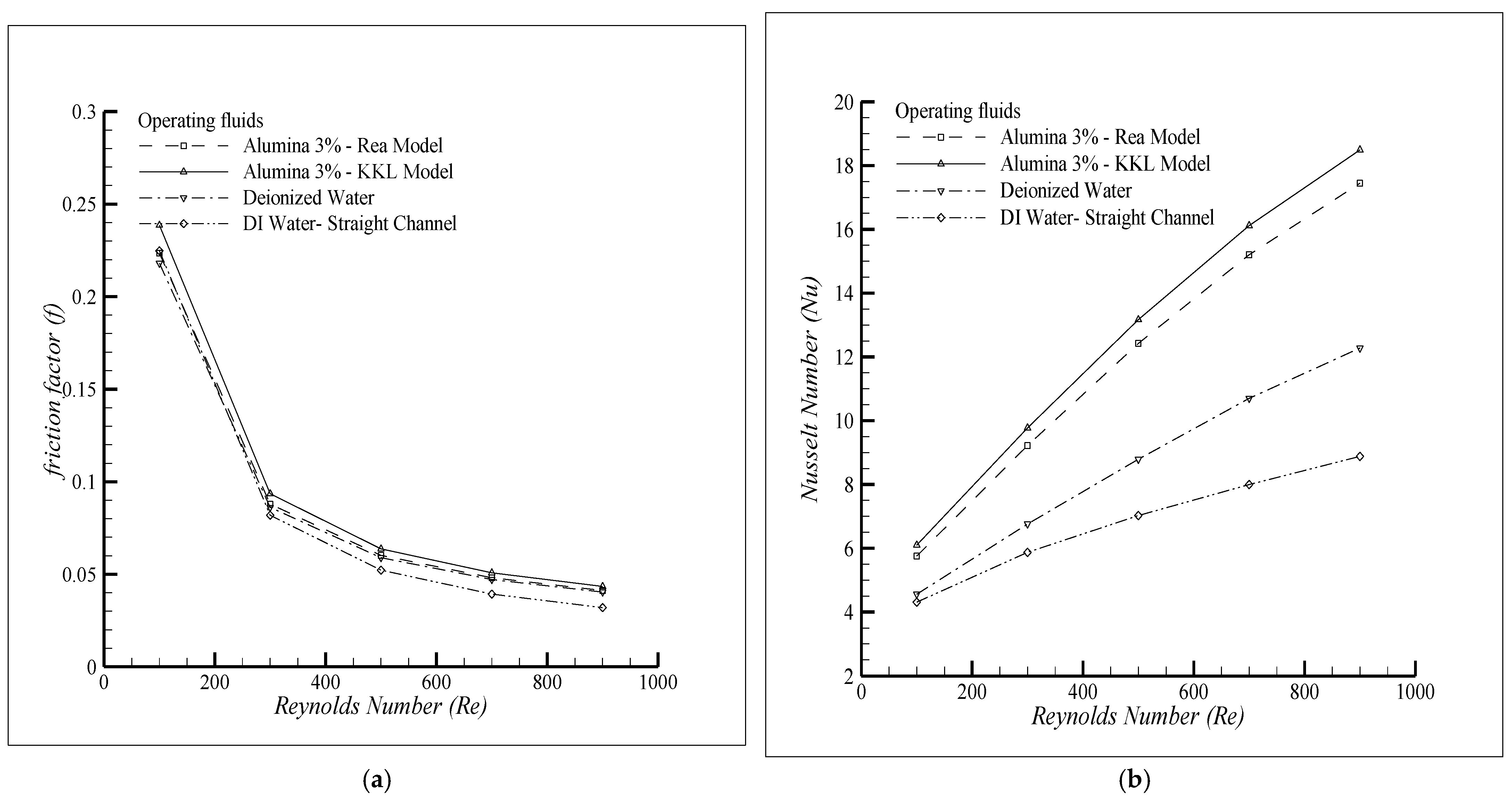
| Serial Number | Width “w” (µm) | Height “h” (µm) | Length “L” (mm) | Reynolds Number | Temperature “T” (Kelvin) | Number of Cases |
|---|---|---|---|---|---|---|
| 1 | 50–350 | 50–350 | 18 | 100–1000 | 323.15 | 490 |
| 2 | 343.15 | 490 | ||||
| 3 | 363.15 | 490 |
| Serial Number | Symbol | Dimensions |
|---|---|---|
| 1 | L | 60 w |
| 2 | L1 | 20 w |
| 3 | (deg.) | Ø −90° |
| 4 | W (µm) | 300 |
| 5 | H | w |
| Serial Number | Symbol | Dimensions |
|---|---|---|
| 1 | L | 60 w |
| 2 | L1 | 10 w |
| 3 | L2 | 40 w |
| 4 | (deg.) | 90° |
| 5 | W (µm) | 300 |
| 6 | H | W |
| 7 | S | W |
| Serial Number | Description | Deionized Water [46] | Copper | Alumina |
|---|---|---|---|---|
| 1 | µ | - | - | |
| 2 | k | 387.6 | - | |
| 3 | Cp | 381 | 880 | |
| 4 | ρ | 998.2 | 8978 | 3920 |
| Serial Number | Discretization Variable | Solution Scheme |
|---|---|---|
| 1 | Pressure | Standard |
| 2 | Pressure–Velocity Coupling | SIMPLEC |
| 3 | Momentum | Second order (upwind) |
| 4 | Energy | Second order (upwind) |
| Serial Number | Number of Elements | Friction Factor | Error % | |
|---|---|---|---|---|
| Present | Shah and London [16] | |||
| 1 | 22,500 (Very Coarse) | 0.03528 | 0.0412 | 14.30 |
| 2 | 45,000 (Coarse) | 0.037195 | 0.0412 | 9.64 |
| 3 | 87,500 (Coarse) | 0.038182 | 0.0412 | 7.25 |
| 4 | 168,000 (Fine) | 0.040658 | 0.0412 | 1.23 |
| 5 | 320,000 (Fine) | 0.041424 | 0.0412 | 0.62 |
| 6 | 600,000 (Fine) | 0.042564 | 0.0412 | 3.39 |
| 7 | 1,080,000 (Very Fine) | 0.042706 | 0.0412 | 3.73 |
| 8 | 2,160,000 (Very Fine) | 0.042758 | 0.0412 | 3.86 |
| 9 | 4,320,000 (Very Fine) | 0.042792 | 0.0412 | 3.94 |
| Serial Number | Width (Microns) | Height (Microns) | Bend Angle (Degree) |
|---|---|---|---|
| 1 | 300 | 300 | 15 |
| 2 | 300 | 300 | 30 |
| 3 | 300 | 300 | 45 |
| 4 | 300 | 300 | 60 |
| 5 | 300 | 300 | 75 |
| 6 | 300 | 300 | 90 |
| S. No. | Width (Microns) | Height (Microns) | Angle (Degrees) | Geometry | Flow |
|---|---|---|---|---|---|
| 1 | 300 | 300 | 90° | Straight Channel | Parallel and Counter flow |
| 2 | 300 | 300 | 35° | Straight Channel | |
| 3 | 300 | 300 | 90° | Curved Channel | |
| 4 | 300 | 300 | 35° | Curved Channel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naqvi, A.A.; Uddin, E.; Khan, M.Z.U. Passive Mixing and Convective Heat Transfer Enhancement for Nanofluid Flow across Corrugated Base Microchannels. Energies 2023, 16, 7893. https://doi.org/10.3390/en16237893
Naqvi AA, Uddin E, Khan MZU. Passive Mixing and Convective Heat Transfer Enhancement for Nanofluid Flow across Corrugated Base Microchannels. Energies. 2023; 16(23):7893. https://doi.org/10.3390/en16237893
Chicago/Turabian StyleNaqvi, Ali Ammar, Emad Uddin, and Muhammad Zia Ullah Khan. 2023. "Passive Mixing and Convective Heat Transfer Enhancement for Nanofluid Flow across Corrugated Base Microchannels" Energies 16, no. 23: 7893. https://doi.org/10.3390/en16237893
APA StyleNaqvi, A. A., Uddin, E., & Khan, M. Z. U. (2023). Passive Mixing and Convective Heat Transfer Enhancement for Nanofluid Flow across Corrugated Base Microchannels. Energies, 16(23), 7893. https://doi.org/10.3390/en16237893







