Machine Learning Assisted Microchannel Geometric Optimization—A Case Study of Channel Designs
Abstract
:1. Introduction
2. Heat Exchanger Modeling
2.1. An Introduction to the Modeling of Heat Exchangers
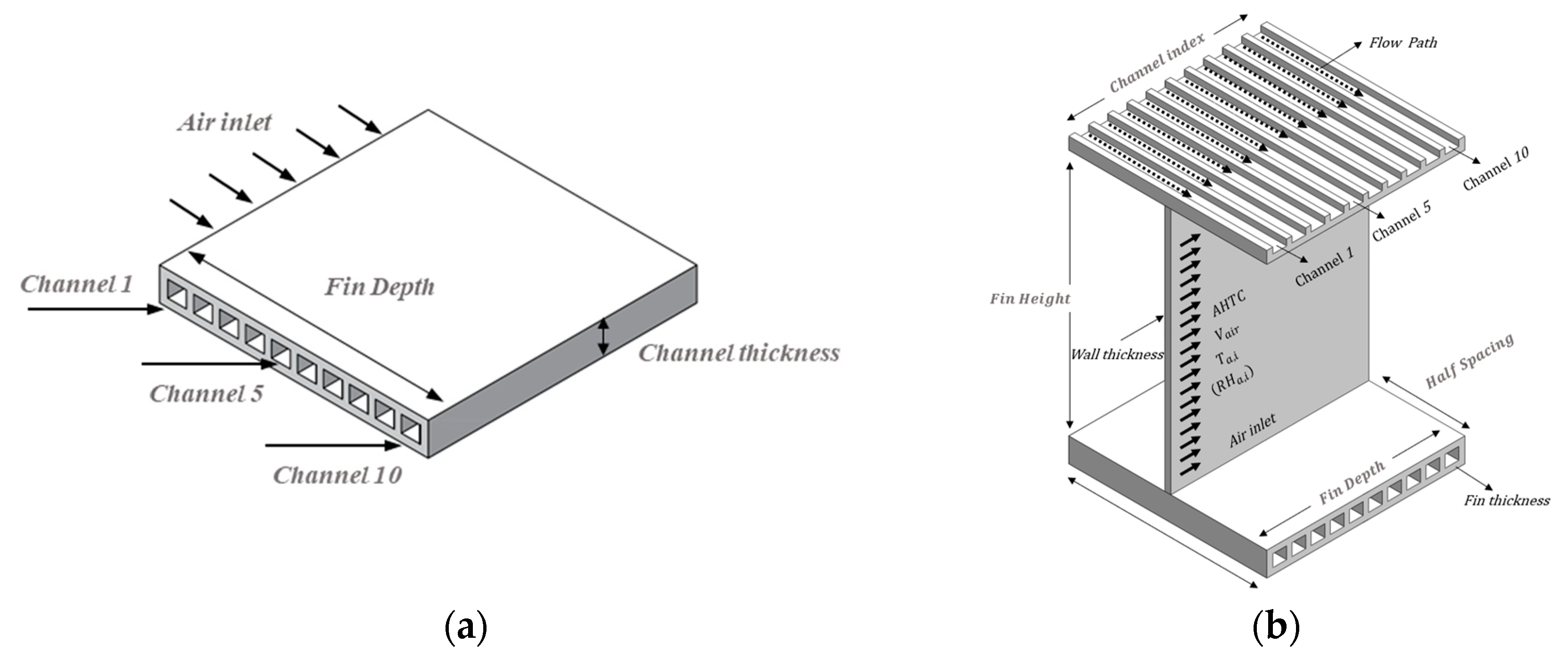
2.2. Heat Exchanger Modeling
2.2.1. Heat Transfer Rate
2.2.2. Pressure Drop
2.2.3. Refrigerant Side Calculation
2.3. Calculation of the Flow Maldistribution
- (1)
- Uniform airflow distribution: the airflow is taken to be uniform in terms of the velocity and temperature in the model. However, this assumption can be modified in future iterations of the model by incorporating velocity and temperature distributions.
- (2)
- Uniform pressure drop across different flow paths: according to the research conducted by Tuo and Hrnjak [23], this assumption is rooted in their demonstration of how the header pressure drop influences the distribution across various flow paths. In the context of their study, a ‘path’ is defined as a specific segment starting from the inlet header, passing through a microchannel tube, and ending at the outlet header. The pressure drop across this path includes the cumulative loss induced by friction, acceleration, gravity, and the contractions and expansions at the interaction points between the header and microchannel tube. As a result, for a microchannel heat exchanger, each flow path within the evaporator experiences a uniform pressure drop from the inlet to the outlet.
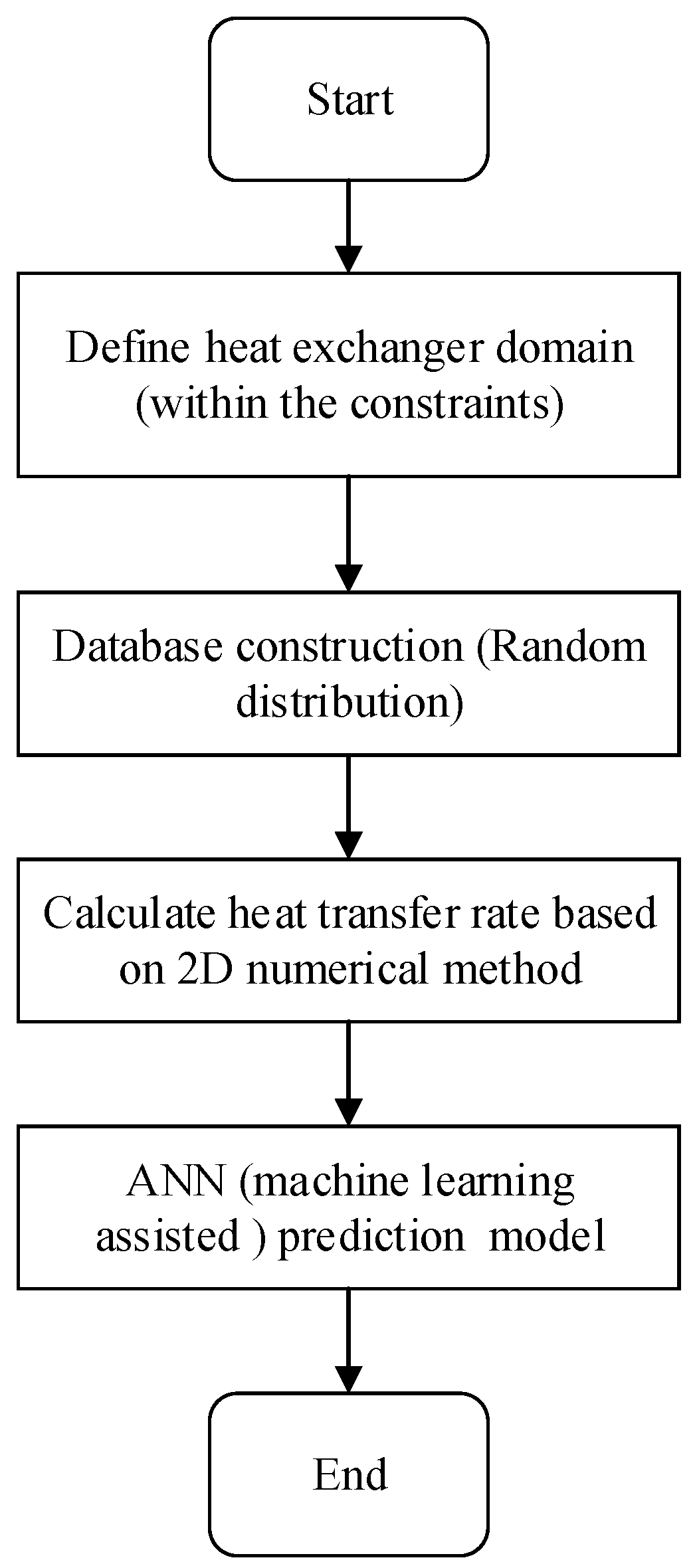
3. ANN-Based Machine-Learning-Assisted Optimization Model
4. Optimization Methodology and Problem Statement
4.1. Methodology
4.2. Baseline Case
4.3. Problem Statement
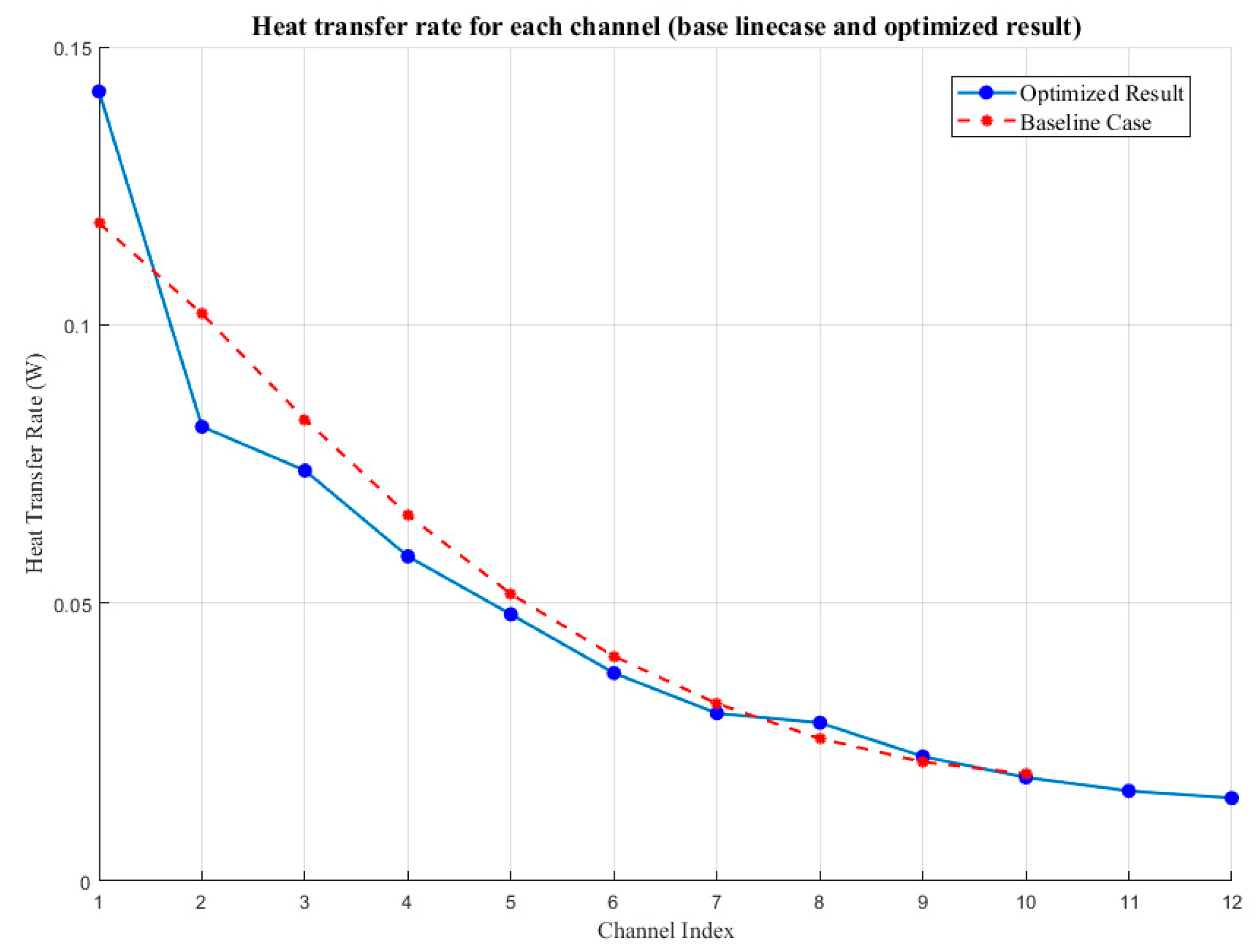
5. Results and Discussion
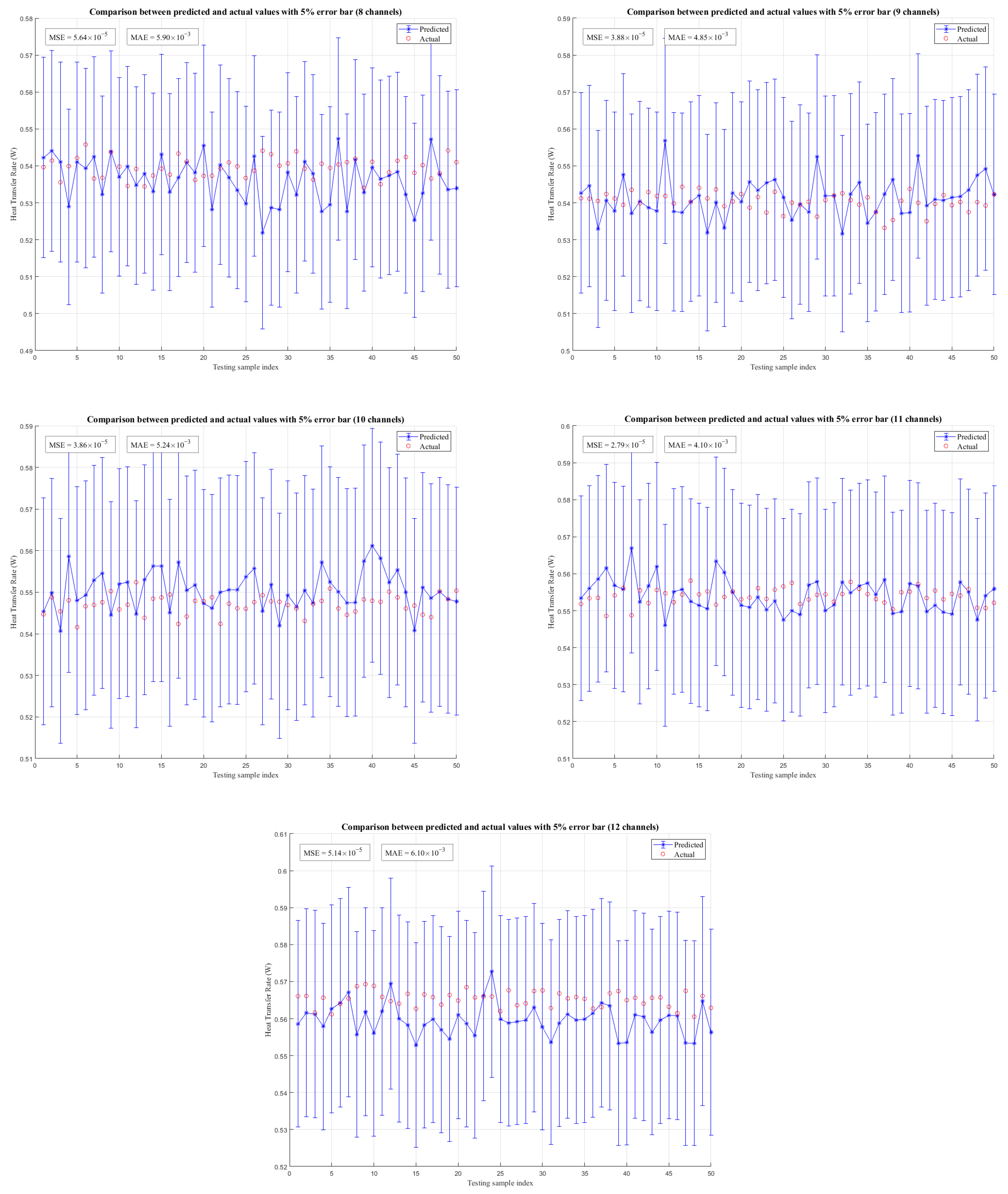
5.1. Scenario A
5.2. Scenarios B and C
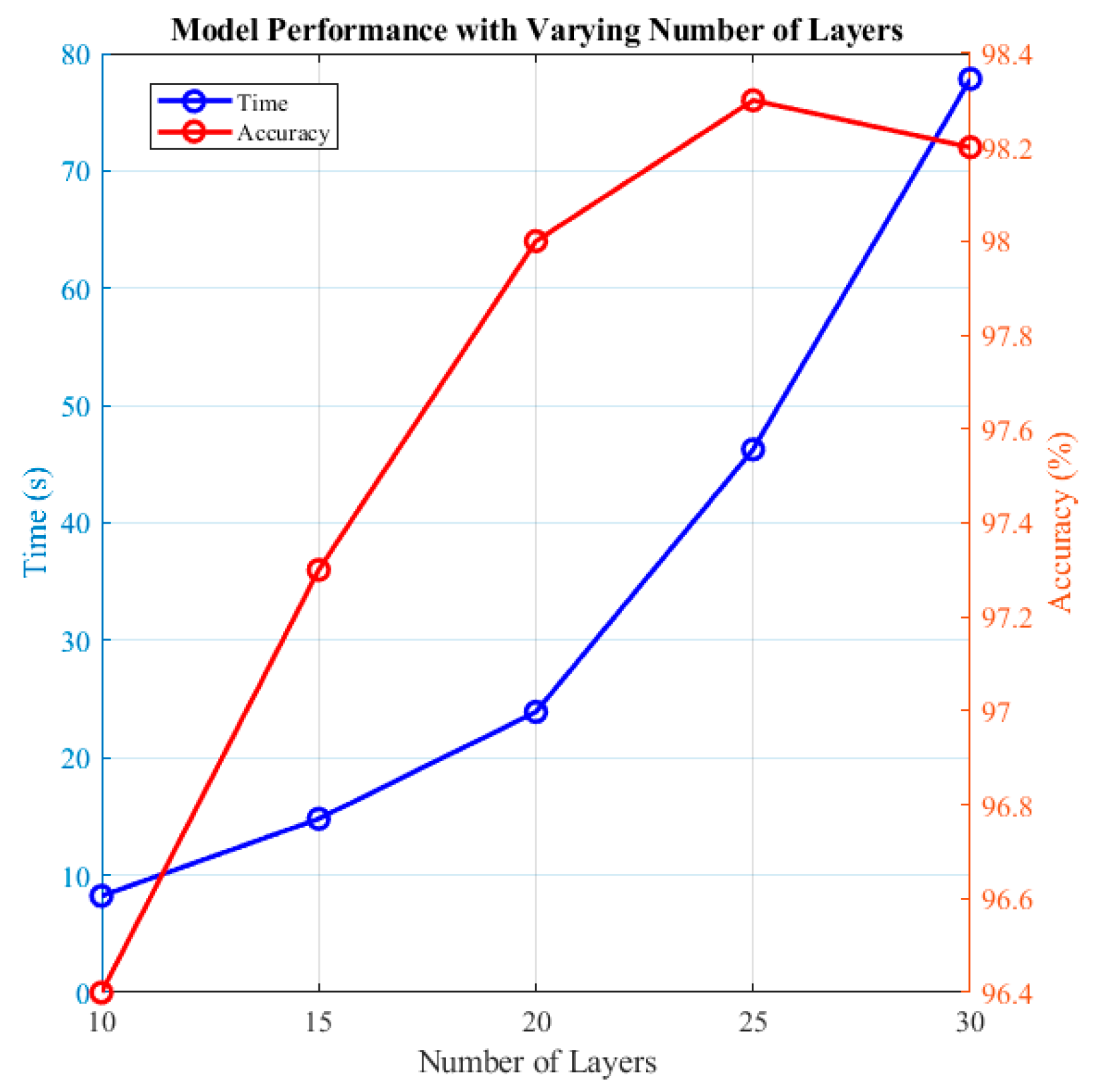
5.3. Computational Cost and ANN Model Application
5.4. Optimized Case Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area ) |
| AHTC | Air-Side heat transfer coefficient |
| RHTC | Refrigerant-Side heat transfer coefficient |
| ANNs | Artificial neural networks |
| Specific heat capacity (KJ/kg/K) | |
| G | Total mass flux (liquid + vapor) |
| g | Acceleration due to gravity |
| h | Heat transfer coefficient |
| Heat transfer coefficient expressed by Equation (10) | |
| Heat transfer coefficient expressed by Equation (11), the Nusselt equation | |
| hyd | Hydraulic diameter |
| ins | Inside |
| Dimensionless vapor velocity defined by Equation (13) | |
| k | Thermal conductivity (KW/m·K) |
| Mass flow rate of air (Kg/s) | |
| L | Tube length |
| ∆P | Pressure drop |
| Reduced pressure | |
| Pr | Prandtl number |
| Heat transfer rate (KJ/Kg) | |
| R | Heat transfer resistance (K/W) |
| Re | Reynolds number |
| Reynolds number assuming liquid phase flowing alone | |
| Temperature (K) | |
| t | Fin thickness (m) |
| Velocity (m/s) | |
| Wall | |
| WP | Wetted perimeter |
| x | Vapor quality |
| Z | Shah’s correlating parameter defined by Equation (14) |
| Greek symbols | |
| μ | Dynamic viscosity |
| ρ | Density |
| π | Ratio of a circle’s circumference |
| Thickness | |
| Subscripts | |
| At this cell | |
| flu | Fluid |
| g | Vapor |
| i | Inlet |
| ins | Inside |
| At the local position | |
| ol | Outlet |
| TP | Two phase |
References
- Harpole, G.; Eninger, J. Micro-channel heat exchanger optimization. In Proceedings of the 7th IEEE SEMI-THERM Symposium, Phoenix, AZ, USA, 12–14 February 1991; pp. 59–63. [Google Scholar]
- Thulukkanam, K. Heat Exchanger Design Handbook; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- bin Abu Bakar, W.; Yek, P.N.Y.; Cheong, K.Y.; Affam, A.C.; Wong, C.C.; Liew, R.K.; Tan, Y.H.; Lam, S.S. Utilization of microwave steam pyrolysis to produce biochar for thermal energy storage. Waste Dispos. Sustain. Energy 2022, 4, 335–341. [Google Scholar] [CrossRef]
- Wang, H.; Xu, W.; Sharif, M.; Cheng, G.; Zhang, Z. Resource utilization of solid waste carbide slag: A brief review of application technologies in various scenes. Waste Dispos. Sustain. Energy 2022, 4, 1–16. [Google Scholar] [CrossRef]
- Moreira, B.R.d.A.; Cruz, V.H.; Cunha, M.L.O.; Lopes, N.P.; Magalhães, A.C.; Miasaki, C.T.; Caraschi, J.C.; Viana, R.d.S. Valorization of semi-solid by-product from distillation of cellulosic ethanol into blends for heating and power. Waste Dispos. Sustain. Energy 2021, 3, 49–61. [Google Scholar] [CrossRef]
- Knight, R.W.; Goodling, J.S.; Hall, D.J. Optimal thermal design of forced convection heat sinks-analytical. J. Electron. Packag. 1991, 113, 313–321. [Google Scholar] [CrossRef]
- Knight, R.; Hall, D.; Goodling, J.; Jaeger, R. Heat sink optimization with application to microchannels. IEEE Trans. Compon. Hybrids Manuf. Technol. 1992, 15, 832–842. [Google Scholar] [CrossRef]
- Bello-Ochende, T.; Liebenberg, L.; Meyer, J. Constructal cooling channels for micro-channel heat sinks. Int. J. Heat Mass Transf. 2007, 50, 4141–4150. [Google Scholar] [CrossRef]
- Husain, A.; Kim, K.-Y. Thermal optimization of a microchannel heat sink with trapezoidal cross section. J. Electron. Packag. 2009, 131, 021005. [Google Scholar] [CrossRef]
- Garcia, J.C.S.; Tanaka, H.; Giannetti, N.; Sei, Y.; Saito, K.; Houfuku, M.; Takafuji, R. Multiobjective geometry optimization of microchannel heat exchanger using real-coded genetic algorithm. Appl. Therm. Eng. 2022, 202, 117821. [Google Scholar] [CrossRef]
- Li, F.; Zhu, W.; He, H. Numerical optimization on microchannel flow and heat transfer performance based on field synergy principle. Int. J. Heat Mass Transf. 2019, 130, 375–385. [Google Scholar] [CrossRef]
- Huang, L.; Aute, V.; Radermacher, R. Air flow distribution and design optimization of variable geometry microchannel heat exchangers. Sci. Technol. Built Environ. 2015, 21, 693–702. [Google Scholar] [CrossRef]
- Gunnasegaran, P.; Mohammed, H.; Shuaib, N.; Saidur, R. The effect of geometrical parameters on heat transfer characteristics of microchannels heat sink with different shapes. Int. Commun. Heat Mass Transf. 2010, 37, 1078–1086. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Gao, J. Influence of geometric parameters on flow and heat transfer performance of micro-channel heat sinks. Appl. Therm. Eng. 2016, 107, 870–879. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, C.; Shi, M.; Wu, J. Three-dimensional numerical simulation of heat and fluid flow in noncircular microchannel heat sinks. Int. Commun. Heat Mass Transf. 2009, 36, 917–920. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, J.; Gong, L.; Duan, X. Thermal performance and structure optimization for slotted microchannel heat sink. Appl. Therm. Eng. 2017, 115, 1266–1276. [Google Scholar] [CrossRef]
- Du, R.; Zou, J.; An, J.; Huang, L. A regression-based approach for the explicit modeling of simultaneous heat and mass transfer of air-to-refrigerant microchannel heat exchangers. Appl. Therm. Eng. 2023, 235, 121366. [Google Scholar] [CrossRef]
- Du, R.; An, J.; Huang, L. A Modified Effectiveness-Based Approach in Performance Prediction of Simultaneous Heat and Mass Transfer of Microchannel Heat Exchanger in Heat Pump Operating Conditions. In Proceedings of the 14th IEA Heat Pump Conference, Chicago, IL, USA, 15–18 May 2023. [Google Scholar]
- Shah, M.M. General Correlation For Heat Transfer During Condensation in Plain Tubes: Further Development and Verifica-tion. ASHRAE Trans. 2013, 119, 3–11. [Google Scholar]
- Hassan, A.H.; Martínez-Ballester, S.; Gonzálvez-Maciá, J. Two-dimensional numerical modeling for the air-side of minichannel evaporators accounting for partial dehumidification scenarios and tube-to-tube heat conduction. Int. J. Refrig. 2016, 67, 90–101. [Google Scholar] [CrossRef]
- Thome, J.R. Engineering Data Book III; Wolverine Tube, Inc.: Huntsville, AL, USA, 2006. [Google Scholar]
- Corberán, J.M.; de Córdoba, P.F.; Gonzálvez, J.; Alias, F. Semiexplicit method for wall temperature linked equations (SEWTLE): A general finite-volume technique for the calculation of complex heat exchangers. Numer. Heat Transf. Part B Fundam. 2001, 40, 37–59. [Google Scholar] [CrossRef]
- Tuo, H.; Hrnjak, P. Effect of the header pressure drop induced flow maldistribution on the microchannel evaporator performance. Int. J. Refrig. 2013, 36, 2176–2186. [Google Scholar] [CrossRef]
- McKay, M.D. Latin hypercube sampling as a tool in uncertainty analysis of computer models. In Proceedings of the 24th Conference on Winter Simulation, Arlington, VA, USA, 13–16 December 1992; pp. 557–564. Available online: https://dl.acm.org/doi/pdf/10.1145/167293.167637 (accessed on 5 December 2023).
- Box, G.E.; Meyer, R.D. Dispersion effects from fractional designs. Technometrics 1986, 28, 19–27. [Google Scholar] [CrossRef]
- Ranganathan, A. The levenberg-marquardt algorithm. Tutoral LM Algorithm 2004, 11, 101–110. [Google Scholar]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef] [PubMed]










| Metric | Unit | Value |
|---|---|---|
| Fin height | m | 0.01 |
| AHTC | KW/m2 K | 0.06104 |
| m/s | 1.5 | |
| K | 300 | |
| Fin depth | m | 0.02 |
| Kg/s | 1.0 × 10−4 (total) | |
| K | 350 | |
| RHTC | KW/m2 K | 8.6521 |
| Half spacing | m | 2.955 × 10−4 |
| Refrigerant vapor quality | - | 0.5 |
| Fin thickness | m | 0.0001 |
| Wall thickness | m | 0.0005 |
| Material (aluminum) | - | - |
| 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|
| Hydraulic diameter (hyd) (mm) | 0.1–1.7 | 0.1–1.6 | 0.1–1.4 | 0.1–1.3 | 0.1–1.2 |
| Cross-sectional area (A) (mm2) | 0.4–2.4 | 0.4–2.2 | 0.4–2.0 | 0.4–1.8 | 0.4–1.6 |
| Scenario No. | Objective 1 | Objective 2 |
|---|---|---|
| A | Maximize heat transfer rate | Minimize pressure drop |
| B | Maximize refrigerant heat transfer coefficient | Minimize pressure drop |
| C | Minimize heat transfer resistance | Minimize pressure drop |
| Calculation Time | |
|---|---|
| Numerical model | 25.92 s (average) |
| ANN model | 0.41 s (average) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Zou, J.; Liu, B.; Jin, Z.; Qian, J. Machine Learning Assisted Microchannel Geometric Optimization—A Case Study of Channel Designs. Energies 2024, 17, 44. https://doi.org/10.3390/en17010044
Huang L, Zou J, Liu B, Jin Z, Qian J. Machine Learning Assisted Microchannel Geometric Optimization—A Case Study of Channel Designs. Energies. 2024; 17(1):44. https://doi.org/10.3390/en17010044
Chicago/Turabian StyleHuang, Long, Junjia Zou, Baoqing Liu, Zhijiang Jin, and Jinyuan Qian. 2024. "Machine Learning Assisted Microchannel Geometric Optimization—A Case Study of Channel Designs" Energies 17, no. 1: 44. https://doi.org/10.3390/en17010044
APA StyleHuang, L., Zou, J., Liu, B., Jin, Z., & Qian, J. (2024). Machine Learning Assisted Microchannel Geometric Optimization—A Case Study of Channel Designs. Energies, 17(1), 44. https://doi.org/10.3390/en17010044









