Techno-Economic Evaluation of a Compressed CO2 Energy Storage System for Load Shifting Based on Dynamic Modelling
Abstract
:1. Introduction
2. Problem Formulation
2.1. Optimization Objective
2.2. Constraints
- (1)
- Operation mode
- (2)
- The SOC of the CCES system
- (3)
- Electric capacity of the compressor
- (4)
- Electric capacity of the expander
2.3. Solving Method
3. Case Study
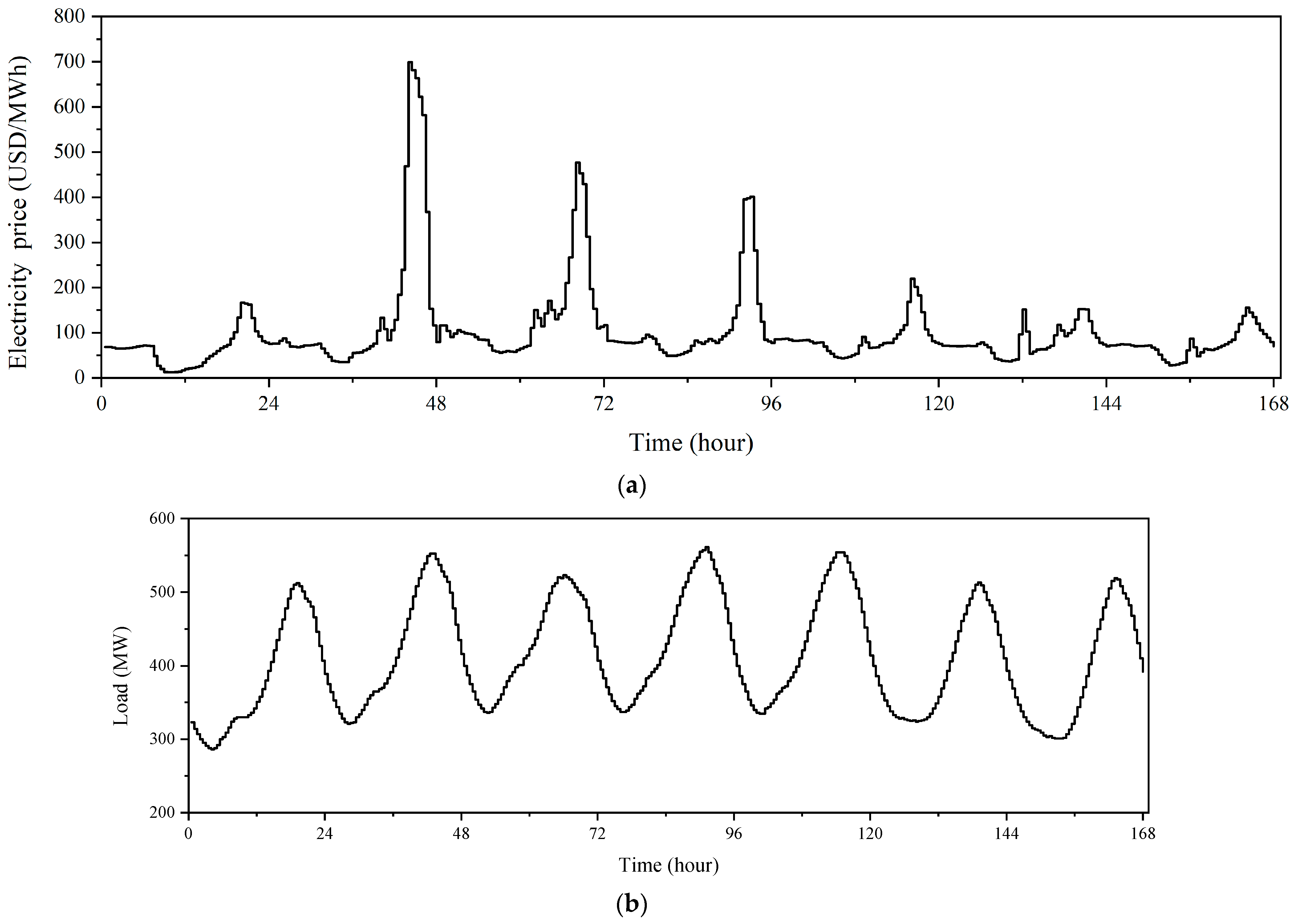
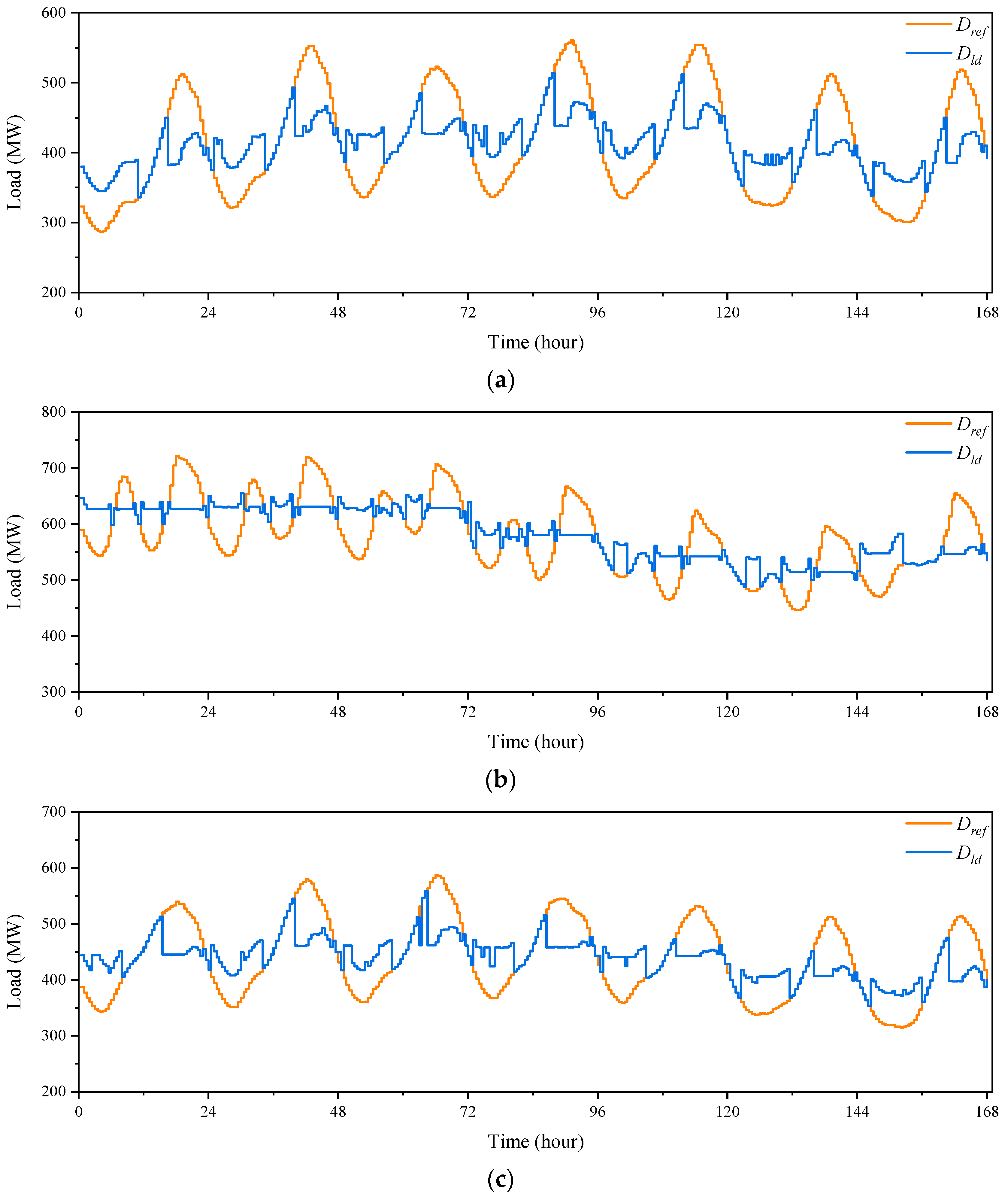
3.1. The Electricity Price and Load Data
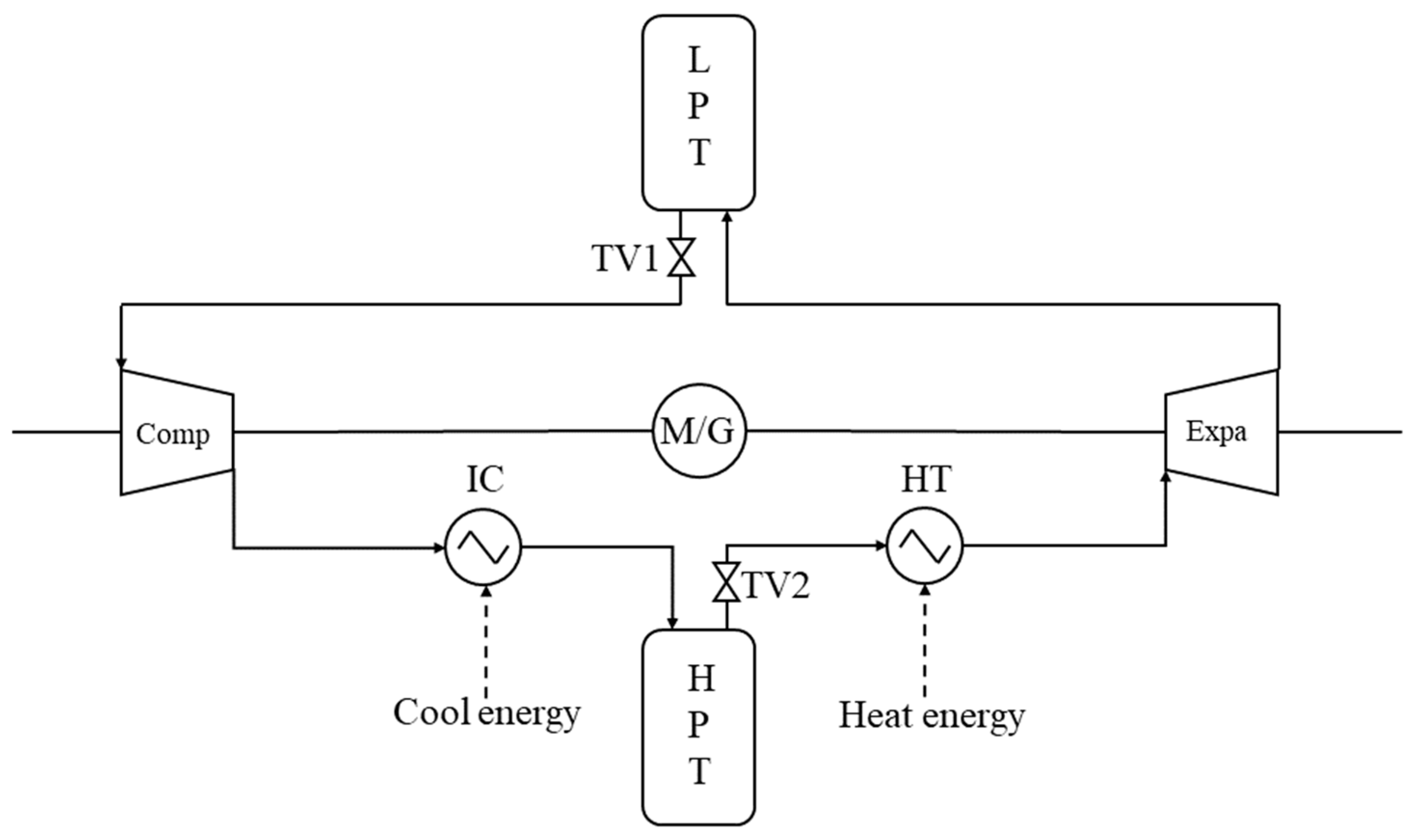
3.2. The Compressed Carbon Dioxide Energy Storage System
3.3. Key Performance Indicator
3.3.1. Energy Flexibility Indicators
3.3.2. Economic Indicators
4. Results and Discussion
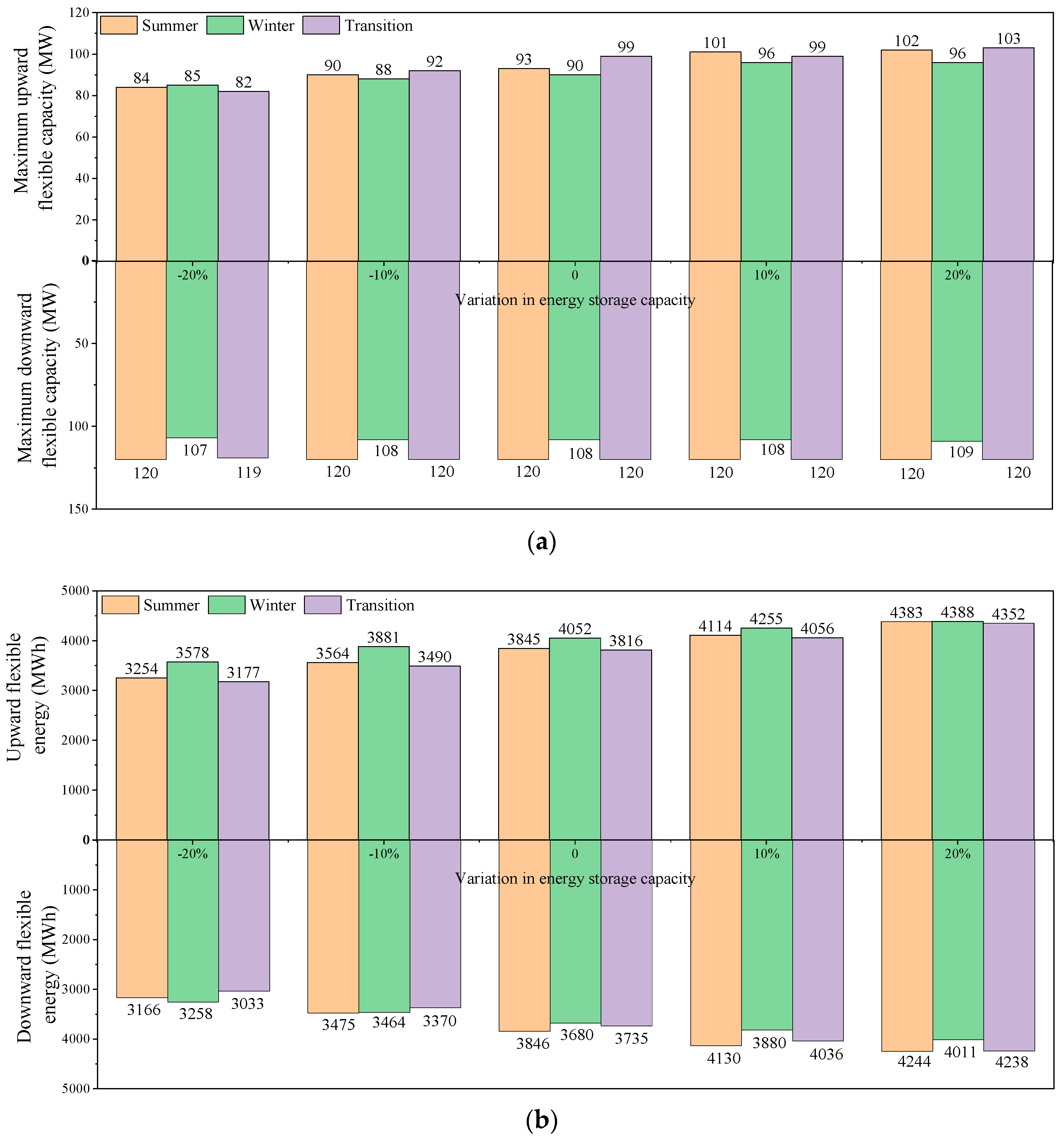
4.1. Electricity Load Energy Flexibility Analysis
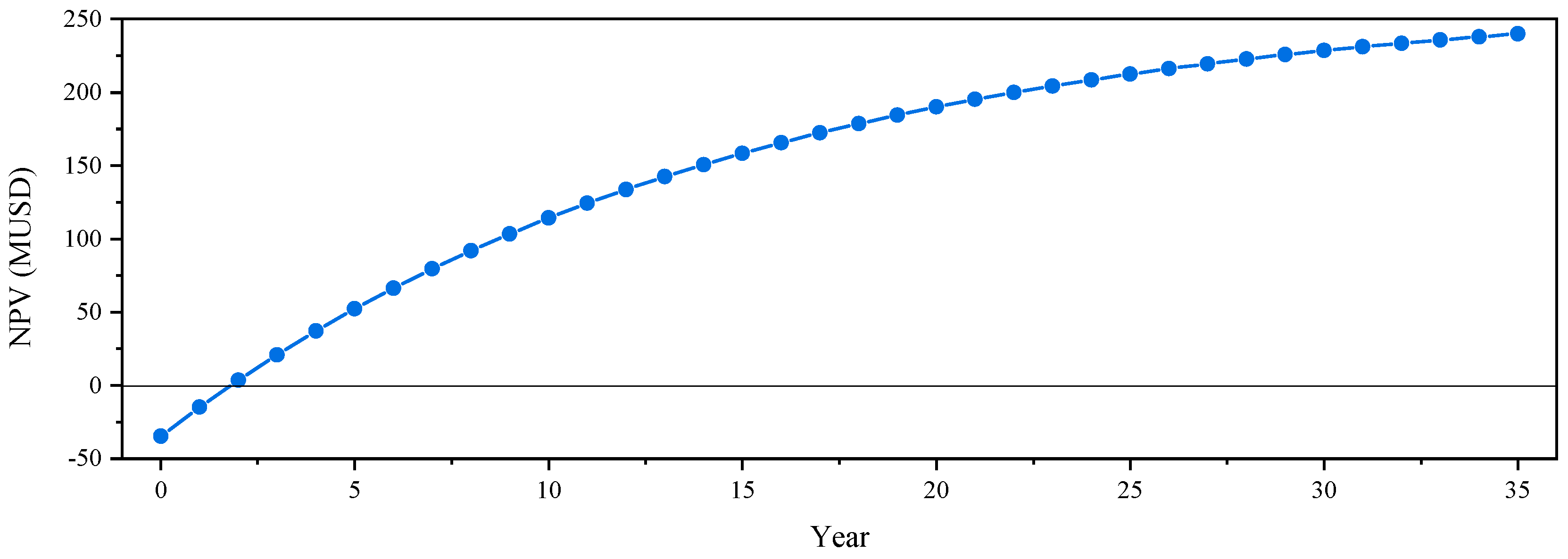
4.2. Economic Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A comprehensive review of stationary energy storage devices for large scale renewable energy sources grid integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Budt, M.; Wolf, D.; Span, R.; Yan, J. A review on compressed air energy storage: Basic principles, past milestones and recent developments. Appl. Energy 2016, 170, 250–268. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Wang, W.; Sun, B.; Li, H.; Sun, Q.; Wennersten, R. An improved min-max power dispatching method for integration of variable renewable energy. Appl. Energy 2020, 276, 115430. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. An updated review of energy storage systems: Classification and applications in distributed generation power systems incorporating renewable energy resources. Int. J. Energy Res. 2019, 43, 6171–6210. [Google Scholar] [CrossRef]
- Guo, C.; Xu, Y.; Guo, H.; Zhang, X.; Lin, X.; Wang, L.; Zhang, Y.; Chen, H. Comprehensive exergy analysis of the dynamic process of compressed air energy storage system with low-temperature thermal energy storage. Appl. Therm. Eng. 2019, 147, 684–693. [Google Scholar] [CrossRef]
- Tong, Z.; Cheng, Z.; Tong, S. A review on the development of compressed air energy storage in China: Technical and economic challenges to commercialization. Renew. Sustain. Energy Rev. 2021, 135, 110178. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, E.; Tian, Z.; Gao, W.; Yang, K. Exergy destruction analysis of a low-temperature Compressed Carbon dioxide Energy Storage system based on conventional and advanced exergy methods. Appl. Therm. Eng. 2021, 185, 116421. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Huang, Q.; Yao, J.; Hu, Y.; Liu, S.; Li, H.; Sun, Q. Integrating compressed CO2 energy storage in an oxy-coal combustion power plant with CO2 capture. Energy 2022, 254, 124493. [Google Scholar] [CrossRef]
- Liu, S.; Wu, S.; Hu, Y.; Li, H. Comparative analysis of air and CO2 as working fluids for compressed and liquefied gas energy storage technologies. Energy Convers. Manag. 2019, 181, 608–620. [Google Scholar] [CrossRef]
- Jia, L.; Chen, H.; Xu, Y.; Liang, W.; Tan, C. A solar energy storage and power generation system based on supercritical carbon dioxide. Renew. Energy 2014, 64, 43–51. [Google Scholar]
- Liu, H.; He, Q.; Borgia, A.; Pan, L.; Oldenburg, C.M. Thermodynamic analysis of a compressed carbon dioxide energy storage system using two saline aquifers at different depths as storage reservoirs. Energy Convers. Manag. 2016, 127, 149–159. [Google Scholar] [CrossRef]
- Hao, Y.; He, Q.; Du, D. A trans-critical carbon dioxide energy storage system with heat pump to recover stored heat of compression. Renew. Energy 2020, 152, 1099–1108. [Google Scholar] [CrossRef]
- Xu, M.; Zhao, P.; Huo, Y.; Han, J.; Wang, J.; Dai, Y. Thermodynamic analysis of a novel liquid carbon dioxide energy storage system and comparison to a liquid air energy storage system. J. Clean. Prod. 2020, 242, 118437. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, P.; Wu, Y.; Dai, Y. Performance analysis of a novel energy storage system based on liquid carbon dioxide. Appl. Therm. Eng. 2015, 91, 812–823. [Google Scholar] [CrossRef]
- Huang, Q.; Feng, B.; Liu, S.; Ma, C.; Li, H.; Sun, Q. Dynamic operating characteristics of a compressed CO2 energy storage system. Appl. Energy 2023, 341, 120985. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Yang, K. Dynamic characteristics of a two-stage compression and two-stage expansion Compressed Carbon dioxide energy storage system under sliding pressure operation. Energy Convers. Manag. 2022, 254, 115218. [Google Scholar] [CrossRef]
- Chaychizadeh, F.; Dehghandorost, H.; Aliabadi, A.; Taklifi, A. Stochastic dynamic simulation of a novel hybrid thermal-compressed carbon dioxide energy storage system (T-CCES) integrated with a wind farm. Energy Convers. Manag. 2018, 166, 500–511. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef]
- Han, X.; Ji, T.; Zhao, Z.; Zhang, H. Economic evaluation of batteries planning in energy storage power stations for load shifting. Renew. Energy 2015, 78, 643–647. [Google Scholar] [CrossRef]
- Parra, D.; Norman, S.A.; Walker, G.S.; Gillott, M. Optimum community energy storage system for demand load shifting. Appl. Energy 2016, 174, 130–143. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, Y.; Liang, R.; Jin, W. An allocative method of hybrid electrical and thermal energy storage capacity for load shifting based on seasonal difference in district energy planning. Energy 2020, 207, 118139. [Google Scholar] [CrossRef]
- Ding, Y.; Lyu, Y.; Lu, S.; Wang, R. Load shifting potential assessment of building thermal storage performance for building design. Energy 2022, 243, 123036. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Vecchi, A.; Ding, Y. Liquid air energy storage (LAES) with packed bed cold thermal storage–From component to system level performance through dynamic modelling. Appl. Energy 2017, 190, 84–98. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, W.; Ma, C.; Feng, B.; Sun, Q.; Li, H.; Wennersten, R. Assessment of the arbitrage by a compressed CO2 energy storage system—Based on dynamic modelling. Adv. Appl. Energy 2023. [Google Scholar] [CrossRef]
- Bao, G.; Lu, C.; Yuan, Z.; Lu, Z. Battery energy storage system load shifting control based on real time load forecast and dynamic programming. In Proceedings of the 2012 IEEE International Conference on Automation Science and Engineering (CASE), Seoul, Republic of Korea, 20–24 August 2012. [Google Scholar]
- CAISO. California ISO Today’s Outlook. Available online: https://www.caiso.com/TodaysOutlook/Pages/default.aspx (accessed on 25 July 2023).
- Zhang, K.; Kummert, M. Evaluating the impact of thermostat control strategies on the energy flexibility of residential buildings for space heating. In Building Simulation; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Zhang, H.; Zhao, J. Joint peak shaving energy consumption optimization model and simulation analysis of pumped storage power unit and coal-fired power units. Chem. Eng. Trans. 2016, 51, 1279–1284. [Google Scholar]
- Zhou, Q.; He, Q.; Lu, C.; Du, D. Techno-economic analysis of advanced adiabatic compressed air energy storage system based on life cycle cost. J. Clean. Prod. 2020, 265, 121768. [Google Scholar] [CrossRef]


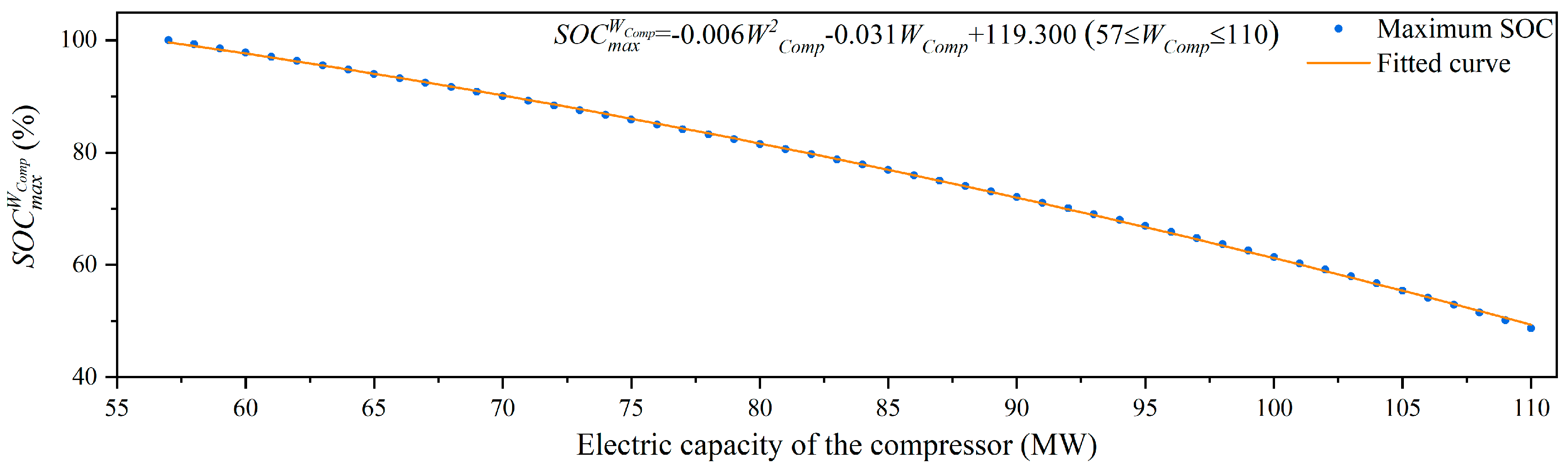
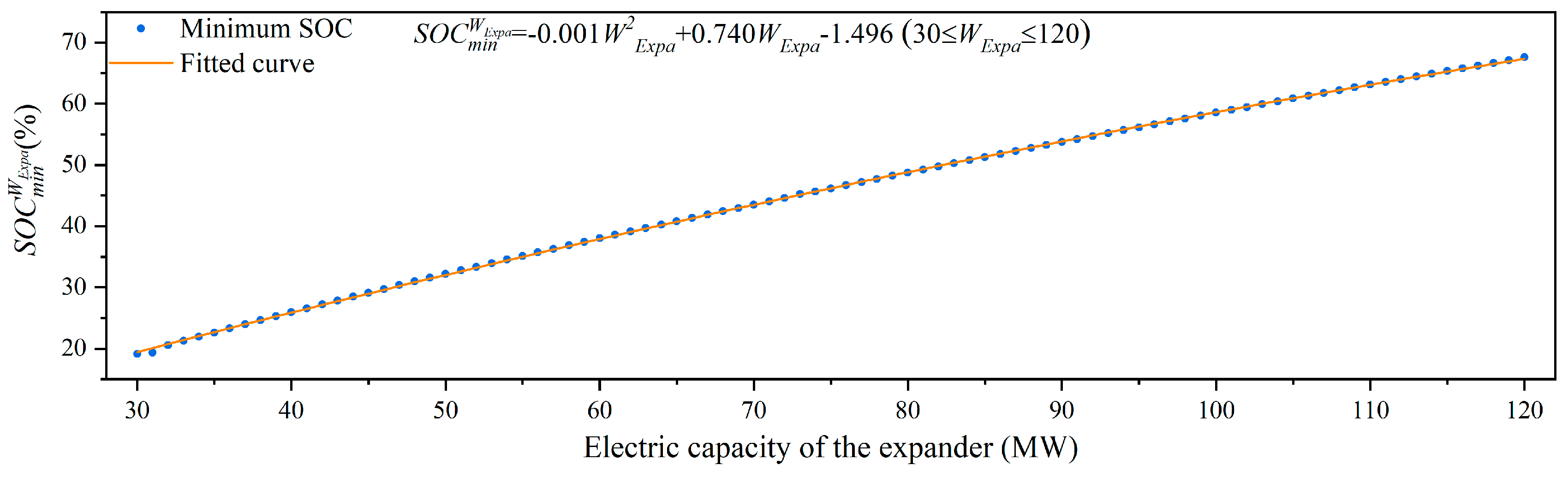

| Parameters | Value |
|---|---|
| Rated isentropic efficiency of compressor (%) | 89 |
| Rated isentropic efficiency of expander (%) | 88 |
| The volume of high-pressure gas tank (m3) | 7600 |
| The volume of low-pressure gas tank (m3) | 36,000.00 |
| The initial pressure of low-pressure gas tank (MPa) | 1.0 |
| The initial pressure of high-pressure gas tank (MPa) | 2.3 |
| Maximum pressure ratio of the compressor | 7.8–14.0 |
| Pressure ratio of the expander | 4.5–10.1 |
| Life cycle (years) | 35 |
| Investment cost (MUSD) | 36.6 |
| Flexibility Indicators | Summer | Winter | Transition Season |
|---|---|---|---|
| (MW) | 93 | 90 | 99 |
| (MWh) | 3845 | 4052 | 3816 |
| (MW) | 120 | 108 | 120 |
| (MWh) | 3846 | 3180 | 3735 |
| Season | Income (MUSD) |
|---|---|
| Summer | 0.63 |
| Winter | 0.29 |
| Transition | 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Yang, J.; Tian, S.; Huang, Q.; Wang, W.; Sun, Q.; Ren, X. Techno-Economic Evaluation of a Compressed CO2 Energy Storage System for Load Shifting Based on Dynamic Modelling. Energies 2023, 16, 7894. https://doi.org/10.3390/en16237894
Zhang B, Yang J, Tian S, Huang Q, Wang W, Sun Q, Ren X. Techno-Economic Evaluation of a Compressed CO2 Energy Storage System for Load Shifting Based on Dynamic Modelling. Energies. 2023; 16(23):7894. https://doi.org/10.3390/en16237894
Chicago/Turabian StyleZhang, Bin, Junbo Yang, Sule Tian, Qingxi Huang, Wei Wang, Qie Sun, and Xiaohan Ren. 2023. "Techno-Economic Evaluation of a Compressed CO2 Energy Storage System for Load Shifting Based on Dynamic Modelling" Energies 16, no. 23: 7894. https://doi.org/10.3390/en16237894
APA StyleZhang, B., Yang, J., Tian, S., Huang, Q., Wang, W., Sun, Q., & Ren, X. (2023). Techno-Economic Evaluation of a Compressed CO2 Energy Storage System for Load Shifting Based on Dynamic Modelling. Energies, 16(23), 7894. https://doi.org/10.3390/en16237894







