Abstract
Many technological advancements in the modern era have made actual use of electrical power and the constrained operating of power systems within stability limits. Some expeditious load variations and rising power demands initiate complications in voltage stability and can put stress on performance, leading to voltage instability. Voltage Stability Indices can be used to perform voltage stability assessment. This review evaluates various VSIs based on mathematical derivations, assumptions, critical values, and methodology. VSIs determine the maximum loadability, voltage collapse proximity, stability margin, weak areas, and contingency ranking. Stability indices can also specify the optimal placing and sizing of Distributed Generators. Thus, VSIs play a vital role in power system voltage stability. This review is a comprehensive survey of various indices and analyses their accuracy in determining the instability of power systems. Voltage stability is a crucial concern in operating a reliable power system, and the systematic evaluation of voltage stability is essential in a power system. This review considered and analyzed 34 indices from 138 articles from the literature for their significant performance in various power system stability problems. Of 33 indices, were 22 derived from transmission line parameters, referred to as line indices, and 12 from bus and line parameters, referred to as bus indices.
1. Introduction
Voltage instability is a crucial phenomenon that effects power systems because it is the main reason for blackouts and voltage collapse. Some unexpected consequences like an unexpected increase in load, line outage, and generator tripping may provoke an excessive load demand in the power system, leading to voltage instability. Consequently, a power system may be disrupted without appropriate action, resulting in cascading failures and large-scale blackouts. The notable blackouts around the world have primarily been caused by voltage instability. From [1], From 1965 to 2005, it can be seen that 22 significant backouts occurred; out of these 22 blackouts, 11 had voltage instability as a leading cause. Voltage instability is also known as voltage collapse; moreover, when instability is developing, the continuity of such events affects the system, resulting in low voltage and even more power outages [2].
According to an IEEE Power System Engineering Committee, “Voltage stability is the ability of a system to maintain voltage so that, when increasing load admittance, load power increases, and so that both power & voltage are manageable”. The consolidation definition of the IEEE and CIGRE is: “Voltage stability refers to the ability of a power system to maintain steady voltages at all buses in the system after being subjected to a disturbance from a given initial operating condition”.
Power system voltage instability may be due to the inadequacy of the source to deliver sufficient reactive power or to faulty power transmission lines not transmitting the desired reactive power. Voltage instability may affect the stability of a wide area or local area, resulting in the voltage collapse of a whole power system—mainly reliable active power delivered from the generators and reactive compensators like shunt capacitors. Voltage instability in a network is most probably the cause of unexpected load demand, transformer tripping, being over the limit of the generators’ reactive power, or defects in the on-load tap changing transformers. Consequently, the regular tracking and forecasting of instability are essential in the power system. In this respect, definite methods for suppressing voltage instability are:
- Strengthen the weak bus while planning the power system, like accurately selecting distributed generators and balancing voltage.
- Temporarily defending the supply by load shedding or improving the power factor by shunt capacitor switching.
- Enhancing the Voltage Stability Margin (VSM) with FACTS devices.
- Blocking on-load tap changers (OLTCs) to operate the transformer.
- Build the generation station near to the load centre and reduce the transmission line length.
- For executive controllers, make use of system voltage fluctuation controllers, Shunt Compensation, step-up transformer controllers, and Automatic Voltage Regulators (AVRs).
- For Real-time Performance: Scheduling the generation according to load demand, evaluating voltage stability, and protecting the load shedding.
- For safeguarding systems: Instant Load Tap Changer (LTC) control, Contingency of load demand, and High Voltage Direct Current (HVDC).
Indeed, over the past few decades, the reliability and stability of power systems have gone through considerable improvements. Stability analysis has evolved from simple static and transient stability analyses to more sophisticated and comprehensive methods.
Voltage Stability Indices (VSIs) generally measure voltage stability. The stability indices’ performance is essential in analyzing and illustrating the consequences of power system operation. Furthermore, the indices assist in predicting eventual improvement and determining long-term advancement. Especially in the last three decades, numerous techniques and methodologies have been developed for easy stability analysis. The performances of various indices for determining voltage stability have been explained in this review. For assessing a system’s stability, several indices consider the system impedance. However, few indices are unconstrained by impedance and performed using the current and voltage of the system. In real-time operation, it is impossible to determine the accurate impedance of a system because of troposphere conditions and inadequate knowledge of the system. Therefore, the accuracy of the impedance-operated indices is repeatedly accompanied by errors.
A taxonomy of comprehensive characteristics, variations in accuracy, and some parameters being inaccurate is presented below, as well as the terminology concerning VSIs, including mathematical derivation, instability conditions, and assumptions of specific parameters. This taxonomy can serve to make researchers aware of the advancements in the VSIs, and the respective operations including voltage stability enhancement, strengthening the weak bus, locating the reactive compensation devices, reducing the cost-effectiveness and location of FACTS devices, and counteracting the prevention of voltage collapse.
Determining the VSI values for a system is carried out in three modes of operation. One is the online mode: In this mode of operation, the engineer observes the voltage stability and operates accordingly to maintain the system’s stability. The statistics used for this in this paper were composed of mathematical models and power system measurements. The second mode of the stability indices is the offline mode: In this mode of operation, the designer gathers the simulated or historical data. The preserved data identify the voltage instability intensity and voltage collapse and do not contain real-time data on voltage instability. The real-time method is the third mode of stability indices, and is obtained using a Phasor Measurement Unit, Power Flow Analysis, and Artificial Intelligence.
This article aims to thoroughly review and scrutinize numerous Voltage Stability Indices. This review indicates the limitations, strengths, underlying principles, and applicability of these indices by sharply examining them. This article provides clarity to researchers, engineers, and power system operators in choosing suitable stability indices depending on the particular characteristics of a system and functional needs. Researchers will gain synthesized knowledge of Voltage Stability Indices, as this article presents the diverse range of stability indices with mathematical formulations, highlighting their peculiar characteristics and underlying principles. This review supports decision-making for system operators with the knowledge needed to estimate instabilities and ensure voltage stability, sustainable energy supply, and grid reliability.
2. Voltage Stability Indices
Voltage Stability Indices are values of an arithmetic sequence adopted for evaluating voltage stability. The indices specify the accessible and equitable regulation of the system’s stability so that voltage levels are within sustainable limits. Indices predominantly assist power engineers in determining voltage stability, predicting voltage collapse, and evaluating the significance of system characteristics. This review elaborates on the numerous methodologies for assessing voltage stability. Furthermore, categorizing the different VSIs in [3,4,5] as line VSIs, Bus VSIs, and overall VSIs. Jacobian matrix-based indices and PMU-based indices fall under overall VSIs.
The overall VSIs’ precision is superior compared to the other stability indices. The overall VSIs are challenging to determine and take more computation time. Line VSIs obtain easy and simple indices that are reasonable in determining all optimization issues through the proficiency of these indices and identifying the critical line and weak bus. These VSIs are derived from a mathematical equation by considering the standard two-bus concept. With these mathematical derivations, the system examines the stability of various stability indices. Similar aspects of voltage collapse points determine the VSIs’ formation. Figure 1 represents an illustration of the interconnected network with a single line in a standard two-bus model.
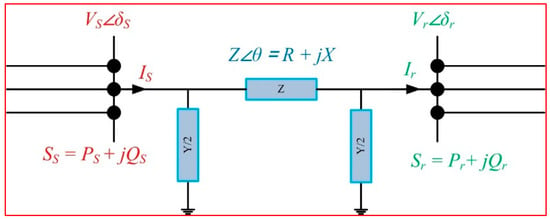
Figure 1.
Standard two-bus model.
Jacobian matrix-based VSIs specify the scope of system stability, determine the voltage collapse point, and evaluate the VSM. However, they consume more time for computation, and in general, mathematical topology variations compel the transformation of the Jacobian matrix, causing the matrix to need to be again; therefore, they are inconvenient in real-time applications. Additionally, Jacobian matrix indices tend to increase the operational time of DG placing and sizing issues. However, the VSIs established by system variables claim lesser computational time and are acceptable for real-time operations. The detriment of these stability indices is that they are less accurate in evaluating the VSM. Consequently, they are not as accurate in determining the weak line and critical bus. In most applications, like placement of the DG and sizing issues, VSIs prevail for identifying the weak bus and critical line or stimulating the deterrents for voltage instability.
Vs, Vr: magnitude of bus voltage at sending and receiving bus; Ss, Ps, Qs: apparent, real, and reactive power at sending bus; Sr, Pr, Qr: apparent, real, and reactive power at receiving bus; δs, δr: voltage angle at sending and receiving bus; R, X, Z, θ = line resistance, line reactance, line impedance, and line impedance angle.
Considering the Kirchhoff Voltage Law (KVL), the current equation for two buses is,
Substituting Equation (3) in Equation (2), we obtain:
Let δs − δr = δ and simplify Equation (5) as:
Transforming VsVr into a rectangular form, we obtain:
Segmenting Equation (7) into real and imaginary parts, we obtain:
Readjusting Equations (8) and (9), we obtain:
Substituting Equation (11) in Equation (10) and vice versa, we obtain:
Rearrange Equations (12) and (13) allows us to obtain:
For a few VSIs, the line resistance (R) and reactance (X) increase with the impedance (Z) and impedance angle (θ); therefore, reducing the current equation, Equation (3) is redefined as:
Substituting Equation (16) into Equation (1), the receiving end’s apparent power concerning the real and reactive power is:
Assuming then Equation (17) is simplified as:
Equating the real and imaginary parts of Equation (18), we obtain:
Simplifying Equations (19) and (20), we obtain:
Most of the stability indices were derived mathematically; the quadratic equation’s voltage discriminant is greater than or equal to zero. The characteristics vary for the index, so different assumptions are considered for deriving the stability indices.
2.1. Line Voltage Stability Indices
2.1.1. Voltage Stability Load Index (VLSI)
The Voltage Stability Load Index (VLSI) derives from the mathematical derivation [6] of a standard two-bus system and Thevenin equivalent circuit. Figure 1 presents the voltage equation considered in this index, obtained from the network. Moreover, we determine the power flow by performing a power flow analysis directed toward speedy converging. Considering the square of the sending-end current, receiving-end active and reactive power with losses, we obtain:
We then substitute Equations (24)–(27) in Equation (23) to simplify it, resulting in:
The analyzed equation is further reduced by equating it to zero and obtaining the sending end voltage equation:
If the obtained receiving end voltage quadratic equation contains real roots, then the discriminant is greater than or equal to zero; hence:
Accordingly, L represents the voltage stability load index,
since
Hence, the value L should be less than 1.0 for the system’s stability. Whenever the index value is more significant than 1.0, corresponding to Equation (32), the voltage emerges as imaginary and collapses. To defend the load instability, the load index value must be Li ≤ 0, and if Li is nearer to 1.0, then bus ‘i’ approaches the stability limit.
2.1.2. Line Stability Index (Lmn)
The Line Stability Index is determined in [7] and derived from the voltage quadratic equations discriminant. Considering this index and Equation (20), we can derive Vr:
Assuming Zsinθ = x,
The above voltage equation should have real roots to obtain absolute values of Vr in terms of Qr. Therefore, the following condition is to manipulate the stability of the system.
Lmn represents the stability index of the line. Voltage collapse is predicted rigorously depending on the stability index’s value. If the obtained value of Lmn is lesser than the unity, then the system is in a stable condition; otherwise, if the value is more significant than the unity, then the system exhausts the stability; moreover, the voltage collapses.
2.1.3. Line Stability Factor (LQP)
The Line Stability Factor (LQP) developed in [8] makes use of a similar theory of the discriminant of the voltage quadratic equation, primarily from receiving end real power:
Reorganizing the power equation as allows us to obtain the roots of Ps:
From Equation (40), it is clear that the system loses its stability when it violates this condition. Further, deriving the reactive power is similar to the derivation of active power:
Since LQP < 1, the system is stable. Here, for deriving the index, it is assumed that the lines are lossless (R/X << 1) and neglect the shunt admittance.
2.1.4. Voltage Collapse Proximity Index (VCPI)
The VCPI [9] evaluates the line voltage stability depending on the theory of maximum power. The analysis assumes a frequent occurrence and varying of the absolute impedance value by keeping ϕ constant. With this inference, the performance may not be accurate, but it is easy to solve. During the operation, the power factor remained constant.
Along with the load demand increase, the current increases with a decrease in Zr, resulting in a receiving-end voltage drop:
Hence, the receiving-end power is Pr = VrIcosϕ and Qr = VrIsinϕ
Simplifying Equation (44) with that for power, we obtain:
Correspondingly, the power loss is and .
Substituting the current equation, we then obtain:
Considering the boundary condition allows us to calculate the maximum active power delivered at the receiving end. Hence, this condition results in the impedance Zr/Zs = 1. The maximum power transfer obtained by substituting this ratio in Equation (45) is:
Similarly, adopting this approach, the following power equation can be derived:
Considering these maximum limits, Voltage Collapse Proximity Indicators can be designed as:
The system may collapse if the values of the VCPIs are more significant than the unity. Therefore, VCPI (1) = VCPI (2) and VCPI (3) = VCPI (4), since only active or reactive terms were considered instead of all proximity indices.
2.1.5. Voltage Stability Index (Lp)
The line stability index proposed in [10] is a similar mathematical formulation to earlier line VSIs. Basically, from the active and reactive power equations, i.e., from Equations (19) and (20), δ can be derived as:
Reorganizing Equation (19) and deriving the voltage equation Vr, we obtain:
Hence, the Vr equation should possess real roots for obtaining the absolute values of Vr expressed in terms of Pr. Accordingly, it is then simplified to be enough to withstand the following conditions:
LP is a line stability index that determines the condition of the transmission line and indicates instability limits. If the calculated value of Lp is more significant to the unity, the system approaches instability. The voltage collapses when the system exceeds the critical limits; moreover, the Vr becomes imaginary.
2.1.6. Fast Voltage Stability Index (FVSI)
The Fast Voltage Stability Index is derived in [11] primarily by considering the current through the line and then calculating the absolute roots of a receiving-end voltage (Equation (15)):
For determining the absolute roots of Vr, the Vr discriminant is greater than or equal to zero.
The angular difference is minute; thus, , Rsin ≈ 0, and Xcos ≈ X. As a result, Equation (62) can be simplified as:
The line is in-transit to the instability limit if the FVSI value is adjacent to 1. With further increases in a stability index value, that line may encounter an unexpected voltage drop accompanying system collapse.
2.1.7. Voltage Stability- Load Bus Index (VSLBI)
VSLBI evaluates the voltage stability by adopting the PMU [12]. Considering the maximum power condition, this stability index is subject to a voltage-drop ΔVr over the transmission impedance Zr that is equivalent to load bus voltage Vr:
ΔVr = Vr
Accordingly, to approach the voltage collapse exposure during the constant power loads, the Voltage Stability Load Bus Index (VLSBI) is represented as:
If the obtained value of the VSLBI is more significant than the unity, then the system is considered stable; if the VSLBI is less than 1, then the system is unstable, and the system may collapse.
2.1.8. Voltage Stability Margin Index (VSMI)
The VSMI, proposed in [13], depends on the correlation between the power transfer from the line and the angular difference between the sending- and receiving-end buses. To derive the fundamental equations of real and reactive power, the receiving end voltage is:
Since , considering Equations (66) and (77), the power Pr maximum value can be calculated for whatever the value of Qr/Pr is. The respective angular differences of the sending- and receiving-end buses (δ), and the receiving-end voltage (Vr), are expressed as:
for any ratio of Qr/Pr
With the correlation between the voltage stability and angular difference, the voltage stability margin that is determined depends on what degree of δ is adjacent to δrmax. Therefore, whatever the operating constraints, the receiving end index can be represented as:
The calculated value of the VSMI should be higher than zero to sustain the system’s stability and protection.
2.1.9. Voltage Collapse Proximity Index (VCPI_1)
The significant motive of VCPI_1 is that, during the voltage collapse, the voltage drop at the Thevenin impedance equals the load voltage. The proximity index derived in [14] is denoted as VCPI_1 to prevent confusion from the VCPI notation. An easy arithmetic prediction indicates that, during the critical situation, the generator phasor voltage () is double the load phasor voltage, . Hence, for the estimation of the possibility of voltage instability, VCPI_1 is represented as:
If the VCPI is greater than or equal to zero, then the system is stable, otherwise it is unstable. In this index, the lines are complicated. However, considering that the sending-end bus connects to the ideal voltage source, the receiving end with the equivalent Thevenin impedance is neglected.
2.1.10. Critical Voltage (Vcr)
The Critical Voltage is an intelligible index that is derived from a single load, an infinite bus system utilizing the Eigen-value theorem, and load flow equations [15]. In this paper, it is used for adapting the power factor cosϕ to be constant. From the active and reactive power flow equations, the bus voltage angle δ is eliminated, and the resulting equation is:
Corresponding to favorable circumstances, Equation (72) contains a specific solution; moreover, the correlation between the , vectors is developed as:
The load bus critical voltage is denoted by Vcr (P-V Curve nose point). V+ and V− are the P-V curves’ upper and lower parts, respectively. Nearer to this, V+ and V− are superposed values of Vcr. The indices concern the maximum power limit as a stability limiting point. Evaluating the simple system by the constant MVA load and cosϕ power factor, Equation (72) is:
To obtain the maximum S, dS/dV is equated to zero. Accordingly:
After the phasor relationship, further reducing Equation (76) allows us to obtain:
2.1.11. Power Transfer Stability Index (PTSI)
The Power Stability Index proposed in [16] is derived with the help of a standard two-bus Thevenin-equivalent system; here, the slack bus and the load bus were connected on a single branch, as represented in Figure 2. The current delivery to load and load power is:
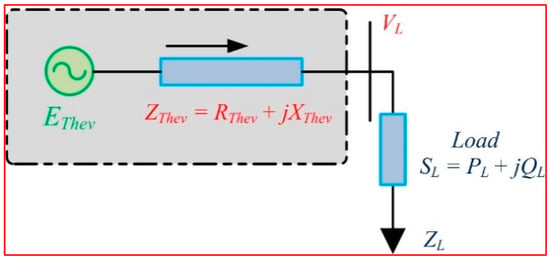
Figure 2.
Simple two-bus Thevenin Equivalent Circuit.
Substituting Equation (78) in (79), we obtain:
Assuming that and , and alternating them into Equation (80), we obtain:
To obtain the maximum value of the apparent power of the load, the SL is differentiated and equated to zero, .
The power margin at the load bus distance when it is approaching voltage collapse is SLmax – SL. If ZL = ZThev,, the power margin is equal to zero; moreover, it indicates no power transfer and may cause voltage collapse. Conversely, a voltage may collapse if the ratio of power is:
Substituting Equations (83) and (84) in Equation (85), the power transfer stability index is:
The value of the PTSI is determined with Equation (86), considering the load’s power, impedance, Thevenin Voltage, Thevenin Impedances, and the Angular phase of the load. The obtained PTSI value lies between 0 and 1. Voltage collapse occurs when the index value reaches 1.
2.1.12. Voltage Stability Index (VSI_1)
The stability index predicts the voltage stability at the steady state operation; this index is proposed in [17]; however, for easy identification, the notation of the stability index is represented as VSI_1. Initially, this index calculates the maximum active, reactive, and apparent power transfer. To obtain the receiving-end voltage (Vr), considering the Equation (19) for active power (Pr) and Equation (20) for reactive power (Qr), we obtain:
Here, , A ≥ 0.
Transmission lines containing a higher X/R ratio and ignoring the resistance value, resulting in Pmax, Qmax, and Smax, can be derived as:
The derived maximum powers identified that the maximum power transfer increases with an increase in the voltage magnitude (Vr) or a decrease in the impedance (ZL). Equivalently, Pmax decreases with an increase in Q, and Qmax decreases with an increase in P.
From the maximum powers, the corresponding load margins can be obtained with Equation (94). Hence, the derived VSI from the obtained load margin is represented in Equation (95). If the obtained VSI is small, the load bus is adjacent to the stability margin and the lesser load margin that is available. The VSI equals zero if the load bus reaches its stability margin point.
2.1.13. Novel Line Stability Index (NLSI)
The NLSI is determined with a similar power transmission approach [18], considering the quadratic Equations (8) and (9):
The discriminant should be greater than or equal to 0 to obtain the absolute value of Vr.
As the angular difference (δ) between receiving and sending ends is usually very small, cosδ ≈ 1. Subsequently, the Novel Line Stability Index can be represented as:
If the value of the NLSI of any line is adjacent to 1, that line is moving closer to the stability limit; consequently, the system may collapse. Hence, the NLSI allows us to find the stability limit, i.e., the index value is lesser than the unity.
2.1.14. Stability Index (SI)
For load flow analysis, the quadratic equation is preferable for calculating the sending-end voltage of a line and can be simplified in general form as:
Further, the receiving-end line active and reactive power is derived as:
Therefore, to obtain the absolute value of the active and reactive power, the corresponding equation should satisfy the following:
Adding both equations, we obtain:
The above equation illustrates that equation values decrease with increased power and impedance. Moreover, Equation (104) considers a stability index [19].
Therefore, the classic stability principle determines the stability index for individual lines of radial distribution networks. The minimum stability index value is the most vulnerable to collapse. If the index is equal to zero, then the system collapses. Here, also, neglecting the shunt admittance to determine the stability index will lead to collapse.
2.1.15. Voltage Stability Margin (VSM)
VSM technique [20] is when the admissible rise in load power occurs during the current operating mode or the critical mode. Considering Figure 1, the voltage (Vs) and load apparent power (SL) are derived as follows:
Concerning the critical point, the load power attains the maximum value and can be written as:
Zr is the available load impedance, and the variation between Zr and Z0 is assumed as an invulnerability limit. Accordingly, the VSM in terms of impedance is as follows:
The allowable power increases until the stability limit is contingent to a higher degree on the angle of the load power factor with a similar VSMs. Therefore, it can be enhanced to signify the margin concerning the load apparent power, VSMs.
Hence, the margin of the apparent load power is derived from the VSM. Two assumptions for the stability margin are (i) that the line shunt admittance neglected and (ii) a constant power factor. The system is unstable when the apparent load power is more significant than the critical one. Even if the value of the VSM is less than zero, the system is unstable.
2.1.16. Voltage Reactive Power Index (VQI)
The line index proposed in [21] has a similar methodology to that of Lp. To insert the relation between the voltage (Vs) and reactive power (Qr) comprised from Equation (19) into Equation (18), we obtain:
As the value of δ is negligible and minimized to zero, then the entire term of (sin(θ − δ)/sin(θ)) is omitted:
Replacing the term Yrs sin(θ) with Brs,, the corresponding equation is:
Extracting the real roots of the quadratic equation in terms of Vr, we obtain:
When the discriminant of Vr equates to zero, the respective equation contains one distinct real root, or two equal roots. Hence, the respective real roots are:
The value of Vr ranges from 0 to 1, illustrating the limitation of real roots as the voltage stability limits. Moreover, real roots should be less than 1 and greater than 0, or the stability is affected. Thus, the derived equation evaluates the system stability and identifies the voltage collapse point as the voltage reactive power index.
If the obtained value of VQI is nearer to 1, then the system is within stability limits. Otherwise, a system beyond the stability limits leads to instability. VQI also identifies the instability point of occurrence and voltage collapse.
2.1.17. Line Collapse Proximity Index (LCPI)
An improved LCPI was developed in [22] to overcome the limitations of specific indices [7,8,11] which ignored the line charging reactance while deriving their values. Since the line charging reactance is a critical factor supporting voltage stability, this proximity index was derived considering the definite transmission line model as well as the consequences of active and reactive power flows through lines. The definite transmission line model primarily represents an equivalent circuit of a two-port network considering the ABCD matrix. Thus, the proposed proximity index is derived from the ABCD matrix.
Hence, the transmission line parameters for a two-port circuit are A, B, C, and D.
Considering the receiving-end current, the sending-end voltage Vs is derived as:
A and B are magnitudes, and their corresponding phase angles are and , respectively. Combining the current with the voltage equation, we obtain:
Here, . Ignoring the imaginary part and considering the real part of the above quadratic equation, we obtain:
Obtaining the roots of the quadratic equation allows us to obtain:
It should contain the actual non-zero values of the Voltage equation and the actual non-zero roots obtained from the voltage equation discriminant.
Therefore, to maintain the system as stable and prevent voltage collapse, the following conditions should be satisfied:
Therefore, the index value should be less than 1 to maintain the system stability, i.e., LCPI < 1. At no load, the LCPI value is zero, and the LCPI value is adjacent to the unity during the system instability.
2.1.18. New Voltage Stability Index (NVSI)
The NLSI derived in [23] is a similar concept of the power transmission quadratic equation represented in Equation (8). Determining the NLSI is similar to the process for determining Lp. Neglecting δ, Equations (19) and (20) represented as:
The Voltage Equation Vr is a second-order equation. The limitation to possessing at least one solution is:
Hence, to sustain stability, the value of the NLSI must be less than 1.00 in order toobtain the NLSI by neglecting the line resistance and line shunt admittances.
2.1.19. Integrated Transmission Line Transfer Index (ITLTI)
An integrated transmission line transfer index depends on the radial topology. The ITLTI’s purpose is identifying the power transfer; moreover, it identifies the weak line depending on the transmission line parameters, consequent to the unity, lagging, and leading power factor states. The transmission line in Figure 1 depicts a constant sending-end voltage transferring the power Ss. Hence, the functional ABCD parameters represent the receiving-end power Sr, Voltage Vr with the respective power factor angle θr. Further, the receiving-end complex power is derived as:
Equivalently, the sending-end complex power is represented as:
Considering the radial transmission line [24], we obtain two-power circles with the same radius and two different centers. Receiving-end complex power circle polar coordinates are represented in Figure 3 with a variable power angle δ.
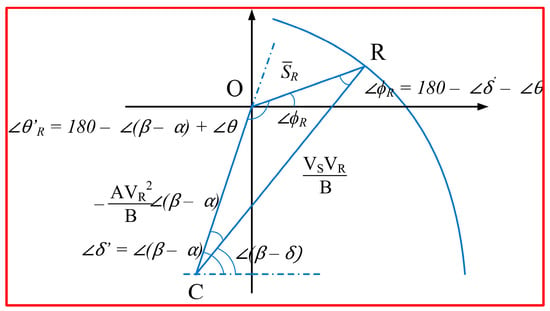
Figure 3.
The receiving-end circle.
Considering the receiving-end circle and ΔOCR, we obtain:
Therefore, the relation between the receiving-end and sending-end voltage can be derived by . Accordingly, an increased power angle at distinct power factors decreases the receiving-end voltage. The receiving-end power magnitude is:
To deliver the maximum power, Sr is partially derived using δ’ and is equated to zero, which determines the critical value of the power angle.
Critical voltage value:
Maximum Power Transfer:
The maximum limit of the receiving-end power for different power angles is as follows:
Moreover, the integrated transmission line transfer index (ITLTI) is expressed as:
Hence, the ITLTI determines the system’s stability for all healthy operations. Determining the Sr_index with varying power angles, the maximum value should be 1; if it exceeds 1, the system is unstable. Therefore, the index value is maintained at less than 1. The loadability concerning the critical power angle increased with an increase in the receiving-end power factor, irrespective of leading or lagging operations. Separating the active and reactive power of Sr, the active power Pr is expressed as follows:
2.1.20. Critical Boundary Index (CBI)
The Critical Boundary Index derived in [25] considers the active and reactive power variations and utilizes arithmetical methods to determine the critical boundaries. This index is preferable because of its high accuracy in predicting system performance and analyzing and adding the actual (Equation (8)) and imaginary (Equation (9)) parts of the power flow equation (Equation (7)).
Imagining that the intensity of the receiving-end and sending-end voltages is more significant than zero, and rearranging Equation (141), we obtain the following:
Hence, the above equation examines that the power transmission had limits for a specific time duration. Those limits are acknowledged as power and voltage stability limits. These limits are logical only when the magnitude of A is 0. Hence, determining the Qr when A = 0 is written as follows:
We plot the power stability limit P-Q characteristics with Qr. The P-V characteristic is the nose curve. The power system stability in Figure 4 includes the unstable and stable boundaries, starting from a current stable point K (Po, Qo) and reaching a critical boundary point C (X, Y). Considering the Lagrange Multipliers, Equation (141) simplifies as:
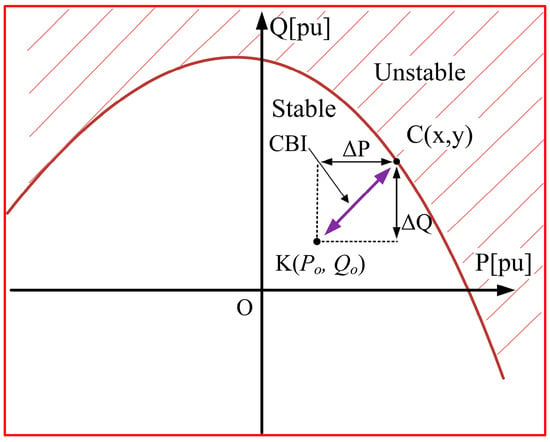
Figure 4.
P-Q Characteristics.
The function f (X, Y) is the length between the current stable point K (Po, Qo) and the adjacent point of voltage collapse C (X, Y). The displacement of f (X, Y) is shown as:
Here, the ΔPik, ΔQik, stability evaluation index, and displacement in the stability curve are represented in Figure 4. Further, as shown in Figure 1, the operating point between the sending-end and receiving-end transmission line can evaluated by:
Due to its high-accuracy prediction, this index is preferable. If the index is close to zero, it is the worst-stability system.
2.1.21. Line Voltage Stability Index (LVSI)
A novel LVSI developed to overcome existing stability indices’ drawbacks, LVSI [26], is derived from the quadratic voltage equation. This index is also derived considering the transmission line ABCD parameters; moreover, the inclusion of line charging capacitance and resistance is ignored by existing stability indices. Consequently, this index evaluates the voltage sensitivity accurately, subject to all circumstances, and predicts the voltage collapse point. The receiving-end active power in terms of transmission line parameters is obtained using:
Rearranging the power equation according to a quadratic equation of voltage is obtained as:
The derivation of the voltage concerning the active power to obtain the sensitivity is shown as:
Hence, the sensitivity should be negative to maintain the system’s stability.
Further simplifying Equation (151), the stability index can be shown as:
It is highly stable if the index value is 2 at no load. If the index value is 1 at the maximum load, it is a collapse point. Therefore, the system to maintain the stability index value must be greater than the unity.
2.1.22. New Line Voltage Stability Index (BVSI)
The index BVSI derived in [27] depends on the power transmission approach. Considering Equation (14), the quadratic equation can be rearranged as follows:
Deriving the quadratic equation roots, we obtain:
For determining the absolute and non-zero values of Vr, the discriminant is made greater than or equal to 0:
Therefore, the index value is less than the unity for the system to be at the stability limit, such that the index value lies between 0 and 1. If the BVSI value exceeds 1, the corresponding line encounters a voltage drop, and the system may collapse. The BVSI line ignores the shunt admittance and the effects of reactive power on stability.
2.2. Bus Voltage Stability Indices
The Bus Voltage Stability Indices evaluate the transmission bus’s voltage stability and do not derive the weak characteristics of the potential voltage issues across the system. Therefore, Bus VSIs are unable to be utilized for determining weak performances.
2.2.1. L-Index
The L-Index [28] is derived from the power flow and standard two-bus system and obtains a detailed analysis. The L index determines peculiar characteristics of power system susceptibility, measuring significant active power, restructuring weak areas or buses, predicting voltage collapse, and identifying instability. Considering the matrix Fij of an ith column and jth row, and elements obtained from the Y matrix, αL, and αG are the load bus and generator bus. The linear transmission system represents a Hybrid matrix (H).
Here, VL, IL: Voltage vector, Current vector at load nodes; VG, IG: Voltage vector, Current vector at generator nodes; ZLL, FLG, KGL, YGG: H submatrices. By partial inversion, the H is obtained from the Y-matrix. For any load node j, j ∈ αL, and the corresponding voltage equation Vj is:
Substituting the equivalent voltage Voj, admittance Yjj+, and power transferred Si+:
Hence, Sj+ contains two parts:
The exceptional characteristic of Equation (159) is that its formation is similar to the admittance equation. Dissimilarities exist between the equivalent voltage Voj and power transferred Sj. The voltage Voj varies slightly, not remaining as a constant value, since the generator voltage remains mostly constant at varying loads. Adopting these limitations can evaluate and regulate local indicators, and Lj can allow us to design for every node j corresponding to the line.
Under stable operations, the Lj ≤ l condition should never disobey any node j. Therefore, the global indicator L represents the stability of the entire subsystem, expressed as:
Here, a series of load nodes is αL, and a series of generator nodes is αG. If the L index value is 0, the system is stable; if the value is 1, the system is approaching instability.
2.2.2. Voltage Instability Proximity Index (VIPI)
The proximity index derived in [29] for estimating instability depends upon coordinating various load flow solutions and instability. The VIPI is a scalar index that analyses the stability margin, considering the angle separating the critical and specified-value vectors. The power flow equation in terms of rectangular coordinates is as follows:
Here, Ys is the specified value; x = ; ei = Bus voltage real value; fi = Bus voltage imaginary value. Assume two types of voltage vectors (Figure 5): x is the operating solution, and x* is the fictitious solution; comply with the uniform specified-value vector. Employing critical vector (a) and deflection vector (b), x and x* can be represented as x = a + b, x* = a − b. Further simplifying them, .
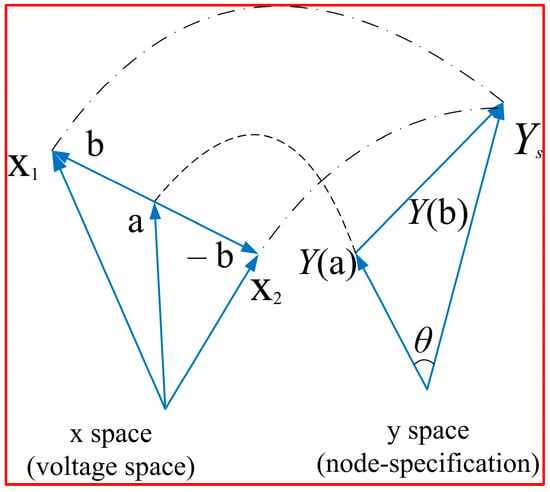
Figure 5.
Concept of VIPI in the Node-Specification Space.
As this proximity index is the angle separating critical vector Y(a), and specified value vector Ys, the VIPI is as follows:
Here, θ is the angle separating two vectors; critical vector Y(a) is in the space of node specification.
2.2.3. Voltage Collapse Proximity Index (VCPIBUS)
VCPIBUS, proposed in [30], is derived out of the standard power flow equation, and considering a network’s voltage phasor measurement and admittance matrix determines the VCPI at every bus. The complex power at bus k of an N bus network is represented as:
The term in the above equation is expressed as:
Hence, the right-hand term in Equation (168) is complex in the form of a − jb. Let the two equations contain two unknown terms (Vk, δ).
A partial derivative matrix is attained by simplifying two equations for evaluating the unknowns with the Newton-Raphson Methodology. During the voltage collapse, the matrix determinant is equal to 0, which results as:
Further simplifying Equation (172), the voltage collapse prediction index (VCPI) determined at bus k is:
Therefore, the above equation is the voltage collapse condition for bus k. The VCPI value fluctuates between 0 and 1, where 0 represents a stable system, and 1 represents voltage collapse.
2.2.4. S Difference Criterion (SDC)
The S Difference Criterion (SDC) [31] needs a protective relay to perform arithmetic derivation and utilizes the successive evaluation of apparent power (S) at the relay point. During the voltage instability environs, the inflation of sending-end power flow delivers the transmission losses. Consequently, the rise in the sending-end apparent power does not afford a rise in receiving-end power. It specifies that ΔS = 0 at the relay point during the voltage instability. Hence, the transfer of apparent power to the receiving end is:
Considering the change in a time period Δt, the time interval changes to tk = tk + Δt. A respective rise in apparent power is as follows:
Here, the term is very small and can be ignored.
Thus, the SDC is a positive real value; then, considering the magnitude of Equation (177), we obtain:
Intending to achieve voltage collapse, the value of ΔS = 0, and correspondingly, the SDC equates to 0. The relay operates if the SDC value is below a predetermined threshold.
2.2.5. Impedance Stability Index (ISI)
The ISI bus stability index depends on Tellegen’s rule, an index derived in [32] made simple in evaluating Thevenin’s variables. Let a bus r with a complex load (Sr) and impedance (Zr) be linked to a power system; the remaining system is expressed as Thevenin’s equivalent with the variables E and Zth. Let the current equation be:
Sr/Vr = Ir* = ((E − Vr)/Zth)*
Vr(E − Vr)* − SrZth* = 0
Two voltage solutions empower the phasor of Equation (180) with a power Sr; if the two solutions are equal, it allows maximum power transfer.
Vr = (E − Vr)*
Equation (181) is fundamental to a local voltage stability approach that conveys predetermined consequences through circuit theory.
The system delivers the maximum power when the load-impedance magnitude equals Thevenin’s impedance magnitude. The adjacent Thevenin network possesses an identical analysis to the base network N. Hence, the derivation is similar to putting a hat (^) on every term, which signifies the adjoint network parameters. The divergence order of Tellegen’s theorem is equivalent to the following:
Here, and Express the advancement of the complex voltage and current at bus ‘r’ regarding the Vr and Ir* base values. The adjacent network load impedance is described as a ratio of phasor voltage to phasor current .
The load impedance specifies that it is the base case; moreover, it is determined at an instant earlier than that of the network that is regulated to power disturbances.
For determining the Thevenin’s impedance, the current equation is substituted in Equation (183) from Equation (179).
Similarly, from Equation (181), the condition for the maximum power transfer of adjacent network can be expressed as:
Analyzing Equations (187) and (188), during the system collapse point, the equivalent Thevenin’s impedance is expressed as:
However, the above two equations are conjugate with each other; for discarding the conjugate values, Thevenin’s impedance absolute value is as follows:
The contingency during the regular loading is:
During the commencement of voltage instability, the dissimilarities among these impedances converge to 0. Moreover, at that instant of collapse, the impedances are identical, i.e., .
This index precisely determines Thevenin’s impedance by evaluating the advancement in voltage and current following the base-case exposure to disturbances. Furthermore, the load impedance is evaluated through the ratio of the voltage to the current. Using Equations (192) and (193), a modest regulated impedance stability index (ISI) for identifying the voltage stability margin is:
Further simplifying by substituting the impedances in terms of voltage and current, the stability index derives as:
2.2.6. Voltage Stability Index (VSIBUS)
The VSI bus index relies on system elements to identify the distance between the operating and collapse points. This index [33] derives from power flow equations that are similar to the assumptions of the SDC. Let ‘i’ be one local bus of the system. The complex load power of bus i is:
The complex bus voltage is Vi = Vi∠δi, and the complex load current is Ii = Ii∠(δi − θi). Employing Taylor’s theorem, the interrelation among the advancement difference between Vi and Ii as a consequence of advancement evolution in Si is expressed as:
Meanwhile, ignoring the higher-order terms,
Usually, if the load increments, there is a corresponding increase in load current and decrease in load voltage. This means that, if the value of is positive, Current is positive and the Voltage is negative. Although the bus reaches a critical point or voltage collapse, adding additional load on a bus might not be able to raise the apparent power Si of the load due to rapid decrement in voltage in contrast to the current increment. Going through this case converges ΔSi to zero. Accordingly, the power through the voltage-stability limit is expressed as:
Considering that the power of Equation (199) is made to α (>1.0), an actual value, it determines almost the same level of linear characteristics. Therefore, excluding the general loss, the voltage stability index at the ‘i’ bus is as follows:
Hence, at no load, the VSI varies from 1, and at voltage collapse, the value varies to 0.
2.2.7. ZL/ZS Ratio
The ZL/Zs ratio index proposed in [34] depends on a similar technique to the ISI. The correspondence index is the load bus impedance (ZL) ratio to Thevenin’s impedance (Zs). The voltage stability margin was generally evaluated from different scenarios. The evaluation of the stability margin depends on the determination of the voltage stability. For an equivalent circuit, the derivation of the apparent load power concerning load admittance is as follows:
Whereas Y = 1/ZL, dividing both sides of the equation with V2:
While dS*/dY* = (Y/S) (dS/dY), thenthe Equation (202) together evaluates (ZL/Zs):
Here, M = (dS*/dY*), and the relevance between ZL/ZS and M relies upon the angle β. The estimation of β is a phase angular difference between the source and the load, i.e., β = φS − φL. The definite value of φS operates on the existent form of the system. The parameter M is determined by evaluating the derivative of the apparent load power to admittance:
Here, S and Y refer to the load power and admittance, respectively. Moreover, suffixes 1 and 2 refer to the starting of a change (time, t1) and completion of the change (time, t2), respectively. The variation between the two-time measurements needs to be around 500 ms. If the index value remains above 1, it is a reliable condition.
2.2.8. Equivalent Node Voltage Collapse Index (ENVCI)
The index ENVCI depends on the ESM (Equivalent System Model) and local voltage phasors [35]. The ENVCI has numerous advantages like accurate evaluation and modeling; moreover, this index is convenient for performing real-time and online operations. The outgoing power at node N of a single-line equivalent model (Figure 6) should perform the consequent equation of plain power flow.
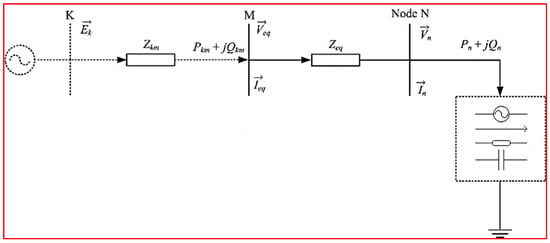
Figure 6.
Equivalent System Model.
Let the phasor voltage equations for two nodes of a single-line equivalent network in terms of rectangular coordinates be and , then the corresponding line impedance is Zkn = Rkn + jXkn. Separating the real terms and imaginary terms of the power flow equation, we obtain:
Hence, the power flow equation, Equation (206), is crucial for determining the phasor voltage at the receiving node, describing the system’s performance. In contrast, the phasor voltage of the sending node is known. Whenever the respective ESMs of all equivalent lines possess an arithmetical solution of the receiving node, signifying that they contain every node voltage of the system, at that instant, the system should possess a complete power flow solution; moreover, this should influence the voltage stability. The system’s stability relies on evaluating Equation (206) at every node. The evaluation of Equation (206) can be examined by the Jacobina matrix singularity:
Therefore, Equation (208) specifies a novel stability index that is known as the Equivalent Node Voltage Collapse Index:
The ENVCI expression in terms of polar coordinates is:
Determining the ENVCI requires only the phasor voltage of two nodes. Every node contains ESM. The system converges to a collapse point if the ENVCI of a minimum of one node is approaching 0; the respective node is the weak node that induces system instability.
2.2.9. Power Stability Index (PSI)
The power stability index [36] was developed to identify the optimal position of the Distributed Generator (DG), including critical buses that are nearer voltage collapse. This index derives from a standard two-bus system, which is stable within the unity margin. Let the power flow in a standard two-bus system without DG be:
where
Now, with DG, the current Ir concerning the active power and reactive power support are expressed as:
Combining Equations (212) and (214), and writing real and imaginary terms separately, we obtain:
Rearranging Equation (215), we obtain:
Hence, Equation (217) is in a quadratic form in terms of Vr. When stable, the node voltage must contain real roots, i.e., the discriminant is more significant than zero, and the index derives as:
If the PSI value is less than 1, the system is stable; if the value is nearer to zero, the system is more stable. Hence, the PSI determines the optimal location of the DG as the calculated value of the PSI for each line patterned from maximum to minimum value. The optimal location of the DG is at the line-end with a maximum value of the PSI.
2.2.10. Voltage Deviation Index (VDI)
The Voltage Deviation Index proposed in [37] determines the voltage deviation’s real value compared to 1 per unit. Assuming an N-bus system, the total VDI is the addition of all N buses’ voltage deviation index.
2.2.11. Simplified Voltage Stability Index (SVSI)
An advanced SVSI proposes [38] to evaluate the system’s stability. This SVSI depends on the Relative Electrical Distance (RED) concept, which considers identifying the convenient generator to a particular load bus; moreover, the relation of electrical parameters for enhancing the performances.
- Relative electrical distance (RED)
The concerned system, the interrelation among the current (I), Generator bus voltage phasor (V), and the load buses (L) represented in the form of an admittance matrix can be shown as:
Rearranging Equation (221), we obtain:
FLG = −|YLL|−1|YLG| represents a composite matrix, which indicates the association between the voltages of the source and load buses. The REDs determined from the matrix FLG are shown as:
Here, the size of matrix A is (n-g) X g, the total number of buses is represented by n, and the total generator count is denoted by g. Matrix A is a particular matrix in that all elements are 1, i.e., a matrix of ones. The data obtained from matrix RLG are considered rather than path algorithms for determining the electrical distance from the generator bus to the load bus. Subsequently, after identifying the shortest distance of the generator to a particular load with the RLG matrix, the Thevenin impedance voltage drop ΔVi can be estimated with:
Vl and Vg are the phasor voltages at the load bus and closest generator. While an increase in demand for power reaches the maximum loading point in one particular bus or various buses in the system, some buses may experience high voltage drops. This process illustrates the potential of voltage collapse and comprises the formation of the SVSI in terms of a correction factor β.
The derived correction factor is proportionate with higher variations between the voltage magnitude of bus m and bus l, which can be determined directly by measuring the PMU during the power system analysis, considering particular operating conditions. Thus, the SVSI is as follows:
Suppose the obtained value of the proposed index is near the unity. In that case, the system considers the voltage instability on these terms: the Thevenin impedance voltage drop equals the voltage of the load bus.
2.2.12. P-Index
The P-index [39] evaluates the distance to collapse and measures the load shedding. The P-index is derived from a standard two-bus system, shown in Figure 1. The load at the receiving end bus is Pr + jQr, and Vr is the voltage magnitude. The equivalent load admittance is Gr − jBr,
Let ΔPr, ΔQr be an incremental increase in load without varying the power factor. The equivalent increment in admittance is ΔGr, ΔBr. The voltage magnitude changed by an amount of ΔVr, is typically negative; therefore, the updated bus voltage is Vr + ΔVr. The corresponding active power variation is as follows:
The substantial consequences of the two terms in Equation (228) are: the primary term is positive and describes the power attained because of the additional load ΔGr, while the secondary term is negative and is the power wasted on the original load Gr because of the voltage drop ΔV. Because of these opposite terms, the overall active power gained is balanced. At the stability limiting point, these two terms diminish, and the overall increment in power is zero.
The P-index bus stability index depends on the ratio of two terms in Equation (228), i.e., the ratio of power lost to power gained. When ΔV is negative for positive ΔGr, a minus sign is added to make the index positive.
In the limiting case, such as ΔGr, ΔV → 0,
Although dVr/dGr is often not defined in terms of network terminology, it is simple to do so in terms of the power and voltage sensitivity of the system. Provided that dVr/dGr:
Thus, differentiating the power, Pr = Vr2 Gr is as follows:
Or:
Substituting Equation (233) in Equation (231), we obtain:
Further simplifying Equation (234), it is reduced as:
Substituting Equation (235) in the P-index Equation (230), we obtain:
Expressing Equation (236) in terms of active power, we obtain:
Therefore, the P-index is expressed in terms of power and voltage sensitivities. When the theoretical value of the stability index is 1.0 at the stability limit. The stability limit varies from 0 (no load) to 1.0 at the collapse point of the system.
3. Summary
The Voltage Stability Indices that are preferred in power system analysis are derived in detail in this paper. Our review of stability indices examined the overall parameters of voltage stability analysis, including the voltage stability margin, stability indices, identifying voltage collapse proximity, and the maximum loadability. This comprehensive review features the significance of definite stability assessment and specifies the effectiveness and vulnerability of various bus and line Voltage Stability Indices.
The line stability indices, like the VSLI, Lmn, LQP, LP, FVSI, NLSI, VQI, and NVSI, and the bus stability indices like the L-Index, Voltage Instability, and VCPI, are derived from the power flow in a standard two-bus system. In contrast, the stability indices like the VCPI, PTSI, VSI_1, VSM, SDC, and PSI are determined by considering the maximum power transfer and maximum power losses. At the same time, stability indices like the SI, LCPI, LVSI, and BVSI derive from the quadratic voltage equation—the overall objectives of the listed stability indices are expressed in Figure 7.
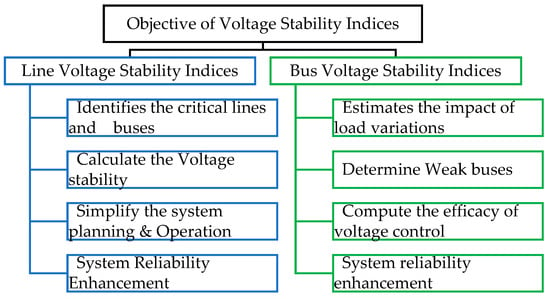
Figure 7.
The objective of Voltage Stability Indices.
The VSLI stability index depends on the load reactive power demand ratio to the available reactive power. It helps to determine the critical points and identifies the load bus nearer to the collapse point. The Lmn stability index is online monitoring that predicts the voltage collapse; the reliability test on the IEEE 24 bus system results in an accurate voltage collapse prediction. It also identifies the stressed lines and weak areas that are exposed to voltage collapse; moreover, it allows for flexible operation. The LQP is a static indicator that performs faster, evaluates stability, and determines the origin of voltage collapse.
The VCPI is a proximity index that determines the range of the collapse point; this index depends upon the systems’ generation and load characteristics and identifies exposure to voltage collapse. The VCPI is a method for the real-time prediction of voltage collapse. This proximity index illustrates the collapse position and is an alarming tool for preventing system collapse. LP performs voltage stability assessment in a radial distribution system. It predicts instabilities easily when changing the load. The FVSI can determine the collapse point, weakest bus, critical line, and maximum loadability. The VSLBI is used for local monitoring of threshold voltage collapse and emergency management during voltage-sensitive loads. The VSLBI operates within a small stability margin and maintains reactive reserve power. The VSMI presents data about weak locations, evaluates the voltage stability margin, and maintains stable voltage levels during load variations. Moreover, the VSMI depends on the relation between voltage stability and angular difference between the receiving- and sending-end buses. VCPI_1 is an online voltage stability evaluation index that depends on power transmission lines and identifies the weakest transmission lines by distinguishing the minor power outage buses, including the electrical distance.
The Critical Voltage (Vcr) specifies the minimum voltage where the system performs away from voltage collapse; the system is unstable if the Jacobian power flow matrix is singular. In Vcr, the Jacobian power matrix is a static voltage stability index specifying the range of the voltage stability limit. The PTSI is an essential technique that forecasts dynamic voltage collapse, calculates the effect of adding additional equipment like generators or transmission lines, and determines the weak points in the system. VSI_1 is a novel online stability index for predicting steady-state voltage stability. Coordinated with the network simplification method, it presents the stability margin of every load bus, sequentially determining the buses which are vulnerable to voltage collapse.
The NLSI performs by varying the active and reactive power and evaluates the voltage stability more accurately than other indices that vary only the reactive power. Moreover, the NLSI evaluates the voltage collapse point, specifies the order of transmission lines based on loadability, and considers the consistency of wind and solar power output and the response time of the system. The SI identifies the most vulnerable bus that is exposed to voltage collapse in the radial distribution system, is easily implemented for load flow analysis, and does not need extra parameters. The VSM is the variation between the minimal permissible voltage and absolute voltage at a particular bus; it determines the loss of voltage contribution during the voltage collapse. The VSM can efficiently prevent voltage collapse from voltage crisis, and can be measured by PV and QV curves. The VQI is an effective technique that determines the critical bus, detects instability in large-scale systems, and determines the distance of the collapse point.
The LCPI combines the influence of the proportional flow of active and reactive power with ABCD parameters, determines the consequences of different power system arrangements, and specifies the most sensitive lines. The NVSI evaluates the voltage stability effectively by varying the active and reactive power, determining the weakest bus and sensitive line, and utilizes the Reactive Power Sensitivity theory. The ITLTI was first derived for radial transmission networks and subsequently adapted for larger systems. The ITLTI contains extended integrated significance; moreover, it is probably a better resolution for online stability assessment and specifies the weakest line and the specific data about a critical voltage instability range. The CBI operates with the Lagrange Constant Computational Method (LCM); the main motive of this index is to determine the critical boundaries and voltage stability with lesser parameters. Varying the active and reactive power predicts voltage stability margin precisely with better accuracy. The LVSI determines the stability margin by considering the transmission line (ABCD) parameters and is expressed in terms of MVA. The LVSI can determine the voltage collapse point and critical lines, and involves only the information on the phasor bus voltage. The BVSI forecasts the voltage security level, considering various operating conditions and identifies the sensitive lines that are nearer to stability. This index can identify the capability of the bus to place a single DG and size effectively; moreover, it can accurately identify the critical lines and weakest bus.
The L-index in online testing depends on the eigenvalues of the Jacobian matrix of a network; these eigenvalues determine the gap between the voltage collapse point and the current operating point. Moreover, the L-index measures stability linearly, and non-linear behavior may not be measured thoroughly. The VIPI determines very sensitive buses that are exposed to voltage instability and finds the possible precautions for preventing voltage collapse; the VIPI depends on the relation between the instability and various load flow solutions. The VCPI is a real-time prediction that determines the system’s proximity to voltage collapse, which is evaluated by analyzing the present voltage and voltage levels at the point of collapse and utilizing the magnitude of voltage and angle; the admittance matrix forecasts the voltage collapse. The SDC’s utilization in the protection algorithm for voltage collapse depends on the local bus phasor of the voltage and current at every line’s relay point. The relay operation is local to voltage collapse, and the overall rise in apparent power is because of transmission losses to the supply.
The ISI calculates the system’s stability; this index illustrates the ratio of variation in system impedance to load impedance. The ISI is a local stability index that is derived using Tellegen’s theorem and adjoint network. The VSIBUS is a simple index which identifies the distance to the collapse point with the help of local data like the magnitude of voltage and load current, and thoroughly examines the influence of line tripping, reactive power limits, and non-linear variation in the load. The ZL/ZS measures the derivation of apparent power concerning admittance, quickly calculating both the power and admittance results in switching the impedance load tap-changing of a transformer. The SVSI utilizes the data of present operating conditions combined with phasor voltage measurement. The SVSI is easily accessible and less computationally derived.
P-index calculation is simple. It involves the system model, nodal power, and only the single datum of system states. The only computation performed is Jacobian matrix inversion, which can be attained smoothly. Therefore, the P-index is appropriate for online voltage stability analysis. Mainly, the load shedding is evaluated by the P-index. Instead of system-wide shedding, the method makes use of single-load shedding.
The Stability index’s concept, assumptions considered during derivation, mathematical equation, condition for index stability, objective, and some references are represented in Table 1 and Table 2 of the line Voltage Stability Indices and bus Voltage Stability Indices, respectively.

Table 1.
Line Voltage Stability Indices.

Table 2.
Bus Voltage Stability Indices.
Figure 8 represents the number of articles published on the line and bus Voltage Stability Indices in the last decade. It shows an eventual rise in research in Voltage Stability Indices to enhance voltage stability and supply the desired power under various load conditions. Table 3 represents some distinct characteristics of Voltage Stability Indices that are the optimal location of the DG and sizing of the DG, as well as dependency on VSI.
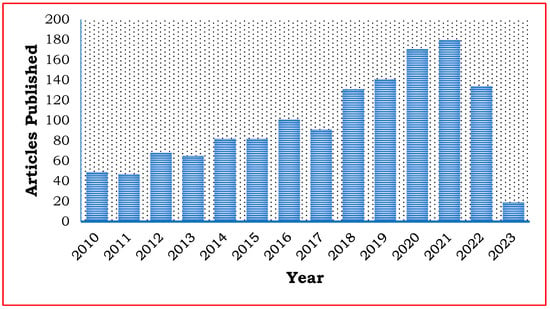
Figure 8.
Number of voltage stability indices articles published.

Table 3.
Characteristics of Stability Indices.
4. Conclusions
Voltage stability indices are essential numerical parameters for measuring and evaluating stability points in the power system network. These indices’ significant roles help detect instability points early, preventing systems from voltage collapse and power outages, minimizing the actual power losses, and enhancing the system’s overall efficiency. The evaluation of these indices indicates the power system operators’ performances of a transmission system. Further, the stability of a system can improve through proper design, reactive power compensation, and optimal power flow. This article discusses the mathematical modeling of 34 line and bus stability indices. The significance of these indices for different power system problems with suitable objectives is also discussed with the help of suitable works from the literature, around 138. This article may be attractive to a researcher who has started researching power system stability analysis, the placement of reactive power compensators, and DG placement for stability enhancement. The main intention of this review is to summarize and highlight how crucial it is to choose suitable stability indices to preserve systems’ reliability and stability. Developing various stability indices for effective utilization in sustaining the instabilities across various operational scenarios has been undertaken.
The VSIs review various elements and perspectives and derive from the concepts of maximum power transfer through a line (VCPI, PTSI, VSI_1, VSMI), solution of voltage equation (VQIline, VSLI, L-index, SI, VCPIbus LCPI, FVSI, Lmn, Lp, LQP, NVSI, NLSI), P-V Curve (SDC, SI, VIPI), and maximum power transfer theorem (SDC, VSIbus, ISI, ZL/ZS, VCPI_1, VSLBI, SVSI). Most VSIs which correspond to the voltage equation concept should have a solution. A few VSIs neglect the sending-end bus Thevenin impedance (VCPI_1, VSLBI), and few VSIs consider bus Thevenin impedance to be extremely sensitive for a minute variation in parameters of two consecutive measurements (VSIbus, SDC, ZL/ZS ratio, and SDC).
In the procedure to enhance the efficiency and minimize the operational time of DG placement and sizing issues, the primary phase considers the simple line and bus VSIs, and the secondary phase considers the bus and overall VSIs operating with improved efficiency. This review article mainly focuses and presents information on the significant measurement of line and bus stability indices for maintaining the voltage and reactive power in a power system network.
Furthermore, this review can assist in choosing the desired stability index for a given scenario. The main findings of this paper can be highlighted as follows:
- The power system stability analysis;
- A comprehensive review of 34 Voltage Stability Indices derived mathematically;
- Voltage Stability Indices evaluated the sizing and placement of distributed energy sources;
- Various power system issues and their corresponding application of Voltage Stability Indices were presented;
- The corresponding data: name, mathematical calculation, concept, assumptions, condition for stability, and objective for each VSI are listed;
- This review article supports researchers, power system operators, and engineers regarding stability indices.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), which is funded by the Ministry of Education under Grant NRF-2021R111A3053429.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eremia, M.; Shahidehpour, M. Handbook of Electrical Power System Dynamics: Modeling, Stability, and Control; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A comprehensive review of the voltage stability indices. Renew. Sustain. Energy Rev. 2016, 63, 1–12. [Google Scholar] [CrossRef]
- Danish, M.S.S.; Senjyu, T.; Danish, S.M.S.; Sabory, N.R.; Narayanan, K.; Mandal, P. A recap of voltage stability indices in the past three decades. Energies 2019, 12, 1544. [Google Scholar] [CrossRef]
- Lim, Z.J.; Mustafa, M.W.; Muda, Z.B. Evaluation of the effectiveness of voltage stability indices on different loadings. In Proceedings of the International Power Engineering and Optimization Conference, Melaka, Malaysia, 6–7 June 2012. [Google Scholar]
- Rahman, T.K.A.; Jasmon, G.B. A new technique for voltage stability analysis in a power system and improved load flow algorithm for the distribution network. In Proceedings of the International Conference on Energy Management and Power Delivery EMPD, Singapore, 21–23 November 1995. [Google Scholar]
- Moghavvemi, M.; Omar, F.M. Technique for contingency monitoring and voltage collapse prediction. IEE Proc. Gener. Transm. Distrib. 1998, 145, 634–640. [Google Scholar] [CrossRef]
- Mohamed, A.; Jasmon, G.B.; Yusof, S. A static voltage collapse indicator using line stability factors. J. Ind. Technol. 1998, 7, 73–85. [Google Scholar]
- Moghavvemi, M.; Faruque, O. Real-time contingency evaluation and ranking technique. IEE Proc.—Gener. Transm. Distrib. 1998, 145, 517–524. [Google Scholar] [CrossRef]
- Moghavvemi, M.; Faruque, M.O. Technique for assessment of voltage stability in the ill-conditioned radial distribution network. IEEE Power Eng. Rev. 2001, 21, 58–60. [Google Scholar] [CrossRef]
- Musirin, I.; Khawa, T.; Rahman, A. Novel fast voltage stability index (FVSI) for voltage stability analysis in a power transmission system. In Proceedings of the Student Conference on Research and Development Proceedings, Shah Alam, Malaysia, 17 July 2002. [Google Scholar]
- Milosevic, B.; Begovic, M. Voltage-stability protection and control using a wide-area network of phasor measurements. IEEE Trans. Power Syst. 2003, 18, 121–127. [Google Scholar] [CrossRef]
- He, T.; Kolluri, S.; Mandal, S.; Galvan, F.; Rastgoufard, P. Identification of weak locations in bulk transmission systems using voltage stability margin index. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004. [Google Scholar]
- Wang, L.; Liu, Y.; Luan, Z. Power transmission paths-based voltage stability assessment. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition: Asia and Pacific, Dalian, China, 18 August 2005. [Google Scholar]
- Sun, H.; Zhou, X.; Li, R. Accuracy analysis of static voltage stability indices based on power flow model. In Proceedings of the 2005 IEEE/PES Transmission and Distribution Conference and Exposition: Asia and Pacific, Dalian, China, 18 August 2005. [Google Scholar]
- Nizam, M.; Mohamed, A.; Hussain, A. Performance evaluation of voltage stability indices for dynamic voltage collapse prediction. Appl. Sci. 2006, 6, 1104–1113. [Google Scholar] [CrossRef]
- Gong, Y.; Schulz, N.; Guzman, A. Synchro phasor-based real-time voltage stability index. In Proceedings of the PSCE Conference, Atlanta, GA, USA, 29 October–1 November 2006. [Google Scholar]
- Yazdanpanah-Goharrizi, A.; Asghari, R. A novel line stability index (NLSI) for voltage stability assessment of power systems. In Proceedings of the 7th WSEAS International Conference on Power Systems, Beijing, China, 15–17 September 2007. [Google Scholar]
- Eminoglu, U.; Hocaoglu, M.H. A voltage stability index for radial distribution networks. In Proceedings of the 42nd International Universities Power Engineering Conference, Brighton, UK, 4–6 September 2007. [Google Scholar]
- Guiping, D.; Yuanzhang, S.; Jian, X. A new index of voltage stability considering distribution network. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
- Althowibi, F.A.; Mustafa, M.W. Line voltage stability calculations in power systems. In Proceedings of the IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010. [Google Scholar]
- Tiwari, R.; Niazi, K.R.; Gupta, V. Line collapse proximity index for prediction of voltage collapse in power systems. Int. J. Electr. Power Energy Syst. 2012, 41, 105–111. [Google Scholar] [CrossRef]
- Kanimozhi, R.; Selvi, K. A novel line stability index for voltage stability analysis and contingency ranking in power system using fuzzy based load flow. J. Electr. Eng. Technol. 2013, 8, 694–703. [Google Scholar] [CrossRef]
- Chuang, S.J.; Hong, C.M.; Chen, C.H. Improvement of integrated transmission line transfer index for power system voltage stability. Int. J. Electr. Power Energy Syst. 2016, 78, 830–836. [Google Scholar] [CrossRef]
- Furukakoi, M.; Adewuyi, O.B.; Danish, M.S.S.; Howlader, A.M.; Senjyu, T.; Funabashi, T. Critical Boundary Index (CBI) based on active and reactive power deviations. Int. J. Electr. Power Energy Syst. 2018, 100, 50–57. [Google Scholar] [CrossRef]
- Ratra, S.; Tiwari, R.; Niazi, K.R. Voltage stability assessment in power systems using line voltage stability index. Comput. Electr. Eng. 2018, 70, 199–211. [Google Scholar] [CrossRef]
- Ismail, B.; Wahab, N.I.A.; Othman, M.L.; Radzi, M.A.M. New Line Voltage Stability Index (BVSI) for Voltage Stability Assessment in Power System: The Comparative Studies. IEEE Access 2022, 10, 103906–103931. [Google Scholar] [CrossRef]
- Kessel, P.; Glavitsch, H. Estimating the voltage stability of a power system. IEEE Trans. Power Deliv. 1986, 1, 346–354. [Google Scholar] [CrossRef]
- Tamura, Y.; Sakamoto, K.; Tayama, Y. Voltage instability proximity index (VIPI) based on multiple load flow solutions in ill-conditioned power systems. In Proceedings of the 27th IEEE Conference on Decision and Control, IEEE, Austin, TX, USA, 7–9 December 1988. [Google Scholar]
- Balamourougan, V.; Sidhu, T.S.; Sachdev, M.S. Technique for online prediction of voltage collapse. IEEE Gener. Transm. Distrib. 2004, 151, 453–460. [Google Scholar] [CrossRef]
- Verbic, G.; Gubina, F. A new concept of voltage-collapse protection based on local phasors. IEEE Trans. Power Deliv. 2004, 19, 576–581. [Google Scholar] [CrossRef]
- Smon, I.; Verbic, G.; Gubina, F. Local voltage-stability index using Tellegen’s theorem. IEEE Trans. Power Syst. 2006, 21, 1267–1275. [Google Scholar] [CrossRef]
- Haque, M.H. Use of local information to determine the distance to voltage collapse. In Proceedings of the International Power Engineering Conference, Singapore, 3–6 December 2007. [Google Scholar]
- Wiszniewski, A. New criteria of voltage stability margin for the purpose of load shedding. IEEE Trans. Power Deliv. 2007, 22, 1367–1371. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Lu, J. A new node voltage stability index based on local voltage phasors. Electr. Power Syst. Res. 2009, 79, 265–271. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Mokhlis, H.; Bakar, A.H.A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Yang, C.F.; Lai, G.G.; Lee, C.H.; Su, C.T.; Chang, G.W. Optimal setting of reactive compensation devices with an improved voltage stability index for voltage stability enhancement. Int. J. Electr. Power Energy Syst. 2012, 37, 50–57. [Google Scholar] [CrossRef]
- Perez-Londõno, S.; Rodríguez, L.F.; Olivar, G. A Simplified Voltage Stability Index (SVSI). Int. J. Electr. Power Energy Syst. 2014, 63, 806–813. [Google Scholar] [CrossRef]
- Kamel, M.; Karrar, A.A.; Eltom, A.H. Development and Application of a New Voltage Stability Index for On-Line Monitoring and Shedding. IEEE Trans. Power Syst. 2018, 33, 1231–1241. [Google Scholar] [CrossRef]
- Makasa, K.J.; Venayagamoorthy, G.K. Online voltage stability load index estimation based on PMU measurements. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Alias, M.R.N.M.; Verayiah, R.; Yin, L.J. Investigation of Power Flow Tracing Strategy Using an Index in a Transmission System with Solar PV for Congestion Management. In Proceedings of the 11th International Conference on Power and Energy Systems (ICPES), Shanghai, China, 18–20 December 2021. [Google Scholar]
- Oukennou, A.; Sandali, A. Analysis and Comparison of Line Voltage Stability Indices. In Proceedings of the 6th International Renewable and Sustainable Energy Conference (IRSEC), Rabat, Morocco, 5–8 December 2018. [Google Scholar]
- Salah, M.; Wang, Y.; Chen, T. A novel collapse prediction index for voltage stability analysis and contingency ranking in power systems. Prot. Control. Mod. Power Syst. 2023, 8, 7. [Google Scholar]
- Shekhawat, N.; Gupta, A.K.; Sharma, A.K. Voltage Stability Assessment Using Line Stability Indices. In Proceedings of the 3rd International Conference and Workshops on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 22–25 November 2018. [Google Scholar]
- Calma, E.R.B.; Pacis, M.C. Artificial Neural Network-based Voltage Stability Analysis of Power Transmission Networks with Distributed Generation Using Phasor Measurement Unit Synthetic Data. In Proceedings of the IEEE 12th Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 6 August 2021. [Google Scholar]
- Singh, P.; Parida, S.K.; Chauhan, B.; Choudhary, N. Online Voltage Stability Assessment Using Artificial Neural Network Considering Voltage Stability Indices. In Proceedings of the 21st National Power Systems Conference (NPSC), Gandhinagar, India, 17–19 December 2020. [Google Scholar]
- Chintakindi, R.; Mitra, A. Detecting Weak Areas in a Real-time Power System on a Static Load Model using Standard Line Voltage Stability Indices. In Proceedings of the IEEE 2nd International Conference on Smart Technologies for Power, Energy, and Control (STPEC), Chhattisgarh, India, 12 November 2021. [Google Scholar]
- Verayiah, R.; Abidin, I.Z. A Study on static voltage collapse proximity indicators. In Proceedings of the IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008. [Google Scholar]
- Isaiah, A.; Yanxia, S. New performance indices for voltage stability analysis in a power system. Energies 2017, 10, 2042. [Google Scholar]
- Salama, M.M.; Saied, E.M.; Abou-Elsaad, M.M.; Ghariany, E.F. Estimating the voltage collapse proximity indicator using an artificial neural network. Energy Convers. Manag. 2001, 42, 69–79. [Google Scholar] [CrossRef]
- Chaithra, A.; Modi, S. Power System Vulnerability Assessment using Voltage Collapse Proximity Index. In Proceedings of the 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018. [Google Scholar]
- Chaithra, A.; Modi, S. Evaluation of Power System Stability using Voltage Proximity Index. In Proceedings of the International Conference on Recent Innovations in Electrical, Electronics & Communication Engineering (ICRIEECE), Bhubaneswar, India, 27–28 July 2018. [Google Scholar]
- Khunkitti, S.; Premrudeepreechacharn, S. Voltage Stability Improvement Using Voltage Stability Index Optimization. In Proceedings of the 2020 International Conference on Power, Energy, and Innovations (ICPEI), Chiangmai, Thailand, 14–16 October 2020. [Google Scholar]
- Xi, Z.; Kong, W.C. Comparison of voltage stability indexes considering dynamic load. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3 October 2011. [Google Scholar]
- Soyemi, A.; Misra, S.; Oluranti, J.; Ahuja, R. Evaluation of Voltage Stability Indices. In Information Systems and Management Science; Springer: Cham, Switzerland, 2022; Volume 303. [Google Scholar]
- Hosseinzadeh, N.; Aziz, A.; Mahmud, A.; Gargoom, A.; Rabbani, M. Voltage Stability of Power Systems with Renewable-Energy Inverter-Based Generators: A Review. Electronics 2021, 10, 115. [Google Scholar] [CrossRef]
- Jirjees, M.A.; Al-Nimma, D.A.; Al-Hafidh, M.S.M. Voltage Stability Enhancement Based on Voltage Stability Indices Using FACTS Controllers. In Proceedings of the 2018 International Conference on Engineering Technology and their Applications (IICETA), Al-Najaf, Iraq, 8–9 May 2018. [Google Scholar]
- Pacis, M.C.; Antonio, I.J.M.; Bañaga, I.J.T. Under Voltage Load Shedding Algorithm using Fast Voltage Stability Index (FVSI) and Line Stability Index (LSI). In Proceedings of the IEEE 13th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management, Manila, Philippines, 28–30 November 2021. [Google Scholar]
- Ali, M.B.; Kazmi, S.A.A.; Khan, Z.A.; Altamimi, A.; Alghassab, M.A.; Alojaiman, B. Voltage Profile Improvement by Integrating Renewable Resources with Utility Grid. Energies 2022, 15, 8561. [Google Scholar] [CrossRef]
- Meena, G.; Verma, K.; Mathur, A. FVSI-Based Meta-heuristic Algorithm for Optimal Load Shedding to Improve Voltage Stability. In Proceedings of the IEEE 10th Power India International Conference (PIICON), New Delhi, India, 25–27 November 2022. [Google Scholar]
- Ramírez-Perdomo, S.L.; Lozano, C.A. Evaluation of indices for voltage stability monitoring using PMU measurements. Ing. E Investig. 2014, 34, 44–49. [Google Scholar] [CrossRef]
- Arbelaez Ramirez Marcela, L. Monitoring Voltage Stability Margin across Several Transmission Lines Using Synchro Phasor Measurements. Ph.D. Thesis, Iowa State University, Ames, Iowa, 2016. [Google Scholar]
- Sajan, K.S.; Kumar, V.; Tyagi, B. Genetic algorithm-based support vector machine for online voltage stability monitoring. Int. J. Electr. Power Energy Syst. 2015, 73, 200–208. [Google Scholar] [CrossRef]
- Naganathan, G.S.; Babulal, C.K. Optimization of support vector machine parameters for voltage stability margin assessment in the deregulated power system. Soft Comput. 2019, 23, 10495–10507. [Google Scholar] [CrossRef]
- Reddy, M.V.; Murthy, V.S.K. Improvement of voltage stability based on static and dynamic criteria. In Proceedings of the 16th National Power Systems Conference, Hyderabad, India, 15–17 December 2010. [Google Scholar]
- Yunhwan, L.; Hwachang, S. Decentralized Load Shedding Method Based on Voltage Stability Margin Index Using Synchrophasor Measurement Technology. Electronics 2018, 7, 277. [Google Scholar]
- Dharmapala, K.D.; Rajapakse, A.; Narendra, K.; Zhang, Y. Machine Learning Based Real-Time Monitoring of Long-Term Voltage Stability Using Voltage Stability Indices. IEEE Access 2020, 8, 222544–222555. [Google Scholar] [CrossRef]
- Mesgarnejad, H.; Shahrtash, S.M. Power system voltage stability assessment employing phasor measurement units. In Proceedings of the 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010. [Google Scholar]
- Ankit, S.; Akash, S. Application of supervised learning for voltage stability assessment using GVSM. Electr. Electron. Technol. Open Access J. 2018, 2, 281–287. [Google Scholar]
- Hameedullah, Z.; Shah, D.M.S.; Tomonobu, S.; Mikaeel, A.; Abdul, N.; Mohebullah, W.; Mahdi, K.; Paras, M. A Contemporary Novel Classification of Voltage Stability Indices. Appl. Sci. 2020, 10, 1639. [Google Scholar]
- Ghassan, S.H.; Husham, I. Assessment of voltage stability based on power transfer stability index using com-putational intelligence models. Int. J. Electr. Comput. Eng. 2021, 11, 2790–2797. [Google Scholar]
- Izzri, N.; Mehdi, O.H.; Abdalla, A.N.; Jaber, A.S.; Shalash, N.A.; Noori, Y.L. Fast Prediction of Power Transfer Stability Index Based on Radial Basis Function Neural Network. Int. J. Phys. Sci. 2011, 6, 7978–7984. [Google Scholar]
- Nizam, M.; Mohamed, A.; Hussain, A. Dynamic Voltage Collapse Prediction on a Practical Power System Using Power Transfer Stability Index. In Proceedings of the 5th Student Conference on Research and Development, Selangor, Malaysia, 11–12 December 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Woldu, T.A.; Ziegler, C.; Wolter, M. A New Method for Prediction of Static and Dynamic Voltage Collapse Using Node Parameters in Large Power Networks. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26–28 October 2020. [Google Scholar]
- Jamroen, C.; Dechanupaprittha, S. Synchrophasor-based early-warning voltage instability index. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017. [Google Scholar]
- Rohikaa, R.M.; Lakshmi, R.; Sunitha, R.; Ashok, S. Assessment of voltage stability in microgrid. In Proceedings of the International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016. [Google Scholar]
- Oukennou, A.; Sandali, A. Assessment and analysis of Voltage Stability Indices in electrical networks using PSAT Software. In Proceedings of the Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016. [Google Scholar]
- Mahiraj, R.S.; Vadhera, S. Voltage Stability Assessment Techniques for Modern Power Systems. In Novel Advancements in Electrical Power Planning and Performance; IGI Global: Hershey, PA, USA, 2020; pp. 128–176. [Google Scholar]
- Gupta, A.R. Effect of optimal allocation of multiple DG and D-STATCOM in the radial distribution system for minimizing losses and THD. In Proceedings of the 7th International Symposium on Embedded Computing and System Design (ISED), Durgapur, India, 18–20 December 2017. [Google Scholar]
- Narayan, K.S.; Kumar, A. Probabilistic analysis of radial distribution network performance with varying wind speed levels. In Proceedings of the 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014. [Google Scholar]
- Pattabhi, M.B.; Lakshmikantha, B.R.; Sundar, K.S. A Novel Method for Contingency Ranking Based on Voltage Stability Criteria in Radial Distribution Systems. Technol. Econ. Smart Grids Sustain. Energy 2022, 7, 9. [Google Scholar] [CrossRef]
- Sagwal, R.; Kumar, A. Voltage Stability Margin, based congestion management for a hybrid system, considering secure bilateral trading: MINLP approach. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016. [Google Scholar]
- Rao, A.R.N.; Vijaya, P.; Kowsalya, M. Voltage stability indices for stability assessment: A review. Int. J. Ambient Energy 2021, 42, 829–845. [Google Scholar]
- Hauqe, M.H. A linear static voltage stability margin for radial distribution systems. In Proceedings of the IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Ahmad, N.; Mohamad, F.; Sulaiman, M.; Fazliana, A.; Kadir, A.; Bin, R.O. Classifications of voltage stability margin (VSM) and load power margin (LPM) using probabilistic neural network (PNN). ARPN J. Eng. Appl. Sci. 2017, 12, 5591–5596. [Google Scholar]
- Merlyn, M.; Suresh, D.; Venkataramu, P.S.; Nagaraj, M.S. Effect of TCSC on Line Voltage Stability Indices under Single Line Outage Condition. Int. J. Innov. Res. Electr. Electron. Instrum. Control Eng. 2015, 3, 101–105. [Google Scholar]
- Singh, B.; Sharma, P.A.K. Voltage Stability Calculations in Power Transmission Lines: Indications and Allocations (IEEE 30 BUS SYSTEM). Int. J. Nov. Res. Electr. Mech. Eng. 2015, 2, 63–66. [Google Scholar]
- Mathew, M.; Gosh, S.; Suresh, D.; Ansari, A.A. An Assessment of Voltage Stability Based on Line Voltage Stability Indices and its Enhancement Using TCSC. IOSR J. Electr. Electron. Eng. 2015, 10, 81–88. [Google Scholar]
- Zhang, Y.; Huang, L.; Chen, X. An Enhanced Voltage-Reactive Power Index Considering Power Injection Limitations for Power System Stability Assessment. IEEE Trans. Power Syst. 2021, 36, 262–273. [Google Scholar]
- Kumar Kavuturu, K.V.; Sai Tejaswi, K.N.V.; Janamala, V. Performance and security enhancement using generalized optimal unified power flow controller under contingency conditions and renewable energy penetrations. J. Electr. Syst. Inf. Technol. 2022, 9, 18. [Google Scholar] [CrossRef]
- Alluri, A.; Lanka, R.S.; Rayapudi, S.R. Optimal Location for FACTS Devices: Hybrid Algorithm to Improve Power Flow and System Security. Cybern. Syst. 2022, 54, 938–960. [Google Scholar] [CrossRef]
- Ismail, B.; Wahab, N.I.A.; Othman, M.L.; Radzi, M.A.M.; Vijyakumar, K.N.; Naain, M.N.M. A Comprehensive Review of Optimal Location and Sizing of Reactive Power Compensation Using Hybrid-Based Approaches for Power Loss Reduction, Voltage Stability Improvement, Voltage Profile Enhancement, and Loadability Enhancement. IEEE Access 2020, 8, 222733–222765. [Google Scholar] [CrossRef]
- Prabhakar, P. Voltage Stability Indices: Formulation and classification perspectives. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 5777–5785. [Google Scholar] [CrossRef]
- Salah, M.; Yifei, W.; Tiancong, C. Modern voltage stability index for prediction of voltage collapse and estimation of maximum load-ability for weak buses and critical lines identification. Int. J. Electr. Power Energy Syst. 2023, 145, 1–19. [Google Scholar]
- Gitanjali, S.; Kabir, C.; Priyanath, D. Enrichment of voltage stability in power system through novel generalized approximate reasoning based intelligent control with African buffalo optimization approach. Soft Comput. 2022, 27, 7473–7496. [Google Scholar]
- Kushwaha, P.K.; Bhattacharjee, C. Research on a selection of appropriate stability index under adverse system conditions for the assessment of voltage stability of an IEEE 14 bus power system. Eur. J. Electr. Eng. 2020, 22, 435–446. [Google Scholar] [CrossRef]
- Samy, A.; Venkadesan, A. Evaluation of Voltage Stability Margin in a Power System using an Artificial Neural Network. In Proceedings of the IEEE 10th Power India International Conference (PIICON), New Delhi, India, 25–27 November 2022. [Google Scholar]
- Ademola, A.S.; Sun, Y. Power system optimization approach to mitigate voltage instability issues: A review. Cogent Eng. 2023, 10, 2153416. [Google Scholar]
- Bode, O.A.; Lotfy, M.E.; Olabisi, B.A.; Rashid, H.O.; Senjyu, H.T.; Narayanan, K. Security-constrained optimal utility-scale solar PV investment planning for weak grids: Short reviews and techno-economic analysis. Appl. Energy 2019, 245, 16–30. [Google Scholar]
- Adewuyi, O.B.; Danish, M.S.S.; Howlader, A.M.; Senjyu, T.; Lotfy, M.E. Network Structure-Based Critical Bus Identification for Power System Considering Line Voltage Stability Margin. J. Power Energy Eng. 2018, 6, 97–111. [Google Scholar] [CrossRef]
- Akito, N.; Miyara, R.; Alharbi, T.; Prabaharan, N. Dynamic Voltage Stability Assessment in Remote Island Power System with Renewable Energy Resources and Virtual Synchronous Generator. Energies 2021, 14, 5851. [Google Scholar]
- Bode, O.A.; Shigenobu, R.; Ooya, K.; Senjyu, T.; Howlader, M.A. Static voltage stability improvement with battery energy storage considering optimal control of active and reactive power injection. Electr. Power Syst. Res. 2019, 172, 303–312. [Google Scholar]
- Ratra, S.; Singh, D.; Bansal, R.C.; Naidoo, R.M. Stochastic Estimation and Enhancement of Voltage Stability Margin considering Load and Wind Power Intermittencies. In Proceedings of the IEEE 6th International Conference on Computing, Communication, and Automation (ICCCA), Arad, Romania, 17–19 December 2021. [Google Scholar]
- Saifullah, M.K.; Kabir, M.M.; Mia, N.; Tanvir, A. Optimal Placement of FACTS Devices in the Power System Using ANN to Increase the System Loadability. Electronic Systems and Intelligent Computing. In Lecture Notes in Electrical Engineering; Mallick, P.K., Meher, P., Majumder, A., Das, S.K., Eds.; Springer: Singapore, 2015; Volume 686. [Google Scholar]
- Kushwaha, P.K.; Bhattacharjee, C. Role of Energy Storage System for improving System Stability considering Customer Behavior Uncertainties. In Proceedings of the International Conference on Contemporary Computing and Applications (IC3A), Lucknow, India, 5–7 February 2020. [Google Scholar]
- Adebayo, I.G.; Sun, Y. Voltage Stability Enhancement Capabilities of LTCT and STATCOM in a Power System. In Proceedings of the IEEE PES/IAS PowerAfrica, Cape Town, South Africa, 28–29 June 2018. [Google Scholar]
- Shuai, C.; Deyou, Y.; Weichun, G.; Chuang, L.; Guowei, C.; Lei, K. Global sensitivity analysis of voltage stability in the power system with correlated renewable energy. Electr. Power Syst. Res. 2021, 192, 106916. [Google Scholar] [CrossRef]
- Adebayo, I.G.; Jimoh, A.A.; Yusuff, A.A.; Sun, Y. An alternative method for the identification of critical nodes leading to voltage instability in a power system. Afr. J. Sci. Technol. Innov. Dev. 2018, 10, 323–333. [Google Scholar] [CrossRef]
- Lakshmi, C.; Manjula, S.S. Detection of Proximity to Voltage Collapse Indicator Using Artificial Neural Networks. Int. J. Sci. Eng. Res. 2019, 10, 59–63. [Google Scholar]
- Salama, H.S.; Vokony, I. Voltage stability indices–A comparison and a review. Comput. Electr. Eng. 2022, 98, 107743. [Google Scholar] [CrossRef]
- Nanba, M.; Huang, Y.; Kai, T.; Iwamoto, S. Studies on VIPI-based control methods for improving voltage stability. Int. J. Electr. Power Energy Syst. 1997, 20, 141–146. [Google Scholar] [CrossRef]
- Takehara, A.; Tanaka, Y.; Iwamoto, S. Voltage stability preventive and emergency-preventive control using VIPI sensitivity. Electr. Eng. Jpn. 2002, 143, 22–30. [Google Scholar] [CrossRef]
- Gubina, F.; Strmcnik, B. Voltage collapse proximity index determination using voltage phasors approach. IEEE Trans. Power Syst. 1995, 10, 788–794. [Google Scholar] [CrossRef]
- Adebayo, I.G.; Jimoh, A.A.; Yusuff, A.A. Prediction of voltage collapse through voltage collapse proximity index and inherent structural characteristics of a power system. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Brisbane, QLD, Australia, 15–18 November 2015. [Google Scholar]
- Venu, Y.; Kanthala, S. Optimal placement and Sizing of Compensator for Voltage Stability improvement Using Voltage Collapse Proximity Indicator. In Proceedings of the 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019. [Google Scholar]
- Adebayo, I.G.; Jimoh, A.A.; Yusuff, A.A. Analysis of Voltage Collapse in a Power System Using Voltage Stability Indices. J. Energy Technol. Policy 2018, 8, 40–45. [Google Scholar]
- Šmon, I.; Pantoš, M.; Gubina, F. An improved voltage-collapse protection algorithm based on local phasors. Electr. Power Syst. Res. 2008, 78, 434–440. [Google Scholar] [CrossRef]
- Maheshkumar, M. Online voltage stability analysis using synchrophasor technology. Int. J. Sci. Res. Dev. 2014, 2, 273–275. [Google Scholar]
- Amroune, M.; Bouktir, T.; Musirin, I. Power system voltage instability risk mitigation via emergency demand response-based whale optimization algorithm. Prot Control Mod Power Syst. 2019, 4, 1–14. [Google Scholar] [CrossRef]
- Gümüş, T.E.; Emiroglu, S.; Yalcin, M.A. Optimal DG allocation and sizing in distribution systems with Thevenin-based impedance stability index. Int. J. Electr. Power Energy Syst. 2023, 144, 108555. [Google Scholar] [CrossRef]
- Cuffe, P.; Milano, F. Validating Two Novel Equivalent Impedance Estimator. IEEE Trans. Power Syst. 2018, 33, 1151–1152. [Google Scholar] [CrossRef]
- Sadeghi, S.E.; Akbari Foroud, A. A new approach for static voltage stability assessment in distribution networks. Int. Trans. Electr. Energy Syst. 2019, 30, 1–21. [Google Scholar] [CrossRef]
- Stefan, P.; Herwig, R. Voltage stability monitoring methods for distribution grids using the Thevenin impedance. CIRED—Open Access Proc. J. 2017, 2017, 1535–1539. [Google Scholar]
- Zhou, Q.; Guan, Y.; Liu, Y.; Zhao, Z. A novel online local voltage stability monitoring approach based on clustering analysis. Int. J. Electr. Power Energy Syst. 2021, 132, 106807. [Google Scholar]
- Pan, J.; Dong, A.; Fan, J.; Li, Y. Online Static Voltage Stability Monitoring for Power Systems Using PMU Data. Math. Probl. Eng. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Alzaareer, K.; Saad, M. Real-Time Voltage Stability Monitoring in Smart Distribution Grids. In Proceedings of the International Conference on Renewable Energy and Power Engineering (REPE), Toronto, ON, Canada, 24–26 November 2018. [Google Scholar]
- Lee, Y.; Han, S. Real-Time Voltage Stability Assessment Method for the Korean Power System Based on Estimation of Thévenin Equivalent Impedance. Appl. Sci. 2019, 9, 1671. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Lin, F.; Li, W.; Wang, L.Y.; Zhao, J. A new transfer impedance-based system equivalent model for voltage stability analysis. Int. J. Electr. Power Energy Syst. 2014, 62, 38–44. [Google Scholar] [CrossRef]
- Akhil, P.; Atul, M.; Prabhakar, K.; Kothari, D.P. Assessment on various node voltage stability indices—A review. In Proceedings of the International Conference on Smart Technologies for Smart Nation (SmartTechCon), Bengaluru, India, 17–19 August 2017. [Google Scholar]
- Nagendra, P.; Datta, T.; Halder, S.; Paul, S. Power System Voltage Stability Assessment Using Network Equivalents-A Review. J. Appl. Sci. 2010, 10, 2147–2153. [Google Scholar] [CrossRef][Green Version]
- Xinglong, W.; Zheng, X.; Zheren, Z. Power Stability Analysis and Evaluation Criteria of Dual-Infeed HVDC with LCC-HVDC and VSC-HVDC. Appl. Sci. 2021, 11, 5847. [Google Scholar]
- Xu, Z.; Xu, Z.; Xiao, L. Analysis and assessment standards of power stability of multi-send HVDC systems. J. Eng. 2018, 2019, 748–753. [Google Scholar] [CrossRef]
- Alam, M. Determination of Power System Contingency Ranking Using Novel Indices. Recent Advances in Power Systems. In Lecture Notes in Electrical Engineering; Gupta, O.H., Sood, V.K., Malik, O.P., Eds.; Springer: Singapore, 2022; Volume 812. [Google Scholar]
- Mehebub, A.; Shubhrajyoti, K.; Sankar, T.S.; Sumit, B. Determination of Critical Contingency Based on L-Index and Impact Assessment on Power System. In Smart Energy and Advancement in Power Technologies; Springer: Berlin, Germany, 2022; pp. 583–596. [Google Scholar]
- Khunkitti, S.; Boonluk, P.; Siritaratiwat, A. Optimal Location and Sizing of BESS for Performance Improvement of Distribution Systems with High DG Penetration. Int. Trans. Electr. Energy Syst. 2022, 2022, 6361243. [Google Scholar] [CrossRef]
- Rodríguez Lopez, D.K.; Perez-Londoño, S.; Rodriguez-Garcia, L. Optimal under voltage load shedding based on voltage stability index. Ing. E Investig. 2016, 36, 43–50. [Google Scholar]
- Shabir, M.; Nawaz, S.; Vijayvargiya, A. Voltage Stability Enhancement Using SVC in PSCAD Software. In Innovations in Electrical and Electronic Engineering. Lecture Notes in Electrical Engineering; Favorskaya, M.N., Mekhilef, S., Pandey, R.K., Singh, N., Eds.; Springer: Singapore, 2021; Volume 661. [Google Scholar]
- Akbarzadeh Aghdam, P.; Khoshkhoo, H. Voltage stability assessment algorithm to predict power system loadability margin. IET Gener. Transm. Distrib. 2020, 14, 1816–1828. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).