Coordinated Control of the Hybrid Electric Ship Power-Based Batteries/Supercapacitors/Variable Speed Diesel Generator
Abstract
:1. Introduction
2. Energy Storage Systems Behavior Modeling
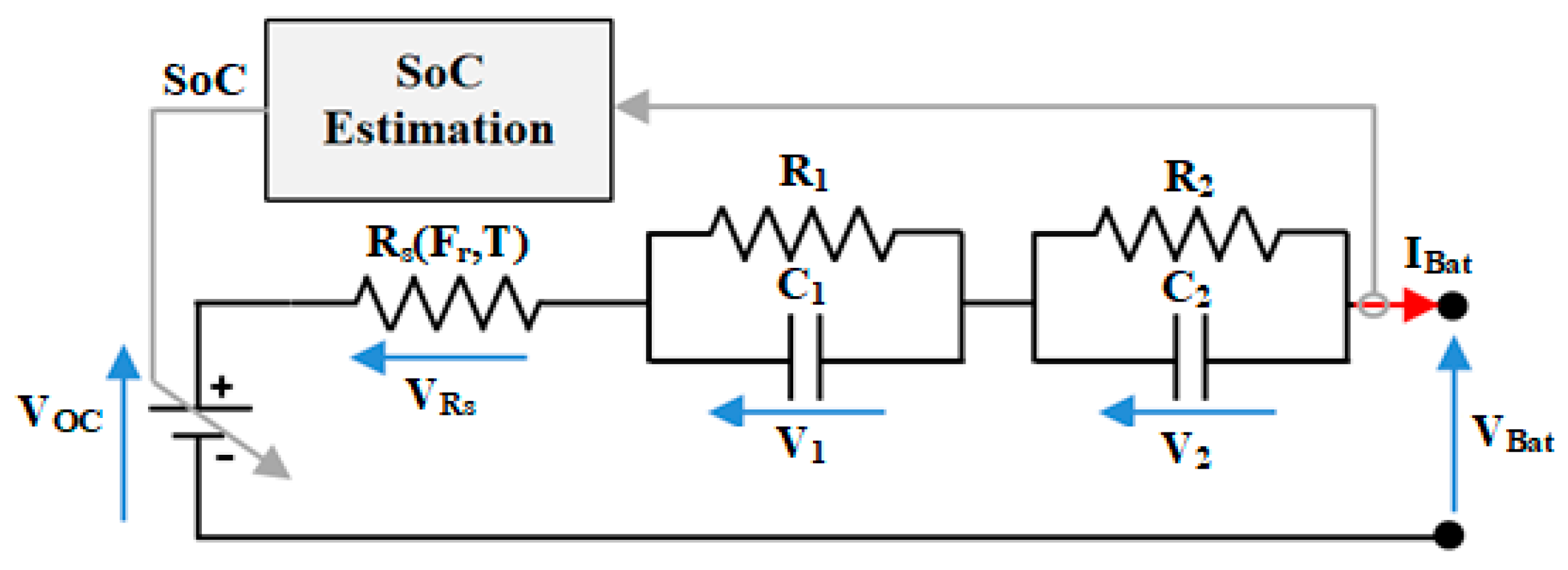
2.1. LiFePO4-Battery Modeling
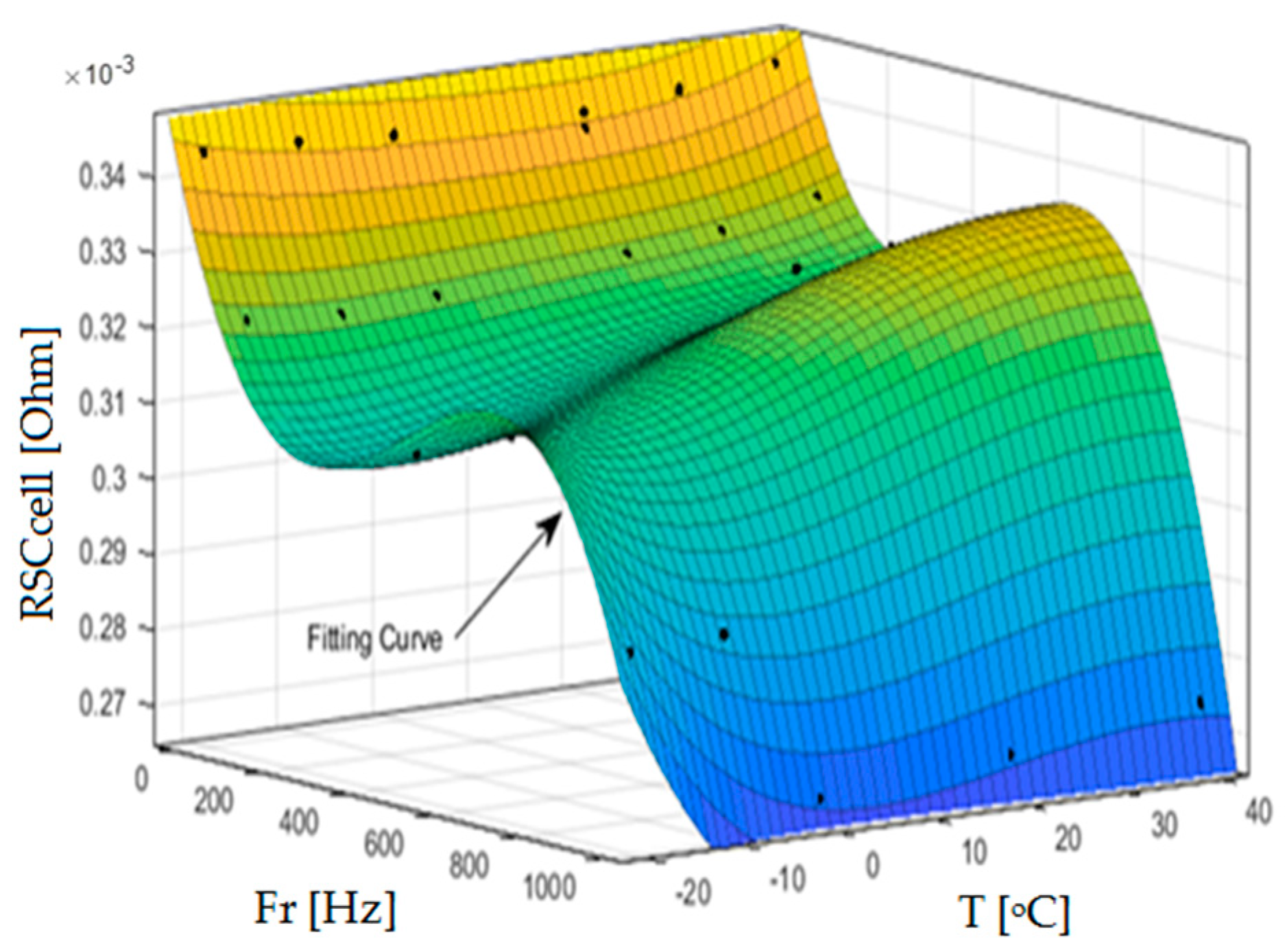
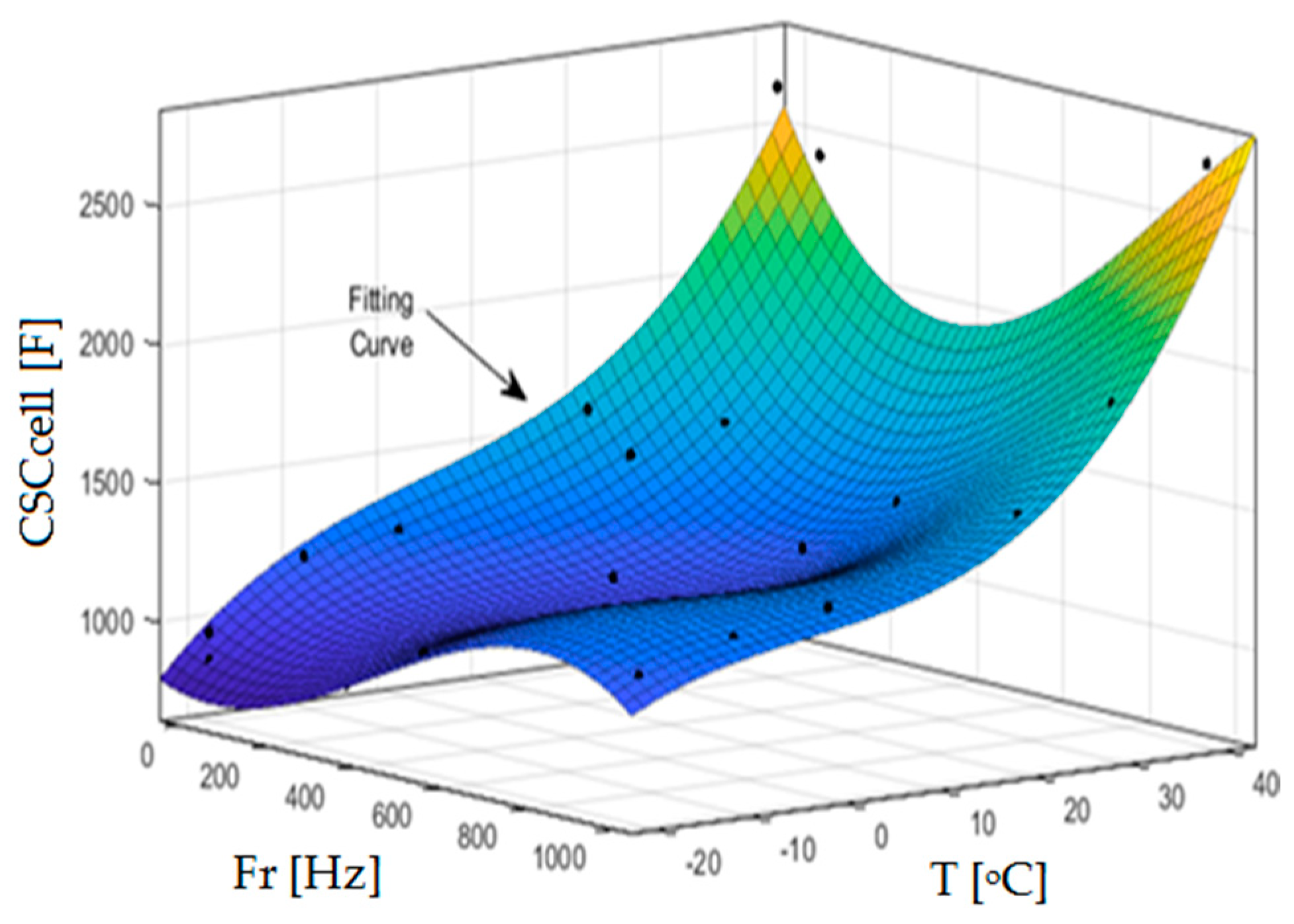
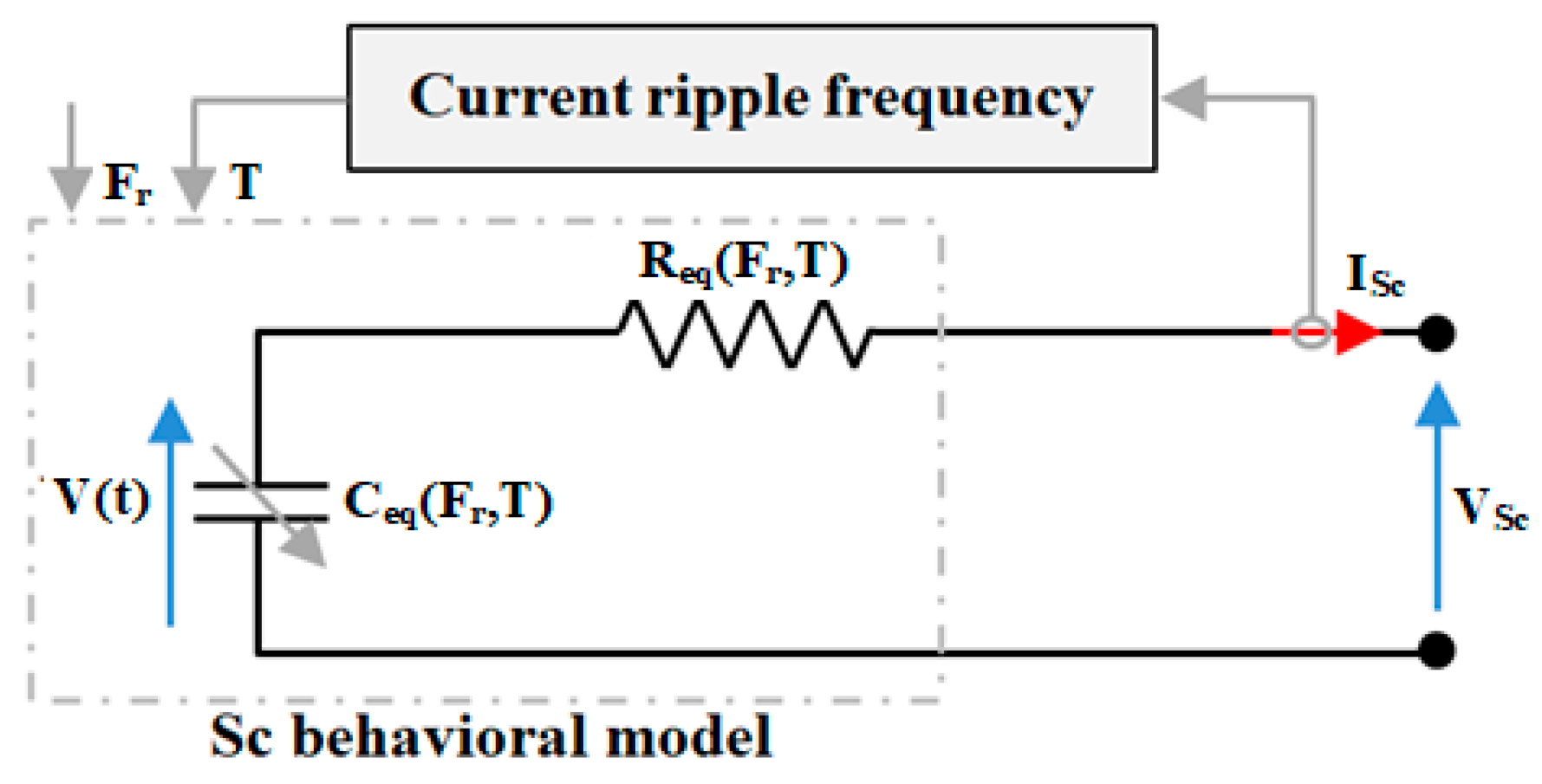
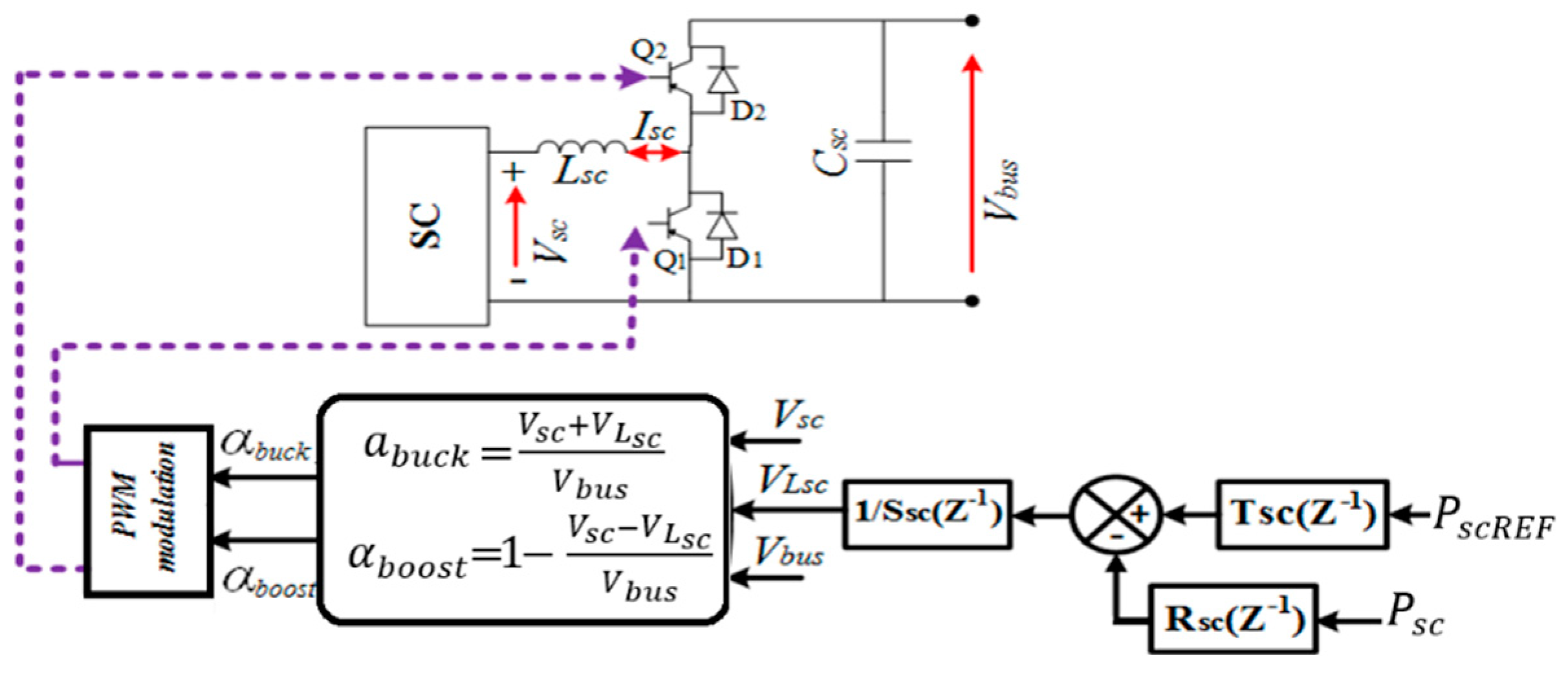
2.2. Supercapacitor Modeling
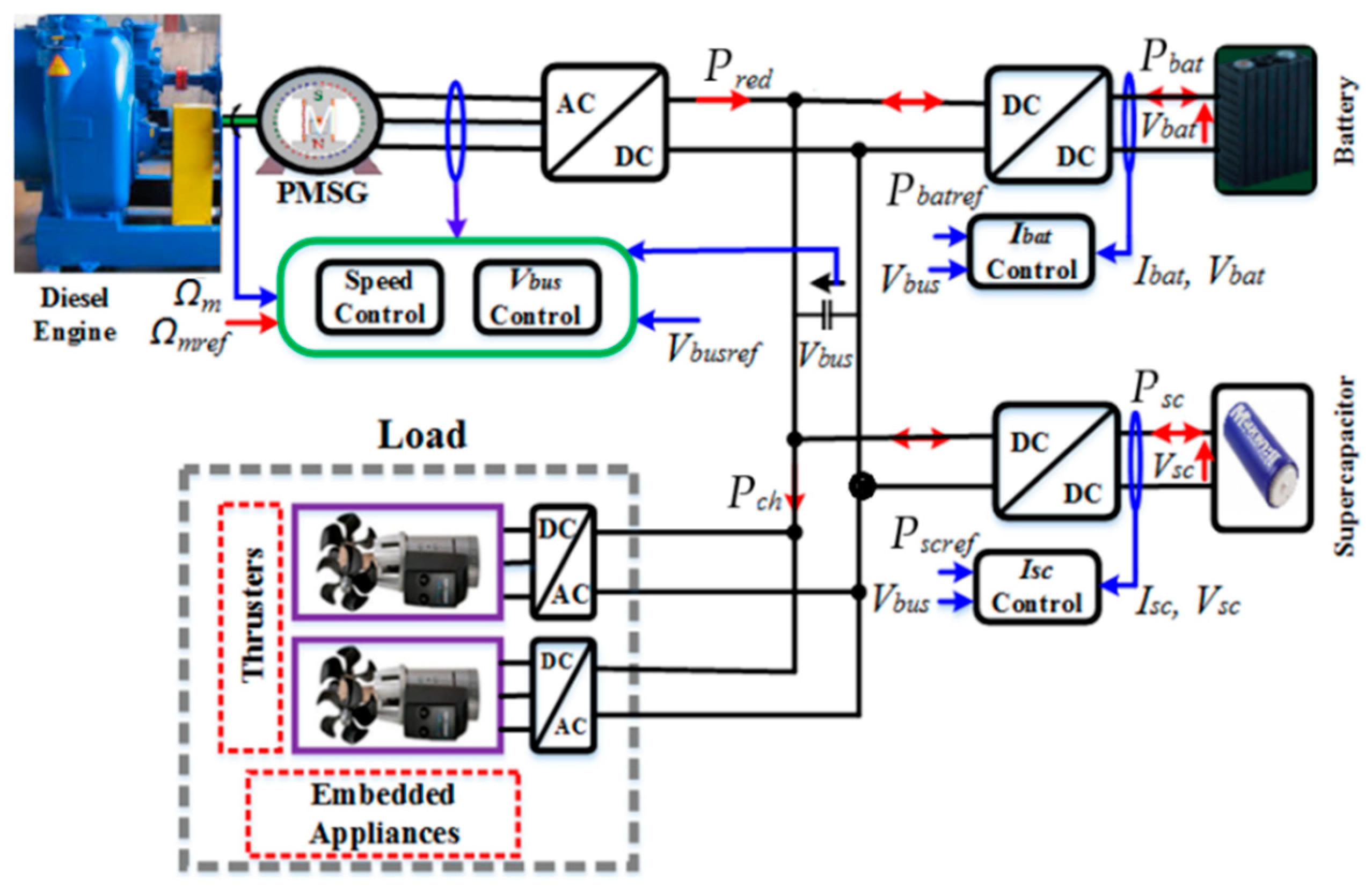
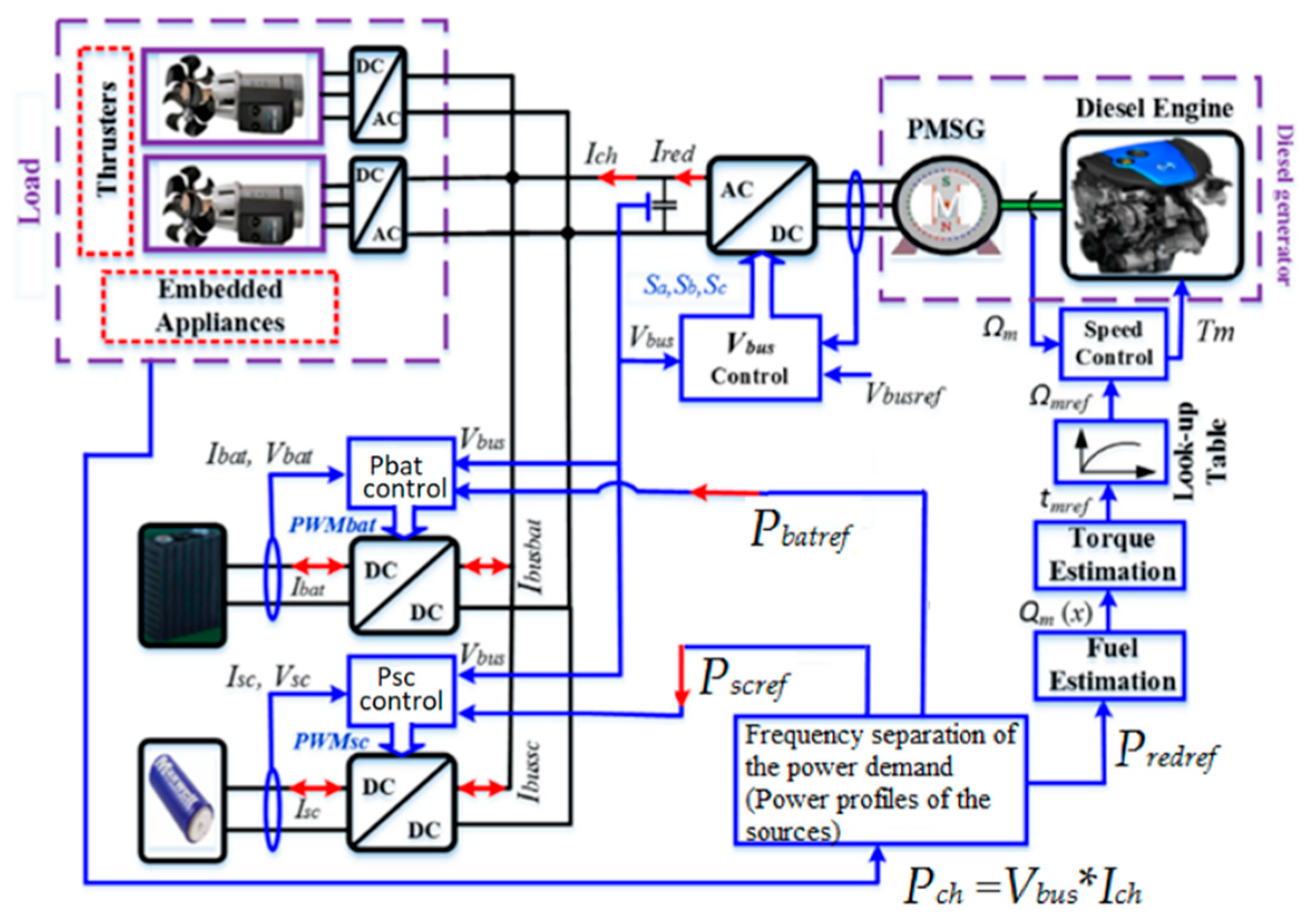
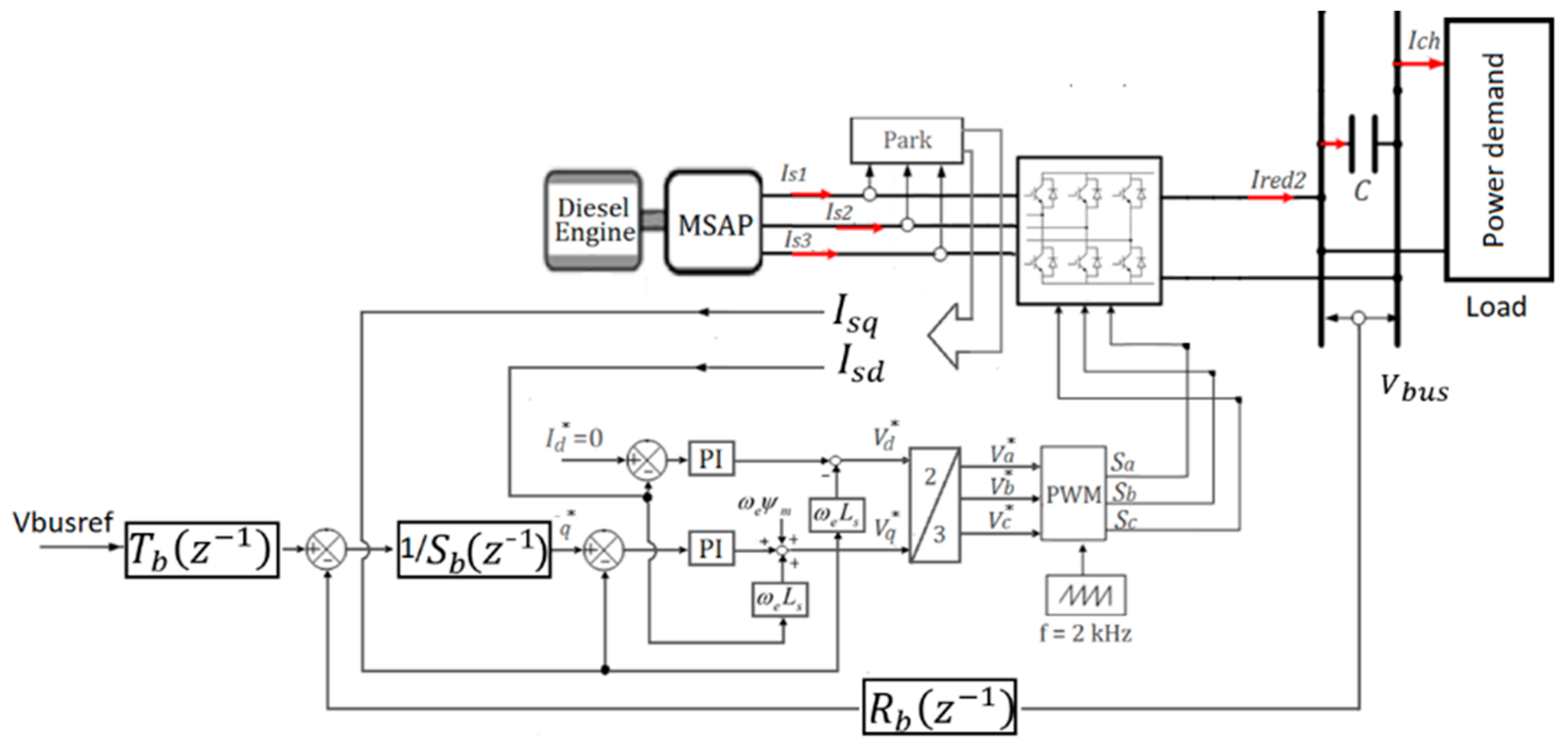
3. Coordinated Power Control of the Hybrid Electric Ship
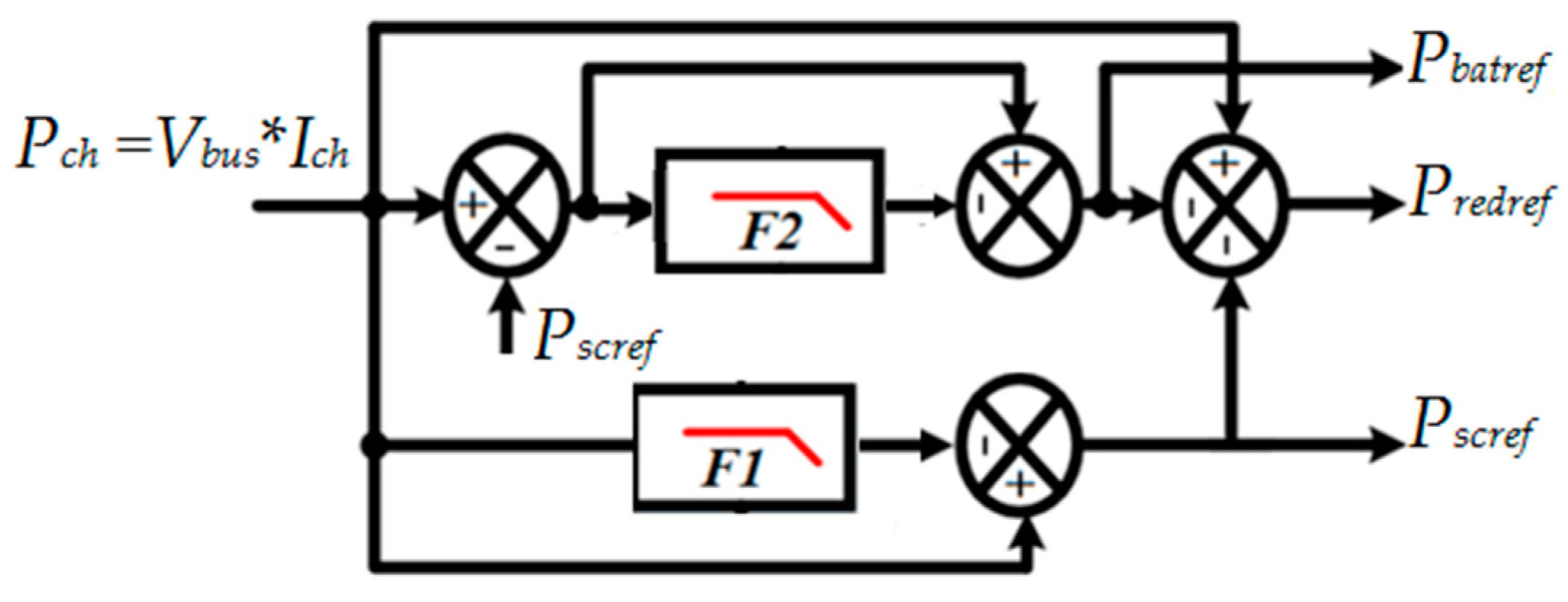
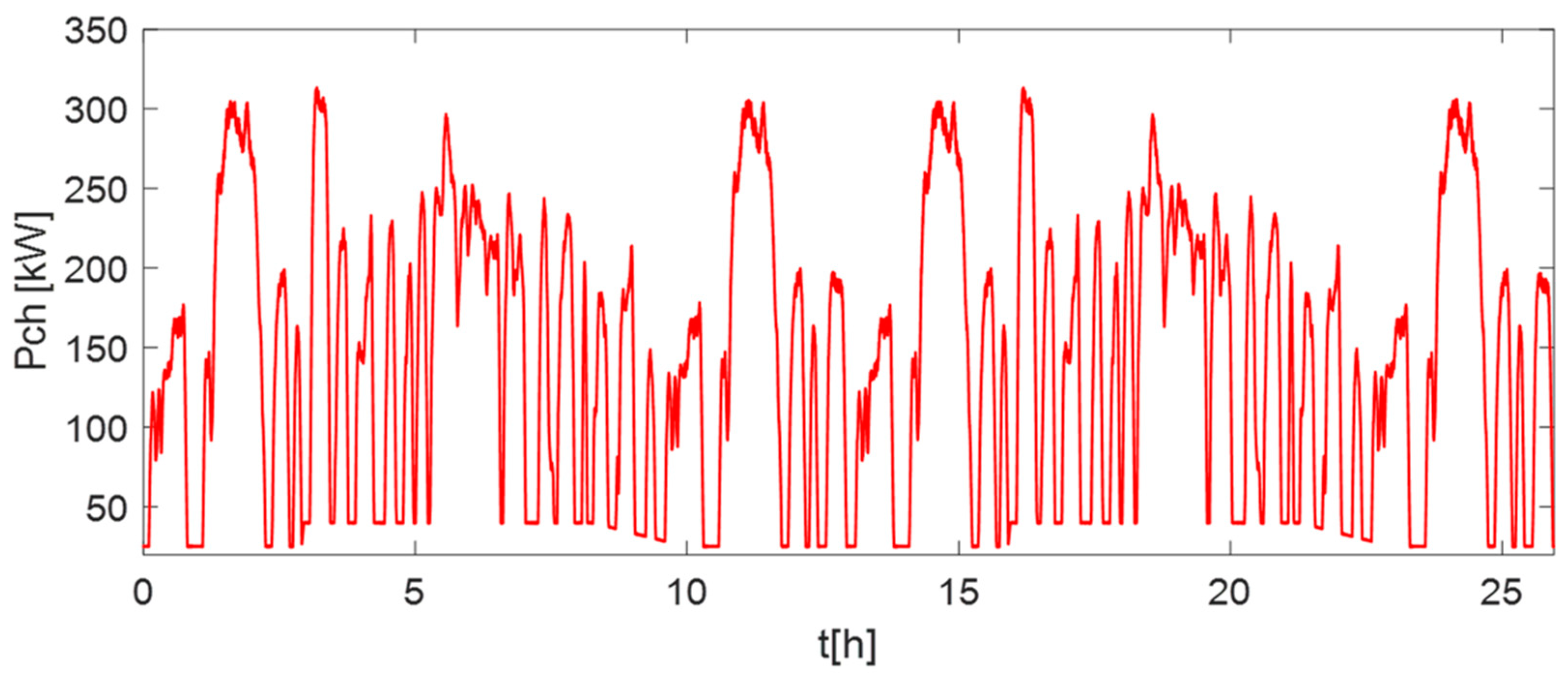
3.1. Power Profiles of the Supercapacitors, Batteries, and Variable-Speed Diesel Generator
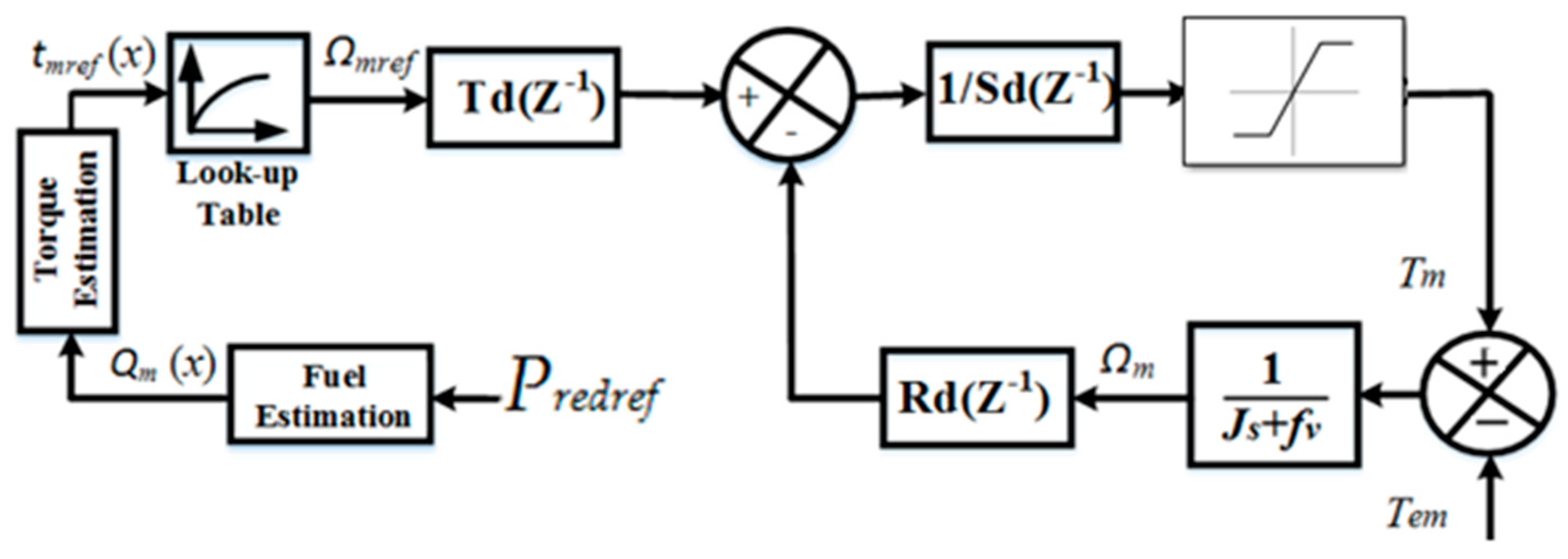
3.2. Diesel Generator Speed Control
3.3. DC-Bus Voltage Control Method
3.4. Batteries’ and Supercapacitors’ Powers Control
4. Electric Ship Behavior Simulations
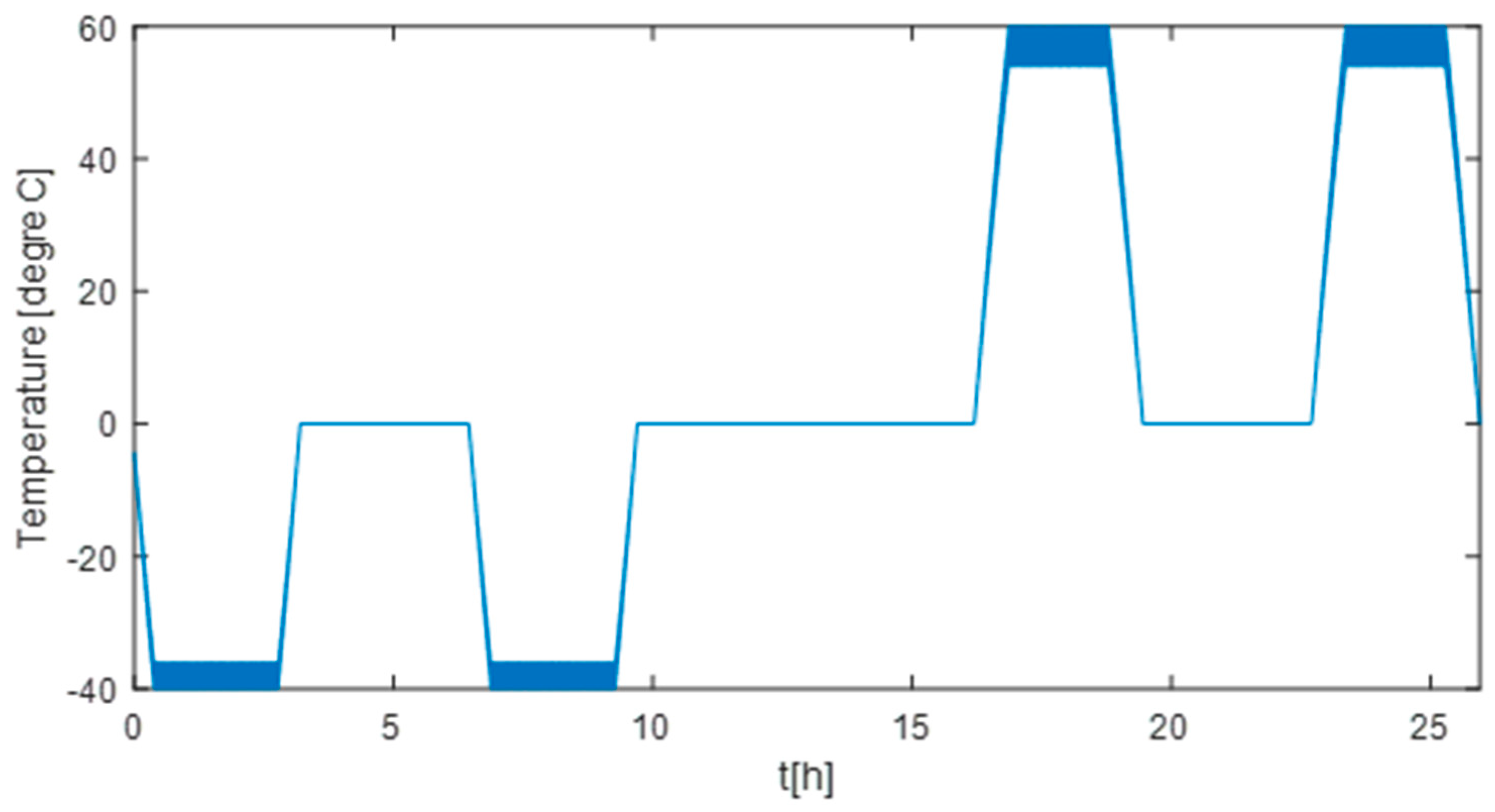
4.1. Conditions of the Simulations
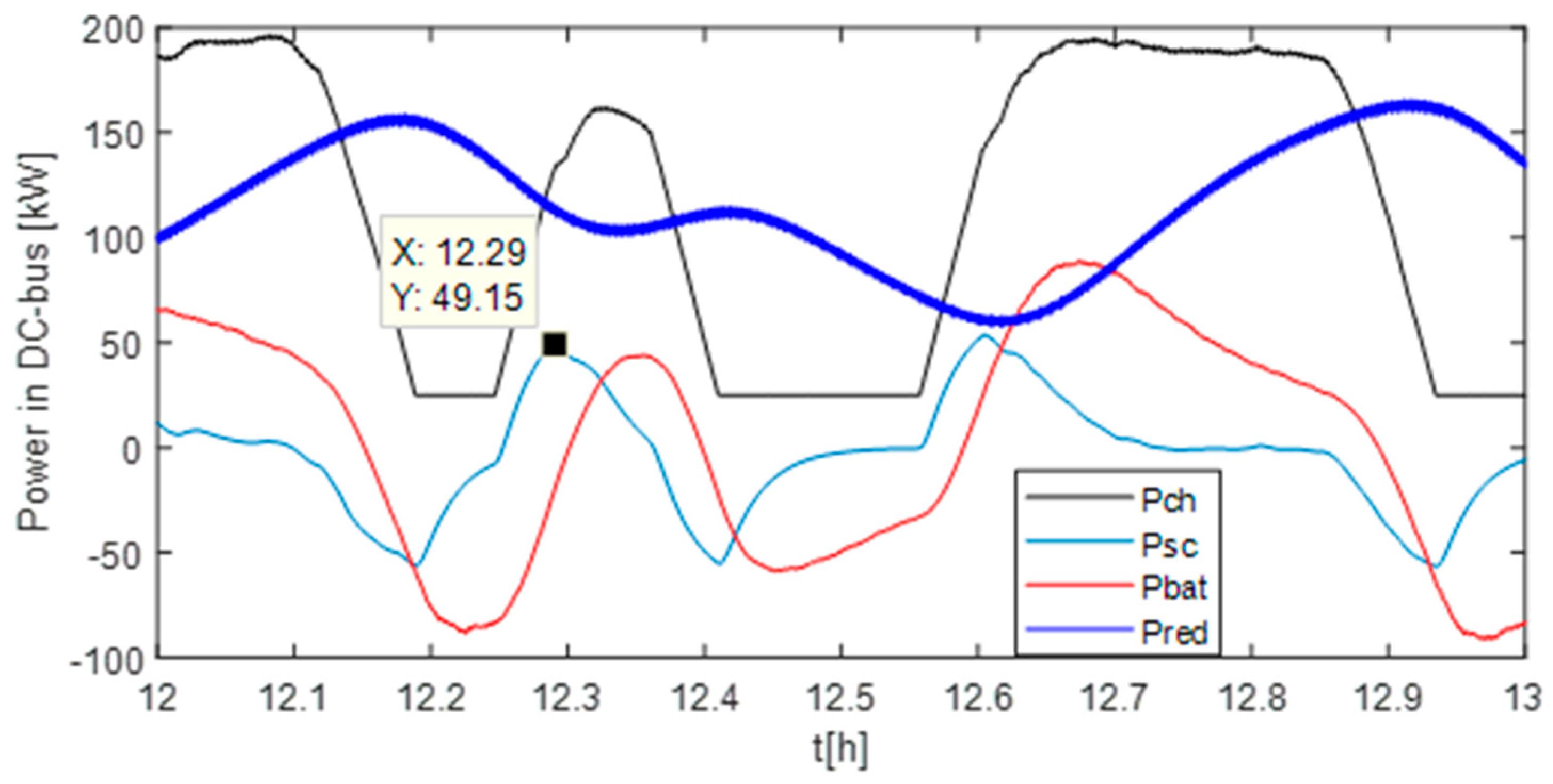
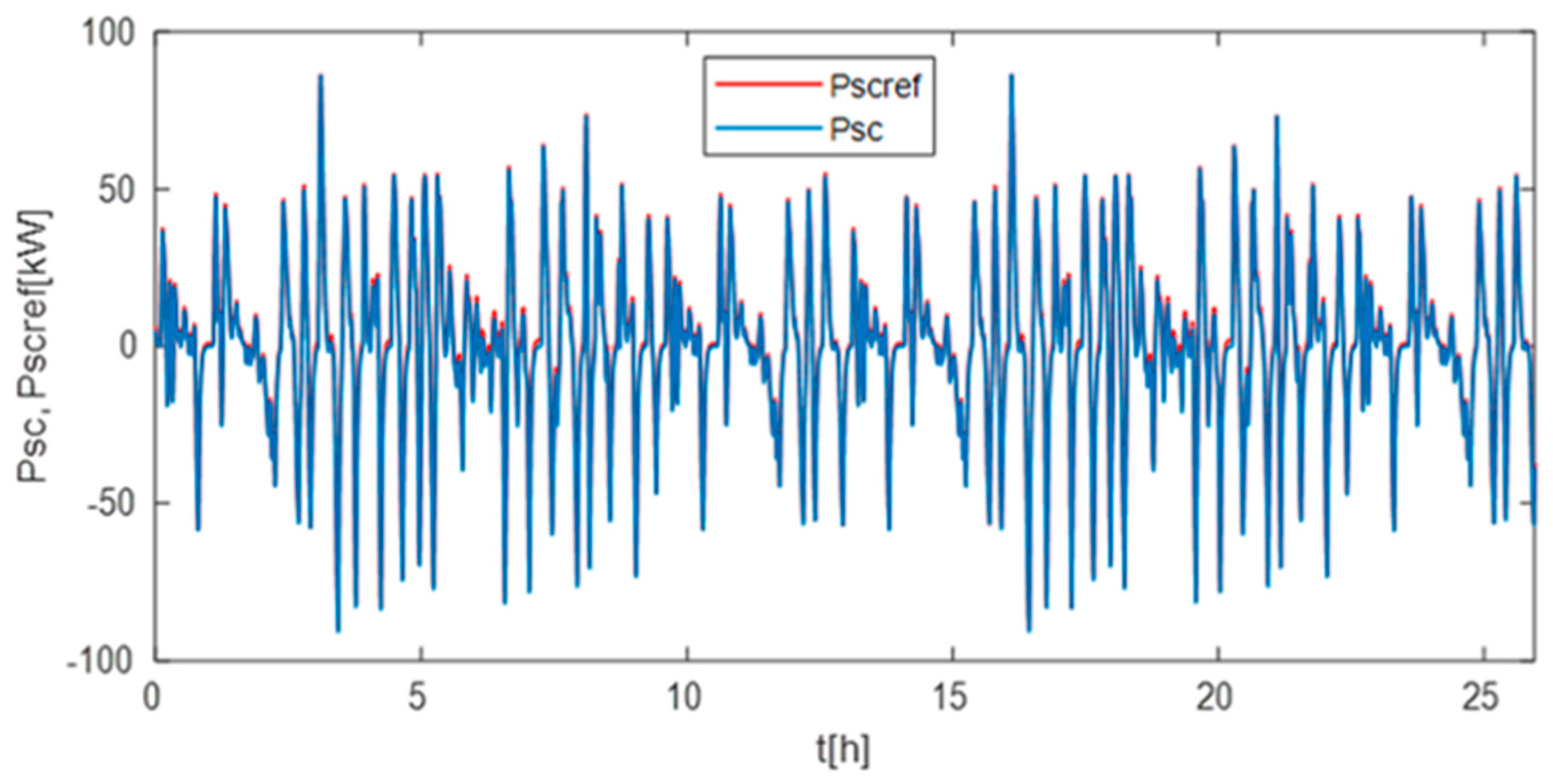
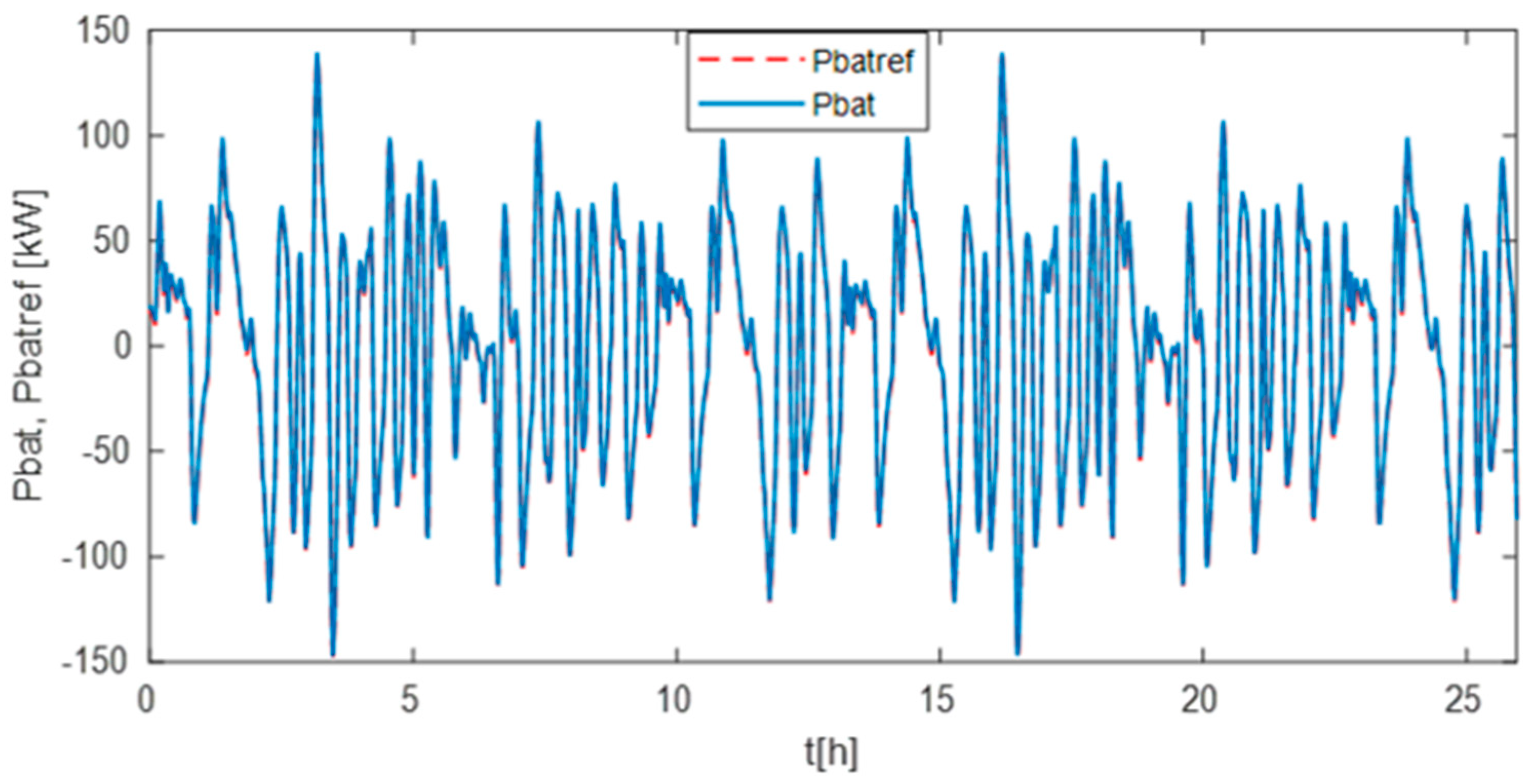
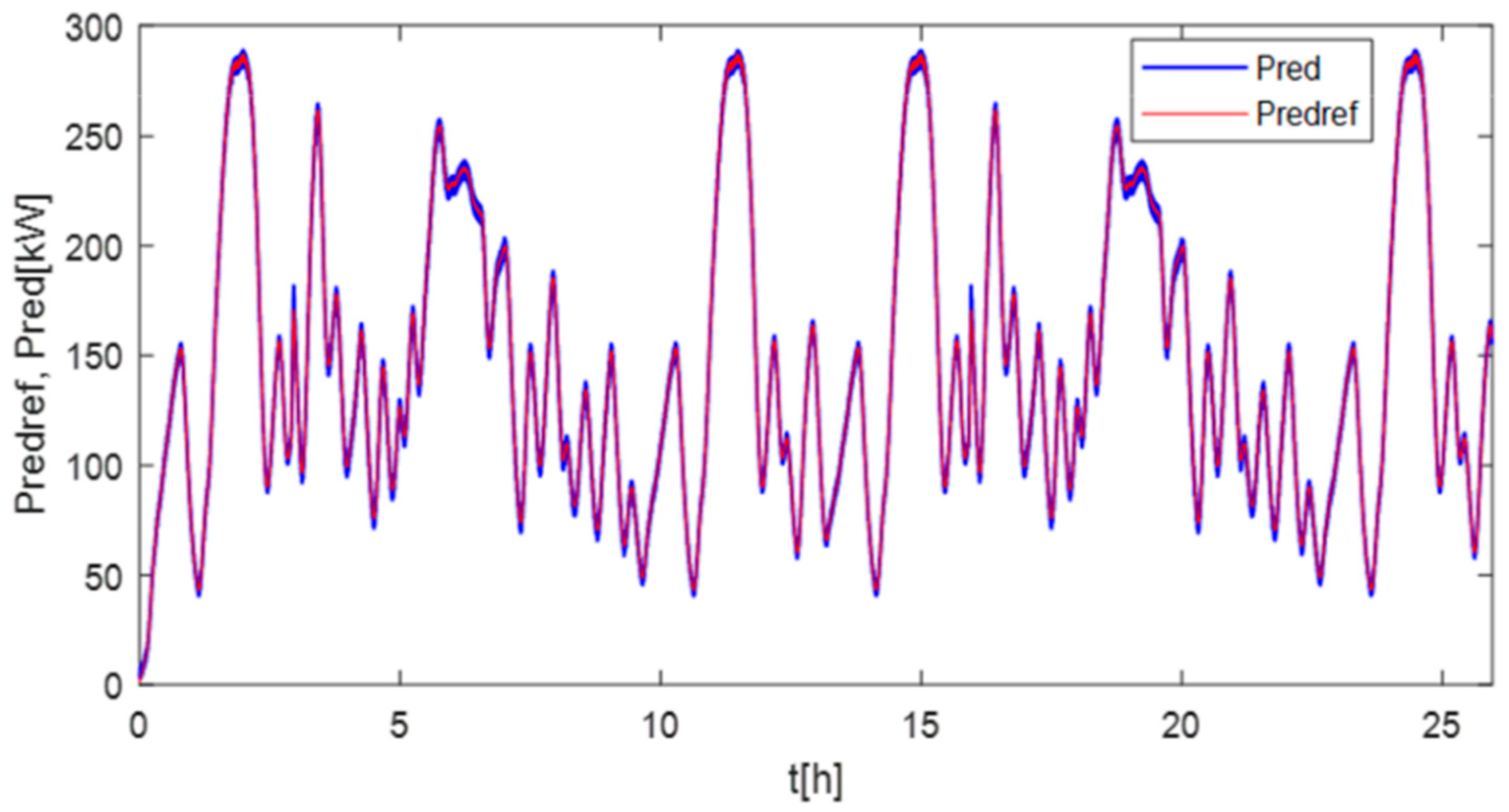
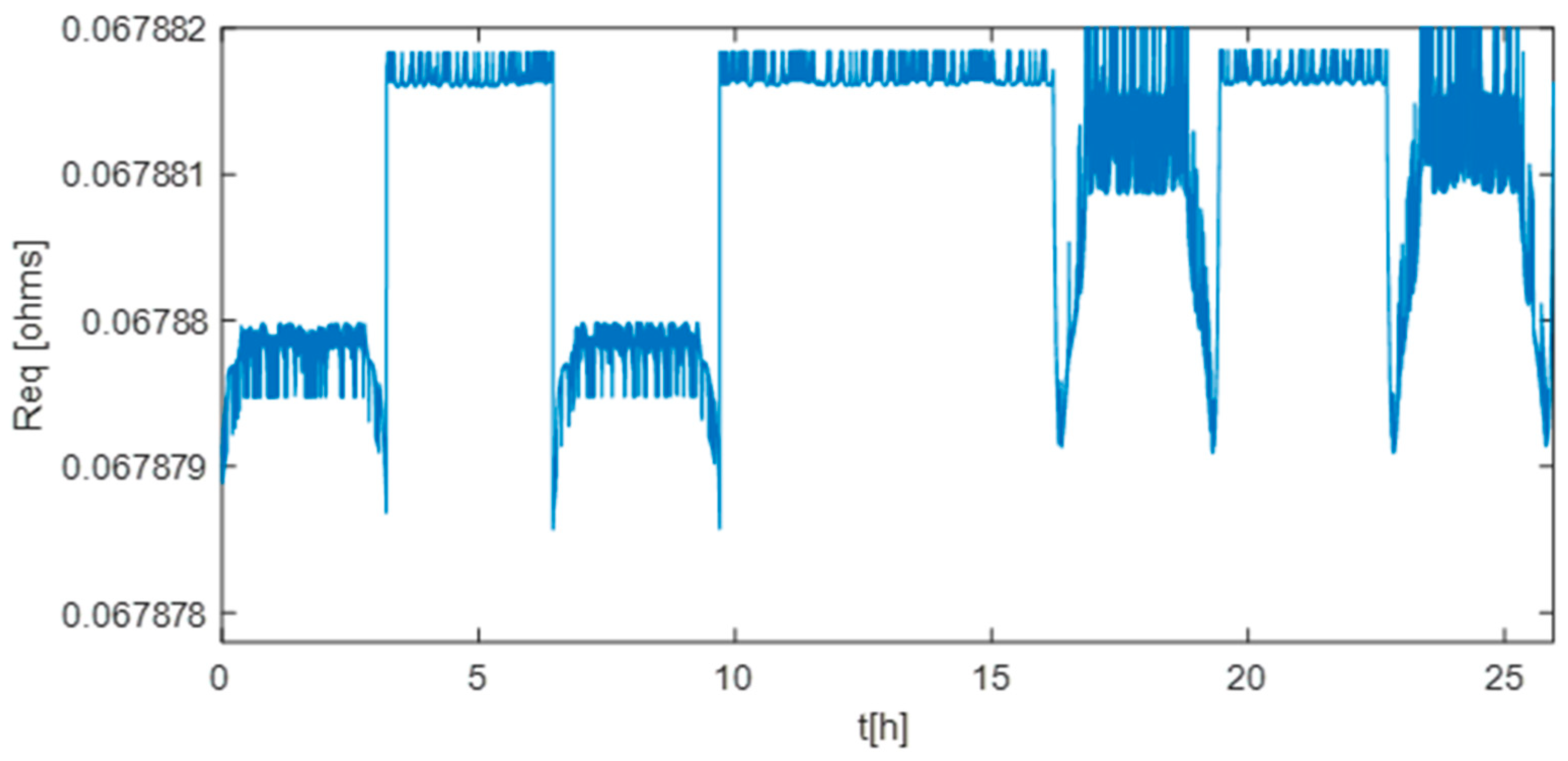
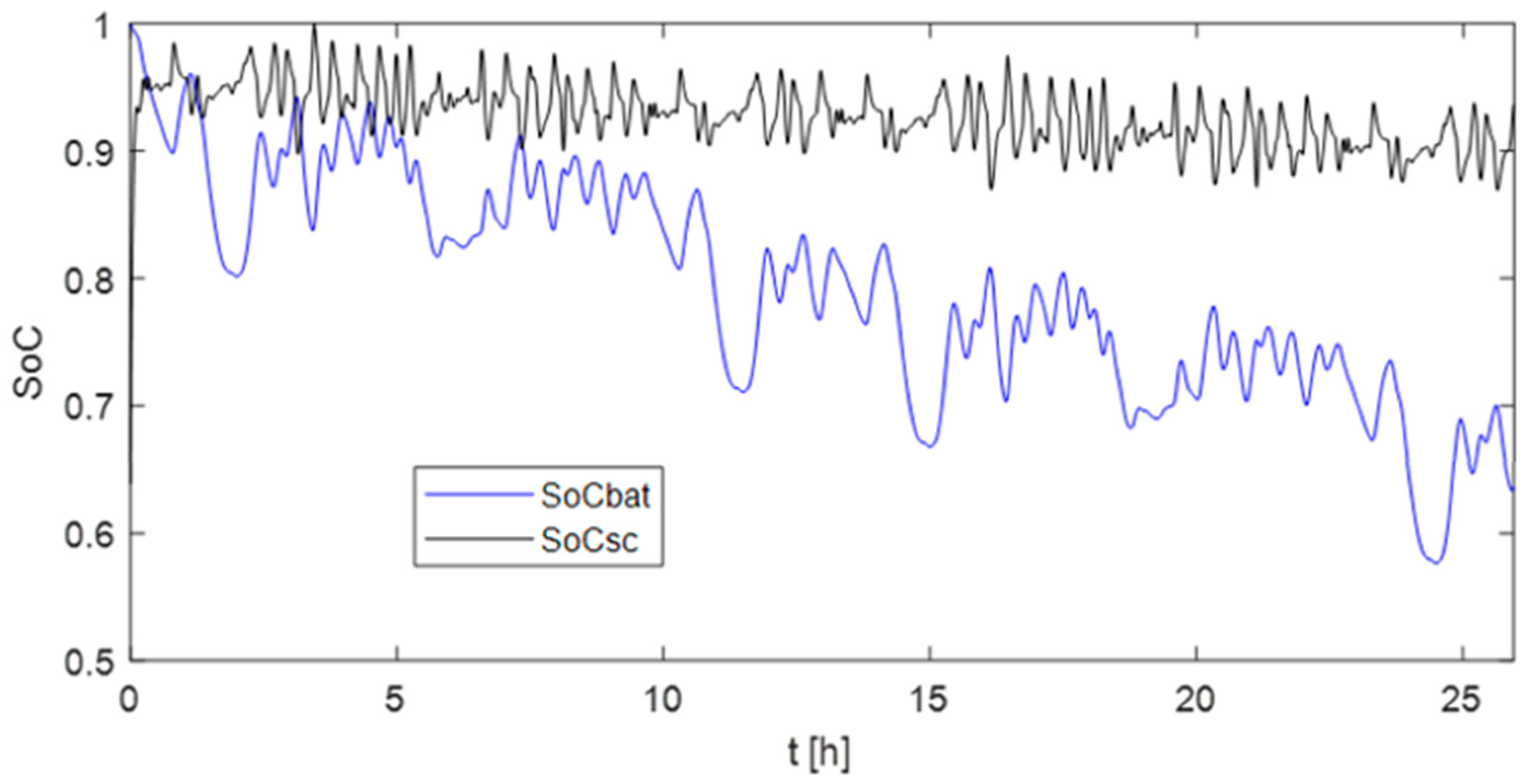
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SC | Supercapacitor |
| PMSG | Permanent Magnet Synchronous Generator |
| VSDG | Variable Speed Diesel Generator |
| HES | Hybrid Electric Ship |
| TESS | Two Energy Storage System |
| Vbus & Vbusref | DC-bus voltage and its reference in [V] |
| Vbat | Batteries voltage in [V] |
| Vsc | Supercapacitors voltage in [V] |
| Psc | Power of the SC |
| Pbat | Power of the batteries |
| Pch | Power of the load in [kW] |
| Pred | Power of the VSDG |
| Sa, Sb, Sc | Control signals of the rectifier |
| Te | Sampling period in [s] |
| Vsd & Vsq | Voltage of the PMSG in dq axis in [V] |
References
- Trovão, J.P.; Machado, F.; Pereirinha, P.G. Hybrid electric excursion ships power supply system based on a multiple energy storage system. IET Electr. Syst. Transp. 2015, 6, 190–201. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.; Dakyo, B. Hybrid Electric Boat based on variable speed Diesel Generator and lithium-battery—Using frequency approach for energy management. In Proceedings of the 2015 Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP), 2015 Intl Conference on Optimization of Electrical & Electronic Equipment (OPTIM) & 2015 Intl Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015; pp. 744–749. [Google Scholar] [CrossRef]
- Lidozzi, A.; Solero, L.; Crescimbini, F. Adaptive Direct-Tuning Control for Variable-Speed Diesel-Electric Generating Units. IEEE Trans. Ind. Electron. 2012, 59, 2126–2134. [Google Scholar] [CrossRef]
- Zhou, Z.; Camara, M.B.; Dakyo, B. Coordinated Power Control of Variable-Speed Diesel Generators and Lithium-Battery on a Hybrid Electric Boat. IEEE Trans. Veh. Technol. 2017, 66, 5775–5784. [Google Scholar] [CrossRef]
- Oukkacha, I.; Camara, M.B.; Dakyo, B. Energy Management in Electric Vehicle based on Frequency sharing approach, using Fuel cells, Lithium batteries and Supercapacitors. In Proceedings of the 2018 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 986–992. [Google Scholar] [CrossRef]
- Trovao, J.P.F.; Santos, V.D.N.; Antunes, C.H.; Pereirinha, P.G.; Jorge, H.M. A Real-Time Energy Management Architecture for Multisource Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 3223–3233. [Google Scholar] [CrossRef]
- Tani, A.; Camara, M.B.; Dakyo, B.; Azzouz, Y. DC/DC and DC/AC Converters Control for Hybrid Electric Vehicles Energy Management-Ultracapacitors and Fuel Cell. IEEE Trans. Ind. Informatics 2013, 9, 686–696. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; Li, B.; Ji, J.; Zhao, K.; Hu, C. A review of power management strategies and component sizing methods for hybrid vehicles. Renew. Sustain. Energy Rev. 2018, 96, 132–144. [Google Scholar] [CrossRef]
- Hossain, M.; Rahim, N.; Selvaraj, J.A. Recent progress and development on power DC-DC converter topology, control, design and applications: A review. Renew. Sustain. Energy Rev. 2018, 81, 205–230. [Google Scholar] [CrossRef]
- Sorlei, I.-S.; Bizon, N.; Thounthong, P.; Varlam, M.; Carcadea, E.; Culcer, M.; Iliescu, M.; Raceanu, M. Fuel Cell Electric Vehicles—A Brief Review of Current Topologies and Energy Management Strategies. Energies 2021, 14, 252. [Google Scholar] [CrossRef]
- Odeim, F.; Roes, J.; Heinzel, A. Power Management Optimization of an Experimental Fuel Cell/Battery/Supercapacitor Hybrid System. Energies 2015, 8, 6302–6327. [Google Scholar] [CrossRef]
- Sampietro, J.L.; Puig, V.; Costa-Castelló, R. Optimal Sizing of Storage Elements for a Vehicle Based on Fuel Cells, Supercapacitors, and Batteries. Energies 2019, 12, 925. [Google Scholar] [CrossRef]
- Gherairi, S. Hybrid Electric Vehicle: Design and Control of a Hybrid System (Fuel Cell/Battery/Ultra-Capacitor) Supplied by Hydrogen. Energies 2019, 12, 1272. [Google Scholar] [CrossRef]
- Nassef, A.M.; Fathy, A.; Rezk, H. An Effective Energy Management Strategy Based on Mine-Blast Optimization Technique Applied to Hybrid PEMFC/Supercapacitor/Batteries System. Energies 2019, 12, 3796. [Google Scholar] [CrossRef]
- Cao, Y.; Kroeze, R.C.; Krein, P.T. Multi-timescale Parametric Electrical Battery Model for Use in Dynamic Electric Vehicle Simulations. IEEE Trans. Transp. Electrif. 2016, 2, 432–442. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.B.; Dakyo, B.; Ramasamy, S. Aging Characterization of Lithium Iron Phosphate Batteries Considering Temperature and Direct Current Undulations as Degrading Factors. IEEE Trans. Ind. Electron. 2020, 68, 9696–9706. [Google Scholar] [CrossRef]
- Lee, Y.-D.; Park, S.-Y.; Han, S.-B. Online Embedded Impedance Measurement Using High-Power Battery Charger. IEEE Trans. Ind. Appl. 2015, 51, 498–508. [Google Scholar] [CrossRef]
- Bruen, T.; Marco, J. Modelling and experimental evaluation of parallel connected lithium ion cells for an electric vehicle battery system. J. Power Sources 2016, 310, 91–101. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, X.; Li, Y.; Tian, H. Energy management strategy of multiple supercapacitors in an autonomous DC microgrid using adaptive virtual impedance. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; pp. 1174–1185. [Google Scholar] [CrossRef]
- Gandolfo, D.; Brandão, A.; Patiño, D.; Molina, M. Dynamic model of lithium polymer battery—Load resistor method for electric parameters identification. J. Energy Inst. 2015, 88, 470–479. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.B.; Dakyo, B. Transient Power Control for Diesel-Generator Assistance in Electric Boat Applications Using Supercapacitors and Batteries. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 416–428. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Chaoui, H.; Gualous, H.; Sabor, J. Online Parameter Identification for Supercapacitor State-of-Health Diagnosis for Vehicular Applications. IEEE Trans. Power Electron. 2017, 32, 9355–9363. [Google Scholar] [CrossRef]
- Ahmad, H.; Wan, W.Y.; Isa, D. Modeling the Ageing Effect of Cycling Using a Supercapacitor-Module Under High Temperature with Electrochemical Impedance Spectroscopy Test. IEEE Trans. Reliab. 2018, 68, 109–121. [Google Scholar] [CrossRef]
- Liu, W.; Song, Y.; Liao, H.; Li, H.; Zhang, X.; Jiao, Y.; Peng, J.; Huang, Z. Distributed Voltage Equalization Design for Supercapacitors Using State Observer. IEEE Trans. Ind. Appl. 2018, 55, 620–630. [Google Scholar] [CrossRef]
- Murray, D.B.; Hayes, J.G. Cycle Testing of Supercapacitors for Long-Life Robust Applications. IEEE Trans. Power Electron. 2015, 30, 2505–2516. [Google Scholar] [CrossRef]
- Bellache, K.; Camara, M.B.; Dakyo, B. Supercapacitors Characterization and Modeling Using Combined Electro-Thermal Stress Approach Batteries. IEEE Trans. Ind. Appl. 2018, 55, 1817–1827. [Google Scholar] [CrossRef]
- Sarr, C.T.; Camara, M.B.; Dakyo, B. Supercapacitors aging assessment in wind/tidal intermittent energies application with variable temperature. J. Energy Storage 2021, 46, 103790. [Google Scholar] [CrossRef]
- Corti, F.; Gulino, M.-S.; Laschi, M.; Lozito, G.M.; Pugi, L.; Reatti, A.; Vangi, D. Time-Domain Circuit Modelling for Hybrid Supercapacitors. Energies 2021, 14, 6837. [Google Scholar] [CrossRef]
- Tankari, M.A.; Camara, M.B.; Dakyo, B.; Lefebvre, G. Use of Ultracapacitors and Batteries for Efficient Energy Management in Wind–Diesel Hybrid System. IEEE Trans. Sustain. Energy 2013, 4, 414–424. [Google Scholar] [CrossRef]
- Broomhead, T.; Manzie, C.; Hield, P.; Shekhar, R.; Brear, M. Economic Model Predictive Control and Applications for Diesel Generators. IEEE Trans. Control. Syst. Technol. 2016, 25, 388–400. [Google Scholar] [CrossRef]
- Hussain, S.; Ali, M.U.; Park, G.-S.; Nengroo, S.H.; Khan, M.A.; Kim, H.-J. A Real-Time Bi-Adaptive Controller-Based Energy Management System for Battery–Supercapacitor Hybrid Electric Vehicles. Energies 2019, 12, 4662. [Google Scholar] [CrossRef]
- Camara, M.B.; Gualous, H.; Gustin, F.; Berthon, A.; Dakyo, B. DC/DC Converter Design for Supercapacitor and Battery Power Management in Hybrid Vehicle Applications—Polynomial Control Strategy. IEEE Trans. Ind. Electron. 2010, 57, 587–597. [Google Scholar] [CrossRef]
- Azuara-Grande, L.S.; Arnaltes, S.; Alonso-Martinez, J.; Rodriguez-Amenedo, J.L. Comparison of Two Energy Management System Strategies for Real-Time Operation of Isolated Hybrid Microgrids. Energies 2021, 14, 6770. [Google Scholar] [CrossRef]
- Lau, H.C.; Ramakrishna, S.; Zhang, K.; Hameed, M.Z.S. A Decarbonization Roadmap for Singapore and Its Energy Policy Implications. Energies 2021, 14, 6455. [Google Scholar] [CrossRef]
- Baqar, A.; Camara, M.B.; Dakyo, B. Supercapacitors Fast Ageing Control in Residential Microgrid Based Photovoltaic/Fuel Cell/Electric Vehicle Charging Station. Energies 2023, 16, 5084. [Google Scholar] [CrossRef]
- Mariscotti, A. Power Quality Phenomena, Standards, and Proposed Metrics for DC Grids. Energies 2021, 14, 6453. [Google Scholar] [CrossRef]






| Basic Characteristics | Supercapacitors | Li-ion Batteries |
|---|---|---|
| Capacity cost in [€/kWh] | 279~18,600 | 465~3534 |
| Life time in [cycles] | 100,000~1,000,000 | 500~2000 |
| Efficiency in [%] | 75~98 | 70~90 |
| Self-discharge in [%/day] | 20~40 | 0.33 |
| Parameters of the Batteries Module | Values | |
|---|---|---|
| VBatmin~VBatmax | Battery’s cell voltage range in [V] | 2.8~3.8 |
| R1* C1 | First order time constant in [Ω* F] | 0.033*92 |
| R2* C2 | Second order time constant in [Ω* F] | 0.375*499 |
| ρPBat | Specific power in [W/kg] | 310 |
| ρEBat | Specific energy in [Wh/kg] | 102 |
| SoC(t0) | Initial value of SoC [%] | 97 |
| Ns_Bat | Number of the battery’s cells in series | 71 |
| NP_Bat | Number of the sub-modules in parallel | 8 |
| Rbwi | Resistance of electric wiring for a battery’s cell in [m Ω] | 4.5 |
| Parameters of the SC Module | Values | |
|---|---|---|
| VSCmin~VSCmax | Voltage range of the SC cell in [V] | 0.7~2.7 |
| ρPSC | Specific power in [W/kg] | 5900 |
| ρESC | Specific energy in [Wh/kg] | 6 |
| SoC(t0) | Initial value of the SoC [%] | 80 |
| Ns_SC | Supercapacitors cells in series | 120 |
| NP_SC | Sub-modules of the supercapacitors in parallel | 7 |
| Rwi | Wiring resistance of a SC cell in [m Ω] | 4.47 |
| Parameters of the VSDG | Values | |
|---|---|---|
| Pnom | DG nominal power in [kW] | 400 |
| n | DG nominal speed in [rpm] | 1500 |
| τD1 | Actuator time constant of DG in [s] | 0.05 |
| τD2 | Fuel combustion delay in [s] | 0.02 |
| p | Pair of poles | 9 |
| Rs | Resistance of the PMSG in [mΩ] | 14 |
| Ls = Ld = Lq | Inductance of the PMSG in [mH] | 8.1 |
| φm | PMSG rotor flux in [Wb] | 0.9 |
| J | Total inertia of VSDG in [kg.m2] | 4.562 |
| fv | Friction coefficient | 0.0024 |
| Parameters of the Control | Values |
|---|---|
| Capacitances in DC-bus | Cbat = Csc = 2 mF; C = 30 mF |
| Inductance in DC/DC converters Tb(Z−1) = Rb (Z−1) = r0b + r1b*Z−1 | Lsc = Lbat = 0.18 mH 28.58–26.09*Z−1 |
| Tbat (Z−1) = Rbat (Z−1) = r0bat + r1bat* Z−1 | 18–16*Z−1 |
| Tsc (Z−1) = Rsc (Z−1) = r0sc + r1sc*Z−1 | 74.44–40.23*Z−1 |
| Td (Z−1) = Rd (Z−1) = r0d + r1d*Z−1 | 1909–1832.3*Z−1 |
| Kpc; Kic | 2.5; 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camara, M.B.; Dakyo, B. Coordinated Control of the Hybrid Electric Ship Power-Based Batteries/Supercapacitors/Variable Speed Diesel Generator. Energies 2023, 16, 6666. https://doi.org/10.3390/en16186666
Camara MB, Dakyo B. Coordinated Control of the Hybrid Electric Ship Power-Based Batteries/Supercapacitors/Variable Speed Diesel Generator. Energies. 2023; 16(18):6666. https://doi.org/10.3390/en16186666
Chicago/Turabian StyleCamara, Mamadou Baïlo, and Brayima Dakyo. 2023. "Coordinated Control of the Hybrid Electric Ship Power-Based Batteries/Supercapacitors/Variable Speed Diesel Generator" Energies 16, no. 18: 6666. https://doi.org/10.3390/en16186666
APA StyleCamara, M. B., & Dakyo, B. (2023). Coordinated Control of the Hybrid Electric Ship Power-Based Batteries/Supercapacitors/Variable Speed Diesel Generator. Energies, 16(18), 6666. https://doi.org/10.3390/en16186666








